Enhanced Bathymetric Inversion for Tectonic Features via Multi-Gravity-Component DenseNet: A Case Study of Rift Identification in the South China Sea
Abstract
Highlights
- We develop a multi-gravity-component fusion model based on an improved DenseNet architecture, which significantly outperforms GEBCO_2024, SRTM15+, and Topo_27.1.
- Removing vertical deflection components (ξ, η) would increase bathymetric prediction errors more significantly than the exclusion of other gravity components.
- The proposed framework enables high-resolution modeling of complex tectonic features such as rifts.
- Our proposed adaptive transition layers and curvature stratification together enhance high-frequency tectonic features’ preservation and terrain generalization.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methods
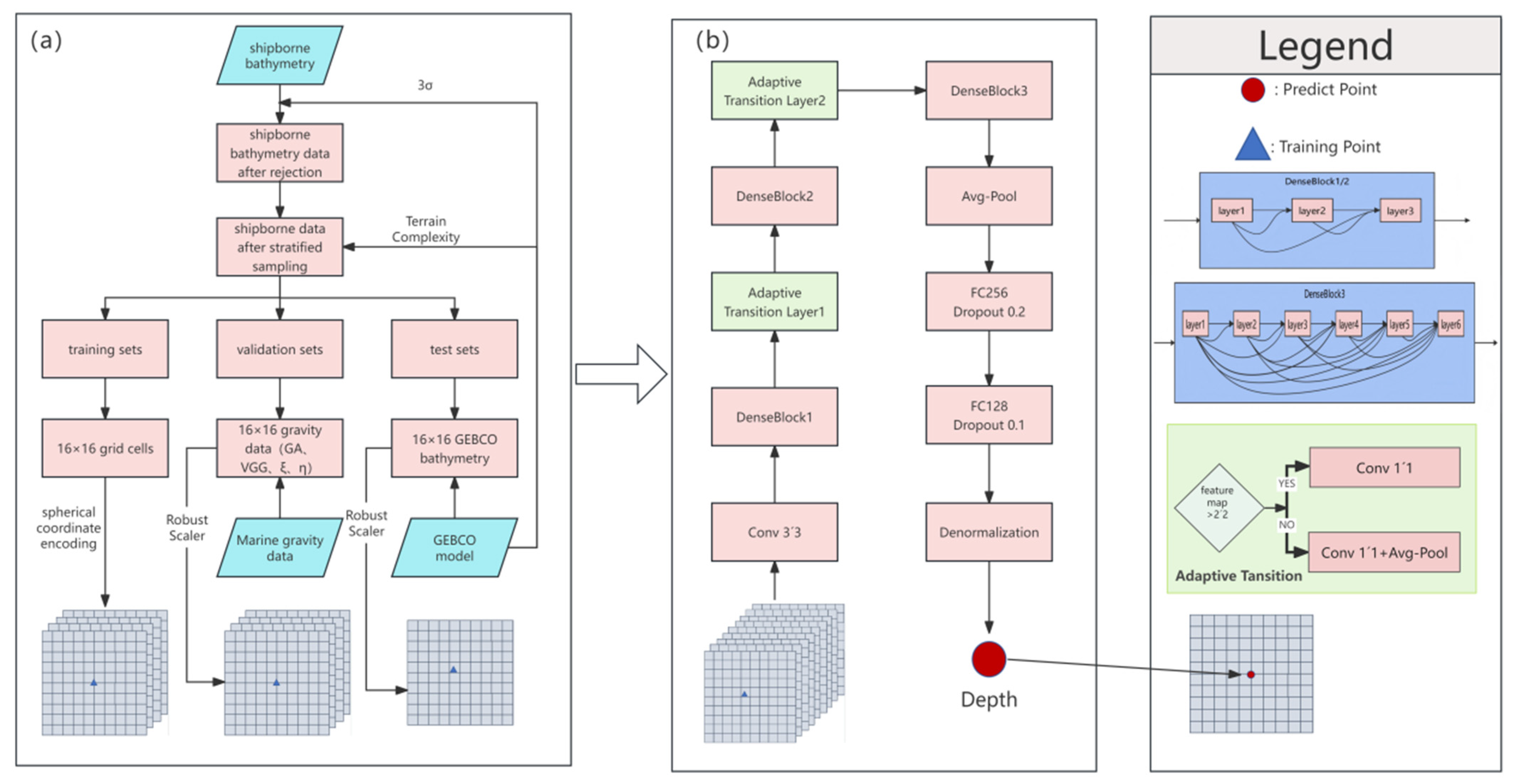
2.2.1. Multi-Source Data Fusion and Feature Tensor Construction
2.2.2. Data Stratification Based on Terrain Complexity
2.2.3. Improved DenseNet Prediction Model Architecture
3. Results
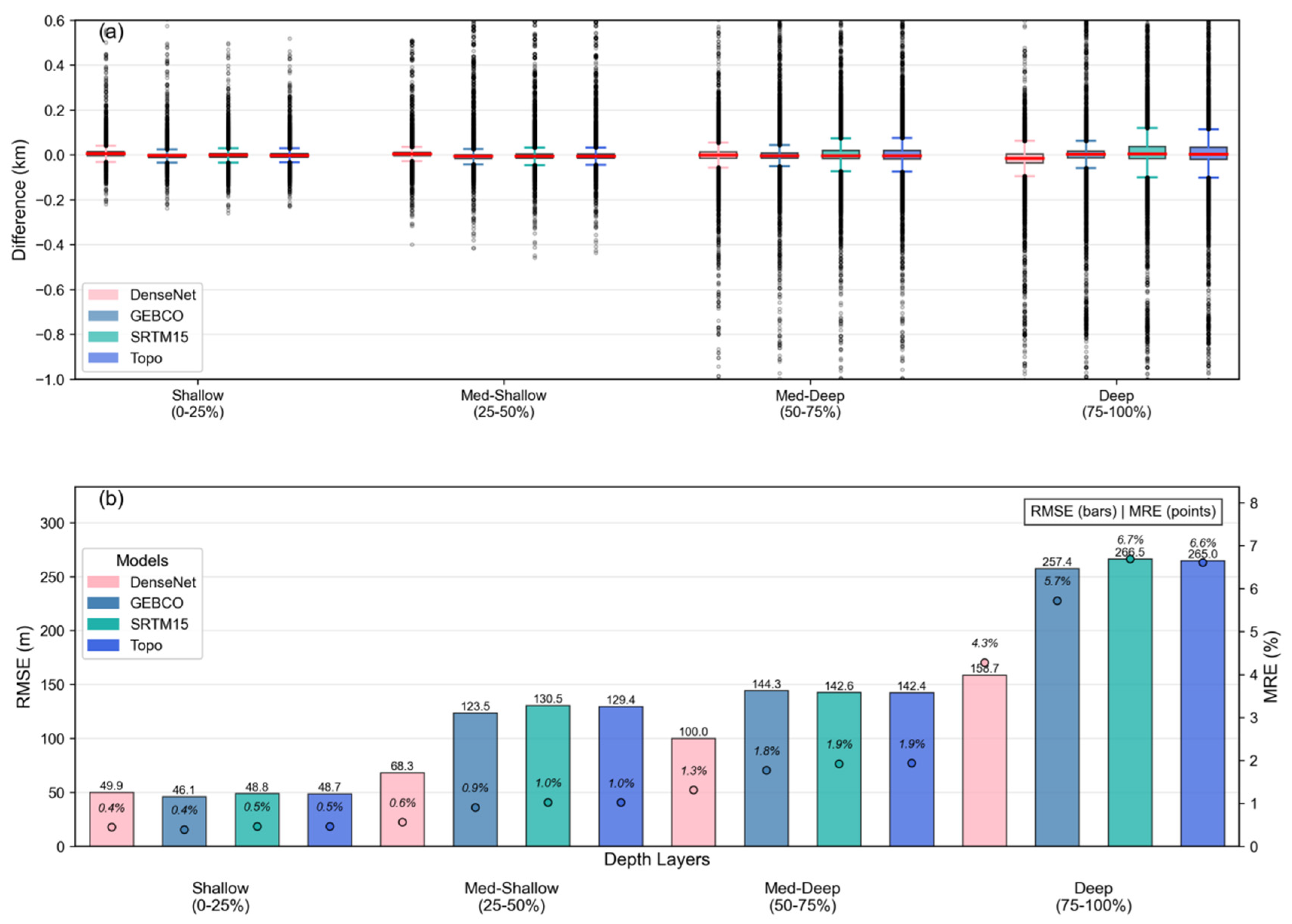
3.1. Inversion Accuracy Comparison
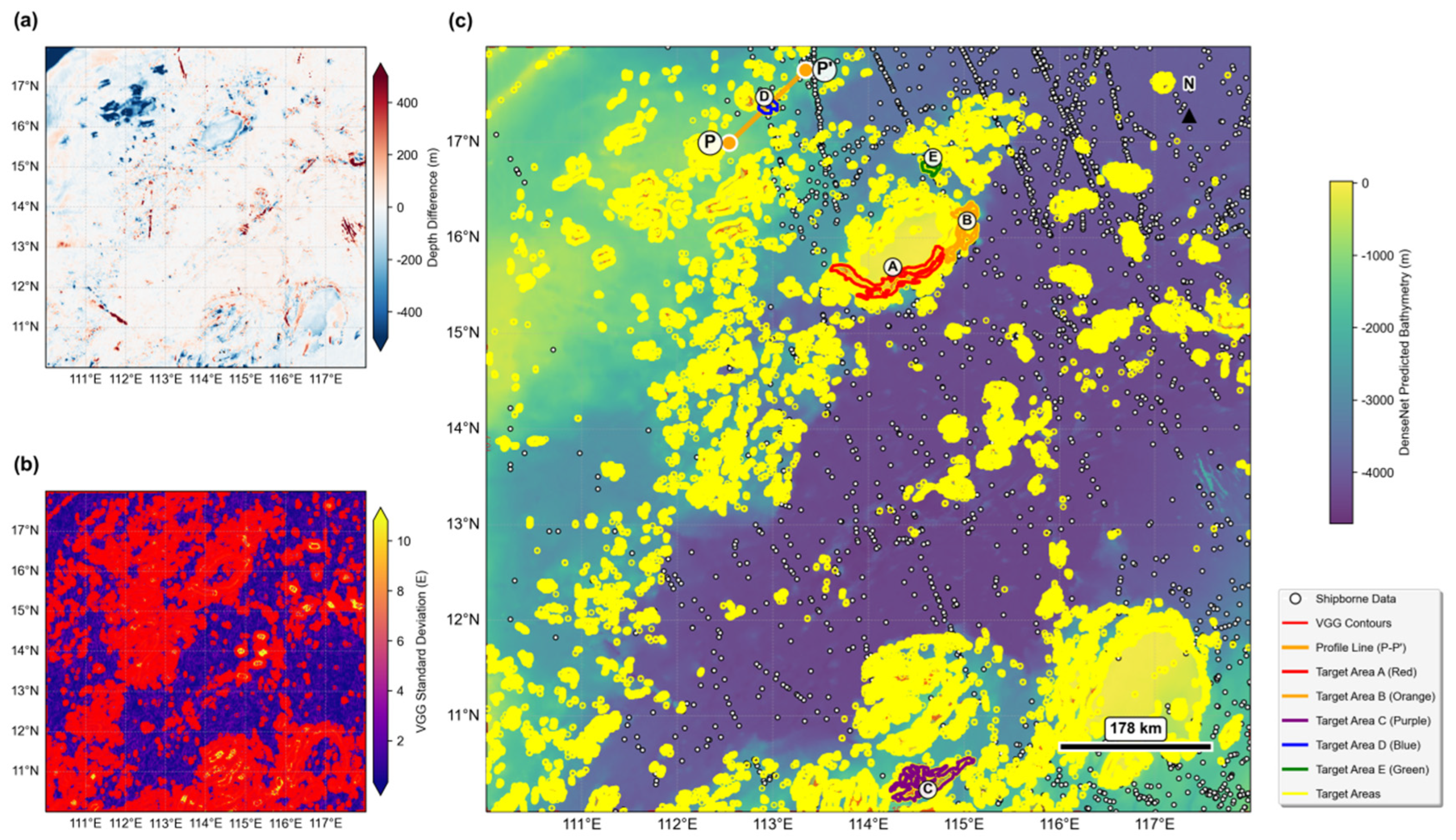
3.2. Complex Rift Terrain Modeling Performance
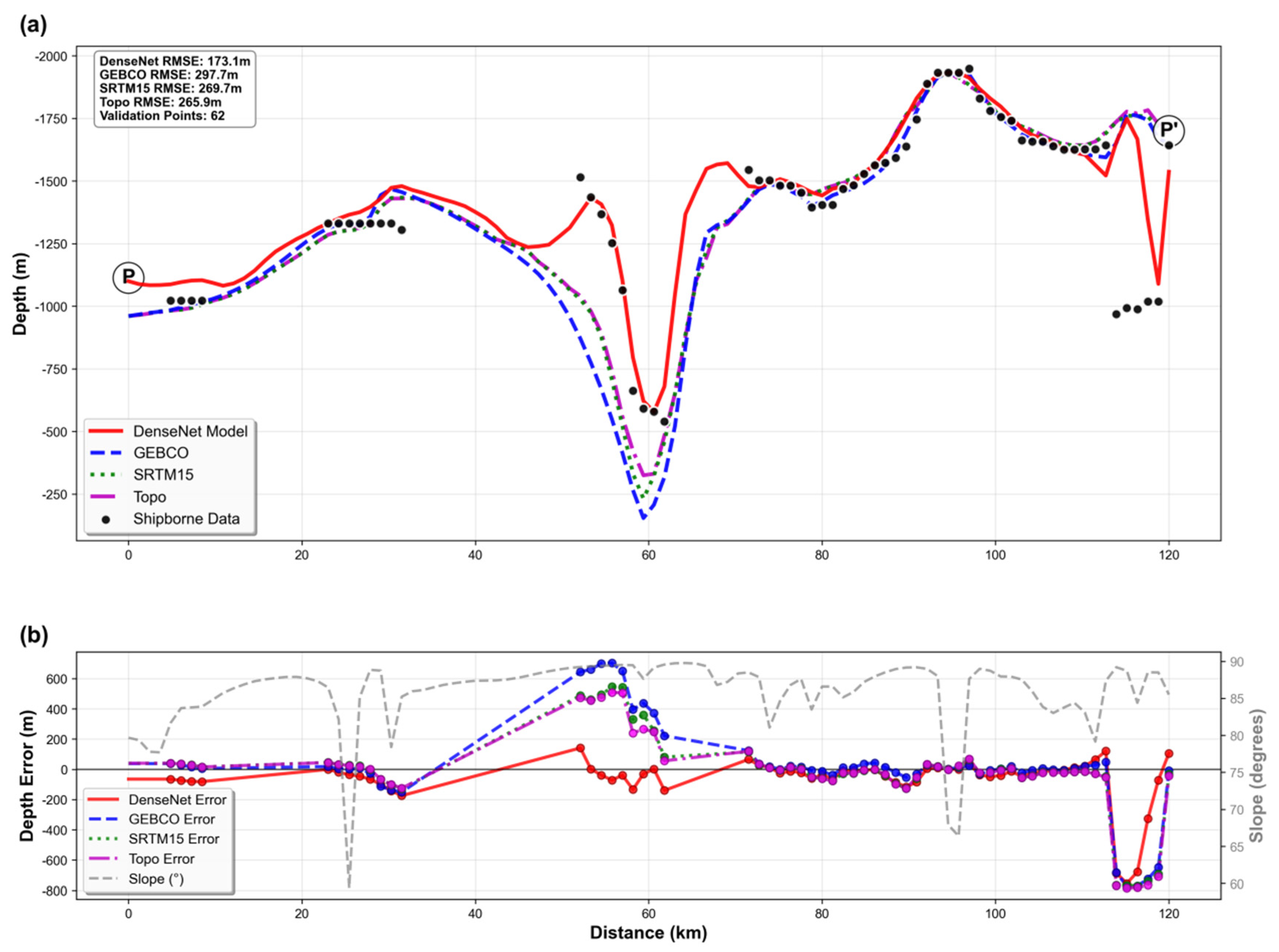
3.3. Typical Structural Profile Validation
4. Discussion
4.1. Dominant Role of Vertical Deflection Components in Rift Identification
4.2. Architectural Innovations for Topographic Complexity Adaptation
4.2.1. Adaptive Transition Layer: Resolving the Detail-Efficiency Trade-Off
4.2.2. Curvature Stratification: Mitigating Data Sparsity Bias
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, D.; Guo, J.; Li, Z.; Ji, B.; Liu, X.; Chang, X. Improved Gravity-Geologic Method Reliably Removing the Long-Wavelength Gravity Effect of Regional Seafloor Topography: A Case of Bathymetric Prediction in the South China Sea. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4211912. [Google Scholar] [CrossRef]
- Zhou, S.; Guo, J.; Zhang, H.; Jia, Y.; Sun, H.; Liu, X.; An, D. SDUST2023BCO: A Global Seafloor Model Determined from a Multi-Layer Perceptron Neural Network Using Multi-Source Differential Marine Geodetic Data. Earth Syst. Sci. Data 2025, 17, 165–179. [Google Scholar] [CrossRef]
- Abulaitijiang, A.; Andersen, O.B.; Sandwell, D. Improved Arctic Ocean Bathymetry Derived DTU17 Gravity Model. Earth Space Sci. 2019, 6, 1336–1347. [Google Scholar] [CrossRef]
- Baudry, N.; Calmant, S. Seafloor Mapping from High-Density Satellite Altimetry. Mar. Geophys. Res. 1996, 18, 135–146. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Feng, J.; Sun, Y.; Xu, Z.; Huang, Z. A New Global Bathymetry Model STO_IEU2020. Remote Sens. 2022, 14, 5744. [Google Scholar] [CrossRef]
- Hu, M.; Jin, T.; Jiang, W.; Chu, Y.; Wen, H.; Li, J. Bathymetry Model in the Northwestern Pacific Ocean Predicted from Satellite Altimetric Vertical Gravity Gradient Anomalies and Ship-Board Depths. Mar. Geod. 2022, 45, 24–46. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Goff, J.A.; Gevorgian, J.; Harper, H.; Kim, S.-S.; Yu, Y.; Tozer, B.; Wessel, P.; Smith, W.H.F. Improved Bathymetric Prediction Using Geological Information: SYNBATH. Earth Space Sci. 2022, 9, e2021EA002069. [Google Scholar] [CrossRef]
- Harper, H.; Sandwell, D.T. Global Predicted Bathymetry Using Neural Networks. Earth Space Sci. 2024, 11, e2023EA003199. [Google Scholar] [CrossRef]
- Hsiao, Y.-S.; Kim, J.; Kim, K.B.; Lee, B.; Hwang, C. Bathymetry Estimation Using the Gravity-Geologic Method: An Investigation of Density Contrast Predicted by the Downward Continuation Method. Terr. Atmos. Ocean. Sci. 2011, 22, 347–358. [Google Scholar] [CrossRef]
- Kim, J.W.; von Frese, R.R.B.; Lee, B.Y.; Roman, D.R.; Doh, S.-J. Altimetry-Derived Gravity Predictions of Bathymetry by the Gravity-Geologic Method. Pure Appl. Geophys. 2011, 168, 815–826. [Google Scholar] [CrossRef]
- Kim, K.B.; Lee, C.K. Bathymetry Change Investigation of the 2011 Tohoku Earthquake. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2015, 33, 181–192. [Google Scholar] [CrossRef]
- Kim, K.B.; Yun, H.S. Satellite-Derived Bathymetry Prediction in Shallow Waters Using the Gravity-Geologic Method: A Case Study in the West Sea of Korea. KSCE J. Civ. Eng. 2018, 22, 2560–2568. [Google Scholar] [CrossRef]
- Hsiao, Y.-S.; Hwang, C.; Cheng, Y.-S.; Chen, L.-C.; Hsu, H.-J.; Tsai, J.-H.; Liu, C.-L.; Wang, C.-C.; Liu, Y.-C.; Kao, Y.-C. High-Resolution Depth and Coastline over Major Atolls of South China Sea from Satellite Altimetry and Imagery. Remote Sens. Environ. 2016, 176, 69–83. [Google Scholar] [CrossRef]
- Wei, Z.; Guo, J.; Zhu, C.; Yuan, J.; Chang, X.; Ji, B. Evaluating Accuracy of HY-2A/GM-Derived Gravity Data with the Gravity-Geologic Method to Predict Bathymetry. Front. Earth Sci. 2021, 9, 636246. [Google Scholar] [CrossRef]
- Dixon, T.H.; Parke, M.E. Bathymetry Estimates in the Southern Oceans from Seasat Altimetry. Nature 1983, 304, 406–411. [Google Scholar] [CrossRef]
- Baudry, N.; Calmant, S. 3-D Modelling of Seamount Topography from Satellite Altimetry. Geophys. Res. Lett. 1991, 18, 1143–1146. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Bathymetric Prediction from Dense Satellite Altimetry and Sparse Shipboard Bathymetry. J. Geophys. Res. Solid Earth 1994, 99, 21803–21824. [Google Scholar] [CrossRef]
- Calmant, S.; Berge-Nguyen, M.; Cazenave, A. Global Seafloor Topography from a Least-Squares Inversion of Altimetry-Based High-Resolution Mean Sea Surface and Shipboard Soundings. Geophys. J. Int. 2002, 151, 795–808. [Google Scholar] [CrossRef]
- Ramillien, G.; Wright, I.C. Predicted Seafloor Topography of the New Zealand Region: A Nonlinear Least Squares Inversion of Satellite Altimetry Data. J. Geophys. Res. Solid Earth 2000, 105, 16577–16590. [Google Scholar] [CrossRef]
- Sun, H.; Jin, T.; Feng, Y.; Sun, W.; Zhou, M.; Sun, H. The Nonlinear Effects in Bathymetric Prediction from Altimetric Gravity Data. J. Geod. 2025, 99, 39. [Google Scholar] [CrossRef]
- Xu, H.; Yu, J. Using an Iterative Algorithm to Predict Topography From Vertical Gravity Gradients and Ship Soundings. Earth Space Sci. 2022, 9, e2022EA002437. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Li, X.; Yang, J.; Wan, X. Seafloor Topography Estimation from Gravity Anomaly and Vertical Gravity Gradient Using Nonlinear Iterative Least Square Method. Remote Sens. 2021, 13, 64. [Google Scholar] [CrossRef]
- Yang, J.; Jekeli, C.; Liu, L. Seafloor Topography Estimation From Gravity Gradients Using Simulated Annealing. J. Geophys. Res. Solid Earth 2018, 123, 6958–6975. [Google Scholar] [CrossRef]
- Xu, C.; Li, J.; Jian, G.; Wu, Y.; Zhang, Y. An Adaptive Nonlinear Iterative Method for Predicting Seafloor Topography From Altimetry-Derived Gravity Data. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025692. [Google Scholar] [CrossRef]
- Jiang, X.; Guo, J.; Lin, M.; Sun, H.; Jiang, T. Enhanced Gravity-Geologic Method to Predict Bathymetry by Considering Non-Linear Effects of Surrounding Seafloor Topography. Geophys. J. Int. 2024, 239, 754–767. [Google Scholar] [CrossRef]
- Sun, H.; Feng, Y.; Fu, Y.; Sun, W.; Peng, C.; Zhou, X.; Zhou, D. Bathymetric Prediction Using Multisource Gravity Data Derived From a Parallel Linked BP Neural Network. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024428. [Google Scholar] [CrossRef]
- An, D.; Feng, W.; Chen, X.; Sun, M.; Zhang, Z.; Meng, Y.; Zhong, M. Predicting Intermediate Wavelength Depth Using a Deep Neural Network Combined with Gravity Data in the Sea of Japan. Int. J. Digit. Earth 2024, 17, 2430679. [Google Scholar] [CrossRef]
- Annan, R.F.; Wan, X. Recovering Bathymetry of the Gulf of Guinea Using Altimetry-Derived Gravity Field Products Combined via Convolutional Neural Network. Surv. Geophys. 2022, 43, 1541–1561. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Sun, Y.; Chang, X.; Jia, Y.; Guo, J.; Sun, H. Predicting Bathymetry Using Multisource Differential Marine Geodetic Data with Multilayer Perceptron Neural Network. Int. J. Digit. Earth 2024, 17, 2393255. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Guo, J.; Jin, X.; Lei, Y.; Sun, Y.; Sun, H. Bathymetry of the Gulf of Mexico Predicted with Multilayer Perceptron From Multisource Marine Geodetic Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4208911. [Google Scholar] [CrossRef]
- Trung, N.N.; Lee, S.-M.; Que, B.C. Satellite Gravity Anomalies and Their Correlation with the Major Tectonic Features in the South China Sea. Gondwana Res. 2004, 7, 407–424. [Google Scholar] [CrossRef]
- Yan, Q.; Shi, X.; Yuan, L.; Yan, S.; Liu, Z. Tectono-Magmatic Evolution of the Philippine Sea Plate: A Review. Geosyst. Geoenviron. 2022, 1, 100018. [Google Scholar] [CrossRef]
- GEBCO. Gridded Bathymetry Data. Available online: https://www.gebco.net/data-products/gridded-bathymetry-data (accessed on 27 July 2025).
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global Bathymetry and Topography at 15 Arc Sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Marks, K.M.; Smith, W.H.F. Radially Symmetric Coherence between Satellite Gravity and Multibeam Bathymetry Grids. Mar. Geophys. Res. 2012, 33, 223–227. [Google Scholar] [CrossRef]
- Wang, D.; Dong, J.; Tang, L.; Ma, M.; Xie, T. An Automatic Generalization Method of a Block-Based Digital Depth Model Based on Surface Curvature Features. J. Mar. Sci. Eng. 2024, 12, 2299. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Zhu, Y.; Newsam, S. DenseNet for Dense Flow. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 790–794. [Google Scholar]
- Ekinci, Y.L. A Comparative Study on Computing Horizontal Derivatives of Gravity Data for Geological Contact Mapping. Geol. Bull. Turk. 2017, 60, 209–221. [Google Scholar] [CrossRef]
- Kim, S.-S.; Wessel, P. New Analytic Solutions for Modeling Vertical Gravity Gradient Anomalies. Geochem. Geophys. Geosyst. 2016, 17, 1915–1924. [Google Scholar] [CrossRef]
- Prasad, K.N.D.; Nguyen, D.V.; Le-Huy, M.; Tran, K.V.; Do, T.D.; Pham, L.T.; Rehman, H. Mapping Structural Geometry and Tectonics of the Central Continental Margin of Vietnam and Adjacent Areas Using an Enhanced Horizontal Gradient of Gravity Data. Tectonophysics 2025, 905, 230719. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]


| Model | MAE (m) | RMSE (m) | R2 | MAPE (%) | Std (m) |
|---|---|---|---|---|---|
| DenseNet | 30.01 | 84.75 | 0.9935 | 1.26 | 84.74 |
| GEBCO_2024 | 48.05 | 161.63 | 0.9762 | 2.19 | 161.53 |
| SRTM15+ | 55.58 | 166.40 | 0.9748 | 2.52 | 166.40 |
| Topo_27.1 | 55.17 | 165.56 | 0.9751 | 2.50 | 165.56 |
| CNN | 50.90 | 122.53 | 0.9863 | 2.56 | 121.81 |
| Rank | Target | Centroid Coordinates | Area (km2) | Validation Points | DenseNet RMSE (m) | GEBCO_2024 RMSE (m) | Improvement (%) |
|---|---|---|---|---|---|---|---|
| 1 | A | 114.242°E, 15.596°N | 1710 | 471 | 64.6 | 229.1 | 71.8 |
| 2 | B | 114.992°E, 16.087°N | 803 | 480 | 75.6 | 283.9 | 73.4 |
| 3 | C | 114.608°E, 10.329°N | 1492 | 117 | 71.1 | 231.7 | 69.3 |
| 4 | D | 112.942°E, 17.375°N | 242 | 108 | 62.8 | 485.2 | 87.1 |
| 5 | E | 114.654°E, 16.742°N | 214 | 138 | 73.9 | 355.2 | 79.2 |
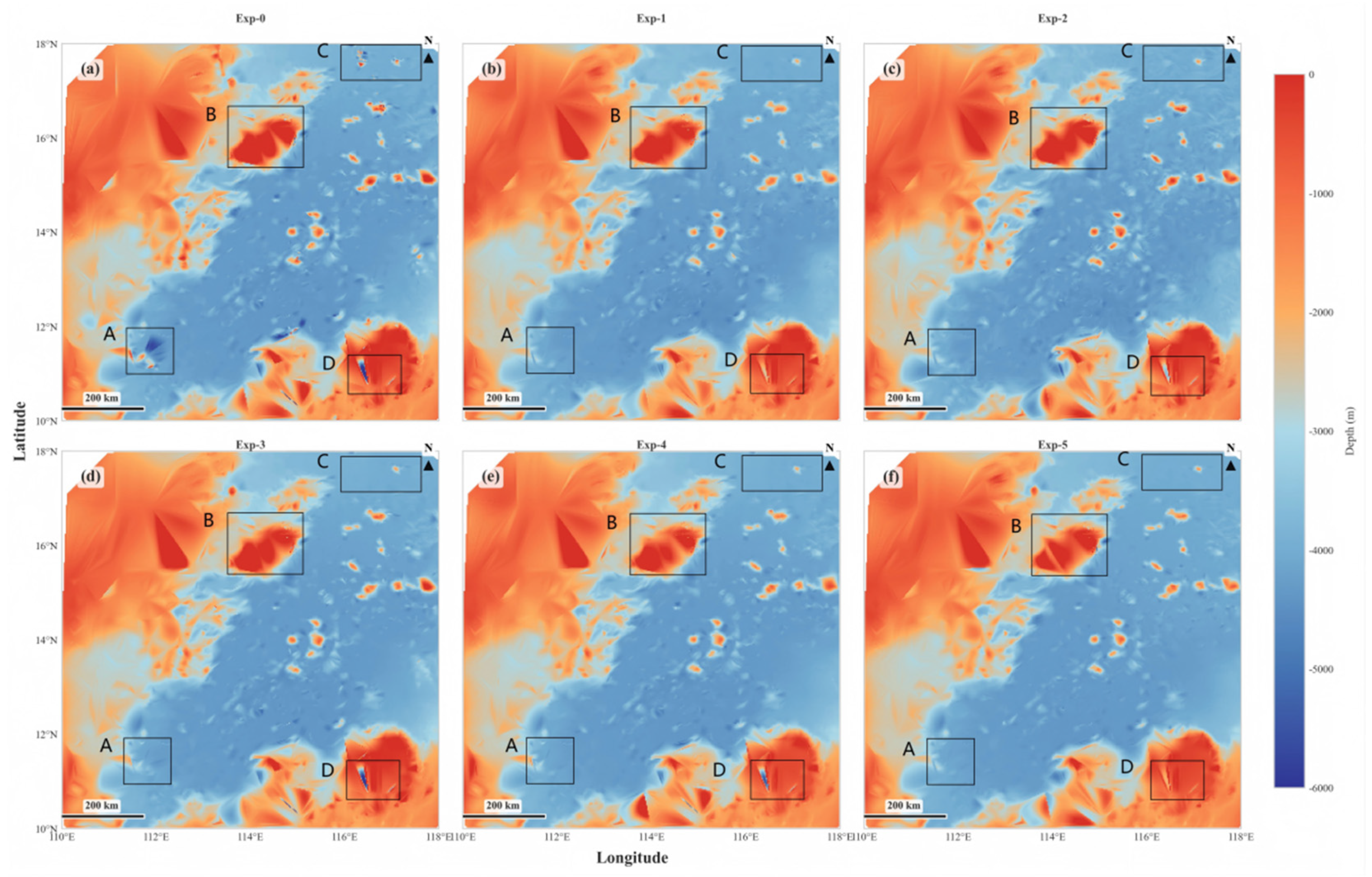
| Model Configuration | RMSE (m) | R2 | ΔRMSE vs. Baseline (m) | Rel. ΔRMSE vs. Baseline (%) |
|---|---|---|---|---|
| Baseline (GA + VGG + ξ + η + Pos + H_ref) | 84.75 | 0.9935 | - | - |
| Exp-1: GA + Pos + H_ref | 178.92 | 0.9709 | +94.17 | +111.1% |
| Exp-2: GA + VGG + Pos + H_ref | 175.83 | 0.9719 | +91.08 | +107.5% |
| Exp-3: GA + ξ+η + Pos + H_ref | 151.61 | 0.9791 | +66.86 | +78.9% |
| Exp-4: ξ + η + Pos + H_ref | 156.62 | 0.9777 | +71.87 | +84.8% |
| Exp-5: No Gravity (Pos + H_ref only) | 177.03 | 0.9715 | +92.28 | +108.9% |
| Complexity Class | Model | MAE (m) | RMSE (m) | R2 | |∆RMSE| (m) |
|---|---|---|---|---|---|
| Overall | DenseNet | 30.01 | 84.75 | 0.9935 | 6.8464 |
| Random | 40.43 | 91.59 | 0.9924 | ||
| Q1 (Flat) | DenseNet | 23.80 | 81.71 | 0.9904 | 5.6911 |
| Random | 32.09 | 87.40 | 0.9890 | ||
| Q2 (Gentle Slope) | DenseNet | 26.18 | 88.41 | 0.9909 | 8.8007 |
| Random | 36.01 | 97.21 | 0.9890 | ||
| Q3 (Slope) | DenseNet | 26.83 | 62.88 | 0.9963 | 6.4344 |
| Random | 37.63 | 69.32 | 0.9955 | ||
| Q4 (Steep Slope) | DenseNet | 43.24 | 101.39 | 0.9917 | 6.6026 |
| Random | 56.00 | 108.00 | 0.9906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, H.; Zhou, S.; Zhu, F.; Li, J.; Bian, S. Enhanced Bathymetric Inversion for Tectonic Features via Multi-Gravity-Component DenseNet: A Case Study of Rift Identification in the South China Sea. Remote Sens. 2025, 17, 3453. https://doi.org/10.3390/rs17203453
Zhang H, Li H, Zhou S, Zhu F, Li J, Bian S. Enhanced Bathymetric Inversion for Tectonic Features via Multi-Gravity-Component DenseNet: A Case Study of Rift Identification in the South China Sea. Remote Sensing. 2025; 17(20):3453. https://doi.org/10.3390/rs17203453
Chicago/Turabian StyleZhang, Huan, Houpu Li, Shuai Zhou, Fengshun Zhu, Jingshu Li, and Shaofeng Bian. 2025. "Enhanced Bathymetric Inversion for Tectonic Features via Multi-Gravity-Component DenseNet: A Case Study of Rift Identification in the South China Sea" Remote Sensing 17, no. 20: 3453. https://doi.org/10.3390/rs17203453
APA StyleZhang, H., Li, H., Zhou, S., Zhu, F., Li, J., & Bian, S. (2025). Enhanced Bathymetric Inversion for Tectonic Features via Multi-Gravity-Component DenseNet: A Case Study of Rift Identification in the South China Sea. Remote Sensing, 17(20), 3453. https://doi.org/10.3390/rs17203453






