Performance of Multi-Antenna GNSS Buoy and Co-Located Mooring Array Deployed Around Qianliyan Islet for Altimetry Satellite Calibration
Highlights
- What are the main findings?
- Validating dual-platform (GNSS buoy + mooring array) calibration for altimetry satellites in the Yellow Sea, achieving 2.76 cm averaged SSH standard deviation during 20-day synchronized observations.
- Demonstrating adaptive low-pass filtering (0.01 Hz cutoff) effectively suppresses high-frequency SSH noise (≤10 s period) while retaining spectral characteristics critical for calibration accuracy.
- What is the implication of the main finding?
- GNSS buoys require correction for attitude variations (±3° under complex seas), necessitating adaptive weighting protocols, whereas mooring arrays better resolve mean SSH trends.
- Establishing a ground-based calibration protocol that integrates multi-platform observations, advancing coastal altimeter methodologies for operational marine monitoring.
Abstract
1. Introduction
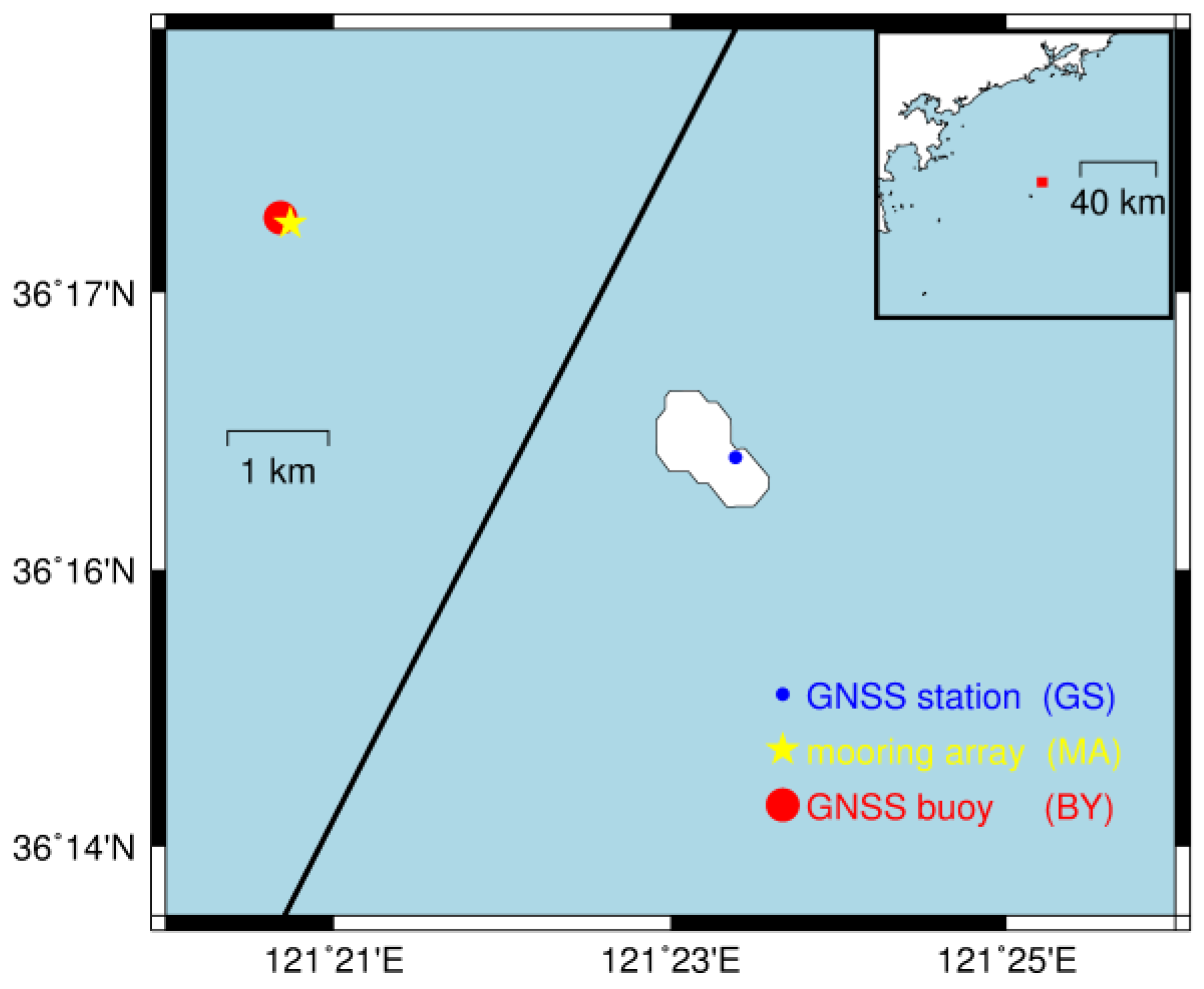
2. Experimental Overview
3. Theoretical Methodology
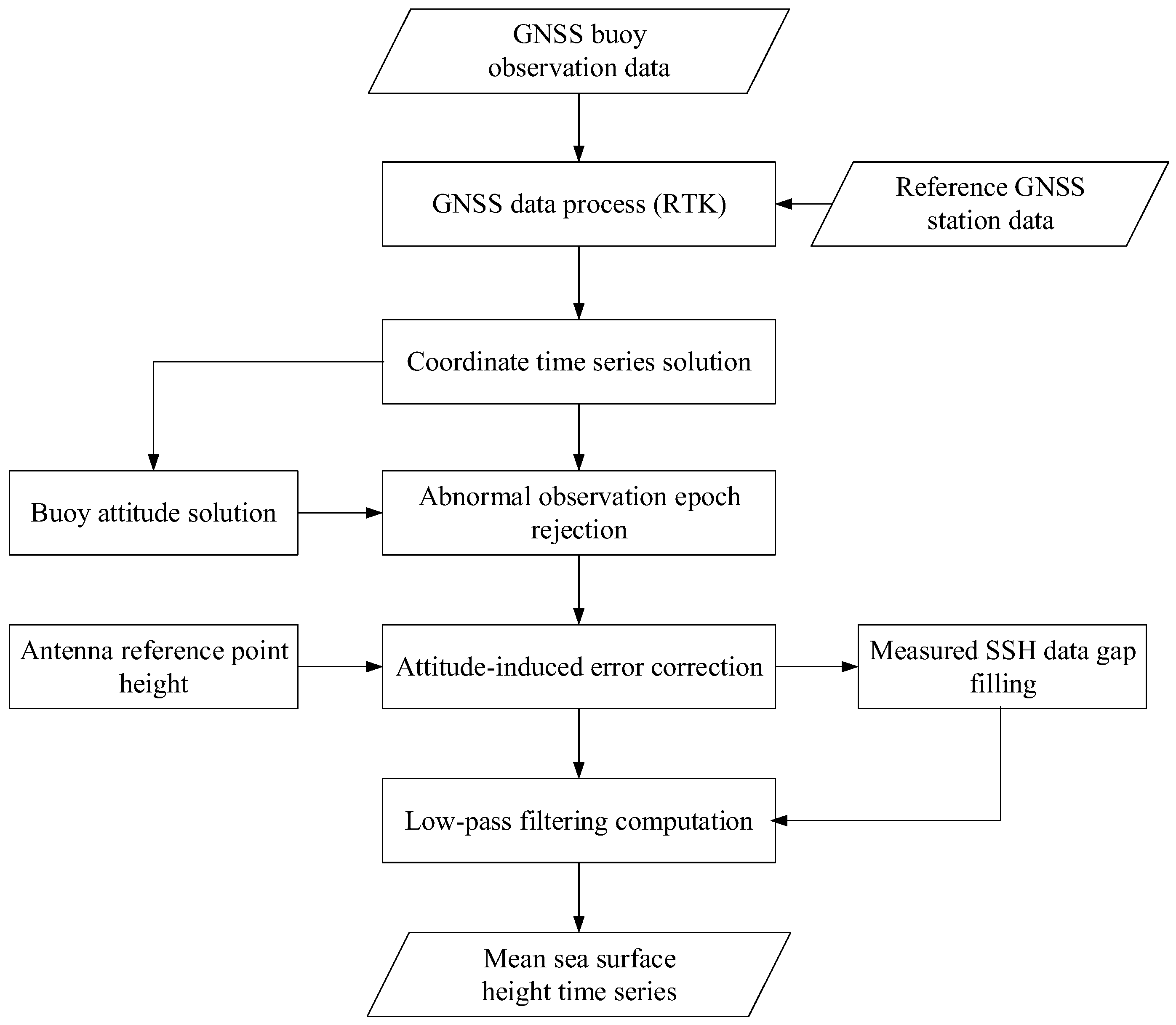
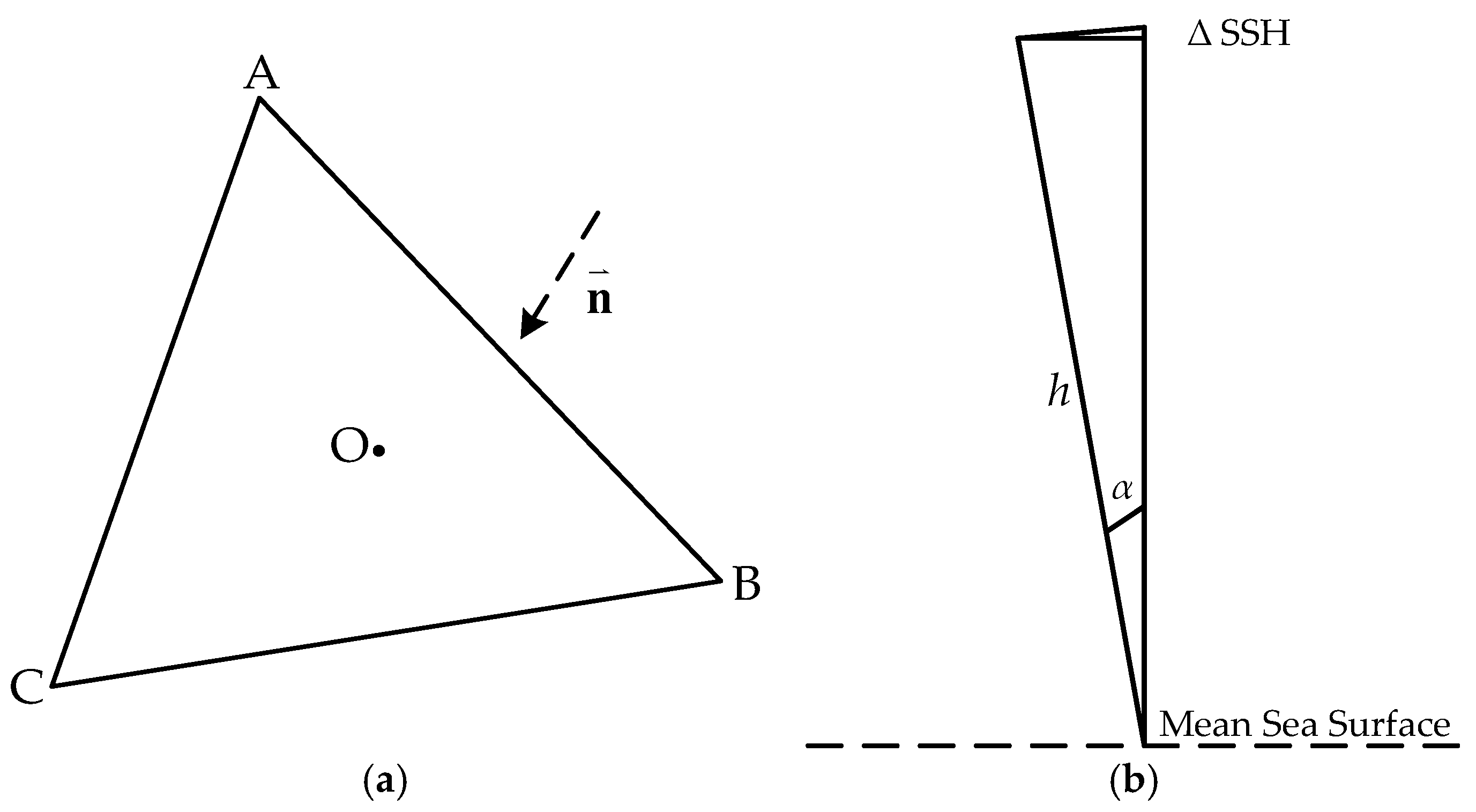
3.1. Method of Processing GNSS Buoy Data
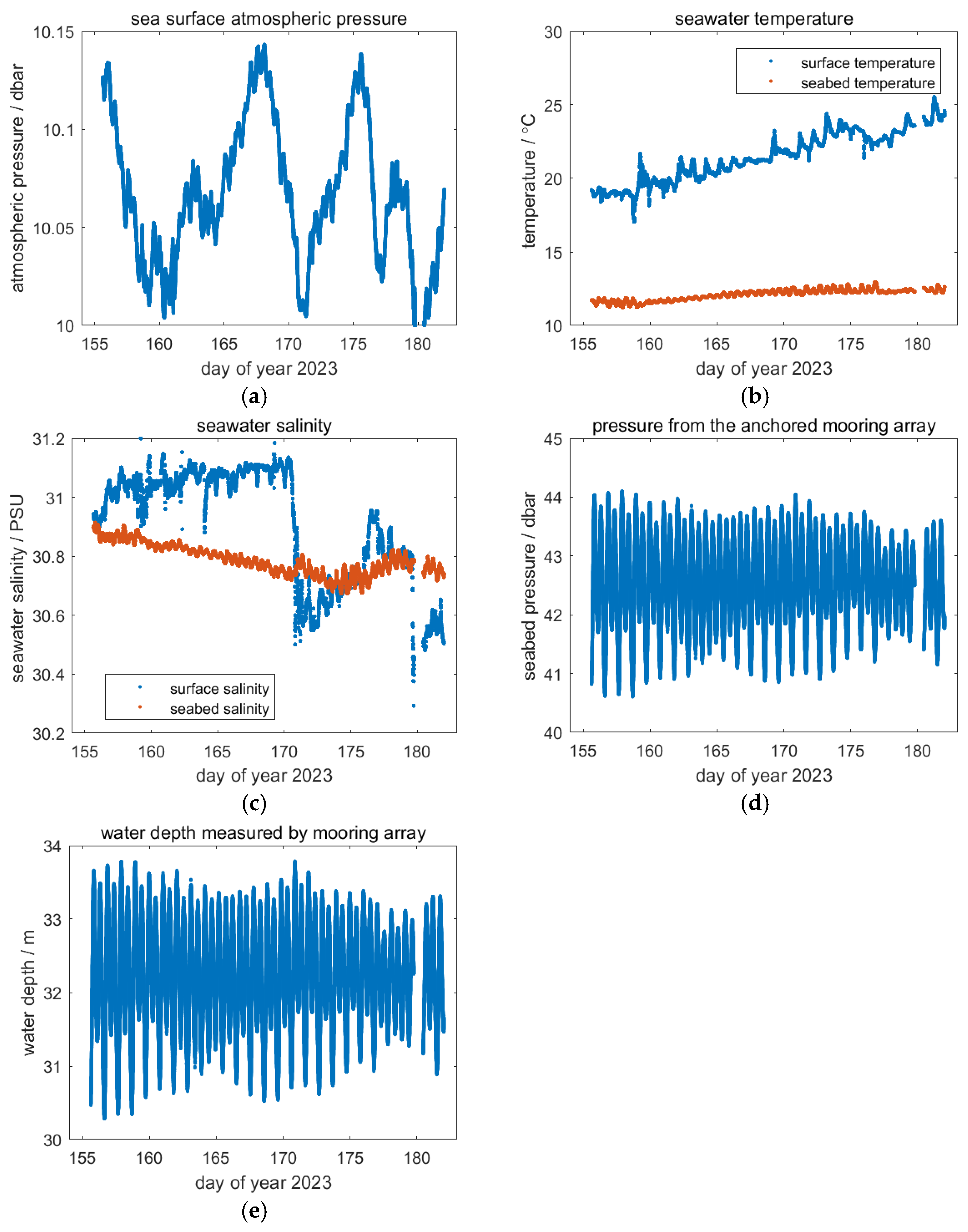
3.2. Method of Processing Mooring Array Data
4. Results
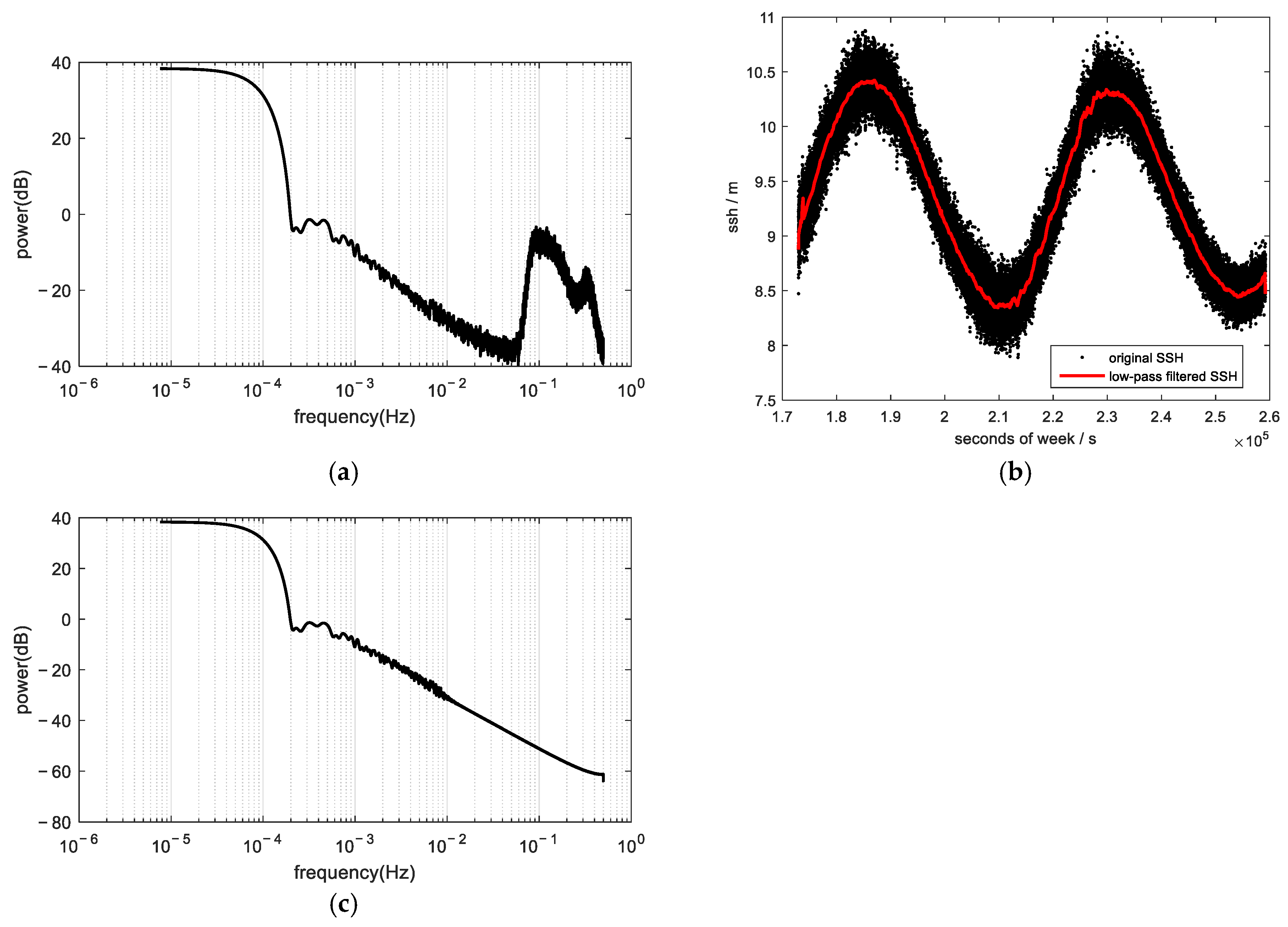
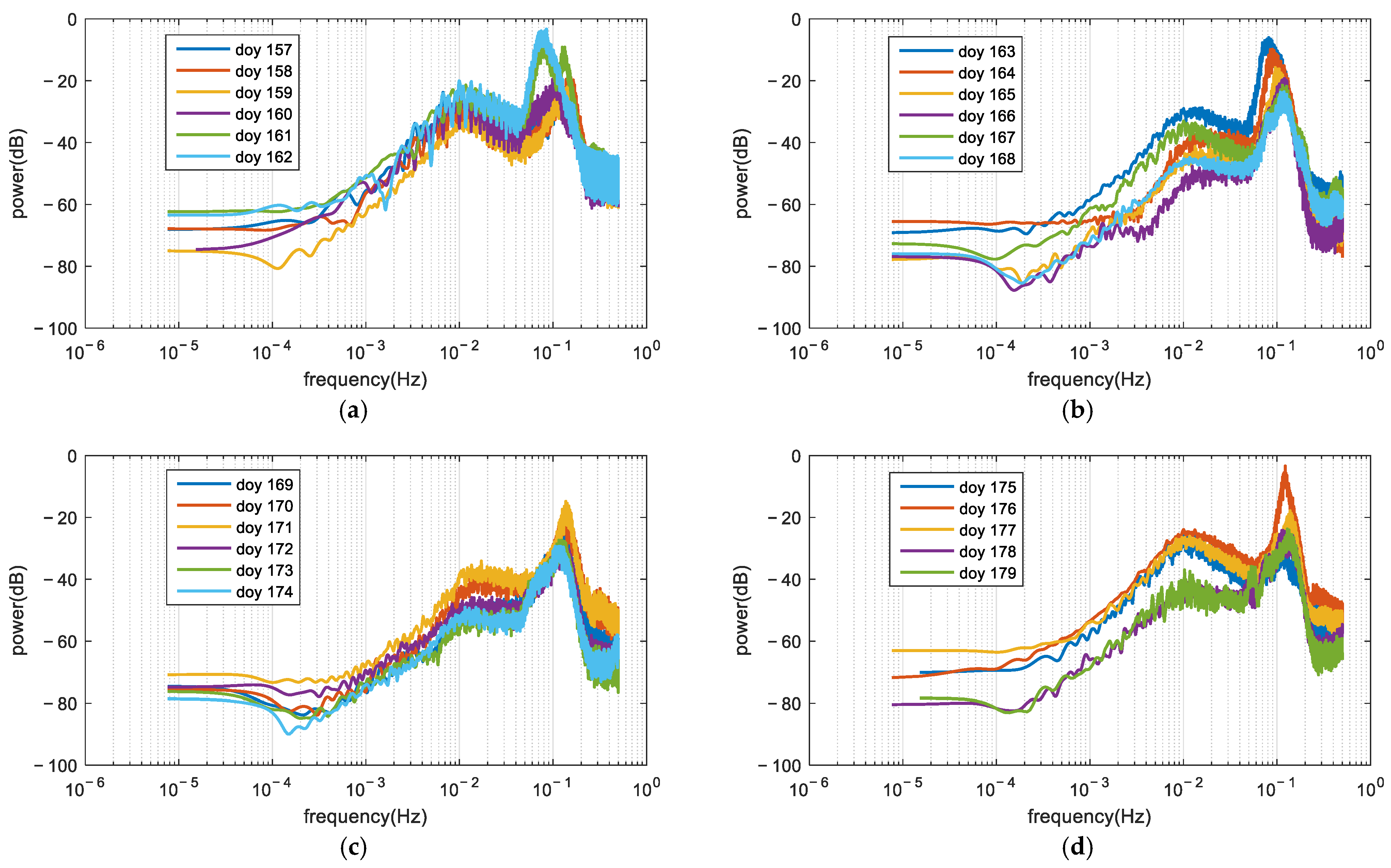
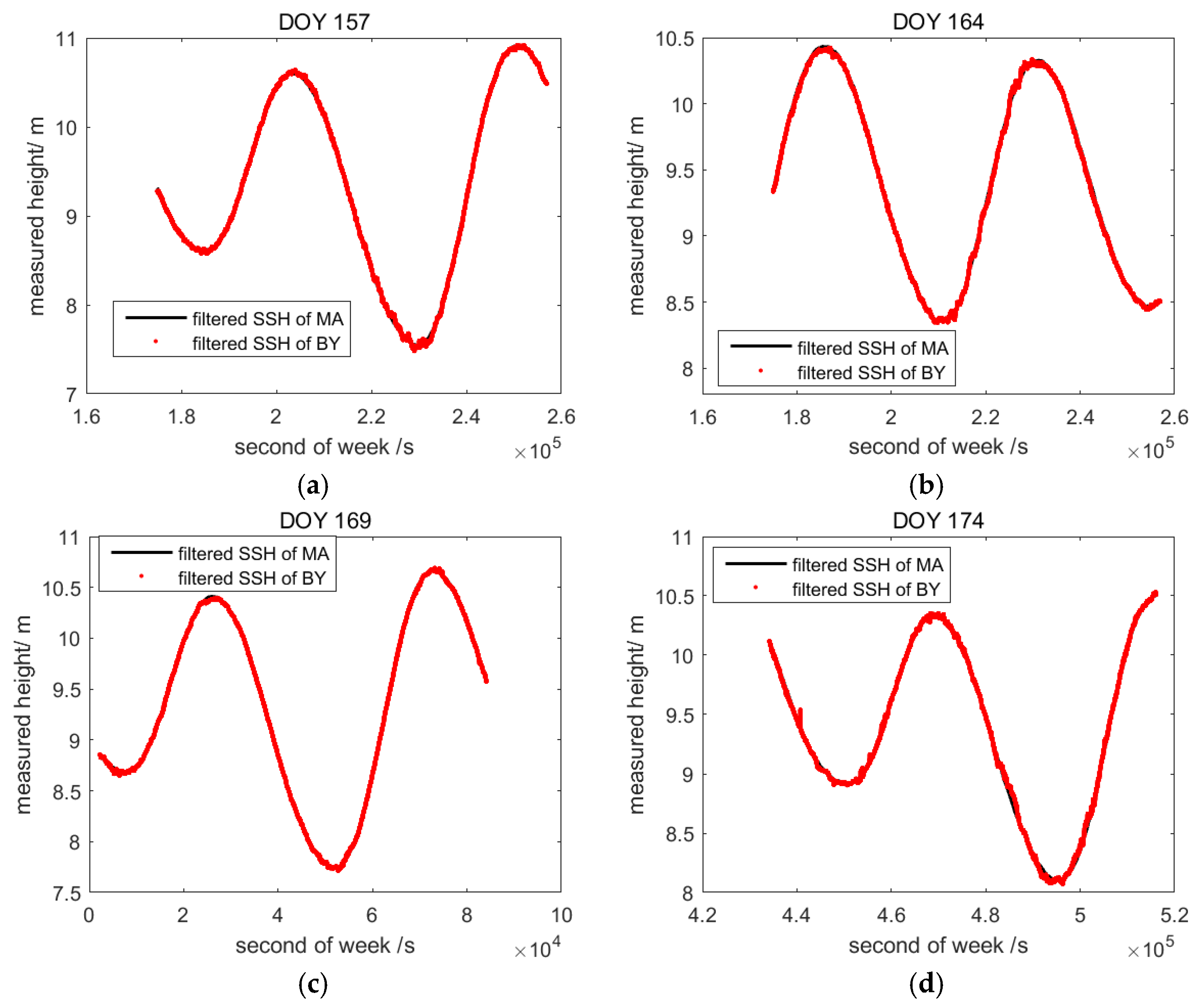
4.1. GNSS Buoy Data Processing
4.2. Mooring Array Data Processing
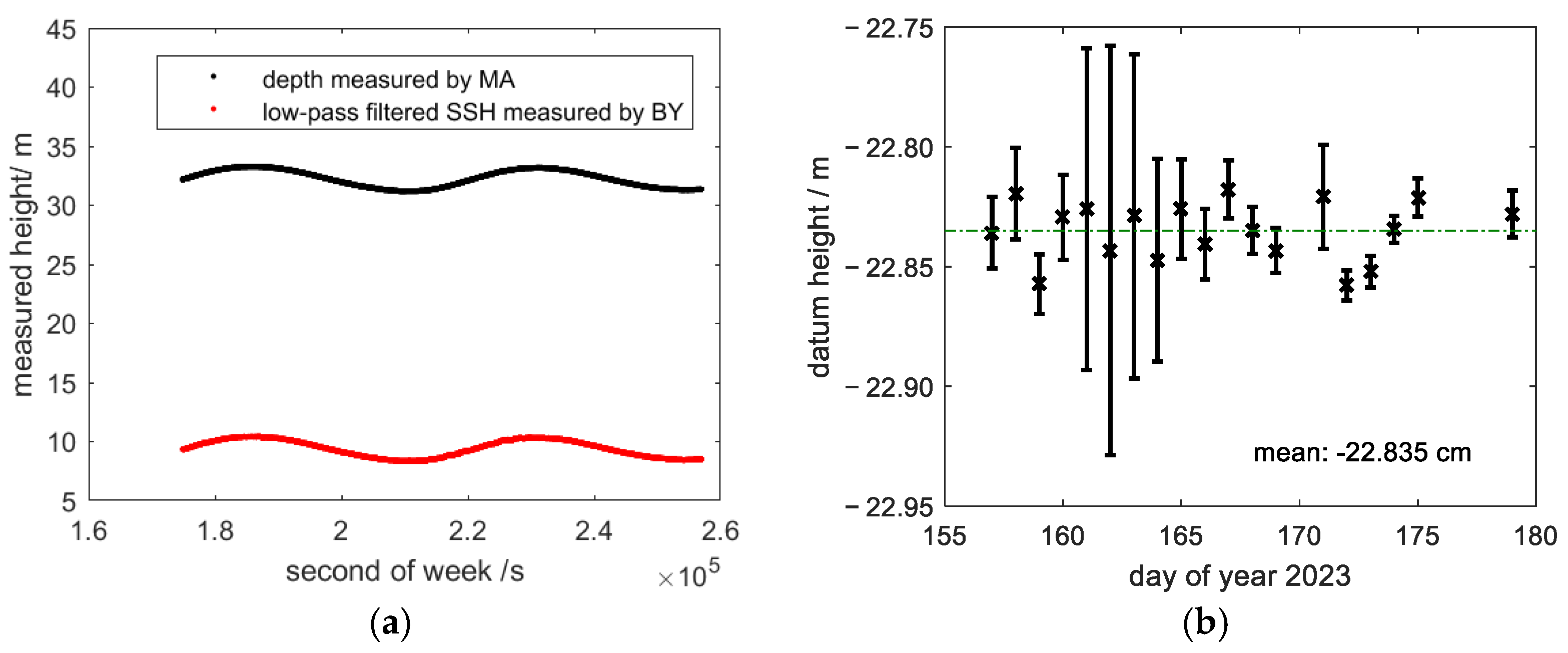
4.3. Consistency Analysis of Synchronous Sea Surface Height Measurements Between GNSS Buoy and Mooring Array
4.4. Error Budget
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donlon, C.J.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, C.R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 mission: Enhanced continuity of satellite sea level measurements from space. Remote Sens. Environ. 2021, 258, 112395. [Google Scholar] [CrossRef]
- Abdalla, S.; Kolahchi, A.A.; Ablain, M.; Adusumilli, S.; Bhowmick, S.A.; Alou-Font, E.; Amarouche, L.; Andersen, O.B.; Antich, H.; Aouf, L.; et al. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Verron, J.; Bonnefond, P.; Andersen, O.; Ardhuin, F.; Bergé-Nguyen, M.; Bhowmick, S.; Blumstein, D.; Boy, F.; Brodeau, L.; Crétaux, J.-F.; et al. The SARAL/AltiKa mission: A step forward to the future of altimetry. Adv. Space Res. 2021, 68, 808–828. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Harper, H.; Tozer, B.; Smith, W.H. Gravity field recovery from geodetic altimeter missions. Adv. Space Res. 2021, 68, 1059–1072. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Gao, J.; Liu, X.; Hwang, C.; Yu, S.; Yuan, J.; Ji, B.; Guan, B. Marine gravity determined frommulti-satellite GM/ERM altimeter data over the South China Sea: SCSGA V1.0. J. Geod. 2020, 94, 50. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global Bathymetry and Topography at 15 Arc Sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Marks, K.M.; Smith, W.H.F. A method of stacking AltiKa repeat cycle data that may reveal 75,000+ possible small seamounts. Earth Space Sci. 2018, 5, 964–969. [Google Scholar] [CrossRef]
- Yu, D.; Deng, X.; Andersen, O.B.; Zhu, H.; Luo, J. A new method for determining geoid gradient components from SWOT wide-swath data for marine gravity field. J. Geod. 2025, 99, 29. [Google Scholar] [CrossRef]
- Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale Eddies Detected by SWOT and Moored Observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
- Das, P.; Hossain, F. Multi-satellite tracking of surface water storage change in the era of Surface Water and Ocean Topography (SWOT) satellite mission. Earth Space Sci. 2025, 12, e2024EA004178. [Google Scholar] [CrossRef]
- Kacimi, S.; Jaruwatanadilok, S.; Kwok, R. SWOT observations over sea ice: A first look. Geophys. Res. Lett. 2025, 52, e2025GL116079. [Google Scholar] [CrossRef]
- Rudenko, S.; Dettmering, D.; Zeitlhöfler, J.; Alkahal, R.; Upadhyay, D.; Bloßfeld, M. Radial Orbit Errors of Contemporary Altimetry Satellite Orbits. Surv. Geophys. 2023, 44, 705–737. [Google Scholar] [CrossRef]
- Haines, B.; Desai, S.D.; Kubitschek, D.; Leben, R.R. A brief history of the Harvest experiment: 1989–2019. Adv. Space Res. 2021, 68, 1161–1170. [Google Scholar] [CrossRef]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Guinle, T.; Féménias, P. Corsica: A 20-Yr Multi-Mission Absolute Altimeter Calibration Site. Adv. Space Res. 2021, 68, 1171–1186. [Google Scholar] [CrossRef]
- Bonnefond, P.; Laurain, O.; Exertier, P.; Boy, F.; Guinle, T.; Picot, N.; Labroue, S.; Raynal, M.; Donlon, C.; Féménias, P.; et al. Calibrating the SAR SSH of Sentinel-3A and CryoSat-2 over the Corsica Facilities. Remote Sens. 2018, 10, 92–103. [Google Scholar] [CrossRef]
- Zhou, B.; Watson, C.; Legresy, B.; King, M.A.; Beardsley, J. Ongoing Development of the Bass Strait GNSS/INS Buoy System for Altimetry Validation in Preparation for SWOT. Remote Sens. 2023, 15, 287. [Google Scholar] [CrossRef]
- Zhou, B.; Watson, C.; Legresy, B.; King, M.A.; Beardsley, J.; Deane, A. GNSS/INS-Equipped Buoys for Altimetry Validation: Lessons Learnt and New Directions from the Bass Strait Validation Facility. Remote Sens. 2020, 12, 3001. [Google Scholar] [CrossRef]
- Watson, C.; Legresy, B.; King, M. Altimeter absolute bias estimates from Bass Strait, Australia. In Proceedings of the Ocean Surface Topography Science Team Meeting 2016, La Rochelle, France, 1–4 November 2016; Available online: https://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclsseminar/files/CVL_01_OSTST2016_Absolute_Bias_Watson_et_al_14h00.pdf (accessed on 10 August 2025).
- Watson, C.; White, N.; Church, J.; Burgette, R.; Tregoning, P.; Coleman, R. Absolute Calibration in Bass Strait, Australia: TOPEX, Jason-1 and OSTM/Jason-2. Mar. Geod. 2011, 34, 242–260. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Kokolakis, C.; Piretzidis, D.; Cullen, R.; Féménias, P.; Fornari, M.; Frantzis, X.; Tripolitsiotis, A.; Bouffard, J.; et al. The ESA Permanent Facility for Altimetry Calibration in Crete: Advanced Services and the Latest Cal/Val Results. Remote Sens. 2024, 16, 223. [Google Scholar] [CrossRef]
- Vergos, G.S.; Tziavos, I.N.; Mertikas, S.; Piretzidis, D.; Frantzis, X.; Donlon, C. Local Gravity and Geoid Improvements around the Gavdos Satellite Altimetry Cal/Val Site. Remote Sens. 2024, 16, 3243. [Google Scholar]
- Mertikas, S.P.; Lin, M.; Piretzidis, D.; Kokolakis, C.; Donlon, C.; Ma, C.; Zhang, Y.; Jia, Y.; Mu, B.; Frantzis, X.; et al. Absolute Calibration of the Chinese HY-2B Altimetric Mission with Fiducial Reference Measurement Standards. Remote Sens. 2023, 15, 1393. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Matsakis, D.; Mavrocordatos, C.; Altamimi, Z.; Kokolakis, C.; Tripolitsiotis, A. Fiducial reference systems for time and coordinates in satellite altimetry. Adv. Space Res. 2021, 68, 1140–1160. [Google Scholar] [CrossRef]
- Mertikas, S.; Tripolitsiotis, A.; Donlon, C.; Mavrocordatos, C.; Féménias, P.; Borde, F.; Frantzis, X.; Kokolakis, C.; Guinle, T.; Vergos, G.; et al. The ESA Permanent Facility for Altimetry Calibration: Monitoring Performance of Radar Altimeters for Sentinel-3A, Sentinel-3B and Jason-3 Using Transponder and Sea-Surface Calibrations with FRM Standards. Remote Sens. 2020, 12, 2642. [Google Scholar]
- Mertikas, S.P.; Donlon, C.; Féménias, P.; Mavrocordatos, C.; Galanakis, D.; Tripolitsiotis, A.; Frantzis, X.; Tziavos, I.N.; Vergos, G.; Guinle, T. Fifteen Years of Cal/Val Service to Reference Altimetry Missions: Calibration of Satellite Altimetry at the Permanent facilities in Gavdos and Crete, Greece. Remote Sens. 2018, 10, 1557–1596. [Google Scholar]
- Zhai, W.; Zhu, J.; Fan, X.; Yan, L.; Chen, C.; Tian, Z. Preliminary calibration results for Jason-3 and Sentinel-3 altimeters in the Wanshan Islands. J. Oceanol. Limnol. 2020, 39, 458–471. [Google Scholar]
- Andersen, O.B.; Zhang, S.; Sandwell, D.T.; Dibarboure, G.; Smith, W.H.; Abulaitijiang, A. The Unique Role of the Jason Geodetic Missions for high Resolution Gravity Field and Mean Sea Surface Modelling. Remote Sens. 2021, 13, 646. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Y.; Lin, M.; Ma, C.; Mertikas, S.P.; Hu, W.; Wang, Z.; Mu, B.; Zhou, X. Monitoring the Performance of HY-2B and Jason-2/3 Sea Surface Height via the China Altimetry Calibration Cooperation Plan. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Y.; Zhou, X.; Zhu, L.; Jiang, Q.; Sun, H.; Chen, G.; Wang, P.; Mertikas, S.P.; Fu, Y.; et al. Calibration of an Airborne Interferometric Radar Altimeter over the Qingdao Coast Sea, China. Remote Sens. 2020, 12, 1651. [Google Scholar]
- Yang, L.; Zhou, X.; Mertikas, S.P.; Zhu, L.; Yang, L.; Lei, N. First calibration results of Jason-2 and SARAL/AltiKa satellite altimeters from the Qianli Yan permanent Cal/Val facilities, China. Adv. Space Res. 2017, 59, 2831–2842. [Google Scholar]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Guillot, A.; Picot, N.; Cancet, M.; Lyard, F. SARAL/AltiKa Absolute Calibration from the Multi-Mission Corsica Facilities. Mar. Geod. 2015, 38 (Suppl. 1), 171–192. [Google Scholar]
- Fofonoff, N.P. Algorithms for Computations of Fundamental Properties of Seawater; Unesco technical papers in marine science; UNESCO: Paris, France, 1983. [Google Scholar]
- Watson, C.; White, N.; Coleman, R.; Church, J.; Morgan, P.; Govind, R. TOPEX/Poseidon and Jason-1: Absolute calibration in bass strait, Australia. Mar. Geod. 2004, 27, 107–131. [Google Scholar]



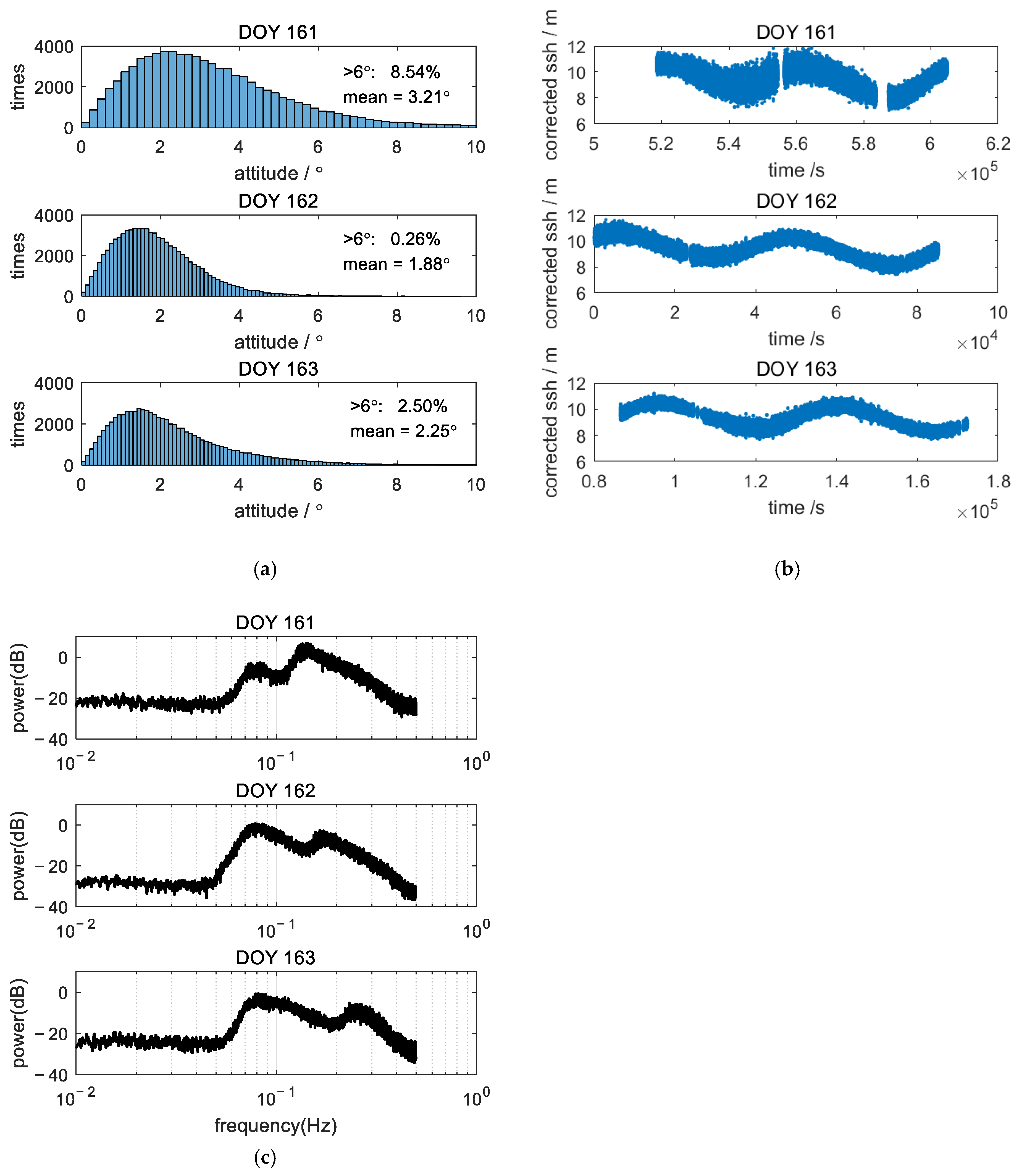

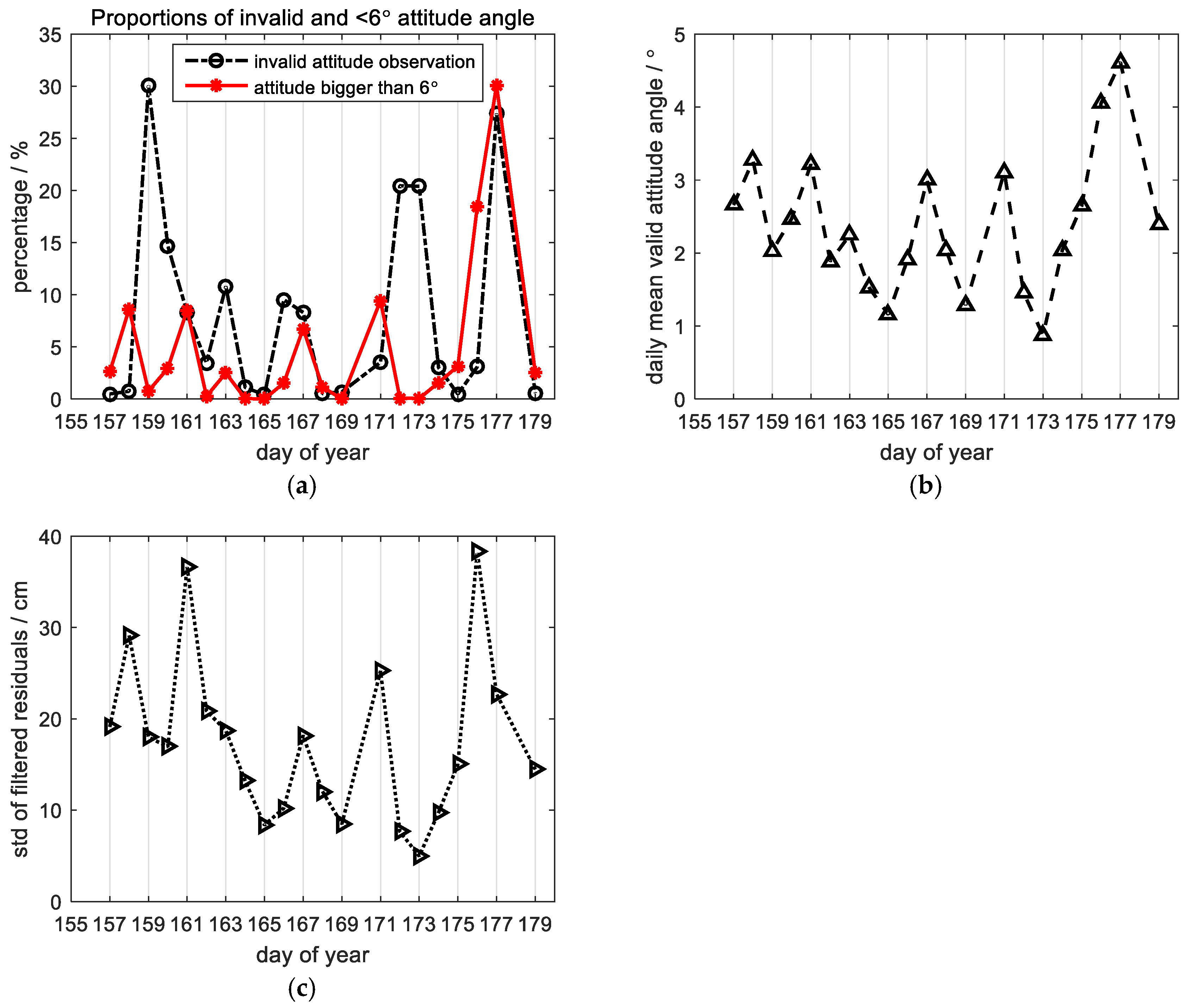

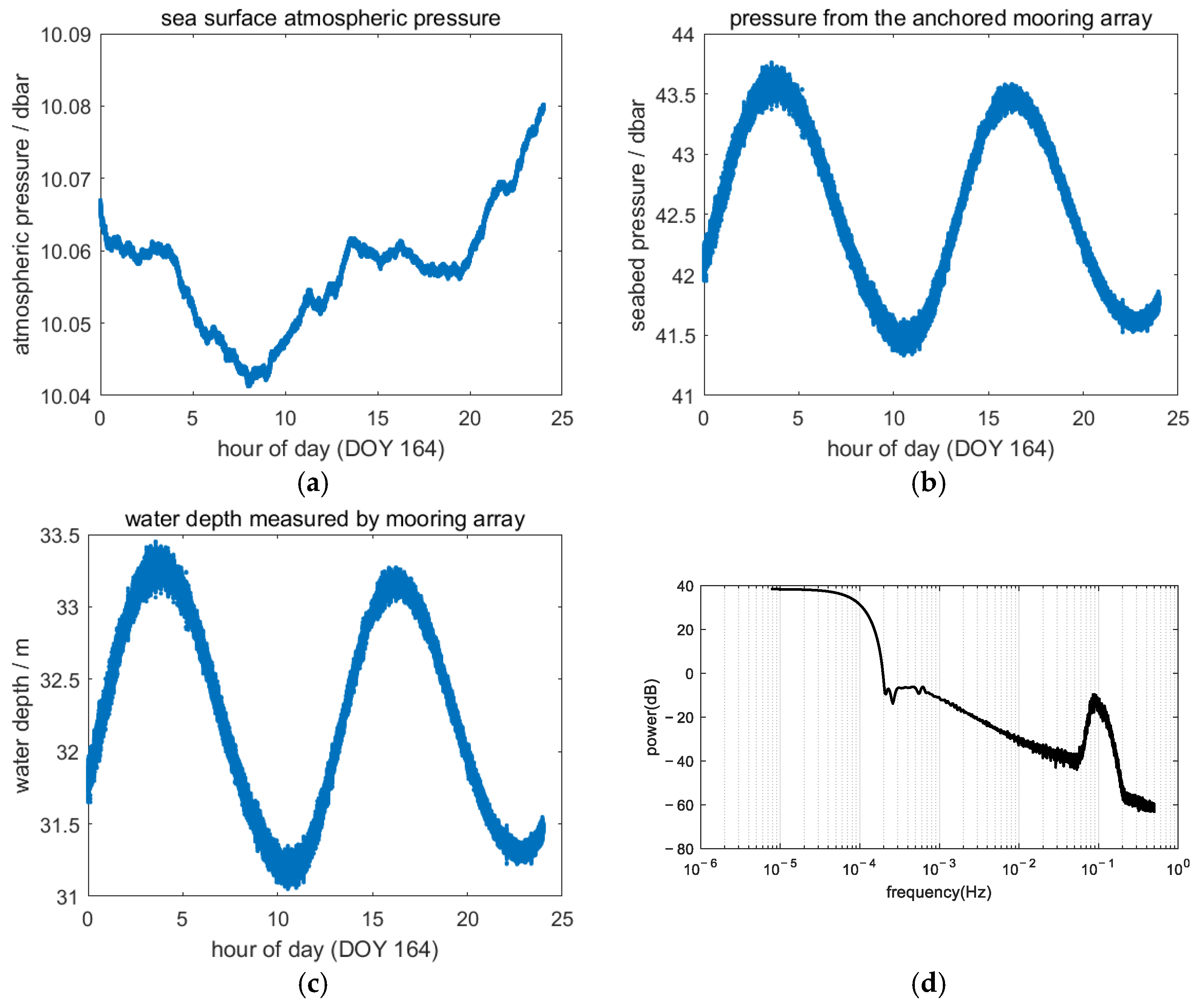
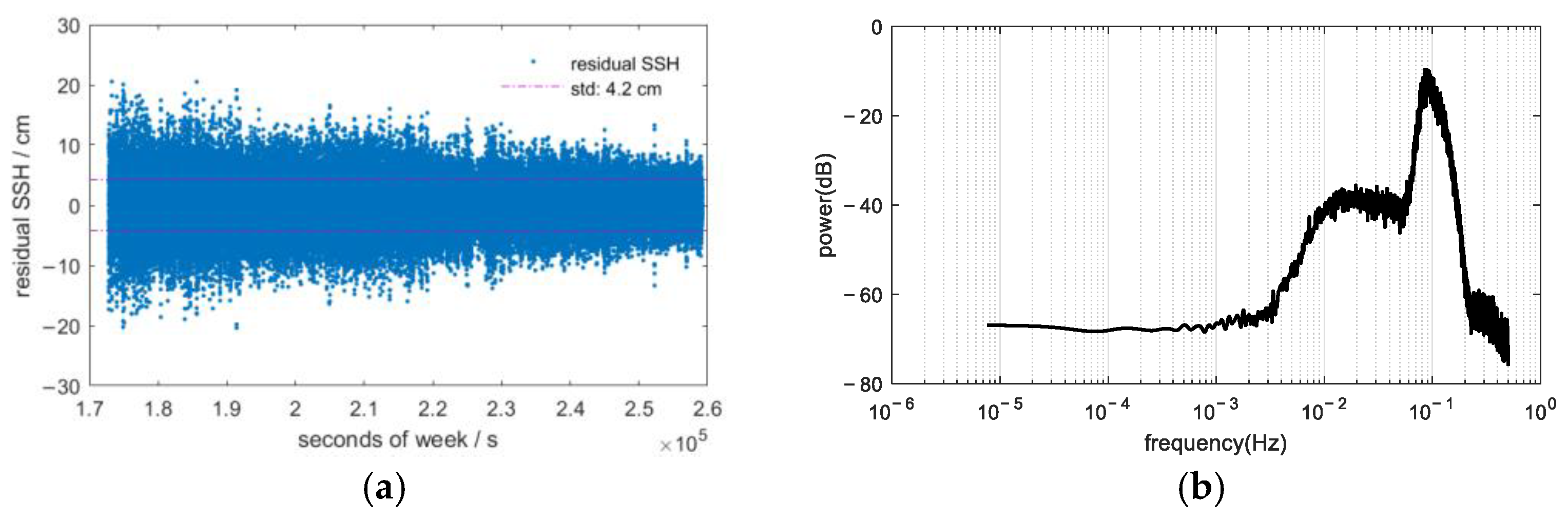


| Antenna Height (m) | Attitude Angle (deg) | Measured SSH Error (cm) |
|---|---|---|
| 10 m | 1 | 0.15 |
| 1.5 | 0.34 | |
| 2 | 0.69 | |
| 3 | 1.37 | |
| 4 | 2.44 | |
| 5 | 3.81 | |
| 6 | 5.49 | |
| 7 | 7.45 | |
| 8 | 9.73 |
| Error Budget (*) | Fixed | Variable |
|---|---|---|
| GNSS Buoy SSH (SSHBuoy) | ||
| 10 | 10 |
| — | 15 |
| 5 | — |
| — | 15 |
| — | 5 |
| (a) SSHBuoy Total: | 11 mm | 24 mm |
| Mooring depth (depthM) | ||
| — | 4 |
| — | 5 |
| — | 2 |
| — | 6 |
| (b) depthM Total: | 0 mm | 9 mm |
| Mooring datum (DatumM) | ||
| 11 | 24 |
| 0 | 9 |
| (c) DatumM Total: (***) | 11 mm | 3 mm |
| Mooring SSH (SSHM) | ||
| 0 | 9 |
| 11 | 3 |
| SSHM Total: | 11 mm | 9 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, B.; Sun, Z.; Huang, H.; Zhai, Z.; Liu, X.; Ma, J.; Huang, L.; Huang, Z.; Ouyang, M.; Zhang, M.; et al. Performance of Multi-Antenna GNSS Buoy and Co-Located Mooring Array Deployed Around Qianliyan Islet for Altimetry Satellite Calibration. Remote Sens. 2025, 17, 3436. https://doi.org/10.3390/rs17203436
Guan B, Sun Z, Huang H, Zhai Z, Liu X, Ma J, Huang L, Huang Z, Ouyang M, Zhang M, et al. Performance of Multi-Antenna GNSS Buoy and Co-Located Mooring Array Deployed Around Qianliyan Islet for Altimetry Satellite Calibration. Remote Sensing. 2025; 17(20):3436. https://doi.org/10.3390/rs17203436
Chicago/Turabian StyleGuan, Bin, Zhongmiao Sun, He Huang, Zhenhe Zhai, Xiaogang Liu, Jian Ma, Lingyong Huang, Zhiyong Huang, Mingda Ouyang, Mimi Zhang, and et al. 2025. "Performance of Multi-Antenna GNSS Buoy and Co-Located Mooring Array Deployed Around Qianliyan Islet for Altimetry Satellite Calibration" Remote Sensing 17, no. 20: 3436. https://doi.org/10.3390/rs17203436
APA StyleGuan, B., Sun, Z., Huang, H., Zhai, Z., Liu, X., Ma, J., Huang, L., Huang, Z., Ouyang, M., Zhang, M., Xu, X., & Yang, L. (2025). Performance of Multi-Antenna GNSS Buoy and Co-Located Mooring Array Deployed Around Qianliyan Islet for Altimetry Satellite Calibration. Remote Sensing, 17(20), 3436. https://doi.org/10.3390/rs17203436






