Spatial Sampling Uncertainty for MODIS Terra Land Surface Temperature Retrievals
Abstract
Highlights
- A spatial sampling uncertainty model is developed for coarsening 1 km MODIS Terra land surface temperature satellite products to resolutions of 0.05° or 0.1°.
- Sampling uncertainty for land surface temperature is dependent on both the underlying land cover and the solar zenith angle at the time of observation.
- The largest sampling uncertainties occur in regions of mixed land cover at 0.05° and for urban areas at 0.1° and the shape of the spatial sampling uncertainty curve with clear-sky fraction differs from previous parameterisations.
- The spatial sampling uncertainty parameterisations presented here can be applied to MODIS Terra LST products and LST products from other morning overpass satellites with similar noise characteristics and spatial resolution.
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite Data Extraction
2.2. Sampling Uncertainty Derivation
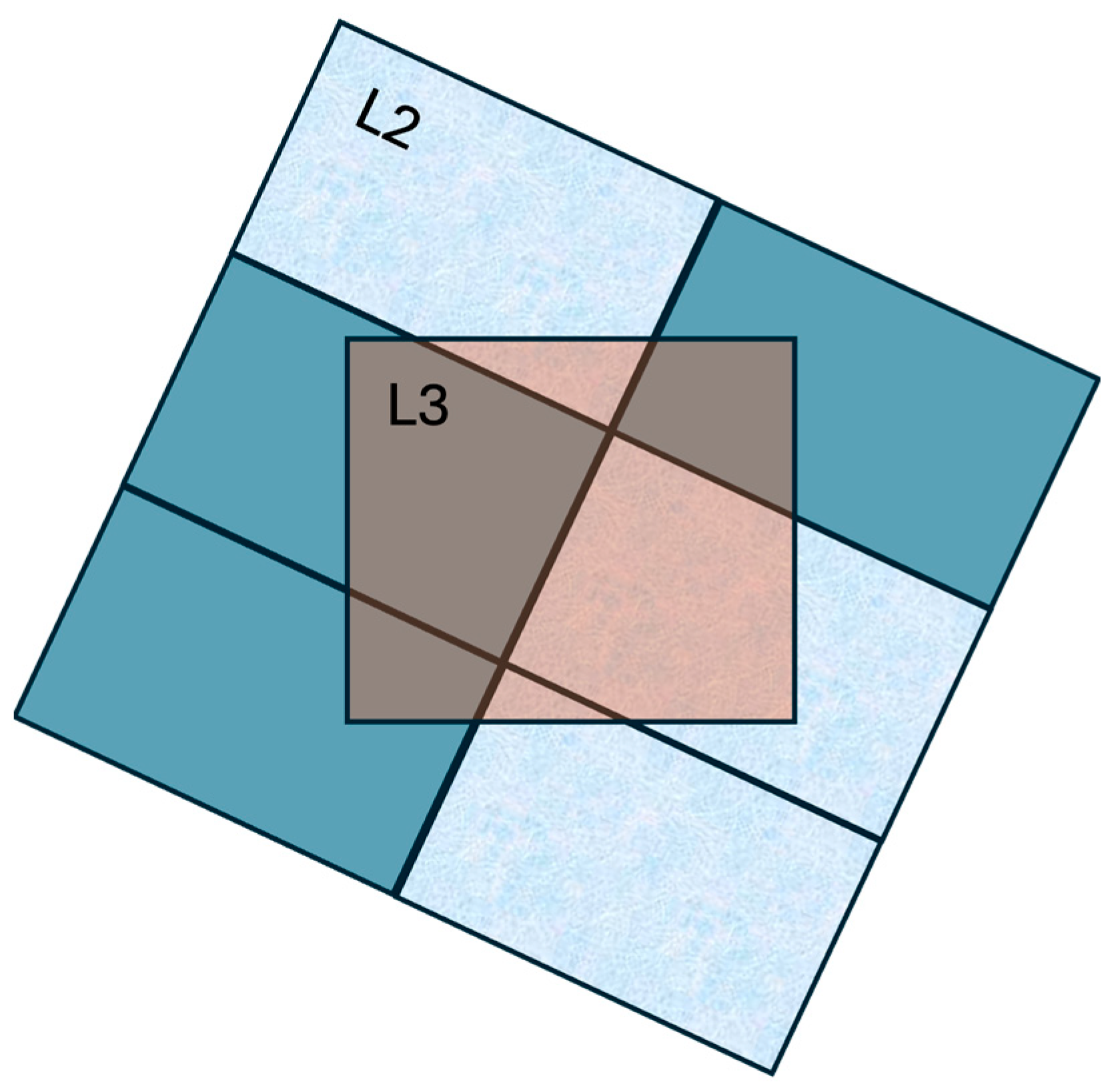
2.3. Subsampling Strategy
3. Results
3.1. Comparing the Sampling Uncertainty Model and Current Parameterisation in ESA LST CCI Products
3.2. Evaluating Other Dependencies of the Sampling Uncertainty Model
3.3. Variability Within Mixed Pixels
3.4. Sampling Uncertainty Modelling Strategy for LST Products at 0.05° and 0.1° Resolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AATSR | Advanced Along-Track Scanning Radiometer |
| ALB-2 | ATSR Land Biome Classification |
| ATSR | Along-Track Scanning Radiometer |
| CCI | Climate Change Initiative |
| CDR | Climate Data Record |
| ECV | Essential Climate Variable |
| ESA | European Space Agency |
| LST | Land Surface Temperature |
| L2 | Level 2 satellite product |
| L3 | Level 3 satellite product |
| L3U | Level 3 uncollated satellite product |
| MODIS | Moderate-Resolution Imaging Spectroradiometer |
| SST | Sea Surface Temperature |
| SU | Sampling uncertainty |
Appendix A
| Biome | a | b | c | d | e |
|---|---|---|---|---|---|
| Tree | 1.09 × 10−8 | −3.05 × 10−6 | 3.47 × 10−4 | −2.12 × 10−2 | 5.99 × 10−1 |
| Flood | 2.17 × 10−8 | −5.53 × 10−6 | 5.33 × 10−4 | −2.52 × 10−2 | 5.59 × 10−1 |
| Urban | 5.22 × 10−8 | −1.29 × 10−5 | 1.15 × 10−3 | −4.61 × 10−2 | 8.04 × 10−1 |
| Crop | 9.68 × 10−9 | −2.70 × 10−6 | 3.06 × 10−4 | −1.83 × 10−2 | 5.07 × 10−1 |
| Bare | 1.16 × 10−8 | −2.98 × 10−6 | 2.99 × 10−4 | −1.55 × 10−2 | 3.88 × 10−1 |
| Shrub | 2.02 × 10−8 | −5.42 × 10−6 | 5.82 × 10−4 | −3.28 × 10−2 | 8.75 × 10−1 |
| Ice | −9.71 × 10−9 | 2.21 × 10−6 | −1.48 × 10−4 | 6.17 × 10−4 | 1.72 × 10−1 |
| Mixed | 3.19 × 10−8 | −8.31 × 10−6 | 8.48 × 10−4 | −4.48 × 10−2 | 1.13 |
| Biome | a | b | c | d | e |
|---|---|---|---|---|---|
| Tree | 6.23 × 10−8 | −1.54 × 10−5 | 1.40 × 10−3 | −6.03 × 10−2 | 1.19 |
| Flood | 5.20 × 10−8 | −1.28 × 10−5 | 1.16 × 10−3 | −4.97 × 10−2 | 9.71 × 10−1 |
| Urban | 1.30 × 10−7 | −3.16 × 10−5 | 2.81 × 10−3 | −1.16 × 10−1 | 2.19 |
| Crop | 4.97 × 10−8 | −1.23 × 10−5 | 1.11 × 10−3 | −4.72 × 10−2 | 9.06 × 10−1 |
| Bare | 3.09 × 10−8 | −7.72 × 10−6 | 7.21 × 10−4 | −3.25 × 10−2 | 6.86 × 10−1 |
| Shrub | 7.95 × 10−8 | −1.96 × 10−5 | 1.78 × 10−3 | −7.68 × 10−2 | 1.52 |
| Ice | 1.93 × 10−8 | −4.90 × 10−6 | 4.81 × 10−4 | −2.40 × 10−2 | 5.71 × 10−1 |
| Mixed | 8.64 × 10−8 | −2.13 × 10−5 | 1.93 × 10−3 | −8.27 × 10−2 | 1.63 |
| Biome | Solar Zenith Angle | a | b | c | d | e |
|---|---|---|---|---|---|---|
| Tree | 0–10 | 5.53 × 10−8 | −1.43 × 10−5 | 1.42 × 10−3 | −7.15 × 10−2 | 1.72 |
| 10–20 | 8.45 × 10−8 | −2.16 × 10−5 | 2.07 × 10−3 | −9.60 × 10−2 | 2.07 | |
| 20–30 | 5.38 × 10−8 | −1.38 × 10−5 | 1.33 × 10−3 | −6.23 × 10−2 | 1.35 | |
| 30–40 | 3.93 × 10−8 | −1.02 × 10−5 | 1.02 × 10−3 | −5.08 × 10−2 | 1.18 | |
| 40–50 | 2.81 × 10−8 | −7.37 × 10−6 | 7.52 × 10−4 | −3.90 × 10−2 | 9.52 × 10−1 | |
| 50–60 | 1.43 × 10−7 | −3.47 × 10−5 | 2.97 × 10−3 | −1.09 × 10−1 | 1.57 | |
| 60–70 | 4.39 × 10−9 | −1.37 × 10−6 | 1.83 × 10−4 | −1.31 × 10−2 | 4.11 × 10−1 | |
| 70–80 | −3.94 × 10−9 | 7.58 × 10−7 | −1.70 × 10−5 | −4.42 × 10−3 | 2.45 × 10−1 | |
| 80–90 | −3.08 × 10−9 | 5.52 × 10−7 | 2.58 × 10−6 | −5.49 × 10−3 | 2.77 × 10−1 | |
| Night | 5.72 × 10−9 | −1.74 × 10−6 | 2.31 × 10−4 | −1.67 × 10−2 | 5.31 × 10−1 | |
| Flood | 0–10 | 5.36 × 10−8 | −1.38 × 10−5 | 1.38 × 10−3 | −7.09 × 10−2 | 1.75 |
| 10–20 | 1.10 × 10−7 | −2.81 × 10−5 | 2.70 × 10−3 | −1.26 × 10−1 | 2.74 | |
| 20–30 | 3.19 × 10−7 | −7.69 × 10−5 | 6.55 × 10−3 | −2.38 × 10−1 | 3.43 | |
| 30–40 | 3.13 × 10−8 | −8.22 × 10−6 | 8.27 × 10−4 | −4.11 × 10−2 | 9.47 × 10−1 | |
| 40–50 | 1.29 × 10−7 | −3.10 × 10−5 | 2.67 × 10−3 | −9.93 × 10−2 | 1.52 | |
| 50–60 | 8.55 × 10−10 | −4.89 × 10−7 | 1.02 × 10−4 | −9.56 × 10−3 | 3.39 × 10−1 | |
| 60–70 | −1.32 × 10−8 | 3.10 × 10−6 | −2.41 × 10−4 | 6.31 × 10−3 | −2.18 × 10−3 | |
| 70–80 | 6.08 × 10−8 | −1.45 × 10−5 | 1.21 × 10−3 | −4.18 × 10−2 | 5.27 × 10−1 | |
| 80–90 | −9.65 × 10−9 | 2.22 × 10−6 | −1.60 × 10−4 | 2.46 × 10−3 | 8.96 × 10−2 | |
| Night | 1.11 × 10−9 | −5.32 × 10−7 | 1.03 × 10−4 | −9.37 × 10−3 | 3.30 × 10−1 | |
| Urban | 0–10 | 5.70 × 10−8 | −1.49 × 10−5 | 1.48 × 10−3 | −7.21 × 10−2 | 1.62 |
| 10–20 | 1.33 × 10−7 | −3.37 × 10−5 | 3.14 × 10−3 | −1.36 × 10−1 | 2.59 | |
| 20–30 | 3.76 × 10−7 | −9.11 × 10−5 | 7.81 × 10−3 | −2.84 × 10−1 | 4.02 | |
| 30–40 | 6.61 × 10−8 | −1.70 × 10−5 | 1.63 × 10−3 | −7.32 × 10−2 | 1.45 | |
| 40–50 | 7.38 × 10−8 | −1.82 × 10−5 | 1.61 × 10−3 | −6.40 × 10−2 | 1.09 | |
| 50–60 | 6.30 × 10−8 | −1.53 × 10−5 | 1.32 × 10−3 | −4.92 × 10−2 | 7.38 × 10−1 | |
| 60–70 | −5.92 × 10−9 | 1.28 × 10−6 | −7.31 × 10−5 | −1.15 × 10−3 | 1.54 × 10−1 | |
| 70–80 | −3.92 × 10−9 | 7.96 × 10−7 | −3.25 × 10−5 | −2.46 × 10−3 | 1.65 × 10−1 | |
| 80–90 | 2.09 × 10−7 | −5.00 × 10−5 | 4.18 × 10−3 | −1.44 × 10−1 | 1.80 | |
| Night | 1.20 × 10−7 | −2.88 × 10−5 | 2.42 × 10−3 | −8.47 × 10−2 | 1.09 | |
| Crop | 0–10 | 7.50 × 10−8 | −1.90 × 10−5 | 1.84 × 10−3 | −8.89 × 10−2 | 2.06 |
| 10–20 | 7.65 × 10−8 | −1.96 × 10−5 | 1.89 × 10−3 | −8.93 × 10−2 | 1.96 | |
| 20–30 | 8.60 × 10−8 | −2.20 × 10−5 | 2.12 × 10−3 | −9.84 × 10−2 | 2.11 | |
| 30–40 | 3.96 × 10−8 | −1.04 × 10−5 | 1.04 × 10−3 | −5.13 × 10−2 | 1.18 | |
| 40–50 | 1.84 × 10−8 | −4.89 × 10−6 | 5.07 × 10−4 | −2.68 × 10−2 | 6.64 × 10−1 | |
| 50–60 | −2.29 × 10−10 | −1.87 × 10−7 | 6.61 × 10−5 | −7.19 × 10−3 | 2.66 × 10−1 | |
| 60–70 | −9.78 × 10−9 | 2.22 × 10−6 | −1.55 × 10−4 | 2.06 × 10−3 | 1.00 × 10−1 | |
| 70–80 | −1.26 × 10−8 | 2.94 × 10−6 | −2.21 × 10−4 | 4.83 × 10−3 | 4.99 × 10−2 | |
| 80–90 | −4.35 × 10−9 | 8.68 × 10−7 | −2.06 × 10−5 | −5.34 × 10−3 | 3.05 × 10−1 | |
| Night | −9.40 × 10−9 | 2.13 × 10−6 | −1.51 × 10−4 | 2.26 × 10−3 | 8.17 × 10−2 | |
| Bare | 0–10 | 1.24 × 10−9 | −5.54 × 10−7 | −9.96 × 10−5 | −8.61 × 10−3 | 2.94 × 10−1 |
| 10–20 | 3.31 × 10−8 | −8.72 × 10−6 | 8.85 × 10−4 | −4.52 × 10−2 | 1.08 | |
| 20–30 | 3.47 × 10−8 | −9.11 × 10−6 | 9.13 × 10−4 | −4.53 × 10−2 | 1.05 | |
| 30–40 | 9.67 × 10−9 | −2.73 × 10−6 | 3.20 × 10−4 | −2.03 × 10−2 | 5.90 × 10−1 | |
| 40–50 | 1.88 × 10−8 | −5.04 × 10−6 | 5.35 × 10−4 | −2.95 × 10−2 | 7.64 × 10−1 | |
| 50–60 | 1.11 × 10−8 | −3.06 × 10−6 | 3.46 × 10−4 | −2.11 × 10−2 | 6.00 × 10−1 | |
| 60–70 | 3.32 × 10−8 | −8.67 × 10−6 | 8.81 × 10−4 | −4.58 × 10−2 | 1.13 | |
| 70–80 | 2.65 × 10−8 | −6.95 × 10−6 | 7.16 × 10−4 | −3.82 × 10−2 | 9.69 × 10−1 | |
| 80–90 | 1.09 × 10−8 | −2.99 × 10−6 | 3.43 × 10−4 | −2.16 × 10−2 | 6.38 × 10−1 | |
| Night | −6.07 × 10−9 | 1.28 × 10−6 | −6.16 × 10−5 | −2.81 × 10−3 | 2.23 × 10−1 | |
| Shrub | 0–10 | 7.86 × 10−8 | −2.03 × 10−5 | 2.01 × 10−3 | −9.89 × 10−2 | 2.29 |
| 10–20 | 7.82 × 10−8 | −2.01 × 10−5 | 1.94 × 10−3 | −9.14 × 10−2 | 1.99 | |
| 20–30 | 7.20 × 10−8 | −1.86 × 10−5 | 1.81 × 10−3 | −8.67 × 10−2 | 1.93 | |
| 30–40 | 4.07 × 10−8 | −1.07 × 10−5 | 1.09 × 10−3 | −5.54 × 10−2 | 1.31 | |
| 40–50 | 2.76 × 10−8 | −7.28 × 10−6 | 7.55 × 10−4 | −4.08 × 10−2 | 1.05 | |
| 50–60 | 4.30 × 10−8 | −1.11 × 10−5 | 1.11 × 10−3 | −5.60 × 10−2 | 1.35 | |
| 60–70 | 2.50 × 10−8 | −6.64 × 10−6 | 7.15 × 10−4 | −4.18 × 10−2 | 1.17 | |
| 70–80 | 1.01 × 10−8 | −2.84 × 10−6 | 3.44 × 10−4 | −2.34 × 10−2 | 7.30 × 10−1 | |
| 80–90 | 3.18 × 10−9 | −1.05 × 10−6 | 1.65 × 10−4 | −1.42 × 10−2 | 5.07 × 10−1 | |
| Night | 2.98 × 10−9 | −1.16 × 10−6 | 1.89 × 10−4 | −1.53 × 10−2 | 5.04 × 10−1 | |
| Ice | 0–10 | 7.86 × 10−8 | −2.03 × 10−5 | 2.01 × 10−3 | −9.89 × 10−2 | 2.29 |
| 10–20 | 7.82 × 10−8 | −2.01 × 10−5 | 1.94 × 10−3 | −9.14 × 10−2 | 1.99 | |
| 20–30 | 7.20 × 10−8 | −1.86 × 10−5 | 1.81 × 10−3 | −8.67 × 10−2 | 1.93 | |
| 30–40 | 4.07 × 10−8 | −1.07 × 10−5 | 1.09 × 10−3 | −5.54 × 10−2 | 1.31 | |
| 40–50 | 2.76 × 10−8 | −7.28 × 10−6 | 7.55 × 10−4 | −4.08 × 10−2 | 1.05 | |
| 50–60 | 4.30 × 10−8 | −1.11 × 10−5 | 1.11 × 10−3 | −5.60 × 10−2 | 1.35 | |
| 60–70 | 2.50 × 10−8 | −6.64 × 10−6 | 7.15 × 10−4 | −4.18 × 10−2 | 1.17 | |
| 70–80 | 1.01 × 10−8 | −2.84 × 10−6 | 3.44 × 10−4 | −2.34 × 10−2 | 7.30 × 10−1 | |
| 80–90 | 3.18 × 10−9 | −1.05 × 10−6 | 1.65 × 10−4 | −1.42 × 10−2 | 5.07 × 10−1 | |
| Night | 2.98 × 10−9 | −1.16 × 10−6 | 1.89 × 10−4 | −1.53 × 10−2 | 5.04 × 10−1 | |
| Mixed | 0–10 | 7.86 × 10−8 | −2.03 × 10−5 | 2.01 × 10−3 | −9.89 × 10−2 | 2.29 |
| 10–20 | 7.82 × 10−8 | −2.01 × 10−5 | 1.94 × 10−3 | −9.14 × 10−2 | 1.99 | |
| 20–30 | 7.20 × 10−8 | −1.86 × 10−5 | 1.81 × 10−3 | −8.67 × 10−2 | 1.93 | |
| 30–40 | 4.07 × 10−8 | −1.07 × 10−5 | 1.09 × 10−3 | −5.54 × 10−2 | 1.31 | |
| 40–50 | 2.76 × 10−8 | −7.28 × 10−6 | 7.55 × 10−4 | −4.08 × 10−2 | 1.05 | |
| 50–60 | 4.30 × 10−8 | −1.11 × 10−5 | 1.11 × 10−3 | −5.60 × 10−2 | 1.35 | |
| 60–70 | 2.50 × 10−8 | −6.64 × 10−6 | 7.15 × 10−4 | −4.18 × 10−2 | 1.17 | |
| 70–80 | 1.01 × 10−8 | −2.84 × 10−6 | 3.44 × 10−4 | −2.34 × 10−2 | 7.30 × 10−1 | |
| 80–90 | 3.18 × 10−9 | −1.05 × 10−6 | 1.65 × 10−4 | −1.42 × 10−2 | 5.07 × 10−1 | |
| Night | 2.98 × 10−9 | −1.16 × 10−6 | 1.89 × 10−4 | −1.53 × 10−2 | 5.04 × 10−1 |
| Biome | Solar Zenith Angle | a | b | c | d | e |
|---|---|---|---|---|---|---|
| Tree | 0–10 | 2.15 × 10−7 | −5.29 × 10−5 | 4.81 × 10−3 | −2.08 × 10−1 | 4.20 |
| 10–20 | 1.95 × 10−7 | −4.76 × 10−5 | 4.25 × 10−3 | −1.75 × 10−1 | 3.26 | |
| 20–30 | 1.56 × 10−7 | −3.82 × 10−5 | 3.42 × 10−3 | −1.41 × 10−1 | 2.60 | |
| 30–40 | 1.42 × 10−7 | −3.48 × 10−5 | 3.11 × 10−3 | −1.28 × 10−1 | 2.37 | |
| 40–50 | 9.17 × 10−8 | −2.26 × 10−5 | 2.04 × 10−3 | −8.67 × 10−2 | 1.67 | |
| 50–60 | 6.90 × 10−8 | −1.70 × 10−5 | 1.54 × 10−3 | −6.54 × 10−2 | 1.27 | |
| 60–70 | 2.46 × 10−8 | −6.18 × 10−6 | 5.82 × 10−4 | −2.66 × 10−2 | 5.69 × 10−1 | |
| 70–80 | 2.46 × 10−8 | −6.18 × 10−6 | 5.83 × 10−4 | −2.66 × 10−2 | 5.63 × 10−1 | |
| 80–90 | 2.57 × 10−8 | −6.48 × 10−6 | 6.16 × 10−4 | −2.86 × 10−2 | 6.19 × 10−1 | |
| Night | 5.28 × 10−8 | −1.31 × 10−5 | 1.20 × 10−3 | −5.23 × 10−2 | 1.05 | |
| Flood | 0–10 | 1.38 × 10−7 | −3.43 × 10−5 | 3.13 × 10−3 | −1.34 × 10−1 | 2.61 |
| 10–20 | 1.95 × 10−7 | −4.73 × 10−5 | 4.16 × 10−3 | −1.67 × 10−1 | 2.96 | |
| 20–30 | 1.88 × 10−7 | −4.58 × 10−5 | 4.03 × 10−3 | −1.60 × 10−1 | 2.80 | |
| 30–40 | 1.12 × 10−7 | −2.73 × 10−5 | 2.43 × 10−3 | −1.00 × 10−1 | 1.84 | |
| 40–50 | 7.42 × 10−8 | −1.81 × 10−5 | 1.61 × 10−3 | −6.60 × 10−2 | 1.20 | |
| 50–60 | 4.82 × 10−8 | −1.19 × 10−5 | 1.09 × 10−3 | −4.78 × 10−2 | 9.71 × 10−1 | |
| 60–70 | 4.64 × 10−8 | −1.14 × 10−5 | 1.04 × 10−3 | −4.56 × 10−2 | 9.34 × 10−1 | |
| 70–80 | 1.04 × 10−8 | −2.74 × 10−6 | 2.80 × 10−4 | −1.44 × 10−2 | 3.48 × 10−1 | |
| 80–90 | 2.21 × 10−8 | −5.55 × 10−6 | 5.27 × 10−4 | −2.45 × 10−2 | 5.33 × 10−1 | |
| Night | 3.19 × 10−8 | −7.96 × 10−6 | 7.44 × 10−4 | −3.34 × 10−2 | 6.98 × 10−1 | |
| Urban | 0–10 | 4.36 × 10−7 | −1.06 × 10−4 | 9.57 × 10−3 | −4.10 × 10−1 | 8.23 |
| 10–20 | 3.32 × 10−7 | −8.12 × 10−5 | 7.32 × 10−3 | −3.14 × 10−1 | 6.30 | |
| 20–30 | 3.06 × 10−7 | −7.50 × 10−5 | 6.77 × 10−3 | −2.87 × 10−1 | 5.56 | |
| 30–40 | 2.66 × 10−7 | −6.46 × 10−5 | 5.71 × 10−3 | −2.33 × 10−1 | 4.29 | |
| 40–50 | 1.66 × 10−7 | −4.05 × 10−5 | 3.64 × 10−3 | −1.55 × 10−1 | 3.04 | |
| 50–60 | 2.81 × 10−7 | −6.78 × 10−5 | 5.92 × 10−3 | −2.35 × 10−1 | 4.17 | |
| 60–70 | 1.99 × 10−7 | −4.90 × 10−5 | 4.47 × 10−3 | −1.94 × 10−1 | 3.87 | |
| 70–80 | 6.51 × 10−9 | −1.78 × 10−6 | 1.88 × 10−4 | −9.90 × 10−3 | 2.37 × 10−1 | |
| 80–90 | 7.53 × 10−9 | −2.06 × 10−6 | 2.30 × 10−4 | −1.36 × 10−2 | 3.78 × 10−1 | |
| Night | 4.86 × 10−8 | −1.21 × 10−5 | 1.11 × 10−3 | −4.89 × 10−2 | 9.92 × 10−1 | |
| Crop | 0–10 | 1.57 × 10−7 | −3.84 × 10−5 | 3.47 × 10−3 | −1.47 × 10−1 | 2.87 |
| 10–20 | 1.97 × 10−7 | −4.80 × 10−5 | 4.25 × 10−3 | −1.72 × 10−1 | 3.11 | |
| 20–30 | 1.74 × 10−7 | −4.23 × 10−5 | 3.73 × 10−3 | −1.49 × 10−1 | 2.63 | |
| 30–40 | 1.12 × 10−7 | −2.74 × 10−5 | 2.44 × 10−3 | −9.94 × 10−2 | 1.79 | |
| 40–50 | 7.98 × 10−8 | −1.95 × 10−5 | 1.75 × 10−3 | −7.22 × 10−2 | 1.34 | |
| 50–60 | 2.63 × 10−8 | −6.56 × 10−6 | 6.08 × 10−4 | −2.67 × 10−2 | 5.36 × 10−1 | |
| 60–70 | 1.12 × 10−8 | −2.92 × 10−6 | 2.92 × 10−4 | −1.45 × 10−2 | 3.36 × 10−1 | |
| 70–80 | 4.24 × 10−9 | −1.23 × 10−6 | 1.43 × 10−4 | −8.54 × 10−3 | 2.30 × 10−1 | |
| 80–90 | 1.88 × 10−8 | −4.74 × 10−6 | 4.52 × 10−4 | −2.12 × 10−2 | 4.68 × 10−1 | |
| Night | 1.84 × 10−8 | −4.67 × 10−6 | 4.45 × 10−4 | −2.04 × 10−2 | 4.33 × 10−1 | |
| Bare | 0–10 | 2.01 × 10−8 | −5.10 × 10−6 | 4.91 × 10−4 | −2.34 × 10−2 | 5.28 × 10−1 |
| 10–20 | 1.22 × 10−7 | −3.01 × 10−5 | 2.73 × 10−3 | −1.17 × 10−1 | 2.29 | |
| 20–30 | 1.12 × 10−7 | −2.76 × 10−5 | 2.49 × 10−3 | −1.05 × 10−1 | 1.99 | |
| 30–40 | 5.08 × 10−8 | −1.26 × 10−5 | 1.17 × 10−3 | −5.20 × 10−2 | 1.08 | |
| 40–50 | 9.28 × 10−8 | −2.27 × 10−5 | 2.05 × 10−3 | −8.64 × 10−2 | 1.67 | |
| 50–60 | 6.75 × 10−8 | −1.66 × 10−5 | 1.50 × 10−3 | −6.39 × 10−2 | 1.25 | |
| 60–70 | 9.55 × 10−8 | −2.34 × 10−5 | 2.10 × 10−3 | −8.89 × 10−2 | 1.72 | |
| 70–80 | 1.01 × 10−7 | −2.48 × 10−5 | 2.24 × 10−3 | −9.52 × 10−2 | 1.86 | |
| 80–90 | 6.75 × 10−8 | −1.67 × 10−5 | 1.54 × 10−3 | −6.80 × 10−2 | 1.38 | |
| Night | 2.20 × 10−8 | −5.58 × 10−6 | 5.35 × 10−4 | −2.52 × 10−2 | 5.58 × 10−1 | |
| Shrub | 0–10 | 1.64 × 10−7 | −4.03 × 10−5 | 3.66 × 10−3 | −1.56 × 10−1 | 3.07 |
| 10–20 | 1.73 × 10−7 | −4.26 × 10−5 | 3.83 × 10−3 | −1.60 × 10−1 | 3.04 | |
| 20–30 | 1.91 × 10−7 | −4.67 × 10−5 | 4.18 × 10−3 | −1.74 × 10−1 | 3.25 | |
| 30–40 | 1.35 × 10−7 | −3.29 × 10−5 | 2.93 × 10−3 | −1.19 × 10−1 | 2.17 | |
| 40–50 | 1.16 × 10−7 | −2.85 × 10−5 | 2.55 × 10−3 | −1.05 × 10−1 | 1.95 | |
| 50–60 | 1.43 × 10−7 | −3.51 × 10−5 | 3.15 × 10−3 | −1.32 × 10−1 | 2.51 | |
| 60–70 | 1.05 × 10−7 | −2.58 × 10−5 | 2.33 × 10−3 | −9.83 × 10−2 | 1.89 | |
| 70–80 | 7.36 × 10−8 | −1.81 × 10−5 | 1.65 × 10−3 | −7.17 × 10−2 | 1.44 | |
| 80–90 | 5.70 × 10−8 | −1.40 × 10−5 | 1.28 × 10−3 | −5.60 × 10−2 | 1.14 | |
| Night | 4.70 × 10−8 | −1.16 × 10−5 | 1.07 × 10−3 | −4.76 × 10−2 | 9.84 × 10−1 | |
| Ice | 0–10 | - | - | - | - | - |
| 10–20 | 1.86 × 10−6 | −4.55 × 10−4 | 4.07 × 10−2 | −1.68 | 3.09 × 101 | |
| 20–30 | 1.99 × 10−6 | −4.87 × 10−4 | 4.40 × 10−2 | −1.87 | 3.68 × 101 | |
| 30–40 | 8.95 × 10−7 | −2.19 × 10−4 | 1.96 × 10−2 | −8.16 × 10−1 | 1.53 × 101 | |
| 40–50 | 4.52 × 10−7 | −1.11 × 10−4 | 1.00 × 10−2 | −4.20 × 10−1 | 7.92 | |
| 50–60 | 2.55 × 10−8 | −6.39 × 10−6 | 6.00 × 10−4 | −2.72 × 10−2 | 5.73 × 10−1 | |
| 60–70 | 2.43 × 10−8 | −6.18 × 10−6 | 6.02 × 10−4 | −2.95 × 10−2 | 6.87 × 10−1 | |
| 70–80 | 1.85 × 10−8 | −4.70 × 10−6 | 4.57 × 10−4 | −2.23 × 10−2 | 5.14 × 10−1 | |
| 80–90 | 3.09 × 10−8 | −7.69 × 10−6 | 7.23 × 10−4 | −3.34 × 10−2 | 7.31 × 10−1 | |
| Night | 3.19 × 10−8 | −7.97 × 10−6 | 7.51 × 10−4 | −3.46 × 10−2 | 7.52 × 10−1 | |
| Mixed | 0–10 | 1.42 × 10−7 | −3.48 × 10−5 | 3.13 × 10−3 | −1.32 × 10−1 | 2.55 |
| 10–20 | 1.83 × 10−7 | −4.46 × 10−5 | 3.98 × 10−3 | −1.65 × 10−1 | 3.08 | |
| 20–30 | 2.18 × 10−7 | −5.31 × 10−5 | 4.71 × 10−3 | −1.91 × 10−1 | 3.45 | |
| 30–40 | 1.54 × 10−7 | −3.77 × 10−5 | 3.37 × 10−3 | −1.39 × 10−1 | 2.57 | |
| 40–50 | 1.08 × 10−7 | −2.65 × 10−5 | 2.38 × 10−3 | −9.87 × 10−2 | 1.84 | |
| 50–60 | 1.08 × 10−7 | −2.65 × 10−5 | 2.38 × 10−3 | −1.00 × 10−1 | 1.94 | |
| 60–70 | 1.44 × 10−7 | −3.50 × 10−5 | 3.09 × 10−3 | −1.26 × 10−1 | 2.29 | |
| 70–80 | 8.64 × 10−8 | −2.13 × 10−5 | 1.93 × 10−3 | −8.31 × 10−2 | 1.65 | |
| 80–90 | 7.97 × 10−8 | −1.95 × 10−5 | 1.75 × 10−3 | −7.43 × 10−2 | 1.45 | |
| Night | 4.60 × 10−8 | −1.14 × 10−5 | 1.06 × 10−3 | −4.67 × 10−2 | 9.56 × 10−1 |
References
- Global Climate Observing System. The 2022 GCOS Implementation Plan; WMO: Geneva, Switzerland, 2022; p. 98. [Google Scholar]
- Embury, O.; Merchant, C.J.; Good, S.A.; Rayner, N.A.; Høyer, J.L.; Atkinson, C.; Block, T.; Alerskans, E.; Pearson, K.J.; Worsfold, M.; et al. Satellite-Based Time-Series of Sea-Surface Temperature since 1980 for Climate Applications. Sci. Data 2024, 11, 326. [Google Scholar] [CrossRef]
- Ghent, D.J.; Corlett, G.K.; Göttsche, F.-M.; Remedios, J.J. Global Land Surface Temperature from the Along-Track Scanning Radiometers. J. Geophys. Res. Atmos. 2017, 122, 12167–12193. [Google Scholar] [CrossRef]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data Records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
- Popp, T.; De Leeuw, G.; Bingen, C.; Brühl, C.; Capelle, V.; Chedin, A.; Clarisse, L.; Dubovik, O.; Grainger, R.; Griesfeller, J.; et al. Development, Production and Evaluation of Aerosol Climate Data Records from European Satellite Observations (Aerosol_cci). Remote Sens. 2016, 8, 421. [Google Scholar] [CrossRef]
- Devasthale, A.; Karlsson, K.-G. Decadal Stability and Trends in the Global Cloud Amount and Cloud Top Temperature in the Satellite-Based Climate Data Records. Remote Sens. 2023, 15, 3819. [Google Scholar] [CrossRef]
- Ablain, M.; Legeais, J.F.; Prandi, P.; Marcos, M.; Fenoglio-Marc, L.; Dieng, H.B.; Benveniste, J.; Cazenave, A. Satellite Altimetry-Based Sea Level at Global and Regional Scales. In Integrative Study of the Mean Sea Level and Its Components; Cazenave, A., Champollion, N., Paul, F., Benveniste, J., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 9–33. ISBN 978-3-319-56490-6. [Google Scholar]
- Zhang, Y.; Pan, M.; Sheffield, J.; Siemann, A.L.; Fisher, C.K.; Liang, M.; Beck, H.E.; Wanders, N.; MacCracken, R.F.; Houser, P.R.; et al. A Climate Data Record (CDR) for the Global Terrestrial Water Budget: 1984–2010. Hydrol. Earth Syst. Sci. 2018, 22, 241–263. [Google Scholar] [CrossRef]
- Preimesberger, W.; Scanlon, T.; Su, C.-H.; Gruber, A.; Dorigo, W. Homogenization of Structural Breaks in the Global ESA CCI Soil Moisture Multisatellite Climate Data Record. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2845–2862. [Google Scholar] [CrossRef]
- Merchant, C.J.; Paul, F.; Popp, T.; Ablain, M.; Bontemps, S.; Defourny, P.; Hollmann, R.; Lavergne, T.; Laeng, A.; de Leeuw, G.; et al. Uncertainty Information in Climate Data Records from Earth Observation. Earth Syst. Sci. Data 2017, 9, 511–527. [Google Scholar] [CrossRef]
- Woolliams, E.R.; Mittaz, J.P.; Merchant, C.J.; Hunt, S.E.; Harris, P.M. Applying Metrological Techniques to Satellite Fundamental Climate Data Records. J. Phys. Conf. Ser. 2018, 972, 012003. [Google Scholar] [CrossRef]
- Mittaz, J.; Merchant, C.J.; Woolliams, E.R. Applying Principles of Metrology to Historical Earth Observations from Satellites. Metrologia 2019, 56, 032002. [Google Scholar] [CrossRef]
- Merchant, C.; Holl, G.; Mittaz, J.; Woolliams, E. Radiance Uncertainty Characterisation to Facilitate Climate Data Record Creation. Remote Sens. 2019, 11, 474. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Embury, O.; Corlett, G.; Merchant, C.J. Independent Uncertainty Estimates for Coefficient Based Sea Surface Temperature Retrieval from the Along-Track Scanning Radiometer Instruments. Remote Sens. Environ. 2016, 178, 213–222. [Google Scholar] [CrossRef]
- Ablain, M.; Meyssignac, B.; Zawadzki, L.; Jugier, R.; Ribes, A.; Spada, G.; Benveniste, J.; Cazenave, A.; Picot, N. Uncertainty in Satellite Estimates of Global Mean Sea-Level Changes, Trend and Acceleration. Earth Syst. Sci. Data 2019, 11, 1189–1202. [Google Scholar] [CrossRef]
- Ghent, D.; Veal, K.; Trent, T.; Dodd, E.; Sembhi, H.; Remedios, J. A New Approach to Defining Uncertainties for MODIS Land Surface Temperature. Remote Sens. 2019, 11, 1021. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Embury, O.; Merchant, C.J. Sampling Uncertainty in Gridded Sea Surface Temperature Products and Advanced Very High Resolution Radiometer (AVHRR) Global Area Coverage (GAC) Data. Remote Sens. Environ. 2016, 177, 287–294. [Google Scholar] [CrossRef]
- Glissenaar, I.; Boersma, K.F.; Anglou, I.; Rijsdijk, P.; Verhoelst, T.; Compernolle, S.; Pinardi, G.; Lambert, J.-C.; Van Roozendael, M.; Eskes, H. TROPOMI Level 3 Tropospheric NO2 Dataset with Advanced Uncertainty Analysis from the ESA CCI+ ECV Precursor Project. Earth Syst. Sci. Data 2025, 17, 4627–4650. [Google Scholar] [CrossRef]
- Merchant, C.J.; Harris, A.R.; Maturi, E.; Maccallum, S. Probabilistic Physically Based Cloud Screening of Satellite Infrared Imagery for Operational Sea Surface Temperature Retrieval. Q. J. R. Meteorol. Soc. 2005, 131, 2735–2755. [Google Scholar] [CrossRef]
- Aldred, F.; Good, E.; Bulgin, C.; Rayner, N. User Requirements Document. 2023. Available online: https://admin.climate.esa.int/documents/2199/LST-CCI-D1.1-URD_-_i3r0_-_User_Requirement_Document.pdf (accessed on 1 August 2025).
- Bontemps, S.; Boettcher, M.; Brockmann, C.; Kirches, G.; Lamarche, C.; Radoux, J.; Santoro, M.; Vanbogaert, E.; Wegmüller, U.; Herold, M.; et al. Multi-Year Global Land Cover Mapping at 300 m and Characterization for Climate Modelling: Achievements of the Land Cover Component of the ESA Climate Change Initiative. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7-W3, 323–328. [Google Scholar] [CrossRef]
- Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lanarche, C.; Schlerf, M.; Santoro, M. Land Cover CCI Product User Guide Version 2. 2014. Available online: https://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 7 October 2025).
- Bulgin, C.E.; Embury, O.; Maidment, R.I.; Merchant, C.J. Bayesian Cloud Detection over Land for Climate Data Records. Remote Sens. 2022, 14, 2231. [Google Scholar] [CrossRef]
- Chi, Y.; Zhao, C.; Yang, Y.; Zhao, X.; Yang, J. Global Characteristics of Cloud Macro-Physical Properties from Active Satellite Remote Sensing. Atmos. Res. 2024, 302, 107316. [Google Scholar] [CrossRef]
- Liu, Y.; Ackerman, S.A.; Maddux, B.C.; Key, J.R.; Frey, R.A. Errors in Cloud Detection over the Arctic Using a Satellite Imager and Implications for Observing Feedback Mechanisms. J. Clim. 2010, 23, 1894–1907. [Google Scholar] [CrossRef]
- Hall, D.K.; Key, J.R.; Casey, K.A.; Riggs, G.A.; Cavalieri, D.J. Sea Ice Surface Temperature Product from MODIS. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1076–1087. [Google Scholar] [CrossRef]
- Bulgin, C.E.; Sembhi, H.; Ghent, D.; Remedios, J.J.; Merchant, C.J. Cloud-Clearing Techniques over Land for Land-Surface Temperature Retrieval from the Advanced Along-Track Scanning Radiometer. Int. J. Remote Sens. 2014, 35, 3594–3615. [Google Scholar] [CrossRef]
- Bulgin, C.; Ermida, S.; Jimenez, C.; Veal, K. End-To-End ECV Uncertainty Budget. 2023. Available online: https://admin.climate.esa.int/media/documents/LST-CCI-D2.3-E3UB_-_i3r0_-_End-to-End_ECV_Uncertainty_Budget.pdf (accessed on 1 August 2025).
- LST CCI. Re-Gridding and Sub-Setting User Manual. 2023. Available online: https://climate.esa.int/en/projects/land-surface-temperature/tool/ (accessed on 1 August 2025).
- Minnett, P.J.; Alvera-Azcárate, A.; Chin, T.M.; Corlett, G.K.; Gentemann, C.L.; Karagali, I.; Li, X.; Marsouin, A.; Marullo, S.; Maturi, E.; et al. Half a Century of Satellite Remote Sensing of Sea-Surface Temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]

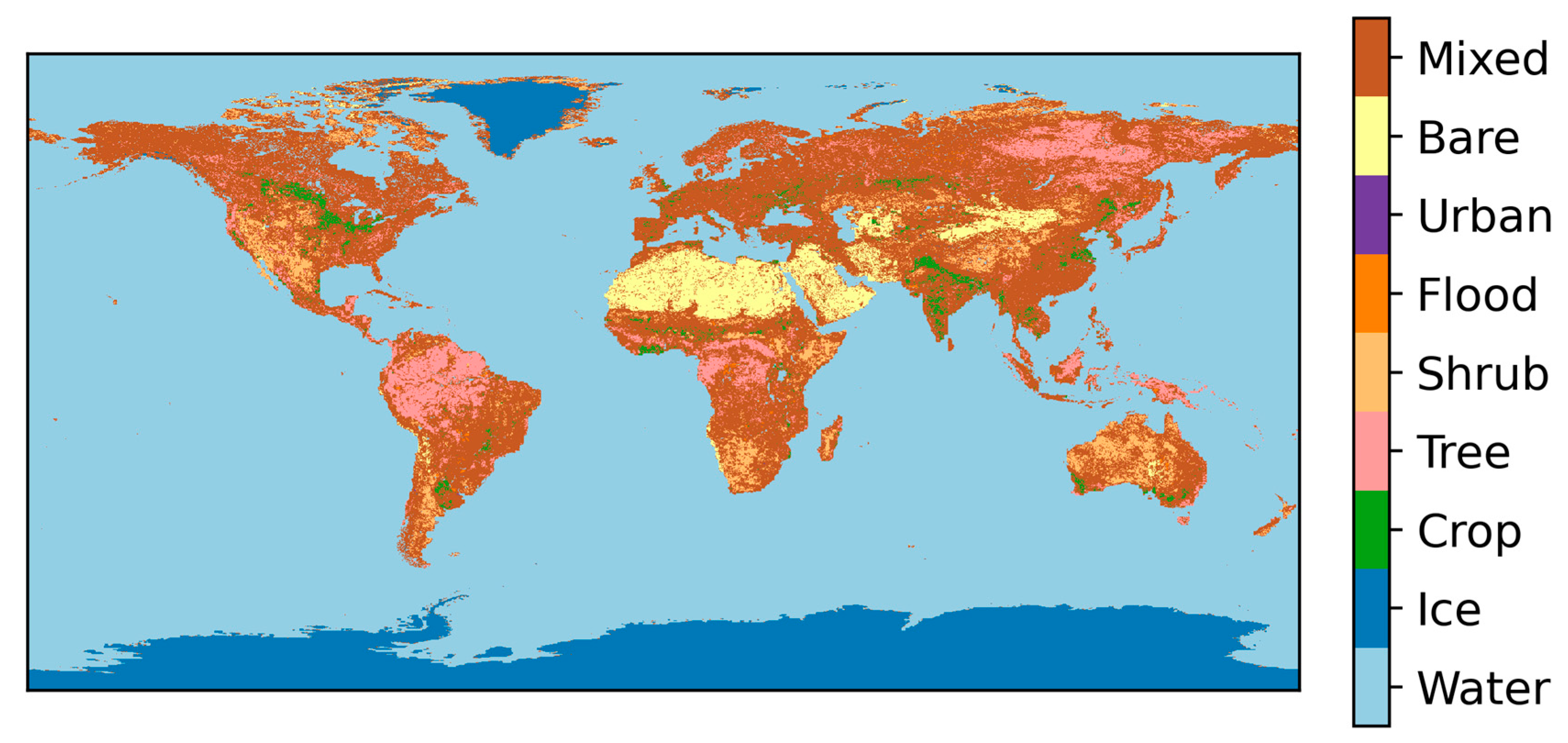

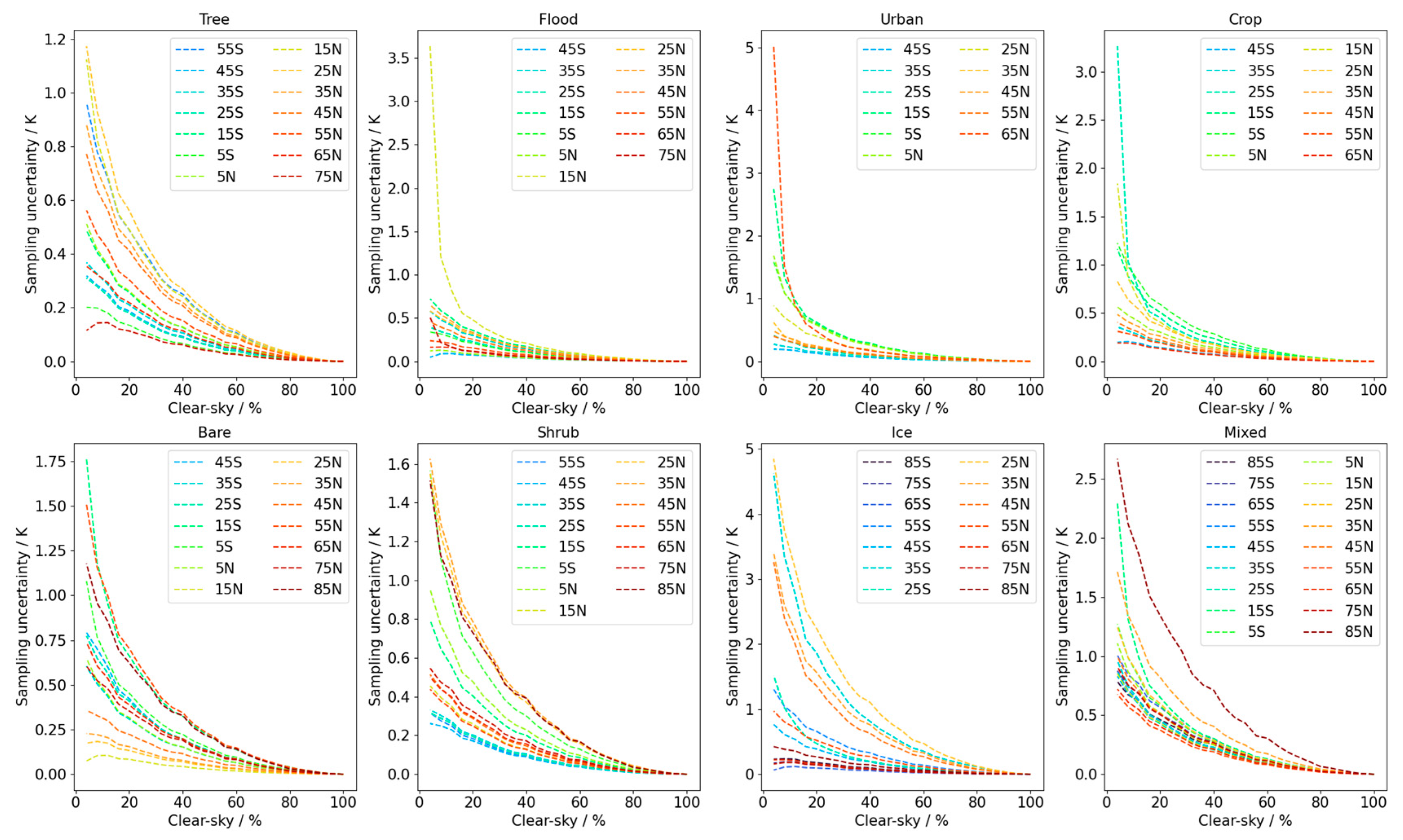
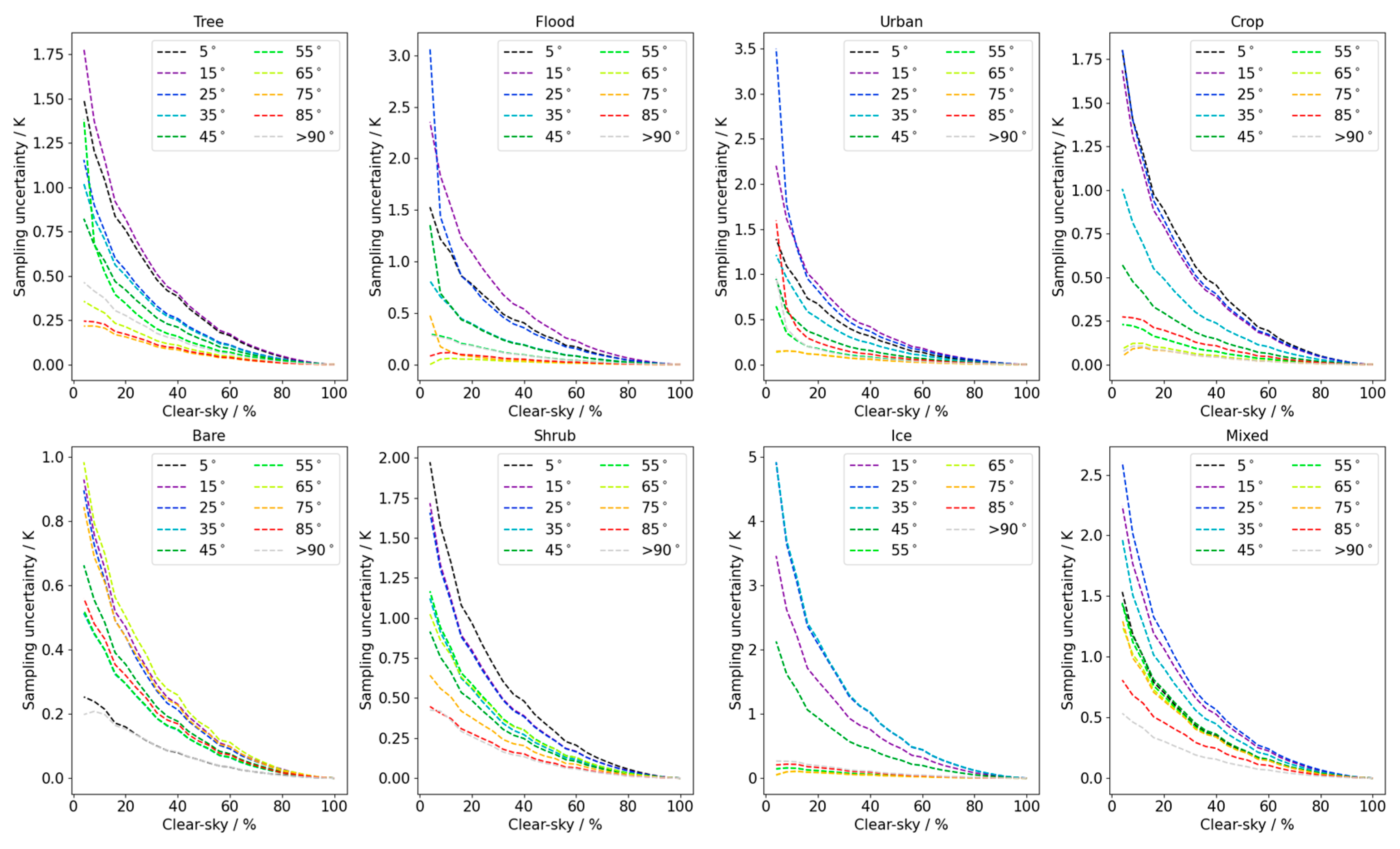
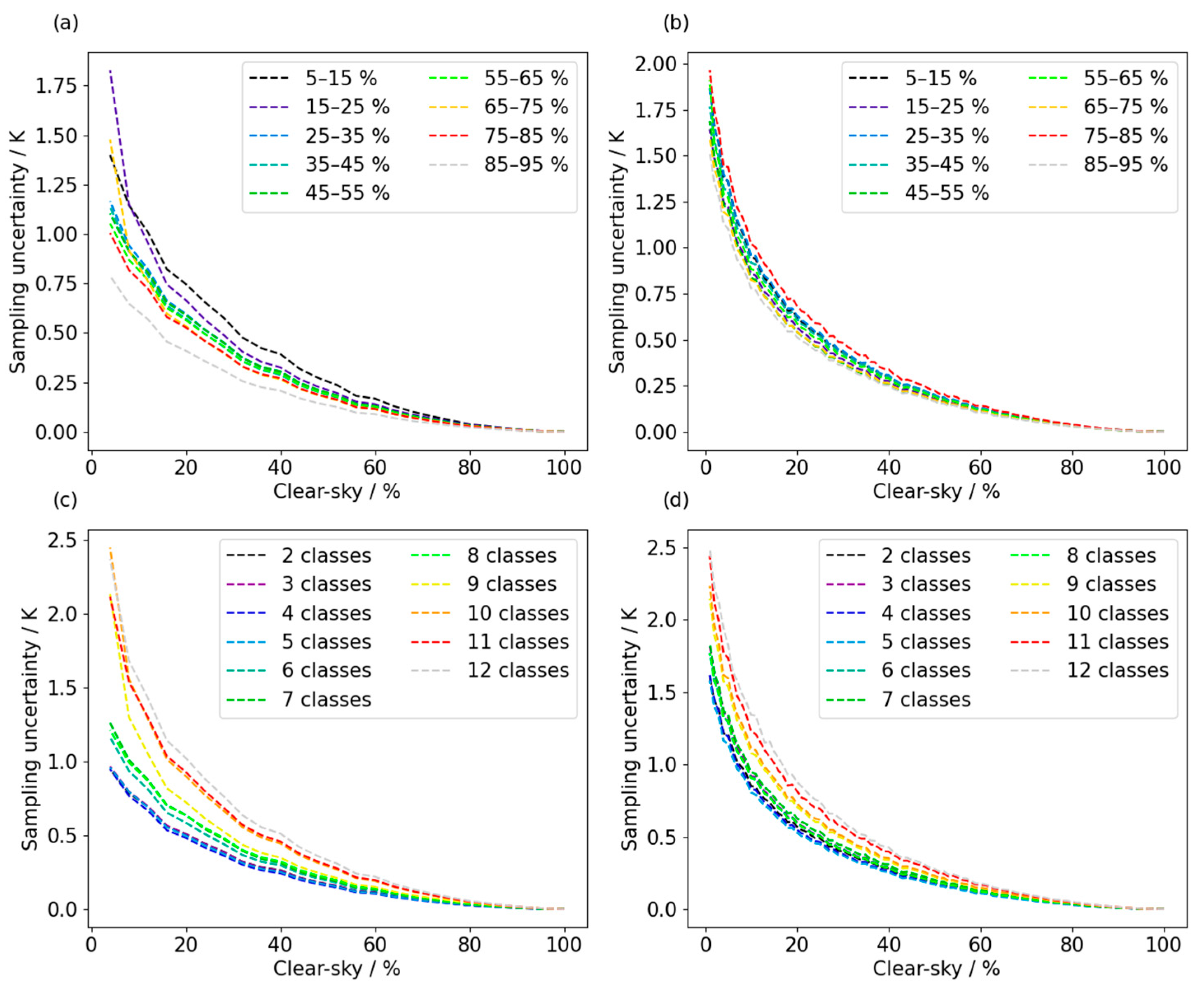
| Biome | 0.05° Target Resolution | 0.1° Target Resolution |
|---|---|---|
| Ice | 28,349 | 61,405 |
| Crop | 4031 | 7460 |
| Tree | 11,287 | 20,489 |
| Shrub | 18,636 | 33,570 |
| Flood | 18,413 | 37,750 |
| Urban | 5105 | 7512 |
| Bare | 20,654 | 43,005 |
| Mixed | 12,732 | 23,170 |
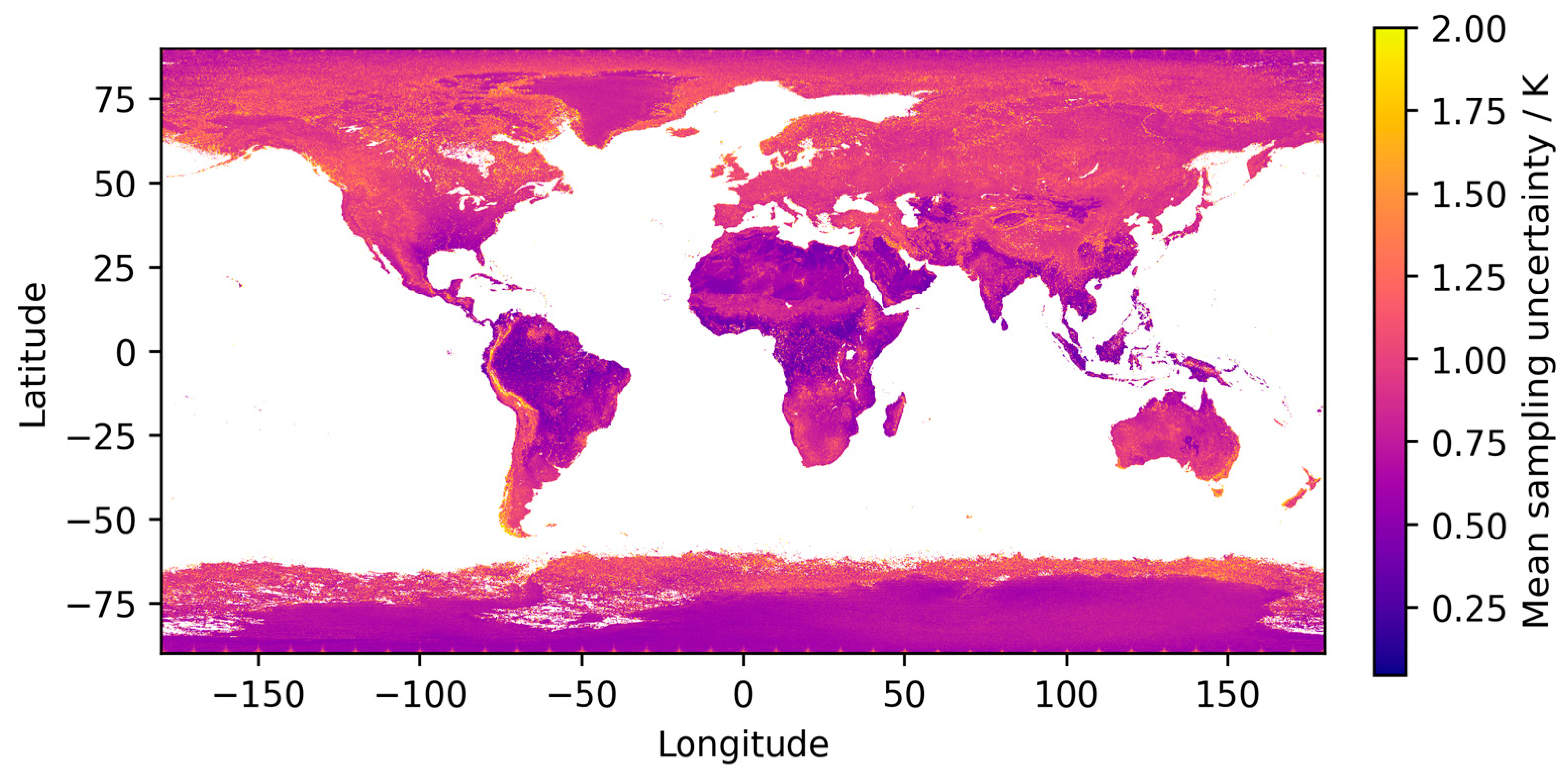
| Biome | Global Mean Sampling Uncertainty/K |
|---|---|
| Ice | 0.95 |
| Crop | 0.74 |
| Tree | 0.86 |
| Shrub | 0.85 |
| Flood | 0.92 |
| Urban | 0.97 |
| Bare | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulgin, C.E.; Ghent, D.J.; Perry, M. Spatial Sampling Uncertainty for MODIS Terra Land Surface Temperature Retrievals. Remote Sens. 2025, 17, 3435. https://doi.org/10.3390/rs17203435
Bulgin CE, Ghent DJ, Perry M. Spatial Sampling Uncertainty for MODIS Terra Land Surface Temperature Retrievals. Remote Sensing. 2025; 17(20):3435. https://doi.org/10.3390/rs17203435
Chicago/Turabian StyleBulgin, Claire E., Darren J. Ghent, and Mike Perry. 2025. "Spatial Sampling Uncertainty for MODIS Terra Land Surface Temperature Retrievals" Remote Sensing 17, no. 20: 3435. https://doi.org/10.3390/rs17203435
APA StyleBulgin, C. E., Ghent, D. J., & Perry, M. (2025). Spatial Sampling Uncertainty for MODIS Terra Land Surface Temperature Retrievals. Remote Sensing, 17(20), 3435. https://doi.org/10.3390/rs17203435





