Enhancing Precipitation Nowcasting Through Dual-Attention RNN: Integrating Satellite Infrared and Radar VIL Data
Abstract
1. Introduction
2. Model, Data, and Methods
2.1. Model Introduction
2.2. Experimental Data
2.3. Evaluation Methods
3. Results and Discussion
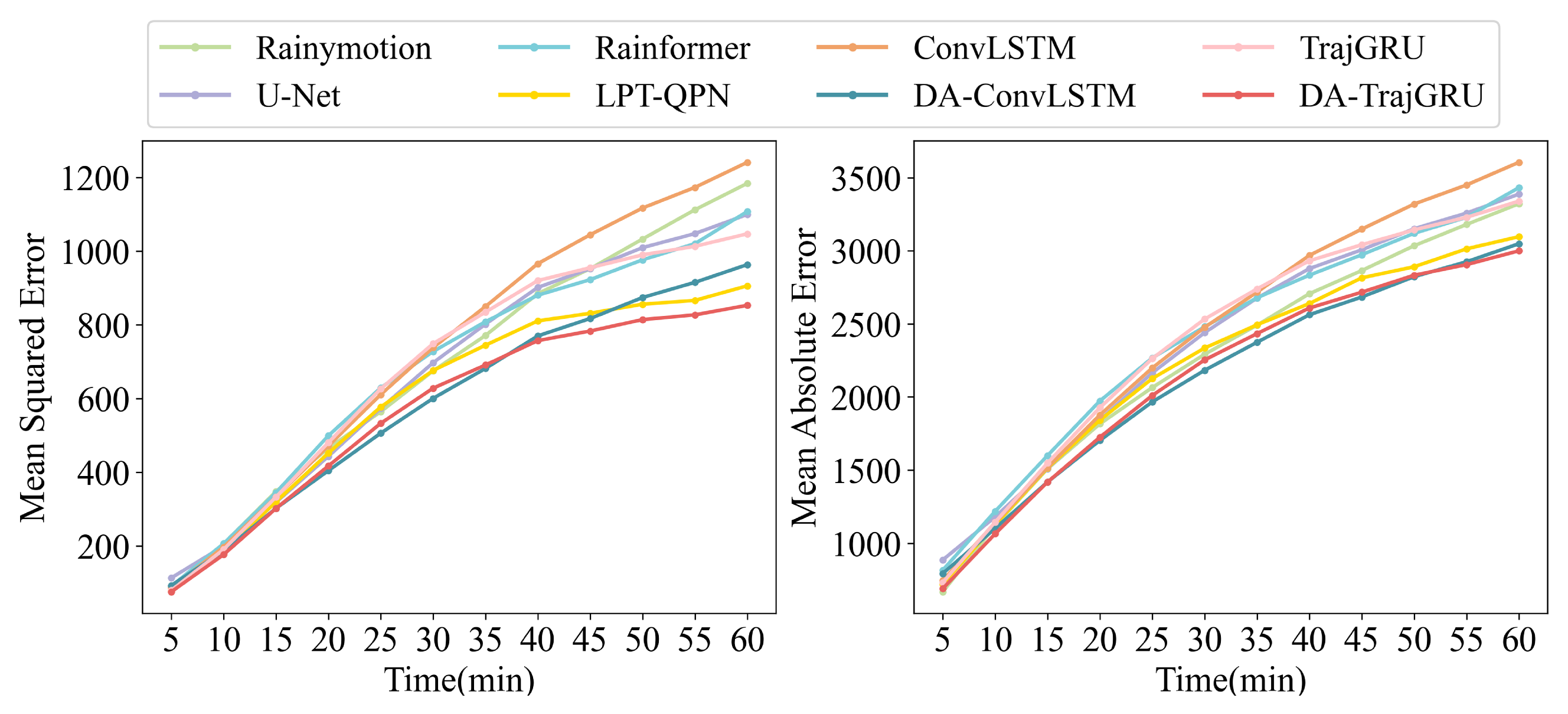
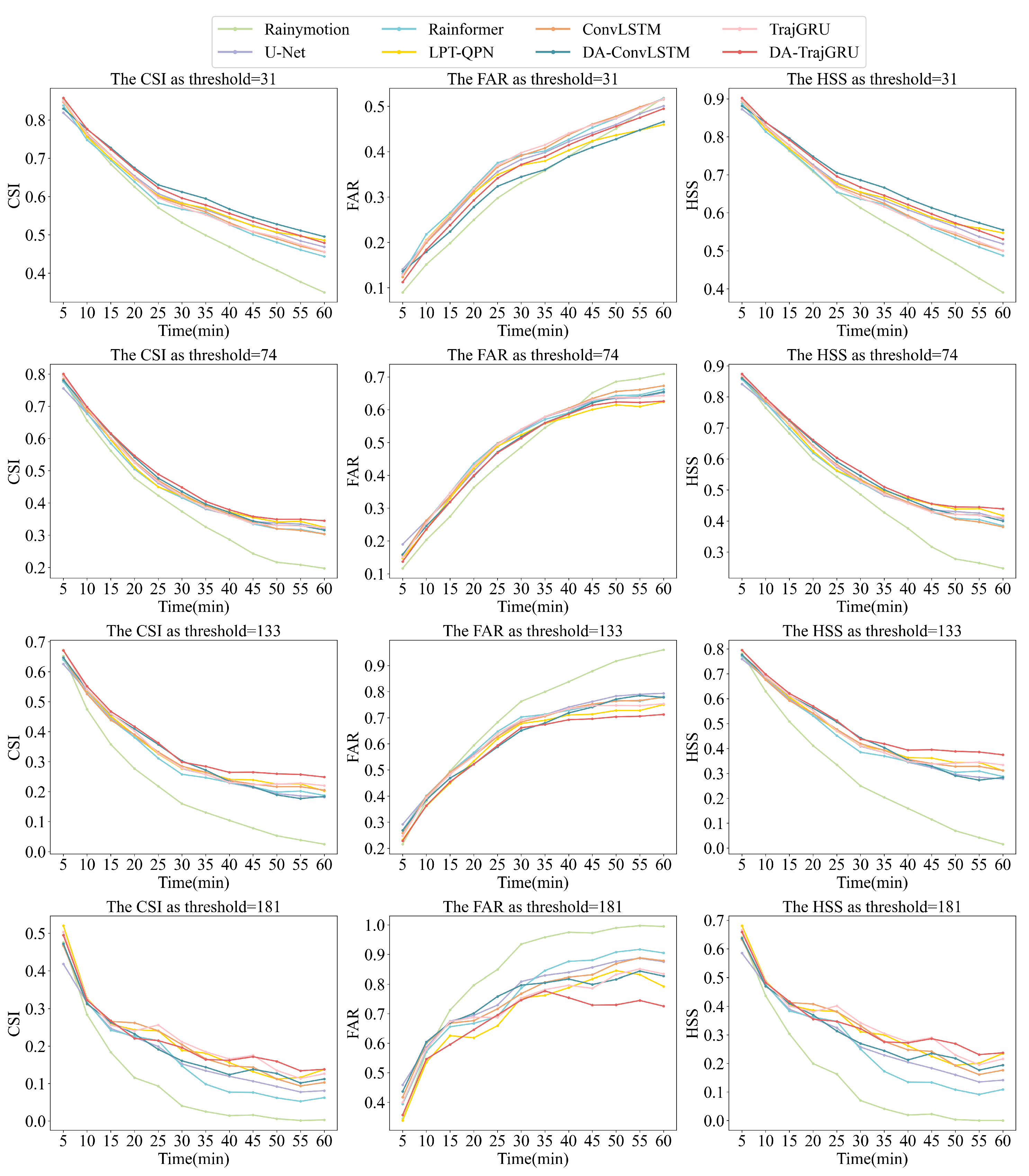
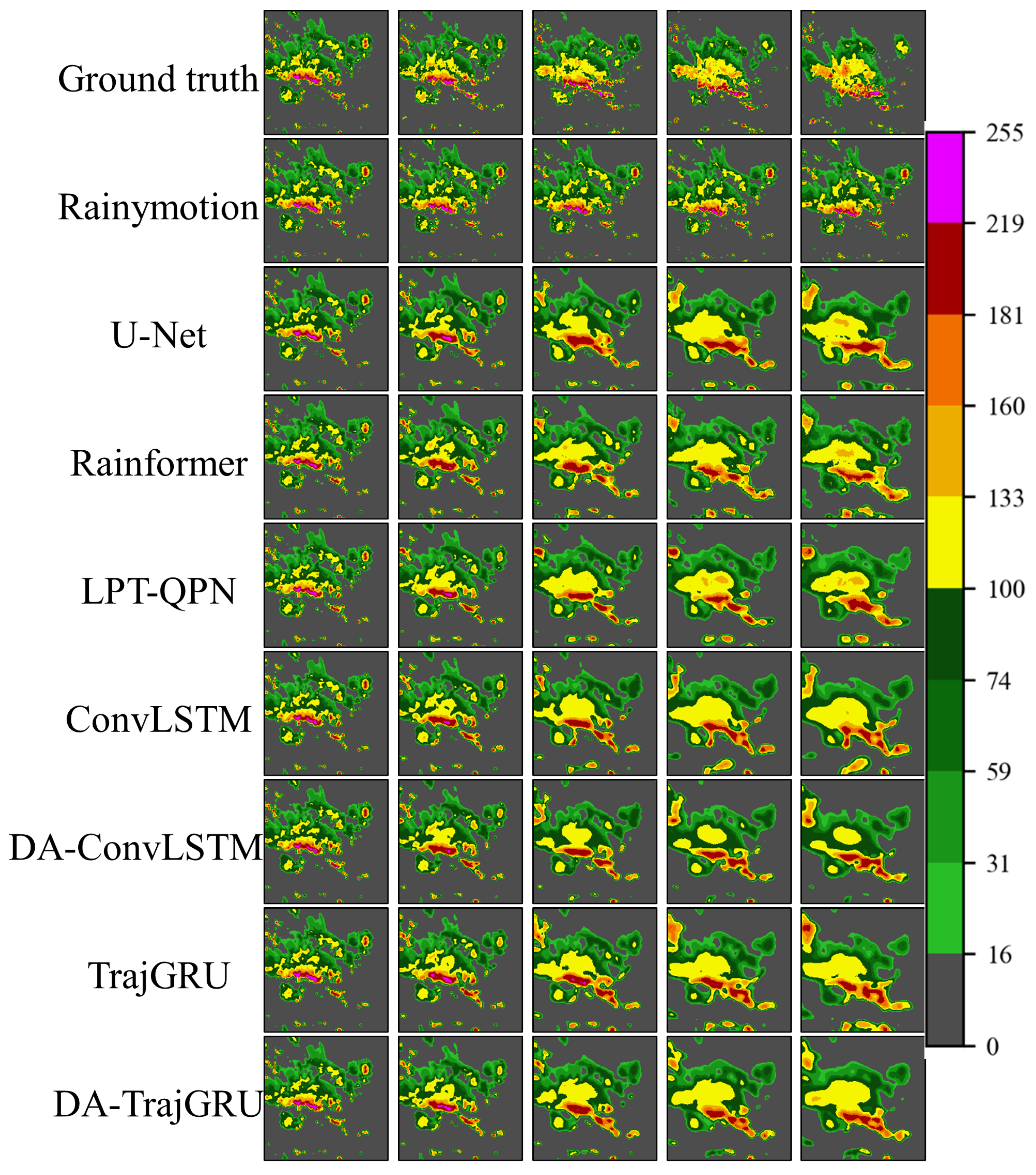
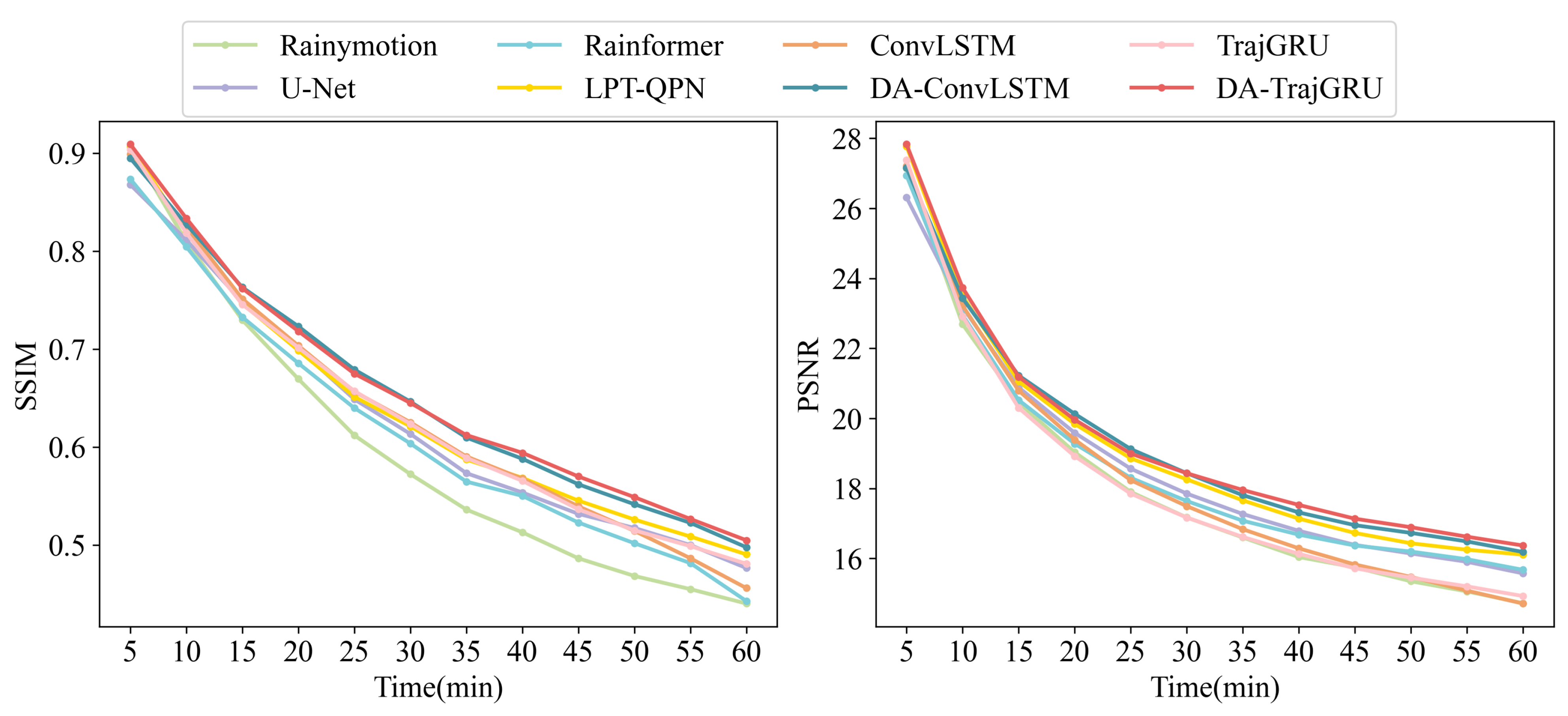
3.1. Test Set Results
3.2. Case 1: Visualization of a Flash Flood
3.3. Case 2: Visualization of a Thunderstorm with High Winds
3.4. Discussion
4. Conclusions
- Enhanced Prediction Performance: The proposed DA-RNN incorporating satellite infrared data demonstrates superior predictive performance compared with traditional RNN models. Specifically, the MSE and MAE of the DA-TrajGRU model were and lower, respectively, compared with those of the TrajGRU model. Similarly, the DA-ConvLSTM model exhibited and reductions in the same metrics compared with the ConvLSTM model.
- Robustness Across Thresholds: The proposed model’s performance across various thresholds indicates that the FAR remains robust in deep learning models, whereas the CSI and HSS tend to decline as the threshold increases. This result can be attributed to the limited amount of information extracted from weather radar VIL images with larger pixel thresholds. The integration of satellite infrared data aids in extracting more comprehensive information, helping to mitigate the overestimation of pixel values in certain areas.
- Accuracy in Real-World Scenarios: The DA-RNN model’s predictions closely aligned with real weather radar images in terms of pixel intensity and envelope. Although the Rainymotion optical flow method offers higher resolution, its predicted envelope and storm positions substantially deviated from the actual observations. Similarly, other models may overestimate pixel values due to insufficient temporal information extraction.
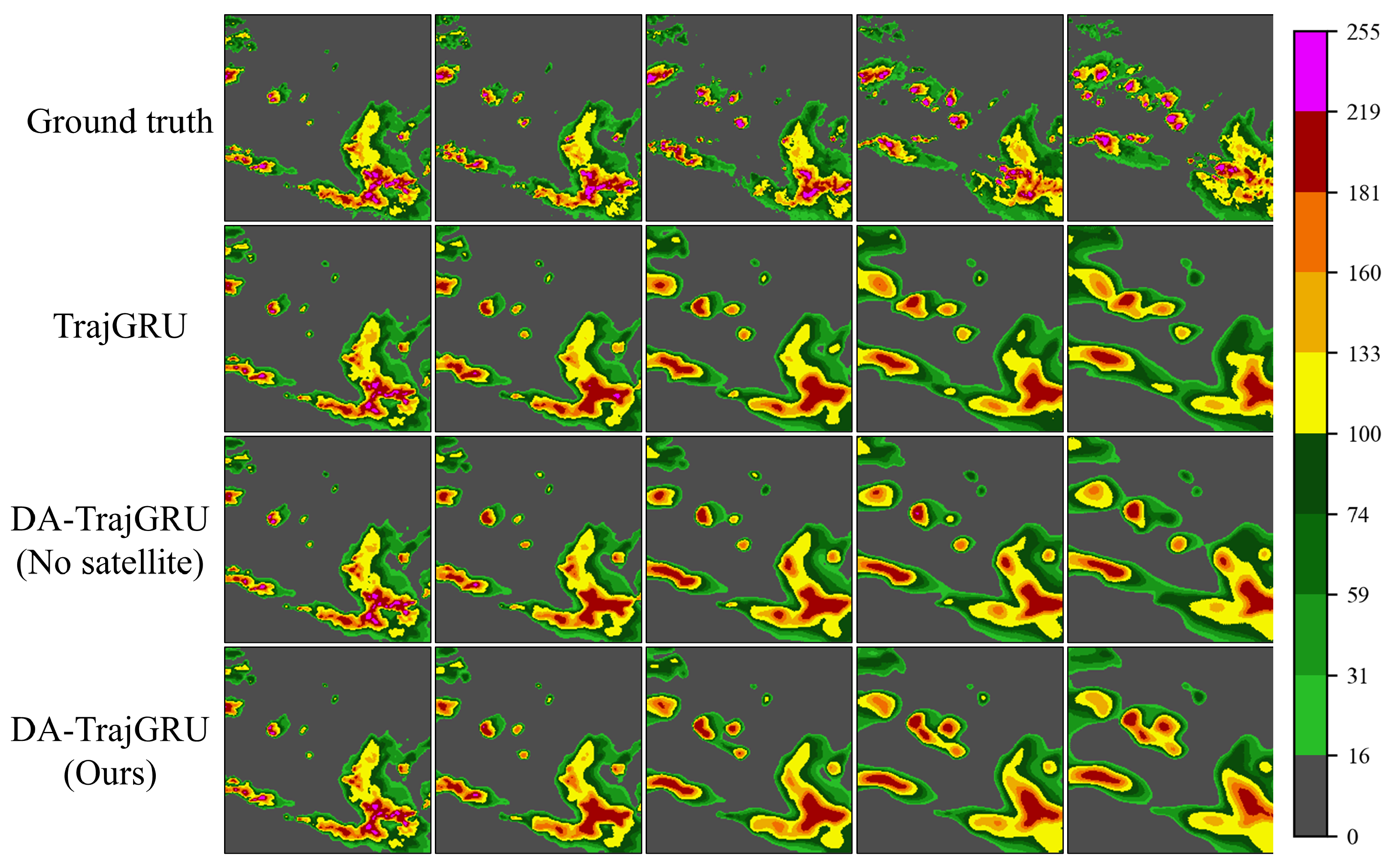
- Importance of Satellite Infrared Data: The results of our ablation tests on the proposed DA-RNN model underscore the critical role of combining DANet with RNN in enhancing the warning rate for precipitation nowcasting. Satellite infrared data are indispensable for increasing the accuracy of these forecasts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chowdhury, A.; Egodawatta, P.; McGree, J. Pattern-based assessment of the influence of rainfall characteristics on urban stormwater quality. Water Sci. Technol. 2023, 87, 2292–2303. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.; Wang, H.; Li, Z.; Bu, Z.; Yang, R.; Liu, Z. Case Study on the Evolution and Precipitation Characteristics of Southwest Vortex in China: Insights from FY-4A and GPM Observations. Remote Sens. 2023, 15, 4114. [Google Scholar] [CrossRef]
- Wang, H.; Tan, L.; Zhang, F.; Zheng, J.; Liu, Y.; Zeng, Q.; Yan, Y.; Ren, X.; Xiang, J. Three-Dimensional Structure Analysis and Droplet Spectrum Characteristics of Southwest Vortex Precipitation System Based on GPM-DPR. Remote Sens. 2022, 14, 4063. [Google Scholar] [CrossRef]
- Zhang, F.; Melhauser, C. Practical and Intrinsic Predictability of Severe and Convective Weather at the Mesoscales. J. Atmos. Sci. 2012, 69, 3350–3371. [Google Scholar]
- Wang, L.; Dong, Y.; Zhang, C.; Heng, Z. Extreme and severe convective weather disasters: A dual-polarization radar nowcasting method based on physical constraints and a deep neural network model. Atmos. Res. 2023, 289, 106750. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.; Li, G.; Xia, J.; Ge, F.; Zeng, Q.; Ren, X.; Tan, L. Projection of Future Extreme Precipitation in China Based on the CMIP6 from a Machine Learning Perspective. Remote Sens. 2022, 14, 4033. [Google Scholar] [CrossRef]
- Che, H.; Niu, D.; Zang, Z.; Cao, Y.; Chen, X. ED-DRAP: Encoder–Decoder Deep Residual Attention Prediction Network for Radar Echoes. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Reinoso-Rondinel, R.; Rempel, M.; Schultze, M.; Tromel, S. Nationwide Radar-Based Precipitation Nowcasting - A Localization Filtering Approach and its Application for Germany. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1670–1691. [Google Scholar] [CrossRef]
- Ehsani, M.; Zarei, A.; Gupta, H.; Barnard, K.; Lyons, E.; Behrangi, A. NowCasting-Nets: Representation Learning to Mitigate Latency Gap of Satellite Precipitation Products Using Convolutional and Recurrent Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–21. [Google Scholar] [CrossRef]
- Ozkaya, A. Assessing the numerical weather prediction (NWP) model in estimating extreme rainfall events: A case study for severe floods in the southwest Mediterranean region, Turkey. J. Earth Syst. Sci. 2023, 132, 125. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Liu, J. Focal Frame Loss: A Simple but Effective Loss for Precipitation Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6781–6788. [Google Scholar] [CrossRef]
- Sun, J.; Xue, M.; Wilson, J.; Zawadzki, I.; Ballard, S.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.; Li, P.W.; Golding, B.; et al. Use of NWP For Nowcasting Convective Precipitation: Recent Progress and Challenges. Ulletin Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
- Jing, J.; Li, Q.; Ma, L.; Chen, L.; Ding, L. REMNet: Recurrent Evolution Memory-Aware Network for Accurate Long-Term Weather Radar Echo Extrapolation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Sun, N.; Zhou, Z.; Li, Q.; Jing, J. Three-Dimensional Gridded Radar Echo Extrapolation for Convective Storm Nowcasting Based on 3D-ConvLSTM Model. Mon. Wea. Rev. 2022, 14, 4256. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, X.; Zhuge, X.; Xu, M. Learnable Optical Flow Network for Radar Echo Extrapolation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1260–1266. [Google Scholar] [CrossRef]
- Chen, Q.; Koltun, V. Full flow: Optical flow estimation by global optimization over regular grids. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4706–4714. [Google Scholar]
- Cheng, Y.; Qu, H.; Wang, J.; Qian, K.; Li, W.; Yang, L.; Han, X.; Liu, M. A Radar Echo Extrapolation Model Based on a Dual-Branch Encoder–Decoder and Spatiotemporal GRU. Atmosphere 2024, 15, 104. [Google Scholar] [CrossRef]
- Yin, J.; Gao, Z.; Han, W. Application of a Radar Echo Extrapolation-Based Deep Learning Method in Strong Convection Nowcasting. Earth Space Sci. 2021, 8, e2020EA001621. [Google Scholar] [CrossRef]
- Geng, H.; Wu, F.; Zhuang, X.; Geng, L.; Xie, B.; Shi, Z. The MS-RadarFormer: A Transformer-Based Multi-Scale Deep Learning Model for Radar Echo Extrapolation. Remote Sens. 2012, 16, 274. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 29th Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, Long Beach CA, USA, 4–9 December 2017; pp. 5618–5628. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Yu, P. PredRNN++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 8122–8131. [Google Scholar]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN Features off-the-shelf: An Astounding Baseline for Recognition. arXiv 2014, arXiv:1403.6382. [Google Scholar]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar]
- Liczbińska, G.; Vögele, J.; Brabec, M. Climate and disease in historical urban space: Evidence from 19th century Poznań, Poland. Clim. Past 2024, 20, 137–150. [Google Scholar] [CrossRef]
- Maryono, A.; Zulaekhah, I.; Nurendyastuti, A. Gradual changes in temperature, humidity, rainfall, and solar irradiation as indicators of city climate change and increasing hydrometeorological disaster: A case study in Yogyakarta, Indonesia. Int. J. Hydrol. Sci. Technol. 2023, 15, 304–326. [Google Scholar] [CrossRef]
- Yokoo, K.; Ishida, K.; Ercan, A.; Tu, T.; Nagasato, T.; Kiyama, M.; Amagasaki, M. Capabilities of deep learning models on learning physical relationships: Case of rainfall-runoff modeling with LSTM. Sci. Total Environ. 2022, 802, 149876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, X.; Guan, J.; Wu, M.; Guo, L. RN-Net: A Deep Learning Approach to 0–2 Hour Rainfall Nowcasting Based on Radar and Automatic Weather Station Data. Sensors 2021, 21, 1981. [Google Scholar] [CrossRef] [PubMed]
- Goyens, C.; Lauwaet, D.; Schroder, M.; Demuzere, M.; Van Lipzig, N. Tracking mesoscale convective systems in the Sahel: Relation between cloud parameters and precipitation. Int. J. Climatol. 2012, 32, 1921–1934. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.; Chen, G.; Tan, X.; Zhu, K. Convective Clouds Extraction from Himawari-8 Satellite Images Based on Double-Stream Fully Convolutional Networks. IEEE Geosci. Remote Sens. Lett. 2022, 17, 553–557. [Google Scholar] [CrossRef]
- Liu, J. An Operational Global Near-Real-Time High-Resolution Seamless Sea Surface Temperature Products From Satellite-Based Thermal Infrared Measurements. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–8. [Google Scholar] [CrossRef]
- Islam, A.; Akter, M.; Fattah, M.; Mallick, J.; Parvin, I.; Islam, H.; Shahid, S.; Kabir, Z.; Kamruzzaman, M. Modulation of coupling climatic extremes and their climate signals in a subtropical monsoon country. Theor. Appl. Climatol. 2024, 155, 4827–4849. [Google Scholar] [CrossRef]
- Chakravarty, K.; Patil, R.; Rakshit, G.; Pandithurai, G. Contrasting features of rainfall microphysics as observed over the coastal and orographic region of western ghat in the inter-seasonal time-scale. J. Atmos. Sol.-Terr. Phys. 2024, 258, 106221. [Google Scholar] [CrossRef]
- Sun, F.; Li, B.; Min, M.; Qin, D. Toward a Deep-Learning-Network-Based Convective Weather Initiation Algorithm from the Joint Observations of Fengyun-4A Geostationary Satellite and Radar for 0-1h Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3455–3468. [Google Scholar]
- Zhang, T.; Wang, H.; Niu, D.; Shi, C.; Chen, X.; Jin, Y. MMSTP: Multi-modal Spatiotemporal Feature Fusion Network for Precipitation Prediction. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023. [Google Scholar]
- Hirano, K.; Maki, M. Imminent Nowcasting for Severe Rainfall Using Vertically Integrated Liquid Water Content Derived from X-Band Polarimetric Radar. J. Meteorol. Soc. Jpn. 2018, 96, 201–220. [Google Scholar]
- Boudevillain, B.; Andrieu, H. Assessment of vertically integrated liquid (VIL) water content radar measurement. J. Atmos. Ocean. Technol. 2023, 20, 807–819. [Google Scholar]
- Ma, Z.; Zhang, H.; Liu, J. DB-RNN: An RNN for Precipitation Nowcasting Deblurring. EEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5026–5041. [Google Scholar] [CrossRef]
- Shafiq, M.; Gu, Z. Deep Residual Learning for Image Recognition: A Survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3141–3149. [Google Scholar]
- Tian, L.; Li, X.; Ye, Y.; Xie, P.; Li, Y. A Generative Adversarial Gated Recurrent Unit Model for Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2020, 17, 601–605. [Google Scholar]
- Veillette, M.; Samsi, S.; Mattioli, C. SEVIR: A storm event imagery dataset for deep learning applications in radar and satellite meteorology. In Proceedings of the NeurIPS, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Gao, Z.; Shi, X.; Han, B.; Maddix, D.; Wang, H.; Zhu, Y.; Li, M.; Jin, X.; Wang, Y. PreDiff: Precipitation Nowcasting with Latent Diffusion Models. In Proceedings of the NeurIPS, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Yang, S.; Yuan, H. A Customized Multi-Scale Deep Learning Framework for Storm Nowcasting. Geophys. Res. Lett. 2023, 50, e2023GL103979. [Google Scholar]
- Bai, C.; Sun, F.; Zhang, J.; Song, Y.; Chen, S. Rainformer: Features Extraction Balanced Network for Radar-Based Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Li, D.; Deng, K.; Zhang, D.; Liu, Y.; Leng, H.; Yin, F.; Ren, K.; Song, J. LPT-QPN: A Lightweight Physics-Informed Transformer for Quantitative Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–19. [Google Scholar] [CrossRef]
- Ayzel, G.; Heistermann, M.W.T. Optical flow models as an open benchmark for radar-based precipitation nowcasting (rainymotion v0.1). Geosci. Model Dev. 2019, 12, 1387–1402. [Google Scholar] [CrossRef]
- Xiong, T.; He, J.; Wang, H.; Tang, X.; Shi, Z.; Zeng, Q. Contextual Sa-Attention Convolutional LSTM for Precipitation Nowcasting: A Spatiotemporal Sequence Forecasting View. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12479–12491. [Google Scholar]
- He, W.; Xiong, T.; Wang, H.; He, J.; Ren, X.; Yan, Y.; Tan, L. Radar Echo Spatiotemporal Sequence Prediction Using an Improved ConvGRU Deep Learning Model. Atmosphere 2022, 13, 88. [Google Scholar] [CrossRef]
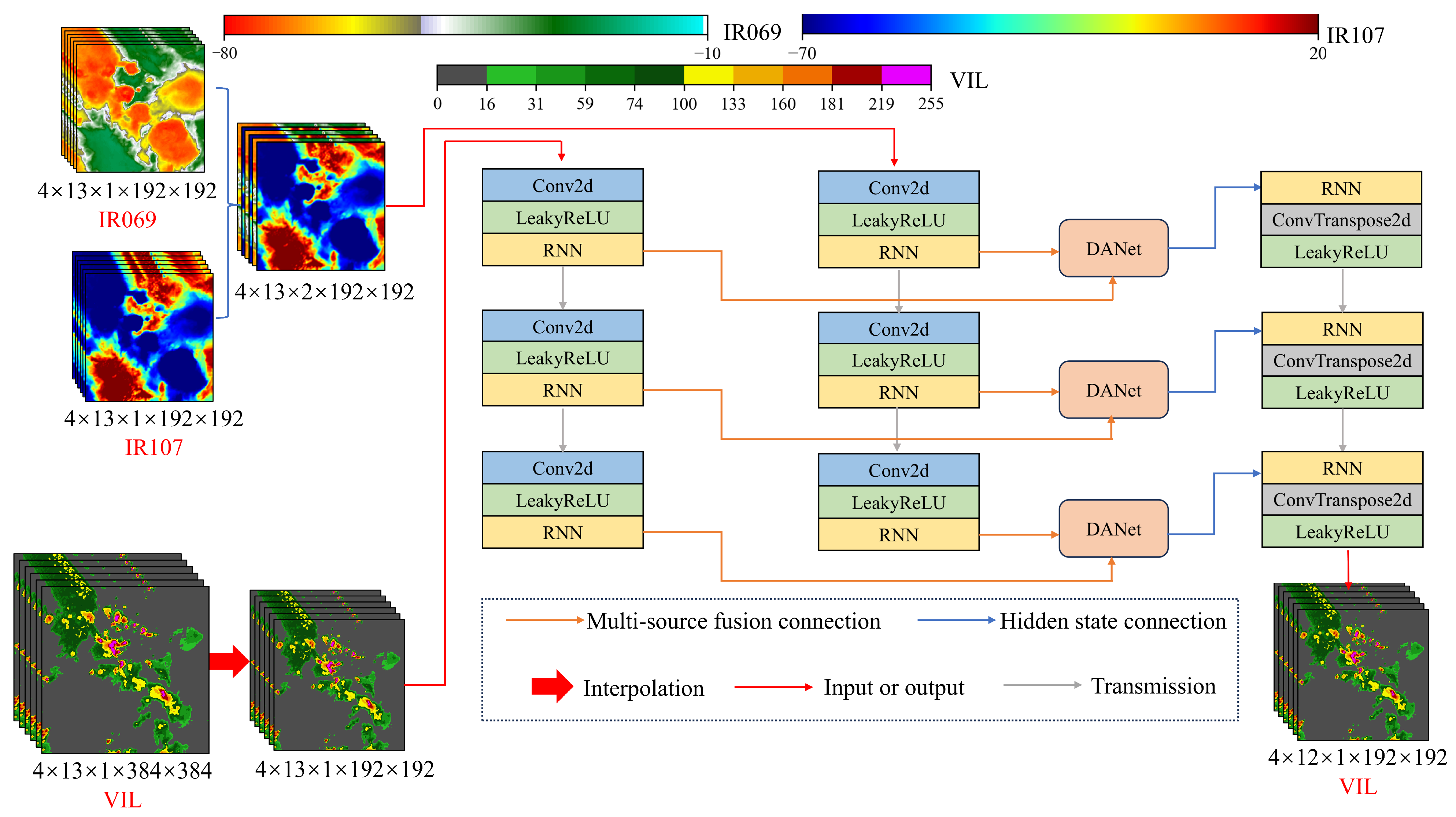
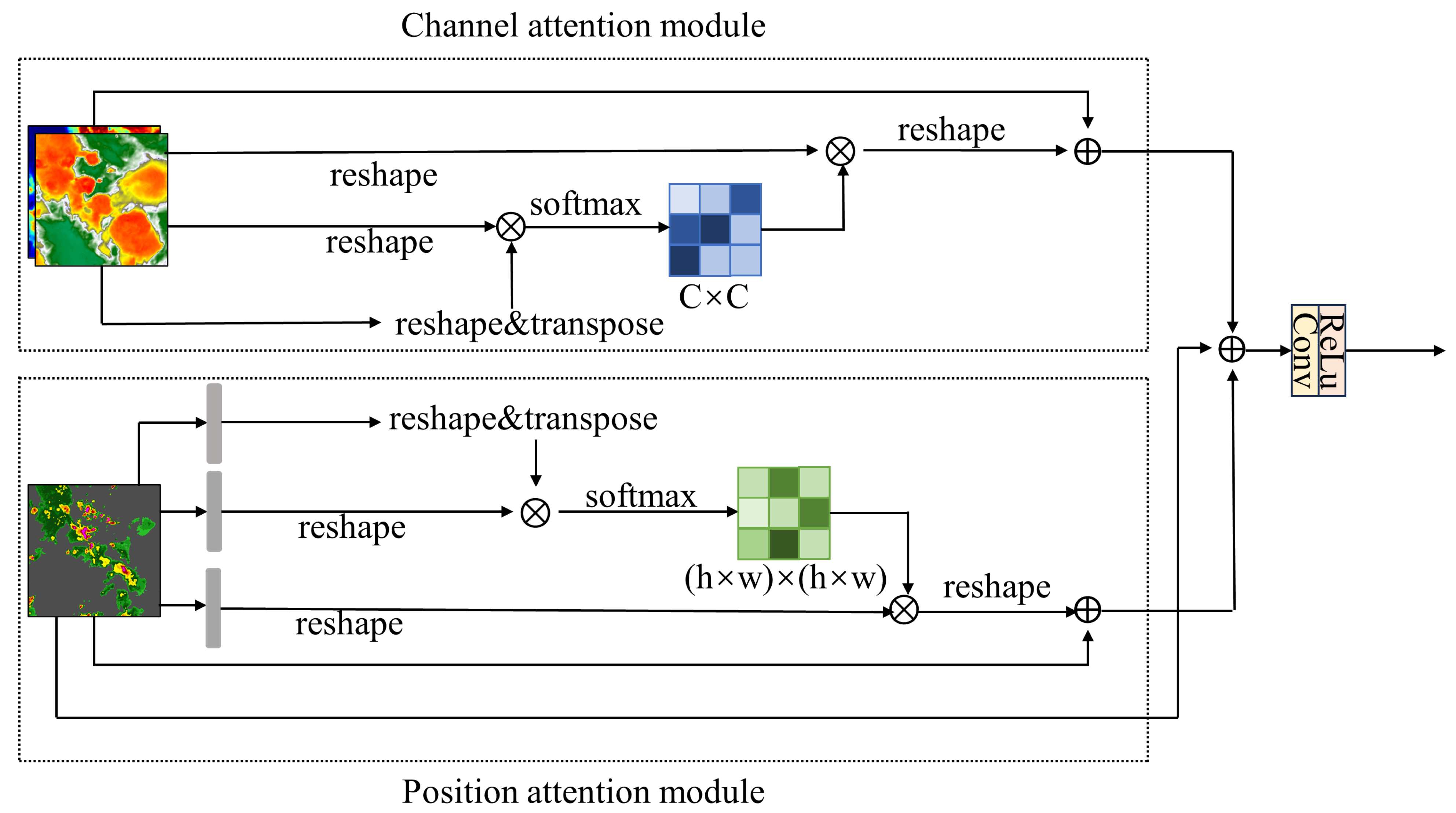



| Data Type | Description | Sensor | Spatial Resolution | Patch Size |
|---|---|---|---|---|
| VIS | Visible satellite imagery | GOES-16 C02 0.64 μm | 0.5 km | 768 × 768 |
| IR069 | Infrared Satellite imagery (mid-level water vapor) | GOES-16 C09 6.9 μm | 2 km | 192 × 192 |
| IR107 | Infrared Satellite imagery (clean longwave window) | GOES-16 C13 10.7 μm | 2 km | 192 × 192 |
| VIL | NEXRAD radar mosaic of VIL | Vertically Integrated Liquid (VIL) | 1 km | 384 × 384 |
| Lightning | Intercloud and cloud to ground lightning events | GOES-16 GLM flashes | 8 km | N/A |
| Name | Configuration |
|---|---|
| Learning Framework | Pytorch 1.8 |
| Graphics card | NVIDIA GeForce RTX 4090 |
| Graphics memory | 24 GB |
| Learning rate | 0.0001 |
| Learning strategy | Cosine AnnealingLR |
| Optimizer | Adam |
| Loss function | MSE |
| Index | Equation | Optimal Value |
|---|---|---|
| Mean Absolute Error (MAE) | 0 | |
| Mean Squared Error (MSE) | 0 | |
| Peak Signal-to-Noise Ratio (PSNR) | ||
| Structural Similarity Index Measure (SSIM) | 1 | |
| Continuous Ranked Probability Score (CRPS) | 0 | |
| Sharpness | ||
| Critical Success Index (CSI) | 1 | |
| False Alarm Rate (FAR) | 0 | |
| Heidke Skill Score (HSS) | 1 | |
| Fraction Skill Score (FSS) | 1 |
| Model | Details | Official Configuration | Our Adaptations |
|---|---|---|---|
| U-Net | Input length | 7 | 13 |
| Output length | 12 | 12 | |
| Rainformer | Input length | 9 | 13 |
| Output length | 9 | 12 | |
| ConvLSTM | Loss function | Balanced MSE | MSE |
| Input length | 5 | 13 | |
| Output length | 20 | 12 | |
| TrajGRU | Loss function | Balanced MSE | MSE |
| Input length | 5 | 13 | |
| Output length | 20 | 12 |
| Algorithm | MSE↓ | MAE↓ | SSIM↑ | PSNR↑ |
|---|---|---|---|---|
| Rainymotion | 356 | 1403 | 0.7161 | 22.179 |
| U-Net | 332 | 1437 | 0.7335 | 22.384 |
| Rainformer | 321 | 1417 | 0.7316 | 22.578 |
| LPT-QPN | 318 | 1384 | 0.7406 | 22.71 |
| ConvLSTM | 321 | 1383 | 0.7467 | 22.643 |
| DA-ConvLSTM | 297 | 1308 | 0.7552 | 22.906 |
| TrajGRU | 321 | 1390 | 0.7476 | 22.645 |
| DA-TrajGRU | 291 | 1301 | 0.7572 | 23.033 |
| Algorithm | CRPS↓ | Sharpness↑ |
|---|---|---|
| U-Net | 5.895 | 46.83 |
| Rainformer | 5.789 | 47.41 |
| LPT-QPN | 5.701 | 43.78 |
| ConvLSTM | 5.789 | 49.46 |
| DA-ConvLSTM | 5.555 | 50.68 |
| TrajGRU | 5.881 | 47.95 |
| DA-TrajGRU | 5.632 | 51.20 |
| Algorithm | Pixel ≥ 31 | Pixel ≥ 74 | Pixel ≥ 133 | Pixel ≥ 181 |
|---|---|---|---|---|
| Rainymotion | 0.6305 | 0.5176 | 0.2986 | 0.1793 |
| U-Net | 0.6509 | 0.5562 | 0.3717 | 0.2443 |
| Rainformer | 0.6555 | 0.5607 | 0.3677 | 0.2403 |
| LPT-QPN | 0.6594 | 0.5661 | 0.3753 | 0.2423 |
| ConvLSTM | 0.6626 | 0.5632 | 0.3796 | 0.2488 |
| DA-ConvLSTM | 0.6732 | 0.5728 | 0.3821 | 0.2496 |
| TrajGRU | 0.6608 | 0.5665 | 0.3841 | 0.2537 |
| DA-TrajGRU | 0.6751 | 0.5783 | 0.3897 | 0.2523 |
| Algorithm | Pixel ≥ 31 | Pixel ≥ 74 | Pixel ≥ 133 | Pixel ≥ 181 |
|---|---|---|---|---|
| Rainymotion | 0.2343 | 0.3273 | 0.5469 | 0.6778 |
| U-Net | 0.2901 | 0.3743 | 0.5026 | 0.5274 |
| Rainformer | 0.2821 | 0.3599 | 0.4928 | 0.5342 |
| LPT-QPN | 0.2724 | 0.3559 | 0.4869 | 0.5195 |
| ConvLSTM | 0.2761 | 0.3688 | 0.4944 | 0.5337 |
| DA-ConvLSTM | 0.2561 | 0.3551 | 0.4801 | 0.5175 |
| TrajGRU | 0.2849 | 0.3636 | 0.4906 | 0.5073 |
| DA-TrajGRU | 0.2630 | 0.3468 | 0.4727 | 0.4896 |
| Algorithm | Pixel ≥ 31 | Pixel ≥ 74 | Pixel ≥ 133 | Pixel ≥ 181 |
|---|---|---|---|---|
| Rainymotion | 0.7042 | 0.6173 | 0.4055 | 0.2620 |
| U-Net | 0.7198 | 0.6537 | 0.4635 | 0.3483 |
| Rainformer | 0.7242 | 0.6583 | 0.4885 | 0.3425 |
| LPT-QPN | 0.7291 | 0.6635 | 0.4962 | 0.3435 |
| ConvLSTM | 0.7307 | 0.6596 | 0.5017 | 0.3534 |
| DA-ConvLSTM | 0.7432 | 0.6705 | 0.5051 | 0.3538 |
| TrajGRU | 0.7291 | 0.6634 | 0.5071 | 0.3583 |
| DA-TrajGRU | 0.7441 | 0.6762 | 0.5137 | 0.3561 |
| Algorithm | Pixel ≥ 31 | Pixel ≥ 74 | Pixel ≥ 133 | Pixel ≥ 181 |
|---|---|---|---|---|
| Rainymotion | 0.7516 | 0.6535 | 0.4253 | 0.2690 |
| U-Net | 0.7718 | 0.6928 | 0.5127 | 0.3543 |
| Rainformer | 0.7752 | 0.6959 | 0.5068 | 0.3484 |
| LPT-QPN | 0.7781 | 0.7004 | 0.5144 | 0.3493 |
| ConvLSTM | 0.7805 | 0.6985 | 0.5202 | 0.3593 |
| DA-ConvLSTM | 0.7891 | 0.7074 | 0.5228 | 0.3596 |
| TrajGRU | 0.7792 | 0.7008 | 0.5253 | 0.3641 |
| DA-TrajGRU | 0.7907 | 0.7119 | 0.5311 | 0.3613 |
| Algorithm | SSIM↑ | PSNR↑ | MSE↓ | MAE↓ |
|---|---|---|---|---|
| TrajGRU | 0.7476 | 22.645 | 321 | 1390 |
| DA-TrajGRU (No satellite) | 0.7521 | 22.845 | 308 | 1340 |
| DA-TrajGRU (Ours) | 0.7572 | 23.033 | 291 | 1301 |
| Algorithm | CSI-M↑ | FAR-M↓ | HSS-M↑ | FAR-31↓ | FAR-74↓ | FAR-133↓ | FAR-181↓ |
|---|---|---|---|---|---|---|---|
| TrajGRU | 0.4662 | 0.4116 | 0.5644 | 0.2849 | 0.3636 | 0.4906 | 0.5073 |
| DA-TrajGRU (No satellite) | 0.4701 | 0.4007 | 0.5692 | 0.2723 | 0.3536 | 0.4861 | 0.4908 |
| DA-TrajGRU (Ours) | 0.4738 | 0.3931 | 0.5725 | 0.2631 | 0.3468 | 0.4727 | 0.4896 |
| Algorithm | Training Time per Epoch (min) | GPU Memory (MB) | Inference Time per Case (S) |
|---|---|---|---|
| TrajGRU | 50 | 10417 | 0.223 |
| DA-TrajGRU (No satellite) | 55 | 15672 | 0.228 |
| DA-TrajGRU (Ours) | 100 | 19707 | 0.324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yang, R.; He, J.; Zeng, Q.; Xiong, T.; Liu, Z.; Jin, H. Enhancing Precipitation Nowcasting Through Dual-Attention RNN: Integrating Satellite Infrared and Radar VIL Data. Remote Sens. 2025, 17, 238. https://doi.org/10.3390/rs17020238
Wang H, Yang R, He J, Zeng Q, Xiong T, Liu Z, Jin H. Enhancing Precipitation Nowcasting Through Dual-Attention RNN: Integrating Satellite Infrared and Radar VIL Data. Remote Sensing. 2025; 17(2):238. https://doi.org/10.3390/rs17020238
Chicago/Turabian StyleWang, Hao, Rong Yang, Jianxin He, Qiangyu Zeng, Taisong Xiong, Zhihao Liu, and Hongfei Jin. 2025. "Enhancing Precipitation Nowcasting Through Dual-Attention RNN: Integrating Satellite Infrared and Radar VIL Data" Remote Sensing 17, no. 2: 238. https://doi.org/10.3390/rs17020238
APA StyleWang, H., Yang, R., He, J., Zeng, Q., Xiong, T., Liu, Z., & Jin, H. (2025). Enhancing Precipitation Nowcasting Through Dual-Attention RNN: Integrating Satellite Infrared and Radar VIL Data. Remote Sensing, 17(2), 238. https://doi.org/10.3390/rs17020238









