Simulation Study of the Effect of Multi-Angle ATI-SAR on Sea Surface Current Retrieval Accuracy
Abstract
Highlights
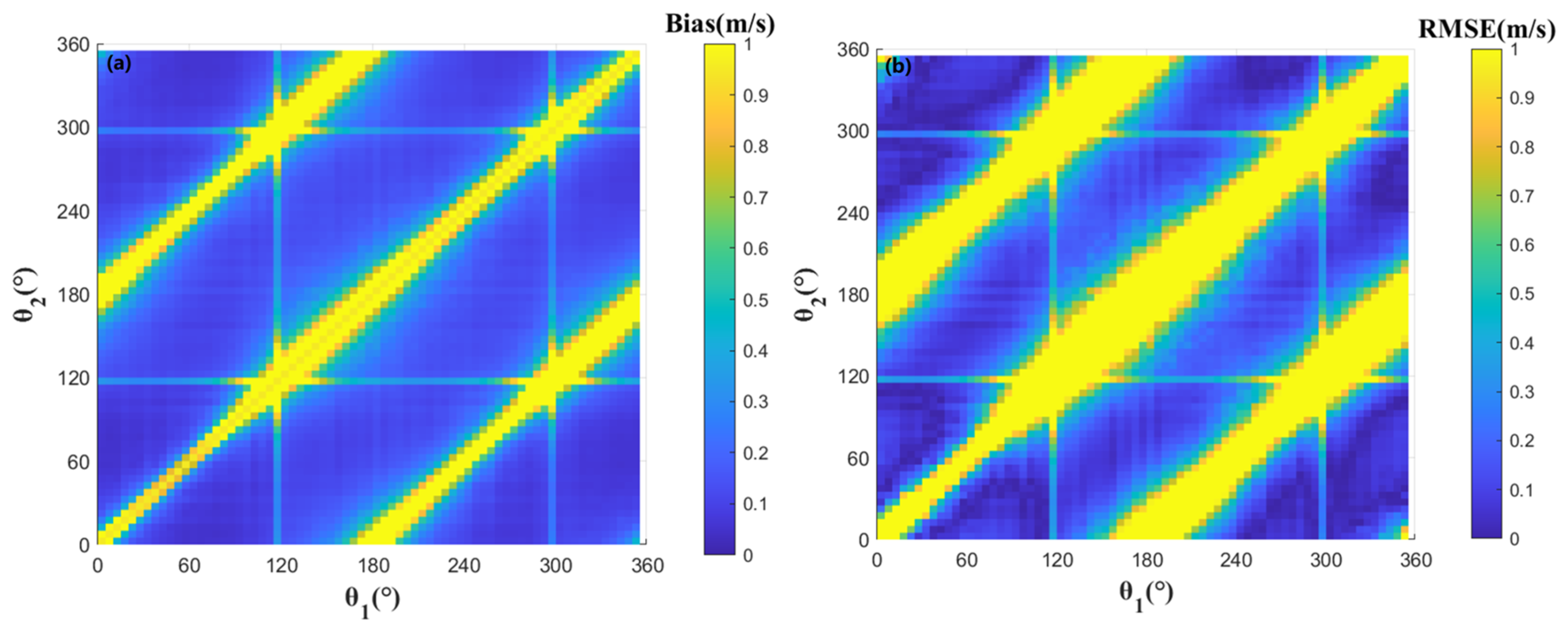
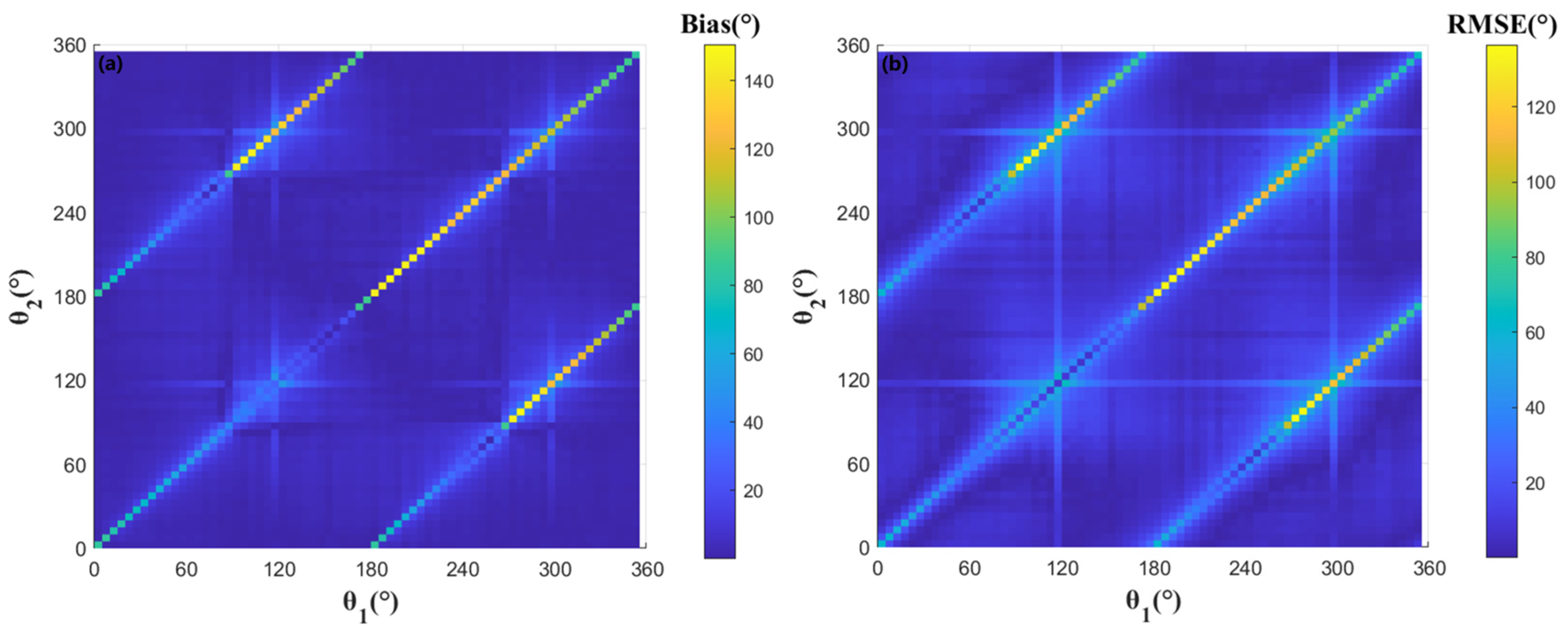
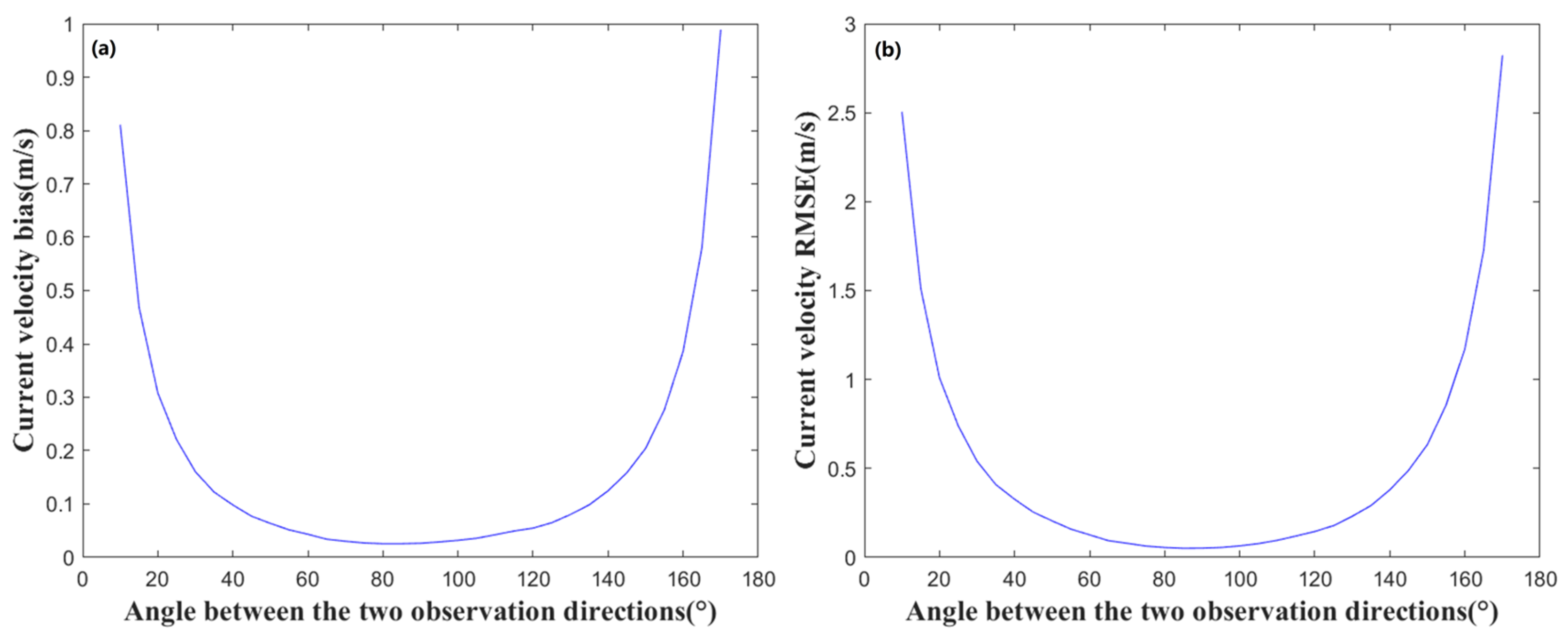
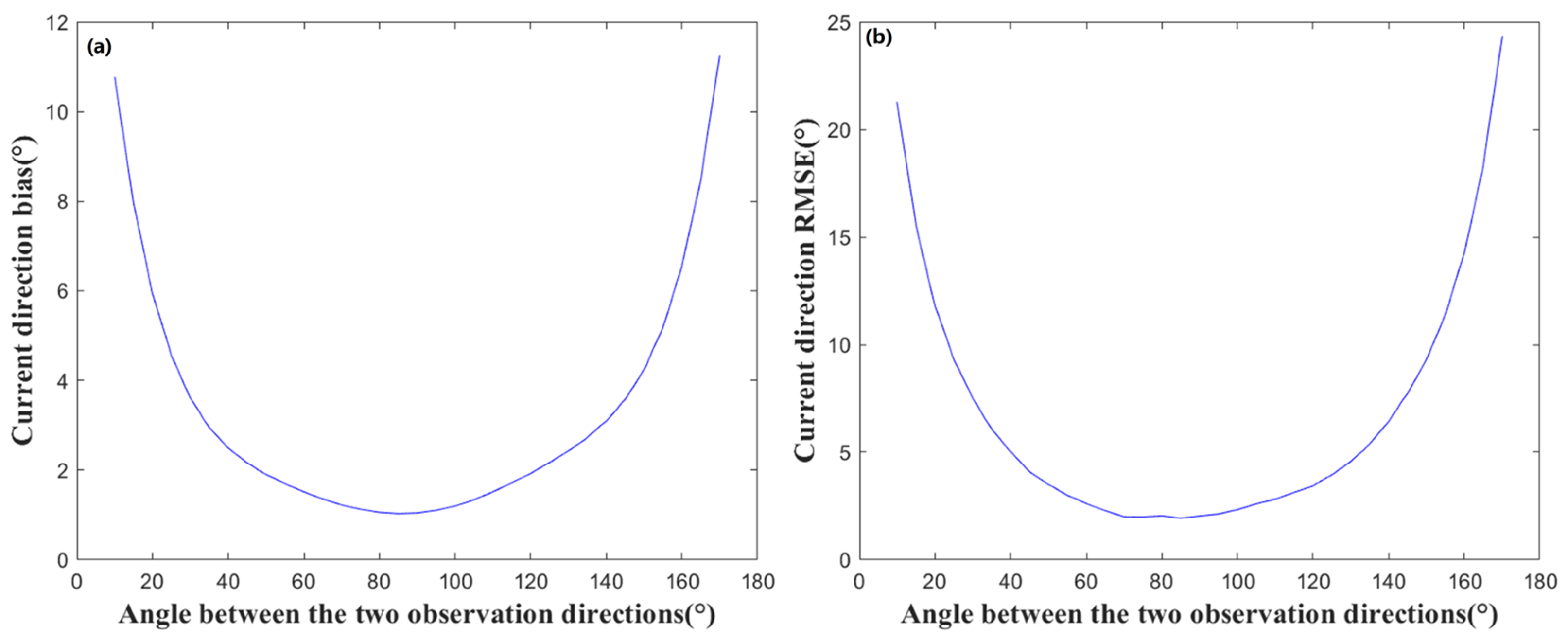
- Retrieval accuracy for 2D currents is maximized when dual ATI-SAR viewing angles are near-orthogonal (~90°) and severely degraded when near-parallel (0°/180°).
- Wind conditions critically impact accuracy: a perpendicular wind-current alignment minimizes velocity error but maximizes direction error, while higher wind speeds degrade both.
- The results provide a quantitative basis for designing future satellite constellation orbits to maximize near-orthogonal observation opportunities over key ocean areas.
- The study highlights the need for advanced retrieval algorithms that can correct for complex, wind-induced biases in multi-angle ATI-SAR data.
Abstract
1. Introduction
2. Principles and Methods
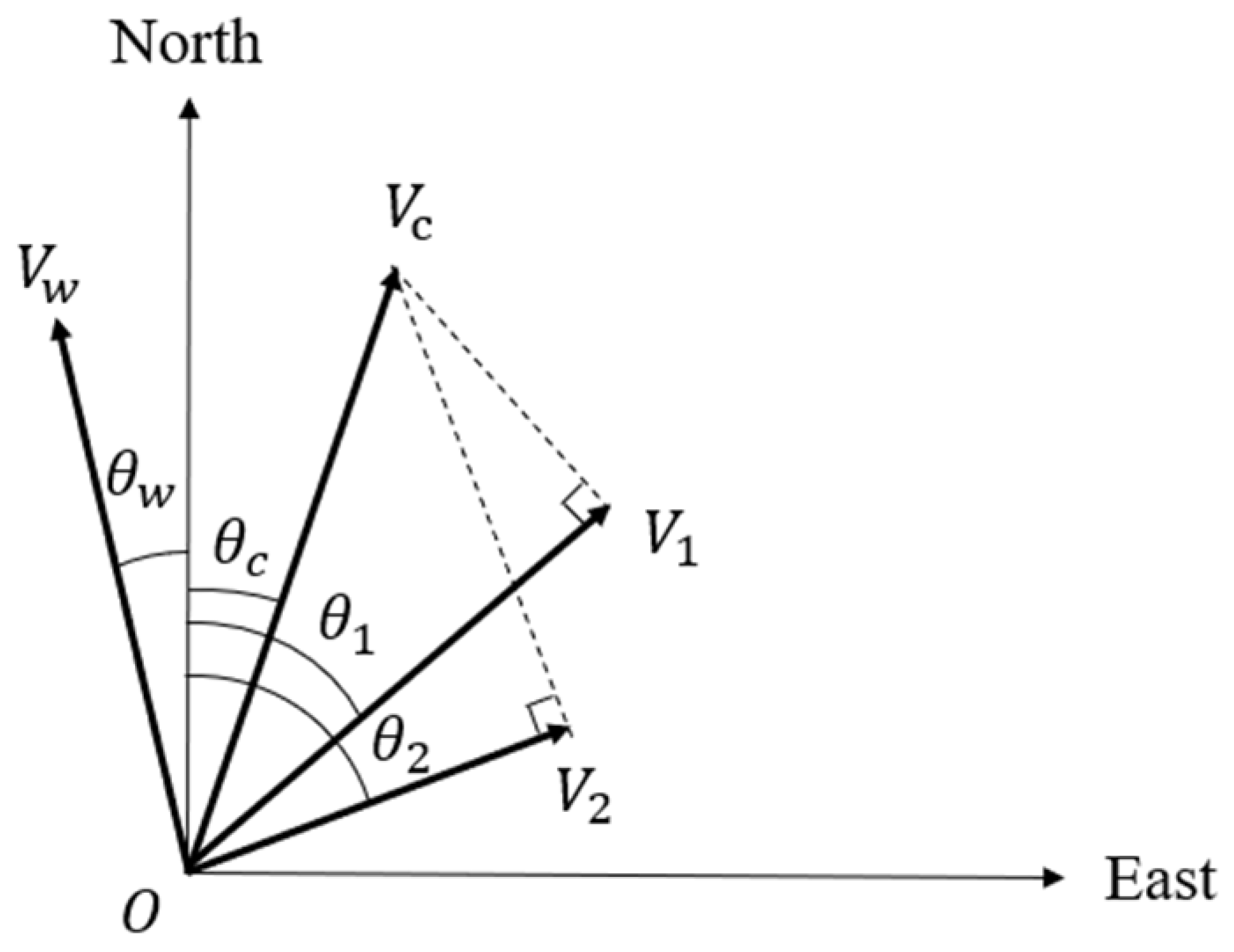
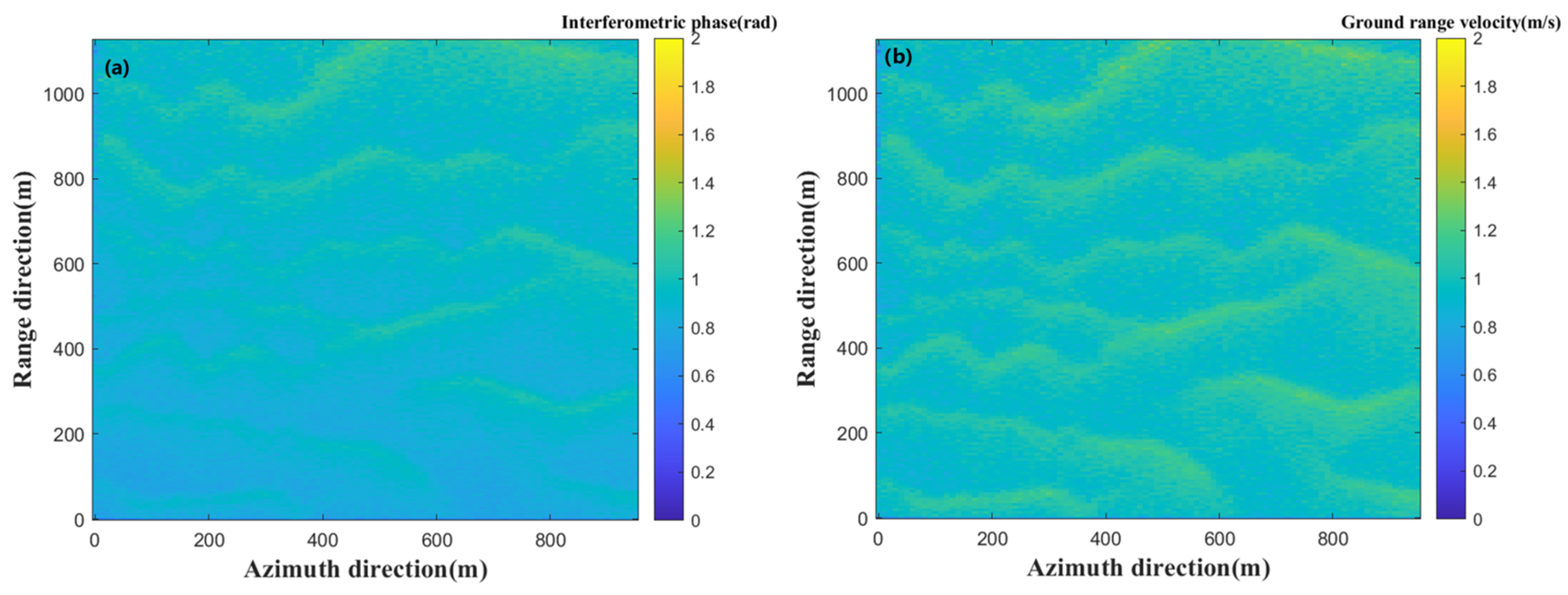
2.1. ATI-SAR Ocean Surface Current Retrieval Principle
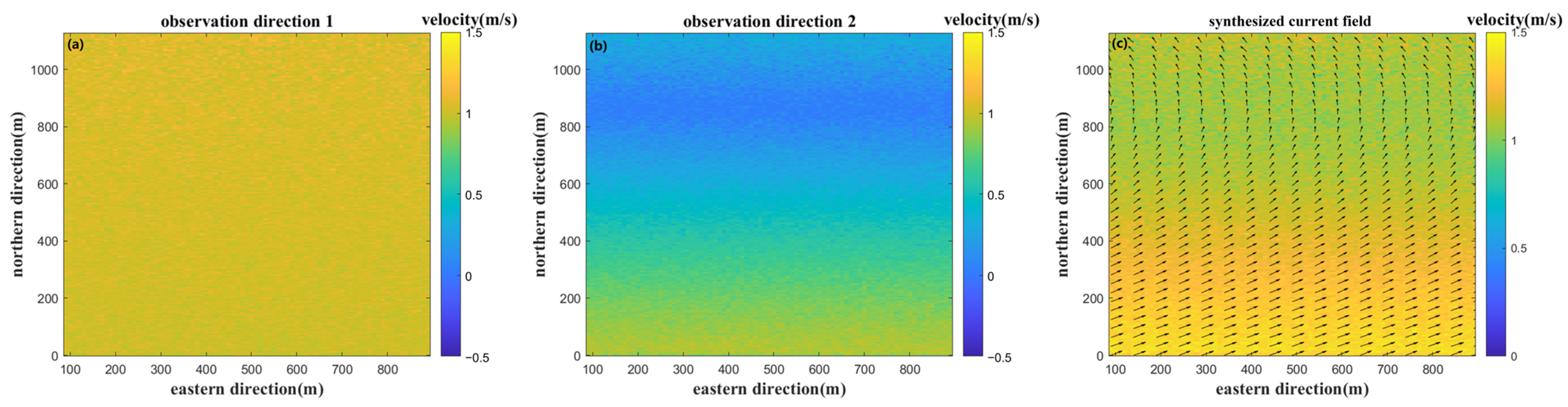
2.2. Multi-Angle Observations Method
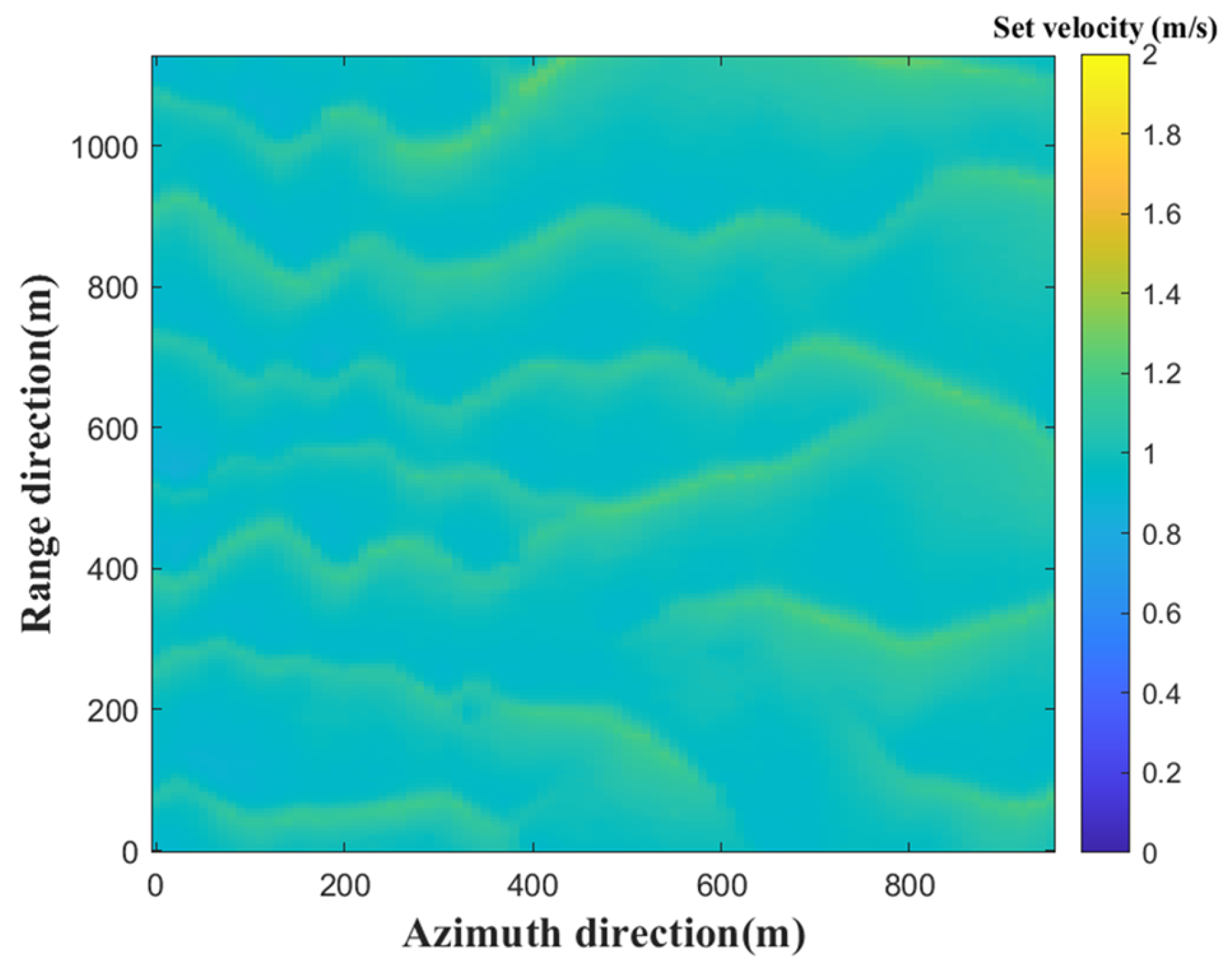
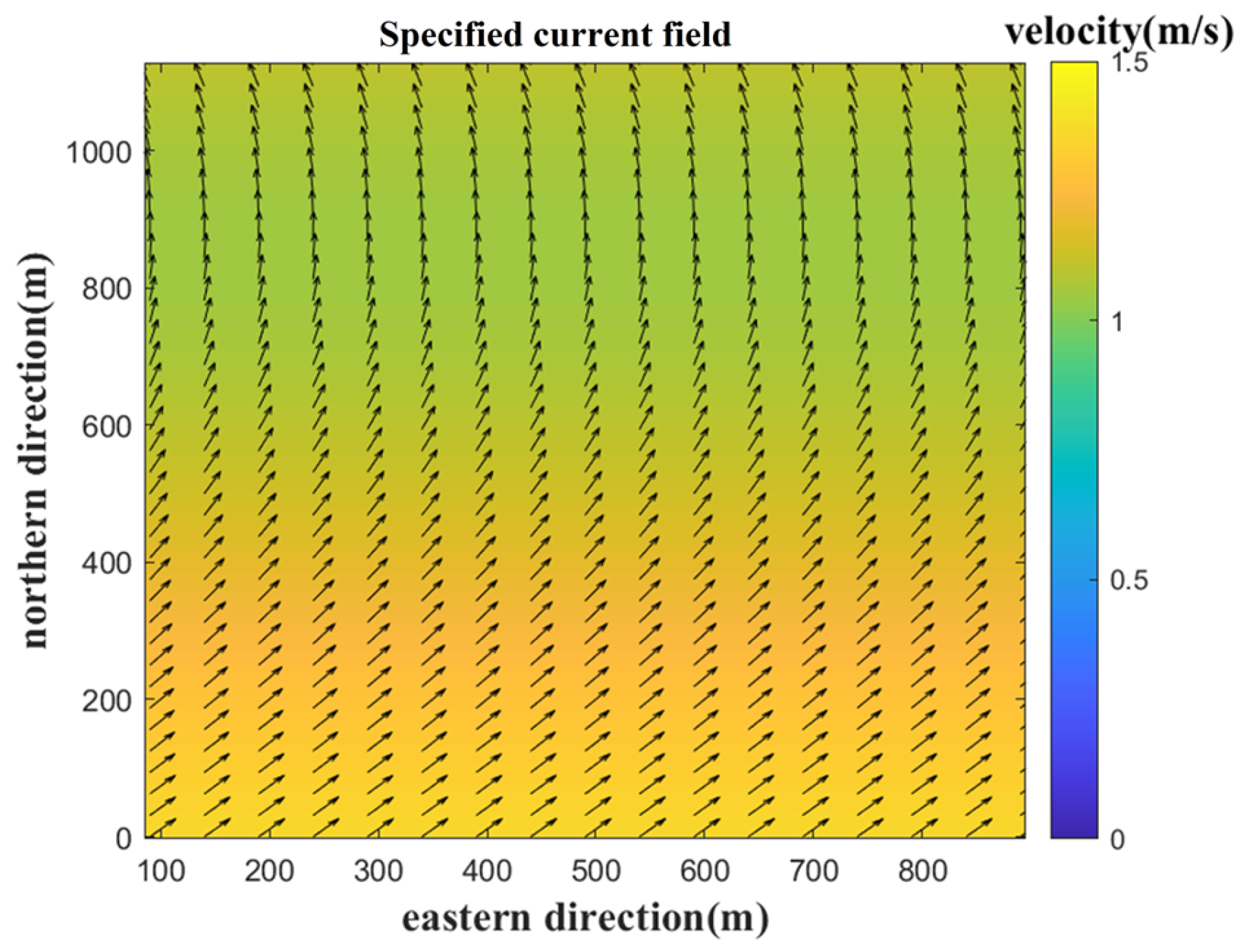
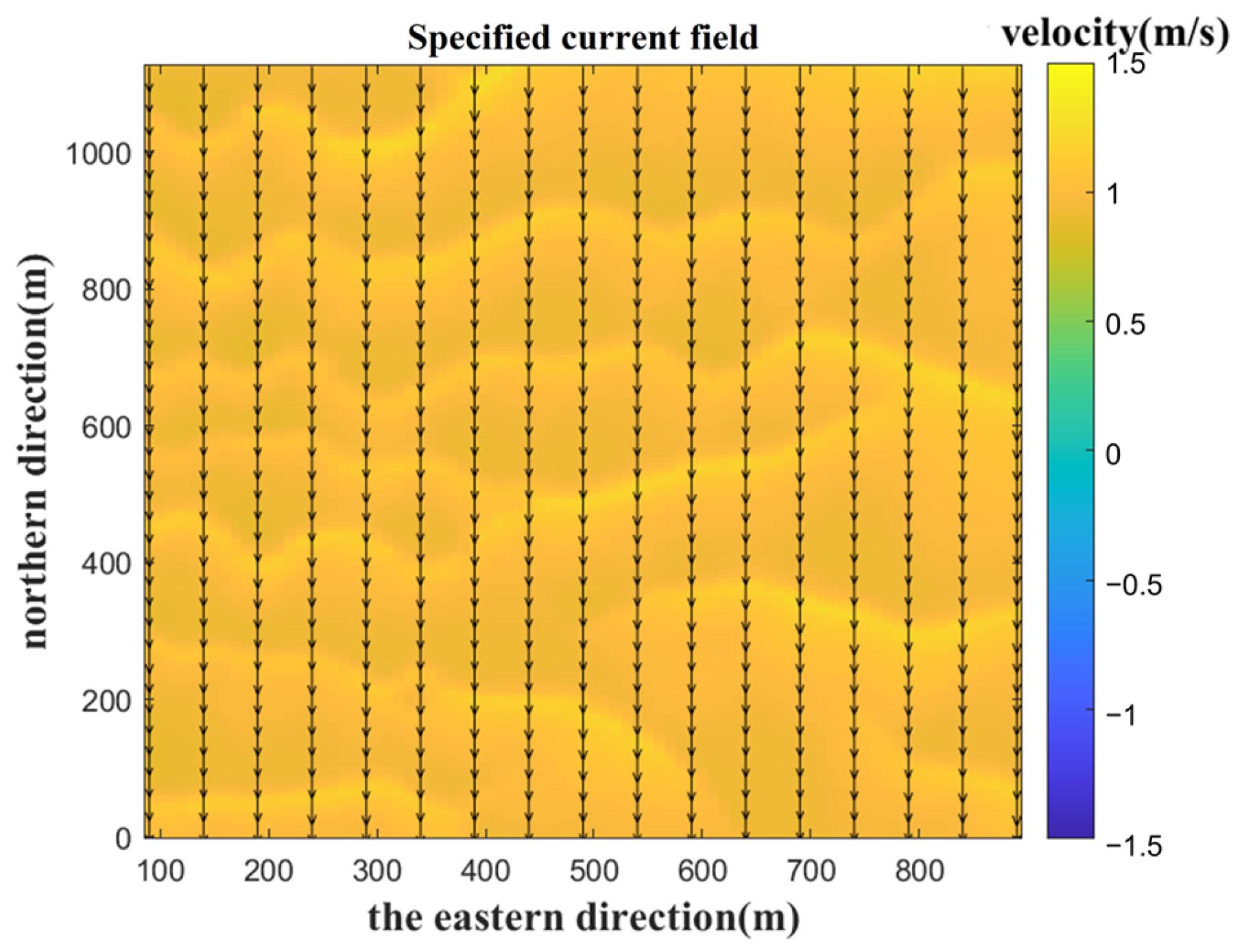
2.3. Simulation Framework
3. Results
3.1. Effect of Observation Angle
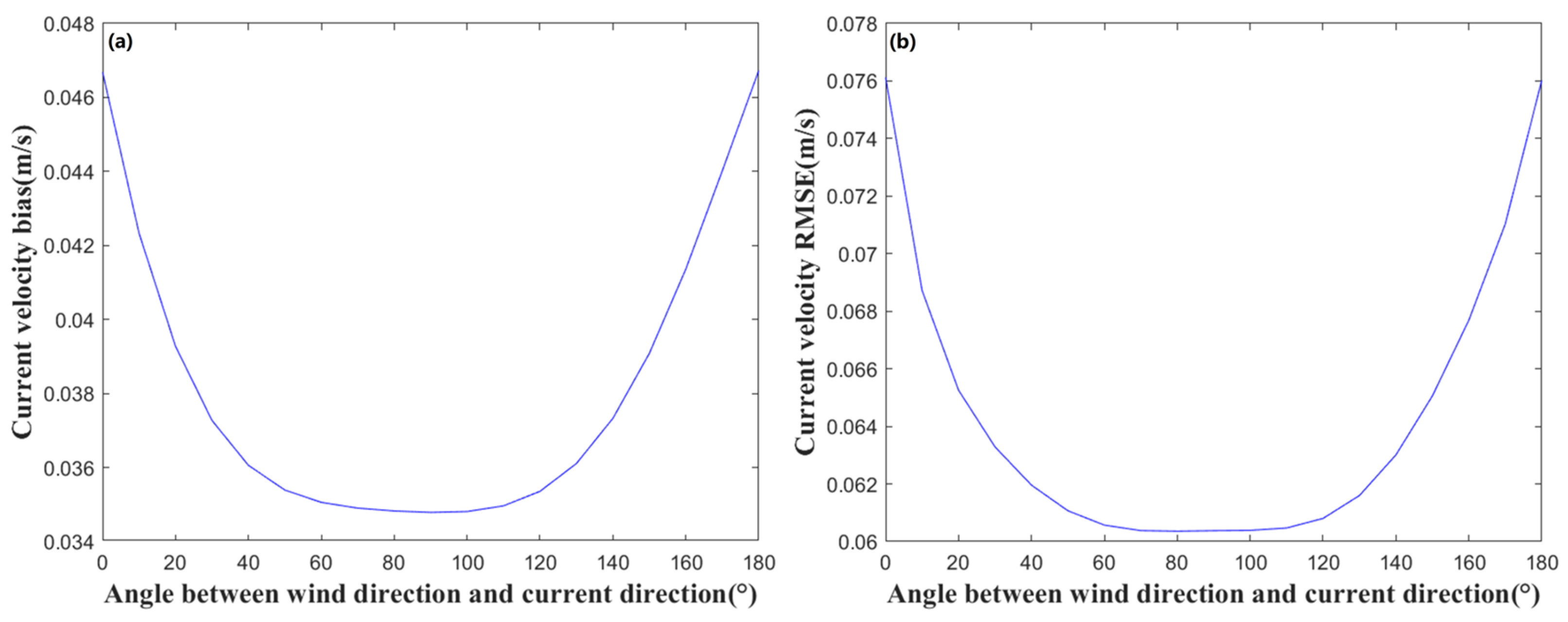
3.2. Effect of Wind and Current Direction
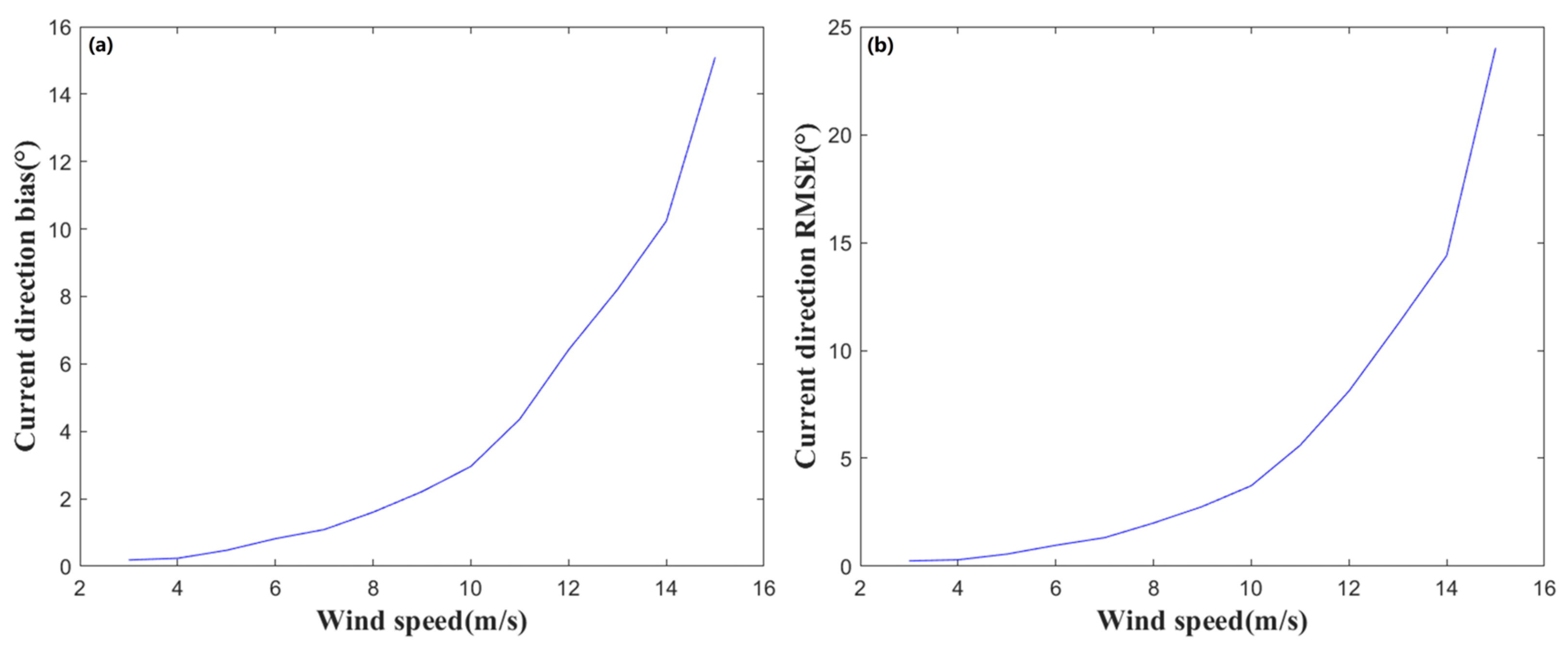
3.3. Effect of Wind Speed
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morrow, R.; Fu, L.-L.; Rio, M.-H.; Ray, R.; Prandi, P.; Le Traon, P.-Y.; Benveniste, J. Ocean Circulation from Space. Surv. Geophys. 2023, 44, 1243–1286. [Google Scholar] [CrossRef]
- Moiseev, A.; Johnsen, H.; Hansen, M.W.; Johannessen, J.A. Evaluation of Radial Ocean Surface Currents Derived from Sentinel-1 IW Doppler Shift Using Coastal Radar and Lagrangian Surface Drifter Observations. JGR Ocean. 2020, 125, e2019JC015743. [Google Scholar] [CrossRef]
- Laurindo, L.C.; Mariano, A.J.; Lumpkin, R. An Improved Near-Surface Velocity Climatology for the Global Ocean from Drifter Observations. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2017, 124, 73–92. [Google Scholar] [CrossRef]
- Du, Y.; Dong, X.; Jiang, X.; Zhang, Y.; Zhu, D.; Sun, Q.; Wang, Z.; Niu, X.; Chen, W.; Zhu, C.; et al. Ocean Surface Current Multiscale Observation Mission (OSCOM): Simultaneous Measurement of Ocean Surface Current, Vector Wind, and Temperature. Prog. Oceanogr. 2021, 193, 102531. [Google Scholar] [CrossRef]
- Espenes, H.; Carrasco, A.; Dagestad, K.-F.; Christensen, K.H.; Drivdal, M.; Isachsen, P.E. Stokes Drift in Crossing Windsea and Swell, and Its Effect on near-Shore Particle Transport in Lofoten, Northern Norway. Ocean Model. 2024, 191, 102407. [Google Scholar] [CrossRef]
- Deyle, L.; Badewien, T.H.; Wurl, O.; Meyerjürgens, J. Lagrangian Surface Drifter Observations in the North Sea: An Overview of High-Resolution Tidal Dynamics and Surface Currents. Earth Syst. Sci. Data 2024, 16, 2099–2112. [Google Scholar] [CrossRef]
- Kulikova, D.Y.; Gorbunov, I.G. Analysis of the Sea Surface Parameters by Doppler X-Band Radar in the Coastal Zone of the Black Sea. In Proceedings of the 2019 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Saint Petersburg and Moscow, Russia, 28–31 January 2019; pp. 1179–1182. [Google Scholar]
- Devi, G.K.; Ganasri, B.P.; Dwarakish, G.S. Applications of Remote Sensing in Satellite Oceanography: A Review. Aquat. Procedia 2015, 4, 579–584. [Google Scholar] [CrossRef]
- Perez, E.; Andres, M.; Gawarkiewicz, G. Is the Regime Shift in Gulf Stream Warm Core Rings Detected by Satellite Altimetry? An Inter-Comparison of Eddy Identification and Tracking Products. JGR Ocean. 2024, 129, e2023JC020761. [Google Scholar] [CrossRef]
- De Carlo, M.; Ardhuin, F. Along-Track Resolution and Uncertainty of Altimeter-Derived Wave Height and Sea Level: Re-Defining the Significant Wave Height in Extreme Storms. JGR Ocean. 2024, 129, e2023JC020832. [Google Scholar] [CrossRef]
- Miao, X.; Wang, J.; Yang, Z.; Mao, P.; Miao, H. Wet Tropospheric Correction Methods for Wide-Swath Altimeters. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4210317. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, W.; Guo, Z.; Xuan, J. The Ocean Surface Current in the East China Sea Computed by the Geostationary Ocean Color Imager Satellite. Remote Sens. 2023, 15, 2210. [Google Scholar] [CrossRef]
- Kugusheva, A.; Bull, H.; Moschos, E.; Ioannou, A.; Le Vu, B.; Stegner, A. Ocean Satellite Data Fusion for High-Resolution Surface Current Maps. Remote Sens. 2024, 16, 1182. [Google Scholar] [CrossRef]
- Yang, X.; Chong, J.; Zhao, Y. Sea Surface Current Retrieval From Sequential SAR and Ocean Color Images for Eddy Kinematics Analysis: A Case Study in the Northern Tyrrhenian Sea. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10126–10136. [Google Scholar] [CrossRef]
- Ye, F.; Hao, Z.; Pan, D. An Optimization Method Based on Decorrelation Scales Analysis for Improving Surface Currents Retrieval From Sea Surface Temperature. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Hauser, D.; Abdalla, S.; Ardhuin, F.; Bidlot, J.-R.; Bourassa, M.; Cotton, D.; Gommenginger, C.; Evers-King, H.; Johnsen, H.; Knaff, J.; et al. Satellite Remote Sensing of Surface Winds, Waves, and Currents: Where Are We Now? Surv. Geophys. 2023, 44, 1357–1446. [Google Scholar] [CrossRef]
- Martin, A.C.H.; Gommenginger, C.; Marquez, J.; Doody, S.; Navarro, V.; Buck, C. Wind-wave-induced Velocity in ATI SAR Ocean Surface Currents: First Experimental Evidence from an Airborne Campaign. JGR Ocean. 2016, 121, 1640–1653. [Google Scholar] [CrossRef]
- Gao, L.; Guo, Y.; Li, X. Weekly Green Tide Mapping in the Yellow Sea with Deep Learning: Integrating Optical and Synthetic Aperture Radar Ocean Imagery. Earth Syst. Sci. Data 2024, 16, 4189–4207. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.-F. Direct Ocean Surface Velocity Measurements from Space: Improved Quantitative Interpretation of Envisat ASAR Observations. Geophys. Res. Lett. 2008, 35, L22608. [Google Scholar] [CrossRef]
- Carande, R.E. Estimating Ocean Coherence Time Using Dual-Baseline Interferometric Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 1994, 32, 846–854. [Google Scholar] [CrossRef]
- Hansen, M.W.; Collard, F.; Dagestad, K.-F.; Johannessen, J.A.; Fabry, P.; Chapron, B. Retrieval of Sea Surface Range Velocities From Envisat ASAR Doppler Centroid Measurements. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3582–3592. [Google Scholar] [CrossRef]
- Johnsen, H.; Nilsen, V.; Engen, G.; Mouche, A.A.; Collard, F. Ocean Doppler Anomaly and Ocean Surface Current from Sentinel 1 Tops Mode. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Beijing, China, 2016; pp. 3993–3996. [Google Scholar]
- Martin, A.C.H.; Gommenginger, C.P.; Jacob, B.; Staneva, J. First Multi-Year Assessment of Sentinel-1 Radial Velocity Products Using HF Radar Currents in a Coastal Environment. Remote Sens. Environ. 2022, 268, 112758. [Google Scholar] [CrossRef]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct Measurements of Ocean Surface Velocity from Space: Interpretation and Validation. J. Geophys. Res. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, L.; Wang, J.; Miao, H.; Zhang, Q. Extrapolation of Electromagnetic Pointing Error Corrections for Sentinel-1 Doppler Currents from Land Areas to the Open Ocean. Remote Sens. Environ. 2023, 297, 113788. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Liu, L.; Miao, H.; Miao, X.; Zhang, Q. Estimating Effects of Wind and Waves on the Doppler Centroid Frequency Shift for the SAR Retrieval of Ocean Currents. Remote Sens. Environ. 2024, 311, 114312. [Google Scholar] [CrossRef]
- Romeiser, R.; Hirsch, O. Possibilities and Limitations of Current Measurements by Airborne and Spaceborne Along-Track Interferometric SAR. In Proceedings of the IGARSS 2001, Scanning the Present and Resolving the Future, Proceedings, IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No.01CH37217), Sydney, NSW, Australia, 9–13 July 2001; IEEE: Sydney, NSW, Australia, 2001; Volume 1, pp. 575–577. [Google Scholar]
- Romeiser, R.; Suchandt, S.; Runge, H.; Steinbrecher, U.; Grunler, S. First Analysis of TerraSAR-X Along-Track InSAR-Derived Current Fields. IEEE Trans. Geosci. Remote Sens. 2010, 48, 820–829. [Google Scholar] [CrossRef]
- Romeiser, R.; Runge, H.; Suchandt, S.; Kahle, R.; Rossi, C.; Bell, P.S. Quality Assessment of Surface Current Fields From TerraSAR-X and TanDEM-X Along-Track Interferometry and Doppler Centroid Analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2759–2772. [Google Scholar] [CrossRef]
- Rashid, M.; Gierull, C.H. Retrieval of Ocean Surface Radial Velocities With RADARSAT-2 Along-Track Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9597–9608. [Google Scholar] [CrossRef]
- Yuan, X.; Lin, M.; Han, B.; Zhao, L.; Wang, W.; Sun, J.; Wang, W. Observing Sea Surface Current by Gaofen-3 Satellite Along-Track Interferometric SAR Experimental Mode. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7762–7770. [Google Scholar] [CrossRef]
- Fernández-Prieto, D.; Sabia, R. Remote Sensing Advances for Earth System Science: The ESA Changing Earth Science Network: Projects 2009–2011; SpringerBriefs in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-32520-5. [Google Scholar]
- Li, Y.; Chong, J.; Sun, K.; Zhao, Y.; Yang, X. Measuring Ocean Surface Current in the Kuroshio Region Using Gaofen-3 SAR Data. Appl. Sci. 2021, 11, 7656. [Google Scholar] [CrossRef]
- Seppke, B.; Gade, M.; Dreschler-Fischer, L. From Multi-Sensor Tracking of Sea Surface Films to Mesoscale and Sub-Mesoscale Sea Surface Current Fields. In Proceedings of the SPIE Remote Sensing, Dresden, Germany, 23–26 September 2013; Volume 8888, pp. 86–96. [Google Scholar]
- Yang, X.; Chong, J.; Diao, L. Estimating MCC Template Size for Ocean Surface Currents Extraction from Sequential SAR Images. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 21 2021; IEEE: Hangzhou, China, 2021; pp. 2859–2862. [Google Scholar]
- Li, Y.; Chong, J.; Li, Z. A Simulation Method of Two-Dimensional Sea-Surface Current Field for Trajectory Crossing Spaceborne SAR. Appl. Sci. 2022, 12, 5900. [Google Scholar] [CrossRef]
- Wang, A.; Wang, X.; Chen, J.; Guo, L.; Huang, H. Wave Spectrum Retrieval Method Based on Full-Link Ocean Surface SAR Imaging Simulation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5219120. [Google Scholar] [CrossRef]
- Wang, X.; Qi, R.; Yao, X.; Xu, C.; Chao, X. High-Precision Simulation of Dynamic Oceans Synthetic Aperture Radar Imaging and Its Typical Application. J. Radars 2025, 14, 712–734. [Google Scholar] [CrossRef]

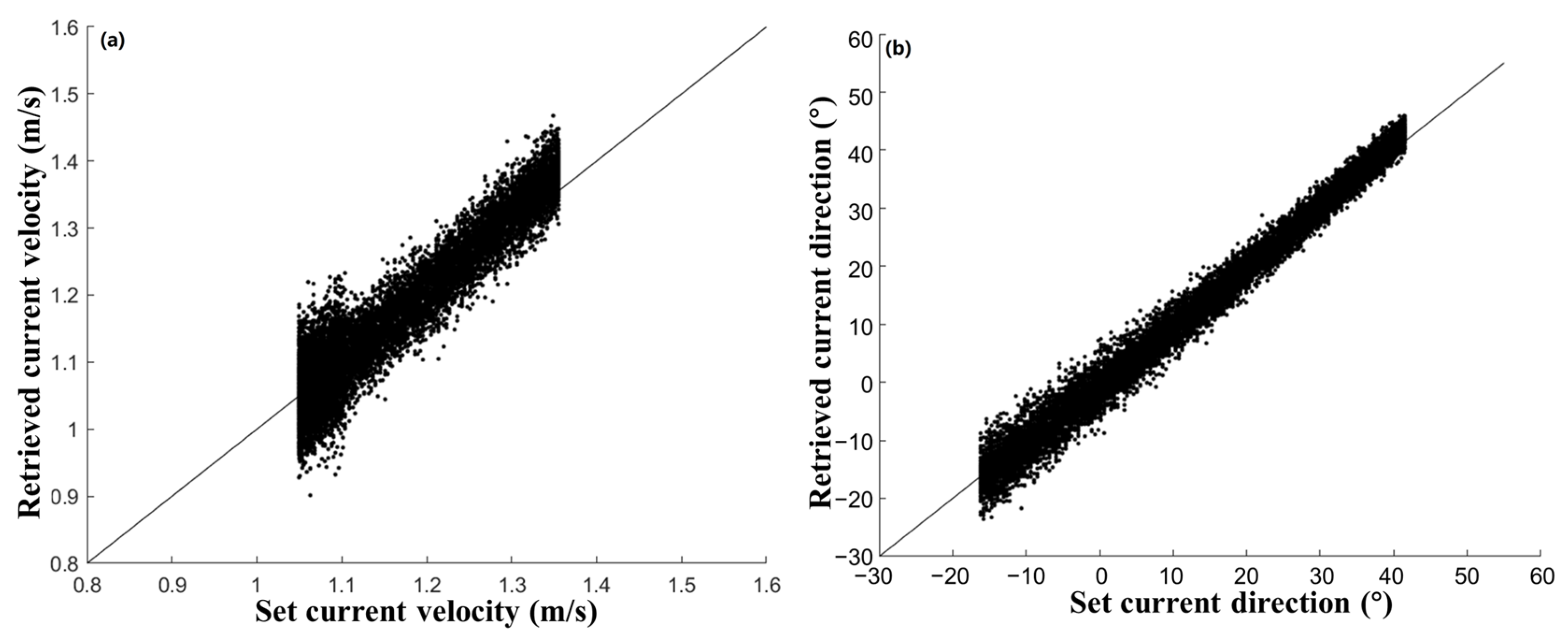

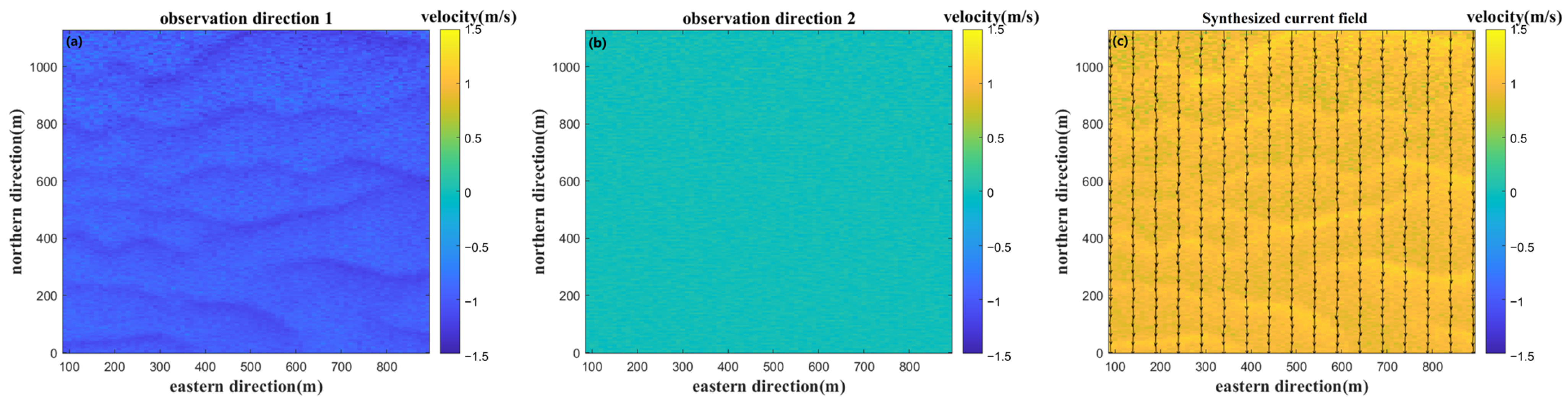
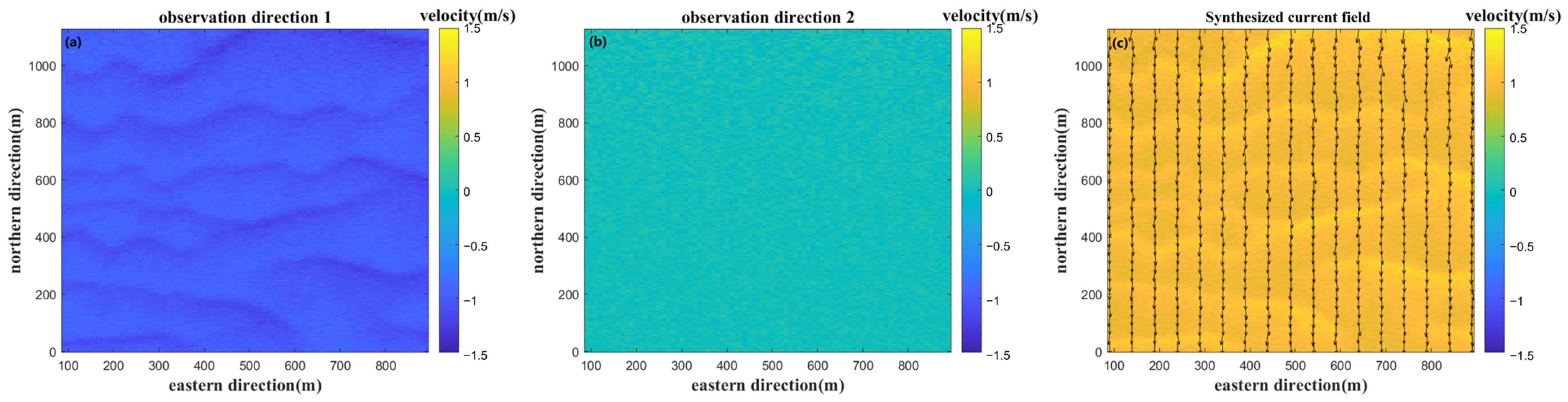

| r | Bias (m/s) | RMSE (m/s) | |
|---|---|---|---|
| current velocity | 0.88 | 0.02 | 0.05 |
| current direction | 0.99 | 1.09 | 2.00 |
| Angle | Current Velocity | Current Direction | ||
|---|---|---|---|---|
| Bias (m/s) | RMSE (m/s) | Bias (°) | RMSE (°) | |
| 0° | 0.03 | 0.07 | 1.14 | 2.00 |
| 90° | 0.02 | 0.05 | 1.95 | 3.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Miao, X.; Wan, Y.; Zhang, J.; Miao, H. Simulation Study of the Effect of Multi-Angle ATI-SAR on Sea Surface Current Retrieval Accuracy. Remote Sens. 2025, 17, 3383. https://doi.org/10.3390/rs17193383
Chen J, Miao X, Wan Y, Zhang J, Miao H. Simulation Study of the Effect of Multi-Angle ATI-SAR on Sea Surface Current Retrieval Accuracy. Remote Sensing. 2025; 17(19):3383. https://doi.org/10.3390/rs17193383
Chicago/Turabian StyleChen, Jiabao, Xiangying Miao, Yong Wan, Jiahui Zhang, and Hongli Miao. 2025. "Simulation Study of the Effect of Multi-Angle ATI-SAR on Sea Surface Current Retrieval Accuracy" Remote Sensing 17, no. 19: 3383. https://doi.org/10.3390/rs17193383
APA StyleChen, J., Miao, X., Wan, Y., Zhang, J., & Miao, H. (2025). Simulation Study of the Effect of Multi-Angle ATI-SAR on Sea Surface Current Retrieval Accuracy. Remote Sensing, 17(19), 3383. https://doi.org/10.3390/rs17193383






