Spatial/Spectral-Frequency Adaptive Network for Hyperspectral Image Reconstruction in CASSI
Abstract
Highlights
- We propose SSFAN, a novel dual-branch transformer network that integrates spatial and channel attention with frequency-domain learning (via a dedicated FDT module and loss) for high-fidelity HSI reconstruction in CASSI.
- The introduced channel compression and expansion modules effectively optimize the computational efficiency of the network, enabling superior detail preservation with moderate resource consumption.
- The integrated spatial/spectral-frequency learning framework achieves breakthrough reconstruction accuracy by simultaneously modeling multi-domain features, particularly in recovering fine textures and suppressing noise.
- This work provides a practical and efficient solution for high-quality hyperspectral imaging, balancing performance and complexity for real-world applications.
Abstract
1. Introduction
2. Related Works
2.1. E2E Neural Networks for CASSI Reconstruction
2.2. Frequency-Domain Processing
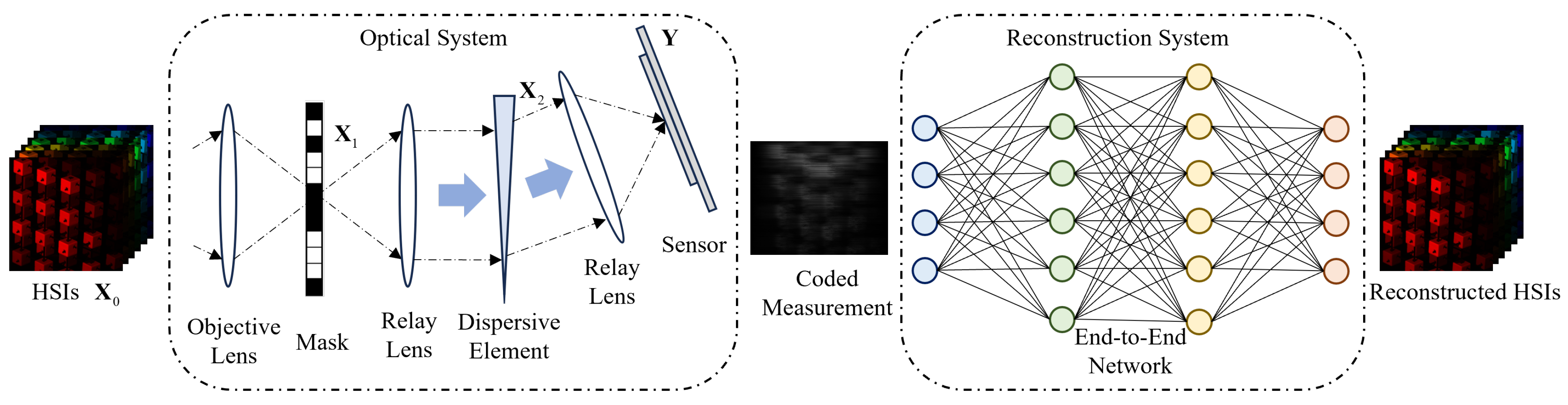
3. Image Formation Model of SD-CASSI
4. Problem Formulation
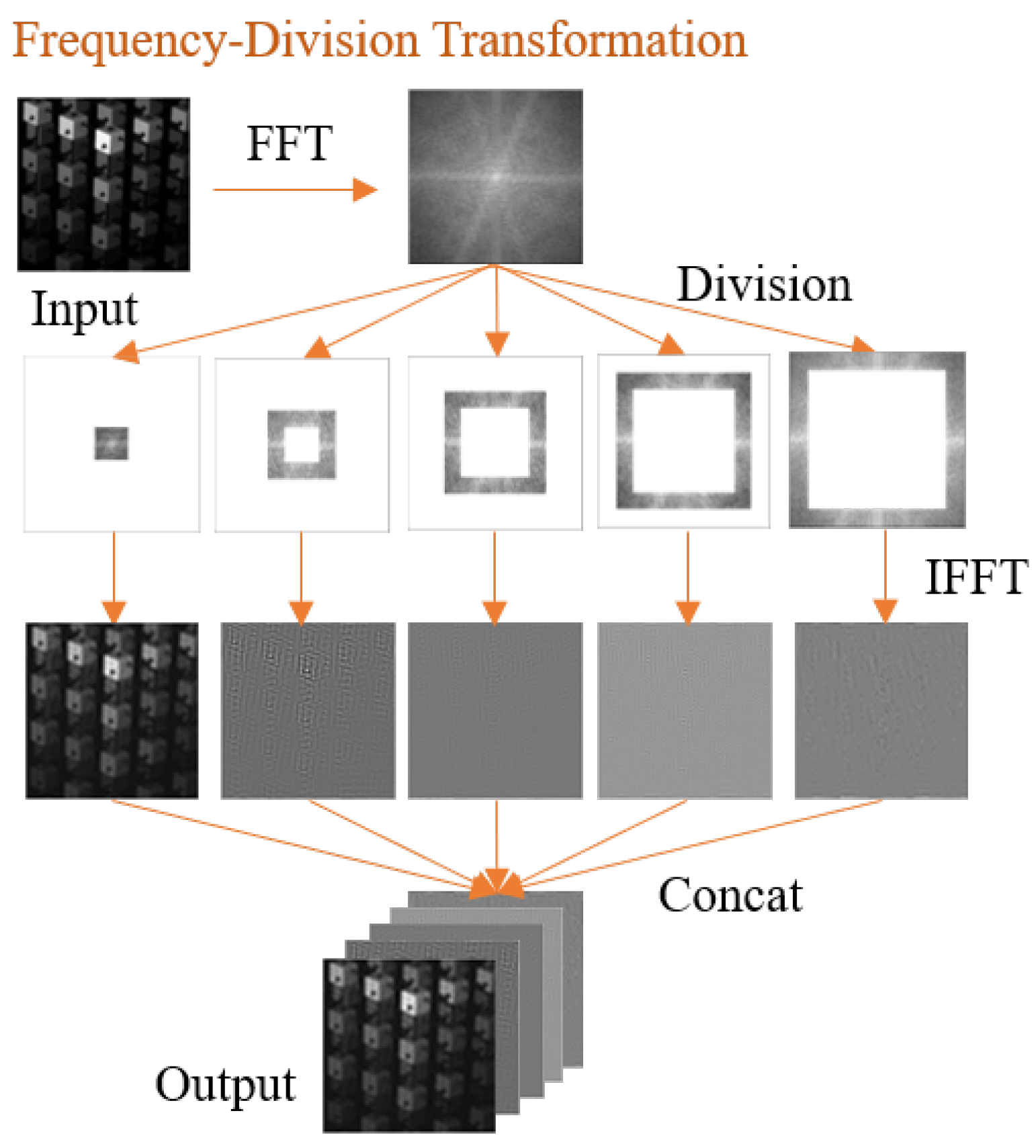
4.1. Frequency-Division Transformation
| Algorithm 1 Frequency-Division Transformation |
Input: Data cube .
|
4.2. Reconstruction Model
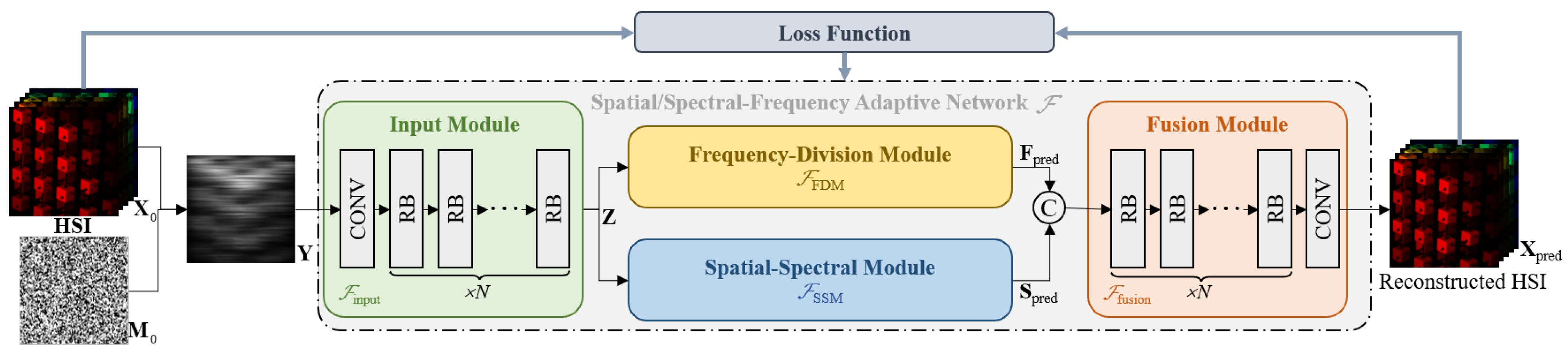
5. Proposed Method
5.1. Network Framework
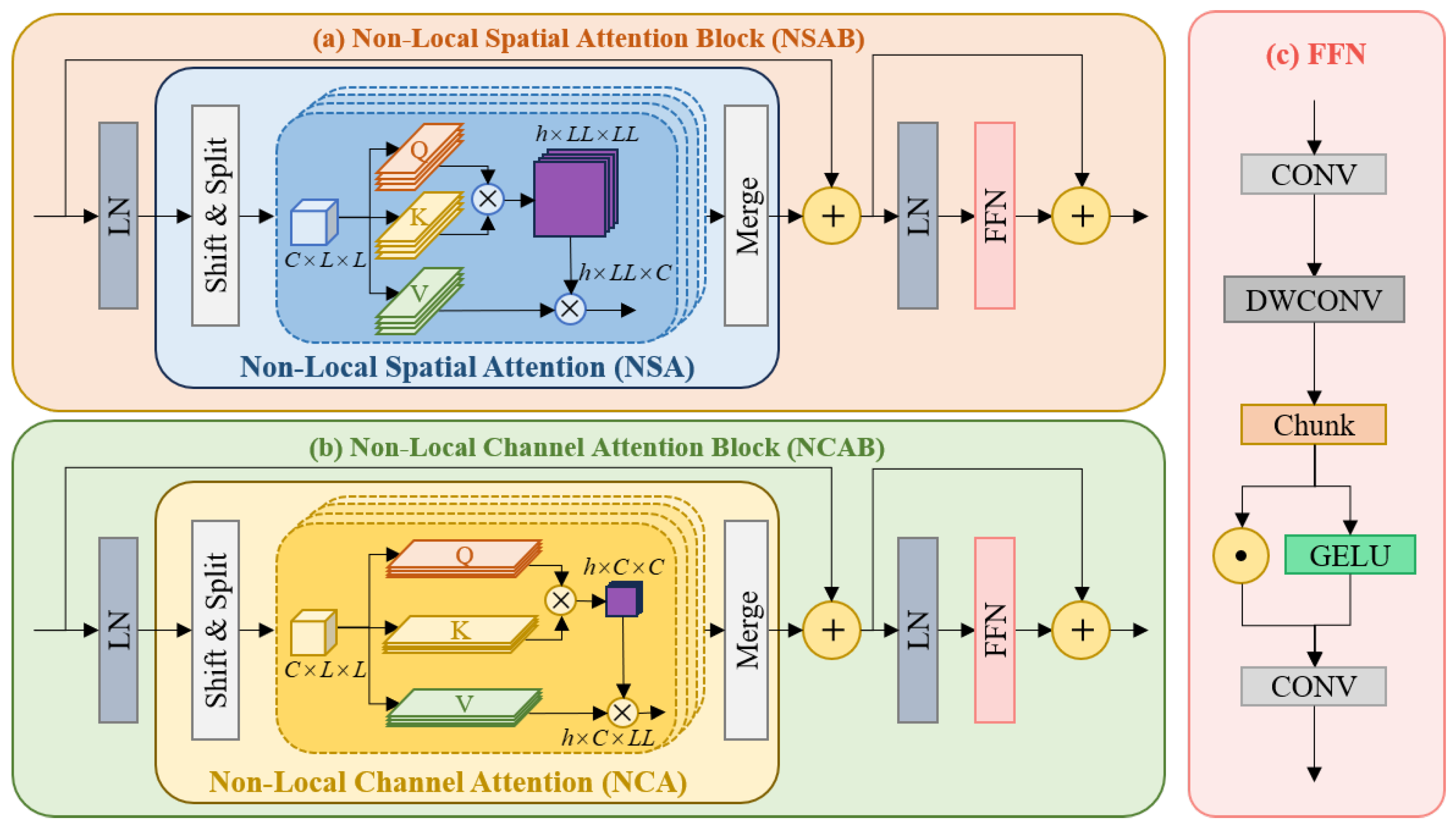
5.2. Spatial–Spectral Module (SSM)
5.3. Frequency-Division Module (FDM)
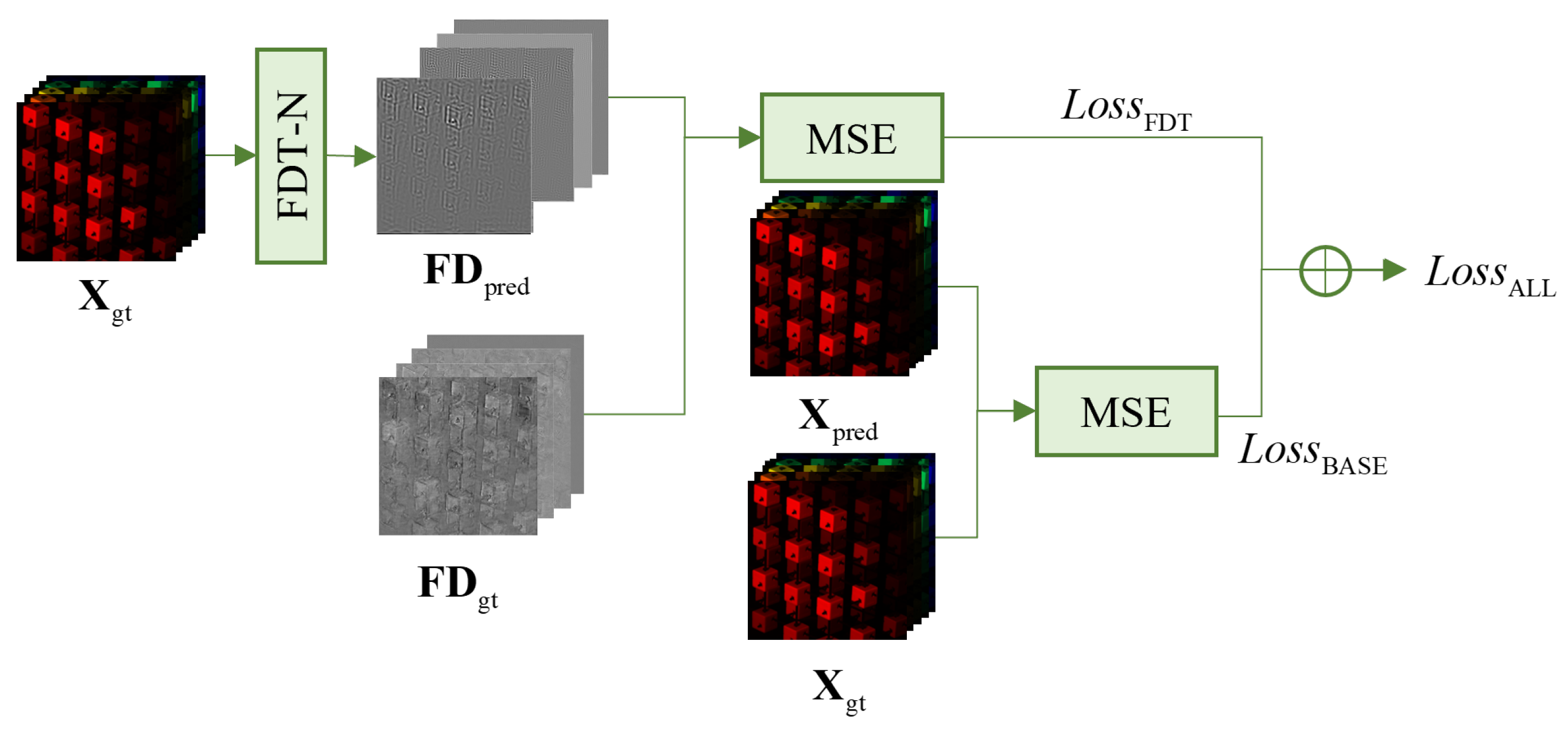
5.4. Loss Function
6. Experimental Results
6.1. Experiment Setup
6.2. Ablation Study
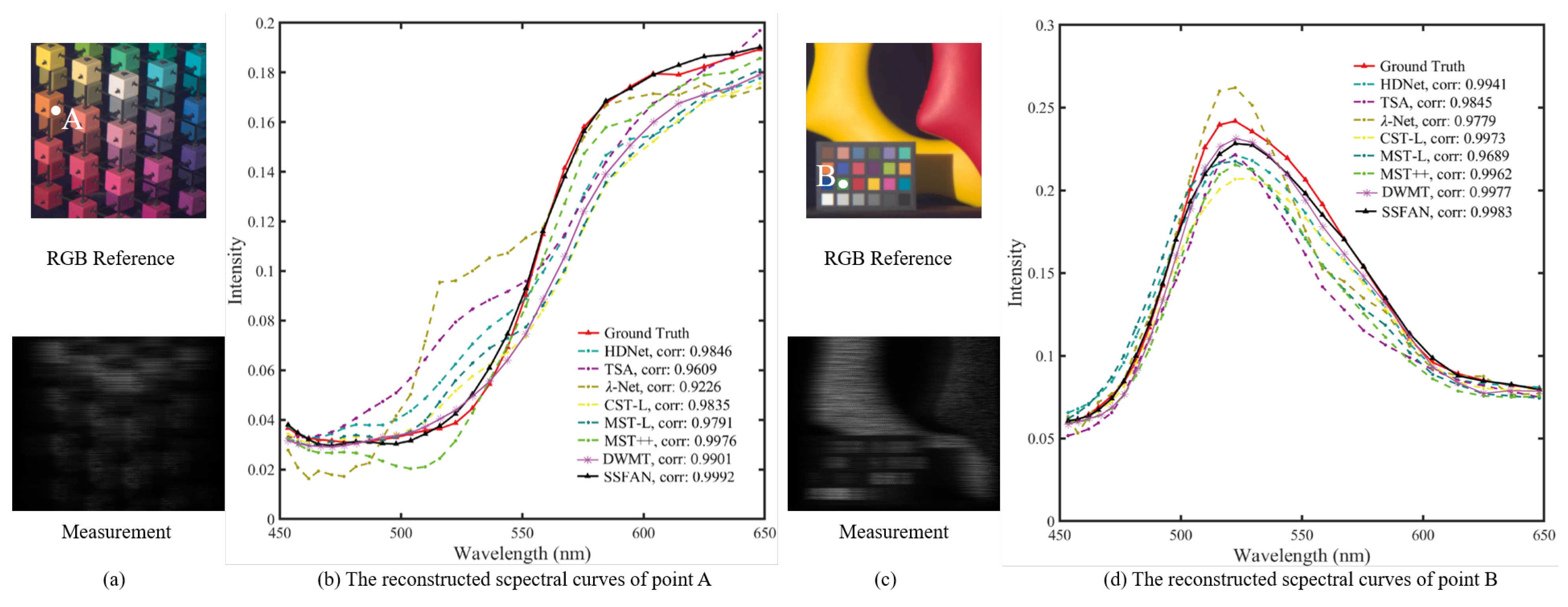
6.3. Performance Evaluation on a Simulation Dataset
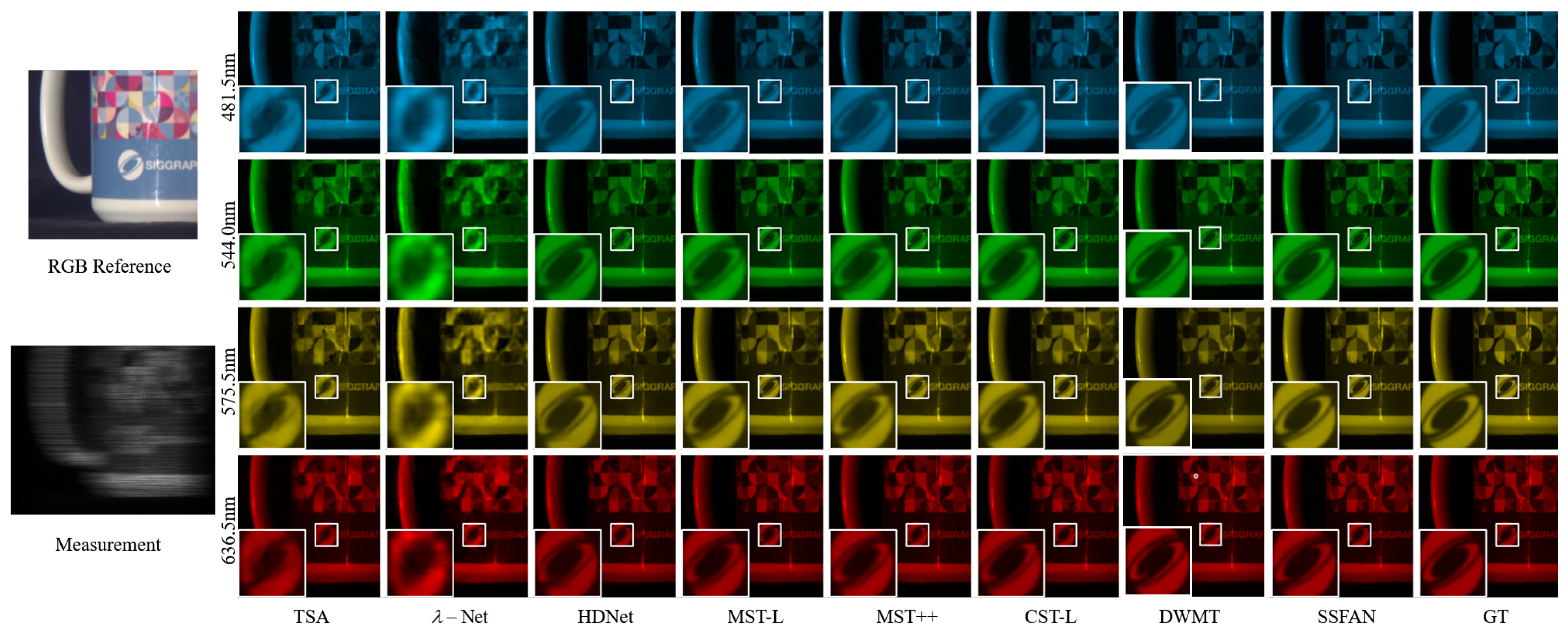
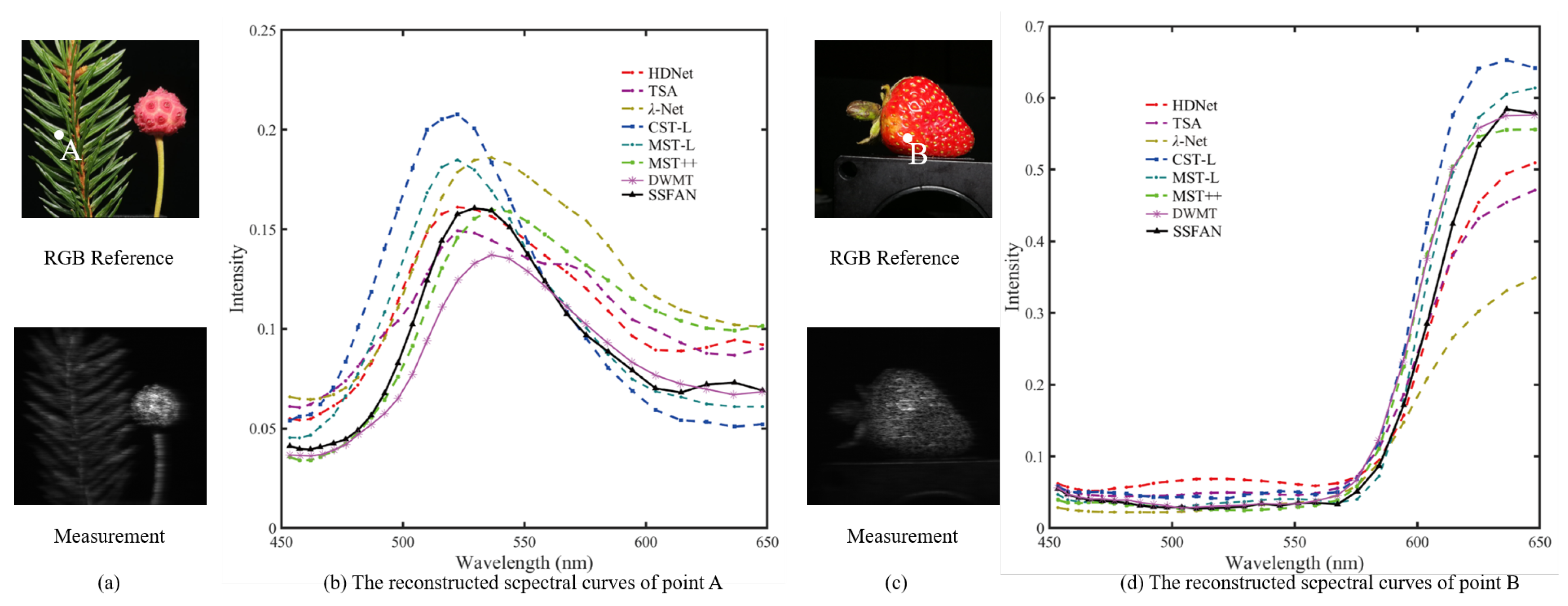
6.4. Performance Evaluation with Real CASSI Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Borengasser, M.; Hungate, W.S.; Watkins, R. Hyperspectral Remote Sensing: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Aburaed, N.; Alkhatib, M.Q.; Marshall, S.; Zabalza, J.; Al Ahmad, H. A review of spatial enhancement of hyperspectral remote sensing imaging techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2275–2300. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Ghamisi, P. Spectral-Spatial Classification of Hyperspectral Remote Sensing Images; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Fei, B. Hyperspectral imaging in medical applications. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2019; Volume 32, pp. 523–565. [Google Scholar]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 010901. [Google Scholar] [CrossRef] [PubMed]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hypersectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Yuen, P.W.; Richardson, M. An introduction to hyperspectral imaging and its application for security, surveillance and target acquisition. Imaging Sci. J. 2010, 58, 241–253. [Google Scholar] [CrossRef]
- Briottet, X.; Boucher, Y.; Dimmeler, A.; Malaplate, A.; Cini, A.; Diani, M.; Bekman, H.; Schwering, P.; Skauli, T.; Kasen, I.; et al. Military applications of hyperspectral imagery. In Proceedings of the Targets and Backgrounds XII: Characterization and Representation, Orlando (Kissimmee), FL, USA, 17–18 April 2006; SPIE: Bellingham, WA, USA, 2006; Volume 6239, pp. 82–89. [Google Scholar]
- Xiong, F.; Zhou, J.; Qian, Y. Material based object tracking in hyperspectral videos. IEEE Trans. Image Process. 2020, 29, 3719–3733. [Google Scholar] [CrossRef]
- Van Nguyen, H.; Banerjee, A.; Chellappa, R. Tracking via object reflectance using a hyperspectral video camera. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops, San Francisco, CA, USA, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 44–51. [Google Scholar]
- Yuan, X.; Brady, D.J.; Katsaggelos, A.K. Snapshot compressive imaging: Theory, algorithms, and applications. IEEE Signal Process. Mag. 2021, 38, 65–88. [Google Scholar] [CrossRef]
- Gao, L.; Wang, L.V. A review of snapshot multidimensional optical imaging: Measuring photon tags in parallel. Phys. Rep. 2016, 616, 1–37. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, H.; Xu, Z.; Li, Q.; Feng, H.; Chen, Y.; Jiang, T.; Xu, W. Practical snapshot hyperspectral imaging with DOE. Opt. Lasers Eng. 2022, 156, 107098. [Google Scholar] [CrossRef]
- Xu, N.; Xu, H.; Chen, S.; Hu, H.; Xu, Z.; Feng, H.; Li, Q.; Jiang, T.; Chen, Y. Snapshot hyperspectral imaging based on equalization designed doe. Opt. Express 2023, 31, 20489–20504. [Google Scholar] [CrossRef]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar] [CrossRef] [PubMed]
- Llull, P.; Liao, X.; Yuan, X.; Yang, J.; Kittle, D.; Carin, L.; Sapiro, G.; Brady, D.J. Coded aperture compressive temporal imaging. Opt. Express 2013, 21, 10526–10545. [Google Scholar] [CrossRef]
- He, K.; Wang, X.; Wang, Z.W.; Yi, H.; Scherer, N.F.; Katsaggelos, A.K.; Cossairt, O. Snapshot multifocal light field microscopy. Opt. Express 2020, 28, 12108–12120. [Google Scholar] [CrossRef]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive coded aperture spectral imaging: An introduction. IEEE Signal Process. Mag. 2013, 31, 105–115. [Google Scholar] [CrossRef]
- Yin, X.; Su, L.; Chen, X.; Liu, H.; Yan, Q.; Yuan, Y. Hyperspectral Image Reconstruction of SD-CASSI Based on Nonlocal Low-Rank Tensor Prior. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Gehm, M.E.; John, R.; Brady, D.J.; Willett, R.M.; Schulz, T.J. Single-shot compressive spectral imaging with a dual-disperser architecture. Opt. Express 2007, 15, 14013–14027. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Liu, L.; Jia, Y.; Zheng, H.; Xu, C.; Xue, L. A refinement boosted and attention guided deep FISTA reconstruction framework for compressive spectral imaging. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Suo, J.; Brady, D.J.; Dai, Q. Rank minimization for snapshot compressive imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2990–3006. [Google Scholar] [CrossRef]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2539–2543. [Google Scholar]
- Zhang, S.; Wang, L.; Fu, Y.; Zhong, X.; Huang, H. Computational hyperspectral imaging based on dimension-discriminative low-rank tensor recovery. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10183–10192. [Google Scholar]
- Chan, S.H.; Wang, X.; Elgendy, O.A. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications. IEEE Trans. Comput. Imaging 2016, 3, 84–98. [Google Scholar] [CrossRef]
- Qiao, M.; Liu, X.; Yuan, X. Snapshot spatial–temporal compressive imaging. Opt. Lett. 2020, 45, 1659–1662. [Google Scholar] [CrossRef]
- Meng, Z.; Yu, Z.; Xu, K.; Yuan, X. Self-supervised neural networks for spectral snapshot compressive imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 2622–2631. [Google Scholar]
- Zheng, S.; Liu, Y.; Meng, Z.; Qiao, M.; Tong, Z.; Yang, X.; Han, S.; Yuan, X. Deep plug-and-play priors for spectral snapshot compressive imaging. Photonics Res. 2021, 9, B18–B29. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Y.; Suo, J.; Durand, F.; Dai, Q. Plug-and-play algorithms for video snapshot compressive imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7093–7111. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Y.; Suo, J.; Dai, Q. Plug-and-play algorithms for large-scale snapshot compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1447–1457. [Google Scholar]
- Ma, J.; Liu, X.Y.; Shou, Z.; Yuan, X. Deep tensor admm-net for snapshot compressive imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 10223–10232. [Google Scholar]
- Huang, T.; Dong, W.; Yuan, X.; Wu, J.; Shi, G. Deep gaussian scale mixture prior for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 16216–16225. [Google Scholar]
- Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Ding, H.; Zhang, Y.; Timofte, R.; Gool, L.V. Degradation-aware unfolding half-shuffle transformer for spectral compressive imaging. Adv. Neural Inf. Process. Syst. 2022, 35, 37749–37761. [Google Scholar]
- Li, M.; Fu, Y.; Liu, J.; Zhang, Y. Pixel adaptive deep unfolding transformer for hyperspectral image reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 12959–12968. [Google Scholar]
- Miao, X.; Yuan, X.; Pu, Y.; Athitsos, V. l-net: Reconstruct hyperspectral images from a snapshot measurement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4059–4069. [Google Scholar]
- Meng, Z.; Ma, J.; Yuan, X. End-to-end low cost compressive spectral imaging with spatial-spectral self-attention. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 187–204. [Google Scholar]
- Hu, X.; Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Hdnet: High-resolution dual-domain learning for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 17542–17551. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Mask-guided spectral-wise transformer for efficient hyperspectral image reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 17502–17511. [Google Scholar]
- Cai, Y.; Lin, J.; Lin, Z.; Wang, H.; Zhang, Y.; Pfister, H.; Timofte, R.; Van Gool, L. Mst++: Multi-stage spectral-wise transformer for efficient spectral reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 745–755. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Van Gool, L. Coarse-to-fine sparse transformer for hyperspectral image reconstruction. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 686–704. [Google Scholar]
- Luo, F.; Chen, X.; Gong, X.; Wu, W.; Guo, T. Dual-window multiscale transformer for hyperspectral snapshot compressive imaging. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; Volume 38, pp. 3972–3980. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Bahdanau, D. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaizer, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; proceedings, part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Mehraban, S.; Adeli, V.; Taati, B. Motionagformer: Enhancing 3d human pose estimation with a transformer-gcnformer network. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 6920–6930. [Google Scholar]
- Zhou, S.; Chen, D.; Pan, J.; Shi, J.; Yang, J. Adapt or perish: Adaptive sparse transformer with attentive feature refinement for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2952–2963. [Google Scholar]
- Gao, J.; Zhang, Y.; Geng, X.; Tang, H.; Bhatti, U.A. PE-Transformer: Path enhanced transformer for improving underwater object detection. Expert Syst. Appl. 2024, 246, 123253. [Google Scholar] [CrossRef]
- Xu, L.; Bennamoun, M.; Boussaid, F.; Laga, H.; Ouyang, W.; Xu, D. Mctformer+: Multi-class token transformer for weakly supervised semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 8380–8395. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Chicchi, L.; Buffoni, L.; Febbe, D.; Giambagli, L.; Marino, R.; Fanelli, D. Automatic Input Feature Relevance via Spectral Neural Networks. arXiv 2024, arXiv:2406.01183. [Google Scholar] [CrossRef]
- Fujieda, S.; Takayama, K.; Hachisuka, T. Wavelet convolutional neural networks. arXiv 2018, arXiv:1805.08620. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, W.; Geng, M. Automatic Seizure Detection Based on S-Transform and Deep Convolutional Neural Network. Int. J. Neural Syst. 2020, 30, 1950024. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Xu, Z.Q.J.; Zhang, Y.; Luo, T.; Xiao, Y.; Ma, Z. Frequency principle: Fourier analysis sheds light on deep neural networks. arXiv 2019, arXiv:1901.06523. [Google Scholar] [CrossRef]
- Xu, K.; Qin, M.; Sun, F.; Wang, Y.; Chen, Y.K.; Ren, F. Learning in the frequency domain. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 1740–1749. [Google Scholar]
- Wei, D.; Deng, Y. Redistributed invariant redundant fractional wavelet transform and its application in watermarking algorithm. Expert Syst. Appl. 2025, 262, 125707. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, P.; Jiang, J.; Xiao, P.; Gao, X. FCIR: Rethink aerial image super resolution with Fourier analysis. In Proceedings of the ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Jiang, L.; Dai, B.; Wu, W.; Loy, C.C. Focal frequency loss for image reconstruction and synthesis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 13919–13929. [Google Scholar]
- Karami, A.; Zanj, B.; Sarkaleh, A.K. Persian sign language (PSL) recognition using wavelet transform and neural networks. Expert Syst. Appl. 2011, 38, 2661–2667. [Google Scholar] [CrossRef]
- Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Bhattacharya, A.; Homayouni, S. PolSAR image classification based on deep convolutional neural networks using wavelet transformation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Deng, J.; Guo, Y.; Liu, S.; Zhang, J. MASFF-Net: Multi-azimuth scattering feature fusion network for SAR target recognition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 19425–19440. [Google Scholar] [CrossRef]
- Wan, X.; Chen, F.; Mo, D.; Liu, H.; Li, Z.; Hu, K. FS-CGNet: Frequency Spectral-Channel Fusion and Cross-Scale Global Aggregation Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–22. [Google Scholar] [CrossRef]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef]
- Choi, I.; Jeon, D.S.; Nam, G.; Gutierrez, D.; Kim, M.H. High-quality hyperspectral reconstruction using a spectral prior. ACM Trans. Graph. (TOG) 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]



| Number of Frequency Bands | PSNR | SSIM | SAM |
|---|---|---|---|
| 3 | 36.70 | 0.964 | 0.097 |
| 4 | 36.82 | 0.964 | 0.093 |
| 5 | 37.02 | 0.966 | 0.091 |
| 6 | 36.93 | 0.965 | 0.092 |
| 7 | 36.98 | 0.965 | 0.094 |
| Number of Compressed Channels | PSNR | SSIM | SAM | GFLOPs | Params |
|---|---|---|---|---|---|
| 28 | 36.73 | 0.964 | 0.097 | 89.46 | 4.24 M |
| 40 | 36.91 | 0.964 | 0.095 | 99.29 | 4.97 M |
| 56 | 37.02 | 0.965 | 0.091 | 117.28 | 6.34 M |
| 64 | 36.39 | 0.963 | 0.100 | 128.44 | 7.19 M |
| Model | GFLOPs | Params |
|---|---|---|
| w/o CCE and CEM | 304.08 | 20.82 M |
| w/ CCE and CEM | 117.28 | 6.34 M |
| SSM | FDM | PSNR | SSIM | SAM |
|---|---|---|---|---|
| ✓ | 36.91 | 0.963 | 0.100 | |
| ✓ | 36.77 | 0.965 | 0.976 | |
| ✓ | ✓ | 37.02 | 0.965 | 0.091 |
| Operation | PSNR | SSIM | SAM |
|---|---|---|---|
| FDT | 37.02 | 0.965 | 0.091 |
| Convoluton Layer | 36.69 | 0.965 | 0.095 |
| Methods | Params | GFLOPs | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | Avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30.10 | 28.46 | 27.73 | 37.01 | 26.19 | 28.64 | 26.47 | 26.09 | 27.50 | 27.13 | 28.53 | |||
| -net | 62.64 M | 117.98 | 0.849 | 0.805 | 0.870 | 0.934 | 0.817 | 0.853 | 0.806 | 0.831 | 0.826 | 0.816 | 0.841 |
| 0.247 | 0.304 | 0.272 | 0.420 | 0.285 | 0.454 | 0.246 | 0.481 | 0.277 | 0.454 | 0.344 | |||
| 32.03 | 31.00 | 32.25 | 39.19 | 29.39 | 31.44 | 20.32 | 29.35 | 30.01 | 29.59 | 31.46 | |||
| TSA-Net | 44.25 M | 110.06 | 0.892 | 0.858 | 0.915 | 0.953 | 0.884 | 0.908 | 0.878 | 0.888 | 0.890 | 0.874 | 0.894 |
| 0.152 | 0.181 | 0.129 | 0.146 | 0.117 | 0.169 | 0.133 | 0.199 | 0.134 | 0.167 | 0.153 | |||
| 35.14 | 35.67 | 36.03 | 42.30 | 32.69 | 34.46 | 33.67 | 32.48 | 34.89 | 32.38 | 34.97 | |||
| HDNet | 2.37 M | 154.76 | 0.935 | 0.940 | 0.943 | 0.969 | 0.946 | 0.952 | 0.926 | 0.941 | 0.942 | 0.937 | 0.943 |
| 0.129 | 0.142 | 0.097 | 0.102 | 0.089 | 0.120 | 0.114 | 0.142 | 0.111 | 0.119 | 0.117 | |||
| 35.40 | 35.87 | 36.51 | 42.27 | 32.77 | 34.80 | 35.87 | 32.67 | 35.39 | 32.50 | 35.18 | |||
| MST-L | 2.03 M | 28.15 | 0.941 | 0.944 | 0.953 | 0.973 | 0.947 | 0.955 | 0.925 | 0.948 | 0.949 | 0.941 | 0.957 |
| 0.123 | 0.142 | 0.106 | 0.130 | 0.101 | 0.137 | 0.110 | 0.180 | 0.130 | 0.146 | 0.131 | |||
| 35.80 | 36.23 | 37.34 | 42.63 | 33.38 | 35.38 | 34.35 | 33.71 | 36.67 | 33.38 | 35.99 | |||
| MST++ | 1.33 M | 19.42 | 0.943 | 0.947 | 0.957 | 0.973 | 0.952 | 0.957 | 0.934 | 0.953 | 0.953 | 0.945 | 0.951 |
| 0.118 | 0.130 | 0.080 | 0.121 | 0.081 | 0.115 | 0.103 | 0.145 | 0.100 | 0.116 | 0.111 | |||
| 35.96 | 36.84 | 38.16 | 42.44 | 33.25 | 35.72 | 36.58 | 34.34 | 36.51 | 33.09 | 36.28 | |||
| CST-L | 3.00 M | 27.81 | 0.949 | 0.955 | 0.962 | 0.975 | 0.955 | 0.963 | 0.944 | 0.961 | 0.957 | 0.945 | 0.956 |
| 0.116 | 0.118 | 0.082 | 0.099 | 0.078 | 0.104 | 0.099 | 0.119 | 0.101 | 0.102 | 0.102 | |||
| 36.54 | 37.85 | 38.59 | 44.66 | 34.05 | 36.24 | 35.29 | 34.62 | 37.52 | 34.05 | 36.94 | |||
| DWMT | 14.48 M | 46.71 | 0.957 | 0.963 | 0.964 | 0.984 | 0.962 | 0.970 | 0.948 | 0.967 | 0.965 | 0.958 | 0.964 |
| 0.109 | 0.114 | 0.073 | 0.097 | 0.071 | 0.103 | 0.092 | 0.119 | 0.088 | 0.098 | 0.096 | |||
| 37.41 | 38.85 | 38.19 | 43.84 | 34.85 | 37.07 | 36.14 | 34.80 | 37.42 | 33.82 | 37.24 | |||
| SSFAN | 6.34 M | 117.28 | 0.965 | 0.971 | 0.965 | 0.985 | 0.969 | 0.973 | 0.955 | 0.969 | 0.965 | 0.959 | 0.968 |
| 0.101 | 0.103 | 0.073 | 0.077 | 0.064 | 0.083 | 0.086 | 0.097 | 0.086 | 0.089 | 0.086 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yuan, Y.; Yin, X.; Su, L. Spatial/Spectral-Frequency Adaptive Network for Hyperspectral Image Reconstruction in CASSI. Remote Sens. 2025, 17, 3382. https://doi.org/10.3390/rs17193382
Liu H, Yuan Y, Yin X, Su L. Spatial/Spectral-Frequency Adaptive Network for Hyperspectral Image Reconstruction in CASSI. Remote Sensing. 2025; 17(19):3382. https://doi.org/10.3390/rs17193382
Chicago/Turabian StyleLiu, Hejian, Yan Yuan, Xiaorui Yin, and Lijuan Su. 2025. "Spatial/Spectral-Frequency Adaptive Network for Hyperspectral Image Reconstruction in CASSI" Remote Sensing 17, no. 19: 3382. https://doi.org/10.3390/rs17193382
APA StyleLiu, H., Yuan, Y., Yin, X., & Su, L. (2025). Spatial/Spectral-Frequency Adaptive Network for Hyperspectral Image Reconstruction in CASSI. Remote Sensing, 17(19), 3382. https://doi.org/10.3390/rs17193382







