Improving the Accuracy of Seasonal Crop Coefficients in Grapevine from Sentinel-2 Data
Abstract
Highlights
- This research presents a novel method to increase the accuracy of grapevine crop coefficients using spectrally unmixed vegetation indices from Sentinel-2 open-source data.
- Spectral unmixing improves the prediction accuracy of crop coefficients in Shiraz, Cabernet Sauvignon, and Chardonnay grapevine cultivars, and our models show transferability across regions and cultivars.
- High-accuracy crop coefficients can increase the efficiency of water use by irrigators and thereby improve sustainability.
- The methodology presented here can be applied to other crop parameters that are modelled using low-resolution satellite data.
Abstract
1. Introduction
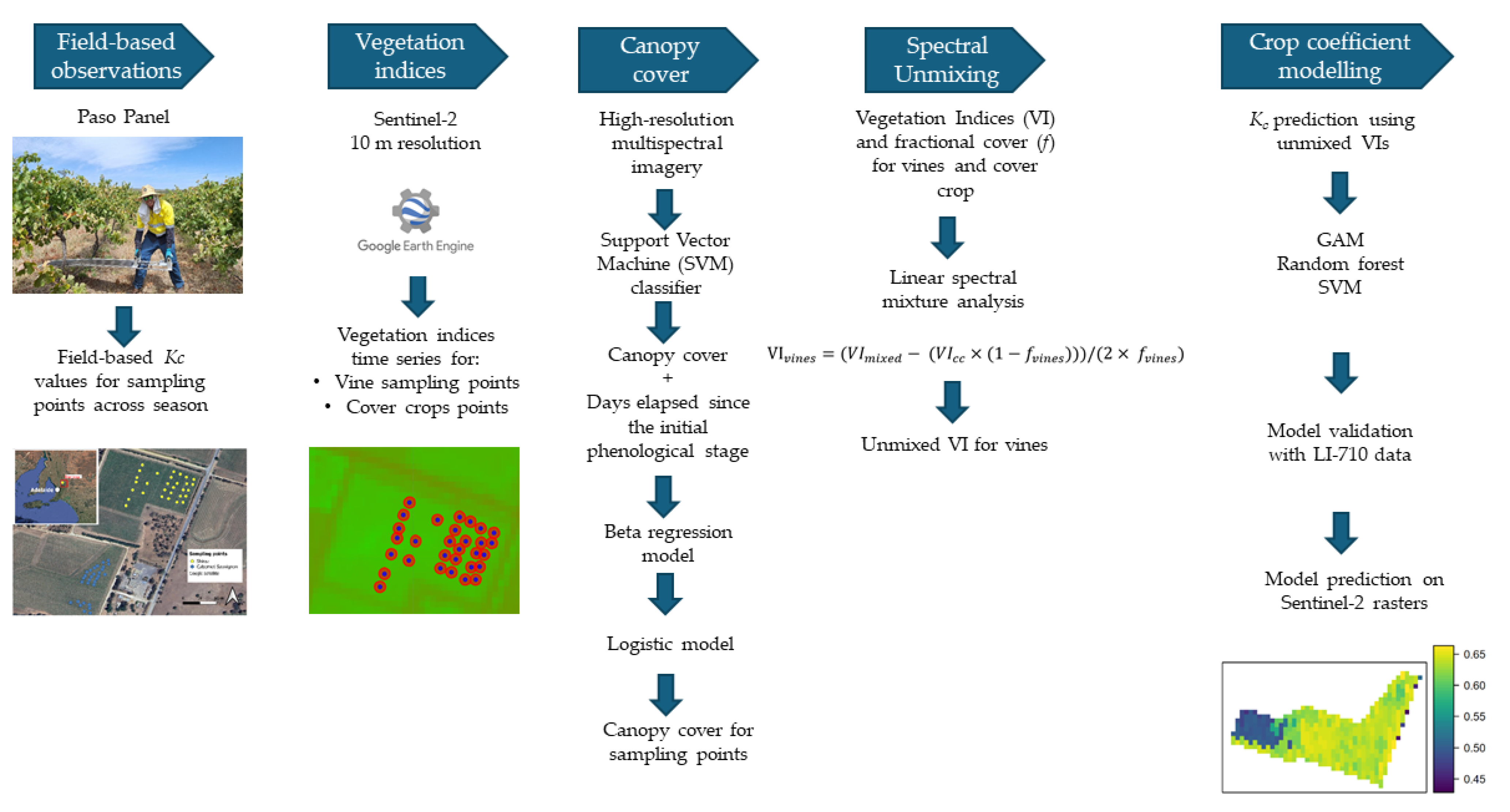
2. Materials and Methods
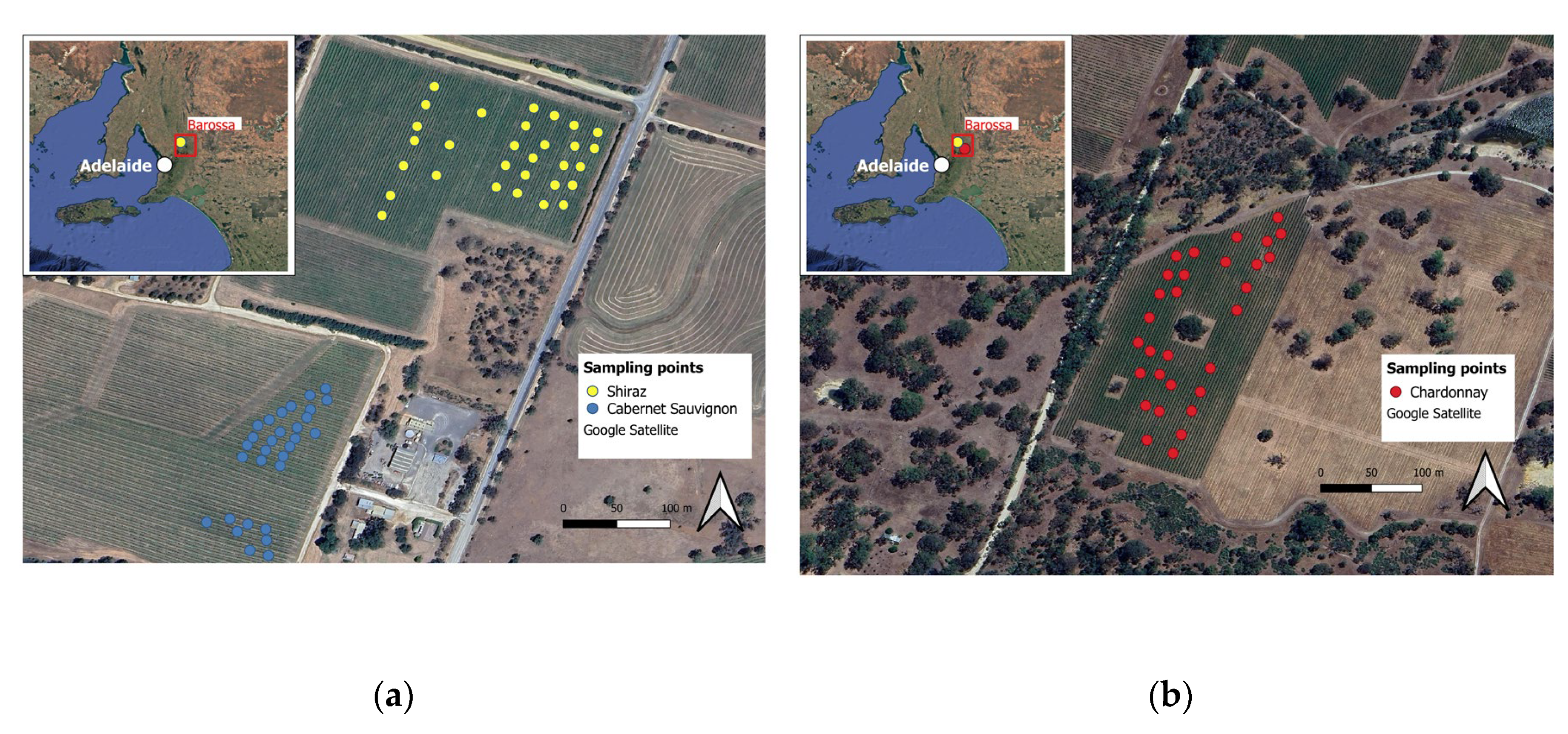
2.1. Study Site
2.2. Crop Coefficient Ground Data
2.3. Remote Sensing Data Acquisition
2.4. Vegetation Indices
2.5. Canopy Cover Data
2.6. Canopy Cover Models
2.7. Spectral Unmixing
2.8. Crop Coefficient Modelling
2.9. Model Validation with Ground Control Data
2.10. Projection to Sentinel-2 Rasters
3. Results
3.1. Crop Coefficient Ground Data
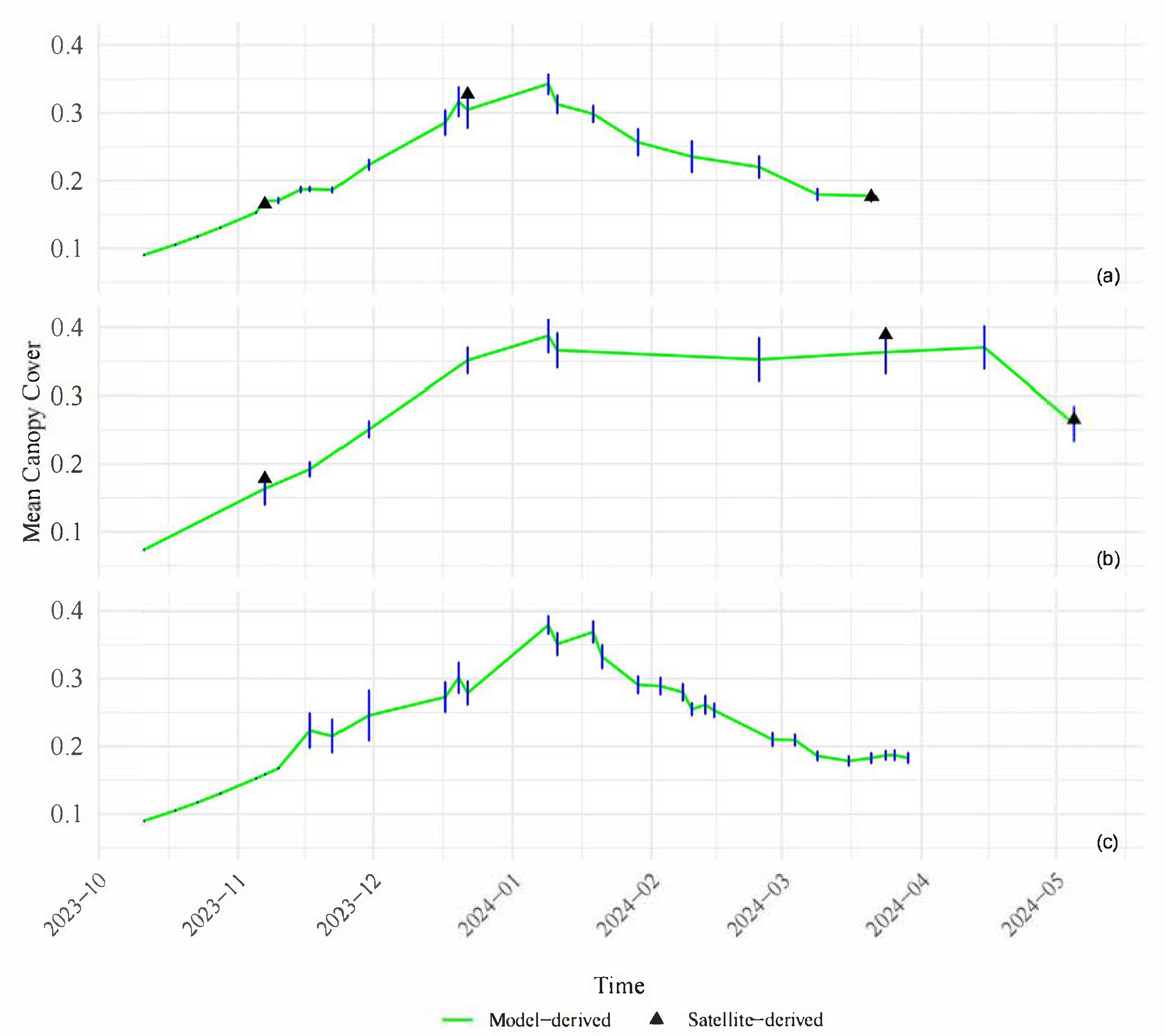
3.2. Canopy Cover Modelling
3.3. Spectral Unmixing
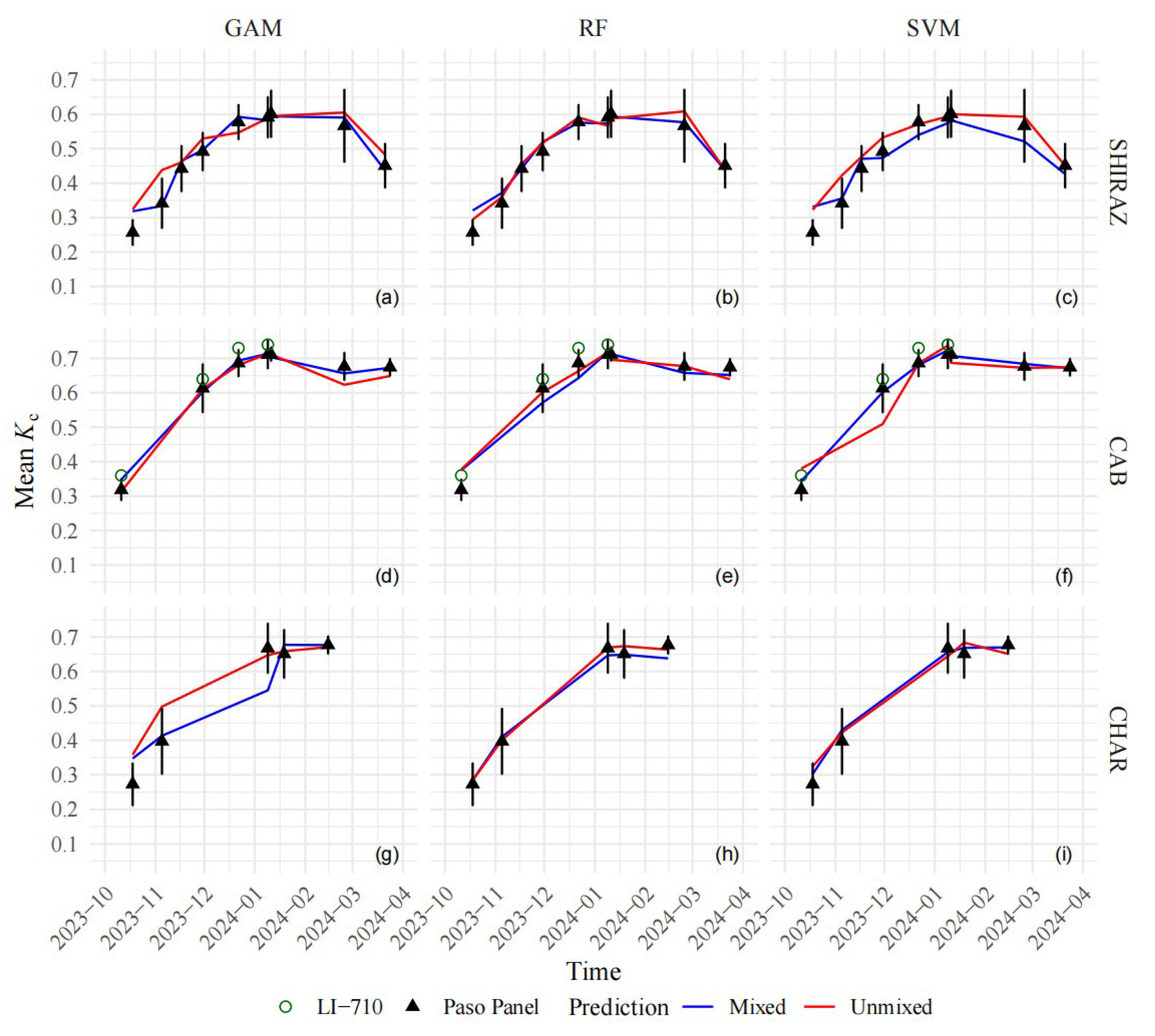
3.4. Crop Coefficient Modelling
3.5. Contribution of Spectral Unmixing and Choice of VIs
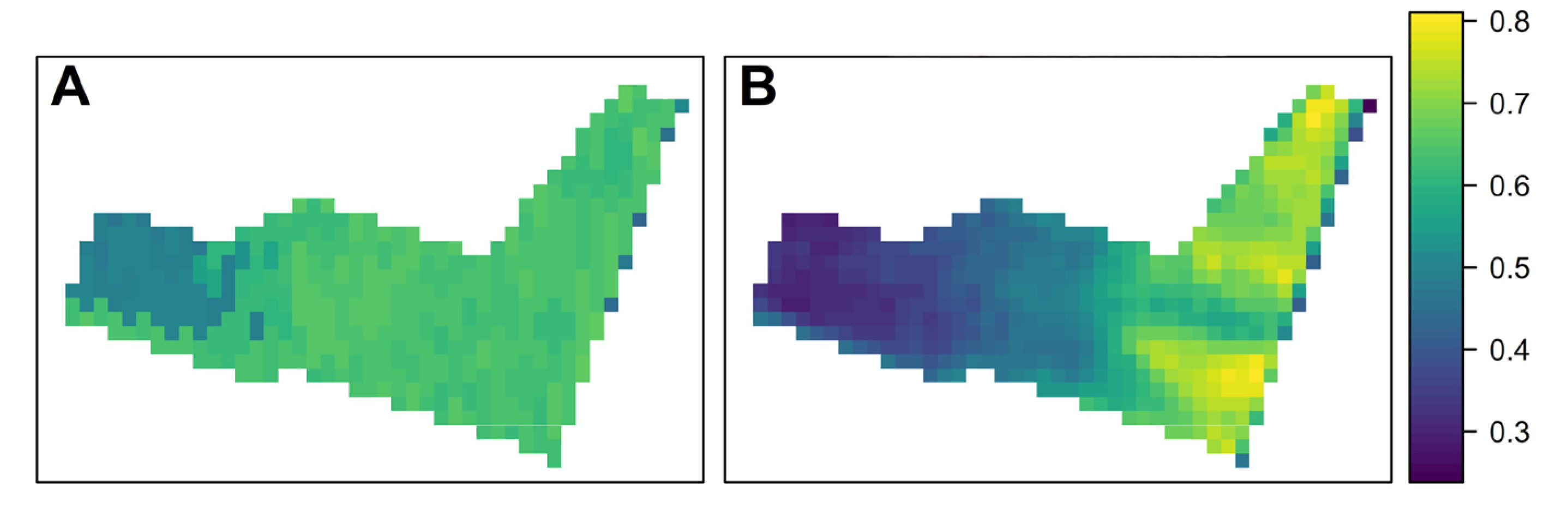
3.6. Projection to Sentinel-2 Rasters
4. Discussion
4.1. Canopy Area Model
4.2. Crop Coefficient Model
4.3. Effectiveness of Spectral Unmixing
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chartzoulakis, K.; Bertaki, M. Sustainable water management in agriculture under climate change. Agric. Agric. Sci. Procedia 2015, 4, 88–98. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Change 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Harrison, M.T.; Cullen, B.R.; Rawnsley, R.P. Modelling the sensitivity of agricultural systems to climate change and extreme climatic events. Agric. Syst. 2016, 148, 135–148. [Google Scholar] [CrossRef]
- Van Leeuwen, C.; Destrac-Irvine, A.; Dubernet, M.; Duchêne, E.; Gowdy, M.; Marguerit, E.; Pieri, P.; Parker, A.; De Resseguier, L.; Ollat, N. An update on the impact of climate change in viticulture and potential adaptations. Agronomy 2019, 9, 514. [Google Scholar] [CrossRef]
- Romero, P.; Navarro, J.M.; Ordaz, P.B. Towards a sustainable viticulture: The combination of deficit irrigation strategies and agroecological practices in Mediterranean vineyards. A review and update. Agric. Water Manag. 2022, 259, 107216. [Google Scholar] [CrossRef]
- Water Use on Australian Farms (2019–20 Financial Year). Available online: https://www.abs.gov.au/statistics/industry/agriculture/water-use-australian-farms/2019-20 (accessed on 8 August 2024).
- Sanchez, L.; Sams, B.; Alsina, M.; Hinds, N.; Klein, L.; Dokoozlian, N. Improving vineyard water use efficiency and yield with variable rate irrigation in California. Adv. Anim. Biosci. 2017, 8, 574–577. [Google Scholar] [CrossRef]
- Gu, Z.; Qi, Z.; Burghate, R.; Yuan, S.; Jiao, X.; Xu, J. Irrigation scheduling approaches and applications: A review. J. Irrig. Drain. Eng. 2020, 146, 04020007. [Google Scholar] [CrossRef]
- Schlank, R.; Kidman, C.M.; Gautam, D.; Jeffery, D.W.; Pagay, V. Data-driven irrigation scheduling increases the crop water use efficiency of Cabernet Sauvignon grapevines. Irrig. Sci. 2024, 42, 29–44. [Google Scholar] [CrossRef]
- Mirás-Avalos, J.M.; Araujo, E.S. Optimization of vineyard water management: Challenges, strategies, and perspectives. Water 2021, 13, 746. [Google Scholar] [CrossRef]
- Zhang, J.; Guan, K.; Peng, B.; Jiang, C.; Zhou, W.; Yang, Y.; Pan, M.; Franz, T.E.; Heeren, D.M.; Rudnick, D.R. Challenges and opportunities in precision irrigation decision-support systems for center pivots. Environ. Res. Lett. 2021, 16, 053003. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; Mañas, F.; López-Fuster, P.; Fereres, E. Evapotranspiration and crop coefficients from lysimeter measurements of mature ‘Tempranillo’ wine grapes. Agric. Water Manag. 2012, 112, 13–20. [Google Scholar] [CrossRef]
- Williams, L.; Phene, C.; Grimes, D.; Trout, T. Water use of mature Thompson Seedless grapevines in California. Irrig. Sci. 2003, 22, 11–18. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Bramley, R.; Hamilton, R. Understanding variability in winegrape production systems: 1. Within vineyard variation in yield over several vintages. Aust. J. Grape Wine Res. 2004, 10, 32–45. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Mota, M.; Wang, T. Prediction of crop coefficients from fraction of ground cover and height: Practical application to vegetable, field and fruit crops with focus on parameterization. Agric. Water Manag. 2021, 252, 106663. [Google Scholar] [CrossRef]
- Williams, L.E.; Levin, A.D.; Fidelibus, M.W. Crop coefficients (Kc) developed from canopy shaded area in California vineyards. Agric. Water Manag. 2022, 271, 107771. [Google Scholar] [CrossRef]
- Using the Paso Panel to Quickly Measure the Canopy Shaded Area and Estimate Vineyard Irrigation Crop Coefficients. Available online: https://ucanr.edu/county-office/county-san-luis-obispo/crop-coefficients-paso-panel (accessed on 25 April 2025).
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates; LI-COR Biosciences: Bad Homburg vor der Höhe, Germany, 2013. [Google Scholar]
- Gautam, D.; Ostendorf, B.; Pagay, V. Estimation of grapevine crop coefficient using a multispectral camera on an unmanned aerial vehicle. Remote Sens. 2021, 13, 2639. [Google Scholar] [CrossRef]
- Marinello, F.; Pezzuolo, A.; Chiumenti, A.; Sartori, L. Technical analysis of unmanned aerial vehicles (drones) for agricultural applications. In Proceedings of the 15th International Scientific Conference: Engineering for Rural Development, Jelgava, Latvia, 25–27 May 2016; pp. 870–875. [Google Scholar]
- Fernández, J. Plant-based sensing to monitor water stress: Applicability to commercial orchards. Agric. Water Manag. 2014, 142, 99–109. [Google Scholar] [CrossRef]
- Berra, E.F.; Fontana, D.C.; Yin, F.; Breunig, F.M. Harmonized Landsat and Sentinel-2 data with Google Earth Engine. Remote Sens. 2024, 16, 2695. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Montgomery, J.; Hornbuckle, J.; Hume, I.; Vleeshouwer, J. IrriSAT—Weather based scheduling and benchmarking technology. In Proceedings of the 17th ASA Conference, Hobart, Australia, 21–24 September 2015; pp. 20–24. [Google Scholar]
- Giovos, R.; Tassopoulos, D.; Kalivas, D.; Lougkos, N.; Priovolou, A. Remote sensing vegetation indices in viticulture: A critical review. Agriculture 2021, 11, 457. [Google Scholar] [CrossRef]
- Balbontín, C.; Campos, I.; Odi-Lara, M.; Ibacache, A.; Calera, A. Irrigation performance assessment in table grape using the reflectance-based crop coefficient. Remote Sens. 2017, 9, 1276. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- Matese, A.; Baraldi, R.; Berton, A.; Cesaraccio, C.; Di Gennaro, S.F.; Duce, P.; Facini, O.; Mameli, M.G.; Piga, A.; Zaldei, A. Estimation of water stress in grapevines using proximal and remote sensing methods. Remote Sens. 2018, 10, 114. [Google Scholar] [CrossRef]
- Reyes-González, A.; Kjaersgaard, J.; Trooien, T.; Hay, C.; Ahiablame, L. Estimation of crop evapotranspiration using satellite remote sensing-Based Vegetation Index. Adv. Meteorol. 2018, 2018, 4525021. [Google Scholar] [CrossRef]
- Vanino, S.; Pulighe, G.; Nino, P.; De Michele, C.; Falanga Bolognesi, S.; D’Urso, G. Estimation of evapotranspiration and crop coefficients of tendone vineyards using multi-sensor remote sensing data in a Mediterranean environment. Remote Sens. 2015, 7, 14708–14730. [Google Scholar] [CrossRef]
- Prabhakara, K.; Hively, W.D.; McCarty, G.W. Evaluating the relationship between biomass, percent groundcover and remote sensing indices across six winter cover crop fields in Maryland, United States. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 88–102. [Google Scholar] [CrossRef]
- Archer, E.; Strauss, H. Effect of plant density on root distribution of three-year-old grafted 99 Richter grapevines. S. Afr. J. Enol. Vitic. 1985, 6, 25–30. [Google Scholar] [CrossRef]
- Gautam, D.; Pagay, V. A review of current and potential applications of remote sensing to study the water status of horticultural crops. Agronomy 2020, 10, 140. [Google Scholar] [CrossRef]
- Rouault, P.; Courault, D.; Flamain, F.; Pouget, G.; Doussan, C.; Lopez-Lozano, R.; McCabe, M.; Debolini, M. High-resolution satellite imagery to assess orchard characteristics impacting water use. Agric. Water Manag. 2024, 295, 108763. [Google Scholar] [CrossRef]
- Palazzi, F.; Biddoccu, M.; Borgogno Mondino, E.C.; Cavallo, E. Use of remotely sensed data for the evaluation of inter-row cover intensity in vineyards. Remote Sens. 2022, 15, 41. [Google Scholar] [CrossRef]
- Hall, A.; Louis, J.; Lamb, D.W. Low-resolution remotely sensed images of winegrape vineyards map spatial variability in planimetric canopy area instead of leaf area index. Aust. J. Grape Wine Res. 2008, 14, 9–17. [Google Scholar] [CrossRef]
- Ferreiro-Arman, M.; Da Costa, J.-P.; Homayouni, S.; Martin-Herrero, J. Hyperspectral image analysis for precision viticulture. In Proceedings of the International Conference Image Analysis and Recognition, Póvoa de Varzim, Portugal, 18–20 September 2006; pp. 730–741. [Google Scholar]
- Cavalli, R.M. Spatial validation of spectral unmixing results: A systematic review. Remote Sens. 2023, 15, 2822. [Google Scholar] [CrossRef]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Quintano, C.; Fernández-Manso, A.; Shimabukuro, Y.E.; Pereira, G. Spectral unmixing. Int. J. Remote Sens. 2012, 33, 5307–5340. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M.; Richard, C.; Chanussot, J.; Drumetz, L.; Tourneret, J.-Y.; Zare, A.; Jutten, C. Spectral variability in hyperspectral data unmixing: A comprehensive review. IEEE Geosci. Remote Sens. Mag. 2021, 9, 223–270. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Gillespie, A.R. Simple models for complex natural surfaces-A strategy for the hyperspectral era of remote sensing. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989. [Google Scholar]
- Iland, P.; Gago, P.; Caillard, A.; Dry, P.R. Australian Wine: Styles and Tastes, People and Places; Patrick Iland Promotions Pty Ltd.: Adelaide, South Australia, 2017. [Google Scholar]
- Region Snapshot 2023–24—Barossa Valley. Available online: https://www.wineaustralia.com/getmedia/cd4203e4-0326-48c7-9516-2287a26887b0/MI_Barossa-Valley-Region-Snapshot-2023-24.pdf (accessed on 30 August 2025).
- Williams, L.; Ayars, J. Grapevine water use and the crop coefficient are linear functions of the shaded area measured beneath the canopy. Agric. For. Meteorol. 2005, 132, 201–211. [Google Scholar] [CrossRef]
- Sentinel-2 Cloud Masking with s2cloudles. Available online: https://developers.google.com/earth-engine/tutorials/community/sentinel-2-s2cloudless (accessed on 4 April 2025).
- Extracting Raster Values for Points. Available online: https://developers.google.com/earth-engine/tutorials/community/extract-raster-values-for-points (accessed on 4 April 2025).
- Misra, G.; Cawkwell, F.; Wingler, A. Status of phenological research using Sentinel-2 data: A review. Remote Sens. 2020, 12, 2760. [Google Scholar] [CrossRef]
- Laroche-Pinel, E.; Albughdadi, M.; Duthoit, S.; Chéret, V.; Rousseau, J.; Clenet, H. Understanding vine hyperspectral signature through different irrigation plans: A first step to monitor vineyard water status. Remote Sens. 2021, 13, 536. [Google Scholar] [CrossRef]
- Tassopoulos, D.; Kalivas, D.; Giovos, R.; Lougkos, N.; Priovolou, A. Sentinel-2 imagery monitoring vine growth related to topography in a protected designation of origin region. Agriculture 2021, 11, 785. [Google Scholar] [CrossRef]
- Gilabert, M.; González-Piqueras, J.; Garcıa-Haro, F.; Meliá, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ. 2002, 82, 303–310. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rouse, J. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third NASA Earth Resources Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973; pp. 309–317. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial color infrared photography for determining early in-season nitrogen requirements in corn. Agron. J. 2006, 98, 968–977. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Morales, A.; Berjón, A.; Agüera, J. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F. Utilisation de la haute resolution spectrale pour suivre l’etat des couverts vegetaux. In Proceedings of the Spectral Signatures of Objects in Remote Sensing, Aussois, France, 18–22 January 1988; p. 279. [Google Scholar]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Klemas, V.; Smart, R. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Rock, B.; Vogelmann, J.; Williams, D.; Vogelmann, A.; Hoshizaki, T. Remote detection of forest damage: Plant responses to stress may have spectral “signatures” that could be used to map, monitor, and measure forest damage. BioScience 1986, 36, 439–445. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- NDVI, Mapping a Function Over a Collection, Quality Mosaicking. Available online: https://developers.google.com/earth-engine/tutorials/tutorial_api_06 (accessed on 4 July 2024).
- Cribari-Neto, F.; Zeileis, A. Beta regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 site. J. Geophys. Res. Solid. Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Xu, F.; Somers, B. Unmixing-based Sentinel-2 downscaling for urban land cover mapping. ISPRS J. Photogramm. Remote Sens. 2021, 171, 133–154. [Google Scholar] [CrossRef]
- Kowalski, K.; Senf, C.; Hostert, P.; Pflugmacher, D. Characterizing spring phenology of temperate broadleaf forests using Landsat and Sentinel-2 time series. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102172. [Google Scholar] [CrossRef]
- Pedersen, E.J.; Miller, D.L.; Simpson, G.L.; Ross, N. Hierarchical generalized additive models in ecology: An introduction with mgcv. PeerJ 2019, 7, e6876. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Fox, E.W.; Hill, R.A.; Leibowitz, S.G.; Olsen, A.R.; Thornbrugh, D.J.; Weber, M.H. Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology. Environ. Monit. Assess. 2017, 189, 316. [Google Scholar] [CrossRef]
- Suykens, J.A. Support vector machines: A nonlinear modelling and control perspective. Eur. J. Control. 2001, 7, 311–327. [Google Scholar] [CrossRef]
- Egipto, R.; Aquino, A.; Costa, J.M.; Andújar, J.M. Predicting crop evapotranspiration under non-standard conditions using machine learning algorithms, a case study for Vitis vinifera L. cv Tempranillo. Agronomy 2023, 13, 2463. [Google Scholar] [CrossRef]
- Tan, X.-H.; Bi, W.-H.; Hou, X.-L.; Wang, W. Reliability analysis using radial basis function networks and support vector machines. Comput. Geotech. 2011, 38, 178–186. [Google Scholar] [CrossRef]
- Ramezan, C.A. Transferability of recursive feature elimination (RFE)-derived feature sets for support vector machine land cover classification. Remote Sens. 2022, 14, 6218. [Google Scholar] [CrossRef]
- Burba, G.; Miller, B.; Fratini, G.; Inkenbrandt, P.C.; Xu, L. Simple direct evapotranspiration measurements with a new cost-optimized ET flux Sensor. In Proceedings of the 104th Annual AMS Meeting 2024, Baltimore, MD, USA, 28 January–1 February 2024; p. 431027. [Google Scholar]
- Peddinti, S.R.; Kisekka, I. Evaluation of the LI-710 evapotranspiration sensor in comparison to full eddy covariance for monitoring energy fluxes in perennial and annual crops. Agric. Water Manag. 2025, 313, 109501. [Google Scholar] [CrossRef]
- Hernández-Ordoñez, E.; Cruz-Alvarez, O.; Orozco-Avitia, J.A.; Hernández-Rodríguez, O.A.; Alonso-Villegas, R.; Jacobo-Cuellar, J.L.; Gardea-Bejar, A.A.; Ojeda-Barrios, D.L. Physiological responses of Cabernet Sauvignon to dividing canopies in the Chihuahuan Desert. Agriculture 2024, 14, 2101. [Google Scholar] [CrossRef]
- Donike, S.; Aybar, C.; Gómez-Chova, L.; Kalaitzis, F. Trustworthy super-resolution of multispectral sentinel-2 imagery with latent diffusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6940–6952. [Google Scholar] [CrossRef]


| Bands | Description | Central Wavelength (nm) |
|---|---|---|
| B2 | Blue | 490 |
| B3 | Green (G) | 560 |
| B4 | Red (R) | 665 |
| B5 | Red-edge (RE) | 705 |
| B8 | Near-infrared (NIR) | 742 |
| B11, B12 | Short Wave Infrared (SWIR) | 1610, 2190 |
| Index | Formula | Index Purpose | Reference |
|---|---|---|---|
| NDVI | Canopy vigour | [54] | |
| EVI2 | Canopy vigour | [55] | |
| GNDVI | Vigour/chlorophyll | [56] | |
| GI | Canopy vigour | [57] | |
| NDRE | Chlorophyll sensitivity | [58] | |
| CIRE | Chlorophyll sensitivity | [59] | |
| IRECI | Chlorophyll sensitivity | [60] | |
| RECAI | Chlorophyll sensitivity | [51] | |
| REP | Chlorophyll sensitivity | [61] | |
| RENDVI2 | Chlorophyll sensitivity | [51] | |
| NDWI | Water | [62] | |
| NDII | Water | [63] | |
| MSI | Water | [64] | |
| SAVI | Soil correction | [53] | |
| SAVIRED | Soil correction | [52] | |
| MSAVI | Soil correction | [65] |
| Date | Cultivar | n | Paso Panel Kc |
|---|---|---|---|
| 11 October 2023 | Cabernet | 25 | 0.348 ± 0.088 |
| 18 October 2023 | Shiraz | 30 | 0.277 ± 0.054 |
| 23 October 2023 | Cabernet | 30 | 0.603 ± 0.097 |
| 28 October 2023 | Cabernet | 23 | 0.679 ± 0.042 |
| 5 November 2023 | Cabernet | 29 | 0.721 ± 0.042 |
| 5 November 2023 | Shiraz | 30 | 0.345 ± 0.077 |
| 7 November 2023 | Cabernet | 29 | 0.713 ± 0.049 |
| 10 November 2023 | Cabernet | 21 | 0.676 ± 0.043 |
| 15 November 2023 | Cabernet | 30 | 0.648 ± 0.062 |
| 17 November 2023 | Shiraz | 30 | 0.456 ± 0.063 |
| 30 November 2023 | Shiraz | 30 | 0.507 ± 0.066 |
| 22 December 2023 | Shiraz | 30 | 0.567 ± 0.084 |
| 9 January 2024 | Shiraz | 30 | 0.589 ± 0.067 |
| 11 January 2024 | Shiraz | 30 | 0.598 ± 0.070 |
| 25 February 2024 | Shiraz | 29 | 0.608 ± 0.087 |
| 21 March 2024 | Shiraz | 30 | 0.443 ± 0.086 |
| Vine Variety | Model | R2 | RMSE | MAE | |
|---|---|---|---|---|---|
| Shiraz | GAM | Unmixed | 0.697 ± 0.025 | 0.083 ± 0.005 | 0.068 ± 0.0.005 |
| Mixed | 0.670 ± 0.026 | 0.090 ± 0.008 | 0.072 ± 0.006 | ||
| RF | Unmixed | 0.625 ± 0.059 | 0.078 ± 0.006 | 0.063 ± 0.004 | |
| Mixed | 0.510 ± 0.077 | 0.090 ± 007 | 0.071 ± 0.006 | ||
| SVM | Unmixed | 0.615 ± 0.064 | 0.084 ± 0.007 | 0.068 ± 0.005 | |
| Mixed | 0.512 ± 0.071 | 0.094 ± 0.008 | 0.074 ± 0.006 | ||
| Cabernet Sauvignon | GAM | Unmixed | 0.697 ± 0.009 | 0.084 ± 0.009 | 0.063 ± 0.006 |
| Mixed | 0.763 ± 0.030 | 0.081 ± 0.112 | 0.061 ± 0.007 | ||
| RF | Unmixed | 0.686 ± 0.067 | 0.072 ± 0.007 | 0.055 ± 0.005 | |
| Mixed | 0.649 ± 0.069 | 0.076 ± 0.009 | 0.056 ± 0.006 | ||
| SVM | Unmixed | 0.713 ± 0.072 | 0.071 ± 0.009 | 0.052 ± 0.005 | |
| Mixed | 0.660 ± 0.081 | 0.078 ± 0.009 | 0.057 ± 0.006 | ||
| Chardonnay | GAM | Unmixed | 0.901 ± 0.015 | 0.090 ± 0.024 | 0.067 ± 0.017 |
| Mixed | 0.877 ± 0.019 | 0.097 ± 0.014 | 0.074 ± 0.0.09 | ||
| RF | Unmixed | 0.814 ± 0.044 | 0.075 ± 0.008 | 0.059 ± 0.007 | |
| Mixed | 0.787 ± 0.056 | 0.081 ± 0.011 | 0.064 ± 0.008 | ||
| SVM | Unmixed | 0.818 ± 0.046 | 0.082 ± 0.012 | 0.064 ± 0.008 | |
| Mixed | 0.824 ± 0.033 | 0.081 ± 0.008 | 0.063 ± 0.007 |
| Year-Month | Model | Shiraz | Cabernet Sauvignon | Chardonnay | |||
|---|---|---|---|---|---|---|---|
| n | Kc | n | Kc | n | Kc | ||
| October 2023 | GAM mx | 12 | 0.318 ± 0.036 | 5 | 0.348 ± 0.129 | 8 | 0.347 ± 0.062 |
| GAM unmx | 12 | 0.324 ± 0.030 | 5 | 0.313 ± 0.051 | 8 | 0.358 ± 0.080 | |
| RF mx | 12 | 0.321 ± 0.042 | 5 | 0.375 ± 0.015 | 8 | 0.284 ± 0.096 | |
| RF unmx | 12 | 0.294 ± 0.022 | 5 | 0.378 ± 0.021 | 8 | 0.284 ± 0.056 | |
| SVM mx | 12 | 0.332 ± 0.063 | 5 | 0.344 ± 0.108 | 8 | 0.302 ± 0.027 | |
| SVM unmx | 12 | 0.323 ± 0.052 | 5 | 0.380 ± 0.085 | 8 | 0.328 ± 0.054 | |
| PP | 12 | 0.257 ± 0.038 | 5 | 0.319 ± 0.0320 | 8 | 0.273 ± 0.062 | |
| ET | 0.36 | ||||||
| November 2023 | GAM mx | 22 | 0.443 ± 0.080 | 8 | 0.603 ± 0.060 | 7 | 0.413 ± 0.089 |
| GAM unmx | 22 | 0.486 ± 0.047 | 8 | 0.612 ± 0.018 | 7 | 0.498 ± 0.166 | |
| RF mx | 22 | 0.458 ± 0.066 | 8 | 0.572 ± 0.097 | 7 | 0.410 ± 0.033 | |
| RF unmx | 22 | 0.457 ± 0.070 | 8 | 0.602 ± 0.035 | 7 | 0.401 ± 0.058 | |
| SVM mx | 22 | 0.441 ± 0.070 | 8 | 0.602 ± 0.039 | 7 | 0.430 ± 0.060 | |
| SVM unmx | 22 | 0.487 ± 0.056 | 8 | 0.510 ± 0.123 | 7 | 0.423 ± 0.090 | |
| PP | 22 | 0.438 ± 0.088 | 8 | 0.614 ± 0.0715 | 7 | 0.397 ± 0.097 | |
| ET | 0.64 | ||||||
| December 2023 | GAM mx | 8 | 0.593 ± 0.044 | 11 | 0.694 ± 0.032 | ||
| GAM unmx | 8 | 0.547 ± 0.020 | 11 | 0.681 ± 0.028 | |||
| RF mx | 8 | 0.576 ± 0.024 | 11 | 0.643 ± 0.090 | |||
| RF unmx | 8 | 0.591 ± 0.011 | 11 | 0.663 ± 0.012 | |||
| SVM mx | 8 | 0.540 ± 0.067 | 11 | 0.681 ± 0.031 | |||
| SVM unmx | 8 | 0.571 ± 0.022 | 11 | 0.685 ± 0.043 | |||
| PP | 8 | 0.578 ± 0.052 | 11 | 0.687 ± 0.040 | |||
| ET | 0.73 | ||||||
| January 2024 | GAM mx | 22 | 0.590 ± 0.026 | 18 | 0.709 ± 0.025 | 19 | 0.601 ± 0.141 |
| GAM unmx | 22 | 0.592 ± 0.012 | 18 | 0.713 ± 0.020 | 19 | 0.652 ± 0.021 | |
| RF mx | 22 | 0.586 ± 0.016 | 18 | 0.716 ± 0.026 | 19 | 0.648 ± 0.072 | |
| RF unmx | 22 | 0.579 ± 0.020 | 18 | 0.708 ± 0.028 | 19 | 0.6709 ± 0.043 | |
| SVM mx | 22 | 0.579 ± 0.031 | 18 | 0.716 ± 0.030 | 19 | 0.6613 ± 0.101 | |
| SVM unmx | 22 | 0.598 ± 0.007 | 18 | 0.715 ± 0.035 | 19 | 0.6609 ± 0.085 | |
| PP | 22 | 0.598 ± 0.065 | 18 | 0.711 ± 0.033 | 19 | 0.6605 ± 0.071 | |
| ET | 0.74 | ||||||
| February 2024 | GAM mx | 9 | 0.591 ± 0.028 | 8 | 0.657 ± 0.047 | 8 | 0.677 ± 0.0347 |
| GAM unmx | 9 | 0.605 ± 0.012 | 8 | 0.624 ± 0.023 | 8 | 0.671 ± 0.0122 | |
| RF mx | 9 | 0.577 ± 0.030 | 8 | 0.658 ± 0.068 | 8 | 0.638 ± 0.0357 | |
| RF unmx | 9 | 0.609 ± 0.033 | 8 | 0.678 ± 0.013 | 8 | 0.663 ± 0.0222 | |
| SVM mx | 9 | 0.521 ± 0.067 | 8 | 0.684 ± 0.021 | 8 | 0.670 ± 0.0188 | |
| SVM unmx | 9 | 0.593 ± 0.051 | 8 | 0.673 ± 0.021 | 8 | 0.651 ± 0.0199 | |
| PP | 9 | 0.567 ± 0.107 | 8 | 0.677 ± 0.041 | 8 | 0.677 ± 0.0270 | |
| March 2024 | GAM mx | 8 | 0.438 ± 0.046 | 8 | 0.673 ± 0.058 | ||
| GAM unmx | 8 | 0.483 ± 0.010 | 8 | 0.649 ± 0.005 | |||
| RF mx | 8 | 0.438 ± 0.027 | 8 | 0.652 ± 0.027 | |||
| RF unmx | 8 | 0.438 ± 0.025 | 8 | 0.640 ± 0.016 | |||
| SVM mx | 8 | 0.427 ± 0.028 | 8 | 0.671 ± 0.034 | |||
| SVM unmx | 8 | 0.451 ± 0.012 | 8 | 0.674 ± 0.018 | |||
| PP | 8 | 0.451 ± 0.066 | 8 | 0.674 ± 0.026 | |||
| Variety | Model | Unmixed | Mixed |
|---|---|---|---|
| Shiraz | RF | CIred, GI, GNDVI, NDRE, NDVI, NDWI, RENDVI2, REP | CIred, GI, GNDVI, IRECI, NDWI, RECAI, RENDVI2, SAVIRED |
| GAM | GI, GNDVI, MSI, NDRE, NDWI, RECAI, RENDVI2, SAVIRED | EVI, GI, IRECI, NDII, NDWI, RENDVI2, REP, SAVIRED | |
| SVM | REP, NDVI, RENDVI2, NDRE, CIred, NDWI, GNDVI, GI | IRECI, GI, RENDVI2, SAVIRED, CIred, GNDVI, NDRE, NDWI | |
| Cabernet Sauvignon | RF | CIred, GI, GNDVI, MSAVI, NDWI, RECAI, REP, SAVI | GI, GNDVI, MSI, NDII, NDRE, NDWI, RECAI, RENDVI2 |
| GAM | CIred, GI, GNDVI, MSI, NDVI, NDWI, RECAI, REP | CIred, GI, MSI, NDII, RENDVI2, REP | |
| SVM | GNDVI, NDWI, GI, RECAI, SAVI, REP, CIred, MSAVI | IRECI, GI, RENDVI2, SAVIRED, CIred, GNDVI, NDRE, NDWI | |
| Chardonnay | RF | CIred, GI, GNDVI, NDRE, NDVI, NDWI, RENDVI2, REP | EVI, GI, MSAVI, MSI, NDII, RENDVI2, REP, SAVI |
| GAM | CIred, EVI, GNDVI, MSAVI, MSI, NDRE, SAVI | GI, GNDVI, IRECI, MSI, NDII, RECAI, SAVIRED | |
| SVM | NDII, RENDVI2, CIred, NDRE, NDWI, REP, MSAVI, MSI | GI, MSI, NDII, EVI, REP, RENDVI2, MSAVI, SAVI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guevara-Torres, D.R.; Luo, H.; Do, C.M.; Ostendorf, B.; Pagay, V. Improving the Accuracy of Seasonal Crop Coefficients in Grapevine from Sentinel-2 Data. Remote Sens. 2025, 17, 3365. https://doi.org/10.3390/rs17193365
Guevara-Torres DR, Luo H, Do CM, Ostendorf B, Pagay V. Improving the Accuracy of Seasonal Crop Coefficients in Grapevine from Sentinel-2 Data. Remote Sensing. 2025; 17(19):3365. https://doi.org/10.3390/rs17193365
Chicago/Turabian StyleGuevara-Torres, Diego R., Hankun Luo, Chi Mai Do, Bertram Ostendorf, and Vinay Pagay. 2025. "Improving the Accuracy of Seasonal Crop Coefficients in Grapevine from Sentinel-2 Data" Remote Sensing 17, no. 19: 3365. https://doi.org/10.3390/rs17193365
APA StyleGuevara-Torres, D. R., Luo, H., Do, C. M., Ostendorf, B., & Pagay, V. (2025). Improving the Accuracy of Seasonal Crop Coefficients in Grapevine from Sentinel-2 Data. Remote Sensing, 17(19), 3365. https://doi.org/10.3390/rs17193365









