2C-Net: A Novel Spatiotemporal Dual-Channel Network for Soil Organic Matter Prediction Using Multi-Temporal Remote Sensing and Environmental Covariates
Abstract
Highlights
- Propose a new framework for soil organic matter (SOM) mapping by combining deep learning.
- Considering multi-temporal remote sensing images (MTRSI) as multi-channel time series data to assist in SOM mapping.
- The accuracy of SOM prediction using this framework surpasses the widely used Random Forest (RF) method.
- The bare soil period after tilling is a more important time window for SOM inversion.
Abstract
1. Introduction
- The 2C-Net model is proposed and applied to SOM mapping: This study proposes a spatiotemporal 2-channel architecture that combines the advantages of cross-attention mechanism and convolutional neural networks (CNNs) to extract features of spatiotemporal information. The temporal channel extracts features from MTRSI data, while the spatial channel captures environmental covariates, such as climate and topography, to model spatial features. By integrating the information captured from both channels, the model enables efficient and accurate prediction of SOM content.
- To map MTRSI data to MTS data and perform global modeling: This study temporally sequentializes MTRSI data along the temporal dimension and maps it into MTS data. Meanwhile, we propose a novel decoder—Multi-Sequence Feature Fusion Module (MFFM)—which aims to model MTRSI from two dimensions: spectral bands and time. Unlike the LSTM that models each sequence independently, MFFM considers the relationships and interactions between different sequences.
- To enrich spatial features and perform feature extraction: This study proposes the Diverse Convolutional Architecture (DCA), which acts as the core module for spatial channels. By utilizing different convolutional kernels in the convolutional space, it effectively captures spatial information while enriching the intermediate features.
2. Materials and Methodology
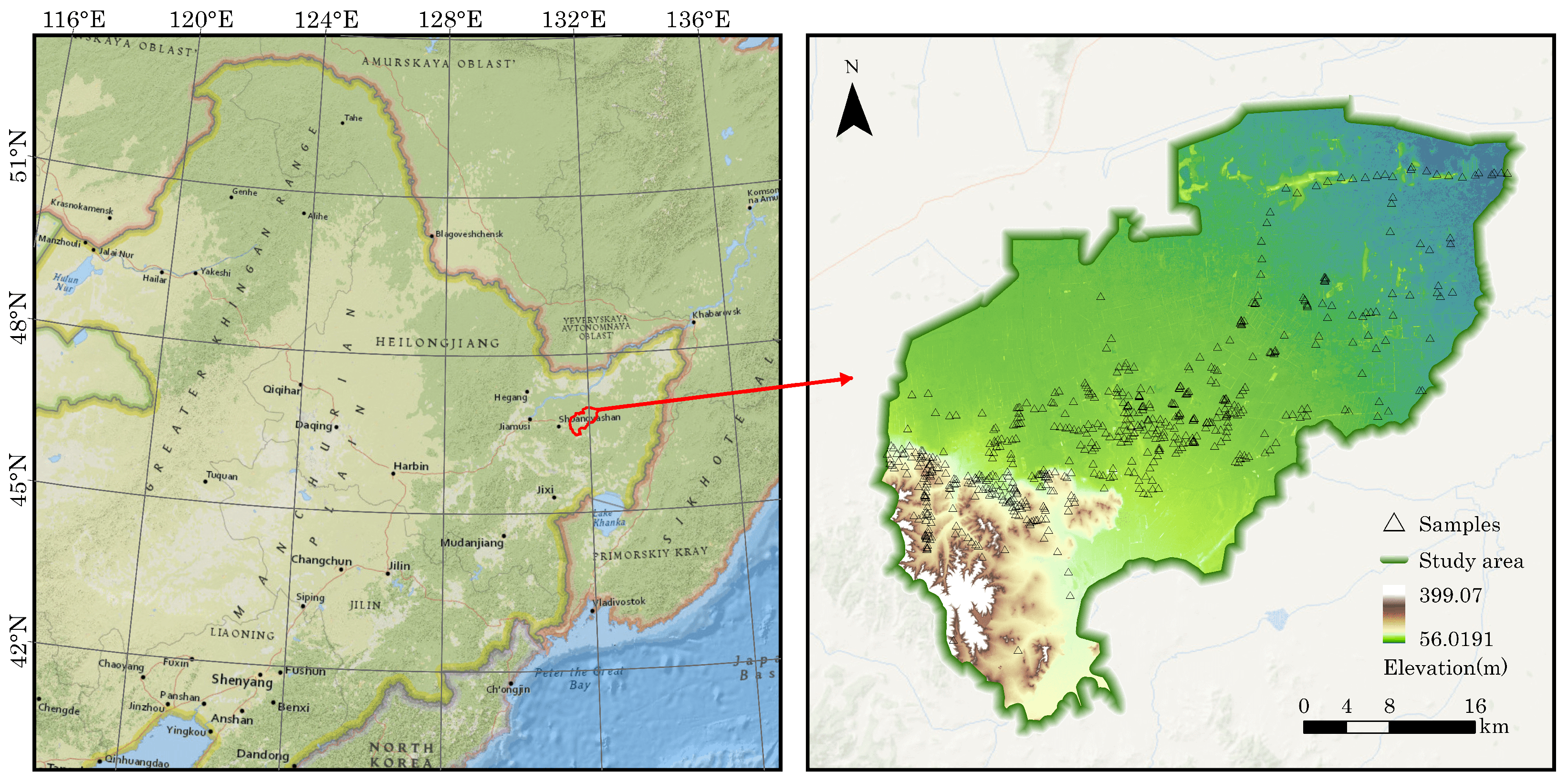
2.1. Study Area
2.2. Dataset
2.2.1. Temporal Data
2.2.2. Spatial Data
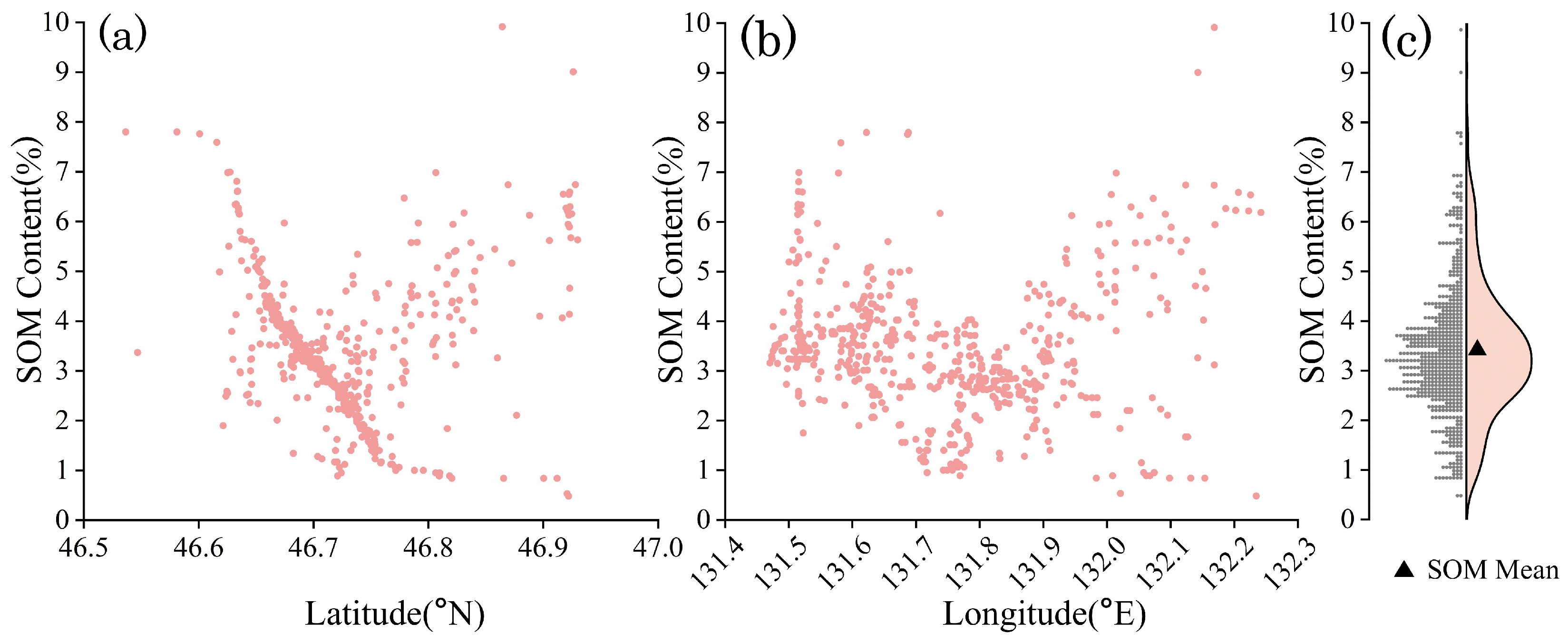
2.2.3. SOM Sampling Data
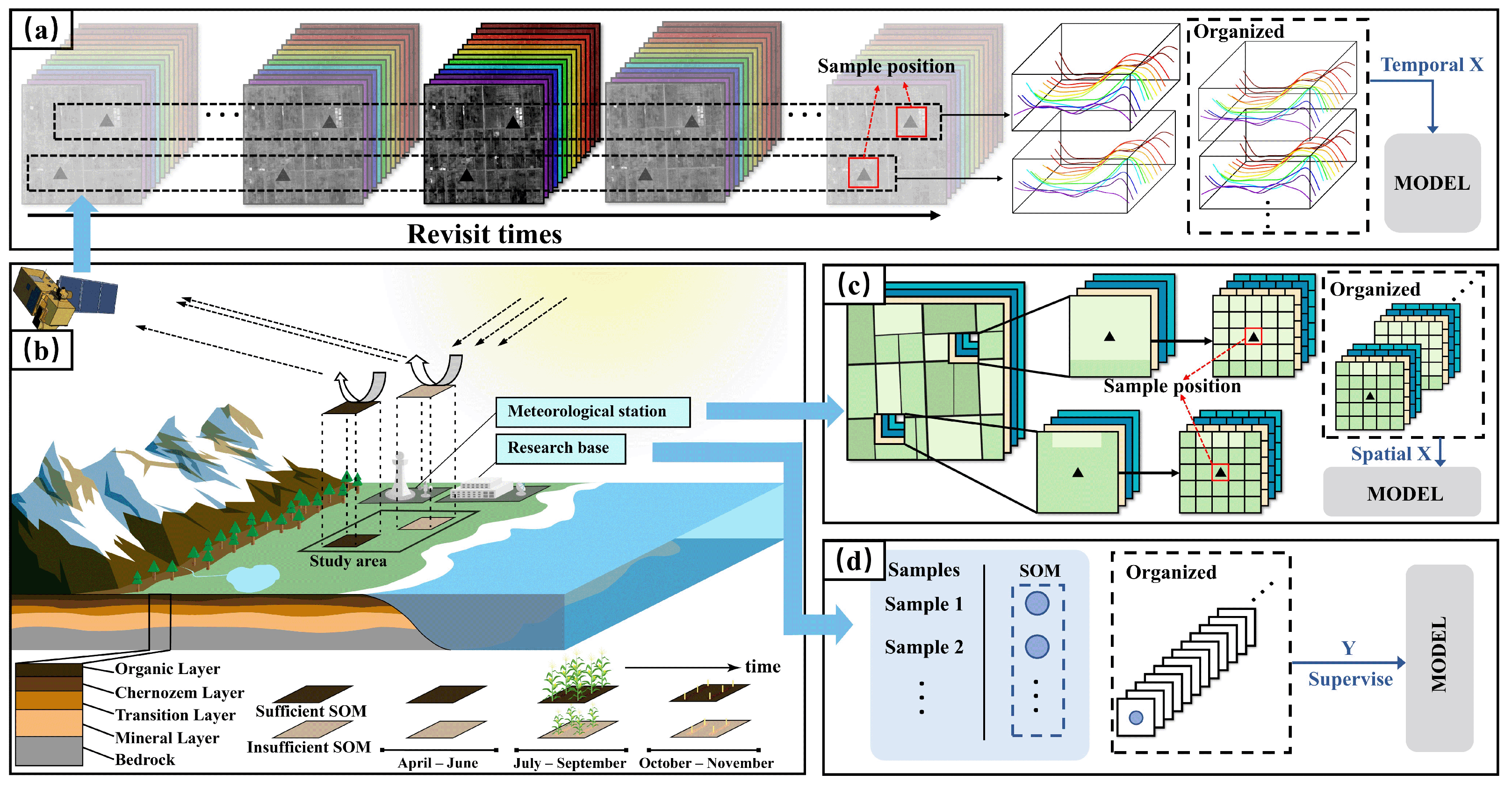
2.3. Basic Scheme
2.4. Workflow and Architecture
2.4.1. Workflow
2.4.2. Model Architecture
2.5. Temporal Channel
2.5.1. Encoder
- Value embedding: The band information of the raw input is passed through a linear layer to obtain MTS vector , with N representing the number of samples and “” is the abbreviation for “value”. The linear layer, as one of the fundamental building blocks in neural networks, is responsible for performing linear transformations of the data. During the subsequent training process, through backpropagation and optimization, the model adjusts its parameters so that the linear layer can optimally map the input information. To keep the encoder simple, this paper does not stack multiple linear layers at this point. A ReLU activation function is applied to introduce non-linearity, thereby enhancing the model’s expressive capability. The process of value embedding can be expressed as follows:
- Coordinate embedding: For each spectral band data, after embedding it as a vector , we incorporate the longitude and latitude information of all samples, denoted as , into the embedding process. This serves two purposes: on the one hand, it provides unique positional information for each spectral band, and on the other hand, it enhances the relevance with the subsequent decoder’s retrieval head. In the fields of natural language processing and computer vision, positional embedding is a widely adopted technique. This approach provides models with positional information for sequences or image patches, thereby improving the model’s understanding of the input [54,74,75]. Similarly, in this paper, after embedding different bands’ information as N vectors , the latitude and longitude information of each sample is treated as default-encoded and embedded into N vectors (as shown in Equation (2)). N represents the number of samples and “p” is the abbreviation for “position”. These vectors are then integrated with the band information by concatenation (as shown in Equation (3)), resulting in the output of the encoder: .
2.5.2. MFFM Decoder
- Decoder initialization: For each sample , the coordinate information of all sample points is embedded and rearranged into vectors . represents the number of samples, represents the number of retrieval heads, and “” is the abbreviation for “head”. This process is as follows:
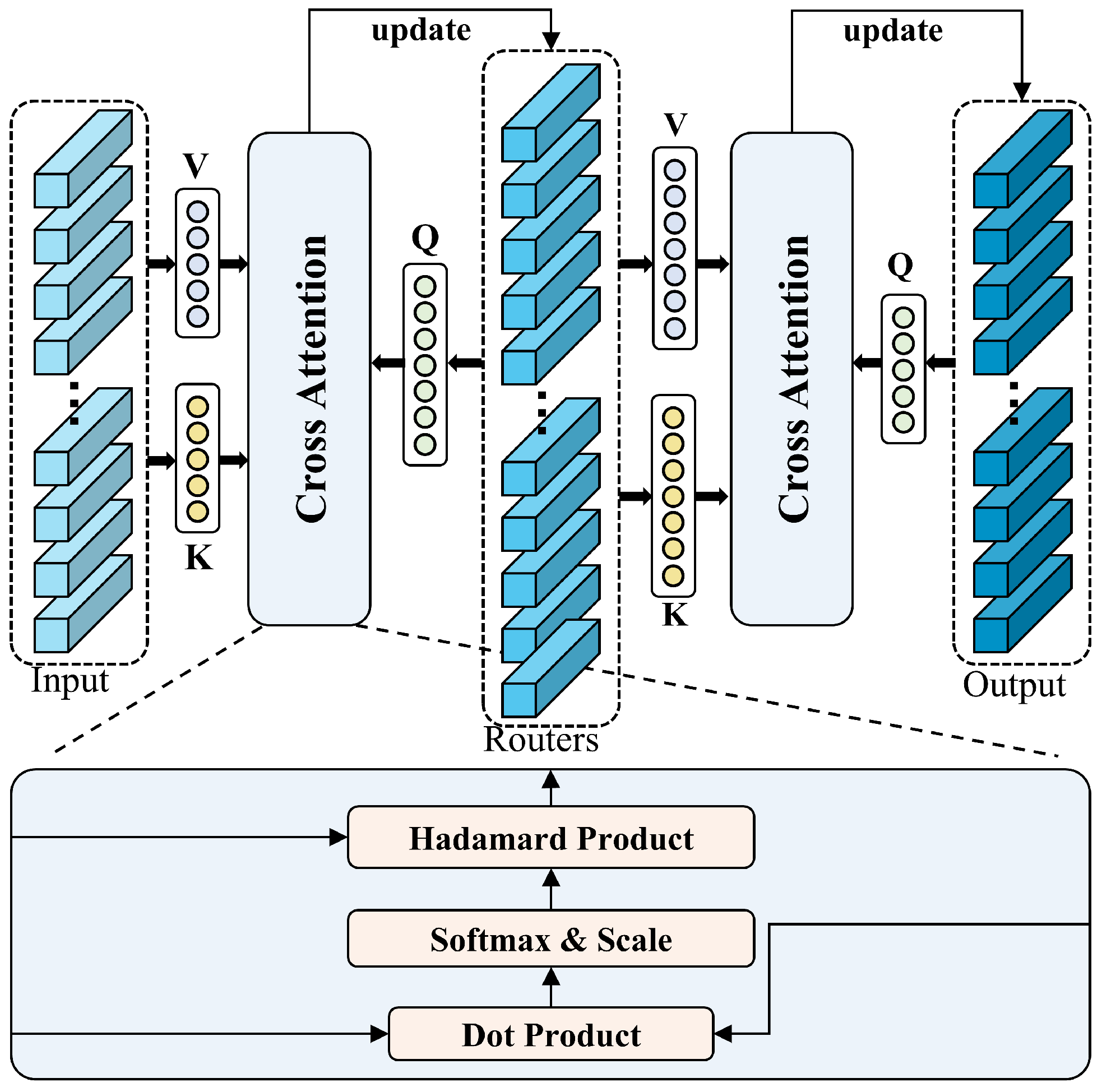
- Head retrieval: Before performing the retrieval, each encoder output is rearranged to align with the corresponding set of retrieval heads from the decoder, resulting in the retrieval targets for the retrieval heads. This process is as follows:Subsequently, for each sample , retrieval heads and the corresponding retrieval targets , the retrieval heads are used as queries , and the retrieval targets are used as keys and values . A cross-attention operation is then performed and then we get retrieval results , which are injected with encoder information; means that it will be input vector of router mechanism. This process is as follows:
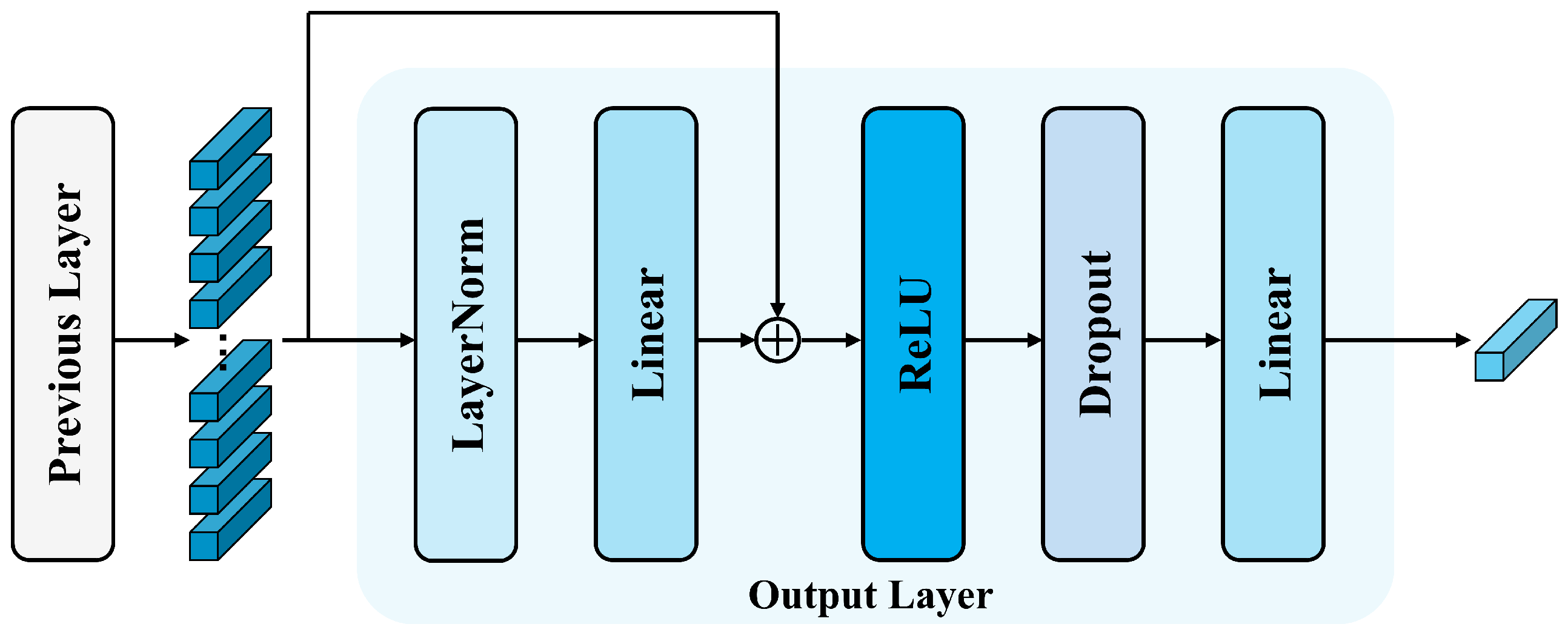
- Head fusion: The retrieval results will be treated as input and fed into the router mechanism, a technique proposed by [73] for MTS forecasting tasks. The router mechanism operates by establishing a routing layer that stores temporary information between input and output vectors of the same dimensionality. In CrossFormer, this layer accepts the input information, integrates it, and then distributes it to the output recipients, resulting in an architecture of , where . , and represent the dimensions of the router, input, and output in the router mechanism, respectively. This mechanism significantly reduces the computational complexity of intermediate vectors through the intermediate routing layer. However, compared to typical MTS forecasting tasks, datasets in the DSM domain have fewer variables, making computational complexity not the primary concern of this study (but it still needs to be considered, as will be mentioned in Section 3.2.2). In this work, by reversing the approach, we set (as shown in Figure 8), where increasing the number of intermediate routers enhances the richness of feature representation while minimizing information loss.For each sample , the retrieval results injected with encoder information are first used as the and , while the initial vectors from the router layer serve as the queries . The first cross-attention operation is then performed among these components (as shown in Equation (7)), yielding initial fused temporary vectors . Subsequently, the temporary router layer vectors are used as the and , and the retrieval results are used as in the second cross-attention operation (as shown in Equation (8)), and we get the final fused vectors after mutual interaction. represent the number of retrieval heads.The fused results are then passed into the output layer (Figure 9), followed by a reshape operation and a fully connected layer (FC), which produces the final output for the temporal channel. This process is as follows:
2.6. Spatial Channel
3. Results
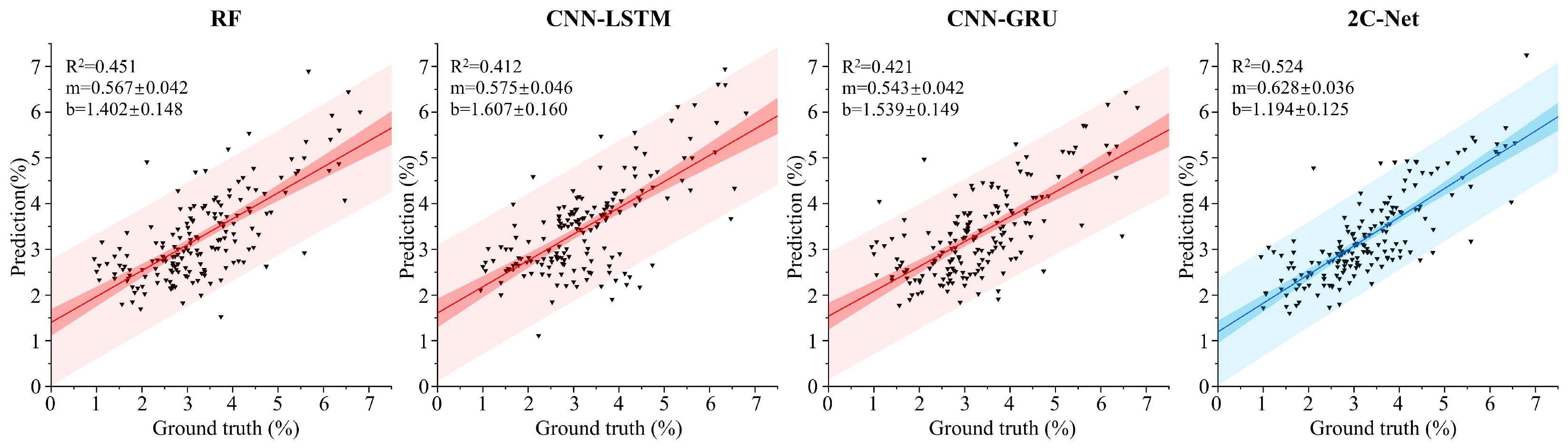
3.1. Compare with Other Models’ Performance
3.2. Ablation Study
3.2.1. Analysis of the Impact of Various Modules on Results
- 2C-Net w/o MFFM DCA CE: In this part, all components are removed from the complete network, and only the two 2 × 2 convolutional layers in the baseline CNN-LSTM architecture are used to extract climate and terrain data, while an MLP is employed to extract spectral data.
- 2C-Net w/o MFFM DCA: In order to compare 1. and validate the effectiveness of the CE component, the MFFM and DCA components are removed from the complete network, and the CE component is added in this part.
- 2C-Net w/o MFFM: In order to compare 2. and validate the effectiveness of the DCA component, the MFFM component is removed from the complete network, while the DCA component and CE are added in this part.
- 2C-Net(with all components): In order to compare 3. and validate the effectiveness of the MFFM component, all components are added in this part.
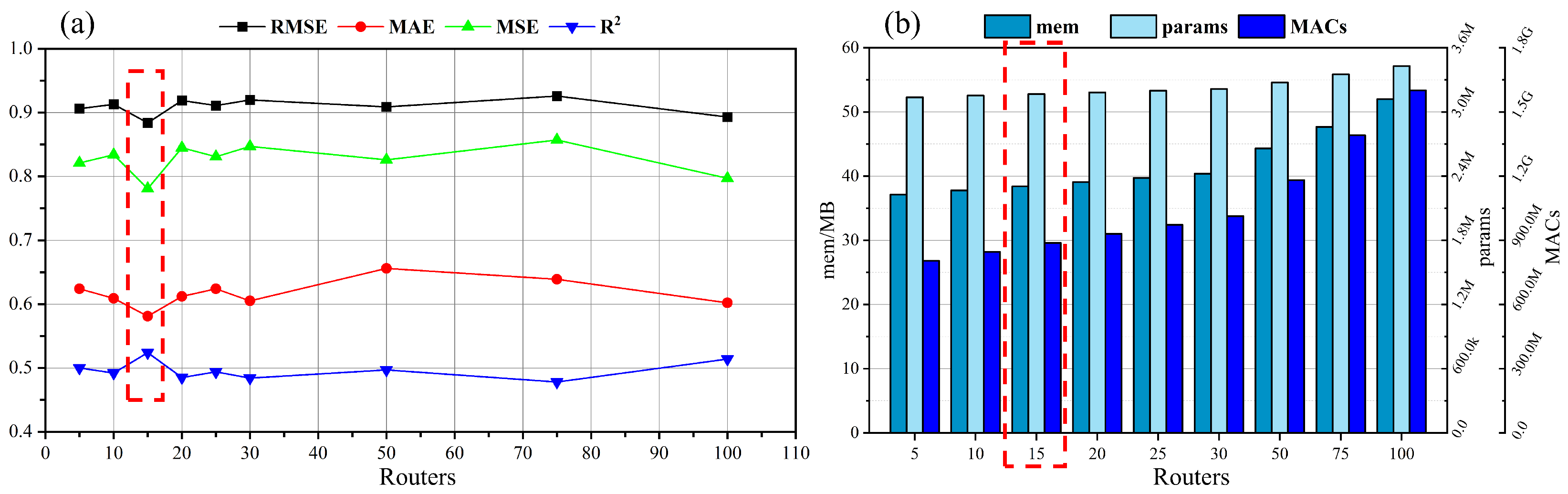
3.2.2. Evaluation of Router Mechanism’s Hyperparameter
3.2.3. Evaluation of Channel Fusion Methods
3.3. Visualization
3.3.1. Visualization of Different Models’ Mapping Results
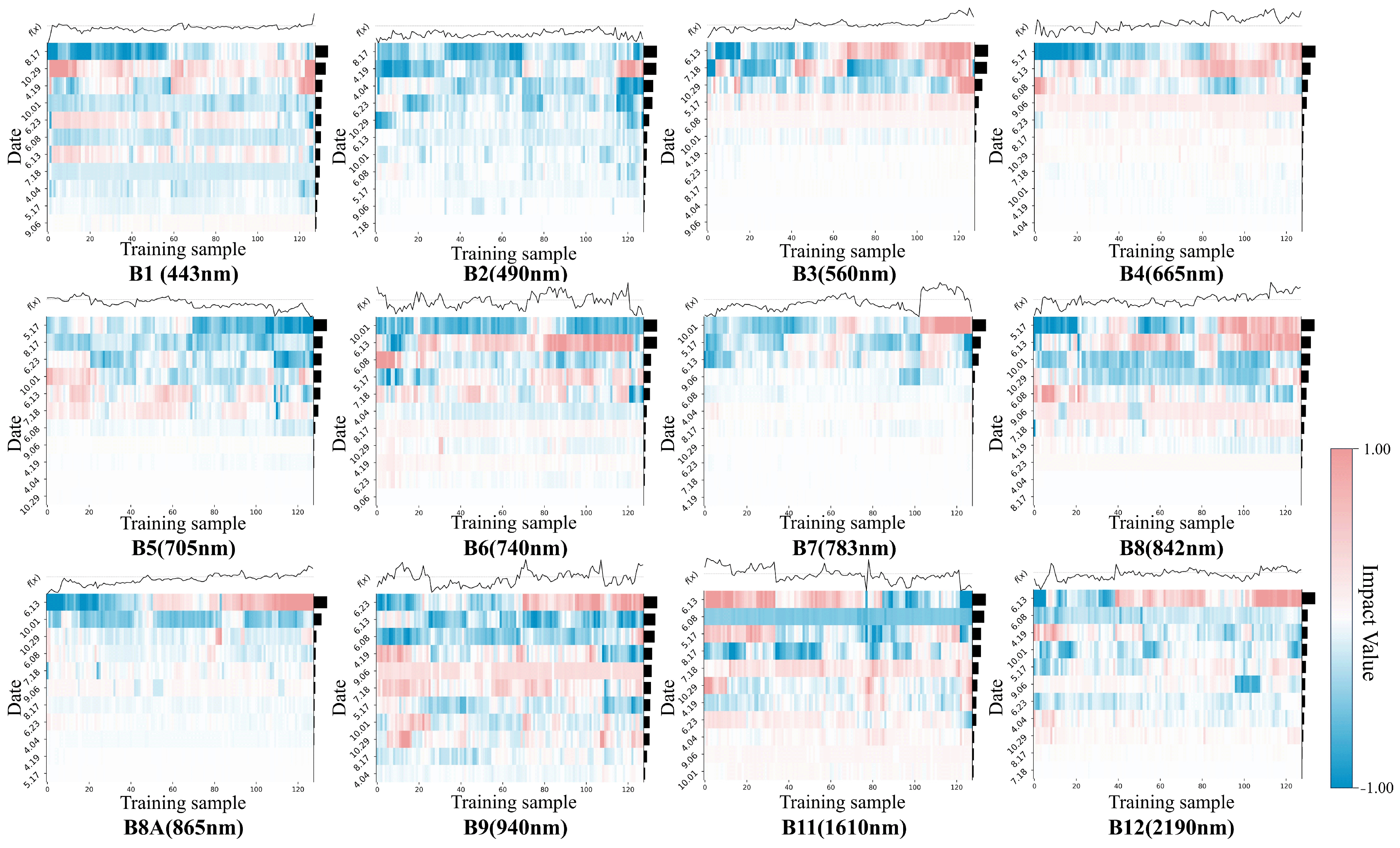
3.3.2. Visualization of Spectral Feature Importance
4. Discussion
4.1. Mapping Result
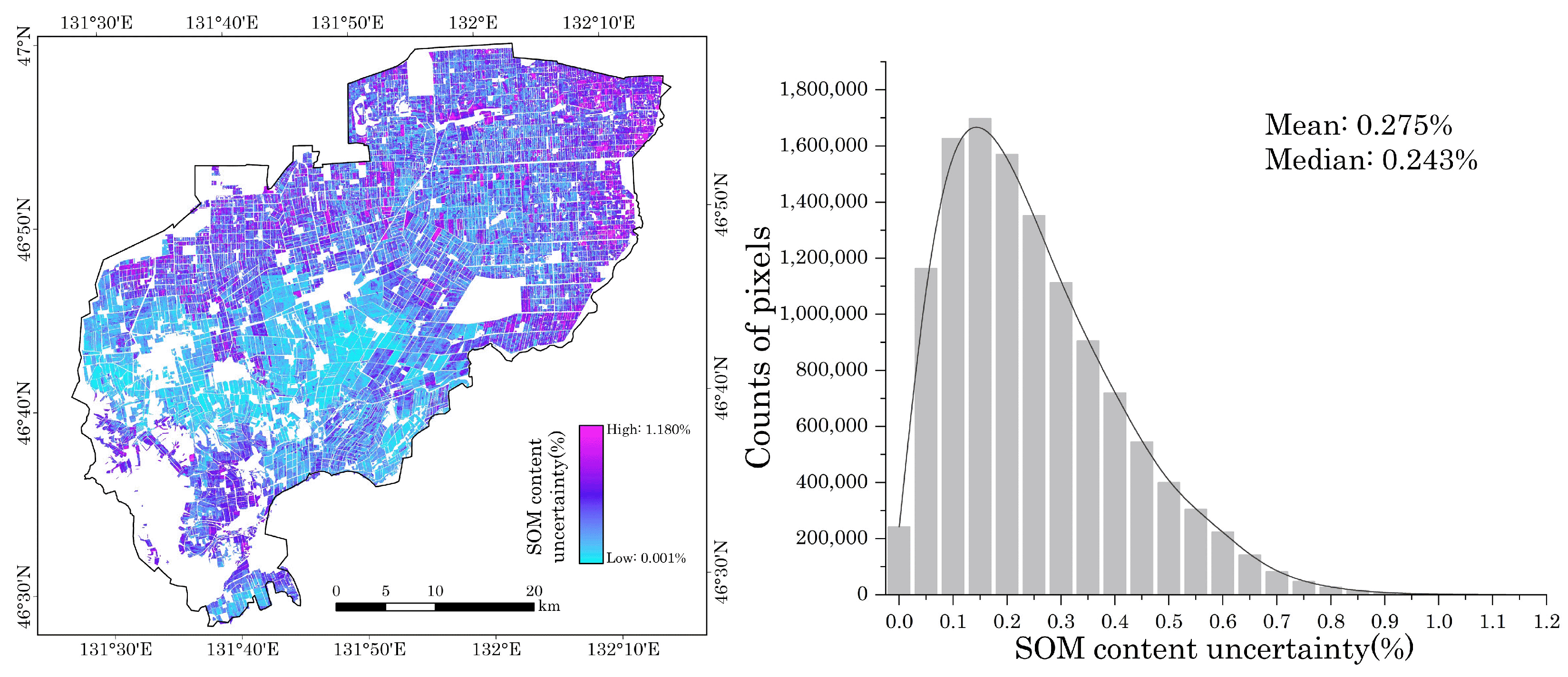
4.2. Uncertainty of Mapping Result
4.3. Feature Importance
4.3.1. From the Perspective of the Spectral Dimension
4.3.2. From the Perspective of the Temporal Dimension
4.4. Limitations of This Study and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tiessen, H.; Cuevas, E.; Chacon, P. The role of soil organic matter in sustaining soil fertility. Nature 1994, 371, 783–785. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Wang, Y.; Men, Z.; Liu, H. Regional soil organic matter mapping models based on the optimal time window, feature selection algorithm and Google Earth Engine. Soil Tillage Res. 2022, 219, 105325. [Google Scholar] [CrossRef]
- Guo, L.; Sun, X.; Fu, P.; Shi, T.; Dang, L.; Chen, Y.; Linderman, M.; Zhang, G.; Zhang, Y.; Jiang, Q.; et al. Mapping soil organic carbon stock by hyperspectral and time-series multispectral remote sensing images in low-relief agricultural areas. Geoderma 2021, 398, 115118. [Google Scholar] [CrossRef]
- Bhattacharyya, S.S.; Ros, G.H.; Furtak, K.; Iqbal, H.M.; Parra-Saldívar, R. Soil carbon sequestration–An interplay between soil microbial community and soil organic matter dynamics. Sci. Total Environ. 2022, 815, 152928. [Google Scholar] [CrossRef] [PubMed]
- Bashir, O.; Ali, T.; Baba, Z.A.; Rather, G.; Bangroo, S.; Mukhtar, S.D.; Naik, N.; Mohiuddin, R.; Bharati, V.; Bhat, R.A. Soil organic matter and its impact on soil properties and nutrient status. In Microbiota and Biofertilizers, Vol 2: Ecofriendly Tools for Reclamation of Degraded Soil Environs; Springer: Cham, Switzerland, 2021; pp. 129–159. [Google Scholar]
- Hamzehpour, N.; Shafizadeh-Moghadam, H.; Valavi, R. Exploring the driving forces and digital mapping of soil organic carbon using remote sensing and soil texture. CATENA 2019, 182, 104141. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Zhang, X.; Liu, H. Mapping the soil organic matter content in a typical black-soil area using optical data, radar data and environmental covariates. Soil Tillage Res. 2024, 235, 105912. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Kung, H.-T.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Ji, C.; Xu, X.; Wang, H.; Pan, J.; Bumberger, J.; Haase, D.; Lausch, A. Prediction of soil organic carbon and the C: N ratio on a national scale using machine learning and satellite data: A comparison between Sentinel-2, Sentinel-3 and Landsat-8 images. Sci. Total Environ. 2021, 755, 142661. [Google Scholar] [CrossRef]
- Du, P.; Liu, S.; Xia, J.; Zhao, Y. Information fusion techniques for change detection from multi-temporal remote sensing images. Inf. Fusion 2013, 14, 19–27. [Google Scholar] [CrossRef]
- Jianya, G.; Haigang, S.; Guorui, M.; Qiming, Z. A review of multi-temporal remote sensing data change detection algorithms. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 757–762. [Google Scholar]
- Du, P.; Li, X.; Cao, W.; Luo, Y.; Zhang, H. Monitoring urban land cover and vegetation change by multi-temporal remote sensing information. Min. Sci. Technol. 2010, 20, 922–932. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Wang, L.; Tian, Y.; Yao, X.; Zhu, Y.; Cao, W. Predicting grain yield and protein content in wheat by fusing multi-sensor and multi-temporal remote-sensing images. Field Crops Res. 2014, 164, 178–188. [Google Scholar] [CrossRef]
- Duan, M.; Song, X.; Liu, X.; Cui, D.; Zhang, X. Mapping the soil types combining multi-temporal remote sensing data with texture features. Comput. Electron. Agric. 2022, 200, 107230. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Zhang, X.; Liu, H. Mapping of soil organic matter in a typical black soil area using Landsat-8 synthetic images at different time periods. CATENA 2023, 231, 107336. [Google Scholar] [CrossRef]
- Zang, D.; Zhao, Y.; Luo, C.; Zhang, S.; Dai, X.; Li, Y.; Liu, H. Improving the accuracy of soil organic matter mapping in typical Planosol areas based on prior knowledge and probability hybrid model. Soil Tillage Res. 2025, 246, 106358. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Luo, C.; Zhang, X.; Liu, H. A new methodology for establishing an SOC content prediction model that is spatiotemporally transferable at multidecadal and intercontinental scales. ISPRS J. Photogramm. Remote Sens. 2024, 218, 531–550. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Zhang, S.; Ai, H.; Han, Y.; Luo, C.; Liu, H. A novel model for mapping soil organic matter: Integrating temporal and spatial characteristics. Ecol. Inform. 2024, 84, 102923. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Meng, X.; Bao, Y.; Zhang, X.; Luo, C.; Liu, H. A long-term global Mollisols SOC content prediction framework: Integrating prior knowledge, geographical partitioning, and deep learning models with spatio-temporal validation. Remote Sens. Environ. 2025, 318, 114592. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Archana, R.; Jeevaraj, P.E. Deep learning models for digital image processing: A review. Artif. Intell. Rev. 2024, 57, 11. [Google Scholar] [CrossRef]
- Odebiri, O.; Odindi, J.; Mutanga, O. Basic and deep learning models in remote sensing of soil organic carbon estimation: A brief review. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102389. [Google Scholar] [CrossRef]
- Jenny, H. Factors of Soil Formation: A System of Quantitative Pedology; Courier Corporation: North Chelmsford, MA, USA, 1994. [Google Scholar]
- Sindayihebura, A.; Ottoy, S.; Dondeyne, S.; Van Meirvenne, M.; Van Orshoven, J. Comparing digital soil mapping techniques for organic carbon and clay content: Case study in Burundi’s central plateaus. CATENA 2017, 156, 161–175. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Hamzehpour, N.; Hassanzadeh, M.; Heung, B.; Goydaragh, M.G.; Schmidt, K.; Scholten, T. Enhancing the accuracy of machine learning models using the super learner technique in digital soil mapping. Geoderma 2021, 399, 115108. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, C.; Zhang, Y.; Gao, L.; Wang, Y.; Wu, Z.; Zhang, W.; Liu, H. Integration of bare soil and crop growth remote sensing data to improve the accuracy of soil organic matter mapping in black soil areas. Soil Tillage Res. 2024, 244, 106269. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Luo, C.; Zhang, X.; Liu, H. SOC content of global Mollisols at a 30 m spatial resolution from 1984 to 2021 generated by the novel ML-CNN prediction model. Remote Sens. Environ. 2024, 300, 113911. [Google Scholar] [CrossRef]
- Liu, Q.; He, L.; Guo, L.; Wang, M.; Deng, D.; Lv, P.; Wang, R.; Jia, Z.; Hu, Z.; Wu, G.; et al. Digital mapping of soil organic carbon density using newly developed bare soil spectral indices and deep neural network. CATENA 2022, 219, 106603. [Google Scholar] [CrossRef]
- Kong, D.; Chu, N.; Luo, C.; Liu, H. Analyzing spatial distribution and influencing factors of soil organic matter in cultivated land of northeast China: Implications for black soil protection. Land 2024, 13, 1028. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Meng, X.; Yu, Y.; Zhang, X.; Liu, H. Mapping the soil organic matter content in Northeast China considering the difference between dry lands and paddy fields. Soil Tillage Res. 2024, 244, 106270. [Google Scholar] [CrossRef]
- Chauhan, N.K.; Singh, K. A review on conventional machine learning vs deep learning. In Proceedings of the 2018 International Conference on Computing, Power and Communication Technologies (GUCON), Greater Noida, India, 28–29 September 2018; pp. 347–352. [Google Scholar]
- Nagendra, B.; Singh, G. Comparing ARIMA, linear regression, random forest, and LSTM for time series forecasting: A study on item stock predictions. In Proceedings of the 2023 4th IEEE Global Conference for Advancement in Technology (GCAT), Bangalore, India, 6–8 October 2023; pp. 1–8. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Kuang, X.; Wang, F.; Hernandez, K.M.; Zhang, Z.; Grossman, R.L. Accurate and rapid prediction of tuberculosis drug resistance from genome sequence data using traditional machine learning algorithms and CNN. Sci. Rep. 2022, 12, 2427. [Google Scholar] [CrossRef]
- Sagar, A.S.; Chen, Y.; Xie, Y.; Kim, H.S. MSA R-CNN: A comprehensive approach to remote sensing object detection and scene understanding. Expert Syst. Appl. 2024, 241, 122788. [Google Scholar] [CrossRef]
- Yao, M.; Zhang, Y.; Liu, G.; Pang, D. SSNet: A novel transformer and CNN hybrid network for remote sensing semantic segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3023–3037. [Google Scholar] [CrossRef]
- Radočaj, D.; Gašparović, M.; Jurišić, M. Open remote sensing data in digital soil organic carbon mapping: A review. Agriculture 2024, 14, 1005. [Google Scholar] [CrossRef]
- Bao, Y.; Yao, F.; Meng, X.; Wang, J.; Liu, H.; Wang, Y.; Liu, Q.; Zhang, J.; Mouazen, A.M. A fine digital soil mapping by integrating remote sensing-based process model and deep learning method in Northeast China. Soil Tillage Res. 2024, 238, 106010. [Google Scholar] [CrossRef]
- Zhao, X.; Heiden, U.; Karlshöfer, P.; Xiong, Z.; Zhu, X.X. Soil Organic Carbon Retrieval from DESIS Images by CNN. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 14–19 April 2024; p. 9731. [Google Scholar]
- Senanayake, S.; Pradhan, B.; Alamri, A.; Park, H.J. A new application of deep neural network (LSTM) and RUSLE models in soil erosion prediction. Sci. Total Environ. 2022, 845, 157220. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Zhang, Y.; Zhang, Y.; Shangguan, W.; Li, Q.; Li, L.; Jiang, S. Interpreting Conv-LSTM for spatio-temporal soil moisture prediction in China. Agriculture 2023, 13, 971. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Shangguan, W.; Li, L.; Dai, Y. A novel local-global dependency deep learning model for soil mapping. Geoderma 2023, 438, 116649. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, Y.; Huang, H.; Li, A.; Yang, L.; Zhou, C. A CNN-LSTM model for soil organic carbon content prediction with long time series of MODIS-based phenological variables. Remote Sens. 2022, 14, 4441. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Lu, J.; Batra, D.; Parikh, D.; Lee, S. Vilbert: Pretraining task-agnostic visiolinguistic representations for vision-and-language tasks. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning (PMLR), Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Zhao, W.; Wu, Z.; Yin, Z.; Li, D. Attention-based CNN ensemble for soil organic carbon content estimation with spectral data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhao, W.; Efremova, N. Soil organic carbon estimation from climate-related features with graph neural network. arXiv 2023, arXiv:2311.15979. [Google Scholar] [CrossRef]
- Luo, C.; Wang, Y.; Zhang, X.; Zhang, W.; Liu, H. Spatial prediction of soil organic matter content using multiyear synthetic images and partitioning algorithms. CATENA 2022, 211, 106023. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, W.; Zhang, X.; Liu, H. Mapping soil organic matter content using Sentinel-2 synthetic images at different time intervals in Northeast China. Int. J. Digit. Earth 2023, 16, 1094–1107. [Google Scholar] [CrossRef]
- He, X.; Yang, L.; Li, A.; Zhang, L.; Shen, F.; Cai, Y.; Zhou, C. Soil organic carbon prediction using phenological parameters and remote sensing variables generated from Sentinel-2 images. CATENA 2021, 205, 105442. [Google Scholar] [CrossRef]
- Guo, L.; Fu, P.; Shi, T.; Chen, Y.; Zeng, C.; Zhang, H.; Wang, S. Exploring influence factors in mapping soil organic carbon on low-relief agricultural lands using time series of remote sensing data. Soil Tillage Res. 2021, 210, 104982. [Google Scholar] [CrossRef]
- Querejeta, J.I.; Schlaeppi, K.; López-García, Á.; Ondoño, S.; Prieto, I.; van Der Heijden, M.G.; del Mar Alguacil, M. Lower relative abundance of ectomycorrhizal fungi under a warmer and drier climate is linked to enhanced soil organic matter decomposition. New Phytol. 2021, 232, 1399–1413. [Google Scholar] [CrossRef] [PubMed]
- Pouladi, N.; Gholizadeh, A.; Khosravi, V.; Borůvka, L. Digital mapping of soil organic carbon using remote sensing data: A systematic review. CATENA 2023, 232, 107409. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter, and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Körschens, M.; Weigel, A.; Schulz, E. Turnover of soil organic matter (SOM) and long-term balances—tools for evaluating sustainable productivity of soils. Z. Pflanzenernährung Bodenkd. 1998, 161, 409–424. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, K.; Hu, N.; Lou, Y.; Wang, F.; Wang, Y. Biochemical composition of soil organic matter physical fractions under 32-year fertilization in Ferralic Cambisol. Carbon Res. 2023, 2, 1. [Google Scholar] [CrossRef]
- Zhou, Y.; Hartemink, A.E.; Shi, Z.; Liang, Z.; Lu, Y. Land use and climate change effects on soil organic carbon in North and Northeast China. Sci. Total Environ. 2019, 647, 1230–1238. [Google Scholar] [CrossRef]
- Dong, Z.; Yao, L.; Bao, Y.; Zhang, J.; Yao, F.; Bai, L.; Zheng, P. Prediction of soil organic carbon content in complex vegetation areas based on CNN-LSTM model. Land 2024, 13, 915. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, J. Crossformer: Transformer utilizing cross-dimension dependency for multivariate time series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 213–229. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1992; pp. 492–518. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
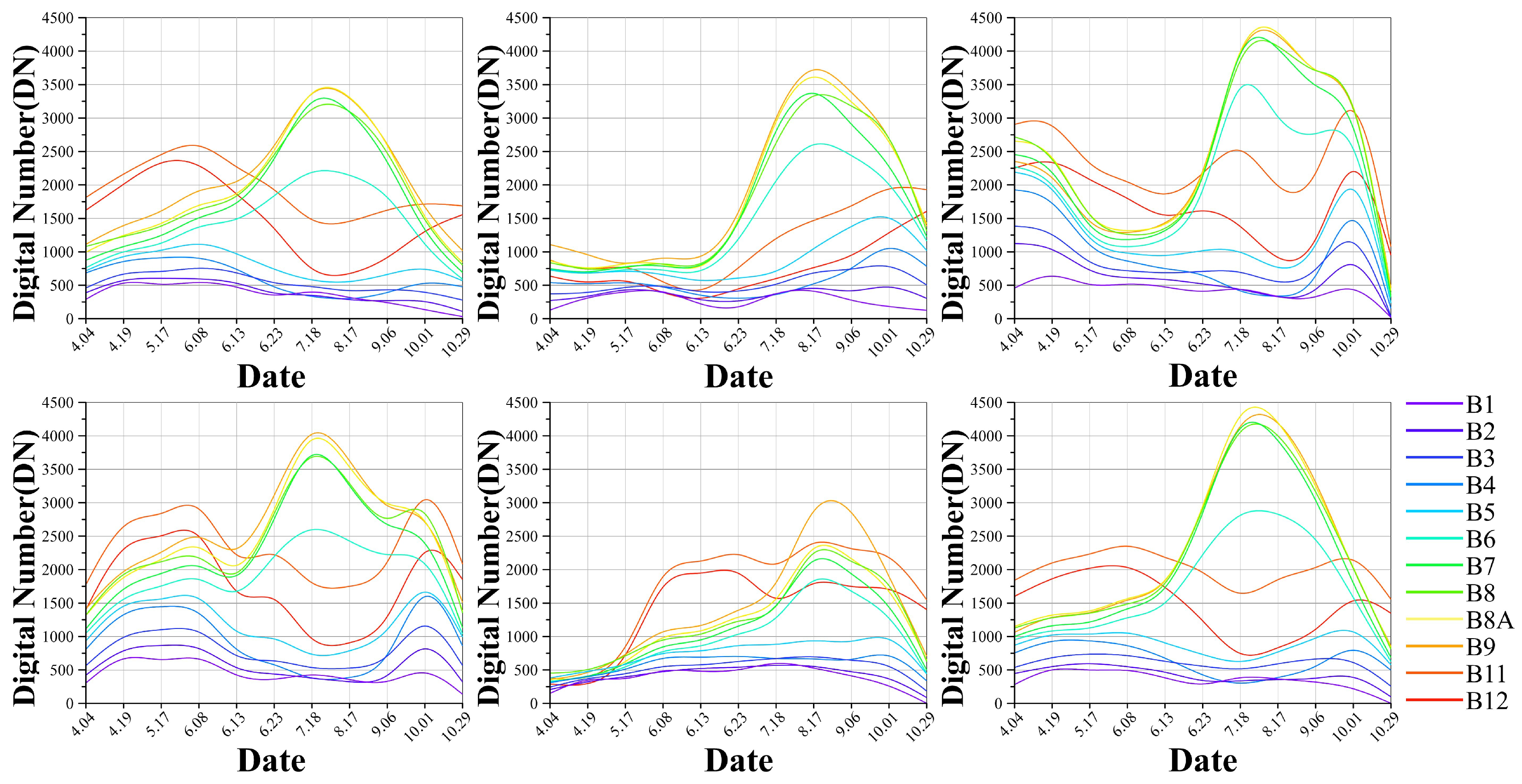




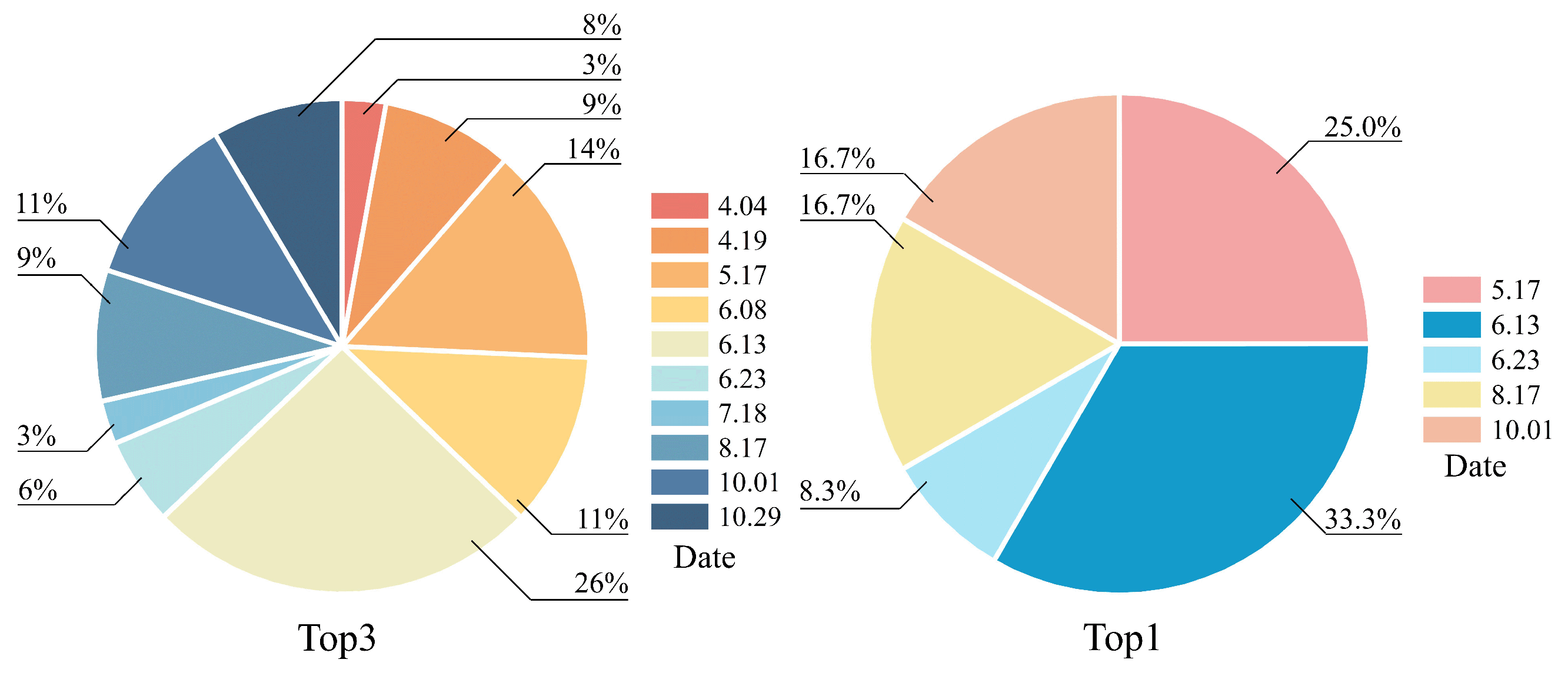
| Various | Pixel Size (m) | Class |
|---|---|---|
| Annual temperature | 1000 | Climate |
| Annual precipitation | 1000 | Climate |
| Elevation | 30 | Terrain |
| CNBL | 27 | Terrain |
| Block | Kernel | I.C. | O.C. | Stride | Padding | Activation |
|---|---|---|---|---|---|---|
| DCA Block 1 | 3 × 3 | 4 | 24 | 1 | 1 | ReLU |
| 3 × 3 | 24 | 24 | 1 | 1 | ReLU | |
| 4 × 4 | 24 | 32 | 1 | 2 | ReLU | |
| 1 × 1 | 32 | 32 | 1 | - | ReLU | |
| DCA Block 2 | 2 × 2 | 32 | 32 | 1 | 1 | ReLU |
| 1 × 1 | 32 | 16 | 1 | - | ReLU |
| Models | RMSE (%) | MAE (%) | MSE (%)2 | R2 | RPIQ | |
|---|---|---|---|---|---|---|
| Machine learning | KNN [22] | 1.181 | 0.869 | 1.395 | 0.151 | 1.44 |
| Elastic Net [21] | 1.110 | 0.796 | 1.232 | 0.249 | 1.51 | |
| LightGBM [25] | 1.141 | 0.791 | 1.302 | 0.206 | 1.50 | |
| SVM [20] | 1.116 | 0.824 | 1.246 | 0.292 | 1.48 | |
| XGBoost [24] | 1.056 | 0.678 | 1.115 | 0.321 | 1.67 | |
| RF [23] | 0.955 | 0.610 | 0.912 | 0.451 | 1.59 | |
| Deep learning | CNN-LSTM [52] | 0.982 | 0.704 | 0.964 | 0.412 | 1.65 |
| CNN-GRU | 0.977 | 0.678 | 0.955 | 0.421 | 1.67 | |
| 2C-Net (Ours) | 0.884 | 0.581 | 0.781 | 0.524 | 1.89 | |
| Models | RMSE | MAE | MSE | R2 | RPIQ |
|---|---|---|---|---|---|
| 2C-Net w/o MFFM DCA CE | 1.112 | 0.824 | 1.237 | 0.347 | 1.47 |
| 2C-Net w/o MFFM DCA | 1.004 | 0.720 | 1.009 | 0.386 | 1.61 |
| 2C-Net w/o MFFM | 0.996 | 0.677 | 0.992 | 0.402 | 1.65 |
| 2C-Net with all | 0.884 | 0.581 | 0.781 | 0.524 | 1.89 |
| Loss Function | RMSE | MAE | MSE | R2 | RPIQ |
|---|---|---|---|---|---|
| MAE Loss | 0.925 | 0.615 | 0.856 | 0.478 | 1.71 |
| MSE Loss | 0.922 | 0.635 | 0.851 | 0.482 | 1.77 |
| Huber Loss | 0.884 | 0.581 | 0.781 | 0.524 | 1.89 |
| Methods | RMSE | MAE | MSE | R2 | RPIQ |
|---|---|---|---|---|---|
| Add | 0.918 | 0.632 | 0.842 | 0.487 | 1.78 |
| Concat | 0.884 | 0.581 | 0.781 | 0.524 | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, J.; Luo, C.; Lu, J.; Kong, D.; Li, X.; Liu, H. 2C-Net: A Novel Spatiotemporal Dual-Channel Network for Soil Organic Matter Prediction Using Multi-Temporal Remote Sensing and Environmental Covariates. Remote Sens. 2025, 17, 3358. https://doi.org/10.3390/rs17193358
Geng J, Luo C, Lu J, Kong D, Li X, Liu H. 2C-Net: A Novel Spatiotemporal Dual-Channel Network for Soil Organic Matter Prediction Using Multi-Temporal Remote Sensing and Environmental Covariates. Remote Sensing. 2025; 17(19):3358. https://doi.org/10.3390/rs17193358
Chicago/Turabian StyleGeng, Jiale, Chong Luo, Jun Lu, Depiao Kong, Xue Li, and Huanjun Liu. 2025. "2C-Net: A Novel Spatiotemporal Dual-Channel Network for Soil Organic Matter Prediction Using Multi-Temporal Remote Sensing and Environmental Covariates" Remote Sensing 17, no. 19: 3358. https://doi.org/10.3390/rs17193358
APA StyleGeng, J., Luo, C., Lu, J., Kong, D., Li, X., & Liu, H. (2025). 2C-Net: A Novel Spatiotemporal Dual-Channel Network for Soil Organic Matter Prediction Using Multi-Temporal Remote Sensing and Environmental Covariates. Remote Sensing, 17(19), 3358. https://doi.org/10.3390/rs17193358








