SS³L: Self-Supervised Spectral–Spatial Subspace Learning for Hyperspectral Image Denoising

Highlights

What are the main findings?

• A dual-domain self-supervised hyperspectral denoising framework that disentangles noise and signal from single noisy inputs without requiring paired training data was developed.
• SS³L integrates adaptive rank subspace representation with a noise-aware spectral–spatial hybrid loss constrained self-supervised learning framework, achieving robust denoising across varying noise levels and different scenes.

What is the implication of the main finding?

• The proposed framework eliminates the requirement for clean training data and manual hyperparameter tuning, addressing key limitations of existing denoising methods in hyperspectral restoration research.
• By enhancing structural fidelity and spectral accuracy under complex noise conditions, SS³L improves the quality and usability of hyperspectral data for remote sensing applications such as classification, detection, and monitoring across different sensors.

Abstract

Hyperspectral imaging (HSI) systems often suffer from complex noise degradation during the imaging process, significantly impacting downstream applications. Deep learning-based methods, though effective, rely on impractical paired training data, while traditional model-based methods require manually tuned hyperparameters and lack generalization. To address these issues, we propose SS³L (Self-Supervised Spectral-Spatial Subspace Learning), a novel HSI denoising framework that requires neither paired data nor manual tuning. Specifically, we introduce a self-supervised spectral–spatial paradigm that learns noisy features from noisy data, rather than paired training data, based on spatial geometric symmetry and spectral local consistency constraints. To avoid manual hyperparameter tuning, we propose an adaptive rank subspace representation and a loss function designed based on the collaborative integration of spectral and spatial losses via noise-aware spectral-spatial weighting, guided by the estimated noise intensity. These components jointly enable a dynamic trade-off between detail preservation and noise reduction under varying noise levels. The proposed SS³L embeds noise-adaptive subspace representations into the dynamic spectral–spatial hybrid loss-constrained network, enabling cross-sensor denoising through prior-informed self-supervision. Experimental results demonstrate that SS³L effectively removes noise while preserving both structural fidelity and spectral accuracy under diverse noise conditions.

1. Introduction

Hyperspectral images (HSIs) retain rich spectral and spatial information, and they have been extensively explored in various kinds of applications, such as biology, ecology, and geoscience [1,2,3]. However, HSIs are often contaminated by noise, which degrades the performance of downstream tasks such as classification, detection, and quantitative analysis, ultimately reducing the accuracy and reliability of HSI-based decision-making. Consequently, numerous HSI denoising techniques have been proposed to address this challenge [4,5].

HSI denoising methods can be broadly categorized into traditional model-based methods and deep-learning-based methods. Traditional approaches typically formulate HSI denoising as an ill-posed inverse problem, which is addressed by incorporating regularization terms based on prior knowledge to transform it into a well-posed problem. For instance, studies in [1,2,4,5,6] encoded both global low-rank and local smoothness priors using the total variation (TV) technique for HSI denoising. Concurrently, Zhuang et al. exploited the non-local low-rank prior by applying a low-rank constraint to non-local HSI blocks in [7]. To address sparse noise, some methods modeled these noise types as sparse components, characterized using distinct paradigms such as the ${\ell }_1$ norm in [8], the ${\ell }_{2,1}$ norm in [9] and Schatten-p norm in [10]. Although knowledge-driven methods can capture intrinsic HSI characteristics, their performance is highly sensitive to parameters such as the assumed rank of the low-rank prior and the number of iterations.

Recent advances in deep learning have demonstrated superior performance in both remote sensing [11,12] and HSI processing [13]. Therefore, in HSI denoising, through convolutional neural networks (CNNs) and vision transformers, many methods are proposed [14,15,16]. For example, Chang et al. [14] introduced HSI-DeNet to evaluate the efficacy of CNNs for HSI denoising, while [15] developed a 3D attention network for this task. Similarly, Zhang et al. [16] proposed a three-dimensional spatial–spectral attention transformer for HSI denoising. Compared to traditional model-based methods, these supervised approaches learn a nonlinear mapping or function using paired clean-noisy data, enabling intuitive and rapid inference. However, their performance depends heavily on the availability and quality of training data, as paired clean-noisy HSI datasets remain scarce in practice. Additionally, hyperspectral sensors exhibit substantial variations in specifications, which means models trained on data from one sensor may not generalize well to HSI from other sensors.

These issues have spurred interest in data-independent approaches, such as self-supervised learning [17,18,19] and unsupervised learning [20,21,22]. A prominent example is Noise2Noise (N2N) [17], a self-supervised method that learns noise distributions by training on multiple noisy observations of the same scene. Another approach, Deep Image Prior (DIP) [20], employs a randomly initialized neural network to generate clean images by mapping a fixed random input (e.g., white noise) to a noise-free output. However, as an iterative optimization-based method, DIP’s performance is highly sensitive to handcrafted hyperparameters (e.g., learning rate, early stopping) and the choice of loss function. Furthermore, adapting the N2N framework to HSI denoising remains challenging. Unlike RGB images with three spectral channels, HSI contains hundreds of spectral bands, making direct application of RGB-oriented N2N methods suboptimal for HSI. These limitations restrict the generalizability of existing data-independent methods when applied to remote sensing HSIs across diverse scenes and sensors.

Despite the success of existing HSI denoising methods, two fundamental challenges remain: (1) supervised deep learning approaches require paired noisy–clean images, which are often unavailable in remote sensing, and (2) model-based methods are sensitive to hyperparameters and require careful parameter tuning. To address these issues, we propose SS³L (Self-Supervised Spectral-Spatial Subspace Learning), a novel dual-constrained framework that integrates self-supervised learning with subspace representation (SR). By leveraging intrinsic redundant features, we design a spectral-spatial hybrid loss function that integrates adaptive rank SR (ARSR), thereby constructing an end-to-end self-supervised framework robust to different noise conditions and various imaging systems. Specifically, we introduce a noise variance estimator called Spectral–Spatial Hybrid Estimation (SSHE) by exploring spatial–spectral local self-similarity priors, which quantifies the noise intensity by analyzing adjacent spectral differences and local variance statistics as the first step of the denoising process. Based on the spectral–spatial isotropy of noise and the structural consistency prior of natural scenes, we develop spatial checkerboard downsampling and spectral difference downsampling strategies to construct complementary spatial and spectral constraints. An adaptive weighting function conditioned on the noise variance estimated via SSHE is employed to formulate the Adaptive Weighted Spectral-Spatial Collaborative Loss Function (AWSSCLF), ensuring robustness under varying noise levels. Concurrently, the ARSR algorithm determines the optimal subspace dimension by dynamically adjusting the latent rank based on the estimated noise energy. Under the constraints of the proposed AWSSCLF, a lightweight network is employed to learn the denoising task within the subspace obtained via ARSR, thereby completing the construction of an end-to-end self-supervised denoising framework.

The main contributions of this article are as follows:

1.

We propose SS³L, a spatial–spectral dual-domain self-supervised framework that embeds domain priors into both model design and optimization via ARSR. By enforcing cross-scale consistency through spatial and spectral downsampling, the framework achieves effective noise-signal disentanglement from a single noisy HSI without corresponding clean image supervision.

2.

We design a spectral–spatial hybrid loss function named AWSSCLF with physics constraints: geometric symmetry and inter-band spectral correlation. Its noise-adaptive weighting mechanism derived from SSHE automatically prioritizes structural fidelity under low noise and enhances denoising under high noise, achieving adaptability to different imaging systems.

3.

The proposed ARSR, guided by singular value energy distribution and noise energy estimation, can dynamically adjust the subspace rank to balance signal fidelity and noise separation, ensuring robustness at varying noise levels.

The rest of this article is organized as follows. Data-independent deep learning methods and SR techniques are reviewed in Section 2. The proposed method is presented in Section 3. Experimental results are shown in Section 4. Finally, conclusions are drawn in Section 5.

2. Related Works

In this section, we analyze three categories of data-independent HSI denoising approaches: model-based and knowledge-driven approaches, self-supervised learning-based techniques, and unsupervised learning-based methods.

2.1. Model-Based Methods

Traditional knowledge-driven methods formulate the HSI denoising problem as an ill-posed inverse problem, subsequently regularizing it into a well-posed formulation via manually designed terms that enforce prior spectral–spatial constraints.

$$\widehat{\mathcal{X}}=\underset{\mathcal{X}}{\mathrm{argmin}}{\parallel \mathcal{Y}-\mathcal{X}\parallel }_F^2+\sum _i^K{\lambda }_i{R}_i\left(X\right)$$

(1)

HSI denoising exploits three core data priors: (1) local/global low-rankness, (2) local smoothness, and (3) non-local self-similarity across spatial–spectral domains to construct the regularization terms. The low-rank prior originates from the intrinsic subspace structure of HSI data cubes, where nuclear norm minimization (e.g., weighted nuclear norm minimization (WNNM) [23], tensor robust principal component analysis (TRPCA) [24]) non-local low-rank tensor decomposition [25]) serve as dominant regularization strategies. Local smoothness priors enforce spatial consistency by constraining neighboring pixel variations, typically implemented through TV regularizers such as LRMR-TV [2], local low-rank spatial–spectral TV (LLRSSTV) [6], and 3D correlation TV (3DCTV) [26]. Non-local self-similarity priors (NLSSP) leverage redundant spatial patterns, integrated via hybrid frameworks like BM4D [27], Kronecker basis representation (KBR) [28], and Non-Local Meets Global (NG-meets) [3]. Sparse representation techniques [5,29] and tensor factorization variants [4,7] further complement these approaches.

However, these optimization-based approaches are highly sensitive to parameter selection, including rank of tensor decomposition, patch size, group numbers, regularization weights, iterations, and so on. Furthermore, handcrafted constraint terms struggle to adapt to complex noise profiles and diverse HSI data distributions. These limitations hinder the generalization of traditional methods when processing HSIs under various noise conditions.

2.2. Self-Supervised Denoising

Although supervised deep learning methods have demonstrated notable empirical success in HSI denoising, acquiring large-scale paired noisy-clean training data, especially remote sensing HSIs, remains challenging. To circumvent this limitation, self-supervised denoising frameworks have been developed to learn intrinsic image features directly from noisy observations. Pioneering work by Lehtinen et al. [17] laid the theoretical foundation for training denoising networks without clean images. Their study shows that, under the assumption of zero-mean and independent noise, a network trained to map between two independently corrupted observations of the same region can implicitly learn to recover the clean image. Formally, given two noisy observations:

$${\mathbf{Y}}_1=\mathbf{X}+{\mathbf{N}}_1,{\mathbf{Y}}_2=\mathbf{X}+{\mathbf{N}}_2$$

where ${\mathbf{N}}_1,{\mathbf{N}}_2$ are independent noise vectors. Minimizing the expected loss:

$$\arg \underset{\theta }{\min }\mathbb{E}\left[\parallel D_{\theta }\left({\mathbf{Y}}_1\right)-{\mathbf{Y}}_2{\parallel }_2^2\right]$$

(2)

is theoretically equivalent to supervised training with clean image $\mathbf{X}$:

$$\arg \underset{\theta }{\min }\mathbb{E}\left[\parallel D_{\theta }\left({\mathbf{Y}}_1\right){-\mathbf{X}\parallel }_2^2\right]$$

This surprising result enables the N2N framework to train a denoiser $D_{\theta }$ using aligned noisy–noisy image pairs to estimate the clean image $\mathbf{X}$ by minimizing the loss $\frac{1}{n}{\sum }_{i=1}^n\parallel D_{\theta }\left({\mathbf{Y}}_1^i\right)-{\mathbf{Y}}_2^i\parallel$.

Based on N2N, Neighbor2Neighbor (Ne2Ne) [19] eliminated the need for aligned pairs by subsampling random neighbors from a single noisy image to generate training pairs. Zero-Shot Noise2Noise (ZSN2N) [30] proposed a symmetric downsampler based on the random neighbor downsampler in Ne2Ne for single-image denoising. Meanwhile, methods like Noise2Void (N2V) [31], Noise2Self (N2S) [32], and Signal2Signal (S2S) [33] employed blind-spot networks (BSNs) to predict target pixels using surrounding neighborhoods, circumventing N2N’s requirement for two independent noisy observations.

All of the above self-supervised networks are designed for RGB images and extending a single-band version of the network directly to the HSI case, band-by-band, often leads to suboptimal performance, which has been presented by the experiment in [29]. There are numerous self-supervised techniques designed for HSI denoising recently. In [34], Qian et al. extended the work of N2N by using two neighboring bands of an HSI as the noisy-noisy training pairs. Zhuang et al. [29] proposed Eigenimage2Eigenimage (E2E) by combining SR [35] with Ne2Ne [19]. E2E learned noise distribution using paired noisy eigenimages obtained by SR instead of HSI data with full bands to overcome the constraint of the number of frequency bands. However, E2E remains a self-supervised method and inherits N2N’s constraints: dependence on curated training data and limited robustness for diverse HSI datasets.

2.3. Unsupervised Methods

DIP [20], a classic unsupervised-learning denoising method, achieves single-image denoising by exploiting the inherent inductive bias of randomly initialized neural networks. Specifically, neural networks prioritize fitting the underlying image structure over noise artifacts when mapping random input to noisy observations. By optimizing the network to reconstruct the noisy input from random noise, guided by the following loss function:

$$\arg \underset{\theta }{\min }\left|\right|f_{\theta }\left(z\right)-\mathbf{Y}{\left|\right|}_2^2$$

(3)

the network captures the clean image’s latent features before overfitting to noise. Early stopping at an optimal iteration step thus yields a denoised output, circumventing the need for pre-trained models or paired training data.

Sidorov et al. [22] extended DIP to HSI denoising, while Miao et al. [36] proposed a disentangled spatial-spectral DIP framework based on HSI decomposition via a linear mixture model. Qiang et al. [37] introduced a self-supervised denoising method combining spectral low-rankness priors with deep spatial priors (SLRP-DSP), and Shi et al. [21] developed a double subspace deep prior approach by integrating sparse representation into the DIP framework.

Although these DIP-based methods achieve notable results and preserve HSI spatial–spectral details effectively, they inherit critical limitations. The DIP-based methods are inherently highly sensitive to iteration counts: insufficient iterations yield suboptimal denoising, while excessive iterations lead to overfitting to noise. Furthermore, integrating handcrafted prior constraints reintroduces the pitfalls of traditional methods: sensitivity to hyperparameters in regularization terms.

To address these issues, we propose a HSI denoising framework named SS³L that generalizes robustly under diverse scenarios, including varying noise levels, noise types, and HSI datasets from heterogeneous sensors. Unlike existing approaches that rely on network architectures designed to model noise structure, our framework learns noise distributions by focusing on the inherent characteristics of both noise and HSI data, thereby decoupling denoising performance from handcrafted priors or sensor-specific training data.

3. Proposed Method

3.1. Overview of SS³L Framework

In this section, we introduce the proposed SS³L (Self-Supervised Spectral–Spatial Subspace Learning) framework for HSI denoising. As illustrated in Figure 1, SS³L consists of two key components:

• Adaptive Rank Subspace Representation (ARSR): A dynamic rank subspace decomposition is applied to the noisy HSI, guided by a hybrid spatial–spectral noise estimation strategy. This step captures the intrinsic low-dimensional structure of the image while suppressing noise.
• Adaptive Weighted Spectral-Spatial Collaborative Loss Function (AWSSCLF): constructed based on spatial geometric symmetry and spectral continuity priors, AWSSCLF incorporates a sigmoid-based adaptive weighting mechanism that dynamically balances the two loss components according to the estimated noise level, ensuring robust and effective denoising under diverse conditions.

The SS³L framework adopts a dual-path training mechanism comprising spatial and spectral supervision branches. Both branches rely on subspace representations derived through ARSR, which dynamically selects the latent dimension based on noise intensity. The spatial path leverages checkerboard downsampling to create paired sub-images, which facilitates a regression–consistency loss design. In parallel, the spectral path performs spectral difference downsampling, with each sub-cube undergoing ARSR before being processing by the network.

The noise variance, estimated through Spectral–Spatial Hybrid Estimator (SSHE), generates adaptive coefficient $\alpha$ that balance influence of the spatial and spectral losses. These components are then integrated into a unified loss function, termed the AWSSCLF, to guide the self-supervised learning of the network $f_{\theta }$ without requiring any clean ground truth.

In the following subsections, we first formulate the denoising problem and define the mathematical notation used throughout the method. Then, we detail each component of the proposed method.

3.2. Problem Formulation

We begin by formulating the HSI denoising problem. In practice, HSIs are often degraded by a combination of additive Gaussian noise (i.e., sensor and atmosphere effects) and sparse noise (e.g., stripes, dead pixels, or impulse interference). These corruptions collectively deteriorate both spatial and spectral fidelity, challenging downstream processing tasks.

The observed noisy HSI $\mathcal{Y}\in {\mathbb{R}}^{H\times W\times B}$ is modeled as the sum of a clean image $\mathcal{X}$, additive Gaussian noise $\mathcal{N}$, and sparse noise $\mathcal{S}$:

$$\mathcal{Y}=\mathcal{X}+\mathcal{N}+\mathcal{S}$$

(4)

where $\mathcal{Y},\mathcal{X}\in {\mathbb{R}}^{H\times W\times B}$ denote the degraded noisy HSI and clean HSI, respectively; $\mathcal{N}$ represents the additive Gaussian noise $\mathbf{N}(0,{\sigma }^2)$ and $\mathcal{S}$ indicates the sparse noise.

The SR can represent the hyperspectral vectors based on the high spectral correlation [8]:

$$\mathcal{X}=\mathcal{Z}{\times }_3\mathbf{E}$$

(5)

where $\mathcal{Z}\in {\mathbb{R}}^{H\times W\times r}$ denotes the eigenimages of the SR, in which $r\ll B$ is the dimension of the subspace and hyperparameter of the SR (i.e., rank r) fixed at $r=4$ in [29], ${\times }_3$ indicates the mode-3 product of a tensor $\mathcal{X}\in {\mathbb{R}}^{I_1\times I_2\times I_3}$ with a matrix $U\in {\mathbb{R}}^{J\times I_3}$ is denoted as $\mathcal{X}{\times }_{3}U$, resulting in a tensor of size ${\mathbb{R}}^{I_1\times I_2\times J}$. The matrix $\mathbf{E}\in {\mathbb{R}}^{r\times B}$ consists of the first r spectral eigenvectors extracted from an orthogonal matrix $\widehat{\mathbf{E}}\in {\mathbb{R}}^{B\times B}$ satisfying ${\widehat{\mathbf{E}}}^T\widehat{\mathbf{E}}=\mathbf{I}$, in which $\mathbf{E}=\widehat{\mathbf{E}}[1:r,:]$ and $\mathbf{I}$ is the identity matrix.

The SR of the noisy HSI $\mathcal{Y}$ with rank r can be formulated as

$$({\mathcal{Z}}_y,{\mathbf{E}}_y)=R(\mathcal{Y},r),$$

(6)

where $R(\mathcal{Y},r)$ denotes the subspace decomposition of $\mathcal{Y}$ with rank r, yielding the coefficient tensor ${\mathcal{Z}}_y$ and the basis matrix ${\mathbf{E}}_y$.

3.3. Adaptive Rank Subspace Representation

The projection of noisy HSIs into a low-dimensional orthogonal subspace enables simultaneous data dimensionality reduction (enhancing computational efficiency) and structural fidelity preservation with noise attenuation. However, conventional fixed-rank SR methods are inherently limited by their static design. These methods impose a binary trade-off: higher ranks retain more high-frequency details (e.g., textures, edges) but tend to preserve more noise under heavy corruption, whereas lower ranks tend to over-smooth the data, which suppresses noise effectively but also leads to loss of semantically important structures. This fundamental rigidity prevents fixed-rank SR from adapting to varying noise levels across different scenarios.

To break the limitation of fixed-rank decomposition, we propose an adaptive framework called ARSR, which dynamically adjusts the subspace rank based on localized noise levels. This is achieved by integrating SSHE, a spectral-spatial hybrid estimation method that quantifies noise variance through joint analysis of spatial homogeneity and spectral correlation, with singular value thresholding to infer optimal SR rank. ARSR enables context-aware dimensionality reduction: in clean, detail-rich regions, it preserves higher ranks (e.g., 12–16), while in noise-dominated areas, it applies more aggressive truncation (e.g., 3–4), thus resolving the fixed-rank trade-off with adaptive precision.

We first introduce SSHE, followed by the ARSR mechanism.

Noise Estimation via SSHE

To accurately estimate noise levels, we design the SSHE method by combining two complementary strategies: Adjacent Band Estimation (ADE) and Marchenko–Pastur Variance Estimation (MPVE).

• ADE leverages the strong spectral correlation between neighboring HSI bands. Since signal components typically vary smoothly between adjacent bands, their differences tend to be small, while uncorrelated noise remains, or becomes more prominent in the residuals.
• MPVE exploits the statistical behavior of noise in the spatial domain. By unfolding the HSI into a matrix and analyzing its singular value distribution, which follows the Marchenko–Pastur (MP) law [38], the noise variance is estimated from the middle singular values.

The formulation of ADE is presented in Equation (7).

$$\begin{array}{cc}\hfill & d_k={\mathcal{Y}}_{:,:,k}-{\mathcal{Y}}_{:,:,k+1},k\in \{1,2,\dots ,B-1\}\hfill \\ \hfill & {\mu }_k=\underset{(i,j)}{\mathrm{median}}\left(d_k^{(i,j)}\right)\hfill \\ \hfill & {\mathrm{MAD}}_k=\underset{(i,j)}{\mathrm{median}}\left|d_k^{(i,j)}-{\mu }_k\right|\hfill \\ \hfill & {\widehat{\sigma }}_{\mathrm{adjacent}}=1.4826\times {\displaystyle \frac{1}{B-1}}\sum _{k=1}^{B-1}{\mathrm{MAD}}_k\hfill \end{array}$$

(7)

in which $d_k$ denotes the differential matrix of band images ${\mathcal{Y}}_{:,:,k}$ and ${\mathcal{Y}}_{:,:,k+1}$, ${\mu }_k$ represents the median of $d_k$, ${\mathrm{MAD}}_k$ (Median Absolute Deviation) quantifies the dispersion of $d_k$. For data that follow a normal distribution, the standard deviation $\sigma$ relates to MAD as $\sigma \approx 1.4826\times \mathrm{MAD}$ (see [39]). Therefore, multiplying by 1.4826 can convert MAD into the estimation of the standard deviation ${\widehat{\sigma }}_{\mathrm{adjacent}}$ of the noise in noisy HSI data $\mathcal{Y}$.

3.4. MP-Based Variance Estimation (MPVE)

MPVE is designed by exploring the statistical regularity of the singular values of a random matrix. Specifically, we unfold the HSI tensor $\mathcal{Y}\in {\mathbb{R}}^{H\times W\times B}$ along the spectral mode into a matrix $\mathbf{Y}\in {\mathbb{R}}^{m\times n}$, where $m=H\times W$ represents the number of spatial pixels and $n=B$ is the number of spectral bands.

Under the assumption of additive white Gaussian noise (AWGN), each row of $\mathbf{Y}$ corresponds to an independent spectral sample contaminated by noise, allowing $\mathbf{Y}$ to be modeled as a random matrix with i.i.d. entries in its noise-dominated part. According to the Marchenko–Pastur (MP) law [38], the empirical spectral distribution of the sample covariance matrix ${\mathbf{Y}}^{\top }\mathbf{Y}/m$ converges to the MP distribution:

$$\rho \left(x\right)={\displaystyle \frac{1}{2\pi {\sigma }^{2}cx}}\sqrt{(x_{+}-x)(x-x_{-})},x\in [x_{-},x_{+}]$$

where $c=m/n$ is the aspect ratio, and $x_{\pm }={\sigma }^2{(1\pm \sqrt{c})}^2$.

In practice, we normalize the matrix by its Frobenius norm:

$${\mathbf{Y}}_n={\displaystyle \frac{\mathbf{Y}-\overline{\mathbf{Y}}}{\parallel \mathbf{Y}-\overline{\mathbf{Y}}{\parallel }_F}},\mathrm{SVD:}{\mathbf{Y}}_n=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T$$

where $\mathrm{\Sigma }=\mathrm{diag}(s_1,s_2,\dots ,s_r)$ contains singular values in descending order.

The empirical noise power is estimated from the bulk of the spectrum by excluding extreme outliers:

$${\tilde{\sigma }}^2=\mathrm{Mean}\left(\left\{s_i^2\mid i\in [5\%, 95\%]\right\}\right)$$

(8)

This estimate is further corrected by the MP expectation to account for the aspect ratio:

$${\widehat{\sigma }}_{mp}^2={\displaystyle \frac{{\tilde{\sigma }}^2}{1+c}}$$

(9)

By combining ADE (spectral-domain analysis) and MPVE (spatial-domain analysis), SSHE provides robust and accurate estimation of the noise variance ${\widehat{\sigma }}^2$ under various HSI conditions.

$$\widehat{\sigma }=\beta \ast {\widehat{\sigma }}_{\mathrm{adjacent}}+(1-\beta )\ast {\widehat{\sigma }}_{mp}$$

(10)

where the weight $\beta$ reflects the relative reliability of ADE and MPVE. The estimated noise variance ${\widehat{\sigma }}^2$ can be used to guide the following steps.

By combining ADE (spectral-domain analysis) and MPVE (spatial-domain analysis), SSHE achieves a robust and accurate estimation of the noise variance ${\widehat{\sigma }}^2$ under various HSI conditions.

Notably, the noise estimation process does not require exact numerical accuracy. Instead, it serves to provide a coarse but meaningful estimation of the noise trend, which is sufficient to guide the subsequent self-supervised denoising module. This design enhances the robustness of our framework and reduces the dependence on dataset-specific tuning.

Adaptive Rank Selection Guided by Noise Statistics

The optimal SR rank is adaptively determined by the estimated variance ${\widehat{\sigma }}^2$. This adaptive mechanism simultaneously accounts for the statistical characteristics of normal distributions and the energy-dominated physical meaning of singular values.

Specifically, we determine the number of components to retain based on the magnitude of singular values obtained from SVD relative to the estimated noise variance and matrix aspect ratio. The selection criterion is given as follows:

$$s_i^2>{\widehat{\sigma }}^2·n·{(1+\sqrt{c})}^2>s_{i+1}^2$$

(11)

where $s_i^2$, $s_{i+1}^2$ represent the i-th and $i+1$-th singular values, ${\widehat{\sigma }}^2$ is the estimated noise variance, n denotes the column dimension of the reshaped HSI matrix (the band numbers B), and  $c=m/n$ is the matrix aspect ratio, with $m=H\times W$ representing the total number of spatial pixels. The index i corresponding to the last singular value that satisfies this inequality is selected as the optimal SR rank. The threshold ${\widehat{\sigma }}^2·n·{(1+\sqrt{c})}^2$ is grounded in the MP distribution [38], which describes the asymptotic singular value distribution of random Gaussian matrices. It establishes a theoretical upper bound on noise-induced singular values. Singular values exceeding this threshold are considered to carry meaningful signal information, whereas smaller ones are dominated by noise.

In the context of SVD, singular values quantify the energy of different components in the data. Therefore, distinguishing signal from noise becomes a matter of identifying where this energy drops below the noise-dominated boundary. The proposed criterion effectively leverages both the statistical behavior of random matrices and the physical significance of singular values, enabling a noise level aware adaptive rank selection mechanism. Notably, this approach is adaptive to matrix dimensionality and avoids reliance on empirically tuned thresholds, thereby preserving signal structures while suppressing noise-induced artifacts.

It is worth noting that SSHE is primarily designed for dense Gaussian-like noise, which typically dominates the total noise energy in hyperspectral imagery. The estimated noise variance serves as a coarse but meaningful reference for subsequent self-supervised denoising, rather than as an exact measure, and sparse noise components (e.g., stripes, impulse noise) are handled in later stages of our framework (e.g., AWSSCLF, ARSR). In practical remote sensing scenarios, such sparse noise usually affects only a small fraction of pixels or bands and exhibits much lower total energy, making the current variance-based approach a valid approximation for modeling the dominant noise components. Nevertheless, in extreme and rare cases where noise consists purely of sparse, non-Gaussian patterns, the Gaussian-based estimation in Equation (7) may be less effective, and integrating robust statistical estimators or sparse modeling techniques could further enhance flexibility.

3.5. Adaptive Weighted Spatial-Spectral Collaborative Loss Function

To achieve robust denoising under diverse noise conditions, we further introduce an adaptive weighting mechanism. This mechanism dynamically balances the contributions of spatial and spectral constraints based on the estimated noise characteristics, ensuring optimal performance without requiring manual hyperparameter tuning. In the following sections, we detail the spatial downsampling strategy and spatial loss formulation, followed by the spectral downsampling and spectral loss, before finally discussing how their adaptive combination leads to an effective spatio-spectral denoising framework.

3.5.1. Spatial Loss Function

Building upon the N2N learning paradigm shown in Equation (2), we adopt symmetric downsampling to generate multiple noisy observations from a single input sample for unsupervised noise distribution learning. Unlike conventional random neighborhood downsampling in Ne2Ne [19] and E2E [29], which introduces spatially uneven degradation, the checkerboard-patterned symmetric downsampling decomposes the original HSI into two geometrically balanced sub-images, preserving structural information while maintaining consistent i.i.d. noise among pixels.

The spatial downsampler, denoted as $D_{\mathrm{spa}}(·)$, operates on eigenimages ${\mathcal{Z}}_y\in {\mathbb{R}}^{H\times W\times r}$ derived from ARSR. As illustrated in Figure 2: $D_{\mathrm{spa}}(·)$ employs checkerboard-patterned decimation to generate two spatially complementary sub-images $D_{\mathrm{spa},1}\left({\mathcal{Z}}_y\right)$, $D_{\mathrm{spa},2}\left({\mathcal{Z}}_y\right)\in {\mathbb{R}}^{H/2\times W/2\times r}$. To improve the computational efficiency of spatial downsampling, we implement two 2D convolutional layers with customized kernels: ${\mathbf{K}}_1=[0.5, 0; 0, 0.5]$ and ${\mathbf{K}}_2=[0, 0.5; 0.5, 0]$ with stride 2 in order to implement the proposed spatial downsampling by convolutional operations.

It is worth emphasizing that the proposed checkerboard sampling differs fundamentally from the random neighborhood subsampling adopted in [19]. In [19], within each $2\times 2$ block, two adjacent pixels are randomly selected and assigned to $g_1\left(\mathbf{y}\right)$ and $g_2\left(\mathbf{y}\right)$, resulting in a stochastic and spatially varying sampling pattern. By contrast, the proposed method employs a deterministic and symmetric checkerboard allocation, where pixels are consistently assigned to $g_1\left(\mathbf{y}\right)$ and $g_2\left(\mathbf{y}\right)$ across the entire image. This symmetry ensures uniform spatial frequency coverage and eliminates randomness, thereby improving the stability and reproducibility of self-supervised training.

Based on the spatial downsampler $D_{\mathrm{spa}}$, the spatial loss function is defined as

$${\mathcal{L}}_{\theta }^{spa}={\mathcal{L}}_{\theta }^{res.}+{\mathcal{L}}_{\theta }^{cons.},$$

(12)

where ${\mathcal{L}}_{\theta }^{res.}$ denotes the regression loss, and ${\mathcal{L}}_{\theta }^{cons.}$ denotes the consistency loss.

A residual learning strategy is employed, in which the network $f_{\theta }$ is trained to predict the noise component, rather than the clean HSI itself. The clean HSI is subsequently recovered by subtracting the estimated noise from the noisy observation:

$$\widehat{\mathcal{X}}=\mathcal{Y}-f_{\theta }\left({\mathcal{Z}}_y\right){\times }_3{\mathbf{E}}_y.$$

(13)

The regression and consistency terms are formulated as

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\theta }^{res.}& =\frac{1}{2}\sum _{i=1}^2\parallel D_{\mathrm{spa},i}\left(\mathcal{Y}\right)-{\widehat{\mathcal{X}}}_{\mathrm{spa},3-i}{\parallel }_2^2,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\theta }^{cons.}& =\frac{1}{2}\sum _{i=1}^2\parallel D_{\mathrm{spa},i}\left(\widehat{\mathcal{X}}\right)-{\widehat{\mathcal{X}}}_{\mathrm{spa},i}{\parallel }_2^2,\hfill \end{array}$$

(15)

where

$${\widehat{\mathcal{X}}}_{\mathrm{spa},i}=D_{\mathrm{spa},i}\left(\mathcal{Y}\right)-f_{\theta }\left(D_{\mathrm{spa},i}\left({\mathcal{Z}}_y\right)\right){\times }_3{\mathbf{E}}_y$$

(16)

represents the estimation of the clean downsampled HSI $D_{\mathrm{spa},i}\left(\mathcal{X}\right)$ from its noisy counterpart $D_{\mathrm{spa},i}\left({\mathcal{Z}}_y\right)$. Here, $D_{\mathrm{spa},i}(·)$ denotes the downsampling operator with kernel ${\mathbf{k}}_i$.

The regression loss (14) enforces fidelity between the downsampled noisy observations and their denoised counterparts, thereby encouraging accurate residual prediction across multiple views. The consistency loss (15) serves as a regularization term by encouraging approximate commutativity between the network and the downsampling operator:

$$f_{\theta }\left(D_{\mathrm{spa},i}\left({\mathcal{Z}}_y\right)\right)\approx D_{\mathrm{spa},i}\left(f_{\theta }\left({\mathcal{Z}}_y\right)\right).$$

(17)

This approximate commutativity stabilizes training, preserves multi-scale spatial structures, and supplies effective supervision in the self-supervised setting, thereby enhancing the robustness of hyperspectral image denoising.

3.5.2. Spectral Loss Function

Given the rich spectral information in HSIs and their inherent smoothness prior, we propose spectral downsampling to effectively exploit this prior and construct a spectral loss function based on the spectral downsampler. This approach not only enhances the spectral consistency but also complements the spatial loss function, which is designed to enhance spatial consistency constraints.

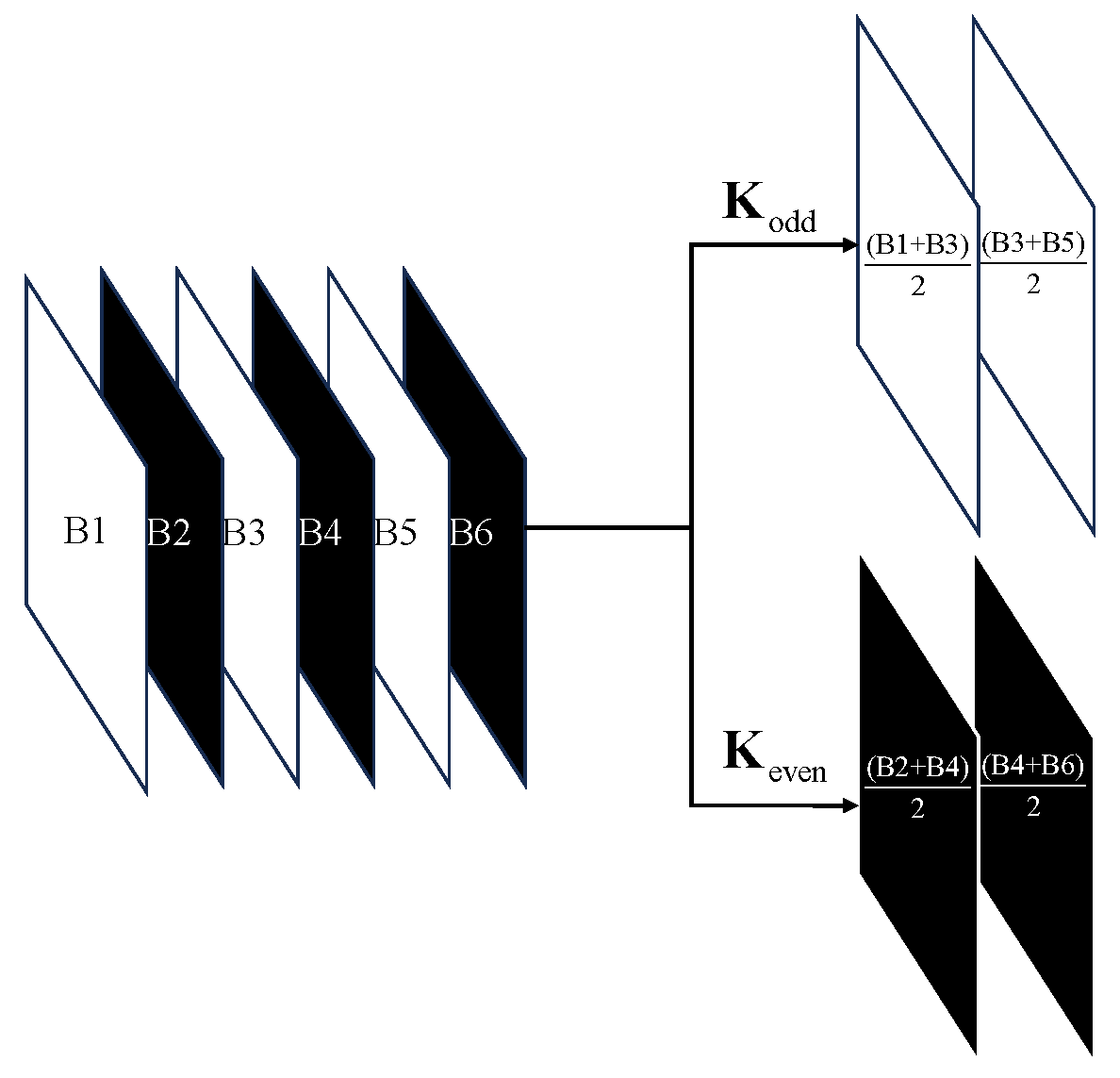
While spatial downsampling operates on geometric structures, spectral downsampling targets inter-band correlations: the HSI is divided along the spectral axis into two sub-cubes, odd and even indexes, and a neighborhood-based smoothing is applied within each sub-cube by averaging adjacent spectral bands. As shown in Figure 3, this process decomposes a 6-band HSI into two 2-band sub-cubes, where the averaged bands inherit material-specific signatures.

Formally, the spectral downsampler $D_{\mathrm{spe}}(·)$ takes an input HSI $\mathcal{Y}\in {\mathbb{R}}^{H\times W\times B}$, producing two spectrally subsampled HSIs $D_{\mathrm{spe},1}\left(\mathcal{Y}\right)$ and $D_{\mathrm{spe},2}\left(\mathcal{Y}\right)\in {\mathbb{R}}^{H\times W\times (B/2-1)}$. If B is odd, the last band is duplicated to ensure equal dimensionality. We applied two 1D Conv with kernels ${\mathbf{K}}_{odd}=[0.5, 0, 0.5, 0]$ and ${\mathbf{K}}_{even}=[0, 0.5, 0, 0.5]$ to accelerate the down-sampling process.

The spectral loss function is theoretically similar to the spatial loss function, but the implementation is quite different. While the spatial loss directly applies spatial downsampling operators to eigenimages ${\mathcal{Z}}_y$ and feeds the reduced-resolution outputs into the network $f_{\theta }\left({\mathcal{Z}}_y\right)$, this approach is fundamentally incompatible with spectral-domain processing. Even when employing 3D convolutional layers to address channel dimensionality constraints, it remains infeasible to reconstruct the denoised results with processed sub-eigenimages $f_{\theta }\left(D_{\mathrm{spe},i}\left({\mathcal{Z}}_y\right)\right)\in {\mathbb{R}}^{H\times W\times (r/2-1)}$ with the eigenmatrix ${\mathbf{E}}_y\in {\mathbb{R}}^{r\times B}$ due to structural mismatches introduced spectral downsampling.

To resolve this, as illustrated in the lower part of Figure 1a, our method employs ARSR on spectrally downsampled HSIs $D_{\mathrm{spe},i}\left(\mathcal{Y}\right)$. This decomposition produces representative eigenimages ${\mathcal{Z}}_{D_{\mathrm{spe},i}\left(\mathcal{Y}\right)},{\mathbf{E}}_{y,i}=R\left(D_{\mathrm{spe},i}\left(\mathcal{Y}\right)\right)$, which are then processed via the network $f_{\theta }$ to yield denoised subsampled data, ${\widehat{\mathcal{X}}}_{\mathrm{spe},i}$. By embedding spectral downsampling into the spatial loss function, we formalize the spectral loss paradigm in Equation (18):

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{\theta }^{spe}={\mathcal{L}}_{\theta }^{res.}+{\mathcal{L}}_{\theta }^{cons.}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{\theta }^{res.}={\displaystyle \frac{1}{2}}(\sum _{i=1}^2\parallel D_{\mathrm{spe},i}\left(\mathcal{Y}\right)-{\widehat{\mathcal{X}}}_{\mathrm{spe},3-i}{\parallel }_2^2)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{\theta }^{cons.}={\displaystyle \frac{1}{2}}(\sum _{i=1}^2\parallel D_{\mathrm{spe},i}\left(\widehat{\mathcal{X}}\right)-{\widehat{\mathcal{X}}}_{\mathrm{spe},i}{\parallel }_2^2)\hfill \end{array}$$

(20)

where $D_{\mathrm{spe},i}(·),(i=1,2)$ denote the spectrally sub-samples; ${\widehat{\mathcal{X}}}_{\mathrm{spe},i}=D_{\mathrm{spe},i}\left(\mathcal{Y}\right)-f_{\theta }\left({\mathcal{Z}}_{D_{\mathrm{spe},i}\left(\mathcal{Y}\right)}\right){\times }_3{\mathbf{E}}_{y,i}$ represent the denoising results corresponding to $D_{\mathrm{spe},i}\left(\mathcal{Y}\right)$.

3.5.3. Collaboration of Spatial and Spectral Losses

A fixed-weight combination of spatial and spectral losses fails to capture the scenario-specific priority each constraint requires in real-world denoising tasks. For instance, spatial priors dominate in high-noise regimes to recover structural coherence, while spectral priors excel at low-noise levels by preserving material-specific signatures. To enable robustness to different scenarios, we formulate the spectral-spatial collaborative loss function as follows:

$${\mathcal{L}}_{\theta }=\alpha {\mathcal{L}}_{\theta }^{spe}+(1-\alpha ){\mathcal{L}}_{\theta }^{spa}$$

(21)

where $\alpha$ controls the balance between the two loss terms, ${\mathcal{L}}_{\theta }^{spa}$ indicates the spatial loss in Equation (12) and ${\mathcal{L}}_{\theta }^{spe}$ refers the spectral loss in Equation (18).

To simultaneously leverage the advantages of both the spatial loss function in high noise scenario and spectral constraint under the low noise condition, we propose a noise adaptive weighting function Equation (22) with the estimated noise level $\widehat{\sigma }$ from Equation (10):

$$\alpha =g\left(\widehat{\sigma }\right)={\displaystyle \frac{1}{1+exp\left\{k(\widehat{\sigma }-\tilde{\sigma })\right\}}}$$

(22)

where $\alpha$ dynamically adjusts the influence of spectral and spatial losses based on the estimated noise level $\widehat{\sigma }$; k is a parameter that can adjust the curvature of the function curve; $\tilde{\sigma }$ denotes the threshold that is generated by ensuring that the signal-to-noise ratio is closest to 10 dB. To distinguish between high and low noise levels, we use SNR = 10 dB as a threshold. This level of noise significantly affects high-frequency information (e.g., texture, edge details), making noise suppression and detail preservation a challenging trade-off. The proposed AWSSCLF not only enhances robustness against diverse noise levels but also eliminates the need for manually tuned hyperparameters, ensuring robust performance.

3.6. End to End Self-Supervised Denoising

With the subspace projection and hybrid loss functions in place, we now describe the end-to-end self-supervised learning procedure. The full workflow of the proposed S${\mathrm{S}}^3$L framework is summarized in Algorithm 1 and shown in Figure 1.

Algorithm 1 Self-supervised HSI denoising with ARSR and AWSSCLF.

Input: Noisy HSI $\mathcal{Y}$ 1: TRAIN  $f_{\theta }(·)$ 2:      SSHE: $\widehat{\sigma }\leftarrow$ {via Equation (10), SSHE} 3:      Select rank: $r\leftarrow$ {via Equation (11)} 4:      Compute weight: $\alpha \leftarrow$ {via Equation (22)} 5:      ARSR: $\mathbf{E},{\mathcal{Z}}_y\leftarrow$ {via Equation (6)} 6: for $k=1$ to T do 7:         Generate spatial sub-images: $D_{\mathrm{spa},i}\leftarrow D_{\mathrm{spa}}\left({\mathcal{Z}}_y\right)$ 8:         Generate spectral sub-images: $D_{\mathrm{spe},i}\leftarrow D_{\mathrm{spe}}\left({\mathcal{Z}}_y\right)$ 9:         Compute spatial loss: ${\mathcal{L}}_{\theta }^{spa}\leftarrow$ Equation (12) 10:       Compute spectral loss: ${\mathcal{L}}_{\theta }^{spe}\leftarrow$ Equation (18) 11:       AWSSCLF: ${\mathcal{L}}_{\theta }\leftarrow \alpha {\mathcal{L}}_{\theta }^{spe}+(1-\alpha ){\mathcal{L}}_{\theta }^{spa}$ {via Equation (21)} 12:       Update parameters: $\theta \leftarrow$ {Adam optimizer} 13: end for 14:      return $r,\theta$

15:

16: PREDICT  $\mathcal{Y}$ 17:      Subspace transform: ${\mathbf{E}}_y,{\mathcal{Z}}_y\leftarrow$ {via Equation (6)} 18:      Noise prediction: $\widehat{\mathcal{N}}\leftarrow f_{\theta }\left({\mathcal{Z}}_y\right){\times }_3\mathbf{E}$ 19:      Reconstruction: $\widehat{\mathcal{X}}\leftarrow \mathcal{Y}-\widehat{\mathcal{N}}$ 20:      return $Clip(\widehat{\mathcal{X}},0,1)$

The Network $f_{\theta }$ used in this work is a lightweight network consisting of three 2D convolutional layers and two LeakyReLU layers. During training, we first apply ARSR to reduce the dimensionality of noisy HSI while preserving its intrinsic structure. The resulting eigenimages serve as the basis for designing spatial and spectral loss functions aimed at enhancing consistency. The spatial loss follows a downsampling-based strategy to enforce spatial consistency, while the spectral loss ensures fidelity along the spectral dimension. These loss functions are computed independently but combined through a noise-aware adaptive weighting scheme. The integrated loss function, AWSSCLF, is used to constrain a lightweight network $f_{\theta }$ within a self-supervised learning framework, as shown in Figure 1a. The network is trained via gradient descent to optimize $\theta$. Once trained, it is applied to the original noisy observation to estimate the denoised image, as illustrated in Figure 1b: $\widehat{\mathcal{X}}=\mathcal{Y}-f_{\theta }\left({\mathcal{Z}}_y\right){\times }_3{\mathbf{E}}_y$.

4. Experiments

4.1. Experimental Setup

4.1.1. Datasets and Evaluation Metrics

We evaluate the proposed method on six HSI datasets under two experimental settings: simulated noise removal and real noise removal. All datasets are preprocessed by removing low-SNR bands (e.g., those affected by water vapor absorption) to ensure reliable evaluation. For large-scale datasets, spatial patches of size $256\times 256\times B$ are extracted for training and evaluation.

For simulated noise removal, experiments are conducted on the Washington DC Mall (WDCM) dataset, the Kennedy Space Center (KSC) dataset, the GF-5 dataset [40], and the AVIRIS dataset [40]. Specifically, WDCM consists of a single HSI of size $1280\times 307\times 191$, acquired via the AVIRIS sensor, with 191 bands retained after low-SNR band removal. KSC consists of a single HSI of size $512\times 614\times 176$, also acquired via AVIRIS. The GF-5 dataset provides hyperspectral data of size $512\times 512\times 330$, acquired by the AHSI sensor, with the number of bands reduced to 305 after removing low-SNR bands affected by atmospheric absorption. The AVIRIS dataset contains hyperspectral data of size $512\times 512\times 224$, also collected using the AVIRIS sensor.

For real noise removal, experiments are conducted on the GF-5 and AVIRIS datasets (the same as in the simulated setting), as well as on the Indian Pines and Botswana datasets. The Indian Pines dataset consists of hyperspectral data of size $145\times 145\times 200$, acquired by AVIRIS, while the Botswana dataset contains a HSI of size $1476\times 256\times 145$, acquired via the EO-1 Hyperion sensor.

To quantitatively assess the denoising performance, we adopt three commonly used evaluation metrics: the mean of the Peak Signal-to-Noise Ratio (mPSNR), the mean of Structural Similarity Index (mSSIM), and the mean of Spectral Angle Mapper (mSAM).

4.1.2. Implementation Details

Throughout all experiments across different HSI datasets and noise conditions, we set $\beta$ in Equation (10) to 0.7 and k in Equation (22) to 0.8.

Experiments of all methods were implemented in Python (v3.10.14, Anaconda, Inc., Austin, TX, USA) with PyTorch = 1.13.1 on Ubuntu 22.04.5, using an Nvidia GeForce RTX 3090 GPU with 24 GB memory. Model training was conducted on the same GPU, with 3000 training iterations. The Adam optimizer was used with parameters (0.9, 0.999) and a learning rate of 0.001.

It should be noted that certain traditional HSI denoising methods, such as NG-Meet, LRTF-DFR, and FastHy, often require dataset-specific hyperparameter tuning to achieve optimal performance. In our experiments, we adopted the default hyperparameters provided by the original authors across all datasets without any manual adjustment. While this may lead to suboptimal performance for some methods in specific scenes, our proposed SS³L framework does not require any hyperparameter tuning, which demonstrates its robustness and stability across diverse datasets. The source code includes implementations of these methods. This design ensures a fair and reproducible comparison.

4.1.3. Comparison Methods

To evaluate the performance of the proposed method, we compared it with eight state-of-the-art methods. These include traditional approaches such as non-local and global prior-based method (NG-meet) [3], and tensor decomposition-based methods like LRTF-DFR [4] and L1HyMixDe [8]. Additionally, we considered a hybrid approach that combines traditional methods and Plug-and-Play deep regularization term (FastHy) [5]. Deep image prior and traditional image prior method combined method (DDS2M) [41]. The deep learning methods include the supervised methods: HSID-CNN [42] and QRNN3D [43], as well as the self-supervised method: Ne2Ne [19].

For HSID-CNN and QRNN3D, since our method operates in a self-supervised paradigm, we directly applied the pre-trained models provided by the original authors, instead of retraining them on our dataset, for a fair comparison. This approach was necessary since our experimental setup only involves six HSI datasets, which are insufficient to meet the data requirements for training these supervised networks.

Methods HSID-CNN and QRNN3D take 32-band and 31-band HSIs as input, respectively. The HSI datasets used in this work are divided into patches with size $256\times 256\times 32$ with a step size of $128\times 128\times 16$ to be fed into these two networks. The results of these two methods are reconstructed via the resulting patches. The Ne2Ne was designed for RGB images. A single-band version was retrained on these HSI datasets and applied to the corresponding HSI datasets.

4.2. Simulated Noise Removal

To assess denoising performance, simulated noisy HSIs were generated by introducing zero-mean additive Gaussian noise to the data that had been normalized to the range [0, 1]. Each spectral band was independently corrupted with Gaussian noise $N(0,{\sigma }^2)$, simulating band-specific sensor noise.

To comprehensively evaluate robustness for varying noise intensities, we constructed a fine-grained simulated noisy HSIs dataset consisting of 20 noise levels, with standard deviations $\sigma \in \left\{\frac{5}{255},\frac{10}{255},\dots ,\frac{100}{255}\right\}$ with the scaled standard deviation ${\sigma }_{\mathrm{scaled}}=\sigma \times 255$ ranging from 5 to 100). This approach provides a thorough assessment of the performance under diverse noise conditions and imaging scenarios.

We define five representative test scenarios (Cases 1–5), which capture key points for the noise intensity and cover both Gaussian and sparse noise situations. These serve as benchmarks for subsequent qualitative and quantitative analyses.

• Cases 1–4: Gaussian noise with scaled noise levels of 5, 25, 50, and 100 was added to simulate various corruption intensities.
• Case 5: To evaluate robustness against sparse structural noise, stripe artifacts were introduced by injecting 200 randomly located 1-pixel-wide vertical stripes into 25% of randomly selected bands, superimposed on the data already corrupted with Gaussian noise at level 50.

4.2.1. Quantitative Comparison

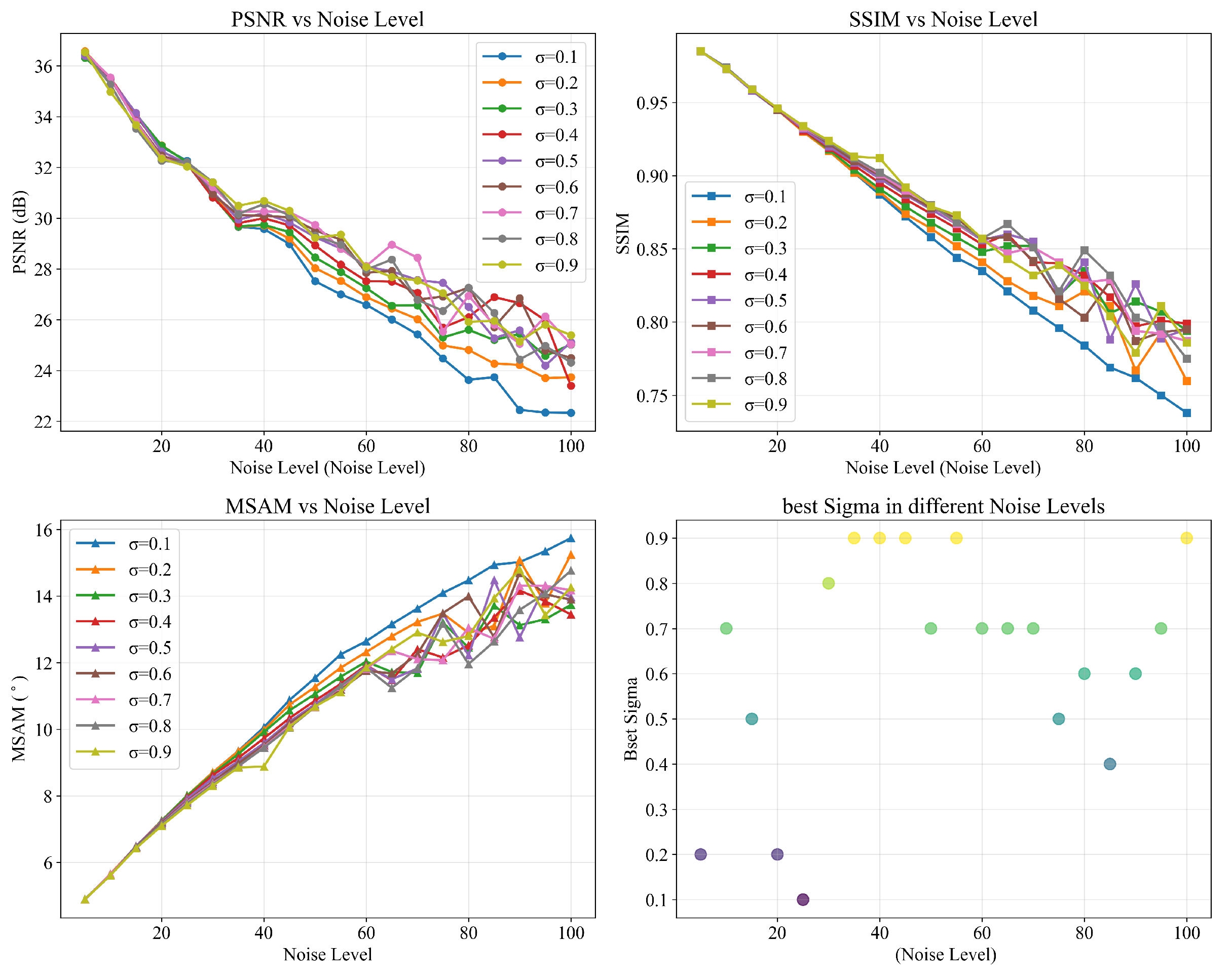
The experimental results for mPSNR, mSSIM, and mSAM across 20 noise levels applied to the WDCM, KSC, GF-5, and AVIRIS datasets are presented in Figure 4. The proposed method achieves superior performance with varying noise levels on the WDCM, GF-5, and KSC datasets.

Traditional methods relying on simple priors underperform for diverse noise conditions. Composite prior-guided approaches such as L1HyMixDe and LRTF-DFR show limited effectiveness: L1HyMixDe achieves competitive results on WDCM and KSC under low noise, while LRTF-DFR performs moderately on WDCM with medium noise. Both degrade significantly in other scenarios.

NG-Meet, which integrates non-local and local priors, underperforms in low-noise regimes but excels under high noise. Notably, its PSNR increases with noise intensity, contrasting with the decline observed in other methods. FastHy, using deep networks as explicit regularizers via a plug-and-play framework, matches our method’s performance on WDCM and KSC but lags on GF-5 (1–3 dB gaps at noise levels 5–60). Supervised deep learning methods (QRNN3D, HSID-CNN) exhibit severe degradation without test-data fine-tuning, revealing training-data dependency. The self-supervised Ne2Ne method, though designed for RGB images, can also get not bad performance through multiple datasets. The AVIRIS dataset’s inherent noise in bands [107–116] and [152–171] leads to marginally lower metrics for our method compared to simulated noisy references. LRTF-DFR shows instability under non-uniform noise, with unstable performance fluctuations at different intensities.

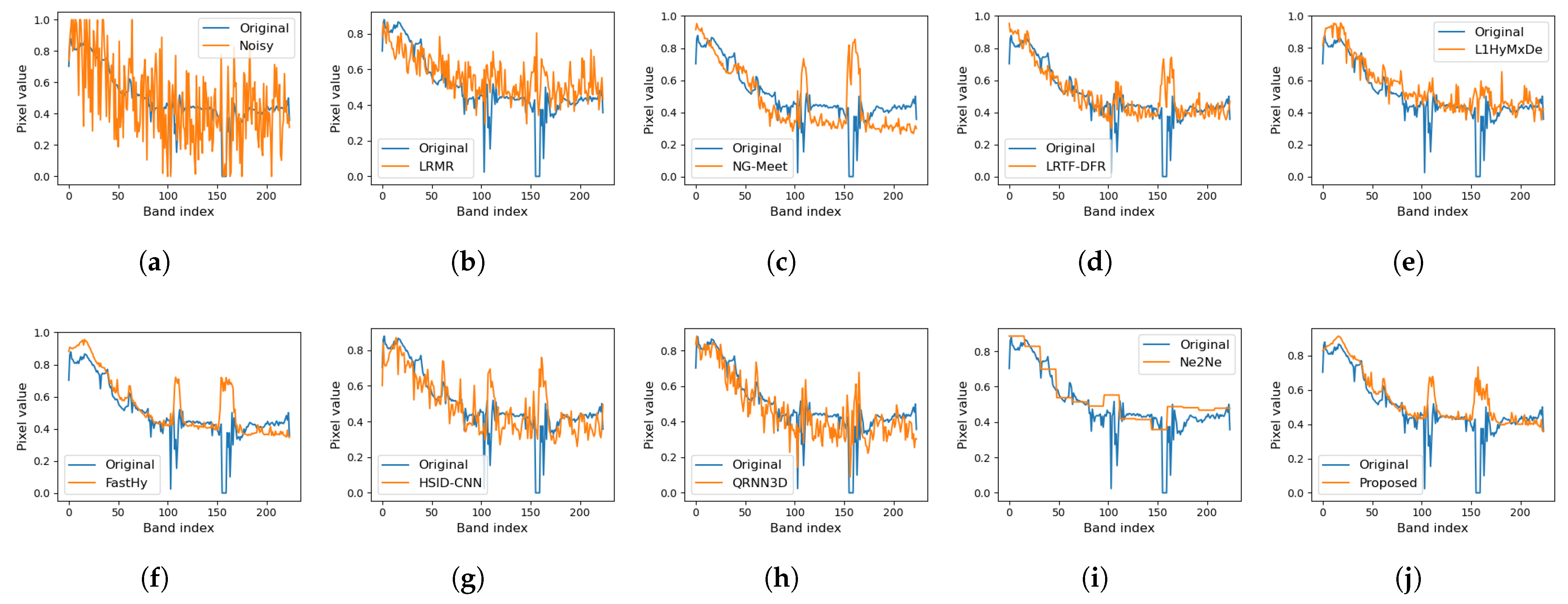
Spectral recovery performance is further validated in Figure 5 and Figure 6, which compare reconstructed spectral curves in Case 2 and Case 5. Most comparison methods exhibit spectral shifting or distortion (Figure 5), while only our approach achieves optimal alignment with real curves (Figure 6). The proposed method gets the best match to real spectral trends and performs well in maintaining spectral fidelity.

Table 1. Quantitative comparison of all competing methods on the WDCM and KSC datasets. The best results are highlighted in bold.

		Noisy	DDS2M	NG-Meet	LRTF-DFR	L1HyMixDe	FastHy	HSID-CNN	Ne2Ne	QRNN3D	Proposed
WDCM
Case1	mPSNR (dB)	34.1996	32.2411	23.7342	34.6905	38.5335	39.6494	16.283	27.1649	23.9383	39.9849
	mSSIM	0.9599	0.9447	0.8409	0.9763	0.9671	0.9578	0.4504	0.8958	0.7878	0.9890
	mSAM (°)	6.7662	7.1999	12.3115	6.1528	4.7864	5.4596	19.8969	13.7181	8.6997	4.1058
Case2	mPSNR (dB)	20.8422	26.884	25.6972	32.1896	31.5029	32.5567	17.0672	26.458	23.2875	32.6666
	mSSIM	0.588	0.8642	0.8543	0.9655	0.8109	0.9237	0.4921	0.8656	0.7368	0.939
	mSAM (°)	23.0836	11.1977	13.8343	7.1798	14.0855	8.0753	17.1872	14.9373	11.6199	9.3564
Case3	mPSNR (dB)	15.47	26.12	24.8601	28.9012	25.5963	29.4901	11.2258	24.0474	21.3145	29.4878
	mSSIM	0.33	0.8723	0.8388	0.9370	0.6985	0.8917	0.3262	0.7934	0.6498	0.9184
	mSAM (°)	33.4264	12.8537	15.0978	8.713	18.0449	10.3574	26.1666	16.7844	14.7021	11.624
Case4	mPSNR (dB)	10.6074	21.9332	25.2726	22.7469	19.6676	24.9552	14.943	18.1661	17.1019	26.621
	mSSIM	0.1441	0.7143	0.8553	0.821	0.5744	0.8554	0.4075	0.6139	0.4917	0.8595
	mSAM (°)	43.5543	17.9286	12.7925	14.5153	21.012	11.1705	21.9956	20.2879	19.3081	13.2
Case5	mPSNR (dB)	15.3399	24.3694	18.6678	23.9983	24.6554	28.231	17.0409	20.1656	20.5653	28.9276
	mSSIM	0.3263	0.7578	0.6655	0.8479	0.7183	0.8639	0.4658	0.6749	0.6348	0.9075
	mSAM (°)	35.0802	17.6427	16.5209	14.3223	18.2969	15.236	19.2434	20.2184	17.2316	11.4248
KSC
Case1	mPSNR (dB)	34.2322	37.5316	24.9481	36.9613	44.3794	43.7204	16.9099	33.2468	23.2345	42.7613
	mSSIM	0.9329	0.9572	0.8409	0.9749	0.9866	0.9878	0.4704	0.9602	0.8398	0.9909
	mSAM (°)	13.6064	6.2507	12.6775	6.7717	3.8436	3.8184	17.0041	8.1344	6.9231	5.0374
Case2	mPSNR (dB)	21.4743	29.1399	26.6868	35.3979	31.3154	34.1601	16.7363	30.71	22.7779	34.5499
	mSSIM	0.4508	0.8224	0.8491	0.9582	0.7784	0.9412	0.5544	0.9114	0.7852	0.9372
	mSAM (°)	33.6641	12.1737	14.5205	8.6318	11.9604	7.8977	16.338	12.0228	11.5781	10.1316
Case3	mPSNR (dB)	16.023	23.9621	27.1994	31.6466	23.8516	32.2211	7.9278	24.8568	19.9464	30.0528
	mSSIM	0.1887	0.7538	0.8286	0.9185	0.5954	0.8178	0.3016	0.7292	0.6069	0.9124
	mSAM (°)	42.5897	16.2702	17.5872	12.2009	15.8523	11.6845	25.2886	15.306	15.9779	11.4229
Case4	mPSNR (dB)	10.8328	22.609	27.6856	25.6783	18.315	27.0152	13.2095	17.3612	14.9885	29.3451
	mSSIM	0.06	0.7501	0.8503	0.8241	0.3877	0.7329	0.3617	0.4313	0.36	0.8716
	mSAM (°)	49.6137	14.4529	13.2766	16.3273	20.0643	13.9542	19.7802	19.4100	20.7138	10.2948
Case5	mPSNR (dB)	16.026	22.0693	19.0167	7.3999	25.3434	30.5901	16.3794	19.9243	19.2514	28.1101
	mSSIM	0.1945	0.6525	0.6323	0.3666	0.573	0.8818	0.4714	0.5315	0.6123	0.8503
	mSAM (°)	43.1404	16.2397	18.1872	24.954	17.4208	12.58	17.8447	20.1234	17.7609	19.4106

and

Table 2. Quantitative comparison of all competing methods on the GF-5 and AVIRIS dataset. The best results are highlighted in bold.

		Noisy	DDS2M	NG-Meet	LRTF-DFR	L1HyMixDe	FastHy	HSID-CNN	Ne2Ne	QRNN3D	Proposed
GF-5
Case 1	mPSNR (dB)	34.0356	38.2413	27.664	37.3411	40.794	38.876	19.8188	33.4585	26.2845	41.0434
	mSSIM	0.9517	0.9865	0.827	0.9782	0.9376	0.9789	0.7178	0.9698	0.8401	0.9911
	mSAM (°)	4.2508	2.2711	6.603	3.7652	2.7712	2.7818	7.0966	5.6999	4.2816	2.3931
Case 2	mPSNR (dB)	20.3603	27.7751	27.6737	33.1085	33.2365	32.6084	20.1893	30.742	25.2399	33.194
	mSSIM	0.4774	0.8738	0.9513	0.9689	0.935	0.9412	0.6989	0.9379	0.7939	0.9653
	mSAM (°)	19.5057	7.0891	6.8497	4.2081	4.8742	3.7523	7.7504	6.6756	6.3891	4.8609
Case 3	mPSNR (dB)	14.9915	25.9239	27.1764	28.0645	26.763	30.5307	12.7354	27.1525	22.907	29.6561
	mSSIM	0.2149	0.9020	0.8259	0.9278	0.8095	0.9221	0.4424	0.8523	0.6931	0.9367
	mSAM (°)	31.9724	8.9945	7.1674	6.9239	9.7997	4.5226	17.2469	8.8428	9.677	6.8598
Case 4	mPSNR (dB)	10.3989	25.2683	26.5495	19.3692	21.161	28.4796	16.5103	20.7051	17.7749	28.9979
	mSSIM	0.0812	0.6731	0.8752	0.7256	0.6551	0.8748	0.5383	0.6371	0.508	0.8943
	mSAM (°)	42.3827	12.2486	8.5733	12.0822	12.7367	5.7872	11.9243	12.517	13.8649	5.7200
Case 5	mPSNR (dB)	15.1019	27.8502	24.0653	8.5861	26.2542	30.238	20.1356	22.8616	22.1065	30.267
	mSSIM	0.2214	0.6449	0.7414	0.4416	0.8503	0.8937	0.6682	0.7383	0.685	0.939
	mSAM (°)	33.2	16.2035	10.0386	17.3323	10.2113	9.9385	10.3601	12.5154	12.011	6.3875
AVIRIS
Case 1	mPSNR (dB)	34.11	30.29	23.88	31.98	35.04	34.00	22.21	28.30	25.96	32.21
	mSSIM	0.9571	0.9046	0.7772	0.9005	0.889	0.9072	0.6831	0.8681	0.8084	0.9136
	mSAM (°)	3.0022	8.2102	13.8491	10.8137	7.6813	7.1497	9.6349	10.5819	7.3689	9.2551
Case 2	mPSNR (dB)	20.28	26.10	24.13	29.74	28.87	29.69	22.03	26.55	24.78	28.80
	mSSIM	0.5183	0.8319	0.7789	0.8876	0.8428	0.886	0.679	0.8397	0.7659	0.8835
	mSAM (°)	14.4262	9.9318	13.9948	11.599	8.2749	7.4654	9.5846	10.8997	8.1789	10.9115
Case 3	mPSNR (dB)	14.63	25.56	24.01	26.34	24.84	26.51	16.07	24.22	22.77	26.56
	mSSIM	0.2495	0.8144	0.7809	0.8417	0.7354	0.8450	0.5191	0.7639	0.67	0.8451
	mSAM (°)	25.587	12.5267	15.4063	12.9843	9.9279	8.3396	14.3058	11.7078	10.0134	13.7923
Case 4	mPSNR (dB)	10.15	23.29	24.03	19.63	20.30	24.57	19.13	20.90	19.79	25.40
	mSSIM	0.102	0.7329	0.7795	0.7203	0.5683	0.8085	0.5531	0.5949	0.4991	0.7961
	mSAM (°)	36.8718	11.1042	14.3703	16.6476	12.2839	8.9728	12.1489	13.6188	13.3766	14.15
Case 5	mPSNR (dB)	14.3825	26.338	21.4547	24.1274	24.0457	26.543	21.0976	21.8417	22.2976	26.5042
	mSSIM	0.2551	0.8156	0.726	0.815	0.7237	0.808	0.6369	0.6732	0.6565	0.8423
	mSAM (°)	27.5759	14.2701	17.0557	15.2223	12.4099	13.5277	11.8106	13.0086	13.2682	13.6372

demonstrate the efficacy of our proposed SS³L, which learns intrinsic data structures directly from feature images, rather than relying on manually designed regularization for denoising. While our method underperforms the advanced plug-and-play framework FastHy on the AVIRIS dataset in Cases 1 and 2, it achieves superior mPSNR values compared to most low-rank prior, local smoothness prior, and supervised learning-based approaches. Case 5, which combines Gaussian noise (level 50) and stripe artifacts, non-local self-similarity methods fail to balance noise removal with structural preservation. Low-rank-prior methods (L1HyMixDe, LRTF-DFR) excel only under low-noise conditions.

4.2.2. Qualitative Comparison

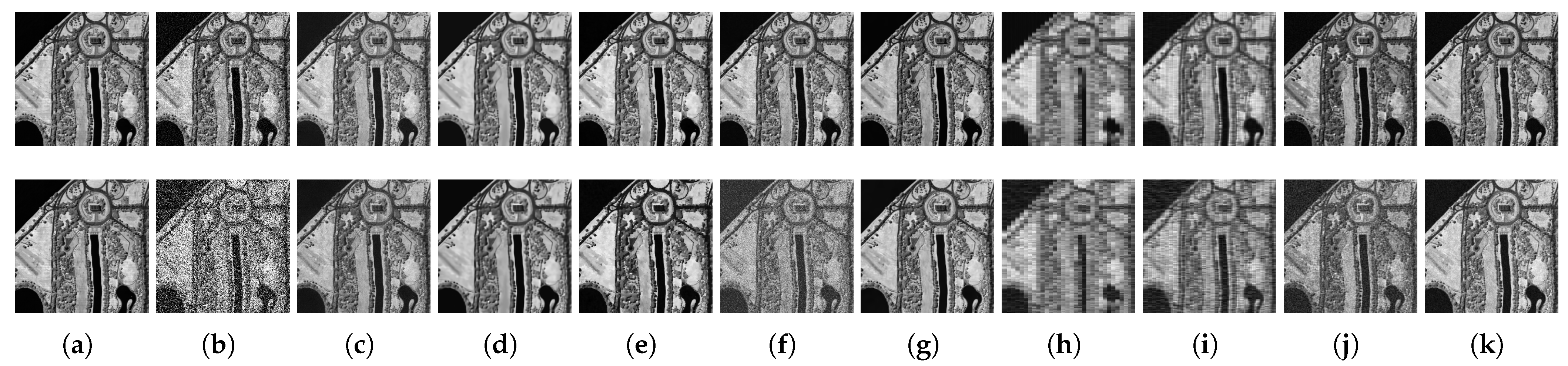
Visual results for Band 100 in Cases 2 and 4 on the WDCM and KSC datasets are shown in Figure 7 and Figure 8, respectively. The L1HyMixDe method performs well in Case 2 but deteriorates significantly under high-noise conditions (Case 4).

To simulate real-world conditions, we evaluated denoising performance on Gaussian-stripe mixed noise (Case 5). Noise was injected into 25% of randomly selected bands, resulting in visualized bands 111 (WDCM), 107 (KSC), 102 (GF-5), and 110 (AVIRIS). Notably, band 110 in AVIRIS belongs to the bands with real stripe noise (107–116), reflecting inherent low-SNR artifacts caused by atmospheric absorption.

As shown in Figure 9, most methods that are competitive under Gaussian noise fail to address mixed noise effectively: NG-Meet removes high-frequency noise but erases critical image details; LRTF-DFR fails to converge on KSC and GF-5 datasets; DDS2M eliminates inherent AVIRIS tilted stripes but introduces artificial vertical stripes into denoised results; FastHy achieves competitive results on WDCM, KSC, and GF-5 but residual stripes remain when processing the AVIRIS dataset.

It should be noted that these traditional methods, including NG-Meet, LRTF-DFR, LRMR, and FastHy, rely on manually tuned hyperparameters for optimal performance. In our experiments, we used the default parameters provided by the authors for all datasets, without dataset-specific adjustment. As a result, some methods may exhibit suboptimal performance in certain scenes. NG-Meet removes high-frequency noise but erases critical image details; LRTF-DFR fails to converge on KSC and GF-5 datasets; FastHy achieves competitive results on WDCM, KSC, and GF-5, but residual stripes remain when processing the AVIRIS dataset. In contrast, our SS³L framework, which requires no hyperparameter tuning, consistently delivers stable and reliable denoising results across all datasets, highlighting its practical advantage and robustness.

4.3. Real HSI Denoising Experiments

To further verify the adaptability of our proposed method on real noise scenes, we executed denoising experiments on four real-world HSI datasets Indian Pines, Botswana, AVIRIS and GF-5.

Each dataset represents distinct noise scenarios: Indian Pines: Gaussian noise with impulse artifacts (first band); Botswana: low-intensity Gaussian noise (final bands); AVIRIS: medium-intensity Gaussian noise (final bands); GF-5: Mixed Gaussian-stripe noise (final bands). Given the lack of ground truth, we take the band at a distance of 5 from the degraded band as the reference noise-free sample.

As shown in Figure 10, all methods achieved satisfactory performance on low-to-medium noise (Botswana, AVIRIS), except supervised deep learning approaches, which perform ineffectively due to training data dependency. NG-Meet’s non-local priors suppressed noise but eroded fine details. L1HyMixDe removed noise completely but introduced luminance distortion. Methods relying on low-rank priors (LRTF-DFR) struggled with sparse noise (e.g., stripes, salt-and-pepper), while NG-Meet eliminated such artifacts at the cost of over-smoothing. Ne2Ne excelled spatially but compromised spectral fidelity, as shown in prior simulations. Our method outperforms all comparison methods, effectively removing complex noise (atmospheric interference, stripes, dead pixels) while preserving structural and spectral integrity for all datasets.

From both the simulated and real noise removal experiments, it can be observed that NG-Meet heavily depends on several hyperparameters, including the coefficients of regularization terms, the number of similar blocks selected for non-local self-similarity estimation, and the number of PCA components retained in subspace projection. In our experiments, these parameters were fixed for high-noise scenarios. Consequently, NG-Meet performs well under heavy noise but exhibits suboptimal performance under other noise conditions. Similarly, LRTF-DFR is even more sensitive to hyperparameter settings. Its performance varies significantly across datasets, and in some cases, it fails to converge due to the challenge of selecting suitable parameters for different noise characteristics. Other methods also show limitations: L1HyMixDe removes noise effectively but introduces luminance distortions, while low-rank-based methods struggle with sparse noise like stripes or salt-and-pepper noise. Ne2Ne preserves spatial structures but may compromise spectral fidelity, as observed in prior simulations. In contrast, our proposed SS³L consistently delivers robust denoising across all datasets and noise levels, effectively removing complex noise—including atmospheric interference, stripes, and dead pixels—while preserving both spatial structures and spectral integrity. Importantly, SS³L does not require manual hyperparameter tuning, highlighting its practical advantage over traditional methods.

4.4. Ablation Study

To analyze how each component in the proposed framework contributes to the denoising performance, we conducted an ablation study on WDCM dataset with different noise levels.

4.4.1. Effectiveness of ARSR and AWSSCLF

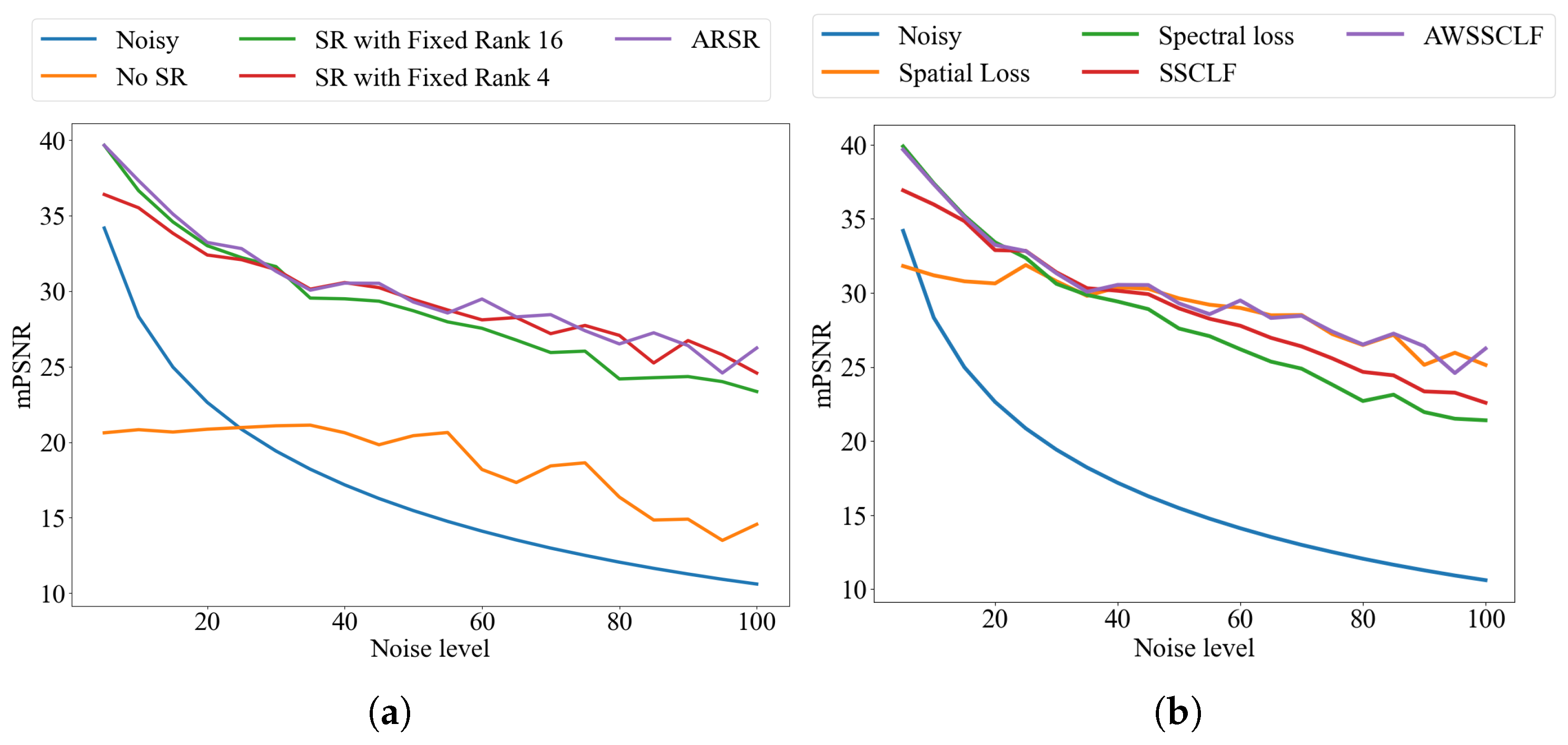
To verify the effectiveness of the proposed ARSR and AWSSCLF strategy, we conducted an ablation study with the following four cases, as shown in

Table 3. Ablation study: component activation status.

Configuration *	ARSR		AWSSCLF
	SR	DynRank	Spatial	Spectral	AdaptW
Subspace Representation Studies
NoSR	×	×	✓	✓	✓
Fixed rank-4 SR	✓	×	✓	✓	✓
Fixed rank-16 SR	✓	×	✓	✓	✓
ARSR	✓	✓	✓	✓	✓
Loss Function Studies
Only spatial loss	✓	✓	✓	×	×
Only spectral loss	✓	✓	×	✓	×
SSCLF	✓	✓	✓	✓	×
AWSSCLF	✓	✓	✓	✓	✓

* Legend: SR = subspace representation, DynRank = dynamic rank, AdaptW = adaptive weighted. ✓: enabled, ×: disabled. Bold configuration names indicate the proposed methods.

. For reference, we also report the mPSNR computed between the noisy HSI and the ground truth, to better assess the effectiveness of the compared strategies. As shown in Figure 11a, the method without SR exhibits the poorest performance, leading to significant information loss in low-noise conditions. The method with a fixed low-rank ($r=4$) SR performs poorly under noise levels below 20 ($\sigma <0.08$), whereas the fixed high-rank ($r=16$) SR variant performs poorly in medium- and high-noise conditions: noise levels higher than 40 ($\sigma >0.16$). In contrast, our proposed ARSR, which dynamically adjusts the rank for SR based on estimated noise variance, consistently outperforms all fixed-rank variants under different noise levels.

The experimental results in Figure 11b show that, under different noise intensities, the spatial loss function and the spectral loss function are complementary. In low-noise scenarios ($\sigma \le 0.1$, noise level lower than 25), relying on spatial loss function results in a 3–5 dB mPSNR reduction, while spectral loss maintains optimal reconstruction quality. This trend significantly reverses when noise level increases ($\sigma >0.16$, noise level greater than 40): the performance decay rate of spectral loss function is larger than that of spatial loss, with the latter demonstrating superior noise robustness. The fixed-weight ($\alpha$ = 0.5) spatial–spectral hybrid loss, although theoretically balanced, exhibits a maximum deviation of 3.8 dB under varying noise levels. In contrast, our AWSSCLF achieves consistently optimal performance under all noise levels ($0.02\le \sigma \le 0.39$).

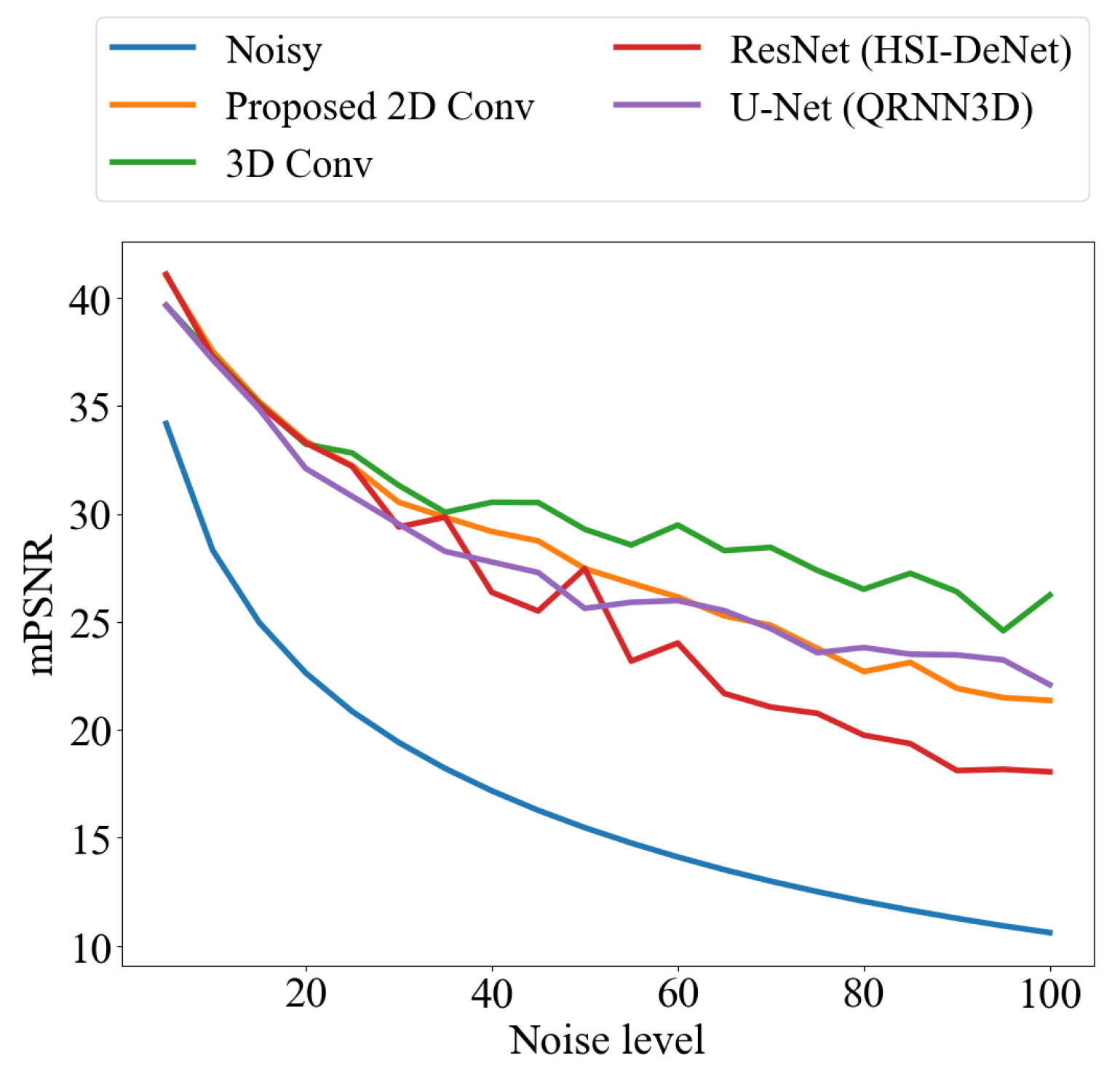
4.4.2. Effectiveness of Network Structure

To evaluate the impact of the network architecture within the proposed framework, we conducted ablation experiments on the WDCM dataset by replacing the network $f_{\theta }$ while keeping the other components unchanged. Specifically, the compared network structures include:

• Proposed lightweight 2D Conv network (3 Conv layers + 2 LeakyReLU layers);
• 3D Conv network;
• ResNet-based network (HSI-DeNet [14]);
• U-Net structure (QRNN3D [43]).

The experimental results shown in Figure 12 reveal that, under low-noise conditions, the noise level in [5,10] ($\sigma \le 0.05$), the 3D Conv network achieves approximately 2 dB PSNR advantage through spectral feature aggregation, and the performance difference of the other methods is less than 0.8 dB. As the noise intensity increases, the a noise level greater than 20 ($\sigma >0.08$), the differences of method performance becomes significant: HSIDeNet deteriorates to 20 dB at noise level 100 ($\sigma =0.39$); U-Net and the 3D model maintain 25 dB via spatial–spectral feature fusion, and our 2D network sustains optimal performance under noise level in [20,100] ($0.08\le \sigma \le 0.39$).

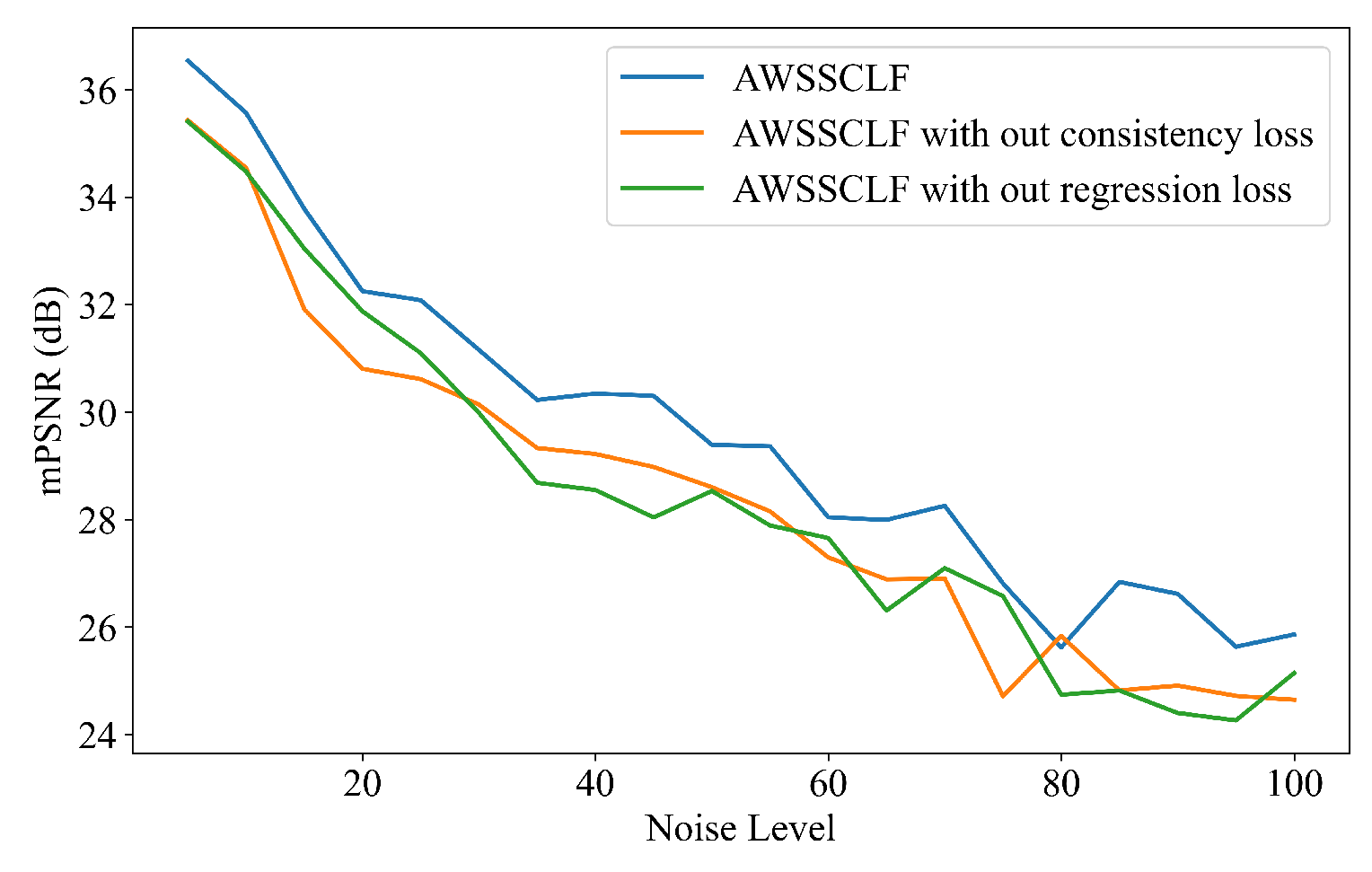
4.4.3. Effectiveness of Regression and Consistency Term

To evaluate the effectiveness of the regression and consistency losses in AWSSCLF, we conducted an ablation study on the WDCM dataset under the following three configurations:

• Proposed AWSSCLF (regression loss and consistency loss);
• AWSSCLF without the regression term (only consistency loss);
• AWSSCLF without the consistency term (only regression loss).

As shown in Figure 13, the full AWSSCLF consistently outperforms its two simplified variants in terms of mPSNR. This demonstrates that combining regression and consistency terms provides complementary benefits, leading to more robust and accurate denoising performance.

4.5. Performance Evaluation of the Proposed Noise Estimator

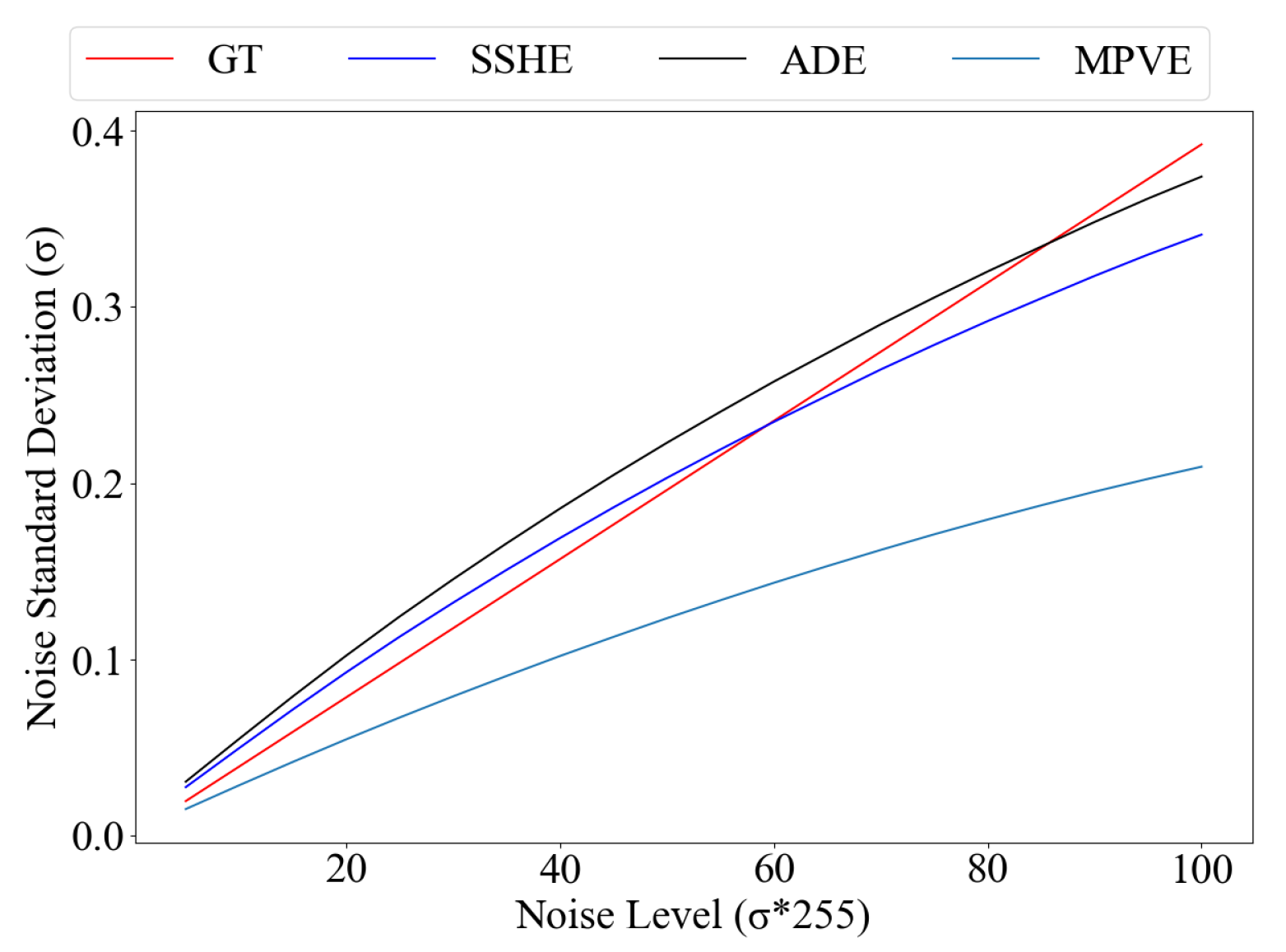
We evaluate the performance of the three proposed noise estimator: ADE, MPVE, and SSHE.

Figure 14 shows the noise estimation results of LAE, ADE, and SSHE under noise levels in [5,100]. By dynamically balancing spatial and spectral information (with $\beta =0.7$), SSHE achieves the closest approximation to the real noise variance, significantly outperforming both ADE and MPVE.

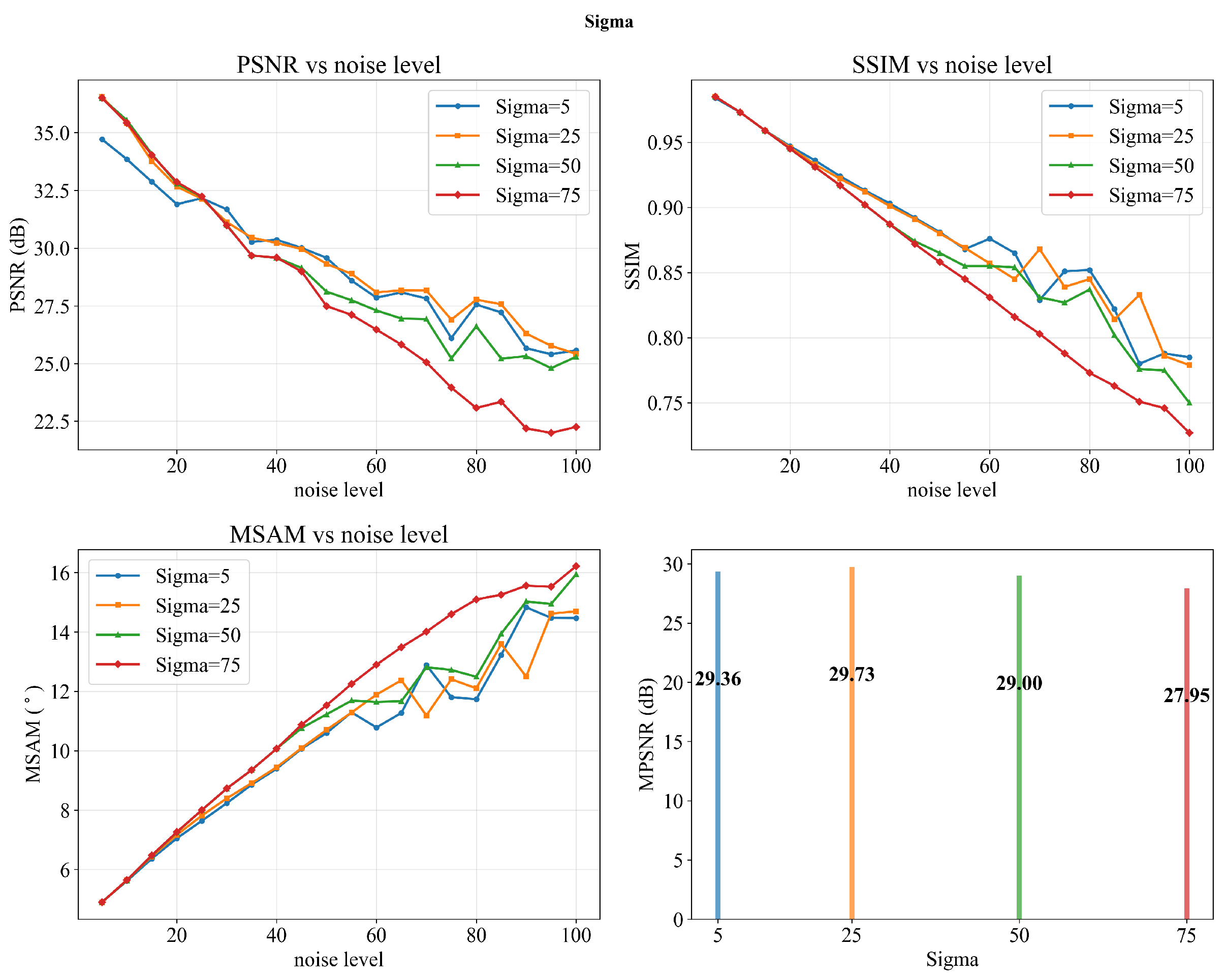
4.6. Parameter Analysis

In this section, we analyze the sensitivity of our framework to the three key parameters, namely k in Equation (22), $\tilde{\sigma }$ in Equation (22), and $\beta$ in Equation (10). The parameter k controls the steepness of the weighting function, $\tilde{\sigma }$ determines the scaling factor for adaptive weighting, and $\beta$ balances the contributions of the two noise level estimators in Equations (9) and (7).

The experimental results are shown in Figure 15, Figure 16 and Figure 17. As can be seen in Figure 15, the parameter k has almost no impact on the performance of our method, which indicates the robustness of the framework to this parameter. For $\tilde{\sigma }$, as shown in Figure 16, the performance consistently peaks at $\tilde{\sigma }=25$ under all conditions, making it a stable and effective choice. Finally, as illustrated in Figure 17, the performance remains stable once $\beta$ exceeds 0.3, suggesting that the method is insensitive to larger $\beta$ values.

Overall, these sensitivity analyses confirm that our framework is robust to parameter variations, and reasonable default settings (e.g., $k=0.8$, $\tilde{\sigma }=25$, and $\beta =0.7$) are sufficient to achieve reliable performance across different datasets and noise conditions.

5. Discussion

The proposed SS³L framework demonstrates several notable strengths. First, by integrating adaptive rank subspace representation (ARSR) with a spatial–spectral hybrid loss, the method effectively balances spatial detail preservation and spectral fidelity across diverse noise conditions. Second, the self-supervised paradigm eliminates the need for clean reference data and manual hyperparameter tuning, which significantly enhances its practicality in real-world remote sensing scenarios where labeled data are scarce. Third, extensive experiments confirm that SS³L achieves competitive or superior results compared with both supervised and traditional self-supervised baselines. Despite these advantages, some limitations remain. The performance of the SSHE module is less robust when handling extremely sparse or structured noise, such as stripe artifacts, where its noise variance estimation may be less accurate. In addition, although the framework is hyperparameter-independent in practice, a limited sensitivity to the preset constants (e.g., $\beta$, k) still exists. Finally, while the method generalizes well across different sensors and noise levels, further validation on larger-scale and more diverse datasets would strengthen its applicability. Looking ahead, integrating more advanced noise modeling strategies (e.g., learning-based priors for sparse noise) and extending the framework to cross-sensor adaptation scenarios are promising directions. These improvements could further enhance the stability, scalability, and generalizability of the SS³L framework in practical remote sensing applications.

6. Conclusions

In this work, we proposed SS³L, which addresses two fundamental challenges in HSI denoising: (1) the paired-data dependency of supervised deep learning and (2) the hyperparameter sensitivity of conventional model-based methods, by employing three key techniques. First, we introduce geometric symmetry and spectral local consistency priors via spatial checkerboard downsampling and spectral difference downsampling, enabling noise–signal disentanglement from a single noisy HSI without clean reference data. Second, we develop the Spectral–Spatial Hybrid Estimation (SSHE) to quantify noise intensity, guiding the Adaptive Weighted Spectral–Spatial Collaborative Loss Function (AWSSCLF) that dynamically balances structural fidelity and denoising strength under varying noise levels. Third, the Adaptive Rank Subspace Representation (ARSR), driven by singular value energy distribution and noise energy estimation, determines the optimal subspace rank without heuristic selection, embedding adaptive subspace representations into the self-supervised network. These components jointly construct a dual-domain, physics-informed self-supervised framework that learns cross-sensor invariant features without requiring paired data or manual hyperparameter tuning, thus achieving robustness across diverse imaging systems. Extensive experiments validate SS³L’s superiority in removing mixed noise types (e.g., Gaussian, stripe, impulse) and generalizing to unseen scenes, achieving competitive performance both in quantitative metrics and visual quality. The current limitations stem from fixed spectral regularization weights and single-scene optimization paradigm. Future work will explore integrating Deep Image Prior (DIP) inductive bias and non-local priors into this self-supervised framework to further enhance generalization across diverse scenarios.