RPC Correction Coefficient Extrapolation for KOMPSAT-3A Imagery in Inaccessible Regions
Abstract
Highlights
- This study proposes a transport-based RPC correction learned on a small head subset, extrapolating downstream while preserving geometry and yielding <3-pixel tails in two of three strips.
- This study models pushbroom error extrapolation by leveraging satellite orbital parameters and terrain characteristics to transport head-of-strip corrections downstream.
- This study provides a practical alternative to strip-wide block adjustment for control-denied or resource-limited settings, operating in image space and tolerating missing segments or ties.
- This study offers a transferable framework for sub-meter platforms; under stronger dynamics, broader calibration and optional higher-order terms further stabilize transport.
Abstract
1. Introduction
1.1. Overview
1.2. Literature Review
1.3. Research Objectives
- Strip segment RPC correction coefficient extrapolation that preserves native scene geometry and reduces GCP dependence. The method calibrates on a small upstream subset and transports correction coefficients to downstream segments, providing a practical alternative to strip-wide block adjustment in control-denied or resource-constrained settings.
- Physically grounded predictor design with morphometry-aware similarity weighting for stable transport. The model uses elapsed time, off-nadir change, and terrain morphometry, and implements a Jarque–Bera- or σDEM-guided similarity weight in a weighted least square fit to emphasize calibration scenes that resemble the target segment.
- Operational validation on KOMPSAT-3A long strips with effective along-track drift control. Experiments on three strips confirm the directional error structure and show sub-3-pixel downstream errors in two strips, clarifying when transport-based extrapolation outperforms strip-replacement strategies.
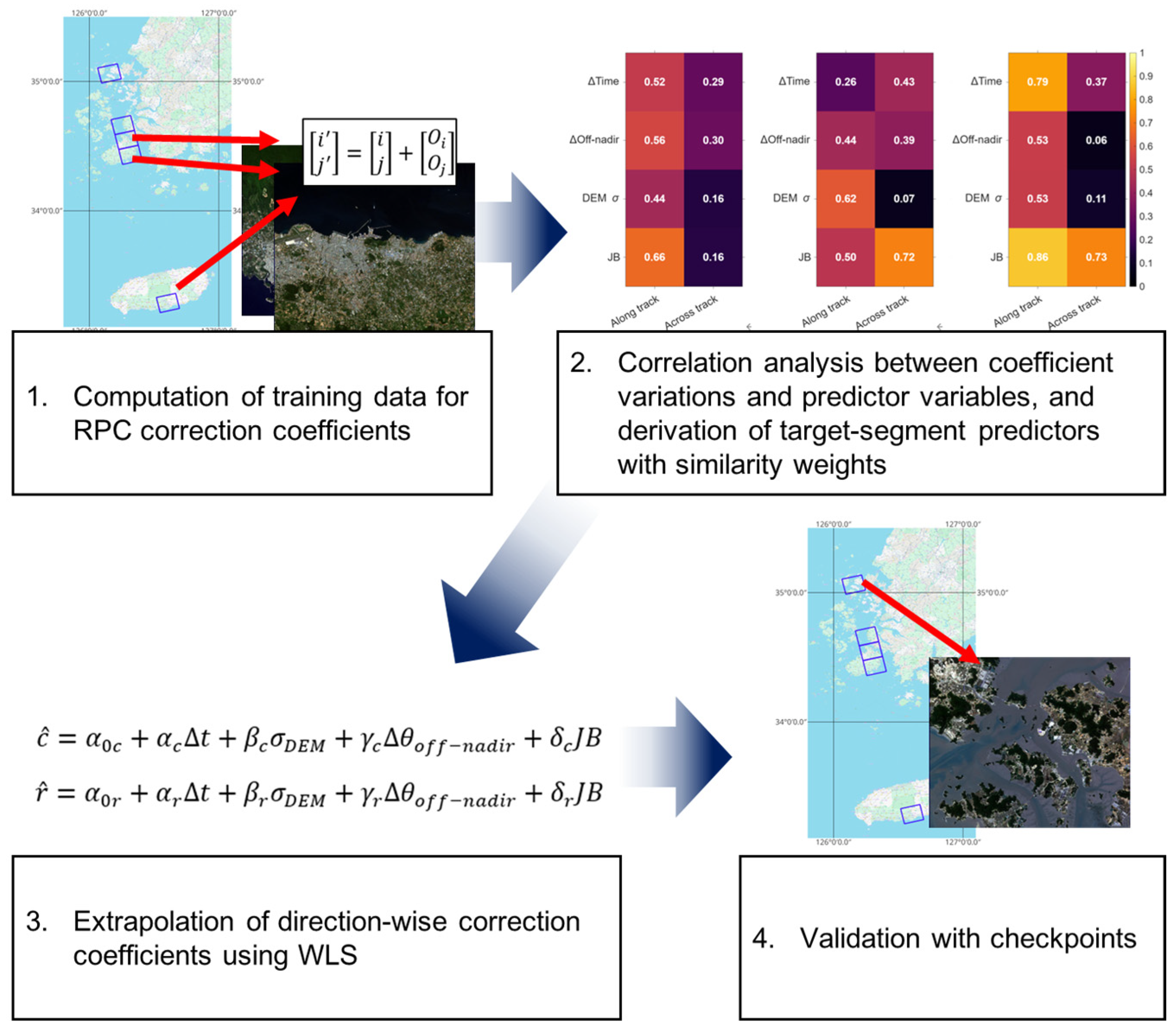
2. Methodology
2.1. Overview
2.2. KOMPSAT-3A Sensor
2.3. KOMPSAT-3A Sensor Modeling
2.4. RFM
2.4.1. RPCs Generation
2.4.2. RPCs Correction Coefficients
2.5. Influencing Factors on RPC Correction Coefficients
2.6. Summary of the Proposed Extrapolation Module
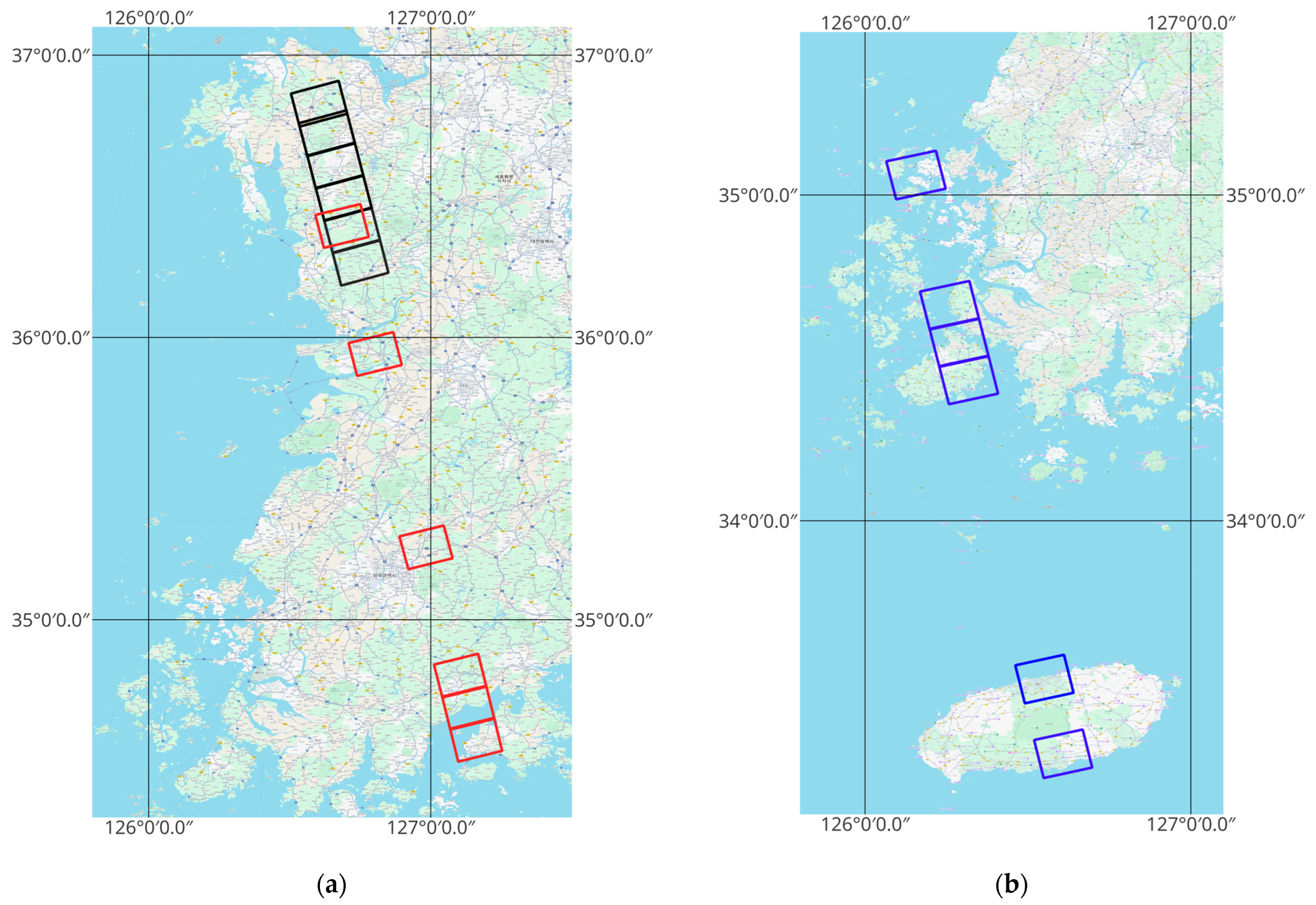
3. Data Preparation
3.1. Strip Image Dataset
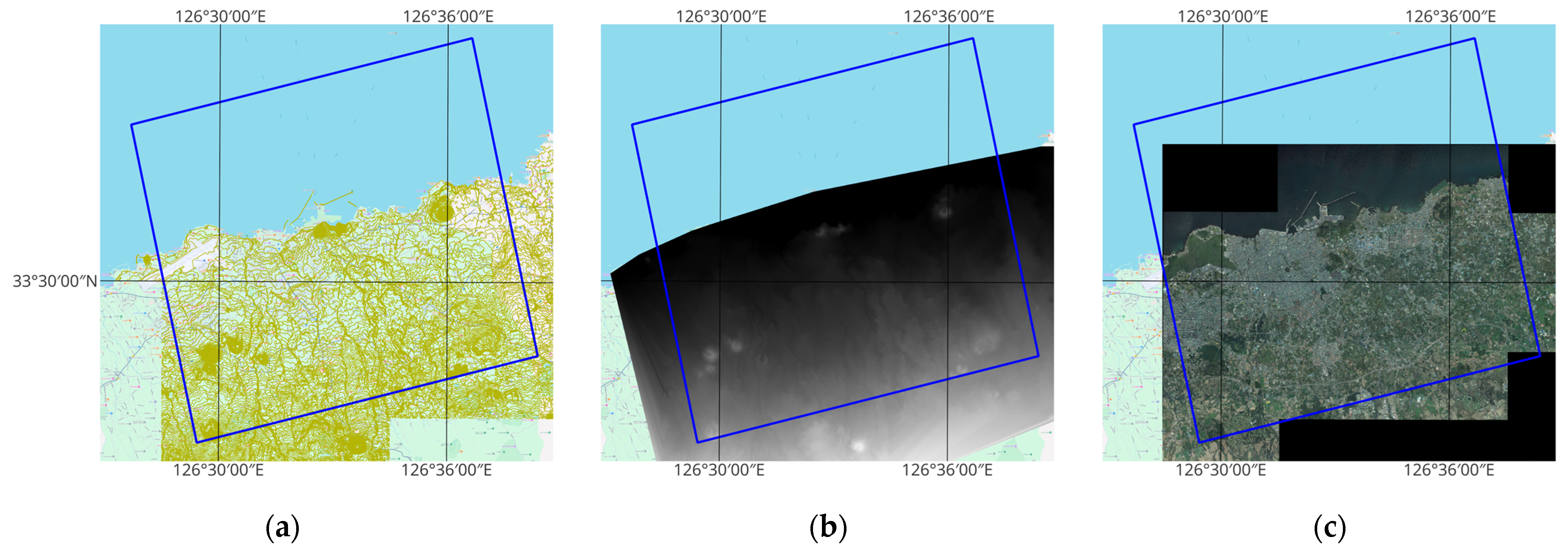
3.2. DEM, Orthophoto, and Digital Map
3.2.1. ASTER GDEM V2
3.2.2. Digital Map and Aerial Orthophoto
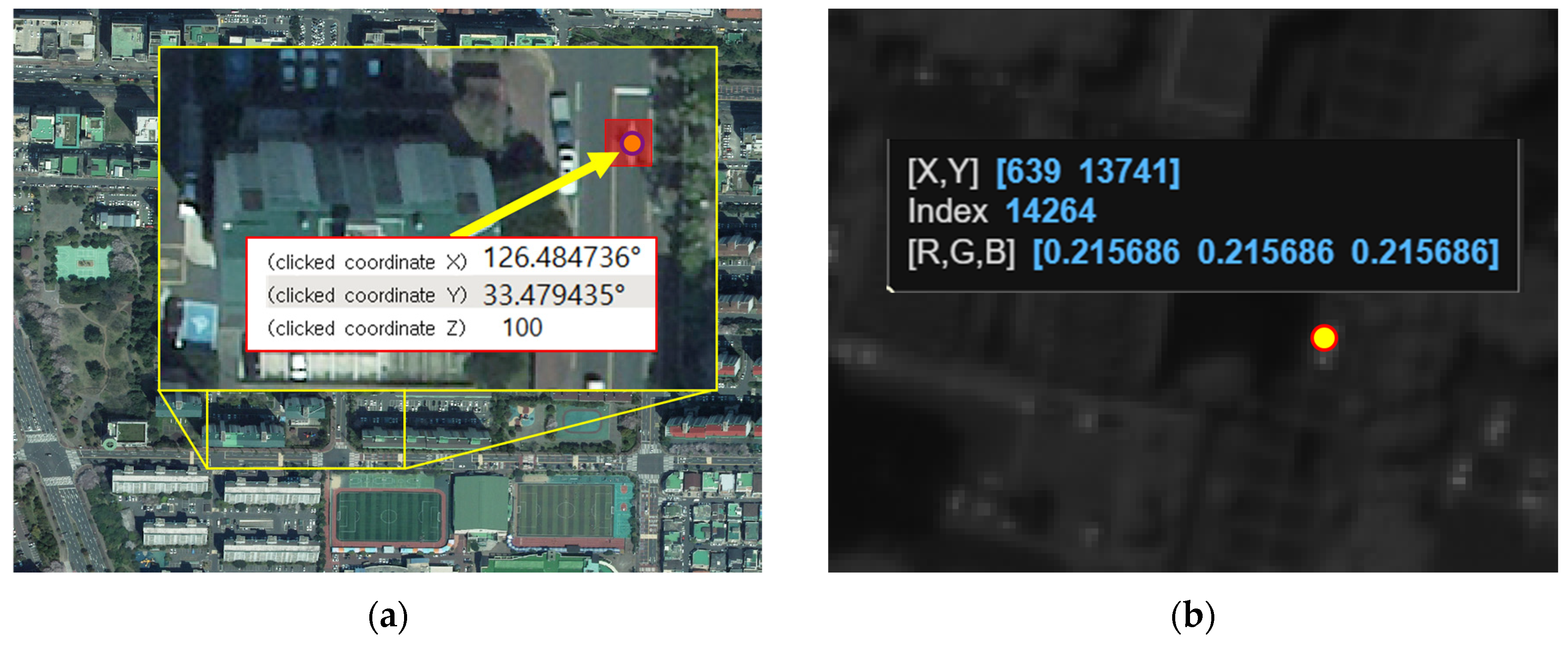
3.3. GCPs and CKPs
4. Results and Discussion
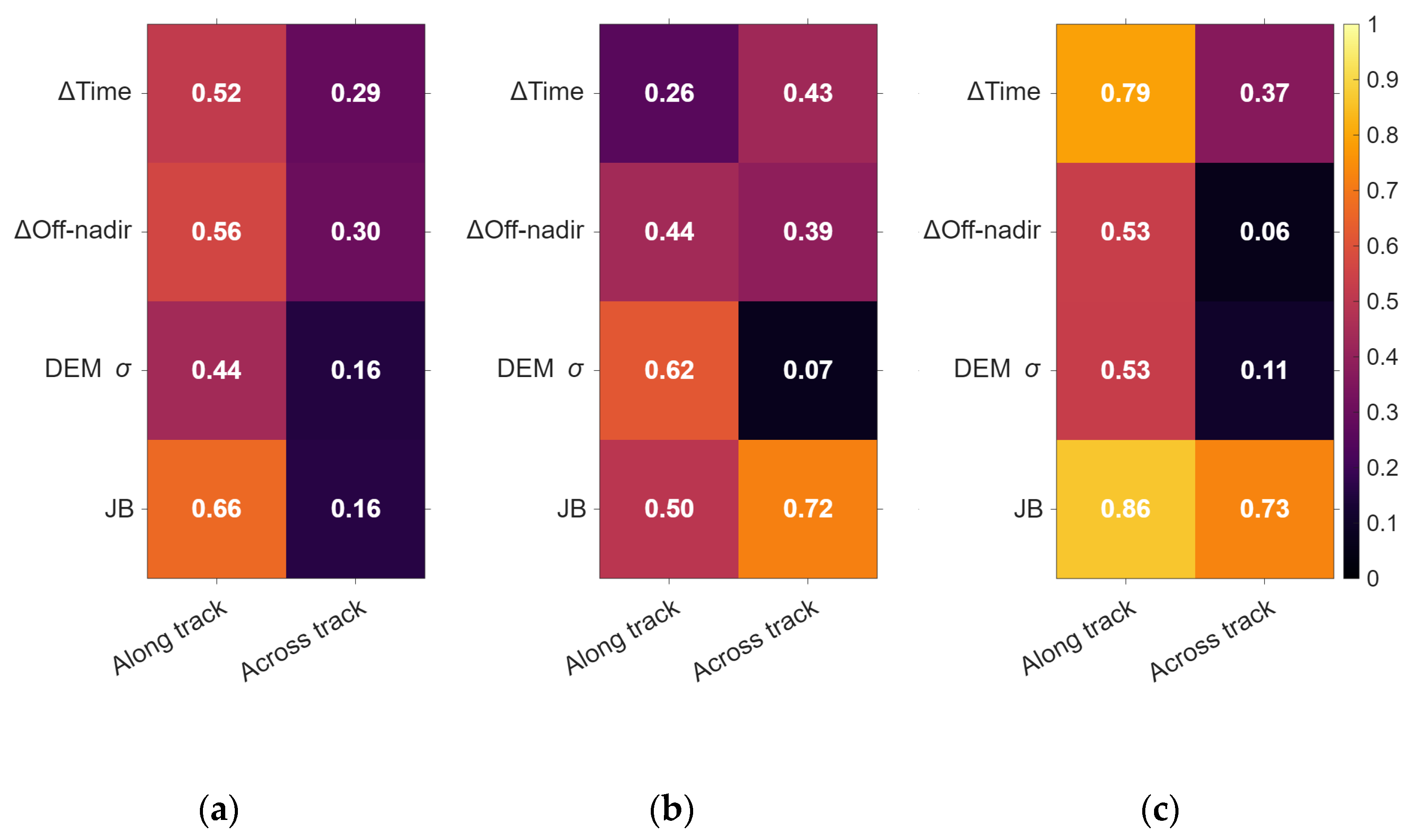
4.1. Results of RPC Correction Coefficient Estimation and Influencing Factors
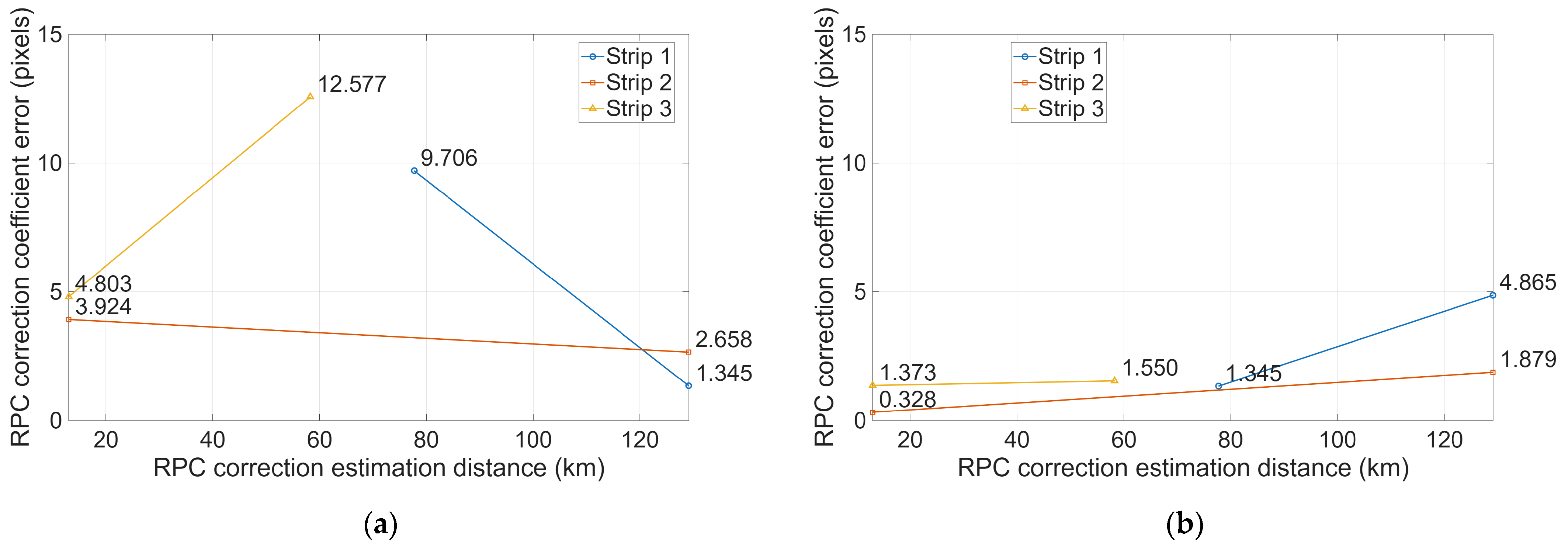
4.2. Extrapolation Modeling of RPC Correction Coefficients
4.3. Comparative Evaluation of RPC Correction Approaches
5. Discussion
5.1. RPC Correction Behavior and Influencing Factors
5.2. Extrapolation Models and Performance of RPC Corrections
5.3. Comparative Discussion with Other Approaches
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Dowman, I.; Li, S.; Li, Z.; Madden, M.; Mills, J.; Paparoditis, N.; Rottensteiner, F.; Sester, M.; Toth, C. Information from Imagery: ISPRS Scientific Vision and Research Agenda. ISPRS J. Photogramm. Remote Sens. 2016, 115, 3–21. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Tu, L.; Zhang, T.; Wang, L. A Review of Building Detection from Very High Resolution Optical Remote Sensing Images. GISci. Remote Sens. 2022, 59, 1199–1225. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Pal, I.; Hati, J.P.; Pramanick, N.; Acharyya, R.; Kumar, A.; Jana, S.K.; Mitra, D. High-Resolution Pléiades Data: An in-Depth Analysis of Applications and Future Prospects. Spat. Inf. Res. 2024, 32, 739–755. [Google Scholar] [CrossRef]
- Shen, X.; Liu, B.; Li, Q.-Q. Correcting Bias in the Rational Polynomial Coefficients of Satellite Imagery Using Thin-Plate Smoothing Splines. ISPRS J. Photogramm. Remote Sens. 2017, 125, 125–131. [Google Scholar] [CrossRef]
- Ban, S.; Kim, T. Rational-Function-Model-Based Rigorous Bundle Adjustment for Improving the Relative Geometric Positioning Accuracy of Multiple Korea Multi-Purpose Satellite-3A Images. Remote Sens. 2024, 16, 2890. [Google Scholar] [CrossRef]
- Berthier, E.; Lebreton, J.; Fontannaz, D.; Hosford, S.; Belart, J.M.-C.; Brun, F.; Andreassen, L.M.; Menounos, B.; Blondel, C. The Pléiades Glacier Observatory: High-Resolution Digital Elevation Models and Ortho-Imagery to Monitor Glacier Change. Cryosphere 2024, 18, 5551–5571. [Google Scholar] [CrossRef]
- Pan, H.; Zou, S.; Guan, L. Block Adjustment with Drift Compensation for Rational Function Model. Photogramm. Eng. Remote Sens. 2018, 84, 791–799. [Google Scholar] [CrossRef]
- Clermont, L.; Michel, C.; Stockman, Y. Stray Light Correction Algorithm for High Performance Optical Instruments: The Case of Metop-3MI. Remote Sens. 2022, 14, 1354. [Google Scholar] [CrossRef]
- Clermont, L.; Michel, C.; Chouffart, Q.; Zhao, Y. Going beyond Hardware Limitations with Advanced Stray Light Calibration for the Metop-3MI Space Instrument. Sci. Rep. 2024, 14, 19490. [Google Scholar] [CrossRef]
- Shen, X.; Li, Q.; Wu, G.; Zhu, J. Bias Compensation for Rational Polynomial Coefficients of High-Resolution Satellite Imagery by Local Polynomial Modeling. Remote Sens. 2017, 9, 200. [Google Scholar] [CrossRef]
- Noh, M.-J.; Howat, I.M. Applications of High-Resolution, Cross-Track, Pushbroom Satellite Images with the SETSM Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3885–3899. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Pradhan, B. Urban Mapping Accuracy Enhancement in High-Rise Built-up Areas Deployed by 3D-Orthorectification Correction from WorldView-3 and LiDAR Imageries. Remote Sens. 2019, 11, 692. [Google Scholar] [CrossRef]
- Ghuffar, S. DEM Generation from Multi Satellite Planetscope Imagery. Remote Sens. 2018, 10, 1462. [Google Scholar] [CrossRef]
- Jo, H.; Lee, C.; Oh, J. The Impact of GCP Chip Distribution on Kompsat-3A RPC Bias Compensation. Appl. Sci. 2024, 14, 3482. [Google Scholar] [CrossRef]
- Loghin, A.-M.; Otepka-Schremmer, J.; Pfeifer, N. Potential of Pléiades and WorldView-3 Tri-Stereo DSMs to Represent Heights of Small Isolated Objects. Sensors 2020, 20, 2695. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, G.; Tang, X.; Li, D. Compensation for Distortion of Basic Satellite Images Based on Rational Function Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5767–5775. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Xu, W.; Li, D.; Gong, J.; Pi, Y. Large-Scale Block Adjustment without Use of Ground Control Points Based on the Compensation of Geometric Calibration for ZY-3 Images. ISPRS J. Photogramm. Remote Sens. 2017, 134, 1–14. [Google Scholar] [CrossRef]
- Pi, Y.; Yang, B.; Li, X.; Wang, M.; Cheng, Y. Large-Scale Planar Block Adjustment of GaoFen1 WFV Images Covering Most of Mainland China. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1368–1379. [Google Scholar] [CrossRef]
- Dai, R.; Wang, M.; Ye, Z. Near-Real-Time Long-Strip Geometric Processing without GCPs for Agile Push-Frame Imaging of LuoJia3-01 Satellite. Remote Sens. 2024, 16, 3281. [Google Scholar] [CrossRef]
- Hong, Z.; Tong, X.; Liu, S.; Chen, P.; Xie, H.; Jin, Y. A Comparison of the Performance of Bias-Corrected RSMs and RFMs for the Geo-Positioning of High-Resolution Satellite Stereo Imagery. Remote Sens. 2015, 7, 16815–16830. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Y. A Generic Method for RPC Refinement Using Ground Control Information. Photogramm. Eng. Remote Sens. 2009, 75, 1083–1092. [Google Scholar] [CrossRef]
- Topan, H.; Oruc, M.; Taşkanat, T.; Cam, A. Combined Efficiency of RPC and DEM Accuracy on Georeferencing Accuracy of Orthoimage: Case Study with Pléiades Panchromatic Mono Image. IEEE Geosci. Remote Sens. Lett. 2013, 11, 1148–1152. [Google Scholar] [CrossRef]
- Toutin, T. Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Li, Q.; Zhong, R.; Yang, C.; Zhao, K.; Zhang, C.; Li, Y. Geometric Quality Improvement Method of Optical Remote Sensing Satellite Images Based on Rational Function Model. Remote Sens. 2022, 14, 4443. [Google Scholar] [CrossRef]
- Titarov, P.S. Evaluation of Cartosat 1 Geometric Potential. In Proceedings of the XXI ISPRS Congress, Beijing, China, 3 July 2008; pp. 841–846. [Google Scholar]
- Liu, H.; Zhao, Y.; Wang, L.; Liu, Y. Comparison of DEM Accuracies Generated from Different Stereo Pairs over a Plateau Mountainous Area. J. Mt. Sci. 2021, 18, 1580–1590. [Google Scholar] [CrossRef]
- Fraser, C.S.; Baltsavias, E.; Gruen, A. Processing of Ikonos Imagery for Submetre 3D Positioning and Building Extraction. ISPRS J. Photogramm. Remote Sens. 2002, 56, 177–194. [Google Scholar] [CrossRef]
- Seo, D.; Oh, J.; Lee, C.; Lee, D.; Choi, H. Geometric Calibration and Validation of Kompsat-3A AEISS-A Camera. Sensors 2016, 16, 1776. [Google Scholar] [CrossRef]
- Pan, H.; Huang, T.; Zhou, P.; Cui, Z. Self-Calibration Dense Bundle Adjustment of Multi-View Worldview-3 Basic Images. ISPRS J. Photogramm. Remote Sens. 2021, 176, 127–138. [Google Scholar] [CrossRef]
- Eftekhari, A.; Saadatseresht, M.; Motagh, M. A Study on Rational Function Model Generation for TerraSAR-X Imagery. Sensors 2013, 13, 12030–12043. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.; Baumgartner, A.; Schwind, P.; Carmona, E.; Storch, T. Differences and Similarities in the Processing of Airborne and Spaceborne Hyperspectral Data Shown on HySpex and EnMap Processing Chains. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9164–9167. [Google Scholar] [CrossRef]
- Yeom, J.-M.; Ko, J.; Hwang, J.; Lee, C.-S.; Choi, C.-U.; Jeong, S. Updating Absolute Radiometric Characteristics for KOMPSAT-3 and KOMPSAT-3A Multispectral Imaging Sensors Using Well-Characterized Pseudo-Invariant Tarps and Microtops II. Remote Sens. 2018, 10, 697. [Google Scholar] [CrossRef]
- Seo, D.-C.; Lee, C.; Oh, J. Merge of Sub-Images from Two PAN CCD Lines of Kompsat-3 AEISS. KSCE J. Civ. Eng. 2016, 20, 863–872. [Google Scholar] [CrossRef]
- Kim, N.; Choi, Y.; Bae, J.; Sohn, H.-G. Estimation and Improvement in the Geolocation Accuracy of Rational Polynomial Coefficients with Minimum GCPs Using KOMPSAT-3A. GISci. Remote Sens. 2020, 57, 719–734. [Google Scholar] [CrossRef]
- EOS Data Analytics. KOMPSAT 3/3A Satellite Images. Available online: https://eos.com/find-satellite/kompsat-3-3a/#:~:text=Pan%20CCD%20detector%20module (accessed on 21 June 2025).
- Hu, Y.; Tao, V.; Croitoru, A. Understanding the Rational Function Model: Methods and Applications. Int. Arch. Photogramm. Remote Sens. 2004, 20, 119–124. [Google Scholar]
- Tao, C.V.; Hu, Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing. Photogramm. Eng. Remote Sens. 2001, 67, 1347–1358. [Google Scholar]
- Fraser, C.S.; Dial, G.; Grodecki, J. Sensor Orientation via RPCs. ISPRS J. Photogramm. Remote Sens. 2006, 60, 182–194. [Google Scholar] [CrossRef]
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.B.; Oimoen, M.J.; Zhang, Z.; Danielson, J.J.; Krieger, T.; Curtis, B.; Haase, J. ASTER Global Digital Elevation Model Version 2-Summary of Validation Results. USGS Rep. 2011, 37. Available online: https://ui.adsabs.harvard.edu/abs/2011usgs.rept...37T/abstract (accessed on 20 September 2025).
- Regulations on the Work and Performance of Digital Topographic Maps. Available online: https://www.law.go.kr/LSW//admRulLsInfoP.do?admRulId=37114&efYd=0 (accessed on 10 May 2025).
- Oh, J.H.; Seo, D.C.; Lee, C.N. A Test Result on the Positional Accuracy of Kompsat-3A Beta Test Images. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 133–142. [Google Scholar] [CrossRef]
- Lee, C.; Seo, D.; Jung, J.; Oh, J. Replacement Sensor Model Generation for a Long High-Resolution Satellite Image Strip. KSCE J. Civ. Eng. 2023, 27, 1751–1759. [Google Scholar] [CrossRef]

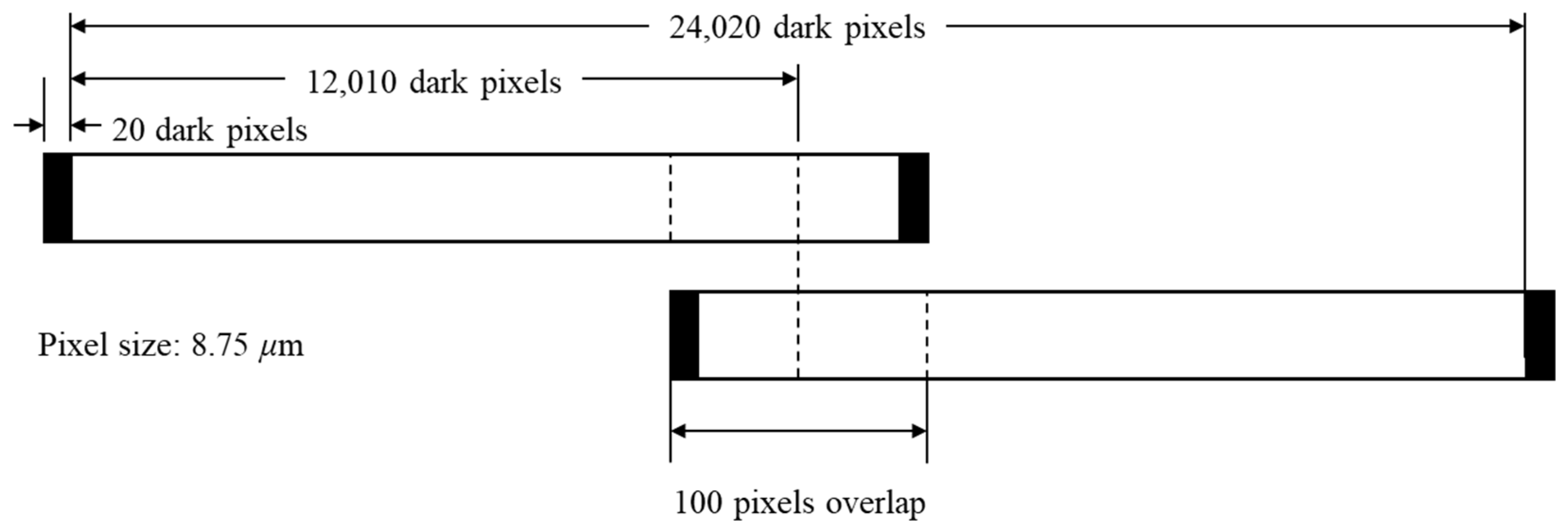
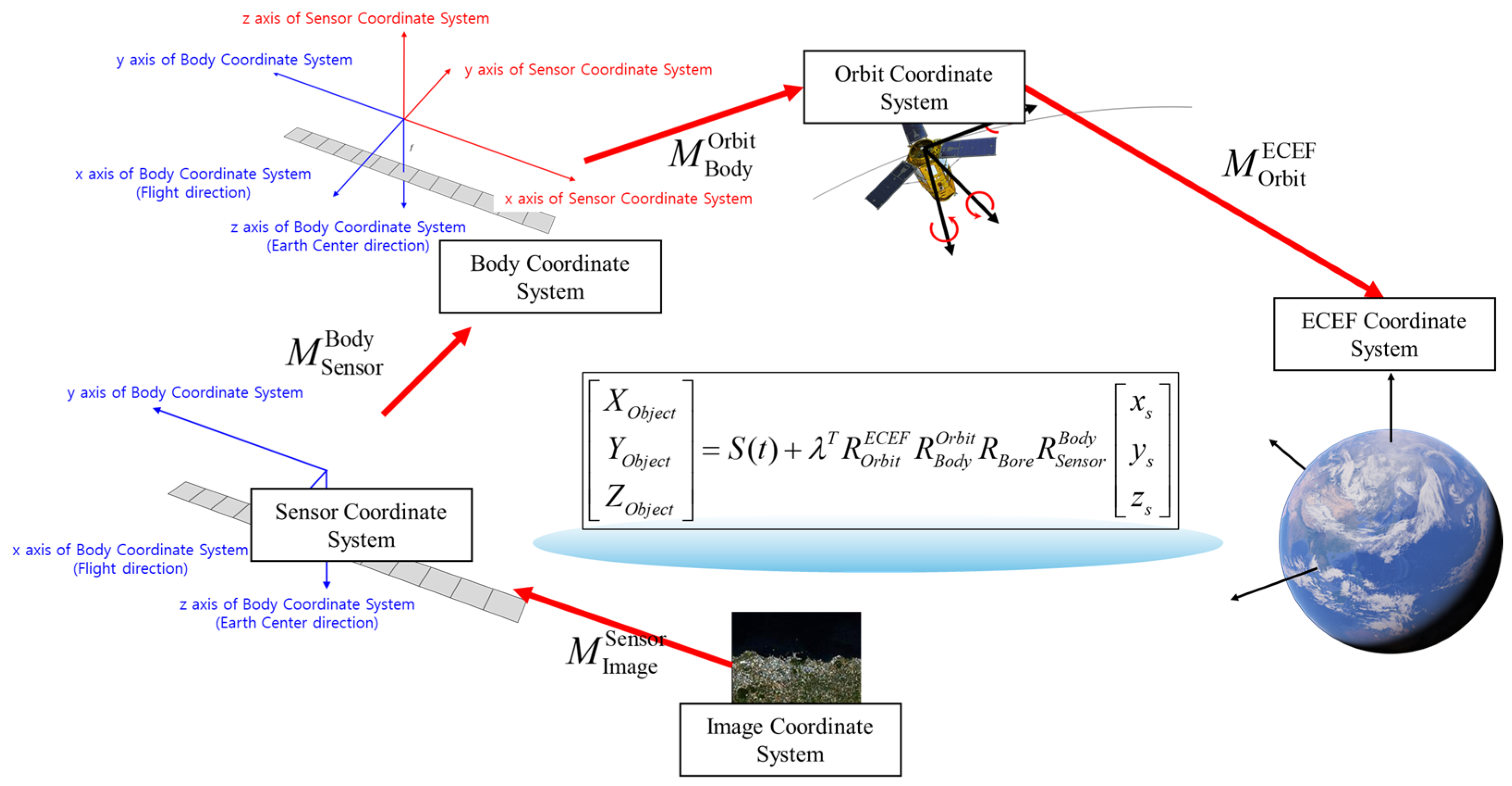
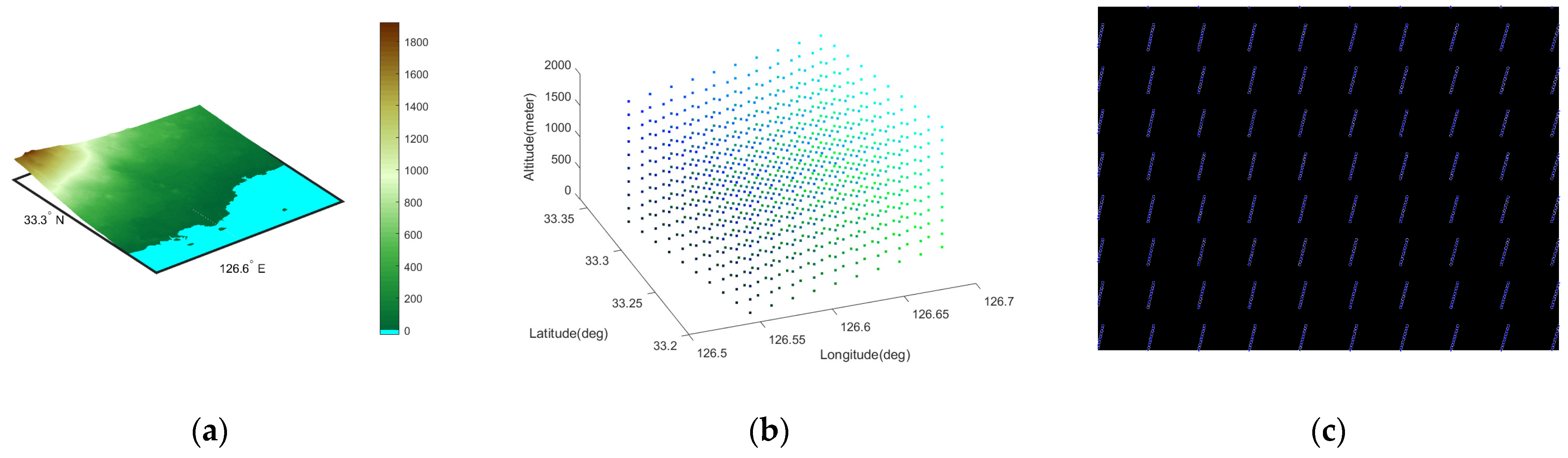
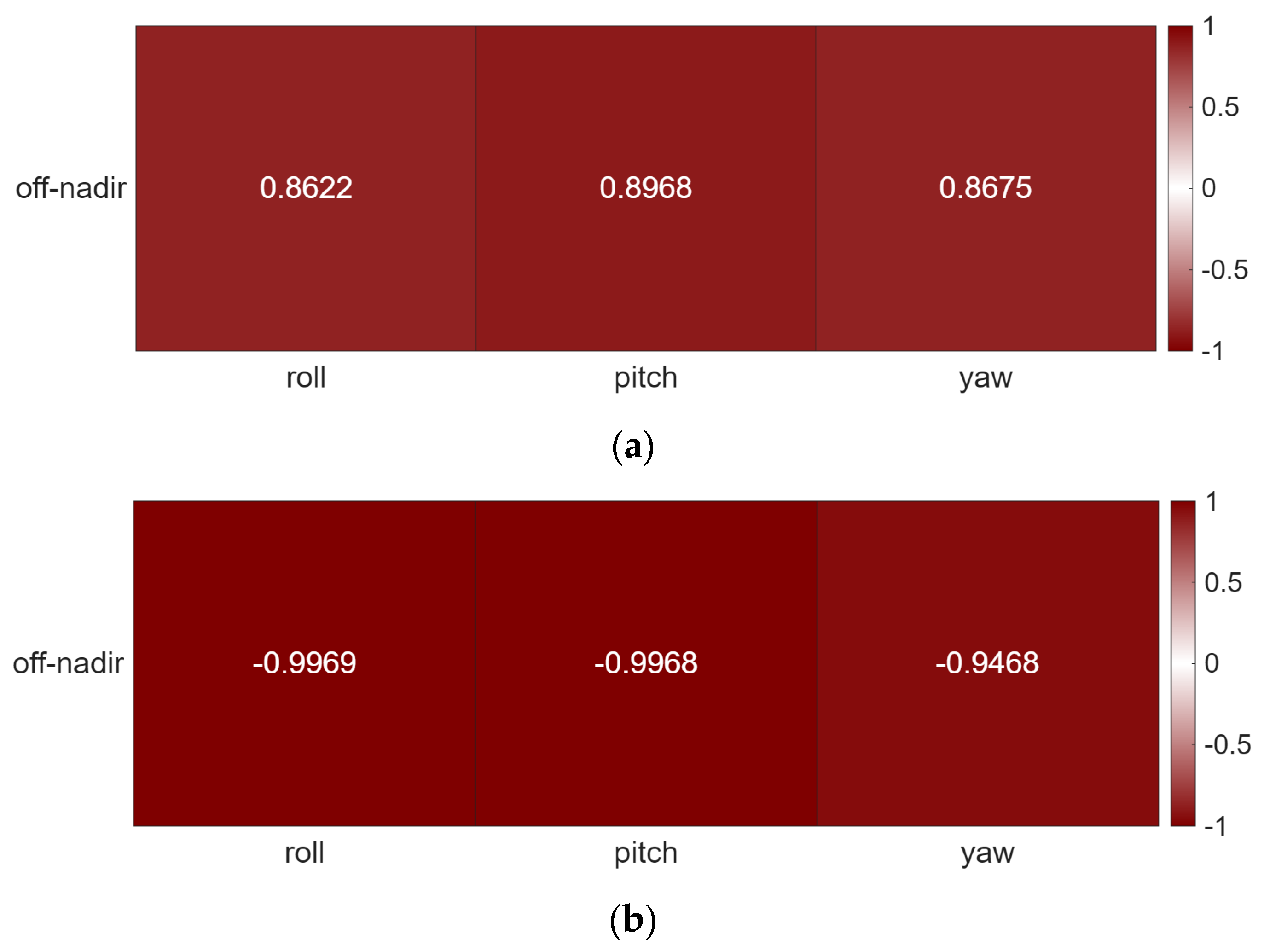

| Strip Number | Target Location | Temporal Change (s) | Satellite Altitude Change (m) | Off-Nadir Change (deg) | σ of Target Area DEM (m) | Skewness of Target Area | Kurtosis of Target Area | JB of Target Area |
|---|---|---|---|---|---|---|---|---|
| Strip 1 K3A 20171021044156 | Goheung | 0 | 0 | 0 | 32.351 | 3.555 | 17.968 | 68.650 |
| Boseong | 1.801 | 0.030 | −0.004 | 95.683 | 1.348 | 3.757 | 1.960 | |
| Miryeok | 3.598 | 0.059 | 0.001 | 89.272 | 0.597 | 3.970 | 0.592 | |
| Gwangju | 10.800 | 0.177 | 0.016 | 116.848 | 1.528 | 4.971 | 3.307 | |
| Gunsan | 21.699 | 0.358 | 0.033 | 19.501 | 3.832 | 21.43 | 99.601 | |
| Boryeong | 28.898 | 0.480 | 0.040 | 126.879 | 1.066 | 4.023 | 1.398 | |
| Strip 2 K3A 20201107044626 | Seobuyeo | 0 | 0 | 0 | 109.847 | 0.962 | 3.630 | 1.0258 |
| Janggok | 3.699 | 0.040 | −0.004 | 95.839 | 2.406 | 11.308 | 23.047 | |
| Hongseong | 5.500 | 0.060 | −0.005 | 68.893 | 1.884 | 6.775 | 7.114 | |
| Deoksan | 7.296 | 0.080 | 0.002 | 107.439 | 1.540 | 5.321 | 3.719 | |
| Dangjin | 9.000 | 0.099 | −0.005 | 57.088 | 1.659 | 6.103 | 5.159 | |
| Strip 3 K3A 20210529045218 | Seogwipo | 0 | 0 | 0 | 355.803 | 1.847 | 6.293 | 6.121 |
| Jeju | 3.601 | 0.032 | −0.003 | 128.563 | 1.352 | 3.878 | 2.021 | |
| Uisin | 18.301 | 0.167 | −0.004 | 73.002 | 2.170 | 7.868 | 10.634 | |
| Gunnae | 20.102 | 0.184 | −0.003 | 54.921 | 3.222 | 15.171 | 47.417 | |
| Hwawon | 22.000 | 0.201 | −0.005 | 41.416 | 2.855 | 11.797 | 27.498 | |
| Shinan | 28.402 | 0.262 | −0.005 | 22.003 | 4.120 | 26.125 | 150.664 |
| Strip 1 (Goheung–Boryeong Strip) | ||||||
|---|---|---|---|---|---|---|
| Goheung | Boseong | Miryeok | Gwangju | Gunsan | Boryeong | |
| Mean across-track error | 32.36 | 40.09 | 46.76 | 42.63 | 33.95 | 31.00 |
| Mean along-track error | 14.64 | 18.25 | 32.55 | 37.65 | 34.25 | 17.13 |
| Across-track correction coefficient | 32.34 | 39.99 | 30.23 | 37.65 | 33.92 | 30.94 |
| Along-track correction coefficient | 11.40 | 7.08 | −25.19 | 0.16 | 28.82 | 13.98 |
| Strip 2 (Seobuyeo–Dangjin Strip) | ||||||
| Seobuyeo | Janggok | Hongseong | Deoksan | Dangjin | ||
| Mean across-track error | 31.95 | 30.32 | 23.80 | 31.34 | 32.07 | |
| Mean along-track error | 11.37 | 7.30 | 9.23 | 6.60 | 16.86 | |
| Across-track correction coefficient | 31.82 | 30.22 | 30.23 | 31.27 | 31.85 | |
| Along-track correction coefficient | −10.27 | −6.19 | −9.19 | −5.85 | −12.22 | |
| Strip 3 (Seogwipo–Shinan Strip) | ||||||
| Seogwipo | Jeju | Uisin | Gunnae | Hwawon | Shinan | |
| Mean across-track error | 19.38 | 24.71 | 23.13 | 21.23 | 21.48 | 17.80 |
| Mean along-track error | 33.05 | 2.11 | 31.39 | 37.80 | 48.79 | 42.65 |
| Across-track correction coefficient | 19.35 | 24.68 | 23.02 | 21.12 | 21.45 | 17.74 |
| Along-track correction coefficient | −32.81 | −30.75 | −31.35 | −37.70 | −38.70 | −42.59 |
| Strip | Extrapolation Model |
|---|---|
| Strip 1 (Goheung–Boryeong) | |
| Strip 2 (Seobuyeo–Dangjin) | |
| Strip 3 (Seogwipo–Shinan) |
| Strip | Test Area | Direction | Estimated Correction Coefficient (pix) | Reference Correction Coefficient (pix) | Correction Coefficient Errors (pix) |
|---|---|---|---|---|---|
| Strip 1 | Boryeong | Across track | 35.530 | 30.941 | 4.589 |
| Along track | 16.358 | 13.981 | 2.377 | ||
| Strip 2 | Dangjin | Across track | 30.026 | 31.849 | 1.823 |
| Along track | −10.068 | −12.223 | 2.155 | ||
| Strip 3 | Shinan | Across track | 19.558 | 17.736 | 1.822 |
| Along track | −42.353 | −42.585 | 0.232 |
| Strip | Test Area | Distance (km) | Along-Track Error (pix) | Across-Track Error (pix) |
|---|---|---|---|---|
| Strip 1 | Gunsan | 77.717 | 9.706 | 1.345 |
| Boryeong | 129.147 | 1.345 | 4.865 | |
| Strip 2 | Deoksan | 12.995 | 3.924 | 0.328 |
| Dangjin | 129.147 | 2.658 | 1.879 | |
| Strip 3 | Hwawon | 12.993 | 4.803 | 1.373 |
| Shinan | 58.309 | 12.577 | 1.550 |
| Previous Approach RPC Correction Coefficient Error | Proposed Approach RPC Correction Coefficient Error | |||
|---|---|---|---|---|
| Along-Track Error | Across-Track Error | Along-Track Error | Across-Track Error | |
| Deoksan | 4.644 | 0.059 | 3.924 | 0.328 |
| Dangjin | 2.801 | 1.794 | 2.658 | 1.879 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, N. RPC Correction Coefficient Extrapolation for KOMPSAT-3A Imagery in Inaccessible Regions. Remote Sens. 2025, 17, 3332. https://doi.org/10.3390/rs17193332
Kim N. RPC Correction Coefficient Extrapolation for KOMPSAT-3A Imagery in Inaccessible Regions. Remote Sensing. 2025; 17(19):3332. https://doi.org/10.3390/rs17193332
Chicago/Turabian StyleKim, Namhoon. 2025. "RPC Correction Coefficient Extrapolation for KOMPSAT-3A Imagery in Inaccessible Regions" Remote Sensing 17, no. 19: 3332. https://doi.org/10.3390/rs17193332
APA StyleKim, N. (2025). RPC Correction Coefficient Extrapolation for KOMPSAT-3A Imagery in Inaccessible Regions. Remote Sensing, 17(19), 3332. https://doi.org/10.3390/rs17193332





