High-Frequency Monitoring and Short-Term Forecasting of Surface Water Temperature Using a Novel Hyperspectral Proximal Sensing System
Abstract
Highlights
- A high-precision lake surface water temperature (LSWT) inversion model was developed using a novel hyperspectral proximal sensing system (HPSs) and a DNN algorithm, achieving an R2 = 0.99, an RMSE = 0.92 °C, and an MAE = 0.64 °C.
- A short-term LSWT forecasting model based on the LSTM algorithm and HPSs data was established, providing accurate 1–3-day predictions (R2 > 0.985).
- The approach enables the real-time, ultra-high-frequency monitoring of lake thermal dynamics, enhancing the detection of rapid temperature fluctuations and extreme events.
- This study provides a practical early warning and management tool to mitigate harmful algal blooms and safeguard drinking water security under climate change.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. In Situ Water Quality Measurement
2.3. HPS Reflectance Measurements
2.4. Matchup of the Data and LSWT Inversion Modeling
2.5. LSWT Forecast Modeling
2.6. Statistical Analysis
3. Results
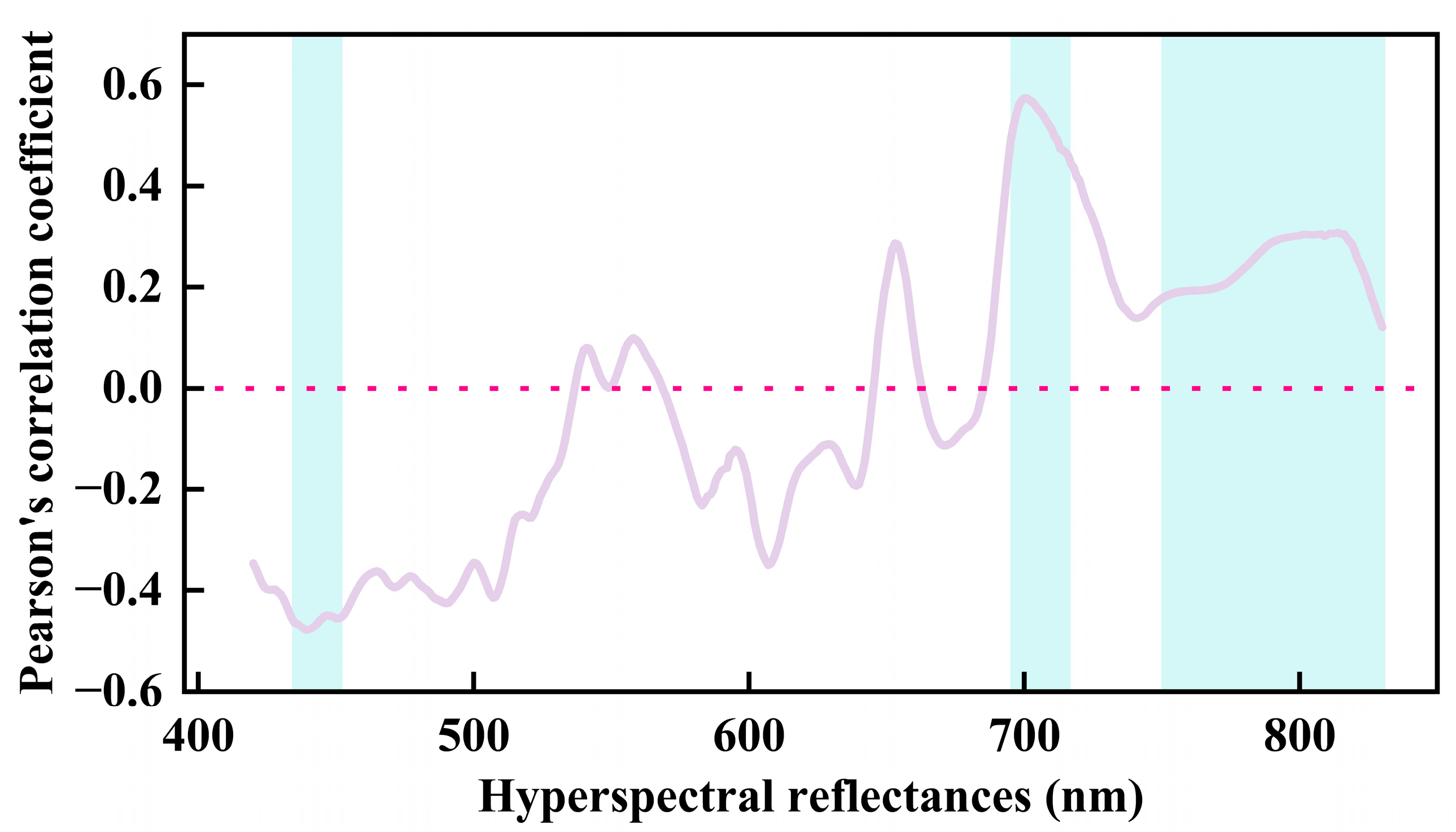
3.1. Analysis of Hyperspectral Sensitivity
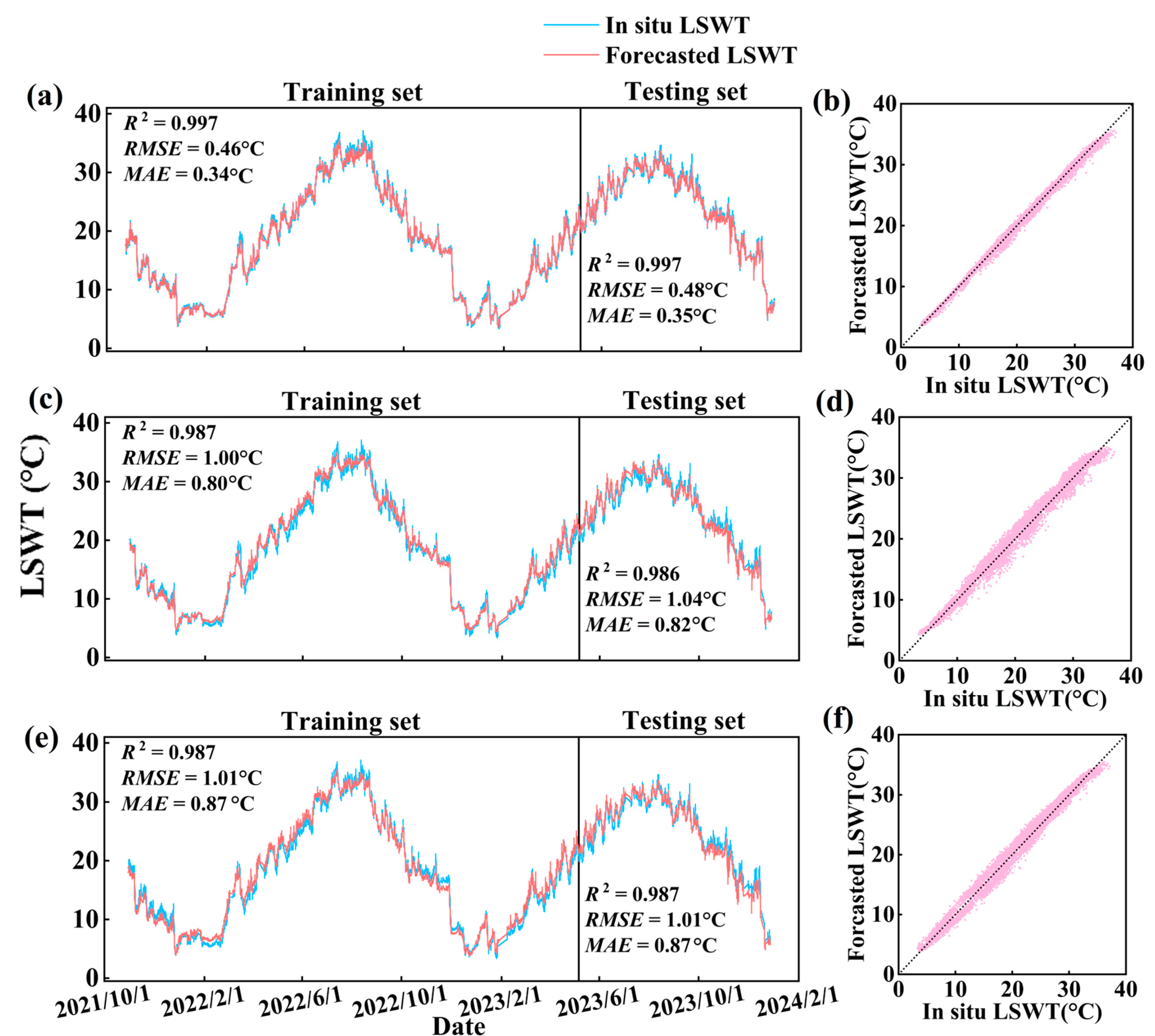
3.2. Development and Validation of LSWT Inversion Models
3.3. Development of LSWT Forecasting Models
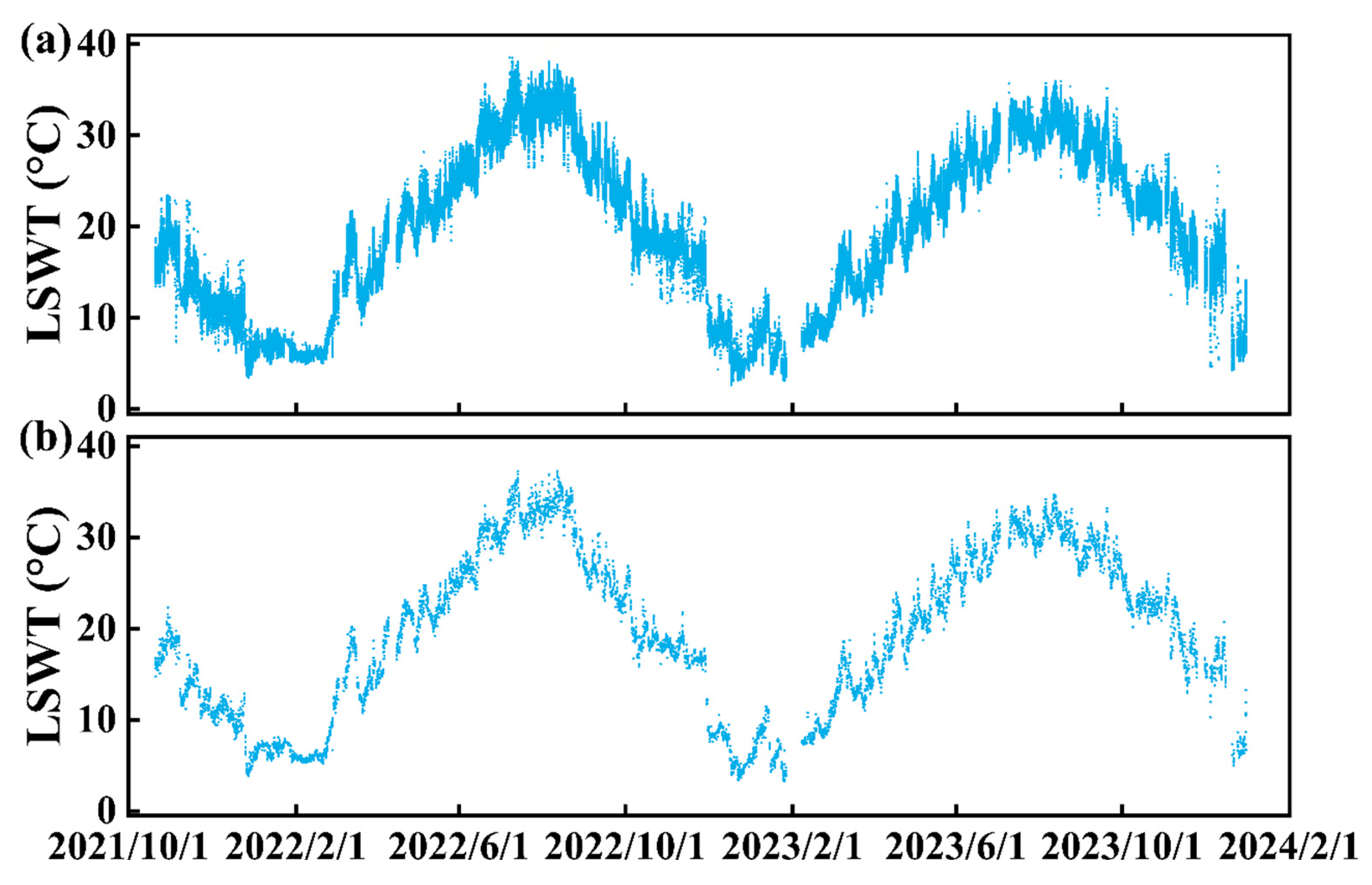
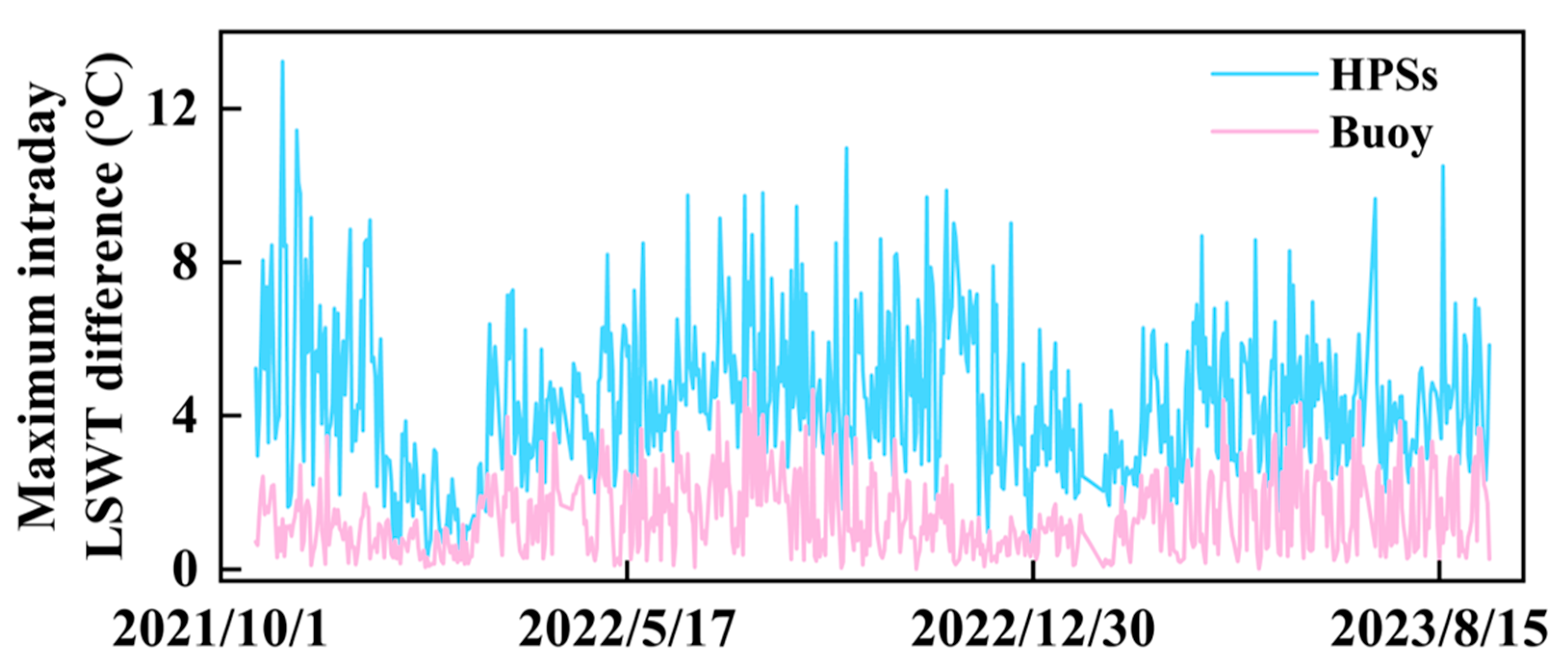
3.4. Temporal Variations in the LSWT in the Northern Part of Lake Taihu
4. Discussion
4.1. Significance of High-Frequency Monitoring and Short-Term Forecasting of LSWT in Lakes
4.2. Strengths and Drawbacks of Models
4.3. Advantages of HPSs for Water Quality Monitoring and Management
5. Conclusions
- (1)
- A DNN-based inversion model was developed using HPSs data, achieving the high-precision inversion of the LSWT with an R2 of 0.990, an RMSE of 0.92 °C, and an MAE of 0.64 °C.
- (2)
- An analysis of high-frequency data from 2021–2023 revealed strong seasonal LSWT variations in northern Lake Taihu. The minute-averaged data exhibited extremes ranging from 2.61 °C to 38.52 °C, while the hourly-averaged data ranged from 3.26 °C to 37.26 °C.
- (3)
- The LSTM forecasting model provided reliable 1–3-day forecasts (R2 > 0.985), offering valuable insights for lake ecosystem management.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Dorber, M.; Barbarossa, V.; Verones, F. Global characterization factors for quantifying the impacts of increasing water temperature on freshwater fish. Ecol. Indic. 2022, 142, 109201. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
- Wang, W.; Shi, K.; Wang, X.; Zhang, Y.; Qin, B.; Zhang, Y.; Woolway, R.I. The impact of extreme heat on lake warming in China. Nat. Commun. 2024, 15, 70. [Google Scholar] [CrossRef]
- Woolway, R.I.; Tong, Y.; Feng, L.; Zhao, G.; Dinh, D.A.; Shi, H.; Zhang, Y.; Shi, K. Multivariate extremes in lakes. Nat. Commun. 2024, 15, 4559. [Google Scholar] [CrossRef] [PubMed]
- Du Plessis, A. Persistent degradation: Global water quality challenges and required actions. One Earth 2022, 5, 129–131. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Stow, C.A. Water Loss from the Great Lakes. Science 2014, 343, 1084–1085. [Google Scholar] [CrossRef]
- Maberly, S.C.; O’Donnell, R.A.; Woolway, R.I.; Cutler, M.E.J.; Gong, M.; Jones, I.D.; Merchant, C.J.; Miller, C.A.; Politi, E.; Scott, E.M.; et al. Global lake thermal regions shift under climate change. Nat. Commun. 2020, 11, 1232. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [PubMed]
- Yang, K.; Yu, Z.; Luo, Y.; Yang, Y.; Zhao, L.; Zhou, X. Spatial and temporal variations in the relationship between lake water surface temperatures and water quality—A case study of Dianchi Lake. Sci. Total Environ. 2018, 624, 859–871. [Google Scholar] [PubMed]
- Woolway, R.I.; Dokulil, M.T.; Marszelewski, W.; Schmid, M.; Bouffard, D.; Merchant, C.J. Warming of Central European lakes and their response to the 1980s climate regime shift. Clim. Chang. 2017, 142, 505–520. [Google Scholar] [CrossRef]
- Qin, B.; Huang, Q. Evaluation of the Climatic Change Impacts on the Inland Lake—A Case Study of Lake Qinghai, China. Clim. Chang. 1998, 39, 695–714. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, K.; Woolway, R.I.; Wang, X.; Zhang, Y. Climate warming and heatwaves accelerate global lake deoxygenation. Sci. Adv. 2025, 11, eadt5369. [Google Scholar] [CrossRef] [PubMed]
- Jane, S.F.; Hansen, G.J.A.; Kraemer, B.M.; Leavitt, P.R.; Mincer, J.L.; North, R.L.; Pilla, R.M.; Stetler, J.T.; Williamson, C.E.; Woolway, R.I.; et al. Widespread deoxygenation of temperate lakes. Nature 2021, 594, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.L.; Wu, Z.X.; Liu, M.L.; He, J.B.; Shi, K.; Zhou, Y.Q.; Wang, M.Z.; Liu, X.H. Dissolved oxygen stratification and response to thermal structure and long-term climate change in a large and deep subtropical reservoir (Lake Qiandaohu, China). Water Res. 2015, 75, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Verburg, P.; Hecky, R.E.; Kling, H. Ecological Consequences of a Century of Warming in Lake Tanganyika. Science 2003, 301, 505–507. [Google Scholar] [CrossRef]
- Qin, B.Q.; Deng, J.M.; Shi, K.; Wang, J.; Brookes, J.; Zhou, J.; Zhang, Y.L.; Zhu, G.W.; Paerl, H.W.; Wu, L. Extreme climate anomalies enhancing cyanobacterial blooms in eutrophic Lake Taihu, China. Water Resour. Res. 2021, 57, e2020WR029371. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Li, N.; Shi, K.; Zhang, Y.; Qin, B.; Zhu, G.; Liu, M.; Shao, K. Summer heatwaves promote harmful algal blooms in the Fuchunjiang Reservoir, an important drinking water source. J. Environ. Manag. 2024, 359, 121056. [Google Scholar] [CrossRef]
- Johnk, K.D.; Huisman, J.; Sharples, J.; Sommeijer, B.; Visser, P.M.; Stroom, J.M. Summer heatwaves promote blooms of harmful cyanobacteria. Glob. Change Biol. 2008, 14, 495–512. [Google Scholar] [CrossRef]
- Jungkeit-Milla, K.; Pérez-Cabello, F.; de Vera-García, A.V.; Galofré, M.; Valero-Garcés, B. Lake Surface Water Temperature in high altitude lakes in the Pyrenees: Combining satellite with monitoring data to assess recent trends. Sci. Total Environ. 2024, 933, 173181. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Zhao, W.; Wu, P.; Huang, C.; Han, X.-J.; Gao, M.; Leng, P.; Shang, G. Validation of Landsat land surface temperature product in the conterminous United States using in situ measurements from SURFRAD, ARM, and NDBC sites. Int. J. Digit. Earth 2021, 14, 640–660. [Google Scholar] [CrossRef]
- Yvon-Durocher, G.; Montoya, J.M.; Trimmer, M.; Woodward, G. Warming alters the size spectrum and shifts the distribution of biomass in freshwater ecosystems. Glob. Change Biol. 2011, 17, 1681–1694. [Google Scholar] [CrossRef]
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Liu, G.; Ou, W.; Zhang, Y.; Wu, T.; Zhu, G.; Shi, K.; Qin, B. Validating and Mapping Surface Water Temperatures in Lake Taihu: Results From MODIS Land Surface Temperature Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1230–1244. [Google Scholar] [CrossRef]
- Kawanishi, T.; Sezai, T.; Ito, Y.; Imaoka, K.; Takeshima, T.; Ishido, Y.; Shibata, A.; Miura, M.; Inahata, H.; Spencer, R.W. The Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E), NASDA’s contribution to the EOS for global energy and water cycle studies. IEEE Trans. Geosci. Remote Sens. 2003, 41, 184–194. [Google Scholar] [CrossRef]
- Chelton, D.B.; Esbensen, S.K.; Schlax, G.; Thum, N.; Freilich, M.H.; Wentz, F.J.; Gentemann, C.L.; McPhaden, M.J.; Schopf, P.S. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical Pacific. J. Clim. 2001, 14, 1479–1498. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.L.; Shi, K.; Zhang, Y.B.; Sun, X.; Wang, W.J.; Huang, X. Monitoring water transparency, total suspended matter and the beam attenuation coefficient in inland water using innovative ground-based proximal sensing technology. J. Environ. Manag. 2022, 306, 114477. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.J.; Shi, K.; Zhang, Y.B.; Li, N.; Sun, X.; Zhang, D.; Zhang, Y.L.; Qin, B.Q.; Zhu, G.W. A ground-based remote sensing system for high-frequency and real-time monitoring of phytoplankton blooms. J. Hazard. Mater. 2022, 439, 129623. [Google Scholar] [CrossRef]
- Hulley, G.C.; Hook, S.J.; Schneider, P. Optimized split-window coefficients for deriving surface temperatures from inland water bodies. Remote Sens. Environ. 2011, 115, 3758–3769. [Google Scholar] [CrossRef]
- Huang, L.; Wang, X.; Sang, Y.; Tang, S.; Jin, L.; Yang, H.; Ottlé, C.; Bernus, A.; Wang, S.; Wang, C.; et al. Optimizing Lake Surface Water Temperature Simulations Over Large Lakes in China With FLake Model. Earth Space Sci. 2021, 8, e2021EA001737. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, K.; Luo, Y.; Shang, C.; Zhu, Y. Lake surface water temperature prediction and changing characteristics analysis—A case study of 11 natural lakes in Yunnan-Guizhou Plateau. J. Clean. Prod. 2020, 276, 122689. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, J.; Yang, X.; Zhang, Y.; Zhang, L.; Ren, H.; Wu, B.; Ye, L. A review of the application of machine learning in water quality evaluation. Eco-Environ. Health 2022, 1, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Virdis, S.G.P.; Kongwarakom, S.; Juneng, L.; Padedda, B.M.; Shrestha, S. Historical and projected response of Southeast Asian lakes surface water temperature to warming climate. Environ. Res. 2024, 247, 118412. [Google Scholar] [CrossRef]
- Su, J.; Lin, Z.Y.; Xu, F.W.; Fathi, G.; Alnowibet, K.A. A hybrid model of ARIMA and MLP with a Grasshopper optimization algorithm for time series forecasting of water quality. Sci. Rep. 2024, 14, 23927. [Google Scholar] [CrossRef] [PubMed]
- Vilhena, L.C.; Hillmer, I.; Imberger, J. The role of climate change in the occurrence of algal blooms: Lake Burragorang, Australia. Limnol. Oceanogr. 2010, 55, 1188–1200. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Kreuzer, D.; Munz, M.; Schlüter, S. Short-term temperature forecasts using a convolutional neural network—An application to different weather stations in Germany. Mach. Learn. Appl. 2020, 2, 100007. [Google Scholar] [CrossRef]
- Xu, H.; Paerl, H.W.; Qin, B.; Zhu, G.; Gaoa, G. Nitrogen and phosphorus inputs control phytoplankton growth in eutrophic Lake Taihu, China. Limnol. Oceanogr. 2010, 55, 420–432. [Google Scholar] [CrossRef]
- Qin, B.Q.; Zhu, G.W.; Gao, G.; Zhang, Y.L.; Li, W.; Paerl, H.W.; Carmichael, W.W. A Drinking Water Crisis in Lake Taihu, China: Linkage to Climatic Variability and Lake Management. Environ. Manag. 2010, 45, 105–112. [Google Scholar] [CrossRef]
- Yan, X.; Xia, Y.; Ti, C.; Shan, J.; Wu, Y.; Yan, X. Thirty years of experience in water pollution control in Taihu Lake: A review. Sci. Total Environ. 2024, 914, 169821. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Liu, P.-W. Strategy of water pollution prevention in Taihu Lake and its effects analysis. J. Great Lakes Res. 2010, 36, 150–158. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Qin, B.Q.; Zhu, G.W.; Shi, K.; Zhou, Y.Q. Profound Changes in the Physical Environment of Lake Taihu From 25 Years of Long-Term Observations: Implications for Algal Bloom Outbreaks and Aquatic Macrophyte Loss. Water Resour. Res. 2018, 54, 4319–4331. [Google Scholar] [CrossRef]
- Woolway, R.I.; Jennings, E.; Shatwell, T.; Golub, M.; Pierson, D.C.; Maberly, S.C. Lake heatwaves under climate change. Nature 2021, 589, 402–407. [Google Scholar] [CrossRef]
- Paerl, H.W.; Huisman, J. Blooms Like It Hot. Science 2008, 320, 57–58. [Google Scholar] [CrossRef]
- Luo, J.; Li, X.; Ma, R.; Li, F.; Duan, H.; Hu, W.; Qin, B.; Huang, W. Applying remote sensing techniques to monitoring seasonal and interannual changes of aquatic vegetation in Taihu Lake, China. Ecol. Indic. 2016, 60, 503–513. [Google Scholar] [CrossRef]
- Huisman, J.; Codd, G.A.; Paerl, H.W.; Ibelings, B.W.; Verspagen, J.M.H.; Visser, P.M. Cyanobacterial blooms. Nat. Rev. Microbiol. 2018, 16, 471–483. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Bentéjac, C.; Csörgo, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Zhang, H.C.; Huang, S.H. Applications of Neural Networks in Manufacturing—A State of the Survey. Int. J. Prod. Res. 1995, 33, 705–728. [Google Scholar] [CrossRef]
- Honda, T.; Kotsuki, S.; Lien, G.-Y.; Maejima, Y.; Okamoto, K.; Miyoshi, T. Assimilation of Himawari-8 All-Sky Radiances Every 10 Minutes: Impact on Precipitation and Flood Risk Prediction. J. Geophys. Res. Atmos. 2018, 123, 965–976. [Google Scholar] [CrossRef]
- Bidder, O.R.; Campbell, H.A.; Gómez-Laich, A.; Urgé, P.; Walker, J.; Cai, Y.Z.; Gao, L.L.; Quintana, F.; Wilson, R.P. Love Thy Neighbour: Automatic Animal Behavioural Classification of Acceleration Data Using the K-Nearest Neighbour Algorithm. PLoS ONE 2014, 9, e88609. [Google Scholar] [CrossRef]
- Xu, L.L.; Li, B.L.; Yuan, Y.C.; Gao, X.Z.; Zhang, T. A Temporal-Spatial Iteration Method to Reconstruct NDVI Time Series Datasets. Remote Sens. 2015, 7, 8906–8924. [Google Scholar] [CrossRef]
- Bautista, P.M.; Duka, M.A.; Delos Reyes, A.; Sobremisana, A.G. Water temperature modeling through regression and artificial neural network using short-term data for a Philippine River. Water Pract. Technol. 2024, 19, 4178–4191. [Google Scholar] [CrossRef]
- Cazzaniga, I.; Zibordi, G.; Alikas, K.; Kratzer, S. Temporal changes in the remote sensing reflectance at Lake VänernNature Reviews Earth and Environment. J. Great Lakes Res. 2023, 49, 357–367. [Google Scholar] [CrossRef]
- Lindemann, B.; Müller, T.; Vietz, H.; Jazdi, N.; Weyrich, M. A survey on long short-term memory networks for time series prediction. Procedia CIRP 2021, 99, 650–655. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Chu, P.; Wang, S.; Yu, W.; Wang, A.; Zong, Y.; Yin, S.; Zhao, C.; Wang, T. The impact of extremely low-temperature changes on fish: A case study on migratory bony fishes (Takifugu fasciatus). Aquaculture 2024, 579, 740155. [Google Scholar] [CrossRef]
- Kayastha, P.; Dzialowski, A.R.; Stoodley, S.H.; Wagner, K.L.; Mansaray, A.S. Effect of Time Window on Satellite and Ground-Based Data for Estimating Chlorophyll-a in Reservoirs. Remote Sens. 2022, 14, 846. [Google Scholar] [CrossRef]
- Mishra, R.K.; Reddy, G.Y.S.; Pathak, H. The Understanding of Deep Learning: A Comprehensive Review. Math. Probl. Eng. 2021, 2021, 5548884. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Tang, L.; Yin, Y.; Liu, D.; Zhang, Y. Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: Comprehensive review and future challenge. Gondwana Res. 2022, 109, 1–17. [Google Scholar] [CrossRef]
- Griffin, C.G.; Finlay, J.C.; Brezonik, P.L.; Olmanson, L.; Hozalski, R.M. Limitations on using CDOM as a proxy for DOC in temperate lakes. Water Res. 2018, 144, 719–727. [Google Scholar] [CrossRef]
- Du, Y.; Chen, F.; Xiao, K.; Song, C.; He, H.; Zhang, Q.; Zhou, Y.; Jang, K.-S.; Zhang, Y.; Xing, P.; et al. Water Residence Time and Temperature Drive the Dynamics of Dissolved Organic Matter in Alpine Lakes in the Tibetan Plateau. Glob. Biogeochem. Cycles 2021, 35, e2020GB006908. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of chl-a concentration in turbid productive waters—Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- Guo, H.W.; Tian, S.; Huang, J.; Zhu, X.T.; Wang, B.; Zhang, Z.J. Performance of deep learning in mapping water quality of Lake Simcoe with long-term Landsat archive. ISPRS J. Photogramm. Remote Sens. 2022, 183, 451–469. [Google Scholar] [CrossRef]
- Donchyts, G.; Winsemius, H.; Baart, F.; Dahm, R.; Schellekens, J.; Gorelick, N.; Iceland, C.; Schmeier, S. High-resolution surface water dynamics in Earth’s small and medium-sized reservoirs. Sci. Rep. 2022, 12, 13776. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Ochoa, C.G.; Li, Q.; Shen, X.; Qian, Z.; Han, S.; Zhang, N.; Yu, M. Forecasting environmental water availability of lakes using temporal fusion transformer: Case studies of China’s two largest freshwater lakes. Environ. Monit. Assess. 2024, 196, 152. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Qian, L.; Pu, N.; Bi, Y.; Wilhelms, A.; Norra, S. An Intelligent Early Warning System for Harmful Algal Blooms: Harnessing the Power of Big Data and Deep Learning. Environ. Sci. Technol. 2024, 58, 15607–15618. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Yang, K.; Zhou, X.; Luo, Y. Temporal and Spatial Dynamics of Surface Water Temperature Changes in China’s Major Lakes. Water Resour. Res. 2025, 61, e2024WR038855. [Google Scholar] [CrossRef]


| Inversion Model | Training Dataset | Testing Dataset | Validation Dataset | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min–Max | Mean ± S.D. | N | Min–Max | Mean ± S.D. | N | Min–Max | Mean ± S.D. | N | |
| LSWT (°C) | 3.18–37.58 | 19.14 ± 9.14 | 7946 | 3.34–37.52 | 19.33 ± 9.07 | 2649 | 3.25–37.32 | 19.50 ± 9.15 | 1178 |
| Training Dataset | Testing Dataset | |||||
|---|---|---|---|---|---|---|
| Input–Output (Days) | R2 | RMSE (°C) | MAE (°C) | R2 | RMSE (°C) | MAE (°C) |
| 1–1 | 0.996 | 0.56 | 0.43 | 0.996 | 0.57 | 0.44 |
| 2–1 | 0.995 | 0.63 | 0.48 | 0.995 | 0.63 | 0.48 |
| 3–1 | 0.997 | 0.46 | 0.34 | 0.997 | 0.48 | 0.35 |
| 4–1 | 0.993 | 0.72 | 0.58 | 0.993 | 0.73 | 0.58 |
| 5–1 | 0.995 | 0.62 | 0.50 | 0.995 | 0.62 | 0.51 |
| 6–1 | 0.995 | 0.63 | 0.50 | 0.995 | 0.61 | 0.49 |
| 7–1 | 0.997 | 0.49 | 0.37 | 0.997 | 0.50 | 0.37 |
| 8–1 | 0.995 | 0.61 | 0.47 | 0.995 | 0.61 | 0.48 |
| 9–1 | 0.994 | 0.68 | 0.53 | 0.994 | 0.70 | 0.54 |
| 10–1 | 0.997 | 0.50 | 0.40 | 0.997 | 0.50 | 0.40 |
| 1–2 | 0.985 | 1.09 | 0.87 | 0.984 | 1.11 | 0.88 |
| 2–2 | 0.985 | 1.08 | 0.80 | 0.985 | 1.07 | 0.80 |
| 3–2 | 0.983 | 1.13 | 0.88 | 0.982 | 1.17 | 0.91 |
| 4–2 | 0.982 | 1.18 | 0.89 | 0.982 | 1.19 | 0.90 |
| 5–2 | 0.984 | 1.12 | 0.88 | 0.984 | 1.12 | 0.87 |
| 6–2 | 0.982 | 1.17 | 0.90 | 0.982 | 1.18 | 0.89 |
| 7–2 | 0.984 | 1.11 | 0.91 | 0.983 | 1.12 | 0.91 |
| 8–2 | 0.983 | 1.15 | 0.91 | 0.983 | 1.15 | 0.90 |
| 9–2 | 0.987 | 1.00 | 0.80 | 0.986 | 1.04 | 0.82 |
| 10–2 | 0.984 | 1.10 | 0.88 | 0.983 | 1.16 | 0.92 |
| 1–3 | 0.983 | 1.15 | 0.93 | 0.983 | 1.14 | 0.93 |
| 2–3 | 0.980 | 1.27 | 0.96 | 0.980 | 1.26 | 0.96 |
| 3–3 | 0.980 | 1.23 | 0.98 | 0.981 | 1.21 | 0.95 |
| 4–3 | 0.974 | 1.40 | 1.11 | 0.975 | 1.40 | 1.12 |
| 5–3 | 0.973 | 1.44 | 1.14 | 0.973 | 1.45 | 1.16 |
| 6–3 | 0.984 | 1.12 | 0.94 | 0.983 | 1.13 | 0.94 |
| 7–3 | 0.987 | 1.01 | 0.87 | 0.987 | 1.01 | 0.87 |
| 8–3 | 0.973 | 1.45 | 1.16 | 0.973 | 1.45 | 1.17 |
| 9–3 | 0.980 | 1.25 | 1.01 | 0.980 | 1.26 | 1.02 |
| 10–3 | 0.982 | 1.20 | 0.98 | 0.980 | 1.24 | 1.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Li, N.; Zhang, Y.; Zhang, Y.; Shi, K.; Qin, B.; Zhu, G. High-Frequency Monitoring and Short-Term Forecasting of Surface Water Temperature Using a Novel Hyperspectral Proximal Sensing System. Remote Sens. 2025, 17, 3303. https://doi.org/10.3390/rs17193303
Luo X, Li N, Zhang Y, Zhang Y, Shi K, Qin B, Zhu G. High-Frequency Monitoring and Short-Term Forecasting of Surface Water Temperature Using a Novel Hyperspectral Proximal Sensing System. Remote Sensing. 2025; 17(19):3303. https://doi.org/10.3390/rs17193303
Chicago/Turabian StyleLuo, Xiayang, Na Li, Yunlin Zhang, Yibo Zhang, Kun Shi, Boqiang Qin, and Guangwei Zhu. 2025. "High-Frequency Monitoring and Short-Term Forecasting of Surface Water Temperature Using a Novel Hyperspectral Proximal Sensing System" Remote Sensing 17, no. 19: 3303. https://doi.org/10.3390/rs17193303
APA StyleLuo, X., Li, N., Zhang, Y., Zhang, Y., Shi, K., Qin, B., & Zhu, G. (2025). High-Frequency Monitoring and Short-Term Forecasting of Surface Water Temperature Using a Novel Hyperspectral Proximal Sensing System. Remote Sensing, 17(19), 3303. https://doi.org/10.3390/rs17193303








