A Semi-Supervised Multi-Scale Convolutional Neural Network for Hyperspectral Image Classification with Limited Labeled Samples
Abstract
Highlights
- A semi-supervised classification model combining a multi-scale convolutional neural network with a novel pseudo-label strategy ensures high-quality classification of hyperspectral remote sensing images.
- By enhancing the discriminative ability of the classifier through the multi-scale convolutional neural network and improving pseudo-label prediction accuracy via a feature-level augmentation-based pseudo-label generation strategy, the model’s classification performance is elevated.
- This approach enhances the classification performance of hyperspectral remote sensing imagery under conditions of insufficient labelled samples.
- It provides a robust solution to the practical challenge of obtaining labelled samples in real-world applications.
Abstract
1. Introduction
- (1)
- An MSCNN is presented that contains spatial and spectral multi-scale information extraction modules. Existing convolutional neural network models primarily focus on multi-scale information extraction in the spatial dimension while overlooking the characteristics of hyperspectral data with hundreds of bands in the spectral dimension. In contrast, this study designed a multi-scale feature extraction module with larger convolutional kernels in the spectral dimension. This enhances the model’s receptive field in the spectral dimension, thereby improving its discrimination capability and significantly increasing the accuracy of pseudo-labels predicted for unlabeled samples.
- (2)
- A new pseudo-label generation strategy based on Dropout [42] is proposed. As a feature-level data augmentation operation, Dropout avoids the problem (which is common in general data augmentation strategies) of changing the spectral response of pixels in HSIs, causing category confusion in spectral response features. Specifically, due to the randomness in Dropout, multiple different classification results for the same unlabeled data can be obtained in multiple Dropout operations. Then, an ensemble learning strategy is adopted to reduce the pseudo-label error by averaging multiple results.
- (3)
- A deep semi-supervised approach (i.e., MSCNN-D-PL) to HSI classification is proposed. The MSCNN-D-PL achieves more reliable pseudo-labels in deep learning mode for hyperspectral imagery classification. In our experiments on four real HSI datasets with limited labeled samples, it improves the classification accuracy by an average of 4.04% compared to the supervised model and 1.92% compared to other semi-supervised models.
2. Related Works and Motivation
2.1. CNN for HSI Classification
2.2. Semi-Supervised Learning for HSI Classification
3. Proposed Approach
3.1. Multi-Scale CNN Model
3.1.1. Spectral and Spatial Multi-Scale Convolutional Blocks
3.1.2. Overview of the Proposed Classification Model
3.2. Dropout-Based Pseudo-Label Generation Strategy
3.3. Multi-Scale CNN Combining Dropout and Pseudo-Labels
| Algorithm 1: MSCNN-D-PL |
| Input: |
Number of unlabeled samples’ predictions, K Total number of epochs, N Number of epochs for training MSCNN at first, N1 Number of epochs for training MSCNN with the updated labeled sample set, N2 |
| Output: |
| Procedure: |
|
4. Experimental Results and Discussion
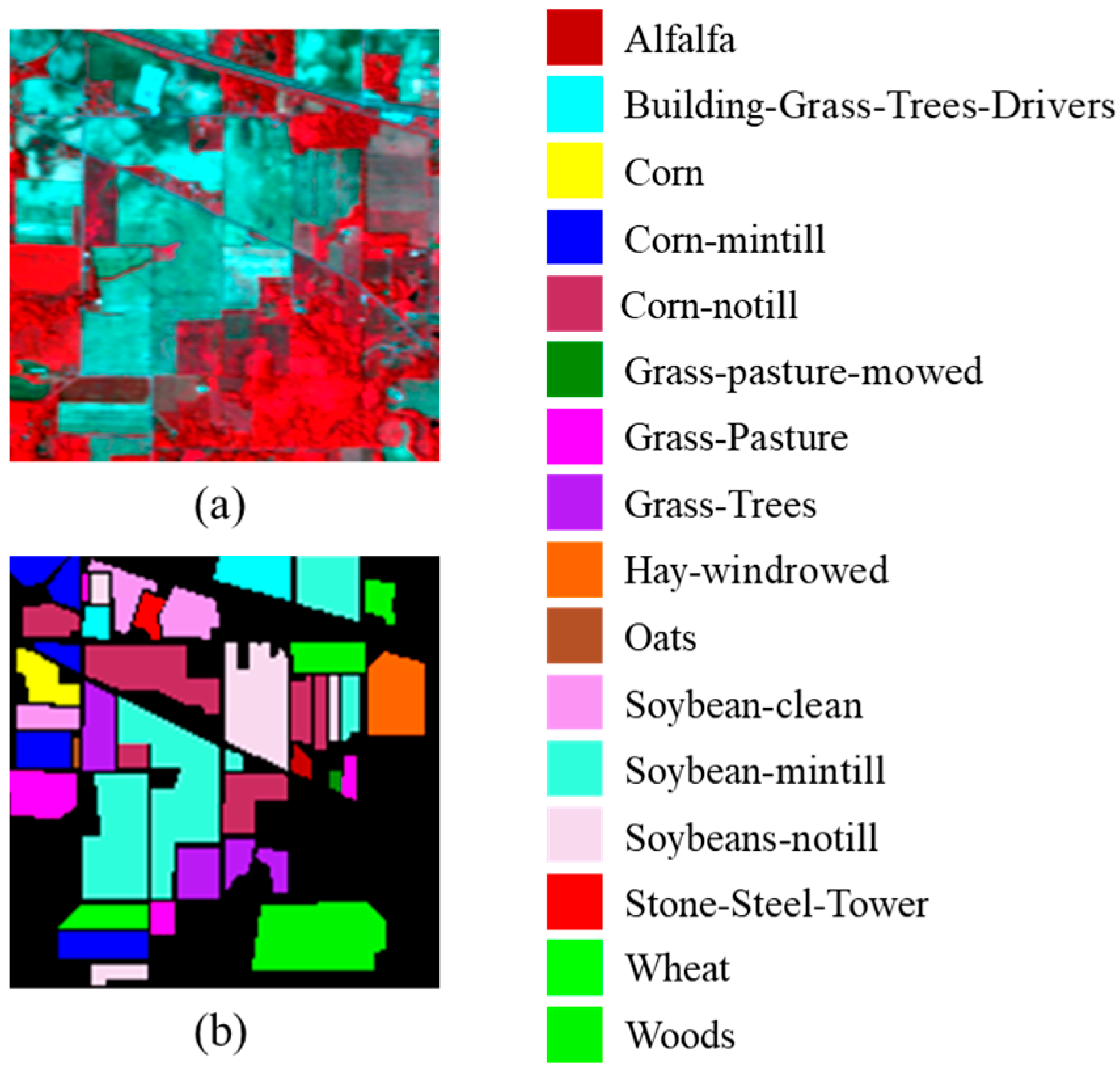
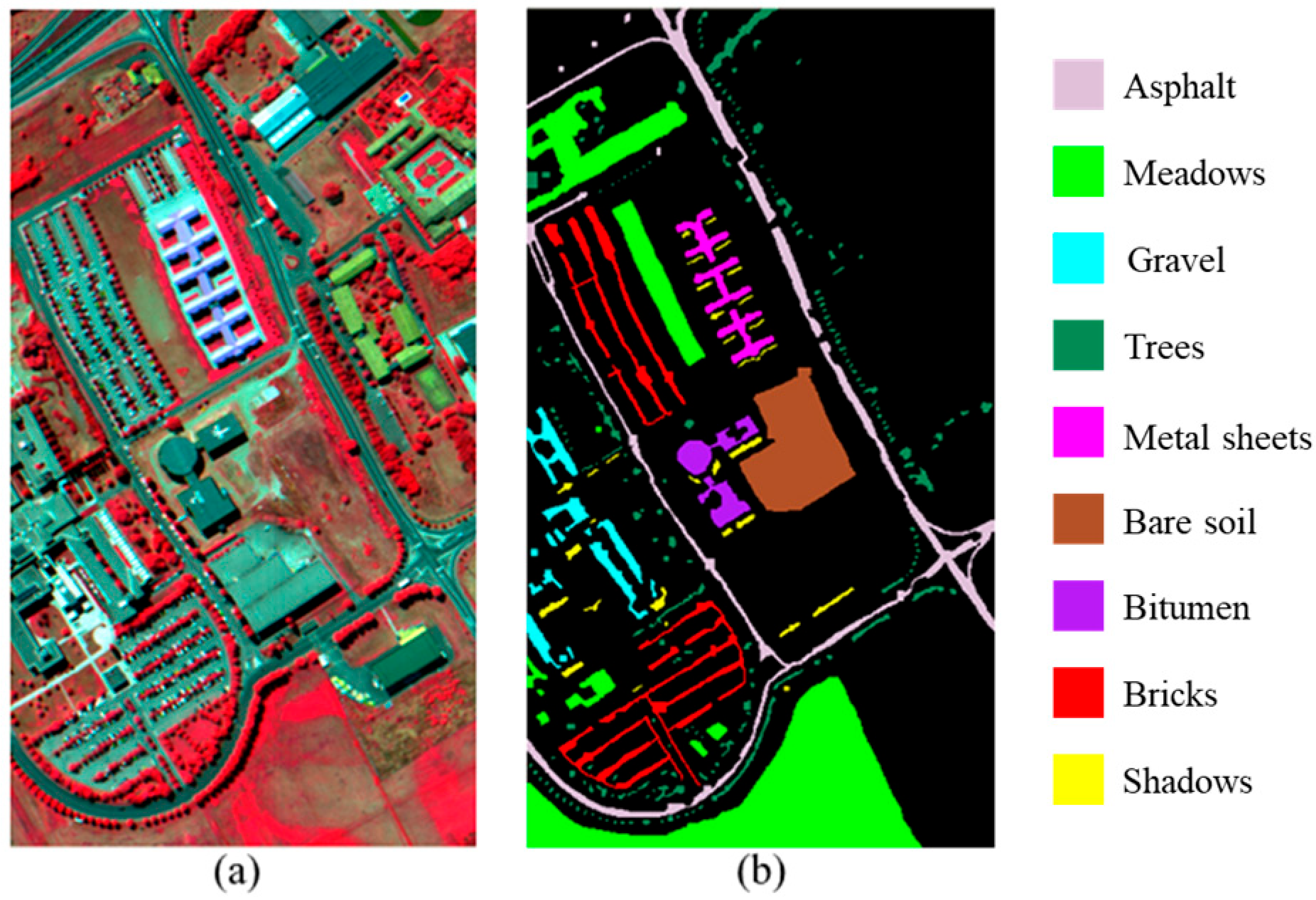
4.1. Description of Datasets
4.2. Experimental Settings
- (1)
- DSR-GCN [60]: A transductive semi-supervised classification model based on a differentiated-scale restricted graph convolutional network.
- (2)
- 3D-GAN [30]: A semi-supervised classification model based on a generative adversarial network (GAN), in which both the generator and discriminator are 3D CNNs.
- (3)
- PseudoLabel [37]: A semi-supervised classification model based on a traditional pseudo-label strategy.
- (4)
- MeanTeacher [61]: A semi-supervised classification model based on consistent regularization.
- (5)
- MixMatch [40]: A deep semi-supervised classification model based on a hybrid strategy combining pseudo-labels and consistent regularization.
- (6)
- FixMatch [41]: A deep semi-supervised classification model based on a hybrid strategy combining pseudo-labels and consistent regularization and achieving impressive performance in the field of natural image classification.
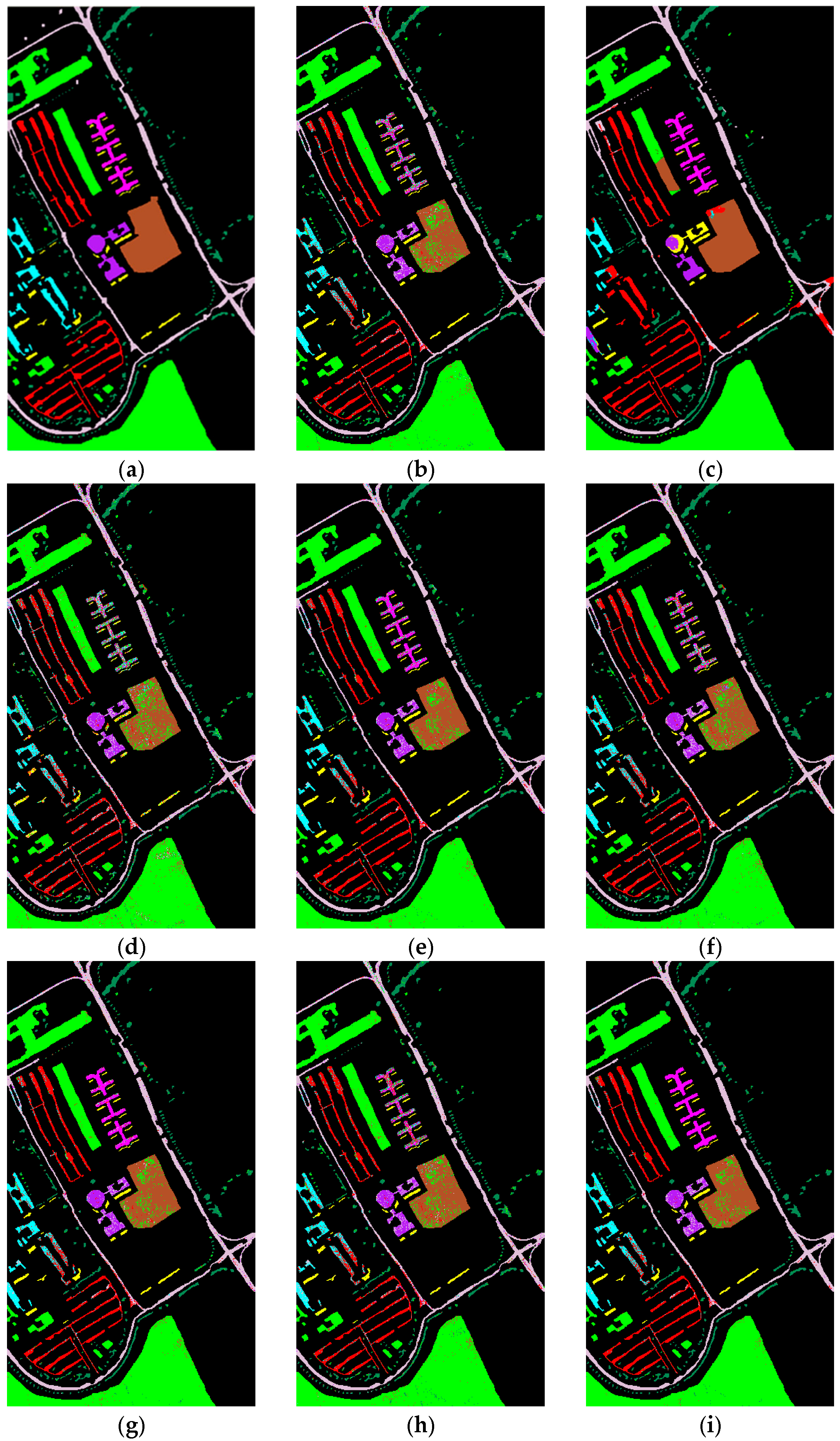
4.3. Results
4.3.1. MSCNN Results
4.3.2. Impact of Data Augmentation on HSI Classification
4.3.3. Comparison with State-of-the-Art Methods
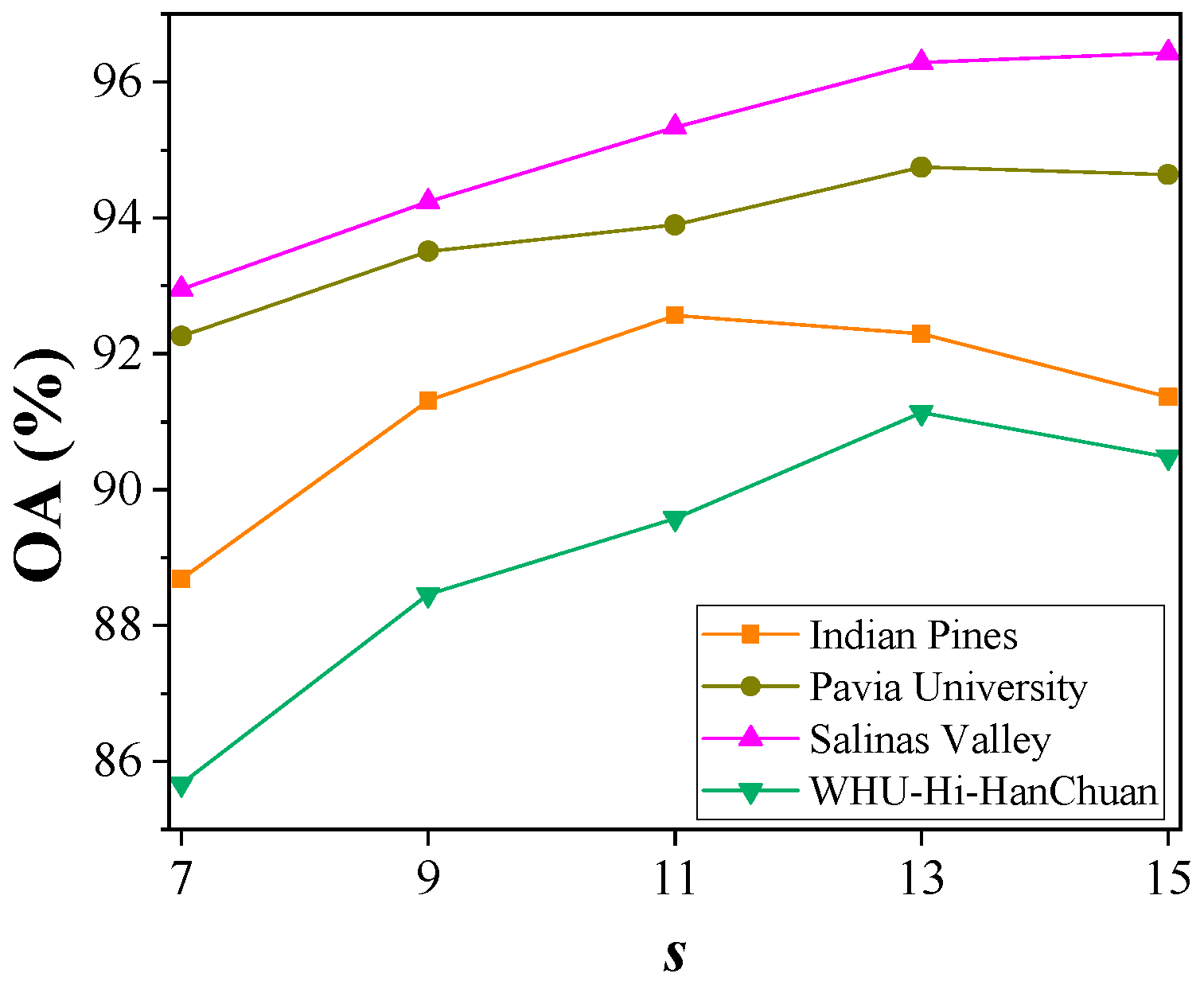
4.4. Hyperparameter Analysis
4.4.1. The Size of the Input Sample
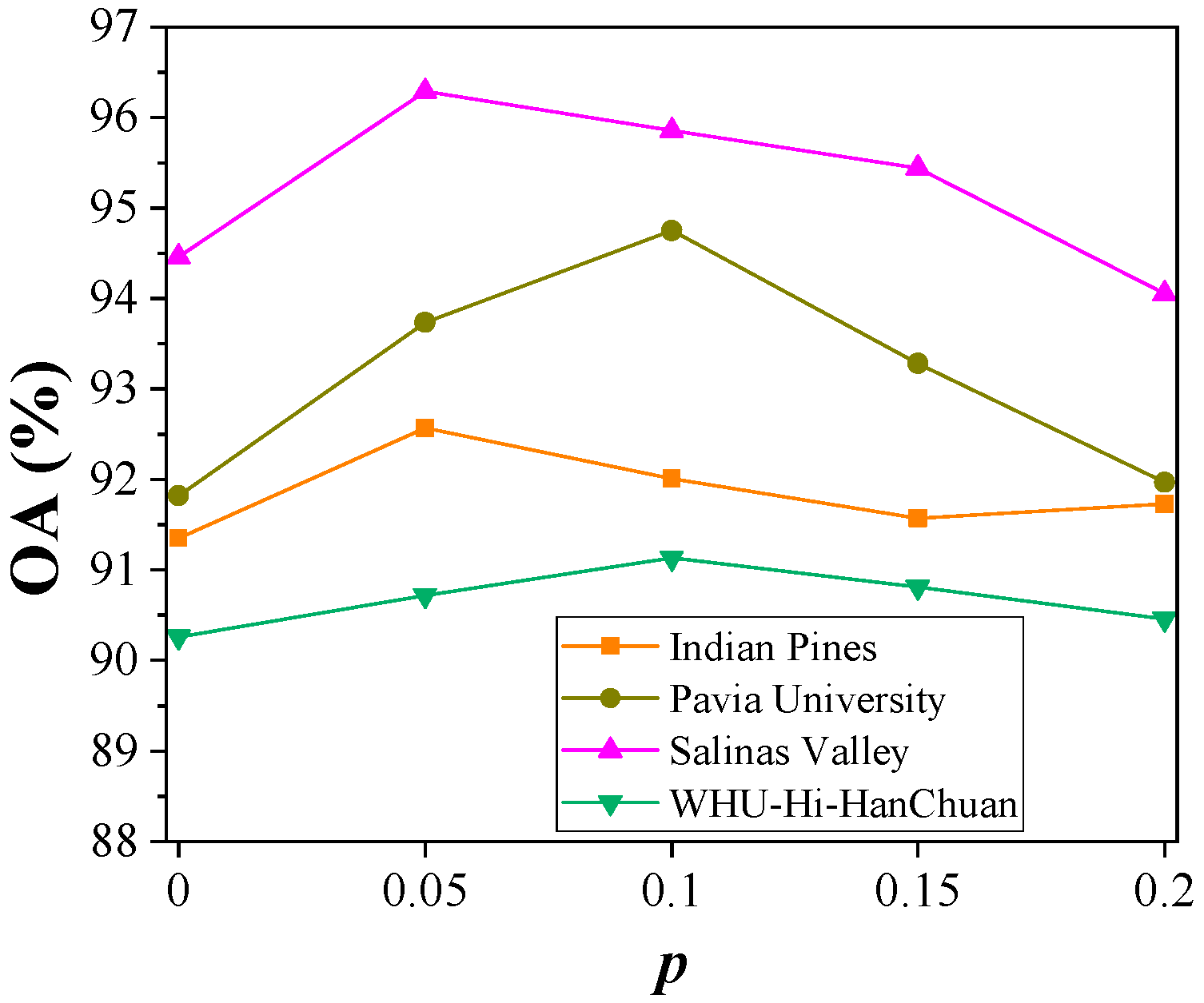
4.4.2. Dropout Probability
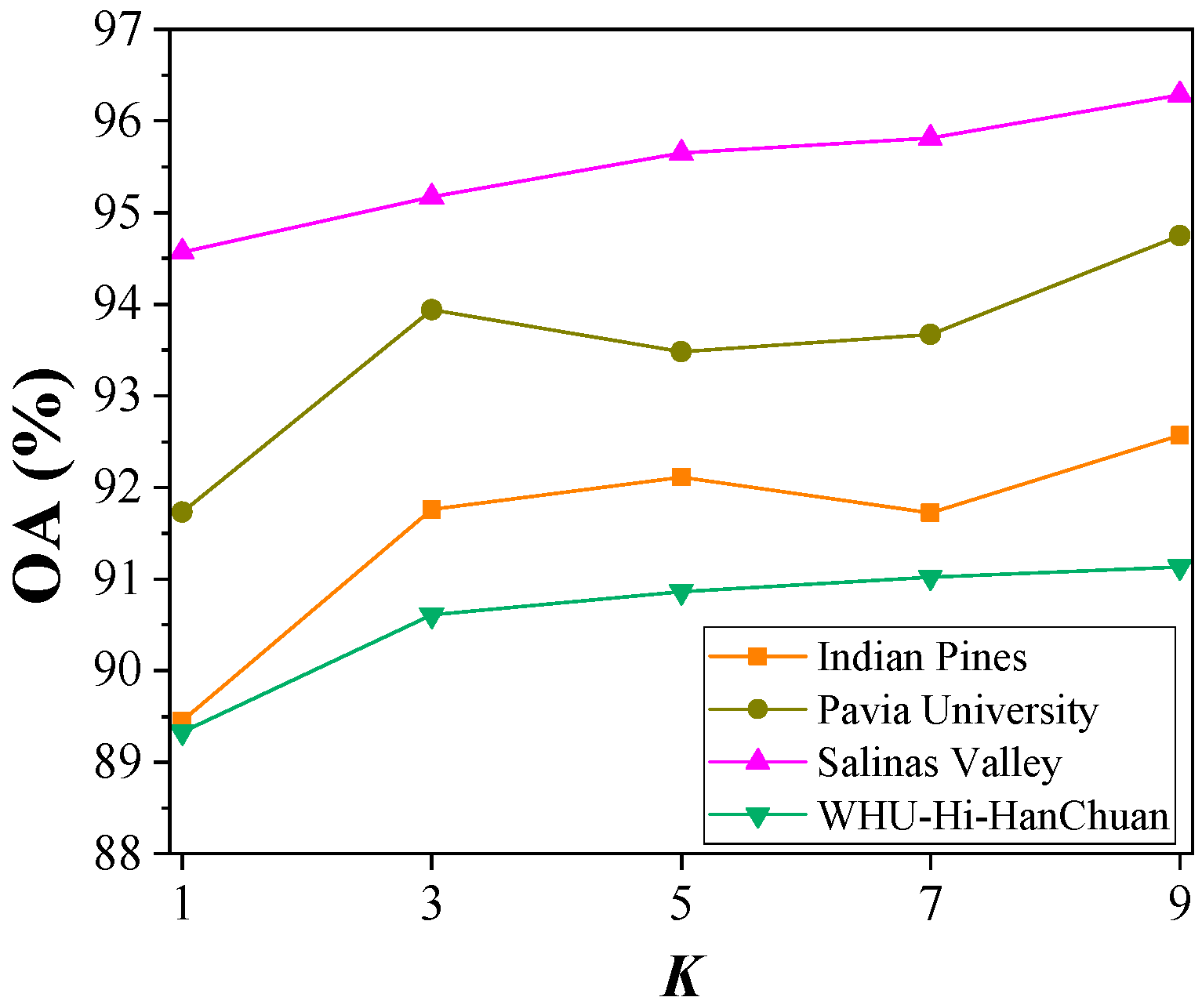
4.4.3. Number of Predictions
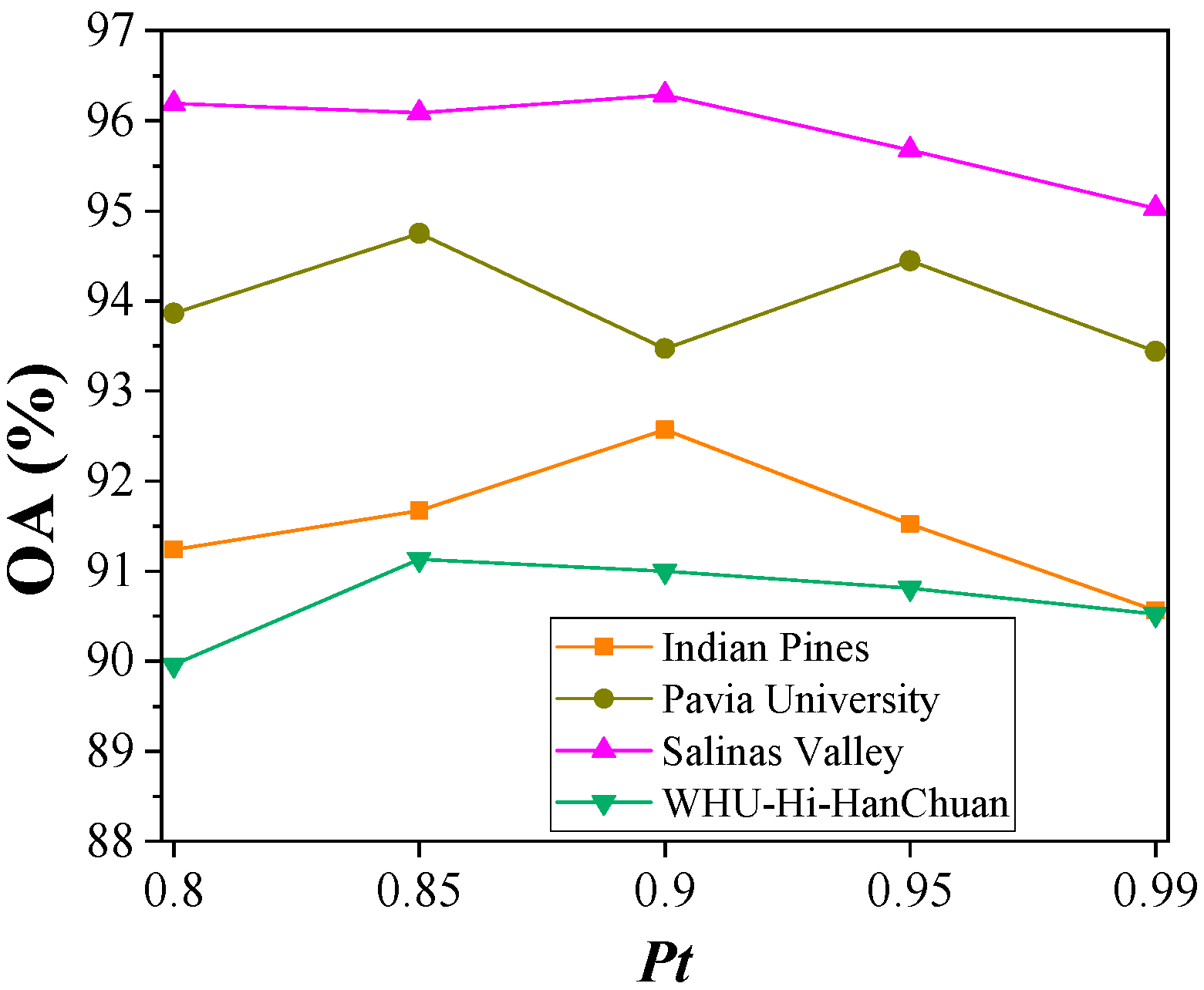
4.4.4. Probability Threshold
4.5. Discussion
4.5.1. Ablation Study
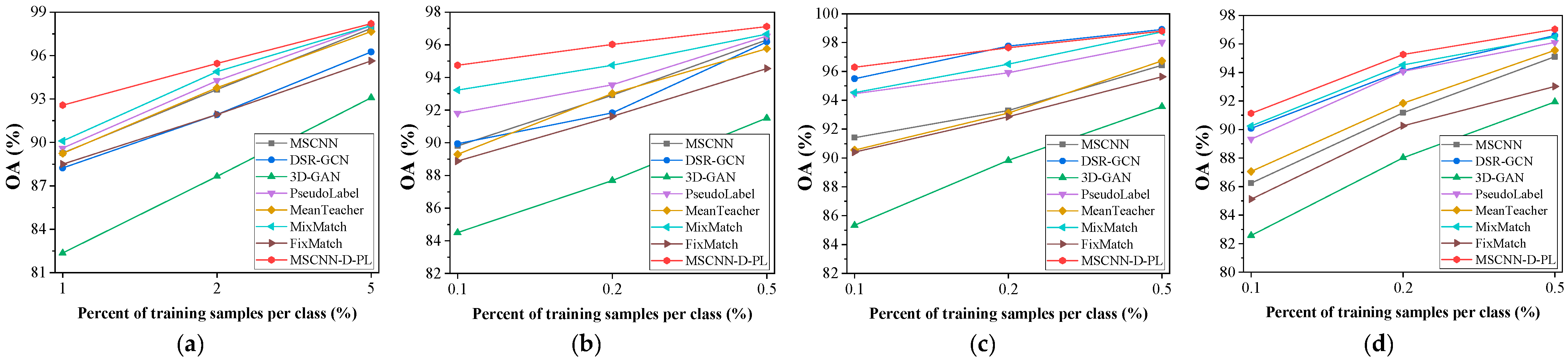
4.5.2. Accuracy Versus the Number of Training Samples
4.5.3. Complexity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Ribeiro, R.; Cruz, G.; Matos, J.; Bernardino, A. A Data Set for Airborne Maritime Surveillance Environments. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2720–2732. [Google Scholar] [CrossRef]
- Yokoya, N.; Chan, J.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef]
- McCann, C.; Repasky, K.S.; Lawrence, R.; Powell, S. Multi-Temporal Mesoscale Hyperspectral Data of Mixed Agricultural and Grassland Regions for Anomaly Detection. ISPRS J. Photogramm. Remote Sens. 2017, 131, 121–133. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An Adaptive Mean-Shift Analysis Approach for Object Extraction and Classification from Urban Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4173–4185. [Google Scholar] [CrossRef]
- Duan, P.; Hu, S.; Kang, X.; Li, S. Shadow Removal of Hyperspectral Remote Sensing Images with Multiexposure Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537211. [Google Scholar] [CrossRef]
- Duan, P.; Ghamisi, P.; Kang, X.; Rasti, B.; Li, S.; Gloaguen, R. Fusion of Dual Spatial Information for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7726–7738. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep Learning Classifiers for Hyperspectral Imaging: A Review. ISPRS J. Photogramm. Remote Sens. 2019, 158, 279–317. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral–Spatial Classification of Hyperspectral Image Based on Deep Auto-Encoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4073–4085. [Google Scholar]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schonlieb, C.-B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–Spatial Classification of Hyperspectral Images Using Deep Convolutional Neural Networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.; Han, J.; Yao, X.; Guo, L. Exploring Hierarchical Convolutional Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Ben Hamida, A.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep Pyramidal Residual Networks for Spectral–Spatial Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction with Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 755–769. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar]
- Ranjan, P.; Girdhar, A. A Comparison of Deep Learning Algorithms Dealing with Limited Samples in Hyperspectral Image Classification. In Proceedings of the 2022 OPJU International Technology Conference on Emerging Technologies for Sustainable Development (OTCON), Raigarh, Chhattisgarh, India, 8–10 February 2023; pp. 1–6. [Google Scholar]
- Huang, L.; Chen, Y. Dual-Path Siamese CNN for Hyperspectral Image Classification with Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2021, 18, 518–522. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, J.; Yang, J.; Geng, J. Data Augmentation and Spatial-Spectral Residual Framework for Hyperspectral Image Classification Using Limited Samples. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems (ICUS), Guangzhou, China, 28–30 October 2022; pp. 1–6. [Google Scholar]
- Xue, Z.; Zhang, M.; Liu, Y.; Du, P. Attention-Based Second-Order Pooling Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9600–9615. [Google Scholar]
- Duan, P.; Xie, Z.; Kang, X.; Li, S. Self-Supervised Learning-Based Oil Spill Detection of Hyperspectral Images. Sci. China Technol. Sci. 2022, 65, 793–801. [Google Scholar]
- Xue, Z.; Zhou, Y.; Du, P. S3Net: Spectral–Spatial Siamese Network for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531219. [Google Scholar] [CrossRef]
- Yang, X.; Song, Z.; King, I.; Xu, Z. A Survey on Deep Semi-Supervised Learning. IEEE Trans. Knowl. Data Eng. 2023, 35, 8934–8954. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27. [Google Scholar]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised Hyperspectral Image Classification Based on Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Clausi, D.A.; Wong, A. Generative Adversarial Networks and Conditional Random Fields for Hyperspectral Image Classification. IEEE Trans. Cybern. 2020, 50, 3318–3329. [Google Scholar]
- Büchel, J.; Ersoy, O. Ladder Networks for Semi-Supervised Hyperspectral Image Classification. arXiv 2018, arXiv:1812.01222. [Google Scholar] [CrossRef]
- Rasmus, A.; Valpola, H.; Honkala, M.; Berglund, M.; Raiko, T. Semi-Supervised Learning with Ladder Networks. In Proceedings of the 29th International Conference on Neural Information Processing Systems, Montreal, Canada, 7–12 December 2015; pp. 3546–3554. [Google Scholar]
- Qin, A.; Shang, Z.; Tian, J.; Wang, Y.; Zhang, T.; Tang, Y.Y. Spectral–Spatial Graph Convolutional Networks for Semisupervised Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2019, 16, 241–245. [Google Scholar] [CrossRef]
- Sha, A.; Wang, B.; Wu, X.; Zhang, L. Semisupervised Classification for Hyperspectral Images Using Graph Attention Networks. IEEE Geosci. Remote Sens. Lett. 2021, 18, 157–161. [Google Scholar] [CrossRef]
- Xie, Y.; Liang, Y.; Gong, M.; Qin, A.K.; Ong, Y.-S.; He, T. Semisupervised Graph Neural Networks for Graph Classification. IEEE Trans. Cybern. 2023, 53, 6222–6235. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Prasad, S. Semi-Supervised Deep Learning Using Pseudo Labels for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 1259–1270. [Google Scholar] [CrossRef]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J. Semi-Supervised Deep Learning Classification for Hyperspectral Image Based on Dual-Strategy Sample Selection. Remote Sens. 2018, 10, 574. [Google Scholar] [CrossRef]
- Kang, X.; Zhuo, B.; Duan, P. Semi-Supervised Deep Learning for Hyperspectral Image Classification. Remote Sens. Lett. 2019, 10, 353–362. [Google Scholar] [CrossRef]
- Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C. MixMatch: A Holistic Approach to Semi-Supervised Learning. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 5049–5059. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.-L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; pp. 596–608. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery Using a Dual-Channel Convolutional Neural Network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Chan, J.C.-W.; Yi, C. Hyperspectral Image Classification Using Two-Channel Deep Convolutional Neural Network. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5079–5082. [Google Scholar]
- Hao, S.; Wang, W.; Ye, Y.; Nie, T.; Bruzzone, L. Two-Stream Deep Architecture for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2349–2361. [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A New Deep Convolutional Neural Network for Fast Hyperspectral Image Classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar] [CrossRef]
- Vinod, N.; Geoffrey, E.H. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Bouthillier, X.; Konda, K.; Vincent, P.; Memisevic, R. Dropout as data augmentation. arXiv 2015, arXiv:1506.08700. [Google Scholar] [CrossRef]
- Zhao, D.; Yu, G.; Xu, P.; Luo, M. Equivalence between Dropout and Data Augmentation: A Mathematical Check. Neural Netw. 2019, 115, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://pytorch.org/ (accessed on 25 March 2023).
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-Borne Hyperspectral with High Spatial Resolution (H2) Benchmark Datasets and Classifier for Precise Crop Identification Based on Deep Convolutional Neural Network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-Borne Hyperspectral Remote Sensing: From Observation and Processing to Applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Xue, Z.; Liu, Z.; Zhang, M. DSR-GCN: Differentiated-Scale Restricted Graph Convolutional Network for Few-Shot Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504918. [Google Scholar] [CrossRef]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1195–1204. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Xue, Z.; Xu, Q.; Zhang, M. Local Transformer with Spatial Partition Restore for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4307–4325. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. RandAugment: Practical Automated Data Augmentation with a Reduced Search Space. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]

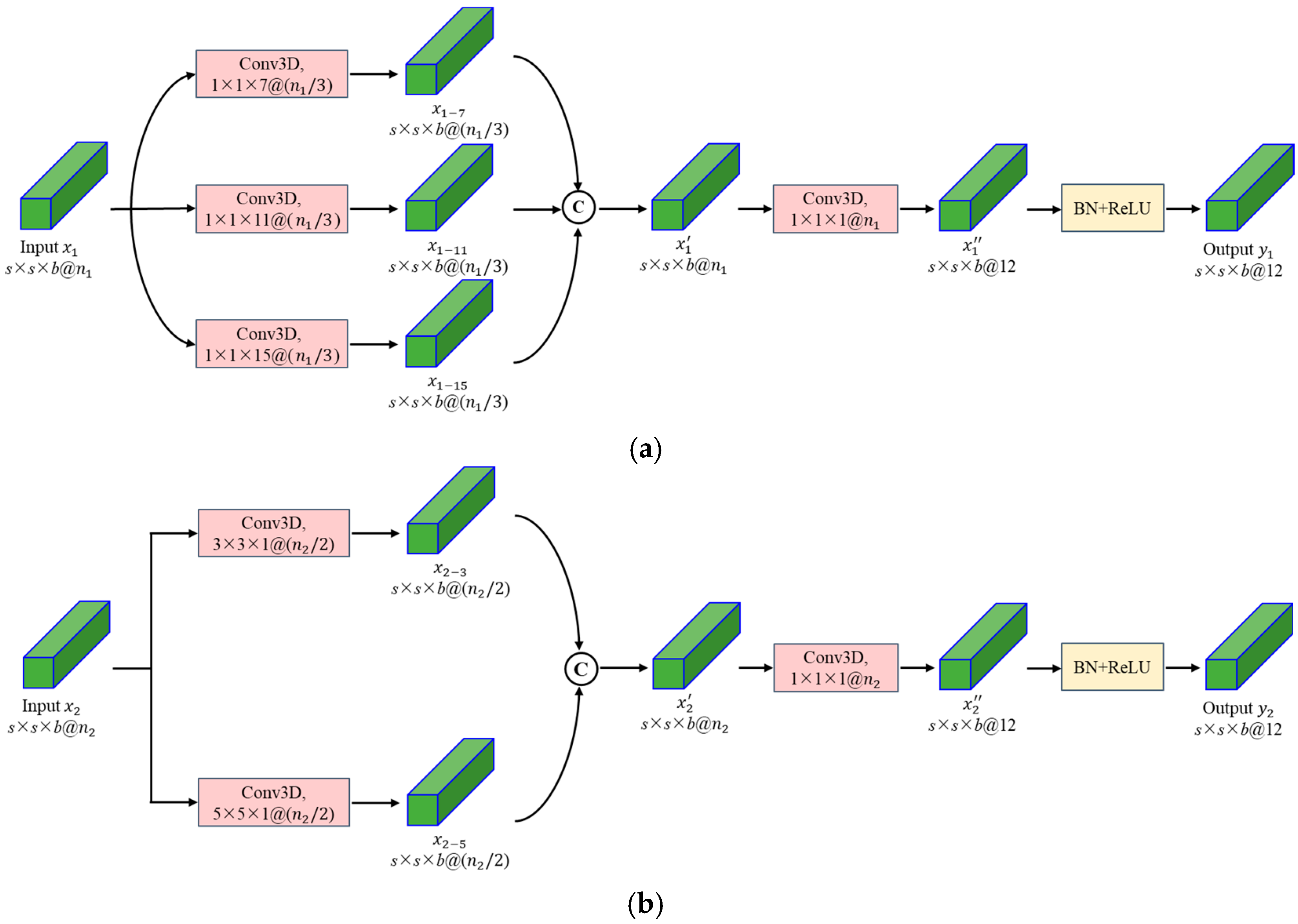
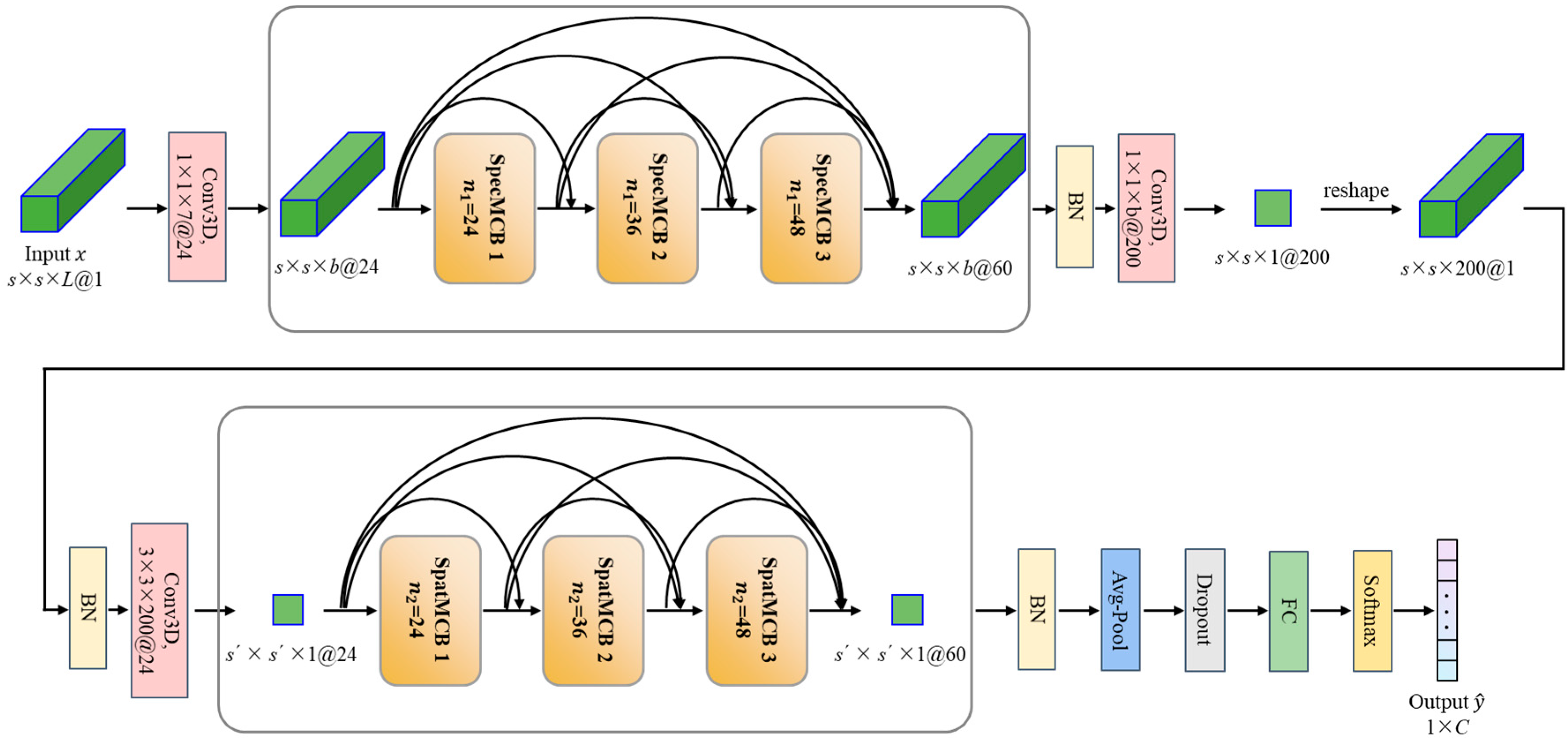



| Module | Input Size | Layer Type | Padding | Output Size | |
|---|---|---|---|---|---|
| Conv3D | (1, 9, 9, 200) | Conv3D (kernelsize = 1 × 1 × 7, stride = 1 × 1 × 2, dim = 24,) | N | (24, 9, 9, 97) | |
| Spectral multi-scale information extraction module | SpecMCB1 | (24, 9, 9, 97) | Parallel {Conv3D (kernelsize = 1 × 1 × 7, dim = 8), Conv3D (kernelsize = 1 × 1 × 11, dim = 8), Conv3D (kernelsize = 1 × 1 × 15, dim = 8)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 9, 9, 97) |
| SpecMCB2 | (36, 9, 9, 97) | Parallel {Conv3D (kernelsize = 1 × 1 × 7, dim = 12), Conv3D (kernelsize = 1 × 1 × 11, dim = 12), Conv3D (kernelsize = 1 × 1 × 15, dim = 12)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 9, 9, 97) | |
| SpecMCB3 | (48, 9, 9, 97) | Parallel {Conv3D (kernelsize = 1 × 1 × 7, dim = 16), Conv3D (kernelsize = 1 × 1 × 11, dim = 16), Conv3D (kernelsize = 1 × 1 × 15, dim = 16)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 9, 9, 97) | |
| Conv3D | (60, 9, 9, 97) | BN, Conv3D (kernelsize = 1 × 1 × 97, dim = 200) | N | (200, 9, 9, 1) | |
| Permute | (200, 9, 9, 1) | - | - | (1, 9, 9, 200) | |
| Conv3D | (1, 9, 9, 200) | BN, ReLU, Conv3D (kernelsize = 3 × 3 × 200, dim = 24) | N | (24, 7, 7, 1) | |
| Spatial multi-scale information extraction module | SpatMCB1 | (24, 7, 7, 1) | Parallel {Conv3D (kernelsize = 3 × 3 × 1, dim = 12), Conv3D (kernelsize = 5 × 5 × 1, dim = 12)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 7, 7, 1) |
| SpatMCB2 | (36, 7, 7, 1) | Parallel {Conv3D (kernelsize = 3 × 3 × 1, dim = 18), Conv3D (kernelsize = 5 × 5 × 1, dim = 18)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 7, 7, 1) | |
| SpatMCB3 | (48, 7, 7, 1) | Parallel {Conv3D (kernelsize = 3 × 3 × 1, dim = 24), Conv3D (kernelsize = 5 × 5 × 1, dim = 24)}, Concat, Conv3D (kernelsize = 1 × 1 × 1, dim = 12), BN, ReLU | Y | (12, 7, 7, 1) | |
| Avg-Pool | (60, 7, 7, 1) | GlobalAvgPooling, Flatten | - | (60) | |
| Dropout | (60,) | Dropout | - | (60) | |
| FC | (60,) | Fully Connected | - | (16) | |
| Dataset | Label | Class | Total Samples | Training Samples |
|---|---|---|---|---|
| Indian Pines | 1 | Alfalfa | 54 | 1 |
| 2 | Bldg-Grass-Trees-Drivers | 380 | 4 | |
| 3 | Corn | 234 | 2 | |
| 4 | Corn-mintill | 834 | 8 | |
| 5 | Corn-notill | 1434 | 14 | |
| 6 | Grass-pasture-mowed | 26 | 1 | |
| 7 | Grass-Pasture | 497 | 5 | |
| 8 | Grass-Trees | 747 | 7 | |
| 9 | Hay-windrowed | 489 | 5 | |
| 10 | Oats | 20 | 1 | |
| 11 | Soybean-clean | 614 | 6 | |
| 12 | Soybean-mintill | 2468 | 25 | |
| 13 | Soybean-notill | 968 | 10 | |
| 14 | Stone-Steel-Tower | 95 | 1 | |
| 15 | Wheat | 212 | 2 | |
| 16 | Woods | 1294 | 13 | |
| Total | 10,366 | 105 | ||
| Dataset | Label | Class | Total Samples | Training Samples |
|---|---|---|---|---|
| Pavia University | 1 | Asphalt | 6631 | 7 |
| 2 | Meadows | 18,649 | 19 | |
| 3 | Gravel | 2099 | 2 | |
| 4 | Trees | 3064 | 3 | |
| 5 | Metal sheets | 1345 | 1 | |
| 6 | Bare soil | 5029 | 5 | |
| 7 | Bitumen | 1330 | 1 | |
| 8 | Bricks | 3682 | 4 | |
| 9 | Shadows | 947 | 1 | |
| Total | 42,776 | 43 | ||
| Dataset | Label | Class | Total Samples | Training Samples |
|---|---|---|---|---|
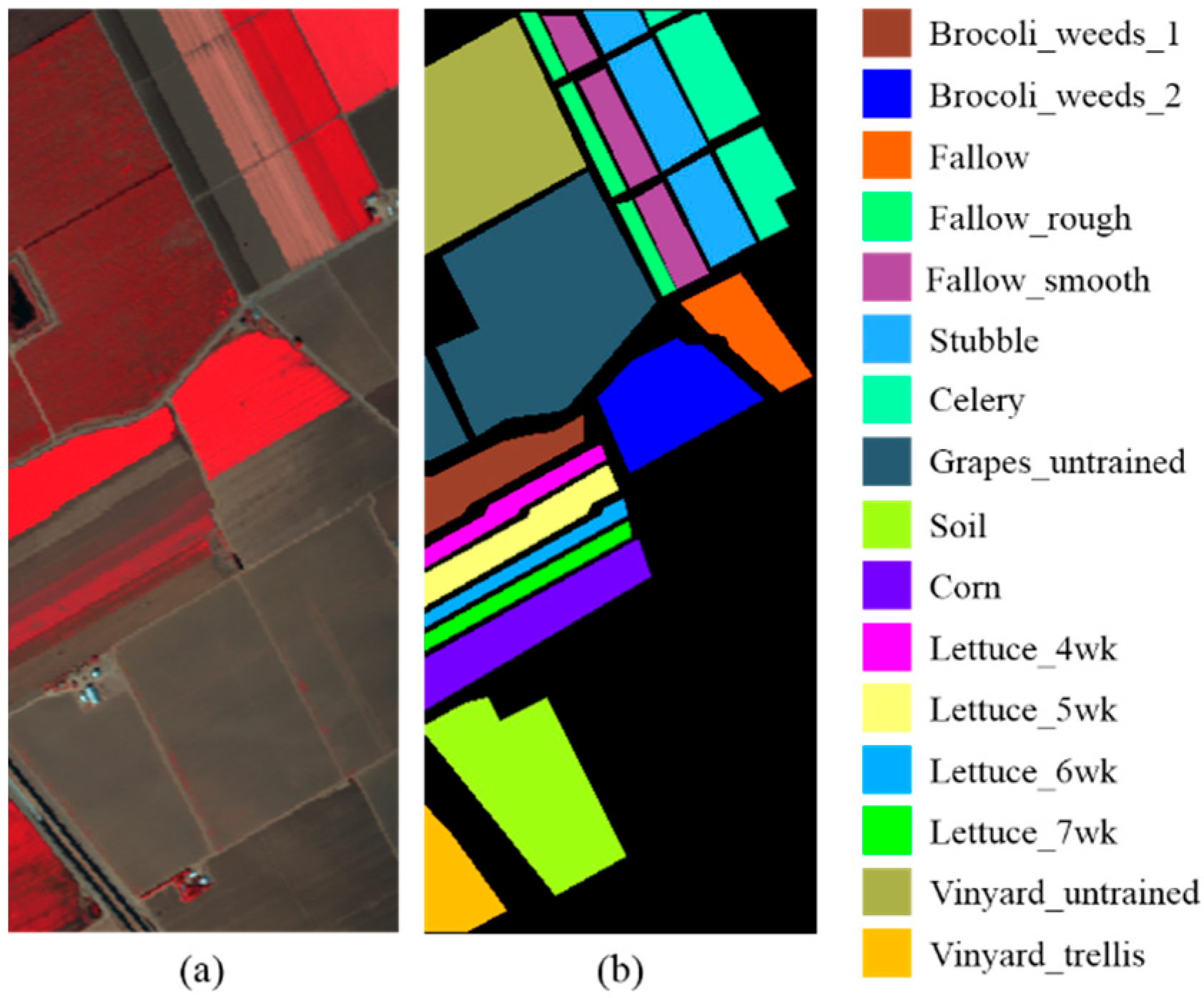
| Salinas Valley | 1 | Brocoli_weeds_1 | 2009 | 2 |
| 2 | Brocoli_weeds_2 | 3726 | 4 | |
| 3 | Fallow | 1976 | 2 | |
| 4 | Fallow_rough | 1394 | 1 | |
| 5 | Fallow_smooth | 2678 | 3 | |
| 6 | Stubble | 3959 | 4 | |
| 7 | Celery | 3579 | 4 | |
| 8 | Grapes_unstrained | 11,271 | 11 | |
| 9 | Soil | 6203 | 6 | |
| 10 | Corn | 3278 | 3 | |
| 11 | Lettuce_4wk | 1068 | 1 | |
| 12 | Lettuce_5wk | 1927 | 2 | |
| 13 | Lettuce_6wk | 916 | 1 | |
| 14 | Lettuce_7wk | 1070 | 1 | |
| 15 | Vinyard_unstrained | 7268 | 7 | |
| 16 | Vinyard_trellis | 1807 | 2 | |
| Total | 54,129 | 54 | ||
| Dataset | Label | Class | Total Samples | Training Samples |
|---|---|---|---|---|
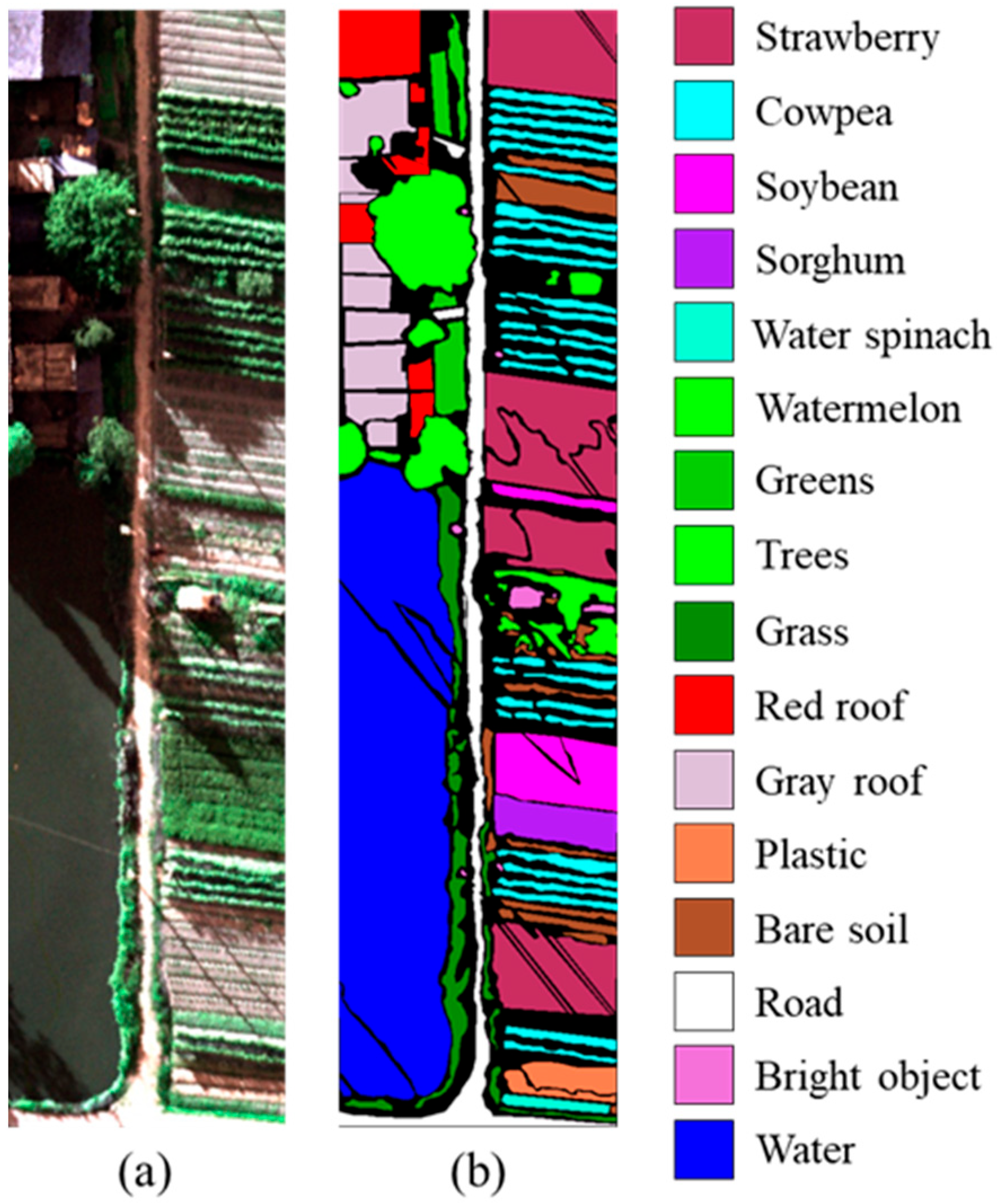
| WHU-Hi-HanChuan | 1 | Strawberry | 44,735 | 45 |
| 2 | Cowpea | 22,753 | 23 | |
| 3 | Soybean | 10,287 | 10 | |
| 4 | Sorghum | 5353 | 5 | |
| 5 | Water spinach | 1200 | 1 | |
| 6 | Watermelon | 4533 | 5 | |
| 7 | Greens | 5903 | 6 | |
| 8 | Trees | 17,978 | 18 | |
| 9 | Grass | 9469 | 9 | |
| 10 | Red roof | 10,516 | 11 | |
| 11 | Gray roof | 16,911 | 17 | |
| 12 | Plastic | 3679 | 4 | |
| 13 | Bare soil | 9116 | 9 | |
| 14 | Road | 18,560 | 19 | |
| 15 | Bright object | 1136 | 1 | |
| 16 | Water | 75,401 | 75 |
| Methods | Indian Pines | Pavia University | Salinas Valley | WHU-Hi-HanChuan | ||||
|---|---|---|---|---|---|---|---|---|
| OA (%) | Kappa (%) | OA (%) | OA (%) | OA (%) | Kappa (%) | OA (%) | Kappa (%) | |
| A-SPN | 84.77 ± 1.43 | 82.51 ± 1.67 | 74.46 ± 2.74 | 64.01 ± 4.37 | 77.65 ± 4.37 | 74.51 ± 5.08 | 82.16 ± 1.63 | 78.63 ± 2.01 |
| S3Net | 75.93 ± 2.17 | 72.68 ± 2.53 | 80.54 ± 2.67 | 74.08 ± 3.19 | 86.84 ± 1.58 | 85.37 ± 1.73 | 80.82 ± 2.96 | 77.42 ± 3.48 |
| SPRLT-Net | 57.40 ± 2.57 | 49.58 ± 3.41 | 68.47 ± 1.34 | 54.62 ± 2.52 | 60.35 ± 5.07 | 54.67 ± 5.97 | 72.63 ± 1.74 | 67.35 ± 2.17 |
| FDSSC | 86.07 ± 2.41 | 84.04 ± 2.48 | 87.21 ± 1.71 | 82.62 ± 2.08 | 89.03 ± 1.68 | 87.77 ± 1.69 | 84.61 ± 1.83 | 81.85 ± 2.23 |
| MSCNN | 89.26 ± 1.21 | 87.77 ± 1.26 | 89.81 ± 1.47 | 85.91 ± 1.89 | 91.41 ± 1.81 | 90.37 ± 1.82 | 86.24 ± 0.98 | 83.83 ± 1.15 |
| ID | Augmentation Operations | Changing the Spectral Value or Not | Adopted or Not |
|---|---|---|---|
| 1 | AutoContrast | √ | √ |
| 2 | Brightness | √ | √ |
| 3 | Color | √ | √ |
| 4 | Contrast | √ | √ |
| 5 | Equalize | √ | × |
| 6 | Identity | × | √ |
| 7 | Posterize | √ | × |
| 8 | Rotate | × | √ |
| 9 | Sharpness | √ | √ |
| 10 | ShearX | × | √ |
| 11 | ShearY | × | √ |
| 12 | Solarize | √ | √ |
| 13 | TranslateX | × | √ |
| 14 | TranslateY | × | √ |
| Dataset | Indian Pines | Pavia University | Salinas Valley | WHU-Hi-HanChuan | |||||
|---|---|---|---|---|---|---|---|---|---|
| Model | FDSSC | MSCNN | FDSSC | MSCNN | FDSSC | FDSSC | MSCNN | FDSSC | |
| Augmentation Type | NoAug | 86.07 ± 2.41 | 89.26 ± 1.21 | 87.21 ± 1.71 | 89.81 ± 1.47 | 89.03 ± 1.68 | 91.41 ± 1.81 | 84.61 ± 1.83 | 86.24 ± 0.98 |
| Aug+ | 85.95 ± 1.86 | 89.40 ± 1.07 | 87.36 ± 1.47 | 89.72 ± 1.23 | 89.11 ± 1.43 | 91.33 ± 1.52 | 84.26 ± 1.43 | 86.15 ± 0.82 | |
| Aug++ | 82.15 ± 3.66 | 86.18 ± 2.35 | 82.01 ± 3.85 | 85.73 ± 1.96 | 85.64 ± 3.19 | 89.26 ± 2.18 | 81.57 ± 2.69 | 83.72 ± 1.87 | |
| Accuracy Metric | Label | Methods | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSCNN | DSR-GCN | 3D-GAN | PseudoLabel | MeanTeacher | MixMatch | FixMatch | MSCNN-D-PL | ||
| PA (%) | 1 | 77.86 ± 4.79 | 83.58 ± 19.06 | 50.49 ± 9.16 | 76.94 ± 4.56 | 75.15 ± 3.09 | 75.14 ± 6.53 | 73.23 ± 2.42 | 82.83 ± 2.38 |
| 2 | 71.52 ± 2.23 | 87.67 ± 8.47 | 51.56 ± 4.36 | 70.72 ± 1.81 | 70.64 ± 1.26 | 71.89 ± 2.49 | 68.06 ± 1.91 | 80.84 ± 1.67 | |
| 3 | 76.32 ± 2.47 | 79.87 ± 8.88 | 55.53 ± 3.05 | 74.55 ± 2.29 | 73.95 ± 2.94 | 77.07 ± 2.63 | 69.70 ± 4.29 | 80.07 ± 2.57 | |
| 4 | 79.80 ± 1.83 | 83.32 ± 8.99 | 67.14 ± 2.88 | 80.44 ± 1.66 | 79.65 ± 1.50 | 80.86 ± 1.29 | 78.05 ± 1.14 | 85.55 ± 1.15 | |
| 5 | 85.64 ± 0.84 | 86.21 ± 5.20 | 77.29 ± 0.76 | 85.50 ± 0.76 | 84.98 ± 0.80 | 86.61 ± 1.05 | 84.24 ± 1.09 | 89.69 ± 0.86 | |
| 6 | 85.06 ± 5.39 | 100.00 ± 0.00 | 65.35 ± 12.96 | 85.66 ± 5.93 | 83.82 ± 8.33 | 89.38 ± 5.39 | 86.01 ± 5.51 | 90.21 ± 3.80 | |
| 7 | 94.17 ± 1.26 | 79.72 ± 11.12 | 90.63 ± 1.81 | 94.81 ± 0.90 | 94.63 ± 1.37 | 96.07 ± 0.91 | 93.78 ± 0.62 | 96.25 ± 0.85 | |
| 8 | 97.85 ± 0.56 | 95.95 ± 1.90 | 96.54 ± 1.50 | 98.11 ± 0.62 | 97.56 ± 0.56 | 98.07 ± 0.76 | 97.72 ± 1.03 | 98.50 ± 0.39 | |
| 9 | 98.34 ± 0.45 | 98.64 ± 2.23 | 98.81 ± 0.57 | 98.75 ± 0.35 | 98.91 ± 0.41 | 98.90 ± 0.50 | 98.81 ± 0.37 | 99.16 ± 0.32 | |
| 10 | 74.30 ± 9.88 | 79.47 ± 27.60 | 53.05 ± 7.79 | 75.91 ± 6.33 | 74.45 ± 11.57 | 80.22 ± 10.00 | 69.55 ± 10.10 | 89.09 ± 5.57 | |
| 11 | 82.65 ± 2.19 | 77.06 ± 18.17 | 68.52 ± 3.63 | 84.20 ± 1.51 | 83.64 ± 1.29 | 85.75 ± 1.49 | 82.51 ± 2.37 | 90.30 ± 1.50 | |
| 12 | 91.07 ± 0.84 | 90.57 ± 7.28 | 85.77 ± 1.14 | 91.84 ± 0.42 | 91.21 ± 0.83 | 91.59 ± 0.41 | 90.70 ± 0.82 | 93.90 ± 0.44 | |
| 13 | 87.31 ± 1.04 | 79.00 ± 5.75 | 79.85 ± 1.89 | 87.69 ± 1.16 | 87.99 ± 0.96 | 88.73 ± 1.59 | 87.23 ± 1.36 | 91.40 ± 0.69 | |
| 14 | 87.69 ± 1.76 | 92.98 ± 10.36 | 83.48 ± 4.66 | 87.85 ± 1.87 | 87.84 ± 1.13 | 88.93 ± 2.77 | 87.66 ± 1.74 | 90.62 ± 3.28 | |
| 15 | 98.81 ± 0.67 | 96.90 ± 2.32 | 96.29 ± 2.47 | 98.80 ± 0.47 | 99.04 ± 0.69 | 98.59 ± 0.79 | 98.54 ± 0.74 | 99.31 ± 0.51 | |
| 16 | 97.11 ± 0.53 | 96.24 ± 8.63 | 95.75 ± 1.31 | 97.20 ± 0.35 | 97.09 ± 0.59 | 97.17 ± 0.72 | 97.07 ± 0.54 | 97.66 ± 0.28 | |
| OA (%) | 89.26 ± 1.21 | 88.23 ± 3.72 | 82.35 ± 1.49 | 89.61 ± 1.33 | 89.24 ± 1.61 | 90.10 ± 1.47 | 88.50 ± 2.23 | 92.57 ± 0.79 | |
| Kappa (%) | 87.77 ± 1.26 | 86.62 ± 4.14 | 79.76 ± 1.56 | 88.13 ± 1.53 | 87.82 ± 1.65 | 88.67 ± 1.50 | 86.86 ± 2.30 | 91.52 ± 0.92 | |
| Accuracy Metric | Label | Methods | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSCNN | DSR-GCN | 3D-GAN | PseudoLabel | MeanTeacher | MixMatch | FixMatch | MSCNN-D-PL | ||
| PA (%) | 1 | 87.81 ± 2.33 | 91.43 ± 7.38 | 84.23 ± 2.69 | 90.69 ± 0.91 | 88.43 ± 3.70 | 92.41 ± 0.65 | 87.94 ± 1.79 | 94.00 ± 0.29 |
| 2 | 98.22 ± 0.44 | 95.85 ± 4.75 | 95.95 ± 1.62 | 98.66 ± 0.15 | 97.81 ± 0.61 | 98.79 ± 0.14 | 97.77 ± 0.75 | 99.10 ± 0.08 | |
| 3 | 64.93 ± 5.87 | 68.38 ± 21.18 | 55.48 ± 11.54 | 69.49 ± 3.62 | 59.06 ± 7.21 | 73.31 ± 1.99 | 58.25 ± 6.27 | 78.41 ± 1.15 | |
| 4 | 89.40 ± 2.73 | 65.39 ± 17.45 | 80.57 ± 6.87 | 92.16 ± 1.39 | 89.44 ± 1.05 | 94.54 ± 0.63 | 87.77 ± 2.33 | 96.03 ± 0.32 | |
| 5 | 97.66 ± 1.27 | 99.53 ± 1.01 | 87.52 ± 12.22 | 98.61 ± 0.45 | 97.14 ± 3.16 | 99.22 ± 0.40 | 96.89 ± 5.04 | 99.43 ± 0.06 | |
| 6 | 72.88 ± 4.79 | 95.90 ± 6.56 | 62.38 ± 10.51 | 82.37 ± 1.33 | 73.77 ± 3.28 | 86.09 ± 1.20 | 72.73 ± 3.52 | 88.96 ± 0.69 | |
| 7 | 58.01 ± 11.37 | 83.43 ± 25.94 | 51.60 ± 14.02 | 66.86 ± 4.19 | 55.88 ± 11.93 | 73.03 ± 2.71 | 57.22 ± 7.37 | 81.61 ± 1.18 | |
| 8 | 88.80 ± 2.35 | 90.75 ± 10.18 | 83.76 ± 4.09 | 88.12 ± 1.97 | 87.68 ± 3.35 | 90.33 ± 1.41 | 87.45 ± 3.16 | 91.99 ± 0.50 | |
| 9 | 99.73 ± 0.15 | 50.94 ± 16.04 | 99.44 ± 0.29 | 99.79 ± 0.14 | 99.66 ± 0.14 | 99.85 ± 0.13 | 99.83 ± 0.08 | 99.84 ± 0.12 | |
| OA (%) | 89.81 ± 1.47 | 89.94 ± 2.37 | 84.50 ± 1.33 | 91.82 ± 1.49 | 89.30 ± 1.53 | 93.23 ± 1.39 | 88.88 ± 1.86 | 94.75 ± 1.93 | |
| Kappa (%) | 85.91 ± 1.89 | 86.65 ± 3.00 | 78.86 ± 1.84 | 89.19 ± 1.96 | 85.31 ± 1.92 | 90.97 ± 1.46 | 84.76 ± 2.12 | 93.03 ± 2.55 | |
| Accuracy Metric | Label | Methods | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSCNN | DSR-GCN | 3D-GAN | PseudoLabel | MeanTeacher | MixMatch | FixMatch | MSCNN-D-PL | ||
| PA (%) | 1 | 97.12 ± 2.14 | 100.00 ± 0.00 | 94.22 ± 4.25 | 98.26 ± 1.28 | 97.13 ± 2.11 | 98.27 ± 1.52 | 96.80 ± 2.26 | 98.97 ± 1.11 |
| 2 | 99.36 ± 1.85 | 100.00 ± 0.00 | 97.99 ± 3.00 | 99.61 ± 0.95 | 99.27 ± 1.74 | 99.58 ± 1.17 | 99.20 ± 2.00 | 99.74 ± 0.97 | |
| 3 | 94.40 ± 2.27 | 90.12 ± 15.84 | 86.70 ± 7.71 | 96.37 ± 1.42 | 93.64 ± 2.11 | 96.58 ± 1.64 | 93.82 ± 2.63 | 97.80 ± 1.13 | |
| 4 | 98.21 ± 1.99 | 82.20 ± 21.04 | 96.68 ± 3.53 | 98.90 ± 1.25 | 98.08 ± 2.01 | 98.95 ± 1.33 | 97.90 ± 2.40 | 99.18 ± 1.12 | |
| 5 | 98.71 ± 1.89 | 94.01 ± 5.22 | 98.31 ± 2.58 | 99.16 ± 1.07 | 98.68 ± 1.73 | 99.23 ± 1.28 | 98.63 ± 2.07 | 99.36 ± 1.02 | |
| 6 | 99.67 ± 1.84 | 99.58 ± 0.28 | 99.45 ± 2.50 | 99.81 ± 0.94 | 99.72 ± 1.72 | 99.77 ± 1.16 | 99.53 ± 2.01 | 99.86 ± 0.95 | |
| 7 | 99.47 ± 1.85 | 99.93 ± 0.09 | 98.68 ± 2.75 | 99.62 ± 0.99 | 99.52 ± 1.75 | 99.62 ± 1.21 | 99.32 ± 2.04 | 99.82 ± 0.98 | |
| 8 | 88.17 ± 2.31 | 96.37 ± 3.49 | 74.03 ± 4.79 | 92.62 ± 1.42 | 86.49 ± 1.99 | 92.67 ± 1.63 | 86.49 ± 2.44 | 95.05 ± 1.44 | |
| 9 | 99.13 ± 1.77 | 100.00 ± 0.00 | 99.01 ± 2.64 | 99.44 ± 0.97 | 99.15 ± 1.65 | 99.40 ± 1.16 | 98.97 ± 1.98 | 99.63 ± 0.96 | |
| 10 | 89.96 ± 2.09 | 88.40 ± 12.18 | 80.07 ± 5.73 | 93.38 ± 1.53 | 88.51 ± 2.20 | 93.50 ± 1.70 | 88.74 ± 2.60 | 95.62 ± 1.51 | |
| 11 | 90.24 ± 2.46 | 99.39 ± 0.56 | 87.91 ± 3.47 | 93.71 ± 1.48 | 90.09 ± 2.34 | 93.56 ± 1.61 | 89.76 ± 2.72 | 95.81 ± 1.78 | |
| 12 | 96.38 ± 1.97 | 90.59 ± 13.95 | 92.87 ± 3.66 | 97.89 ± 1.18 | 96.07 ± 1.82 | 97.71 ± 1.41 | 95.87 ± 2.20 | 98.42 ± 1.12 | |
| 13 | 98.13 ± 2.03 | 81.01 ± 16.10 | 98.06 ± 2.80 | 98.91 ± 1.27 | 98.20 ± 1.94 | 98.80 ± 1.35 | 97.97 ± 2.17 | 99.30 ± 1.08 | |
| 14 | 94.44 ± 2.12 | 78.97 ± 21.72 | 91.21 ± 3.95 | 96.45 ± 1.28 | 93.81 ± 2.36 | 96.53 ± 1.57 | 94.22 ± 2.44 | 97.67 ± 1.26 | |
| 15 | 67.30 ± 2.28 | 96.43 ± 3.95 | 56.55 ± 4.82 | 78.63 ± 2.33 | 64.91 ± 2.24 | 79.07 ± 2.65 | 64.22 ± 2.25 | 85.58 ± 2.12 | |
| 16 | 97.52 ± 2.14 | 90.37 ± 10.30 | 91.87 ± 4.98 | 98.81 ± 1.08 | 97.29 ± 2.33 | 98.68 ± 1.22 | 97.29 ± 2.31 | 99.21 ± 1.07 | |
| OA (%) | 91.41 ± 1.81 | 95.50 ± 1.85 | 85.33 ± 2.76 | 94.46 ± 1.28 | 90.55 ± 1.74 | 94.53 ± 1.49 | 90.40 ± 2.02 | 96.29 ± 1.15 | |
| Kappa (%) | 90.37 ± 1.82 | 95.00 ± 2.06 | 83.62 ± 2.71 | 93.84 ± 1.43 | 89.44 ± 1.76 | 93.91 ± 1.54 | 89.29 ± 2.04 | 95.87 ± 1.28 | |
| Accuracy Metric | Label | Methods | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MSCNN | DSR-GCN | 3D-GAN | PseudoLabel | MeanTeacher | MixMatch | FixMatch | MSCNN-D-PL | ||
| PA (%) | 1 | 97.16 ± 0.12 | 97.61 ± 1.68 | 95.89 ± 1.13 | 97.90 ± 0.06 | 97.49 ± 0.05 | 98.07 ± 0.06 | 96.91 ± 0.09 | 98.23 ± 0.11 |
| 2 | 84.45 ± 1.39 | 85.88 ± 3.41 | 77.05 ± 1.15 | 88.15 ± 1.34 | 85.49 ± 1.25 | 89.13 ± 1.24 | 82.74 ± 1.23 | 90.20 ± 0.71 | |
| 3 | 74.63 ± 1.66 | 87.87 ± 6.52 | 67.96 ± 1.67 | 79.72 ± 1.40 | 76.10 ± 1.35 | 81.75 ± 1.35 | 71.63 ± 1.66 | 83.54 ± 1.18 | |
| 4 | 96.33 ± 0.22 | 94.20 ± 2.21 | 94.09 ± 1.33 | 97.09 ± 0.15 | 96.56 ± 0.36 | 97.28 ± 0.20 | 95.89 ± 0.26 | 97.72 ± 0.17 | |
| 5 | 18.17 ± 1.33 | 37.61 ± 21.62 | 5.67 ± 1.42 | 35.92 ± 1.48 | 22.85 ± 1.78 | 40.67 ± 1.33 | 11.20 ± 2.37 | 46.28 ± 1.13 | |
| 6 | 22.05 ± 2.56 | 70.37 ± 14.73 | 12.07 ± 2.47 | 39.11 ± 1.43 | 26.18 ± 1.68 | 43.25 ± 1.33 | 15.85 ± 2.59 | 48.90 ± 1.36 | |
| 7 | 86.46 ± 1.65 | 87.56 ± 13.10 | 81.52 ± 1.30 | 89.17 ± 0.54 | 86.86 ± 1.33 | 89.65 ± 1.47 | 84.31 ± 1.47 | 90.91 ± 1.32 | |
| 8 | 81.85 ± 1.40 | 83.65 ± 5.07 | 74.53 ± 1.88 | 86.35 ± 1.22 | 83.06 ± 1.37 | 86.95 ± 1.11 | 79.97 ± 1.46 | 88.38 ± 1.28 | |
| 9 | 69.38 ± 2.63 | 74.03 ± 5.01 | 57.50 ± 2.23 | 75.44 ± 1.74 | 68.75 ± 2.09 | 77.54 ± 1.99 | 63.80 ± 2.06 | 79.52 ± 1.49 | |
| 10 | 89.48 ± 1.73 | 79.26 ± 13.10 | 85.13 ± 1.51 | 91.66 ± 1.51 | 89.73 ± 1.31 | 92.23 ± 0.98 | 88.46 ± 1.87 | 93.20 ± 0.84 | |
| 11 | 77.93 ± 1.76 | 96.23 ± 3.26 | 74.60 ± 2.17 | 82.60 ± 1.01 | 79.43 ± 1.87 | 84.11 ± 1.48 | 76.63 ± 1.73 | 85.36 ± 1.32 | |
| 12 | 17.42 ± 1.20 | 76.23 ± 28.27 | 4.93 ± 3.46 | 35.13 ± 2.10 | 22.21 ± 2.08 | 40.14 ± 2.03 | 10.42 ± 2.22 | 46.13 ± 1.06 | |
| 13 | 50.22 ± 1.97 | 62.65 ± 10.56 | 42.07 ± 1.58 | 60.34 ± 1.65 | 53.49 ± 2.55 | 64.08 ± 1.81 | 46.47 ± 1.96 | 67.78 ± 1.44 | |
| 14 | 84.76 ± 1.45 | 83.69 ± 7.73 | 78.69 ± 1.55 | 88.29 ± 1.29 | 85.57 ± 1.41 | 88.92 ± 1.17 | 83.10 ± 1.30 | 90.09 ± 1.21 | |
| 15 | 59.58 ± 2.84 | 21.25 ± 12.30 | 30.77 ± 3.18 | 70.81 ± 1.57 | 62.89 ± 2.30 | 72.20 ± 1.17 | 51.51 ± 2.34 | 75.95 ± 1.65 | |
| 16 | 99.53 ± 0.04 | 99.34 ± 0.40 | 99.39 ± 0.05 | 99.66 ± 0.03 | 99.59 ± 0.04 | 99.67 ± 0.01 | 99.49 ± 0.04 | 99.71 ± 0.03 | |
| OA (%) | 86.24 ± 0.98 | 90.07 ± 1.17 | 82.57 ± 1.76 | 89.33 ± 1.06 | 87.06 ± 1.12 | 90.25 ± 0.86 | 85.11 ± 1.63 | 91.13 ± 0.55 | |
| Kappa (%) | 83.83 ± 1.15 | 88.35 ± 1.37 | 79.38 ± 1.91 | 87.42 ± 1.15 | 84.71 ± 1.09 | 88.51 ± 0.79 | 82.40 ± 1.76 | 89.58 ± 0.65 | |
| Method | Indian Pines | Pavia University | Salinas Valley | WHU-Hi-HanChuan | ||||
|---|---|---|---|---|---|---|---|---|
| OA (%) | Kappa (%) | OA (%) | Kappa (%) | OA (%) | Kappa (%) | OA (%) | Kappa (%) | |
| FDSSC (baseline) | 86.07 ± 2.41 | 84.04 ± 2.48 | 87.21 ± 1.71 | 82.62 ± 2.08 | 89.03 ± 1.68 | 87.77 ± 1.69 | 84.61 ± 1.83 | 81.85 ± 2.23 |
| baseline + MS (MSCNN) | 89.26 ± 1.21 | 87.77 ± 1.26 | 89.81 ± 1.47 | 85.91 ± 1.89 | 91.41 ± 1.81 | 90.37 ± 1.82 | 86.24 ± 0.98 | 83.83 ± 1.15 |
| Baseline + MS + D-PL (MSCNN-D-PL) | 92.57 ± 0.79 | 91.52 ± 0.92 | 94.75 ± 1.93 | 93.03 ± 2.55 | 96.29 ± 1.15 | 95.87 ± 1.28 | 91.13 ± 0.55 | 89.58 ± 0.65 |
| Dataset | Stage | # Samples | Methods | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSCNN | DSR-GCN | 3D-GAN | PseudoLabel | MeanTeacher | MixMatch | FixMatch | MSCNN-D-PL | |||
| Indian Pines | Train | 105 | 215.86 | 66.65 | 428.23 | 232.52 | 390.26 | 400.52 | 405.77 | 393.38 |
| Test | 10,261 | 2.38 | 0.41 | 1.29 | 2.40 | 2.36 | 2.43 | 2.33 | 2.32 | |
| Parameters | 2.31 | 0.33 | 4.28 | 2.31 | 2.31 | 2.31 | 2.31 | 2.31 | ||
| Pavia University | Train | 43 | 35.96 | 110.19 | 106.41 | 38.03 | 61.58 | 64.62 | 68.49 | 62.23 |
| Test | 42,733 | 5.63 | 0.31 | 2.64 | 5.66 | 5.70 | 5.61 | 5.60 | 5.68 | |
| Parameters | 1.20 | 3.64 | 2.23 | 1.20 | 1.20 | 1.20 | 1.20 | 1.20 | ||
| Salinas Valley | Train | 54 | 123.33 | 193.63 | 243.89 | 129.52 | 185.59 | 189.43 | 191.30 | 184.95 |
| Test | 54,075 | 13.20 | 0.19 | 6.91 | 13.18 | 13.11 | 13.21 | 13.23 | 13.14 | |
| Parameters | 2.36 | 0.38 | 4.37 | 2.36 | 2.36 | 2.36 | 2.36 | 2.36 | ||
| WHU-Hi-HanChuan | Train | 258 | 1799.04 | 722.78 | 2975.71 | 1851.84 | 2306.44 | 2311.96 | 2348.55 | 2257.07 |
| Test | 257,272 | 91.72 | 0.80 | 44.83 | 92.03 | 91.85 | 92.38 | 91.67 | 91.53 | |
| Parameters | 3.16 | 0.29 | 5.85 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Liu, Z.; Guan, R.; Zhao, H. A Semi-Supervised Multi-Scale Convolutional Neural Network for Hyperspectral Image Classification with Limited Labeled Samples. Remote Sens. 2025, 17, 3273. https://doi.org/10.3390/rs17193273
Yang C, Liu Z, Guan R, Zhao H. A Semi-Supervised Multi-Scale Convolutional Neural Network for Hyperspectral Image Classification with Limited Labeled Samples. Remote Sensing. 2025; 17(19):3273. https://doi.org/10.3390/rs17193273
Chicago/Turabian StyleYang, Chen, Zizhuo Liu, Renchu Guan, and Haishi Zhao. 2025. "A Semi-Supervised Multi-Scale Convolutional Neural Network for Hyperspectral Image Classification with Limited Labeled Samples" Remote Sensing 17, no. 19: 3273. https://doi.org/10.3390/rs17193273
APA StyleYang, C., Liu, Z., Guan, R., & Zhao, H. (2025). A Semi-Supervised Multi-Scale Convolutional Neural Network for Hyperspectral Image Classification with Limited Labeled Samples. Remote Sensing, 17(19), 3273. https://doi.org/10.3390/rs17193273






