Space–Ground Joint Support Method in Autonomous Orbit Determination of BeiDou Satellites

Highlights

What are the main findings?

• A novel space–ground joint support method was proposed, integrating space-based orientation observations with ground anchor stations to achieve a 3D orbit accuracy of 0.45 m during 90-day inertial-frame operation, while star-sensor-aided inertial alignment effectively resolved Earth-fixed frame rotation ambiguity, reducing along-track error from 10.35 m to 0.28 m.
• A breakthrough in ERP estimation was achieved, demonstrating polar motion accuracy of 2.23 mas (xp) and 3.55 mas (yp), along with onboard UT1-UTC determination at 0.42 ms precision—without reliance on VLBI/SLR—by integrating inter-satellite links with star-sensor data to overcome rank deficiency in GNSS-only solutions, as validated against IERS benchmarks.

What are the implications of the main findings?

• System resilience was significantly enhanced, enabling meter-level autonomous navigation (8.42 m in Earth-fixed frame) during ground station outages, which is critical in wartime and ground-scarce scenarios, while semi-autonomous operation with ERP updates achieved 0.29 m 3D orbit accuracy.
• A strategic PNT infrastructure was established, providing independent spaceborne ERP determination capability.

Abstract

When relying exclusively on inter-satellite links for autonomous orbit determination, it cannot suppress or eliminate the constellation overall rotation, rendering it incapable of determining its spatial orientation relative to terrestrial and celestial reference frames. To address these limitations, an autonomous orbit determination method for BeiDou Satellites is proposed by integrating satellite-to-ground, inter-satellite, and space-based orientation observations. This study introduces space-based orientation data between navigation satellites to provide inertial frame orientation references for the BeiDou constellation, while utilizing ground-based anchor stations to establish orientation references in the Earth-fixed frame. The results demonstrate that (1) In a 90-day autonomous operation within the inertial frame, the combined use of inter-satellite links and space-based orientation data achieves a 3D orbit position accuracy of 0.45 m. (2) In semi-autonomous operation, with Earth rotation parameter (ERP) updates every three days from ground stations, the 3D orbit determination accuracy reaches the decimeter level; using long-term predicted ERPs in conjunction with satellite-to-ground data, meter-level accuracy is maintained. (3) When the space-based orientation measurement noise is limited to 5 milliarcseconds, the accuracies of polar motion parameters xp and yp reach 2.23 milliarcseconds and 3.55 milliarcseconds, respectively, while the UT1–UTC parameter achieves an accuracy of 0.42 milliseconds. This work provides critical technical support for flexible autonomous navigation of the BeiDou system when the ground control stations are destroyed in the wartime and contributes to the independent determination of ERP within China.

1. Introduction

As a critical component of national strategic infrastructure, satellite navigation systems must maintain high precision, reliability, and longevity under diverse and often challenging conditions. To support these capabilities, the Global Navigation Satellite System (GNSS) typically relies on a ground-based operation and control networks to continuously monitor satellite status and upload precise ephemeris data and clock offset corrections. However, this ground-based infrastructure is inherently vulnerable due to its limited concealment, rendering it susceptible to targeted attacks in extreme scenarios such as wartime. In the absence of ground-based maintenance, the precision of satellite ephemeris and clock data deteriorates rapidly, potentially leading to the swift incapacitation of the entire system. To mitigate this vulnerability and strengthen autonomous operational capabilities during conflict, autonomous navigation algorithms have been developed and explored across various satellite navigation systems. Notably, the BDS-3 incorporates an inter-satellite link measurement system and has conducted relevant autonomous navigation experiments [1,2].

During autonomous navigation of constellations, autonomous orbit determination on the basis of inter-satellite ranging can lead to two immeasurability problems. First, the overall constellation rotation cannot be measured [3]. The basis for the autonomous operation of a navigation constellation is the maintenance of its spatial reference, which requires ensuring that the coordinates of each satellite conform to the coordinate system defined by the positioning and navigation service. Furthermore, broadcast navigation messages must align with the terrestrial reference system and be convertible into the celestial reference system. However, when autonomous orbit determination is based solely on inter-satellite ranging, satellites lack direct physical measurement capabilities tied to either geodetic or celestial reference frames, resulting in the loss of spatial anchoring. In the absence of spatial reference information fixed relative to the Earth and the celestial sphere, it becomes virtually impossible to suppress or correct the overall rotation of the satellite constellation. This leads to an inability to determine the spatial orientation of the navigation constellation relative to terrestrial and celestial reference systems. Even with long-term predicted ephemeris uploaded from the ground, the effectiveness of constellation rotation correction is constrained by the prediction accuracy, which degrades over time—a limitation observed in both GPS Block IIR and BDS-3 satellites [4,5,6,7]. Additionally, Earth rotation parameters (ERPs) cannot be independently measured in space. When converting between inertial and Earth-fixed coordinate systems onboard satellites, ERPs must be sourced from ground-uploaded prediction models. These predictions, however, have limited temporal accuracy, rapidly degrading over short timeframes, which in turn restricts both the precision of autonomous orbit determination and the duration of independent service time [8]. Together, these two unmeasurable factors present significant technical challenges for maintaining spatial orientation of satellite constellations during autonomous operation.

To address these two problems, scholars have proposed two types of solutions in the literature. The first type strengthens the satellite’s autonomous orbit determination capability. One approach in this category is to add star sensors to the satellite for star observation, obtain space-based orientation observation information, and determine the position and attitude of the satellite [9,10]. X-ray pulsar observations or optical inter-satellite links (OISLs) can also be adopted to achieve autonomous navigation of satellite constellations [11,12,13,14]. One approach employs time difference of arrival (TDOA) measurements of radiation photons from solar active regions for the autonomous orbit determination of navigation constellation [15]. Another method involves increasing the number of ground anchor stations to enhance the geometric linkage between satellites and the ground; however, these stations remain vulnerable to hostile attacks [5,6]. In this context, the integration of astronomical observation data with inter-satellite ranging information has garnered significant attention. This approach leverages the strengths of astronomical navigation to address the issue of overall constellation rotation inherent in inter-satellite ranging-based autonomous orbit determination. Currently, most research concentrates on managing constellation rotation within the inertial frame, despite the requirement for broadcast navigation messages in autonomous systems to align with the terrestrial reference frame. A core challenge in satellite autonomous orbit determination lies in resolving the ERP issue. Nonetheless, there is a paucity of studies addressing how to synergize satellite-to-ground links, inter-satellite links, and space-based orientation observations to mitigate constellation rotation within the Earth-fixed reference frame. Furthermore, the issue of unmeasurable ERPs during autonomous satellite operation has received limited attention, particularly in relation to the integrated design of ground anchor station support and space-based orientation observation frameworks. These represent critical challenges that must be addressed in the development of the next-generation BeiDou system.

In response to the aforementioned challenges, this study integrates measured satellite-to-ground link data, inter-satellite link data, and space-based orientation measurements to explore a space–ground joint support strategy for the autonomous orbit determination of BeiDou satellites. The proposed approach first presents an orbit determination method that combines observations from satellite-to-ground links, inter-satellite links, and space-based orientation sensors, along with a corresponding methodology for ERP estimation. A joint support strategy is then developed, coordinating both space-based and ground-based resources to accommodate BeiDou satellites operating under autonomous and semi-autonomous modes. Finally, an experimental analysis based on measured BeiDou data is conducted, offering technical validation and foundational support for the future deployment of space-based orientation instruments on BeiDou satellites.

2. Orbit Determination Method of BeiDou Satellites Integrating Satellite-to-Ground, Inter-Satellite, and Space-Based Orientation Observations

A space-based integrated monitoring resource based on the BeiDou satellite constellation, with high-precision, miniaturized star sensors deployed on satellites, can comprehensively utilize inter-satellite Ka-band link ranging, satellite-to-ground Ka-band ranging, and inter-satellite space-based orientation measurements. Independently constructing a complete and unified spatial reference, including the position and velocity of navigation satellites and the spatial orientation of the constellation, can significantly improve the resilience and anti-destruction ability of China’s spatial reference system. This architecture is a critical new means for achieving an independent, controllable, secure spatial reference in China, especially under adversarial conditions.

Considering the constellation satellites’ orbit characteristics, platform features, and onboard processing capabilities, star sensors are placed on high-altitude orbit satellites for space-based orientation observations. Bidirectional Ka-band inter-satellite measurements are conducted between the BeiDou satellites, and Ka-band satellite-to-ground measurements are performed between the satellites and ground stations. For the autonomous operation of BeiDou satellites, space-based orientation measurements and inter-satellite ranging information are used as the observed quantities. The navigation information, such as the satellite’s position and velocity, is determined through the least squares algorithm, thereby achieving autonomous orbit determination of BeiDou satellites on the basis of inter-satellite links and space-based orientation. For the semi-autonomous operation of the BeiDou satellites, satellite-to-ground ranging information is added on top of the above observations.

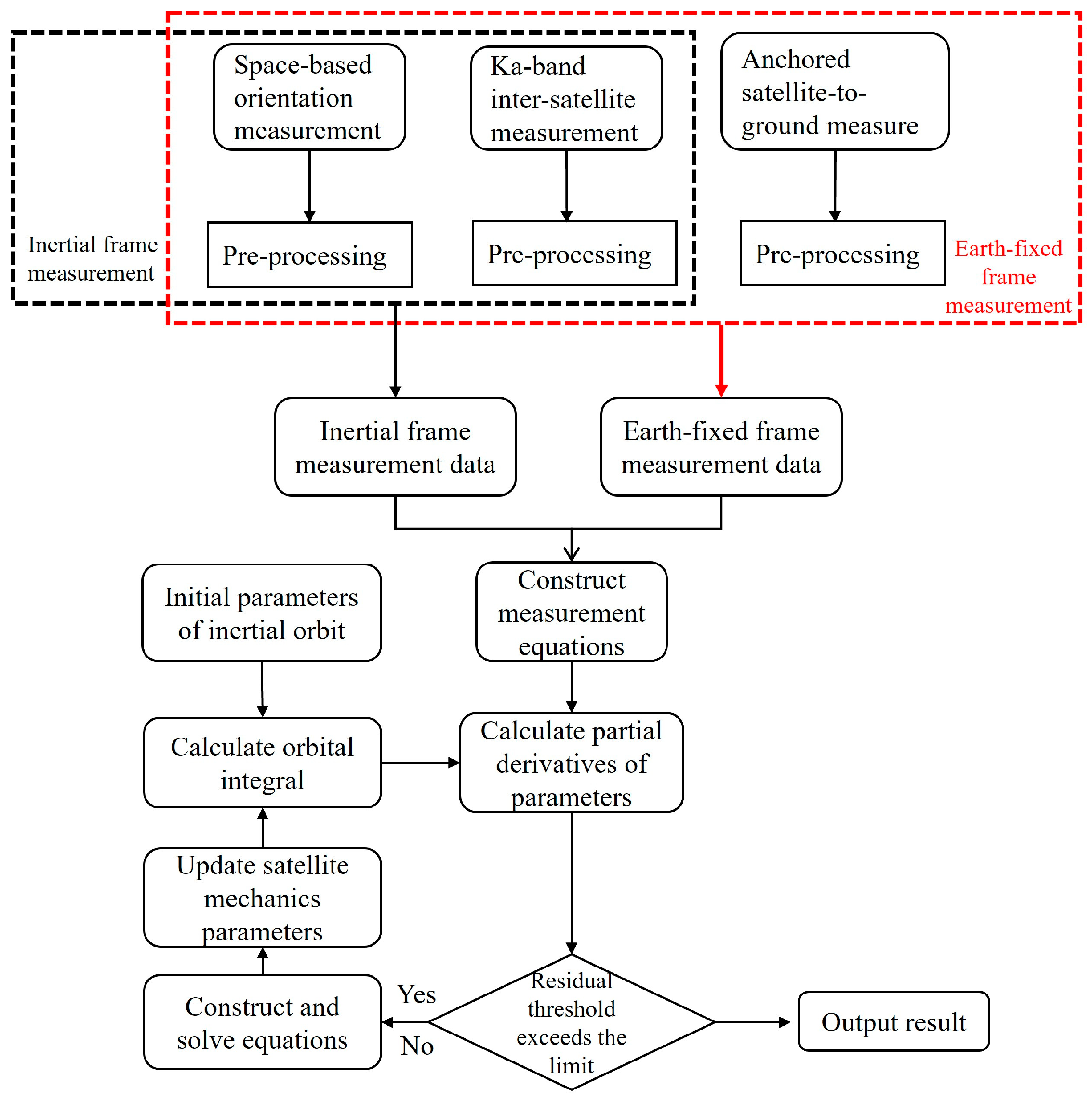
The integrated processing framework for BeiDou satellite orbit determination—combining satellite-to-ground, inter-satellite, and space-based orientation observations—proceeds as Figure 1. In the autonomous orbit determination mode, space-based orientation data and inter-satellite navigation measurements are first subjected to preprocessing. Subsequently, measurement models are formulated, partial derivatives of the relevant parameters are computed, and orbit integration is conducted. The satellite’s dynamical parameters are iteratively updated, and a residual threshold criterion is applied to determine the convergence of the solution, at which point the satellite orbit is resolved in the inertial reference frame. In the semi-autonomous orbit determination mode, the incorporation of satellite-to-ground measurement data from ground anchor stations enables the establishment of geometric links between satellite-to-ground and inter-satellite observations. This integrated dataset facilitates the estimation of satellite orbit parameters within the Earth-fixed reference frame.

For space-based orientation observations, angular distance measurements of the observation satellite, target satellite, and background star can be obtained through star sensors, and the relative right ascension and declination $\left({\alpha }_{ij},{\delta }_{ij}\right)$ in the direction of the line connecting the two satellites can be calculated as the observed quantity. For Ka-band inter-satellite measurements, the Ka-band inter-satellite link is adopted for the BDS-3 satellites, with 3 s as one time slot. The forward and reverse inter-satellite ranging values observed in each time slot are reduced to the same epoch [16]. The forward and reverse ranging values after reduction are summed to obtain the relative distance between the satellites for orbit determination. Ka-band satellite-to-ground measurements are performed between satellite i and ground station sta. These three types of observation data are combined to establish the measurement equation shown below.

$$\begin{array}{c}{\alpha }_{ij}=\left\{\begin{array}{c}arctan\left({\displaystyle \frac{\Delta y}{\Delta x}}\right),\Delta x\ge 0\\ arctan\left({\displaystyle \frac{\Delta y}{\Delta x}}\right)+\pi ,\Delta x<0\end{array}\right.\\ {\delta }_{ij}=arctan\left({\displaystyle \frac{\Delta z}{\sqrt{\Delta x^2+\Delta y^2}}}\right)\end{array}$$

(1)

where $\left({\alpha }_{ij},{\delta }_{ij}\right)$ is the relative right ascension and declination along the line connecting observation satellite $i$ and target satellite $j$. $\Delta \overrightarrow{r}={\overrightarrow{r}}_i-{\overrightarrow{r}}_j={\left[\Delta x,\Delta y,\Delta z\right]}^T$, where ${\overrightarrow{r}}_i={\left[x_i,y_i,z_i\right]}^T$ and ${\overrightarrow{r}}_j={\left[x_j,y_j,z_j\right]}^T$ are the position vectors of satellites $i$ and $j$ in the inertial coordinate system, respectively.

$${\rho }_{ijISL}\left(t_0\right)={\displaystyle \frac{{\tilde{\rho }}_{ij}\left(t_0\right)+{\tilde{\rho }}_{ji}\left(t_0\right)}{2c}}=\left|{\overrightarrow{R}}_i\left(t_0\right)-{\overrightarrow{R}}_j\left(t_0\right)\right|+{\displaystyle \frac{{\tau }_i^{send}+{\tau }_i^{rcv}}{2}}+{\displaystyle \frac{{\tau }_j^{send}+{\tau }_j^{rcv}}{2}}+{\displaystyle \frac{\Delta {\rho }_{cor}^{ij}+\Delta {\rho }_{cor}^{ji}}{2}}+\xi$$

(2)

where ${\rho }_{ijISL}\left(t_0\right)$ denotes the relative distance of the inter-satellite Ka-band link between satellites $i$ and $j$ at the reduction time $t_0$. ${\tilde{\rho }}_{ij}$ and ${\tilde{\rho }}_{ji}$ are the forward and reverse ranging values of the inter-satellite Ka-band link at $t_0$. ${\overrightarrow{R}}_i$ and ${\overrightarrow{R}}_j$ are the three-dimensional (3D) position vectors of the two satellites. ${\tau }_i^{send}$, ${\tau }_i^{rcv}$, ${\tau }_j^{send}$, and ${\tau }_j^{rcv}$ are the transmit and receive delays of the inter-satellite link equipment for satellites i and j, respectively. $\Delta {\rho }_{cor}^{ij}$ and $\Delta {\rho }_{cor}^{ji}$ represent the model corrections of the two ranging values, including the phase center correction of the satellite antenna and the relativistic effect correction, where $\xi$ is the random noise in the inter-satellite measurement and where $c$ is the speed of light.

For the Ka-band satellite-to-ground measurement between satellite i and ground station sta, we need only to treat the ground station as another satellite j in the above observation equation and denote the Ka-band satellite-to-ground measurement between i and sta at $t_0$ as ${\rho }_{istaISL}\left(t_0\right)$.

For the autonomous operation mode of BeiDou satellites, only the relative distance between satellites and space-based orientation observations are used for orbit determination, and the satellite orbit in the J2000 coordinate system is obtained. The relative distance between satellites at time $t_k$, ${\rho }_{ijISL}$, and the space-based orientation observation, $\left({\alpha }_{ij},{\delta }_{ij}\right)$, are combined as the observed quantity $L_{or{b}_k}$ at $t_k$. The orbit parameter $X_{or{b}_k}$ of a certain BeiDou satellite at $t_k$ is treated as the quantity to be estimated. The basic equation for calculating the BeiDou satellite orbit parameter is established as follows:

$$\left\{\begin{array}{c}{L}_{or{b}_k}=\left(\begin{array}{c}{\rho }_{ijISL}\left(t_k\right)\\ {\alpha }_{ij}\left(t_k\right)\\ {\delta }_{ij}\left(t_k\right)\end{array}\right)=A_{or{b}_k}{X}_{or{b}_k}+{\Delta }_{or{b}_k}\\ X_{or{b}_k}={\Phi }_{or{b}_{k,k-1}}{X}_{or{b}_{k-1}}+W_{or{b}_k}\end{array}\right.$$

(3)

where $X_{or{b}_k}$ and $X_{or{b}_{k-1}}$ are the orbit parameters of the BeiDou satellite at epochs $t_k$ and $t_{k-1}$, respectively; $X_{or{b}_0}$ is the known orbit parameter at $t_0$; $L_{or{b}_k}$ is the orbit observation at $t_k$; ${\Phi }_{or{b}_{k,k-1}}$ is the state transition matrix between the orbit parameters; $A_{or{b}_k}$ is the orbit parameter design matrix expressing the relationship between the observed quantity and the orbit parameter vector; ${\Delta }_{or{b}_k}$ is the orbit observation noise vector; and $W_{or{b}_k}$ is the system process noise matrix in the orbit parameter calculation.

For the semi-autonomous operation mode of BeiDou satellites, the satellite-to-ground distance is added on the basis of the inter-satellite distance and space-based orientation observations. The observation equation is then reformulated as follows:

$$L_{or{b}_k}=\left(\begin{array}{c}{\rho }_{ijISL}\left(t_k\right)\\ {\alpha }_{ij}\left(t_k\right)\\ {\delta }_{ij}\left(t_k\right)\\ {\rho }_{istaISL}\left(t_k\right)\end{array}\right)=A_{or{b}_k}^{\prime }{X}_{or{b}_k}+{\Delta }_{or{b}_k}^{\prime }$$

(4)

$A_{or{b}_k}$ is the orbit parameter design matrix, ${\Delta }_{or{b}_k}$ is the noise vector in the orbit observation.

$$A_{or{b}_k}={\displaystyle \frac{𝜕L_{or{b}_k}}{𝜕\overrightarrow{r}}}=\left(\begin{array}{c}{\displaystyle \frac{𝜕{\rho }_{ijISL}}{𝜕\overrightarrow{X}}}\\ {\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕\overrightarrow{X}}}\\ {\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕\overrightarrow{X}}}\\ {\displaystyle \frac{𝜕{\rho }_{istaISL}}{𝜕\overrightarrow{X}}}\end{array}\right)$$

(5)

Here, the observation partial derivatives between the space-based orientation data and orbital parameters to be estimated are expressed by

$$\left\{\begin{array}{c}{\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕{\overrightarrow{r}}_i}}={\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}{\displaystyle \frac{𝜕\Delta {\overrightarrow{r}}_{ij}}{𝜕{\overrightarrow{r}}_i}}=-{\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}\hspace{1em} {\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕{\overrightarrow{r}}_j}}={\displaystyle \frac{𝜕{\alpha }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}\\ {\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕{\overrightarrow{r}}_i}}={\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}{\displaystyle \frac{𝜕\Delta {\overrightarrow{r}}_{ij}}{𝜕{\overrightarrow{r}}_i}}=-{\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}\hspace{1em} {\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕{\overrightarrow{r}}_i}}={\displaystyle \frac{𝜕{\delta }_{ij}}{𝜕\Delta {\overrightarrow{r}}_{ij}}}\end{array}\right.$$

(6)

$$\left\{\begin{array}{c}{\displaystyle \frac{𝜕\alpha }{𝜕\Delta \overrightarrow{r}}}={\displaystyle \frac{\Delta x^2}{\Delta x^2+\Delta y^2}}\left(-{\displaystyle \frac{\Delta y}{\Delta x^2}},{\displaystyle \frac{1}{\Delta x}},0\right)\\ {\displaystyle \frac{𝜕\delta }{𝜕\Delta \overrightarrow{r}}}={\displaystyle \frac{1}{\sqrt{\Delta x^2+\Delta y^2}\left(\Delta x^2+\Delta y^2+\Delta z^2\right)}}\left(-\Delta x\Delta z,-\Delta y\Delta z,\Delta x^2+\Delta y^2\right)\end{array}\right.$$

(7)

The partial derivative matrix corresponding to space-based orientation data with respect to dynamic parameters (e.g., optical pressure), tropospheric model parameters, and ambiguity terms is null. The partial derivative matrices for satellite-to-ground and inter-satellite link measurements are available in the literature [16,17]. Utilizing these three categories of measurement data, the least squares method is employed to estimate the orbital parameters, dynamic parameters, and ambiguity terms of the BeiDou satellites. The least-squares algorithm we use is linear, in which the sum of squared residuals U must be minimized.

$$U=V_l^T{V}_l=\mathit{min}\left(l=1,2,\dots ,k\right)$$

(8)

$$U={\displaystyle \sum }_{l=1}^k{\left(L_{orbl}-L_{orb{l}_c}\right)}^T\left(L_{orbl}-L_{orb{l}_c}\right)$$

(9)

At a given measurement epoch $l$, $L_{orbl}$ represents the observed quantity, while $L_{orb{l}_c}$ denotes the estimated observable.

3. ERP Calculation Method

ERPs include the difference between Universal Time 1 (UT1) and Coordinated Universal Time (UTC), as well as the polar motion coordinates $x_p,y_p$. The ERP products released by the International Earth Rotation Service (IERS) are based on a comprehensive solution by space geodetic techniques, mainly very long baseline interferometry (VLBI), satellite laser ranging (SLR), Doppler orbiting system (DORIS), and GNSS. However, technologies such as SLR and VLBI are bulky, expensive, and have poor accessibility and mobility, coupled with limited observation data. These characteristics limit the application of ERPs in high temporal resolution scenarios. This paper proposes an ERP calculation method that combines BeiDou satellite-to-ground, inter-satellite, and space-based orientation measurements.

The UT1-UTC parameter and the orbit’s right ascension point of the ascending node ($\mathrm{\Omega }$) are linearly correlated. When only satellite-to-ground data or satellite-to-ground and inter-satellite data are used for orbit determination, if satellite orbit parameters and ERPs are calculated simultaneously, it is impossible to estimate UT1-UTC on the basis of GNSS satellite-to-ground and inter-satellite data during orbit determination. After adding the space-based orientation data, however, we can determine the direction of the connecting line between the two navigation satellites in inertial space and provide direct measurements of the overall constellation orientation in the inertial frame, thereby removing the correlation between UT1-UTC and $\mathrm{\Omega }$. Under these circumstances, the ERPs can be solved. After epoch reduction of the Ka-band bidirectional satellite-to-ground measurements, the unidirectional satellite-to-ground distance $\rho$ can be obtained as follows:

$$\rho =\left|P{\stackrel{\rightharpoonup }{X}}_{sat}-P{\stackrel{\rightharpoonup }{X}}_{sta}\right|$$

(10)

$$P=RNSU, {\stackrel{\rightharpoonup }{x}}_{sta}=P {\stackrel{\rightharpoonup }{X}}_{sta}$$

(11)

where ${\stackrel{\rightharpoonup }{X}}_{sat}$ represents a satellite’s coordinates in the inertial coordinate system, while ${\stackrel{\rightharpoonup }{X}}_{sta}$ and ${\stackrel{\rightharpoonup }{x}}_{sta}$ represent the coordinates of the station in the inertial and Earth-fixed coordinate systems, respectively. P is the rotation matrix that transforms from the inertial coordinate system to the Earth-fixed coordinate system, where R, N, S and U represent the precession transformation matrix, nutation transformation matrix, Earth’s rotation matrix, the polar motion matrix. The Earth’s rotation matrix is related to the UT1-UTC parameter ${\epsilon }_{UT1}$, and the polar motion matrix is related to the polar motion parameters ${\epsilon }_x,{\epsilon }_y$.

The Earth’s rotation angle ERA is the angle between the terrestrial intermediate origin (TIO) and the celestial intermediate origin (CIO), which is measured along the intermediate equator corresponding to the celestial intermediate pole (CIP), with the direction of regression being positive. ERA is a linear function of ${\epsilon }_{UT1}$, and JD is the Julian day at the current moment, as shown in IERS 2010 Formula 5.15 [18].

$$\begin{array}{c}ERA\left(T_u\right)=2\pi \left({\epsilon }_{UT1}\hspace{0.33em}+0.7790572732640+0.00273781191135448T_u\right)\\ T_u=\left(JD-2451545.0\right)\end{array}$$

(12)

The Earth’s rotation matrix is a function of the ERA:

$$R_z\left(ERA\right)=\left[\begin{array}{ccc}cos\left(ERA\right)& sin\left(ERA\right)& 0\\ -sin\left(ERA\right)& cos\left(ERA\right)& 0\\ 0& 0& 1\end{array}\right]$$

(13)

The partial derivative of the geometric distance $\rho$ to ${\epsilon }_{UT1}$ is as follows:

$${\displaystyle \frac{𝜕\rho }{𝜕{\epsilon }_{UT1}}}={\displaystyle \frac{𝜕\rho }{𝜕{\stackrel{\rightharpoonup }{X}}_{sta}}}\cdot {\displaystyle \frac{𝜕{\stackrel{\rightharpoonup }{X}}_{sta}}{𝜕{\epsilon }_{UT1}}}={\displaystyle \frac{𝜕\rho }{𝜕{\stackrel{\rightharpoonup }{X}}_{sta}}}\cdot {\left[RC2I\right]}^T\cdot {\displaystyle \frac{𝜕{\left[R_z\left(ERA\right)\right]}^T}{𝜕UT1}}\cdot {\left[RPOM\right]}^T\cdot {\stackrel{\rightharpoonup }{x}}_{sta}$$

(14)

where

$${\displaystyle \frac{𝜕\rho }{𝜕{\stackrel{\rightharpoonup }{X}}_{sta}}}={\displaystyle \frac{{\stackrel{\rightharpoonup }{X}}_{sta}-{\stackrel{\rightharpoonup }{X}}_{sat}}{\rho }}$$

(15)

The partial derivative of the Earth’s rotation matrix to ${\epsilon }_{UT1}$ is:

$${\displaystyle \frac{𝜕R_z\left(ERA\right)}{𝜕{\epsilon }_{UT1}}}={\displaystyle \frac{𝜕R_z\left(ERA\right)}{𝜕ERA}}\cdot {\displaystyle \frac{𝜕ERA}{𝜕{\epsilon }_{UT1}}}=2\pi \left[\begin{array}{ccc}-sin\left(ERA\right)& cos\left(ERA\right)& 0\\ -cos\left(ERA\right)& -sin\left(ERA\right)& 0\\ 0& 0& 1\end{array}\right]$$

(16)

The partial derivative of $\rho$ with respect to the pole motion is:

$${\displaystyle \frac{\delta \rho }{{\epsilon }_x}}=-{\displaystyle \frac{\delta \rho }{\delta \left[RPOM\right]}}\cdot {\displaystyle \frac{\delta \left[RPOM\right]}{{\epsilon }_x}}$$

(17)

$${\displaystyle \frac{\delta \rho }{{\epsilon }_y}}=-{\displaystyle \frac{\delta \rho }{\delta \left[RPOM\right]}}\cdot {\displaystyle \frac{\delta \left[RPOM\right]}{{\epsilon }_y}}$$

(18)

On the basis of the above partial derivative matrices and the satellite dynamics equation, the normal equation can be constructed [19]. If only satellite-to-ground and inter-satellite link data are available, the normal equation suffers from rank deficiency when the orbit and ERPs are solved simultaneously. After adding space-based orientation data, we can determine the orientation of navigation satellite links in inertial space and the orbit’s right ascension point of the ascending node $\mathrm{\Omega }$, thereby removing the correlation between UT1-UTC and $\mathrm{\Omega }$. This integration solves the rank deficiency problem of the normal equation, thereby obtaining the ERPs. The satellite orbit and ERPs can thus be simultaneously determined through least squares batch processing.

4. Design of Autonomous and Semi-Autonomous Operation Modes for BeiDou Satellites

4.1. Simulation and Error Modeling of Space-Based Orientation Observation Data

As no actual space-based orientation observations currently exist for BeiDou satellites, such data must be generated through simulation. This section describes the methodology employed for this simulation. Initially, error-free right ascension and declination values for both the target and observation satellites are produced using the inertial-frame orbits of the BeiDou constellation and corresponding stellar observation ephemerides. Subsequently, a measurement error model is constructed by thoroughly analyzing the operational principles and error characteristics of star sensors. Finally, varying levels of simulated measurement noise are superimposed onto the right ascension and declination data to produce realistic space-based orientation observations for use in orbit determination analyses.

This study simulates space-based orientation measurement data based on the BDS satellite precise ephemeris provided by the Multi-GNSS Experiment (MGEX) [20] and the Earth orientation parameter (EOP) product issued by the International Earth Rotation Service (IERS) [21]. Ignoring the actual generation process of on-board photogrammetric data, the simulation process is as follows:

Firstly, the generation of precise ephemerides follows the standards of the International Terrestrial Reference Frame (ITRF). To simulate orientation measurements in a celestial coordinate system, it is essential to employ EOP provided by the International IERS or derived from the precise ephemeris itself. The transformation process involves applying corrections for polar motion, performing a rotation based on the true equinox hour angle, and incorporating precession and nutation effects. This conversion yields the required celestial-frame data, which serve as the basis for simulating space-based orientation measurements.

Secondly, the criterion for determining inter-satellite visibility is whether one satellite is within the visible angle range between the positive and negative zenith angles of another satellite. Inter-satellite visibility is a prerequisite for inter-satellite orientation measurements. Thirdly, Calculate the unit vector between satellites in the celestial coordinate system. Finally, star sensors are subject to multiple sources of measurement error, including uncalibrated systematic biases, stochastic measurement noise, and periodic low-frequency errors (LFE) resulting from thermal deformation of the optical head and its mounting structure. These error components must be incorporated into the data simulation process to ensure realism, as represented by the following equations [17,22,23].

The precise ephemeris utilized in this study is sourced from the MGEX. The terms ${error}_{\alpha }$ and ${error}_{\delta }$ denote the simulated errors associated with right ascension and declination, respectively. In the simulation framework, both Gaussian white noise and a constant systematic bias are incorporated. The constant systematic bias of the space-based orientation data can be solved by data processing method, and then the systematic difference solved can be deducted from the original measurement data, so as to eliminate the influence of systematic bias on the orbital accuracy. The systematic bias of the space-based orientation data in our manuscript is the residual systematic error after data processing modification.

4.2. Design of Autonomous and Semi-Autonomous Operation Modes for BeiDou Satellites

4.2.1. Autonomous Operation Mode

At the onset of autonomous operation, ERPs are uploaded from the ground a single time, serving as predicted values for autonomous operation durations of 60 or 90 days. During this period, the orbital parameters of BeiDou satellites are determined using data from inter-satellite links and space-based orientation measurements. To obtain orientation data, star sensors are installed on three inclined geosynchronous orbit (IGSO) satellites. Each IGSO satellite observes a visible medium Earth orbit (MEO) satellite located on a fixed orbital plane. When a particular MEO satellite becomes non-visible, the observation seamlessly transitions to another visible MEO satellite within the same orbital plane. At each observation epoch, occurring every 15 min, a single orientation measurement is acquired from each IGSO satellite, resulting in a total of three orientation measurements per epoch. This observational strategy is referred to as the “staring mode” in this study.

4.2.2. Semi-Autonomous Operation Mode

Semi-autonomous operation Mode 1: In this mode, the ground anchor station uploads ERPs every 3 days and makes satellite-to-ground Ka-band link observations with visible satellites every 5 min. The three IGSO satellites are employed to measure the space-based orientation data and inter-satellite pseudorange data, with a rotation period of 8 h. During this period, each IGSO satellite fixedly observes one visible MEO satellite on a single orbital plane. Space-based orientation measurement observations and inter-satellite pseudorange observations are obtained every 15 min. At the beginning of the next scanning period, the IGSO satellites switch to another orbital plane, each following the same rule to ensure that MEO satellites participate in observations on all three orbital planes during each rotation period. This orientation measurement approach is referred to as the scanning mode in this study.

Semi-autonomous operation Mode 2: This mode is the same as Mode 1 except that the ground anchor station no longer conducts Ka-band satellite-to-ground link observations. The satellite obtains precise ERPs every 3 days, and then orbit determination is implemented on the basis of the inter-satellite link and space-based orientation data.

Semi-autonomous operation Mode 3: In this mode, the ground anchor station uploads the ERPs only once at the beginning of semi-autonomous operation. In other words, long-term predicted ERPs are used, and the other configurations are taken the same as those in Mode 1. Here, BeiDou satellite orbit determination is based on three types of data: satellite-to-ground data, inter-satellite data, and orientation data.

Semi-autonomous Operation Mode 4: BeiDou satellites employ a “visibility equals observability” full-constellation orientation measurement strategy, wherein orientation measurements are performed whenever mutual visibility between satellites is achieved. All other configuration settings remain consistent with those in Mode 3. In this mode, orbit determination continues to rely on satellite-to-ground, inter-satellite, and orientation measurement data. While Mode 1 yields three orientation measurements per epoch, Mode 4 allows for a substantially greater volume of orientation data due to the relaxation of observational constraints—any satellite pair that maintains line-of-sight can contribute to orientation measurements.

The autonomous and semi-autonomous operation modes of the BeiDou satellites mentioned above are summarized in

Table 1. Design of the autonomous and semi-autonomous operation modes of BeiDou satellites.

Mode	ERP	Satellite-to-Ground Data	Ka-Band Inter-Satellite Data	Orientation Data and Measurement Mode
				Staring	Scanning	Visibility Equals Observability
Autonomous Mode	Predicted		√	√
Semi-autonomous Mode 1	Uploaded every 3 days	√	√		√
Semi-autonomous Mode 2	Uploaded every 3 days		√		√
Semi-autonomous Mode 3	Predicted	√	√		√
Semi-autonomous Mode 4	Predicted	√	√			√

.

5. Experimental Analysis

In this section, experiments are conducted on the autonomous and semi-autonomous operation modes of the BeiDou satellites designed in Section 4.2. Satellite orbit determination involves four main aspects: satellite dynamics models, measurement models, parameter estimation methods, and orbit determination strategies. The first three methods are detailed in Refs. [24,25,26]. and will not be repeated here. In this study, ground anchor stations are deployed in Hainan, Central China, Southwest China, and Northeast China. The data selected are from 1 October 2024 to 31 December 2024, with satellite-to-ground and inter-satellite data being actual measurement data and space-based orientation measurement data being simulated. The basic strategy for orbit determination is shown in

Table 2. Autonomous orbit determination strategy for BeiDou satellites.

Orbit Determination Arc Length	72 h
Cutoff elevation angle	5°
Data types	Satellite-to-ground, inter-satellite, and space-based orientation data
Sampling interval	Satellite-to-ground, inter-satellite data: 5 min; space-based orientation data: 15 min
Observation weighting	$\mathrm{Elevation}\text{-}\mathrm{dependent} \mathrm{weighting}: \sin \left(E\right)$
Attitude model	China Academy of Space Technology (CAST)/Space Environment Monitoring and Warning Center (SECM) official model
Antenna thrust	igs_metadata_2081.snx
Phase entanglement and relativistic effects	IERS conventions (2010)
Satellite clock offset	White noise
Receiver inter-signal bias (ISB)	Constant estimation
Ambiguity	Float ambiguity solution
Tropospheric delay	A priori value: Saastamoinen model; wet delay: Global Mapping Function (GMF) estimation
Antenna model	BDS B1I/B3I: IGS14.atx
ERP	3-day predicted ERPs are uploaded

; it integrates satellite-to-ground and inter-satellite data sampled at 5 min intervals, as well as space-based orientation data sampled at 15 min intervals, and utilizes 3-day predicted Earth rotation parameters (ERPs) to achieve high-precision orbit determination through optimized data synthesis and temporal resolution.

5.1. Accuracy Analysis of BeiDou Satellite Orbit Determination Under Autonomous Operation Mode

Under autonomous navigation, there is no ground station to support information uploading, so the ERPs are predicted values. This section analyzes the orbit determination accuracy of the BeiDou satellites during a 90-day autonomous navigation operation. The simulation is based on the BeiDou satellite orbit with the 90-day predicted ERPs, which include the overall rotation error of the constellation. The experimental analysis is conducted with this orbit as the initial orbital state for the 90-day autonomous operation.

In the autonomous operation mode, the absence of satellite-to-ground data from ground stations precludes the resolution of the overall rotation of the BeiDou satellite constellation relative to the Earth-fixed reference frame. Consequently, orientation data can only be utilized to correct for the constellation’s overall rotation with respect to the inertial reference frame. Therefore, precise ephemerides in the J2000 inertial coordinate system are employed as the reference for assessing the orbit determination accuracy of BeiDou satellites when using 90-day predicted ERPs. This assessment reflects the spatial reference accuracy of the BeiDou constellation relative to the inertial frame. The random noise in the orientation data is modeled as a normally distributed error with a mean of 5 mas. Additionally, constant systematic errors are introduced for the MEO satellites across the three orbital planes, with values of 5 mas, −5 mas, and 4 mas, respectively. The residual RMS of the ISL measurements is 10 cm. The data sources used in this evaluation consist of measured inter-satellite link data and simulated orientation observations.

Two experiments are designed, which are, respectively, 90 days of autonomous operation for BeiDou satellites supported only by inter-satellite link data (ISL), 90 days of autonomous operation for BeiDou satellites supported by the inter-satellite link data and space-based orientation data (ISL + SO). After 90 days of autonomous operation for BeiDou satellites supported only by inter-satellite link data, the time series of the radial (R), tangential (T), and normal (N) determination errors and the 3D positions under the Earth-fixed reference system are illustrated in Figure 2. C19, C20,…, C46 are the PRN of the Beidou satellite.

Next, on the basis of inter-satellite link data, space-based orientation data are added for BeiDou satellite orbit determination. After 90 days of autonomous operation, the time series of orbit determination errors in the R, T, and N directions and 3D positions under the Earth-fixed reference system are shown in Figure 3.

The accuracy of the orbit is evaluated through RMS values in the Earth-fixed frame and the inertial frame. As shown in Figure 4, the one-day RMS errors in the R, T, and N directions, as well as the 3D position accuracy in the Earth-fixed frame, are presented, respectively, supported by inter-satellite link data (ISL) and inter-satellite link data/space-based orientation data (ISL + SO). Corresponding results in the inertial frame are provided in Figure 5.

The orbit determination accuracies of BeiDou satellites in autonomous operation mode, which are based on inter-satellite link data and inter-satellite link+space-based orientation data, are summarized in

Table 3. Orbit determination accuracy statistics of the BeiDou satellites in autonomous mode (unit: m).

Measurement Data	Reference System	R	T	N	Pos
Inter-satellite link	Inertial reference system	0.20	10.35	10.62	14.83
	Earth-fixed reference system	0.18	7.28	4.66	9.31
Inter-satellite link+space-based orientation	Inertial reference system	0.06	0.28	0.34	0.45
	Earth-fixed reference system	0.19	6.68	3.99	8.42

. The orbit accuracies of 27 BeiDou satellites, including 3 IGSO satellites and 24 MEO satellites, in inertial and Earth-fixed frames are calculated for the 90th day of autonomous operation. The average orbit determination accuracy of these 27 BeiDou satellites is taken as the final result.

The following can be seen:

(1) Relying exclusively on inter-satellite links, the BeiDou satellites make forecasts for 90 days. The R-, T-, and N-direction satellite orbit accuracies and 3D position accuracies are 0.2, 0.35, 10.62, and 14.83 m in the inertial frame (Figure 5) and 0.18, 7.28, 4.66, and 9.31 m in the Earth-fixed reference system (Figure 4). The overall rotation of the constellation results in low orbit accuracies.

(2) Following 90 days of autonomous operation incorporating both space-based orientation observations and inter-satellite link measurements, the orbit determination accuracies of BeiDou satellites in the inertial frame reached 0.06 m (radial), 0.28 m (along-track), 0.34 m (cross-track), and 0.45 m in overall 3D positioning (Figure 5). The 3D orbital accuracy thus remained within 0.5 m relative to the inertial reference frame. These results confirm that space-based orientation measurements can effectively detect and correct for constellation-wide rotational errors in real time, thereby enabling reliable and precise autonomous orbit determination. When the error of the space-based orientation data is 5 mas and the inter-satellite distance of the BeiDou satellites is taken as 40,000 km, this angular measurement accuracy corresponds to an inter-satellite range error of approximately 0.96 m. The Ka-band inter-satellite ranging accuracy is about 0.09 m. The weighting of measurement data depends on their respective accuracies. Denoting the error of the angular measurement data as ${\mathrm{\sigma }}_1$ and the error of the Ka inter-satellite ranging data as ${\mathrm{\sigma }}_2$, the weighting ratio between the angular measurement data and the Ka inter-satellite ranging data in data processing is (${\mathrm{\sigma }}_1$/${\mathrm{\sigma }}_2$)2 ≈ 100:1. Therefore, in the orbit determination process, the Ka inter-satellite ranging data play a decisive role in orbit accuracy, while the angular measurement data are primarily used to correct the overall rotation of the constellation. Consequently, considering space-based measurements even with included noise does not degrade the results compared to using inter-satellite links alone.

(3) After 90 days of autonomous operation, the integration of inter-satellite link data with space-based orientation measurements yields a 3D orbit positioning accuracy of 8.42 m (Figure 4) for BeiDou satellites in the Earth-fixed reference frame. The predominant sources of error lie in the along-track and cross-track directions, primarily resulting from unresolved constellation rotation relative to the Earth-fixed frame. When compared to orbit determination relying solely on inter-satellite link data, the incorporation of space-based orientation data offers only a modest improvement in positioning accuracy within the Earth-fixed system. This limited gain can be attributed to the dual nature of orbit errors, which comprise both inertial-frame orbit deviations and inaccuracies in ERPs. While space-based orientation data effectively addresses rotational errors in the inertial frame, it does not rectify ERP-related inaccuracies—identified as the dominant error source, so the results considering Earth-fixed reference system provides much larger errors than that considering inertial reference system. As such, the combined measurement approach of inter-satellite links and space-based orientation can only resolve rotational discrepancies in the inertial frame. To mitigate the constellation’s rotational offset relative to the Earth-fixed reference frame, satellite-to-ground observations supported by ground anchor stations remain essential.

5.2. Accuracy Analysis of BeiDou Satellite Orbit Determination Under Semi-Autonomous Operation Mode

Experimental analysis is also conducted under the four semi-autonomous operation modes designed in Section 4.2.2. The random noise and constant systematic error of space-based orientation data are consistent with the settings in Section 5.1. Using the BeiDou precision orbit released by the Multi-GNSS Experiment (MGEX) analysis center as the reference, the orbit determination accuracy of the BeiDou satellites after 90 days of semi-autonomous operation is evaluated, which represents the absolute processing accuracy of the spatial reference of the BeiDou satellite in the Earth-fixed reference system. The orbit accuracy details of BeiDou satellite C27 after 90 days of semi-autonomous operation in the four modes are compared in Figure 6.

The following can be seen from the figure:

(1) Compared with Modes 1 and 2, Modes 3 and 4 exhibit lower orbit determination accuracy, accompanied by pronounced fluctuations in the R, T, and N directions. In Modes 1 and 2, ERPs are updated via ground anchor station uploads every three days, whereas Modes 3 and 4 rely on long-term predicted ERP values. During the 90-day semi-autonomous operation, the ERP prediction arc length for orbit determination in Modes 1 and 2 does not exceed three days, while Modes 3 and 4 utilize ERP predictions spanning the entire 90-day period. Among ERP components, the UT1–UTC parameter demonstrates significantly higher prediction error compared to polar motion parameters. Specifically, the UT1–UTC errors reach 0.198 milliseconds for a 5-day prediction and 19.983 milliseconds for a 90-day predictions [26] (IERS Annual Report 2019, p.137). Since ground station coordinates are defined in the Earth-fixed reference frame, the use of inaccurately predicted ERPs for coordinate transformations introduces substantial errors in station positions when expressed in the inertial frame. These positional errors subsequently degrade orbit determination accuracy in the inertial reference system. Therefore, the large uncertainties associated with long-term ERP predictions impose a critical limitation on orbit determination performance.

(2) The orbit determination accuracy in Mode 4 is marginally superior to that in Mode 3. This improvement is attributed to the differing space-based orientation measurement strategies employed by the two modes. Mode 3 utilizes a scanning observation mode with an 8 h cycle, resulting in only three orientation measurements per epoch. In contrast, Mode 4 implements a “visibility equals observability” approach, which significantly increases the volume of orientation data by enabling measurements whenever satellites are mutually visible.

The orbit accuracies of the BeiDou satellites in the four semi-autonomous operation modes are shown in Figure 7.

The orbit determination accuracies of the BeiDou satellites in the four semi-autonomous operation modes are listed in

Table 4. Orbit determination accuracy statistics of the BeiDou satellites in various semi-autonomous modes (unit: m).

Mode	R	T	N	Pos
1	0.06	0.19	0.20	0.29
2	0.06	0.29	0.38	0.49
3	0.42	2.16	2.10	3.10
4	0.06	1.52	1.47	2.17

. The orbit determination accuracies of the 27 BeiDou satellites (including 3 IGSO satellites and 24 MEO satellites) in the Earth-fixed reference system on the 90th day of semi-autonomous operation are determined and averaged to obtain the final result.

The following conclusions can be drawn:

(1) The 3D position accuracies for satellite orbit determination in Modes 1, 2, 3, and 4 are 0.29 m, 0.49 m, 3.10 m, and 2.17 m, respectively. The corresponding user range error (URE) accuracies are 0.06 m, 0.06 m, 0.59 m, and 0.30 m. Compared with Modes 1 and 2, Modes 3 and 4 demonstrate slightly reduced orbit determination accuracy, primarily due to their reliance on long-term predicted ERPs. These results underscore the critical influence of ERP accuracy on the performance of autonomous orbit determination.

(2) The orbit determination accuracies of Modes 1 and 2 are largely equivalent. In both modes, ERPs are uploaded from ground anchor stations every three days; however, Mode 1 additionally incorporates satellite-to-ground observational data. These findings suggest that when ERP updates can be transmitted to satellites at regular intervals, the continuous satellite-to-ground measurement link can be omitted without significant loss of accuracy. This strategy substantially enhances the operational flexibility of ground stations, as it eliminates the need for prolonged observation sessions. Instead, ground anchor stations only need to establish brief communication links for ERP uploads before relocating, thereby significantly improving their survivability and resilience in wartime scenarios.

(3) The 3D position accuracies in orbit determination are 0.49 m and 17.70 m for autonomous operation mode and semi-autonomous operation Mode 2, respectively. Neither mode has satellite-to-ground link data support. However, Mode 2 updates ERPs every 3 days, whereas the autonomous operation mode uses long-term predicted ERPs. Therefore, for semi-autonomous operation, if ERPs can be frequently uploaded, the overall constellation rotation problem in the Earth-fixed reference system can be solved without long-term satellite-to-ground link measurements.

(4) The 3D position accuracy in orbit determination is 17.70 m under autonomous operation mode and improves to 3.10 m in semi-autonomous operation Mode 3. Both modes use long-term predicted ERPs, but Mode 3 incorporates satellite-to-ground link measurement data, which effectively solves the overall constellation rotation problem in the Earth-fixed reference system.

(5) The 3D position accuracies for orbit determination under semi-autonomous operation Modes 2 and 3 are 0.49 m and 3.10 m, respectively. In Mode 2, ERPs are updated frequently, although satellite-to-ground measurements are not performed. Conversely, Mode 3 relies on long-term predicted ERPs in conjunction with satellite-to-ground observations. These results indicate that frequent ERP updates play a more critical role in maintaining orbit accuracy than continuous satellite-to-ground measurements. Accordingly, adopting a semi-autonomous operation mode that emphasizes regular ERP uploads is recommended. This approach reduces the operational burden of establishing and maintaining satellite-to-ground measurement links and enhances the wartime survivability of ground anchor stations by enabling short-duration, mobile deployments.

(6) The only difference between semi-autonomous operation Modes 3 and 4 lies in the space-based orientation measurement mode. Mode 3 adopts a scanning measurement approach with an 8 h cycle, whereas Mode 4 adopts the “visibility equals observability” setting. The amount of orientation observation data at a certain moment increases from 3 in Mode 3 to hundreds in Mode 4, so Mode 4 yields a higher orbit accuracy, although it does not differ by an order of magnitude. Considering the satellite platform characteristics and engineering implementation costs, the scanning measurement mode is recommended.

5.3. Accuracy Analysis of ERP Calculation

This section evaluates the feasibility of estimating the z-axis orientation parameter of the navigation constellation relative to the inertial reference frame using orientation data, with simultaneous estimation of satellite orbits and ERPs. The accuracy of the estimated ERPs is assessed against the final IERS ERP product as the reference standard. In the observation setup, each IGSO satellite monitors a visible MEO satellite located on a fixed orbital plane. When the observed MEO satellite becomes non-visible, another visible MEO satellite within the same orbital plane is selected for observation. Measurements are acquired at 15 min intervals, with simulated orientation noise levels of 0.05, 0.5, and 5 mas. Five technical schemes are designed for comparison, as detailed in

Table 5. ERP estimation strategies under different schemes.

Scheme	Data Source	Orientation Noise	Polar Motion Parameter Around the x-Axis	Polar Motion Parameter Around the y-Axis	UT1-UTC
1	Satellite-to-ground + inter-satellite	-	Weak constraint (0.1)	Weak constraint (0.1)	-
2	Satellite-to-ground + orientation	5 mas	No constraint	No constraint	No constraint
3	Satellite-to-ground + inter-satellite + orientation	5 mas	No constraint	No constraint	No constraint
4	Satellite-to-ground + inter-satellite + orientation	0.5 mas	No constraint	No constraint	No constraint
5	Satellite-to-ground + inter-satellite + orientation	0.05 mas	No constraint	No constraint	No constraint

. Scheme 1 utilizes satellite-to-ground and inter-satellite data. Scheme 2 combines satellite-to-ground and orientation data with 5 mas measurement noise. Scheme 3 integrates satellite-to-ground, inter-satellite, and orientation data (5 mas noise). Scheme 4 uses the same data sources as Scheme 3 but with 0.5 mas orientation noise. Scheme 5 further reduces the orientation measurement noise to 0.05 mas while maintaining the same data configuration.

The ERP estimation accuracy statistics under the five schemes are summarized in

Table 6. Statistics of ERP estimation results under different schemes.

Scheme	Polar Motion Parameter Around the x-Axis (mas)	Polar Motion Parameter Around the y-Axis (mas)	UT1-UTC (ms)
1	1.13	−6.38	-
2	13.91	−22.68	1.37
3	2.23	−3.55	0.42
4	2.01	−3.50	0.41
5	2.07	−3.41	0.39

.

The following conclusions can be drawn from the table:

(1) Under satellite-to-ground and inter-satellite joint measurement conditions, owing to the linear correlation between $\mathrm{\Omega }$ and UT1-UTC, simultaneously estimating the orbital and ERPs results in a rank deficiency in the normal equation, making it impossible to solve for the UT1-UTC parameter.

(2) The combination of satellite-to-ground measurement and space-based orientation data can facilitate the estimation of ERPs, but the estimation accuracy is relatively low. The accuracies of the polar motion parameters xp and yp are 13.91 mas and 22.68 mas, respectively, and the accuracy of the UT1-UTC parameter is 1.37 ms. This is because, under these circumstances, only regional stations impose strong constraints on satellite orbits, resulting in low accuracies of the calculated satellite orbits and thus inferior ERP calculation accuracies.

(3) After inter-satellite measurements are added to satellite-to-ground and space-based orientation measurements, the accuracy of ERPs is significantly improved. When the noise of space-based orientation measurements is 5 mas, the accuracies of the polar motion parameters xp and yp are 2.23 mas and 3.55 mas, respectively, and the accuracy of the UT1-UTC parameter is 0.42 ms.

(4) Under the joint support of satellite-to-ground, inter-satellite, and space-based orientation data, the ERP accuracy gradually improves as the space-based orientation measurement noise is reduced from 5 mas to 0.5 mas and then to 0.05 mas, but the accuracies are all comparable without any difference in the order of magnitude. The good constellation geometry and rich measurement data determine the accuracy of the ERP calculation, and a space-based orientation measurement noise error within 5 mas will not significantly reduce the orbit determination accuracy.

At present, the precision of the polar motion parameters xp and yp in the IERS ERP rapid product is better than 0.1 mas, and the precision of the UT1-UTC parameter is better than 0.1 ms [27]. Although the accuracy of the ERPs calculated in this study is not as high as that of the IERS products, the proposed method can achieve ERP calculations on the basis solely of the BeiDou satellite navigation system. It only requires the deployment of star sensors on BeiDou satellites, without relying on other measurement methods such as the SLR and VLBI. With the addition of space-based orientation measurements to satellite-to-ground and inter-satellite measurements, all-weather and continuous measurements can be achieved for BeiDou satellites. In practical BeiDou engineering applications, the proposed ERP calculation method can be used in semi-autonomous operation mode, which can serve as a backup for ERP determination and provide technical support for China’s independent ERP determination.

6. Conclusions

This study systematically investigated an autonomous orbit determination method for BeiDou satellites by integrating satellite-to-ground, inter-satellite, and space-based orientation observations and introduced a method to calculate ERP. Autonomous and semi-autonomous operation modes are designed for BeiDou satellites, and the orbit determination and ERP calculation accuracies under different satellite operation modes are analyzed via measured BeiDou data. The following conclusions are drawn:

(1) Under autonomous operation with 90-day predicted ERPs, the 3D position accuracy of BeiDou satellite orbits in the Earth-fixed reference frame is 9.31 m when relying solely on inter-satellite link data. With the incorporation of space-based orientation observations, this accuracy improves to 8.42 m. However, significant errors persist in the along-track and cross-track directions, primarily due to unresolved overall constellation rotation relative to the Earth-fixed frame. In contrast, the 3D orbit accuracy in the inertial reference frame under the same prediction conditions reaches 0.45 m, representing a substantial improvement over the Earth-fixed frame results. These findings demonstrate that space-based orientation data effectively addresses the constellation rotation issue within the inertial frame. Nevertheless, achieving accurate spatial orientation of BeiDou satellites relative to the Earth-fixed reference system necessitates the inclusion of ground-based station measurements.

(2) Compared to autonomous operation, uploading ERPs from a mobile ground station to the satellite every three days enhances the 3D orbit determination accuracy from 8.42 m to 0.49 m. In the absence of ERP updates, establishing a Ka-band link between the ground station and the satellite for satellite-to-ground measurements improves the 3D position accuracy from 8.42 m to 3.1 m. Thus, incorporating high-precision ERPs and satellite-to-ground measurement data effectively compensates for the overall constellation rotation in the Earth-fixed reference frame.

(3) With the support of inter-satellite links and space-based orientation data in semi-autonomous mode, updating the ERPs on the satellite every three days enables decimeter-level accuracy in 3D orbit determination. When the satellite relies on ERPs predicted over a 90-day horizon, the 3D position accuracy remains at the meter level, even with the inclusion of satellite-to-ground measurement data. In summary, large errors in ERPs significantly degrade the accuracy of autonomous orbit determination.

(4) When the ERPs of the satellite are updated every 3 days in semi-autonomous mode, the 3D position accuracy of the BeiDou satellite orbit is 0.29 m without satellite-to-ground data support, which is comparable to the 0.49 m accuracy with satellite-to-ground data support. Therefore, the mobile ground station can only establish a link with the satellite for a short period when necessary and change its location after the ERPs are uploaded, which can greatly improve the wartime resistance of the ground anchor station.

(5) In semi-autonomous operation mode, when the space-based orientation measurement adopts the 8 h cycle scanning mode and the “visibility equals observability” mode, the 3D position accuracies of the BeiDou satellite orbit are 3.1 m and 2.17 m, respectively. The scanning mode has only three orientation observation data records at a certain moment, whereas the “visibility equals observability” mode increases the number of orientation observation data to hundreds. Therefore, the orbit accuracy of the latter is higher than that of the former, although it does not differ by an order of magnitude. Considering the satellite platform characteristics and engineering implementation costs, the use of the scanning measurement mode for space-based orientation measurement is recommended.

(6) Relying solely on satellite-to-ground and inter-satellite measurements is insufficient for calculating the complete set of ERPs. However, incorporating space-based orientation measurements enables integrated, high-precision estimation of both satellite orbits and ERPs. When the noise level of space-based orientation measurements is 5 mas, the resulting accuracies for the polar motion parameters xp and yp are 2.23 mas and 3.55 mas, respectively, while the accuracy of the UT1–UTC parameter reaches 0.42 ms. Although the ERP accuracy obtained in this study does not match that of IERS products, the proposed method enables ERP estimation solely through the BeiDou satellite navigation system, without reliance on external measurement techniques such as SLR or VLBI. This novel approach offers a foundation for independent ERP determination in China.

This study investigates a joint space-based and ground-based support methodology for autonomous orbit determination of BeiDou satellites, along with an ERP calculation approach that integrates space-based orientation data. The proposed framework aims to provide technical support for the development of the next-generation BeiDou navigation system. It is recommended that star sensors be deployed on BeiDou IGSO satellites, utilizing either staring or scanning measurement modes, with orientation measurement errors constrained to within 10 mas. Mobile ground stations can establish short-term communication with satellites and relocate after uploading ERPs. This strategy eliminates the need for sustained satellite-to-ground measurements and enhances the resilience of ground anchor stations under wartime conditions.