Future Scenarios of Global Urban Expansion and Carbon Emissions with National Heterogeneity: A Mixed-Effects Model Based on Urban Nighttime Lights
Abstract
Highlights
- Scenario-based projections of urban expansion and CO2 emissions for 555 global cities from 2017 to 2053 are generated using a mixed-effects model under five Shared Socioeconomic Pathways–Representative Concentration Pathways (SSP–RCP) scenarios.
- National and regional heterogeneity is evident: developed cities may experience stabilization or even shrinkage under certain scenarios, whereas developing cities, particularly in Asia and Africa, are projected to undergo rapid expansion.
- Total urban area is projected to increase across all scenarios. In regionally fragmented and socially unequal pathways (e.g., SSP3–RCP6.0), urban growth is constrained but emissions remain high. Meanwhile, high-growth, fossil fuel–driven pathways are associated with extensive urban sprawl and elevated emissions, while sustainable scenarios foster compact, low-carbon development.
- The results indicate that region-specific policies and early planning are essential to align urbanization trajectories with global climate mitigation goals.
Abstract
1. Introduction
2. Literature Review
2.1. Urban Expansion Studies
2.2. Urban CO2 Emissions Studies
2.3. Contributions of This Study
3. Materials and Methods
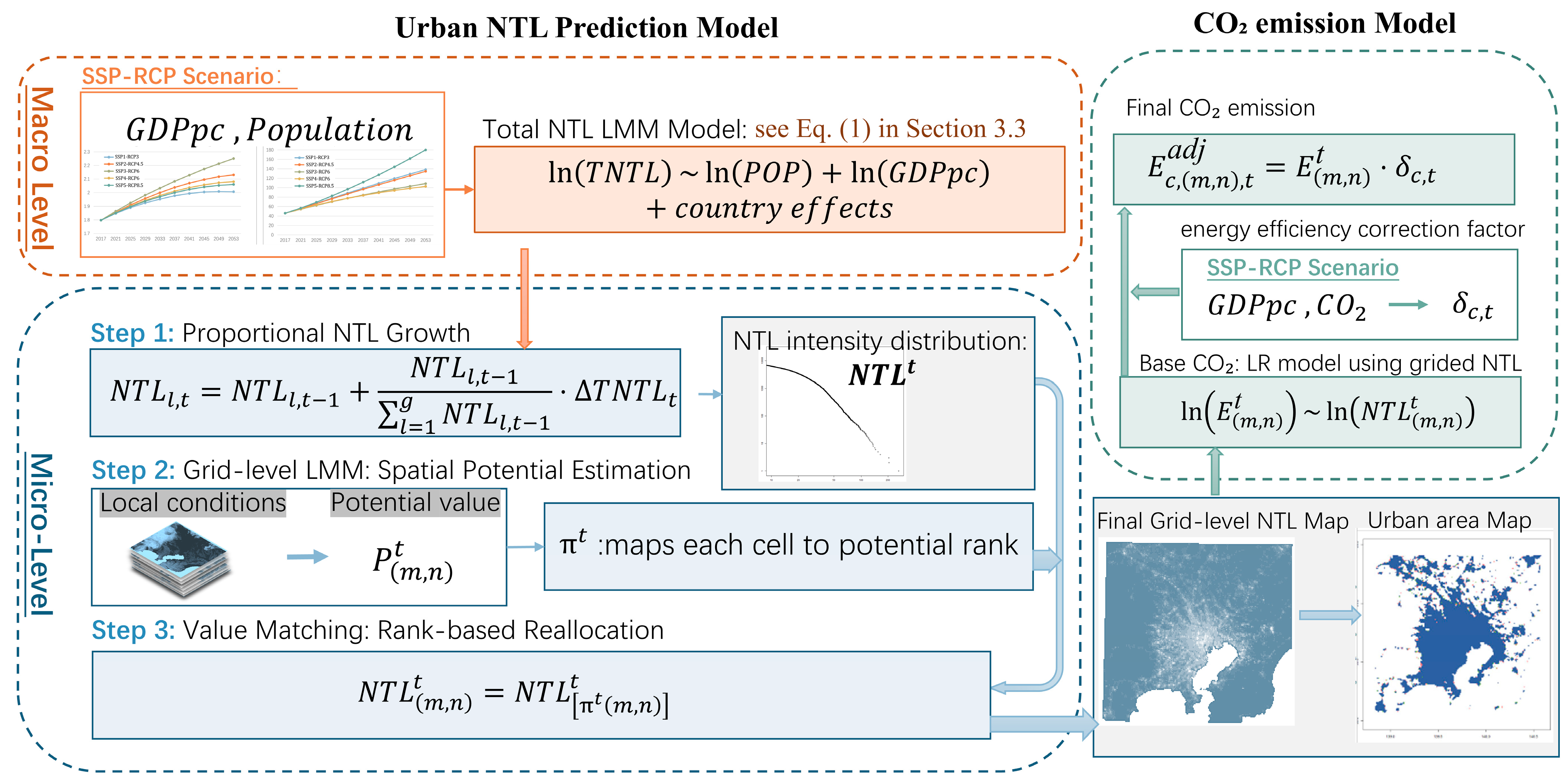
3.1. Framework Overview
3.2. Data Sources and Preprocessing
3.3. Modeling Framework
3.3.1. Urban Nighttime Light (NTL) Prediction Model
- (i)
- Macro-Level Model
- (ii)
- Micro-Level Model
3.3.2. Emissions Estimation Model
3.4. Validation
3.4.1. Macro-Level Model
3.4.2. Grid-Level Potential Model in Micro-Level Model
3.4.3. CO2 Emission Prediction Model
4. Results
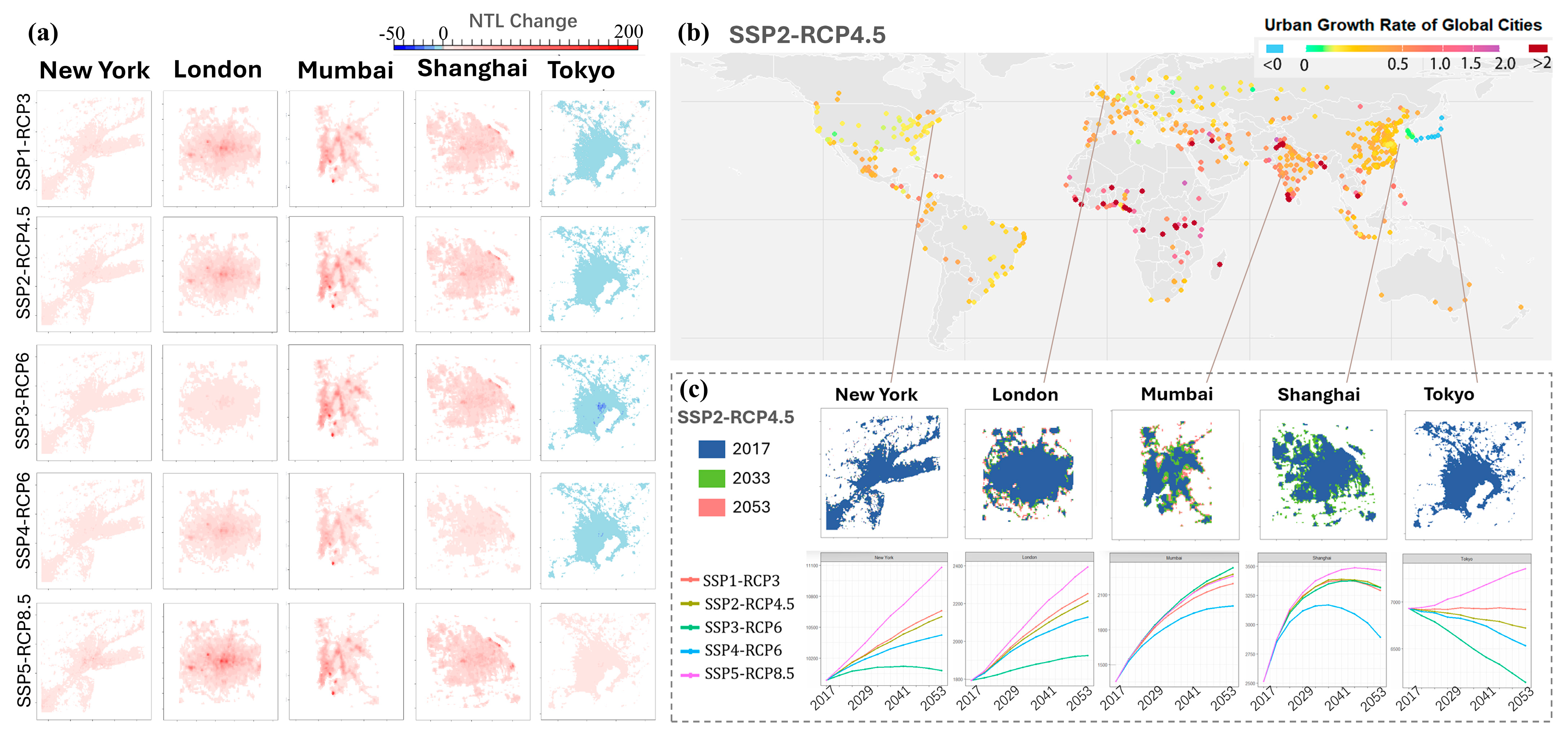
4.1. NTL and Urban Area Results for Selected Cities
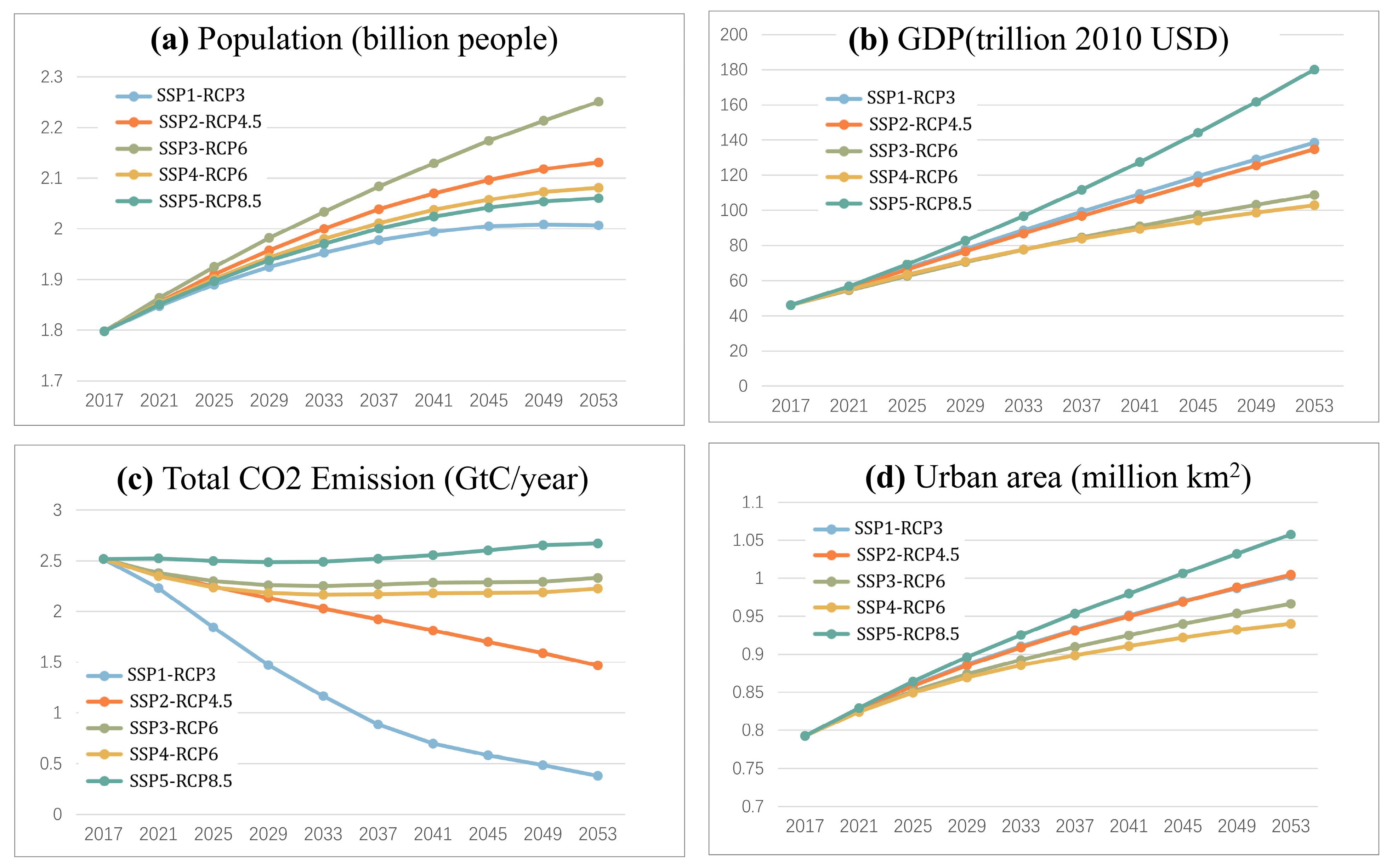
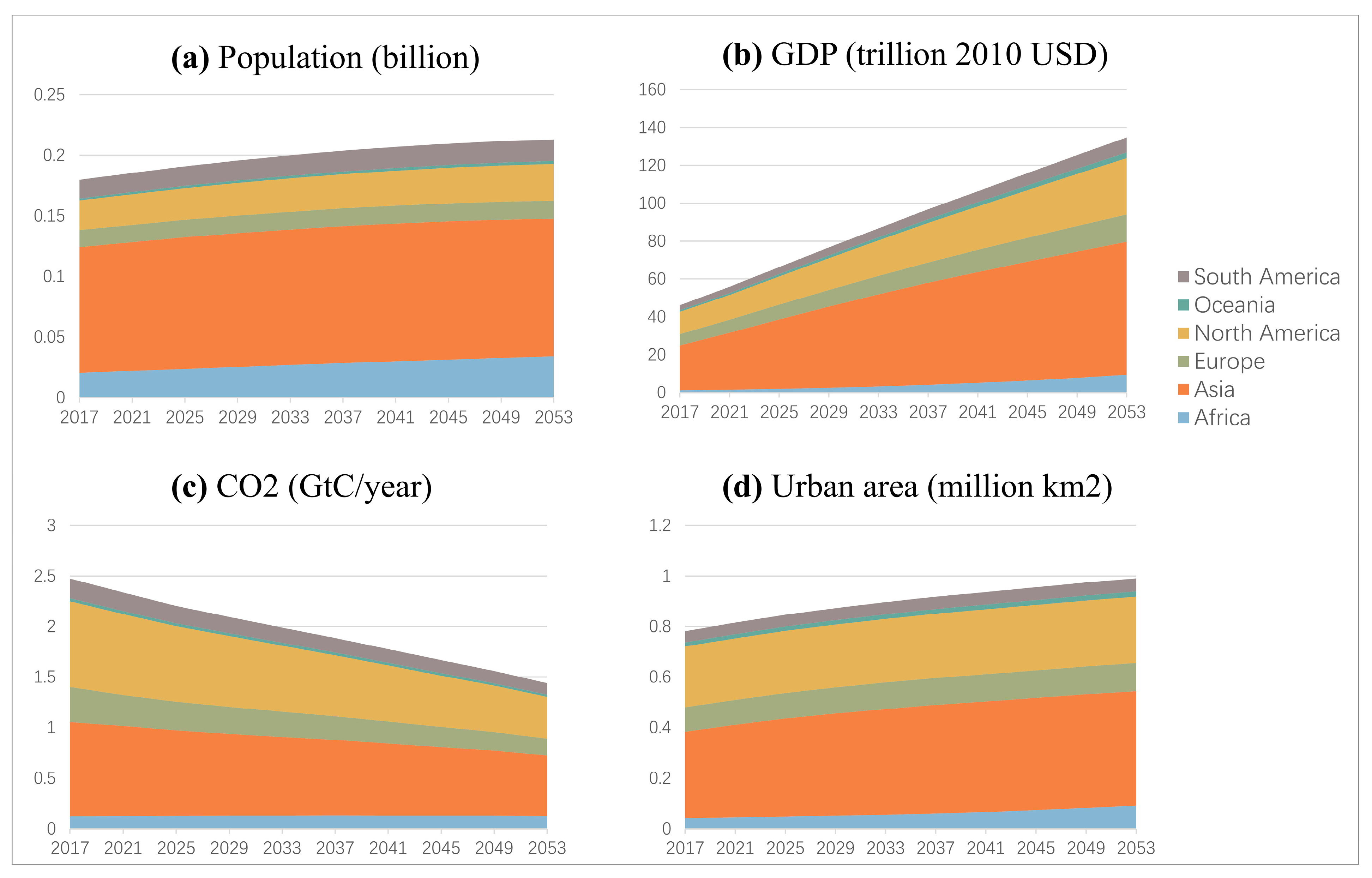
4.2. Projected Urban Expansion and CO2 Emissions of 555 Global Cities
5. Discussion
5.1. Scenario-Based Urban Expansion Trends and Their Policy Implications
5.2. Carbon Emission and Spatial Expansion Risks Under Diverging Urbanization Pathways
5.3. Limitations and Directions for Future Research
5.3.1. Model Structure and Theoretical Simplifications
5.3.2. Spatial and Temporal Limitations
5.3.3. Scaling and Representation Constraints
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Human Settlements Programme (UN-Habitat). World Cities Report 2022: Envisaging the Future of Cities; UN-Habitat: Nairobi, Kenya, 2022. [Google Scholar]
- Krayenhoff, E.S.; Moustaoui, M.; Broadbent, A.M.; Gupta, V.; Georgescu, M. Diurnal interaction between urban expansion, climate change and adaptation in US cities. Nat. Clim. Change 2018, 8, 1097–1103. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Z.; Zhao, X.; Wang, X.; Zuo, L.; Wen, Q.; Yi, L.; Xu, J.; Hu, S.; Liu, B. Chinese cropland losses due to urban expansion in the past four decades. Sci. Total Environ. 2019, 650, 847–857. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhan, J.; Zhao, F.; Yan, H.; Zhang, F.; Wei, X. Impacts of urbanization-induced land-use changes on ecosystem services: A case study of the Pearl River Delta Metropolitan Region, China. Ecol. Indic. 2019, 98, 228–238. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M.; Güneralp, B.; Reilly, M.K. A meta-analysis of global urban land expansion. PLoS ONE 2011, 6, e23777. [Google Scholar] [CrossRef] [PubMed]
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Liu, F.; Zhao, X.; Wang, X.; Shi, L.; Xu, J.; Yu, S.; Wen, Q.; Zuo, L.; Yi, L. Urban expansion in China based on remote sensing technology: A review. Chin. Geogr. Sci. 2018, 28, 727–743. [Google Scholar] [CrossRef]
- Poelmans, L.; Van Rompaey, A. Complexity and performance of urban expansion models. Comput. Environ. Urban Syst. 2010, 34, 17–27. [Google Scholar] [CrossRef]
- Din, S.U.; Yamamoto, K. Urban spatial dynamics and geo-informatics prediction of Karachi from 1990–2050 using remote sensing and CA-ANN simulation. Earth Syst. Environ. 2024, 8, 849–868. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Shi, K.; Liu, S.; Chang, Z. Exploring the effect of urban sprawl on carbon dioxide emissions: An urban sprawl model analysis from remotely sensed nighttime light data. Environ. Impact Assess. Rev. 2022, 93, 106731. [Google Scholar] [CrossRef]
- Duan, X.; Hu, Q.; Zhao, P.; Wang, S.; Ai, M. An approach of identifying and extracting urban commercial areas using the nighttime lights satellite imagery. Remote Sens. 2020, 12, 1029. [Google Scholar] [CrossRef]
- Tong, L.; Hu, S.; Frazier, A.E. Mixed accuracy of nighttime lights (NTL)-based urban land identification using thresholds: Evidence from a hierarchical analysis in Wuhan Metropolis, China. Appl. Geogr. 2018, 98, 201–214. [Google Scholar] [CrossRef]
- Liu, H.; Luo, N.; Hu, C. Detection of county economic development using LJ1-01 nighttime light imagery: A comparison with NPP-VIIRS data. Sensors 2020, 20, 6633. [Google Scholar] [CrossRef]
- Wan, W.; Chen, H.; Yang, X.; Li, R.; Cui, Y.; Hu, Y. Identifying the Hierarchical Structure of Nighttime Economic Agglomerations Based on the Fusion of Multisource Data. ISPRS Int. J. Geo-Inf. 2024, 13, 188. [Google Scholar] [CrossRef]
- Wu, J.; Tu, Y.; Chen, Z.; Yu, B. Analyzing the Spatially Heterogeneous Relationships between Nighttime Light Intensity and Human Activities across Chongqing, China. Remote Sens. 2022, 14, 5695. [Google Scholar] [CrossRef]
- Liu, B.; Lv, J. Spatiotemporal Evolution and Tapio Decoupling Analysis of Energy-Related Carbon Emissions Using Nighttime Light Data: A Quantitative Case Study at the City Scale in Northeast China. Energies 2024, 17, 4795. [Google Scholar] [CrossRef]
- Kii, M.; Matsumoto, K.; Sugita, S. Future Scenarios of Urban Nighttime Lights: A Method for Global Cities and Its Application to Urban Expansion and Carbon Emission Estimation. Remote Sens. 2024, 16, 1018. [Google Scholar] [CrossRef]
- Laird, N.M.; Ware, J.H. Random-effects models for longitudinal data. Biometrics 1982, 38, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Van Vuuren, D.P.; Kriegler, E.; O’Neill, B.C.; Ebi, K.L.; Riahi, K.; Carter, T.R.; Edmonds, J.; Hallegatte, S.; Kram, T.; Mathur, R. A new scenario framework for climate change research: Scenario matrix architecture. Clim. Change 2014, 122, 373–386. [Google Scholar] [CrossRef]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.; Potere, D. The dimensions of global urban expansion: Estimates and projections for all countries, 2000–2050. Prog. Plan. 2011, 75, 53–107. [Google Scholar] [CrossRef]
- Gao, C.; Feng, Y.; Tong, X.; Lei, Z.; Chen, S.; Zhai, S. Modeling urban growth using spatially heterogeneous cellular automata models: Comparison of spatial lag, spatial error and GWR. Comput. Environ. Urban Syst. 2020, 81, 101459. [Google Scholar] [CrossRef]
- Huang, B.; Xie, C.; Tay, R. Support vector machines for urban growth modeling. Geoinformatica 2010, 14, 83–99. [Google Scholar] [CrossRef]
- Mohammady, S.; Delavar, M.R. Urban sprawl assessment and modeling using landsat images and GIS. Model. Earth Syst. Environ. 2016, 2, 155. [Google Scholar] [CrossRef]
- Mozaffaree Pour, N.; Oja, T. Prediction Power of Logistic Regression (LR) and Multi-Layer Perceptron (MLP) Models in Exploring Driving Forces of Urban Expansion to Be Sustainable in Estonia. Sustainability 2022, 14, 160. [Google Scholar] [CrossRef]
- Rana, M.S.; Sarkar, S. Prediction of urban expansion by using land cover change detection approach. Heliyon 2021, 7, e08437. [Google Scholar] [CrossRef] [PubMed]
- Al-shalabi, M.; Billa, L.; Pradhan, B.; Mansor, S.; Al-Sharif, A.A. Modelling urban growth evolution and land-use changes using GIS based cellular automata and SLEUTH models: The case of Sana’a metropolitan city, Yemen. Environ. Earth Sci. 2013, 70, 425–437. [Google Scholar] [CrossRef]
- Boulila, W.; Ghandorh, H.; Khan, M.A.; Ahmed, F.; Ahmad, J. A novel CNN-LSTM-based approach to predict urban expansion. Ecol. Inform. 2021, 64, 101325. [Google Scholar] [CrossRef]
- Chettry, V.; Surawar, M. Delineating urban growth boundary using remote sensing, ANN-MLP and CA model: A case study of Thiruvananthapuram urban agglomeration, India. J. Indian Soc. Remote Sens. 2021, 49, 2437–2450. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Gao, J.; O’Neill, B.C. Mapping global urban land for the 21st century with data-driven simulations and Shared Socioeconomic Pathways. Nat. Commun. 2020, 11, 2302. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.; Liu, X.; Chen, Y.; Liang, X.; Leng, J.; Xu, X.; Liao, W.; Qiu, Y.; Wu, Q. Global projections of future urban land expansion under shared socioeconomic pathways. Nat. Commun. 2020, 11, 537. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Mertes, C.M.; Schneider, A.; Sulla-Menashe, D.; Tatem, A.; Tan, B. Detecting change in urban areas at continental scales with MODIS data. Remote Sens. Environ. 2015, 158, 331–347. [Google Scholar] [CrossRef]
- Matci, D.K. Development of a new index for mapping urban areas in Türkiye using Sentinel-2 images. Adv. Space Res. 2023, 72, 4677–4691. [Google Scholar] [CrossRef]
- Bagan, H.; Yamagata, Y. Analysis of urban growth and estimating population density using satellite images of nighttime lights and land-use and population data. GISci. Remote Sens. 2015, 52, 765–780. [Google Scholar] [CrossRef]
- Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Pettit, C.; Jiang, B.; Haworth, J.; Stein, A. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef]
- Zhang, Q.; Schaaf, C.; Seto, K.C. The vegetation adjusted NTL urban index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ. 2013, 129, 32–41. [Google Scholar] [CrossRef]
- He, X.; Zhang, Z.; Yang, Z. Extraction of urban built-up area based on the fusion of night-time light data and point of interest data. R. Soc. Open Sci. 2021, 8, 210838. [Google Scholar] [CrossRef]
- Kii, M.; Tamaki, T.; Suzuki, T.; Nonomura, A. Estimating urban spatial structure based on remote sensing data. Sci. Rep. 2023, 13, 8804. [Google Scholar] [CrossRef]
- Xin, X.; Liu, B.; Di, K.; Zhu, Z.; Zhao, Z.; Liu, J.; Yue, Z.; Zhang, G. Monitoring urban expansion using time series of night-time light data: A case study in Wuhan, China. In Remote Sensing of Night-Time Light; Routledge: London, UK, 2021; pp. 256–274. [Google Scholar]
- Liu, Z.; He, C.; Zhang, Q.; Huang, Q.; Yang, Y. Extracting the dynamics of urban expansion in China using DMSP-OLS nighttime light data from 1992 to 2008. Landsc. Urban Plan. 2012, 106, 62–72. [Google Scholar] [CrossRef]
- Kii, M.; Matsumoto, K. Detecting Urban Sprawl through Nighttime Light Changes. Sustainability 2023, 15, 16506. [Google Scholar] [CrossRef]
- Xiao, P.; Wang, X.; Feng, X.; Zhang, X.; Yang, Y. Detecting China’s urban expansion over the past three decades using nighttime light data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4095–4106. [Google Scholar] [CrossRef]
- Moran, D.; Kanemoto, K.; Jiborn, M.; Wood, R.; Többen, J.; Seto, K.C. Carbon footprints of 13,000 cities. Environ. Res. Lett. 2018, 13, 064041. [Google Scholar] [CrossRef]
- Wang, G.; Han, Q.; de Vries, B. A geographic carbon emission estimating framework on the city scale. J. Clean. Prod. 2020, 244, 118793. [Google Scholar] [CrossRef]
- Fang, G.; Gao, Z.; Tian, L.; Fu, M. What drives urban carbon emission efficiency?—Spatial analysis based on nighttime light data. Appl. Energy 2022, 312, 118772. [Google Scholar] [CrossRef]
- Song, M.; Wang, Y.; Han, Y.; Ji, Y. Estimation Model and Spatio-Temporal Analysis of Carbon Emissions from Energy Consumption with NPP-VIIRS-like Nighttime Light Images: A Case Study in the Pearl River Delta Urban Agglomeration of China. Remote Sens. 2024, 16, 3407. [Google Scholar] [CrossRef]
- Jin, Y.; Sharifi, A.; Li, Z.; Chen, S.; Zeng, S.; Zhao, S. Carbon emission prediction models: A review. Sci. Total Environ. 2024, 927, 172319. [Google Scholar] [CrossRef]
- O’neill, B.C.; Dalton, M.; Fuchs, R.; Jiang, L.; Pachauri, S.; Zigova, K. Global demographic trends and future carbon emissions. Proc. Natl. Acad. Sci. USA 2010, 107, 17521–17526. [Google Scholar] [CrossRef]
- Gurney, K.R.; Kılkış, Ş.; Seto, K.C.; Lwasa, S.; Moran, D.; Riahi, K.; Keller, M.; Rayner, P.; Luqman, M. Greenhouse gas emissions from global cities under SSP/RCP scenarios, 1990 to 2100. Glob. Environ. Change 2022, 73, 102478. [Google Scholar] [CrossRef]
- Gütschow, J.; Jeffery, M.L.; Günther, A.; Meinshausen, M. Country-resolved combined emission and socio-economic pathways based on the Representative Concentration Pathway (RCP) and Shared Socio-Economic Pathway (SSP) scenarios. Earth Syst. Sci. Data 2021, 13, 1005–1040. [Google Scholar] [CrossRef]
- Kummu, M.; Taka, M.; Guillaume, J.H. Gridded global datasets for gross domestic product and human development index over 1990–2015. Sci. Data 2018, 5, 180004. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Zhizhin, M.; Ghosh, T.; Hsu, F.-C.; Taneja, J. Annual time series of global VIIRS nighttime lights derived from monthly averages: 2012 to 2019. Remote Sens. 2021, 13, 922. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S. A very high-resolution (1 km× 1 km) global fossil fuel CO2 emission inventory derived using a point source database and satellite observations of nighttime lights. Atmos. Chem. Phys. 2011, 11, 543–556. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S.; Andres, R.J. The Open-source Data Inventory for Anthropogenic Carbon dioxide (CO2), version 1 2016 (ODIAC2016): A global, monthly fossil-fuel CO2 gridded emission data product for 2 tracer transport simulations and surface flux inversions 3. Earth Syst. Sci. Data 2018, 10, 87–107. [Google Scholar] [CrossRef]
- ESA. Land Cover CCI Product User Guide Version 2; European Space Agency: Brussels, Belgium, 2017; p. 105. [Google Scholar]
- Kaya, Y. Impact of Carbon Dioxide Emission Control on GNP Growth: Interpretation of Proposed Scenarios; Intergovernmental Panel on Climate Change/Response Strategies Working Group (IPCC): Geneva, Switzerland, 1989. [Google Scholar]
- Lee, K.; Yun, S.-J.; Park, S. Varied drivers for reducing CO2 emissions in countries with legislated carbon neutrality targets: A Kaya identity clustering analysis. Environ. Dev. Sustain. 2025, 1–23. [Google Scholar] [CrossRef]
- Kii, M.; Akimoto, K.; Doi, K. Random-growth urban model with geographical fitness. Phys. A Stat. Mech. Its Appl. 2012, 391, 5960–5970. [Google Scholar] [CrossRef]
- Kii, M. Projecting future populations of urban agglomerations around the world and through the 21st century. Npj Urban Sustain. 2021, 1, 10. [Google Scholar] [CrossRef]
| Fixed Effects | Estimate | t-Value | Random Effects | Std. Dev. |
|---|---|---|---|---|
| −2.941 | −5.261 | 3.358 | ||
| 0.8413 | 19.865 | 0.2412 | ||
| 0.5973 | 10.513 | 0.3278 | ||
| 0.5019 | ||||
| Number of samples | 1665 | |||
| groups | 109 | |||
| Conditional R2 | 0.8496 | |||
| Variable Name | Description | Fixed Effects (Estimate) | Fixed Effects (t-Value) | Random Effects (Std. Dev.) |
|---|---|---|---|---|
| Nighttime light intensity in the previous year | 139.543 | |||
| Road travel time to city center | −4.335 | |||
| Distance to nearest road | −5.620 | |||
| Railway travel time to city center | −1.468 | |||
| Standard deviation of slope | −23.932 | |||
| Maximum daily precipitation | −0.244 | |||
| Focal total NTL from 8 surrounding cells in year t − 1 | 30.087 | |||
| Annual average temperature | −0.771 | |||
| Annual temperature variability (standard deviation) | −4.382 | |||
| Annual average precipitation | 4.468 | |||
| Population density of agglomeration | 2.211 | |||
| Per capita GDP of agglomeration | −0.802 | |||
| Intercept | 8.401 | |||
| Residual | ||||
| Number of samples | 2,555,832 | |||
| groups | 571 | |||
| Train R2 | 0.579 | test R2 | 0.566 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Kii, M.; Okano, Y.; Chou, C.-C. Future Scenarios of Global Urban Expansion and Carbon Emissions with National Heterogeneity: A Mixed-Effects Model Based on Urban Nighttime Lights. Remote Sens. 2025, 17, 3251. https://doi.org/10.3390/rs17183251
Xu J, Kii M, Okano Y, Chou C-C. Future Scenarios of Global Urban Expansion and Carbon Emissions with National Heterogeneity: A Mixed-Effects Model Based on Urban Nighttime Lights. Remote Sensing. 2025; 17(18):3251. https://doi.org/10.3390/rs17183251
Chicago/Turabian StyleXu, Jiaoyi, Masanobu Kii, Yoshinori Okano, and Chun-Chen Chou. 2025. "Future Scenarios of Global Urban Expansion and Carbon Emissions with National Heterogeneity: A Mixed-Effects Model Based on Urban Nighttime Lights" Remote Sensing 17, no. 18: 3251. https://doi.org/10.3390/rs17183251
APA StyleXu, J., Kii, M., Okano, Y., & Chou, C.-C. (2025). Future Scenarios of Global Urban Expansion and Carbon Emissions with National Heterogeneity: A Mixed-Effects Model Based on Urban Nighttime Lights. Remote Sensing, 17(18), 3251. https://doi.org/10.3390/rs17183251







