WSC-Net: A Wavelet-Enhanced Swin Transformer with Cross-Domain Attention for Hyperspectral Image Classification

Highlights

What are the main findings?

• A novel dual-branch architecture, WSC-Net, was developed to synergistically integrate a Swin Transformer backbone with a parallel Wavelet Transform Module via a new Cross-Domain Attention Fusion (CDAF) mechanism.
• The proposed WSC-Net consistently outperforms state-of-the-art hyperspectral image classification methods, demonstrating a superior ability to preserve fine-grained local details without sacrificing global contextual understanding.

What are the implications of the main findings?

• This study demonstrates that the intelligent fusion of spatial-domain and frequency-domain features is a highly effective strategy to overcome the inherent performance trade-offs of single-paradigm deep learning models in HSI analysis.
• The proposed Cross-Domain Attention Fusion (CDAF) module provides a flexible and powerful blueprint for integrating features from disparate domains, offering a promising pathway for developing more robust multi-modal and multi-scale models in remote sensing.

Abstract

This paper introduces the Wavelet-Enhanced Swin Transformer Network (WSC-Net), a novel dual-branch architecture that resolves the inherent tradeoff between global spatial contextual and fine-grained spectral details in hyperspectral image (HSI) classification. While transformer-based models excel at capturing long-range dependencies, their patch-based nature often overlooks intra-patch high-frequency details, hindering the discrimination of spectrally similar classes. Our framework synergistically couples a two-stage Swin transformer with a parallel Wavelet Transform Module (WTM) for local frequency information capture. To address the semantic gap between spatial and frequency domains, we propose the Cross-Domain Attention Fusion (CDAF) module—a bi-directional attention mechanism that facilitates intelligent feature exchange between the two streams. CDAF explicitly models cross-domain dependencies, amplifies complementary features, and suppresses noise through attention-guided integration. Extensive experiments on four benchmark datasets demonstrate that WSC-Net consistently outperforms state-of-the-art methods, confirming its effectiveness in balancing global contextual modeling with local detail preservation.

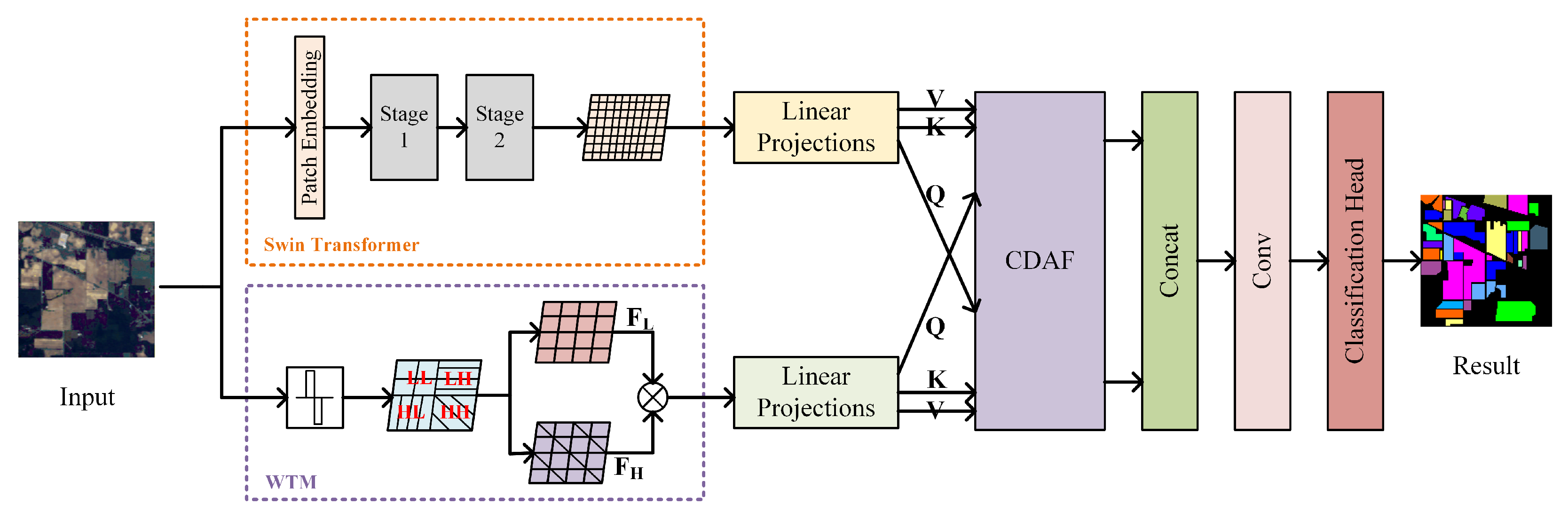
1. Introduction

Different sensors have been used for Earth observation, like infrared and synthetic aperture radar (SAR) [1,2,3]. Within this context, hyperspectral imaging, a cornerstone of modern remote sensing, can capture a wealth of information across hundreds of contiguous, narrow spectral bands, enabling fine-grained material discrimination and revolutionizing applications such as precision agriculture [4], environmental monitoring [5], urban planning [6], and mineral exploration [7,8]. The unique spectral signature contained in each pixel offers unparalleled potential for detailed land-cover mapping. However, the richness of HSI data also poses a major challenge. The so-called curse of dimensionality (Hughes phenomenon) [9] arises from the high number of spectral bands relative to the limited number of labeled training samples, which often leads to overfitting and poor generalization. In addition, HSI data commonly exhibit high intra-class spectral variability, inter-class similarity, the presence of mixed pixels due to low spatial resolution, and atmospheric or sensor-induced noise, making accurate pixel-wise classification challenging [10,11]. At the same time, accurately capturing the microscopic spectral–spatial details that are crucial for classification while effectively modeling the macroscopic spatial context and suppressing noise remains a core bottleneck for current advanced methods.

Traditional machine-learning algorithms, including Support Vector Machines (SVMs) [12], Random Forests (RFs) [13], k-Nearest Neighbors (KNNs) [14], and Multinomial Logistic Regression (MLR) [15], have been widely used for HSI classification. These approaches typically rely on spectral information, sometimes augmented with handcrafted spatial features, such as Gabor filters or Local Binary Patterns. While they can perform reasonably well on a small amount of data, these methods often struggle to capture the complex nonlinear relationships inherent in hyperspectral data and require extensive feature engineering [16].

The advent of deep learning, particularly convolutional neural networks (CNNs), has significantly advanced HSI classification by enabling hierarchical and automatic learning of spatial–spectral features [17,18]. Multiple CNN variants have been explored: 1D CNNs focus on deep spectral features [19], 2D CNNs utilize the spatial context of selected or reduced bands [20,21], and 3D CNNs jointly extract spatial and spectral features by convolving over the full data cube [22,23]. Hybrid architectures, such as HybridSN [24], which combine 3D CNNs for local feature extraction with 2D CNNs for broader spatial modeling, have shown promising performance in HSI classification. Building on this concept, several studies have further explored 2D-3D fusion strategies. For instance, Zhong et al. [25] developed the Spectral–Spatial Residual Network (SSRN), employing a hierarchical design that utilizes 3D convolutions for the initial feature extraction followed by 2D residual blocks to capture multi-level representations. Feng et al. [26] developed a hybrid convolutional neural network (OCT-MCNN) that integrates 3D octave convolutions with 2D vanilla convolutions for HSI classification. Additionally, the MDGCN framework [27] synergistically combines 3D CNNs and graph-based contextual modeling. To further enhance CNN performance, techniques like attention mechanisms [28], residual connections [29], and dilated convolutions [30] have been incorporated. However, a fundamental limitation of CNNs lies in their local receptive fields. While stacking many layers can enlarge the effective receptive field, capturing truly long-range dependencies and global contextual relationships efficiently remains a challenge, which is crucial for distinguishing spectrally ambiguous classes in complex scenes [31].

To overcome the global contextual modeling limitations of CNNs, transformer architectures, which have revolutionized Natural Language Processing (NLP) through their self-attention mechanism, have been successfully adapted for computer vision. The Vision Transformer (ViT) [32] has shown that pure transformer architectures can achieve state-of-the-art performance in image classification by treating image patches as token sequences. This has spurred significant interest in applying transformers to HSI classification [33,34]. The Swin transformer [35] has taken this further by introducing a hierarchical architecture and a shifted window-based self-attention mechanism, enabling more efficient modeling of multi-scale features and reducing computational complexity, making it particularly suitable for dense prediction tasks in remote sensing [36].

Building upon these foundation models, several studies have explored combining CNNs with transformers to leverage the local feature extraction strengths of CNNs and the global modeling capabilities of transformers for HSI classification. For example, Hong et al. [37] presented SpectralFormer, one of the first works that applied the transformer architecture, for HSI classification by modeling spectral sequences. Wang et al. [38] introduced a transformer architecture with CNN-enhanced cross-attention to fuse local and global features for improved HSI classification. Guerri et al. [39] introduced a gate-shift fuse block to a CNN–transformer model to improve the extraction of local features and global features by attention-driven fusion. These hybrid CNN–transformer approaches have demonstrated superior performance in HSI classification by effectively capturing both local spatial–spectral patterns and long-range dependencies through sophisticated attention mechanisms. However, because they rely primarily on CNNs for the perception of local features, these methods have inherited the limitations of CNNs in capturing non-local, frequency-based features. Fundamentally, the patch-based paradigm of the transformer backbone itself, while powerful for context, remains the primary bottleneck for preserving the fidelity of intra-patch details.

This patch-based limitation manifests in several critical shortcomings for current transformer-based HSI classification methods. First, the tokenization process, which flattens 2D or 3D patches to 1D vectors, inherently risks the loss of fine-grained local information. Subtle but diagnostically crucial details, such as the precise shape of a narrow spectral absorption feature or a delicate spatial texture, can be disrupted or averaged out before the self-attention mechanism even processes them [40]. The model operates on coarse, patch-level representations, potentially smoothing over the very high-frequency cues needed to distinguish spectrally similar classes. Then, transformers lack the strong inductive biases that are innate to CNNs [32]. This makes them more vulnerable to the noise and high spectral redundancy common in HSI data. The self-attention mechanism, without these constraints, can sometimes learn spurious correlations from noisy pixels or over-attend to redundant bands, degrading the quality of the learned features. Finally, it is well established that transformers are data-hungry models that typically require large-scale pretraining or extensive labeled data to achieve the optimal performance. This presents a significant practical challenge in remote sensing, where acquiring a large number of high-quality labeled samples for HSI is often difficult and expensive [41]. These limitations collectively motivate the exploration of alternative domains to complement the transformer’s powerful contextual modeling with enhanced fine-grained feature extraction and improved robustness.

To address these limitations and enhance fine-grained feature extraction, frequency-domain analysis, in particular, the wavelet transform, offers a powerful complementary approach for signal and image processing. Wavelet transforms decompose signals to frequency sub-bands at multiple scales and are excellent for capturing local transient features (e.g., edges and subtle peaks in spectra) and representing texture, while exhibiting inherent noise reduction capabilities through multi-resolution decomposition [42,43]. In the HSI domain, wavelet transforms have traditionally been used for tasks such as noise reduction [44], feature extraction for conventional classifiers [45], and band selection [46]. Some recent work has also begun to integrate wavelet transforms with CNNs for HSI classification, often using wavelet coefficients as input features or designing wavelet-inspired network layers [47,48]. While these applications demonstrate the utility of wavelets, the deep and synergistic integration with advanced transformer architectures remains a challenge. A critical, yet often overlooked, issue is the semantic gap between the hierarchical, context-rich features from a transformer and the fine-grained, location-specific details from a wavelet decomposition. Simply concatenating these features is unlikely to fully exploit their complementary strengths, potentially leading to suboptimal performance due to feature redundancy and semantic misalignment.

This work directly tackles the above-mentioned challenges. In brief, a novel framework, WSC-Net (Wavelet-Enhanced Swin Transformer with Cross-Domain Attention), that synergistically merges the features of these two distinct but complementary domains, is proposed. Its core is to introduce a dedicated wavelet analysis branch to extract multi-scale detailed features that might be overlooked by the Swin-transformer-based backbone. Crucially, and as the primary contribution of this work, we develop a Cross-Domain Attention Fusion (CDAF) module to enable intelligent and adaptive interaction between the wavelet-derived features and the Swin transformer’s contextual representations. This CDAF module is not a generic attention block but a purpose-built mechanism that allows features from one domain to selectively attend to and enhance features from the other, fostering a more discriminative and robust feature space for HSI classification. The main contributions of this work are summarized as follows:

• This paper proposes WSC-Net, a novel dual-branch architecture that effectively integrates wavelet-transform-based feature enhancement with a two-stage Swin transformer backbone, specifically adapted for HSI patch analysis, aiming to capture both global contextual and fine-grained local details;
• We introduce a Cross-Domain Attention Fusion (CDAF) module, the core innovation of WSC-Net. It facilitates the synergistic, bi-directional interaction and adaptive fusion of features from the wavelet domain and the spatial–spectral domain, overcoming the semantic gap that hinders simple fusion strategies and leading to richer and more robust feature representations;
• Extensive experiments on benchmark HSI datasets demonstrate that the proposed WSC-Net achieves superior classification performance compared to those of several state-of-the-art HSI classification methods.

The subsequent sections of this paper are organized as follows: Section 2 details the methodology, Section 3 reports on the experiments and delivers an analysis of the results. Section 4 provides an in-depth discussion of our findings and the model’s implications. Finally, Section 5 concludes the paper and suggests directions for future research.

2. Materials and Methods

The proposed Wavelet-Enhanced Swin Transformer with a Cross-Domain Attention Network (WSC-Net) is designed to accurately classify HSI by synergistically fusing multi-scale contextual information with fine-grained detail features. As illustrated in Figure 1, the architecture is structured as a dual-branch network. This process begins with data preprocessing, followed by two parallel feature extraction streams: a two-stage Swin transformer backbone for contextual features and a Wavelet Transform Module (WTM) for frequency-domain details. The core innovation lies in our Cross-Domain Attention Fusion (CDAF) module, which intelligently integrates features from both branches before a final classification head produces the land-cover predictions.

2.1. Dual-Branch Feature Extraction

Recognizing that spatial contextual and frequency-domain details are fundamentally different but complementary aspects of HSI data, we adopt a dual-branch architecture. This parallel design enables specialized and unimpeded feature extraction within each domain before their intelligent fusion, avoiding the potential feature degradation that can occur in sequential processing.

Both branches operate on preprocessed HSI data, which undergo a standardized preparation pipeline. The input HSI cube, $\mathcal{X}\in {\mathbb{R}}^{H\times W\times B}$ (where H and W denote the spatial height and width, and B represents the number of spectral bands), is first dimensionally reduced to ${\mathcal{X}}_{pca}\in {\mathbb{R}}^{H\times W\times B^{\prime }}$ via Principal Component Analysis (PCA) to reduce spectral redundancy and computational cost, where $B^{\prime }$ represents the reduced number of spectral bands. The reduced data are then partitioned into non-overlapping patches ($x_p\in {\mathbb{R}}^{P\times P\times B^{\prime }}$), where P denotes the patch size, providing the input format for both feature extraction branches.

2.1.1. Swin Transformer Backbone for Contextual Features

The primary branch of our network employs a two-stage Swin transformer backbone, adapted from the Swin–Tiny configuration [35], to extract a hierarchical pyramid of spatial–spectral features. The process begins with a patch embedding layer that projects each input patch (${\mathbf{x}}_p\in {\mathbb{R}}^{P\times P\times B^{\prime }}$) to a D-dimensional token. The core of the backbone is structured in two sequential stages to build a multi-scale representation suitable for HSI patch analysis. The first stage consists of a pair of Swin transformer blocks operating at the initial patch resolution. This is followed by a single patch-merging layer, which downsamples the spatial resolution of the feature map by a factor of 2 while doubling the feature dimension. The second stage then processes these downsampled, higher-dimension features with its own pair of Swin transformer blocks. This adaptation is necessary because the small spatial size of HSI patches (11 × 11) cannot sustain the multiple downsampling steps of a standard four-stage Swin transformer.

A pair of consecutive Swin transformer blocks is the fundamental computational unit. As illustrated in Figure 2, this pair comprises a block with Window-based Multi-head Self-Attention (W-MSA) and another with Shifted-Window-based MSA (SW-MSA). This design allows for efficient local attention computation within non-overlapping windows of size $M\times M$, while the shifting mechanism enables cross-window information flow, which is crucial for building a global receptive field. The process for two consecutive blocks (l and $l+1$) is formulated as follows:

$$\left\{\begin{array}{cc}\hfill {\widehat{\mathbf{z}}}^l& =\mathrm{W}-\mathrm{MSA}\left(\mathrm{LN}\left({\mathbf{z}}^{l-1}\right)\right)+{\mathbf{z}}^{l-1}\hfill \\ \hfill {\mathbf{z}}^l& =\mathrm{MLP}\left(\mathrm{LN}\left({\widehat{\mathbf{z}}}^l\right)\right)+{\widehat{\mathbf{z}}}^l\hfill \\ \hfill {\widehat{\mathbf{z}}}^{l+1}& =\mathrm{SW}-\mathrm{MSA}\left(\mathrm{LN}\left({\mathbf{z}}^l\right)\right)+{\mathbf{z}}^l\hfill \\ \hfill {\mathbf{z}}^{l+1}& =\mathrm{MLP}\left(\mathrm{LN}\left({\widehat{\mathbf{z}}}^{l+1}\right)\right)+{\widehat{\mathbf{z}}}^{l+1},\hfill \end{array}\right.$$

(1)

where ${\mathbf{z}}^{l-1}$ and ${\mathbf{z}}^{l+1}$ represent the input and output feature sequences, respectively, ${\widehat{\mathbf{z}}}^l$ and ${\widehat{\mathbf{z}}}^{l+1}$ denote intermediate feature representations, MLP represents the multi-layer perceptron, and LN(·) denotes layer normalization. To handle input feature maps of varying sizes that may not be perfectly divisible by the window size, dynamic padding is employed before the window-partitioning step. This two-stage hierarchical processing ultimately produces a rich feature representation ($F_{swin}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times D_{swin}}$), which encapsulates comprehensive multi-scale contextual understanding.

2.1.2. Wavelet Transform Module (WTM) for Detail Features

While the Swin transformer branch focuses on extracting hierarchical contextual features, the Wavelet Transform Module (WTM) operates in parallel to capture complementary fine-grained detail features. It takes the same preprocessed data ${\mathcal{X}}_{\mathrm{pca}}$ as input and applies a 2D Discrete Wavelet Transform (DWT). We select the Haar wavelet for its computational efficiency and its effectiveness in capturing step changes and local discontinuities, which are prevalent at object boundaries in HSI data.

As illustrated in Figure 3, for each spectral channel, ${\mathcal{X}}_{\mathrm{pca}}^{\left(b\right)}$ (where $b\in \{1,\dots ,B^{\prime }\}$), the DWT decomposes it to four sub-bands as follows:

$$L{L}^{\left(b\right)},L{H}^{\left(b\right)},H{L}^{\left(b\right)},H{H}^{\left(b\right)}=\mathrm{DWT}\left({\mathcal{X}}_{\mathrm{pca}}^{\left(b\right)}\right),$$

(2)

where $L{L}^{\left(b\right)}$ is the low-frequency approximation sub-band, and $L{H}^{\left(b\right)}, H{L}^{\left(b\right)}$, and $H{H}^{\left(b\right)}$ are the high-frequency detail sub-bands capturing horizontal, vertical, and diagonal information, respectively. After decomposing all the spectral channels, the sub-bands of the same type are stacked to form four multi-channel feature maps: $LL\in {\mathbb{R}}^{H/2\times W/2\times B^{\prime }}$, $LH\in {\mathbb{R}}^{H/2\times W/2\times B^{\prime }}$, $HL\in {\mathbb{R}}^{H/2\times W/2\times B^{\prime }}$, and $HH\in {\mathbb{R}}^{H/2\times W/2\times B^{\prime }}$. These multi-channel feature maps are then processed through separate convolutional mappings, ${\varphi }_L$ and ${\varphi }_H$, to create dedicated low-frequency and high-frequency feature streams as follows:

$$\left\{\begin{array}{cc}\hfill F_L& ={\varphi }_L\left(LL\right)\hfill \\ \hfill F_H& ={\varphi }_H\left(\mathrm{Concat}(LH,HL,HH)\right),\hfill \end{array}\right.$$

(3)

where $\mathrm{Concat}(·)$ denotes concatenation along the channel dimension. The two feature streams are then combined to form the complete wavelet feature representation as follows:

$$F_{\mathrm{wave}}=\mathrm{Concat}(F_L,F_H).$$

(4)

To ensure dimensional compatibility with the Swin transformer features for subsequent fusion, a spatial alignment operation,

$${\widehat{F}}_{\mathrm{wave}}=\mathrm{Align}\left(F_{\mathrm{wave}}\right)$$

(5)

is applied to $F_{\mathrm{wave}}$ to match the spatial resolution of $F_{\mathrm{swin}}$, where $\mathrm{Align}(·)$ can be implemented using strided convolution or adaptive pooling, resulting in the final aligned wavelet feature map (${\widehat{F}}_{\mathrm{wave}}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times D_{\mathrm{wave}}}$).

2.2. Cross-Domain Attention Fusion (CDAF) Module

To bridge the semantic gap between the context-rich spatial features extracted by the Swin transformer and the fine-grained frequency features captured by the WTM, WSC-Net introduces the Cross-Domain Attention Fusion (CDAF) module as its core component. This module adopts a bi-directional cross-attention mechanism to enable adaptive and synergistic integration between spatial and frequency-domain representations. Specifically, it allows features from each domain to dynamically query the other, selecting the most relevant information in a mutually reinforced manner. The overall architecture of the CDAF module is illustrated in Figure 4.

The module takes the Swin transformer output ($F_{\mathrm{swin}}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times D_{\mathrm{swin}}}$) and the aligned wavelet features (${\widehat{F}}_{\mathrm{wave}}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times D_{\mathrm{wave}}}$) as inputs. For compatibility with the attention mechanism, both feature maps are first flattened from their 2D spatial format to 1D sequences of tokens, resulting in a shape of ${\mathbb{R}}^{L\times D}$ (where $L=H^{\prime }{W}^{\prime }$). Following this, the reshaped features are projected to Query (Q), Key (K), and Value (V) spaces using separate learnable linear projections, ${\varphi }_s$ and ${\varphi }_w$ as follows:

$$Q_s,K_s,V_s={\varphi }_s\left(F_{\mathrm{swin}}\right);Q_w,K_w,V_w={\varphi }_w\left({\widehat{F}}_{\mathrm{wave}}\right).$$

(6)

where all the Q, K, and V tensors have the dimension ${\mathbb{R}}^{H^{\prime }{W}^{\prime }\times d_k}$, with $d_k$ being the feature dimension per attention head. With these projections, the cross-attention mechanism computes the attention-enhanced information, where features from one domain attend to the other. This bi-directional enhancement is formulated as follows:

$$A_{w\to s}=\mathrm{Softmax}\left({\displaystyle \frac{Q_s{K}_w^T}{\sqrt{d_k}}}\right)V_w;A_{s\to w}=\mathrm{Softmax}\left({\displaystyle \frac{Q_w{K}_s^T}{\sqrt{d_k}}}\right)V_s.$$

(7)

where $A_{w\to s}$ represents the wavelet information aggregated for the Swin branch, and $A_{s\to w}$ is the Swin context aggregated for the wavelet branch. The resulting attention outputs, $A_{w\to s}$ and $A_{s\to w}$, are subsequently integrated back into the original feature streams via learnable, weighted residual connections.

To accommodate potential dimensional inconsistencies before the residual addition, projection layers ${\pi }_s$ and ${\pi }_w$ are employed to align the attention outputs with the original feature dimensions as follows:

$$F_{\mathrm{swin}}^{\prime }=F_{\mathrm{swin}}+\alpha ·{\pi }_s\left(A_{w\to s}\right);{\widehat{F}}_{\mathrm{wave}}^{\prime }={\widehat{F}}_{\mathrm{wave}}+\beta ·{\pi }_w\left(A_{s\to w}\right),$$

(8)

where $\alpha$ and $\beta$ are learnable scalar parameters that are initialized to 1 and balance the fusion. These parameters act as dynamic gates, allowing the network to autonomously learn the optimal contribution level from each domain during training, thus preventing a static, hand-tuned fusion ratio and enabling a truly adaptive integration. Finally, the two enhanced feature maps are concatenated and passed through a fusion convolutional layer to produce the final output:

$$F_{\mathrm{fused}}={\mathrm{Conv}}_{\mathrm{fuse}}\left(\mathrm{Concat}(F_{\mathrm{swin}}^{\prime },{\widehat{F}}_{\mathrm{wave}}^{\prime })\right),$$

(9)

where $F_{\mathrm{fused}}\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times D_{\mathrm{fused}}}$, with $D_{\mathrm{fused}}$ being the desired output feature dimension. This resulting feature map, $F_{\mathrm{fused}}$, now contains a rich blend of global contextual and fine-grained details, making it a highly discriminative representation.

2.3. Loss Function

The entire WSC-Net is trained in an end-to-end fashion, guided by a unified optimization objective. To this end, the final discriminative feature map, $F_{\mathrm{fused}}$, is first passed through a classification head to generate class-wise predictions. This head comprises a Global Average Pooling (GAP) layer and a subsequent fully connected (FC) layer, which map the features to a vector of logits, $L\in {\mathbb{R}}^C$. These logits are then converted to a probability distribution using the Softmax function as follows:

$${\widehat{y}}_c={\displaystyle \frac{e^{L_c}}{{\sum }_{j=1}^C{e}^{L_j}}},$$

(10)

where ${\widehat{y}}_c$ represents the predicted probability for class c, and C is the total number of classes.

For the multi-class classification task, we employ the standard Cross-Entropy (CE) loss to measure the discrepancy between this predicted probability distribution and the one-hot encoded ground-truth label (y). The CE loss is formulated as follows:

$${\mathcal{L}}_{CE}=-\sum _{c=1}^C{y}_{c}log\left({\widehat{y}}_c\right),$$

(11)

where $y_c$ is the binary indicator (0 or 1) signifying if c is the correct class. By minimizing this loss function using backpropagation with the AdamW optimizer, all the learnable parameters in the network—including those in the Swin transformer backbone, the WTM, and the CDAF module—are jointly optimized to produce a highly discriminative model for HSI classification. The overall training and testing procedure of the proposed WSC-Net is summarized in Algorithm 1.

Algorithm 1: Training and testing procedures of WSC-Net.

3. Experiments and Results

3.1. Experimental Datasets and Evaluation Indicators

To comprehensively evaluate the performance of the proposed WSC-Net, we conducted extensive experiments on four widely used HSI datasets: Indian Pines (IP), Pavia University (PU), Salinas (SA), and Longkou (LK). These datasets were selected to cover a diverse range of characteristics, including varying spatial resolutions, spectral properties, scene complexities, and class distributions. This diversity provides a robust testbed for assessing the model’s effectiveness, generalization capability, and robustness. An overview of these datasets, including their false-color images and ground-truth maps, is presented in Figure 5. Detailed information on the land-cover classes and sample counts for each dataset is provided in

Table 1. Land-cover classes and the number of labeled samples for the experimental datasets.

Indian Pines			Pavia University			Salinas			Longkou
Category	Color	Samples	Category	Color	Samples	Category	Color	Samples	Category	Color	Samples
Alfalfa		46	Asphalt		6631	Broccoli 1		2009	Corn		34,511
Corn-notill		1428	Meadows		18,649	Broccoli 2		3726	Cotton		8374
Corn-mintill		830	Gravel		2099	Fallow		1976	Sesame		3031
Corn		237	Trees		3064	Rough Plow		1394	B-L soybean		63,212
Grass-pasture		483	P-metal sheets		1345	Smooth		2678	N-L soybean		4151
Grass-trees		730	Bare soil		5029	Stubble		3959	Rice		11,854
Grass-p-mowed		28	Bitumen		1330	Celery		3579	Water		67,056
Hay-windowed		478	S-B bricks		3682	U-Grapes		11,271	Roads/Houses		7124
Oats		20	Shadows		947	Vineyard Soil		6203	Mixed weed		5229
Soybean-notill		972				Green Weeds		3278
Soybean-mintill		2455				Romaine 4wk		1068
Soybean-clean		593				Romaine 5wk		1927
Wheat		205				Romaine 6wk		916
Woods		1265				Romaine 7wk		1070
B-G-T-Drives		386				U-Vineyard		7268
Stone-S-Towers		93				V-Trellis		1807
Total		10,249	Total		42,776	Total		54,129	Total		204,542

.

• Indian Pines (IP): The Indian Pines dataset was acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over a mixed agricultural and forest area in northwestern Indiana, USA. The scene comprises a spatial dimension of 145 × 145 pixels. It originally consists of 224 spectral bands spanning wavelengths from 0.4 to 2.5 μm, from which 24 water absorption and noisy bands were removed, resulting in 200 bands retained for experimentation. This dataset has 16 distinct land-cover classes. The classification task is particularly challenging due to the high spectral similarity among certain vegetation types and the severe class imbalance, where minority classes contain as few as 20 samples [49].
• Pavia University (PU): The Pavia University dataset was collected by the Reflective Optics System Imaging Spectrometer (ROSIS) sensor over an urban environment at the University of Pavia, Italy. The image has a spatial dimension of 610 × 340 pixels and a high spatial resolution of 1.3 m. After discarding 12 noisy bands, 103 spectral bands ranging from 0.43 to 0.86 μm were used for the analysis. This dataset encompasses nine urban structure classes. The complex urban scene, with its intricate spatial layouts and spectrally similar human-made materials, makes it a standard benchmark for testing a model’s fine-grained discrimination ability [50].
• Salinas (SA): The Salinas dataset was also captured by the AVIRIS sensor but over the Salinas Valley, California, an area with high agricultural uniformity. The image covers 512 × 217 pixels, with a high spatial resolution of 3.7 m. From the original 224 bands, 20 noisy and water absorption bands were removed, leaving 204 bands for the experiments. The dataset contains 16 agriculture-related classes, including various vegetables, fallow fields, and vineyard vines.
• Longkou (LK): The Longkou dataset was acquired by an airborne Headwall A-series hyperspectral imaging sensor over a coastal farming area in Longkou, Shandong Province, China [51]. This large-scale dataset has a spatial dimension of 550 × 400 pixels and a spatial resolution of about 0.46 m. It contains 270 spectral bands covering the 0.4 to 1.0 μm range. The dataset comprises 19 distinct classes, featuring a diverse mix of crops, trees, water, and human-made structures.

We evaluate WSC-Net and baseline methods using three widely adopted metrics for hyperspectral image classification: the overall accuracy (OA), average accuracy (AA), and kappa coefficient ($\kappa$). These metrics provide complementary insights into different aspects of the classification performance. Let N be the total number of test samples, C be the number of land-cover classes, and $M\in {\mathbb{R}}^{C\times C}$ be the confusion matrix, where the element $M_{ij}$ represents the number of samples from class i that were classified as class j.

• Overall Accuracy (OA): This metric represents the proportion of correctly classified pixels relative to the total number of test pixels. OA is

  $$\mathrm{OA}={\displaystyle \frac{{\sum }_{i=1}^C{M}_{ii}}{N}}.$$

  (12)
  However, OA can be biased toward majority classes in imbalanced datasets.
• Average Accuracy (AA): AA calculates the mean classification accuracy for each class, giving equal weight to all the classes regardless of the sample size. This provides a more balanced assessment across all the categories. AA is defined as follows:

  $$\mathrm{AA}={\displaystyle \frac{1}{C}}\sum _{i=1}^C{\displaystyle \frac{M_{ii}}{{\sum }_{j=1}^C{M}_{ij}}}.$$

  (13)
• Kappa Coefficient ($\kappa$): The kappa coefficient measures the agreement between the classification results and ground truth while correcting for chance agreement. It is computed as follows:

  $$\kappa ={\displaystyle \frac{N{\sum }_{i=1}^C{M}_{ii}-{\sum }_{i=1}^C\left({\sum }_{j=1}^C{M}_{ij}{\sum }_{j=1}^C{M}_{ji}\right)}{N^2-{\sum }_{i=1}^C\left({\sum }_{j=1}^C{M}_{ij}{\sum }_{j=1}^C{M}_{ji}\right)}}.$$

  (14)
  Higher kappa values (closer to 1) indicate better classification performance.

In addition to these three metrics, individual class accuracies will be reported to enable a fine-grained analysis of the model performance on specific land-cover types. All the results are averaged over multiple independent runs to ensure statistical significance.

3.2. Implementation Details

To ensure a fair comparison and reproducibility, all the experiments were conducted within a unified framework on a single NVIDIA Tesla V100 GPU using the PyTorch 1.12.1 framework. For data preparation, we first applied PCA to each HSI cube to reduce its spectral dimensionality, setting the number of principal components at 30 for the IP, SA, and LK datasets and at 15 for the PU dataset. These values were chosen based on common practice to retain over 99% of the spectral variance while reducing the computational overhead. From these reduced data cubes, spatial patches of size 11 × 11 were extracted around each labeled pixel to form the input for the networks. This patch size was determined to be optimal through a dedicated ablation study (Section 3.6), which balances the need for sufficient spatial context with the risk of introducing noise from irrelevant neighboring pixels. The training set for the IP dataset consisted of 5% of the samples from each class. For the SA, PU, and LK datasets, the training sets were composed of 0.5%, 1%, and 5% of the samples per class, respectively. These challenging, small-sample ratios were selected to rigorously test the model’s generalization capability. The remaining samples in each dataset were used for testing.

The architecture of our proposed WSC-Net is configured based on the Swin–Tiny variant, which has been adapted to effectively process the low spatial dimensions of HSI patches. The two-stage Swin transformer backbone is configured with depths of [2, 2] and numbers of attention heads of [3, 6] for each stage, respectively. This two-stage design is a specific adaptation for the small 11×11 HSI patches to prevent the excessive spatial downsampling that would occur in a standard four-stage architecture. The initial embedding dimension is set at ninety-six, and the attention window size is seven. WTM employs a single-level 2D Haar wavelet, chosen for its computational efficiency and effectiveness in capturing sharp local features, as validated in our ablation study (Section 3.6). The attention dimension ($d_k$) within the CDAF module was set at 64, a standard value for such mechanisms.

During training, all the models were optimized for 100 epochs using the AdamW optimizer with a learning rate of $5\times {10}^{-4}$ and a weight decay of 0.05. A cosine-annealing scheduler was used to adjust the learning rate, and the batch size was set at 64. These training hyperparameters were determined through preliminary experiments to ensure stable and efficient convergence across all the datasets. To ensure statistical significance, the final results reported are the average and standard deviation of 10 independent runs, each with a different random seed for data splitting and model initialization.

3.3. Comparison Methods

To thoroughly validate the effectiveness of the proposed method, we conducted a comprehensive comparative analysis against eight representative methods. These baselines were carefully selected to cover the main technological paradigms in HSI classification, including Support Vector Machines (SVMs) [12], 3D CNNs [22], the Hybrid Spectral–Spatial Network (HybridSN) [24], Vision Transformer (ViT) [32], the Hyperspectral Image Transformer (HiT) [52], Discrete Wavelet Transform and Dense CNN (DWTDense) [53], the Spectral–Spatial Feature Tokenization Transformer (SSFTT) [54], and the Spectral–Spatial Morphological Attention Transformer (MorphFormer) [55]. All the methods were implemented under the same experimental conditions for a fair and rigorous comparison.

3.4. Quantitative Results and Analysis

The comprehensive quantitative results of the proposed WSC-Net and the eight comparative methods across the four benchmark datasets are presented in

Table 2. Classification accuracy (%) for the IP dataset. The best result in each row is highlighted in bold.

No.	SVM	3D CNN	HybridSN	ViT	HiT	DWTDense	SSFTT	MorphFormer	Ours
1	0.00 ± 0.00	40.91 ± 1.05	45.45 ± 0.98	0.00 ± 0.00	27.50 ± 0.65	55.15 ± 0.88	47.73 ± 0.43	79.55 ± 0.15	68.29 ± 0.22
2	74.80 ± 1.02	88.87 ± 0.87	84.16 ± 0.65	80.62 ± 0.55	83.37 ± 0.41	91.52 ± 0.55	95.43 ± 0.32	94.18 ± 0.25	97.20 ± 0.18
3	48.67 ± 1.11	90.75 ± 0.92	89.99 ± 0.78	67.43 ± 0.64	85.75 ± 0.51	92.80 ± 0.61	95.18 ± 0.45	88.97 ± 0.33	96.92 ± 0.35
4	0.00 ± 0.00	89.33 ± 1.02	88.44 ± 0.88	82.22 ± 0.71	69.38 ± 0.63	91.22 ± 0.75	96.00 ± 0.54	94.67 ± 0.48	96.71 ± 0.41
5	75.16 ± 0.98	97.60 ± 0.76	95.86 ± 0.54	93.46 ± 0.43	91.53 ± 0.33	97.10 ± 0.31	96.30 ± 0.21	98.04 ± 0.11	94.48 ± 0.15
6	97.55 ± 0.87	99.71 ± 0.29	97.98 ± 0.43	99.28 ± 0.32	97.66 ± 0.21	98.80 ± 0.25	98.70 ± 0.15	99.57 ± 0.09	99.09 ± 0.08
7	0.00 ± 0.00	37.04 ± 1.54	59.26 ± 1.32	0.00 ± 0.00	60.00 ± 1.15	68.52 ± 1.21	66.67 ± 1.02	85.19 ± 0.98	100.00 ± 0.00
8	97.80 ± 0.76	100.00 ± 0.00	100.00 ± 0.00	99.78 ± 0.21	99.29 ± 0.15	100.00 ± 0.00	100.00 ± 0.00	99.34 ± 0.05	99.53 ± 0.00
9	0.00 ± 0.00	57.89 ± 1.87	36.84 ± 1.54	0.00 ± 0.00	33.33 ± 1.21	64.71 ± 1.95	15.79 ± 1.11	47.37 ± 1.01	72.22 ± 1.45
10	57.85 ± 1.21	88.30 ± 0.95	89.82 ± 0.87	78.11 ± 0.76	84.09 ± 0.65	91.14 ± 0.71	97.94 ± 0.54	95.34 ± 0.43	98.74 ± 0.28
11	91.47 ± 0.95	91.55 ± 0.76	90.01 ± 0.65	84.52 ± 0.54	88.85 ± 0.43	93.62 ± 0.41	95.63 ± 0.32	95.45 ± 0.21	98.37 ± 0.11
12	32.15 ± 1.11	75.67 ± 0.87	81.71 ± 0.76	69.27 ± 0.65	70.11 ± 0.54	85.30 ± 0.65	98.40 ± 0.43	97.69 ± 0.32	98.13 ± 0.23
13	69.74 ± 0.87	99.43 ± 0.20	97.44 ± 0.54	98.46 ± 0.43	97.78 ± 0.32	98.92 ± 0.28	92.82 ± 0.21	100.00 ± 0.00	95.14 ± 0.09
14	98.17 ± 0.76	98.00 ± 0.54	98.09 ± 0.43	95.34 ± 0.32	98.83 ± 0.15	98.51 ± 0.18	99.92 ± 0.08	100.00 ± 0.00	99.82 ± 0.05
15	6.81 ± 1.87	87.74 ± 1.32	84.47 ± 1.21	85.01 ± 1.01	91.18 ± 0.98	88.94 ± 1.05	98.09 ± 0.87	100.00 ± 0.00	99.14 ± 0.85
16	1.14 ± 0.98	100.00 ± 0.00	100.00 ± 0.00	76.14 ± 1.11	91.46 ± 1.01	95.52 ± 0.98	92.05 ± 0.95	98.86 ± 0.87	82.14 ± 1.05
OA (%)	72.45 ± 0.54	91.54 ± 0.41	90.60 ± 0.35	84.01 ± 0.28	88.15 ± 0.21	92.87 ± 0.38	96.49 ± 0.18	96.11 ± 0.16	97.81 ± 0.15
AA (%)	46.96 ± 0.65	83.93 ± 0.48	83.72 ± 0.41	69.35 ± 0.35	79.38 ± 0.28	87.14 ± 0.45	86.67 ± 0.21	92.14 ± 0.19	93.50 ± 0.11
$\kappa$ (×100)	67.42 ± 0.58	90.36 ± 0.45	89.31 ± 0.38	81.73 ± 0.31	86.46 ± 0.25	91.89 ± 0.42	96.00 ± 0.19	95.57 ± 0.17	97.50 ± 0.18

,

Table 3. Classification accuracy (%) for the PU dataset. The best result in each row is highlighted in bold.

No.	SVM	3D CNN	HybridSN	ViT	HiT	DWTDense	SSFTT	MorphFormer	Ours
1	95.80 ± 0.75	98.78 ± 0.31	98.26 ± 0.38	89.43 ± 1.12	94.14 ± 0.81	99.15 ± 0.25	98.77 ± 0.29	96.51 ± 0.25	99.92 ± 0.05
2	99.78 ± 0.11	99.68 ± 0.11	99.11 ± 0.19	98.80 ± 0.25	99.87 ± 0.08	99.75 ± 0.15	99.92 ± 0.06	97.87 ± 0.03	99.59 ± 0.12
3	58.52 ± 2.81	79.60 ± 1.82	83.69 ± 1.41	64.00 ± 2.51	74.01 ± 2.01	85.20 ± 1.35	83.64 ± 1.38	82.60 ± 1.25	86.62 ± 1.15
4	87.21 ± 1.32	94.13 ± 0.72	89.68 ± 1.15	88.36 ± 1.28	85.20 ± 1.48	93.50 ± 0.85	91.06 ± 0.95	93.35 ± 0.61	93.18 ± 0.82
5	99.89 ± 0.11	99.98 ± 0.02	99.96 ± 0.04	99.91 ± 0.09	96.10 ± 0.55	99.97 ± 0.03	99.97 ± 0.03	99.98 ± 0.02	100.00 ± 0.00
6	85.40 ± 1.38	93.50 ± 0.81	93.01 ± 0.88	89.30 ± 1.22	91.50 ± 0.99	95.80 ± 0.65	98.68 ± 0.21	96.63 ± 0.18	97.87 ± 0.35
7	35.76 ± 3.55	99.01 ± 0.25	98.71 ± 0.31	17.31 ± 4.51	76.92 ± 1.95	98.90 ± 0.28	96.23 ± 0.58	97.44 ± 0.15	100.00 ± 0.00
8	77.34 ± 1.85	83.21 ± 1.49	79.78 ± 1.75	76.24 ± 1.98	71.03 ± 2.21	90.50 ± 1.15	94.60 ± 0.68	92.02 ± 0.75	97.61 ± 0.41
9	47.92 ± 3.12	91.14 ± 0.98	92.42 ± 0.89	66.60 ± 2.45	77.80 ± 1.88	91.80 ± 0.95	93.00 ± 0.81	93.63 ± 0.55	87.19 ± 1.11
OA (%)	89.48 ± 0.95	95.81 ± 0.45	95.03 ± 0.49	88.63 ± 1.05	91.87 ± 0.85	96.55 ± 0.41	97.43 ± 0.28	95.72 ± 0.21	97.92 ± 0.22
AA (%)	76.40 ± 1.55	93.22 ± 0.61	92.73 ± 0.65	76.66 ± 1.81	85.17 ± 1.25	95.51 ± 0.52	95.06 ± 0.41	94.00 ± 0.32	95.78 ± 0.39
$\kappa$ (×100)	85.83 ± 1.15	94.43 ± 0.51	93.38 ± 0.56	84.78 ± 1.25	89.08 ± 0.98	95.42 ± 0.48	96.58 ± 0.35	94.84 ± 0.28	97.24 ± 0.29

,

Table 4. Classification accuracy (%) for the SA dataset. The best result in each row is highlighted in bold.

No.	SVM	3D CNN	HybridSN	ViT	HiT	DWTDense	SSFTT	MorphFormer	Ours
1	90.86 ± 0.95	99.95 ± 0.05	100.00 ± 0.00	94.85 ± 0.68	94.90 ± 0.65	98.10 ± 0.35	98.35 ± 0.25	97.50 ± 0.31	93.75 ± 0.75
2	100.00 ± 0.00	100.00 ± 0.00	99.89 ± 0.08	99.95 ± 0.05	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00
3	99.54 ± 0.15	99.69 ± 0.12	97.66 ± 0.35	99.49 ± 0.16	93.44 ± 0.78	100.00 ± 0.00	99.90 ± 0.07	100.00 ± 0.00	100.00 ± 0.00
4	49.50 ± 2.51	99.21 ± 0.21	96.25 ± 0.48	85.15 ± 1.25	89.47 ± 1.05	98.50 ± 0.55	99.86 ± 0.08	98.85 ± 0.25	99.64 ± 0.13
5	95.88 ± 0.55	94.41 ± 0.68	98.39 ± 0.28	94.75 ± 0.65	94.90 ± 0.63	98.80 ± 0.32	98.95 ± 0.22	99.47 ± 0.15	99.32 ± 0.18
6	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	99.95 ± 0.05	98.20 ± 0.12	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00
7	98.68 ± 0.25	99.94 ± 0.06	99.80 ± 0.10	99.52 ± 0.15	99.13 ± 0.21	99.90 ± 0.08	99.94 ± 0.06	100.00 ± 0.00	99.92 ± 0.07
8	87.27 ± 1.15	84.51 ± 1.35	79.04 ± 1.65	87.68 ± 1.11	82.28 ± 1.45	91.50 ± 0.95	85.25 ± 1.31	88.48 ± 1.05	92.96 ± 0.81
9	99.64 ± 0.13	99.98 ± 0.02	99.71 ± 0.11	99.61 ± 0.13	99.71 ± 0.11	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00	100.00 ± 0.00
10	96.30 ± 0.48	96.69 ± 0.45	95.46 ± 0.55	94.39 ± 0.68	95.80 ± 0.52	97.90 ± 0.38	98.93 ± 0.22	98.22 ± 0.29	98.74 ± 0.24
11	70.80 ± 1.85	87.11 ± 1.18	46.85 ± 2.65	96.80 ± 0.45	74.32 ± 1.75	97.50 ± 0.52	94.37 ± 0.68	95.01 ± 0.61	99.53 ± 0.15
12	99.84 ± 0.09	97.70 ± 0.33	97.70 ± 0.33	92.91 ± 0.81	99.58 ± 0.14	99.80 ± 0.11	99.95 ± 0.05	99.95 ± 0.05	99.95 ± 0.05
13	89.81 ± 1.01	99.89 ± 0.08	97.59 ± 0.35	55.43 ± 2.25	94.18 ± 0.71	98.60 ± 0.45	99.78 ± 0.11	98.90 ± 0.23	99.34 ± 0.17
14	67.39 ± 1.95	98.31 ± 0.29	92.86 ± 0.82	89.39 ± 1.05	84.79 ± 1.31	96.50 ± 0.68	78.82 ± 1.55	84.51 ± 1.33	87.51 ± 1.15
15	72.76 ± 1.78	81.73 ± 1.48	86.95 ± 1.19	73.66 ± 1.75	77.32 ± 1.65	89.60 ± 1.25	92.24 ± 0.85	87.54 ± 1.15	92.52 ± 0.83
16	98.72 ± 0.24	99.28 ± 0.18	99.39 ± 0.17	99.33 ± 0.18	74.19 ± 1.71	100.00 ± 0.00	99.89 ± 0.08	99.67 ± 0.12	100.00 ± 0.00
OA (%)	90.04 ± 0.95	93.41 ± 0.58	91.96 ± 0.71	91.32 ± 0.82	90.18 ± 0.91	94.85 ± 0.48	95.16 ± 0.41	95.24 ± 0.39	96.90 ± 0.28
AA (%)	88.56 ± 1.05	96.15 ± 0.42	92.97 ± 0.65	91.43 ± 0.85	90.87 ± 0.88	96.88 ± 0.36	96.64 ± 0.35	96.76 ± 0.31	97.70 ± 0.25
$\kappa$ (×100)	88.87 ± 1.01	92.67 ± 0.65	91.06 ± 0.78	90.33 ± 0.91	89.06 ± 1.01	94.26 ± 0.53	94.62 ± 0.45	94.70 ± 0.43	96.55 ± 0.31

and

Table 5. Classification accuracy (%) for the LK dataset. The best result in each row is highlighted in bold.

No.	SVM	3D CNN	HybridSN	ViT	HiT	DWTDense	SSFTT	MorphFormer	Ours
1	88.51 ± 1.11	97.15 ± 0.38	97.63 ± 0.33	92.95 ± 0.81	96.11 ± 0.52	98.10 ± 0.28	99.05 ± 0.18	99.32 ± 0.14	99.86 ± 0.08
2	85.12 ± 1.35	95.23 ± 0.59	95.88 ± 0.52	90.55 ± 0.95	93.48 ± 0.72	96.50 ± 0.45	97.11 ± 0.38	97.35 ± 0.35	97.66 ± 0.41
3	82.55 ± 1.48	96.55 ± 0.46	97.01 ± 0.41	91.88 ± 0.85	94.99 ± 0.61	97.80 ± 0.35	98.88 ± 0.21	99.15 ± 0.18	99.87 ± 0.07
4	92.54 ± 0.82	98.48 ± 0.24	98.95 ± 0.21	96.01 ± 0.51	98.87 ± 0.24	98.90 ± 0.22	99.05 ± 0.19	98.99 ± 0.20	99.14 ± 0.18
5	75.33 ± 1.85	87.99 ± 1.15	88.15 ± 1.11	81.05 ± 1.55	85.88 ± 1.35	88.50 ± 1.08	88.85 ± 1.03	88.67 ± 1.05	89.35 ± 0.99
6	88.67 ± 1.08	98.01 ± 0.30	98.23 ± 0.28	94.88 ± 0.62	97.12 ± 0.41	98.85 ± 0.24	99.48 ± 0.14	99.55 ± 0.12	99.74 ± 0.10
7	98.81 ± 0.25	99.88 ± 0.08	99.91 ± 0.07	98.78 ± 0.24	99.72 ± 0.16	99.95 ± 0.05	99.96 ± 0.04	99.98 ± 0.02	99.99 ± 0.01
8	80.88 ± 1.55	92.18 ± 0.81	93.88 ± 0.71	88.54 ± 1.11	91.88 ± 0.88	94.50 ± 0.65	94.98 ± 0.59	95.15 ± 0.57	95.40 ± 0.55
9	72.54 ± 1.95	83.87 ± 1.38	84.11 ± 1.35	80.55 ± 1.61	81.33 ± 1.58	85.10 ± 1.28	84.88 ± 1.24	84.99 ± 1.23	85.20 ± 1.20
OA (%)	84.81 ± 1.15	96.35 ± 0.43	96.88 ± 0.39	91.98 ± 0.85	95.01 ± 0.55	97.58 ± 0.31	98.15 ± 0.25	98.33 ± 0.22	98.84 ± 0.18
AA (%)	85.18 ± 1.25	95.09 ± 0.55	95.58 ± 0.51	90.43 ± 0.95	93.28 ± 0.68	94.80 ± 0.58	95.23 ± 0.48	95.48 ± 0.46	96.25 ± 0.42
$\kappa$ (×100)	82.75 ± 1.35	95.51 ± 0.49	96.05 ± 0.45	89.85 ± 0.98	93.55 ± 0.65	97.03 ± 0.36	97.68 ± 0.30	97.89 ± 0.27	98.48 ± 0.21

. These tables provide per-class accuracy, OA, AA, and $\kappa$ values. A thorough analysis of these results reveals the clear superiority of our proposed approach.

WSC-Net establishes new state-of-the-art performances across all four datasets, consistently achieving the highest or near-highest scores in the three primary metrics. This validates both its exceptional performance and strong generalization capability. Specifically, in the IP, PU, SA, and LK datasets, WSC-Net achieves leading OA scores of 97.81%, 97.92%, 96.90%, and 98.84%, respectively. Such remarkable performance spans datasets with vastly different characteristics—from the low-resolution, noisy environment of IP to the complex, high-resolution agricultural scenes of LK—confirming the effectiveness and adaptability of our architecture. The most compelling evidence emerges from a detailed examination of the challenging IP dataset. Here, WSC-Net achieves an outstanding AA of 93.50%, substantially outperforming competing methods, including recent powerful models, like MorphFormer (92.14%) and SSFTT (86.67%). This superior AA is particularly meaningful, given the dataset’s severe class imbalance, as it reflects more balanced performance across all the classes. The model’s strength becomes especially apparent in notoriously difficult, low-sample classes. For instance, WSC-Net achieves perfect (100.00%) accuracy in Class 7 (Grass-p-mowed) and a highly competitive accuracy of 72.22% in Class 9 (Oats), significantly surpassing those of the other advanced transformer models. Similar excellence in challenging classes appears throughout all the datasets, including outstanding results in Class 8 (Untrained grapes) in SA and Class 7 (Bitumen) in PU.

These results illuminate the fundamental value of our architectural innovations. While advanced transformer models, like HiT and MorphFormer, excel at capturing spatial context, they often struggle with fine-grained details and noise resilience. Notably, even when compared to DWTDense, a strong baseline that also leverages wavelet transforms with a powerful DenseNet backbone, our WSC-Net consistently maintains a performance advantage across all the datasets. This is a critical finding, as it suggests that the superiority of our model stems not merely from the inclusion of wavelet features but also fundamentally from the intelligent, adaptive fusion mechanism of the CDAF module. WSC-Net addresses these limitations through two key components: WTM extracts subtle frequency-domain features, while the CDAF module intelligently integrates this information with the spatial context. The consistently high AA scores further validate this approach, demonstrating that our model delivers more balanced and reliable classification across diverse land-cover types. Rather than offering merely incremental improvements, WSC-Net provides a principled solution to the fundamental challenges inherent in HSI classification.

3.5. Visual Analysis and Classification Maps

To complement the quantitative metrics, a qualitative assessment of the classification maps provides a more intuitive understanding of our model’s practical advantages. Figure 6, Figure 7, Figure 8 and Figure 9 display the classification results generated by several representative methods for selected sub-regions of the four datasets, alongside the ground-truth maps. Visual inspection immediately reveals a clear performance hierarchy among the different approaches.

The maps from classical SVMs are characterized by significant “salt-and-pepper” noise, indicating a lack of spatial contextual awareness. While CNN-based architectures, like HybridSN, produce more homogeneous regions, they often struggle with accurately delineating class boundaries, resulting in overly smoothed or blurred edges. Even advanced transformer-based models, such as SSFTT, despite their strong performances, can occasionally produce blocky artifacts or exhibit confusion in areas with complex textural patterns. These limitations become particularly apparent when examining fine-grained spatial details or transitional zones between different land-cover types. In striking contrast, the classification maps produced by WSC-Net demonstrate remarkable fidelity to the ground truth across all the tested scenarios. This visual excellence manifests through several distinctive characteristics. First, the intra-class regions exhibit exceptional smoothness and uniformity, with drastically reduced misclassified pixels. This is particularly evident in the large agricultural fields of the SA dataset. Second, WSC-Net maintains sharp and precise boundaries between different land-cover types, as observed in the intricate urban layout of the PU map, where building edges remain clearly defined. Third, our model demonstrates outstanding capability in correctly identifying small or irregularly shaped objects, a task where competing methods frequently fail. A clear example is the accurate classification of the small ’Oats’ class in the IP dataset.

This enhanced spatial coherence and detail preservation stem directly from our architectural innovations. The wavelet features from the WTM provide crucial textural and edge information, which is then intelligently integrated by the CDAF module with the global context from the Swin transformer. This synergistic fusion enables WSC-Net to not only generate accurate pixel-wise predictions but also reconstruct the underlying spatial structure of scenes with high fidelity. The result is more reliable and interpretable classification outcomes that better reflect the true complexity of real-world landscapes.

3.6. Ablation Studies

Ablation study of different model configurations: To validate the effectiveness of the proposed architectural components, we conducted a comprehensive ablation study on the IP dataset. This analysis systematically deconstructs WSC-Net to isolate and quantify the contributions of both the WTM and the CDAF module. The results, presented in

Table 6. Ablation study of WSC-Net’s components in the IP dataset.

Model Configuration	WTM	CDAF	OA (%)	AA (%)	$\mathit{\kappa }$ (×100)
w/o WTM and CDAF	✗	✗	94.89 ± 0.18	86.34 ± 0.21	94.17 ± 0.19
w/o WTM	✗	✓	95.82 ± 0.19	90.55 ± 0.23	96.38 ± 0.20
w/o CDAF	✓	✗	97.15 ± 0.22	91.82 ± 0.25	96.75 ± 0.24
WSC-Net (Full Model)	✓	✓	97.81 ± 0.15	93.50 ± 0.11	97.50 ± 0.18

, demonstrate a clear and synergistic relationship between the components, where each part plays a vital role in achieving the final performance.

The baseline model consists solely of our customized two-stage Swin transformer backbone (w/o WTM and CDAF), which achieves a strong OA of 94.89%. When the CDAF module is introduced without the wavelet branch (w/o WTM), it functions as a self-attention enhancement and increases the OA to 95.82%, confirming its independent effectiveness in refining spatial–spectral features. In contrast, adding the WTM with simple concatenation (w/o CDAF) leads to a more substantial improvement, achieving an OA of 97.15%, thereby providing direct evidence that wavelet-derived features supply crucial complementary information. Finally, the full WSC-Net model integrates both components, where the CDAF module intelligently fuses the spatial–spectral and frequency-domain streams, boosting performance to the highest OA of 97.81%. This step-by-step progression demonstrates that both WTM and CDAF contribute distinct and complementary benefits: wavelet features provide significant enhancement, while CDAF unlocks their full potential through adaptive cross-domain fusion.

Ablation study of the per-class performance: To further investigate the classification behavior of the proposed WSC-Net, we present the normalized confusion matrices for four datasets in Figure 10. These matrices visualize the per-class recall rates, offering a granular view of the model’s performance. A consistent pattern of strongly weighted diagonals is evident across all four datasets, confirming that WSC-Net achieves high and balanced recall rates for the vast majority of the classes. This demonstrates the model’s robustness and adaptability to diverse spectral and spatial characteristics, ranging from the complex agricultural landscapes of the IP and SA datasets to the urban–rural environments in the PU and LK datasets.

Ablation study of the wavelet basis selection: To validate our choice of the Haar wavelet, an additional ablation study was conducted on the IP dataset to compare its performance against those of other commonly used wavelet bases, namely, Daubechies 4 (db4) and Symlets 4 (sym4). The results, presented in

Table 7. Ablation study of different wavelet bases in the IP dataset.

Wavelet Basis	OA (%)	AA (%)	$\mathit{\kappa }$ (×100)
Haar	97.81 ± 0.15	93.50 ± 0.11	97.50 ± 0.18
Daubechies 4 (db4)	95.52 ± 0.39	91.67 ± 0.26	95.18 ± 0.21
Symlets 4 (sym4)	96.46 ± 0.30	92.51 ± 0.24	95.10 ± 0.43

, provide valuable insights into the model’s sensitivity to the choice of the wavelet.

The experimental results indicate that while all the tested wavelet bases enable the model to achieve high-quality classification, the Haar wavelet yields the best performance across all three metrics. The db4 and sym4 wavelets, which are smoother and have longer filters, result in a slight but consistent decrease in performance. A plausible explanation is that the simple, discontinuous nature of the Haar wavelet is particularly well suited for capturing the sharp, step-like changes often present in hyperspectral signatures at material boundaries and in specific absorption features. Smoother wavelets, like db4 and sym4, might slightly blur these critical high-frequency details during decomposition. Therefore, considering its marginally superior accuracy and well-known computational efficiency, the Haar wavelet is confirmed as the most effective choice for the WSC-Net architecture.

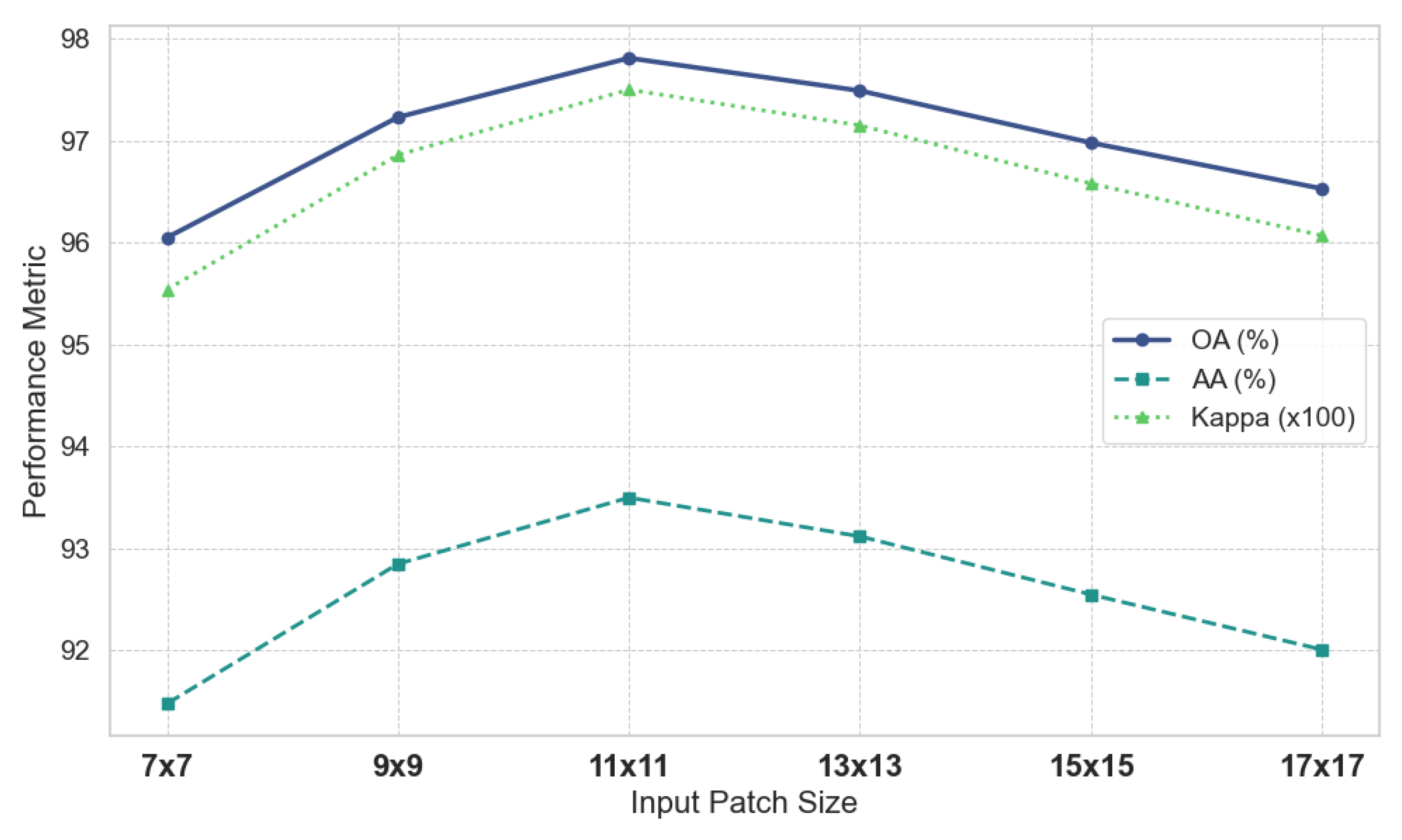
Ablation study of the input patch size: To determine the optimal spatial input, we evaluated WSC-Net’s performance in the IP dataset with patch sizes ranging from $7\times 7$ to $17\times 17$. As illustrated in Figure 11, the results reveal a distinct “peaking” behavior. Performance improves from $7\times 7$ to its maximum at $11\times 11$, demonstrating the benefit of a moderate spatial context. Beyond this peak, however, the accuracy consistently declines, indicating that larger patches introduce noise from irrelevant neighboring pixels, a phenomenon known as the “curse of the context.” This finding strongly supports our model’s design rationale. WSC-Net achieves its best performance with a relatively compact $11\times 11$ patch because its WTM already captures the fine-grained details that other models seek from larger, potentially noisy receptive fields. The $11\times 11$ size strikes an optimal balance between sufficient context for the Swin transformer backbone and minimal noise introduction. Therefore, this configuration is confirmed as the ideal setting and is used for all the experiments in this paper.

4. Discussion

The experimental results presented in the previous sections confirm the quantitative and qualitative effectiveness of WSC-Net. This section provides a broader context for these findings by discussing the rationale behind our patch-based methodology, analyzing the architectural principles that contribute to the model’s performance and acknowledging its current limitations.

A pertinent consideration in HSI classification is the role of patch-based deep learning models in relation to object-based approaches, which have demonstrated high accuracies on certain benchmarks. These two paradigms, however, address distinct scientific questions and application needs. Object-based methods excel in scenarios requiring cartographically clean outputs for large, homogeneous regions. In contrast, our patch-based methodology is aligned with the objective of advancing fine-grained analysis at the highest possible spatial resolution. This approach is fundamental for applications such as mineral exploration or precision agriculture, where the classification of individual pixels or small pixel groups is critical. It provides an end-to-end framework that learns features directly from the data, offering greater generalizability to scenes with complex or fragmented landscapes, where pre-segmentation is often challenging. Therefore, research into advanced patch-based models remains a vital frontier for developing foundational feature extractors with broad applicability in remote sensing.

Furthermore, a key inquiry into any new model is to understand why it is effective, beyond simply achieving higher metrics. The advantages of WSC-Net are rooted in its dual-branch architecture and the intelligent fusion enabled by the CDAF module. A logical inference of this mechanism’s behavior can be drawn directly from the experimental evidence. For instance, the model’s high AA in the imbalanced IP dataset points to its enhanced ability to classify small or minority classes, which often depend on subtle, high-frequency textural or spectral cues that a standard transformer might average out. WSC-Net’s success in these cases suggests that the CDAF module is effectively leveraging the detail-rich features from the wavelet branch. Concurrently, the high spatial coherence and low noise in the classification maps for large, uniform areas (e.g., in the SA dataset) indicate that the model is not simply overfitting to high-frequency information. This observed balance between sensitivity to fine details and stability in homogeneous regions provides strong evidence that the CDAF module functions as an adaptive arbitrator. It likely learns to dynamically prioritize high-frequency information from the WTM when classifying complex, boundary-like regions, while relying on the robust, context-rich features from the Swin transformer for simpler, uniform areas. This capacity for adaptive, data-driven feature synthesis is the primary reason for WSC-Net’s robust and well-balanced performance.

Finally, it is important to acknowledge the limitations of the proposed architecture. The dual-branch design, while effective, results in a higher parameter count and increased computational cost compared to those of single-stream models. This tradeoff between accuracy and efficiency is a key consideration for practical deployment on resource-constrained platforms. Future work could focus on model compression or the development of more computationally efficient cross-domain interaction mechanisms. The principles of fusing spatial and frequency domains validated herein could also be extended to other challenging remote sensing tasks, presenting a clear path for continued research.

5. Conclusions

This paper addresses a fundamental challenge in HSI classification: the tradeoff between global contextual and fine-grained local details. We propose WSC-Net, a novel dual-branch architecture that synergistically fuses spatial–spectral features from a two-stage Swin transformer backbone, specifically adapted for HSI patch analysis, with high-frequency details from WTM. This approach leverages the complementary nature of these two domains to create a more comprehensive feature representation. The cornerstone of WSC-Net is the CDAF module. Rather than employing simple concatenation, CDAF enables intelligent, bi-directional information exchange, allowing features from each branch to dynamically enhance and refine the other for optimal integration. Extensive experiments on four datasets demonstrate WSC-Net’s superiority over a wide range of state-of-the-art methods. The results particularly highlight its exceptional capability in classifying challenging, low-sample classes while maintaining spatial coherence, establishing new performance benchmarks in HSI classification. Future work could explore extending this fusion paradigm to other remote sensing tasks or developing more efficient implementations. In summary, WSC-Net provides a principled and robust framework that effectively bridges macroscopic contextual modeling and microscopic detail perception.