Two-Step Forward Modeling for GPR Data of Metal Pipes Based on Image Translation and Style Transfer
Abstract
Highlights
- The two-step strategy, combining image translation and style transfer, achieves accurate Ground-penetrating radar (GPR) data simulation. Image translation generates precise simulated clutter-free images, and style transfer converts them to match real-world heterogeneous medium characteristics.
- Compared to finite-difference time-domain (FDTD), the proposed method drastically reduces time costs while maintaining good performance.
- It offers an efficient and reliable solution for GPR data simulation and analysis, sup-porting applications in geophysics, civil engineering, and other fields.
- It enables rapid generation of high-quality GPR data, facilitating deep learning tasks like target recognition that require large labeled datasets.
Abstract
1. Introduction
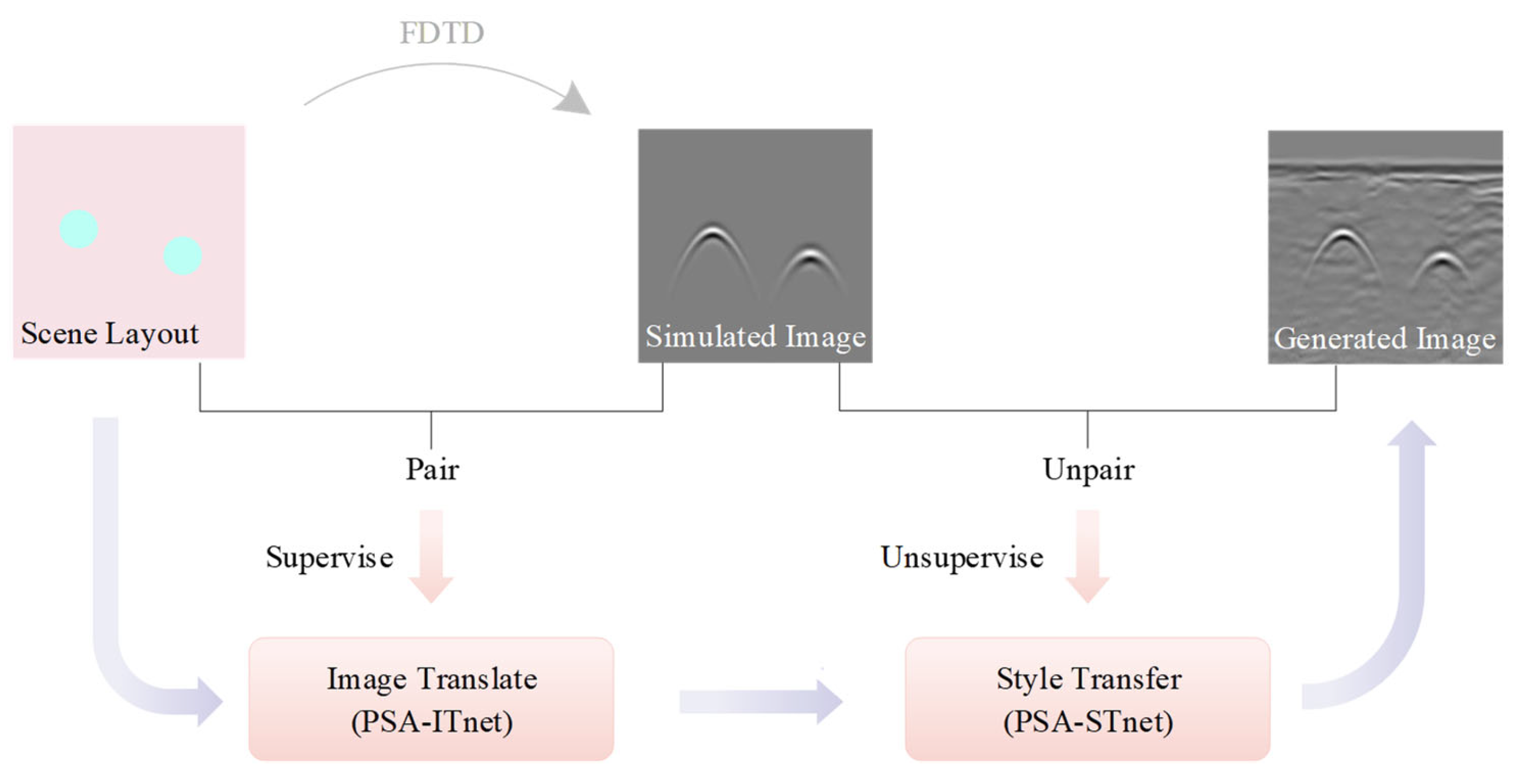
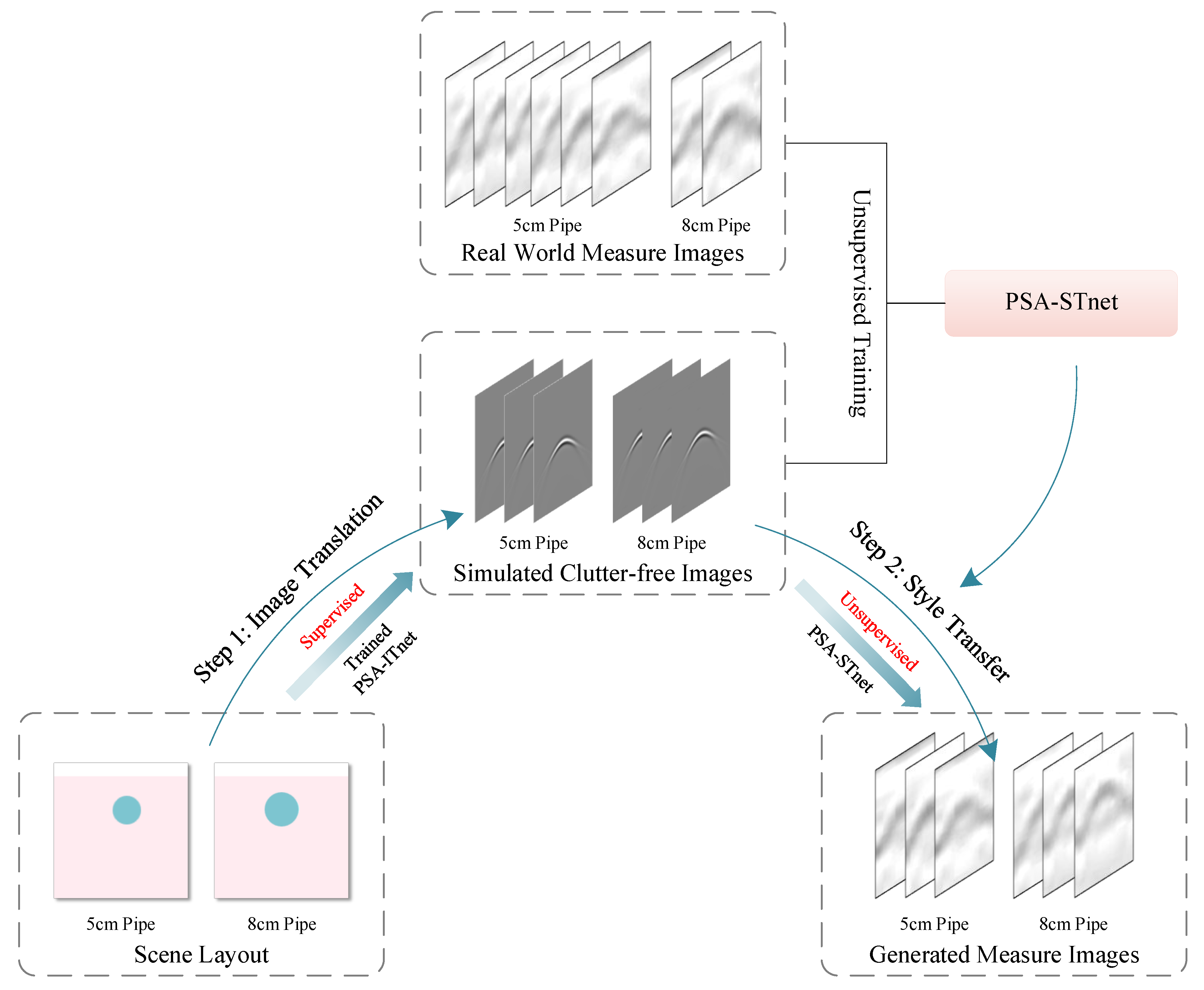
- Propose a two-step forward modeling strategy based on image translation and style transfer, enabling GPR data simulation without relying on extensive labeled data or expensive numerical calculations.
- Develop a Polarized Self-Attention Image Translation network (PSA-ITnet) to convert scene layout images (geometric schematics of metal pipes and surrounding media) into simulated clutter-free GPR B-scan images, capturing critical longitudinal time-delay properties.
- Design a Polarized Self-Attention Style Transfer network (PSA-STnet) to transform simulated clutter-free images into data matching the distribution of real-world heterogeneous media, preserving target information under unsupervised conditions.
2. Methods
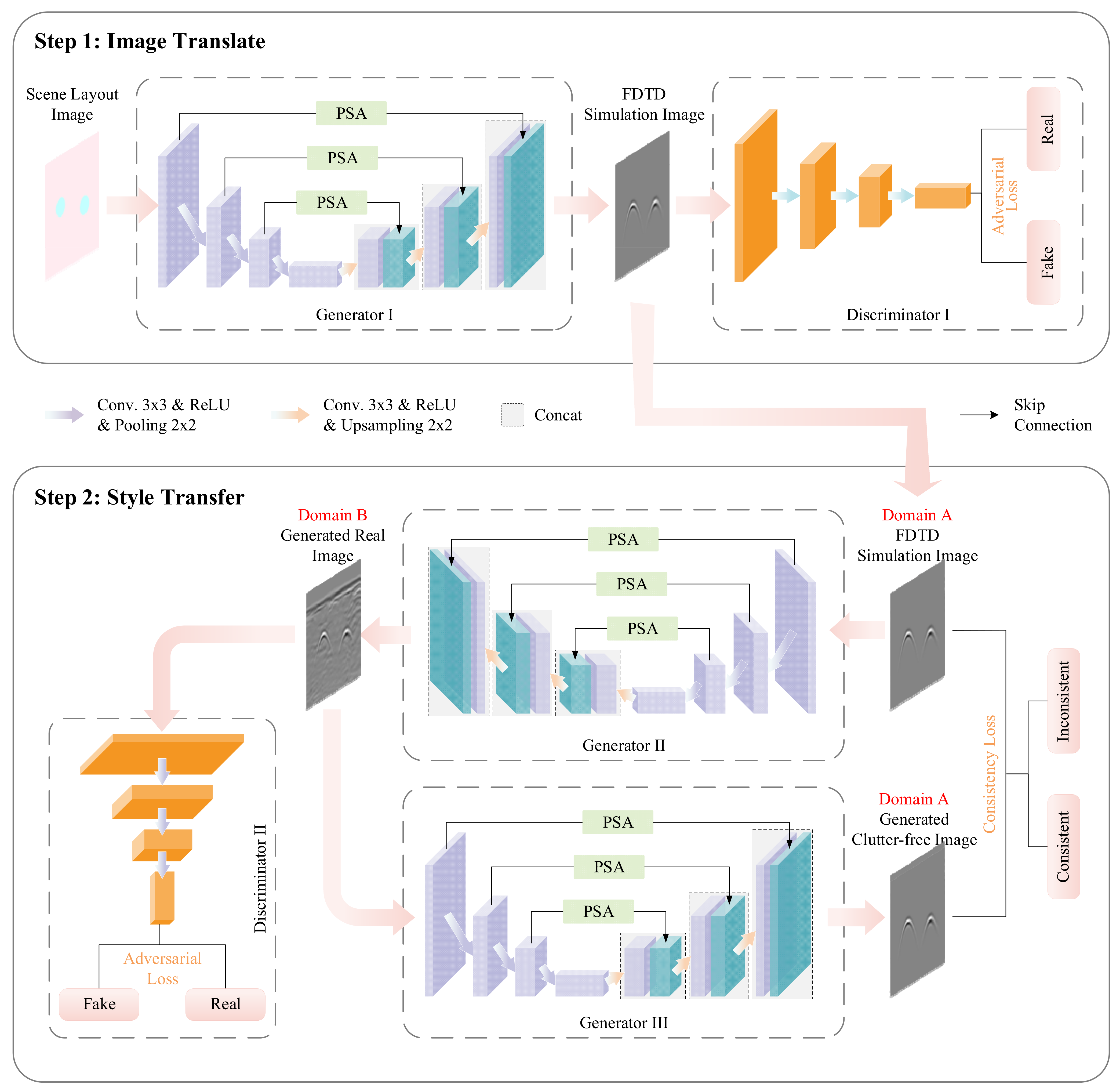
2.1. Step 1: Image Translation
2.1.1. PSA-ITnet Structure
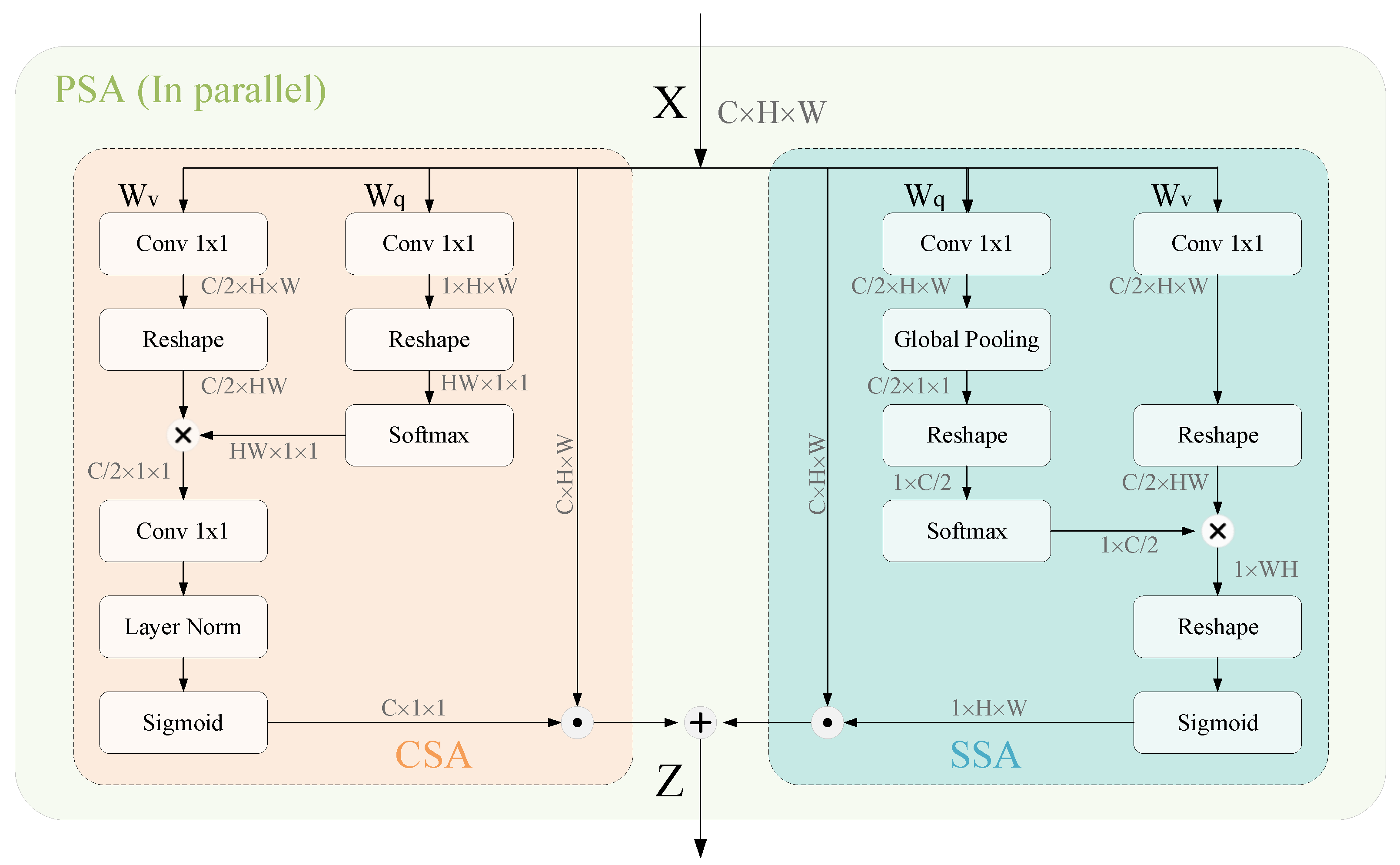
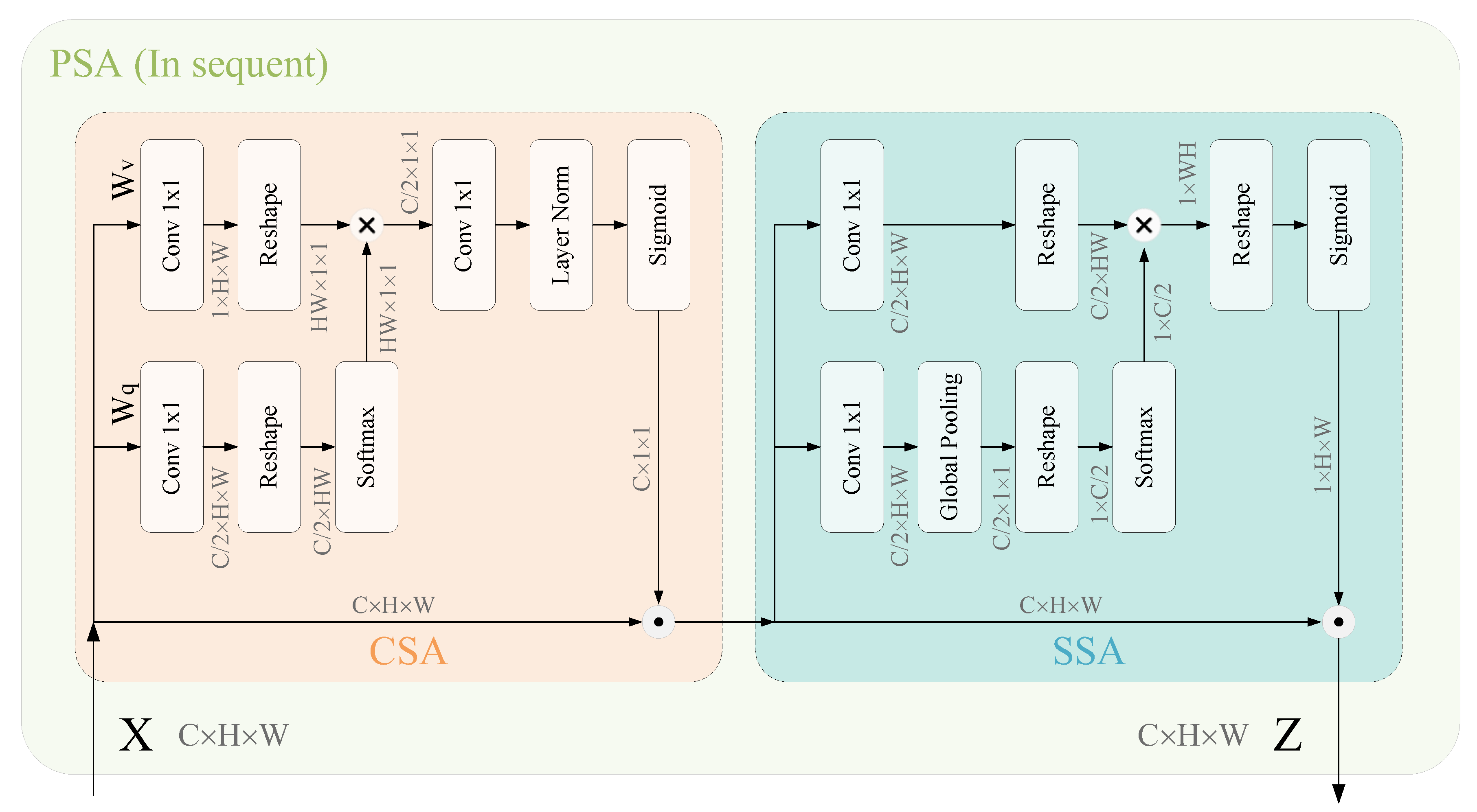
2.1.2. Polarized Self-Attention Mechanism
- Channel self-attention branch
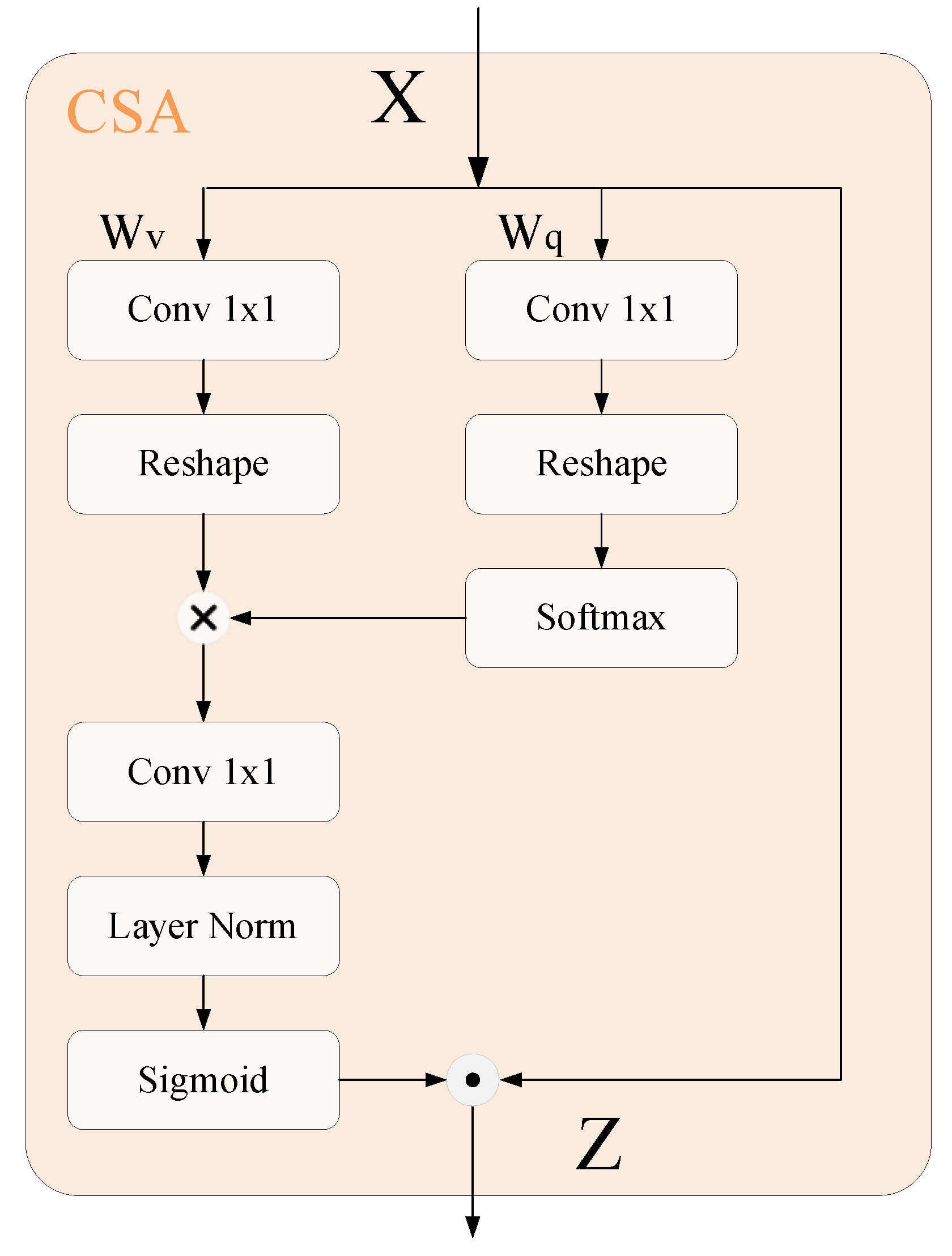
- Spatial self-attention branch
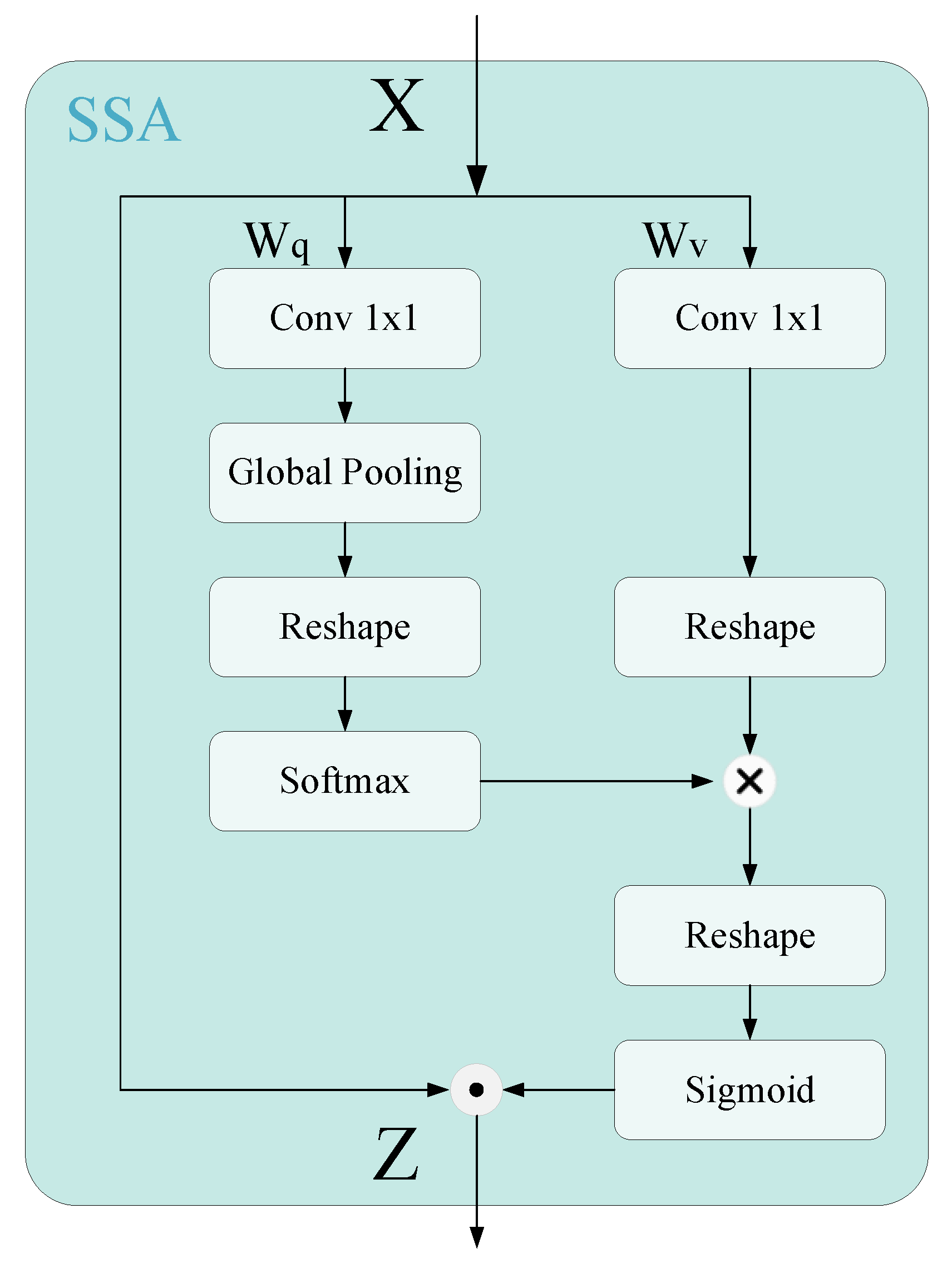
2.2. Step 2: Style Transfer
2.2.1. Adversarial Loss
2.2.2. Consistency Loss
3. Simulation Experiments
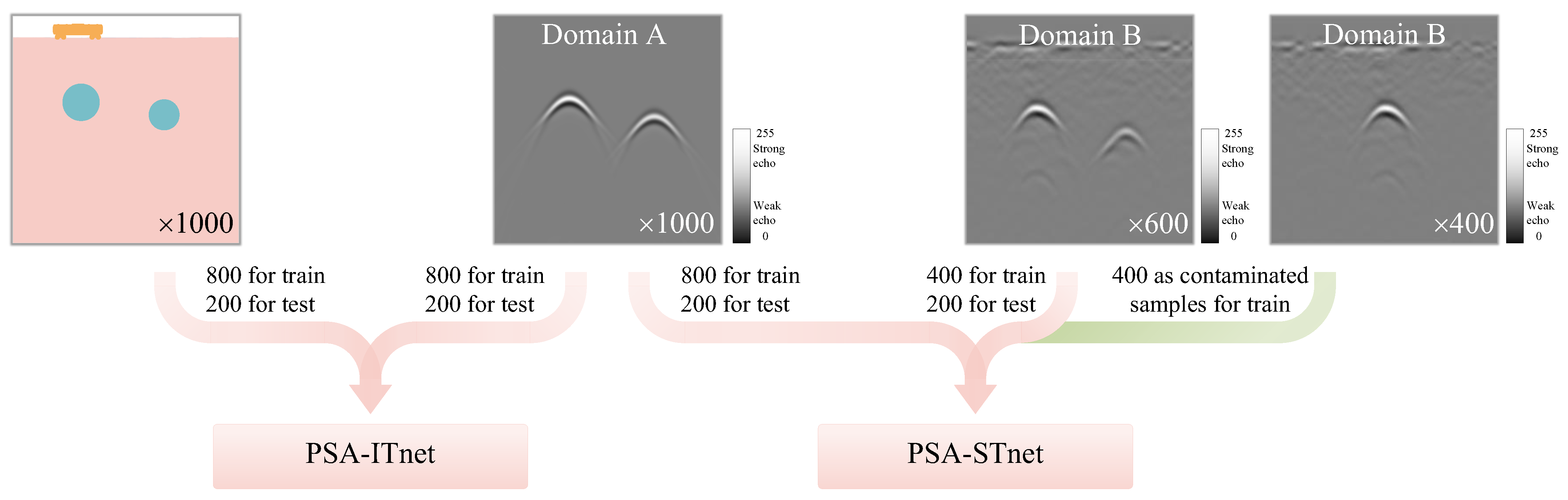
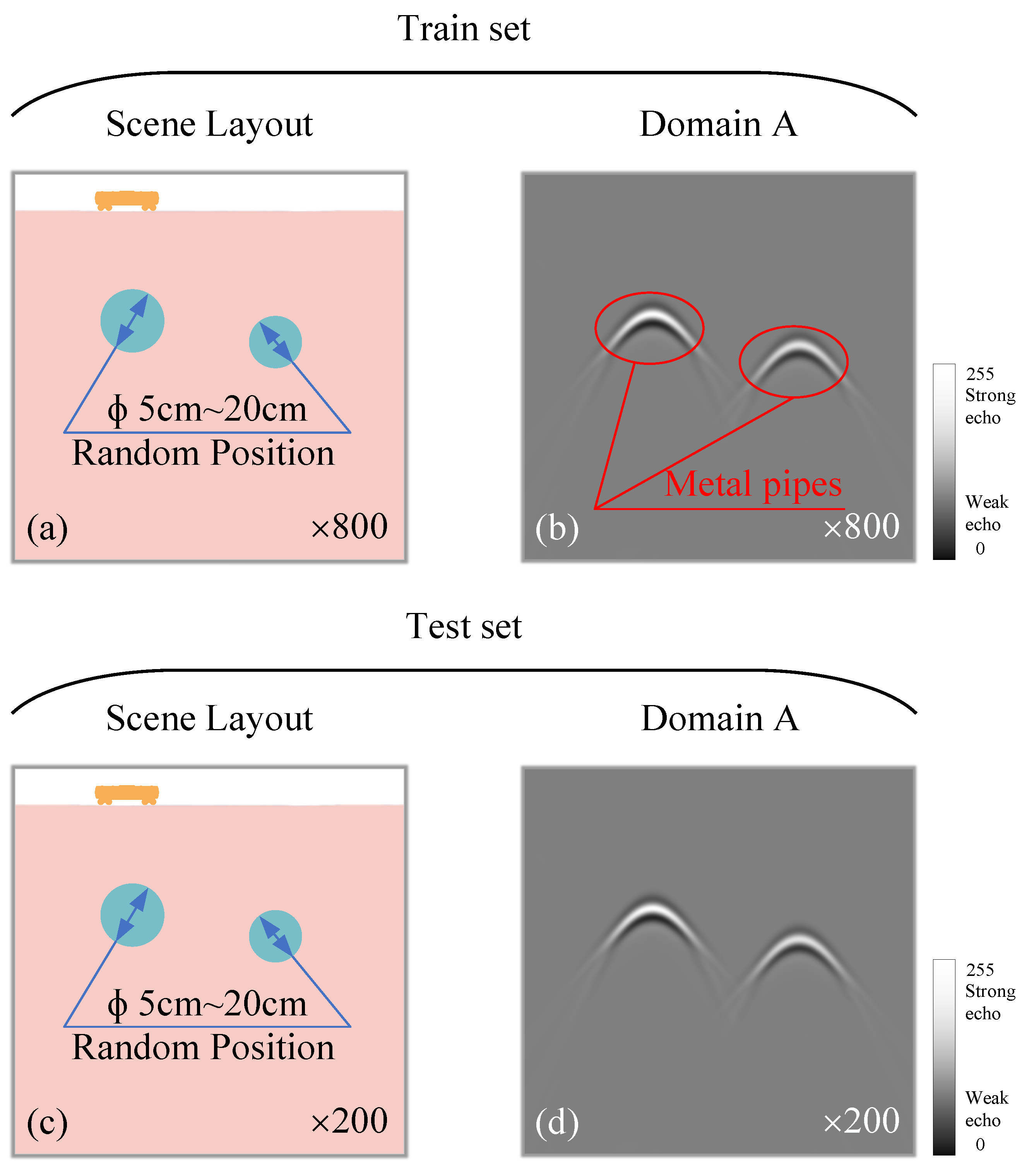
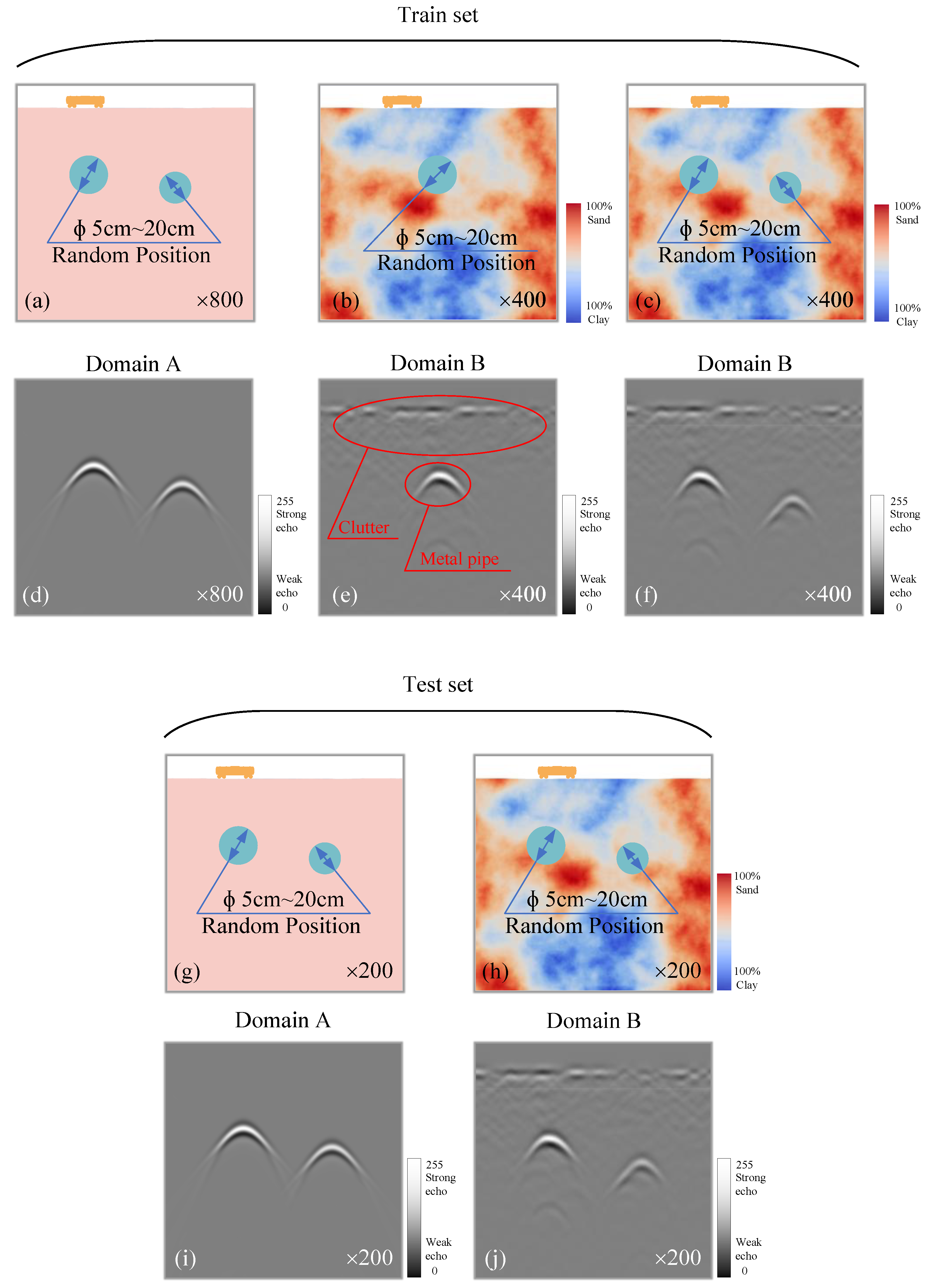
3.1. Dataset Preparation
3.2. Analysis of Image Translation Results
3.3. Analysis of Style Transfer Results
4. Real-World Experimental Verification
4.1. Data Preparation
4.2. Experimental Verification
5. Conclusions
6. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yamaguchi, T.; Mizutani, T.; Meguro, K.; Hirano, T. Detecting Subsurface Voids from GPR Images by 3-D Convolutional Neural Network Using 2-D Finite Difference Time Domain Method. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 3061–3073. [Google Scholar] [CrossRef]
- Lu, X.; Song, A.; Qian, R.; Liu, L. Anisotropic Reverse-Time Migration of Ground-Penetrating Radar Data Collected on the Sand Dunes in the Badain Jaran Desert. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 647–654. [Google Scholar] [CrossRef]
- Ma, Y.; Lei, W.; Pang, Z.; Zheng, Z.; Tan, X. Rebar Clutter Suppression and Road Defects Localization in GPR B-Scan Images Based on SuppRebar-GAN and EC-Yolov7 Networks. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Kaur, P.; Dana, K.J.; Romero, F.A.; Gucunski, N. Automated GPR Rebar Analysis for Robotic Bridge Deck Evaluation. IEEE Trans. Cybern. 2016, 46, 2265–2276. [Google Scholar] [CrossRef]
- Liu, B.; Ren, Y.; Liu, H.; Xu, H.; Wang, Z.; Cohn, A.; Jiang, P. GPRInvNet: Deep Learning-Based Ground-Penetrating Radar Data Inversion for Tunnel Linings. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8305–8325. [Google Scholar] [CrossRef]
- Porsani, J.; Navarro, A.; Rangel, R.; Neto, A.; Lima, L.; Stangari, M.; Souza, L.; Santos, V. GPR survey on underwater archaeological site: A case study at Jenipapo stilt village in the eastern Amazon region, Brazil. J. Archaeol. Sci. Rep. 2023, 51, 104114. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Z.; Wang, B.; Yu, T. GPR impedance inversion for imaging and characterization of buried archaeological remains: A case study at Mudu city cite in Suzhou, China. J. Appl. Geophys. 2018, 148, 226–233. [Google Scholar] [CrossRef]
- Lopera, O.; Slob, E.C.; Milisavljevic, N.; Lambot, S. Filtering Soil Surface and Antenna Effects From GPR Data to Enhance Landmine Detection. IEEE Trans. Geosci. Remote Sens. 2007, 45, 707–717. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Multiparameter Adaptive Target Classification Using Full-Polarimetric GPR: A Novel Approach to Landmine Detection. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 2592–2606. [Google Scholar] [CrossRef]
- Benedetto, A.; Benedetto, F.; De Blasiis, M.R.; Giunta, G. Reliability of signal processing technique for pavement damages detection and classification using ground penetrating radar. IEEE Sens. J. 2005, 5, 471–480. [Google Scholar] [CrossRef]
- Zou, L.; Liu, H.; Alani, A.M.; Fang, G. Surface Permittivity Estimation of Southern Utopia Planitia by High-Frequency RoPeR in Tianwen-1 Mars Exploration. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2002809. [Google Scholar] [CrossRef]
- Alsharahi, G.; Faize, A.; Louzazni, M.; Mostapha, A.M.M.; Bayjja, M.; Driouach, A. Detection of cavities and fragile areas by numerical methods and GPR application. J. Appl. Geophys. 2019, 164, 225–236. [Google Scholar] [CrossRef]
- Yee, K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Di, Q.; Wang, M. Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion. Geophysics 2004, 69, 472–477. [Google Scholar] [CrossRef]
- Liu, H.; Dai, D.; Zou, L.; He, Q.; Meng, X.; Chen, J. Refined Modeling of Heterogeneous Medium for Ground-Penetrating Radar Simulation. Remote Sens. 2024, 16, 3010. [Google Scholar] [CrossRef]
- Liu, Q.; Fan, G. Simulations of GPR in dispersive media using a frequency-dependent PSTD algorithm. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2317–2324. [Google Scholar]
- Zarei, S.; Oskooi, B.; Amini, N.; Dalkhani, A.R. 2D spectral element modeling of GPR wave propagation in inhomogeneous media. J. Appl. Geophys. 2016, 133, 92–97. [Google Scholar] [CrossRef]
- Ma, Y.; Song, X.; Li, Z.; Li, H.; Qu, Z. A Prior Knowledge-Guided Semi-Supervised Deep Learning Method for Improving Buried Pipe Detection on GPR Data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4508015. [Google Scholar] [CrossRef]
- Jin, A.; Chen, C.; Yang, B.; Zou, Q.; Wang, Z.; Yan, Z. GPR-Former: Detection and Parametric Reconstruction of Hyperbolas in GPR B-Scan Images with Transformers. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4507113. [Google Scholar] [CrossRef]
- Kim, N.; Kim, S.; An, Y.-K.; Lee, J.-J. Triplanar Imaging of 3-D GPR Data for Deep-Learning-Based Underground Object Detection. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 4446–4456. [Google Scholar] [CrossRef]
- Dai, Q.; Lee, Y.H.; Sun, H.-H.; Ow, G.; Yusof, M.L.M.; Yucel, A.C. DMRF-UNet: A Two-Stage Deep Learning Scheme for GPR Data Inversion Under Heterogeneous Soil Conditions. IEEE Trans. Antennas Propagat. 2022, 70, 6313–6328. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, G.; Meng, X.; Liu, H. FusionInv-GAN: Advancing GPR Data Inversion With RTM-Guided Deep Learning Techniques. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5930511. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, F.; Zhang, M.; Miao, Y.; Wan, T.; Xu, D. A novel FDTD-based 3-D RTM imaging method for GPR working on dispersive medium. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1002813. [Google Scholar] [CrossRef]
- Ni, Z.-K.; Shi, C.; Pan, J.; Zheng, Z.; Ye, S.; Fang, G. Declutter-GAN: GPR B-Scan Data Clutter Removal Using Conditional Generative Adversarial Nets. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023105. [Google Scholar] [CrossRef]
- Kayacan, Y.E.; Erer, I. A Vision-Transformer-Based Approach to Clutter Removal in GPR: DC-ViT. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3505105. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wang, C.J.; Rost, N.S.; Golland, P. Spatial-Intensity Transforms for Medical Image-to-Image Translation. IEEE Trans. Med. Image 2023, 42, 3362–3373. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Liu, H.; Liu, F.; Fan, X.; Huang, D. Polarized self-attention: Towards high-quality pixel-wise mapping. Neurocomputing 2022, 506, 158–167. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Cai, W. A Unified Framework for Generalizable Style Transfer: Style and Content Separation. IEEE Trans. Image Process. 2020, 29, 4085–4098. [Google Scholar] [CrossRef]
- Zhu, J.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Behera, A.P.; Prakash, S.; Khanna, S.; Nigam, S.; Verma, S. CNN-Based Metrics for Performance Evaluation of Generative Adversarial Networks. IEEE Trans. Artif. Intell. 2024, 5, 5040–5049. [Google Scholar] [CrossRef]
- Yang, B.; Rappaport, C. Response of realistic soil for GPR applications with 2-D FDTD. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1198–1205. [Google Scholar] [CrossRef]
- Wei, X.-K.; Zhang, X.; Diamanti, N.; Shao, W.; Sarris, C.D. Subgridded FDTD Modeling of Ground Penetrating Radar Scenarios Beyond the Courant Stability Limit. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7189–7198. [Google Scholar] [CrossRef]
- Takekura, S.; Miyamoto, H.; Kobayashi, M. Detecting Lunar Subsurface Water Ice Using FMCW Ground Penetrating Radar: Numerical Analysis with Realistic Permittivity Variations. Remote Sens. 2025, 17, 1050. [Google Scholar] [CrossRef]
- Mao, L.; Wang, X.; Chi, Y.; Pang, S.; Wang, X.; Huang, Q. A Three-Dimensional FDTD(2,4) Subgridding Algorithm for the Airborne Ground-Penetrating Radar Detection of Landslide Models. Remote Sens. 2025, 17, 1107. [Google Scholar] [CrossRef]
- Cheng, Q.; Cui, F.; Dong, G.; Wang, R.; Li, S. A Method of Reconstructing Ground Penetrating Radar Bscan for Advanced Detection Based on High-Order Synchrosqueezing Transform. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5910313. [Google Scholar] [CrossRef]
- McDonald, T.; Plattner, A.; Warren, C.; Robinson, M.; Tian, G. 3-D Visualization of New Hybrid-Rotational Ground-Penetrating Radar for Subsurface Inspection of Transport Infrastructure. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5101613. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, W.; Min, X.; Wang, T.; Lu, W.; Zhai, G. A Full-Reference Quality Assessment Metric for Fine-Grained Compressed Images. In Proceedings of the 2021 International Conference on Visual Communications and Image Processing (VCIP), Munich, Germany, 5–8 December 2021; pp. 1–4. [Google Scholar]



| Materials | Size (cm) | Dielectric Constant |
|---|---|---|
| Air | 5 | 1 |
| Underground medium | 95 | 9 |
| Metal pipes | 5~20 | ∞ |
| FDTD | GAN | UnetGAN | Pix2Pix | FusionInv-GAN | PSA-ITnet in Sequent | PSA-ITnet in Parallel | |
|---|---|---|---|---|---|---|---|
| MSE | 0 | 95.232 | 18.736 | 27.840 | 14.181 | 4.352 | 4.182 |
| PSNR (dB) | +∞ | 28.343 | 35.404 | 33.684 | 36.614 | 41.744 | 41.917 |
| SSIM | 1 | 0.864 | 0.915 | 0.904 | 0.923 | 0.950 | 0.953 |
| FDTD | GAN | UnetGAN | Pix2Pix | FusionInv-GAN | PSA-STnet in Sequence | PSA-STnet in Parallel | |
|---|---|---|---|---|---|---|---|
| MSE | 0 | 228.578 | 35.153 | 33.439 | 10.910 | 5.152 | 4.806 |
| PSNR (dB) | +∞ | 24.540 | 32.671 | 32.872 | 37.753 | 41.011 | 41.313 |
| SSIM | 1 | 0.762 | 0.854 | 0.861 | 0.907 | 0.979 | 0.987 |
| Methods | Time Cost of a B-Scan Image (s) | |
|---|---|---|
| FDTD | Homogeneous medium | 292.580 |
| Heterogeneous medium | 486.460 | |
| Proposed method | PSA-ITnet | 0.060 |
| PSA-STnet | 0.165 |
| GAN | UnetGAN | Pix2Pix | FusionInv-GAN | PSA-STnet in Sequence | PSA-STnet in Parallel | |
|---|---|---|---|---|---|---|
| MSE | 389.296 | 127.609 | 135.284 | 144.487 | 62.890 | 33.089 |
| PSNR (dB) | 22.228 | 27.072 | 26.818 | 26.533 | 30.145 | 32.934 |
| SSIM | 0.751 | 0.904 | 0.858 | 0.846 | 0.923 | 0.972 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Gao, Y.; Huang, Z.; Shi, M.; Liu, X. Two-Step Forward Modeling for GPR Data of Metal Pipes Based on Image Translation and Style Transfer. Remote Sens. 2025, 17, 3215. https://doi.org/10.3390/rs17183215
Guo Z, Gao Y, Huang Z, Shi M, Liu X. Two-Step Forward Modeling for GPR Data of Metal Pipes Based on Image Translation and Style Transfer. Remote Sensing. 2025; 17(18):3215. https://doi.org/10.3390/rs17183215
Chicago/Turabian StyleGuo, Zhishun, Yesheng Gao, Zicheng Huang, Mengyang Shi, and Xingzhao Liu. 2025. "Two-Step Forward Modeling for GPR Data of Metal Pipes Based on Image Translation and Style Transfer" Remote Sensing 17, no. 18: 3215. https://doi.org/10.3390/rs17183215
APA StyleGuo, Z., Gao, Y., Huang, Z., Shi, M., & Liu, X. (2025). Two-Step Forward Modeling for GPR Data of Metal Pipes Based on Image Translation and Style Transfer. Remote Sensing, 17(18), 3215. https://doi.org/10.3390/rs17183215





