Deep Learning Retrieval and Prediction of Summer Average Near-Surface Air Temperature in China with Vegetation Regionalization
Abstract
1. Introduction
2. Materials and Methods
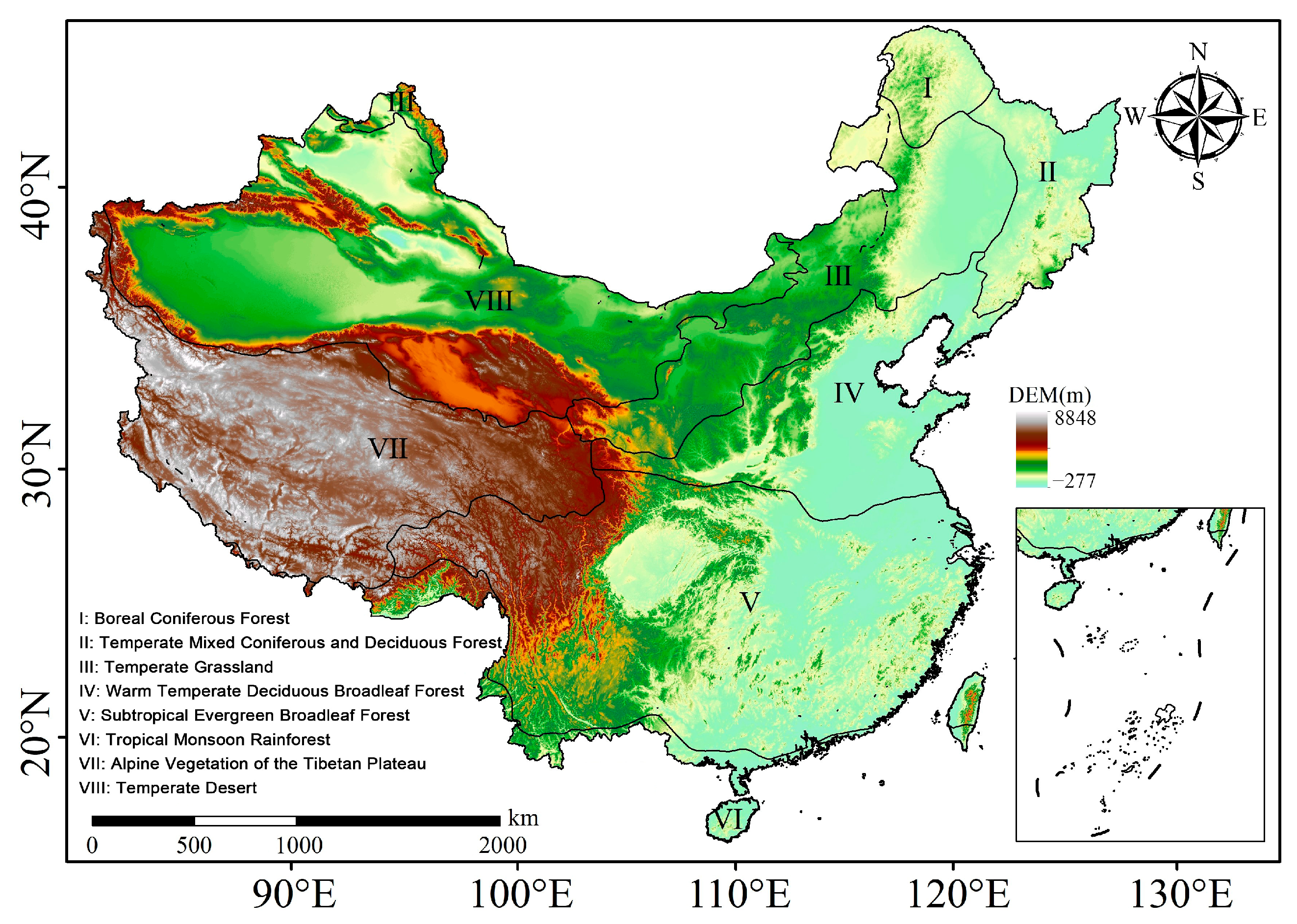
2.1. Study Area
2.2. Data
2.2.1. Satellite Data
2.2.2. Meteorological Data
2.2.3. Geographic Data
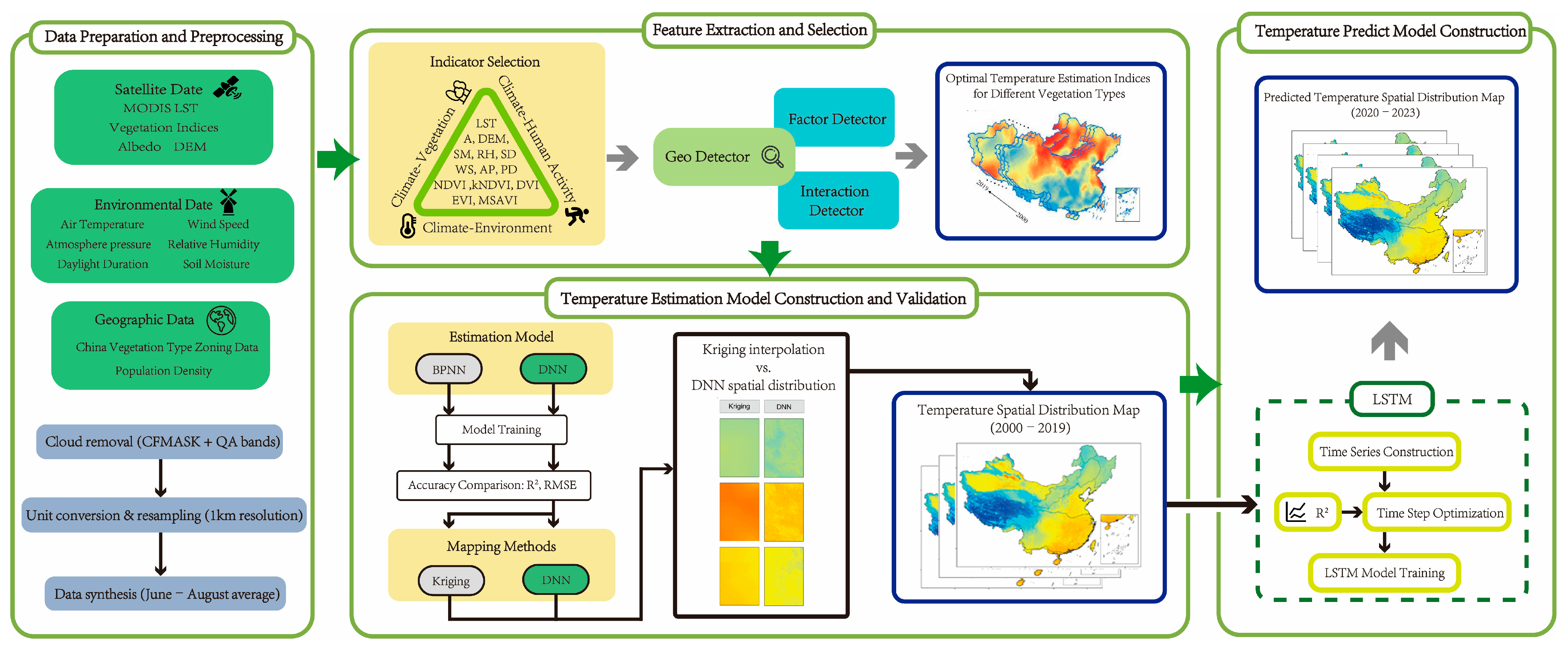
2.3. Data Processing
2.4. Methods
2.4.1. Extraction of SANSAT Retrieval Indicators
- (1)
- Surface Albedo (SA)
- (2)
- Normalized Difference Vegetation Index (NDVI)
- (3)
- Kernel Normalized Difference Vegetation Index (KNDVI)
- (4)
- Difference Vegetation Index (DVI)
- (5)
- Enhanced vegetation index (EVI)
- (6)
- Modified Soil Adjusted Vegetation Index (MSAVI)
2.4.2. Selection of Optimal Indicators for SANSAT Retrieval
2.4.3. Model Construction for SANSAT Retrieval
- (1)
- DNN model
- (2)
- BPNN model
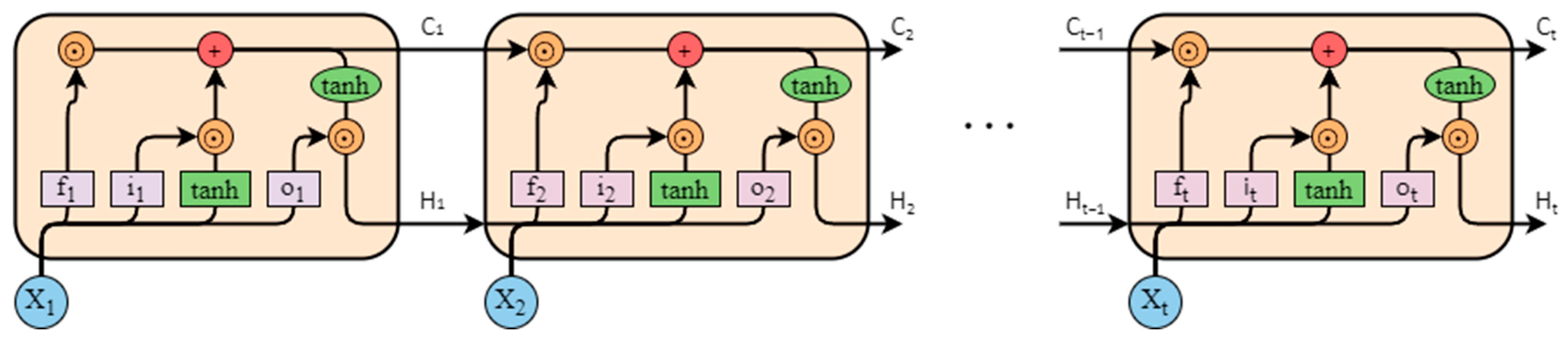
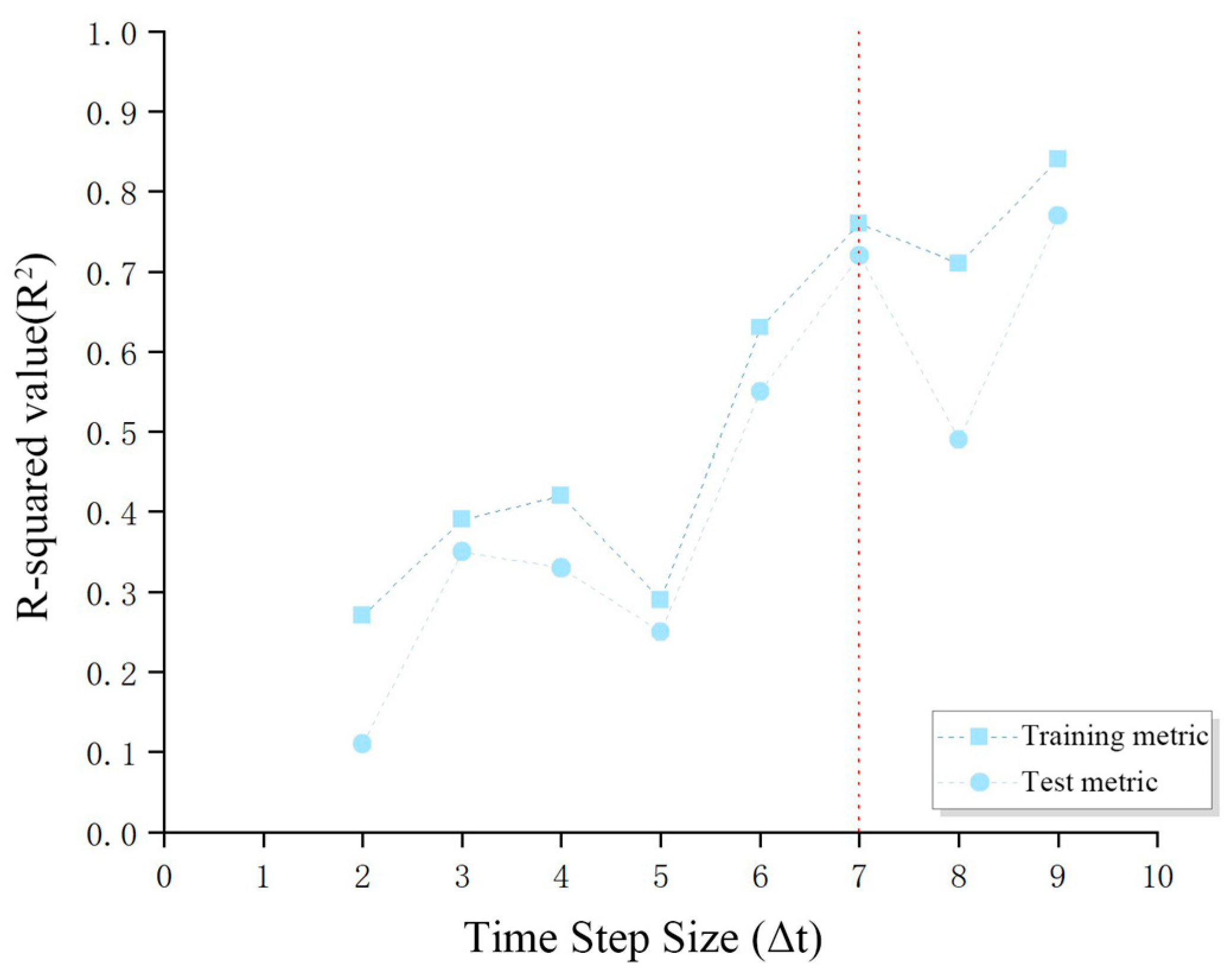
2.4.4. Model Construction for SANAST Prediction
2.4.5. Model Accuracy Verification
3. Results
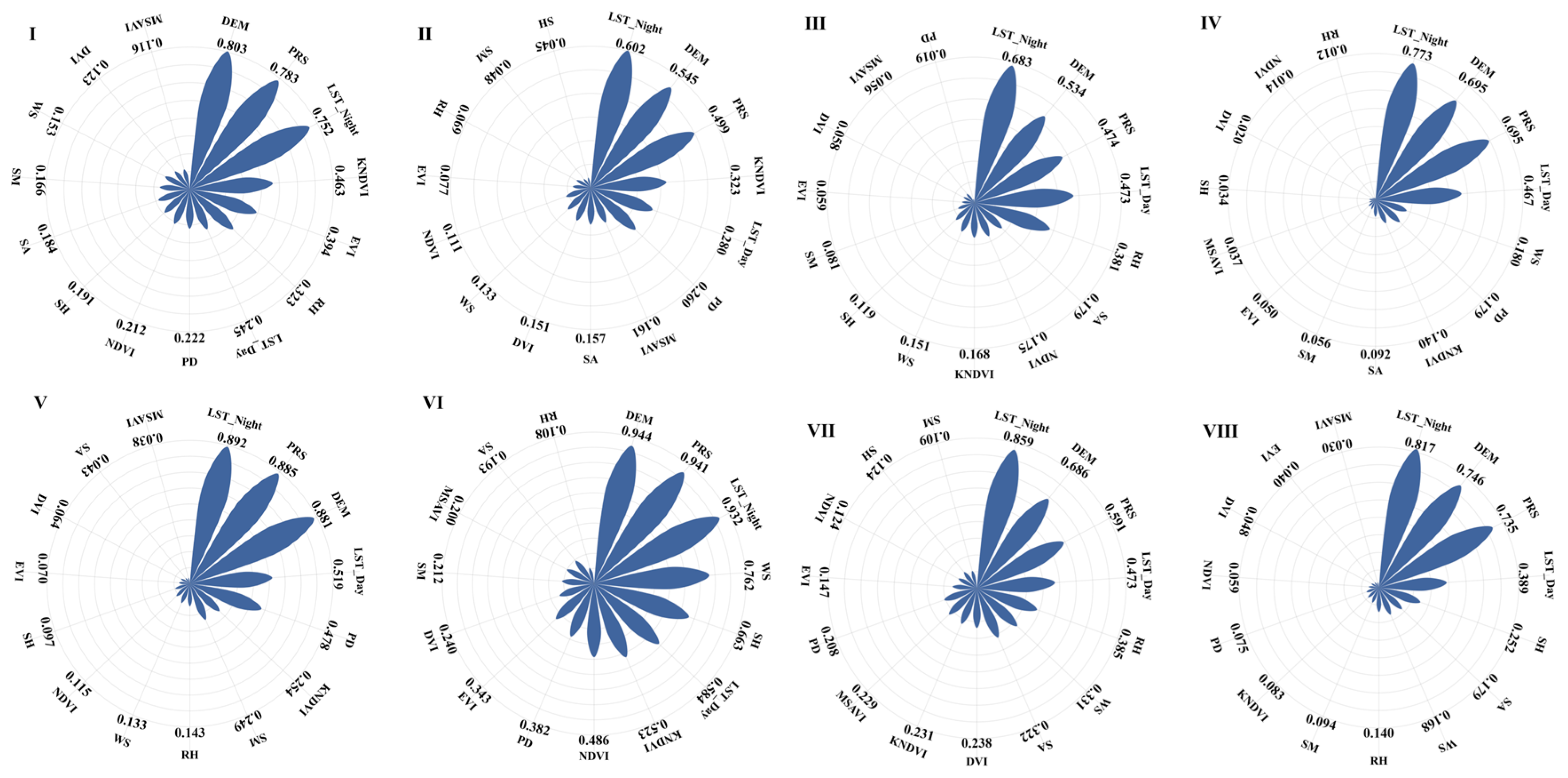
3.1. Selection of the Optimal Indicators for SANAST Retrieval
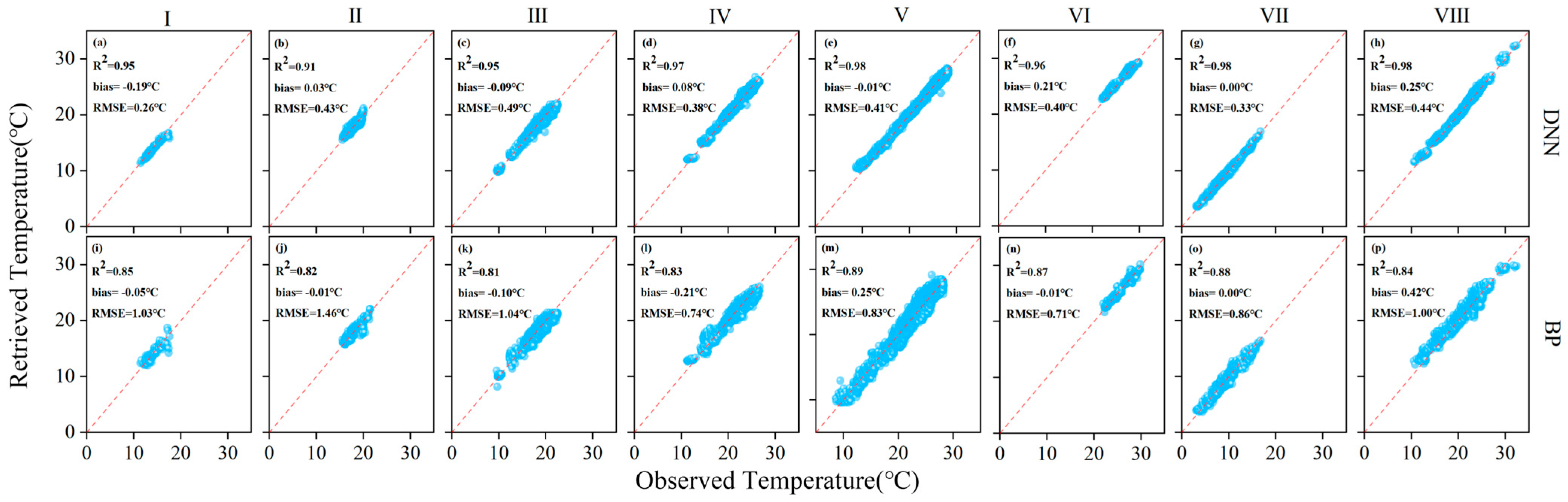
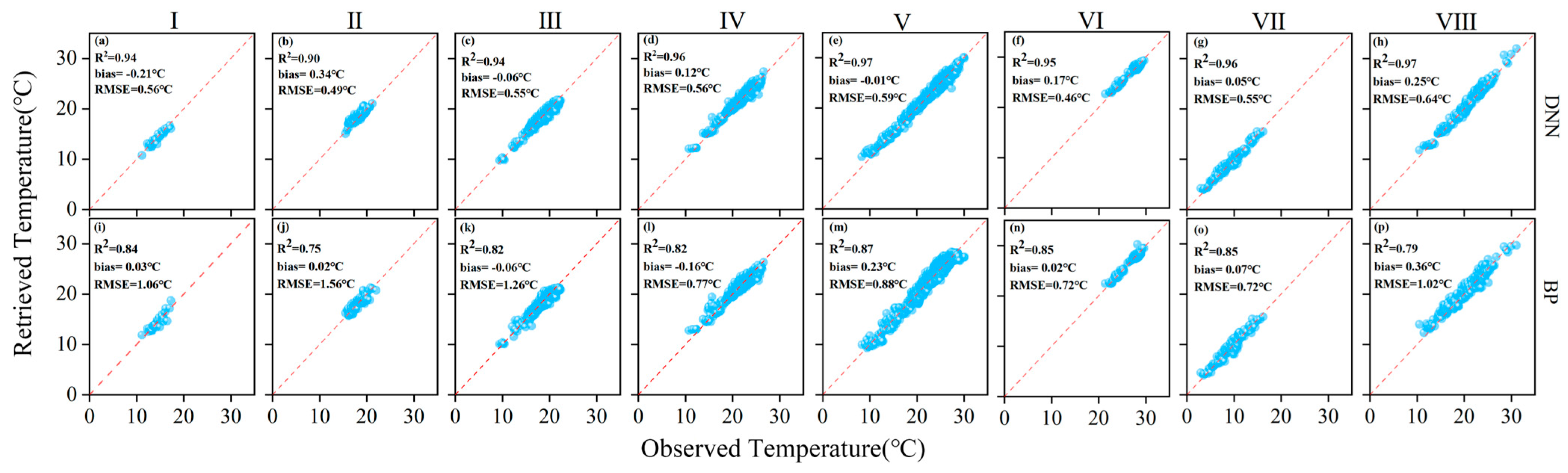
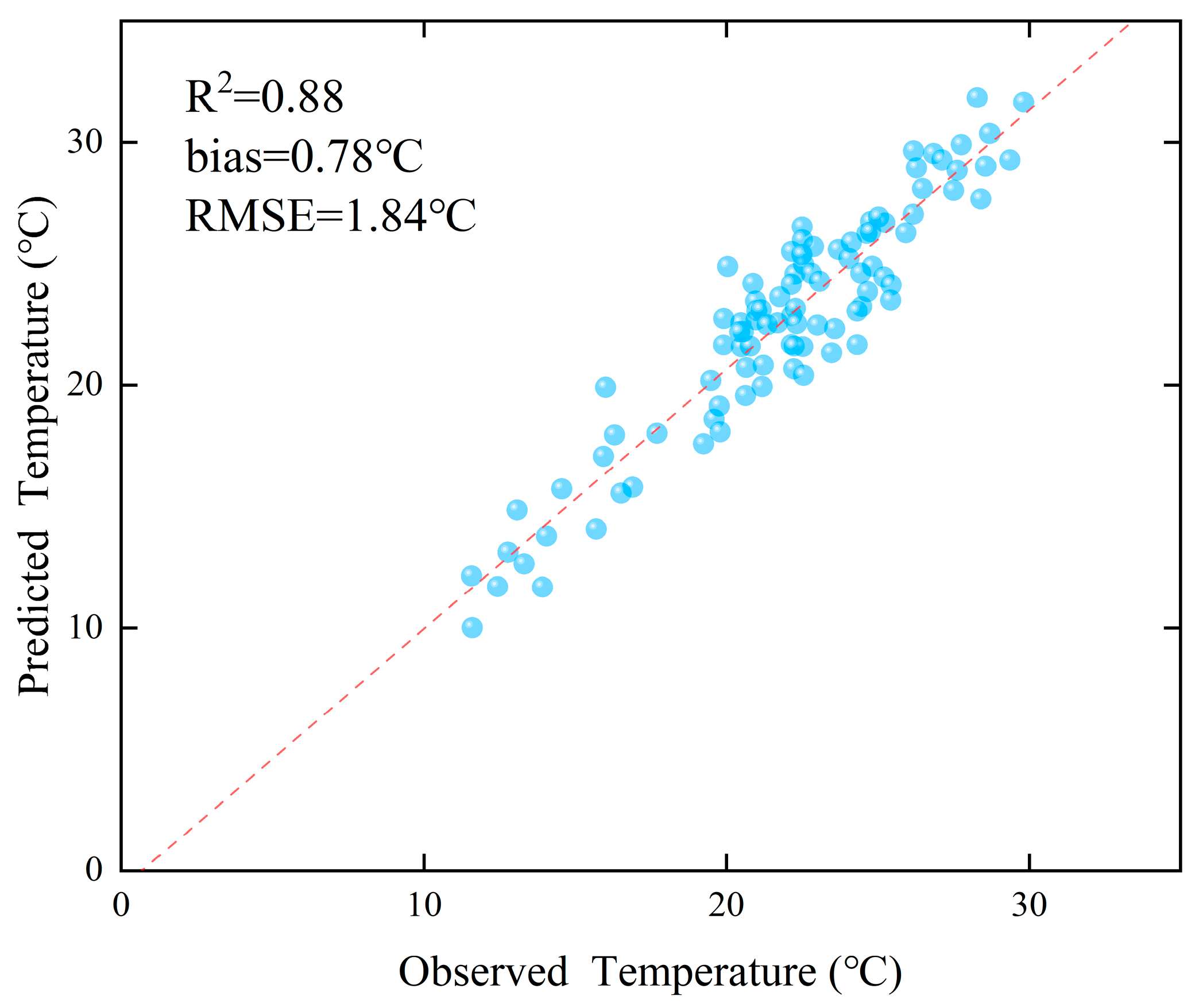
3.2. Optimized SANAST Retrieval Model
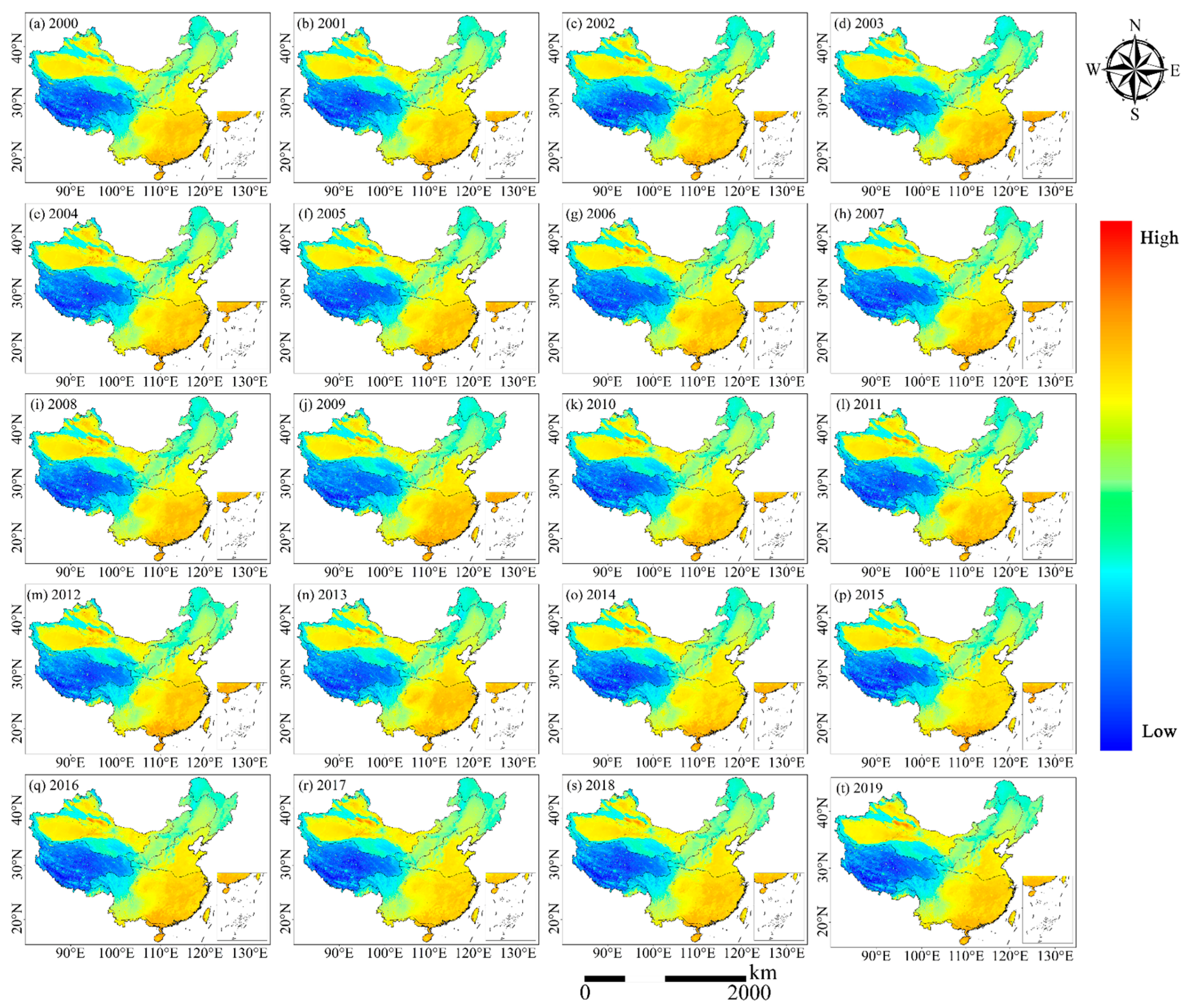
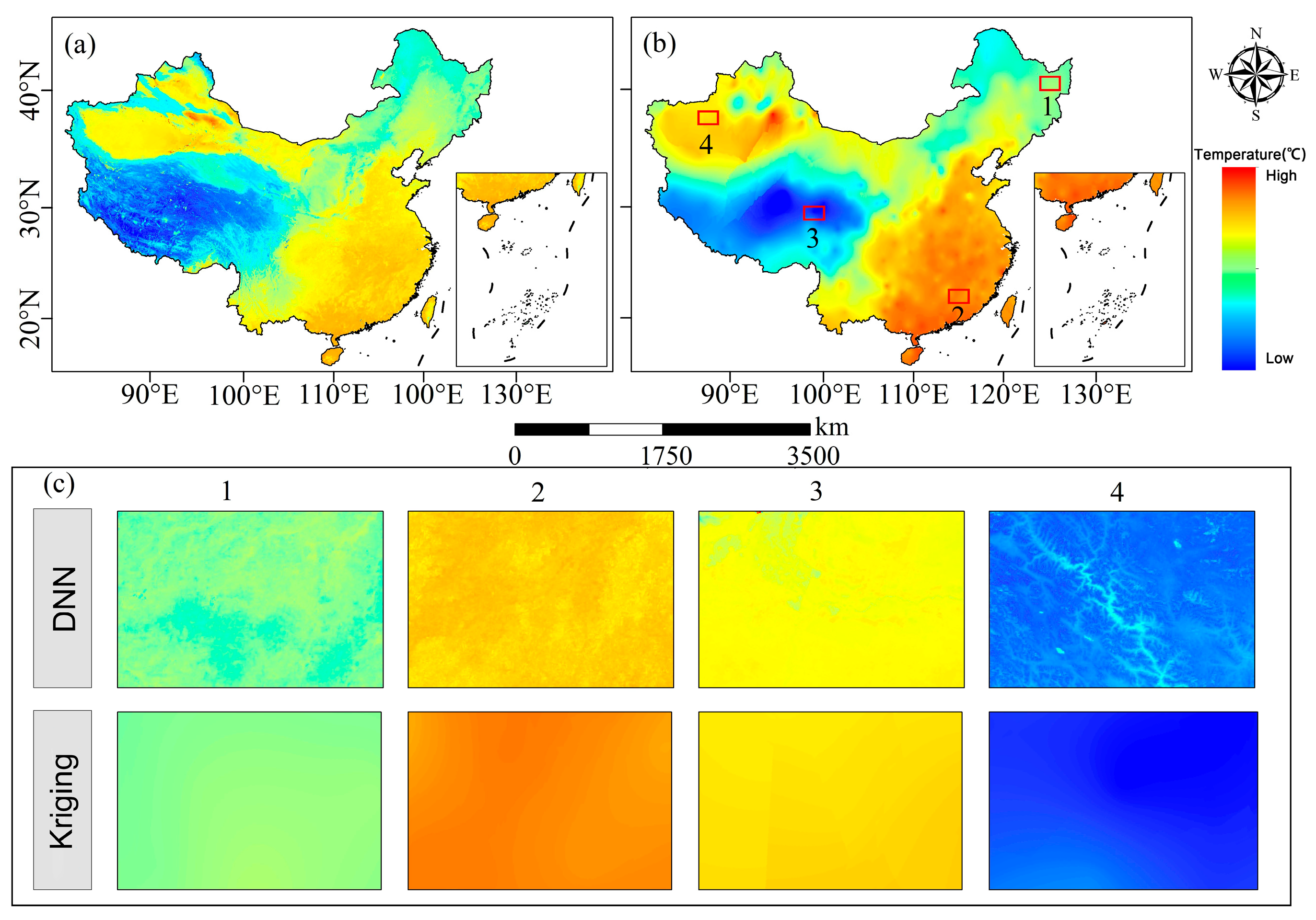
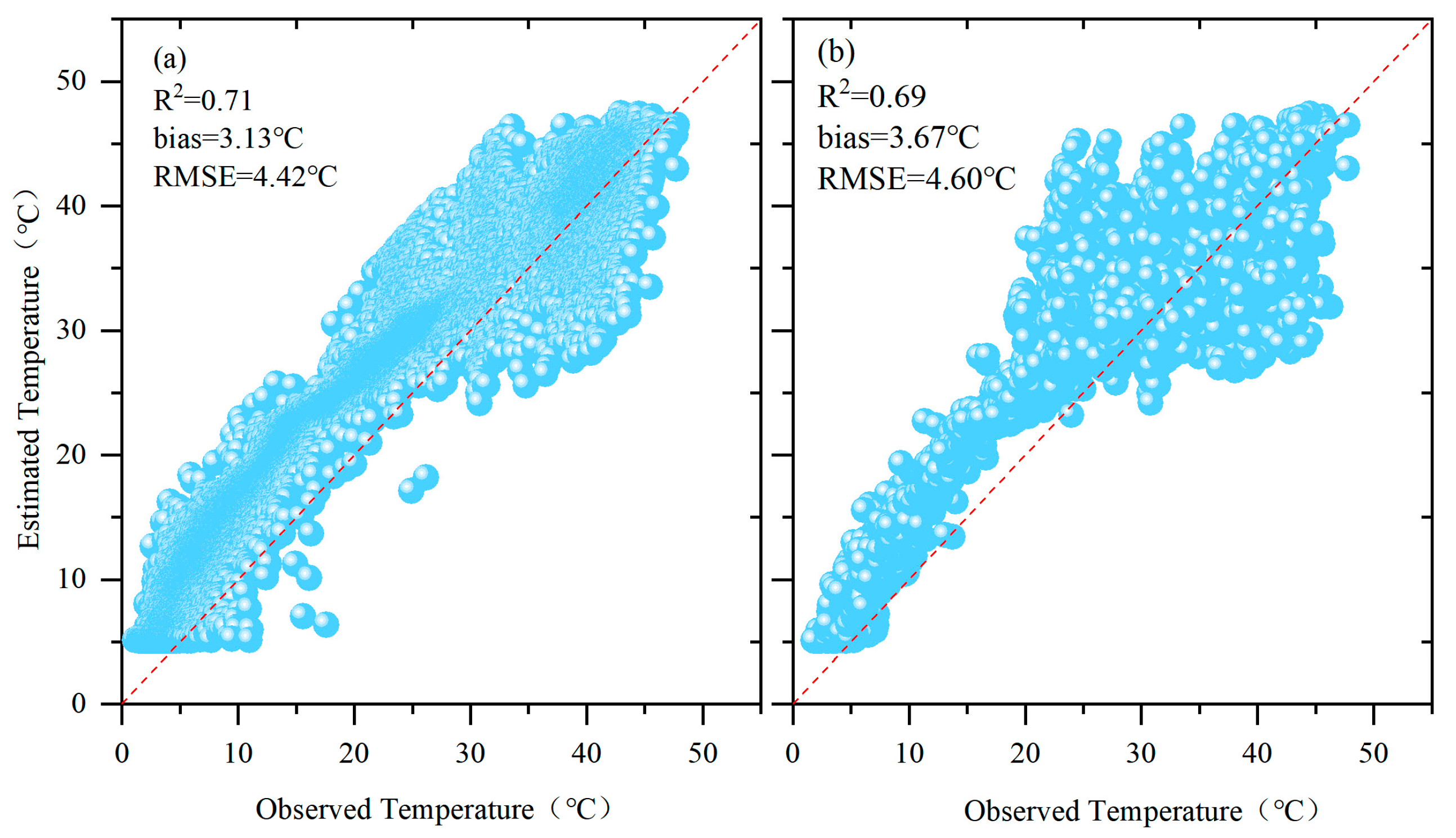
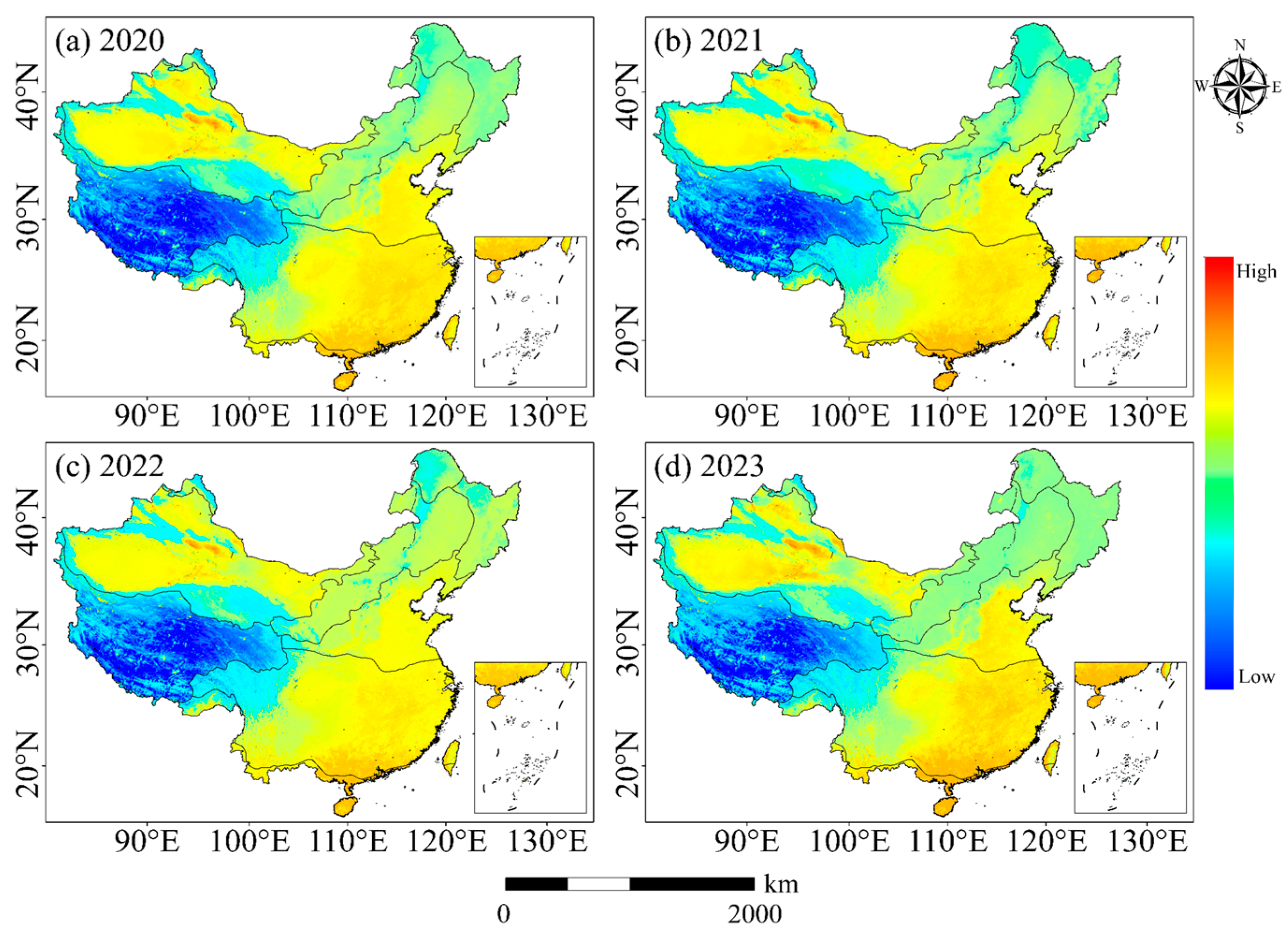
3.3. Optimized SANAST Prediction Model
4. Discussion
4.1. Comparison with Existing Research
4.2. Prospects for Future Research
5. Conclusions
- (1)
- Nighttime land surface temperature (LST_Night), elevation (DEM), and air pressure (PRS) emerged as the primary drivers of temperature variation across vegetation regions, with their influence further amplified when combined with other environmental variables. The eastern regions are influenced by both anthropogenic activities and topographic factors, whereas the western regions—particularly the Qinghai–Tibet Plateau and non-monsoon zones—are predominantly shaped by natural factors. Furthermore, in regions with substantial vegetation cover, vegetation-related factors generally contribute more than 20% to temperature variation, whereas in temperate desert areas their contribution is below 10%, indicating that vegetation plays a major role in SANAST changes in most regions.
- (2)
- By integrating multi-source remote sensing, geographic, and meteorological datasets, and employing region-specific modeling tailored to vegetation types, the DNN models achieved high fitting accuracy (R2 = 0.90–0.97) and low RMSE values (0.46–0.64 °C) across vegetation regions. Compared with BPNN models, the DNN approach demonstrated superior accuracy and stability, markedly improving the spatial adaptability and reliability of SANSAT retrieval at the national scale.
- (3)
- Building on these results, an LSTM network was applied to predict SANAST for 2020–2023. The model achieved R2 values of 0.71 and 0.69 for the training and testing sets, respectively, with corresponding RMSE values of 4.42 °C and 4.60 °C. The predicted spatial patterns were consistent with observed summer climate distributions across China, confirming the model’s feasibility and stability for time-series forecasting.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, W.; Zhou, L.; Zhang, H.; Zhang, Y.; Dai, X. Air temperature field distribution estimations over a Chinese mega-city using MODIS land surface temperature data: The case of Shanghai. Front. Earth Sci. 2016, 10, 38–48. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Obahoundje, S.; N’Guessan Bi, V.H.; Diedhiou, A.; Kravitz, B.; Moore, J.C. Influence of stratospheric aerosol geoengineering on temperature mean and precipitation extremes indices in Africa. Int. J. Clim. Chang. Strat. Manag. 2022, 14, 399–423. [Google Scholar] [CrossRef]
- Zhou, X.; Yi, Z.; Wang, Y.; Wang, D.; Zhang, L.; Huo, H. Estimating near-surface air temperature in urban functional zones in China using spatial-temporal attention. Build. Environ. 2025, 276, 112860. [Google Scholar] [CrossRef]
- Xue, X.; Wu, Y.-X.; Chen, Z.; Liu, R.; Zhao, Z. Interannual variation and statistical prediction of summer dry and hot days in South China from 1970 to 2018. J. Trop. Meteorol. 2023, 29, 431–447. [Google Scholar] [CrossRef]
- Liu, T.; Chen, H.; Jiang, W.; Li, Z. Prediction of summer precipitation in China based on soil moisture and interannual increment approach. Atmos. Sci. 2016, 40, 591–603. [Google Scholar] [CrossRef]
- Jiang, Y.; Fan, G.; Zhou, D.; Wu, Z. Changes in autumn persistent rain in Sichuan and its spatial distribution. Meteorol. Sci. 2013, 33, 316–324. [Google Scholar] [CrossRef]
- Fan, Z.; Yue, T.; Chen, C.; Sun, X. Analysis of spatial and temporal variation trends of temperature and precipitation in China. J. Earth Inf. Sci. 2011, 13, 526–533. [Google Scholar] [CrossRef]
- Shen, D.; Shi, W.-F.; Tang, W.; Wang, Y.; Liao, J. The agricultural economic value of weather forecasting in China. Sustainability 2022, 14, 17026. [Google Scholar] [CrossRef]
- Shi, Y.; Jiang, Z.; Dong, L.; Shen, S. Statistical estimation of high-resolution surface air temperature from MODIS over the Yangtze River Delta, China. J. Meteorol. Res. 2017, 31, 448–454. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.; Chen, D.; Liu, Y.; Xia, P. Retrieving precipitable water vapor data using GPS zenith delays and global reanalysis data in China. Remote Sens. 2016, 8, 389. [Google Scholar] [CrossRef]
- Dirksen, M.; Knap, W.H.; Steeneveld, G.J.; Ronda, R.J. Downscaling daily air-temperature measurements in the Netherlands. Theor. Appl. Climatol. 2020, 142, 751–767. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Y.; Fan, Y.; Li, Y.; Ge, J. Machine learning-assisted mapping of city-scale air temperature: Using sparse meteorological data for urban climate modeling and adaptation. Build. Environ. 2023, 234, 110211. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Navarro-Serrano, F.; López-Moreno, J.I.; Azorin-Molina, C.; Alonso-González, E.; Aznarez-Balta, M.; Buisán, S.T.; Revuelto, J. Elevation effects on air temperature in a topographically complex mountain valley in the Spanish Pyrenees. Atmosphere 2020, 11, 656. [Google Scholar] [CrossRef]
- Jiang, K.; Pan, Z.; Pan, F.; Wang, J.; Han, G.; Song, Y.; Zhang, Z.; Huang, N.; Ma, S.; Chen, X.; et al. The global spatiotemporal heterogeneity of land surface-air temperature difference and its influencing factors. Sci. Total Environ. 2022, 838, 156214. [Google Scholar] [CrossRef]
- Che, J.; Ding, M.; Zhang, Q.; Wang, Y.; Sun, W.; Wang, Y.; Wang, L.; Huai, B. Reconstruction of near-surface air temperature over the Greenland Ice Sheet based on MODIS data and machine learning approaches. Remote Sens. 2022, 14, 5775. [Google Scholar] [CrossRef]
- Sun, H.; Gao, J.; Yan, T.; Hu, K.; Xu, Z.; Wang, Y.; Meng, J.; Zhao, Z. Research progress in remote sensing monitoring of vegetation drought. J. Remote Sens. 2024, 28, 1395–1411. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, W.; Huang, Y.; Sun, W.; Han, P.; Yu, L.; Sun, F. Empirical estimation of near-surface air temperature in China from MODIS LST data by considering physiographic features. Remote Sens. 2016, 8, 629. [Google Scholar] [CrossRef]
- Yu, L.; Jin, X. A regime-dependent retrieval algorithm for near-surface air temperature and specific humidity from multi-microwave sensors. Remote Sens. Environ. 2018, 215, 199–216. [Google Scholar] [CrossRef]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Lin, S.; Moore, N.J.; Messina, J.P.; DeVisser, M.H.; Wu, J. Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 128–140. [Google Scholar] [CrossRef]
- Montanaro, M.; Gerace, A.; Rohrbach, S. Toward an operational stray light correction for the Landsat 8 thermal infrared sensor. Appl. Opt. 2015, 54, 3704–3715. [Google Scholar] [CrossRef]
- Santana, R.A.; Dias-Júnior, C.Q.; Vale, R.D.; Tóta, J.; Fitzjarrald, D.R. Observing and modeling the vertical wind profile at multiple sites in and above the Amazon rainforest canopy. Adv. Meteorol. 2017, 2017, 1–8. [Google Scholar] [CrossRef]
- Eccel, E.; Ghielmi, L.; Granitto, P.; Barbiero, R.; Grazzini, F.; Cesari, D. Prediction of minimum temperatures in an Alpine region by linear and non-linear post-processing of meteorological models. Nonlinear Process. Geophys. 2007, 14, 211–222. [Google Scholar] [CrossRef]
- Jiang, P.; Pan, X.M.; Zeng, X.Y. Temporal and spatial variation of temperature and precipitation in each agricultural sub-region of China. Res. Soil Water Conserv. 2020, 27, 270–278. [Google Scholar] [CrossRef]
- Yang, D.; Zhong, S.; Mei, X.; Ye, X.; Niu, F.; Zhong, W. A comparative study of several popular models for near-land surface air temperature estimation. Remote Sens. 2023, 15, 1136. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Luo, T.; Dan, Y.; Zhou, L.; Lv, X. Variation of net primary productivity and its drivers in China’s forests during 2000–2018. Forest Ecosyst. 2020, 7, 15. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, Y.; Shen, X.; Li, G.; Zhou, D. Rising air temperature and its asymmetry under different vegetation regions in China. Sci. Geogr. Sin. 2018, 38, 272–283. [Google Scholar] [CrossRef]
- Bonan, G. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Piao, S.; Yin, G.; Tan, J.; Cheng, L.; Huang, M.; Li, Y.; Liu, R.; Mao, J.; Myneni, R.B.; Peng, S.; et al. Detection and attribution of vegetation greening trend in China over the last 30 years. Global Change Biol. 2015, 21, 1601–1609. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; He, J.; Zhou, X.; Chen, L.; Zhu, C. The regional variabilities of the summer rainfall in China and its relation with anomalous moisture transport during the recent 50 years. Acta Meteorol. Sin. 2010, 68, 918–931. [Google Scholar] [CrossRef]
- Li, J.-X.; Liu, G.; Wu, R.; Ren, H.-L.; Wang, H.-M.; Mao, X.; Wei, X.-C. Narrow and wide India–Burma trough-like circulations: Their different impacts on precipitation over southern China. Geosci. Lett. 2022, 9, 7. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B. MODIS-based estimation of air temperature of the Tibetan Plateau. J. Geogr. Sci. 2013, 23, 627–640. [Google Scholar] [CrossRef]
- Wu, G.; Zhou, X.; Xu, X.; Huang, J.; Duan, A.; Yang, S.; Hu, W.; Ma, Y.; Liu, Y.; Bian, J.; et al. An integrated research plan for the Tibetan Plateau land–air coupled system and its impacts on the global climate. Bull. Am. Meteorol. Soc. 2023, 104, E158–E177. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Kimball, J.S.; Hong, S.Y. Retrievals of all-weather daily air temperature using MODIS and AMSR-E data. Remote Sens. 2014, 6, 8387–8404. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, J.; Zhang, X.; Wang, S.; Tang, W.; Wang, Z.; Ma, J.; Ai, L.; Li, M.; Wang, W. Progress and challenges in all-weather remote sensing of land surface temperature. J. Remote Sens. 2023, 27, 1534–1553. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Pan, M.; Beck, H.; Coccia, G.; Serrat-Capdevila, A.; Verbist, K. Satellite remote sensing for water resources management: Potential for supporting sustainable development in data-poor regions. Water Resour. Res. 2018, 54, 9724–9758. [Google Scholar] [CrossRef]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4, 7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Qiu, Y.; Chai, D. A deep learning method for Landsat image cloud detection without manually labeled data. Remote Sens. Land Resour. 2021, 33, 102–107. [Google Scholar] [CrossRef]
- Yang, X.; Tang, G.; Xiao, C.; Deng, F. Terrain revised model for air temperature in mountainous area based on DEMs: A case study in Yaoxian county. J. Geogr. Sci. 2007, 17, 399–408. [Google Scholar] [CrossRef]
- Zhu, S.; Zhou, C.; Zhang, G.; Zhang, H.; Hua, G. Preliminary verification of instantaneous air temperature estimation for clear sky conditions based on SEBAL. Meteorol. Atmos. Phys. 2017, 129, 71–81. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Zhao, C.; Qu, Y.; Liu, Q.; Zhang, H.; Tong, Y.; Wang, C.; Li, S.; Guo, J.; et al. Review of land surface albedo: Variance characteristics, climate effect and management strategy. Remote Sens. 2022, 14, 1382. [Google Scholar] [CrossRef]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 225–240. [Google Scholar] [CrossRef]
- Chen, A.; Meng, W.; Hu, S.; Bian, L. Comparative analysis on land surface albedo from MODIS and GLASS over the Tibetan Plateau. Trans. Atmos. Sci. 2020, 43, 932–942. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, X.; Sun, L.; Liu, Q.; Liu, S. Validation of GLASS albedo product through Landsat TM data and ground measurements. J. Remote Sens. 2014, 18, 547–558. [Google Scholar] [CrossRef]
- Andres-Anaya, P.; Sanchez-Aparicio, M.; Del Pozo, S.; Lagüela, S.; Hernández-López, D.; Gonzalez-Aguilera, D. A new methodology for estimating surface albedo in heterogeneous areas from satellite imagery. Appl. Sci. 2024, 14, 75. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Jiménez-Muñoz, J.-C. Land use classification from multitemporal Landsat imagery using the Yearly Land Cover Dynamics (YLCD) method. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 711–720. [Google Scholar] [CrossRef]
- Karmaoui, A.; Moumane, A.; El Jaafari, S.; Menouni, A.; Al Karkouri, J.; Yacoubi, M.; Hajji, L. Thirty years of change in the land use and land cover of the Ziz Oases (Pre-Sahara of Morocco) combining remote sensing, GIS, and field observations. Land 2023, 12, 2127. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, Z.; Liu, Z.; Si, J.; Ou, J. Assessment and dynamic prediction of green space ecological service value in Guangzhou City, China. Remote Sens. 2024, 16, 4180. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Wang, C.; Liu, L.; Zhou, Y.; Liu, X.; Wu, J.; Tan, W.; Xu, C.; Xiong, X. Comparison between satellite derived solar-induced chlorophyll fluorescence, NDVI and kNDVI in detecting water stress for dense vegetation across southern China. Remote Sens. 2024, 16, 1735. [Google Scholar] [CrossRef]
- Lu, J.; Li, J.; Fu, H.; Tang, X.; Liu, Z.; Chen, H.; Sun, Y.; Ning, X. Deep learning for multi-source data-driven crop yield prediction in Northeast China. Agriculture 2024, 14, 794. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Bao, N.; Li, W.; Gu, X.; Liu, Y. Biomass estimation for semiarid vegetation and mine rehabilitation using Worldview-3 and Sentinel-1 SAR imagery. Remote Sens. 2019, 11, 2855. [Google Scholar] [CrossRef]
- Vijith, H.; Dodge-Wan, D. Applicability of MODIS land cover and Enhanced Vegetation Index (EVI) for the assessment of spatial and temporal changes in strength of vegetation in tropical rainforest region of Borneo. Remote Sens. Appl. Soc. Environ. 2020, 18, 100311. [Google Scholar] [CrossRef]
- Hao, B.; Xu, X.; Wu, F.; Tan, L. Long-term effects of fire severity and climatic factors on post-forest-fire vegetation recovery. Forests 2022, 13, 883. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Y.; Li, H.; Guo, J. Soil moisture retrieval in farmland areas with Sentinel multi-source data based on regression convolutional neural networks. Sensors 2021, 21, 877. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Ma, P.; Kwan, M.-P.; Liu, Y. How did urban environmental characteristics influence land surface temperature in Hong Kong from 2017 to 2022? Evidence from remote sensing and land use data. Sustainability 2023, 15, 15511. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Fu, B. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, L.; Duan, Y.; Fan, S. Spatial and temporal patterns and evolution of traditional villages in Jiangxi Province. J. Remote Sens. 2021, 25, 2460–2471. [Google Scholar] [CrossRef]
- Zhang, X.; Lyu, C.; Fan, X.; Bi, R.; Xia, L.; Xu, C.; Sun, B.; Li, T.; Jiang, C. Spatiotemporal variation and influence factors of habitat quality in Loess Hilly and Gully Area of Yellow River Basin: A case study of Liulin County, China. Land 2022, 11, 127. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, L.; Wan, H.; Wu, Q.; Liu, C. Remote sensing monitoring and analysis of landscape pattern changes in Bayinbuluke Heritage Area over the past 30 years. J. Remote Sens. 2021, 25, 2488–2506. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gong, J. Deep neural network for remote-sensing image interpretation: Status and perspectives. Natl. Sci. Rev. 2019, 6, 1082–1086. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Tian, S.; Ma, L.; Li, H.; Tian, F.; Mao, J. Research on a coal seam gas content prediction method based on an improved extreme learning machine. Appl. Sci. 2023, 13, 8753. [Google Scholar] [CrossRef]
- He, X.; Zhao, X.; Sun, Y.; Geng, P.; Zhang, X. Application of TBSS-based machine learning models in the diagnosis of pediatric autism. Front. Neurol. 2023, 13, 1078147. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Gu, F.; Travacca, B.; Askari, A.; Tsai, A. Implicit deep learning. SIAM J. Math. Data Sci. 2021, 3, 930–958. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Mehrkanoon, S. Deep shared representation learning for weather elements forecasting. Knowl.-Based Syst. 2019, 179, 120–128. [Google Scholar] [CrossRef]
- Hutasavi, S.; Chen, D. Estimating district-level electricity consumption using remotely sensed data in Eastern Economic Corridor, Thailand. Remote Sens. 2021, 13, 4654. [Google Scholar] [CrossRef]
- Zhu, J.; Cao, S.; Shang, G.; Shi, J.; Wang, X.; Zheng, Z.; Liu, C.; Yang, H.; Xie, B. Subpixel snow mapping using daily AVHRR/2 data over Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 2899. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, T.; Cheng, Q.; Shen, H.-F. Inversion of air temperature in the Yangtze River Economic Belt using spatiotemporal neural network model. J. Trop. Meteorol. 2023, 48, 325–332. [Google Scholar] [CrossRef]
- Wang, M. Spatial Estimation of Air Temperature Based on Multi-Source Information Fusion and Its Application. Master’s Thesis, Hubei University, Wuhan, China, 2021. [Google Scholar]
- Jang, J.D.; Viau, A.A.; Anctil, F. Neural network estimation of air temperatures from AVHRR data. Int. J. Remote Sens. 2004, 25, 4541–4554. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, Y. Regression model of spatial air-temperature distribution and monthly variation characteristics in Sichuan Province. Sichuan Meteorol. 2006, 2, 17–18. [Google Scholar]
- Bai, L.; Xu, Y.M.; He, M.; Li, N. Study on remote sensing retrieval of near-surface air temperature based on random forest algorithm. J. Geo-Inf. Sci. 2017, 19, 390–397. [Google Scholar]
- Han, P.; Ji, Z. Ridge regression prediction model for May air temperature in South China. J. Appl. Meteorol. Sci. 2024, 35, 480–492. [Google Scholar] [CrossRef]



| Data Type | Dataset Source | Time Resolution | Spatial Resolution |
|---|---|---|---|
| Surface temperature | MODIS Land surface temperature and emissivity dataset (MOD11A1) | Daily | 1 km |
| Vegetation index | MODIS Vegetation index dataset (MOD13A2) | 8 days | 1 km |
| Surface albedo | MODIS Albedo dataset (MCD43A3) | 9 days | 500 m |
| Elevation | NASA SRTM Digital elevation dataset | — | 30 m |
| Soil moisture | GLDAS-2.1: Global land assimilation system dataset | Monthly | 1 km |
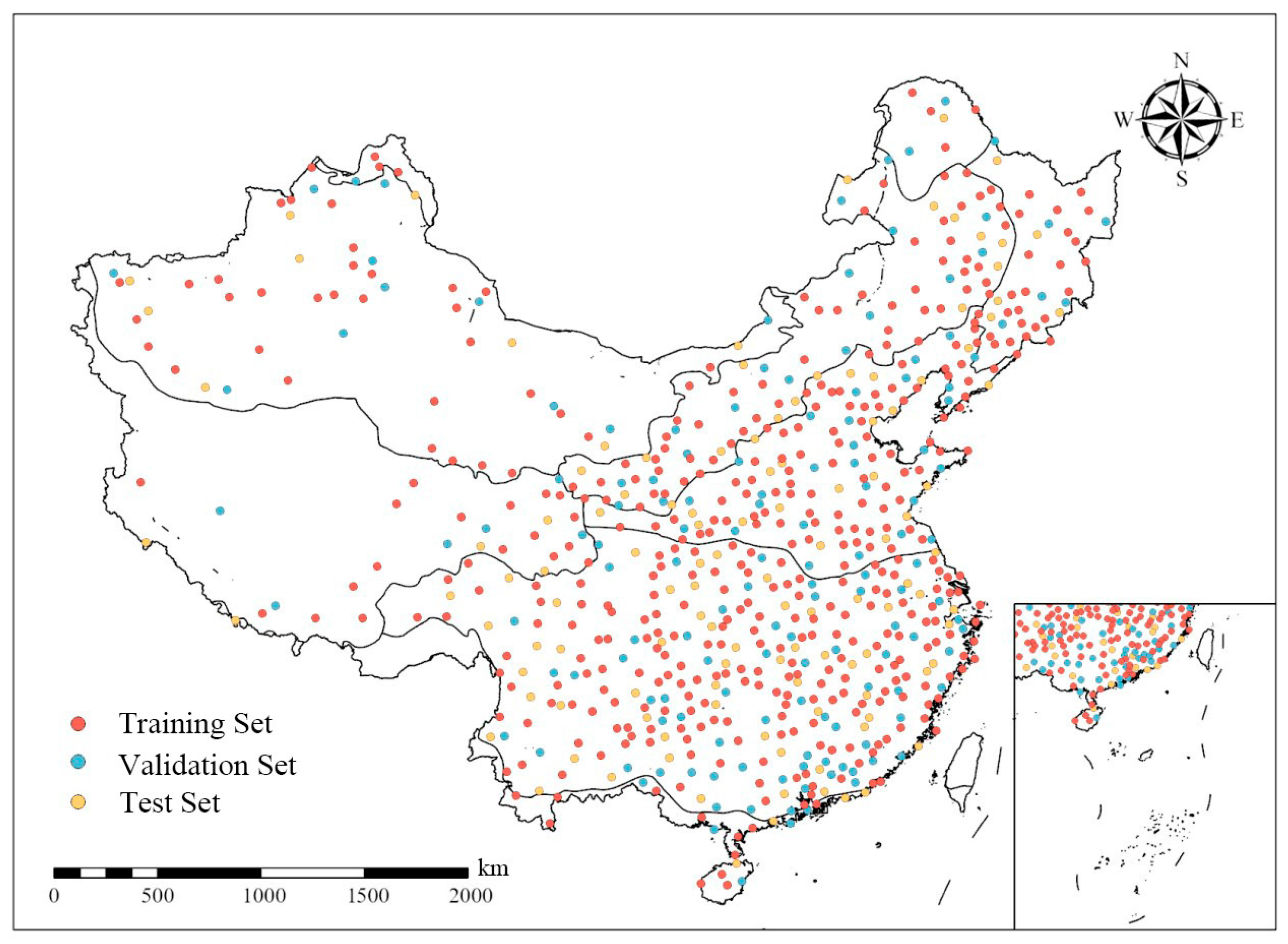
| Sample Type | Number of Samples in Each Vegetation Region | |||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | |
| Training set | 80 | 500 | 1200 | 1780 | 3860 | 260 | 360 | 660 |
| Test set | 40 | 120 | 380 | 560 | 1340 | 100 | 120 | 220 |
| Verification set | 20 | 100 | 300 | 440 | 1360 | 80 | 120 | 180 |
| Relationship Description | Interaction | Implication |
|---|---|---|
| Nonlinear attenuation | Strong negative interaction | |
| Single-factor nonlinear attenuation | Weak negative interaction | |
| Two-factor enhancement | Synergistic effect | |
| Independent role | No interference with each other | |
| Nonlinear enhancement | Strong synergistic effect |
| Region Code | Vegetation Region | Indicator |
|---|---|---|
| I | Cold temperate coniferous forest region | DEM, PRS, LST_Night, KNDVI, EVI, RH, LST_Day, PD, NDVI, SH, SA, SM, WS |
| II | Temperate coniferous and deciduous forest mixed forest region | LST_Night, DEM, PRS, KNDVI, LST_Day, PD, MSAVI, SA, DVI |
| III | Temperate grassland region | LST_Night, DEM, PRS, LST_Day, RH, SA, NDVI, KNDVI, WS |
| IV | Warm temperate deciduous broad-leaved forest region | LST_Night, DEM, PRS, LST_Day, WS, PD, KNDVI |
| V | Subtropical evergreen broad-leaved forest region | LST_Night, PRS, DEM, LST_Day, PD, KNDVI, SM |
| VI | Tropical monsoon forest and rainforest region | DEM, PRS, LST_Night, WS, SH, LST_Day, KNDVI, NDVI, PD, EVI, DVI, SM, MSAVI, SA |
| VII | Alpine vegetation region in Qinghai–Tibet Plateau | LST_Night, DEM, PRS, LST_Day, RH, WS, SA, DVI, KNDVI, MSAVI, PD, EVI |
| VIII | Temperate desert region | LST_Night, DEM, PRS, LST_Day, SH, SA, WS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Li, Z.; Wen, Y.; Xie, S.; Ou, J.; Wang, J.; Liu, Z.; Si, J.; Gan, Z.; Lyu, Y.; et al. Deep Learning Retrieval and Prediction of Summer Average Near-Surface Air Temperature in China with Vegetation Regionalization. Remote Sens. 2025, 17, 3209. https://doi.org/10.3390/rs17183209
Lu W, Li Z, Wen Y, Xie S, Ou J, Wang J, Liu Z, Si J, Gan Z, Lyu Y, et al. Deep Learning Retrieval and Prediction of Summer Average Near-Surface Air Temperature in China with Vegetation Regionalization. Remote Sensing. 2025; 17(18):3209. https://doi.org/10.3390/rs17183209
Chicago/Turabian StyleLu, Wenting, Zhefan Li, Ya Wen, Shujuan Xie, Jiaming Ou, Jianfang Wang, Zhenhua Liu, Jiahe Si, Zheyu Gan, Yue Lyu, and et al. 2025. "Deep Learning Retrieval and Prediction of Summer Average Near-Surface Air Temperature in China with Vegetation Regionalization" Remote Sensing 17, no. 18: 3209. https://doi.org/10.3390/rs17183209
APA StyleLu, W., Li, Z., Wen, Y., Xie, S., Ou, J., Wang, J., Liu, Z., Si, J., Gan, Z., Lyu, Y., Ji, Z., Fang, Q., & Jin, M. (2025). Deep Learning Retrieval and Prediction of Summer Average Near-Surface Air Temperature in China with Vegetation Regionalization. Remote Sensing, 17(18), 3209. https://doi.org/10.3390/rs17183209






