Precipitation Data Accuracy and Extreme Rainfall Detection for Flood Risk Analysis in the Akçay Sub-Basin
Abstract
Highlights
- GPM-IMERG outperforms CHIRPS in the Türkiye’s Akçay Sub-Basin, with higher accuracy at the monthly scale (Pearson = 0.943; RMSE = 50.81 mm) but lower performance at the daily scale (Pearson = 0.592; RMSE = 12.45 mm).
- Extreme rainfall analysis indicated that the Beta distribution best fits monthly precipitation, while the Weibull distribution fits daily precipitation, improving threshold-based flood risk assessments.
- GPM-IMERG is suitable for long-term precipitation monitoring and monthly extreme event detection in data-scarce basins, supporting hydrological modeling and flood risk management.
Abstract
1. Introduction
2. Materials and Methods
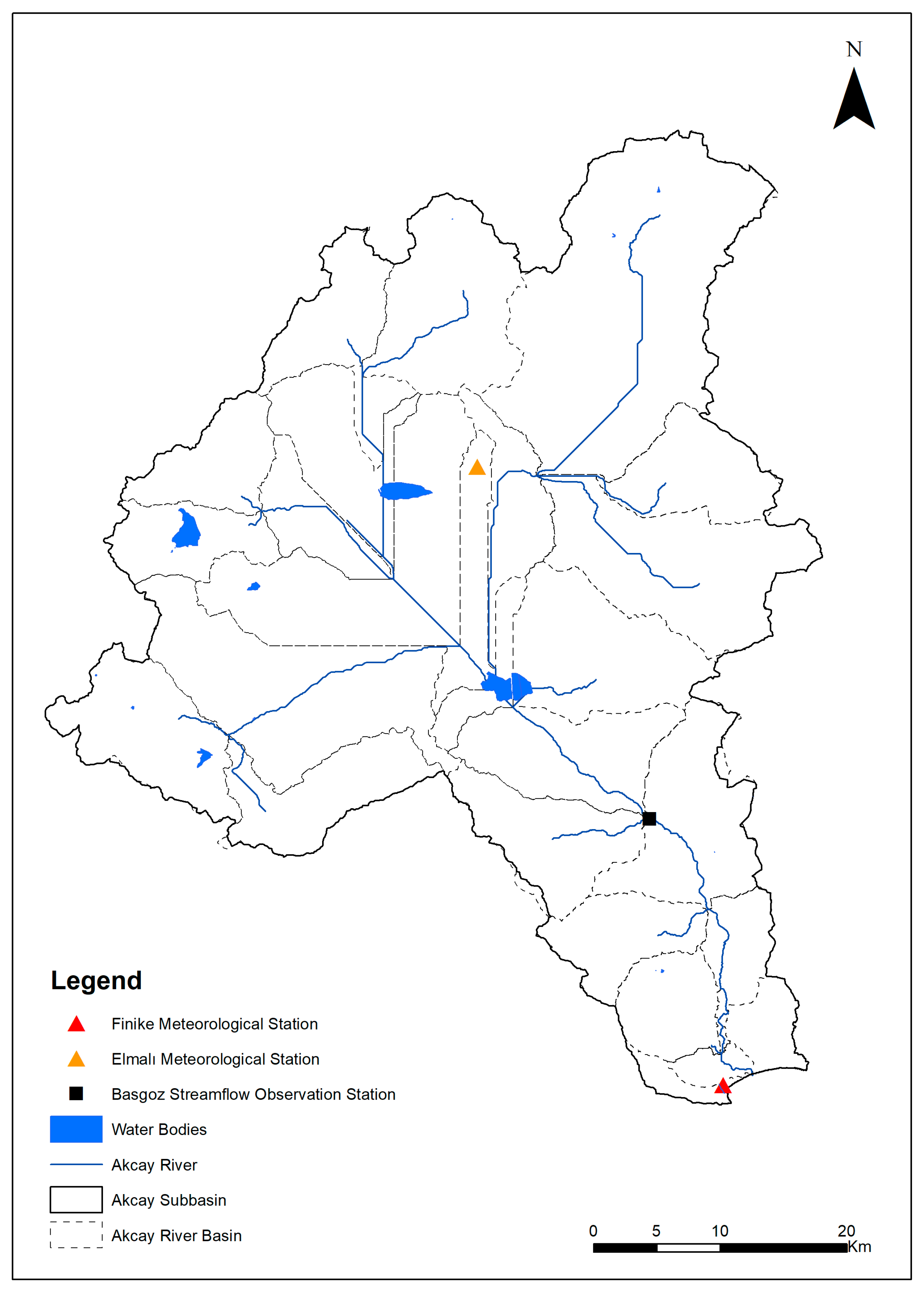
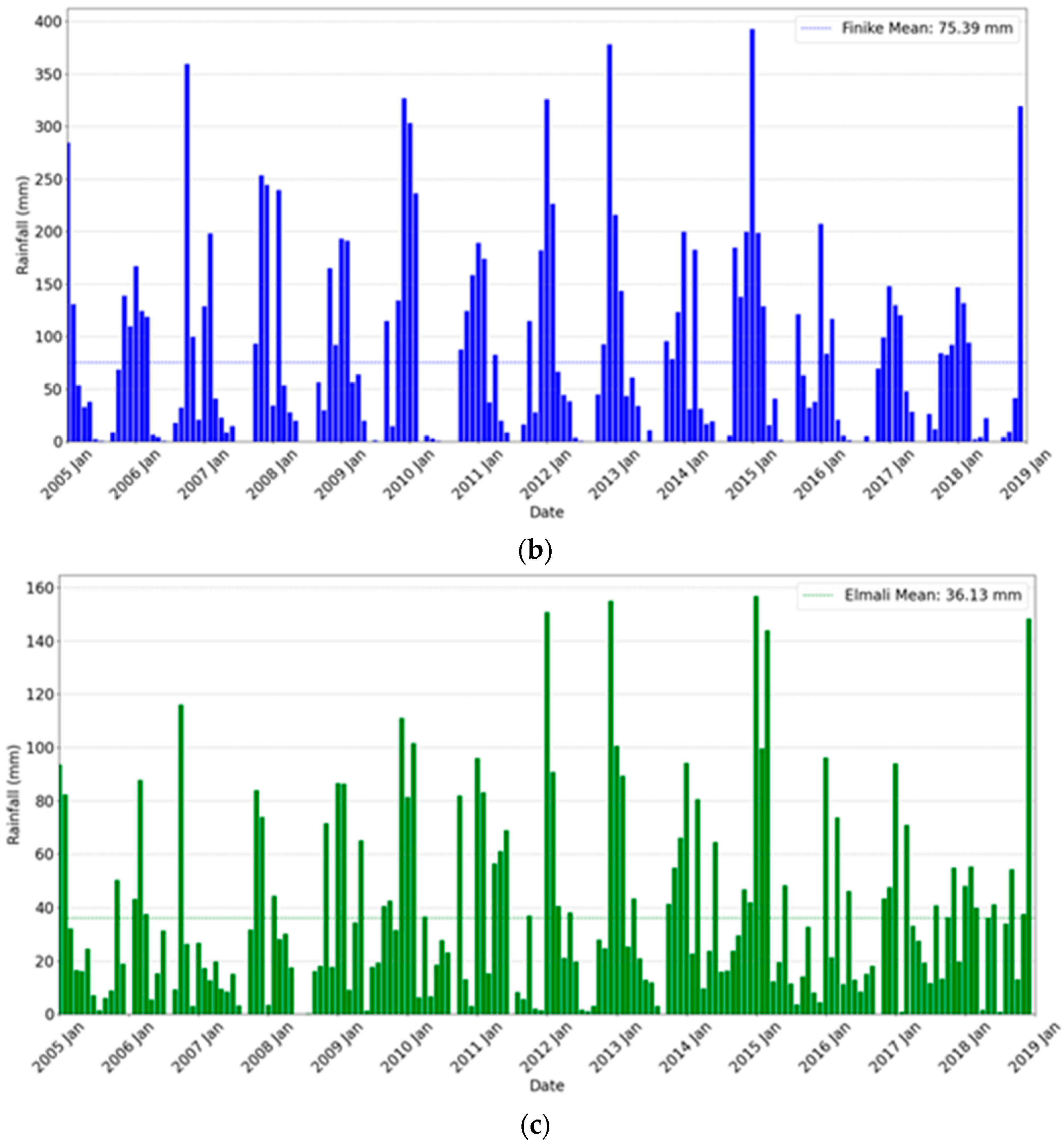
2.1. Study Area and Datasets
2.2. Correlation Analysis Between Meteorological Station and Remotely Sensed Datasets
2.3. Extreme Rainfall Detection Metrics
3. Results
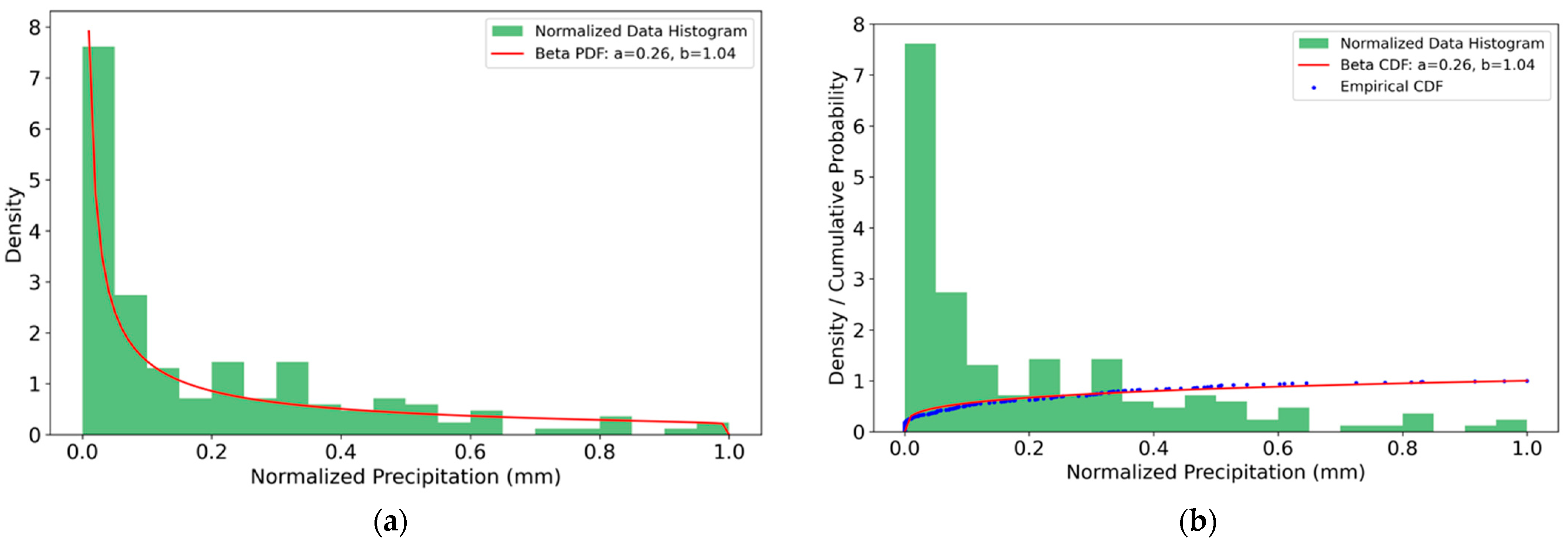
3.1. Kolmogorov–Smirnov (K-S) Tests and Probability Distribution Analysis
3.2. Performance of Extreme Rainfall Event Detection
4. Discussion and Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Ali, S.; Zhang, Q.; He, Y. Impacts of climate change on extreme precipitation and river flow in Asia: A systematic review. J. Hydrol. 2022, 602, 126689. [Google Scholar]
- Gudmundsson, L.; Decharme, B.; Blöschl, G. Observed climate variability and extremes in global river flow. Nat. Rev. Earth Environ. 2023, 4, 44–59. [Google Scholar]
- Westra, S.; Fowler, H.J.; Evans, J.P.; Alexander, L.V.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N.M. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
- Dottori, F.; Szewczyk, W.; Ciscar, J.-C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Change 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Change 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Change 2016, 134, 387–401. [Google Scholar]
- Mondal, A.; Lakshmi, V.; Hashemi, H. Intercomparison of trend analysis of multi satellite monthly precipitation products and gage measurements for river basins of India. J. Hydrol. 2018, 565, 779–790. [Google Scholar] [CrossRef]
- Lakshmi, V. Remote Sensing of the Terrestrial Water Cycle; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Dandridge, C.; Lakshmi, V.; Bolten, J.; Srinivasan, R. Evaluation of satellite-based rainfall estimates in the Lower Mekong River Basin. Remote Sens. 2019, 11, 2709. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.I.F.; Allan, R.P.; Greatrex, H.; Rojas, O.; Leo, O. Evaluation of satellite based and model re analysis rainfall estimates for Uganda. Meteorol. Appl. 2013, 20, 308–317. [Google Scholar]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P. Integrated Multi satellite Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document; NASA Goddard Space Flight Center. 2020. Available online: https://gpm.nasa.gov (accessed on 15 April 2024).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Rowland, J.; Michaelsen, J. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.H.M.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Le, M.-H.; Lakshmi, V.; Bolten, J.; Bui, D. Adequacy of satellite derived precipitation estimate for hydrological modeling in Vietnam basins. J. Hydrol. 2020, 586, 124820. [Google Scholar] [CrossRef]
- Tran, D.; Le, M.-H.; Zhang, R.; Nguyen, B.; Bolten, J.; Lakshmi, V. Robustness of gridded precipitation products for Vietnam basins using the comprehensive assessment framework of rainfall. Atmos. Res. 2023, 293, 106293. [Google Scholar] [CrossRef]
- Prat, O.P.; Nelson, B.R. Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge data sets at daily to annual scales (2002–2012). Hydrol. Earth Syst. Sci. 2015, 19, 2037–2056. [Google Scholar] [CrossRef]
- Hashemi, H.; Nordin, M.; Lakshmi, V.; Huffman, G.; Knight, R. Bias correction of long term satellite monthly precipitation product (TRMM 3B43) over the conterminous United States. J. Hydrometeorol. 2017, 18, 2491–2509. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, D.; Qin, Z.; Zheng, Y.; Guo, J. Assessment of the GPM and TRMM precipitation products using the rain gauge network over the Tibetan Plateau. J. Meteorol. Res. 2018, 32, 324–336. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.K.; Dehghani, M. Evaluation of satellite rainfall climatology using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef]
- Fayne, J.; Hashemi, H.; Huffman, G.; Lakshmi, V. Very high resolution altitude corrected, TMPA based monthly satellite precipitation product over the CONUS. Sci. Data 2020, 7, 96. [Google Scholar] [CrossRef]
- Tran, D.; Nguyen, B.; Zhang, R.; Aryal, A.; Grodzka Lukaszewska, M.; Sinicyn, G.; Lakshmi, V. Quantification of gridded precipitation products on the Mekong River Basin: A case study for the Srepok River subbasin, Central Highland Vietnam. Remote Sens. 2023, 15, 1030. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–294. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov–Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1958, 46, 68–76. [Google Scholar] [CrossRef]
- Beguería, S. Uncertainties in partial duration series modelling of extremes related to the choice of the threshold value. J. Hydrol. 2005, 303, 215–230. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation. Hydrol. Sci. J. 2004, 49, 575–590. [Google Scholar] [CrossRef]
- Yu, Y.; Choi, Y.J.; Kim, J.H.; Lee, S. Evaluating the performance of satellite precipitation products for extreme rainfall detection. Remote Sens. 2022, 14, 567. [Google Scholar] [CrossRef]
- Doswell, C.A., III; Davies-Jones, R.; Keller, D.L. On summary measures of skill in rare event forecasting based on contingency tables. Wea. Forecast. 1990, 5, 576–585. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification: A Practitioner’s Guide in Atmospheric Science, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Schaefer, J.T. The critical success index as an indicator of warning skill. Wea. Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Marzban, C. Scalar measures of performance in rare-event situations. Wea. Forecast. 1998, 13, 753–763. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- United States Geological Survey. Shuttle Radar Topography Mission (SRTM) Elevation Data; USGS: Reston, VA, USA, 2000. Available online: https://www.usgs.gov (accessed on 18 April 2024).
- Gupta, P.; Singh, P.; Singh, P.; Joshi, V. Assessment of satellite based precipitation products for hydrological applications in the Himalayan region. J. Hydrol. 2020, 591, 125579. [Google Scholar] [CrossRef]
- Hordofa, T.; Kiggundu, N.; Girma, M. Performance evaluation of satellite based rainfall estimates for drought monitoring in the Upper Blue Nile Basin, Ethiopia. Meteorol. Appl. 2021, 28, e2007. [Google Scholar] [CrossRef]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over the last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhao, J.; Duan, J.; Liu, X. Assessment of the accuracy of satellite based precipitation products in the Tibetan Plateau. Water 2020, 12, 510. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Chen, X.; Ma, Y.; Su, Z. Assessing the quality of satellite based precipitation estimates over the Tibetan Plateau. Atmos. Res. 2021, 249, 105307. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Da Silva, N.A.; Webber, B.G.M.; Matthews, A.J.; Feist, M.M.; Stein, T.H.M.; Holloway, C.E.; Abdullah, M.F.A.B. Validation of GPM IMERG extreme precipitation in the Maritime Continent by station and radar data. Earth Space Sci. 2021, 8, e2021EA001738. [Google Scholar] [CrossRef]
- Ji, H.; Peng, D.; Gu, Y.; Liang, Y.; Luo, X. Evaluation of multiple satellite precipitation products and their potential utilities in the Yarlung Zangbo River Basin. Sci. Rep. 2022, 12, 14071. [Google Scholar] [CrossRef]
- Hameed, I.A.; Al Nuaimi, K.; Idrees, N.M. Reliability of GPM IMERG satellite precipitation data for modelling flash flood events in selected watersheds in the UAE. Remote Sens. 2023, 15, 3991. [Google Scholar] [CrossRef]
- Ebert, E.E.; Damrath, U.; Wergen, W.; Baldwin, M.E. The WGNE assessment of short-term quantitative precipitation forecasts. Bull. Am. Meteorol. Soc. 2007, 84, 483–494. [Google Scholar] [CrossRef]
- Öztopal, A. Forecast verification: A practitioner’s guide in atmospheric science. Meteorol. Atmos. Phys. 2007, 101, 279–280. [Google Scholar]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Aitchison, J.; Brown, J.A.C. The Lognormal Distribution; Cambridge University Press: Cambridge, UK, 1957. [Google Scholar]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. A 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Pareto, V. Cours d’économie Politique; Rouge: Lausanne, Switzerland, 1896. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Aksu, H.; Akgül, M.A. Performance evaluation of CHIRPS satellite precipitation estimates over Turkey. Theor. Appl. Climatol. 2020, 142, 71–84. [Google Scholar] [CrossRef]
- Hisam, E. Evaluation of Grid Based Precipitation Products over the Mediterranean Region in Turkey. M.S. Thesis, İstanbul Technical University, Graduate School, İstanbul, Turkey, 2022. Available online: http://hdl.handle.net/11527/25494 (accessed on 18 October 2024).
- Hafizi, H.; Sorman, A.A. Performance assessment of CHIRPSv2.0 and MERRA 2 gridded precipitation datasets over complex topography of Turkey. Environ. Sci. Proc. 2022, 19, 21. [Google Scholar] [CrossRef]
- Aksu, H.; Taflan, G.Y.; Yaldiz, S.G.; Akgül, M.A. Evaluation of IMERG for GPM satellite-based precipitation products for extreme precipitation indices over Turkiye. Atmos. Res. 2023, 291, 106826. [Google Scholar] [CrossRef]
- Aksu, H.; Yaldiz, S.G.; Taflan, G.Y.; Akgül, M.A. Frequency analysis based on peaks-over-threshold approach for GPM IMERG precipitation product. Theor. Appl. Climatol. 2023, 154, 275–289. [Google Scholar] [CrossRef]
- Koçak, R.; Dönmez, S.; Tor, M.A.; Tekeli, A. Utilizing GPM IMERG Early, Late and Final Runs for Flood Estimation over Aralık District, Iğdır City; General Assembly of the International Union of Geodesy and Geophysics (IUGG): Berlin, Germany, 2023. [Google Scholar] [CrossRef]





| Remote Datasets (Precipitation) | Temporal Coverage | Temporal Resolution | Spatial Resolution | File Format |
|---|---|---|---|---|
| CHIRPS (Observation) | 1981–Present | Daily | 0.05° | netCDF |
| GPM-IMERG (Observation) | 2000–Present | Daily, half hourly | 0.1° | netCDF |
| Statistical Metrics | Elmali | Finike | ||
|---|---|---|---|---|
| CHIRPS | GPM-IMERG | CHIRPS | GPM-IMERG | |
| Correlation Coefficient (r) | 0.765 | 0.818 | 0.899 | 0.943 |
| Nash-Sutcliffe Efficiency (NSE) | −0.993 | −0.549 | 0.679 | 0.887 |
| Root Mean Square Error (RMSE) (mm) | 49.682 | 43.800 | 50.813 | 30.146 |
| Percent Bias (PBIAS) (%) | 71.698 | 65.283 | 19.045 | −4.870 |
| Mean Absolute Error (MAE) (mm) | 32.133 | 28.056 | 30.811 | 18.117 |
| Statistical Metrics | Elmali | Finike | ||
|---|---|---|---|---|
| CHIRPS | GPM-IMERG | CHIRPS | GPM-IMERG | |
| Correlation Coefficient (r) | 0.345 | 0.420 | 0.350 | 0.592 |
| Nash-Sutcliffe Efficiency (NSE) | −2 | −0.868 | −0.697 | 0.239 |
| Root Mean Square Error (RMSE) (mm) | 7.367 | 5.812 | 12.455 | 8.341 |
| Percent Bias (PBIAS) (%) | 71.466 | 65.060 | 19.291 | −4.673 |
| Mean Absolute Error (MAE) (mm) | 2.384 | 2.034 | 3.772 | 2.632 |
| Distributions | Monthly Dataset | Daily Dataset | ||
|---|---|---|---|---|
| Statistic | p-Value | Statistic | p-Value | |
| Gamma | 0.12 | 0.013 | 0.42 | 0.001 |
| Lognormal | 0.17 | 0.001 | 0.41 | 0.001 |
| Normal | 0.75 | 0.001 | 0.54 | 0.001 |
| Weibull | 0.14 | 0.003 | 0.36 | 0.001 |
| Exponential | 0.22 | 0.001 | 0.75 | 0.001 |
| Gumbel | 0.15 | 0.001 | 0.47 | 0.001 |
| Pareto | 0.30 | 0.001 | 0.70 | 0.001 |
| Beta | 0.11 | 0.033 | 0.43 | 0.001 |
| Generalized Extreme Value | 0.36 | 0.001 | 0.58 | 0.001 |
| Performance Metrics | Monthly Comparison (Finike vs. GPM-IMERG) | Daily Comparison (Finike vs. GPM-IMERG) |
|---|---|---|
| POD (Probability of Detection) | 0.778 | 0.478 |
| FAR (False Alarm Ratio) | 0.222 | 0.388 |
| POFD (Probability of False Detection) | 0.013 | 0.048 |
| CSI (Critical Success Index) | 0.636 | 0.366 |
| ACC (Accuracy) | 0.976 | 0.887 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakshmi, V.; Kir, E.G.; Fang, B. Precipitation Data Accuracy and Extreme Rainfall Detection for Flood Risk Analysis in the Akçay Sub-Basin. Remote Sens. 2025, 17, 3199. https://doi.org/10.3390/rs17183199
Lakshmi V, Kir EG, Fang B. Precipitation Data Accuracy and Extreme Rainfall Detection for Flood Risk Analysis in the Akçay Sub-Basin. Remote Sensing. 2025; 17(18):3199. https://doi.org/10.3390/rs17183199
Chicago/Turabian StyleLakshmi, Venkataraman, Elif Gulen Kir, and Bin Fang. 2025. "Precipitation Data Accuracy and Extreme Rainfall Detection for Flood Risk Analysis in the Akçay Sub-Basin" Remote Sensing 17, no. 18: 3199. https://doi.org/10.3390/rs17183199
APA StyleLakshmi, V., Kir, E. G., & Fang, B. (2025). Precipitation Data Accuracy and Extreme Rainfall Detection for Flood Risk Analysis in the Akçay Sub-Basin. Remote Sensing, 17(18), 3199. https://doi.org/10.3390/rs17183199







