Developing a Quality Flag for SAR Ocean Wave Spectrum Partitioning with Machine Learning

Highlights

What are the main findings?

• A refined classification framework is applied to Sentinel-1 Wave Mode products, enabling more accurate characterization of ocean wave partitions based on comparisons with WW3 numerical wave model.
• Advanced AI techniques using SAR features, selected based on physical relevance, are used to predict errors on individual wave partition integral parameters which are then combined in a unique quality indicator.

What is the implication of the main finding?

• The qualification of S1 wave partition enables the development of robust, interpretable solutions supporting both scientific research and operational ocean monitoring, for ocean wave analysis and forecasting.
• Identifying errors arising from the current S1 wave retrieval can highlight issues caused by imperfect modeling (e.g. azimuth cut-off, Modulation Transfer Function (MTF) but also partitions cross-assignment limitations) and can help refining wave inversion methods.

Abstract

Synthetic Aperture Radar (SAR) is one of the few instruments capable of providing high-resolution global two-dimensional (2D) measurements of ocean waves. Since 2014 and then 2016, the Sentinel-1A/B satellites, whenever operating in a specific wave mode (WV), have been providing ocean swell spectrum data as Level-2 (L2) OCeaN products (OCN), derived through a quasi-linear inversion process. This WV acquires small SAR images of 20 × 20 km footprints alternating between two sub-beams, WV1 and WV2, with incidence angles of approximately 23° and 36°, respectively, to capture ocean surface dynamics. The SAR imaging process is influenced by various modulations, including hydrodynamic, tilt, and velocity bunching. While hydrodynamic and tilt modulations can be approximated as linear processes, velocity bunching introduces significant distortion due to the satellite’s relative motion with respect to the ocean surface and leads to constructive but also destructive effects on the wave imaging process. Due to the associated azimuth cut-off, the quasi-linear inversion primarily detects ocean swells with, on average, wavelengths longer than 200 m in the SAR azimuth direction, limiting the resolution of smaller-scale wave features in azimuth but reaching 10 m resolution along range. The 2D spectral partitioning technique used in the Sentinel-1 WV OCN product separates different swell systems, known as partitions, based on their frequency, directional, and spectral characteristics. The accuracy of these partitions can be affected by several factors, including non-linear effects, large-scale surface features, and the relative direction of the swell peak to the satellite’s flight path. To address these challenges, this study proposes a novel quality control framework using a machine learning (ML) approach to develop a quality flag (QF) parameter associated with each swell partition provided in the OCN products. By pairing collocated data from Sentinel-1 (S1) and WaveWatch III (WW3) partitions, the QF parameter assigns each SAR-derived swell partition one of five quality levels: “very good,” “good,” “medium,” “low,” or “poor”. This ML-based method enhances the accuracy of wave partitions, especially in cases where non-linear effects or large-scale oceanic features distort the data. The proposed algorithm provides a robust tool for filtering out problematic partitions, improving the overall quality of ocean wave measurements obtained from SAR. Moreover, the variability in the accuracy of swell partitions, depending on the swell direction relative to the satellite’s flight heading, is effectively addressed, enabling more reliable data for oceanographic studies. This work contributes to a better understanding of ocean swell dynamics derived from SAR observations and supports the numerical swell modeling community by aiding in the refinement of models and their integration into operational systems, thereby advancing both theoretical and practical aspects of ocean wave forecasting.

1. Introduction

Copernicus, the Earth observation component of the European Union’s space program, plays a vital role in monitoring the planet and its environment for the benefit of European citizens [1]. As part of this initiative, the Sentinel-1 (S1) mission, operated by the European Space Agency (ESA), deploys satellites equipped with Synthetic Aperture Radar (SAR). These satellites operate in the C-band (central frequency 5.405 GHz) and support multiple acquisition modes. In particular, the WV mainly uses vertical–vertical (VV) polarization to observe open ocean conditions [2]. Sentinel-1A was launched on 3 April 2014, followed by Sentinel-1B on 25 April 2016. Both satellites shared the same orbital plane with a 180° phase difference. Sentinel-1B stopped transmitting data on 23 December 2021, was officially decommissioned in 2023, and was replaced by Sentinel-1C, launched on 5 December 2024.

Data acquired in WV mode are routinely processed into L2 OCN products, which include directional ocean wave spectra generated using a quasi-linear inversion method [3,4]. This inversion provides valuable information on the distribution of wave energy across frequency and direction. SAR-based inversion is mainly effective for long ocean swells (wavelengths greater than 200 m) [5,6,7,8] and for wave propagation in the marginal ice zone [9,10].

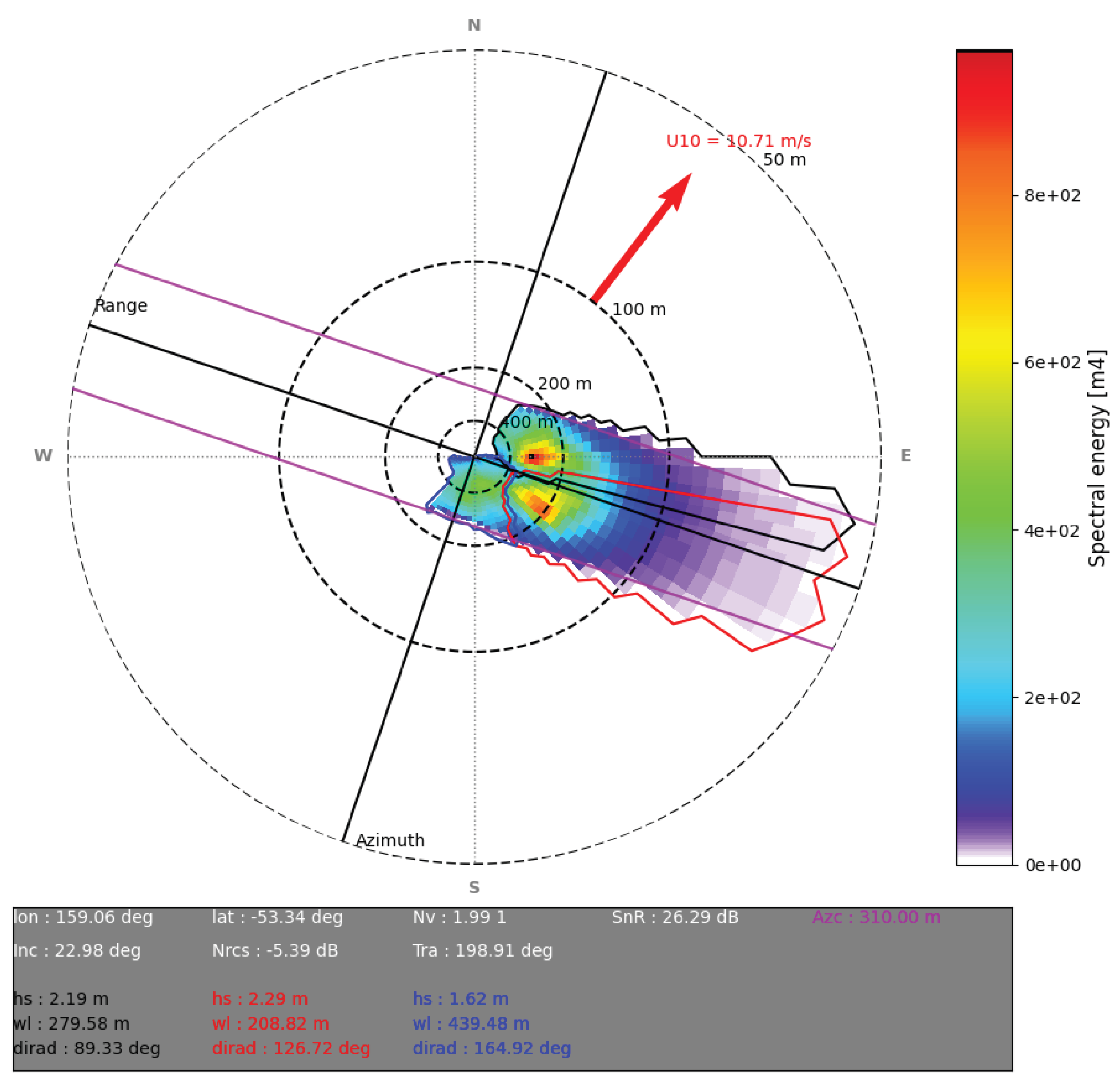
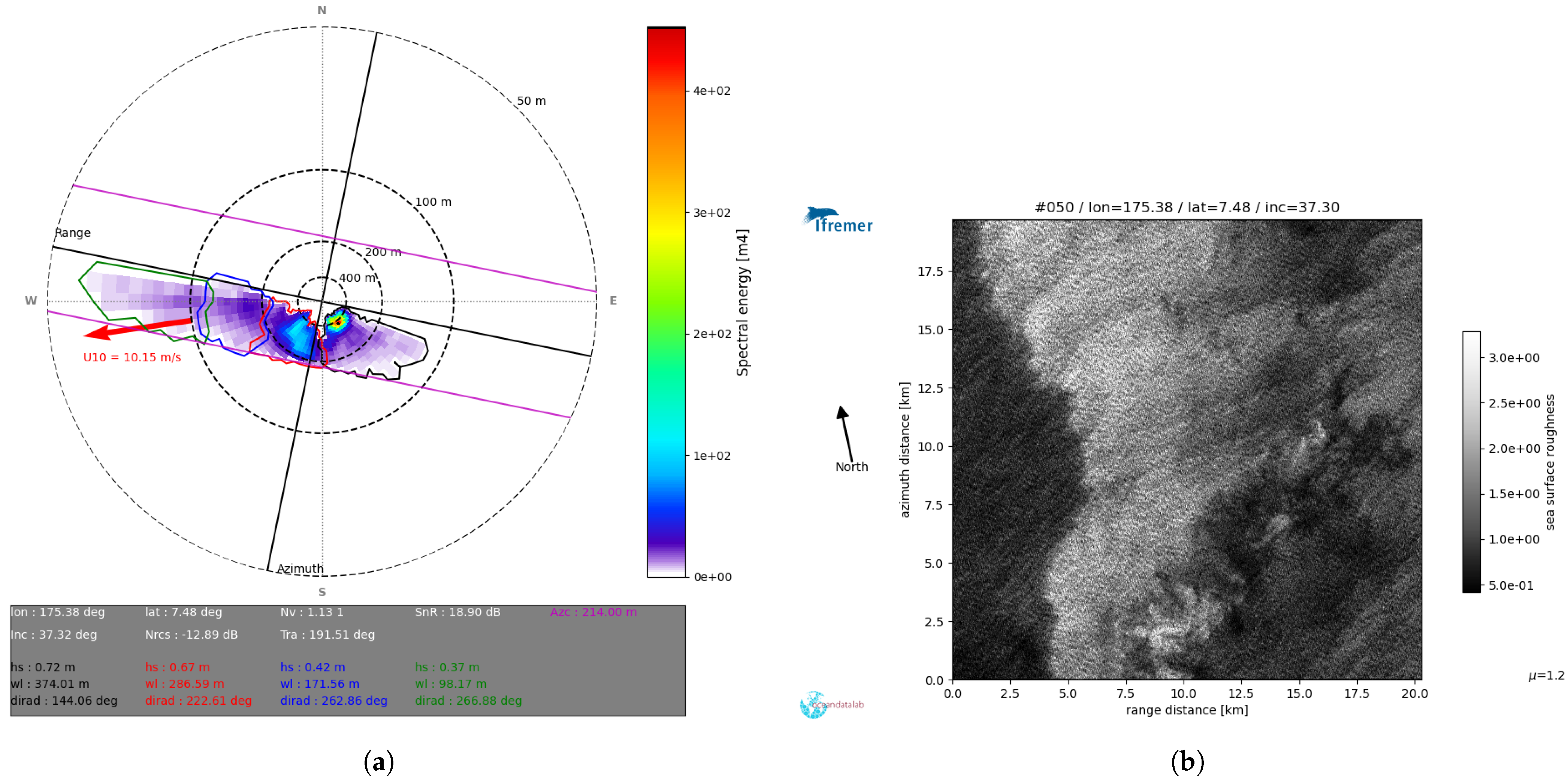
Although integral parameters derived from SAR spectra can effectively characterize single-swell systems, they become less informative when multiple, overlapping wave systems are present (Figure 1). In such cases, partitioning the ocean wave spectrum into distinct wave systems is essential for accurate analysis and quality control. Within the L2 OCN product, the wave spectrum is divided into up to five separate partitions [3] using the “watershed” algorithm, originally introduced by [11,12]. Each partition is described by its corresponding integral parameters, including partition effective significant wave height (Hs), peak wavelength, and peak wave direction (Figure 1).

A direct comparison between wave partitions derived from SAR observations and those produced by the WW3 model [13] reveals notable discrepancies, particularly between the dominant and secondary swell systems. These differences are not random; instead, they exhibit systematic spatial patterns, with positive clustering of partitioned wavelengths observed along the azimuth direction and negative clustering along the range direction [14,15,16].

Such discrepancies underscore the broader challenge of accurately retrieving ocean wave spectra from SAR data. At the core of this challenge lies the modeling of the Modulation Transfer Function (MTF), which governs the transformation from the observed SAR image to the true ocean wave field. Most existing retrieval methods rely on quasi-linear approximations to represent this mapping. However, these approaches remain affected by significant non-linearities that are not yet fully taken into account, limiting the fidelity of the retrieved wave parameters.

One of the primary sources of distortion is the Doppler shift induced by the radial component of the wave orbital motion, which modulates the SAR backscatter signal. As described in [6], this results in either constructive or destructive velocity bunching effects: the well-organized orbital motion of the longest waves of the wave spectrum (swell) leads to deterministic misregistration in the azimuth direction and an apparent constructive redistribution of the backscatter intensity along the azimuth direction; on the other hand, the shortest waves lead to random misregistration in the azimuth direction, leading to possible significant degradation in the azimuth resolution and to distortions of the resulting SAR ocean image spectra (non-linear relationship between SAR image spectra and ocean wave spectra).

Destructive effects prevent one from directly recovering the sea surface profile and individual waves, but, indirectly, methods have been developed to retrieve information of the wave spectra, including the shortest part of the wave spectra (e.g., total Hs, as discussed by [17]). The constructive effects distort the apparent wave spectrum by shifting energy away from its true frequency and direction, resulting in biased estimates of wave height and other integral parameters if left uncorrected.

Compared to the WW3 model, ref. [18] reports Root Mean Square Errors (RMSEs) of 0.70 m for significant wave height (Hs), 0.9 s for mean wave period, and 30° for wave direction, highlighting the limitations of SAR-based wave spectrum retrieval in accurately capturing key oceanographic parameters.

To address these limitations, recent studies have explored machine learning techniques as post-processing tools. Rather than directly resolving the non-linearities inherent in SAR imaging, these approaches aim to correct integral parameters, such as total Hs, as discussed by [17], and reduce uncertainties associated with MTF-induced distortions.

Building on this concept, our proposed method also operates as a post-processing approach, but with a distinct focus: it seeks to qualify the retrieved SAR wave spectrum partitions by evaluating their reliability and consistency. This is particularly important in complex sea states where multiple wave systems coexist and interact.

To achieve this, we applied data-driven machine learning techniques to define a prior quality flag (QF) for each of the five wave partitions derived from Sentinel-1 WV OCN products. The QF is determined by learning partition error parameters, including the relative error in the effective significant wave height (Equation (1)), the relative error in the peak period (Equation (2)), and the absolute error in the peak wave direction (Equation (4)). This enables a more targeted and interpretable assessment of partition quality, which is essential to ensure the robustness of downstream oceanographic analyses and applications.

$$\Delta Hs=2{\displaystyle \frac{\left(H{s}_{\mathrm{SAR}}-H{s}_{\mathrm{WW}3}\right)}{H{s}_{\mathrm{SAR}}+H{s}_{\mathrm{WW}3}}}$$

(1)

$$\Delta \mathit{T}=2{\displaystyle \frac{\left(T_{\mathrm{SAR}}-T_{\mathrm{WW}3}\right)}{T_{\mathrm{SAR}}+T_{\mathrm{WW}3}}}$$

(2)

where

$$T_{\mathrm{SAR}}=\sqrt{{\displaystyle \frac{w{l}_{\mathrm{SAR}}}{1.56}}},T_{\mathrm{WW}3}=\sqrt{{\displaystyle \frac{w{l}_{\mathrm{WW}3}}{1.56}}}$$

(3)

$$\Delta \varphi ={\varphi }_{\mathrm{SAR}}-{\varphi }_{\mathrm{WW}3}$$

(4)

Building on previously defined error metrics, we implement the qualification framework using collocated SAR and WW3 partition pairs. Specifically, the effective significant wave height and peak period are expressed as relative errors (Equations (1) and (2)), while the peak wave direction is evaluated using an absolute error (Equation (4)). This distinction ensures that each parameter is assessed in a way that reflects its physical characteristics and variability.

Moreover, the use of relative errors for certain parameters helps achieve a more balanced distribution of values across the QF classes. This adjustment mitigates the disproportionate influence of higher $\mathit{Hs}$ values on error estimation, thereby reducing bias and enabling a more fair and more representative evaluation of partition quality.

The primary contributions of this research are threefold: (1) the application of machine learning algorithms to improve the qualification of the Sentinel-1 ocean wave spectrum partitioning; (2) an interpretability analysis of the model’s predictions in relation to the geophysical inversion process underlying the SAR data; and (3) the establishment of a framework to support future research aimed at improving the retrieval of the ocean wave spectrum from SAR observations.

This manuscript is structured as follows: Section 2 presents the dataset utilized in this study. Section 3 outlines the complete machine learning methodology. Section 4 details the results and model validation. Section 5 provides an in-depth discussion of the findings, and Section 6 concludes this paper with perspectives for future research.

2. Dataset Collection

2.1. Sentinel-1 WV OCN Products

The S1A/B WV mode operates by acquiring SAR images, or imagettes, spaced 100 km apart, with two alternating incidence angles, WV1 and WV2, along the satellite’s flight path using a “leap frog” acquisition strategy [19]. In each acquisition, the S1 WV mode can only operate in a single polarization, VV or HH, with VV polarization being the default for global ocean observations. Each acquired imagette covers an area of approximately 20 × 20 km, with a high spatial resolution of 5 m. The ocean wave spectrum (OSW) component of the WV OCN product is derived from SAR images of the Level-1 (L1) single look complex (SLC), processed through the ESA L2 spectral inversion unit [3].

The inversion process begins with the estimation and removal of non-linear contributions from the SAR data, which is essential for improving the accuracy of the final results. Once the non-linearity is treated, the cross-spectra technique is applied to resolve the 180° directional ambiguity in wave propagation, which is crucial for obtaining reliable directional information. This method allows retrieval of the ocean wave spectrum with a directional resolution of 10° and 30 exponentially spaced wave numbers, spanning from 30 to 800 m. The final step of the process involves partitioning the 2D ocean wave spectrum into five independent ocean wave systems using the watershed algorithm, after which the integral parameters (such as effective significant wave height, peak wavelength, and peak wave direction) for each partition are computed.

For the purposes of this study, we used data acquired exclusively from the S1A satellite, covering both the WV1 and WV2 modes with VV polarization, collected between December 2024 and February 2025. This time period was selected because it corresponds to the deployment of version 3.90 of the S1 L2 Instrument Processing Facility (IPF), which includes a new SAR MTF tuning. This upgrade significantly improves the wave inversion performance of SAR images [3].

Furthermore, to ensure the integrity of the ocean wave data, products acquired at latitudes above 55° north and south are filtered out to exclude any possible contamination from sea ice, which could distort wave measurements.

The publicly available S1 L2 WV OCN data used in this study can be accessed through the Copernicus Open Access Hub [20].

2.2. WW3 Hindcasts

The WW3 hindcast, part of the Integrated Ocean Waves for Geophysical and other Applications (IOWAGA) project led by IFREMER, is a third-generation wave model that resolves the spectral action density equilibrium equation for wavenumber–directional spectra. It is driven by data on 3 h wind and ice concentration from the European Center for Medium-Range Weather Forecasts (ECMWF) product [21,22]. The model operates with spatial and temporal resolutions of 0.5° and 3 h, respectively. The spectral data are organized into 32 frequency bins, exponentially spaced from 0.038 to 0.7159 Hz, and 24 directional bins, each separated by 15°. To partition the wave spectra, the model employs the “watershed” algorithm, which divides the spectra into five partitions corresponding to different swells, as well as one partition for wind seas. Wind seas are represented by Partition 0, while Partitions 1 through 5 correspond to various swell systems. The accuracy of the model’s wave parameter has been validated against buoy and altimeter measurements, showing strong agreement [21,23,24]. The WW3 Hindcast data are available for download through the IFREMER FTP server accessed on 7 March 2025 (ftp://ftp.ifremer.fr/ifremer/ww3/HINDCAST/).

Our method quantifies the discrepancies between SAR and WW3. Although WW3 cannot fully capture complex effects such as coastal refraction, bathymetry, or diffraction near islands, it serves as a reference to evaluate SAR-derived wave observations, focusing on open-ocean regions to minimize errors.

Instead of using WW3 as a direct target, which could propagate model biases into SAR predictions, we define the ML target as the difference between SAR and WW3. This emphasizes the degree of agreement rather than reproducing the model, allowing high consistency to indicate reliable SAR retrievals, while large discrepancies highlight potential limitations in either dataset.

2.3. Match-Up Partitions

The S1 L2 WV OCN products were collocated with the WW3 hindcasts based on the closest spatial and temporal grid points, within a window of 0.25° in latitude/longitude and 1.5 h in time. To ensure the best match-ups at the partitioned swell level, these spatiotemporal collocations were further refined by identifying, for each SAR partition, the closest WW3 partition match. For this step, referred to as the partition cross-assignment, the spectral distance $D_{\mathrm{spec}}$ between the partitions was defined, as proposed by [25], according to the following equation:

$$D_{\mathrm{spec}}={\displaystyle \frac{1}{q}}\left(\left|{\varphi }_1-{\varphi }_2\right|mod360+2·r·{\displaystyle \frac{\left|T_1-T_2\right|}{T_1+T_2}}\right)$$

(5)

In this equation, ${\varphi }_i$ and $T_i$ represent the peak wave direction and peak period of each swell system, respectively. The constant r was set to 250, which appropriately scales the period error: a 20° directional error is treated as equivalent to an 8% error in the wave period, reflecting the typical SAR swell measurement accuracy. Furthermore, the value of $q=30$ was chosen to define the error thresholds to ensure a 30° directional error and a 12% period error to give a spectral distance equal to one [26].

No further filtering was applied to the dataset to preserve a comprehensive representation of the various errors inherent in the inversion and partitioning processes, as well as any nongeophysical contributions present at the ocean surface.

3. Method Details

3.1. Quality Flag Definition

The Normalized Radar Cross-Section (NRCS) is influenced by several error sources, including geometric distortions, sensor-specific acquisition errors, and the presence of nongeophysical factors such as atmospheric influences and surface roughness at the air–sea interface. Additionally, the quasi-linear inversion process employed to derive ocean wave spectra from SAR data introduces further inaccuracies. The partitioning algorithm, which divides the ocean wave spectrum into distinct wave systems, is also subject to its own set of errors. To address these complexities, the first critical step in our algorithmic approach is to independently quantify the errors in $\Delta \mathit{Hs}$, $\Delta \mathit{T}$, and $\Delta \varphi$ at the partition level with respect to the WW3 model data.

These errors are estimated using a supervised ML algorithm, which leverages a set of observables derived from SAR (that is, features) to predict discrepancies in partition wave parameters [27]. The features used for the error estimation process are detailed in

Table 1. SAR features used to learn partition integral parameter error.

Feature	Description
$\mathrm{p}$	The partition index
$\mathrm{Hs}$	The effective significant wave height in the partition p
${\varphi }_{\mathrm{peak}}$	The dominant wave direction in the partition p projected in the SAR geometry
${\lambda }_{\mathrm{azimuth}}$	The dominant wavelength in the azimuth direction in the partition p
$N_{\mathrm{v}}^{\left(p\right)}$	The normalized variance of significant wave height in the partition p
${\mathrm{R}}_{\mathrm{energy}}$	The energy ratio between the partition energy peak and the maximum boundary energy
${\mathrm{T}}_{\mathrm{cutoff}}^{\mathrm{peak}}$	The wave peak period in the azimuth cut-off direction in the partition p
${\mathrm{T}}_{\mathrm{peak}}$	The wave peak period in the partition p
$\mathrm{Ambiguity}$  $\mathrm{factor}$	The absolute value of the ambiguity factor related to the wave propagation direction
$\mathrm{Nrcs}$	The Normalized Radar Cross-Section of the SLC WV imagette
$\mathrm{Wind}$  $\mathrm{speed}$	The estimated SAR wind speed at 10 m from the SLC WV imagette
$\mathrm{Snr}$	The Signal-to-Noise Ratio (SNR) of the SLC WV imagette
$\mathrm{Skewness}$	The skewness of the SLC WV imagette
$\mathrm{Kurtosis}$	The kurtosis of the SLC WV imagette
$\mathrm{Nv}$	The normalized variance of the SLC WV imagette

. The calculation of some features is described in detail in [3].

Regardless of the acquisition mode (WV1 or WV2), the same set of features is used to estimate the three primary errors. This requires the training of six separate models tailored to the S1A mission, each aimed at improving the accuracy of partition-level error quantification and ultimately refining the ocean wave parameter retrieval process.

The second step of the algorithm focuses on computing a combined error metric for each individual acquisition mode (i.e., WV1 and WV2). This combined error, denoted as $C_{\mathrm{error}}$ and defined in Equation (6), is calculated by multiplying the three primary error estimates—$\Delta \mathit{Hs}$, $\Delta \mathit{T}$, and $\Delta \varphi$—previously inferred using the trained models applied to the validation dataset, which consists of all S1A acquisitions from February 2025. The metric is expressed as follows:

$$C_{\mathrm{error}}=\Delta \mathit{Hs}·\Delta \mathit{T}·\Delta \varphi$$

(6)

The combined error is not designed to preserve the individual error magnitudes, but rather to serve as a synthetic indicator of partition quality. In general, the combined error related to such artificial SAR partitions is much higher than the one related to real SAR partitions for which the associated WW3 partition shows different integral parameters but of the same order magnitude. Moreover, discrepancies between a SAR partition and a WW3-modeled partition often affect all three integral parameters simultaneously. For example, if a SAR partition is split into two while WW3 models a single-wave partition, this will influence the partition parameters together.

Alternative tests using a weighted sum yielded similar results, but the multiplicative approach preserves the equal influence of each partition characteristic and provides a robust general formulation.

Since the ultimate goal is to assess the quality of ocean swell systems in a manner that is independent of the SAR acquisition mode, a unified combined error metric is produced by merging the mode-specific error estimates from both WV1 and WV2. This approach is motivated by the need for consistent and homogeneous error characterization across different SAR configurations. Since both WV1 and WV2 data are used interchangeably in operational wave monitoring and analysis, having a mode-agnostic quality metric ensures comparability between partitions retrieved under different acquisition conditions. By assembling the combined error from both modes, we enable a seamless interpretation of partition-level quality, facilitating the identification and classification of ocean swell systems without bias introduced by the acquisition geometry.

This reference error is then partitioned into five equally probable intervals using the q-quintile method, commonly referred to as Quintile. These intervals represent different levels of error severity, ranging from low to high. Once this reference error distribution is established, the calculated $C_{error}$ for each partition is matched to the corresponding quintile range. Based on this comparison, each partition is assigned a quality label: “very good,” “good,” “medium,” “low,” or “poor.” This classification serves as an indication of the reliability and accuracy of the partition, facilitating informed decision making in further analyses.

3.2. Machine Learning Dataset

In the context of algorithm development, we focused on the S1 L2 OCN WV dataset, which was acquired over two months: December 2024 and January 2025. These data were assigned to the training phase, with an 80–20% split for training and validation, respectively. This approach ensures that the model is rigorously tested on unseen data during training. Data from February 2025 were used exclusively for model evaluation, providing an independent test set to assess the model’s generalizing ability.

During the training process, no data normalization was performed, as the chosen machine learning algorithm is inherently robust to raw, unnormalized data, facilitating direct input handling without additional pre-processing steps and data transformation.

Our ML approach relies on previously defined error metrics. Relative errors are used to allow the model to take account of the scale of these parameters and to ensure a balanced representation across the QF classes. In contrast, the peak wave direction is evaluated using an absolute error, which is more appropriate given its angular nature and bounded range. Consequently, ML targets are defined as $\left|\Delta \mathit{Hs}\right|$, $\left|\Delta \mathit{T}\right|$, and $\left|\Delta \varphi \right|$.

This design focuses on the magnitude of the discrepancy between SAR and WW3, rather than its sign, and avoids depending on the absolute accuracy of the WW3 model, which may be limited in capturing certain geophysical conditions.

3.3. Machine Learning Modeling

In this study, we initially used a traditional Random Forest algorithm; however, it soon revealed limitations in terms of interpretability. Consequently, we shifted our focus to the eXtreme Gradient Boosting (XGBoost) supervised learning algorithm, which offered improved performance and explainability. XGBoost is a scalable distributed machine learning library based on gradient-boosted decision trees (GBDTs). A decision tree is a model that makes decisions by splitting data into branches based on simple conditions, forming a set of “true or false” statements. Since its debut in 2014, XGBoost has become one of the most widely adopted algorithms among data scientists and machine learning practitioners due to its high performance, particularly for structured data problems. The library is open-source [28] and is able to efficiently train and test models on large datasets.

One of the primary reasons for selecting XGBoost in our study is its regularization capabilities. Regularization helps to control overfitting, where the model fits too closely to the training data, thereby reducing its ability to generalize to unseen data. XGBoost applies L1 and L2 penalties to the weights and biases of each tree, helping to maintain model simplicity and prevent overfitting. Additionally, XGBoost is highly optimized, with features that make it more memory-efficient, such as cache awareness, which is crucial when working with large datasets.

XGBoost also stands out for its ability to handle missing data, eliminating the need for imputation, and its ability to work with data in their raw, unnormalized state, simplifying the data processing workflow. These advantages make XGBoost an attractive choice for dealing with complex data problems.

To fine-tune the XGBoost model and achieve optimal performance, hyperparameter tuning was performed. Hyperparameters are critical settings that influence how the model learns, and selecting the right ones can significantly improve model accuracy. Given the large number of hyperparameters, finding the best combination manually is impractical. Therefore, we used the GridSearch technique [29] to systematically explore different combinations of hyperparameters. In this process, multiple sets of hyperparameters are tested within a defined search space, and the performance of the model is evaluated on a validation dataset. Although this method is effective, it can be computationally expensive, particularly as the number of parameters and their possible values increases. A list of the hyperparameters most commonly tuned in XGBoost is provided in

Table 2. The main XGBoost hyperparameters selected for tuning.

Hyperparameter	Range	Default	Search Range	Definition
$\mathrm{colsample}\_\mathrm{bytree}$	(0,1]	1	[0.7,1]	The fraction of features that will be used to construct each tree
$\mathrm{learning}\_\mathrm{rate}$	[0,1]	0.3	[0.01,0.4]	Step size at each iteration while the objective function is being optimized
$\max \_\mathrm{depth}$	[0,∞)	6	[4,10]	The maximum depth of each tree
$\max \_\mathrm{leaves}$	[0,∞)	1	[5,10]	Maximum number of nodes to be added
$\mathrm{num}\_\mathrm{parallel}\_\mathrm{tree}$	[0,∞)	1	[5,15]	Number of parallel trees constructed during each iteration
$\mathrm{subsample}$	(0,1]	1	[0.7,1]	The proportion of data that will be sampled for each tree
$\mathrm{n}\_\mathrm{estimators}$	[0,1)	100	[100,300]	The highest number of gradient-boosted trees
$\mathrm{gamma}$	[0,∞)	0	[0,0.5]	Minimum loss reduction necessary to create a new partition on a tree leaf node
$\mathrm{alpha}$	[0,∞)	0	[0,10]	L1 regularization term on weights. Increasing this value will make model more conservative
$\mathrm{lambda}$	[0,∞)	1	[0,10]	L2 regularization term on weights. Increasing this value will make model more conservative

, with additional parameters available in [28].

Machine learning models must exhibit robustness, meaning that they should minimize the impact of outliers and prioritize the influence of typical data points. In tasks such as parameter estimation, using a robust loss function (e.g., absolute error) is often preferred over a non-robust one (e.g., squared error) because it is less sensitive to large deviations. Common loss functions in regression tasks are squared loss $L\left(x\right)=x^2$ and absolute loss $L\left(x\right)=\left|x\right|$. Although squared loss is highly sensitive to outliers, making it less reliable in such cases, absolute loss is more resilient because it focuses on the order of the data rather than their absolute magnitude [30].

To take advantage of both, the pseudo-Huber [31,32,33] loss function is often used. This hybrid function blends the properties of both quadratic and absolute loss while maintaining the smooth differentiability required for optimization. It is mathematically expressed as follows:

$$L_{Hp}\left(x\right)={\delta }^2\left(\sqrt{1+{\displaystyle \frac{x^2}{{\delta }^2}}}-1\right),$$

(7)

where $\delta >0$ is the threshold parameter that controls the transition between the quadratic and linear behavior of the loss.

For small values of x, the pseudo-Huber loss behaves like a quadratic function,

$$L_{Hp}\left(x\right)\approx {\displaystyle \frac{x^2}{2}},$$

while for large values of x, it approximates the absolute loss,

$$L_{Hp}\left(x\right)\approx \delta \left|x\right|-{\delta }^2.$$

In XGBoost, the model is optimized using gradient-based methods, such as gradient descent, to minimize the chosen loss function while incorporating regularization to prevent overfitting. The objective function of the model combines the loss function and a regularization term, as shown in Equation (8):

$${\mathcal{L}}^{\left(t\right)}=\sum _{i=1}^{n}l\left(y_i,{\widehat{y}}_i^{(t-1)}+f_t\left(x_i\right)\right)+\Omega \left(f_t\right).$$

(8)

Here, l represents the loss function (for example, pseudo-Huber), $f_t$ denotes the prediction from the t-th tree, and $\Omega \left(f_t\right)$ is the regularization term that helps avoid overfitting by penalizing overly complex models. The gradient descent process iteratively updates the model parameters to minimize this objective. Additional details on regularization can be found in [27].

4. Results

4.1. Metric Definition

Model training was performed using an 8GB NVIDIA RTX A2000 graphics card. Due to XGBoost’s ability to leverage parallel processing, the grid search and model training time for each model was approximately three hours. The performance of XGBoost models in predicting errors in the partitioning parameters and controlling the final partitioning labeling was assessed using several evaluation metrics. These metrics include $RMSE$, Normalized Root Mean Squared Error ($NRMSE$), standard deviation ($STD$), Median Absolute Error ($MAE$), Scatter Index ($SI$), coefficient of determination ($R^2$), and explained variance score ($EVS$).

The $RMSE$ is a widely used metric that measures the square root of the average squared differences between predicted and observed values. It is sensitive to large errors, thus providing a strong indication of how far the predictions are from the actual values. The RMSE is defined as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2}$$

(9)

where $\widehat{y_i}$ is the predicted value obtained with the model and $y_i$ is the true value.

The NRMSE is a normalized version of the RMSE that scales the error by the range or the mean of the observed values. This allows for a comparison of error across different datasets with different ranges or units. It is calculated as follows:

$$NRMSE={\displaystyle \frac{RMSE}{\mathrm{Range}\mathrm{or}\mathrm{Mean}\mathrm{of}{y}_i}}$$

(10)

The STD measures the amount of variation or dispersion of a set of values. In the context of model evaluation, it is useful for understanding the variability in the errors and is given by

$$STD=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-\mu )}^2}$$

(11)

where $\mu$ is the mean of $y_i$.

The MAE measures the median of the absolute differences between the predicted and true values, making it a robust metric to outliers, as it gives equal weight to each error regardless of magnitude. The MAE is defined as follows:

$$MAE=\mathrm{median}\left(|y_i-\widehat{y_i}|\right)$$

(12)

SI is a metric used to assess the consistency of the model predictions by calculating the ratio of the RMSE to the mean of the observed values. It provides insight into the relative error of the predictions and is given by:

$$SI={\displaystyle \frac{RMSE}{\mathrm{mean}\mathrm{of}{y}_i}}$$

(13)

R² is a statistical measure that indicates how well the predicted values match the actual values. It measures the proportion of variance in the dependent variable that is predictable from the independent variables. An R² value of 1 means perfect predictions, while a value of 0 indicates no correlation between predicted and actual values. R² is computed as follows:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(14)

The EVS is similar to R² but with the key difference that it does not penalize for systematic offsets in the predictions. It measures the proportion of variance in the target variable that is explained by the model and is defined as follows:

$$EVS=1-{\displaystyle \frac{\mathrm{Var}(y-\widehat{y})}{\mathrm{Var}\left(y\right)}}$$

(15)

where $\mathrm{Var}\left(y\right)$ is the variance of the true values, and $\mathrm{Var}(y-\widehat{y})$ is the variance of the residuals.

For a more detailed description, the reader is referred to [34].

4.2. Overall Model Performances

The results for the two acquisition modes, classified by partition QF, are derived from the validation dataset using the partition effective significant wave height, peak wavelength, and peak wave direction with respect to WW3 and are presented in

Table 3. Performance of quality flags by acquisition mode (WV1 and WV2) for partition effective significant wave height.

Quality Flag	${\mathit{R}}^2$	$\mathit{RMSE}$	$\mathit{SI}$
Very Good	(0.73, 0.68)	(0.53, 0.52)	(32.74, 36.52)
Good	(0.54, 0.53)	(0.58, 0.65)	(50.16, 51.06)
Medium	(0.37, 0.35)	(0.69, 0.78)	(63.21, 62.43)
Low	(0.14, 0.12)	(0.87, 0.94)	(86.77, 78.67)
Poor	(−0.24, −0.20)	(1.37, 1.26)	(120.54, 102.07)

,

Table 4. Performance of quality flags by acquisition mode (WV1 and WV2) for partition peak wavelength.

Quality Flag	${\mathit{R}}^2$	$\mathit{RMSE}$	$\mathit{SI}$
Very Good	(0.82, 0.81)	(38.70, 40.93)	(13.64, 13.66)
Good	(0.76, 0.74)	(45.86, 45.87)	(18.97, 18.27)
Medium	(0.65, 0.62)	(55.82, 55.25)	(24.11, 23.58)
Low	(0.48, 0.42)	(71.85, 71.36)	(28.85, 29.98)
Poor	(−0.29, −0.36)	(132.43, 130.32)	(42.21, 47.47)

and

Table 5. Performance of quality flags by acquisition mode (WV1 and WV2) for partition wave peak direction.

Quality Flag	${\mathit{R}}^2$	$\mathit{RMSE}$	$\mathit{SI}$
Very Good	(0.82, 0.73)	(36.35, 43.92)	(33.24, 41.16)
Good	(0.52, 0.52)	(70.03, 67.15)	(49.50, 49.22)
Medium	(0.37, 0.43)	(82.07, 76.09)	(53.20, 51.20)
Low	(−0.05, 0.21)	(103.99, 90.72)	(68.25, 59.30)
Poor	(−0.84, −0.26)	(135.11, 114.30)	(87.28, 73.32)

, respectively. This analysis provides a clear view of how the model distinguishes between good and bad partitions.

Performance metrics for each class, evaluated based on partition parameters and compared to the WW3 model, reveal insightful trends. For each parameter, the model demonstrates strong initial agreement with WW3. Specifically, for the “very good” class, the agreement is excellent, with an R² value of 0.77 (overall mean). However, as the class quality decreases towards “poor,” the agreement progressively weakens. In the “poorest” class, the distributions of SAR and WW3 diverge significantly, reflecting a clear mismatch between the two. This trend holds true for almost the entire range of partition wave parameters.

For the subsequent analysis, we will focus exclusively on the extreme classes—“very good” and “poor”—along with the “medium” class, as these categories represent the most relevant distinctions in partition quality for our purposes.

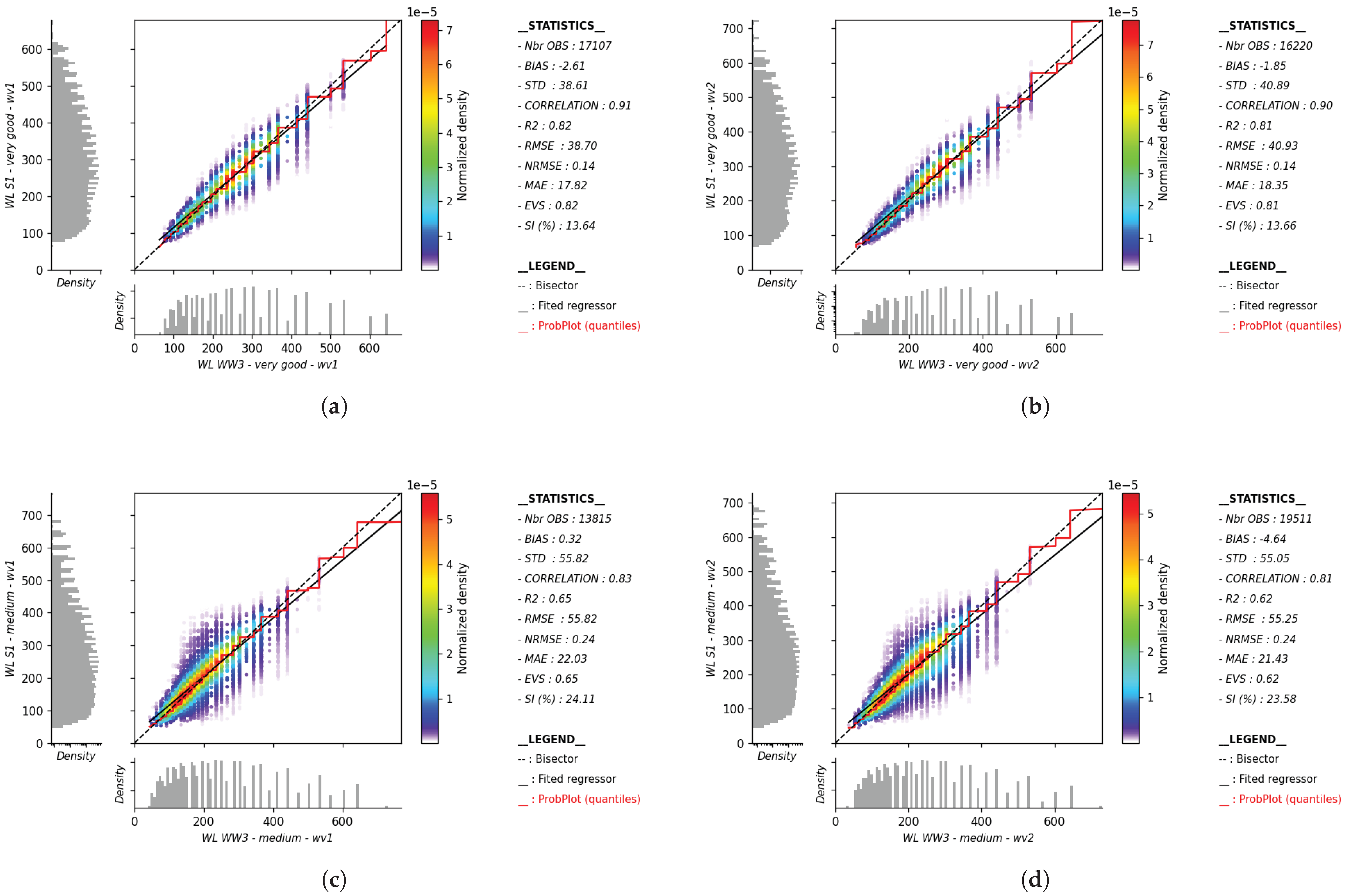
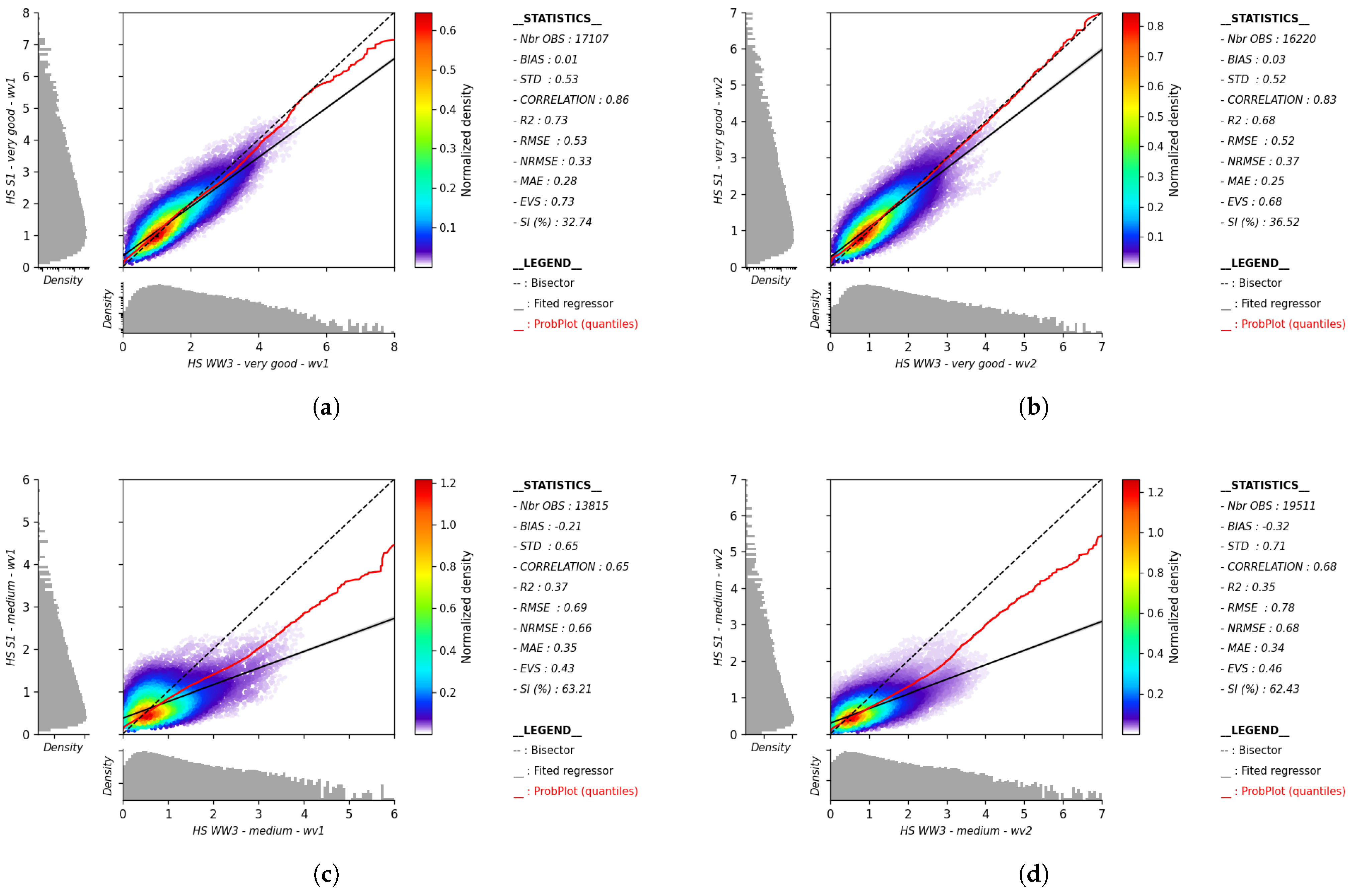
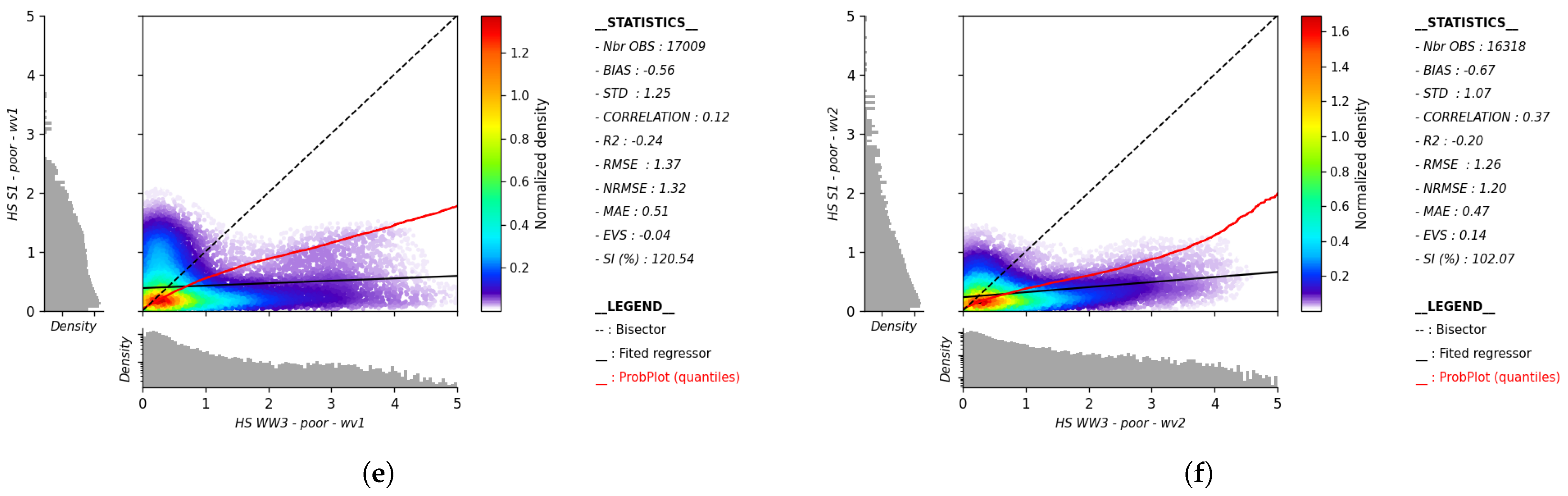
To showcase the robustness of the methodology in partition classification, from high-quality (very good) to low-quality (poor) classes for both WV1 and WV2 across partition parameter ranges, scatter plots are presented in Figure 2 for the integral parameter Hs. In addition to the clear class separation, the plots reveal a consistent trend of increasing error as partition quality declines, with a notable mismatch in the poor class. This mismatch underscores the model’s ability to effectively capture variations in error distribution, reinforcing the reliability of the classification approach. These findings highlight the strength of the model in preserving accuracy across diverse data quality levels, even under challenging conditions. Further partition parameters, including peak wavelength and peak wave direction, are detailed in Appendices Appendix A and Appendix B.

4.3. Focused Analysis of Partition Classification Performance

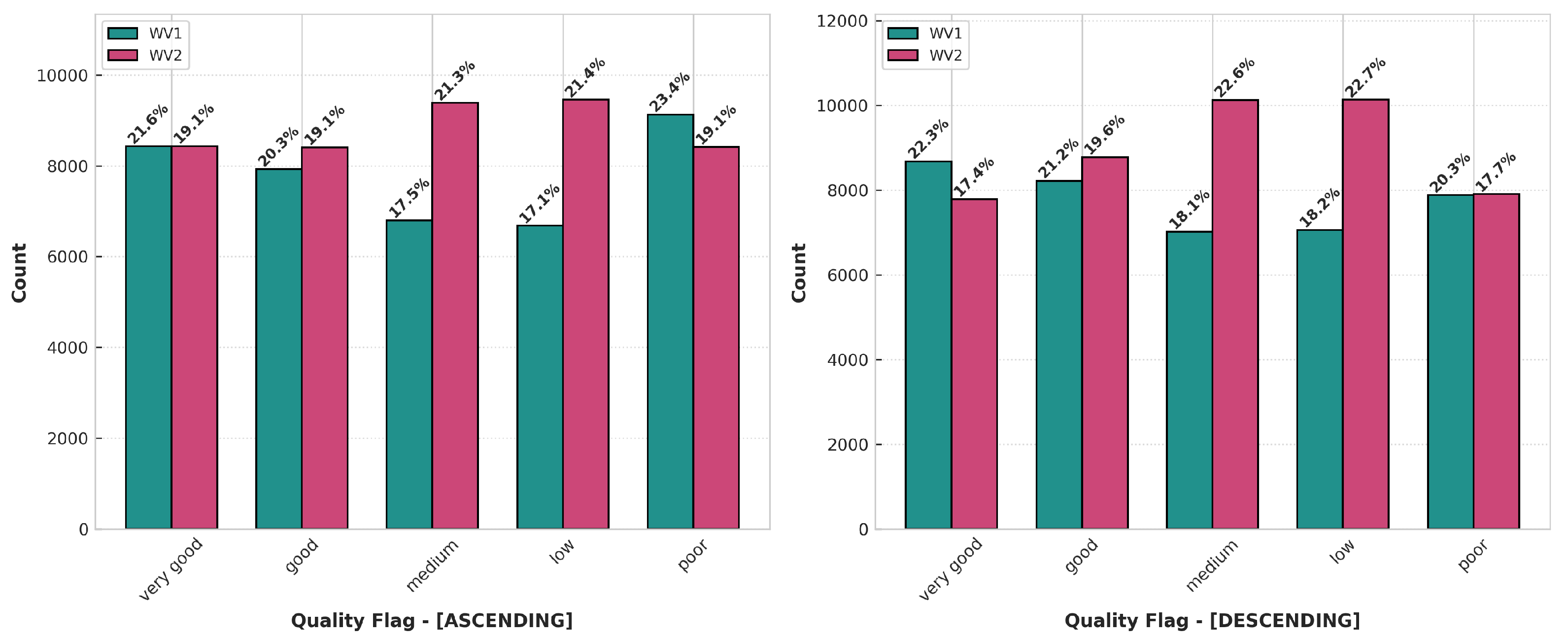
The class distribution depicted in Figure 3 is largely uniform across all partitions, indicating an overall balanced classification with no evident bias toward any particular class.

Minor deviations are observed in the medium and low classes between ascending and descending passes. These differences likely reflect the aggregation of error metrics across both modes, which alters the percentile thresholds relative to evaluating each mode independently, rather than indicating systematic discrepancies.

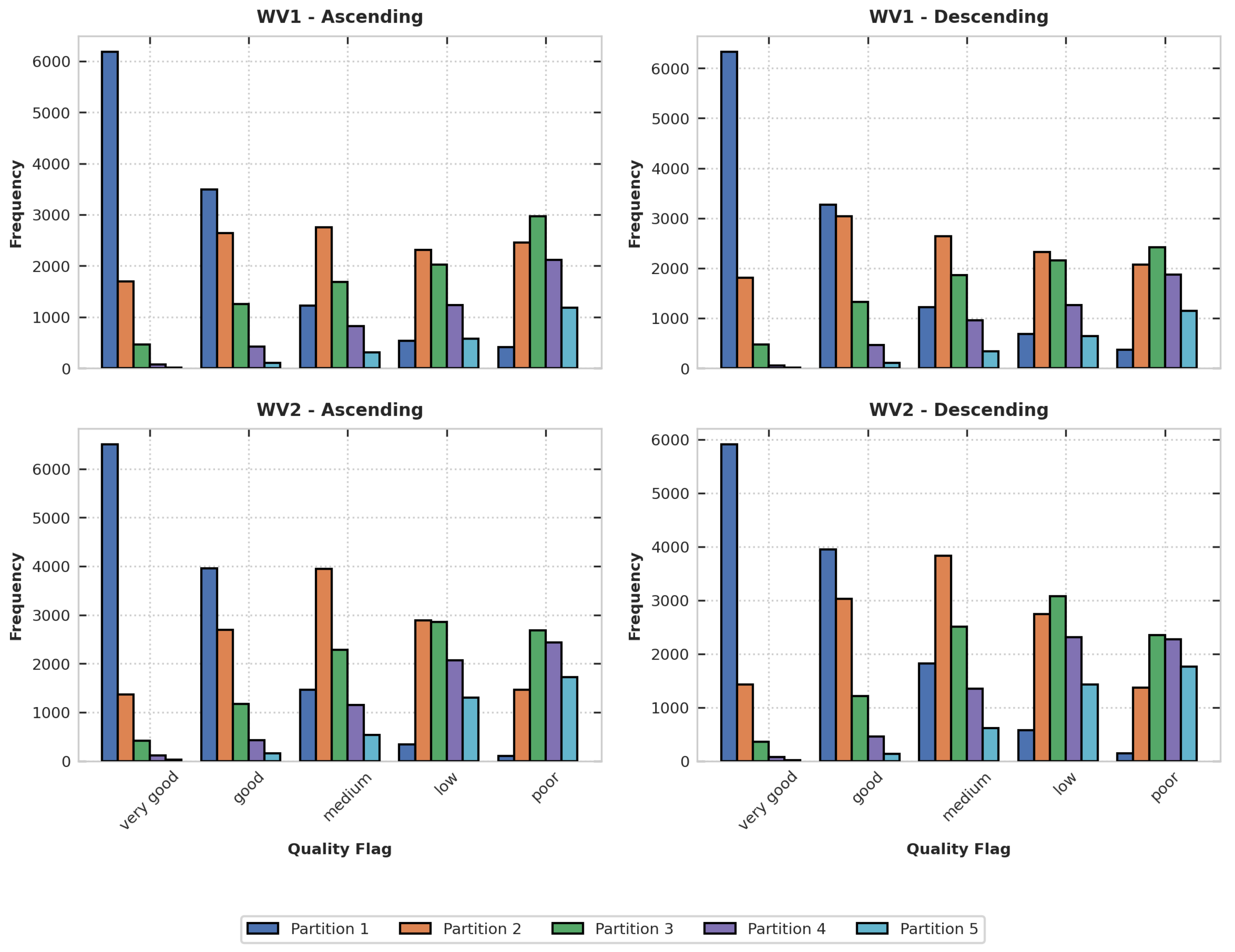
A detailed analysis of Figure 4 highlights how the algorithm assigns quality classifications across wave partitions. The first partition, typically representing the dominant swell, is consistently identified as the most significant and is predominantly classified as “very good” or “good.” This outcome aligns with expectations, as the algorithm is designed to prioritize the most geophysically relevant wave information extracted from the SAR data.

The second partition, often associated with a secondary swell, shows a more evenly distributed classification between quality levels. This trend is particularly noticeable in the WV1 data and appears to be largely unaffected by the heading of the satellite. In contrast, WV2 displays a slightly different pattern, which may be due to the uncertainty introduced by merging classification thresholds across acquisition modes.

Lower-ranked partitions tend to be classified as “low” or “poor,” reflecting their reduced geophysical relevance. This clear stratification in partition quality helps end users focus on the most significant components of the sea state when interpreting SAR wave data.

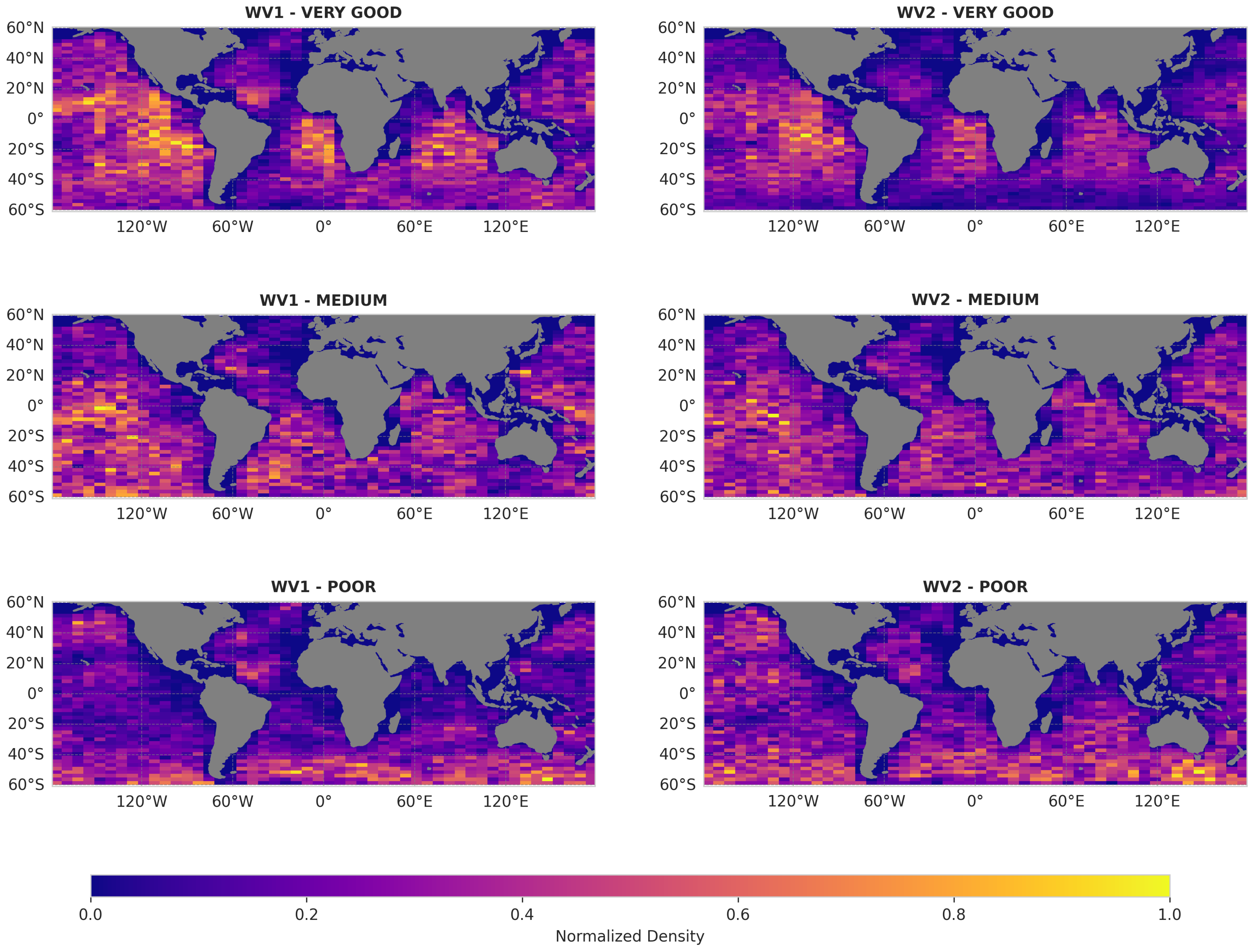
The mapping of the spatial distribution of classes (“very good,” “medium,” and “poor”) across WV1 and WV2 modes (Figure 5) reveals the performance of the classification in different regions. The distributions are largely consistent between the two modes, suggesting that the observed patterns are primarily dictated by the algorithm rather than by differences in the acquisition mode.

Some regional variations can be attributed to differences in WV acquisition coverage. For example, coverage over Europe is relatively sparse due to the use of alternative Sentinel-1 acquisition modes: Interferometric Wide Swath (IW) is mainly employed for mainland land monitoring, while Extra-Wide Swath (EW) is more frequently used in regions such as the Azores. Consequently, fewer WV observations are available for quality assessment in these areas.

A more detailed examination of the spatial distribution highlights certain regional tendencies.

• Very Good: This class tends to be more frequent in mid-latitude. In contrast, it is less commonly observed in the northern Indian Ocean and in coastal regions, where environmental factors such as monsoon activity, coastal topography, and proximity to land can affect the quality of wave retrievals.
• Medium: This class is relatively evenly distributed across the globe, with an increased presence in transition zones near the equator and subpolar regions. These areas are characterized by more variable conditions that often result in intermediate-quality inversions.
• Poor: This class is more frequently observed in high-latitude regions, where strong and variable winds, complex atmospheric dynamics, and environmental variability can affect both SAR retrievals and the performance of the WW3 model. Importantly, this classification does not exclusively reflect the limitations of SAR. It captures the general inconsistency between SAR and WW3 outputs, which may stem from either a dataset or geophysical conditions that influence both. The aim is to characterize the reliability of the partition based on observed disagreement, rather than attributing the error to a single source.

5. Discussion

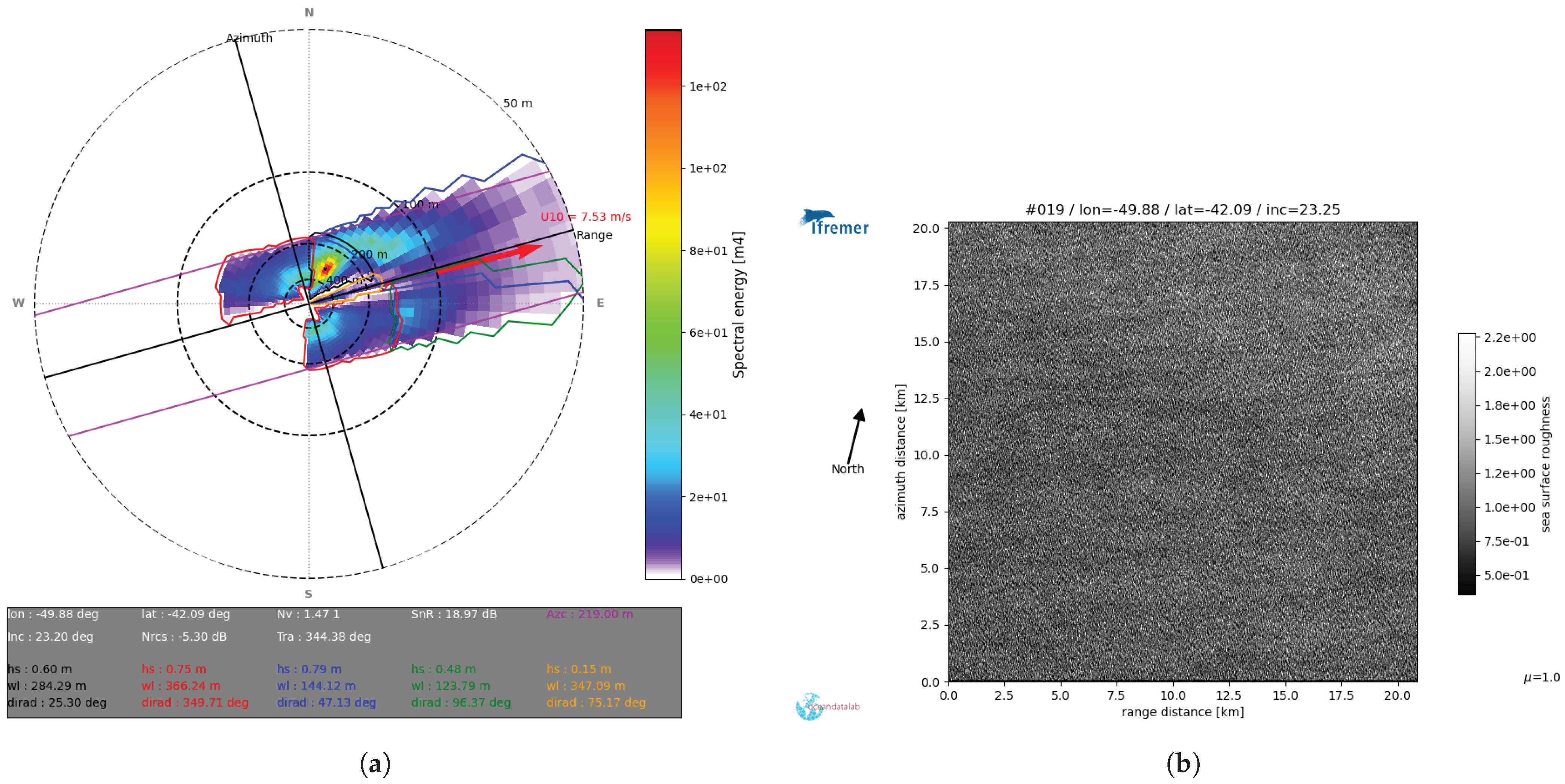
Retrieving ocean wave parameters from SAR data is inherently complex due to the limitations of the radar system and environmental variability. The MTF plays a central role in translating SAR cross-spectrum information into wave spectra, but factors such as wave motion, whether moving toward or away from the radar, can distort this process (Figure 6). Some inconsistencies can thus be directly attributed to the SAR inversion process. This is illustrated in Figure 6, where the red partition represents an artificial azimuth-oriented feature caused by underestimation of the azimuthal MTF, and the yellow partition reflects a comparable range-oriented artifact. The errors associated with such artificial partitions are substantially larger than those of genuine SAR-derived partitions, for which the corresponding WW3 partitions differ in integral parameters but remain of the same order of magnitude.

In addition to MTF-related challenges, environmental phenomena such as rainfall and other atmospheric or oceanic characteristics further impact NRCS, affecting wave retrieval. Rainfall (Figure 7) can influence the NRCS by altering surface roughness, potentially masking the geophysical signal. Oceanic fronts, characterized by sharp gradients in sea surface temperature and salinity, and atmospheric fronts (Figure 8), marked by strong near-surface wind variations, also introduce discontinuities in the NRCS, further complicating the retrieval of the wave spectrum.

To go deeper into model explanation and interpretability, an illustrative example of model interpretation is provided using SHAP-based explanations [35] to estimate errors in the three partition-integral parameters for the WV1 acquisition (see Figure 9, Figure 10 and Figure 11). The explanation for the WV2 acquisition is essentially the same and is therefore not shown. Each plot investigation contains two types of analysis, one for the model explanation: this explanation helps to interpret the importance of each feature (Table 1) and how they affect the model’s predictions. A second plot based on the importance of features introduces the concept of feature clustering to help visualize redundancy among features. This clustering aims to group features that provide information similar to the model. This means that a model might be able to use one of two related features and achieve similar predictive performance. Traditional methods such as correlation matrices can identify such relationships. In the context of SHAP’s feature clustering, “distance” between features is typically scaled between 0 and 1, where a distance of 0 means the features are perfectly redundant, and a distance of 1 means they are completely independent. In our case, we set the clustering cut-off at 0.5: the bar plot will only show clusters (or groups) of features that have a clustering distance of less than 0.5. This means that only highly redundant features (those sharing more than 50% of their explanation power) will be visually grouped together. Less redundant features, even if they have some relationship, will be displayed individually.

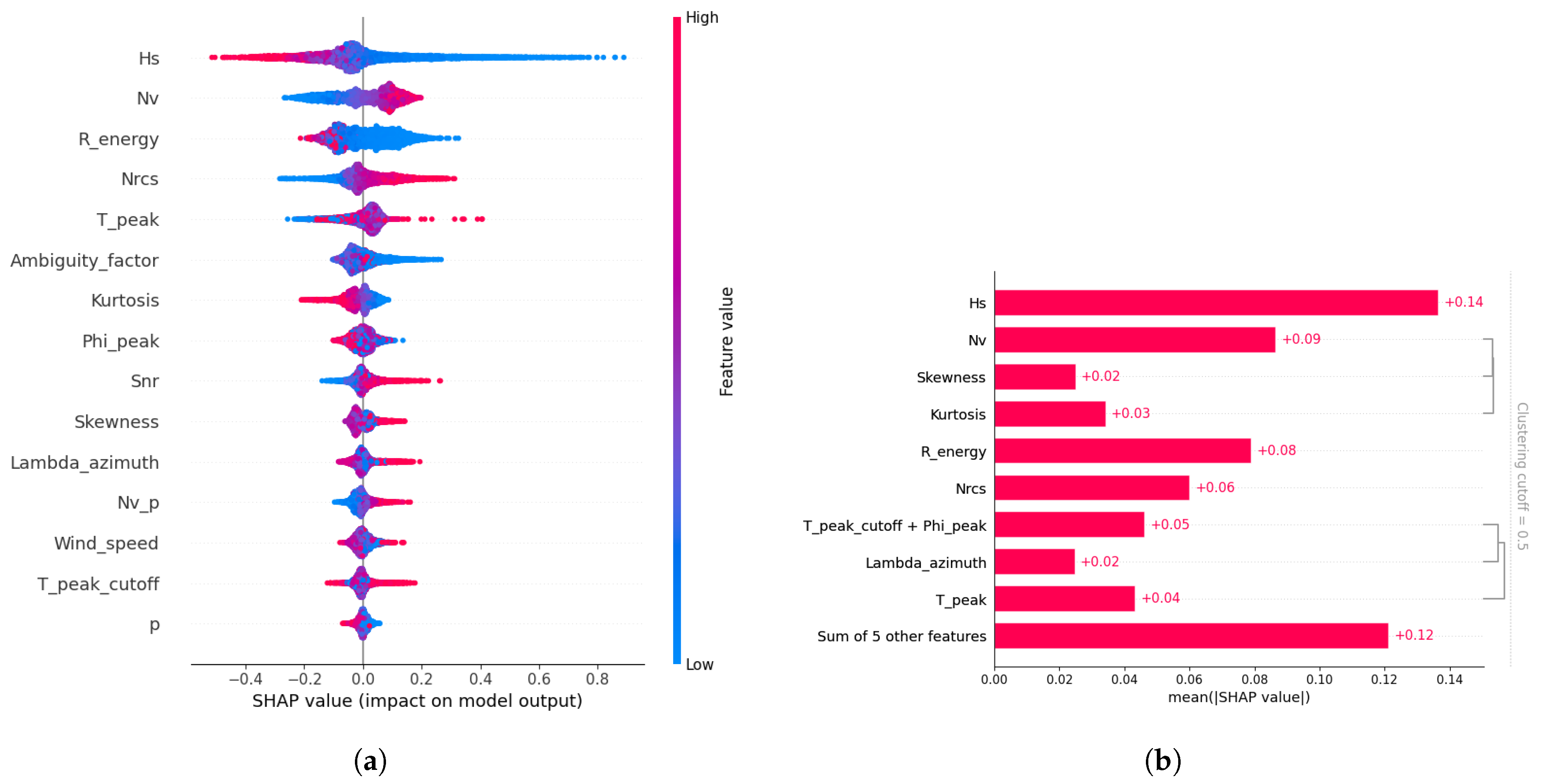
The main predictors for the estimation of $\left|\Delta \mathit{Hs}\right|$ (as depicted in Figure 9a) are the effective partition $\mathit{Hs}$ and the normalized variance of the SLC imagette. These features are physically meaningful, as they directly relate to wave energy and sea surface texture, and their influence is clearly reflected in the behavior of the model. Specifically, the model tends to associate higher effective values $\mathit{Hs}$ with a lower predicted error, leading to a higher quality classification for those partitions. In contrast, lower $\mathit{Hs}$ values are typically associated with higher predicted errors and lower quality assessments. This indicates that the model prioritizes energetic sea states, while treating weaker partitions more conservatively.

A further insight comes from the feature clustering (Figure 9b): statistical moments derived from the SLC imagette—namely skewness, kurtosis, and normalized variance—form a single cluster, indicating that they collectively explain a significant portion (over 50%) of the model’s behavior. Another correlated group includes peak wave parameters such as peak direction and peak period. Most other features appear relatively independent of their contribution to predict $\left|\Delta \mathit{Hs}\right|$, suggesting that the model relies on a focused subset of physically meaningful indicators to make its predictions.

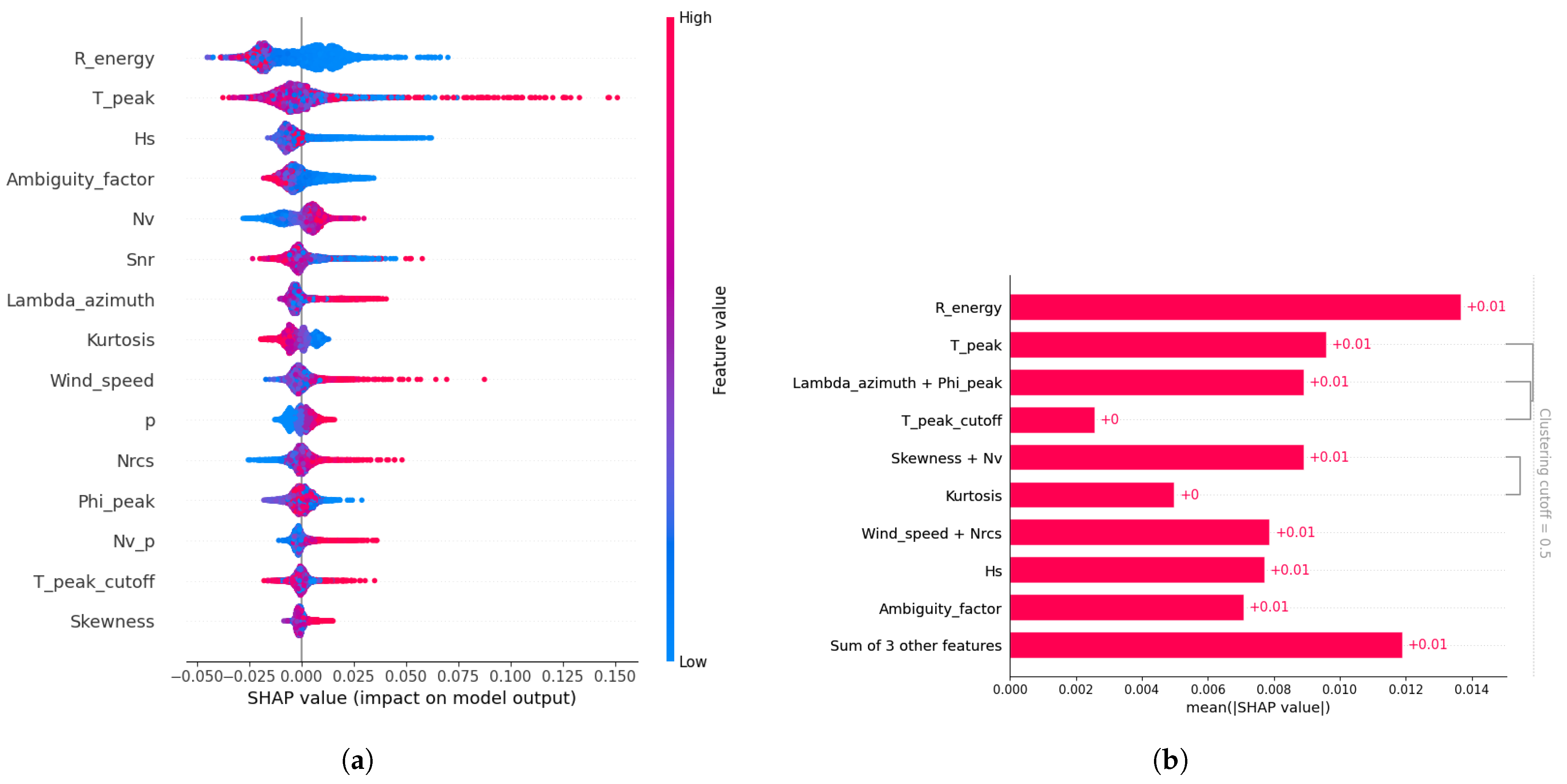
In the context of the estimation of the peak period error $\left|\Delta \mathit{T}\right|$ (Figure 10a), the predominant determinant of the fidelity of the model is the energy ratio between the spectral peak of the partition and the maximum energy boundary. A decreased energy ratio corresponds to an increase in relative error, underscoring its critical influence on the model’s uncertainty quantification. In contrast, elevated energy ratios are associated with reduced error magnitudes, indicating enhanced precision in the peak period retrieval. Smaller energy ratio predominantly plays a role in higher sensitivity of the partitioning process and reduced ability to cross-assign the right partitions between the model and the SAR: typically, swell systems seen by the model as a single energy peak may have a double peak in the corresponding SAR spectrum domain.

Consistent with the objective of the model, the peak period itself constitutes the second most significant feature that impacts error prediction. Its influence manifests non-linearly and is modulated by the swell propagation direction relative to the SAR azimuth, as well as hydrodynamic effects and tilt modulation intrinsic to the SAR wave retrieval mechanism.

In particular, while the partition index has a limited influence on the estimation of $\left|\Delta \mathit{Hs}\right|$, the model leverages the partition rank (i.e., the “p” feature) more substantially when predicting $\left|\Delta \mathit{T}\right|$. This suggests that the model attempts to refine its error estimation by accounting for the sequential ordering of swell systems, which aligns with the earlier observations regarding the distribution of quality classes across partition ranks. This strategy reflects the model’s recognition of the varying relevance and complexity of each partition in accurately retrieving peak period information.

Furthermore, we observe a similar behavior to $\left|\Delta \mathit{Hs}\right|$ in terms of feature redundancy (Figure 10b): the SLC imagette statistics are often redundant, leading the model to group them together. This redundancy extends to some other peak partition parameters computed in different geometries, which also appear to be redundant for the model.

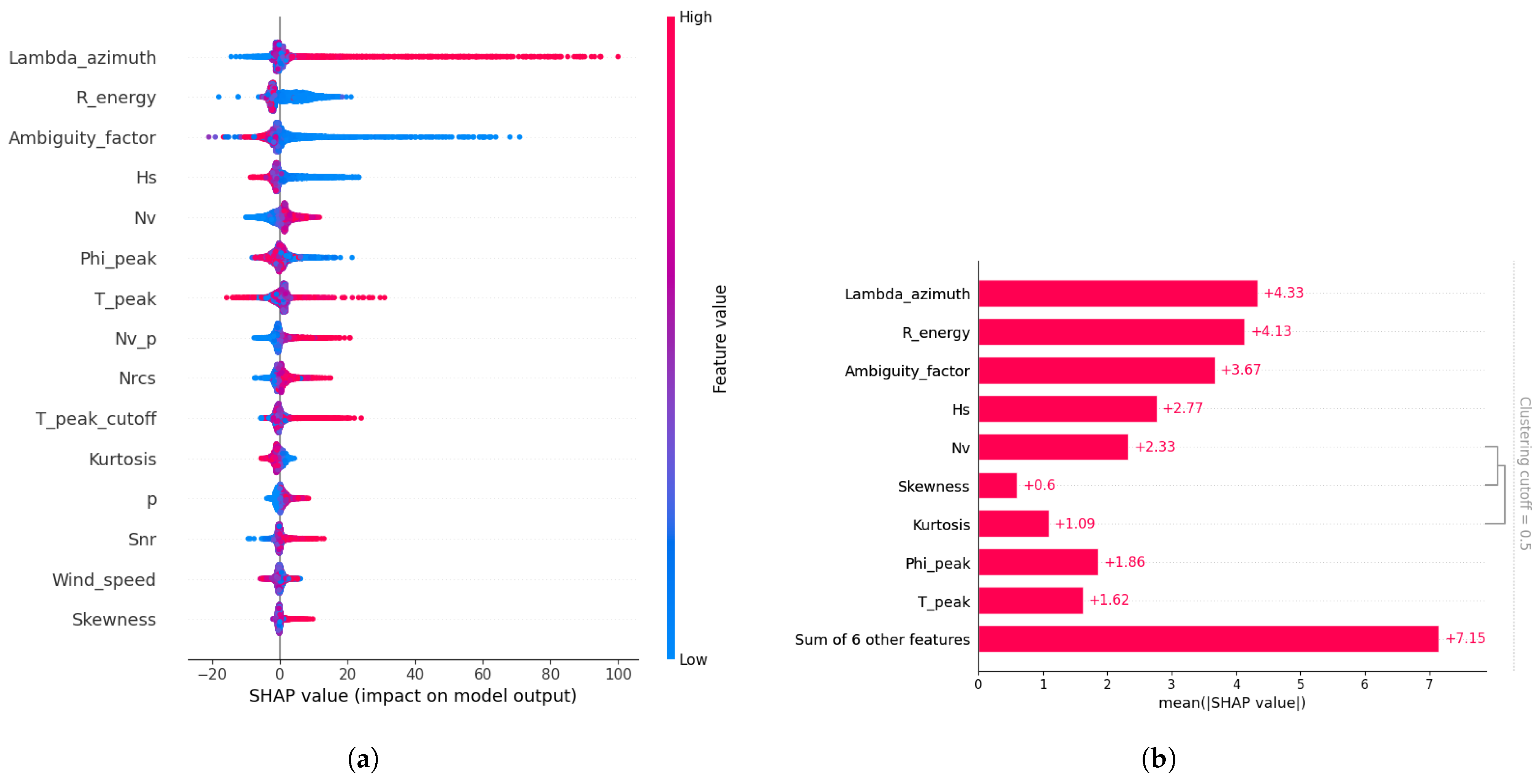
Analysis of the error estimation of the partition wave direction $\left|\Delta \mathsf{\Phi }\right|$ (Figure 11a) reveals a pronounced sensitivity to alignment between the dominant wave direction and the direction of the satellite. This confirms the fundamental influence of wave propagation dynamics relative to the SAR flight azimuth, which imposes intrinsic constraints on the inversion accuracy, as previously described. The elevated importance of the ambiguity factor—ranked third among predictors—further highlights its critical role in modulating directional uncertainty, distinguishing this error metric from others.

Consistent with patterns observed in the estimation of other wave parameters, the energy ratio once again proves to be a principal driver, ranking as the second most important feature. The peak wave direction $\mathsf{\Phi }$ also contributes significantly, occupying the sixth position in the feature importance hierarchy, emphasizing its relevance in capturing directional variability.

In addition to the correlated statistical features derived from the SLC imagette (Figure 11b), the model does not identify additional significant groups of features influencing $\left|\Delta \mathsf{\Phi }\right|$. This suggests that directional error arises from a more discrete set of physical and retrieval factors, underscoring the complex interplay between wave dynamics and SAR observation geometry. These insights pave the way for targeted improvements in SAR wave inversion methodologies with the potential to enhance the fidelity of directional retrieval under challenging environmental conditions.

6. Conclusions

This study proposes a novel methodology to improve the reliability of SAR-based ocean wave retrieval by introducing an advanced partition classification algorithm. Through the integration of machine learning and explainability techniques, the approach effectively mitigates persistent challenges in the interpretation of wave spectra, particularly those associated with system-induced distortions such as azimuth cut-off effects and MTF limitations.

Looking forward, the proposed QF classification framework holds promise in enabling a more systematic identification of error sources, especially those that recur under specific SAR observation conditions. Furthermore, it may serve as a foundation for targeted advancements in wave inversion methodologies, including the refinement of MTF models and the development of sophisticated filtering techniques to suppress non-wave signals.

What sets this work apart is not just the classification accuracy, but the intelligent selection of physically meaningful features that align with the behavior of ocean waves. This synergy between data-driven modeling and geophysical understanding enables a deeper insight into SAR performance under varying sea conditions. The model’s capacity to isolate the most reliable partitions creates opportunities for more targeted and confident use of SAR data in both scientific research and operational settings.

Beyond technical contributions, the integration of interpretability adds a valuable layer of transparency. Rather than treating the algorithm as a black box, the use of SHAP-based analysis illuminates the factors influencing each decision, allowing users to validate outcomes and potentially refine the input data or retrieval strategies.

In a broader sense, this work contributes to a growing effort in Earth observation to make remote sensing tools not only more accurate but also more accountable and accessible. The proposed method offers a foundation upon which future SAR-based systems can be built: systems that are capable of adapting to complex marine environments while providing clear, interpretable results. As ocean monitoring becomes increasingly vital in the context of climate change and maritime activity, such tools will be essential for both research and real-world applications.