Improving Atmospheric Noise Correction from InSAR Time Series Using Variational Autoencoder with Clustering (VAE-Clustering) Method
Abstract
1. Introduction
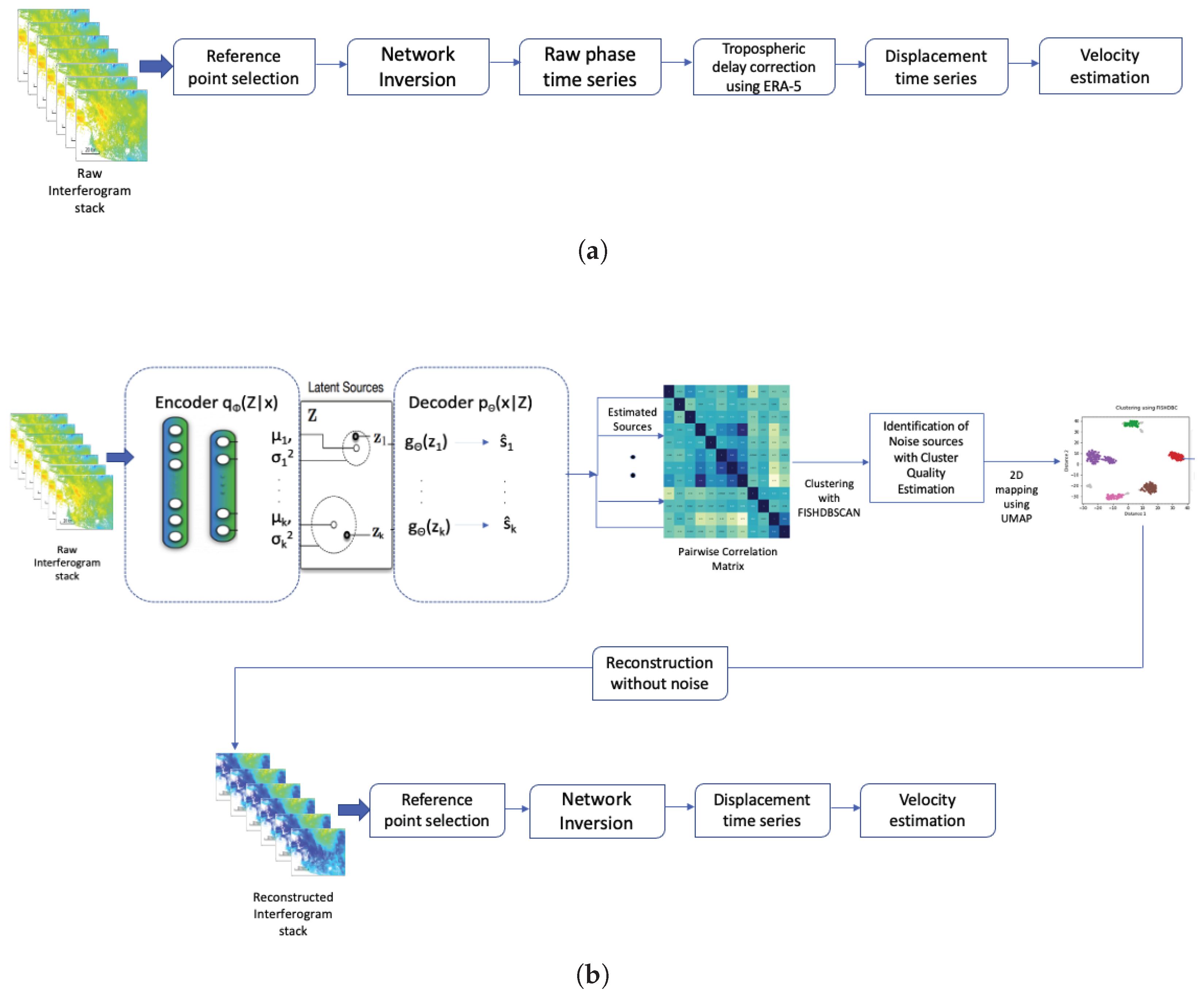
2. Method
2.1. Variational Autoencoder
2.1.1. Encoder
2.1.2. Decoder
2.1.3. Architecture
2.2. Clustering
2.3. Integration into MintPy
- First, with the original uncorrected interferograms as inputs and keeping the rest of the modules the same and estimating the tropospheric delay using the delay maps acquired from ERA5. In this method, the tropospheric phase delay of the interferograms was estimated by subtracting the ZTD maps from the original phase of the interferograms. This data is downloaded for the corresponding interferogram dates from the CDS website [32,33,34,35]. To account for residual orbital errors, the original interferograms were corrected from a linear trend in range. This is implemented as a module in MintPy before estimating the velocity.
- Second, by reducing the noise of the interferograms using the VAE-clustering method, then providing the corrected interferogram as input to the MintPy module, and finally estimating the velocity. The step for correcting the stratified tropospheric delay using ERA5 was removed in this workflow.
3. Data
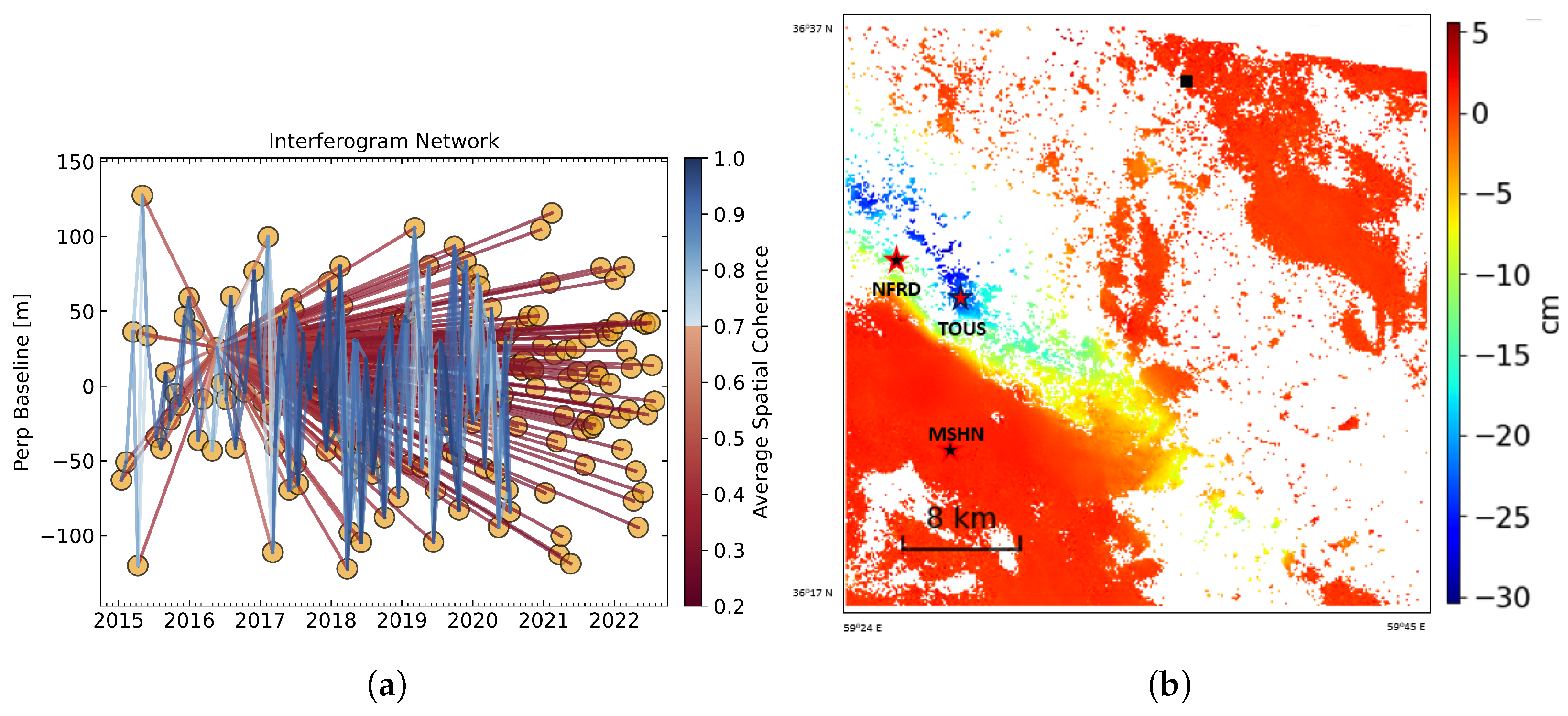
3.1. Mashhad, Iran
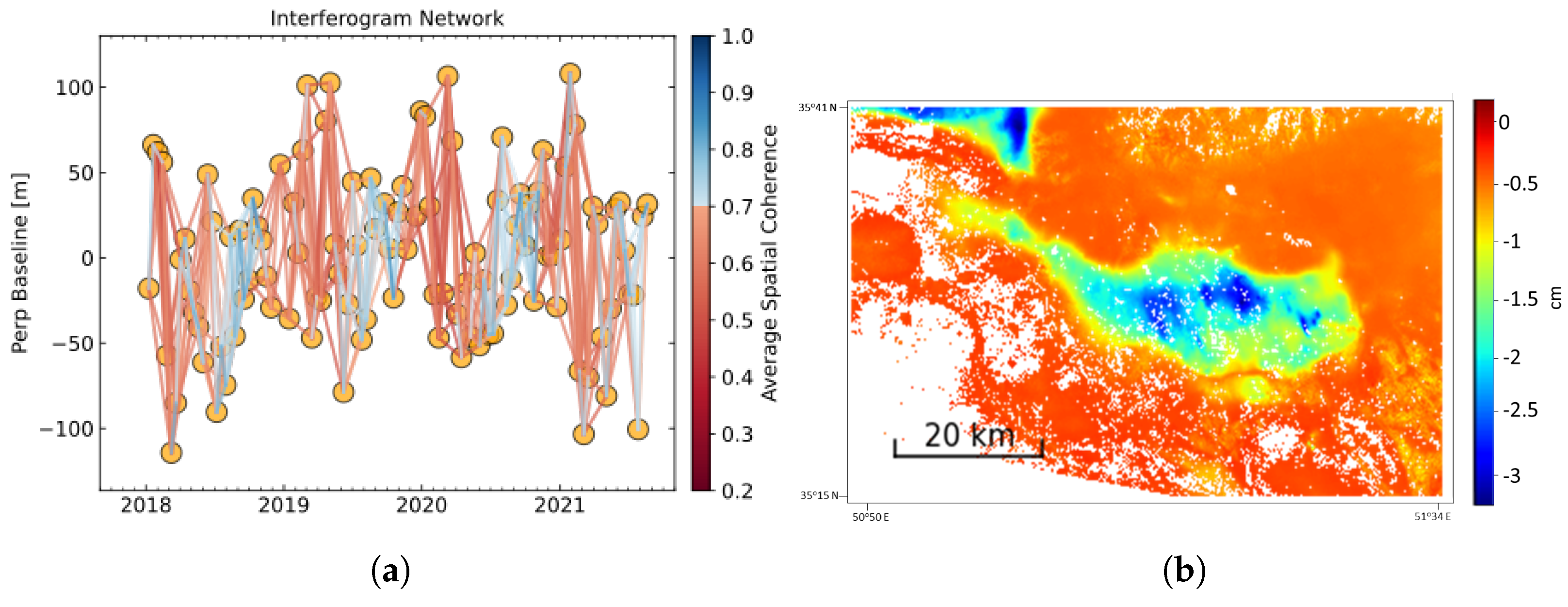
3.2. Tehran, Iran
3.3. Acapulco, Mexico
4. Training Details
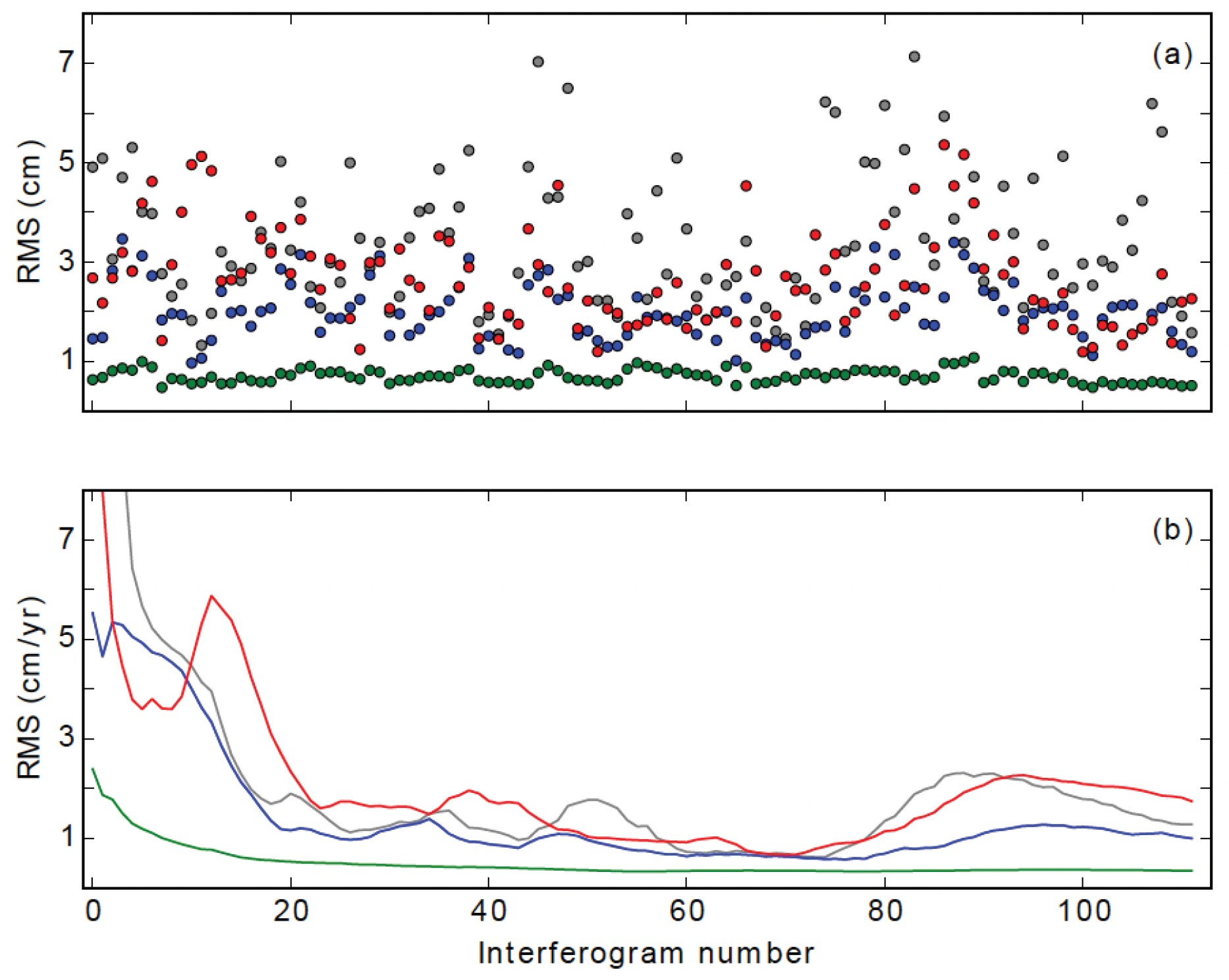
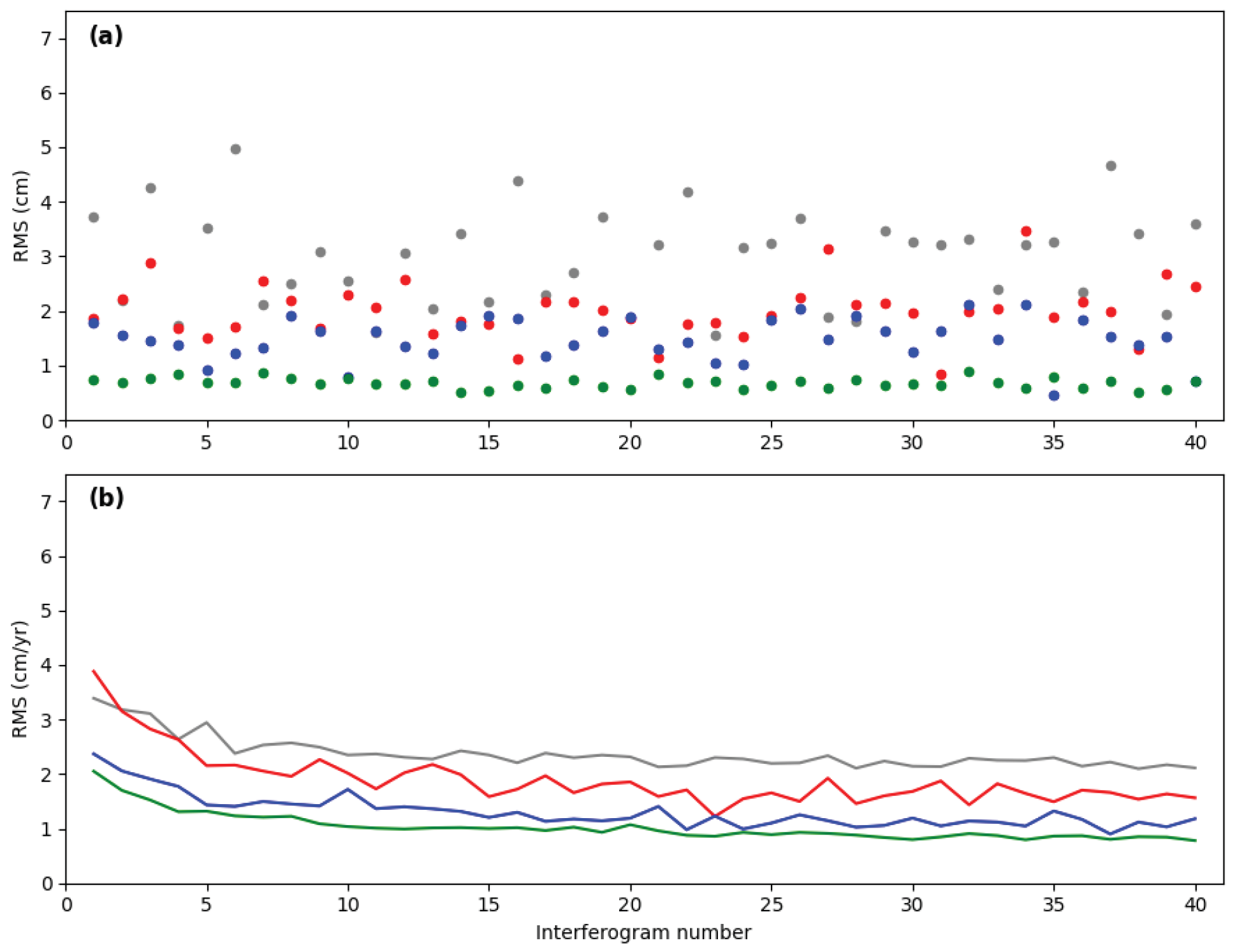
5. Results
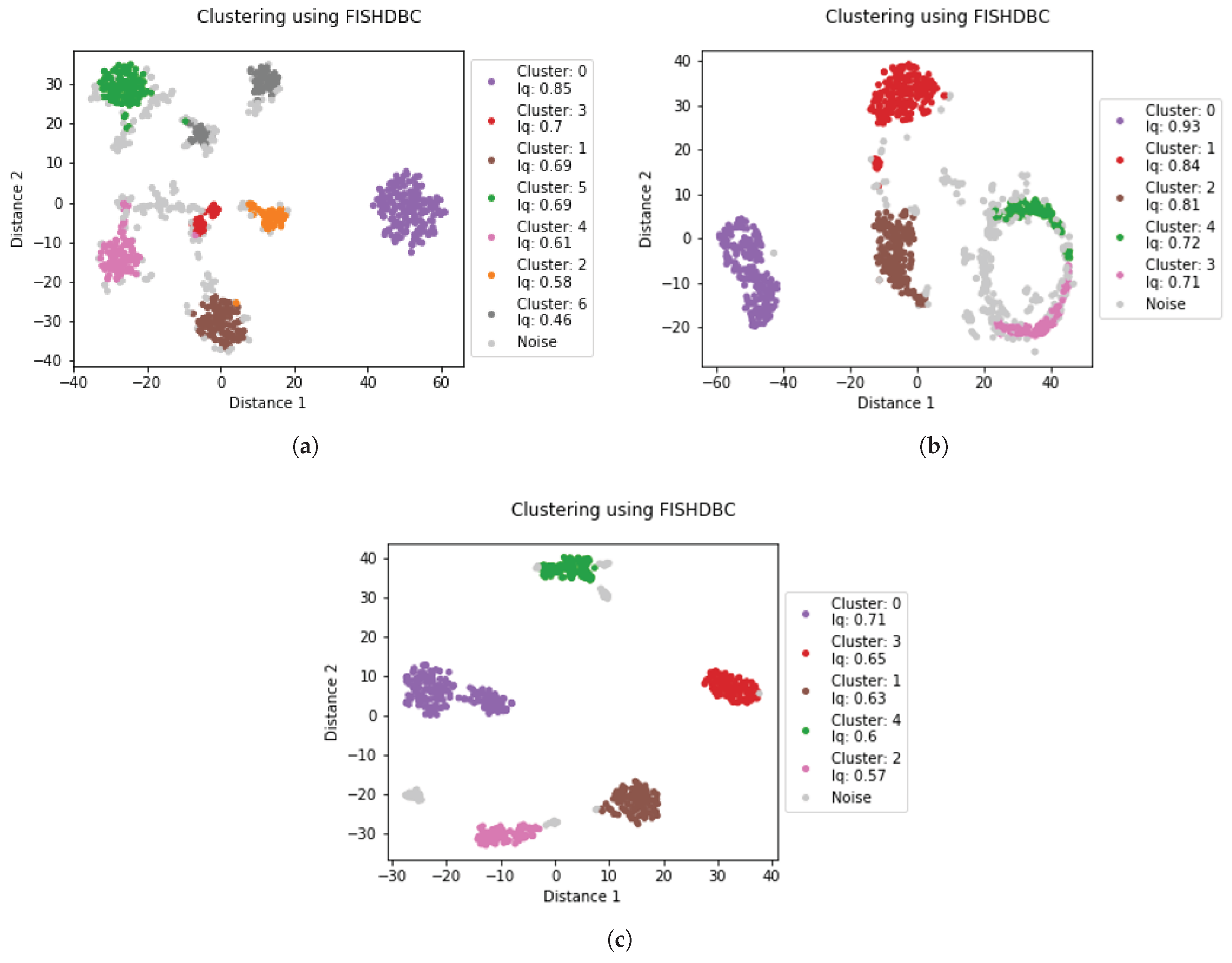
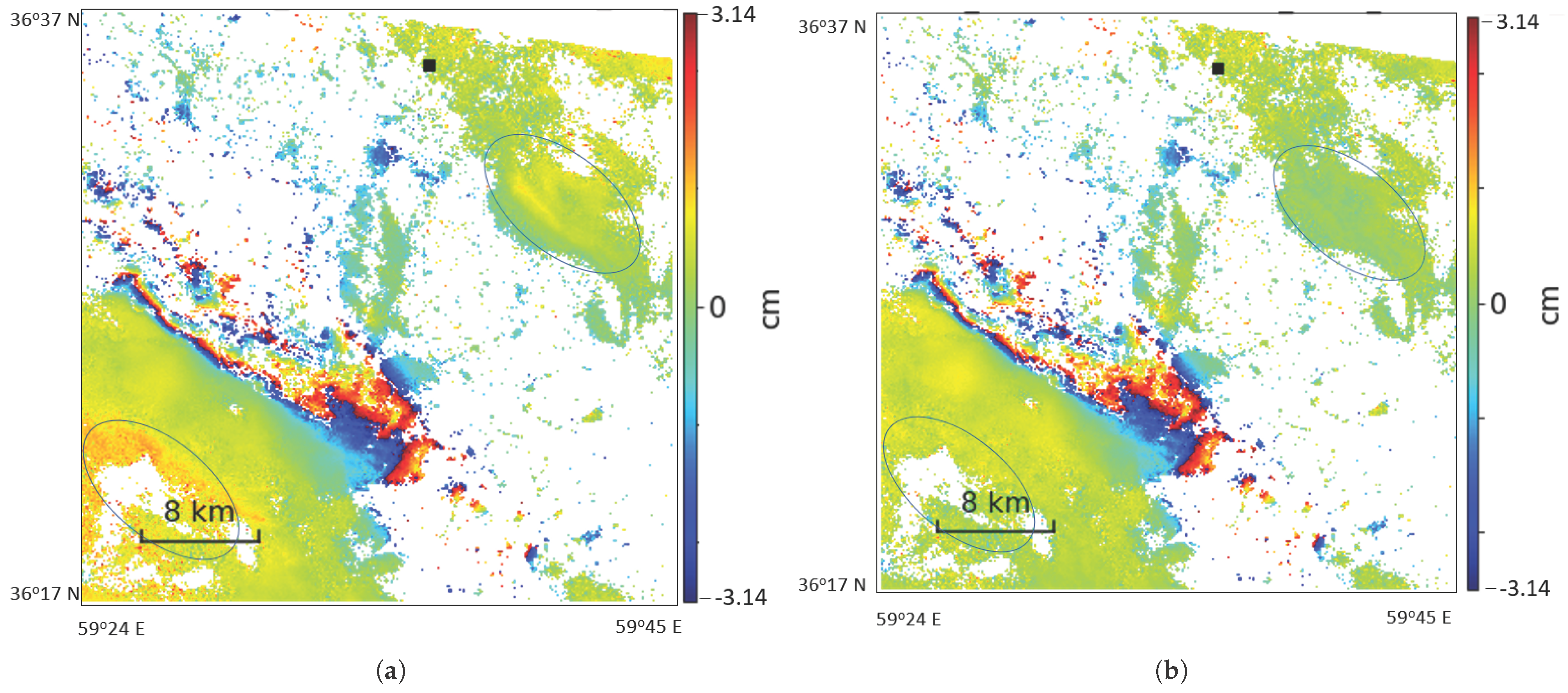
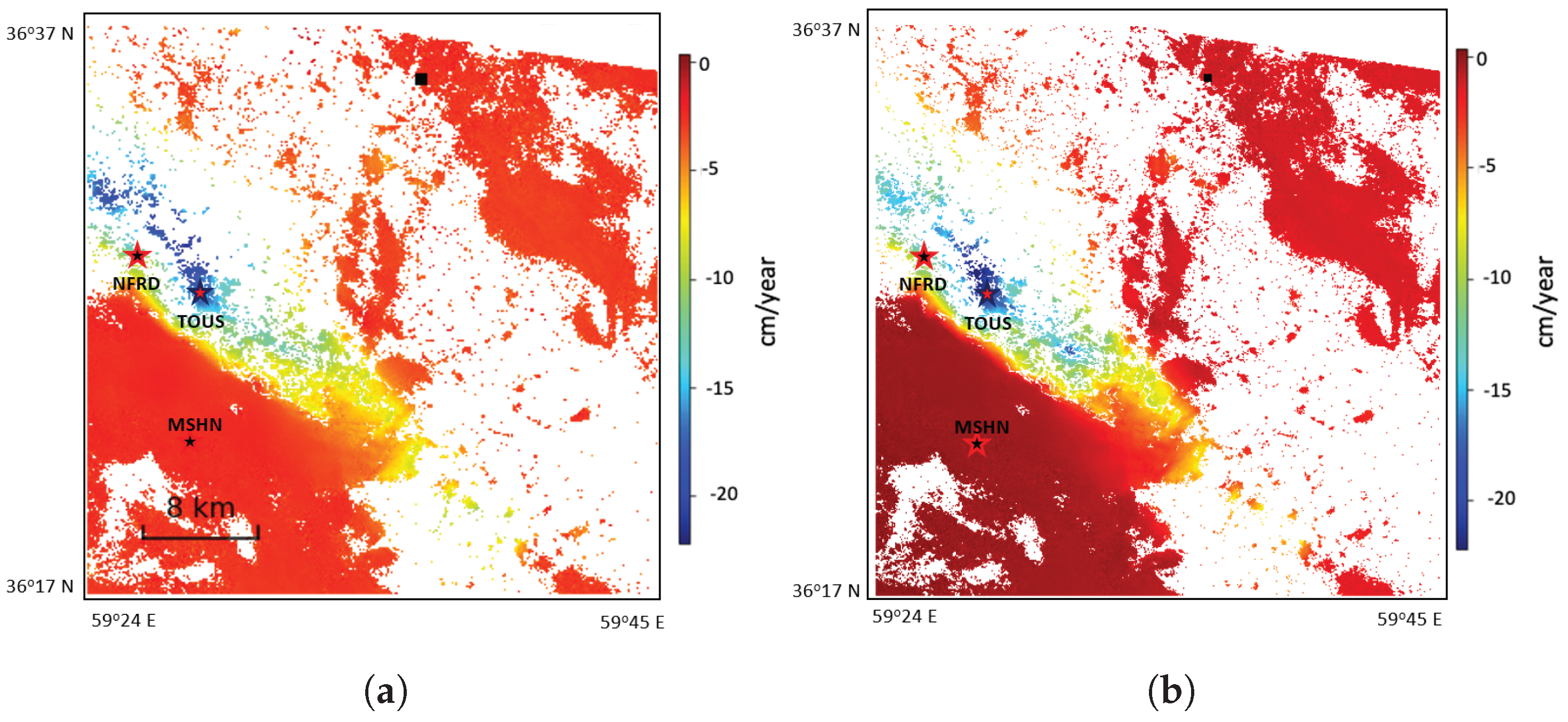
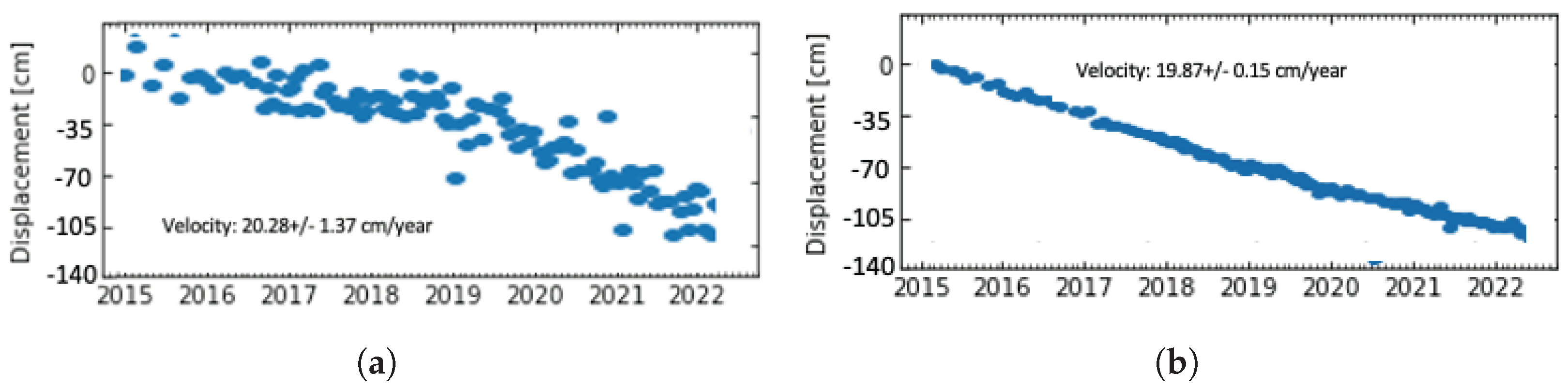
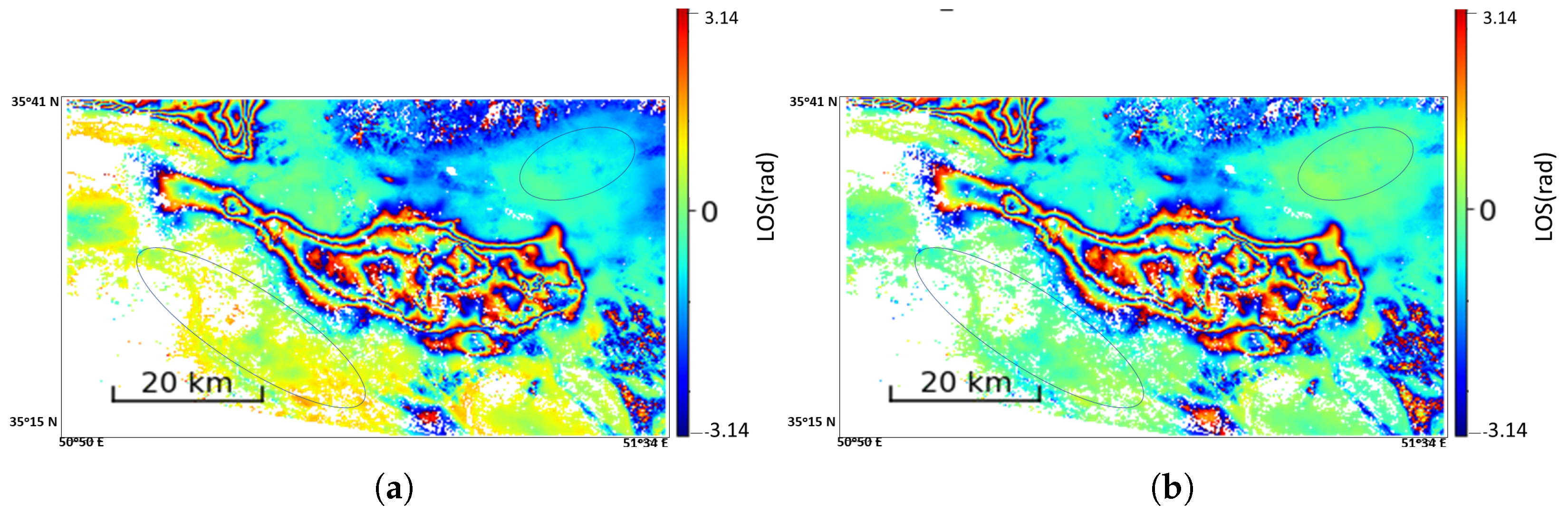
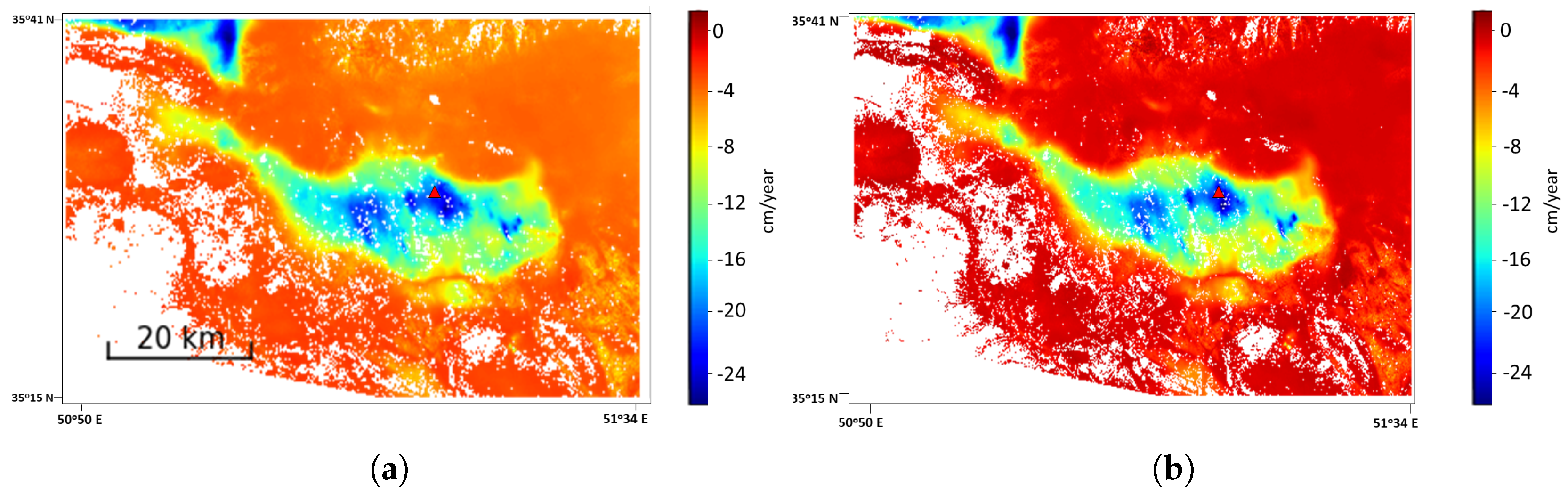
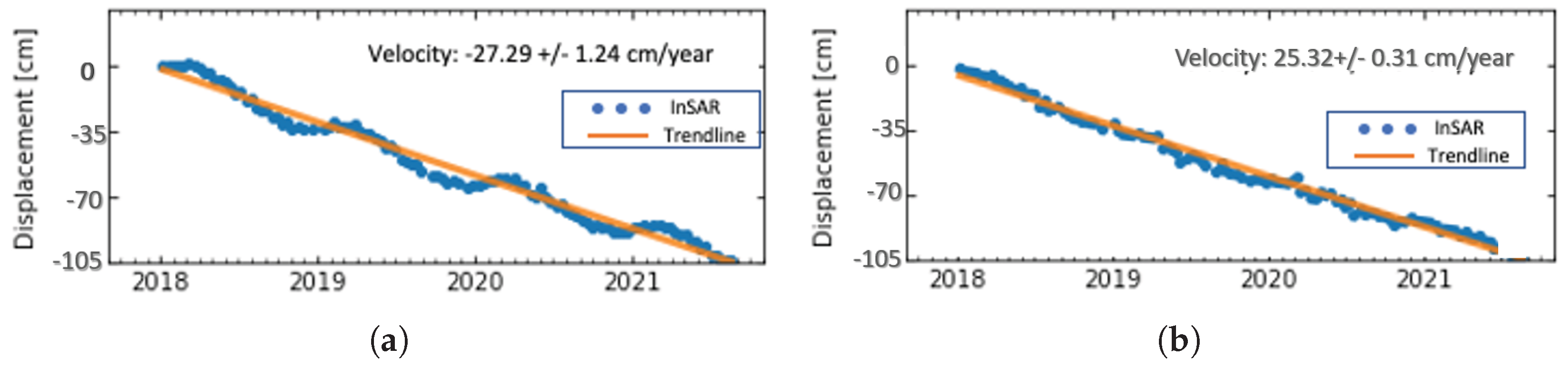
5.1. Results from Mashhad
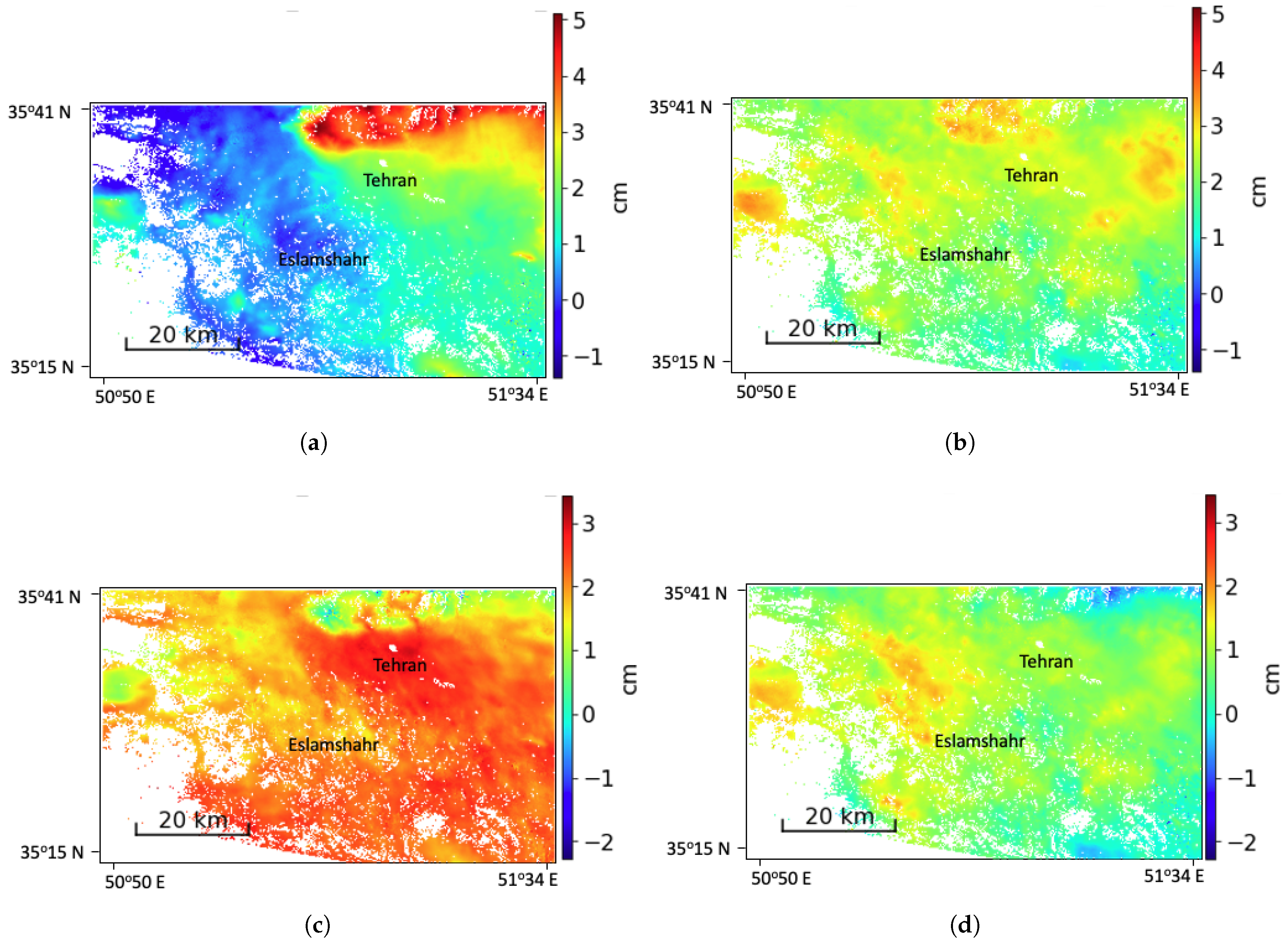
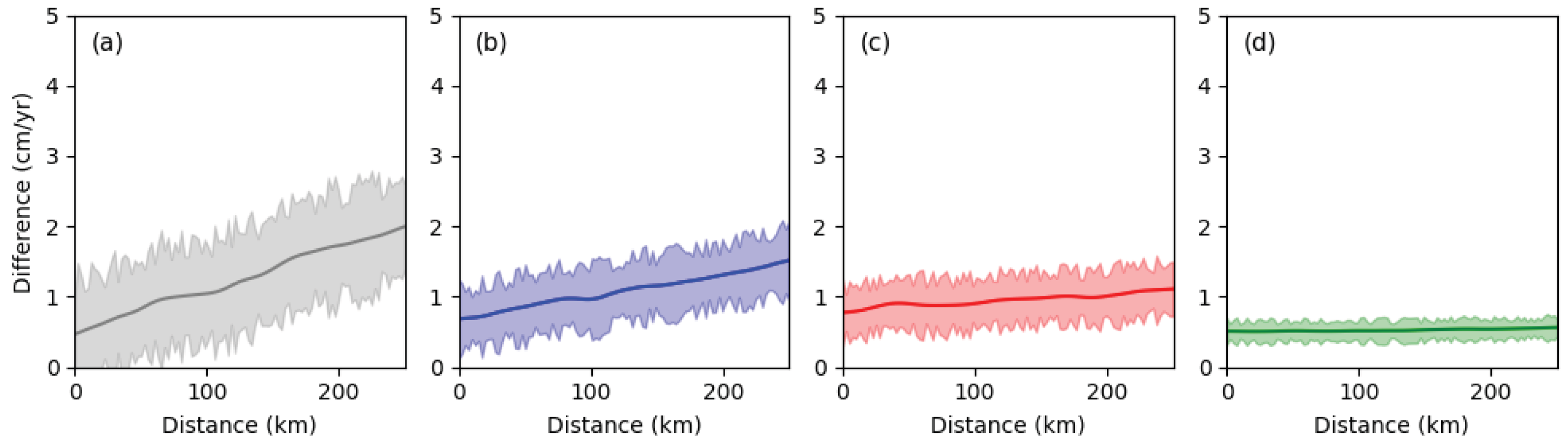
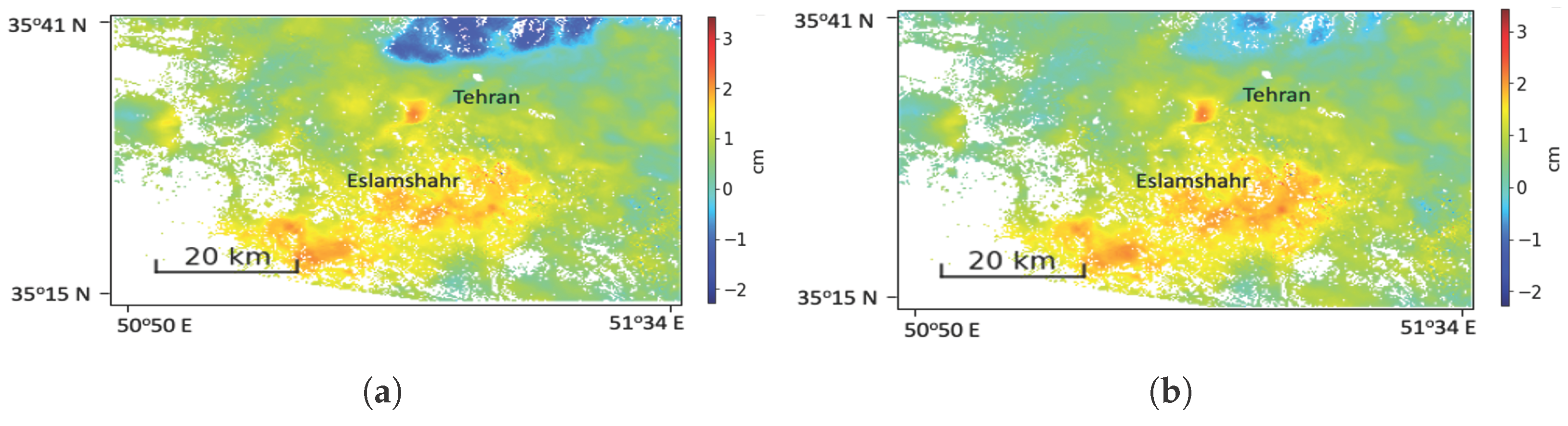
5.2. Results from Tehran
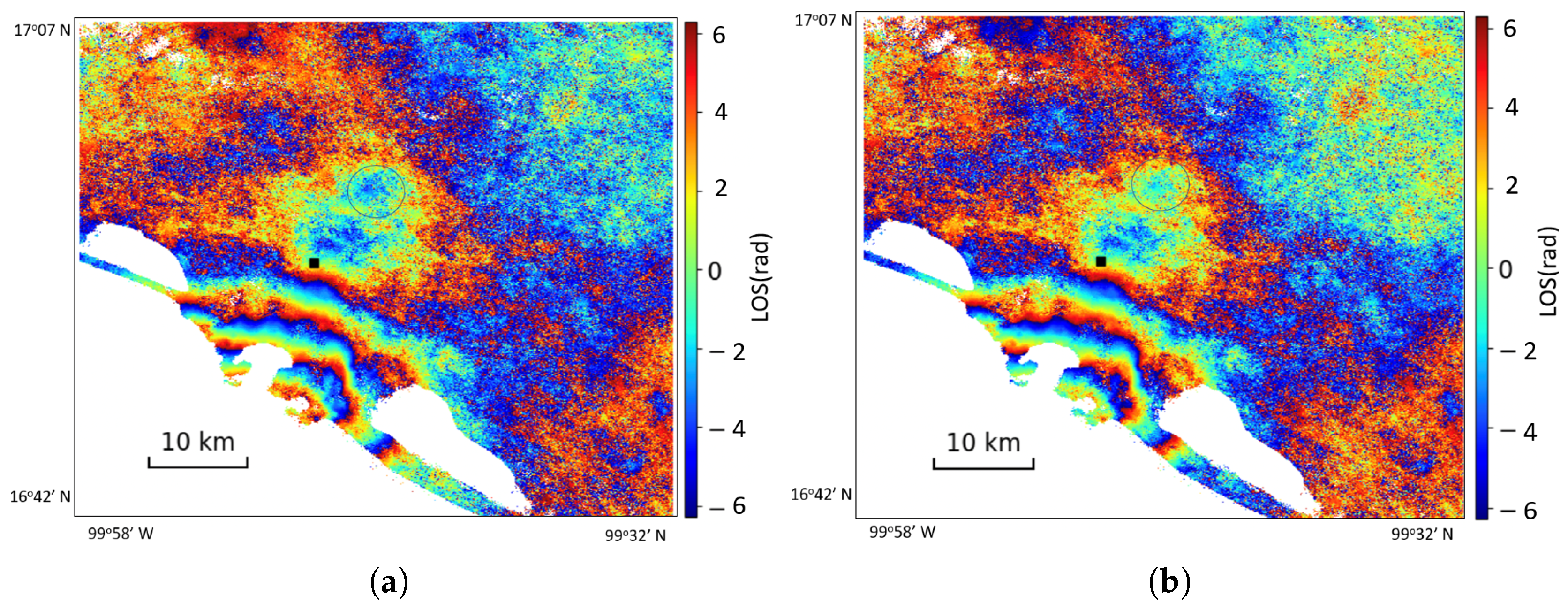
5.3. Results from Acapulco, Mexico
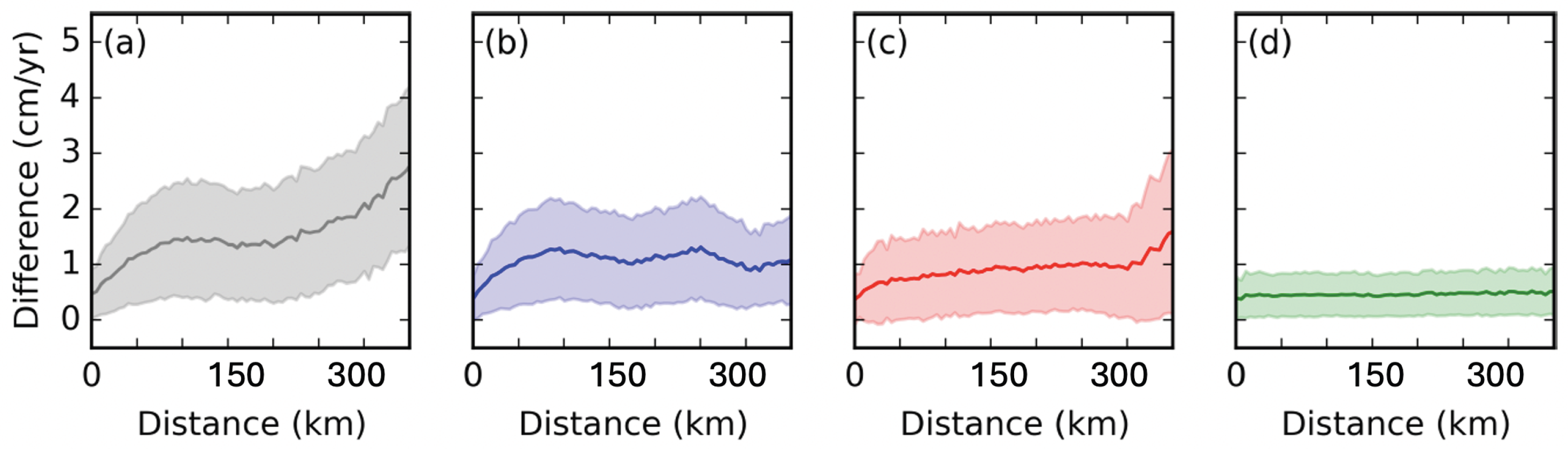
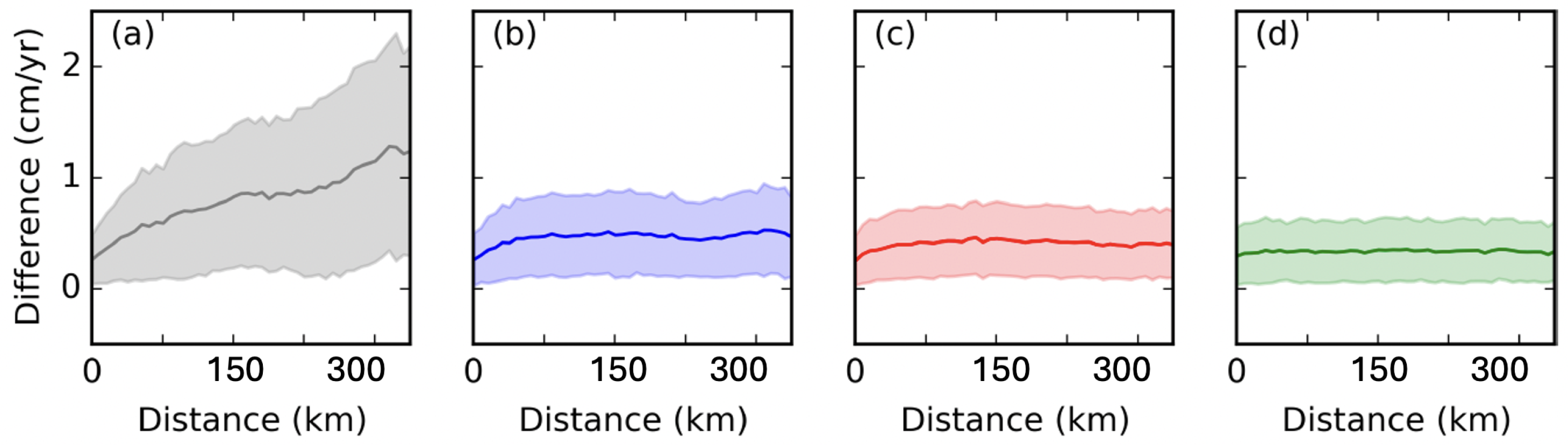
6. Discussion
6.1. Comparison of Performance of VAE-Clustering Method with Adaptive Localized Phase Topography Correction Method
6.2. Some Cases of Exceptions for the VAE-Clustering Approach
6.3. Analysis and Comparison of Application of Algorithms like ICA, NMF, or PCA to the VAE-Clustering Approach
- is the number of interferograms in the dataset;
- is the total number of pixels per interferogram (e.g., spatial resolution × image size).
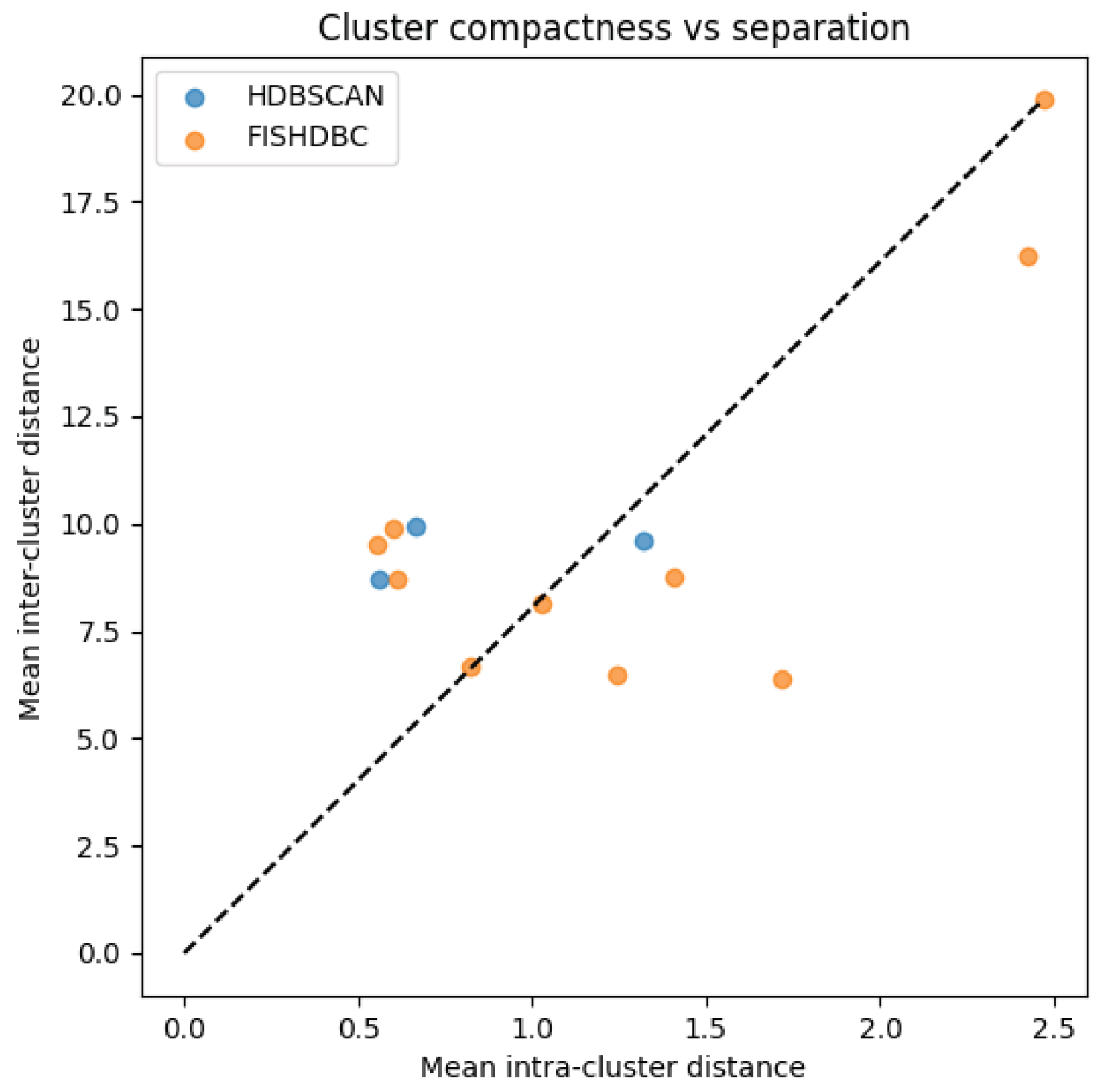
6.4. Comparison of Using FISHDBC Clustering Against Clustering Using HDBSCAN
7. Conclusions
8. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Massonnet, D.; Feigl, K. Radar interferometry and its application to changes in the Earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.; Fieldling, E. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Annu. Rev. Earth Planet. Sci. 2008, 28, 169–209. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M. Sentinel-1 InSAR over Germany: Large-scale interferometry, atmospheric effects, and ground deformation mapping. ZFV—Z. Geodasie Geoinf. Landmanag. 2017, 142, 245–246. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Li, Z. Interferometric synthetic aperture radar (INSAR) atmospheric correction: GPS, moderate resolution imaging Spectroradiometer (MODIS), and insar integration. J. Geophys. Res. 2005, 110, B03410. [Google Scholar] [CrossRef]
- Ghosh, B.; Haghshenas Haghighi, M.; Motagh, M.; Maghsudi, S. Using Generative Adversarial Networks for Extraction of Insar Signals from Large-Scale Sentinel-1 Interferograms by Improving Tropospheric Noise Correction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, V-3-2021, 57–64. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic insar tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38, L17311. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Jolivet, R.; Dalaison, M.; Johnson, P.A.; Hulbert, C. Autonomous extraction of millimeter-scale deformation in InSAR time series using deep learning. Nat. Commun. 2021, 12, 6480. [Google Scholar] [CrossRef]
- Gaddes, M.E.; Hooper, A.; Bagnardi, M. Using Machine Learning to Automatically Detect Volcanic Unrest in a Time Series of Interferograms. J. Geophys. Res. Solid Earth 2019, 124, 12304–12322. [Google Scholar] [CrossRef]
- Ghosh, B.; Motagh, M.; Haghighi, M.H.; Vassileva, M.S.; Walter, T.R.; Maghsudi, S. Automatic Detection of Volcanic Unrest Using Blind Source Separation With a Minimum Spanning Tree Based Stability Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7771–7787. [Google Scholar] [CrossRef]
- Chen, C.; Dai, K.; Tang, X.; Cheng, J.; Pirasteh, S.; Wu, M.; Shi, X.; Zhou, H.; Li, Z. Removing insar topography-dependent atmospheric effect based on Deep Learning. Remote Sens. 2022, 14, 4171. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Bull, D. The Application of Convolutional Neural Networks to Detect Slow, Sustained Deformation in InSAR Time Series. Geophys. Res. Lett. 2019, 46, 11850–11858. [Google Scholar] [CrossRef]
- Zhou, H.; Dai, K.; Tang, X.; Xiang, J.; Li, R.; Wu, M.; Peng, Y.; Li, Z. Time-series insar with deep-learning-based topography-dependent atmospheric delay correction for potential landslide detection. Remote Sens. 2023, 15, 5287. [Google Scholar] [CrossRef]
- Zhou, H.; Dai, K.; Pirasteh, S.; Li, R.; Xiang, J.; Li, Z. InSAR Spatial-Heterogeneity Tropospheric Delay Correction in Steep Mountainous Areas Based on Deep Learning for Landslides Monitoring. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5215014. [Google Scholar] [CrossRef]
- Ma, P.; Yu, C.; Jiao, Z.; Zheng, Y.; Wu, Z.; Mao, W.; Lin, H. Improving time-series InSAR deformation estimation for city clusters by deep learning-based atmospheric delay correction. Remote Sens. Environ. 2024, 304, 114004. [Google Scholar] [CrossRef]
- Cardoso, J.F. Blind signal separation: Statistical principles. Proc. IEEE 1998, 86, 2009–2025. [Google Scholar] [CrossRef]
- Huang, P.S.; Chen, S.D.; Smaragdis, P.; Hasegawa-Johnson, M. Singing-voice separation from monaural recordings using robust principal component analysis. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar] [CrossRef]
- Févotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura-Saito Divergence: With Application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef] [PubMed]
- Badeau, R.; Dremeau, A. Variational Bayesian EM algorithm for modeling mixtures of non-stationary signals in the time-frequency domain (HR-NMF). In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar] [CrossRef]
- Hoshen, Y. Towards Unsupervised Single-channel Blind Source Separation Using Adversarial Pair Unmix-and-remix. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Neri, J.; Badeau, R.; Depalle, P. Unsupervised Blind Source Separation with Variational Auto-Encoders. In Proceedings of the 2021 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021. [Google Scholar] [CrossRef]
- Calhoun, V.; Adali, T.; Pearlson, G.; Pekar, J. A method for making group inferences from functional MRI data using independent component analysis. Hum. Brain Mapp. 2001, 14, 140–151. [Google Scholar] [CrossRef]
- Kingma, D.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Wei, Y.H.; Ni, Y.Q. Parameter-adaptive variational autoencoder for linear/nonlinear blind source separation. J. Civ. Struct. Health Monit. 2024, 15, 1161–1184. [Google Scholar] [CrossRef]
- Neri, J.; Depalle, P.; Badeau, R. Approximate inference and learning of state space models with Laplace Noise. IEEE Trans. Signal Process. 2021, 69, 3176–3189. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Gaddes, M.E. Automatic Detection of Volcanic Unrest Using Interferometric Synthetic Aperture Radar. Ph.D. Thesis, University of Leeds, Leeds, UK, 2019. [Google Scholar]
- Dell’Amico, M. FISHDBC: Flexible, Incremental, Scalable, Hierarchical Density-Based Clustering for Arbitrary Data and Distance. arXiv 2019, arXiv:1910.07283. [Google Scholar] [CrossRef]
- Sainburg, T.; McInnes, L.; Gentner, T.Q. Parametric UMAP Embeddings for Representation and Semisupervised Learning. Neural Comput. 2021, 33, 2881–2907. [Google Scholar] [CrossRef] [PubMed]
- van der Maaten, L.; Hinton, G. Viualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Copernicus Climate Data Store, 2022. ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Available online: https://cds.climate.copernicus.eu/ (accessed on 9 September 2025).
- Khorrami, M.; Abrishami, S.; Maghsoudi, Y.; Alizadeh, B.; Perissin, D. Extreme subsidence in a populated city (Mashhad) detected by PSInSAR considering groundwater withdrawal and geotechnical properties. Sci. Rep. 2020, 10, 11357. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M. Ground surface response to continuous compaction of aquifer system in Tehran, Iran: Results from a long-term multi-sensor InSAR analysis. Remote Sens. Environ. 2019, 221, 534–550. [Google Scholar] [CrossRef]
- Gonzalez-Huizar, H.; Pérez-Campos, X.; Velasco, A.A. Acapulco Earthquake Struck the Edge of a Seismic Gap. Temblor.net. 2022. Available online: https://temblor.net/earthquake-insights/acapulco-earthquake-struck-the-edge-of-a-seismic-gap-13465/ (accessed on 9 September 2025).
- Iglesias, A.; Singh, S.K.; Castro-Artola, O.; Pérez-Campos, X.; Corona-Fernandez, R.D.; Santoyo, M.A.; Espíndola, V.H.; Arroyo, D.; Franco, S.I. A source study of the MW 7.0 Acapulco, Mexico, earthquake of 8 September 2021. Seismol. Res. Lett. 2022, 93, 3205–3218. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M. Local and Large Scale InSAR Measurement of Ground Surface Deformation. Dissertation, Gottfried Wilhelm Leibniz Universität Hannover, Fakultät für Bauingenieurwesen und Geodäsie. Veröffentlichungen der DGK, Reihe C: Dissertationen, Heft Nr. 840. Verlag der Bayerischen Akademie derWissenschaften: München, 2019. ISBN 978-3-7696-5252-9, ISSN 0065-5325. Also Published inWissenschaftliche Arbeiten der Fachrichtung Geodäsie und Geoinformatik der Universität Hannover, Nr. 354, ISSN 0174-1454. Available online: https://dgk.badw.de/fileadmin/user_upload/Files/DGK/docs/c-840.pdf (accessed on 1 June 2025).








| Parameter | Value |
|---|---|
| Track (Path) | 93 |
| Frame | 472 |
| Orbit | 43,565 |
| Flight Direction | Descending |
| Time Span | 2015–2021 |
| Interferograms | ≈500 |
| Reference GPS Station | MSHN |
| Active GPS Station for Validation | NFRD |
| Parameter | Value |
|---|---|
| Track (Path) | 78 |
| Frame | 52 |
| Orbit | 26,179 |
| Flight Direction | Ascending |
| Time Span | 2018–2021 |
| Interferograms | ≈500 |
| Processing Method | SBAS via ASF HyP3 |
| Parameter | Value |
|---|---|
| Track (Path) | 58 |
| Flight Direction | Ascending |
| Time Span | January 2021–April 2022 |
| Interferograms | ≈100 |
| Temporal Baselines | 6, 12, 18, 24 days |
| Processing Method | SBAS via ASF HyP3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, B.; Motagh, M.; Anvari, M.A.; Maghsudi, S. Improving Atmospheric Noise Correction from InSAR Time Series Using Variational Autoencoder with Clustering (VAE-Clustering) Method. Remote Sens. 2025, 17, 3189. https://doi.org/10.3390/rs17183189
Ghosh B, Motagh M, Anvari MA, Maghsudi S. Improving Atmospheric Noise Correction from InSAR Time Series Using Variational Autoencoder with Clustering (VAE-Clustering) Method. Remote Sensing. 2025; 17(18):3189. https://doi.org/10.3390/rs17183189
Chicago/Turabian StyleGhosh, Binayak, Mahdi Motagh, Mohammad Ali Anvari, and Setareh Maghsudi. 2025. "Improving Atmospheric Noise Correction from InSAR Time Series Using Variational Autoencoder with Clustering (VAE-Clustering) Method" Remote Sensing 17, no. 18: 3189. https://doi.org/10.3390/rs17183189
APA StyleGhosh, B., Motagh, M., Anvari, M. A., & Maghsudi, S. (2025). Improving Atmospheric Noise Correction from InSAR Time Series Using Variational Autoencoder with Clustering (VAE-Clustering) Method. Remote Sensing, 17(18), 3189. https://doi.org/10.3390/rs17183189







