Machine Learning-Constrained Semi-Analysis Model for Efficient Bathymetric Mapping in Data-Scarce Coastal Waters
Abstract
Highlights
- Substrate classification maps effectively constrain bottom reflectance albedo in the semi-analytical bathymetry inversion algorithm.
- The improved HOPE-PW achieves promising accuracy in Case I/II transitional waters with a 56% reduction in runtime and 68% lower memory usage.
- Provides an efficient, practical framework for bathymetric mapping in data-scarce coastal waters without relying on extensive in-situ measurements.
- Establishes a robust validation paradigm by extending ICESat-2 applications to anthropogenically impacted coastal zones with complex water types.
Abstract
1. Introduction
2. Materials and Methods
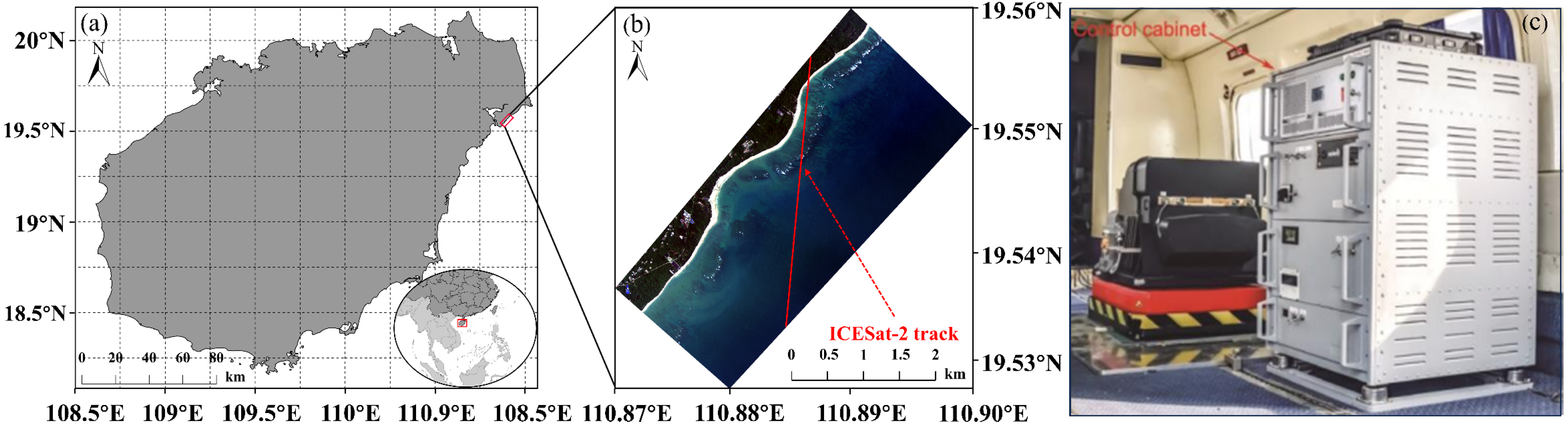
2.1. Areas of Study
2.2. Data
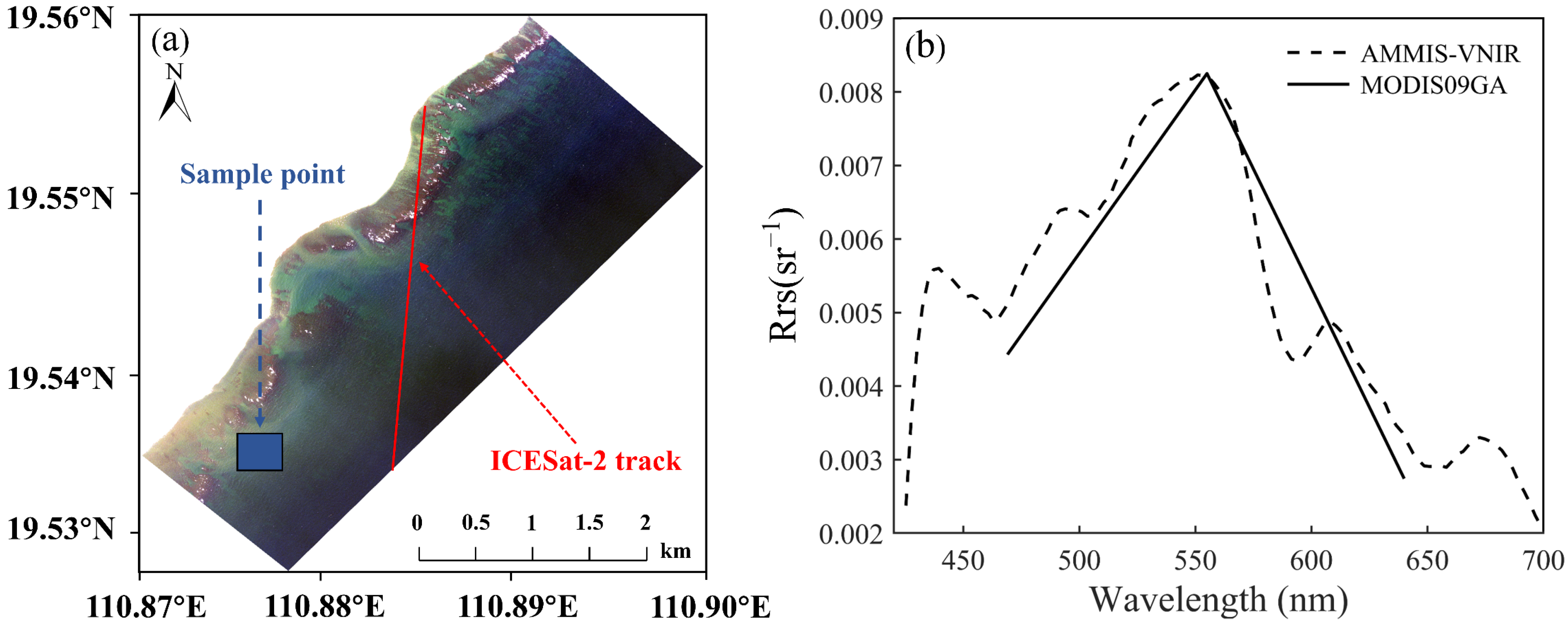
2.2.1. Hyperspectral Data
2.2.2. Satellite LiDAR Data
2.3. Methodology
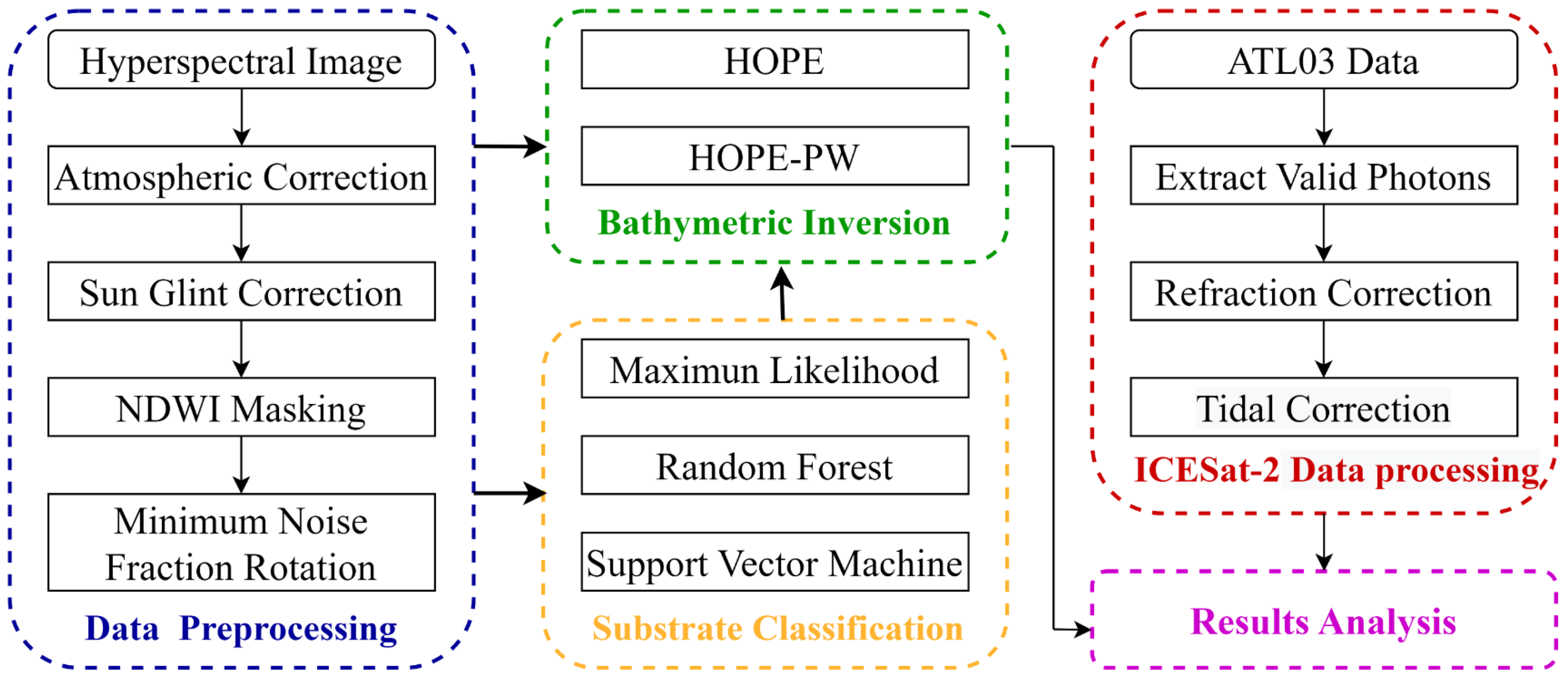
2.3.1. Data Processing
2.3.2. Machine Learning-Based Substrate Classification
2.3.3. Semi-Analytical Bathymetric Inversion Models
2.3.4. Evaluating the Accuracy of Results
3. Results
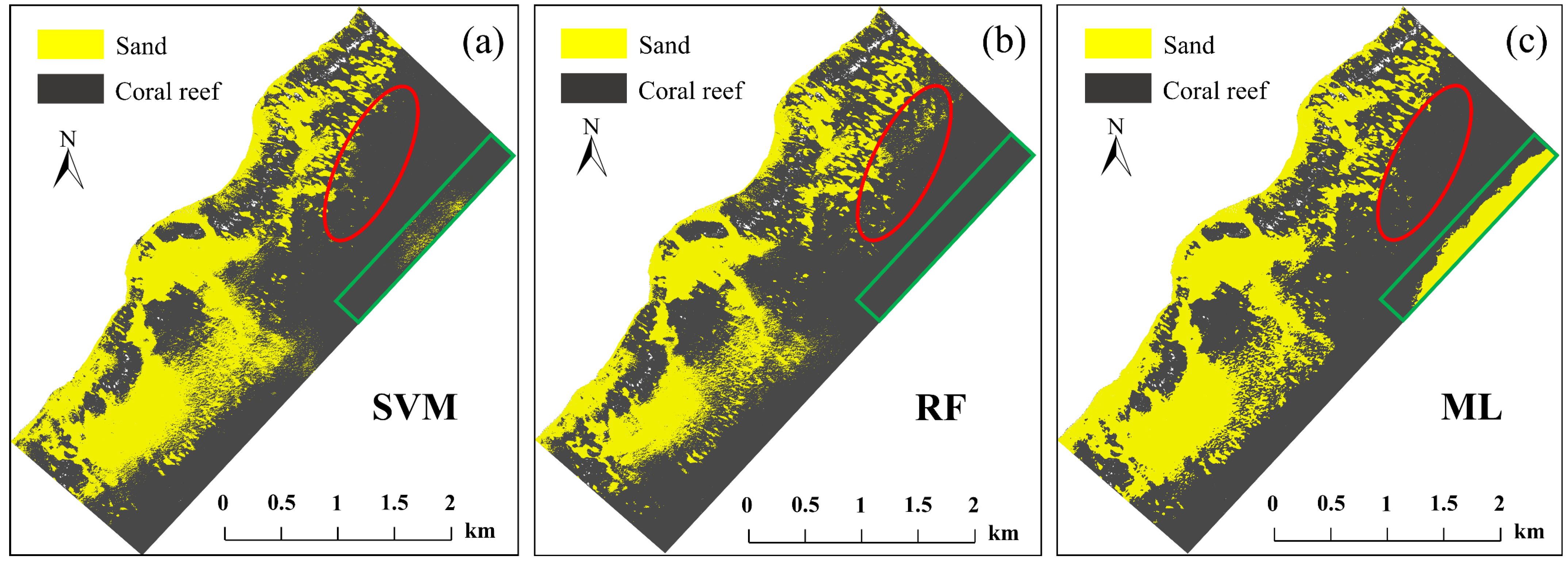
3.1. Substrate Classification Results
3.2. Bathymetric Inversion Results
3.3. Quantitative Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muir, P.R.; Wallace, C.C.; Done, T.; Aguirre, J.D. Limited Scope for Latitudinal Extension of Reef Corals. Science 2015, 348, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Ferrario, F.; Beck, M.W.; Storlazzi, C.D.; Micheli, F.; Shepard, C.C.; Airoldi, L. The Effectiveness of Coral Reefs for Coastal Hazard Risk Reduction and Adaptation. Nat. Commun. 2014, 5, 3794. [Google Scholar] [CrossRef]
- Sondak, C.F.A.; Ang, P.O.; Beardall, J.; Bellgrove, A.; Boo, S.M.; Gerung, G.S.; Hepburn, C.D.; Hong, D.D.; Hu, Z.; Kawai, H.; et al. Carbon Dioxide Mitigation Potential of Seaweed Aquaculture Beds (SABs). J. Appl. Phycol. 2017, 29, 2363–2373. [Google Scholar] [CrossRef]
- Roelfsema, C.; Kovacs, E.; Ortiz, J.C.; Wolff, N.H.; Callaghan, D.; Wettle, M.; Ronan, M.; Hamylton, S.M.; Mumby, P.J.; Phinn, S. Coral Reef Habitat Mapping: A Combination of Object-Based Image Analysis and Ecological Modelling. Remote Sens. Environ. 2018, 208, 27–41. [Google Scholar] [CrossRef]
- Lugendo, B.; Wegoro, J.; Shaghude, Y.; Pamba, S.; Makemie, M.; Hollander, J. Seagrass Mapping across the Coast of Tanzania. Ocean. Coast. Manag. 2024, 253, 107169. [Google Scholar] [CrossRef]
- Mederos-Barrera, A.; Marcello, J.; Eugenio, F.; Hernández, E. Seagrass Mapping Using High Resolution Multispectral Satellite Imagery: A Comparison of Water Column Correction Models. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 102990. [Google Scholar] [CrossRef]
- Qin, X.; Wu, Z.; Luo, X.; Shang, J.; Zhao, D.; Zhou, J.; Cui, J.; Wan, H.; Xu, G. MuSRFM: Multiple Scale Resolution Fusion Based Precise and Robust Satellite Derived Bathymetry Model for Island Nearshore Shallow Water Regions Using Sentinel-2 Multi-Spectral Imagery. ISPRS J. Photogramm. Remote Sens. 2024, 218, 150–169. [Google Scholar] [CrossRef]
- Tejaswi, A.; Sahoo, B.; Kale, R.V.; Murty, P.L.N.; Mohanty, A. A Method for Simulating Coastal Inundation and Inland Flooding by Integrating Inland Hydrology with Ocean Hydrodynamics. Nat. Hazards 2025, 121, 8827–8848. [Google Scholar] [CrossRef]
- Diruit, W.; Le Bris, A.; Bajjouk, T.; Richier, S.; Helias, M.; Burel, T.; Lennon, M.; Guyot, A.; Ar Gall, E. Seaweed Habitats on the Shore: Characterization through Hyperspectral UAV Imagery and Field Sampling. Remote Sens. 2022, 14, 3124. [Google Scholar] [CrossRef]
- Xu, N.; Wang, L.; Zhang, H.-S.; Tang, S.; Mo, F.; Ma, X. Machine Learning Based Estimation of Coastal Bathymetry From ICESat-2 and Sentinel-2 Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1748–1755. [Google Scholar] [CrossRef]
- Zuo, X.; Teng, J.; Su, F.; Duan, Z.; Yu, K. Multimodel Combination Bathymetry Inversion Approach Based on Geomorphic Segmentation in Coral Reef Habitats Using ICESat-2 and Multispectral Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 3267–3280. [Google Scholar] [CrossRef]
- Rende, S.F.; Bosman, A.; Di Mento, R.; Bruno, F.; Lagudi, A.; Irving, A.D.; Dattola, L.; Giambattista, L.D.; Lanera, P.; Proietti, R.; et al. Ultra-High-Resolution Mapping of Posidonia oceanica (L.) Delile Meadows through Acoustic, Optical Data and Object-Based Image Classification. J. Mar. Sci. Eng. 2020, 8, 647. [Google Scholar] [CrossRef]
- Zhong, J.; Sun, J.; Lai, Z. ICESat-2 and Multispectral Images Based Coral Reefs Geomorphic Zone Mapping Using a Deep Learning Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6085–6098. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Chen, R.F.; Peacock, T.G. Properties of the Water Column and Bottom Derived from Airborne Visible Infrared Imaging Spectrometer (AVIRIS) Data. J. Geophys. Res. 2001, 106, 11639–11651. [Google Scholar] [CrossRef]
- Valdazo, J.; Ferrer, N.; Vega, C.; Martín, J.; Luque, Á.; Bergasa, O. Mapping Marine Habitats in a Shallow Beach-Reef Environment Combining Direct Methods and Hyperspectral Remote Sensing. Ocean. Coast. Manag. 2024, 255, 107231. [Google Scholar] [CrossRef]
- Wu, Z.; Tao, B.; Mao, Z.; Huang, H. Bathymetry Retrieval Algorithm Based on Hyperspectral Features of Pure Water Absorption From 570 to 600 Nm. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503219. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters: 2 Deriving Bottom Depths and Water Properties by Optimization. Appl. Opt. 1999, 38, 3831. [Google Scholar] [CrossRef]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of Near-Shore Satellite Derived Bathymetry: Classification and Account of Five Decades of Coastal Bathymetry Research. J. Ocean Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, Y.; Wu, S.; Chen, H.; Song, C.; Mao, Z.; Shen, W. Satellite-Derived Bathymetry Using a Fast Feature Cascade Learning Model in Turbid Coastal Waters. J. Remote Sens. 2024, 4, 0272. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote Sensing of Bottom Reflectance and Water Attenuation Parameters in Shallow Water Using Aircraft and Landsat Data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of Water Depth with High-resolution Satellite Imagery over Variable Bottom Types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the Use of Sentinel-2 for Coastal Habitat Mapping and Satellite-Derived Bathymetry Estimation Using Downscaled Coastal Aerosol Band. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters. I. A Semianalytical Model. Appl. Opt. 1998, 37, 6329. [Google Scholar] [CrossRef]
- Klonowski, W.M. Retrieving Key Benthic Cover Types and Bathymetry from Hyperspectral Imagery. J. Appl. Remote Sens. 2007, 1, 011505. [Google Scholar] [CrossRef]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A Physics Based Retrieval and Quality Assessment of Bathymetry from Suboptimal Hyperspectral Data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Jay, S.; Guillaume, M.; Minghelli, A.; Deville, Y.; Chami, M.; Lafrance, B.; Serfaty, V. Hyperspectral Remote Sensing of Shallow Waters: Considering Environmental Noise and Bottom Intra-Class Variability for Modeling and Inversion of Water Reflectance. Remote Sens. Environ. 2017, 200, 352–367. [Google Scholar] [CrossRef]
- Petit, T.; Bajjouk, T.; Mouquet, P.; Rochette, S.; Vozel, B.; Delacourt, C. Hyperspectral Remote Sensing of Coral Reefs by Semi-Analytical Model Inversion—Comparison of Different Inversion Setups. Remote Sens. Environ. 2017, 190, 348–365. [Google Scholar] [CrossRef]
- Garcia, R.A.; Lee, Z.; Hochberg, E.J. Hyperspectral Shallow—Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sens. 2018, 10, 147. [Google Scholar] [CrossRef]
- Lee, Z.; Weidemann, A.; Arnone, R. Combined Effect of Reduced Band Number and Increased Bandwidth on Shallow Water Remote Sensing: The Case of WorldView 2. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2577–2586. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, R.; Qin, Y.; Cao, B.; Liang, Y.; Liu, Y.; Tian, J.; Wang, S. Rapid Estimation of Bathymetry from Multispectral Imagery without in Situ Bathymetry Data. Appl. Opt. 2019, 58, 7538. [Google Scholar] [CrossRef]
- Xia, H.; Li, X.; Zhang, H.; Wang, J.; Lou, X.; Fan, K.; Shi, A.; Li, D. A Bathymetry Mapping Approach Combining Log-Ratio and Semianalytical Models Using Four-Band Multispectral Imagery Without Ground Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2695–2709. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Paavel, B.; Kutser, T. How Much Benthic Information Can Be Retrieved with Hyperspectral Sensor from the Optically Complex Coastal Waters? J. Appl. Rem. Sens. 2020, 14, 016504. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of Shallow Water Bathymetry, Hydro-optics, and Benthos Mapping Techniques in Australian and Caribbean Coastal Environments. Limnol. Ocean. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Chen, Y.; Le, Y.; Zhang, D.; Wang, Y.; Qiu, Z.; Wang, L. A Photon-Counting LiDAR Bathymetric Method Based on Adaptive Variable Ellipse Filtering. Remote Sens. Environ. 2021, 256, 112326. [Google Scholar] [CrossRef]
- Sun, S.; Chen, Y.; Mu, L.; Le, Y.; Zhao, H. Improving Shallow Water Bathymetry Inversion through Nonlinear Transformation and Deep Convolutional Neural Networks. Remote Sens. 2023, 15, 4247. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-Derived Bathymetry Using the ICESat-2 Lidar and Sentinel-2 Imagery Datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Zhang, S.; Huang, H. Nearshore Bathymetry from ICESat-2 LiDAR and Sentinel-2 Imagery Datasets Using Physics-Informed CNN. Remote Sens. 2024, 16, 511. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Lang, S.; Chen, S.; Wu, Z.; Wang, D. Ecological Status and Degradation Factors in Seagrass Meadows along the Coast of Wenchang, Hainan. J. Appl. Oceanogr. 2022, 4, 614–624. [Google Scholar] [CrossRef]
- Jia, J.; Wang, Y.; Zheng, X.; Yuan, L.; Li, C.; Cen, Y.; Si, F.; Lv, G.; Wang, C.; Wang, S.; et al. Design, Performance, and Applications of AMMIS: A Novel Airborne Multimodular Imaging Spectrometer for High-Resolution Earth Observations. Engineering 2025, 47, 38–56. [Google Scholar] [CrossRef]
- Xi, L.; Si, F.; Jiang, Y.; Zhou, H.; Zhan, K.; Chang, Z.; Qiu, X.; Yang, D. First High-Resolution Tropospheric NO2 Observations from the Ultraviolet Visible Hyperspectral Imaging Spectrometer (UVHIS). Atmos. Meas. Technol. 2021, 14, 435–454. [Google Scholar] [CrossRef]
- Liu, C.; Xu, R.; Xie, F.; Jin, J.; Yuan, L.; Lv, G.; Wang, Y.; Li, C.; Wang, J. New Airborne Thermal-Infrared Hyperspectral Imager System: Initial Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4149–4165. [Google Scholar] [CrossRef]
- Niu, C.; Tan, K.; Wang, X.; Du, P.; Pan, C. A Semi-Analytical Approach for Estimating Inland Water Inherent Optical Properties and Chlorophyll a Using Airborne Hyperspectral Imagery. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103774. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Parrish, C.; Magruder, L.; Neuenschwander, A.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Kotta, J.; Lõugas, L.; Kutser, T. Mapping Spatial Distribution, Percent Cover and Biomass of Benthic Vegetation in Optically Complex Coastal Waters Using Hyperspectral CASI and Multispectral Sentinel-2 Sensors. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102444. [Google Scholar] [CrossRef]
- Le Quilleuc, A.; Collin, A.; Jasinski, M.F.; Devillers, R. Very High-Resolution Satellite-Derived Bathymetry and Habitat Mapping Using Pleiades-1 and ICESat-2. Remote Sens. 2021, 14, 133. [Google Scholar] [CrossRef]
- Widya, L.K.; Kim, C.-H.; Do, J.-D.; Park, S.-J.; Kim, B.-C.; Lee, C.-W. Comparison of Satellite Imagery for Identifying Seagrass Distribution Using a Machine Learning Algorithm on the Eastern Coast of South Korea. J. Mar. Sci. Eng. 2023, 11, 701. [Google Scholar] [CrossRef]
- Wilson, K.L.; Wong, M.C.; Devred, E. Comparing Sentinel-2 and WorldView-3 Imagery for Coastal Bottom Habitat Mapping in Atlantic Canada. Remote Sens. 2022, 14, 1254. [Google Scholar] [CrossRef]
- Kutser, T.; Vahtmäe, E.; Praks, J. A Sun Glint Correction Method for Hyperspectral Imagery Containing Areas with Non-Negligible Water Leaving NIR Signal. Remote Sens. Environ. 2009, 113, 2267–2274. [Google Scholar] [CrossRef]
- Wicaksono, P.; Aryaguna, P.A.; Lazuardi, W. Benthic Habitat Mapping Model and Cross Validation Using Machine-Learning Classification Algorithms. Remote Sens. 2019, 11, 1279. [Google Scholar] [CrossRef]
- Bakirman, T.; Gumusay, M.U. Assessment of Machine Learning Methods for Seagrass Classification in the Mediterranean. Balt. J. Mod. Comput. 2020, 8, 315–326. [Google Scholar] [CrossRef]
- Marcello, J.; Eugenio, F.; Gonzalo-Martin, C.; Rodriguez-Esparragon, D.; Marques, F. Advanced Processing of Multiplatform Remote Sensing Imagery for the Monitoring of Coastal and Mountain Ecosystems. IEEE Access 2021, 9, 6536–6549. [Google Scholar] [CrossRef]
- Hafizt, M.; Yuwono, D.M.; Janwar, Z.; Suyarso; Wouthuyzen, S. Benthic Habitat Mapping for Estimating Seagrass Carbon Stock across Takabonerate Islands, Indonesia. Reg. Stud. Mar. Sci. 2024, 77, 103703. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical Properties of the Clearest Natural Waters (200–800 Nm). Appl. Opt. 1981, 20, 177. [Google Scholar] [CrossRef]



| Authors | Platform | Classifier | Max Depth |
|---|---|---|---|
| Poursanidis et al. (2019) [22] | Sentinel-2 | SVM, RF | 30 m |
| Wicaksono et al. (2019) [50] | WorldView-2 | RF, DT, SVM | 7 m |
| Vahtmäe et al. (2020) [32] | CASI-2 | MD, ML, SAM | 7.6 m |
| Bakirman et al. (2020) [51] | WorldView-2 | RF, SVM | 20 m |
| Rende et al. (2020) [12] | Pleiades-1 | KNN, RT, DT | 10 m |
| Marcello et al. (2021) [52] | Sentinel-2, Pika-L, WorldView-2 | ML, SVM, SAM | 20 m |
| Vahtmäe et al. (2021) [45] | CASI-2, Sentinel-2 | MD | 3 m |
| Le Quilleuc et al. (2021) [46] | Pleiades-1 | ANN, ML, SVM | 15 m |
| Diruit et al. (2022) [9] | HySpex | ML, SAM | 9 m |
| Mederos-Barrera et al. (2022) [6] | WorldView-2, WorldView-3 | GNB, SVM, KNN | 35 m |
| Wilson et al. (2022) [48] | Sentinel-2, WorldView-3 | RF | / |
| Widya et al. (2023) [47] | Geoeye-1, Sentinel-2, Landsat-8 | SVM | 10 m |
| Valdazo et al. (2024) [15] | Pika-L | ML | 1.5 m |
| Hafizt et al. (2024) [53] | Sentinel-2 | ANN | / |
| Lugendo et al. (2024) [5] | Sentinel-2 | RF, SVM, ANN | 25 m |
| Parameters | HOPE | HOPE-PW |
|---|---|---|
| Wavelength | 400–675 and 750–800 nm | 570–600 nm |
| Optimization | ||
| HOPE | HOPE-PW | |||
|---|---|---|---|---|
| Parameter | Initial Value | (Min, Max) | Initial Value | (Min, Max) |
| (0, 1) | (0, 0.01) | |||
| (0, 1) | ||||
| (0, 0.2) | 0 | (0, 0.05) | ||
| 0.6 | (0, 1) | 0.6 | (0, 1) | |
| 3 | (0, 20) | 3 | (0, 20) | |
| ) | (0, 1) | |||
| (0, 2) | ||||
| Classifier | Overall Accuracy | Kappa Coefficient |
|---|---|---|
| SVM | 91.49% | 0.89 |
| RF | 96.76% | 0.93 |
| ML | 86.47% | 0.83 |
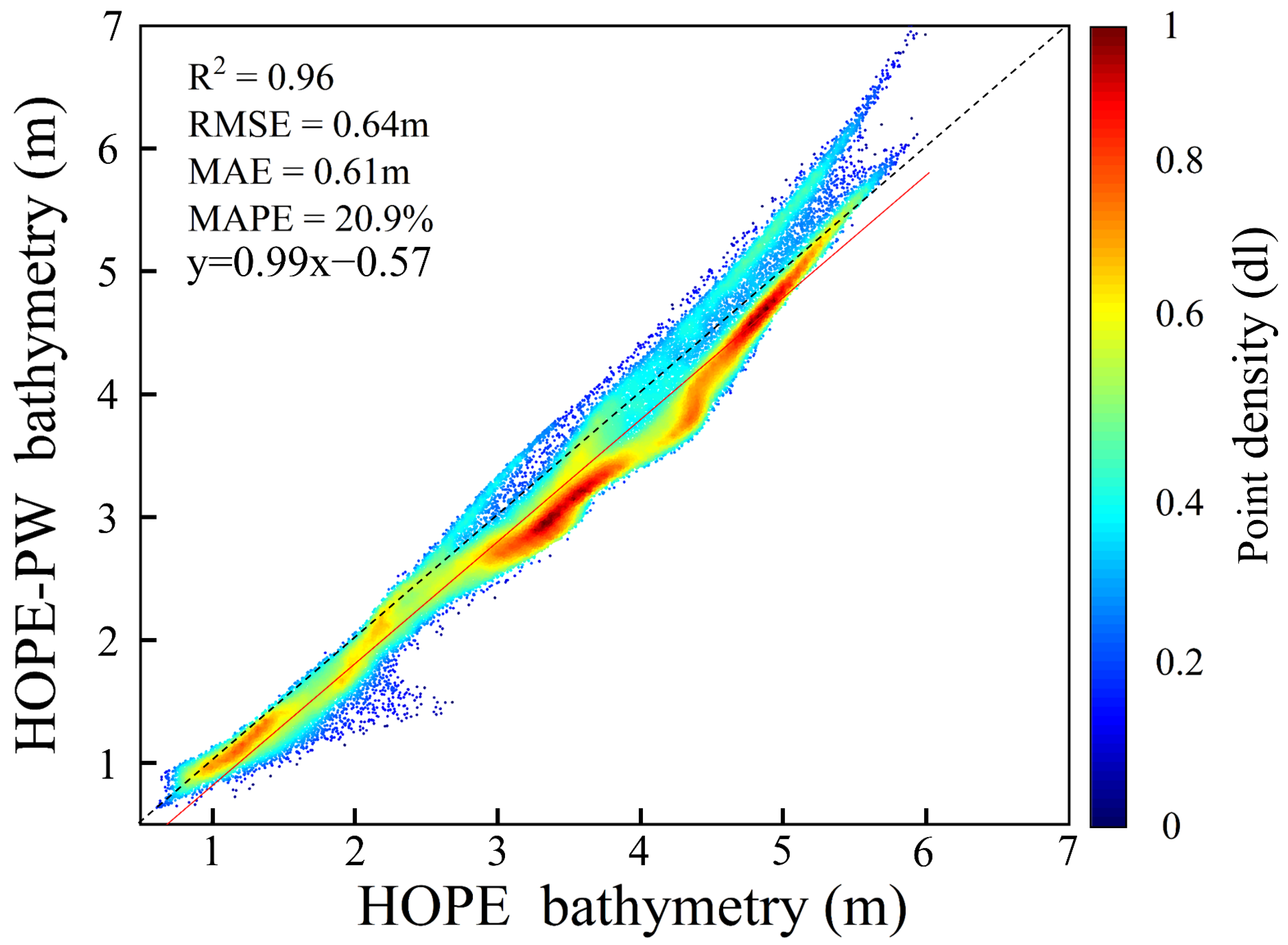
| Metrics | HOPE | HOPE-PW |
|---|---|---|
| R2 | 0.53 | 0.47 |
| RMSE (m) | 0.38 | 0.48 |
| MAE (m) | 0.30 | 0.32 |
| MAPE (%) | 19.8 | 21.1 |
| Throughput (pixel·s−1) | 0.09359 | 0.04085 |
| Resident Set Size (GB) | 16.24 | 5.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, X.; Wu, Z.; Han, C.; Zhang, L.; Xu, P.; Mao, Z.; Wang, Y.; Zhang, C. Machine Learning-Constrained Semi-Analysis Model for Efficient Bathymetric Mapping in Data-Scarce Coastal Waters. Remote Sens. 2025, 17, 3179. https://doi.org/10.3390/rs17183179
Wang Q, Zhang X, Wu Z, Han C, Zhang L, Xu P, Mao Z, Wang Y, Zhang C. Machine Learning-Constrained Semi-Analysis Model for Efficient Bathymetric Mapping in Data-Scarce Coastal Waters. Remote Sensing. 2025; 17(18):3179. https://doi.org/10.3390/rs17183179
Chicago/Turabian StyleWang, Qifei, Xianliang Zhang, Zhongqiang Wu, Chang Han, Longwei Zhang, Pinyan Xu, Zhihua Mao, Yueming Wang, and Changxing Zhang. 2025. "Machine Learning-Constrained Semi-Analysis Model for Efficient Bathymetric Mapping in Data-Scarce Coastal Waters" Remote Sensing 17, no. 18: 3179. https://doi.org/10.3390/rs17183179
APA StyleWang, Q., Zhang, X., Wu, Z., Han, C., Zhang, L., Xu, P., Mao, Z., Wang, Y., & Zhang, C. (2025). Machine Learning-Constrained Semi-Analysis Model for Efficient Bathymetric Mapping in Data-Scarce Coastal Waters. Remote Sensing, 17(18), 3179. https://doi.org/10.3390/rs17183179







