Elevation-Dependent Trends in Himalayan Snow Cover (2004–2024) Based on MODIS Terra Observations
Abstract
1. Introduction
2. Materials and Methods
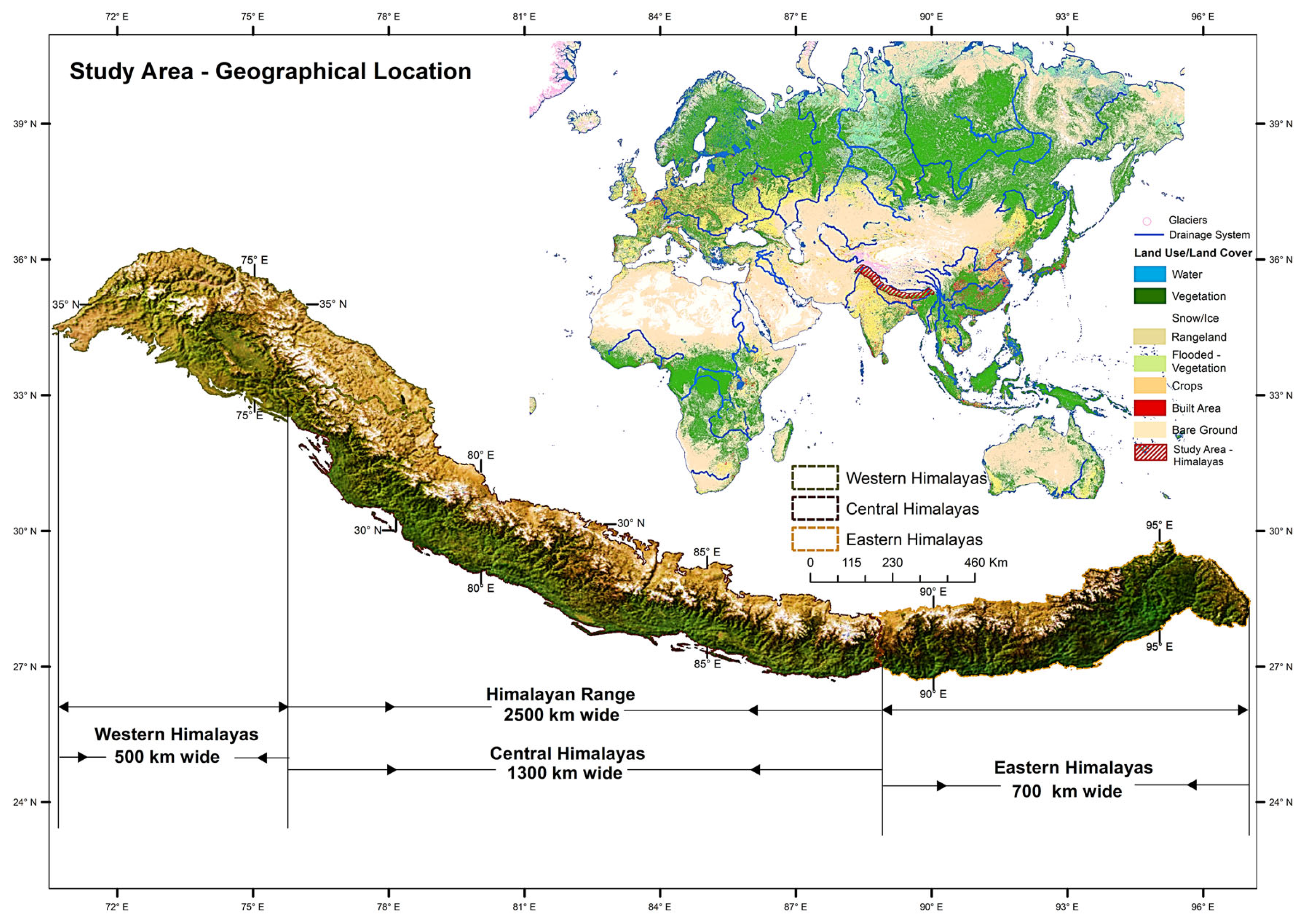
2.1. Study Area
2.2. Datasets
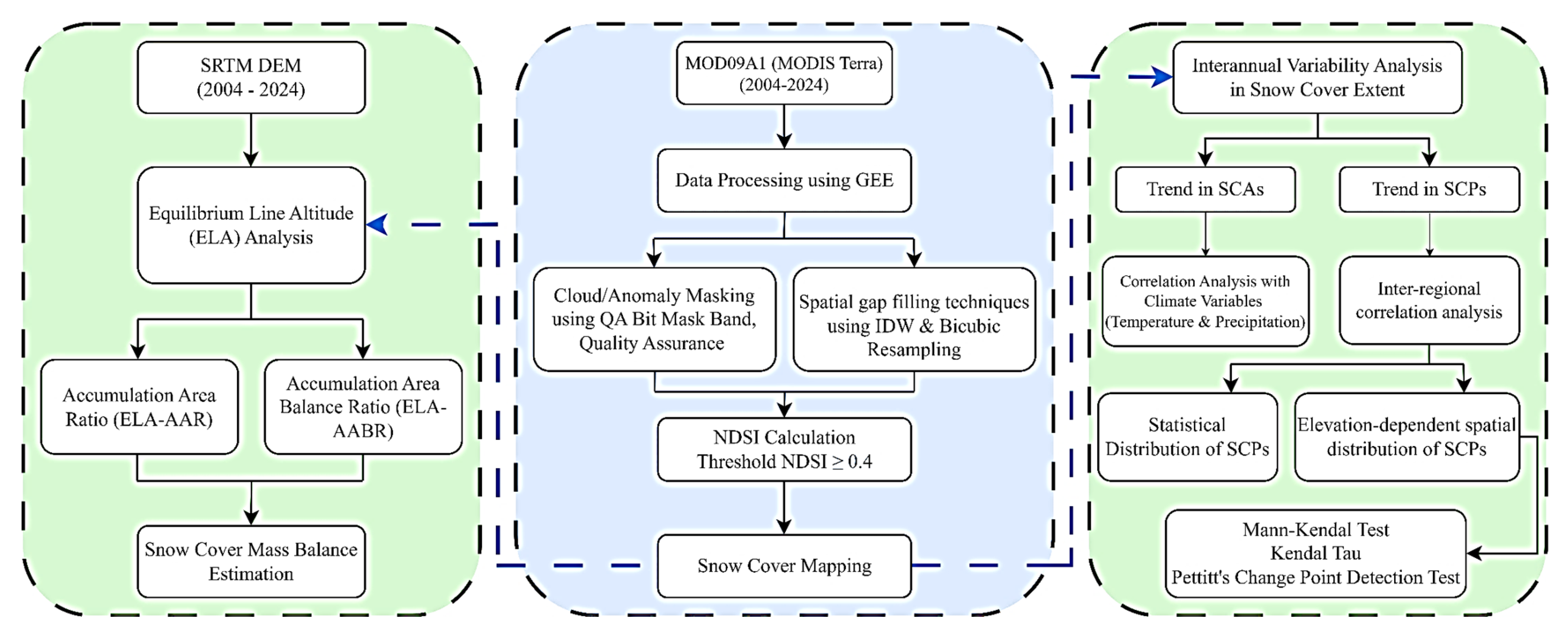
2.3. Methodology
2.3.1. Data Preprocessing
2.3.2. Snow Cover Pixels Detection
2.3.3. SCPs Variability Analysis
- (i)
- Mann–Kendall (MK) Test
- (ii)
- Kendall’s τ
- (iii)
- Pettitt’s Test (for change point detection)
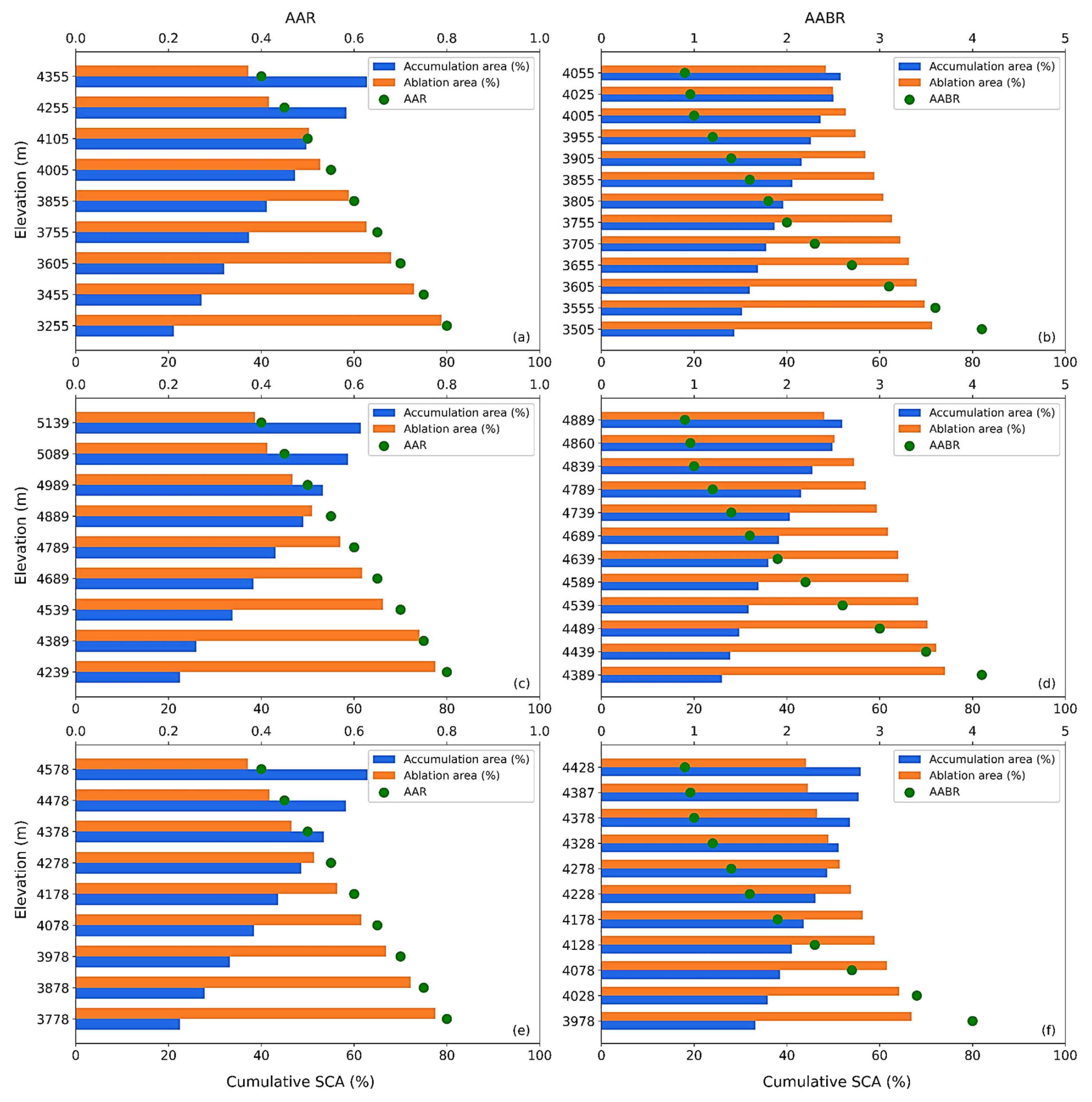
2.3.4. Snow Mass Balance Estimation Using ELA-Based AAR and AABR Methods
2.3.5. Model Performance Evaluation
- ▪
- True Positives (TP): snow pixels correctly classified as snow;
- ▪
- False Positives (FP): non-snow pixels incorrectly classified as snow;
- ▪
- False Negatives (FN): snow pixels missed by the classifier; and
- ▪
- True Negatives (TN): non-snow pixels correctly classified as non-snow.
3. Results
3.1. Snow Cover Validation
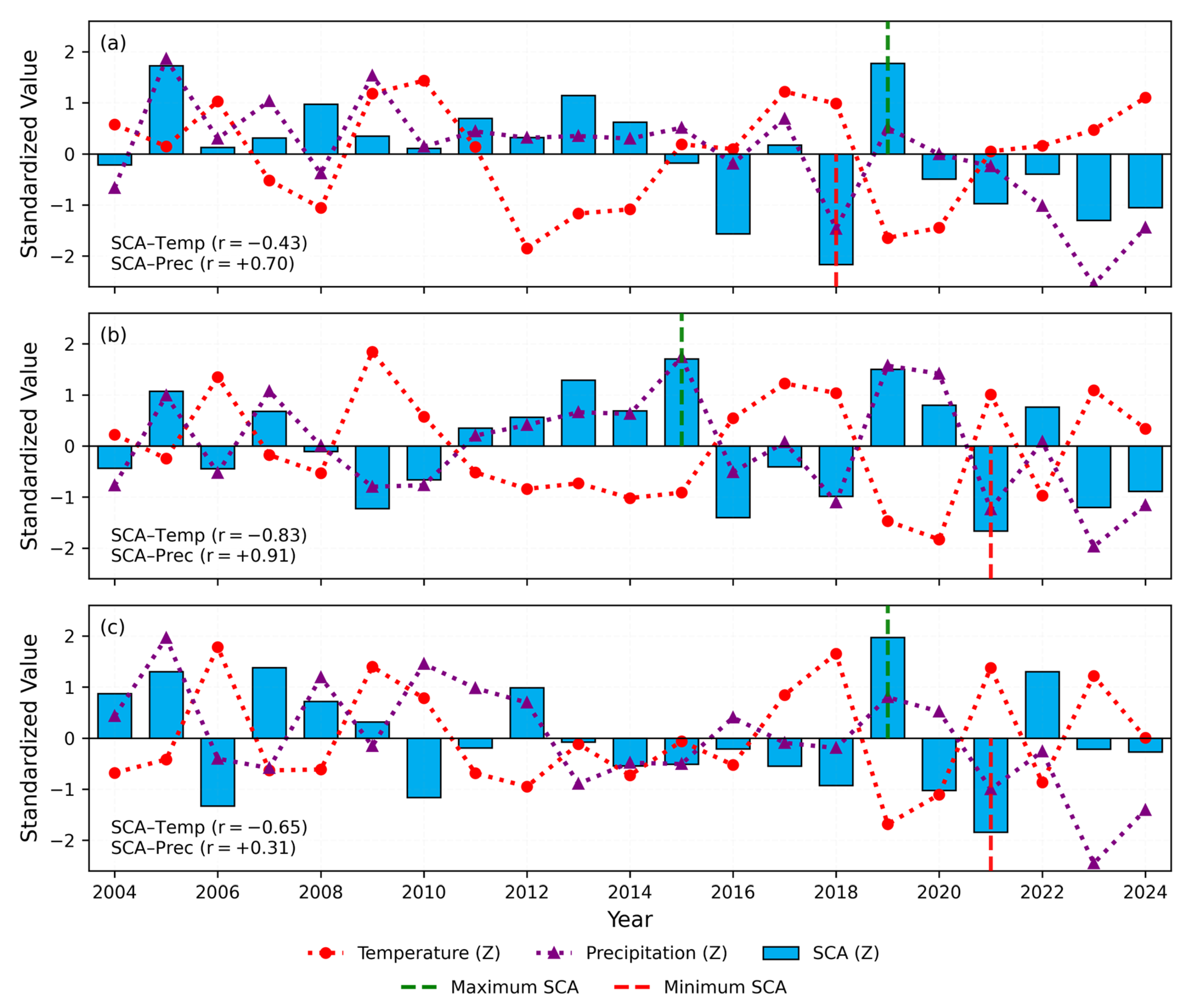
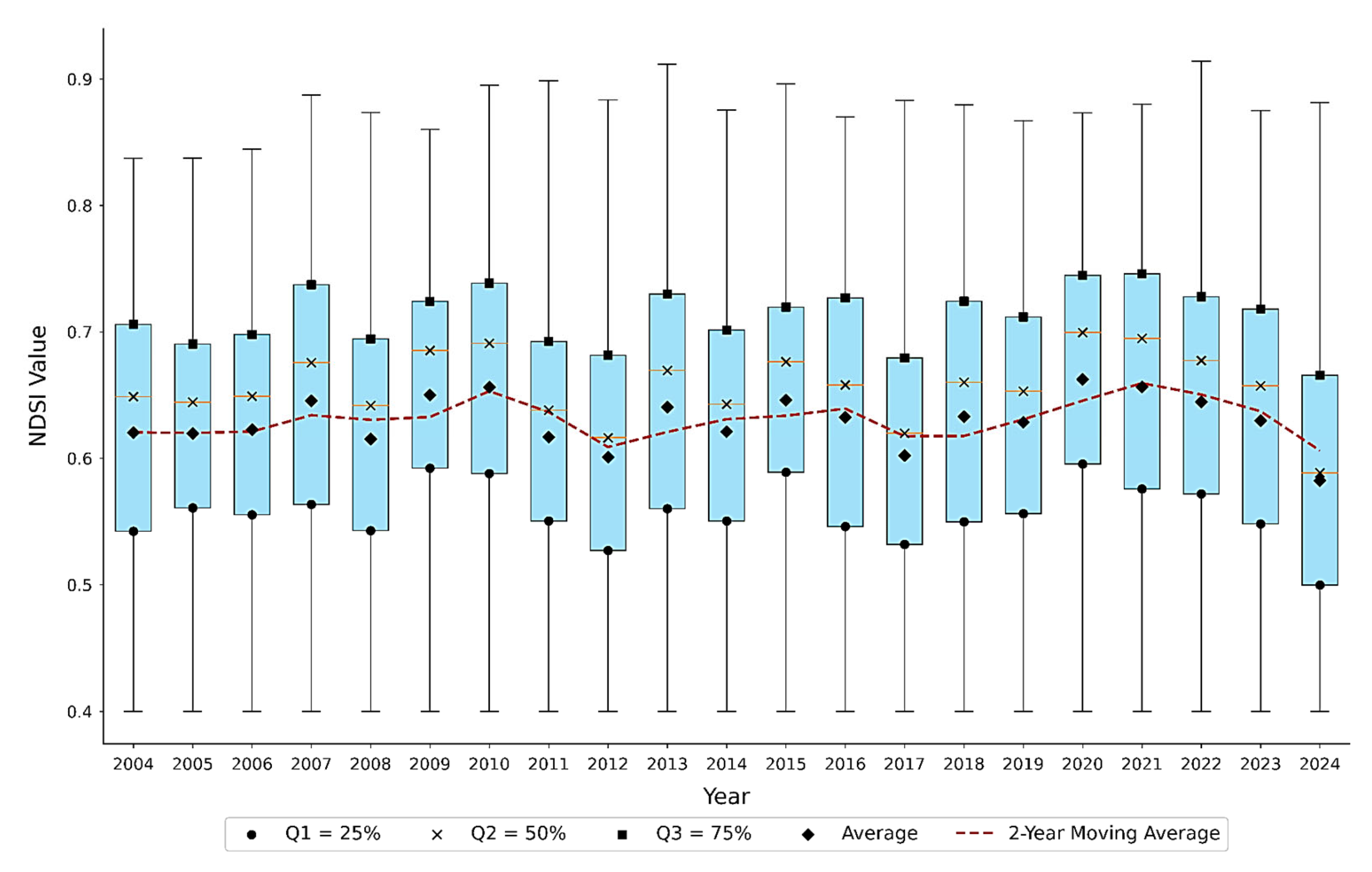
3.2. Interannual Variability in SCAs
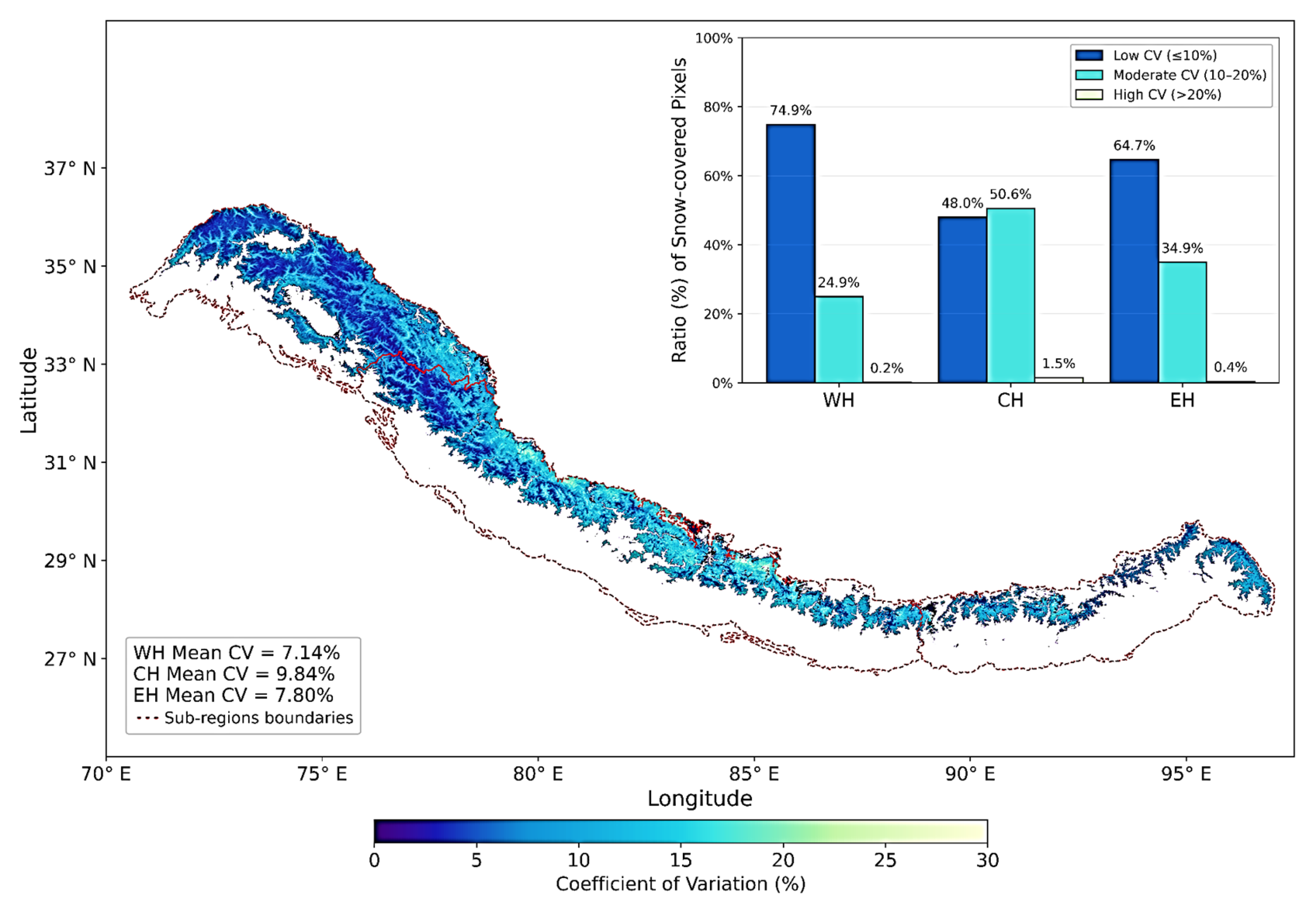
3.3. Temporal Variability of Snow Cover at Pixel Scale
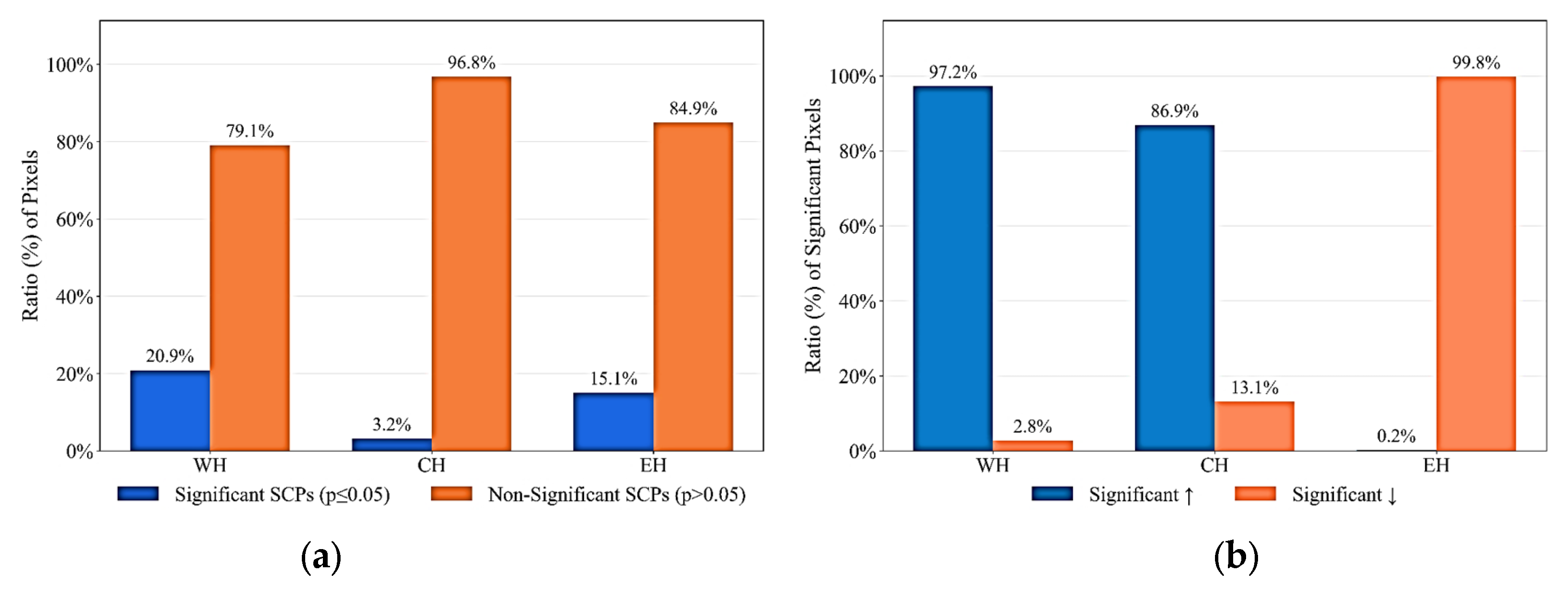
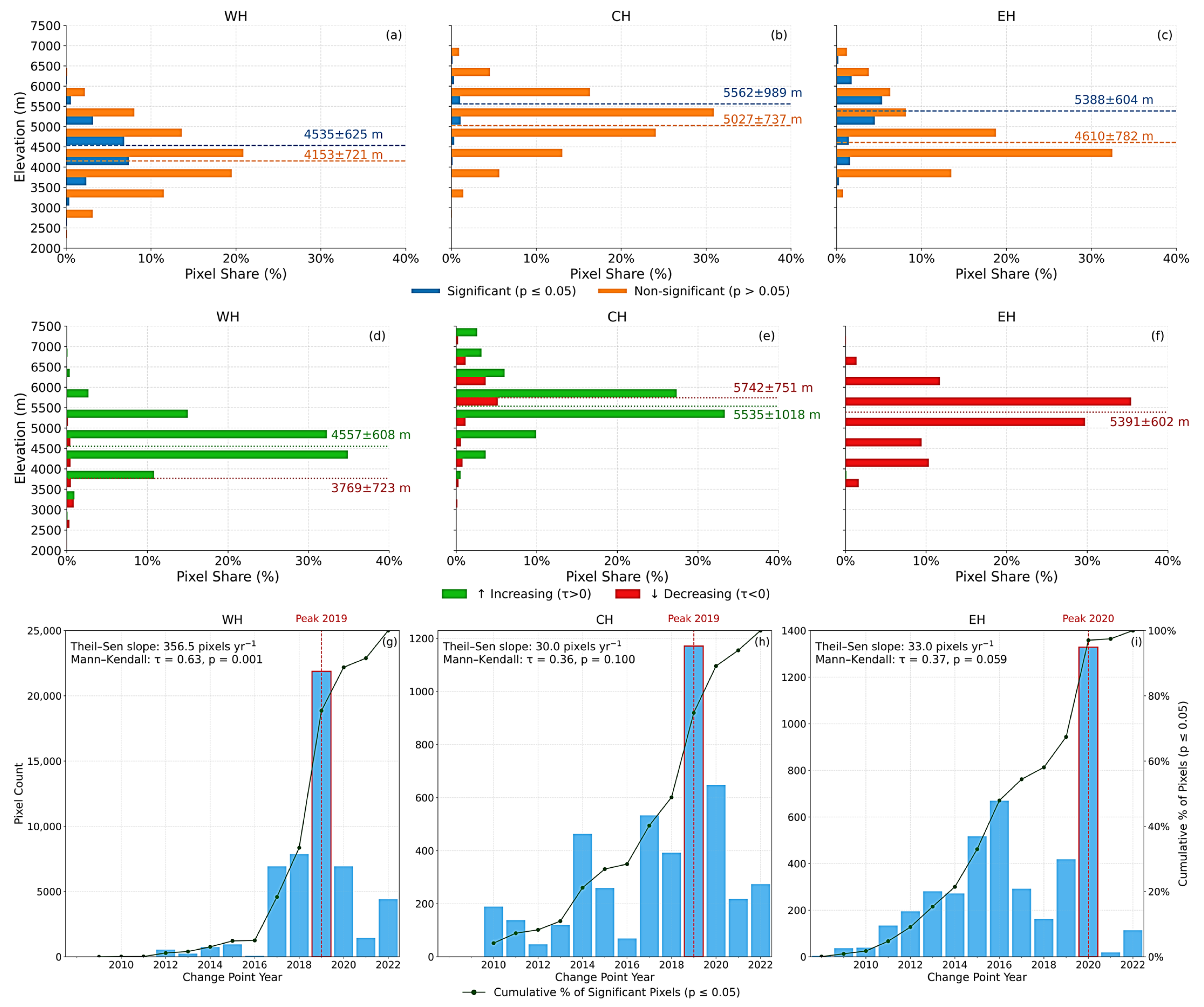
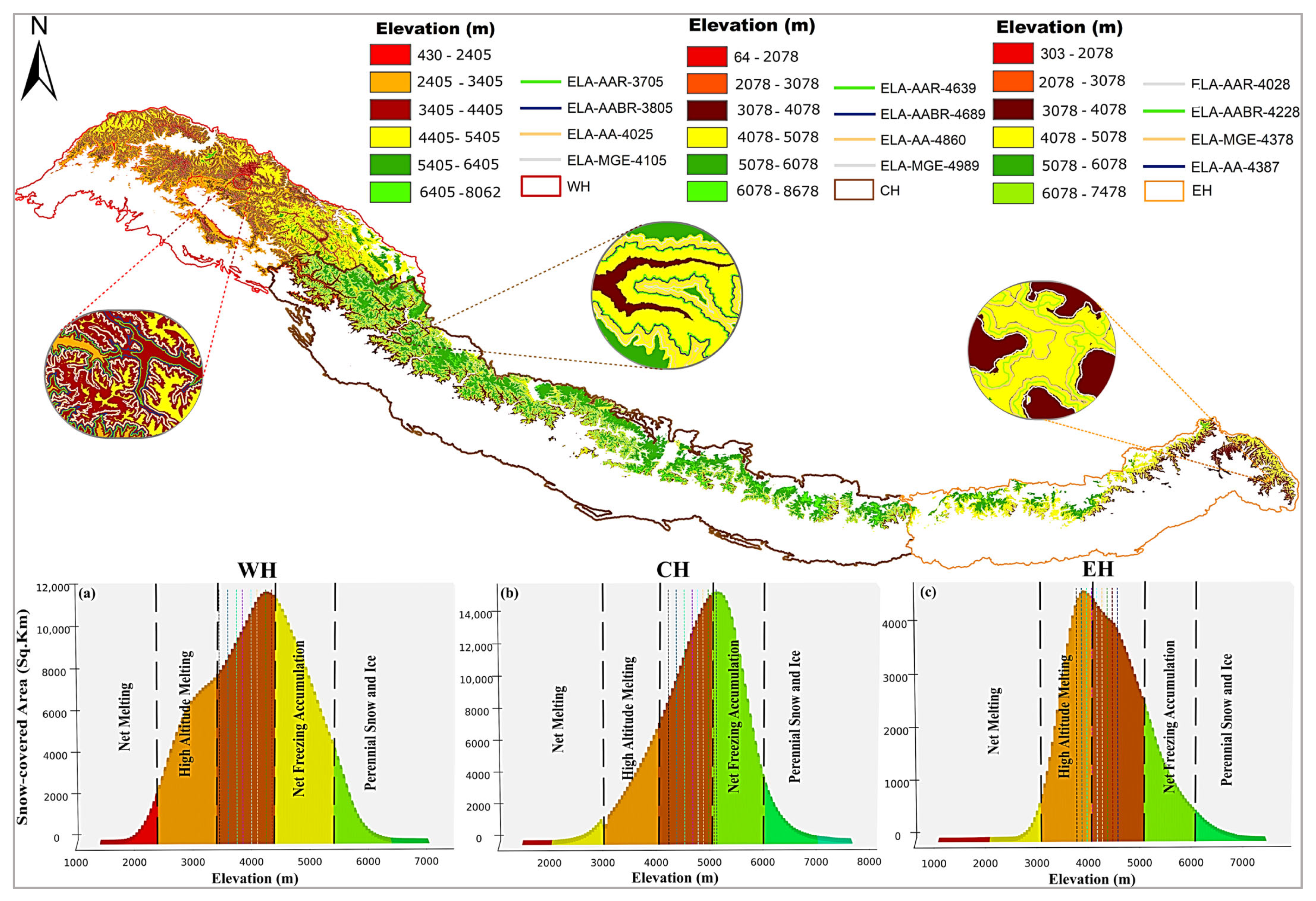
3.4. Elevation-Dependent Spatial Distribution of the SCPs Across the Himalayas
3.5. Snow Cover Mass Balance Estimation Based on AAR and AABR
4. Discussion
4.1. Variations in Snow Cover Trends Across Different Regions of the Himalayas
4.2. Climatic Influences and Spatial Variability
4.3. Snow Mass Balance and ELA
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AA | Area-Altitude |
| AABR | Accumulation-Area Balance Ratio |
| AAR | Accumulation Area Ratio |
| CGF | Cloud-gap-filled |
| CH | Central Himalayas |
| DJFM | December, January, February, March |
| EDW | Elevation-dependent warming |
| EH | Eastern Himalayas |
| ELA | Equilibrium Line Altitude |
| FN | False Negatives |
| FP | False Positives |
| GEE | Google Earth Engine |
| HMA | High Mountain Asia |
| IDW | Inverse Distance Weighting |
| IQRs | Interquartile ranges |
| ISM | Indian Summer Monsoon |
| MGE | Median Glacier Elevation |
| MK | Mann-Kendall test |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MR | Misclassification rate |
| Ka | Kappa statistic |
| CV | Coefficient of Variation |
| NDSI | Normalized Difference Snow Index |
| OA | Overall Accuracy |
| QA | Quality Assurance |
| SCA | Snow-covered Area |
| SCE | Snow cover extent |
| SCPs | Snow-covered Pixels |
| SRTM | Shuttle Radar Topography Mission |
| TN | True Negatives (TN) |
| TP | True Positives |
| WDs | Western Disturbances |
| WH | Western Himalayas |
References
- Immerzeel, W.W.; van Beek, L.P.H.; Konz, M.; Shrestha, A.B.; Bierkens, M.F.P. Hydrological response to climate change in a glacierized catchment in the Himalayas. Clim. Change 2012, 110, 721–736. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. Earth Surf. 2010, 115, F03019. [Google Scholar] [CrossRef]
- Hock, R.; Rasul, G.; Adler, C.; Cáceres, B.; Gruber, S.; Hirabayashi, Y.; Jackson, M.; Kääb, A.; Kang, S.; Kutuzov, S. High mountain areas. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; IPCC: Geneva, Switzerland, 2019; pp. 131–202. [Google Scholar]
- Xiao, L.; Che, T.; Chen, L.; Xie, H.; Dai, L. Quantifying snow albedo radiative forcing and its feedback during 2003–2016. Remote Sens. 2017, 9, 883. [Google Scholar] [CrossRef]
- Li, Y.; Tao, H.; Su, B.; Kundzewicz, Z.W.; Jiang, T. Impacts of 1.5 °C and 2 °C global warming on winter snow depth in Central Asia. Sci. Total Environ. 2019, 651, 2866–2873. [Google Scholar]
- Sankey, T.; Donald, J.; McVay, J.; Ashley, M.; O’Donnell, F.; Lopez, S.M.; Springer, A. Multi-scale analysis of snow dynamics at the southern margin of the North American continental snow distribution. Remote Sens. Environ. 2015, 169, 307–319. [Google Scholar] [CrossRef]
- Banerjee, A.; Chen, R.; Meadows, M.E.; Sengupta, D.; Pathak, S.; Xia, Z.; Mal, S. Tracking 21st century climate dynamics of the Third Pole: An analysis of topo-climate impacts on snow cover in the central Himalaya using Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102490. [Google Scholar]
- Frei, A.; Robinson, D.A. Northern Hemisphere snow extent: Regional variability 1972–1994. Int. J. Climatol. 1999, 19, 1535–1560. [Google Scholar] [CrossRef]
- Joshi, R.; Tamang, N.D.; Balraju, W.; Singh, S.P. Spatial and seasonal patterns of temperature lapse rate along elevation transects leading to treelines in different climate regimes of the Himalaya. Biodivers. Conserv. 2024, 33, 3517–3538. [Google Scholar] [CrossRef]
- Kattel, D.B.; Yao, T.; Yang, K.; Tian, L.; Yang, G.; Joswiak, D. Temperature lapse rate in complex mountain terrain on the southern slope of the central Himalayas. Theor. Appl. Climatol. 2013, 113, 671–682. [Google Scholar] [CrossRef]
- Sabin, T.P.; Krishnan, R.; Vellore, R.; Priya, P.; Borgaonkar, H.P.; Singh, B.B.; Sagar, A. Climate Change Over the Himalayas. In Assessment of Climate Change over the Indian Region: A Report of the Ministry of Earth Sciences (MoES), Government of India; Krishnan, R., Sanjay, J., Gnanaseelan, C., Mujumdar, M., Kulkarni, A., Chakraborty, S., Eds.; Springer: Singapore, 2020; pp. 207–222. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, Y.; Ullah, S.; Pepin, N.; Ma, Q. Changes in snow depth under elevation-dependent warming over the Tibetan Plateau. Atmos. Sci. Lett. 2021, 22, e1041. [Google Scholar] [CrossRef]
- Wester, P.; Chaudhary, S.; Maharjan, A.; Steiner, J.F.; Chettri, N.; Chettri, R.; Jackson, M.; Nepal, S.; Wang, X. Water, Ice, Society, and Ecosystems in the Hindu Kush Himalaya: An Introduction; International Centre for Integrated Mountain Development (ICIMOD): Khumaltar, Nepal, 2023; pp. 1–15. [Google Scholar]
- Mukhtar, H.; Yang, Y.; Xu, M.; Wu, J.; Abbas, S.; Wei, D.; Zhao, W. Elevation-Dependent Vegetation Greening and Its Responses to Climate Changes in the South Slope of the Himalayas. Geophys. Res. Lett. 2025, 52, e2024GL113276. [Google Scholar] [CrossRef]
- Notarnicola, C. Overall negative trends for snow cover extent and duration in global mountain regions over 1982–2020. Sci. Rep. 2022, 12, 13731. [Google Scholar] [CrossRef]
- Fugazza, D.; Manara, V.; Senese, A.; Diolaiuti, G.; Maugeri, M. Snow cover variability in the greater alpine region in the MODIS era (2000–2019). Remote Sens. 2021, 13, 2945. [Google Scholar] [CrossRef]
- Rohrer, M.; Salzmann, N.; Kulkarni, A. Missing (in-situ) snow cover data hampers climate change and runoff studies in the Greater Himalayas. Sci. Total Environ. 2013, 468, S60–S70. [Google Scholar] [CrossRef] [PubMed]
- Lievens, H.; Demuzere, M.; Marshall, H.P.; Reichle, R.H.; Brucker, L.; Brangers, I.; de Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow depth variability in the Northern Hemisphere mountains observed from space. Nat. Commun. 2019, 10, 4629. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zeng, J.; Li, Z.; Letu, H.; Zhang, P.; Huang, L.; Qiao, H.; Chen, Q. Measuring global snow water equivalent from passive microwave remote sensing: Opportunities and challenges. Innov. Geosci. 2024, 2, 100062. [Google Scholar] [CrossRef]
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. Global snow zone maps and trends in snow persistence 2001–2016. Int. J. Climatol. 2018, 38, 4369–4383. [Google Scholar] [CrossRef]
- Notarnicola, C. Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 2020, 243, 111781. [Google Scholar] [CrossRef]
- Huang, Y.; Song, Z.; Yang, H.; Yu, B.; Liu, H.; Che, T.; Chen, J.; Wu, J.; Shu, S.; Peng, X.; et al. Snow cover detection in mid-latitude mountainous and polar regions using nighttime light data. Remote Sens. Environ. 2022, 268, 112766. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; DiGirolamo, N.E.; Román, M.O. Evaluation of MODIS and VIIRS cloud-gap-filled snow-cover products for production of an Earth science data record. Hydrol. Earth Syst. Sci. 2019, 23, 5227–5241. [Google Scholar] [CrossRef]
- Gascoin, S.; Hagolle, O.; Huc, M.; Jarlan, L.; Dejoux, J.F.; Szczypta, C.; Marti, R.; Sánchez, R. A snow cover climatology for the Pyrenees from MODIS snow products. Hydrol. Earth Syst. Sci. 2015, 19, 2337–2351. [Google Scholar] [CrossRef]
- Xu, N.; Li, W.; Gong, P.; Lu, H. Satellite altimeter observed surface water increase across lake-rich regions of the Arctic. Innovation 2024, 5, 100714. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.K.; Riggs, G.A.; DiGirolamo, N.E.; Román, M.O. MODIS cloud-gap filled snow-cover products: Advantages and uncertainties. Hydrol. Earth Syst. Sci. Discuss. 2019, 123, 1–23. [Google Scholar]
- Li, Y.; Chen, Y. The continuing shrinkage of snow cover in High Mountain Asia over the last four decades. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 24–28 April 2023; p. EGU-16661. [Google Scholar]
- Desinayak, N.; Prasad, A.K.; El Askary, H.; Kafatos, M.; Asrar, G.R. Snow cover variability and trend over the Hindu Kush Himalayan region using MODIS and SRTM data. Ann. Geophys. 2022, 40, 67–82. [Google Scholar] [CrossRef]
- Rikiishi, K.; Nakasato, H. Height dependence of the tendency for reduction in seasonal snow cover in the Himalaya and the Tibetan Plateau region, 1966–2001. Ann. Glaciol. 2006, 43, 369–377. [Google Scholar] [CrossRef]
- IPCC. Impacts, Adaptation and Vulnerability; Cambridge University Press: Cambridge, UK, 2007; p. 828. [Google Scholar]
- Khali, H.; Pandey, P.; Ali, S.N.; Champatiray, P.K. MODIS Observed Spatiotemporal Variation of Snow Cover in Zanskar Valley, North-Western Himalaya. Front. Water 2022, 4, 853146. [Google Scholar] [CrossRef]
- Mishra, B.; Babel, M.S.; Tripathi, N.K. Analysis of climatic variability and snow cover in the Kaligandaki River Basin, Himalaya, Nepal. Theor. Appl. Climatol. 2014, 116, 681–694. [Google Scholar] [CrossRef]
- Mishra, B.; Tripathi, N.K.; Babel, M.S. An artificial neural network-based snow cover predictive modeling in the higher Himalayas. J. Mt. Sci. 2014, 11, 825–837. [Google Scholar] [CrossRef]
- Moazzam, M.F.U.; Rahman, G.; Lee, B.G.; Ansari, N.A. Trend of snow cover under the influence of climate change using Google Earth Engine platform: A case study of Astore (Western Himalayas) and Shigar (Karakoram region). Front. Environ. Sci. 2022, 10, 1006399. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Chen, H.; Yong, B.; Qi, W.; Wu, H.; Ren, L.; Hong, Y. Investigating the evaluation uncertainty for satellite precipitation estimates based on two different ground precipitation observation products. J. Hydrometeorol. 2020, 21, 2595–2606. [Google Scholar] [CrossRef]
- Luo, L.; Zhang, J.; Wang, H.; Chen, M.; Jiang, Q.; Yang, W.; Wang, F.; Zhang, J.; Swain, R.B.; Meadows, M.E.; et al. Innovations in science, technology, engineering, and policy (iSTEP) for addressing environmental issues towards sustainable development. Innov. Geosci. 2024, 2, 100087. [Google Scholar] [CrossRef]
- Yang, G.; Zha, D.; Cao, D.; Zhang, G. Time for a change: Rethinking the global renewable energy transition from the Sustainable Development Goals and the Paris Climate Agreement. Innovation 2024, 5, 100582. [Google Scholar] [CrossRef]
- Vermote, E. MODIS/Terra Surface Reflectance 8-Day L3 Global 500m SIN Grid, V061; National Snow and Ice Data Center: Boulder, CO, USA, 2021. [Google Scholar]
- USGS. Land Processes DAAC (LP DAAC). Available online: https://earthexplorer.usgs.gov/ (accessed on 12 July 2024).
- Patil, R.; Mohanty, B.; Liu, B.; Chandrashekaran, I.R.; Headey, S.J.; Williams, M.L.; Clements, C.S.; Ilyichova, O.; Doak, B.C.; Genissel, P.; et al. A ligand-induced structural change in fatty acid–binding protein 1 is associated with potentiation of peroxisome proliferator–activated receptor α agonists. J. Biol. Chem. 2019, 294, 3720–3734. [Google Scholar] [CrossRef]
- Riggs, G.; Hall, D. Continuity of MODIS and VIIRS Snow Cover Extent Data Products for Development of an Earth Science Data Record. Remote Sens. 2020, 12, 3781. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Available online: https://cds.climate.copernicus.eu (accessed on 27 August 2025).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- NASA JPL. NASA Shuttle Radar Topography Mission Global 1 Arc Second. 2013. Available online: https://www.earthdata.nasa.gov/data/catalog/lpcloud-srtmgl1-003 (accessed on 12 July 2024).
- Pellitero, R.; Rea, B.R.; Spagnolo, M.; Bakke, J.; Hughes, P.; Ivy Ochs, S.; Lukas, S.; Ribolini, A. A GIS tool for automatic calculation of glacier equilibrium-line altitudes. Comput. Geosci. 2015, 82, 55–62. [Google Scholar] [CrossRef]
- Chi, M.; Plaza, A.; Benediktsson, J.A.; Sun, Z.; Shen, J.; Zhu, Y. Big data for remote sensing: Challenges and opportunities. Proc. IEEE 2016, 104, 2207–2219. [Google Scholar] [CrossRef]
- Mahale, G.; Mahale, H.; Parimi, R.B.; Nandy, S.K.; Bhattacharya, S. Hardware architecture of bi-cubic convolution interpolation for real-time image scaling. In Proceedings of the 2014 International Conference on Field-Programmable Technology (FPT), Shanghai, China, 10–12 December 2014; pp. 264–267. [Google Scholar]
- Parajka, J.; Blöschl, G. Validation of MODIS snow cover images over Austria. Hydrol. Earth Syst. Sci. 2006, 10, 679–689. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, H.; Zhang, L.; Li, P. Inpainting for remotely sensed images with a multichannel nonlocal total variation model. IEEE Trans. Geosci. Remote Sens. 2013, 52, 175–187. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin & Co., Ltd.: London, UK, 1948; p. 160. [Google Scholar]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Kurowski, L. Die Höhe der Schneegrenze: Mit besonderer Berücksichtigung der Finsteraarhorn-Gruppe; Hlözel Ed.: Vienna, Austria, 1891; p. 160. [Google Scholar]
- Osmaston, H. Estimates of glacier equilibrium line altitudes by the Area×Altitude, the Area × Altitude Balance Ratio and the Area × Altitude Balance Index methods and their validation. Quat. Int. 2005, 138–139, 22–31. [Google Scholar] [CrossRef]
- Furbish, D.J.; Andrews, J.T. The use of hypsometry to indicate long-term stability and response of valley glaciers to changes in mass transfer. J. Glaciol. 1984, 30, 199–211. [Google Scholar] [CrossRef]
- Baig, S.U.; Muneeb, F. Adjustment of glacier geometries to future equilibrium line altitudes in the Shigar River Basin of Karakoram Range, Pakistan. SN Appl. Sci. 2021, 3, 482. [Google Scholar] [CrossRef]
- Kern, Z.; László, P. Size specific steady-state accumulation-area ratio: An improvement for equilibrium-line estimation of small palaeoglaciers. Quat. Sci. Rev. 2010, 29, 2781–2787. [Google Scholar] [CrossRef]
- Sim, J.; Wright, C.C. The kappa statistic in reliability studies: Use, interpretation, and sample size requirements. Phys. Ther. 2005, 85, 257–268. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Stillinger, T.; Roberts, D.A.; Collar, N.M.; Dozier, J. Cloud masking for Landsat 8 and MODIS Terra over snow-covered terrain: Error analysis and spectral similarity between snow and cloud. Water Resour. Res. 2019, 55, 6169–6184. [Google Scholar] [CrossRef]
- Liu, A.; Che, T.; Huang, X.; Dai, L.; Wang, J.; Deng, J. Effect of Cloud Mask on the Consistency of Snow Cover Products from MODIS and VIIRS. Remote Sens. 2022, 14, 6134. [Google Scholar] [CrossRef]
- Gurung, D.R.; Maharjan, S.B.; Shrestha, A.B.; Shrestha, M.S.; Bajracharya, S.R.; Murthy, M.S.R. Climate and topographic controls on snow cover dynamics in the Hindu Kush Himalaya. Int. J. Climatol. 2017, 37, 3873–3882. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Liu, J.; Ahmad, I.; Ijaz, M.W.; Khan, M.I. Quantification of spatial temporal variability of snow cover and hydro-climatic variables based on multi-source remote sensing data in the Swat watershed, Hindukush Mountains, Pakistan. Meteor. Atmos. Phys. 2019, 131, 467–486. [Google Scholar] [CrossRef]
- Muhammad Tahir, K.; Yin, Y.; Wang, Y.; Babar, Z.A.; Yan, D. Impact assessment of orography on the extreme precipitation event of July 2010 over Pakistan: A numerical study: A numerical study. Adv. Meteorol. 2015, 2015, 510417. [Google Scholar] [CrossRef]
- Shafiq, M.u.; Ahmed, P.; Islam, Z.u.; Joshi, P.K.; Bhat, W.A. Snow cover area change and its relations with climatic variability in Kashmir Himalayas, India. Geocarto Int. 2019, 34, 688–702. [Google Scholar] [CrossRef]
- Tahir, A.A.; Adamowski, J.F.; Chevallier, P.; Haq, A.U.; Terzago, S. Comparative assessment of spatiotemporal snow cover changes and hydrological behavior of the Gilgit, Astore and Hunza River basins (Hindukush–Karakoram–Himalaya region, Pakistan). Meteorol. Atmos. Phys. 2016, 128, 793–811. [Google Scholar] [CrossRef]
- Stocker, T. Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; 110705799X; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; p. 1535. [Google Scholar]
- Midhuna, T.M.; Kumar, P.; Dimri, A.P. A new Western Disturbance Index for the Indian winter monsoon. J. Earth Syst. Sci. 2020, 129, 59. [Google Scholar] [CrossRef]
- Dimri, A.P. Decoding the Karakoram anomaly. Sci. Total Environ. 2021, 788, 147864. [Google Scholar] [CrossRef]
- Dimri, A.P.; Niyogi, D.; Barros, A.P.; Ridley, J.; Mohanty, U.C.; Yasunari, T.; Sikka, D.R. Western Disturbances: A review. Rev. Geophys. 2015, 53, 225–246. [Google Scholar] [CrossRef]
- Dharpure, J.K.; Goswami, A.; Patel, A.; Kulkarni, A.V.; Snehmani. Assessment of snow cover variability and its sensitivity to hydrometeorological factors in the Karakoram and Himalayan region. Hydrol. Sci. J. 2021, 66, 2198–2215. [Google Scholar] [CrossRef]
- Choudhury, A.; Yadav, A.C.; Bonafoni, S. A Response of Snow Cover to the Climate in the Northwest Himalaya (NWH) Using Satellite Products. Remote Sens. 2021, 13, 655. [Google Scholar] [CrossRef]
- Qureshi, M.A.; Yi, C.; Xu, X.; Li, Y. Glacier status during the period 1973–2014 in the Hunza Basin, Western Karakoram. Quat. Int. 2017, 444, 125–136. [Google Scholar] [CrossRef]
- Ali, S.; Khan, G.; Hassan, W.; Qureshi, J.A.; Bano, I. Assessment of glacier status and its controlling parameters from 1990 to 2018 of Hunza Basin, Western Karakorum. Environ. Sci. Pollut. Res. 2021, 28, 63178–63190. [Google Scholar] [CrossRef] [PubMed]
- Saydi, M.; Ding, J.l. Impacts of topographic factors on regional snow cover characteristics. Water Sci. Eng. 2020, 13, 171–180. [Google Scholar] [CrossRef]
- Hasson, S.; Lucarini, V.; Pascale, S.; Böhner, J. Seasonality of the hydrological cycle in major South and Southeast Asian river basins as simulated by PCMDI/CMIP3 experiments. Earth Syst. Dyn. 2014, 5, 67–87. [Google Scholar] [CrossRef]
- Sharma, A.; Choudhury, M. Chapter 17—Changing climate and depleting water resources in the mountains with a case study from the Himalayas. In Water Conservation in the Era of Global Climate Change; Thokchom, B., Qiu, P., Singh, P., Iyer, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 411–436. [Google Scholar]
- Negi, H.S.; Kumar, A.; Kanda, N.; Thakur, N.K.; Singh, K.K. Status of glaciers and climate change of East Karakoram in early twenty-first century. Sci. Total Environ. 2021, 753, 141914. [Google Scholar] [CrossRef]
- Krishnan, R.; Shrestha, A.B.; Ren, G.; Rajbhandari, R.; Saeed, S.; Sanjay, J.; Syed, M.A.; Vellore, R.; Xu, Y.; You, Q.; et al. Unravelling Climate Change in the Hindu Kush Himalaya: Rapid Warming in the Mountains and Increasing Extremes. In The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People; Wester, P., Mishra, A., Mukherji, A., Shrestha, A.B., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 57–97. [Google Scholar]
- Hewitt, K. The Karakoram anomaly? Glacier expansion and the’elevation effect,’Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar] [CrossRef]
- Farinotti, D.; Immerzeel, W.W.; de Kok, R.J.; Quincey, D.J.; Dehecq, A. Manifestations and mechanisms of the Karakoram glacier Anomaly. Nat. Geosci. 2020, 13, 8–16. [Google Scholar] [CrossRef]
- Bolch, T.; Pieczonka, T.; Mukherjee, K.; Shea, J. Brief communication: Glaciers in the Hunza catchment (Karakoram) have been nearly in balance since the 1970s. Cryosphere 2017, 11, 531–539. [Google Scholar] [CrossRef]
- Maurer, J.M.; Schaefer, J.M.; Rupper, S.; Corley, A. Acceleration of ice loss across the Himalayas over the past 40 years. Sci. Adv. 2019, 5, eaav7266. [Google Scholar] [CrossRef]
- Lin, H.; Li, G.; Cuo, L.; Hooper, A.; Ye, Q. A decreasing glacier mass balance gradient from the edge of the Upper Tarim Basin to the Karakoram during 2000–2014. Sci. Rep. 2017, 7, 6712. [Google Scholar] [CrossRef]
- Kuttippurath, J.; Patel, V.K.; Sharma, B.R. Observed changes in the climate and snow dynamics of the Third Pole. npj Clim. Atmos. Sci. 2024, 7, 162. [Google Scholar] [CrossRef]
- Trueba, J.J.G.; Canadas, E.S. The AAR Method for Palaeo-ELA determination: Methodological analysis and application to Valdecebollas Massif (Cantabrian Range). Geophys. Res. Lett. 2004, 30, 7–34. [Google Scholar]
- Zasadni, J.; Świąder, A.; Kłapyta, P. A novel (raster input/output) method of equilibrium line altitude (AAR, AABR) estimation and glacier hypsometry analysis. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 4–13 April 2018; p. 18556. [Google Scholar]

| Year | True Negative | False Positive | False Negative | True Positive | Overall Accuracy | Precision (Snow) | Recall (Snow) | F1 Score | Kappa Statistic | Misclassification Rate |
|---|---|---|---|---|---|---|---|---|---|---|
| (TN) | (FP) | (FN) | (TP) | (OA) | (Ka) | (MR) | ||||
| 2004 | 11,838,948 | 77,921 | 38,494 | 682,437 | 0.9908 | 0.8975 | 0.9466 | 0.9214 | 0.9165 | 0.0092 |
| 2005 | 11,641,374 | 163,161 | 22,526 | 810,739 | 0.9853 | 0.8325 | 0.9730 | 0.8972 | 0.8894 | 0.0147 |
| 2006 | 11,858,926 | 124,242 | 23,976 | 630,656 | 0.9883 | 0.8354 | 0.9634 | 0.8948 | 0.8887 | 0.0117 |
| 2007 | 11,710,598 | 126,439 | 29,097 | 771,666 | 0.9877 | 0.8592 | 0.9637 | 0.9084 | 0.9019 | 0.0123 |
| 2008 | 11,787,311 | 111,820 | 24,796 | 713,873 | 0.9892 | 0.8646 | 0.9664 | 0.9127 | 0.9069 | 0.0108 |
| 2009 | 11,835,634 | 66,844 | 25,012 | 710,310 | 0.9927 | 0.9140 | 0.9660 | 0.9393 | 0.9354 | 0.0073 |
| 2010 | 11,831,359 | 46,176 | 35,238 | 725,027 | 0.9936 | 0.9401 | 0.9537 | 0.9468 | 0.9434 | 0.0064 |
| 2011 | 11,766,435 | 210,256 | 16,287 | 644,822 | 0.9821 | 0.7541 | 0.9754 | 0.8506 | 0.8412 | 0.0179 |
| 2012 | 11,749,961 | 227,134 | 36,843 | 623,862 | 0.9791 | 0.7331 | 0.9442 | 0.8254 | 0.8145 | 0.0209 |
| 2013 | 11,654,108 | 170,621 | 33,045 | 780,026 | 0.9839 | 0.8205 | 0.9594 | 0.8845 | 0.8759 | 0.0161 |
| 2014 | 11,731,121 | 185,073 | 29,714 | 691,892 | 0.9830 | 0.7890 | 0.9588 | 0.8656 | 0.8567 | 0.0170 |
| 2015 | 11,646,289 | 113,399 | 25,108 | 853,004 | 0.9890 | 0.8827 | 0.9714 | 0.9249 | 0.9190 | 0.0110 |
| 2016 | 11,931,844 | 74,468 | 37,898 | 593,590 | 0.9911 | 0.8885 | 0.9400 | 0.9135 | 0.9089 | 0.0089 |
| 2017 | 11,849,531 | 202,106 | 13,932 | 572,231 | 0.9829 | 0.7390 | 0.9762 | 0.8412 | 0.8324 | 0.0171 |
| 2018 | 11,942,945 | 104,631 | 17,822 | 572,402 | 0.9903 | 0.8455 | 0.9698 | 0.9034 | 0.8983 | 0.0097 |
| 2019 | 11,573,962 | 191,270 | 21,768 | 850,800 | 0.9831 | 0.8165 | 0.9751 | 0.8887 | 0.8797 | 0.0169 |
| 2020 | 11,613,299 | 64,161 | 46,315 | 914,025 | 0.9913 | 0.9344 | 0.9518 | 0.9430 | 0.9383 | 0.0087 |
| 2021 | 11,934,850 | 43,342 | 46,142 | 613,466 | 0.9929 | 0.9340 | 0.9300 | 0.9320 | 0.9283 | 0.0071 |
| 2022 | 11,679,405 | 79,434 | 35,619 | 843,342 | 0.9909 | 0.9139 | 0.9595 | 0.9361 | 0.9312 | 0.0091 |
| 2023 | 11,918,071 | 81,725 | 31,951 | 606,053 | 0.9910 | 0.8812 | 0.9499 | 0.9143 | 0.9095 | 0.0090 |
| 2024 | 11,936,909 | 209,141 | 24,625 | 467,125 | 0.9815 | 0.6907 | 0.9499 | 0.7999 | 0.7904 | 0.0185 |
| Mean | 11,817,989 | 97,818 | 26,273 | 695,720 | 0.9902 | 0.8767 | 0.9636 | 0.9181 | 0.9129 | 0.0098 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tauqir, G.; Zhao, W.; Xu, M.; Fu, D. Elevation-Dependent Trends in Himalayan Snow Cover (2004–2024) Based on MODIS Terra Observations. Remote Sens. 2025, 17, 3175. https://doi.org/10.3390/rs17183175
Tauqir G, Zhao W, Xu M, Fu D. Elevation-Dependent Trends in Himalayan Snow Cover (2004–2024) Based on MODIS Terra Observations. Remote Sensing. 2025; 17(18):3175. https://doi.org/10.3390/rs17183175
Chicago/Turabian StyleTauqir, Ghania, Wei Zhao, Mengjiao Xu, and Dongjie Fu. 2025. "Elevation-Dependent Trends in Himalayan Snow Cover (2004–2024) Based on MODIS Terra Observations" Remote Sensing 17, no. 18: 3175. https://doi.org/10.3390/rs17183175
APA StyleTauqir, G., Zhao, W., Xu, M., & Fu, D. (2025). Elevation-Dependent Trends in Himalayan Snow Cover (2004–2024) Based on MODIS Terra Observations. Remote Sensing, 17(18), 3175. https://doi.org/10.3390/rs17183175








