A Cloud-Based Framework for the Quantification of the Uncertainty of a Machine Learning Produced Satellite-Derived Bathymetry
Abstract
1. Introduction
2. Methodology
2.1. Study Site
2.2. Remote Sensing and Reference Data
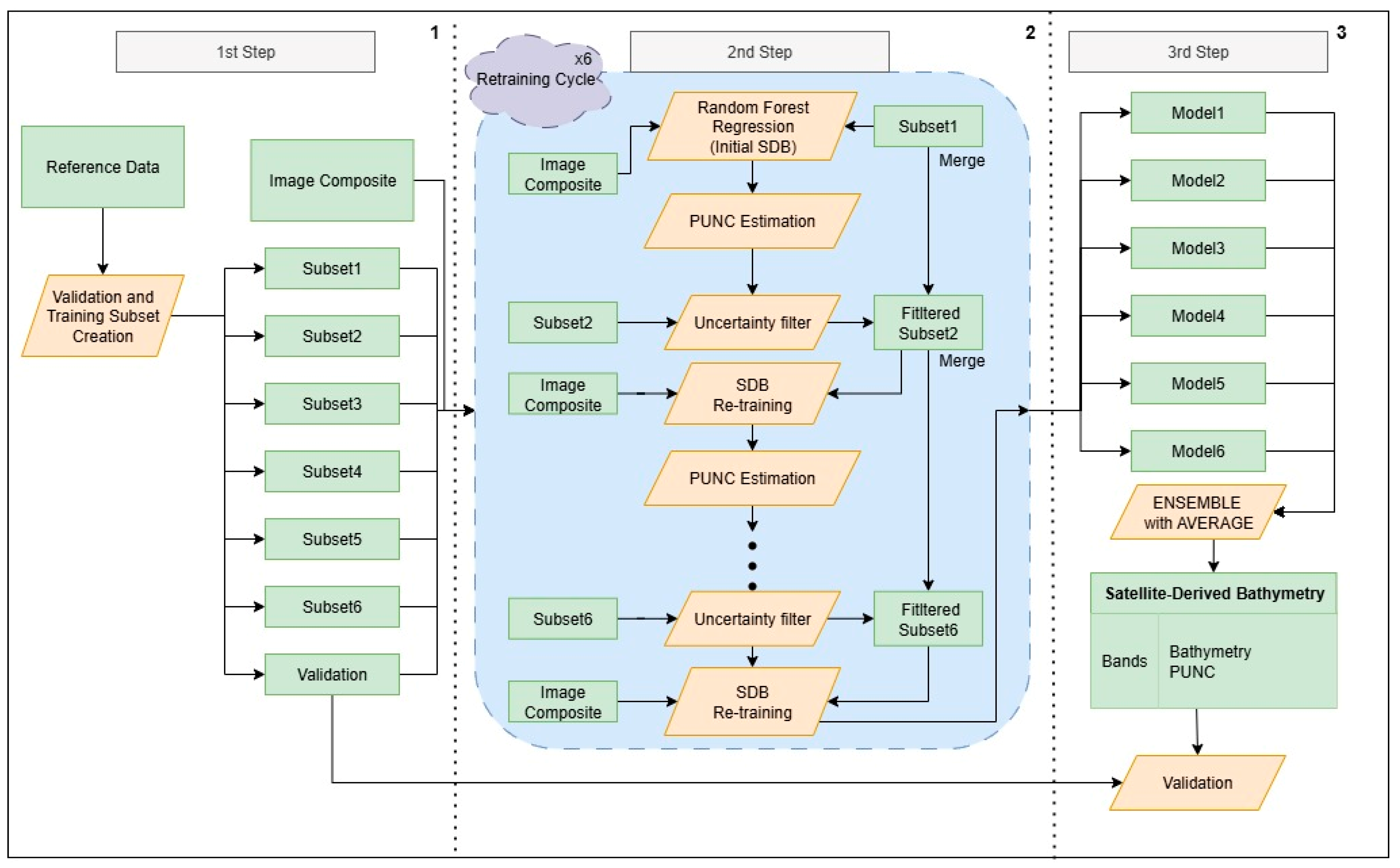
2.3. The Workflow, the Pixel UNCertainty (PUNC), and the Model Retraining
2.3.1. PUNC Estimation in ML Products with Continuous Distribution
2.3.2. Retraining the SDB Model with Bootstrapping
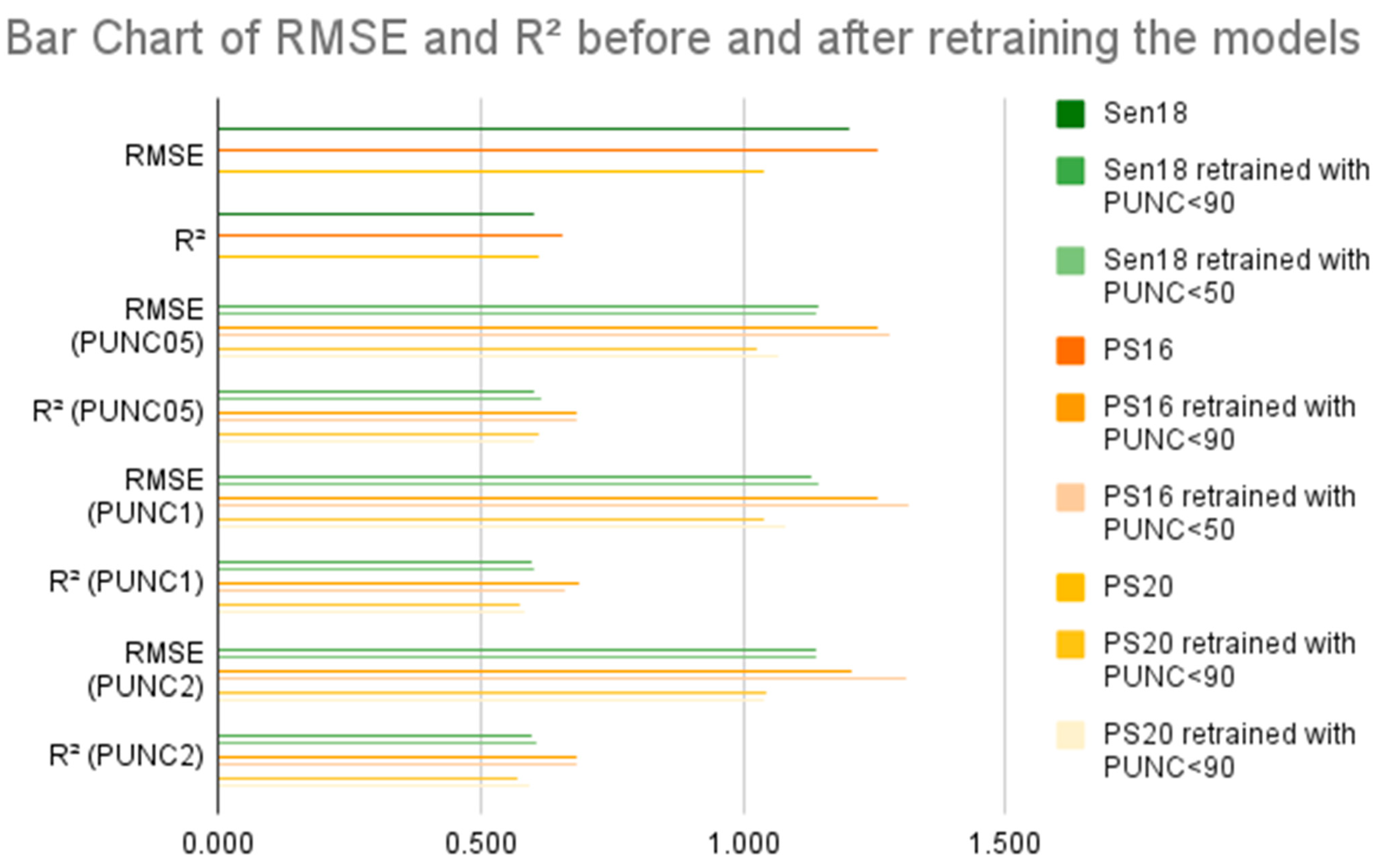
2.4. Accuracy Assessment
3. Results
3.1. PUNC Values on S2 Data
3.2. PUNC Values on PS Data
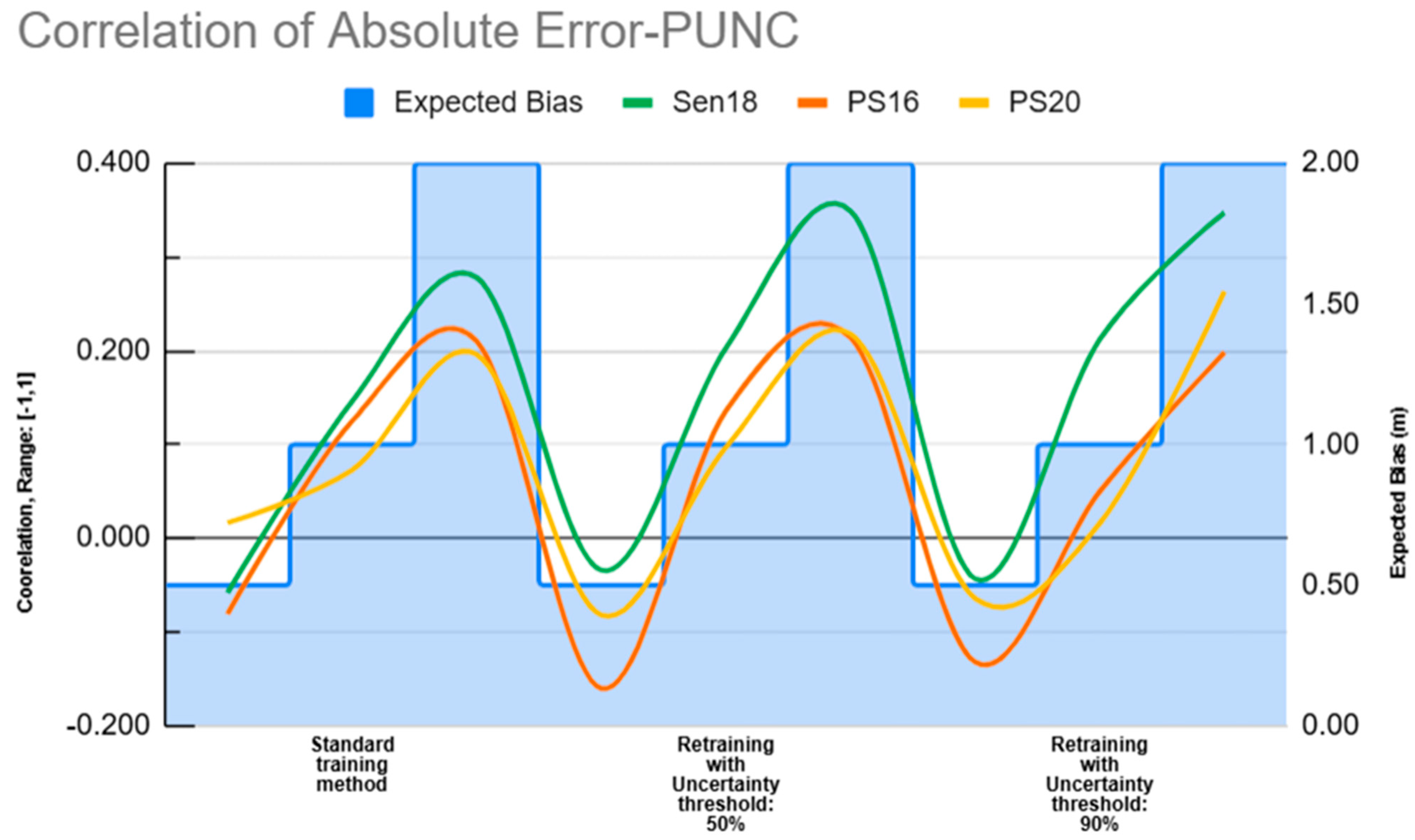
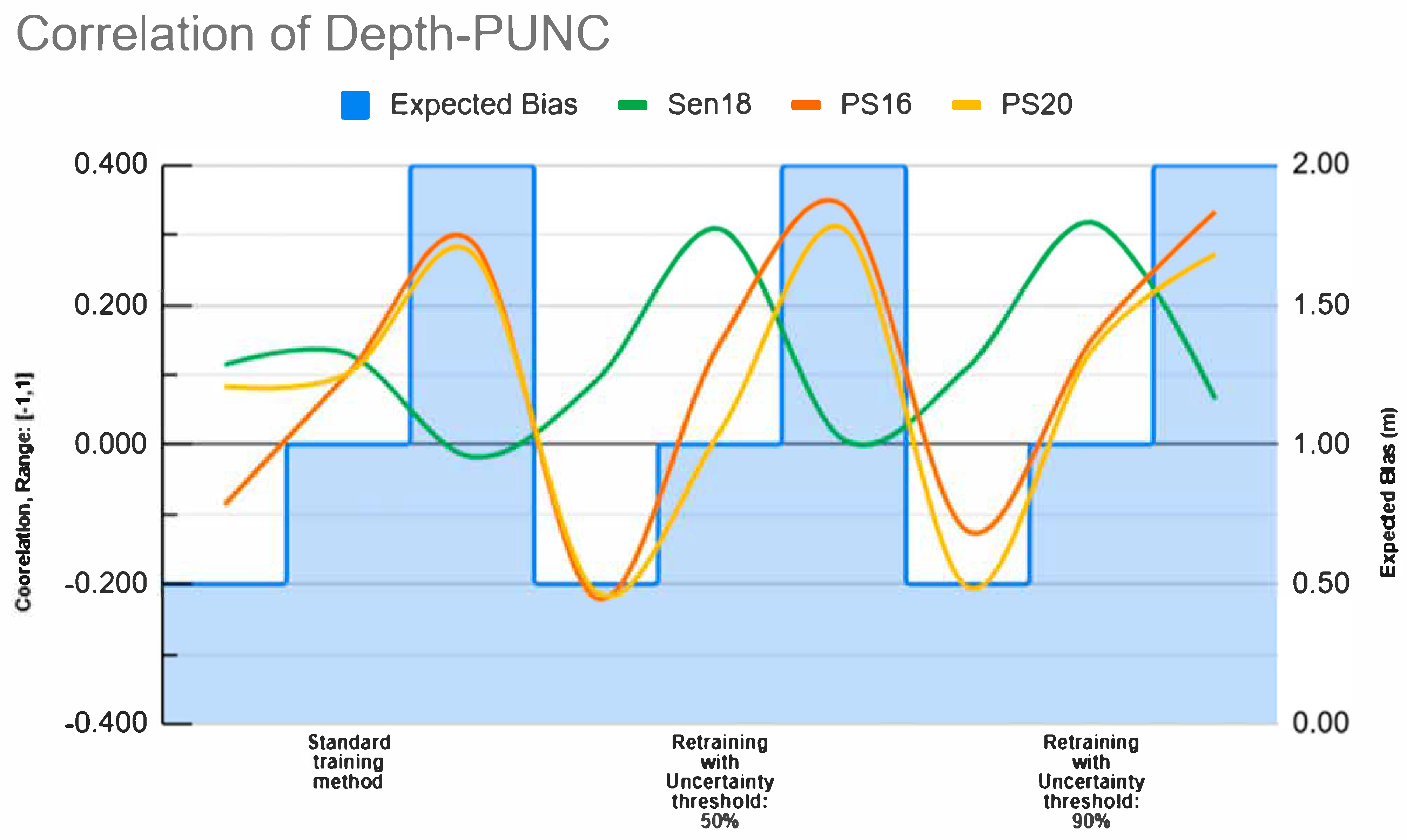
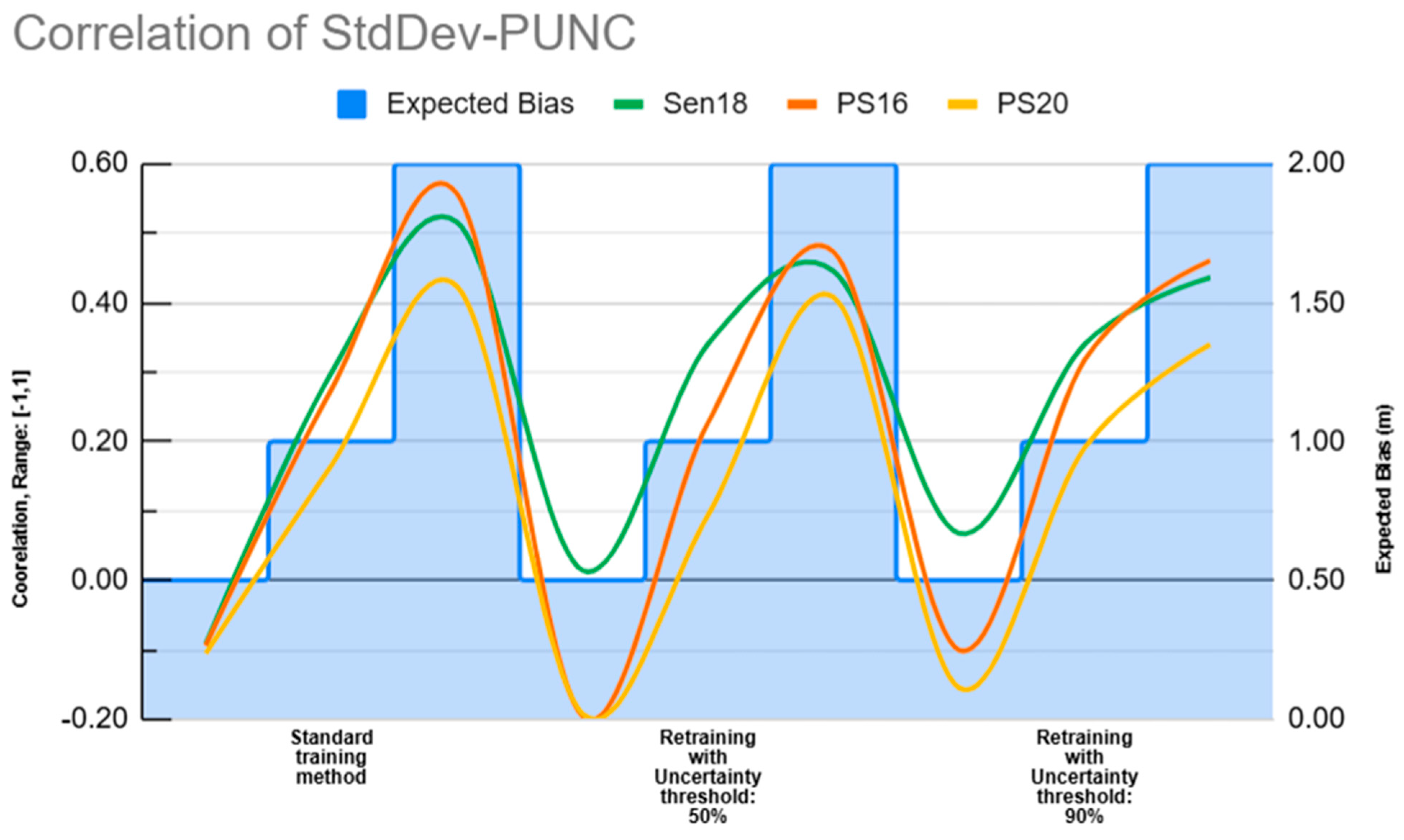
3.3. T-Test and Observed Correlation Between Absolute Error, True Depth, and Standard Deviation with PUNC
4. Discussion
4.1. Usage and Challenges of PUNC
4.1.1. Usage of PUNC
4.1.2. Uncertainties of PUNC
4.2. Future Prospects
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2023: Synthesis Report Contribution of Working Groups, I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 35–115. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-Resolution Maps of Bathymetry and Benthic Habitats in Shallow-Water Environments Using Multispectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Garcia, R.A.; Hedley, J.D.; Tin, H.C.; Fearns, P.R.C.S. A method to analyze the potential of optical remote sensing for benthic habitat mapping. Remote Sens. 2015, 7, 13157–13189. [Google Scholar] [CrossRef]
- Misiuk, B.; Brown, C.J. Benthic habitat mapping: A review of three decades of mapping biological patterns on the seafloor. Estuar. Coast. Shelf Sci. 2024, 296, 108599. [Google Scholar] [CrossRef]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of near-shore satellite derived bathymetry: Classification and account of five decades of coastal bathymetry research. J. Ocean. Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite derived bathymetry using machine learning and multi-temporal satellite images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
- Adebisi, N.; Balogun, A.L.; Mahdianpari, M.; Min, T.H. Assessing the impacts of rising sea level on coastal morpho-dynamics with automated high-frequency shoreline mapping using multi-sensor optical satellites. Remote Sens. 2021, 13, 3587. [Google Scholar] [CrossRef]
- Velegrakis, A.F.; Chatzistratis, D.; Chalazas, T.; Armaroli, C.; Schiavon, E.; Alves, B.; Grigoriadis, D.; Hasiotis, T.; Ieronymidi, E. Earth observation technologies, policies and legislation for the coastal flood risk assessment and management: A European perspective. Anthr. Coasts 2024, 7, 3. [Google Scholar] [CrossRef]
- Naboureh, A.; Ebrahimy, H.; Azadbakht, M.; Bian, J.; Amani, M. Ruesvms: An ensemble method to handle the class imbalance problem in land cover mapping using google earth engine. Remote Sens. 2020, 12, 3484. [Google Scholar] [CrossRef]
- Araya-Lopez, R.; de Paula Costa, M.D.; Wartman, M.; Macreadie, P.I. Trends in the application of remote sensing in blue carbon science. Ecol. Evol. 2023, 13, e10559. [Google Scholar] [CrossRef] [PubMed]
- Blume, A.; Pertiwi, A.P.; Lee, C.B.; Traganos, D. Bahamian seagrass extent and blue carbon accounting using Earth Observation. Front. Mar. Sci. 2023, 10, 1058460. [Google Scholar] [CrossRef]
- Christianson, A.B.; Cabré, A.; Bernal, B.; Baez, S.K.; Leung, S.; Pérez-Porro, A.; Poloczanska, E. The Promise of Blue Carbon Climate Solutions: Where the Science Supports Ocean-Climate Policy. Front. Mar. Sci. 2022, 9, 851448. [Google Scholar] [CrossRef]
- Liu, J.; Failler, P.; Ramrattan, D. Blue carbon accounting to monitor coastal blue carbon ecosystems. J. Environ. Manag. 2024, 352, 120008. [Google Scholar] [CrossRef]
- Malerba, M.E.; Duarte de Paula Costa, M.; Friess, D.A.; Schuster, L.; Young, M.A.; Lagomasino, D.; Serrano, O.; Hickey, S.M.; York, P.H.; Rasheed, M.; et al. Remote sensing for cost-effective blue carbon accounting. Earth-Sci. Rev. 2023, 238, 104337. [Google Scholar] [CrossRef]
- Macreadie, P.I.; Anton, A.; Raven, J.A.; Beaumont, N.; Connolly, R.M.; Friess, D.A.; Kelleway, J.J.; Kennedy, H.; Kuwae, T.; Lavery, P.S.; et al. The future of Blue Carbon science. Nat. Commun. 2019, 10, 3998. [Google Scholar] [CrossRef] [PubMed]
- Macreadie, P.I.; Costa, M.D.P.; Atwood, T.B.; Friess, D.A.; Kelleway, J.J.; Kennedy, H.; Lovelock, C.E.; Serrano, O.; Duarte, C.M. Blue carbon as a natural climate solution. Nat. Rev. Earth Environ. 2021, 2, 826–839. [Google Scholar] [CrossRef]
- Pham-Duc, B.; Nguyen, H.; Phan, H.; Tran-Anh, Q. Trends and applications of google earth engine in remote sensing and earth science research: A bibliometric analysis using scopus database. Earth Sci. Inform. 2023, 16, 2355–2371. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Pérez-Cutillas, P.; Pérez-Navarro, A.; Conesa-García, C.; Zema, D.A.; Amado-Álvarez, J.P. What is going on within google earth engine? A systematic review and meta-analysis. Remote Sens. Appl. Soc. Environ. 2023, 29, 100907. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, X.; Zou, Z.; Chen, B.; Ma, J.; Dong, J.; Doughty, R.B.; Zhong, Q.; Qin, Y.; Dai, S.; et al. Tracking annual changes of coastal tidal flats in China during 1986–2016 through analyses of Landsat images with Google Earth Engine. Remote Sens. Environ. 2020, 238, 110987. [Google Scholar] [CrossRef]
- Arjasakusuma, S.; Kusuma, S.S.; Saringatin, S.; Wicaksono, P.; Mutaqin, B.W.; Rafif, R. Shoreline dynamics in East Java Province, Indonesia, from 2000 to 2019 using multi-sensor remote sensing data. Land 2021, 10, 100. [Google Scholar] [CrossRef]
- Caballero, I.; Roca, M.; Dunbar, M.B.; Navarro, G. Water Quality and Flooding Impact of the Record-Breaking Storm Gloria in the Ebro Delta (Western Mediterranean). Remote Sens. 2024, 16, 41. [Google Scholar] [CrossRef]
- Roca, M.; Navarro, G.; García-Sanabria, J.; Caballero, I. Monitoring Sand Spit Variability Using Sentinel-2 and Google Earth Engine in a Mediterranean Estuary. Remote Sens. 2022, 14, 2345. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Sayer, A.M.; Govaerts, Y.; Kolmonen, P.; Lipponen, A.; Luffarelli, M.; Mielonen, T.; Patadia, F.; Popp, T.; Povey, A.C.; Stebel, K.; et al. A review and framework for the evaluation of pixel-level uncertainty estimates in satellite aerosol remote sensing. Atmos. Meas. Tech. 2020, 13, 373–404. [Google Scholar] [CrossRef]
- Tran, B.N.; Van Der Kwast, J.; Seyoum, S.; Uijlenhoet, R.; Jewitt, G.; Mul, M. Uncertainty assessment of satellite remote-sensing-based evapotranspiration estimates: A systematic review of methods and gaps. Hydrol. Earth Syst. Sci. 2023, 27, 4505–4528. [Google Scholar] [CrossRef]
- Lubac, B.; Burvingt, O.; Nicolae Lerma, A.; Sénéchal, N. Performance and Uncertainty of Satellite-Derived Bathymetry Empirical Approaches in an Energetic Coastal Environment. Remote Sens. 2022, 14, 2350. [Google Scholar] [CrossRef]
- Thomas, N.; Lee, B.; Coutts, O.; Bunting, P.; Lagomasino, D.; Fatoyinbo, L. A Purely Spaceborne Open Source Approach for Regional Bathymetry Mapping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4708109. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, X.; Wu, Z.; Yang, F.; Zhu, H.; Zhao, D.; Zhu, J. Improving Statistical Uncertainty Estimate of Satellite-Derived Bathymetry by Accounting for Depth-Dependent Uncertainty. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5401309. [Google Scholar] [CrossRef]
- Chénier, R.; Ahola, R.; Sagram, M.; Faucher, M.-A.; Shelat, Y. Consideration of Level of Confidence within Multi-Approach Satellite-Derived Bathymetry. ISPRS Int. J. Geo-Inf. 2019, 8, 48. [Google Scholar] [CrossRef]
- Christofilakos, S.; Blume, A.; Pertiwi, A.P.; Lee, C.B.; Traganos, D.; Reinartz, P. A cloud-based framework for the quantification of the spatially-explicit uncertainty of remotely sensed benthic habitats. Int. J. Appl. Earth Obs. Geoinf. 2025, 141, 104670. [Google Scholar] [CrossRef]
- Cho, L. Marine protected areas: A tool for integrated coastal management in Belize. Ocean Coast. Manag. 2005, 48, 932–947. [Google Scholar] [CrossRef]
- Verutes, G.M.; Arkema, K.K.; Clarke-Samuels, C.; Wood, S.A.; Rosenthal, A.; Rosado, S.; Canto, M.; Bood, N.; Ruckelshaus, M. Integrated planning that safeguards ecosystems and balances multiple objectives in coastal Belize. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2017, 13, 1–17. [Google Scholar] [CrossRef]
- Karlsson, M.; van Oort, B.; Romstad, B. What we have lost and cannot become: Societal outcomes of coastal erosion in southern Belize. Ecol. Soc. 2015, 20, 4. [Google Scholar] [CrossRef]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Technical note: Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Lee, C.B.; Traganos, D.; Reinartz, P. A Simple Cloud-Native Spectral Transformation Method to Disentangle Optically Shallow and DeepWaters in Sentinel-2 Images. Remote Sens. 2022, 14, 590. [Google Scholar] [CrossRef]
- Traganos, D.; Aggarwal, B.; Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N.; Reinartz, P. Towards Global-Scale Seagrass Mapping and Monitoring Using Sentinel-2 on Google Earth Engine: The Case Study of the Aegean and Ionian Seas. Remote Sens. 2018, 10, 1227. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Chrysoulakis, N.; Reinartz, P. Cubesats allow high spatiotemporal estimates of satellite-derived bathymetry. Remote Sens. 2019, 11, 1299. [Google Scholar] [CrossRef]
- Thomas, N.; Pertiwi, A.P.; Traganos, D.; Lagomasino, D.; Poursanidis, D.; Moreno, S.; Fatoyinbo, L. Space-Borne Cloud-Native Satellite-Derived Bathymetry (SDB) Models Using ICESat-2 And Sentinel-2. Geophys. Res. Lett. 2021, 48, e2020GL092170. [Google Scholar] [CrossRef]
- Neumann, T.A.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.B.; Rebold, T.; et al. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Han, R.; Liu, P.; Wang, G.; Zhang, H.; Wu, X. Advantage of combining ObiA and classifier ensemble method for very high-resolution satellite imagery classification. J. Sens. 2020, 2020, 8855509. [Google Scholar] [CrossRef]
- Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N. Mapping coastal marine habitats and delineating the deep limits of the Neptune’s seagrass meadows using very high resolution Earth observation data. Int. J. Remote Sens. 2018, 39, 8670–8687. [Google Scholar] [CrossRef]
- Topouzelis, K.; Papakonstantinou, A.; Doukari, M.; Stamatis, P.; Makri, D.; Katsanevakis, S. Coastal habitat mapping in the Aegean Sea using high resolution orthophoto maps. Proc. SPIE 2017, 10444, 389–394. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global canopy height regression and uncertainty estimation from GEDI LIDAR waveforms with deep ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Student. The Probable Error of a Mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Gruber, C.; Schenk, P.O.; Schierholz, M.; Kreuter, F.; Kauermann, G. Sources of Uncertainty in Machine Learning—A Statisticians’ View. arXiv 2023, arXiv:2305.16703. [Google Scholar]
- Khakhim, N.; Kurniawan, A.; Wicaksono, P.; Hasrul, A. Assessment of Empirical Near-Shore Bathymetry Model Using New Emerged PlanetScope Instrument and Sentinel-2 Data in Coastal Shallow Waters. Int. J. Geoinform. 2024, 20, 95–105. [Google Scholar] [CrossRef]
- Casal, G.; Harris, P.; Monteys, X.; Hedley, J.; Cahalane, C.; McCarthy, T. Understanding satellite-derived bathymetry using Sentinel 2 imagery and spatial prediction models. GISci. Remote Sens. 2020, 57, 271–286. [Google Scholar] [CrossRef]
- Phillips, O.M. Remote Sensing of the Sea Surface. Ann. Rev. Fluid Mech. 1988, 20, 89–109. [Google Scholar] [CrossRef]





| Composite | # of Image/Tiles Used for Composites | Bands | Number of TD | Number of VD |
|---|---|---|---|---|
| SEN18 | 876 | 24 in total, 6 pixel-based and 18 object-based. Pixel-based: Three optical channels, DIV, Hue, and Value. Object-based: Mean, Median, and StdDev of all the pixel-based bands. | 2753 | 777 |
| PS16 | 8 (NICFI basemaps every semester) | 2852 | 742 | |
| PS20 | 29 (besides the first composite that is a NICFI six-month basemap, all the others are monthly mosaics) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christofilakos, S.; Pertiwi, A.P.; Reyes, A.C.; Carpenter, S.; Thomas, N.; Traganos, D.; Reinartz, P. A Cloud-Based Framework for the Quantification of the Uncertainty of a Machine Learning Produced Satellite-Derived Bathymetry. Remote Sens. 2025, 17, 3060. https://doi.org/10.3390/rs17173060
Christofilakos S, Pertiwi AP, Reyes AC, Carpenter S, Thomas N, Traganos D, Reinartz P. A Cloud-Based Framework for the Quantification of the Uncertainty of a Machine Learning Produced Satellite-Derived Bathymetry. Remote Sensing. 2025; 17(17):3060. https://doi.org/10.3390/rs17173060
Chicago/Turabian StyleChristofilakos, Spyridon, Avi Putri Pertiwi, Andrea Cárdenas Reyes, Stephen Carpenter, Nathan Thomas, Dimosthenis Traganos, and Peter Reinartz. 2025. "A Cloud-Based Framework for the Quantification of the Uncertainty of a Machine Learning Produced Satellite-Derived Bathymetry" Remote Sensing 17, no. 17: 3060. https://doi.org/10.3390/rs17173060
APA StyleChristofilakos, S., Pertiwi, A. P., Reyes, A. C., Carpenter, S., Thomas, N., Traganos, D., & Reinartz, P. (2025). A Cloud-Based Framework for the Quantification of the Uncertainty of a Machine Learning Produced Satellite-Derived Bathymetry. Remote Sensing, 17(17), 3060. https://doi.org/10.3390/rs17173060









