HTMNet: Hybrid Transformer–Mamba Network for Hyperspectral Target Detection
Abstract
1. Introduction
- A novel HTMNet is designed for HTD, which effectively models high-fidelity background samples by jointly leveraging Transformer and Mamba architectures. This hybrid design significantly improves the network’s capability to distinguish target information from complex background by capturing both multi-scale and global–local features.
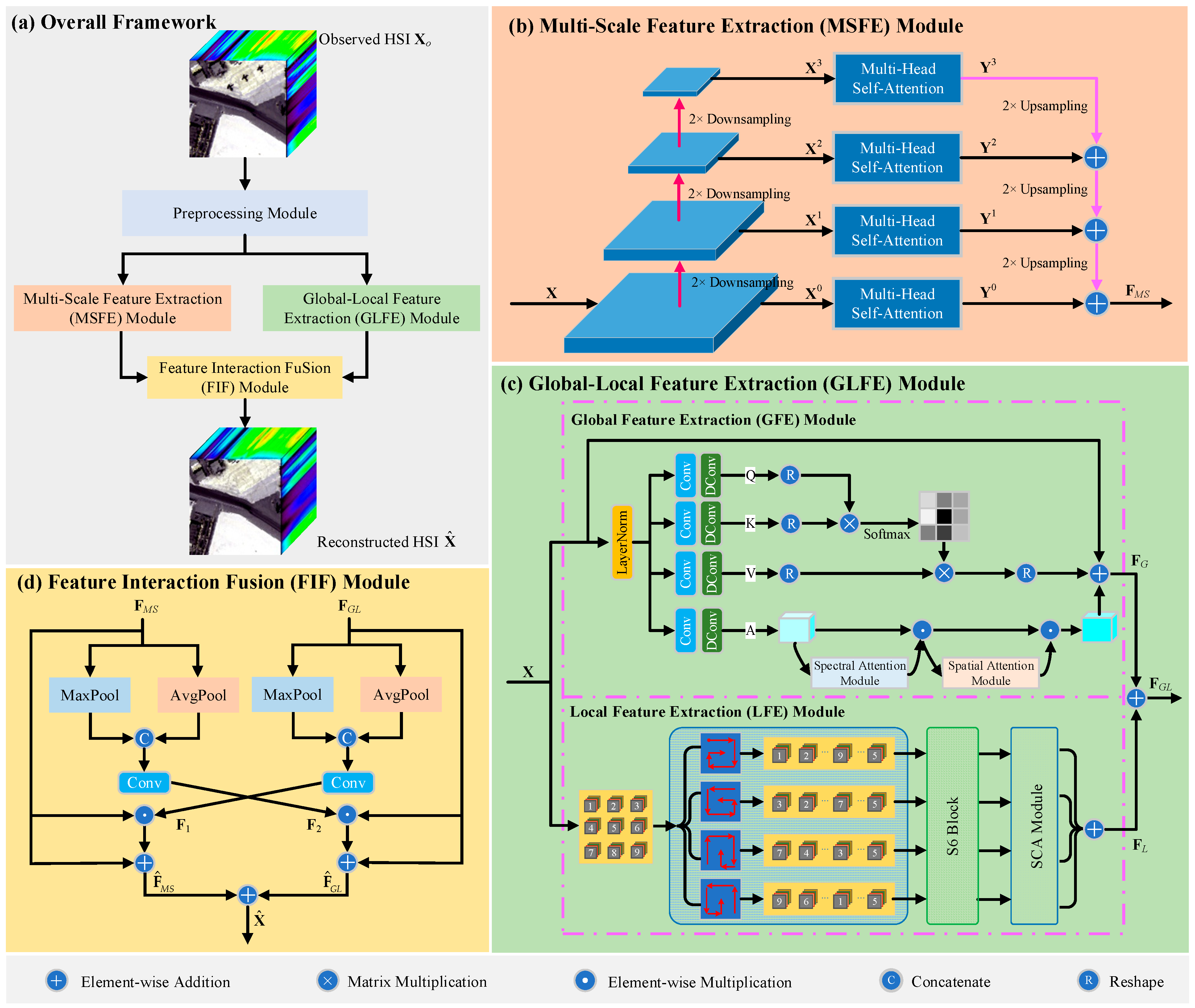
- A dual-branch architecture is designed, consisting of an MSFE module and a GLFE module. The MSFE module employs a Transformer-based strategy to capture and fuse features at multiple spatial scales. The GLFE module further complements this by capturing global background features through incorporating a spectral–spatial attention module into the Transformer and extracting local background features via a novel circular scanning strategy embedded within the LocalMamba. This dual-perspective design can capture background features from multiple perspectives, enhancing both multi-scale and global–local representation capabilities.
- A FIF module is further devised to facilitate the integration and interaction of features extracted from the two branches. By promoting multi-scale and global–local feature fusion, the FIF module enhances contextual consistency and semantic complementarity among features, enhancing background modeling accuracy and robustness.
2. Methods
2.1. Preliminary
2.2. Preprocessing Module
2.3. Multi-Scale Feature Extraction Module
2.4. Global–Local Feature Extraction Module
2.4.1. Global Feature Extraction Module
- (1)
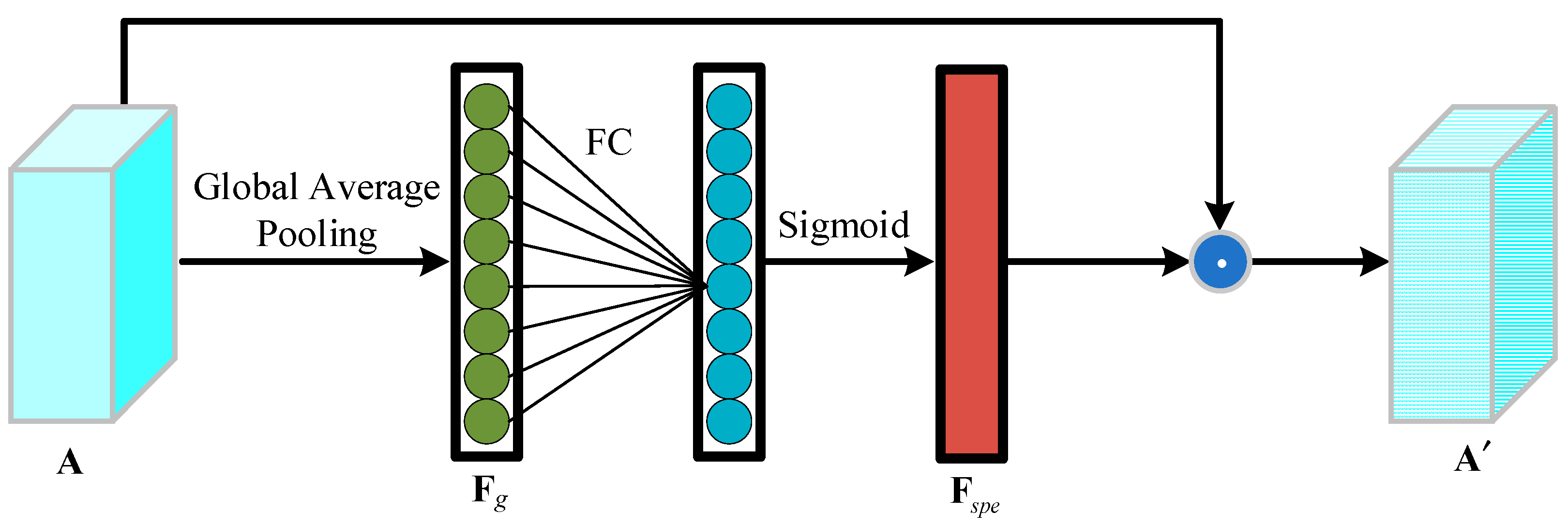
- Spectral attention module: Figure 3 corresponds to the spectral attention module in Figure 1c, specifically, first, a global average pooling operation is performed on the features to obtain the global feature representation of each channel. Then, the is imported into the fully connected (FC) layer and Sigmoid function to obtain spectral attention weights . Finally, we obtain the enhanced spectral features by element-wise multiplication of and . The processes are formulated as follows.where signifies the global average pooling layer, signifies the FC layer, represents the Sigmoid activation function, and denotes the element-wise multiplication.
- (2)
- Spatial attention module: Figure 4 corresponds to the spatial attention module in Figure 1c, specifically, first, a max and average of the pooling layers are performed on the features to obtain pooled features and . Then, after concatenating and , a convolution followed by a Sigmoid function is performed to attain the spatial attention features . Finally, we obtain the output of the spectral–spatial attention module by element-wise multiplication of and . The processes are formulated as follows.where signifies the max pooling layer, signifies the average pooling layer, denotes the concatenate operation along the channel dimension, and denotes the convolution with kernel 3.
2.4.2. Local Feature Extraction Module
2.5. Feature Interaction Fusion Module
2.6. Model Training and Inference
3. Results
3.1. Experimental Setup
3.1.1. Dataset Setup
- (1)
- San Diego I and San Diego II [48]: The first two datasets, San Diego I and San Diego II, were acquired using the Airborne Visible Infrared Imaging Spectrometer (AVIRIS) at San Diego Airport, California, USA. Both HSIs have dimensions of 100 × 100 × 224, featuring a spatial resolution of 3.5 m and covering the wavelength range from 400 to 2500 nm. Following the removal of low-quality bands, 189 spectral bands were retained for the experimental analysis. The targets to be inspected are three aircraft.
- (2)
- Abu-airport-2 [49]: The third dataset, Abu-airport-2, was collected by AVIRIS on the Los Angeles Airport scene in California. The size of HSI is 100 × 100 × 205, featuring 100 × 100 pixels and 205 spectral bands, with a wavelength range of 400 to 2500 nm. Spatial resolution of this dataset is 7.1 m. The targets to be detected are two aircraft, consisting of 87 pixels.
- (3)
- Abu-beach-4 [49]: The fourth dataset, Abu-beach-4, was collected by the Reflectometry Imaging Spectrometer (ROSIS-03) sensor in the Pavia Beach area of Italy. The spatial size of HSI is 150 × 150 and the spatial resolution is 1.3 m. It consists of 115 spectral bands, ranging from 430 nm to 860 nm. After removing the low-quality bands, there were still 102 bands in the experiment. Some Vehicles on the bridge are marked as targets.
3.1.2. Evaluation Metric
3.1.3. Implementation Details
3.2. Ablation Study
- (1)
- Effectiveness of MSFE: To assess the effectiveness of MSFE, we conducted an experiment by integrating the multi-scale module into the baseline. As shown in Table 1, MSFE outperforms the baseline by 0.74%, 0.58%, 0.35%, and 0.26% on the four datasets, respectively, demonstrating its effectiveness. These improvements indicate that MSFE is capable of effectively extracting multi-scale features for better background modeling.
- (2)
- Effectiveness of GLFE: To assess the effectiveness of GLFE, we conducted an experiment by combining MSFE and GLFE, where their outputs were added directly to obtain the final result. As shown in Table 1, MSFE + GLFE outperforms MSFE alone by 0.08%, 0.09%, 0.21%, and 0.65% on the four datasets, respectively. These results show that GLFE is effective in capturing complementary global and local contextual information, which further enhances the representational capability of the model.
- (3)
- Effectiveness of FIF: By incorporating the FIF module to fuse the outputs of MSFE and GLFE, we conducted an experiment aimed at assessing the effectiveness of FIF. As shown in Table 1, the configuration MSFE + GLFE + FIF outperforms MSFE + GLFE by 0.03%, 0.02%, 0.10%, and 0.32% on the four datasets, respectively. These results demonstrate that FIF effectively enhances feature interaction and fusion, contributing to improved detection performance.
3.3. Comparison with Other Advanced HTD Methods
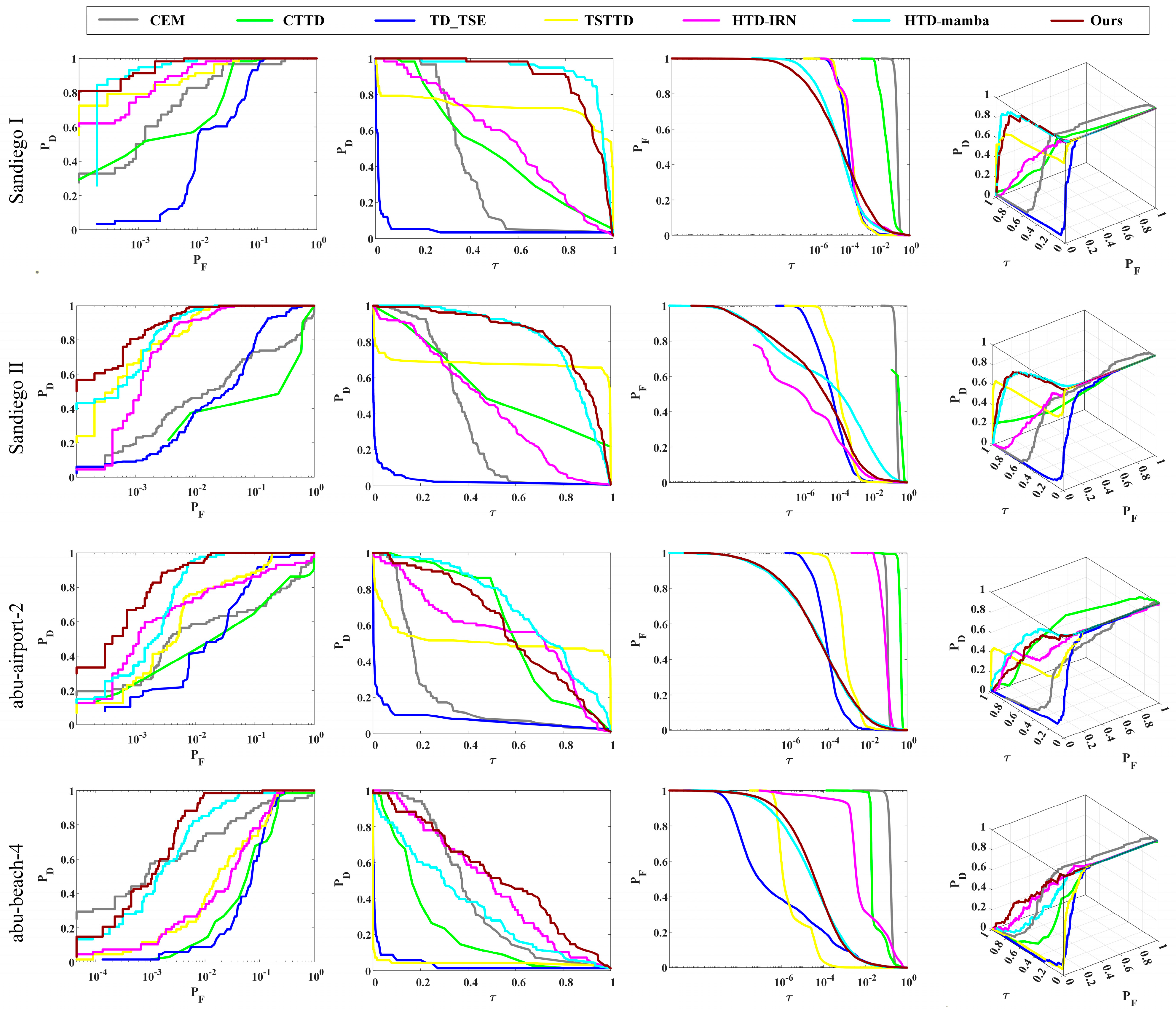
3.3.1. Qualitative Comparison
- (1)
- ROC curve comparisons
- (2)
- Background-target separation map comparisons
- (3)
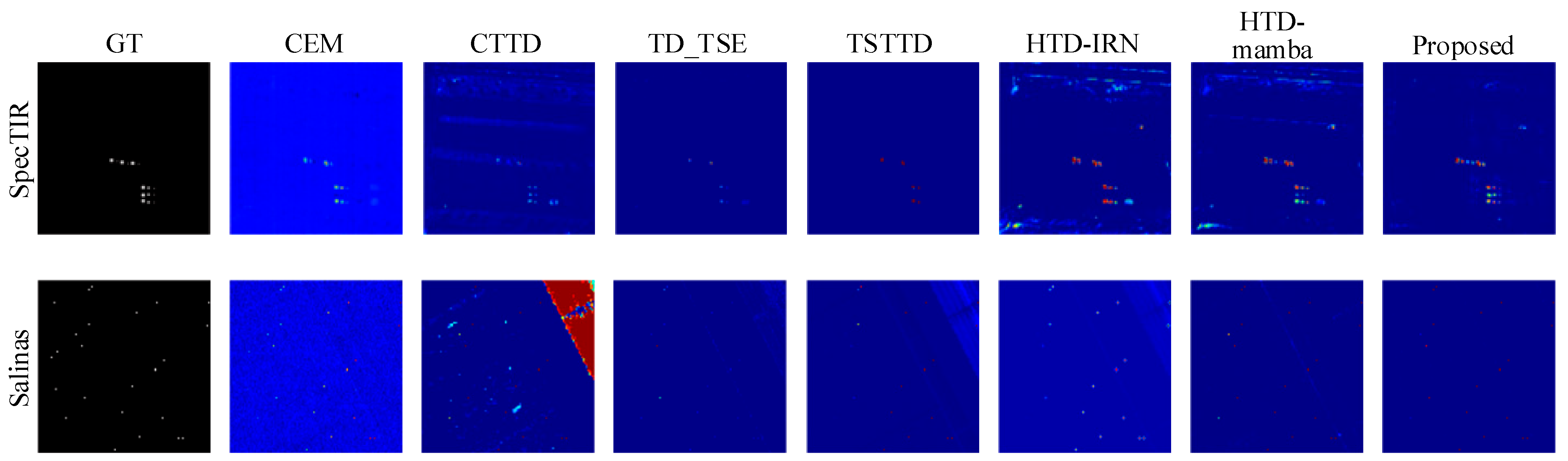
- Detection map comparisons
3.3.2. Quantitative Comparison
4. Discussion
4.1. Impact of Fusion Strategy
4.2. Impact of the Larger Dataset
4.3. Impact of the Low-Contrast Dataset
4.4. Analyses of Computational Efficiency
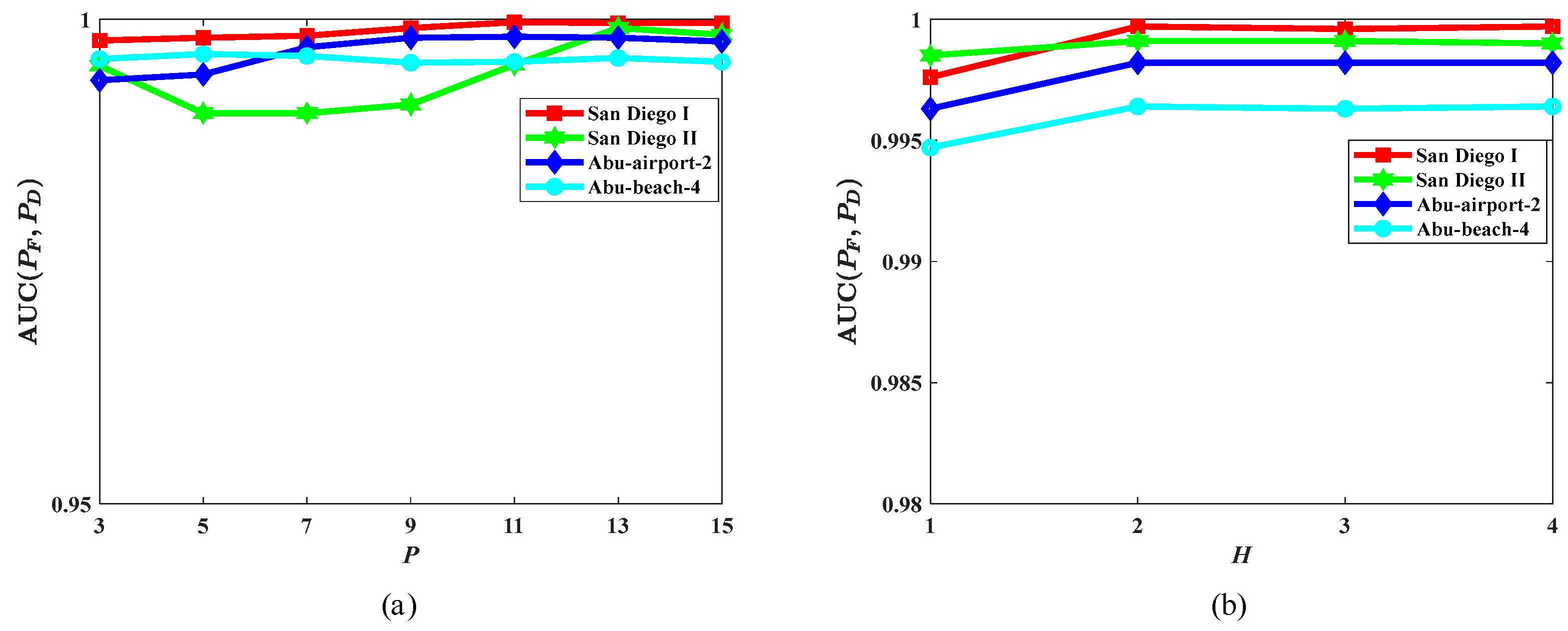
4.5. Impact of Hyperparameters
- (1)
- Patch size P: For the patch sizes, as shown in Figure 12a, the highest AUC(PF, PD) values were achieved when the patch sizes were set to 11 × 11, 13 × 13, 11 × 11, and 5 × 5 for the San Diego I, San Diego II, Abu-airport-2, and Abu-beach-4 datasets, respectively. Therefore, these sizes were adopted to ensure optimal detection performance for each dataset.
- (2)
- Number of attention heads H: For the number of attention heads, as shown in Figure 12b, when the number of attention heads exceeds 2, the AUC(PF, PD) value remains stable and reaches its maximum. Therefore, considering both detection accuracy and computational efficiency, the number of attention heads is set to 2.
- (3)
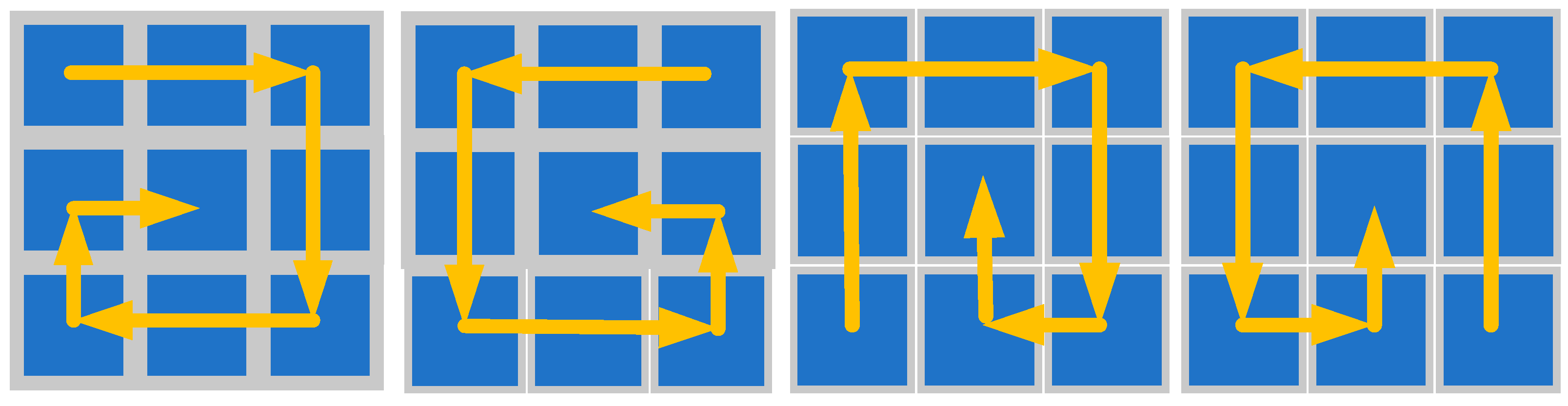
- For the scan orientations in the proposed circular scanning strategy, as illustrated in Figure 5, we designed four orientations starting from the four corner points and scanning towards the center in a circular manner. This configuration enables comprehensive local feature extraction from multiple perspectives.
4.6. Impact of Spectral–Spatial Attention (SSA) Block
4.7. Impact of Similarity Strategy
4.8. Differences with Existing Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, Q.; Xue, Y.; Zhang, L. Progress in hyperspectral remote sensing science and technology in China over the past three decades. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 70–91. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2013, 31, 34–44. [Google Scholar] [CrossRef]
- Chen, B.; Liu, L.; Zou, Z.; Shi, Z. Target detection in hyperspectral remote sensing image: Current status and challenges. Remote Sens. 2023, 15, 3223. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent advances on spectral–spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1579–1597. [Google Scholar] [CrossRef]
- Wang, X.; Hu, Q.; Cheng, Y.; Ma, J. Hyperspectral image super-resolution meets deep learning: A survey and perspective. IEEE/CAA J. Autom. Sin. 2023, 10, 1668–1691. [Google Scholar] [CrossRef]
- Chen, C.; Sun, Y.; Hu, X.; Zhang, N.; Feng, H.; Li, Z.; Wang, Y. Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution. Remote Sens. 2025, 17, 1947. [Google Scholar] [CrossRef]
- Huo, Y.; Cheng, X.; Lin, S.; Zhang, M.; Wang, H. Memory-Augmented Autoencoder with Adaptive Reconstruction and Sample Attribution Mining for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5518118. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, C.; Huo, Y.; Zhang, M.; Wang, H.; Ren, J. Prototype-Guided Spatial-Spectral Interaction Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5516517. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Chen, X.; Zheng, H. Deep bidirectional hierarchical matrix factorization model for hyperspectral unmixing. Appl. Math. Model. 2025, 137, 115736. [Google Scholar] [CrossRef]
- Chang, S.; Du, B.; Zhang, L.; Zhao, R. IBRS: An iterative background reconstruction and suppression framework for hyperspectral target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3406–3417. [Google Scholar] [CrossRef]
- Zhao, X.; Hou, Z.; Wu, X.; Li, W.; Ma, P.; Tao, R. Hyperspectral target detection based on transform domain adaptive constrained energy minimization. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102461. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, H.; Xu, F.; Zhu, Y.; Fu, X. Constrained-target band selection with subspace partition for hyperspectral target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9147–9161. [Google Scholar] [CrossRef]
- Qin, H.; Wang, S.; Li, Y.; Xie, W.; Jiang, K.; Cao, K. A Signature-constrained Two-stage Framework for Hyperspectral Target Detection Based on Generative Self-supervised Learning. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5514917. [Google Scholar] [CrossRef]
- Bayarri, V.; Prada, A.; García, F.; De Las Heras, C.; Fatás, P. Remote Sensing and Environmental Monitoring Analysis of Pigment Migrations in Cave of Altamira’s Prehistoric Paintings. Remote Sens. 2024, 16, 2099. [Google Scholar] [CrossRef]
- Luo, F.; Shi, S.; Qin, K.; Guo, T.; Fu, C.; Lin, Z. SelfMTL: Self-Supervised Meta-Transfer Learning via Contrastive Representation for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5508613. [Google Scholar] [CrossRef]
- West, J.E.; Messinger, D.W.; Ientilucci, E.J.; Kerekes, J.P. Matched filter stochastic background characterization for hyperspectral target detection. In Proceedings of the SPIE 5806, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Orlando, FL, USA, 1 June 2005; Volume 5806, pp. 1–12. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Chang, C.I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef]
- Kelly, E.J. An adaptive detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 2007, AES-22, 115–127. [Google Scholar] [CrossRef]
- Kraut, S.; Scharf, L.L. The CFAR adaptive subspace detector is a scale-invariant GLRT. IEEE Trans. Signal Process. 2002, 47, 2538–2541. [Google Scholar] [CrossRef]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the Coeur d’Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Chang, C.I.; Ren, H.; Hsueh, M.; Du, Q.; D’Amico, F.M.; Jensen, J.O. Revisiting the target-constrained interference-minimized filter (TCIMF). In Proceedings of the SPIE 5159, Imaging Spectrometry IX, San Diego, CA, USA, 7 January 2004; Volume 5159, pp. 339–348. [Google Scholar]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L. A sparse representation-based binary hypothesis model for target detection in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1346–1354. [Google Scholar] [CrossRef]
- Li, W.; Du, Q.; Zhang, B. Combined sparse and collaborative representation for hyperspectral target detection. Pattern Recognit. 2015, 48, 3904–3916. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, Y.; Zhang, L. Spatially adaptive sparse representation for target detection in hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1923–1927. [Google Scholar] [CrossRef]
- Zhao, X.; Li, W.; Zhao, C.; Tao, R. Hyperspectral target detection based on weighted Cauchy distance graph and local adaptive collaborative representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527313. [Google Scholar] [CrossRef]
- Huo, Y.; Qian, X.; Li, C.; Wang, W. Multiple instance complementary detection and difficulty evaluation for weakly supervised object detection in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6006505. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Hyperspectral remote sensing image subpixel target detection based on supervised metric learning. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4955–4965. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, K.; Gao, K.; Gao, K.; Li, W. Hyperspectral time-series target detection based on spectral perception and spatial–temporal tensor decomposition. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5520812. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, K.; Wang, X.; Zhao, S.; Gao, K.; Lin, H. Tensor Adaptive Reconstruction Cascaded with Global and Local Feature Fusion for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 607–620. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, H.; Lu, Z.; Zhang, Y.; Ding, Y.; Li, X.; Zhang, B. MDA-HTD: Mask-driven dual autoencoders meet hyperspectral target detection. Inf. Process. Manag. 2025, 62, 104106. [Google Scholar] [CrossRef]
- Tian, Q.; He, C.; Xu, Y.; Wu, Z.; Wei, Z. Hyperspectral target detection: Learning faithful background representations via orthogonal subspace-guided variational autoencoder. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5516714. [Google Scholar] [CrossRef]
- Sun, L.; Ma, Z.; Zhang, Y. ABLAL: Adaptive background latent space adversarial learning algorithm for hyperspectral target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 411–427. [Google Scholar] [CrossRef]
- Qin, H.; Xie, W.; Li, Y.; Jiang, K.; Lei, J.; Du, Q. Weakly supervised adversarial learning via latent space for hyperspectral target detection. Pattern Recognit. 2023, 135, 109125. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Yu, X.; Mei, S. Robust signature-based hyperspectral target detection using dual networks. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5500605. [Google Scholar] [CrossRef]
- Xu, S.; Geng, S.; Xu, P.; Chen, Z.; Gao, H. Cognitive fusion of graph neural network and convolutional neural network for enhanced hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5515915. [Google Scholar] [CrossRef]
- Qin, H.; Xie, W.; Li, Y.; Du, Q. HTD-VIT: Spectral-spatial joint hyperspectral target detection with vision transformer. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1967–1970. [Google Scholar]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese transformer network for hyperspectral image target detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526419. [Google Scholar] [CrossRef]
- Jiao, J.; Gong, Z.; Zhong, P. Triplet spectralwise transformer network for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5519817. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Shen, D.; Zhu, X.; Tian, J.; Liu, J.; Du, Z.; Wang, H. HTD-Mamba: Efficient Hyperspectral Target Detection with Pyramid State Space Model. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5507315. [Google Scholar] [CrossRef]
- Huang, T.; Pei, X.; You, S.; Wang, F.; Qian, C.; Xu, C. Localmamba: Visual state space model with windowed selective scan. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Cham, Switzerland, 2025; pp. 12–22. [Google Scholar]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Liu, Y. Vmamba: Visual state space model. arXiv 2024, arXiv:2401.10166. [Google Scholar] [PubMed]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1990–2000. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Chang, C.I. Comprehensive analysis of receiver operating characteristic (ROC) curves for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511720. [Google Scholar] [CrossRef]
- Chang, C.I. An effective evaluation tool for hyperspectral target detection: 3D receiver operating characteristic curve analysis. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5131–5153. [Google Scholar] [CrossRef]
- Sun, X.; Zhuang, L.; Gao, L.; Gao, H.; Sun, X.; Zhang, B. Information retrieval with chessboard-shaped topology for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5514515. [Google Scholar] [CrossRef]
- Sun, X.; Qu, Y.; Gao, L.; Sun, X.; Qi, H.; Zhang, B. Target detection through tree-structured encoding for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4233–4249. [Google Scholar] [CrossRef]
- Shen, D.; Ma, X.; Kong, W.; Liu, J.; Wang, J.; Wang, H. Hyperspectral target detection based on interpretable representation network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5519416. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.J. CrossFuse: A novel cross attention mechanism based infrared and visible image fusion approach. Inf. Fusion 2024, 103, 102147. [Google Scholar] [CrossRef]
- Herwegab, J.A.; Kerekesa, J.P.; Weatherbeec, O.; Messinger, D.; van Aardt, J.; Ientilucci, E.; Ninkov, Z.; Faulring, J.; Raqueño, N.; Meola, J. Spectir hyperspectral airborne rochester experiment data collection campaign. In Proceedings of the SPIE Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII, Baltimore, MD, USA, 23–27 April 2012; Volume 8390, pp. 839028-1–839028-10. [Google Scholar]
- Feng, R.; Li, H.; Wang, L.; Zhong, Y.; Zhang, L.; Zeng, T. Local spatial constraint and total variation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5512216. [Google Scholar] [CrossRef]






| SSFE (Baseline) | MSFE | GLFE | FIF | San Diego I | San Diego II | Abu-Airport-2 | Abu-Beach-4 |
|---|---|---|---|---|---|---|---|
| √ | 0.9912 | 0.9922 | 0.9916 | 0.9841 | |||
| √ | 0.9986 | 0.9980 | 0.9951 | 0.9867 | |||
| √ | √ | 0.9994 | 0.9989 | 0.9972 | 0.9932 | ||
| √ | √ | √ | 0.9997 | 0.9991 | 0.9982 | 0.9964 |
| Dataset | AUC Values | CEM | CTTD | TD_TSE | TSTTD | HTD-IRN | HTD-Mamba | Ours |
|---|---|---|---|---|---|---|---|---|
| San Diego I | AUC(PF, PD) ↑ | 0.8151 | 0.6929 | 0.9309 | 0.9971 | 0.9983 | 0.9994 | 0.9997 |
| AUC(τ, PD) ↑ | 0.3591 | 0.5534 | 0.0306 | 0.7296 | 0.5633 | 0.9311 | 0.8998 | |
| AUC(τ, PF) ↓ | 0.2504 | 0.3170 | 0.0004 | 0.0008 | 0.0044 | 0.0066 | 0.0074 | |
| AUCODP ↑ | 0.9238 | 0.9293 | 0.9611 | 1.7259 | 1.5572 | 1.9241 | 1.8921 | |
| AUCSNPR ↑ | 1.4340 | 1.7456 | 77.3617 | 974.6511 | 127.0831 | 140.2938 | 121.3924 | |
| Inference time ↓ | 0.3410 | 0.3560 | 0.5620 | 2.8900 | 2.7262 | 1.7562 | 1.8530 | |
| San Diego II | AUC(PF, PD) ↑ | 0.9865 | 0.9869 | 0.9695 | 0.9978 | 0.9967 | 0.9986 | 0.9991 |
| AUC(τ, PD) ↑ | 0.3868 | 0.5053 | 0.0499 | 0.6804 | 0.4500 | 0.8280 | 0.8435 | |
| AUC(τ, PF) ↓ | 0.1668 | 0.0525 | 0.0011 | 0.0015 | 0.0032 | 0.0172 | 0.0057 | |
| AUCODP ↑ | 1.2065 | 1.4397 | 1.0183 | 1.6767 | 1.4435 | 1.8094 | 1.8368 | |
| AUCSNPR ↑ | 2.3188 | 9.6307 | 44.6177 | 461.7719 | 140.8711 | 48.2789 | 147.2270 | |
| Inference time ↓ | 0.4265 | 0.3256 | 0.4236 | 2.6500 | 2.8626 | 1.7652 | 1.8226 | |
| Abu-airport-2 | AUC(PF, PD) ↑ | 0.8361 | 0.8036 | 0.9511 | 0.9745 | 0.9250 | 0.9968 | 0.9982 |
| AUC(τ, PD) ↑ | 0.2230 | 0.6124 | 0.0773 | 0.5154 | 0.5633 | 0.7051 | 0.6043 | |
| AUC(τ, PF) ↓ | 0.1043 | 0.4669 | 0.0006 | 0.0063 | 0.0852 | 0.0090 | 0.0052 | |
| AUCODP ↑ | 0.9548 | 0.9491 | 1.0278 | 1.4836 | 1.4031 | 1.6929 | 1.5973 | |
| AUCSNPR ↑ | 2.1381 | 1.3116 | 132.8010 | 82.4463 | 6.6085 | 78.2876 | 116.8085 | |
| Inference time ↓ | 0.3659 | 0.2652 | 0.3952 | 2.9556 | 2.9652 | 1.7966 | 1.7952 | |
| Abu-beach-4 | AUC(PF, PD) ↑ | 0.9419 | 0.9034 | 0.9174 | 0.9481 | 0.9483 | 0.9923 | 0.9964 |
| AUC(τ, PD) ↑ | 0.4089 | 0.2201 | 0.0332 | 0.0427 | 0.4822 | 0.3482 | 0.5306 | |
| AUC(τ, PF) ↓ | 0.1704 | 0.0489 | 0.0023 | 0.0002 | 0.0613 | 0.0025 | 0.0033 | |
| AUCODP ↑ | 1.1804 | 1.0746 | 0.9483 | 0.9907 | 1.3692 | 1.3380 | 1.5237 | |
| AUCSNPR ↑ | 2.3988 | 4.5018 | 14.3010 | 227.3069 | 7.8677 | 138.7763 | 161.0973 | |
| Inference time ↓ | 0.0896 | 0.5624 | 0.3562 | 2.8654 | 3.9521 | 2.9535 | 2.3655 |
| Addition | Cross-Attention | FIF | San Diego I | San Diego II | Abu-Airport-2 | Abu-Beach-4 |
|---|---|---|---|---|---|---|
| √ | 0.9994 | 0.9989 | 0.9972 | 0.9932 | ||
| √ | 0.9997 | 0.9990 | 0.9979 | 0.9955 | ||
| √ | 0.9997 | 0.9991 | 0.9982 | 0.9964 |
| Dataset | AUC Values | CEM | CTTD | TD_TSE | TSTTD | HTD-IRN | HTD-Mamba | Ours |
|---|---|---|---|---|---|---|---|---|
| SpecTIR | AUC(PF, PD) ↑ | 0.7478 | 0.9303 | 0.9836 | 0.9922 | 0.8568 | 0.9930 | 0.9993 |
| AUC(τ, PD) ↑ | 0.3747 | 0.3985 | 0.1148 | 0.5223 | 0.6464 | 0.6090 | 0.6996 | |
| AUC(τ, PF) ↓ | 0.1208 | 0.0227 | 0.0001 | 0.0002 | 0.0111 | 0.0074 | 0.0034 | |
| AUCODP ↑ | 1.0017 | 1.3061 | 1.0983 | 1.5143 | 1.4922 | 1.5946 | 1.6955 | |
| AUCSNPR ↑ | 3.1009 | 17.5420 | 1116.8857 | 2694.8164 | 58.0937 | 82.7502 | 207.2633 | |
| Salinas | AUC(PF, PD) ↑ | 0.9954 | 0.8849 | 0.9774 | 0.9695 | 0.9524 | 0.9984 | 0.9994 |
| AUC(τ, PD) ↑ | 0.5821 | 0.7881 | 0.1464 | 0.6512 | 0.5571 | 0.8186 | 0.7809 | |
| AUC(τ, PF) ↓ | 0.0893 | 0.1022 | 0.0015 | 0.0104 | 0.0366 | 0.0008 | 0.0002 | |
| AUCODP ↑ | 1.4881 | 1.5708 | 1.1223 | 1.6102 | 1.4729 | 1.8162 | 1.7801 | |
| AUCSNPR ↑ | 6.5155 | 7.7134 | 96.7823 | 62.3423 | 15.2363 | 975.0307 | 4207.4922 |
| Methods | TSTTD | HTD-IRN | HTD-Mamba | HTMNet |
|---|---|---|---|---|
| Params. (M) | 0.91 | 0.41 | 0.34 | 1.43 |
| Memory usage (M) | 895.8 | 774.3 | 890.4 | 1057.6 |
| FLOPs (G) | 1.95 | 1.76 | 0.22 | 2.55 |
| San Diego I | San Diego II | Abu-Airport-2 | Abu-Beach-4 | |
|---|---|---|---|---|
| w/o SSA | 0.9989 | 0.9984 | 0.9960 | 0.9911 |
| w/SSA | 0.9994 | 0.9989 | 0.9972 | 0.9932 |
| San Diego I | San Diego II | Abu-Airport-2 | Abu-Beach-4 | |
|---|---|---|---|---|
| Euclidean distance | 0.9995 | 0.9989 | 0.9978 | 0.9962 |
| Cosine similarity | 0.9997 | 0.9991 | 0.9982 | 0.9964 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Kuang, Y.; Huo, Y.; Zhu, W.; Zhang, M.; Wang, H. HTMNet: Hybrid Transformer–Mamba Network for Hyperspectral Target Detection. Remote Sens. 2025, 17, 3015. https://doi.org/10.3390/rs17173015
Zheng X, Kuang Y, Huo Y, Zhu W, Zhang M, Wang H. HTMNet: Hybrid Transformer–Mamba Network for Hyperspectral Target Detection. Remote Sensing. 2025; 17(17):3015. https://doi.org/10.3390/rs17173015
Chicago/Turabian StyleZheng, Xiaosong, Yin Kuang, Yu Huo, Wenbo Zhu, Min Zhang, and Hai Wang. 2025. "HTMNet: Hybrid Transformer–Mamba Network for Hyperspectral Target Detection" Remote Sensing 17, no. 17: 3015. https://doi.org/10.3390/rs17173015
APA StyleZheng, X., Kuang, Y., Huo, Y., Zhu, W., Zhang, M., & Wang, H. (2025). HTMNet: Hybrid Transformer–Mamba Network for Hyperspectral Target Detection. Remote Sensing, 17(17), 3015. https://doi.org/10.3390/rs17173015









