Texture-Adaptive Hierarchical Encryption Method for Large-Scale HR Remote Sensing Image Data

Abstract

High-resolution (HR) remote sensing images contain rich, sensitive information regarding the distribution of geospatial objects and natural resources. With the widespread application of HR remote sensing images, there is an urgent need to protect the data security of HR remote sensing images during transmission and sharing. Existing encryption approaches typically employ a global encryption strategy, overlooking the varying texture complexity across different sub-regions in HR remote sensing images. This oversight results in low efficiency and flexibility for encrypting large-scale remote sensing image data. To address these limitations, this paper presents a texture-adaptive hierarchical encryption method that combines region-specific security levels. The method first decomposes remote sensing images into grid-based sub-blocks and classifies them into three texture complexity types (i.e., simple, medium, and complex) through gradient and frequency metrics. Then, chaotic systems of different dimensions are adaptively adopted to encrypt the sub-blocks according to their texture complexity. A more complex chaotic system encrypts a sub-block with a more complex texture to ensure security while reducing computational complexity. The experimental results on publicly available high-resolution remote sensing datasets demonstrate that the proposed method achieves adequate information concealment while maintaining an optimal balance between encryption security and computational efficiency. The proposed method is more competitive in encrypting large-scale HR remote sensing data compared to conventional approaches, and it shows significant potential for the secure sharing and processing of HR remote sensing images in the big data era.

1. Introduction

High-resolution (HR) remote sensing image data are an essential type of national fundamental geographic data that can clearly and intuitively represent the distribution of geographical features on the Earth’s surface, such as urban distribution and land use [1,2,3,4,5,6]. With the advancement of satellite technology and enhanced remote sensing capabilities, data acquisition and applications have significantly improved [7,8,9,10]. HR remote sensing images contain rich, sensitive information regarding the distribution of geospatial objects and natural resources. Given the widespread use of HR remote sensing images, there is an urgent need to safeguard the data security of these images during transmission and sharing [11,12,13]. The rapid development of remote sensing big models and deep learning applications has introduced new security vulnerabilities during the training and application phases. These include model inversion attacks that can reconstruct sensitive geographical features from training data, adversarial sample attacks that manipulate environmental monitoring results, gradient leakage that exposes satellite imaging characteristics, and metadata inference that reveals the protected geolocation patterns. These AI-specific vulnerabilities, compounded by traditional security challenges during network transmission and data sharing, necessitate advanced protection frameworks that address both data-level encryption and model-level privacy preservation. However, existing encryption approaches typically employ a global encryption strategy, overlooking the varying texture complexity across different sub-regions in remote sensing images. This oversight results in low efficiency and flexibility in encrypting large-scale HR remote sensing image data.

Although remote sensing image encryption possesses unique characteristics, its underlying techniques remain rooted in the evolutionary trajectory of general-purpose image encryption methodologies. Traditional approaches can be broadly categorized into symmetric encryption, asymmetric encryption, and hybrid encryption. Symmetric schemes, exemplified by AES and DES, employ a single secret key for both encryption and decryption, leveraging computational efficiency to dominate real-time encryption scenarios; however, their key-distribution mechanisms face significant challenges in distributed remote sensing environments [14]. Asymmetric algorithms, such as RSA and ECC, resolve key-management issues through public-key infrastructures, yet their high computational complexity limits applicability to large-scale remote sensing datasets. Hybrid encryption achieves a pragmatic balance by utilizing asymmetric techniques for key exchange while relying on symmetric ciphers for bulk data encryption, thereby emerging as a compromise solution for current remote sensing data-sharing paradigms. Recent advancements have integrated chaotic systems and DNA encoding to enhance randomness and resistance against statistical attacks [15]. Some neural-network-based image encryption methods employing deep learning models have also been proposed to optimize cryptographic transformations adaptively, offering novel perspectives for protecting complex remote sensing textures [14]. Nevertheless, these generic methods predominantly adopt global encryption strategies, disregarding spatial disparities in texture complexity within remote sensing imagery. Consequently, low-entropy regions are excessively encrypted, whereas high-entropy areas receive insufficient protection, resulting in computational redundancy and flexibility deficits [1]. Furthermore, emerging technologies such as homomorphic encryption and lattice-based cryptography, while enabling ciphertext-domain remote sensing analyses, suffer from prohibitive latency that undermines real-time requirements [16].

To address the limitations of global encryption strategies and reconcile the tension between security, efficiency, and real-time performance, this study presents a texture-adaptive hierarchical encryption method for large-scale HR remote sensing image data. In this study, texture complexity is formally defined and quantified using information entropy, which measures the uncertainty and information content of pixel distributions in a given image block. Entropy is adopted because it provides a concise and computationally efficient proxy for texture variability, and it has been widely used as a statistical measure in remote sensing analysis. By leveraging entropy as the guiding metric, our method can adaptively assign stronger encryption operations to regions with higher texture complexity while reducing unnecessary computation in low-complexity areas. The goal of this paper is to solve the problem of how to balance high security and computational efficiency in the encryption of HR remote sensing image data. To solve this problem, a new selective encryption method based on texture complexity classification is designed.

The remainder of this paper is organized as follows. Section 2 reviews related work on remote sensing image-data encryption. In Section 3, the framework and details of the proposed texture-adaptive hierarchical encryption method are described. Section 4 presents experiments and a comparative study to evaluate the effectiveness of the proposed method. Finally, conclusions and a discussion are presented in Section 5.

2. Related Work

2.1. Traditional Image Encryption Methods

Raster geographic data (remote sensing imagery) mostly share similar data representations with conventional image data, allowing encryption research to draw on established image encryption theories [17,18]. The earliest image encryption theories originated from classical text encryption theories and cryptosystems, transforming image information into chaotic ciphertexts using mathematical or physical approaches to make the plaintext invisible to the human eye after encryption [19,20,21]. Currently, research on image encryption theory is relatively abundant, mainly including image encryption methods based on traditional encryption algorithms [22,23,24,25], chaos-based image encryption [26,27,28,29,30,31], block-based image encryption [32,33,34,35], compressed sensing-based image encryption [27,36,37], and DNA coding-based image encryption [38,39,40,41,42].

In the initial stages of image encryption research, traditional encryption algorithms were predominantly used to secure image data. These methods typically involved symmetric or asymmetric algorithms to encrypt crucial pixel information, taking advantage of the security features of the established encryption techniques for robust defense against attacks [43,44,45]. However, unlike ordinary text, image data have unique formats and characteristics, such as large volume, high redundancy, strong correlation, and a two-dimensional distribution, which means that traditional encryption methods are only partially suitable for image encryption needs [46,47]. Chaos-based encryption employs chaotic systems to encrypt the positions or values of image pixels [48]. Chaotic systems, renowned for their sensitivity to initial conditions, unpredictability, and complex bifurcation properties, offer exceptional cryptographic capabilities [49]. Therefore, they have been widely applied in image encryption, particularly through two-dimensional chaotic map functions that shuffle the pixel positions to achieve encryption. The performance of chaotic systems directly affects the encryption outcomes. Many researchers have explored new chaotic systems based on classical systems to enhance performance, induce more complex chaotic behaviors, and expand the range of chaos, thereby increasing the security of encrypted images [49,50,51]. Although more complex chaotic systems offer superior protection, they also incur greater computational complexity. To address this issue, some researchers have integrated image compression into chaotic image encryption schemes [52,53,54,55]. Directly applying nonlinear transformations in low-dimensional chaos-based encryption may pose security risks and lead to data expansion issues [56,57]. The inherent “high security–high complexity” dilemma is particularly pronounced in continuous chaotic systems. Early image encryption schemes predominantly relied on such systems: Yang et al. [58] constructed a fractional-order hyperchaotic system derived from the Lorenz oscillator, which theoretically yields two positive Lyapunov exponents. However, the associated differential equations must be solved by Adomian decomposition or Runge–Kutta integrators, resulting in an encryption time >3 s for a single 512 × 512 image [59]. Ma et al. introduced an offset-based multi-stable continuous system capable of exhibiting four coexisting attractors simultaneously, yet the unavoidable numerical integration overhead prevents real-time deployment on FPGA/ARM platforms [60]. This “high security–low efficiency” trade-off has motivated a paradigm shift toward discrete maps. One-dimensional maps such as Logistic and Tent gained immediate popularity due to their simple iterations and hardware-friendly implementations. Nevertheless, Hua et al. [61] demonstrated that their monolithic structure limits the number of positive LEs to at most one and renders them susceptible to periodic windows and dynamical degradation under finite-precision arithmetic. Choi et al. [62] combined the Arnold transformation with a Laplace expansion to construct a higher-dimensional Arnold system. Hua et al. [63] fused Logistic and Sine maps via an XOR-coupling mechanism to realize 2D/3D chaos. Despite these efforts, Liu et al. [64] proved that the positive-LE count in such systems remains far below the system dimension, failing to satisfy the “non-degenerate” condition and tending to collapse into short periodic sequences after quantization. To achieve the non-degenerate requirement “dimension = number of positive LEs,” Hua et al. [65] generalized the Arnold parameter matrix to arbitrary dimensions. They proposed the first configurable high-dimensional discrete system for which a positive-LE count can be prescribed. Wang et al. [66] and Zang et al. [67] further ensured that every dimension contributes a positive LE by employing “chaos inverse control” and “strictly diagonally dominant matrix” strategies, respectively. Liu et al. [68] incorporated nonlinear filters and feed-forward/feedback architectures to generate uniformly ergodic trajectories; their 4-D system encrypts a 1024 × 1024 image in only 0.42 s while achieving NPCR/UACI scores of 99.61%/33.47%. These results corroborate that discrete systems with ≤4 dimensions can be executed in real time on FPGA, and non-degenerate designs effectively suppress finite-precision degradation, thereby establishing both theoretical and practical foundations for 1-D/2-D/4-D hierarchical encryption. However, single-attractor systems become globally vulnerable once the key is compromised. Qin [69] observed that the number of equilibrium points is positively correlated with coexisting attractors. Ali et al. [70] devised a 1-D multi-stable map using dual sinusoidal functions with a phase parameter that enables switching among period-2, chaotic, and hyperchaotic regimes. Huang et al. [71] proposed a 3-D multi-stable hyperchaotic map featuring eight symmetric attractors. After introducing memristive elements, Ma et al. [72] realized seven coexisting dynamic modes. Further, Liu et al. [73] and Marco et al. [74] constructed discrete memristive multi-stable systems, theoretically expanding the key space to 2⁵¹². Regrettably, existing schemes have not yet simultaneously fulfilled the dual requirements of “non-degenerate + multi-stable,” leaving a critical challenge for future research. Although compressed sensing improves transmission efficiency and reduces storage space, its sparse sampling nature might result in lossy image post-decryption. With the development of DNA computing, DNA coding has emerged as a novel field of cryptography [75]. This method uses DNA as an information carrier to convert binary sequences into DNA representations. It supports massive parallel computing, offers vast storage capacity, and has low power consumption, aligning well with the demands of image encryption in terms of efficiency and transmission [76,77,78]. Thus, combining molecular computations with biological methodologies has led to the proposal of many novel image encryption schemes.

2.2. Encryption Methods for Remote Sensing Images

Although traditional image encryption methods can be applied to remote sensing image encryption, considering the large data volume and comprehensive coverage of remote sensing images, standard image encryption methods cannot balance security and efficiency. Therefore, many studies on HR remote sensing image encryption have been conducted. For example, Zhang et al. improved an AES-based image block encryption method by introducing chaotic systems [79]. They grouped sequences from remote sensing images and random sequences generated by chaotic systems into large fixed-length integers to realize AES block encryption. This symmetric approach was experimentally validated and demonstrated high security and efficiency. Given the large data volume of remote sensing images, drawbacks of small critical space, and poor randomness of low-dimensional chaotic systems, Xu et al. presented a remote sensing image encryption approach using compound chaotic neurons and tent maps [80]. Ye et al. introduced a new block-based encryption technique for remote sensing images that employs image partitioning [81]. These block shuffling and diffusing operations are applied to large images with fast encryption speed. Encryption methods primarily address the issues of large amounts of remote sensing image data and communication security, building upon and innovating existing image encryption methods.

Although in-depth studies on image encryption have been conducted from different perspectives, most current image encryption methods apply the same encryption algorithm to the entire spatial area of remote sensing images, neglecting the differences in texture complexity in remote sensing images, which leads to high computational complexity and poor adaptability and scalability of the encryption algorithms for HR remote sensing image content. HR remote sensing images are characterized by high resolution, large data volume, comprehensive coverage, multiple bands, and rich texture features, with different regions containing varying amounts of information [82]. As illustrated in Figure 1, the texture features and information content embodied in various areas of remote sensing images vary significantly. Regions such as region A (lakes) show simpler textures with less valuable geographic information. In contrast, regions such as regions B (harbors) and C (building groups) show complex textures with richer and more sensitive geographic information.

Most existing remote sensing image encryption methods use a unified global encryption strategy that overlooks the uneven distribution of information content within remote sensing images. The uniform global encryption paradigm is inherently limited in two fundamental respects. First, it incurs unnecessary computational overhead: in high-resolution remote sensing images, 30–70% of the pixels—typically found in texture-flat and semantically low-value regions such as lakes, bare soil, or cloud cover—demand only modest security. Yet global encryption methods usually apply the same high-intensity permutation-diffusion primitives to these low-value pixels as it does to high-value regions, resulting in substantial redundant computation. Second, they fail to provide differentiated protection: a monolithic security level cannot discriminate between semantically dense areas and semantically sparse ones. Consequently, the scheme cannot simultaneously optimize efficiency and fidelity. In short, global encryption methods lack a content-adaptive authorization mechanism; they neither afford additional safeguards for sensitive regions nor release computational resources for sparse areas, thereby rendering them ill-suited to the complex security requirements of HR remote sensing imagery across diverse application and terminal contexts [83]. Inspired by content-based multilevel authorization schemes for remote sensing image data [84,85,86], this study proposes a texture-adaptive hierarchical encryption method for large-scale HR remote sensing image data. The novel idea involves applying encryption techniques of varying security levels to sub-regions with differing degrees of texture complexity in the remote sensing image. A simple and faster encryption algorithm is used for regions with less available information, while a safe and slower encryption algorithm is employed for areas with complex texture features (characterizing regions with rich and sensitive information). This hierarchical encryption strategy allows for the adaptive selection of more appropriate encryption algorithms based on the regional characteristics of remote sensing image data. In this manner, remote sensing image data can be effectively protected while avoiding the pitfalls of weak security or low efficiency associated with the indiscriminate use of simple or complex encryption algorithms.

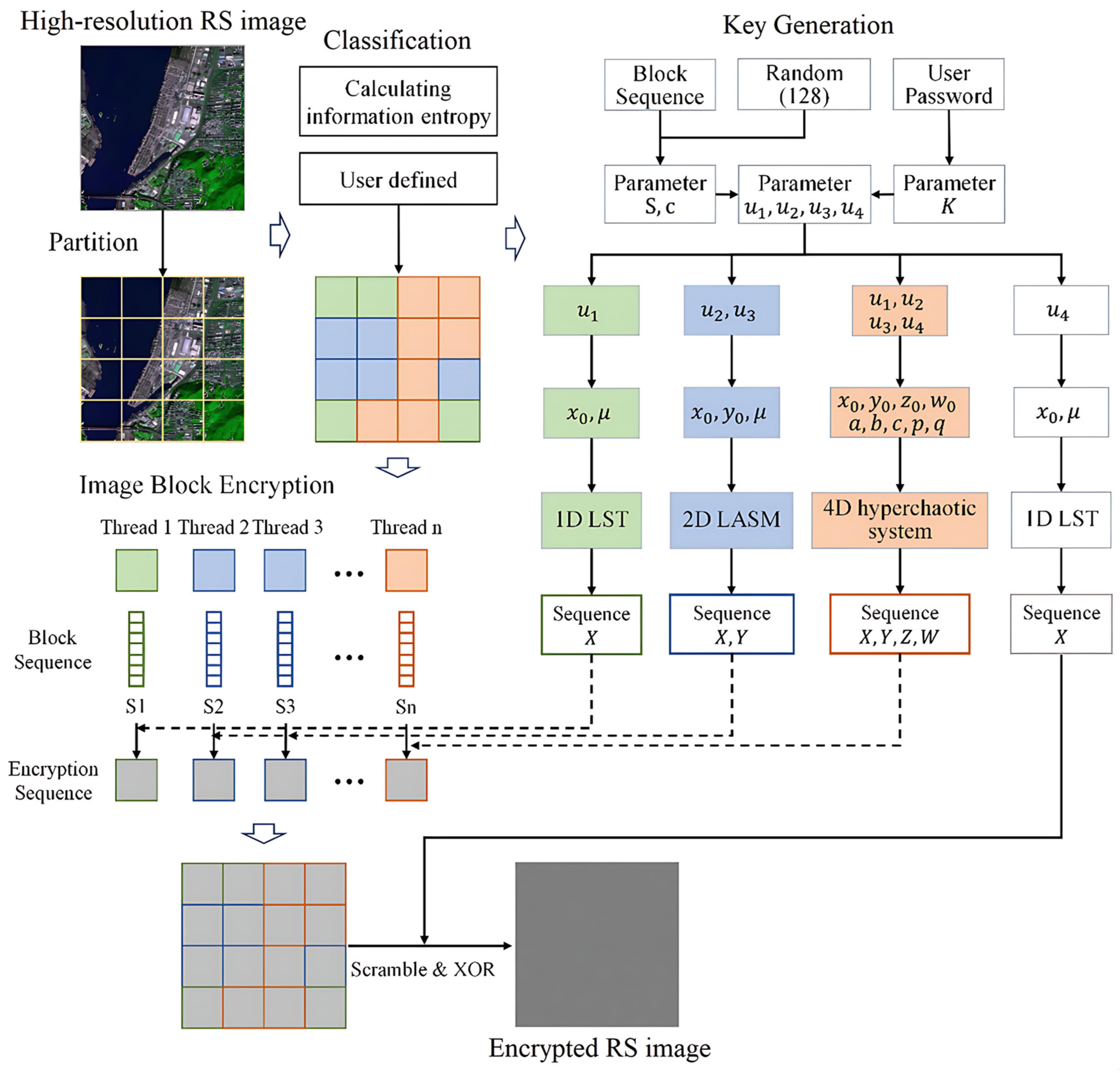
3. Methodology

3.1. Preliminaries

Chaotic systems are commonly used to generate random sequences in cryptography, which is also the basis of many image-data encryption methods. Thus, this paper first defines and introduces concepts related to the chaotic systems used in our method.

3.1.1. One-Dimensional Logistic-Tent Chaotic System

The Logistic–Tent chaotic system (LTS) proposed by Zhou et al. is a novel one-dimensional (1D) chaotic system developed by integrating the Logistic and Tent chaotic systems as seed maps [87]. Compared with the seed maps, LTS has a more significant phase space and better chaotic performance. The 1D LTS is defined as follows:

$$x_{n+1}=\left\{\begin{array}{c}{(\mu x}_n\left(1-x_n\right)+\left(4-\mu \right){\displaystyle \frac{x_n}{2}}) mod 1,x_nϵ[\mathrm{0,0.5})\\ {(\mu x}_n\left(1-x_n\right)+{\displaystyle \frac{\left(4-\mu \right)\left(1-x_n\right)}{2}}) mod 1,x_nϵ\left[\mathrm{0.5,1}\right]\end{array}\right.$$

(1)

where the control parameter $\mu \in \left(0, 4\right)$, $x$ is the variable of the system with values within $\left[0, 1\right]$, and n is the iteration number.

Through n iterations, n random numbers can be generated, and the sequence formed by these random numbers is the pseudo-random sequence produced by the chaotic system. This system maintains a chaotic state within the range of μ, offering better chaotic characteristics than the Logistic and Tent chaotic systems.

3.1.2. Two-Dimensional Logistic-Adjusted-Sine Map

The two-dimensional Logistic-Adjusted-Sine Map (2D-LASM) chaotic system is a novel two-dimensional (2D) chaotic system constructed by modulating the Logistic and Sine maps [88]. The 2D-LASM model is defined as follows:

$$\left\{\begin{array}{c}{x}_{n+1}=\mathit{sin}\left(\pi \mu \left(y_n+3\right)x_n\left(1-x_n\right)\right)\\ y_{n+1}=\mathit{sin}\left(\pi \mu \left(x_{n+1}+3\right)y_n\left(1-y_n\right)\right)\end{array}\right.$$

(2)

where the control parameter $\mu \in \left[\mathrm{0,1}\right]$, $x$ and $y$ are the variables of the system, and n is the iteration number. A 2D-LASM is constructed by integrating the Sine map and Logistic map; in the construction process, the logistic equation is first scaled by a factor of μ, and then the scaling result is fed as input to the Sine map; finally, the phase plane is extended from 1D to 2D. Unlike the individual Sine and Logistic maps, the interaction between the two input variables $x$ and $y$ in 2D-LASM creates a more complex system and makes output prediction more difficult.

3.1.3. Four-Dimensional Hyperchaotic System

Laarem proposed an improved four-dimensional (4D) autonomous chaotic system by introducing nonlinear state feedback to the first equation and a nonlinear cross-product term to the third equation of a three-dimensional Rössler chaotic system [89]. This leads to a hyperchaotic system with 12 terms and three nonlinearities and is formulated as follows:

$$\left\{\begin{array}{l}{x}_{n+1}=-y_n-z_n+w_n\\ y_{n+1}=x_n+a{y}_n-z_n\\ z_{n+1}=b_n+z_n\left(x_n-c\right)+p{x}_n{w}_n\\ w_{n+1}=-x_n{y}_n+q{w}_n\end{array}\right.$$

(3)

where $x$, $y$, $z$, and $w$ are the state variables, and $a$, $b$, $c$, $p$, and $q$ are the system parameters. When $a$ = 0.1, $b$ = 0.1, $c$ = 14, $p$ = −20, and $q$ = −0.28, the system exhibits hyperchaotic behavior. The two positive Lyapunov exponents prove that it exhibits hyperchaotic behavior, and it is challenging to crack its parameters through brute-force attacks.

3.2. Texture-Adaptive Hierarchical Encryption Method

Inspired by content-based multilevel authorization of remote sensing image data, this paper proposes a texture-adaptive hierarchical encryption method for HR remote sensing images. This method is based on the complexity of texture features and adopts different encryption algorithms ranging from simple to complex with varying levels of security to match the diverse texture complexities within HR remote sensing (RS) images. Specifically, simple encryption is used for uncomplicated textures (less sensitive information), whereas complex encryption algorithms are employed for regions with complex textures (more sensitive information). This approach allows for the adaptive selection of encryption algorithms that best fit the regional characteristics of RS images, thereby effectively protecting the data while avoiding the pitfalls of weak security or inefficiency associated with the blanket application of basic or advanced encryption algorithms. The overall workflow of the proposed encryption approach is illustrated in Figure 2. First, the RS image was divided into blocks, and the information entropy of each sub-block was computed to categorize them into distinct levels. Second, encryption algorithms are selected based on the characteristics of the image blocks to generate and encrypt the keys. Finally, the sub-blocks are stitched together, and further encryption is performed on the entire image to obtain the final encrypted image. The decryption process is the inverse of the steps above.

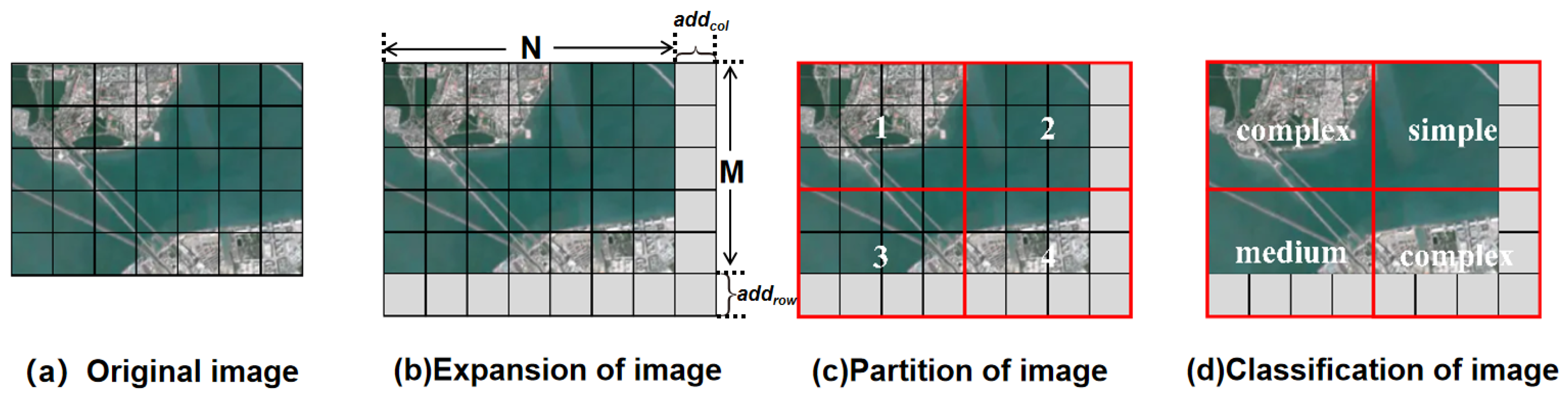
3.2.1. Partition and Texture Complexity Classification of RS Images

The method divides the RS image into equal-sized image blocks to measure the amount of information in different regions. Encryption processing is then applied to these image blocks. We assume that the original RS image is I, with a size of $M\times N$, and the size of each image block is $m\times n$. The numbers of rows and columns of the resulting blocks can be determined using the following formula:

$$Row=\left\{\begin{array}{c}{\displaystyle \frac{M}{m}}, M mod m=0\\ ⌈{\displaystyle \frac{M}{n}}⌉, M mod m\ne 0\end{array}\right.$$

(4)

$$Col=\left\{\begin{array}{c}{\displaystyle \frac{N}{n}}, N mod n=0\\ ⌈{\displaystyle \frac{N}{n}}⌉, N mod n\ne 0\end{array}\right.$$

(5)

where Row is the row number of the image blocks, Col is the column number of the image blocks, $⌈\ast ⌉$ represents rounding, and mod refers to the modulo operation. The size of the image blocks (m, n) can be set according to the original image resolution and user requirements. In this study, m and n were set to 128. The image-processing flow is shown in Figure 3.

Furthermore, based on the number of rows and columns required for blocking, the original remote sensing image was divided into blocks to obtain the image block set $ImgSet=\left\{I_1, I_2,\dots , I_s\right\}$, where $s=Row\times Col$, and s is the number of image blocks. Because the original remote sensing image may not be perfectly divided into image blocks, a row or column extension of the original image is required. This section calculates the number of extended rows and columns using Equations (6) and (7), respectively.

$$\left\{{\displaystyle \genfrac{}{}{0pt}{}{f_m=M mod m}{ad{d}_{row}=\left\{\begin{array}{c}0, { f}_m=0\\ m-f_m, f_m\ne 0\end{array}\right.}}\right.$$

(6)

$$\left\{{\displaystyle \genfrac{}{}{0pt}{}{f_n=N mod n}{ad{d}_{col}=\left\{\begin{array}{c}0, { f}_n=0\\ n-f_n, f_n\ne 0\end{array}\right.}}\right.$$

(7)

where $ad{d}_{row}$ and $ad{d}_{col}$ are the number of rows and columns to expand, respectively, and mod is the remaining operation function.

The size of the comprehensive row matrix was $ad{d}_{row}\times N$, and that of the extended column matrix was $ad{d}_{col}\times \left(M+ ad{d}_{row}\right)$. This is based on the principle that better randomness of encrypted pixel values leads to higher security of RS images. Each element of the matrix was generated by a random number generator with a range of [0, 255]. By default, the extended row matrix is concatenated at the bottom of the image and the comprehensive column matrix is attached to the rightmost side. Moreover, to ensure that the decrypted image is the same size as the original image, the number of vast rows and columns must be recorded as auxiliary information and saved in the header of the encrypted image for decryption.

To ensure the security of image block encryption and enhance the sensitivity of the encryption key, the proposed method correlates the encryption key with remote sensing image data. Specifically, the sum of pixel values ${SUM}_t$ for each image block is first calculated. Then, to obtain the same encryption key during decryption, the sum of pixel values needs to be converted to the pixel value range of the image and stored; that is, the modulo 256 value ${SUM}_t^{\prime }$ of each pixel sum is calculated using formula 8, and $NumP$ is calculated using formula 9. We use ${SUM}_t^{\prime }$ and $NumP$ as parameters to generate the encryption key for each image block.

$${\displaystyle \genfrac{}{}{0pt}{}{{SUM}_t={\sum }_{j=1}^n{\sum }_{i=1}^m{P}_{i,j}}{{SUM}_t^{\prime }={SUM}_t mod 256}}$$

(8)

$$NumP=(\sum _{t=1}^s{SUM}_t) mod 256$$

(9)

where $P_{i,j}$ is the pixel value in row $i$ and column $j$, m and n are the number of rows and columns of the image block, ${SUM}_t$ is the sum of the pixel values in the t-th image block, and $s$ is the number of all image blocks.

Specifically, assuming that the sum of pixel values of each image block is $SUM=\left\{{SUM}_1, {SUM}_2,\dots , {SUM}_s\right\}$, a random integer matrix Q is constructed with elements ranging from 0 to 255, where the size of Q is $1\times \left(M+addrow\right)$. The first s positions ($M+{add}_{row}\ge s$) of Q are used to record the ${SUM}_t^{\prime }$ of each image block and record $NumP$ at the (s+1)-th position of $Q=\left[{SUM}_1^{\prime }, {SUM}_2^{\prime },\dots , {SUM}_s^{\prime }, NumP, \dots \right]$. Matrix Q is used as an input variable for encrypting each image block in the next step.

Texture is an essential characteristic of remote sensing imagery, with more intricate textures containing richer details and representing a more significant amount of knowledge, embodying a greater amount of information from the image. Therefore, greater attention and protection should be provided during encryption in areas with more complex textures. This study introduces the concept of information entropy to assess texture complexity in remote sensing images. The image blocks are then classified into different levels based on their information entropy, as shown in Figure 3. Specifically, the information entropy proposed by Shannon was utilized to quantify the information content of each image block [27]:

$$H_t=-\sum _{i=1}^L{p}_{i}log{p}_i$$

(10)

where $H_t$ represents the information entropy of the t-th image block $I_t$, L is the gray level of the image, $p_i$ is the ratio of the number of pixels with a value i in the block, and $I_t$ is the total number of pixels in this block. For remote sensing image data with pixel values ranging from 0 to 255, the value range of information entropy is from 0 to 8. A greater value indicates that the image block contains more information and may have relatively complex texture features.

The proposed method suggests that different RS images be divided based on user-defined thresholds. However, this study established threshold reference values by dividing a large sample of RS images into equal intervals, setting these thresholds at 2.67 and 5.34. Based on the information entropy of each image block, they were divided into three types: simple ($C_t=0$), medium ($C_t=1$), and complex ($C_t=2$).

$$C_t=\left\{\begin{array}{l}0, H_t\in \left[0, 2.67\right)\\ 1, H_t\in \left[2.67, 5.34\right)\\ 2, H_t\in \left[5.34, 8\right]\end{array}\right.$$

(11)

where $C_t$ represents the type label of the image block $I_t$, $H_t$ is the information entropy of $I_t$.

The decryption process selects the corresponding decryption algorithm according to the type of each image block. Given that the decryption process selects the appropriate decryption algorithm based on the type of each image block, it is essential to save the type information ($C_t$) during encryption for subsequent retrieval during decryption. In this step, a random integer matrix W with a range of [0, 255] is generated to maintain the type information of each image block. The size of W is $1\times \left(M+{add}_{row}\right)$, where $M+{add}_{row}\ge s$, and the type information ($C_t$) of each image block is replaced in the first s numbers of W in the order of its block number t.

3.2.2. Initial Encryption Parameter Generation

This study adopts different local encryptions for different image blocks to improve the security of the entire encrypted RS image. For each image block $I_t$ in the image block set, $NumP$ and the corresponding ${SUM}_t^{\prime }$ in the matrix Q as parameters are taken, and the commonly used password-based key derivation function PBKDF is applied to compute a derived key for each image block [90]. Then, the encryption key for each image block is calculated based on the derived key, so that the encryption keys for different image blocks are distinct. Here, the encryption key for each sub-image refers to the initial parameters of the chaotic system used, whereas for simple image blocks, the encryption key contains three parameters: the initial variable $x_0$, control parameter $\mu$, and iteration number $k$. For medium image blocks, it contains four parameters: initial variables $x_0$ and $y_0$, control parameter $\mu$, and iteration number $k$. For complex image blocks, it has ten parameters: initial variables $x_0$, $y_0$, $z_0$, and $w_0$; control parameters $a$, $b$, $c$, $p$, and $q$; and iteration number $k$. The specific steps for generating image block encryption keys are as follows:

(1) The salt value S and iteration count c are calculated using the following formulas:

$$S=SM3\left(random\left(128\right)\right)⨁SM3\left(P{S_t}^{\prime }+NumP\right)$$

(12)

$$c=NumP mod 100+1$$

(13)

where $\mathrm{S}\mathrm{M}3$ is a cryptographic hash algorithm, $\oplus$ represents XOR operation, $P{S}_t$ is the value obtained by taking the sum of the pixel values of each image block modulo 256, $mod$ represents modulo operation, and $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\left(·\right)$ is a random number generator.

(2) The passphrase P (the result of the user’s password after the SM3 calculation), salt S, and iteration count c are applied as inputs to the password-based key derivation function to generate the derived key DK.

$$M\left(P,U\right)=SM3\left(P⨁U\right)$$

(14)

$$\left\{\begin{array}{c}{U}_1=M(P,S||INT\left(i\right))\hfill \\ U_2=M\left(P,U_1\right)\hfill \\ \dots \dots \\ U_c=M(P,U_{c-1})\hfill \end{array}\right.$$

(15)

$$T_{\left(256\right)}=U_1⨁U_2\dots \dots ⨁U_c$$

(16)

$${DK}_1\left|\right|{DK}_2\left|\right|\dots \dots \left|\right|{DK}_8=T_{\left(256\right)}$$

(17)

where $\mathrm{M}\left(P,U\right)$ denotes the hash message authentication code function based on SM3; $\mathrm{U}$ is a per-run, non-secret input that transforms the static master key P into a dynamic, unique output M; $\oplus$ represents XOR operation; and $\left|\right|$ represents the byte concatenation operator.

(3) An 8×32-bit Derived Key Sequence DK is generated. From this sequence, the initial parameters for the chaotic encryption functions are calculated according to the complexity of the image block.

For simple image blocks, the initial value $x_0$, control variable $\mu$ and iteration number $k$ are calculated as follows:

$$\left\{\begin{array}{c}{x}_0={\displaystyle \frac{\left|{DK}_1\right|}{2^{32}}}\\ \mu =\left(\left|{DK}_2\right| mod 4\right)+x_0\\ k=\left|{DK}_1+{DK}_2\right| mod 2^8+2^8\end{array}\right.$$

(18)

where $\left|·\right|$ denotes the absolute value and mod represents the modulo operation.

For medium-complexity image blocks, the initial values $x_0$, $y_0$, control variable $\mu$ and iteration number $k$ are calculated as follows:

$$\left\{\begin{array}{c}{x}_0={\displaystyle \frac{\left|{DK}_3\right|}{2^{32}}}\\ y_0={\displaystyle \frac{\left|{DK}_4\right|}{2^{32}}}\\ \mu ={\displaystyle \frac{c}{{SUM}_t^{\prime }}}\left({DK}_3⨁{DK}_4\right)-\left[{\displaystyle \frac{c}{{SUM}_t^{\prime }}}\left({DK}_3⨁{DK}_4\right)\right]\\ k=\left|{DK}_3+{DK}_4\right| mod 2^8+2^8\end{array}\right.$$

(19)

where [·] represents the round-down operator, and ${SUM}_t^{\prime }$ is calculated according to Equation (6).

For complex image blocks, the initial values $x_0$, $y_0$, $z_0$, and $w_0$ and iteration number $k$ are calculated as follows:

$$\left\{\begin{array}{c}\begin{array}{c}{x}_0={\displaystyle \frac{c}{{SUM}_t^{\prime }}}({DK}_5⨁{DK}_6)-[{\displaystyle \frac{c}{{SUM}_t^{\prime }}}({DK}_5⨁{DK}_6)]\\ y_0={\displaystyle \frac{c}{{SUM}_t^{\prime }}}\left({DK}_6⨁{DK}_7\right)-[{\displaystyle \frac{c}{{SUM}_t^{\prime }}}({DK}_6⨁{DK}_7)]\\ z_0={\displaystyle \frac{c}{{SUM}_t^{\prime }}}\left({DK}_7⨁{DK}_8\right)-[{\displaystyle \frac{c}{{SUM}_t^{\prime }}}({DK}_7⨁{DK}_8)]\\ w_0={\displaystyle \frac{c}{{SUM}_t^{\prime }}}\left({DK}_8⨁{DK}_5\right)-[{\displaystyle \frac{c}{{SUM}_t^{\prime }}}({DK}_8⨁{DK}_5)]\end{array}\\ k=\left|{DK}_5+{DK}_6+{DK}_7+{DK}_8\right| mod 2^8+2^8\end{array}\right.$$

(20)

where the parameters $x_0$, $y_0$, $z_0$, and $w_0$ are the initial values of the 4D hyperchaotic system. To make the system exhibit hyperchaotic behavior, we set $a$ = 0.1, $b$ = 0.1, $c$ = 14, $p$ = −20, and $q$ = −0.28 [89].

For the overall RS image, a 1D chaotic function is used for encryption. Similarly, the values of the initial value $x_0$, control variable $\mu$, and iteration number $k$ are calculated as follows:

$$\left\{\begin{array}{c}{x}_0={\displaystyle \frac{\left|{DK}_7\right|}{2^{32}}}\\ \mu =\left(\left|{DK}_8\right| mod 4\right)+x_0\\ k=\left|{DK}_7+{DK}_8\right| mod 2^8+2^8\end{array}\right.$$

(21)

3.2.3. Encryption of Image Blocks with a Texture-Adaptive Strategy

Because the information content in RS images is spatially unevenly distributed, the importance of local regions also differs. Local areas with less sensitive information may not require high security with slow encryption algorithms, whereas areas with abundant information require more robust protection. Therefore, this study uses encryption methods of different levels for various types of image blocks. As described in Section 2, the 1D LTS chaotic system is a one-dimensional chaotic system with simple structures and fast computing speed but a relatively small key space; therefore, it is used to encrypt simple image blocks in this study. The 2D LASM chaotic system is a two-dimensional chaotic system with a more complex system structure and better chaotic performance than one-dimensional chaotic systems, making it suitable for encrypting medium image blocks. The 4D hyperchaotic system is a high-dimensional chaotic system with four random variables, making its chaotic trajectory a more complex structure and computationally complex. However, with a larger key space and more robust anti-attack capability, it encrypts complex image blocks. Using the pseudo-random sequences generated from low-to high-dimensional chaotic systems to encrypt the corresponding-level image blocks, different encryption needs of other images can be met, achieving a better balance between encryption efficiency and security.

For familiar color RS images, first, the different component matrices $I_{tC}$ of each image block $I_t$ are extracted; then, corresponding-level encryption is performed to obtain the ciphertext image block $I_t^{\prime }$ based on the image block category. To ensure the randomness of the chaotic system output sequences and avoid transient effects, random numbers are taken after k iterations of each chaotic system to generate random sequences. In the computation process, the encryption calculations for different image blocks operate independently; therefore, parallel computing can be utilized to enhance the efficiency significantly.

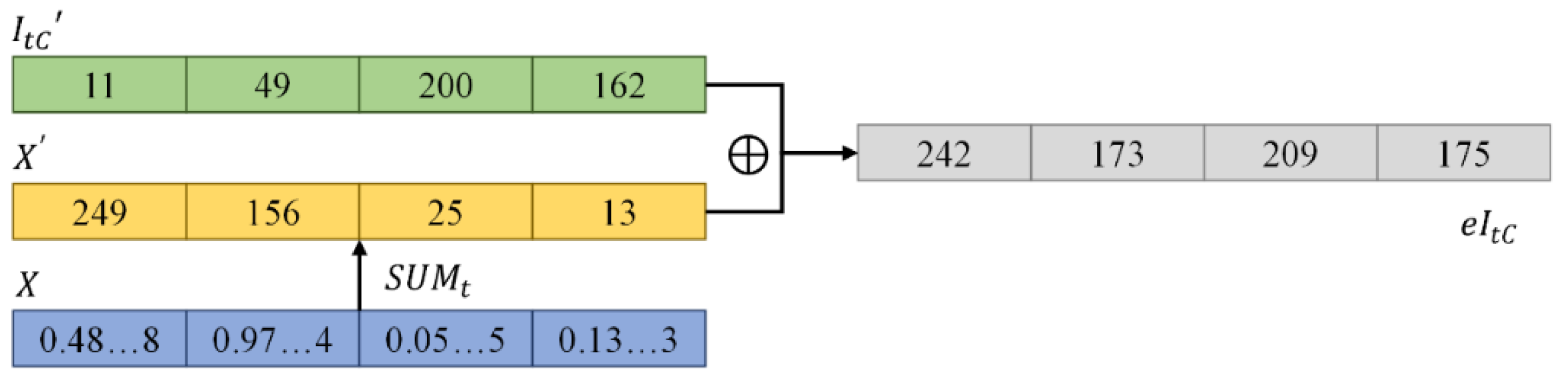
• Encryption of simple image block: The pixel values of the component matrices of the image block are encrypted by replacing the pixel values. The encryption steps for a simple image block $I_t$ component matrices $I_{tC}$ (i.e., $I_{tR}$, $I_{tG}$ and $I_{tB}$) are as follows: First, $I_{tC}$ is converted to a 1D image vector $I_{tC}^{\prime }=\left[P_1,P_2,\dots ,P_i\right]$, where $p_i$ denotes the value of a component of the i-th pixel. The maximum value of i is the number of rows multiplied by the number of columns, w $m\times n$. Then, the 1D LTS initial parameters ($x_0$, $\mu$, and $k$) are calculated based on the passphrase P, related image block parameter ${SUM}_t^{\prime }$, and $NumP$ using the method in Section 3.2. Further, according to Equation (16), the system is iterated ($k+m\times n$) times to obtain a random sequence and remove the first $k$ random numbers to obtain $X=\left[x_1, x_2,\dots , x_{m\times n}\right]$. $X_s$ is processed according to Equation (22) to obtain the random vector $X^{\prime }=\left[x_1^{\prime },x_2^{\prime },\dots , x_{m\times n}^{\prime }\right]$, and pixel-wise XOR is performed on $I_{tC}^{\prime }$ and $X_s^{\prime }$ to obtain the encrypted 1D vector $I_{tC}^{″}$.

$$\left\{\begin{array}{c}{X}_i^{\prime }=⌈X_i\times {SUM}_t⌉ mod 2^8\\ {I_{tC}}_i^{″}={I_{tC}}_i^{\prime }\oplus X_i^{\prime }\end{array}\right.$$

(22)

where $⌈·⌉$ represents round-down operator, $i=\mathrm{1,2},\dots ,m\times n$.

Finally, $I_{tC}^{″}$ is converted back to the 2D encrypted component matrix ${eI}_{tC}$, and all ciphertext matrices are merged to obtain the encrypted image block ${eI}_t$. Figure 4 illustrates the encryption process for the simple image blocks.

• Encryption of medium image block: The encryption steps for the medium image block $I_t$ are more complex compared to that for simple blocks; first, convert one component matrix $I_{tC}$ into a 1D image vector $I_{tC}^{\prime }$. According to the parameters ${SUM}_t^{\prime }$, $NumP$, and passphrase P, calculate the 2D LASM initial parameters ($x_0$, $y_0$, $\mu$ and $k$) using the method in Section 3.2. According to Equation (19), iterate the system ($k+m\times n$) times to obtain two groups of random sequences; remove the first $k$ random numbers from each group to generate two 1D random sequences $X=\left[x_1, x_2,\dots , x_{m\times n}\right]$ and $Y=\left[y_1, y_2,\dots , y_{m\times n}\right]$. Then, sort $X$ in ascending order to obtain the sorted sequence $X^{\prime }$ and index sequence $X^{″}$, and perform a position permutation on $I_{tC}^{\prime }$ according to Equation (23) to obtain $I_{tC}^{″}$. Sequence $Y$ obtains a new 1D random sequence $Y^{\prime }=\left[y_1^{\prime },y_2^{\prime },\dots , y_{m\times n}^{\prime }\right]$. Perform pixel-wise XOR between $Y^{\prime }$ and $I_{tC}^{″}$ according to Equation (23) to obtain the encrypted 1D vector $I_{tC}^{‴}$:

$$\left\{\begin{array}{c}{I}_{tC}^{″}=\left\{{I_{tC}^{\prime }}_{X_1^{″}},{I_{tC}^{\prime }}_{X_2^{″}},\dots ,{I_{tC}^{\prime }}_{X_{m\times n}^{″}}\right\}\\ Y_i^{\prime }=⌈Y_i\times {SUM}_t⌉ mod 2^8\\ {I_{tC}}_i^{‴}={I_{tC}}_i^{″}\oplus Y_i^{\prime }\end{array}\right.$$

(23)

where $I_{tC}^{″}$ denotes the position scrambling result based on the index sequence $X^{″}$.

Finally, convert $I_{tC}^{‴}$ is converted back to the 2D encrypted component matrix ${eI}_{tC}$ and merge all ciphertext matrices to obtain the encrypted image block ${eI}_t$. Figure 5 illustrates the encryption process for the medium image blocks.

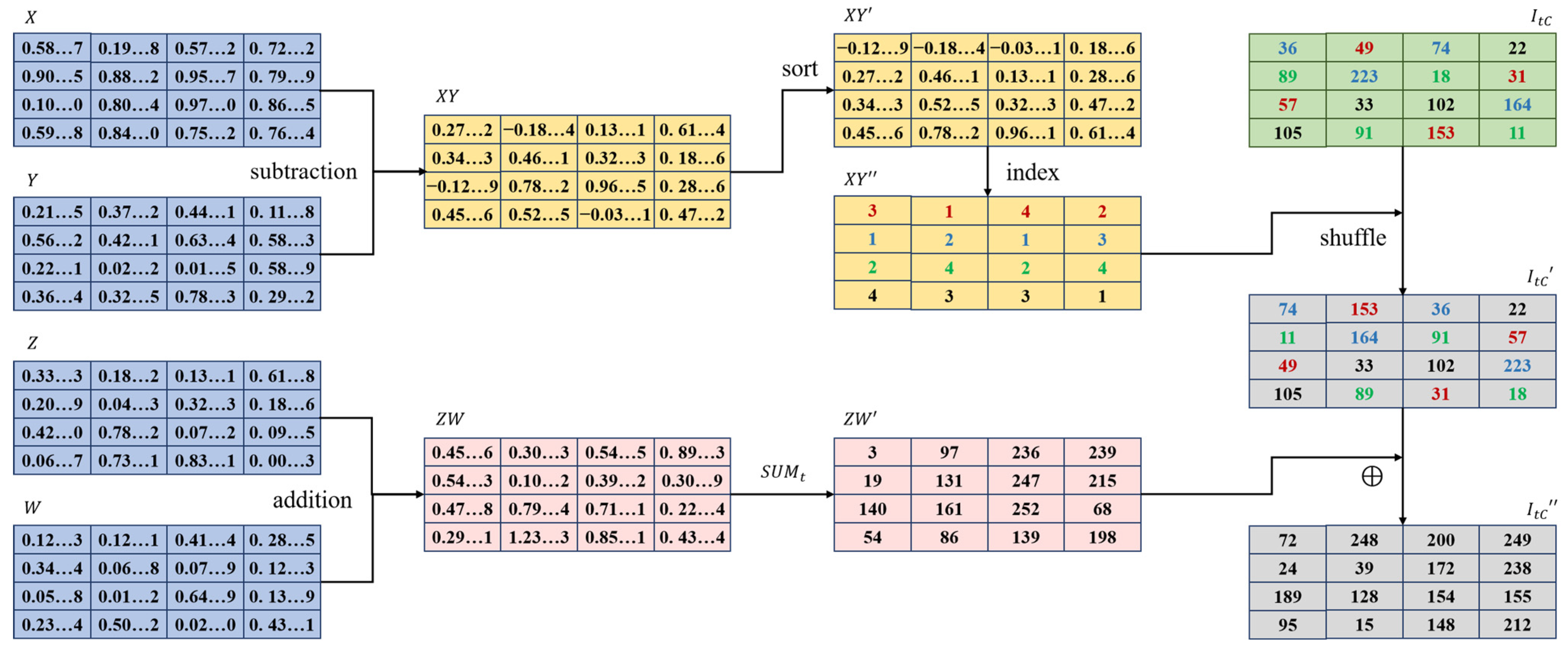
• Encryption of complex image block: The encryption steps for complex image blocks also take the pixel values of the component matrices as encryption objects, but the process of generating scrambling and substitution matrices is more complicated. The encryption steps for difficult image block $I_t$’s one-component matrices $I_{tC}$ are as follows: First, calculate the 4D hyperchaotic system initial parameters ($x_0$, $y_0$, $z_0$, $w_0$ and $k$) based on ${SUM}_t^{\prime }$, $umP$, and passphrase P using the method in Section 3.2. According to Equation (20), iterate the system ($k+m\times n$) to generate four groups of random sequences, remove the first k random numbers from each group, and use the remaining random numbers in each group to generate four $m\times n$ 2D random matrices $X$, $Y$, $Z$, and $W,$ respectively. Then, perform one-to-one subtraction on matrices $X$ and $Y$ to obtain the index matrix $XY$, and perform one-to-one addition on $Z$ and $W$ to obtain the scrambling matrix $ZW$ and the scramble matrix $I_{tC}$ according to the index matrix $XY$ using the chaos magic transformation method (CMT) proposed by [91] to obtain the scrambled matrix $I_{tC}^{\prime }$. Further, perform pixel-wise XOR operations between $I_{tC}^{\prime }$ and $ZW$ according to Formula (24) to obtain the encrypted component matrix $I_{tC}^{″}$.

$$\left\{\begin{array}{c}XY=X-Y\\ ZW=Z+W\\ I_{tC}^{\prime }=\left\{{I_{tC}}_{{XY}_1^{″}},{I_{tC}}_{{XY}_2^{″}},\dots ,{I_{tC}}_{{XY}_{m\times n}^{″}}\right\}\\ {ZW}_i^{\prime }=⌈{ZW}_i\times {SUM}_t⌉ mod 2^8\\ {I_{tC}}_i^{″}={I_{tC}}_i^{\prime }\oplus {ZW}_i^{\prime }\end{array}\right.$$

(24)

Finally, the encrypted component matrices are merged to obtain the ciphertext image block ${eI}_t$. Figure 6 illustrates the encryption process for the complex image blocks.

After encrypting the image blocks, the ciphertext image blocks must be stitched together to form the ciphertext image $cI$. Because extension matrices and plaintext pixel values are also required for decryption, this section concatenates two information matrices Q and W to the ciphertext image to obtain ${cI}^{\prime }$. There are two primary concerns with this approach. First, directly concatenating the plaintext information matrices may expose some details of the original remote sensing image, thereby increasing the risk of cracking the ciphertext image to some extent. Second, block-wise encryption introduces confusion within each image block and does not mitigate inter-block correlation. The ciphertext image, formed by stitching image blocks encrypted using different methods, exhibits noticeable block traces that can reveal information about the encryption methods to potential attackers. Therefore, to enhance security, an additional overall encryption operation on the stitched ciphertext image is necessary to conceal the block information and concatenate the plaintext information.

Specifically, the component matrices ${cI}_C^{\prime }$ of ${cI}^{\prime }$ are extracted, and the following encryption steps are performed on each component matrix: first, ${cI}_C^{\prime }$ is converted to a 1D image vector ${cI}_C^{\prime }=\left[p_1,p_2,\dots ,p_{\left(M+addrow\right)\times \left(N+addcol+2\right)}\right]$, where $p_i$ is the C component value of the i-th pixel. Then, the logistic initial parameters ($x_0$, $\mu$, and $k$) are calculated according to Equation (21). Furthermore, according to Equation (1), the system $k+\left(M+addrow\right)\times \left(N+addcol+2\right)$ obtains a random sequence, and the first $k$ random numbers are removed to obtain a 1D random sequence $X=\left[x_1, x_2,\dots , x_{\left(M+ addrow\right)\times \left(N+addcol+2\right)}\right]$. Furthermore, $X$ is processed according to formula 25 to obtain $X^{\prime }$, and pixel-wise XOR is performed between ${cI}_C^{\prime }$ and $X^{\prime }$ to generate the ciphertext matrix ${fcI}_C$ using Equation (26). Finally, the component ciphertext matrices are merged to obtain the encrypted RS image $fcI$.

$$X_i^{\prime }=⌈X_i\times {SUM}_{I_C}⌉ mod 2^8$$

(25)

$${{fcI}_C}_i=\left\{\begin{array}{c}{p}_i\oplus p_{\left(M+addrow\right)\times \left(N+addcol+2\right)}\oplus X_i^{\prime },i=1\\ p_i\oplus p_{i-1}\oplus X_i^{\prime },i>1\end{array}\right.$$

(26)

where ${SUM}_{I_C}$ represents the sum of all raw pixel values of the component matrix $I_C$.

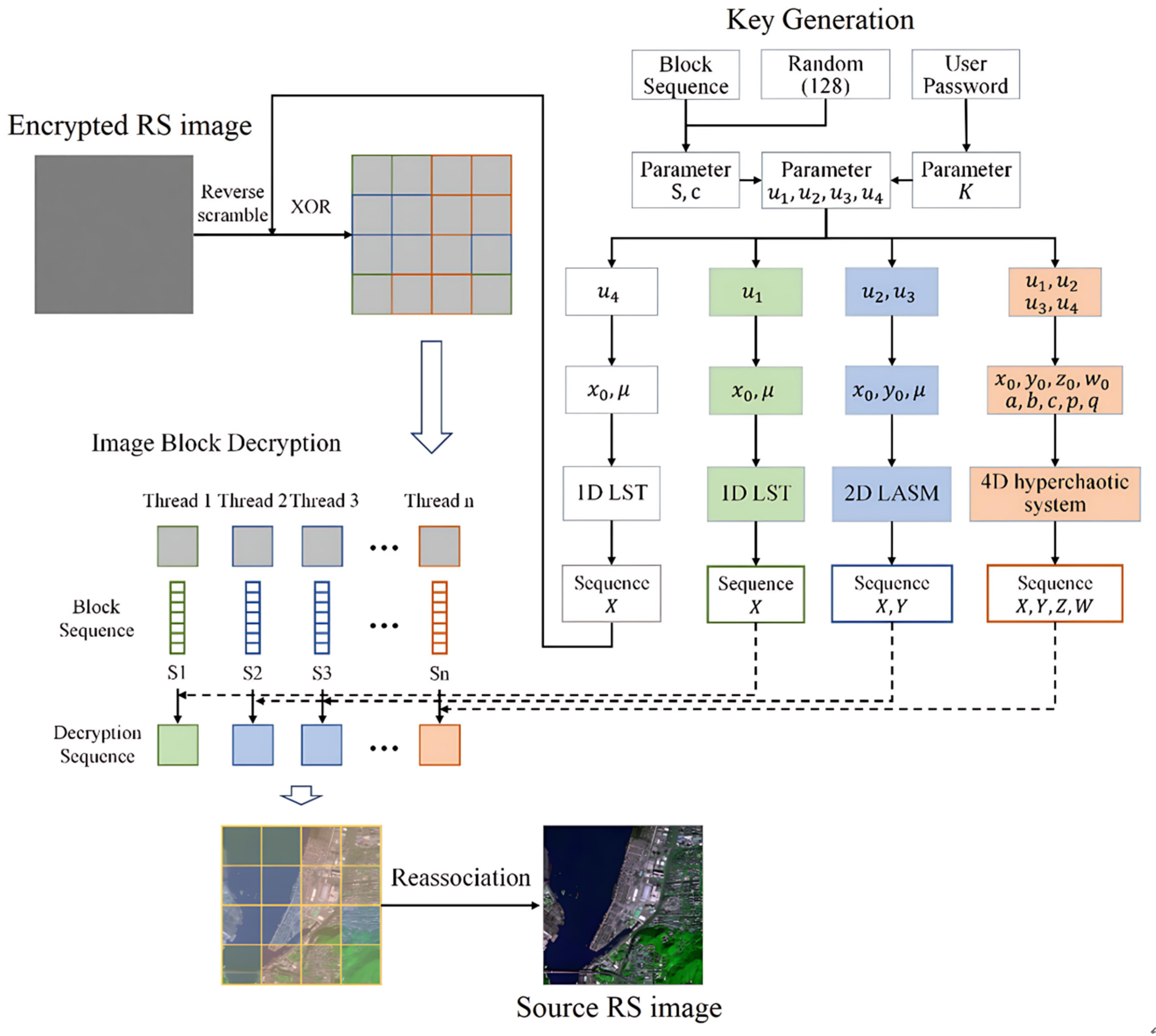
3.3. Encrypted Image Decryption

The decryption process for an encrypted RS image is the reverse of the encryption process. First, global decryption is performed on the encrypted image, and the result is partitioned and inversely graded. Then, decryption is conducted separately on the simple, medium, and complex image blocks based on the specific information associated with each image block. Subsequently, the decrypted image blocks are spliced back together according to their original positions to obtain the final source RS image, as shown in Figure 7.

4. Experiment

Remote sensing images of different sizes were used as experimental data to analyze the validity and security of the proposed encryption method. The algorithm was implemented in JDK8, and the experiments were carried out on a desktop computer with an Intel i5-8265U CPU, 8G memory, and Windows 10 operating system.

4.1. Encryption of Image Blocks

The following figures show the encryption and decryption results for remote sensing images of different sizes. Figure 8a–e show the original remote sensing images with dimensions of 256 × 256, 512 × 512, 1024 × 1024, 2048 × 2048, and 4096 × 4096, respectively. Figure 8f–j show the corresponding encrypted RS images. Figure 8k–o show the decrypted RS images. It can be observed from the encrypted images that the original RS images are encrypted into wholly random and meaningless images, from which no valuable information can be obtained visually. In addition, the proposed method is reversible, and the original images can be restored using the correct user passphrases. Figure 8p–t show the histograms of the source images and Figure 8u–y show the histograms of the encrypted images. The original R, G, and B histograms exhibit noticeable aggregated distributions, whereas those of the encrypted images are uniformly random. This indicates that the proposed method can effectively conceal the information and characteristics of the original data after encryption and can withstand statistical attacks to some extent. These results confirm that the proposed method can securely encrypt and faithfully recover remote sensing images while resisting statistical analysis.

4.2. Comparative Analysis of Efficiency

Comparative analyses with current chaos-based remote sensing image encryption methods were conducted to verify the efficiency of the proposed method. The runtimes for encrypting images using a simple 1D Logistic–Tent chaotic system (1D TLS) and a complex 4D hyperchaotic system were compared. The running-time comparisons of the different encryption methods are presented in

Table 1. Comparison of the running times of different encryption methods (ms).

Methods	Size
	256 × 256	512 × 512	1024 × 1024	2048 × 2048	4096 × 4096
Encryption method based on composite chaos [92]	1996	2248	2974	5163	13,909
Encryption method based on chaotic system and AES [46]	2736	3251	4616	8961	32,163
Global encryption method based on 1D LTS	1916	2005	2697	5159	12,652
Global encryption method based on 4D hyperchaotic system	2075	2366	3003	6378	24,807
Our method	1947	2249	2649	4480	9014

. Compared to other methods, the proposed method has a faster encryption efficiency for large remote sensing images. When the data size is small, a global encryption method based on a simple chaotic system is the most efficient. However, for extensive data, by utilizing parallel processing and hierarchical encryption, the proposed block-wise hierarchical encryption strategy can take full advantage and achieve better efficiency compared to other global encryption methods. This demonstrates that the proposed method achieves superior efficiency for large-scale remote sensing images compared to existing chaos-based methods.

4.3. Key Security Analysis

The security of the key can be analyzed from two aspects: key space size and key sensitivity. A secure encryption scheme must possess a key space large enough to render brute-force attacks computationally infeasible. The generally accepted standard is a key space larger than 2¹⁰⁰. The key used in the proposed method mainly contains several parameters: (1) ${SUM}_t^{\prime }$, $NumP$ related to the pixel value sum of image blocks, (2) derived key DK generated based on passphrase $P$, ${SUM}_t^{\prime }$, and $NumP$; and (3) initial parameters of chaotic systems obtained from DK. Assuming a double number precision of the computer is ${10}^{-15}$. Our method’s security is anchored by the highest-level 4-D hyperchaotic system, which requires at least four initial values as its secret key. The minimum key space of the 4D hyperchaotic system’s initial parameters is ${10}^{60}$, which is far larger than $2^{100}$ [27]. The total key space will be even larger considering the ranges of other parameters. When considering the additional control parameters of all three chaotic systems, the total key space is even larger. Therefore, the key space of the proposed method satisfies the security requirement and can resist brute-force attacks. Key sensitivity refers to imperceptible changes in the key value that lead to an entirely different encrypted image. In this section, the original passphrase is $P$= 1dbab33b8808edc0f5349ec7c20fe03847e5f4deca 8e37790cefe22c1ed6a76e, and a slightly changed version is $P^{\prime }$= 1dbab33b8808edc0f5349ec7c20fe038 47e5f4deca8e37790cefe22c1ed6a76a. The encrypted images obtained using these two keys are described below. Figure 9c shows that even a slight change in the key can result in very different encrypted images. Therefore, the proposed method has a high key sensitivity. With a sufficiently large key space and high key sensitivity, the proposed method meets modern security requirements.

4.4. Information Entropy Analysis

Information entropy can be used to measure the uncertainty of random variables. An excellent image encryption method should result in encrypted images with high uncertainty and unpredictability of pixel values. The information entropy of the remote sensing images was calculated as follows: for images with 256 gray levels, the information entropy ranges from 0 to 8, and the ideal value for encrypted images should be as close to 8 as possible [27].

Table 2. Comparison of information entropy before and after encryption.

Name	Size	Information Entropy of the Source RS Image	Information Entropy of the Encrypted RS Image
Test1.tif	256 × 256	5.66774	7.99717
Test2.tif	512 × 512	6.95465	7.99929
Test3.tif	1024 × 1024	5.94480	7.99982
Test4.tif	2048 × 2048	6.41338	7.99995
Test5.tif	4096 × 4096	6.42870	7.99998

lists the information entropy of the remote sensing images before and after encryption. For different image sizes, the information entropy of the ciphertext images encrypted using the proposed method is very close to a maximum of 8. Therefore, ciphertext images exhibit high randomness and unpredictability. It should also be noted that the experimental data are derived from publicly available high-resolution remote sensing datasets, which inherently contain diverse land-cover types (e.g., urban, vegetation, and water). Because these are real-world large-scale images rather than synthetic samples, it is challenging to obtain cases with completely simple or completely complex textures. Nevertheless, the selected data ensure sufficient diversity of texture complexity across different scenes, thereby providing a representative and realistic evaluation scenario. In summary, high information entropy indicates that the proposed method can effectively enhance the randomness and uncertainty of encrypted remote sensing images. Thus, the ciphertext images exhibit high randomness and unpredictability, validating the robustness of our encryption.

4.5. Correlation Analysis of Adjacent Pixels

Owing to the spatial continuity in sampling, the pixel values in the original remote sensing images exhibit a strong correlation in the horizontal, vertical, and diagonal directions. To conceal the information in the original images and avoid leakage, remote sensing image encryption algorithms should eliminate or reduce the strong correlation between adjacent pixels in encrypted images as much as possible. The correlation coefficient of adjacent pixels in remote sensing images was calculated as follows [93]:

$$\left\{\begin{array}{c}{C}_r={\displaystyle \frac{\frac{1}{L}{\sum }_{i=1}^L\left[x_i-E\left(x\right)\right]\left[y_i-E\left(y\right)\right]}{\sqrt{DX}\sqrt{DY}}}\\ E\left(x\right)={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^L}{x}_i\\ E\left(y\right)={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^L}{y}_i\\ DX={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=1}^L}{\left(x_i-E\left(x\right)\right)}^2\\ DY={\displaystyle \frac{1}{L}}\sum _{i=1}^L{\left(y_i-E\left(y\right)\right)}^2\end{array}\right.$$

(27)

where $x$ and $y$ are the gray values of $L$ pairs of adjacent pixels in the image, $i$ represents the $i$-th pair of adjacent pixels, $E\left(·\right)$ is the expected value, and $DX$ and $DY$ are the variances.

A total of 3000 pairs of adjacent pixels ($L=3000$) were selected in the horizontal, vertical, and diagonal directions to test the correlation between adjacent pixels before and after encryption, as shown in Figure 10 and

Table 3. Correlation between adjacent pixels before and after image encryption.

Image	Component	Horizontal Direction	Vertical Direction	Diagonal Direction
Source RS image	R	0.9569	0.9393	0.9363
	G	0.9615	0.9338	0.9325
	B	0.9826	0.9698	0.9672
Encrypted RS image	R	−0.0181	0.0149	0.0141
	G	−0.0069	−0.0031	−0.0090
	B	0.0097	−0.0163	0.0028

. The correlation coefficients are close to 1, and adjacent pixels are distributed as a straight line in the original image, indicating a strong correlation. In the encrypted image, adjacent pixels are randomly distributed, and the correlation coefficient is almost 0. Therefore, the proposed method effectively reduces the correlation between adjacent pixels in encrypted remote sensing images. The results show that our method effectively eliminates adjacent-pixel correlations, thereby enhancing encryption security.

4.6. Analysis of Resistance to Differential Attack

A differential attack is a chosen-plaintext attack. Since most remote sensing image encryption algorithms rely on a single key for encryption, attackers can modify the original image slightly to generate multiple images. By analyzing the impact of these small changes on the encrypted images, they can attempt to establish a relationship between the plaintext and ciphertext, thereby decrypting the ciphertext without the key. The ability to resist differential attacks can be evaluated by the number of pixel change rate (NPCR) and Unified Average Changing Intensity (UACI) [27]. Let $P_1$, $P_2$ be two original images with slight differences, and $C_1$, $C_2$ are their encrypted images. The NPCR measures the percentage of different pixels between $C_1$ and $C_2$, and UACI measures the average change rate of the pixel values. They are calculated as follows:

$$\left\{\begin{array}{c}{NPCR}_{\left(C_1,C_2\right)}={\displaystyle \frac{{\sum }_{i=1}^M{\sum }_{j=1}^{N}W\left(i,j\right)}{H}}\times 100\% \\ W\left(i,j\right)=\left\{\begin{array}{c}0, if{C}_1\left(i,j\right)=C_2\left(i,j\right)\\ 1, if{C}_1\left(i,j\right)\ne C_2\left(i,j\right)\end{array}\right.\\ {UACI}_{\left(C_1,C_2\right)}={\displaystyle \frac{1}{H}}\left[{\displaystyle \sum _{i=1}^M}{\displaystyle \sum _{j=1}^N}{\displaystyle \frac{\left|C_1\left(i,j\right)-C_2\left(i,j\right)\right|}{g}}\right]\times 100\% \end{array}\right.$$

(28)

where $M$, $N$ are the image width and height, $H=M\times N$, and $g$ is the maximum pixel value in images $P_1$ and $P_2$.

Wu et al. [94] derived the expectation and variance of NPCR and UACI for ideal encrypted images based on mathematical modeling and proposed standard values for different image sizes. The NPCR threshold ${N^{\ast }}_{\alpha }$ under the significance level α can be calculated as follows: if NPCR > ${N^{\ast }}_{\alpha }$, the method passes the NPCR test. The UACI standard interval is (${u^{\ast -}}_{\alpha }$, ${u^{\ast +}}_{\alpha }$), and the method passes the UACI test if the UACI is within (${u^{\ast -}}_{\alpha }$, ${u^{\ast +}}_{\alpha }$). The formulas for calculating the NPCR and UACI thresholds are as follows:

$$\left\{\begin{array}{c}{N^{\ast }}_{\alpha }={\displaystyle \frac{g-{\Phi }^{-1}\left(\alpha \right)\sqrt{\frac{g}{H}}}{g+1}}\\ \begin{array}{c}{u^{\ast -}}_{\alpha }={\mu }_u-{\Phi }^{-1}\left({\displaystyle \frac{\alpha }{2}}\right){\sigma }_u\\ {u^{\ast +}}_{\alpha }={\mu }_u+{\Phi }^{-1}\left({\displaystyle \frac{\alpha }{2}}\right){\sigma }_u\end{array}\\ {\mu }_u={\displaystyle \frac{g+2}{3g+3}}\\ {{\sigma }^2}_u={\displaystyle \frac{\left(g+2\right)\left(g^2+2g+3\right)}{18{\left(g+1\right)}^{2}gH}}\end{array}\right.$$

(29)

where $\alpha$ is typically set to 0.05.

As shown in

Table 4. Results for NPCR and UACI.

Size of the RS Image	NPCR	UACI
256 × 256	99.6205%	33.5417%
512 × 512	99.6066%	33.4559%
1024 × 1024	99.6054%	33.4659%
2048 × 2048	99.6095%	33.4514%
4096 × 4096	99.6112%	33.4690%

, the NPCR and UACI values of the proposed method are higher than the thresholds, indicating that it can resist differential attacks.

5. Discussion and Conclusions

This study comprehensively addresses the challenges associated with the large data volume, multiple bands, and complex texture features of remote sensing images. Based on spatial partitioning, a region-level multigradation remote sensing image encryption method incorporating texture complexity is proposed. The experimental results robustly validate the method’s effectiveness, security, and efficiency.

First, remote sensing images are partitioned and encrypted in a graded manner according to data size and texture complexity. Then, a separate encryption key is generated for each image block using the key generation method. With hierarchical partitioning and key generation, multidimensional chaotic systems encrypt simple, medium, and complex image blocks. Finally, the ciphertext image blocks are integrated. A fast XOR operation using a one-dimensional chaotic system is applied to the entire image to conceal the block information and reduce the inter-block pixel correlation. Experiments conducted on authentic remote sensing images validated their security and effectiveness. The experimental results comprehensively validated the proposed method’s security and efficiency. The method passed a suite of standard cryptographic tests, demonstrating high randomness (information entropy approaching the ideal value of 8), the elimination of strong pixel correlations, and proven resilience against statistical, brute-force, and differential attacks. A standout advantage is the method’s superior efficiency for large-scale data. For a 4096 × 4096 image, our method’s encryption time (9014 ms) was significantly shorter than those of competing approaches, which took up to 32,163 ms. This performance gain is directly attributed to the block-wise hierarchical strategy designed for parallel processing, confirming the method’s suitability for handling the massive datasets in modern remote sensing.

The proposed method demonstrates a significant efficiency advantage in vector map data encryption compared with existing methods. It improves encryption efficiency by leveraging parallel computation in remote sensing image processing while maintaining security. Thus, it holds significant application value in the encrypted acquisition and transmission of remote sensing data.

Despite its advantages, the proposed method has certain limitations. The hierarchical partitioning strategy for image blocks, which classifies them into simple, medium, and complex categories, relies on predefined thresholds based on prior knowledge and empiricism. These parameters may not be universally optimal for all remote sensing images with highly diverse textures and features. While the method supports manual annotation and user selection to enhance adaptability, this introduces a degree of subjectivity and reduces the potential for full automation. Additionally, the overall algorithm, with its multiple stages (partitioning, key generation, multilevel chaotic encryption, and XOR), is also more complex to implement than a single global encryption scheme.

Another limitation lies in the key generation process, which partially depends on plaintext information through pixel-sum values of image blocks. Although these sums are never used directly as keys but are combined with a strong external passphrase-derived key and mapped into nonlinear chaotic systems—where minimal input differences yield drastically different outputs—this dependence may still pose a theoretical inference risk. Future work should therefore explore more robust key derivation, such as hash-chain strategies or local feature-based mechanisms, to further reduce plaintext dependence and strengthen security.

Finally, although this study compares the proposed method with several chaos-based schemes, it does not provide systematic experimental comparisons with mainstream approaches such as AES, DNA-based encryption, or compressive sensing. Because these methods have fundamentally different objectives and computational models—AES performance being largely hardware-dependent, DNA relying on specialized encoding, and compressive sensing integrating compression with encryption—a direct runtime comparison would be neither fair nor conclusive. Instead, our framework is conceptually complementary and could potentially incorporate such techniques rather than compete with them directly. Nevertheless, broader comparative studies remain a critical direction for future research.

In summary, the proposed approach offers distinct advantages but also highlights clear avenues for improvement. Future research should focus on developing adaptive partitioning mechanisms, possibly using machine learning to automatically classify image blocks and optimize encryption levels and exploring dynamic chaotic systems with parameters that evolve with image statistics to enhance unpredictability. Extending the framework to other geospatial data types, such as hyperspectral cubes or remote sensing video streams, also represents a valuable and challenging direction.