Leaf Area Index Estimation of Grassland Based on UAV-Borne Hyperspectral Data and Multiple Machine Learning Models in Hulun Lake Basin
Abstract
1. Introduction
2. Materials and Methods
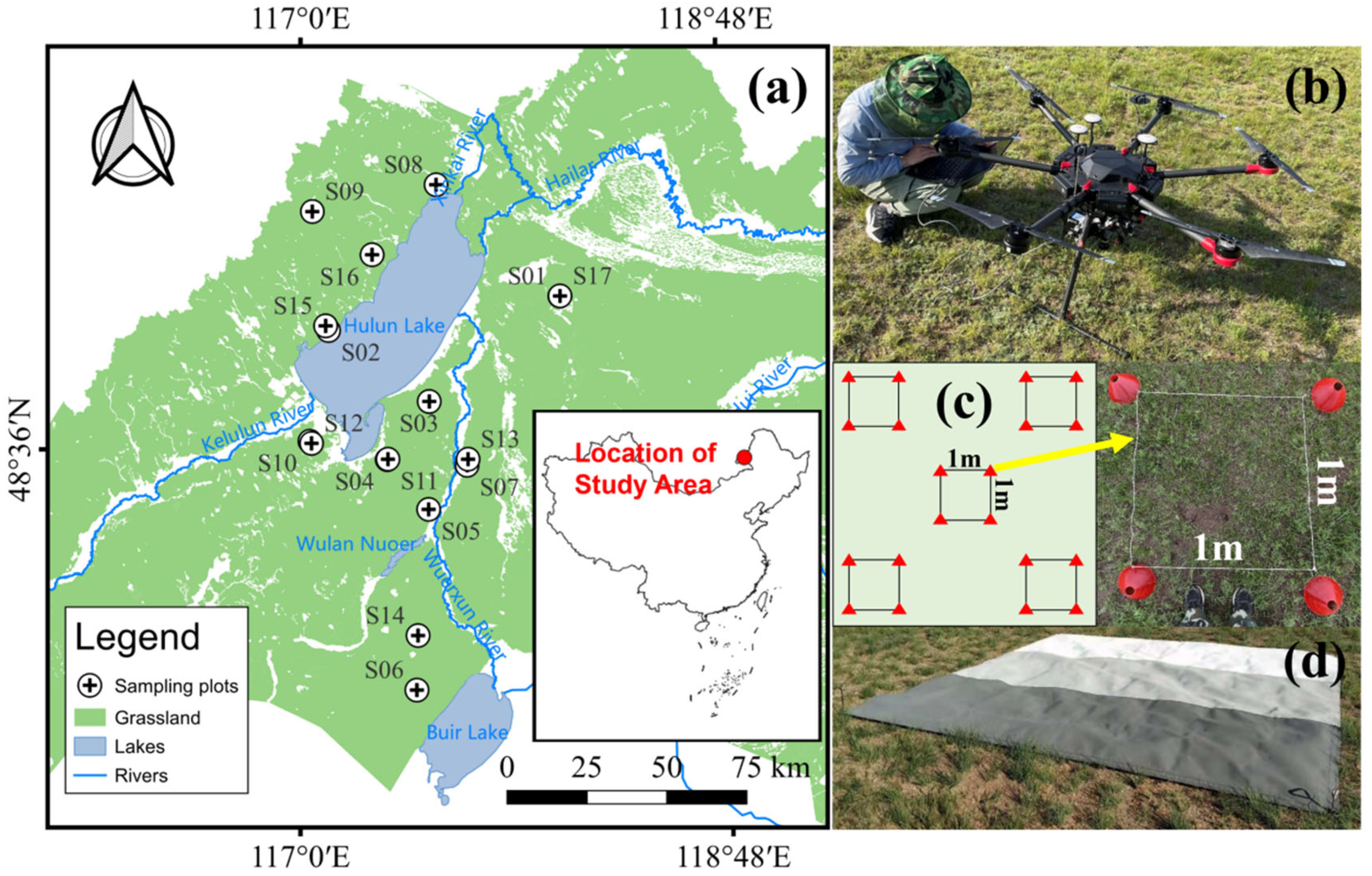
2.1. Overview of the Research Area and Data Collection
2.2. Hyperspectral Data Processing and Quality Control
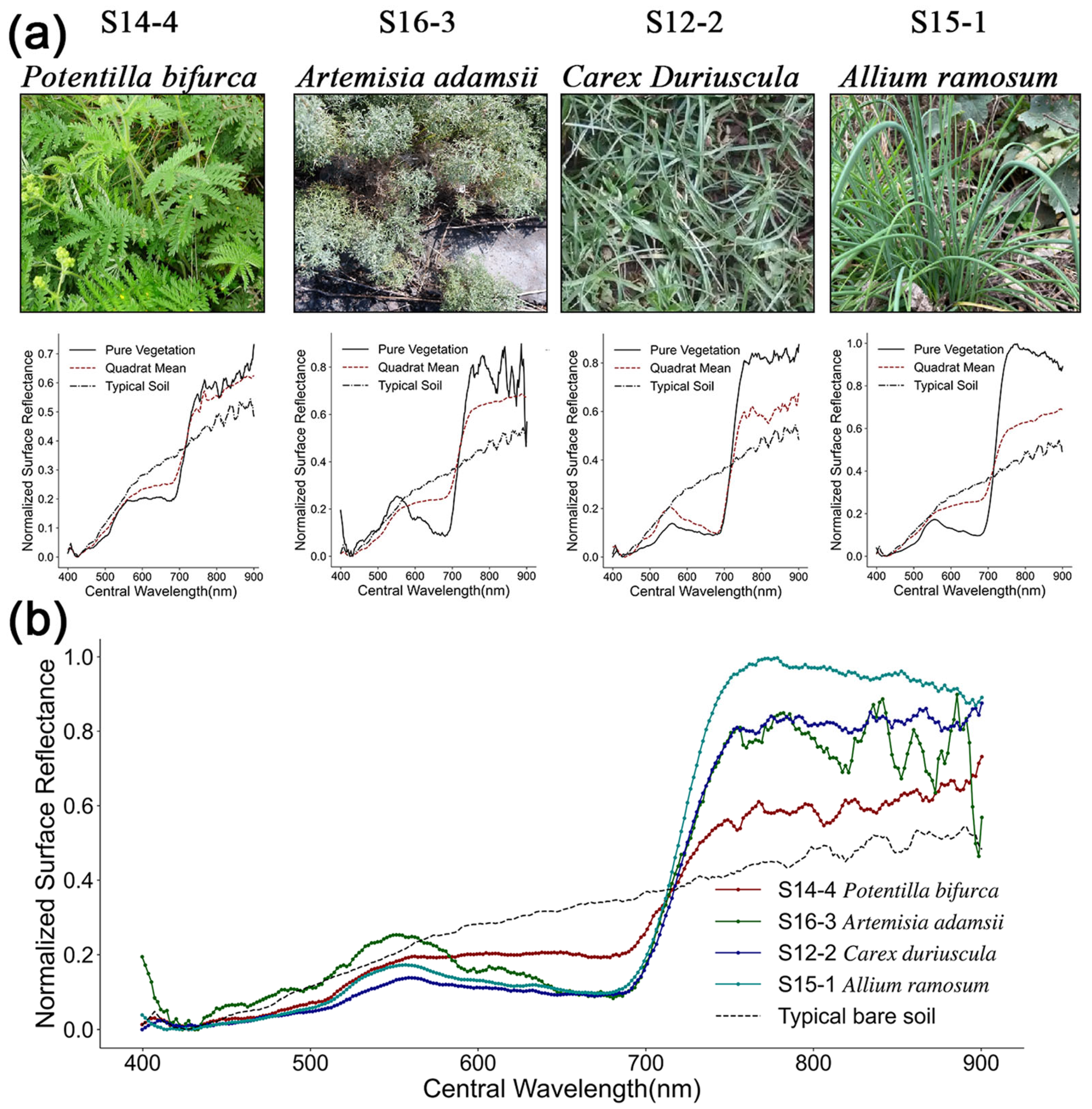
2.3. Spectral Information Extraction and Data Screening
2.4. Model Construction and Accuracy Evaluation Method
- (1)
- Random Forest
- (2)
- Support Vector Machine
- (3)
- K-Nearest Neighbor
- (4)
- Partial Least Squares Regression
2.5. Quadrat-Level Species Richness
2.6. SHAP Explains Models
3. Results
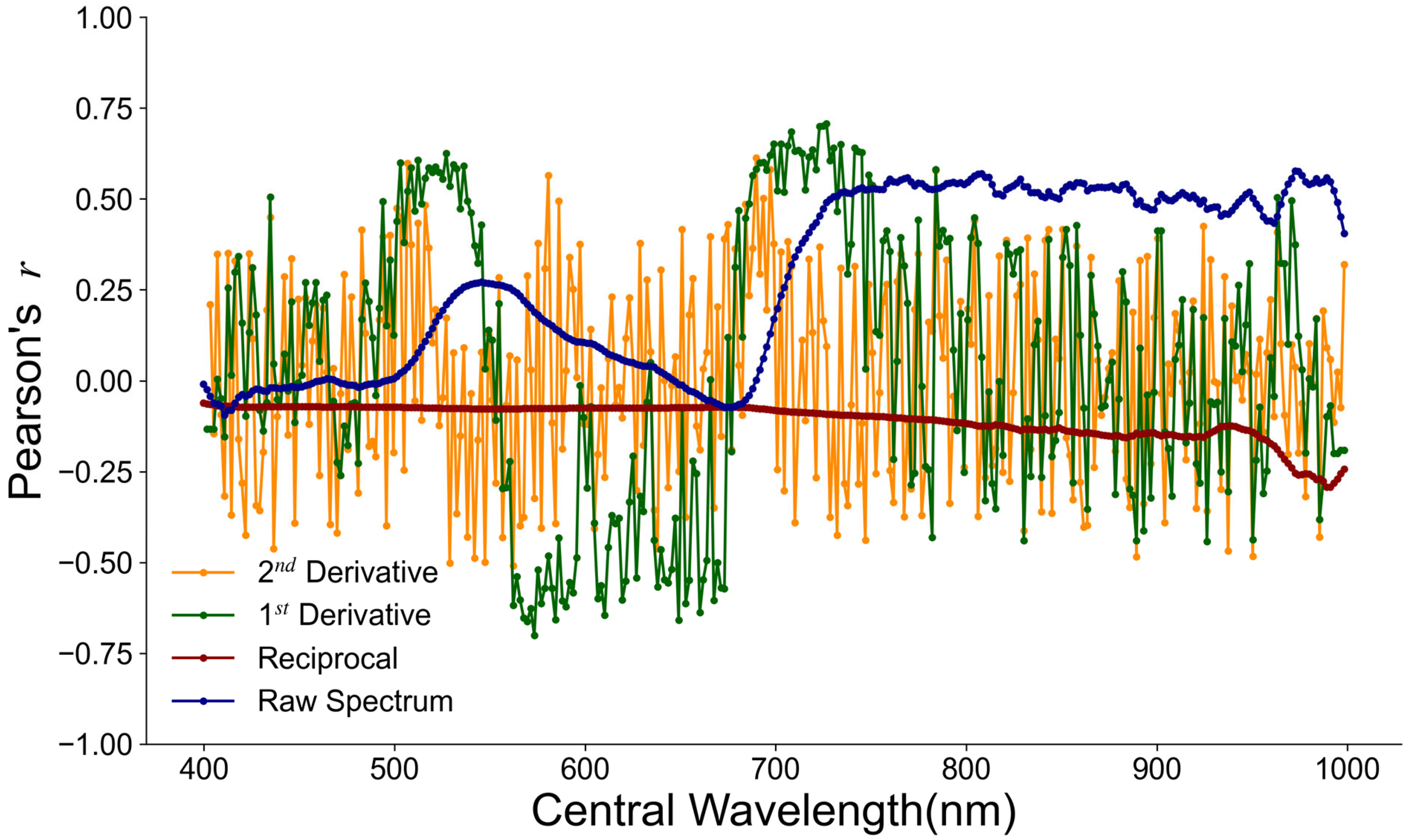
3.1. Feature Band and Vegetation Index Selection
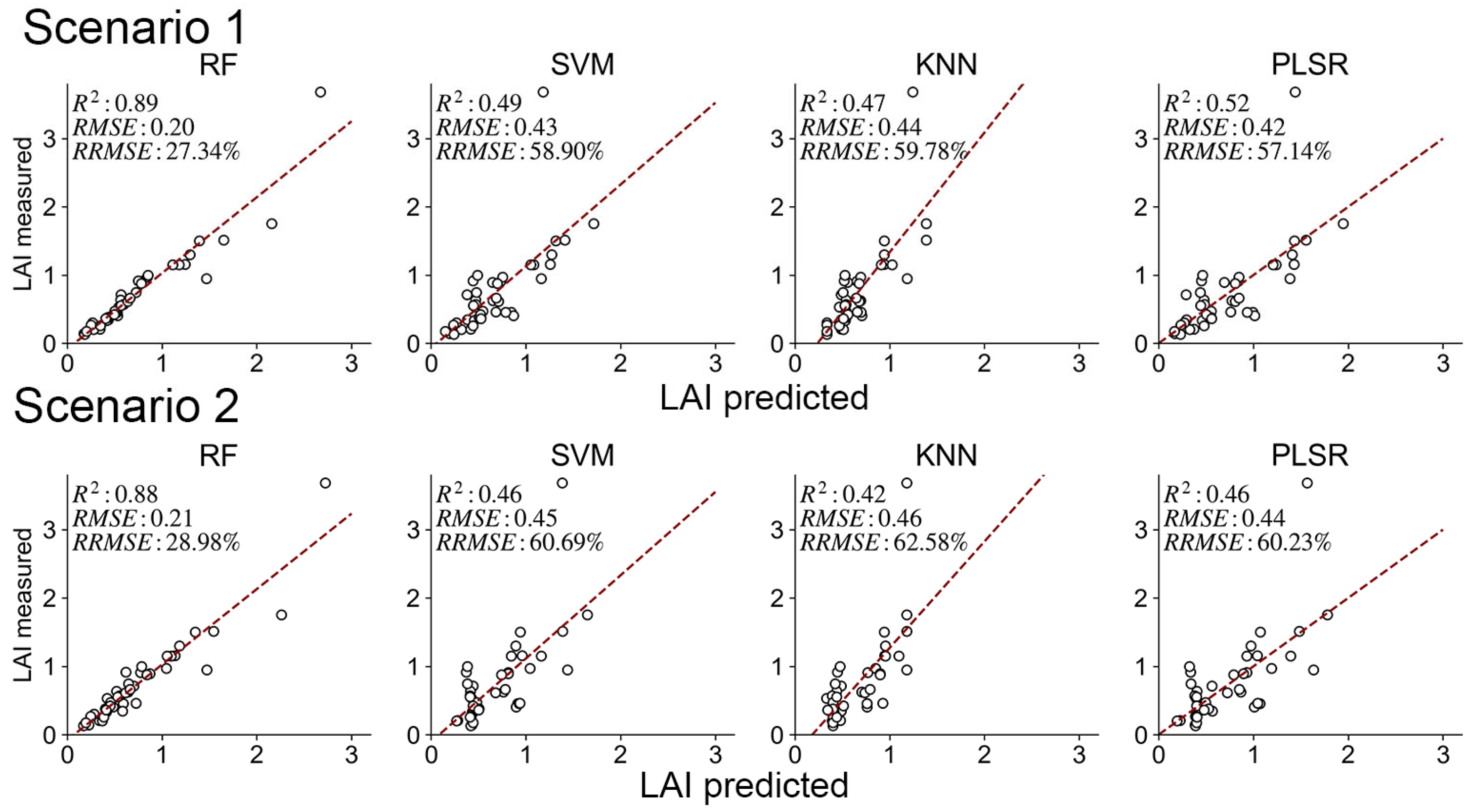
3.2. Model Performance and Validation Between Current LAI Products
3.3. Uncertainty and Mapping of LAI Estimation Model Predictions
3.4. Analysis of the Eigenvalue Contribution of SHAP
4. Discussion
4.1. The Influence of Spatial Heterogeneity on Model Performance
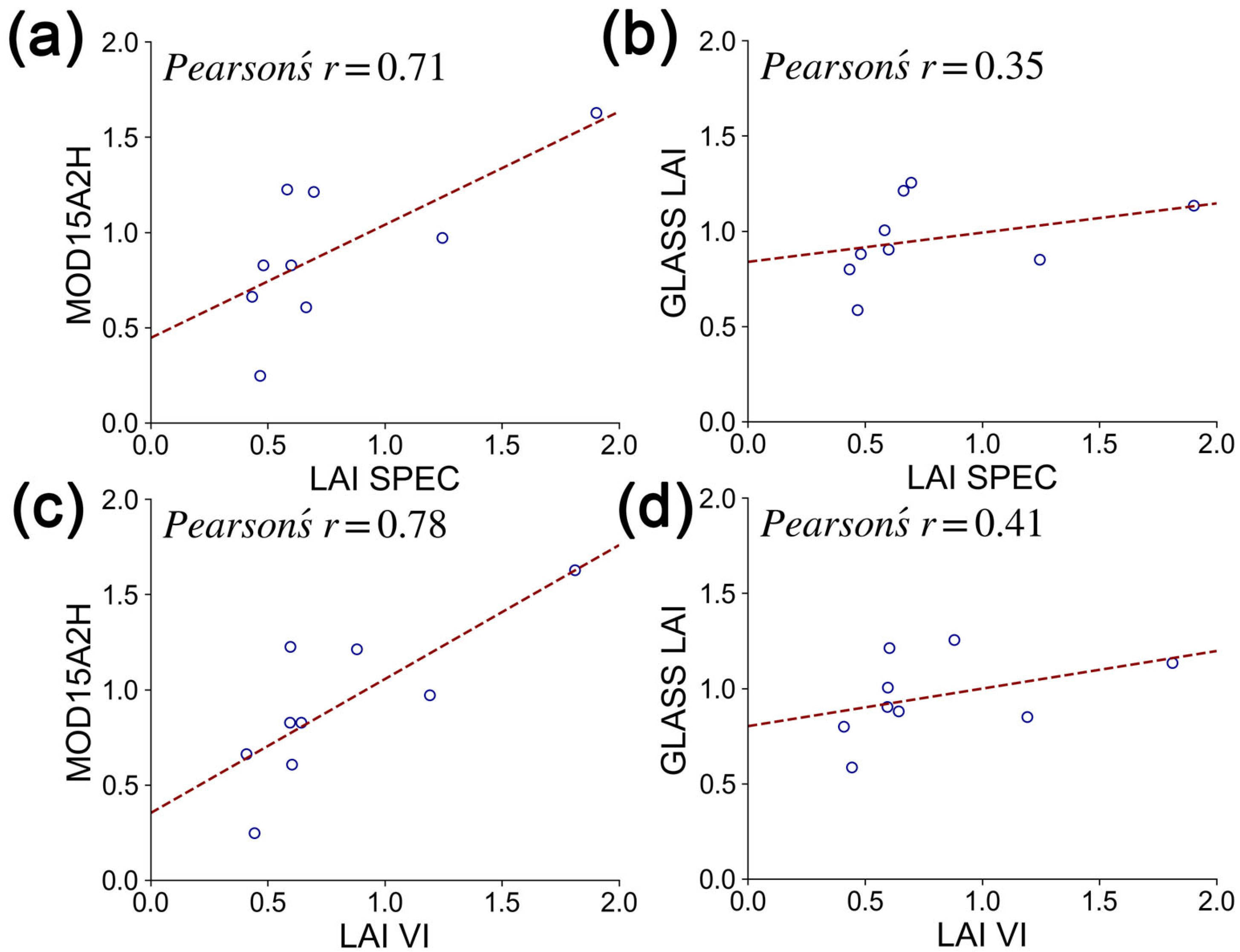
4.2. Comparison of This Study with Existing LAI Products
4.3. Potential and Limitations of Grassland UAV Hyperspectral LAI Estimation for Optimizing the Accuracy of Regional-Scale Carbon Sink Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lal, R. Carbon Cycling in Global Drylands. Curr. Clim. Chang. Rep. 2019, 5, 221–232. [Google Scholar] [CrossRef]
- Bardgett, R.D.; Bullock, J.M.; Lavorel, S.; Manning, P.; Schaffner, U.; Ostle, N.; Chomel, M.; Durigan, G.; Fry, E.L.; Johnson, D.; et al. Combatting global grassland degradation. Nat. Rev. Earth Environ. 2021, 2, 720–735. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Osem, Y.; O’Hara, K. An ecohydrological approach to managing dryland forests: Integration of leaf area metrics into assessment and management. Forestry 2016, 89, 338–349. [Google Scholar] [CrossRef]
- De Bock, A.; Belmans, B.; Vanlanduit, S.; Blom, J.; Alvarado-Alvarado, A.A.; Audenaert, A. A review on the leaf area index (LAI) in vertical greening systems. Build. Environ. 2023, 229, 109926. [Google Scholar] [CrossRef]
- Fang, H.L.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Cho, M.A.; Ramoelo, A.; Math, R. Estimation of leaf area index (LAI) of South Africa from MODIS imagery by inversion of PROSAIL radiative transfer model. In Proceedings of the IEEE Joint International Geoscience and Remote Sensing Symposium (IGARSS)/35th Canadian Symposium on Remote Sensing, Quebec City, QC, Canada, 13–18 July 2014; pp. 2590–2593. [Google Scholar]
- López-Lozano, R.; Casterad, M.A. LAI estimation by scaling up and inversion of radiative transfer models from Quickbird images. Rev. De Teledetec. 2005, 24, 43–47. [Google Scholar]
- Fang, H.L.; Wang, Y.; Zhang, Y.H.; Li, S.J. Long-Term Variation of Global GEOV2 and MODIS Leaf Area Index (LAI) and Their Uncertainties: An Insight into the Product Stabilities. J. Remote Sens. 2021, 2021, 9842830. [Google Scholar] [CrossRef]
- Fang, H.L.; Wei, S.S.; Jiang, C.Y.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Liu, Y.B.; Xiao, J.F.; Ju, W.M.; Zhu, G.L.; Wu, X.C.; Fan, W.L.; Li, D.Q.; Zhou, Y.L. Satellite-derived LAI products exhibit large discrepancies and can lead to substantial uncertainty in simulated carbon and water fluxes. Remote Sens. Environ. 2018, 206, 174–188. [Google Scholar] [CrossRef]
- Tian, Y.H.; Woodcock, C.E.; Wang, Y.J.; Privette, J.L.; Shabanov, N.V.; Zhou, L.M.; Zhang, Y.; Buermann, W.; Dong, J.R.; Veikkanen, B.; et al. Multiscale analysis and validation of the MODIS LAI product: I. Uncertainty assessment. Remote Sens. Environ. 2002, 83, 414–430. [Google Scholar] [CrossRef]
- Mateen, M.; Wen, J.H.; Nasrullah; Akbar, M.A. The Role of Hyperspectral Imaging: A Literature Review. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 51–62. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.M.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. Ieee Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Jain, N.; Ray, S.S.; Singh, J.P.; Panigrahy, S. Use of hyperspectral data to assess the effects of different nitrogen applications on a potato crop. Precis. Agric. 2007, 8, 225–239. [Google Scholar] [CrossRef]
- Yang, Y.C.; Nan, R.; Mi, T.X.; Song, Y.X.; Shi, F.H.; Liu, X.R.; Wang, Y.Q.; Sun, F.L.; Xi, Y.J.; Zhang, C. Rapid and Nondestructive Evaluation of Wheat Chlorophyll under Drought Stress Using Hyperspectral Imaging. Int. J. Mol. Sci. 2023, 24, 5825. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, S.S.; Peng, Z.P.; Huang, J.C.A.; Wang, C.Y.; Jiang, H.; Zheng, Q.; Li, D. Phenology Effects on Physically Based Estimation of Paddy Rice Canopy Traits from UAV Hyperspectral Imagery. Remote Sens. 2021, 13, 1792. [Google Scholar] [CrossRef]
- Toth, C.; Józków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Kanning, M.; Kühling, I.; Trautz, D.; Jarmer, T. High-Resolution UAV-Based Hyperspectral Imagery for LAI and Chlorophyll Estimations from Wheat for Yield Prediction. Remote Sens. 2018, 10, 2000. [Google Scholar] [CrossRef]
- Yu, K.Q.; Zhao, Y.R.; Zhu, F.L.; Li, X.L.; He, Y. Mapping of Chlorophyll and SPAD Distribution in Pepper Leaves During Leaf Senescence Using Visible and Near-Infrared Hyperspectral Imaging. Trans. Asabe 2016, 59, 13–24. [Google Scholar]
- Bayat, B.; Van der Tol, C.; Verhoef, W. Remote Sensing of Grass Response to Drought Stress Using Spectroscopic Techniques and Canopy Reflectance Model Inversion. Remote Sens. 2016, 8, 557. [Google Scholar] [CrossRef]
- Ding, Z.; Zhu, X.; Ma, L.; Zhao, Y. Estimating LAI and uncertainty in grassland using UAV hyperspectral data and PROSAIL. Adv. Comput. Signals Syst. 2024, 8, 13–22. [Google Scholar] [CrossRef]
- Si, Y.L.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T.J. Mapping spatio-temporal variation of grassland quantity and quality using MERIS data and the PROSAIL model. Remote Sens. Environ. 2012, 121, 415–425. [Google Scholar] [CrossRef]
- Lu, B.; Proctor, C.; He, Y.H. Investigating different versions of PROSPECT and PROSAIL for estimating spectral and biophysical properties of photosynthetic and non-photosynthetic vegetation in mixed grasslands. Gisci. Remote Sens. 2021, 58, 354–371. [Google Scholar] [CrossRef]
- Fern, R.R.; Foxley, E.A.; Bruno, A.; Morrison, M.L. Suitability of NDVI and OSAVI as estimators of green biomass and coverage in a semi-arid rangeland. Ecol. Indic. 2018, 94, 16–21. [Google Scholar] [CrossRef]
- He, Y.H.; Guo, X.L.; Wilmshurst, J.F. Comparison of different methods for measuring leaf area index in a mixed grassland. Can. J. Plant Sci. 2007, 87, 803–813. [Google Scholar] [CrossRef]
- Imran, H.A.; Gianelle, D.; Rocchini, D.; Dalponte, M.; Martín, M.P.; Sakowska, K.; Wohlfahrt, G.; Vescovo, L. VIS-NIR, Red-Edge and NIR-Shoulder Based Normalized Vegetation Indices Response to Co-Varying Leaf and Canopy Structural Traits in Heterogeneous Grasslands. Remote Sens. 2020, 12, 2254. [Google Scholar] [CrossRef]
- Shen, B.B.; Ding, L.; Ma, L.C.; Li, Z.W.; Pulatov, A.; Kulenbekov, Z.; Chen, J.Q.; Mambetova, S.; Hou, L.L.; Xu, D.W.; et al. Modeling the Leaf Area Index of Inner Mongolia Grassland Based on Machine Learning Regression Algorithms Incorporating Empirical Knowledge. Remote Sens. 2022, 14, 4196. [Google Scholar] [CrossRef]
- Qin, G.X.; Wu, J.; Li, C.B.; Meng, Z.Y. Comparison of the hybrid of radiative transfer model and machine learning methods in leaf area index of grassland mapping. Theor. Appl. Climatol. 2024, 155, 2757–2773. [Google Scholar] [CrossRef]
- Tsele, P.; Ramoelo, A. Integrating Active Learning and Regression Methods for Estimation of Grass Lai Over a Mountainous Region using Sentinel-2 Satellite Data. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 10516–10519. [Google Scholar]
- Doepper, V.; Rocha, A.D.; Berger, K.; Graenzig, T.; Verrelst, J.; Kleinschmit, B.; Foerster, M. Estimating soil moisture content under grassland with hyperspectral data using radiative transfer modelling and machine learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102817. [Google Scholar] [CrossRef]
- Liu, Z.W.; Jiang, J.B.; Du, Y.; Xu, Z.F. A Band Influence Algorithm for Hyperspectral Band Selection to Classify Moldy Peanuts. IEEE Access 2021, 9, 147527–147536. [Google Scholar] [CrossRef]
- Li, J.H.; Li, Q.Z.; Wang, F.; Liu, F. Hyperspectral redundancy detection and modeling with local Hurst exponent. Phys. A-Stat. Mech. Its Appl. 2022, 592, 126830. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.W.; Cao, C.X.; Yang, H.; Gao, M.X.; Zheng, S.; Xu, M.; Xie, D.H.; Jia, H.C.; Ji, W.; et al. Scale effects of leaf area index inversion based on environmental and disaster monitoring satellite data. Sci. China-Earth Sci. 2010, 53, 92–98. [Google Scholar] [CrossRef]
- Fan, W.J.; Gai, Y.Y.; Xu, X.R.; Yan, B.Y. The spatial scaling effect of the discrete-canopy effective leaf area index retrieved by remote sensing. Sci. China-Earth Sci. 2013, 56, 1548–1554. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Gong, M.G.; Chan, Y.Q. Hyperspectral band selection based on multi-objective optimization with high information and low redundancy. Appl. Soft Comput. 2018, 70, 604–621. [Google Scholar] [CrossRef]
- Yang, C.B.; Feng, M.C.; Song, L.F.; Jing, B.H.; Xie, Y.K.; Wang, C.; Yang, W.D.; Xiao, L.J.; Zhang, M.J.; Song, X.Y. Study on hyperspectral monitoring model of soil total nitrogen content based on fractional-order derivative. Comput. Electron. Agric. 2022, 201, 107307. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Lin, Y.H.; Shen, H.F.; Tian, Q.J.; Gu, X.F.; Yang, R.R.; Qiao, B.J. Mechanisms underlying diurnal variations in the canopy spectral reflectance of winter wheat in the jointing stage. Curr. Sci. 2020, 118, 1401–1406. [Google Scholar] [CrossRef]
- Shebl, A.; Abriha, D.; Fahil, A.S.; El-Dokouny, H.A.; Elrasheed, A.A.; Csámer, A. PRISMA hyperspectral data for lithological mapping in the Egyptian Eastern Desert: Evaluating the support vector machine, random forest, and XG boost machine learning algorithms. Ore Geol. Rev. 2023, 161, 105652. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Evolution of Support Vector Machine and Regression Modeling in Chemoinformatics and Drug Discovery. J. Comput. Aided Mol. Des. 2022, 36, 355–362. [Google Scholar] [CrossRef]
- Sumayli, M. Development of advanced machine learning models for optimization of methyl ester biofuel production from papaya oil: Gaussian process regression (GPR), multilayer perceptron (MLP), and K-nearest neighbor (KNN) regression models. Arab. J. Chem. 2023, 16, 104833. [Google Scholar] [CrossRef]
- Burnett, A.C.; Anderson, J.; Davidson, K.J.; Ely, K.S.; Lamour, J.; Li, Q.Y.; Morrison, B.D.; Yang, D.D.; Rogers, A.; Serbin, S.P. A best-practice guide to predicting plant traits from leaf-level hyperspectral data using partial least squares regression. J. Exp. Bot. 2021, 72, 6175–6189. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Z.; Cui, Y.X.; Liu, Z.H.; Zhao, Y.; Hu, M.; Hu, J.J. Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation. Comput. Mater. Sci. 2020, 171, 109203. [Google Scholar] [CrossRef]
- Qureshi, H.; Anwar, T.; Mohibullah, M.; Fatima, S.; Younas, R.; Habiba, U.; Malik, L.; Hanif, A.; Iqbal, M. Paired plot experiments to assess impact of invasive species on native floral diversity in Pakistan. Front. Environ. Sci. 2023, 10, 1037319. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ma, X.L.; Zhang, J.L.; Sun, D.L.; Zhou, X.Z.; Mi, C.L.; Wen, H.J. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Psomas, A.; Kneubühler, M.; Huber, S.; Itten, K.; Zimmermann, N.E. Hyperspectral remote sensing for estimating aboveground biomass and for exploring species richness pat-terns of grassland habitats. Int. J. Remote Sens. 2011, 32, 9007–9031. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Gamon, J.A.; Townsend, P.A.; Zygielbaum, A.I.; Helzer, C.J.; Hmimina, G.Y.; Yu, R.; Moore, R.M.; Schweiger, A.K.; Cavender-Bares, J. Detecting prairie biodiversity with airborne remote sensing. Remote Sens. Environ. 2019, 221, 38–49. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C.; Pan, K.; Guo, Z.; Liu, J.; Xu, A.; Ma, H.; Pan, X. The Simultaneous Prediction of Soil Properties and Vegetation Coverage from Vis-NIR Hyperspectral Data with a One-Dimensional Convolutional Neural Network: A Laboratory Simulation Study. Remote Sens. 2022, 14, 397. [Google Scholar] [CrossRef]
- Pervin, R.; Robeson, S.M.; MacBean, N. Fusion of airborne hyperspectral and LiDAR canopy-height data for estimating fractional cover of tall woody plants, herbaceous vegetation, and other soil cover types in a semi-arid savanna ecosystem. Int. J. Remote Sens. 2022, 43, 3890–3926. [Google Scholar] [CrossRef]
- Pu, Y.; Wilmshurst, F.J.; Guo, X. Separating Shrub Cover From Green Vegetation in Grasslands Using Hyperspectral Vegetation Indices. Can. J. Remote Sens. 2024, 50, 2347630. [Google Scholar] [CrossRef]
- Liu, W.; Han, W.; Jin, G.; Gong, K.; Ma, J. Classification of major species in the sericite–Artemisia desert grassland using hyperspectral images and spectral feature identification. PeerJ 2024, 12, e17663. [Google Scholar] [CrossRef]
- Zhu, X.; Bi, Y.; Du, J.; Gao, X.; Zhang, T.; Pi, W.; Zhang, Y.; Wang, Y.; Zhang, H. Research on deep learning method recognition and a classification model of grassland grass species based on unmanned aerial vehicle hyperspectral remote sensing. Grassl. Sci. 2023, 69, 3–11. [Google Scholar] [CrossRef]
- Srinet, R.; Nandy, S.; Patel, N.R.; Padalia, H.; Watham, T.; Singh, S.K.; Chauhan, P. Simulation of forest carbon fluxes by integrating remote sensing data into biome-BGC model. Ecol. Model. 2023, 475, 110185. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.H.; Bai, Y.; Koju, U.A.; Igbawua, T.; Chang, Q.; Zhang, D.; Yao, F.M. Evaluation and improvement of the daily boreal ecosystem productivity simulator in simulating gross primary productivity at 41 flux sites across Europe. Ecol. Model. 2018, 368, 205–232. [Google Scholar] [CrossRef]
- Amiro, B.D.; Chen, J.M.; Liu, J. Net primary productivity following forest fire for Canadian ecoregions. Can. J. For. Res. 2000, 30, 939–947. [Google Scholar] [CrossRef]
- Fu, G.; Wu, J.S. Validation of MODIS collection 6 FPAR/LAI in the alpine grassland of the Northern Tibetan Plateau. Remote Sens. Lett. 2017, 8, 831–838. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Chen, C.; Xu, B.D.; Song, W.J.; Yang, B.; Zeng, Y.L.; Liu, Z.; Yan, G.J.; Knyazikhin, Y.; et al. Generating Global Products of LAI and FPAR From SNPP-VIIRS Data: Theoretical Background and Implementation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2119–2137. [Google Scholar] [CrossRef]
- Ma, H.; Liang, S.L. Development of the GLASS 250-m leaf area index product (version 6) from MODIS data using the bidirectional LSTM deep learning model. Remote Sens. Environ. 2022, 273, 112985. [Google Scholar] [CrossRef]
- Sara, D.; Mandava, A.K.; Kumar, A.; Duela, S.; Jude, A. Hyperspectral and multispectral image fusion techniques for high resolution applications: A review. Earth Sci. Inform. 2021, 14, 1685–1705. [Google Scholar] [CrossRef]
- Cheng, J.P.; Yang, H.; Qi, J.B.; Sun, Z.D.; Han, S.Y.; Feng, H.K.; Jiang, J.Y.; Xu, W.M.; Li, Z.H.; Yang, G.J.; et al. Estimating canopy-scale chlorophyll content in apple orchards using a 3D radiative transfer model and UAV multispectral imagery. Comput. Electron. Agric. 2022, 202, 107401. [Google Scholar] [CrossRef]
- Mudi, S.; Paramanik, S.; Behera, M.D.; Prakash, A.J.; Deep, N.R.; Kale, M.P.; Kumar, S.; Sharma, N.; Pradhan, P.; Chavan, M.; et al. Moderate resolution LAI prediction using Sentinel-2 satellite data and indirect field measurements in Sikkim Himalaya. Environ. Monit. Assess. 2022, 194, 897. [Google Scholar] [CrossRef]
- Tsele, P.; Ramoelo, A.; Qabaqaba, M.; Mafanya, M.; Chirima, G. Validation of LAI, chlorophyll and FVC biophysical estimates from sentinel-2 level 2 prototype processor over a heterogeneous savanna and grassland environment in South Africa. Geocarto Int. 2022, 37, 14355–14378. [Google Scholar] [CrossRef]



| Quality Control Standards | Threshold |
|---|---|
| Surface reflectance (ρ) | 0 < ρ < 1 |
| Noise–signal ratio | |
| Solar zenith angle | |
| Light conditions | Clear and cloudless |
| Name | Formula | Name | Formula | ||
|---|---|---|---|---|---|
| Conventional VIs | Normalized difference vegetation index (NDVI) | (R800 − R670)/(R800 + R670) | Hyperspectral-specific VIs | Normalized difference red-edge index (NDRE) | (R790 − R720)/(R790 + R720) |
| Soil-adjusted vegetation index (SAVI) | 1.5 × (R800 − R670)/(R800 + R670 + 0.5) | Chlorophyll red-edge index (Clre) | R750/R720 − 1 | ||
| Optimized soil-adjusted vegetation index (OSAVI) | 1.16 × (R800 − R670)/(R800 + R670 + 0.16) | Modified red-edge simple ratio index (mSR705) | (R750 − R445)/(R705 − R445) | ||
| Green-normalized difference vegetation index (GNDVI) | (R750 − R550)/(R750 + R550) | Modified red-edge-normalized difference vegetation index (mND705) | (R750 − R705)/(R750 + R705 − 2R445) | ||
| Chlorophyll green index (Clgreen) | R800/R560−1 | Meris terrestrial chlorophyll index (MTCI) | (R750 − R710)/(R710 − R680) | ||
| Plant pigment ratio (PPR) | (R550 − R450)/(R550 + R450) | Anthocyanin reflectance index (ARI) | (1/R559)/(1/R721) | ||
| Two-band enhanced vegetation index (EVI2) | 2.5 × (R800 − R670)/(R800 + 2.4 × R670 + 1) | Greenness index (GI) | R554/R667 | ||
| Red-edge normalized vegetation index (NDVI705) | (R750 − R705)/(R750 + R705) | Plant biochemical index (PBI) | R810/R560 | ||
| Triangular vegetation index (TVI) | 0.5 × [120(R800 − R550) − 200(R670 − R550)] | Spectral polygon vegetation index (SPVI) | 0.4 × [3.7(R800 − R670) − 1.2(R530 − R670)] | ||
| Enhanced vegetation index (EVI) | 2.5(R864 − R660)/(R864 + 6R660 − 7.5R487 + 1) | Transformed chlorophyll absorption in reflectance index (TCARI) | 3 × [(R700 − R670)− 0.2(R700 − R550)(R700/R670)] |
| Spectrum Variables | Central Wavelength (nm) | Vegetation Indices | ||
|---|---|---|---|---|
| X1 | 972.5 | 0.58 | NDVI | 0.55 |
| X2 | 808 | 0.57 | SAVI | 0.63 |
| X3 | 769.2 | 0.56 | PPR | 0.54 |
| Y1 | 726.7 | 0.71 | EVI2 | 0.65 |
| Y2 | 573.3 | -0.70 | TCARI | 0.62 |
| Y3 | 649.1 | -0.66 | TVI | 0.67 |
| Z1 | 689.3 | 0.61 | SPVI | 0.65 |
| Z2 | 506.8 | 0.60 | EVI | 0.59 |
| Z3 | 784.0 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Bao, S.; Tong, Y.; Fan, Y.; Lu, L.; Liu, S.; Li, W.; Xue, M.; Cao, B.; Li, Q.; et al. Leaf Area Index Estimation of Grassland Based on UAV-Borne Hyperspectral Data and Multiple Machine Learning Models in Hulun Lake Basin. Remote Sens. 2025, 17, 2914. https://doi.org/10.3390/rs17162914
Wu D, Bao S, Tong Y, Fan Y, Lu L, Liu S, Li W, Xue M, Cao B, Li Q, et al. Leaf Area Index Estimation of Grassland Based on UAV-Borne Hyperspectral Data and Multiple Machine Learning Models in Hulun Lake Basin. Remote Sensing. 2025; 17(16):2914. https://doi.org/10.3390/rs17162914
Chicago/Turabian StyleWu, Dazhou, Saru Bao, Yi Tong, Yifan Fan, Lu Lu, Songtao Liu, Wenjing Li, Mengyong Xue, Bingshuai Cao, Quan Li, and et al. 2025. "Leaf Area Index Estimation of Grassland Based on UAV-Borne Hyperspectral Data and Multiple Machine Learning Models in Hulun Lake Basin" Remote Sensing 17, no. 16: 2914. https://doi.org/10.3390/rs17162914
APA StyleWu, D., Bao, S., Tong, Y., Fan, Y., Lu, L., Liu, S., Li, W., Xue, M., Cao, B., Li, Q., Cha, M., Zhang, Q., & Shan, N. (2025). Leaf Area Index Estimation of Grassland Based on UAV-Borne Hyperspectral Data and Multiple Machine Learning Models in Hulun Lake Basin. Remote Sensing, 17(16), 2914. https://doi.org/10.3390/rs17162914






