Determination of Trends in GPS Time Series Using Complementary Ensemble Empirical Mode Decomposition
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Complementary Ensemble Empirical Mode Decomposition
- Generating a pair of signals by adding and subtracting white noise ε(t) from the original time series
- Separate decomposition of signals and using the EMD method as follows:
- (a)
- Identification of extrema at and ;
- (b)
- Determination of upper and lower envelope, by separately connecting all local minima and maxima using cubic spline line;
- (c)
- Determination of envelope mean and and first components and as follows:and then verifying whether and meet the condition for IMF. If the condition is met, then and , otherwise the procedure is repeated —times until the condition is met, and during the repetition, the next and are considered accordingly in the following way
- (d)
- Separation of the first component from the datawhere and will be considered as new datums, for which the procedure at points a–d will be repeated times, until is so small that no more local extrema and can be extracted, or until and become monotonic functions.
2.3. Bootstrap
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPS | Global Positioning System |
| CEEMD | Complementary Ensemble Empirical Mode Decomposition |
| NGL | Nevada Geodetic Laboratory |
| GNSSs | Global Navigation Satellite Systems |
| RMSE | Root Mean Square Error |
| MIDAS | Median Interannual Difference Adjusted for Skewness |
| MLE | Maximum Likelihood Estimation |
| SSA | Singular Spectrum Analysis |
| PPP | Precise Point Positioning |
| EPN | EUREF Permanent Network |
| MAD | Median Absolute Deviation |
| EMD | Empirical Mode Decomposition |
| IMFs | Intrinsic Mode Functions |
| ITRF | International Terrestrial Reference Frame |
| LSs | Last Squares |
| ITRS | International Terrestrial Reference System |
| PSD | Post-Seismic Deformation |
| USGS | U. S. Geological Survey |
References
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of Earth deformation: Seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef]
- Banerjee, P.; Pollitz, F.F.; Nagarajan, B.; Burgmann, R. Coseismic slip distributions of the 26 December 2004 Sumatra-Andaman and 28 March 2005 Nias earthquakes from GPS static offsets. Bull. Seismol. Soc. Am. 2007, 97, S86–S102. [Google Scholar] [CrossRef]
- Tregoning, P.; Burgette, R.; McClusky, S.C.; Lejeune, S.; Watson, C.S.; McQueen, H. A decade of horizontal deformation from great earthquakes. J. Geophys. Res. 2013, 118, 2371–2381. [Google Scholar] [CrossRef]
- Nistor, S.; Suba, N.S.; El-Mowafy, A.; Apollo, M.; Malkin, Z.; Nastase, E.I.; Kudrys, J.; Maciuk, K. Implication between Geophysical Events and the Variation of Seasonal Signal Determined in GNSS Position Time Series. Remote Sens. 2021, 13, 3478. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S.I. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. Solid Earth 2002, 107, ETG-9. [Google Scholar] [CrossRef]
- Kermarrec, G.; Maddanu, F.; Klos, A.; Proietti, T.; Bogusz, J. Modeling trends and periodic components in geodetic time series: A unified approach. J. Geod. 2024, 98, 17. [Google Scholar] [CrossRef]
- Oelsmann, J.; Passaro, M.; Sánchez, L.; Dettmering, D.; Schwatke, C.; Seitz, F. Bayesian modelling of piecewise trends and discontinuities to improve the estimation of coastal vertical land motion: DiscoTimeS: A method to detect change points in GNSS, satellite altimetry, tide gauge and other geophysical time series. J. Geod. 2022, 96, 62. [Google Scholar] [CrossRef]
- Klos, A.; Kusche, J.; Fenoglio-Marc, L.; Bos, M.S.; Bogusz, J. Introducing a vertical land motion model for improving estimates of sea level rates derived from tide gauge records affected by earthquakes. GPS Solut. 2019, 23, 102. [Google Scholar] [CrossRef]
- Bogusz, J. Geodetic aspects of GPS permanent station nonlinearity studies. Acta Geodyn. Geomater. 2015, 12, 180. [Google Scholar] [CrossRef]
- Hobbs, B.; Ord, A. Nonlinear dynamical analysis of GNSS data: Quantification, precursors and synchronisation. Prog. Earth Planet. Sci. 2018, 5, 36. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068.b. [Google Scholar] [CrossRef]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missingdata. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Heflin, M.; Donnellan, A.; Parker, J.; Lyzenga, G.; Moore, A.; Ludwig, L.G.; Rundle, J.; Wang, J.; Pierce, M. Automated estimation and tools to extract positions, velocities, breaks, and seasonal terms from daily GNSS measurements: Illuminating nonlinear Salton Trough deformation. Earth Space Sci. 2020, 7, e2019EA000644. [Google Scholar] [CrossRef]
- Bos, M.S.; Bastos, L.; Fernandes, R.M.S. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef]
- Klos, A.; Bos, M.S.; Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut. 2018, 22, 21. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Ji, K.; Shen, Y.; Wang, F. Signal Extraction from GNSS Position Time Series Using Weighted Wavelet Analysis. Remote Sens. 2020, 12, 992. [Google Scholar] [CrossRef]
- Kaczmarek, A.; Kontny, B. Identification of the Noise Model in the Time Series of GNSS Stations Coordinates Using Wavelet Analysis. Remote Sens. 2018, 10, 1611. [Google Scholar] [CrossRef]
- Gruszczynska, M.; Klos, A.; Gruszczynski, M.; Bogusz, J. Investigation of time-changeable seasonal components in the GPS height time series: A case study for Central Europe. Acta. Geodyn. Geomater. 2016, 13, 281–289. [Google Scholar] [CrossRef]
- Khazraei, S.M.; Amiri-Simkooei, A.R. On the application of Monte Carlo singular spectrum analysis to GPS position time series. J. Geod. 2019, 93, 1401–1418. [Google Scholar] [CrossRef]
- Ji, K.; Shen, Y.; Chen, Q.; Wang, F. Extended singular spectrum analysis for processing incomplete heterogeneous geodetic time series. J. Geod. 2023, 97, 74. [Google Scholar] [CrossRef]
- Ji, K.; Shen, Y.; Wang, F.; Chen, Q. An efficient improved singular spectrum analysis for processing GNSS position time series with missing data. Geophys. J. Int. 2025, 240, 189–200. [Google Scholar] [CrossRef]
- Wnęk, A.; Kudas, D. Modeling seasonal oscillations in GNSS time series with Complementary Ensemble Empirical Mode Decomposition. GPS Solut. 2022, 26, 101. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
- Li, Y.; Han, L.; Yi, L.; Zhong, S.; Chen, C. Feature extraction and improved denoising method for nonlinear and nonstationary high-rate GNSS coseismic displacements applied to earthquake focal mechanism inversion of the El Mayor-Cucapah earthquake. Adv. Space Res. 2021, 68, 3971–3991. [Google Scholar] [CrossRef]
- Montillet, J.P.; Tregoning, P.; McClusky, S.; Yu, K. Extracting white noise statistics in GPS coordinate time series. IEEE Geosci. Remote Sens. Lett. 2012, 10, 563–567. [Google Scholar] [CrossRef]
- Niu, Y.; Ye, Y.; Zhao, W.; Shu, J. Dynamic monitoring and data analysis of a long-span arch bridge based on high-rate GNSS-RTK measurement combining CF-CEEMD method. J. Civ. Struct. Health Monit. 2021, 11, 35–48. [Google Scholar] [CrossRef]
- Yang, B.; Yang, Z.; Tian, Z.; Liang, P. Weakening the Flicker Noise in GPS Vertical Coordinate Time Series Using Hybrid Approaches. Remote Sens. 2023, 15, 1716. [Google Scholar] [CrossRef]
- Li, Y.; Han, L.; Liu, X. Accuracy Enhancement and Feature Extraction for GNSS Daily Time Series Using Adaptive CEEMD-Multi-PCA-Based Filter. Remote Sens. 2023, 15, 1902. [Google Scholar] [CrossRef]
- Wnęk, A.; Kudas, D. Application of combination of denoising methods and Complementary Ensemble Empirical Mode Decomposition in GNSS time series analysis. GPS Solut. 2025, 29, 141. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99, e2020943118. [Google Scholar] [CrossRef]
- Klein, J.; Valkama, M.; Staudt, M.; Schmidt-Thomé, P.; Kallio, H. ESPON-TITAN: Territorial patterns of natural hazards in Europe. Nat. Hazards 2024, 1–23. [Google Scholar] [CrossRef]
- U. S. Geological Survey. Search Earthquake Catalog. Available online: https://earthquake.usgs.gov/earthquakes/search (accessed on 14 July 2025).
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophys. Geosyst. 2003, 4, 1027. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- Tretyak, K.; Dosyn, S. Study of vertical movements of the European crust using tide gauge and GNSS observations. Rep. Geod. Geoinform. 2014, 97, 112–131. [Google Scholar] [CrossRef]
- NGL Steps 2024. Available online: http://geodesy.unr.edu/NGLStationPages/steps.txt (accessed on 20 April 2025).
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, Y.; Schmitt, F.G.; Lu, Z.; Liu, Y. Analysis of daily river flow fluctuations using empirical mode decomposition and arbitrary order Hilbert spectral analysis. J. Hydrol. 2009, 373, 103–111. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert–Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46, RG2006. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 1994. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, Version: 23.2.0.2485118 (R2023b) Update 6; The MathWorks Inc.: Natick, MA, USA, 2023; Available online: https://www.mathworks.com (accessed on 20 April 2025).
- Herring, T.A.; Melbourne, T.I.; Murray, M.H.; Floyd, M.A.; Szeliga, W.M.; King, R.W.; Phillips, D.A.; Puskas, C.M.; Santillan, M.; Wang, L. Plate Boundary Observatory and related networks: GPS data analysis methods and geodetic products. Rev. Geophys. 2016, 54, 759–808. [Google Scholar] [CrossRef]
- He, X.; Bos, M.S.; Montillet, J.-P.; Fernandes, R.; Melbourne, T.; Jiang, W.; Li, W. Spatial Variations of Stochastic Noise Properties in GPS Time Series. Remote Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
- Kowalczyk, K.; Rapinski, J. Verification of a GNSS time series discontinuity detection approach in support of the estimation of vertical crustal movements. ISPRS Int. J. Geo-Inf. 2018, 7, 149. [Google Scholar] [CrossRef]
- Kreemer, C.; Blewitt, G.; Maerten, F. Co- and postseismic deformation of the 28 March 2005 Nias Mw 8.7 earthquake from continuous GPS data. Geophys. Res. Lett. 2006, 33, L07307. [Google Scholar] [CrossRef]
- Tobita, M. Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 2016, 68, 41. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, B03412. [Google Scholar] [CrossRef]
- Montillet, J.P.; Williams, S.D.P.; Koulali, A.; McClusky, S.C. Estimation of offsets in GPS time-series and application to the detection of earthquake deformation in the far-field. Geophys. J. Int. 2015, 200, 1207–1221. [Google Scholar] [CrossRef]
- Clarke, D.; Brenguier, F.; Froger, J.-L.; Shapiro, N.M.; Peltier, A.; Staudacher, T. Timing of a large volcanic flank movement at Piton de la Fournaise Volcano using noise-based seismic monitoring and ground deformation measurements. Geophys. J. Int. 2013, 195, 1132–1140. [Google Scholar] [CrossRef]
- Zhang, P.; Dai, Y.; Zhang, H.; Wang, C.; Zhang, Y. Combining CEEMD and recursive least square for the extraction of time-varying seismic wavelets. J. Appl. Geophys. 2019, 170, 103854. [Google Scholar] [CrossRef]
- Shao, Q.; Li, W.; Hou, G.; Han, G.; Wu, X. Mid-term simultaneous spatiotemporal prediction of sea surface height anomaly and sea surface temperature using satellite data in the South China Sea. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1501705. [Google Scholar] [CrossRef]
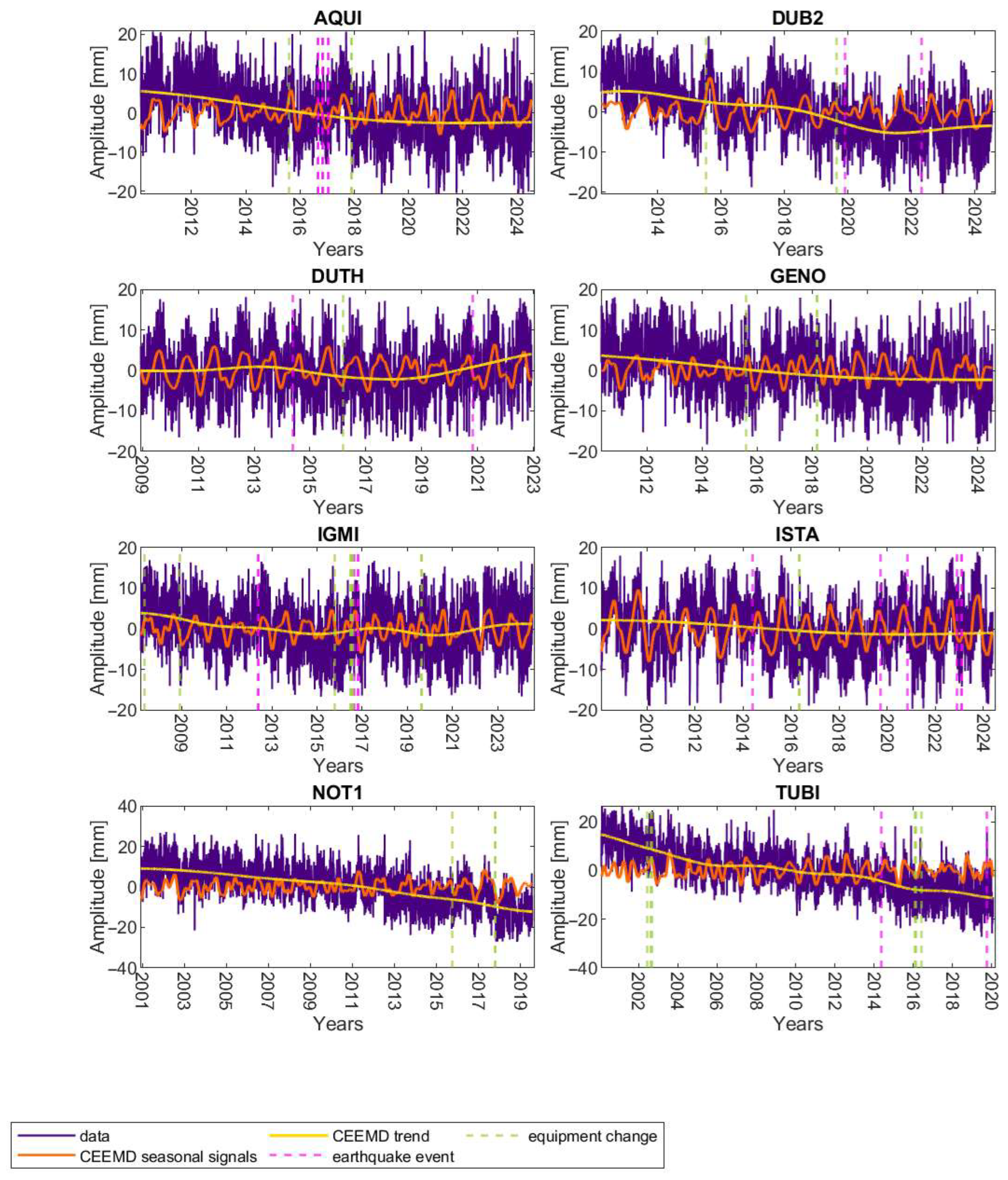
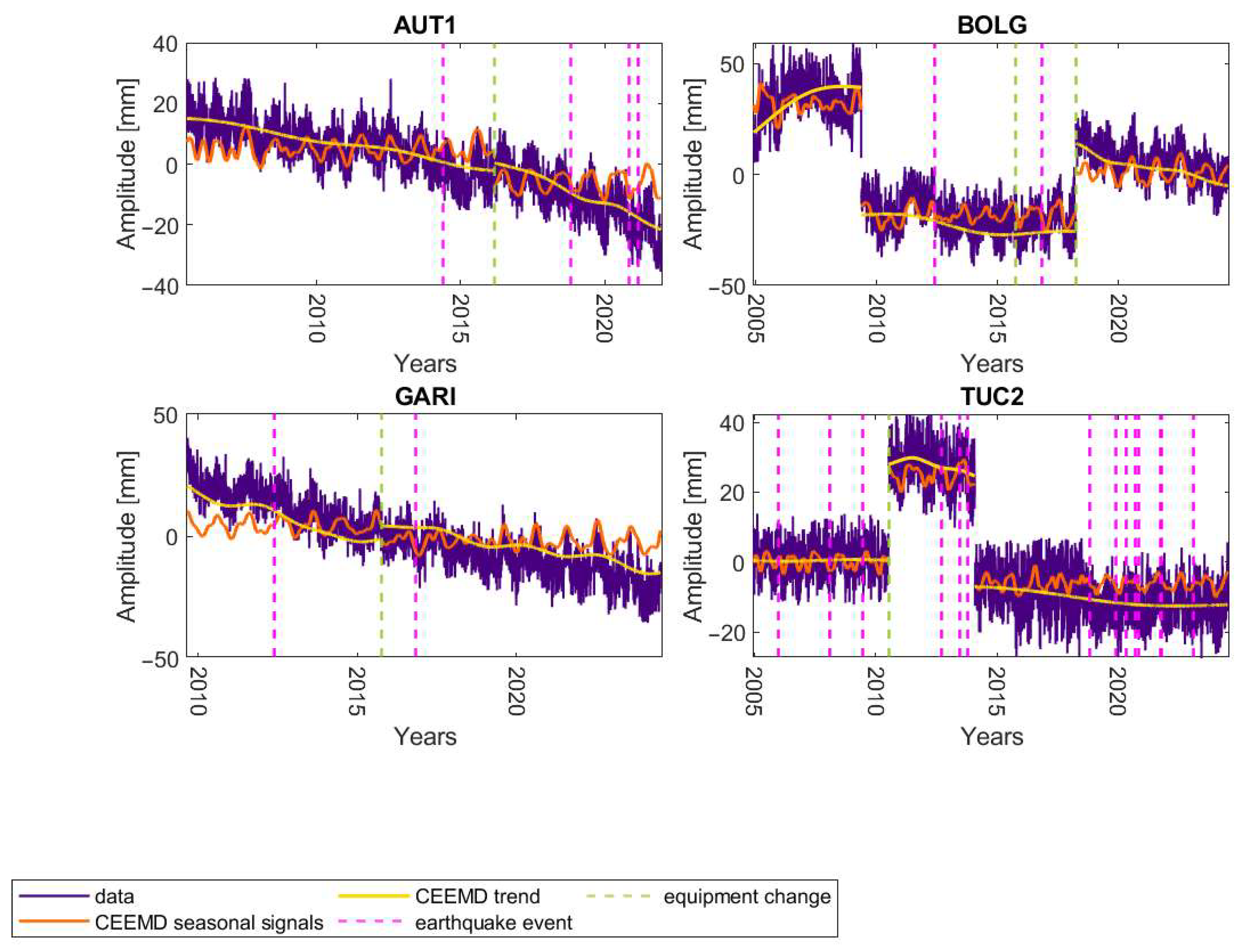

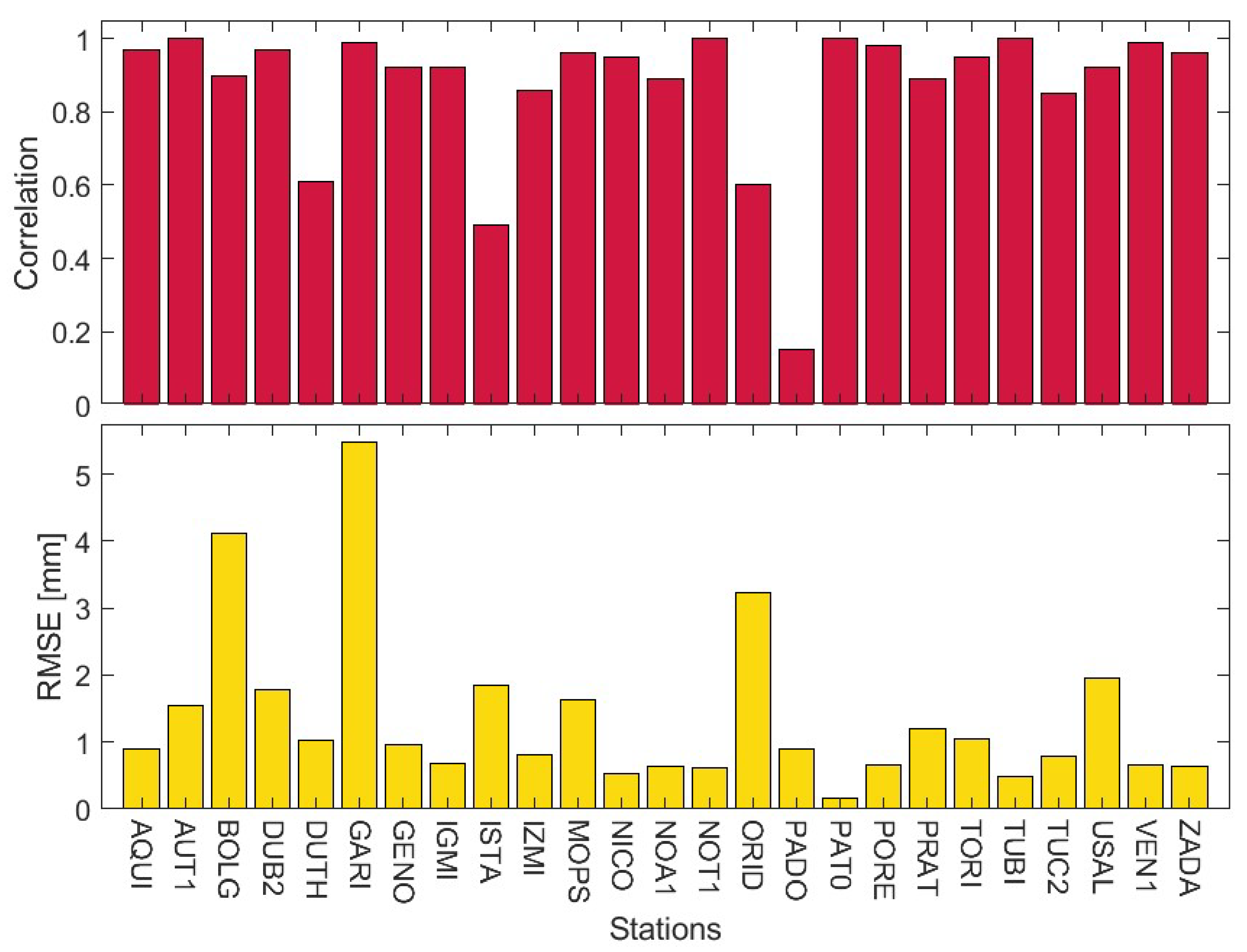
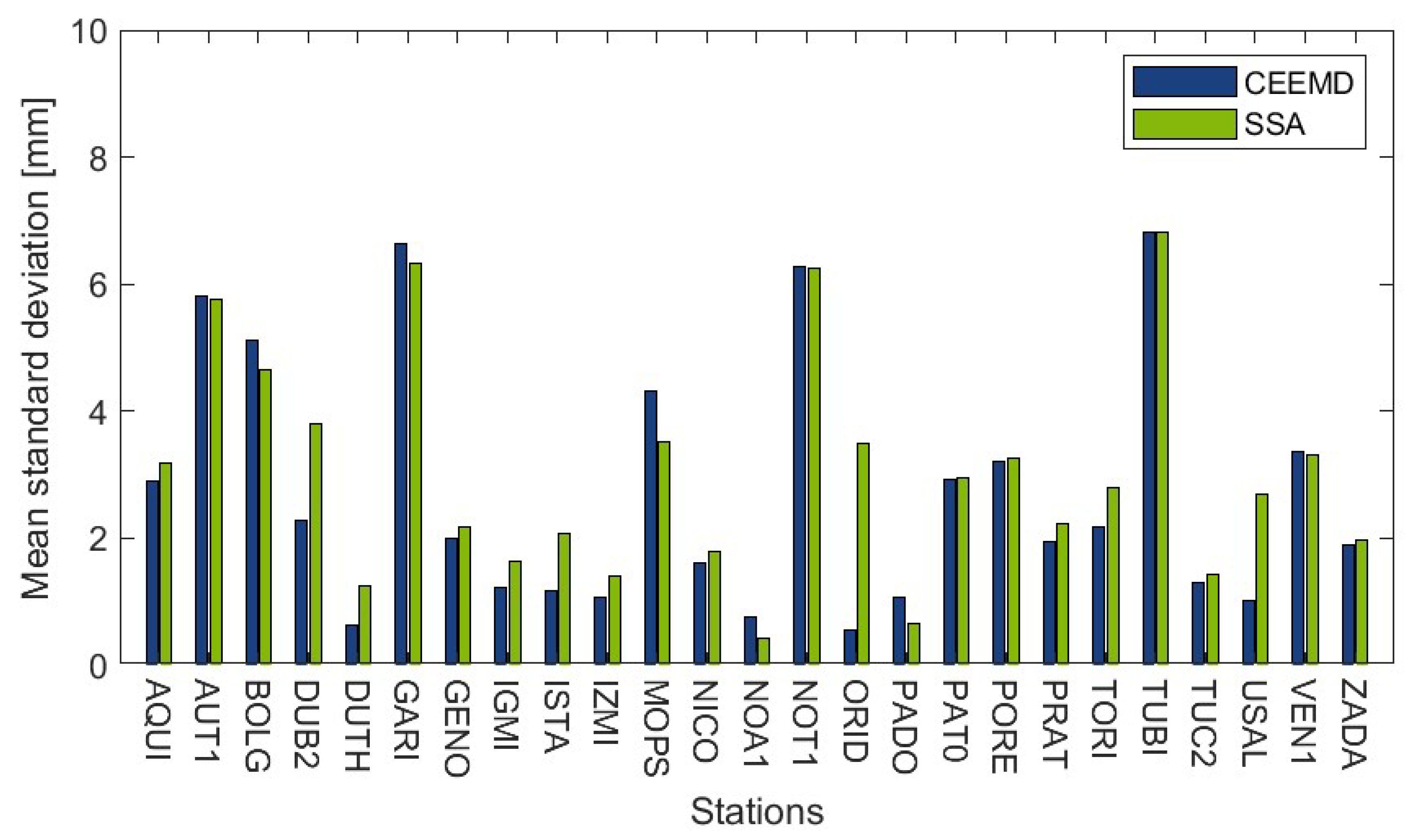
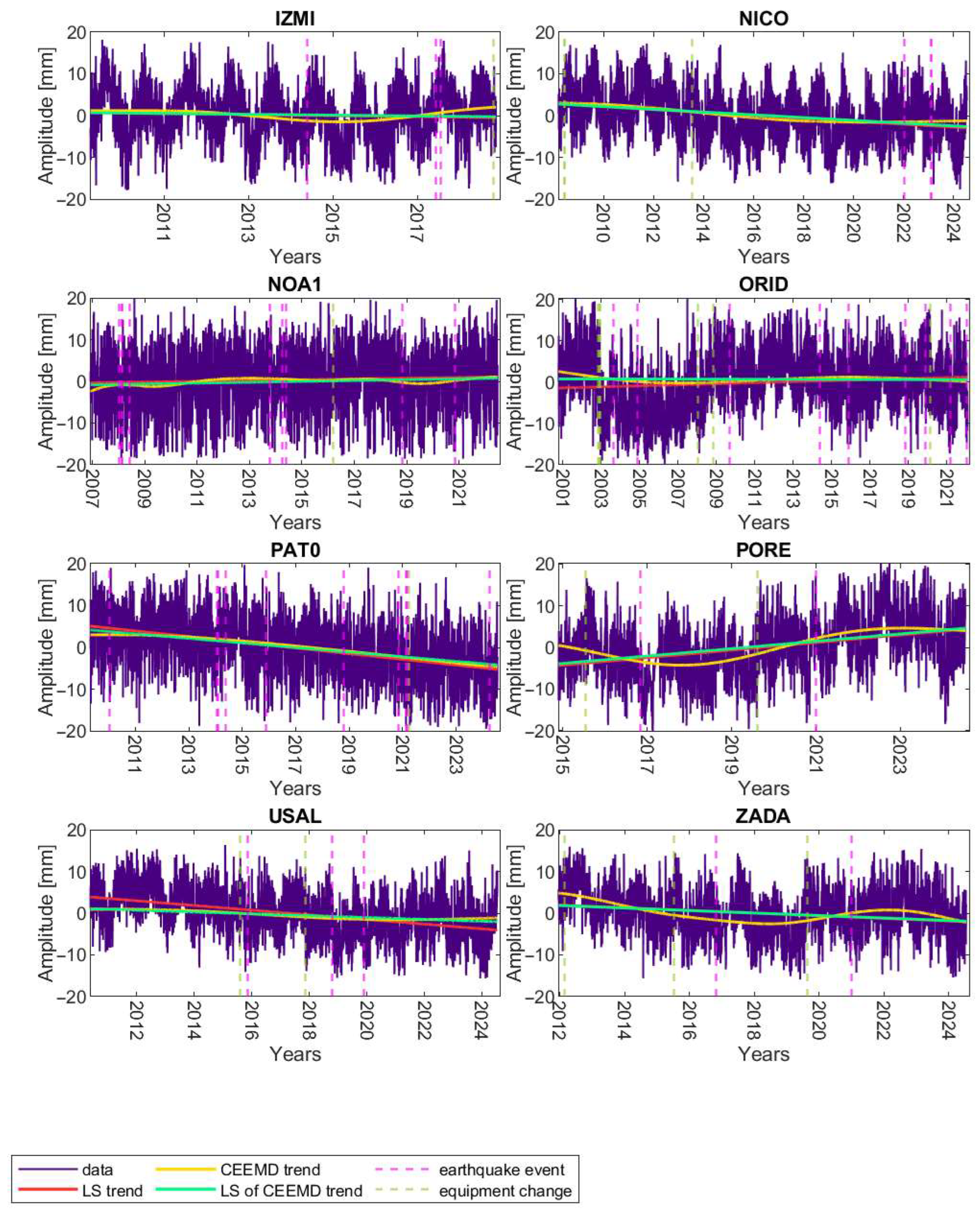
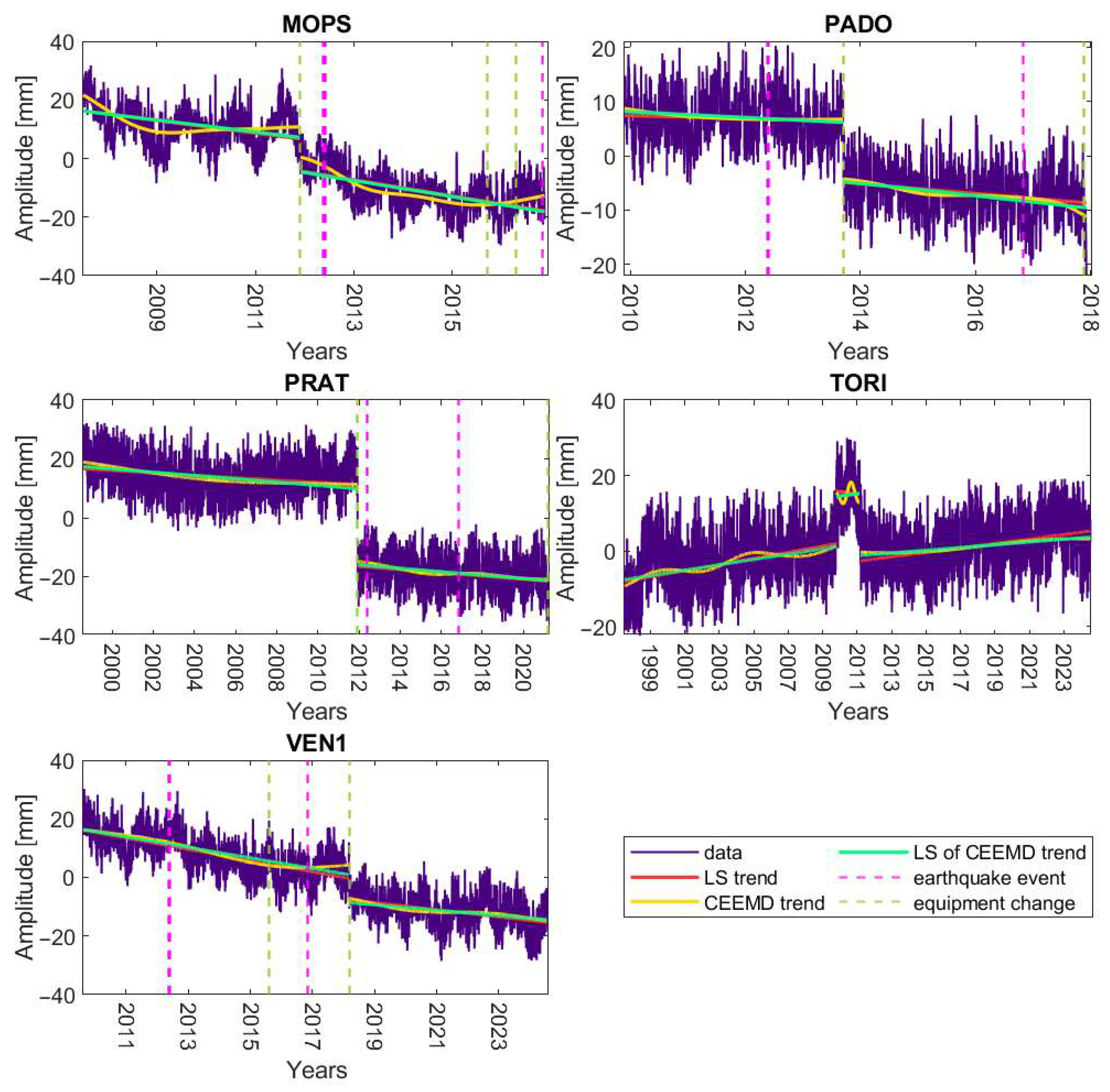
| Station ID | Start Date | End Date | Time Series Length [Years] | Completeness | Longest Period of Missing Data [Days] | |
|---|---|---|---|---|---|---|
| 1 | AQUI | 2009.8810 | 2024.5343 | 14.6533 | 99% | 38 |
| 2 | AUT1 | 2005.2458 | 2021.9552 | 16.7095 | 97% | 35 |
| 3 | BOLG | 2004.6790 | 2024.5343 | 19.8553 | 97% | 19 |
| 4 | DUB2 | 2011.9755 | 2024.5343 | 12.5588 | 94% | 46 |
| 5 | DUTH | 2008.7010 | 2022.9217 | 14.2207 | 98% | 35 |
| 6 | GARI | 2009.3964 | 2024.5343 | 15.1379 | 97% | 34 |
| 7 | GENO | 2010.0973 | 2024.5343 | 14.4370 | 98% | 22 |
| 8 | IGMI | 2006.9405 | 2024.5343 | 17.5938 | 95% | 45 |
| 9 | ISTA | 2007.8605 | 2024.3837 | 16.5233 | 99% | 11 |
| 10 | IZMI | 2009.0049 | 2018.8586 | 9.8537 | 98% | 7 |
| 11 | MOPS | 2007.2581 | 2016.8682 | 9.6101 | 99% | 11 |
| 12 | NICO | 2007.9453 | 2024.5343 | 16.5890 | 99% | 16 |
| 13 | NOA1 | 2006.6804 | 2022.4672 | 15.7868 | 98% | 16 |
| 14 | NOT1 | 2000.6871 | 2019.5541 | 18.8669 | 96% | 26 |
| 15 | ORID | 2000.5283 | 2022.0702 | 21.5419 | 95% | 31 |
| 16 | PADO | 2009.6510 | 2017.9250 | 8.2740 | 98% | 4 |
| 17 | PAT0 | 2009.0706 | 2024.5508 | 15.4801 | 97% | 35 |
| 18 | PORE | 2014.6477 | 2024.5343 | 9.8866 | 95% | 48 |
| 19 | PRAT | 1998.3462 | 2021.1722 | 22.8259 | 94% | 27 |
| 20 | TORI | 1997.2483 | 2024.5343 | 27.2860 | 95% | 32 |
| 21 | TUBI | 1999.8439 | 2020.0715 | 20.2277 | 97% | 25 |
| 22 | TUC2 | 2004.7365 | 2024.5343 | 19.7978 | 97% | 35 |
| 23 | USAL | 2010.1521 | 2024.5343 | 14.3822 | 98% | 9 |
| 24 | VEN1 | 2009.3690 | 2024.5343 | 15.1653 | 99% | 9 |
| 25 | ZADA | 2011.7182 | 2024.5343 | 12.8162 | 95% | 47 |
| Station ID | Slope of Curve [mm/Year] | Standard Error of the LS Trend Fit [mm] | RMSE [mm] | |||
|---|---|---|---|---|---|---|
| MIDAS [11] | LS | LS of CEEMD | ||||
| 1 | AQUI | −0.460 | −0.722 | −0.644 | 6.04 | 0.90 |
| 2 | AUT1 | −1.356 | −1.775 | −1.616 | 5.28 | 0.43 |
| −3.884 | −3.834 | 5.26 | 0.67 | |||
| 3 | BOLG | −1.032 | 3.084 | 4.756 | 9.43 | 2.57 |
| −1.101 | −1.262 | 7.52 | 1.66 | |||
| −2.543 | −2.486 | 6.31 | 1.21 | |||
| 4 | DUB2 | −1.567 | −1.114 | −0.956 | 5.47 | 1.08 |
| 5 | DUTH | 0.463 | 0.047 | 0.061 | 6.10 | 1.45 |
| 6 | GARI | −3.213 | −3.965 | −3.869 | 5.68 | 1.43 |
| −2.404 | −2.281 | 6.02 | 1.26 | |||
| 7 | GENO | −0.624 | −0.493 | −0.463 | 5.82 | 0.53 |
| 8 | IGMI | −0.747 | −0.193 | −0.158 | 5.71 | 1.23 |
| 9 | ISTA | 0.502 | −0.138 | −0.245 | 6.38 | 0.44 |
| 10 | IZMI | −0.306 | −0.120 | −0.100 | 6.08 | 1.08 |
| 11 | MOPS | −3.182 | −2.159 | −2.059 | 6.97 | 2.96 |
| −2.748 | −2.774 | 5.87 | 2.51 | |||
| 12 | NICO | 0.000 | −0.348 | −0.324 | 5.46 | 0.61 |
| 13 | NOA1 | 0.729 | 0.092 | 0.103 | 6.69 | 0.65 |
| 14 | NOT1 | −0.796 | −1.154 | −1.156 | 6.57 | 0.88 |
| 15 | ORID | 0.793 | 0.126 | −0.009 | 6.66 | 0.57 |
| 16 | PADO | −0.473 | −0.235 | −0.230 | 4.74 | 0.91 |
| −0.897 | −1.157 | 4.67 | 0.61 | |||
| 17 | PAT0 | −0.469 | −0.678 | −0.538 | 5.66 | 0.42 |
| 18 | PORE | −1.128 | 0.908 | 0.872 | 6.37 | 2.04 |
| 19 | PRAT | −0.623 | −0.404 | −0.581 | 6.06 | 0.93 |
| −0.550 | −0.585 | 5.35 | 0.61 | |||
| 20 | TORI | −0.019 | 0.810 | 0.710 | 6.36 | 0.93 |
| −0.562 | 0.694 | 5.63 | 1.80 | |||
| 0.590 | 0.550 | 5.70 | 1.00 | |||
| 21 | TUBI | 0.179 | −1.163 | −1.148 | 5.86 | 1.35 |
| 22 | TUC2 | 2.868 | 0.078 | 0.121 | 4.56 | 0.10 |
| −1.174 | −1.220 | 5.46 | 0.71 | |||
| −0.762 | −0.744 | 5.40 | 1.44 | |||
| 23 | USAL | 0.106 | −0.560 | −0.206 | 4.90 | 0.27 |
| 24 | VEN1 | −1.707 | −1.919 | −1.836 | 5.18 | 1.09 |
| −1.224 | −0.895 | 5.39 | 0.59 | |||
| 25 | ZADA | −1.928 | −0.317 | −0.303 | 5.37 | 1.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wnęk, A.; Kudas, D. Determination of Trends in GPS Time Series Using Complementary Ensemble Empirical Mode Decomposition. Remote Sens. 2025, 17, 2802. https://doi.org/10.3390/rs17162802
Wnęk A, Kudas D. Determination of Trends in GPS Time Series Using Complementary Ensemble Empirical Mode Decomposition. Remote Sensing. 2025; 17(16):2802. https://doi.org/10.3390/rs17162802
Chicago/Turabian StyleWnęk, Agnieszka, and Dawid Kudas. 2025. "Determination of Trends in GPS Time Series Using Complementary Ensemble Empirical Mode Decomposition" Remote Sensing 17, no. 16: 2802. https://doi.org/10.3390/rs17162802
APA StyleWnęk, A., & Kudas, D. (2025). Determination of Trends in GPS Time Series Using Complementary Ensemble Empirical Mode Decomposition. Remote Sensing, 17(16), 2802. https://doi.org/10.3390/rs17162802






