A Deep Transfer Contrastive Learning Network for Few-Shot Hyperspectral Image Classification
Abstract
1. Introduction
- (1)
- Spectral data augmentation module: Improves sample diversity through random spectral shift and noise injection
- (2)
- Transfer learning and residual networks are introduced into few-shot hyperspectral classification in a collaborative way, and spectral–spatial dual-branch feature extraction is designed. By combining ImageNet pre-trained spatial features with spectral residual networks, feature expression is optimized. In addition, a spatial attention module (SAM) is introduced to adaptively weight multi-scale spatial features
- (3)
- The cross-entropy and supervised contrast loss are jointly optimized to explicitly maximize the ratio of “inter-class margin/intra-class radius”, directly alleviating the inherent problem of HSIs with similar inter-classes and large intra-class variance.
2. Methodology
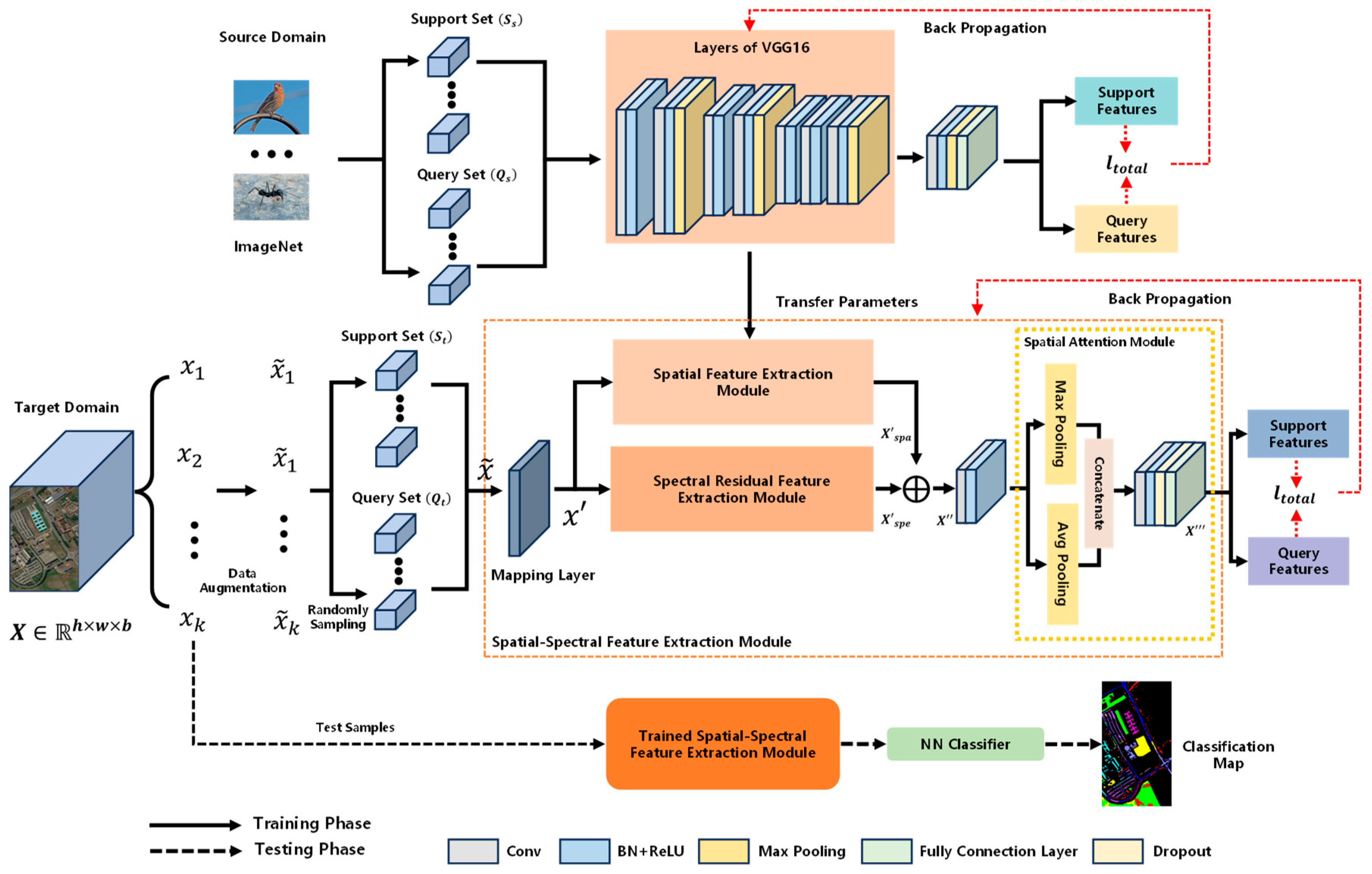
2.1. Overview of the Proposed Network
2.2. Few-Shot Pre-Training Phase
2.2.1. Pre-Training Phase on the Source-Domain
2.2.2. Pre-Training Phase on the Target Domain
3. Experiments and Analyses
3.1. Datasets and Configuration
3.2. Ablation Experiments
3.2.1. Combination of Different Modules
3.2.2. SAM Contribution Analysis
3.2.3. Loss Function
3.3. Comparison with State-of-the-Art Algorithms
3.3.1. The Quantitative Evaluations
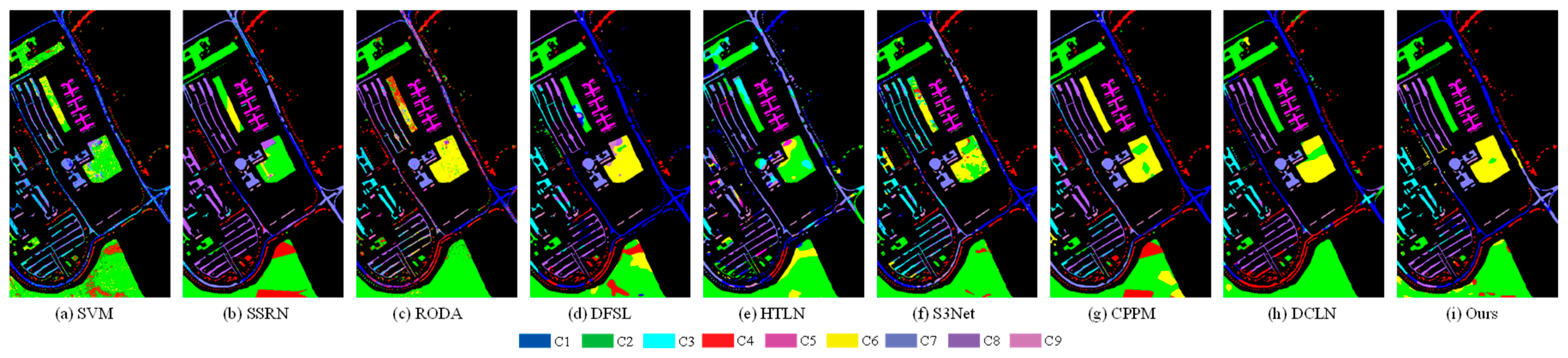
3.3.2. The Qualitative Evaluations
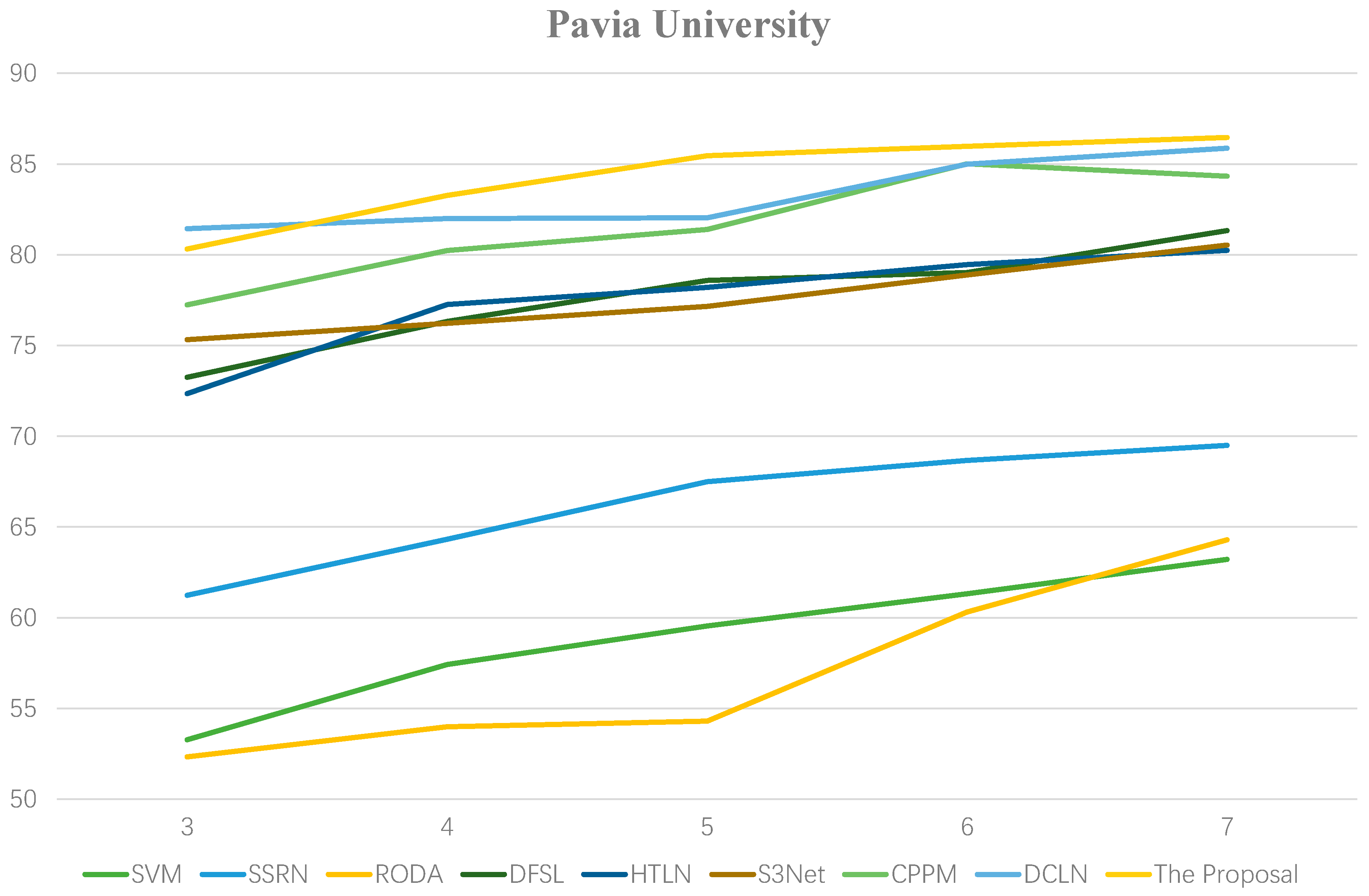
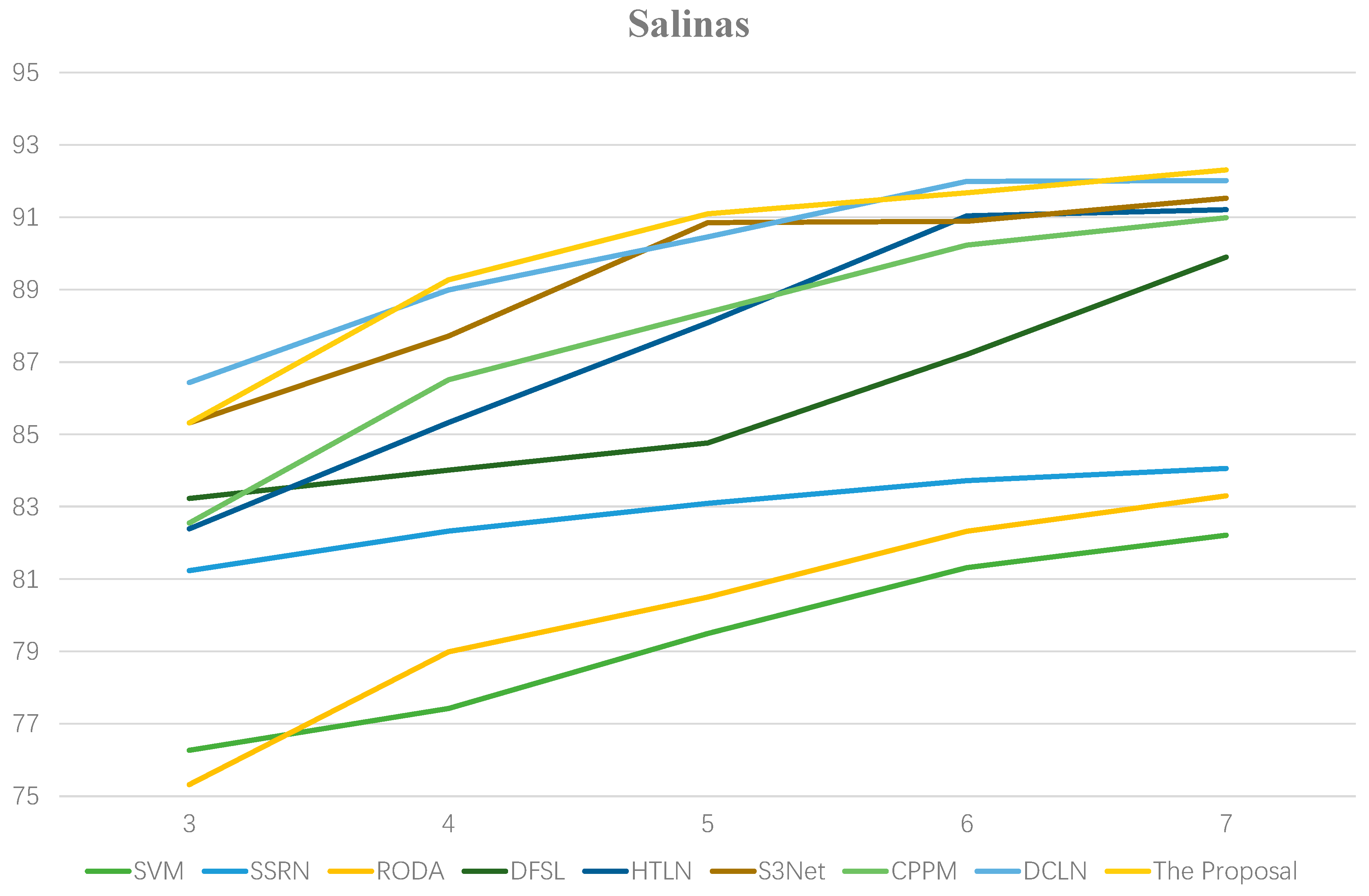
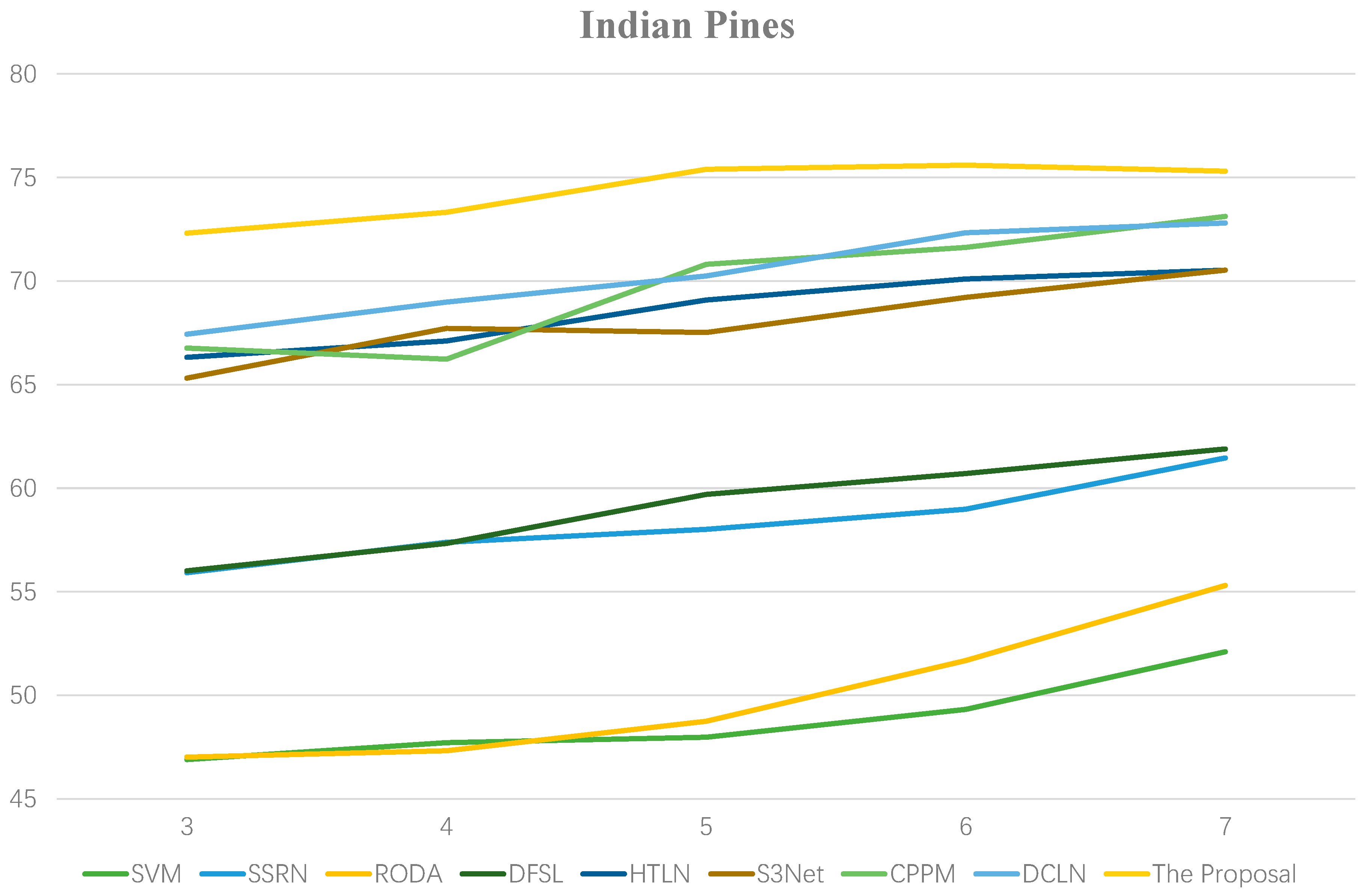
3.4. Effect of the Labeled Samples
3.5. Analysis of Computational Complexity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Cao, Z.; Xin, H.; Wang, R. Efficient Unsupervised Clustering of Hyperspectral Images via Flexible Multi-Anchor Graphs. Remote Sens. 2025, 17, 2647. [Google Scholar] [CrossRef]
- Peng, J.; Sun, W.; Li, W.; Li, H.-C.; Meng, X.; Ge, C.; Du, Q. Low-rank and sparse representation for hyperspectral image processing: A review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 10–43. [Google Scholar] [CrossRef]
- Li, N.; Wang, Z.; Cheikh, F.A. Discriminating spectral–spatial feature extraction for hyperspectral image classification: A review. Sensors 2024, 24, 2987. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Q.; Liang, T.; Yin, J.; Gao, J.; Ge, J.; Hou, M.; Wu, C.; Li, W. Estimating the forage neutral detergent fiber content of alpine grassland in the Tibetan Plateau using hyperspectral data and machine learning algorithms. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4405017. [Google Scholar] [CrossRef]
- Anand, R.; Veni, S.; Araint, J. Big data challenges in airborne hyperspectral image for urban landuse classification. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 1808–1814. [Google Scholar]
- Yang, X.; Yu, Y. Estimating soil salinity under various moisture conditions: An experimental study. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2525–2533. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Z. Self-supervised contrastive learning residual network for hyperspectral image classification under limited labeled samples. In Proceedings of the 2024 7th International Conference on Image and Graphics Processing, Beijing, China, 19–21 January 2024; pp. 116–121. [Google Scholar]
- Démoulin, R.; Gastellu-Etchegorry, J.-P.; Briottet, X.; Marionneau, M.; Zhen, Z.; Adeline, K.; Dantec, V.L. Hyperspectral Remote Sensing and 3D Radiative Transfer Modelling for Maize Crop Monitoring. In Proceedings of the 13th EARSeL Workshop on Imaging Spectroscopy, Valence, Spain, 24–26 April 2024. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; Volime 1, pp. 886–893. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local binary patterns and extreme learning machine for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Wang, X. Hyperspectral image classification powered by Khatri-Rao decomposition-based multinomial logistic regression. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530015. [Google Scholar] [CrossRef]
- Maffei, A.; Haut, J.M.; Paoletti, M.E.; Plaza, J.; Bruzzone, L.; Plaza, A. A single model CNN for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2516–2529. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised spectral-spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Zhang, X.; Gao, H.; Yang, Y.; Wang, J. Deep belief network for spectral–spatial classification of hyperspectral remote sensor data. Sensors 2019, 19, 204. [Google Scholar] [CrossRef] [PubMed]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep few-shot learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Hyperspectral image classification using random occlusion data augmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1751–1755. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Aburaed, N.; Alkhatib, M.Q.; Marshall, S.; Zabalza, J.; Al Ahmad, H. Hyperspectral data scarcity problem from a super resolution perspective: Data augmentation analysis and scheme. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 5056–5057. [Google Scholar]
- Liu, S.; Li, H.; Jiang, C.; Feng, J. Spectral–spatial graph convolutional network with dynamic-synchronized multiscale features for few-shot hyperspectral image classification. Remote Sens. 2024, 16, 895. [Google Scholar] [CrossRef]
- Shi, M.; Ren, J. A lightweight dense relation network with attention for hyperspectral image few-shot classification. Eng. Appl. Artif. Intell. 2023, 126, 106842. [Google Scholar] [CrossRef]
- Zhang, Z.; Gao, D.; Liu, D. Spectral-spatial domain attention network for hyperspectral image few-shot classification. Remote Sens. 2024, 16, 592. [Google Scholar] [CrossRef]
- Jiang, S.; Jia, S. A 3D lightweight Siamese network for hyperspectral image classification with limited samples. In Proceedings of the 10th International Conference on Computing and Pattern Recognition, Shanghai, China, 15–17 October 2021; pp. 142–148. [Google Scholar]
- Gao, K.; Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Sun, Y. Small sample classification of hyperspectral image using model-agnostic meta-learning algorithm and convolutional neural network. Int. J. Remote Sens. 2020, 42, 3090–3122. [Google Scholar] [CrossRef]
- Zhou, F.; Zhang, L.; Wei, W.; Bai, Z.; Zhang, Y. Meta transfer learning for few-shot hyperspectral image classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021; pp. 3681–3684. [Google Scholar]
- Gao, K.; Liu, B.; Yu, X.; Yu, A. Unsupervised meta learning with multiview constraints for hyperspectral image small sample set classification. IEEE Trans. Image Process. 2022, 31, 3449–3462. [Google Scholar] [CrossRef]
- Zhao, L.; Luo, W.; Liao, Q.; Chen, S.; Wu, J. Hyperspectral image classification with contrastive self-supervised learning under limited labeled samples. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6008205. [Google Scholar] [CrossRef]
- Qu, Y.; Baghbaderani, R.K.; Qi, H. Few-shot hyperspectral image classification through multitask transfer learning. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar]
- He, X.; Chen, Y.; Ghamisi, P. Heterogeneous transfer learning for hyperspectral image classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3246–3263. [Google Scholar] [CrossRef]
- Li, X.; Cao, Z.; Zhao, L.; Jiang, J. ALPN: Active-learning-based prototypical network for few-shot hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5508305. [Google Scholar] [CrossRef]
- Thoreau, R.; Achard, V.; Risser, L.; Berthelot, B.; Briottet, X. Active learning for hyperspectral image classification: A comparative review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 256–278. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Z.; Wang, D.; Wang, Z.J. Cross-domain few-shot contrastive learning for hyperspectral images classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5514505. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, J.; Zhang, G.; Sun, W.; Du, Q. Deep contrastive learning network for small-sample hyperspectral image classification. J. Remote Sens. 2023, 3, 0025. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, J.; Chen, N.; Sun, W.; Du, Q.; Zhou, Y. Refined prototypical contrastive learning for few-shot hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506214. [Google Scholar] [CrossRef]
- Jaiswal, A.; Babu, A.R.; Zadeh, M.Z.; Banerjee, D.; Makedon, F. A survey on contrastive self-supervised learning. Technologies 2020, 9, 2. [Google Scholar] [CrossRef]
- Devabathini, N.J.; Mathivanan, P. Sign language recognition through video frame feature extraction using transfer learning and neural networks. In Proceedings of the 2023 International Conference on Next Generation Electronics (NEleX), Vellore, India, 14–16 December 2023; pp. 1–6. [Google Scholar]
- Dhillon, G.S.; Chaudhari, P.; Ravichandran, A.; Soatto, S. A baseline for few-shot image classification. arXiv 2019, arXiv:1909.02729. [Google Scholar]
- Settles, B. Active Learning Literature Survey; University of Wisconsin-Madison: Madison, WI, USA, 2009. [Google Scholar]
- Li, Z.; Liu, M.; Chen, Y.; Xu, Y.; Li, W.; Du, Q. Deep cross-domain few-shot learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5501618. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1359. [Google Scholar] [CrossRef]
- Xue, Z.; Zhou, Y.; Du, P. S3Net: Spectral–spatial Siamese network for few-shot hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5531219. [Google Scholar] [CrossRef]
- Theckedath, D.; Sedamkar, R.R. Detecting affect states using VGG16, ResNet50 and SE-ResNet50 networks. SN Comput. Sci. 2020, 1, 79. [Google Scholar] [CrossRef]
- Elsayed, G.; Krishnan, D.; Mobahi, H.; Regan, K.; Bengio, S. Large margin deep networks for classification. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, Canada, 3–8 December 2018; pp. 850–860. [Google Scholar]
- Song, L.; Feng, Z.; Yang, S.; Zhang, X.; Jiao, L. Self-supervised assisted semi-supervised residual network for hyperspectral image classification. Remote Sens. 2022, 14, 2997. [Google Scholar] [CrossRef]
- Yang, H.; Ni, J.; Gao, J.; Han, Z.; Luan, T. A novel method for peanut variety identification and classification by improved VGG16. Sci. Rep. 2021, 11, 15756. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the Machine Learning Research (PMLR), Virtual Event, 13–18 July 2020; Volume 119, pp. 1597–1607. [Google Scholar]
- Braham, N.A.A.; Mairal, J.; Chanussot, J.; Mou, L.; Zhu, X.X. Enhancing contrastive learning with positive pair mining for few-shot hyperspectral image classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2024, 17, 8509–8526. [Google Scholar] [CrossRef]





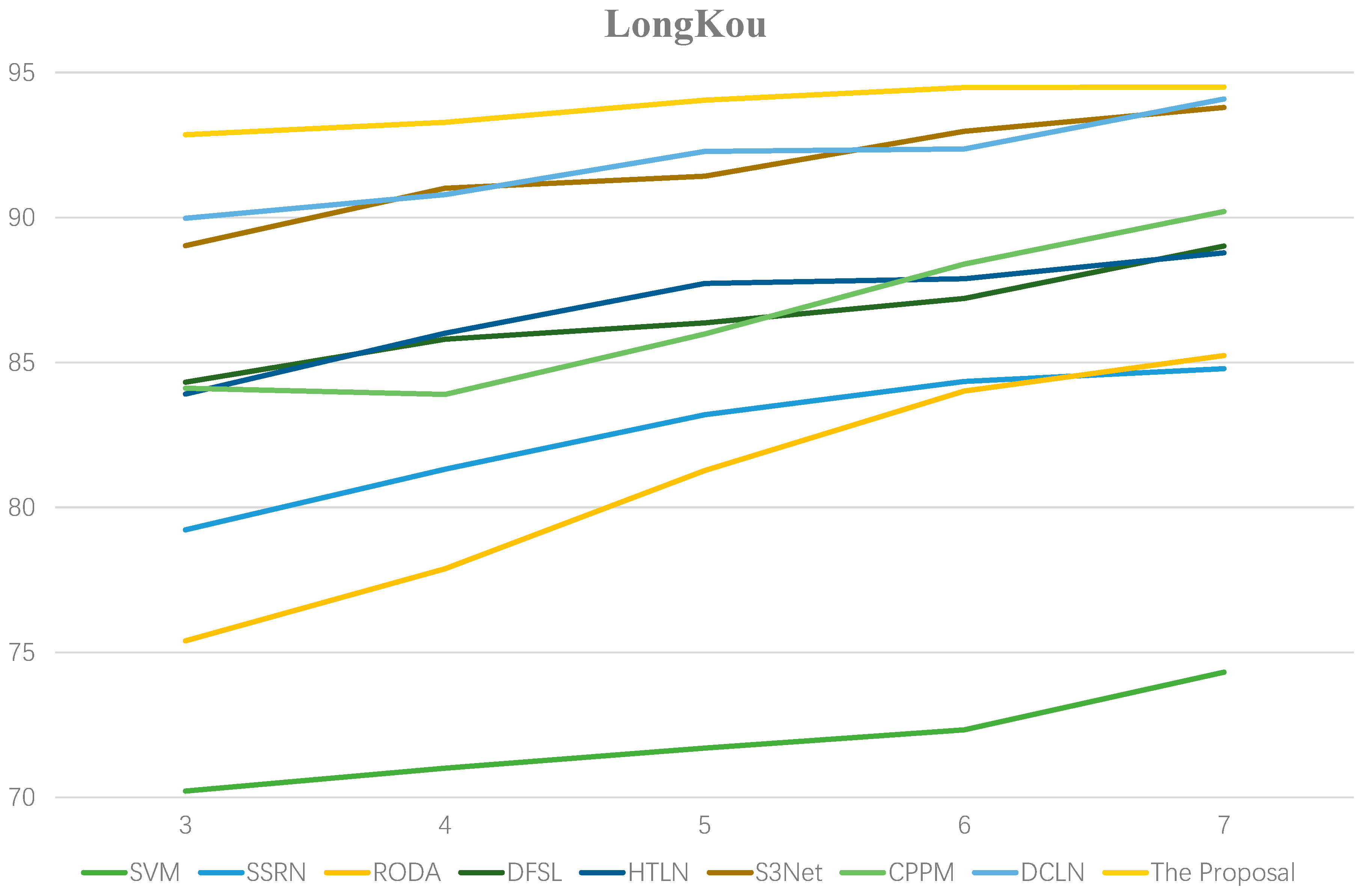
| Pavia University | |||
|---|---|---|---|
| No. | Land-Cover Type | Training | Test |
| 1 | Asphalt | 5 | 6626 |
| 2 | Medows | 5 | 18,644 |
| 3 | Gravel | 5 | 2094 |
| 4 | Trees | 5 | 3059 |
| 5 | Metal-sheets | 5 | 1340 |
| 6 | Bare-soil | 5 | 5024 |
| 7 | Bitumen | 5 | 1325 |
| 8 | Bricks | 5 | 3677 |
| 9 | Shadows | 5 | 942 |
| Total | 45 | 42,731 | |
| Salinas | |||
|---|---|---|---|
| No. | Land-Cover Type | Training | Test |
| 1 | Brocoli 1 | 5 | 2004 |
| 2 | Brocoli 2 | 5 | 3721 |
| 3 | Fallow | 5 | 1971 |
| 4 | Fallow_plow | 5 | 1389 |
| 5 | Fallow_smooth | 5 | 2673 |
| 6 | Stubble | 5 | 3954 |
| 7 | Celery | 5 | 3574 |
| 8 | Grapes_untrained | 5 | 11,266 |
| 9 | Soil | 5 | 6198 |
| 10 | Corn | 5 | 3273 |
| 11 | Lettuce_4_wk | 5 | 1063 |
| 12 | Lettuce_5_wk | 5 | 1922 |
| 13 | Lettuce_6_wk | 5 | 911 |
| 14 | Lettuce_7_wk | 5 | 1065 |
| 15 | Vinyard-untrained | 5 | 7263 |
| 16 | Vinyard-vertical | 5 | 1802 |
| Total | 80 | 54,049 | |
| Indian Pines | |||
|---|---|---|---|
| No. | Land-Cover Type | Training | Test |
| 1 | Alfalfa | 5 | 41 |
| 2 | Corn-notill | 5 | 1432 |
| 3 | Corn-mintill | 5 | 825 |
| 4 | Corn | 5 | 232 |
| 5 | Grass-pasture | 5 | 478 |
| 6 | Grass-trees | 5 | 725 |
| 7 | Grass-pasture mowed | 5 | 23 |
| 8 | Hay-windrowed | 5 | 473 |
| 9 | Oats | 5 | 15 |
| 10 | Soybean-notill | 5 | 967 |
| 11 | Soybean-mintill | 5 | 2450 |
| 12 | Soybean-clean | 5 | 588 |
| 13 | Wheat | 5 | 200 |
| 14 | Woods | 5 | 1260 |
| 15 | Buildings-grass | 5 | 381 |
| 16 | Stone-steel | 5 | 88 |
| Total | 80 | 10,169 | |
| LongKou | |||
|---|---|---|---|
| No. | Land-Cover Type | Training | Test |
| 1 | Corn | 5 | 34,506 |
| 2 | Cotton | 5 | 8369 |
| 3 | Sesame | 5 | 3026 |
| 4 | Broad-leaf soy-bean | 5 | 63,207 |
| 5 | Narrow-leaf soybean | 5 | 4146 |
| 6 | Rice | 5 | 11,849 |
| 7 | Water | 5 | 67,051 |
| 8 | Roads and Houses | 5 | 7119 |
| 9 | Mixed weed | 5 | 5224 |
| Total | 45 | 204,497 | |
| Dataset | Schemes | OA (%) |
|---|---|---|
| Pavia University | SpaM (Pre-trained) | |
| SpaM (Scratch) | ||
| SpeM | ||
| SpaM (Pre-trained) + SpeM | ||
| Salinas | SpaM (Pre-trained) | |
| SpaM (Scratch) | ||
| SpeM | ||
| SpaM (Pre-trained) + SpeM | ||
| Indian Pines | SpaM (Pre-trained) | |
| SpaM (Scratch) | ||
| SpeM | ||
| SpaM (Pre-trained) + SpeM | ||
| LongKou | SpaM (Pre-trained) | |
| SpaM (Scratch) | ||
| SpeM | ||
| SpaM (Pre-trained) + SpeM |
| Dataset | With SAM | Without SAM | ∆OA (%) |
|---|---|---|---|
| Pavia University | |||
| Salinas | |||
| Indian Pines | |||
| LongKou | +2.31 |
| Dataset | Loss Function | OA (%) |
|---|---|---|
| Pavia University | ||
| Salinas | ||
| Indian Pines | ||
| LongKou | ||
| SVM | SSRN | RODA | DFSL | HTLN | S3Net | CPPM | DCLN | Ours | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 72.42 | 76.99 | 35.53 | 98.24 | 89.77 | 81.76 | 79.12 | 73.86 | 83.21 |
| 2 | 82.69 | 63.97 | 51.80 | 98.45 | 74.37 | 75.51 | 85.48 | 61.77 | 91.14 |
| 3 | 40.71 | 55.98 | 84.78 | 48.04 | 62.87 | 70.08 | 63.13 | 39.89 | 80.47 |
| 4 | 67.90 | 91.82 | 86.77 | 50.94 | 94.69 | 85.83 | 92.07 | 94.34 | 92.54 |
| 5 | 99.99 | 99.51 | 100 | 99.92 | 99.86 | 99.93 | 99.72 | 98.79 | 98.48 |
| 6 | 27.83 | 63.29 | 49.78 | 77.96 | 57.79 | 64.17 | 71.07 | 86.05 | 70.34 |
| 7 | 41.89 | 55.67 | 94.72 | 73.53 | 93.12 | 95.14 | 79.17 | 90.76 | 89.60 |
| 8 | 54.84 | 45.85 | 20.44 | 84.24 | 81.35 | 72.45 | 69.97 | 63.91 | 74.43 |
| 9 | 81.75 | 99.63 | 96.82 | 75.68 | 98.06 | 94.90 | 97.60 | 98.97 | 99.18 |
| OA | 59.54 ±2.38 | 67.49 ±1.27 | 54.30 ±1.03 | 78.58 ±2.77 | 78.20 ±0.98 | 77.15 ±1.11 | 81.39 ±2.93 | 82.04 ±1.42 | 85.46 ±1.56 |
| AA | 63.36 ±3.85 | 72.52 ±2.89 | 68.96 ±0.12 | 78.56 ±1.65 | 83.53 ±0.45 | 82.19 ±0.67 | 81.93 ±1.94 | 68.92 ±2.31 | 86.60 ±1.32 |
| 49.49 ±2.71 | 58.97 ±0.56 | 44.88 ±2.34 | 78.50 ±2.01 | 72.10 ±1.88 | 71.02 ±2.56 | 76.24 ±3.58 | 75.10 ±1.87 | 81.18 ±2.12 |
| SVM | SSRN | RODA | DFSL | HTLN | S3Net | CPPM | DCLN | Ours | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 89.94 | 94.17 | 81.26 | 99.70 | 100 | 99.91 | 99.12 | 99.27 | 98.54 |
| 2 | 97.36 | 98.57 | 87.92 | 99.60 | 99.80 | 94.24 | 97.50 | 99.51 | 98.49 |
| 3 | 84.33 | 90.56 | 75.26 | 98.83 | 96.40 | 96.94 | 96.43 | 90.60 | 99.79 |
| 4 | 99.31 | 98.93 | 75.94 | 98.20 | 83.27 | 98.80 | 96.65 | 99.67 | 99.54 |
| 5 | 92.13 | 95.23 | 87.41 | 73.19 | 89.22 | 97.52 | 98.36 | 92.20 | 96.38 |
| 6 | 97.13 | 99.25 | 90.02 | 97.60 | 99.97 | 99.28 | 98.07 | 98.73 | 97.96 |
| 7 | 96.58 | 98.82 | 85.57 | 99.22 | 98.48 | 98.89 | 99.03 | 99.33 | 98.65 |
| 8 | 66.48 | 78.50 | 83.63 | 80.24 | 89.48 | 81.66 | 63.39 | 72.28 | 76.02 |
| 9 | 97.41 | 94.11 | 93.53 | 100 | 99.45 | 99.71 | 98.99 | 99.95 | 98.61 |
| 10 | 76.63 | 85.56 | 84.84 | 74.83 | 90.05 | 92.57 | 92.90 | 91.43 | 93.99 |
| 11 | 76.39 | 90.63 | 62.94 | 95.30 | 97.06 | 99.53 | 98.42 | 98.16 | 98.20 |
| 12 | 88.41 | 99.48 | 79.74 | 81.12 | 97.41 | 88.67 | 83.17 | 98.90 | 99.34 |
| 13 | 91.20 | 20.08 | 62.15 | 100 | 97.09 | 97.96 | 99.02 | 98.75 | 98.10 |
| 14 | 79.13 | 66.29 | 65.63 | 32.83 | 81.96 | 91.57 | 96.99 | 97.97 | 97.98 |
| 15 | 46.37 | 59.14 | 69.97 | 57.72 | 60.39 | 73.39 | 88.14 | 85.96 | 81.33 |
| 16 | 91.23 | 66.96 | 72.47 | 95.62 | 99.48 | 96.10 | 86.50 | 91.56 | 97.09 |
| OA | 79.50 ±2.09 | 83.09 ±1.42 | 80.50 ±1.19 | 84.76 ±2.22 | 88.08 ±1.36 | 90.85 ±1.74 | 88.37 ±0.75 | 90.46 ±1.21 | 91.10 ±2.32 |
| AA | 85.63 ±2.08 | 85.46 ±2.67 | 78.64 ±2.45 | 86.50 ±0.76 | 92.47 ±1.79 | 94.29 ±2.09 | 93.30 ± 0.54 | 94.64 ±0.31 | 95.62 ±0.62 |
| 77.26 ±3.51 | 81.07 ±2.81 | 78.42 ±1.93 | 83.07 ±1.58 | 86.80 ±2.83 | 89.82 ±0.34 | 87.12 ±0.81 | 89.42 ±0.57 | 90.11 ±1.44 |
| SVM | SSRN | RODA | DFSL | HTLN | S3Net | CPPM | DCLN | Ours | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 28.19 | 77.35 | 92.68 | 80.56 | 36.53 | 99.76 | 100 | 82.41 | 89.23 |
| 2 | 39.74 | 18.52 | 55.31 | 29.20 | 68.15 | 47.38 | 38.44 | 57.12 | 72.97 |
| 3 | 37.05 | 54.66 | 51.52 | 79.02 | 65.64 | 58.82 | 56.70 | 62.47 | 74.01 |
| 4 | 26.06 | 32.30 | 37.50 | 87.22 | 49.04 | 89.61 | 74.70 | 89.24 | 84.31 |
| 5 | 42.93 | 9.73 | 85.36 | 85.20 | 86.01 | 78.97 | 85.33 | 65.24 | 90.99 |
| 6 | 80.92 | 85.53 | 88.14 | 88.75 | 97.58 | 95.45 | 91.27 | 70.15 | 94.14 |
| 7 | 23.70 | 10.27 | 100 | 100 | 19.00 | 100 | 100 | 97.42 | 95.00 |
| 8 | 92.34 | 78.50 | 61.31 | 100 | 47.06 | 83.30 | 85.90 | 91.42 | 97.94 |
| 9 | 12.92 | 12.32 | 93.33 | 100 | 25.86 | 100 | 100 | 93.24 | 85.00 |
| 10 | 38.63 | 62.28 | 15.31 | 54.16 | 64.71 | 57.23 | 68.63 | 64.70 | 78.97 |
| 11 | 56.25 | 66.86 | 30.57 | 42.54 | 74.96 | 58.13 | 74.44 | 60.17 | 59.71 |
| 12 | 22.23 | 28.25 | 9.18 | 37.91 | 56.76 | 60.41 | 43.91 | 67.04 | 82.76 |
| 13 | 83.20 | 99.18 | 96.00 | 97.95 | 76.92 | 99.05 | 99.70 | 84.28 | 99.14 |
| 14 | 83.40 | 85.98 | 68.17 | 73.39 | 92.32 | 83.16 | 89.35 | 86.27 | 77.48 |
| 15 | 27.96 | 13.82 | 40.68 | 58.24 | 51.46 | 76.27 | 79.74 | 92.84 | 79.65 |
| 16 | 85.20 | 87.78 | 100 | 100 | 57.14 | 99.43 | 95.00 | 84.57 | 99.44 |
| OA | 47.98 ±3.72 | 58.01 ±1.13 | 48.74 ±2.90 | 59.70 ±2.97 | 69.08 ±3.01 | 67.52 ±3.19 | 70.82 +1.30 | 70.25 ±2.50 | 75.40 ±2.21 |
| AA | 48.79 ±2.91 | 50.56 ±2.26 | 64.07 ±2.39 | 75.88 ±3.28 | 60.57 ±2.77 | 80.43 ±2.38 | 80.19 +1.61 | 77.97 ±1.61 | 85.05 ±1.32 |
| 41.91 ±2.45 | 52.07 ±1.69 | 42.44 ±4.82 | 55.17 ±4.33 | 65.21 ±2.54 | 63.57 ±3.71 | 66.85 +1.47 | 68.38 ±1.24 | 72.06 ±0.97 |
| SVM | SSRN | RODA | DFSL | HTLN | S3Net | CPPM | DCLN | Ours | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 87.00 | 90.49 | 81.32 | 91.08 | 77.61 | 95.25 | 89.29 | 88.17 | 92.3 |
| 2 | 64.61 | 80.13 | 78.42 | 78.79 | 92.93 | 87.28 | 76.07 | 97.08 | 72.22 |
| 3 | 57.40 | 78.84 | 80.33 | 93.66 | 87.13 | 97.56 | 97.90 | 75.29 | 97.63 |
| 4 | 95.55 | 92.64 | 94.13 | 94.26 | 77.60 | 96.93 | 77.49 | 97.88 | 90.15 |
| 5 | 99.82 | 99.77 | 98.75 | 99.96 | 88.11 | 99.23 | 80.12 | 100.0 | 92.35 |
| 6 | 58.82 | 69.78 | 75.96 | 91.18 | 96.12 | 92.25 | 91.02 | 93.97 | 85.53 |
| 7 | 78.75 | 97.93 | 91.42 | 80.77 | 89.27 | 94.92 | 98.69 | 75.35 | 86.65 |
| 8 | 66.12 | 86.53 | 79.24 | 92.64 | 83.94 | 97.50 | 53.25 | 79.88 | 81.71 |
| 9 | 99.26 | 86.05 | 99.93 | 99.99 | 56.41 | 95.11 | 51.03 | 97.27 | 87.58 |
| OA | 71.70 ±4.53 | 83.20 ±2.64 | 81.28 ±1.72 | 86.37 ±2.46 | 87.73 ±2.33 | 91.43 ±1.24 | 85.99 ± 2.11 | 92.29 ±1.08 | 94.05 ±1.37 |
| AA | 78.59 ±3.76 | 86.92 ±1.31 | 86.61 ±3.23 | 91.37 ±1.96 | 83.24 ±2.33 | 93.87 ±1.22 | 79.43 ±3.10 | 89.43 ±1.79 | 93.84 ±2.54 |
| 64.42 ±4.22 | 78.31 ±1.77 | 75.81 ±2.64 | 82.66 ±2.77 | 83.63 ±3.79 | 89.83 ±2.68 | 82.11 ±4.02 | 89.74 ±2.01 | 94.99 ±1.79 |
| SVM | SSRN | RODA | DFSL | HTLN | S3Net | CPPM | DCLN | The Proposal | ||
|---|---|---|---|---|---|---|---|---|---|---|
| PU | Train | 4.24 | 722.43 | 634.23 | 809.58 | 1482.30 | 1204.34 | 1847.30 | 1437.82 | 1567.34 |
| Test | 0.57 | 3.89 | 3.38 | 4.57 | 8.42 | 6.23 | 7.98 | 7.32 | 8.61 | |
| Params | - | 0.35 | 0.20 | 0.03 | 0.68 | 0.05 | 0.85 | 0.63 | 0.46 | |
| SA | Train | 7.32 | 1029.4 | 874.87 | 1198.32 | 1624.06 | 1352.33 | 1629.04 | 1577.95 | 1431.51 |
| Test | 0.82 | 6.22 | 5.29 | 7.32 | 8.11 | 7.39 | 8.23 | 7.91 | 8.92 | |
| Params | - | 0.40 | 0.20 | 0.03 | 0.68 | 0.09 | 0.85 | 0.65 | 0.46 | |
| IP | Train | 3.97 | 463.21 | 423.25 | 927.43 | 1432.57 | 983.46 | 1563.97 | 1360.32 | 1523.95 |
| Test | 0.49 | 3.78 | 3.12 | 5.43 | 7.29 | 5.88 | 7.92 | 8.13 | 7.33 | |
| Params | - | 0.35 | 0.20 | 0.03 | 0.68 | 0.09 | 0.85 | 0.63 | 0.46 | |
| LongKou | Train | 9.42 | 509.32 | 1302.34 | 1628.94 | 1937.32 | 1799.21 | 2384.22 | 1988.29 | 1803.98 |
| Test | 2.35 | 13.97 | 20.21 | 19.39 | 22.34 | 21.15 | 21.33 | 24.90 | 20.32 | |
| Params | - | 0.35 | 0.20 | 0.03 | 0.68 | 0.09 | 0.85 | 0.65 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Wang, Z. A Deep Transfer Contrastive Learning Network for Few-Shot Hyperspectral Image Classification. Remote Sens. 2025, 17, 2800. https://doi.org/10.3390/rs17162800
Yang G, Wang Z. A Deep Transfer Contrastive Learning Network for Few-Shot Hyperspectral Image Classification. Remote Sensing. 2025; 17(16):2800. https://doi.org/10.3390/rs17162800
Chicago/Turabian StyleYang, Gan, and Zhaohui Wang. 2025. "A Deep Transfer Contrastive Learning Network for Few-Shot Hyperspectral Image Classification" Remote Sensing 17, no. 16: 2800. https://doi.org/10.3390/rs17162800
APA StyleYang, G., & Wang, Z. (2025). A Deep Transfer Contrastive Learning Network for Few-Shot Hyperspectral Image Classification. Remote Sensing, 17(16), 2800. https://doi.org/10.3390/rs17162800





