Diverse Techniques in Estimating Integrated Water Vapor for Calibration and Validation of Satellite Altimetry
Abstract
1. Introduction
2. Data and Instruments
2.1. GNSS Meteorology
2.2. Radiosondes
2.3. Ground-Based Μicrowave Radiometer
2.4. Satellite Sensors for the IWV Estimation
2.5. Atmospheric Models
3. Methods
3.1. GNSS Meteorology
3.2. Ground-Based Μicrowave Radiometer and Radiosondes
3.3. Satellite Sensors for the IWV Estimation
3.4. Atmospheric Models
4. Results
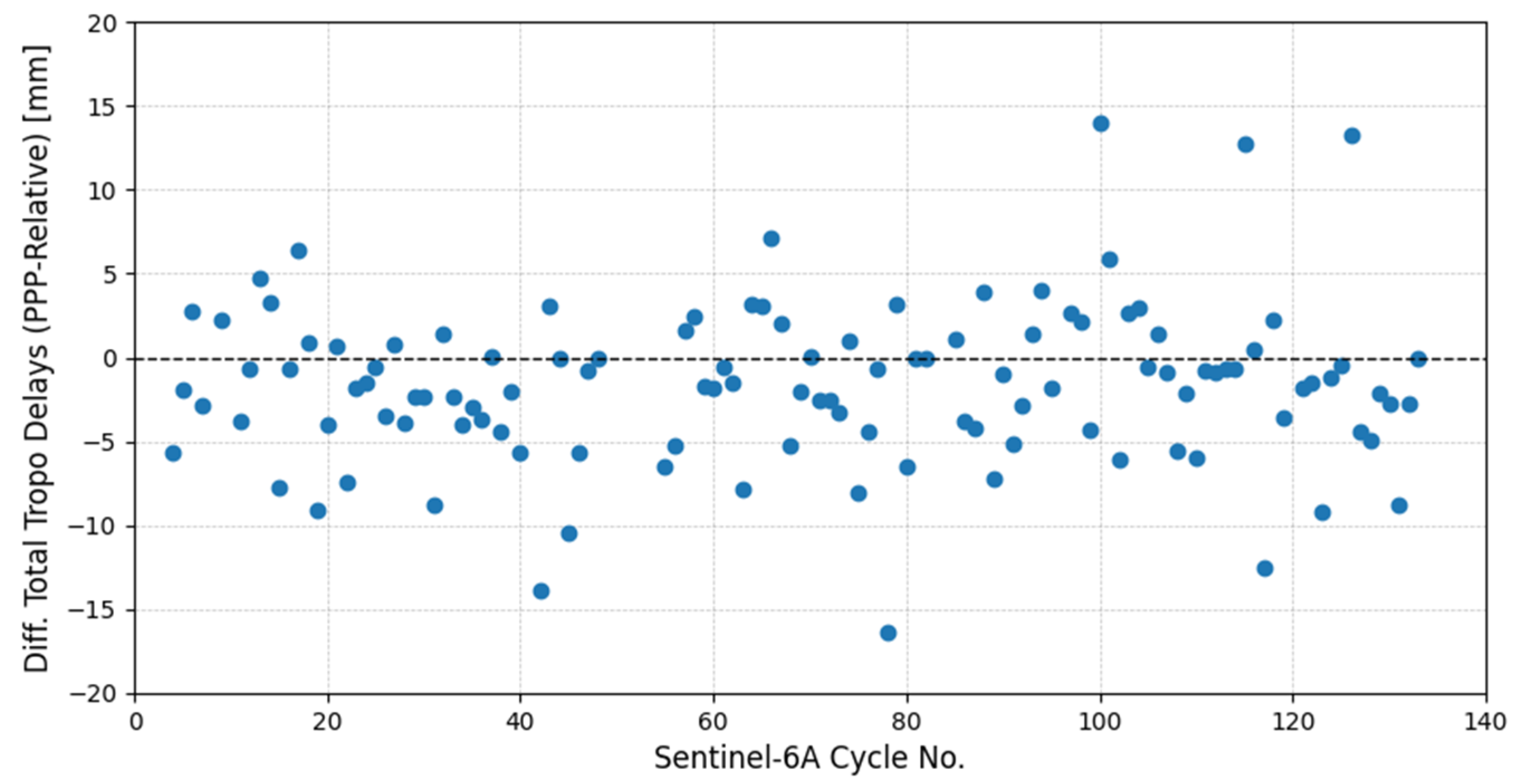
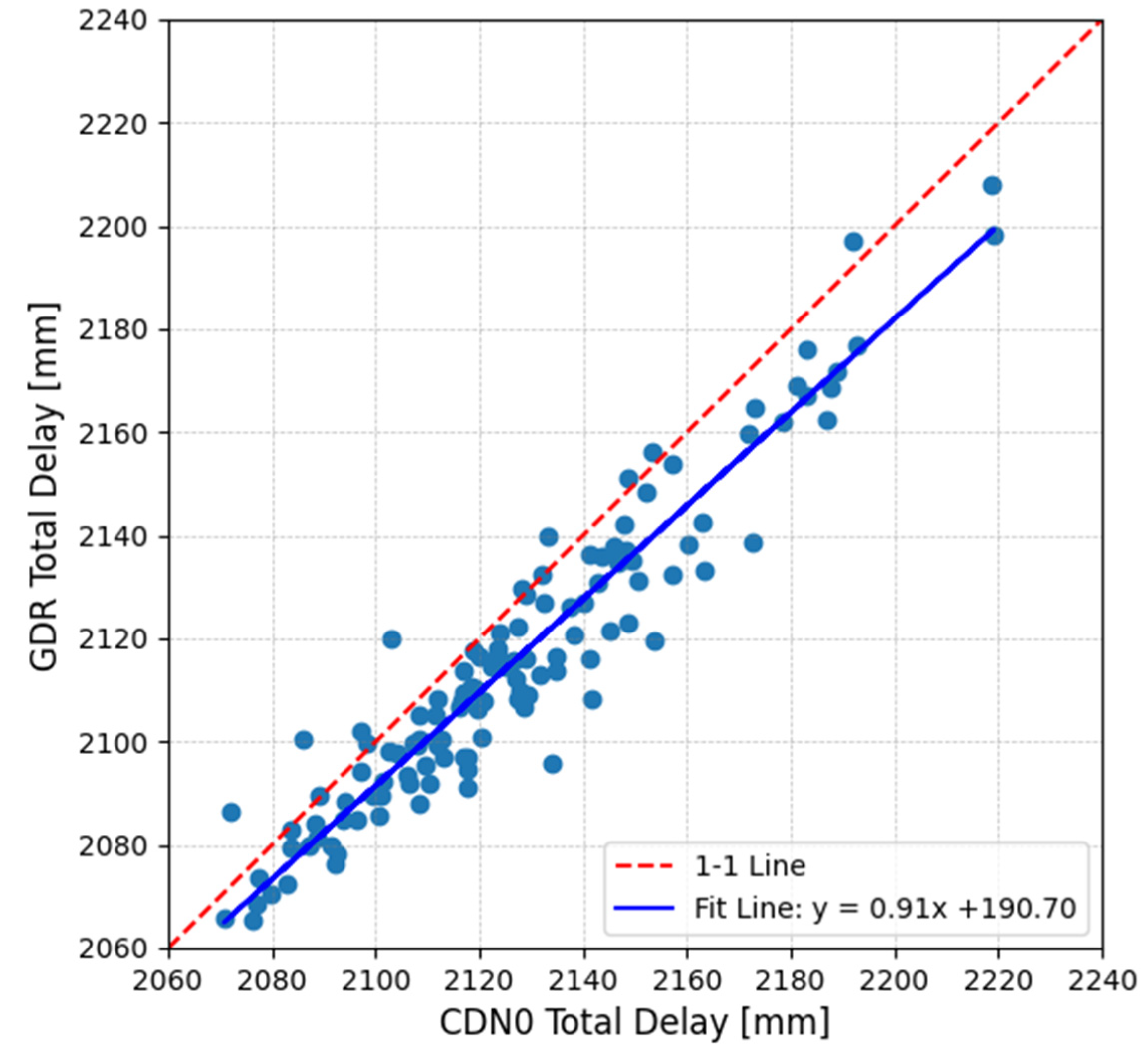
4.1. Total Tropospheric Delay from GNSS
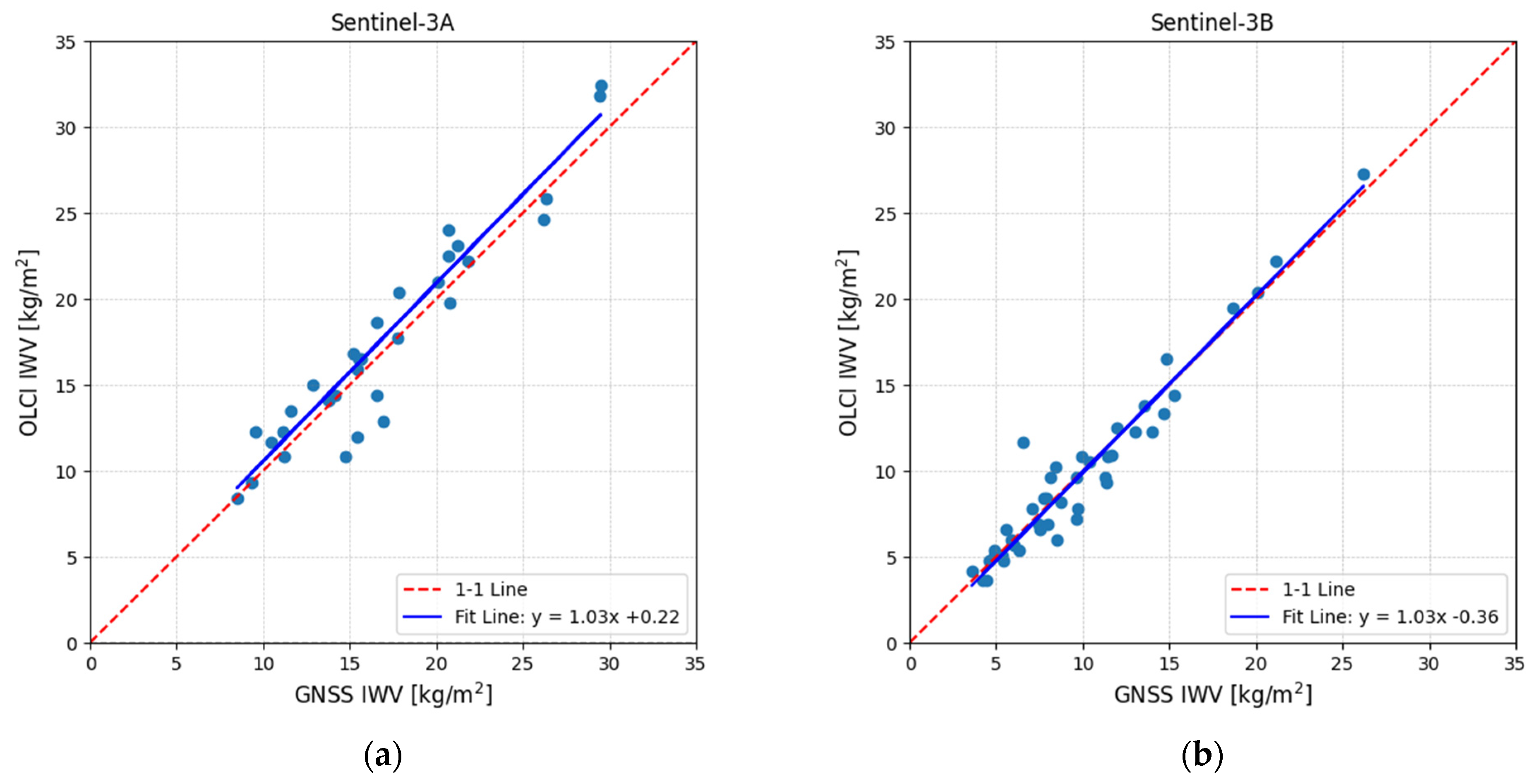
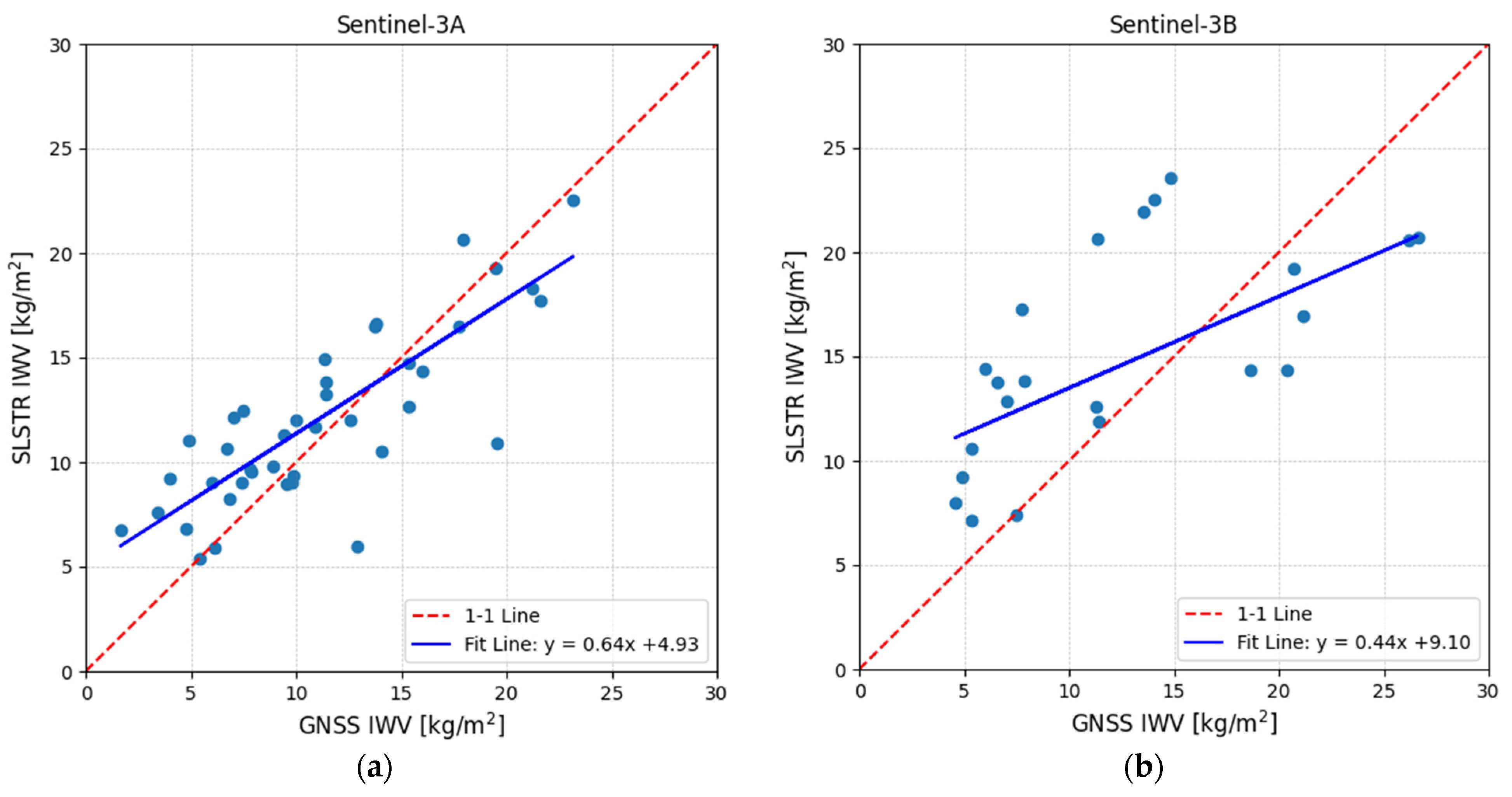
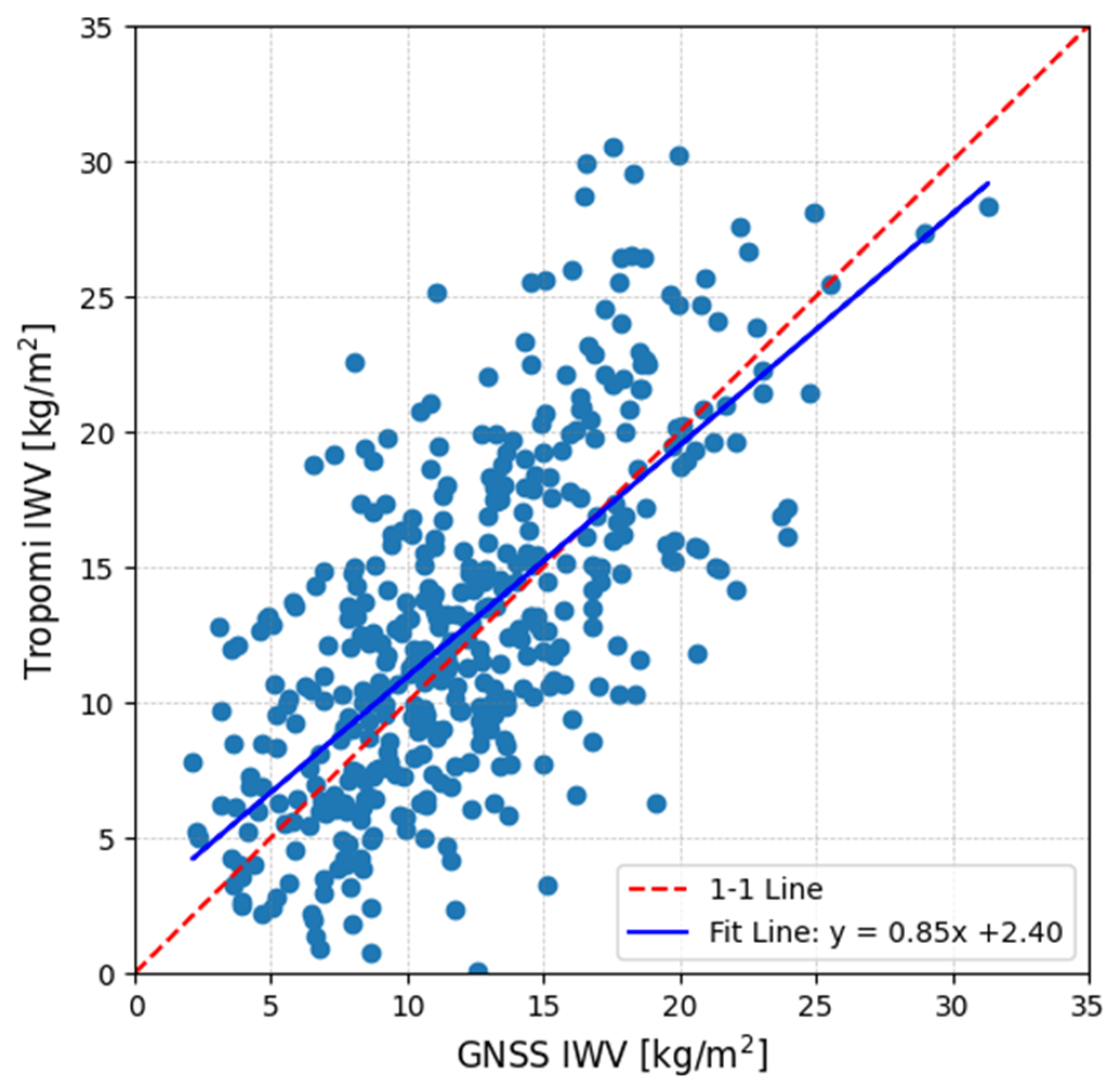
4.2. Integrated Water Vapor Derived from Satellite Sensors
4.2.1. The OLCI Instrument of Sentinel-3A/B
4.2.2. The SLSTR Instrument of Sentinel-3A/B
4.2.3. The TROPOMI Instrument of Sentinel-5P
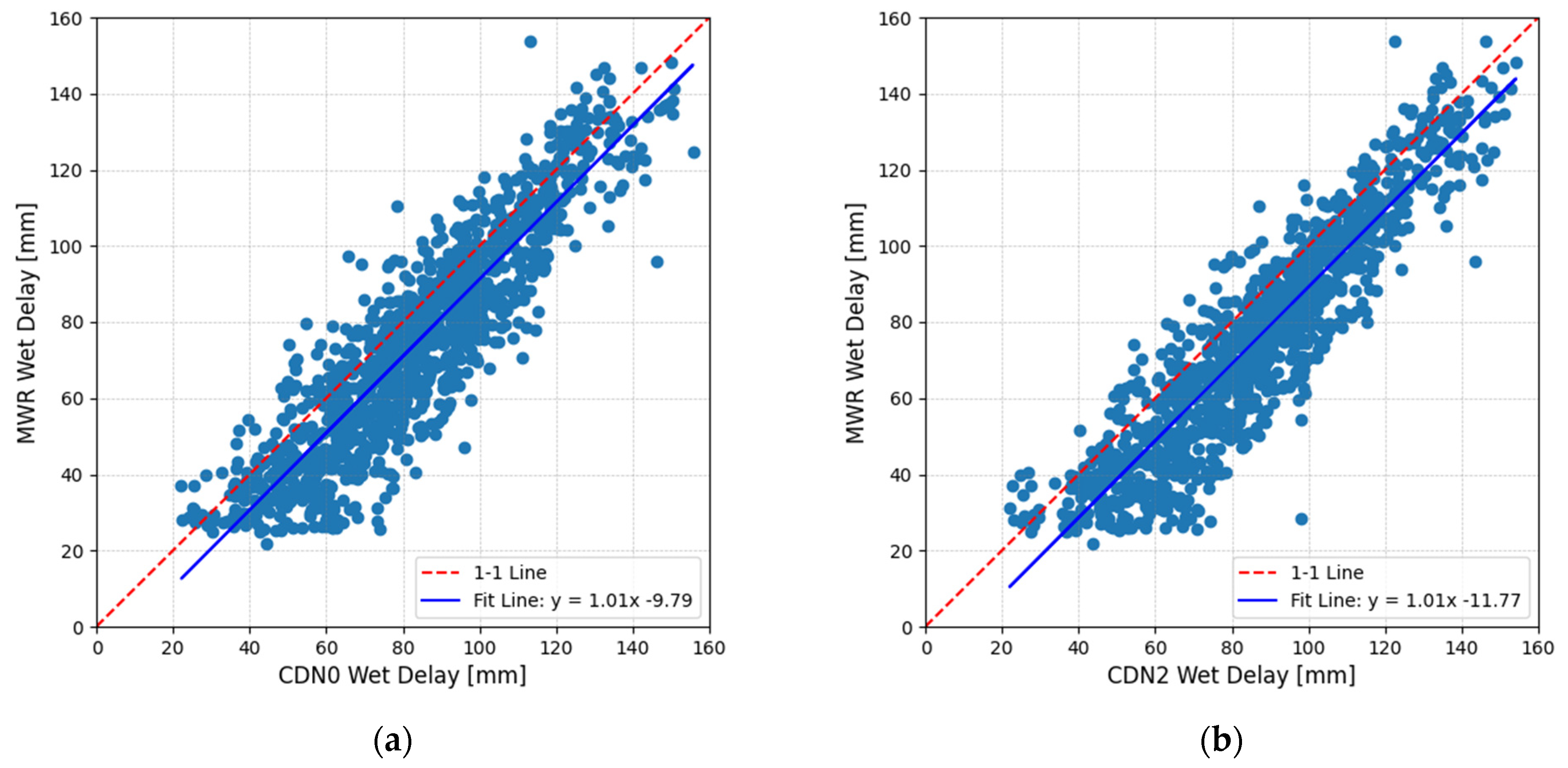
4.3. Ground Radiometer Measurements in Crete
4.4. The ECMWF Operational Analysis
5. Discussion and Concluding Remarks
- GNSS meteorology is currently the reference technique for the integrated water vapor estimation in support of satellite altimetry Cal/Val, due to its proven accuracy, temporal continuity, and robustness under a wide range of weather conditions.
- Diverse GNSS processing techniques (i.e., relative positioning and PPP-AR) should be employed to reduce the uncertainty of GNSS-derived IWV results, particularly in high-precision applications like Cal/Val.
- Complementary use of satellite-based IWV products from Copernicus Sentinel missions (e.g., OLCI, SLSTR, TROPOMI) provides valuable redundancy and spatial coverage, enhancing the reliability of Cal/Val operations, especially when ground-based data are limited.
- Ground-based microwave radiometers provide accurate integrated water vapor values and wet troposphere delay measurements directly along the path to the satellite (due to the narrow field of view) and with high temporal resolution, when compared to GNSS-derived observations. In addition, ground radiometers can operationally provide other atmospheric and propagation parameters, like total cloud liquid content, vertical profiles of temperature and water vapor, and atmospheric attenuation at any frequency between Ka-band and V-band. However, operating ground-based microwave radiometers at remote, high-altitude sites such as CDN1 presents major challenges, primarily due to their high and continuous power requirements. Furthermore, the reliance on precipitation-free circumstances for data retrieval raises the possibility of irregular observations of zenith wet delay. This limitation is especially problematic for satellite altimetry calibration and validation that require ZWD data only during satellite overpasses. Despite these operational challenges, ground radiometers are extremely useful for intercomparison with co-located GNSS observations. Based on our experience, ground MWRs are very effective for short-term intercalibration campaigns at various Cal/Val sites, ideally conducted during the summer months to take advantage of clear sky and the benefit of better power supply conditions.
- Future work will focus on optimizing the use of SLSTR-derived IWV data, with an emphasis on tailoring the processing chain for the ESA Primary Fiducial Reference Cal/Val site.
- Extending MWR intercalibration campaigns to additional ESA PFAC Cal/Val sites (e.g., GVD1 transponder in Gavdos and the ALX1/ALX2 corner reflectors in Crete) would improve spatial coverage and support comprehensive validation of satellite altimeters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AR | Ambiguity Resolution |
| ATSR | Along-Track Scanning Radiometers |
| Cal/Val | Calibration and Validation |
| DOAS | Differential Optical Absorption Spectrometry |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| ESA | European Space Agency |
| FRM | Fiducial Reference Measurements |
| GMSL | Global Mean Sea Level |
| GNSS | Global Navigation Satellite Systems |
| IWV | Integrated Water Vapor |
| MWR | Microwave Radiometer |
| OLCI | Ocean Land Color Instrument |
| PFAC | Permanent Facility for Altimetry Calibration |
| PPP | Precise Point Positioning |
| RP | Relative Positioning |
| SAR | Synthetic Aperture Radar |
| S6-MF | Sentinel-6 Michael Freilich |
| SLSTR | Sea Land Surface Temperature Radiometer |
| TCWV | Total Column Water Vapor |
| TWD | Tropospheric Wet Delay |
| ZWD | Zenith Wet Delay |
References
- International Altimetry Team; Verron, J.; Ryan, B.; Bonnefond, P.; Benveniste, J. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Veng, T.; Andersen, O.B. Consolidating sea level acceleration estimates from satellite altimetry. Adv. Space Res. 2021, 68, 496–503. [Google Scholar] [CrossRef]
- Nerem, R.S.; Frederikse, T.; Hamlington, B.D. Extrapolating empirical models of satellite-observed global mean sea level to estimate future sea level change. Earth’s Future 2022, 10, e2021EF002290. [Google Scholar] [CrossRef]
- Guérou, A.; Meyssignac, B.; Prandi, P.; Ablain, M.; Ribes, A.; Bignalet-Cazalet, F. Current observed global mean sea level rise and acceleration estimated from satellite altimetry and the associated measurement uncertainty. Ocean Sci. 2023, 19, 431–451. [Google Scholar] [CrossRef]
- Legeais, J.-F.; Meyssignac, B.; Faugère, Y.; Guerou, A.; Ablain, M.; Pujol, M.-I.; Dufau, C.; Dibarboure, G. Copernicus Sea Level Space Observations: A Basis for Assessing Mitigation and Developing Adaptation Strategies to Sea Level Rise. Front. Mar. Sci. 2021, 8, 704721. [Google Scholar] [CrossRef]
- Hunt, S.E.; Albinet, C.; Nickeson, J.; Hall, A.; Fox, N.; Boccia, V.; Goryl, P. A Quality Assurance Framework for Satellite Earth Observation Missions. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 608–611. [Google Scholar] [CrossRef]
- Niro, F.; Cosh, M.; Nickeson, J. Trustworthy satellite Earth observations for science and society. Eos 2024, 105. [Google Scholar] [CrossRef]
- Sterckx, S.; Brown, I.; Kääb, A.; Krol, M.; Morrow, R.; Veefkind, P.; Folkert Boersma, K.; De Mazière, M.; Fox, N.; Thorne, P. Towards a European Cal/Val service for earth observation. Int. J. Remote Sens. 2020, 41, 4496–4511. [Google Scholar] [CrossRef]
- Badatala, S.; Sharma, S.; Tripathi, S.; Patel, P.R.; Mathur, A.K. Radiometric calibration stability assessment of Sentinel-1B using point targets at Surat Basin, Australia. Int. J. Microw. Wirel. Technol. 2022, 14, 1262–1269. [Google Scholar] [CrossRef]
- Gibert, F.; Gómez-Olivé, A.; Garcia-Mondéjar, A.; Francis, R.; Hernández, S.; Flores de la Cruz, A.; Vendrell, E.; Roca, M. A trihedral corner reflector for radar altimeter calibration. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5101408. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Kokolakis, C.; Piretzidis, D.; Cullen, R.; Féménias, P.; Fornari, M.; Frantzis, X.; Tripolitsiotis, A.; Bouffard, J.; et al. The ESA Permanent Facility for Altimetry Calibration in Crete: Advanced Services and the Latest Cal/Val Results. Remote Sens. 2024, 16, 223. [Google Scholar] [CrossRef]
- Goryl, P.; Fox, N.; Donlon, C.; Castracane, P. Fiducial Reference Measurements (FRMs): What are They? Remote Sens. 2023, 15, 5017. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Féménias, P.; Cullen, R.; Galanakis, D.; Frantzis, X.; Tripolitsiotis, A. Fiducial Reference Measurements for Satellite Altimetry Calibration: The Constituents. In Fiducial Reference Measurements for Altimetry. International Association of Geodesy Symposia; Mertikas, S., Pail, R., Eds.; Springer: Cham, Switzerland, 2019; Volume 150. [Google Scholar]
- Dettmering, D.; Schwatke, C. Ionospheric Correction for Satellite Altimetry—Impact on Global Mean Sea Level Trends. Earth Space Sci. 2022, 9, e2021EA002098. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Frery, M.-L.; Siméon, M.; Goldstein, C.; Féménias, P.; Borde, F.; Houpert, A.; Olea Garcia, A. Sentinel-3 Microwave Radiometers: Instrument Description, Calibration and Geophysical Products Performances. Remote Sens. 2020, 12, 2590. [Google Scholar] [CrossRef]
- Prado, A.; Vieira, T.; Pires, N.; Fernandes, M.J. Wet tropospheric correction for satellite altimetry using SIRGAS-CON products. J. Geod. Sci. 2022, 12, 211–229. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lazaro, C.; Viera, T. On the role of the troposphere in satellite altimetry. Remote Sens. Environ. 2021, 252, 112149. [Google Scholar] [CrossRef]
- Hay, A.; Watson, C.; Legresy, B.; King, M.; Beardsley, J. Small scale variability in the wet troposphere impacts the interpretation of SWOT satellite observations. Geophys. Res. Lett. 2025, 52, e2024GL112778. [Google Scholar] [CrossRef]
- Mendes, V.B. Modeling the Neutral-Atmosphere Propagation Delay in Radiometric Space Techniques. Ph.D. Thesis, Department of Geodesy and Geomatics Engineering Technical Report No. 199. University of New Brunswick, Fredericton, NB, Canada, 1999; 353p. [Google Scholar]
- Li, L.; Wu, S.; Zhang, K.; Wang, X.; Li, W.; Shen, Z.; Zhu, D.; He, Q.; Wan, M. A new zenith hydrostatic delay model for real-time retrievals of GNSS-PWV. Atmos. Meas. Tech. 2021, 14, 6379–6394. [Google Scholar] [CrossRef]
- Vieira, E.; Lazaro, C.; Fernandes, M.J. Spatio-temporal variability of the wet component of the troposphere—Application to satellite altimetry. Adv. Space Res. 2018, 63, 1737–1753. [Google Scholar] [CrossRef]
- Hadas, T.; Hobiger, T.; Hordyniec, P. Considering different recent advancements in GNSS on real-time zenith troposphere estimates. GPS Solut. 2020, 24, 99. [Google Scholar] [CrossRef]
- Ablain, M.; Meyssignac, B.; Zawadzki, L.; Jugier, R.; Ribes, A.; Spada, G.; Benveniste, J.; Cazenave, A.; Picot, N. Uncertainty in satellite estimates of global mean sea level changes, trends and acceleration. Earth Syst. Sci. Data 2019, 11, 1189–1202. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M. Review on the Role of GNSS Meteorology in Monitoring Water Vapor for Atmospheric Physics. Remote Sens. 2021, 13, 2287. [Google Scholar] [CrossRef]
- Muñoz, L.E.; Campozano, L.V.; Guevara, D.C.; Parra, R.; Tonato, D.; Suntaxi, A.; Maisincho, L.; Páez, C.; Villacís, M.; Córdova, J.; et al. Comparison of Radiosonde Measurements of Meteorological Variables with Drone, Satellite Products, and WRF Simulations in the Tropical Andes: The Case of Quito, Ecuador. Atmosphere 2023, 14, 264. [Google Scholar] [CrossRef]
- Gradinarsky, L.P.; Haas, R.; Elgered, G.; Johansson, J.M. Wet path delay and delay gradients inferred from microwave radiometer, GPS and VLBI observations. Earth Planet 2000, 52, 695–698. [Google Scholar] [CrossRef]
- Aparicio, A.J.P.; Vaquero-Martinez, J.; Gallego, M.C.; Anton, M.; Vaqueto, J.M. Validation of precipitable water vapor estimates from an inexpensive infrared thermometer. J. Atmos. Sol. Terr. Phys. 2023, 249, 106107. [Google Scholar] [CrossRef]
- Kloosterman, J.L.; Brown, S.; Koch, T.; Vo, N.; Nicaise, F.; Schlecht, E.; Bloom, M.; Milligan, L.; Scott Tripp, K.; Kangaslahti, P.; et al. The Advanced Microwave Radiometer—Climate Quality (AMR-C) Instrument for Sentinel-6. In Proceedings of the 28th International Symposium on Space Terahertz Technology, Cologne, Germany, 13–15 March 2017. [Google Scholar]
- Preusker, R.; Carbajal Henken, C.; Fischer, J. Retrieval of Daytime Total Column Water Vapour from OLCI Measurements over Land Surfaces. Remote Sens. 2021, 13, 932. [Google Scholar] [CrossRef]
- Coppo, P.; Mastrandrea, C.; Stagi, M.; Calamai, L.; Nieke, J. Sea and Land Surface Temperature Radiometer detection assembly design and performance. J. Appl. Remote Sens. 2014, 8, 084979. [Google Scholar] [CrossRef]
- Vaquero-Martinez, J.; Anton, M.; Chan, K.L.; Loyola, D. Evaluation of Water Vapor Product from TROPOMI and GOME-2 Satellites Against Ground-Based GNSS Data over Europe. Atmosphere 2022, 13, 1079. [Google Scholar] [CrossRef]
- International GNSS Service. Guidelines for Continuously Operating Reference Stations in the IGS. Available online: https://igs.org/news/new-cors-guidelines/ (accessed on 15 July 2025).
- Vömel, H.; Ingleby, B. Ballon-borne radiosondes. In Field Measurements for Passive Environmental Remote Sensing; Nalli, N.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2023; Chapter 2; pp. 23–35. [Google Scholar] [CrossRef]
- Wilgan, K.; Stauffer, R.; Meindl, M.; Geiger, A. Comparison of tropospheric parameters from Meteodrone measurements with GNSS estimated from ground-based stations. Adv. Space Res. 2020, 66, 2812–2826. [Google Scholar] [CrossRef]
- Imke, D.; Yin, X.; Russell, S.V.; Scott, A.; Jeff, A.; Bryant, K.; Bruce, H. Integrated Global Radiosonde Archive (IGRA), Version 2; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2016. [CrossRef]
- Karavaev, D.M.; Shchukin, G.G.; Efremenko, A.N. Ground-based microwave radiometry for measurements of atmospheric water vapour and cloud liquid water contents. J. Phys. Conf. Ser. 2020, 1632, 012026. [Google Scholar] [CrossRef]
- Borger, C.; Beirle, S.; Wagner, T. A 16-year global climate data record of total column water vapour generated from OMI observations in the visible blue spectral range. Earth Syst. Sci. Data 2023, 15, 3023–3049. [Google Scholar] [CrossRef]
- Smith, D.; Barillot, M.; Bianchi, S.; Brandani, F.; Coppo, P.; Etxaluze, M.; Frerick, J.; Kirschstein, S.; Lee, A.; Maddison, B.; et al. Sentinel-3A/B SLSTR Pre-Launch Calibration of the Thermal InfraRed Channels. Remote Sens. 2020, 12, 2510. [Google Scholar] [CrossRef]
- Herbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyl, A.; Munoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, E.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Jin, S.; Wang, Q.; Dardanelli, G. A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sens. 2022, 14, 3930. [Google Scholar] [CrossRef]
- Zhao, Q.; Yaho, Y.; Yao, W.; Li, Z. Real-time precise point positioning-based zenith tropospheric delay for precipitation forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correction satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Geophys. Monogr. Ser. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, K.; Zhang, T.; He, L.; Shen, Z.; Xiong, S.; Shi, Y.; Chen, L.; Liao, W. A Global Conversion Factor Model for Mapping Zenith Total Delay onto Precipitable Water. Remote Sens. 2022, 14, 1086. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. Climatol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Han, Y.; Westwater, R. Analysis and improvement of tipping calibration for ground-based microwave radiometers. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1260–1276. [Google Scholar] [CrossRef]
- Liljegren, J.C. Automatic self-calibration of ARM microwave radiometers. In Microwave Radiometry and Remote Sensing of the Earth’s Surface and Atmosphere; Pampaloni, P., Paloscia, S., Lorton, V.A., Eds.; VSP Book: Herndon, VA, USA, 2000; pp. 433–443. [Google Scholar]
- Clough, S.A.; Shephard, M.W.; Mlawer, E.J.; Delamere, J.S.; Iacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Fionda, E.; Cadeddu, M.; Mattioli, V.; Pacione, R. Intercomparison of Integrated Water Vapor Measurements at High Latitudes from Co-Located and Near-Located Instruments. Remote Sens. 2019, 11, 2130. [Google Scholar] [CrossRef]
- Negusini, M.; Petkov, B.H.; Tornatore, V.; Barindelli, S.; Martelli, L.; Sarti, P.; Tomasi, C. Water Vapour Assessment Using GNSS and Radiosondes over Polar Regions and Estimation of Climatological Trends from Long-Term Time Series Analysis. Remote Sens. 2021, 13, 4871. [Google Scholar] [CrossRef]
- Leinweber, R. Remote Sensing of Atmospheric Water Vapor over Land Areas Using MERIS Measurements and Application to Numerical Weather Prediction Model Validation. Ph.D. Thesis, Freien Universität Berlin, Berlin, Germany, 22 June 2010. [Google Scholar]
- Casadio, S.; Castelli, E.; Papandrea, E.; Dinelli, B.M.; Pisacane, G.; Burini, A.; Bojkov, B.R. Total column water vapour from along track scanning radiometer series using thermal infrared dual view ocean cloud free measurements: The advanced infrared water vapour estimator (AIRWAVE) algorithm. Remote Sens. Environ. 2016, 172, 1–14. [Google Scholar] [CrossRef]
- Castelli, E.; Papandrea, E.; Di Roma, A.; Dinelli, B.M.; Casadio, S.; Bojkov, B. The advanced infrared water vapour estimator (AIRWAVE) version 2: Algorithm evolution, dataset description and performance improvements. Atmos. Meas. Tech. 2019, 12, 371–388. [Google Scholar] [CrossRef]
- Li, Z.L.; Jia, L.; Su, Z.; Wan, Z.; Zhang, R. A new approach for retrieving precipitable water from ATSR2 split-window channel data over land area. Int. J. Remote Sens. 2003, 24, 5095–5117. [Google Scholar] [CrossRef]
- Chan, K.L.; Slijkhuis, S. S5P/TROPOMI Total Column Water Vapour Algorithm Theoretical Basis Document. DLR 2021, S5P-L2-DLR-ATBD-TCWV. Available online: https://data-portal.s5p-pal.com/product-docs/tcwv/S5P-L2-DLR-ATBD-TCWV_1.2_signed.pdf (accessed on 24 April 2024).
- Herring, T.A.; King, R.W.; McClusky, S.C. GAMIT Reference Manual: GPS Analysis at MIT, Release 10.7; Massachesetts Institue of Technology: Cambridge, MA, USA, 2018; Available online: http://geoweb.mit.edu/gg/docs/GAMIT_Ref.pdf (accessed on 14 February 2024).
- Tserolas, V.; Mertikas, S.P.; Frantzis, X. The western Crete geodetic infrastructure: Long-range power law correlations in GPS time series using Detrended Fluctuation Analysis. Adv. Space Res. 2013, 51, 1448–1467. [Google Scholar] [CrossRef]
- Banville, S.; Hassen, E.; Lamothe, P.; Farinaccio, J.; Donahue, B.; Mireault, Y.; Goudarzi, M.A.; Collins, P.; Ghoddousi-Fard, R.; Kamali, O. Enabling ambiguity resolution in CSRS-PPP. Navigation 2021, 68, 433–451. [Google Scholar] [CrossRef]
- Mertikas, S.; Partsinevelos, P.; Tripolitsiotis, A.; Kokolakis, C.; Petrakis, G.; Frantzis, X. Validation of Sentinel-3 OLCI Integrated Water Vapor Products Using Regional GNSS Measurements in Crete, Greece. Remote Sens. 2020, 12, 2606. [Google Scholar] [CrossRef]
- Donlon, J.C.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 mission: Enhanced continuity of satellite sea level measurements from space. Remote Sens. Environ. 2021, 258, 112395. [Google Scholar] [CrossRef]
- Sentinel-3/Jason-CS-Sentinel-6 Product Handbook, Issue 5 rev.1, 2024, SALP-MU-P-EA-23014-CLS. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_L2P_S3_S6.pdf (accessed on 14 February 2024).
- Campanelli, M.; Mascitelli, A.; Sano, P.; Diemoz, H.; Estelles, V.; Federic, S.; Lannarelli, A.M.; Fratarcangeli, F.; Mazzoni, A.; Realini, E.; et al. Precipitable water vapour content from ESR/SKYNET sun–sky radiometers: Validation against GNSS/GPS and AERONET over three different sites in Europe. Atmos. Meas. Tech. 2018, 11, 81–94. [Google Scholar] [CrossRef]
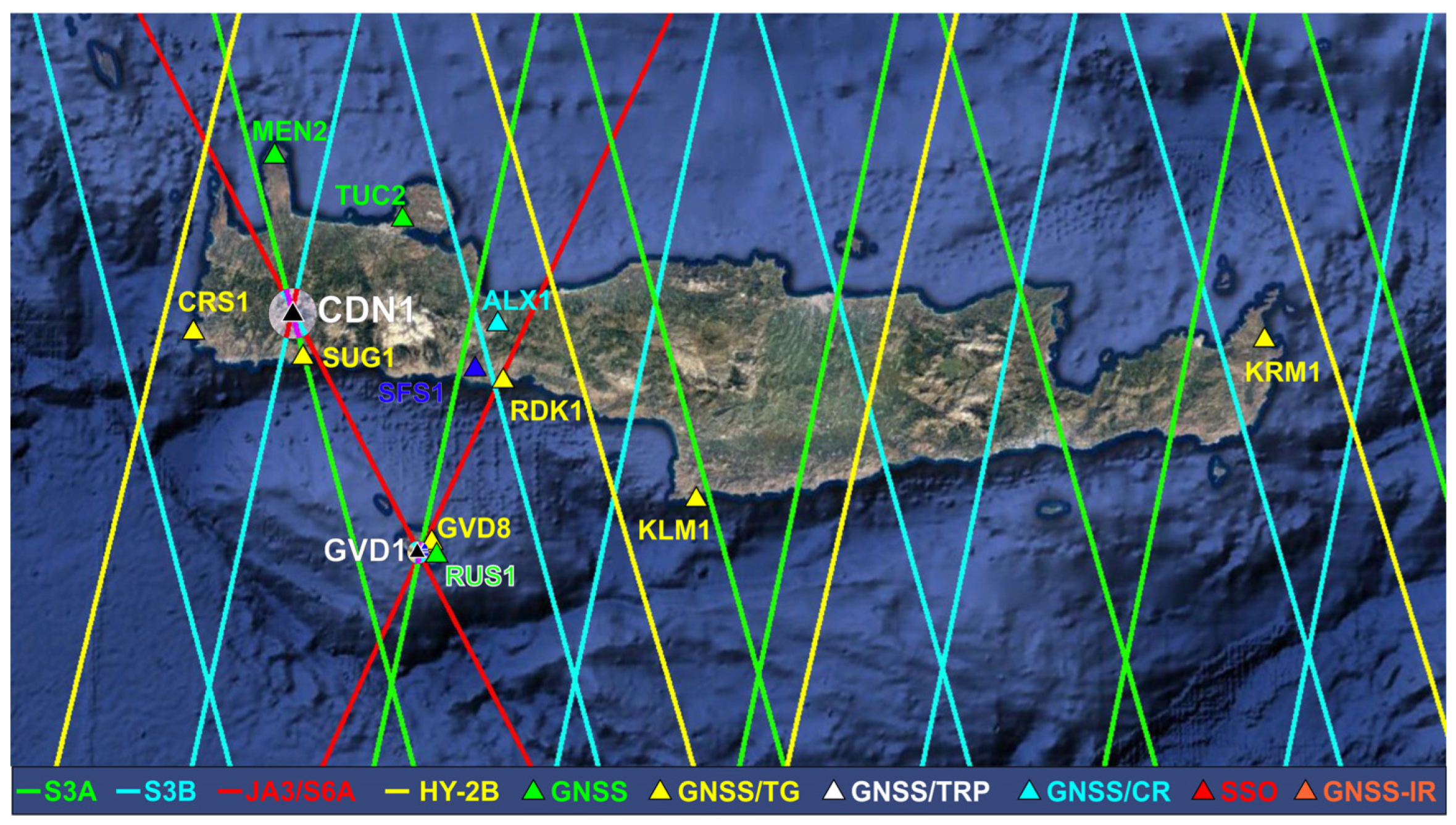



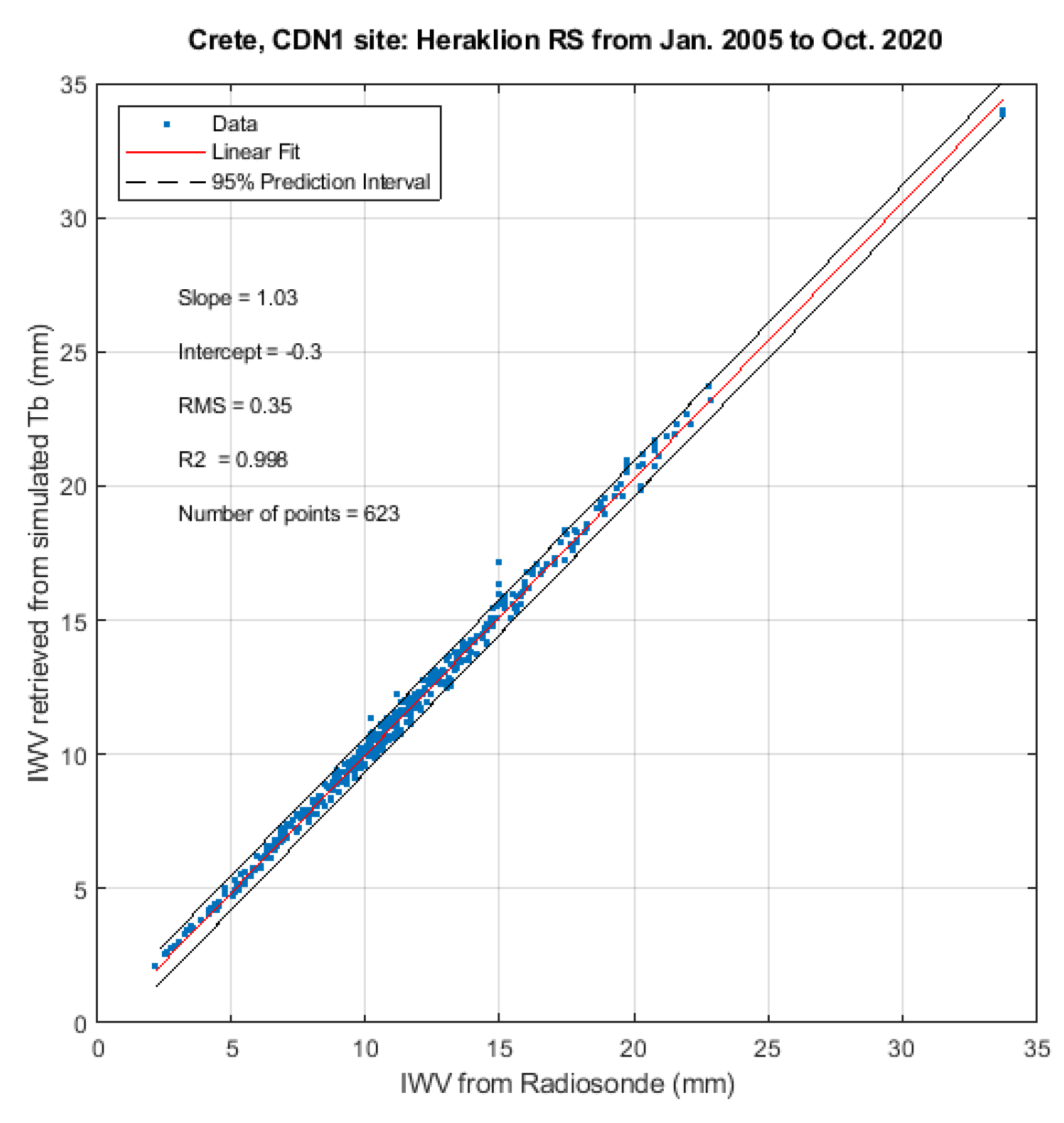
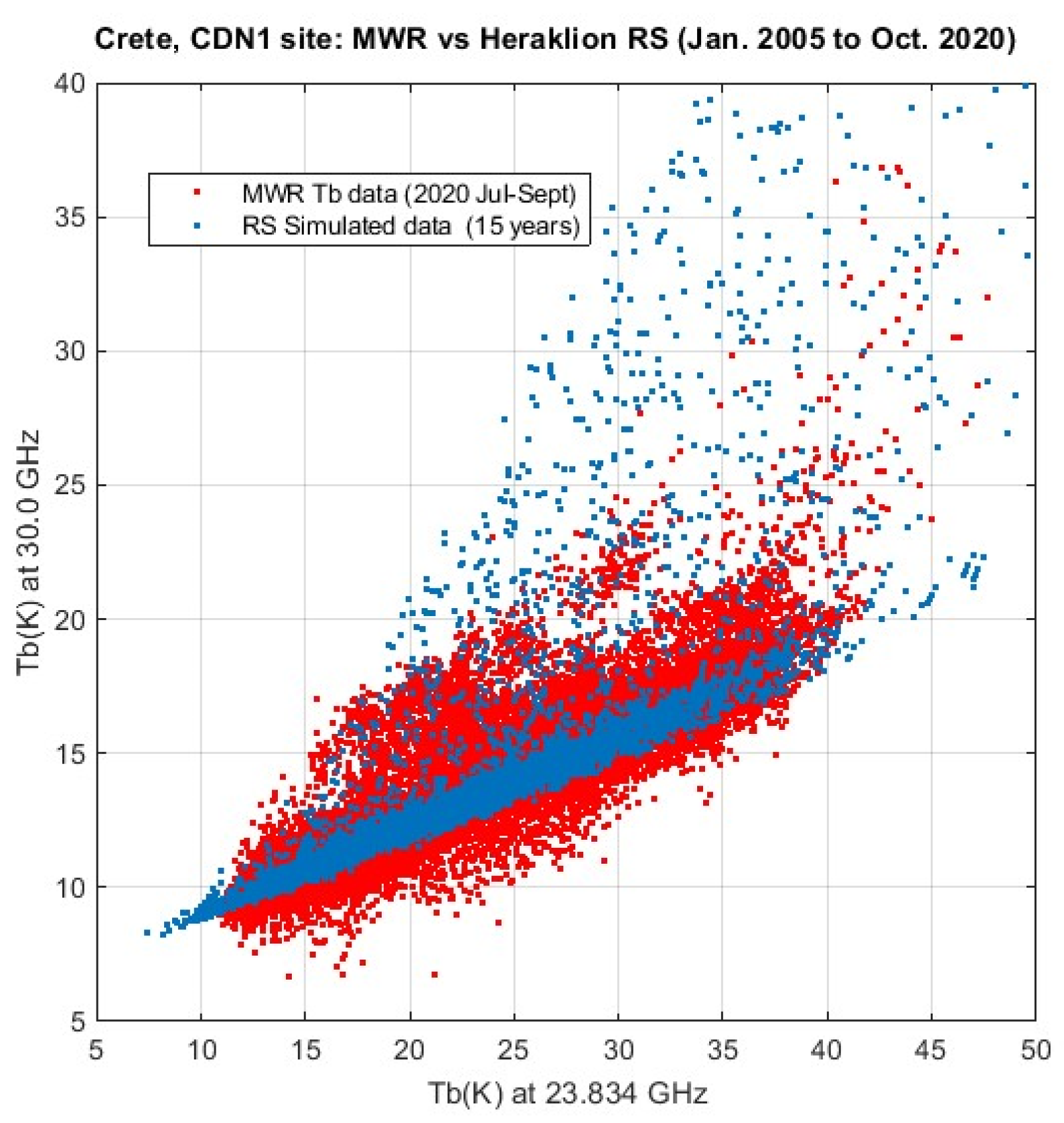
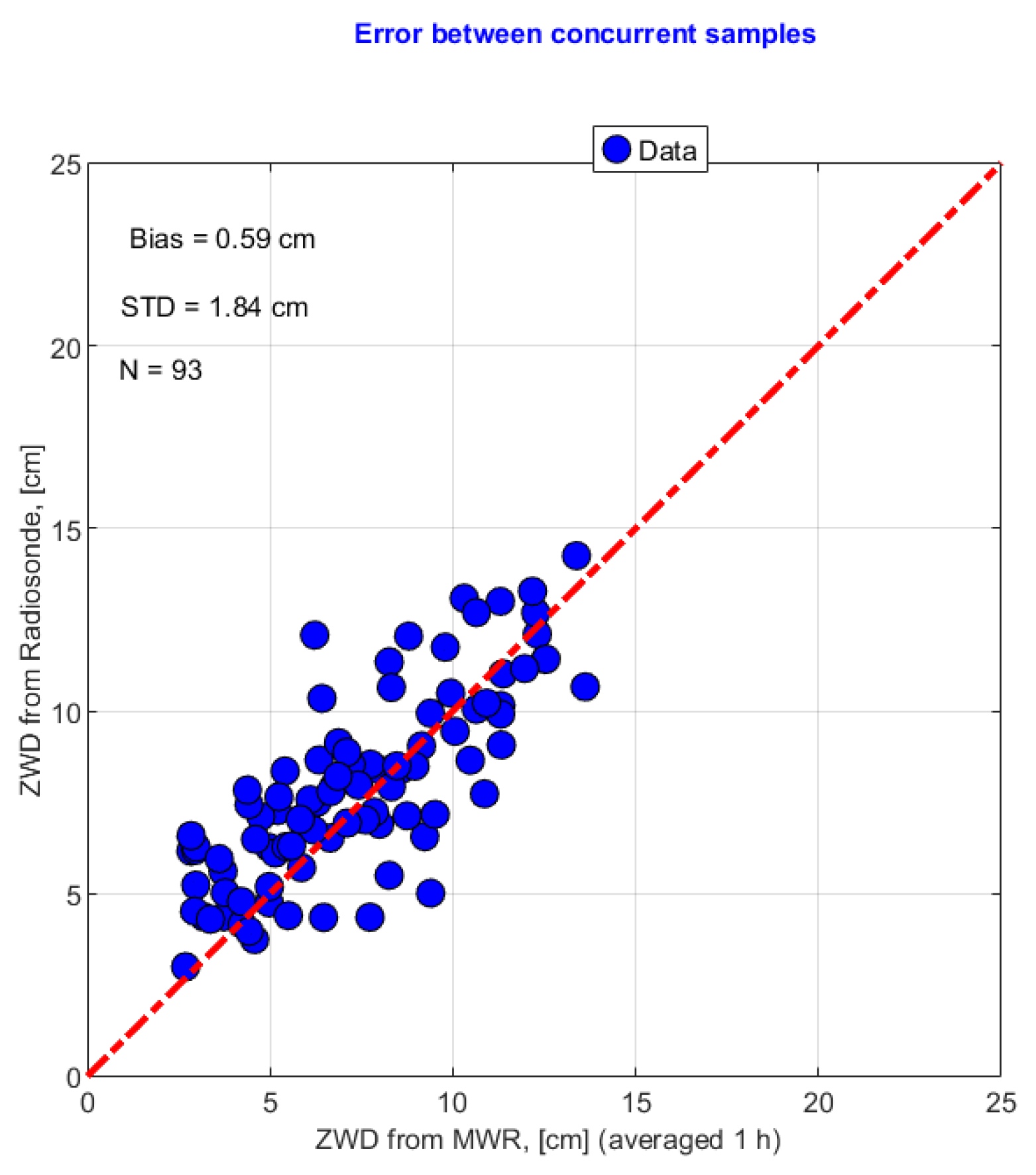
| GNSS Station ID | Latitude | Longitude | Time Span (Years) |
|---|---|---|---|
| Crete: “CDN1” Transponder Cal/Val | |||
| CDN0 | 35°20′16.0236″ N | 23°46′46.855153″ E | 30 August 2014–25 May 2025 |
| CDN2 | 35°20′16.2903″ N | 23°46′46.829304″ E | 27 May 2016–25 May 2025 |
| Gavdos: “GVD1” Transponder Cal/Val | |||
| GVD0 | 34°50′18.5775″ N | 24°06′31.9084″ E | 15 January 2003–25 May 2025 |
| GVD2 | 34°50′18.5775″ N | 24°06′31.3900″ E | 9 October 2021–25 May 2025 |
| Altimetry Mission | S3A D335 | S3B D335 | S3A A14 | S3B D335 | Multi-Mission |
|---|---|---|---|---|---|
| Satellite Instrument | OLCI | OLCI | SLSTR | SLSTR | TROPOMI |
| GNSS Station | GVD0 (Gavdos) | CDN0 (Crete) | CDN0 (Crete) | CDN0 (Crete) | CDN0 (Crete) |
| Sample Size | N = 31 | N = 46 | N = 22 | N = 34 | N = 432 |
| Bias | −0.64 kg/m2 | 0.14 kg/m2 | −1.01 kg/m2 | −2.78 kg/m2 | −0.76 kg/m2 |
| Standard Deviation | ±1.79 kg/m2 | ±1.19 kg/m2 | ±3.02 kg/m2 | ±6.19 kg/m2 | ±4.66 kg/m2 |
| Regression Fit Slope | 1.03 | 1.03 | 0.64 | 0.44 | 0.85 |
| Regression Fit Offset | 0.22 | −0.36 | 4.93 | 9.10 | 2.40 |
| Pearson Coefficient | 0.9495 | 0.9658 | 0.8101 | 0.6374 | 0.631 |
| Date | Satellite Altimeter | Radiometer [kg/m2] | CDN0 GNSS [kg/m2] | IWV Difference [kg/m2] |
|---|---|---|---|---|
| 02-July-2020 | Sentinel-3B | 11.00 | 14.86 | −3.86 |
| 02-July-2020 | Jason-3 | 6.94 | 9.94 | −1.00 |
| 12-July-2020 | Jason-3 | 5.90 | 7.54 | −1.64 |
| 22-July-2020 | Jason-3 | 4.42 | 9.17 | −4.75 |
| 23-July-2020 | Sentinel-3A | 7.80 | 9.54 | −1.74 |
| 29-July-2020 | Sentinel-3B | 10.02 | 11.01 | −0.99 |
| 01-August-2020 | Jason-3 | 10.79 | 12.62 | −1.83 |
| 19-August-2020 | Sentinel-3A | 12.91 | 15.34 | −2.43 |
| 09-September-2020 | Jason-3 | 10.14 | 14.75 | −4.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mertikas, S.P.; Donlon, C.; Tripolitsiotis, A.; Kokolakis, C.; Martellucci, A.; Fionda, E.; Cadeddu, M.; Piretzidis, D.; Frantzis, X.; Kalamarakis, T.; et al. Diverse Techniques in Estimating Integrated Water Vapor for Calibration and Validation of Satellite Altimetry. Remote Sens. 2025, 17, 2779. https://doi.org/10.3390/rs17162779
Mertikas SP, Donlon C, Tripolitsiotis A, Kokolakis C, Martellucci A, Fionda E, Cadeddu M, Piretzidis D, Frantzis X, Kalamarakis T, et al. Diverse Techniques in Estimating Integrated Water Vapor for Calibration and Validation of Satellite Altimetry. Remote Sensing. 2025; 17(16):2779. https://doi.org/10.3390/rs17162779
Chicago/Turabian StyleMertikas, Stelios P., Craig Donlon, Achilles Tripolitsiotis, Costas Kokolakis, Antonio Martellucci, Ermanno Fionda, Maria Cadeddu, Dimitrios Piretzidis, Xenofon Frantzis, Theodoros Kalamarakis, and et al. 2025. "Diverse Techniques in Estimating Integrated Water Vapor for Calibration and Validation of Satellite Altimetry" Remote Sensing 17, no. 16: 2779. https://doi.org/10.3390/rs17162779
APA StyleMertikas, S. P., Donlon, C., Tripolitsiotis, A., Kokolakis, C., Martellucci, A., Fionda, E., Cadeddu, M., Piretzidis, D., Frantzis, X., Kalamarakis, T., & Femenias, P. (2025). Diverse Techniques in Estimating Integrated Water Vapor for Calibration and Validation of Satellite Altimetry. Remote Sensing, 17(16), 2779. https://doi.org/10.3390/rs17162779










