1. Introduction
This paper presents an alternative method of LiDAR data adjustment based on photogrammetric geometric principles. This method can be employed without trajectory processing, making it ideal for archival data or data affected by GPS signal jamming.
It is evident that the adjustment of LiDAR data represents a pivotal phase in the overall processing procedure. Consequently, numerous sophisticated methodologies, founded upon trajectory adjustment, have been employed to facilitate the large-scale generation of geodata. In the contemporary era, the technology that utilizes direct georeferencing as basic input data is especially susceptible to disruption caused by GNSS signal jamming, a phenomenon that is precipitated by political and military considerations. The implementation of a flexible methodology for the assessment, correction and enhancement of LiDAR data is imperative to ensure the reliability of LiDAR data. It is evident that a significant proportion of scanning platforms are equipped with RGB or RGB and IR cameras. The integration of LiDAR and photogrammetric techniques has been demonstrated to be an effective method for enhancing data quality.
The present paper sets forth the findings of research undertaken with a view to the development of a flexible methodology for the enhancement of LiDAR data registration by means of lidargrammetry. Lidargrammetry can be defined as the application of photogrammetric methodologies to LiDAR data, whereby the point clouds are represented by means of lidargrams. Lidargrams are synthetic images in central projection. In this approach, synthetic images of the point cloud are generated, and the relationship between points in the cloud and their coordinates when projected onto specific images (lidargrams) is recorded in unique LiDAR point identifiers (ULPIs). This unique solution facilitates the utilization of conventional image processing algorithms for the processing of point clouds, while preserving the pixel–point relationship and ensuring the integrity of the final LiDAR data.
The hypothesis under investigation is that a solution based on lidargrammetry and ULPIs is a flexible and efficient method for improving the geometric quality of airborne laser scanning (ALS) data in the absence of a trajectory, or when the trajectory is affected by GNSS errors or disruption.
The objective of the research is to validate the efficacy of the method and its implementation. Furthermore, the optional workflow for LiDAR data adjustment is presented, and the potential of the lidargrammetric approach is confirmed.
1.1. ALS LiDAR Data Adjustment
The conventional registration process of ALS data typically involves a two-step orientation procedure [
1]. The process entails trajectory alignment, subsequently followed by point cloud calculation based on the adjusted trajectory. The three-dimensional coordinates of each point are determined by a specific trajectory point defined by six degrees of freedom: three linear and three angular. These are analogous to photogrammetric EOPs and LiDAR observations, including angles and distance. It is customary for the resulting raw data to be consolidated into a single strip, which is then typically subjected to vertical adjustment. In the conventional approach, precise trajectory adjustment is imperative for ensuring the accuracy of LiDAR data. There are many commercial solutions. The most popular are the three listed below.
One of the most common solutions is the TerraSolid/TerraMatch (024.029) software, which is characterized by a workflow that is divided into several steps. These include point computation, strip overlap area analysis, and optionally, surface-to-surface matching or tie-line-based matching [
2]. The initial option pertains to the rectification of angular orientation, scale (for the entirety of the block), elevation or roll and elevation (for individual flight lines), and fluctuating elevation within strips. The second option, tie-line-based matching, utilizes found tie lines for angular, horizontal and vertical corrections of the block, groups of flight lines, individual flight lines, and finally, corrections of points’ positions within strips.
Riegl RiProcess is a commercial software solution for the alignment of Riegl ALS data, offering three fundamental options: rigid transformation with translation (rigid strip, all strips may be translated), and two non-rigid transformations, both with and without translation, where strips can be deformed. It is important to note that all options recalculate the trajectory. However, it should be noted that the results depend on the chosen option, and the LiDAR strips are recalculated either rigidly or flexibly [
3].
Leica’s sensor data can be adjusted by utilizing two options provided in HyMap software. The first option is patch-based matching, which “utilizes well-defined patches and decomposes the observed vertical errors into roll, pitch, and dZ errors based on the angular location of the patch”. The second option is phase correlation, which “calculates the 3D shifts between two objects using phase correlation” [
4].
These conventional workflows are employed in the field of mapping, and the precision of the resulting product is contingent on two primary factors: trajectory accuracy and calibration errors [
5]. It is evident that ground control data are not considered essential in these commercial software solutions. The aforementioned commercial software is efficient and designed for large-scale data processing.
In addition to the aforementioned solutions, there is the option of selecting more specialized tools for further quality analysis. One such example is OPALS, which was developed by a research group at TU Wien [
6].
In the conventional photogrammetric approach, direct georeferencing was not imperative for precise aerial triangulation; only approximate exterior orientation parameters (EOPs) were required. The utilisation of ground control points and check points proved to be of paramount importance in enhancing the three-dimensional accuracy of the final result and in the assessment of the result. However, this relationship is inverted in the context of aerial LiDAR point clouds.
A further salient distinction pertains to the processing of LiDAR strips, which are the primary data to be processed (rigidly or non-rigidly), and for which vertical accuracy is frequently regulated with greater rigour than their horizontal accuracy, utilizing ground truth data. Conversely, basic photogrammetric data comprise individual images with their EOPs, which are the primary objects for adjustment. The photogrammetric block is characterised by enhanced flexibility, enabling deformation across smaller areas. While this flexibility can be advantageous, it can also result in the introduction of undetected minor gross errors that are challenging to identify.
This characteristic is exploited as an advantage by generating virtual images of LiDAR data and applying corrections to the block of images with greater flexibility than is typically possible in the LiDAR data adjustment process.
1.2. LiDAR Accuracy Evaluation
The accuracy of LiDAR is a primary area of research in this technology. The initial and most critical consideration is that of vertical accuracy. The evaluation of LiDAR data can be conducted using survey marks [
7], and can be assessed as the accuracy of individual measured points or the TIN generated from the LiDAR point cloud [
8].
1.2.1. 3D Accuracy Evaluation
Horizontal accuracy poses a more substantial challenge in this technology. The majority of assessment solutions employ building roofs, such as automatically extracted ridge lines of overlapping strips [
9], “the distances between points in one strip and their corresponding planes in the overlapping strip” [
10], or check points selected as points of intersection of the modelled ridge lines [
11].
The complex evaluation of spatial accuracy is presented in several papers. The comparison of strips provides statistics on XYZ accuracy [
12]. In their paper, Habib et al. set out four QC (quality control) procedures for the detection and quantification of both systematic and random errors in overlapping parallel LiDAR strips [
13]. The increased availability of LiDAR equipment dedicated to UAVs has resulted in a global increase in the number of reported investigations [
14,
15].
There are a number of examples that assess the accuracy of UAV LiDAR data georeferenced directly without using control points, planes, or patches [
16,
17]. Conversely, an accuracy assessment of LiDAR strip adjustment in the absence of direct georeferencing was conducted prior to the widespread utilisation of UAVs [
18].
1.2.2. Alternative Methods for the Assessment
It is important to note that alternative methods for the assessment of LiDAR data do exist. For instance, Pirotti et al. compare LiDAR data with the point cloud generated by dense matching [
19]. Research of a similar nature has been documented in the paper of Bakuła et al. [
20]. The accuracy of LiDAR data in vegetated terrain is addressed in the work [
21,
22]. A plethora of other examples of LiDAR data assessment have been documented, including the assessment of DTM accuracy for UAV LiDAR data captured from varying flight heights over a range of terrain characteristics [
23], the utilisation of novel sensors for topo-bathymetric UAV acquisition [
24], and the evaluation of UAV LiDAR data for the purpose of deformation monitoring of engineering facilities [
25].
The errors present in LiDAR data are intricate, with some proving challenging to detect and others impossible to eliminate. A plethora of methodologies exist for the purpose of error detection; however, the most prevalent approach involves a comparison between overlapping LiDAR strips and LiDAR strips with the ground truth. The elimination of errors can be achieved through the correction of the source data, as follows: The observations may be obtained from GNSS, IMU or scanner sources, or alternatively through the correction of the result point cloud. It is imperative that the trajectory is known in both cases in all commercial tools. A challenging solution to this problem would be to resolve it without trajectory.
1.3. Data Enhancement Methods
The vertical accuracy of ALS data has been established for various sensors and registration methods, with a range of 2–10 cm being reported. The validity of the results is contingent upon the flight altitude above the terrain, in addition to other factors, including the type of scanner, GNSS receiver, and IMU. However, it is important to note that such accuracy is now achievable. Furthermore, a plethora of methodologies have been formulated and evaluated with a view to enhancing data precision, predominantly within the domain of registration.
There are two primary groups of solutions for improving the absolute accuracy of ALS point clouds.
The initial group pertains to the enhancement of LiDAR data, either with or without the adjustment of auxiliary data such as GNSS/INS, but without the incorporation of additional data such as imagery. The second group involves integrating LiDAR data with photogrammetric data.
1.3.1. LiDAR Data Enhancement Without Auxiliary Imagery Data
There are four main methods for the enhancement of LiDAR data:
more precise calibration of the sensor and platform [
13,
26,
27];
correction of the trajectory [
28,
29];
and the utilization of ground information [
36,
37].
It is evident that auxiliary data, such as GNSS/INS data, are not a prerequisite for the analysis of strip correspondence and ground information. A geometrical analysis of the relative position of the strips or their relation to the ground truth is sufficient.
1.3.2. LiDAR Data Enhancement with Auxiliary Imagery Data
The second major group of methods for LiDAR data enhancement involves integrating ALS data with photogrammetric imagery in one of the following ways:
calibration of the LiDAR–camera system [
38];
depth maps for the purpose of co-registration between both datasets [
39,
40,
41];
dense matching of the image sequence captured by LiDAR data for cloud-to-cloud alignment [
42,
43,
44,
45];
ALS and image integration using and adjusting the platform’s trajectory: trajectory adjustment and enhancement of both datasets [
46,
47,
48] and image block triangulation, which is utilized for the adjusted camera trajectory. This trajectory is then applied (taking into account the boresights and excentres of both the camera and scanner). The application of this trajectory results in the recalculation of refined and enhanced LiDAR strips [
49].
1.4. Lidargrammetry—State of the Art
1.4.1. Lidargrammetry—General Approach
Lidargrammetry is an integration method involving the generation and utilisation of synthetic images, frequently described as “virtually taking photographs of the point cloud”. These images are then employed in a photogrammetric manner. Lidargrammetry is a variant of data integration for stereo observation of the point cloud [
50,
51].
The generation of synthetic images is facilitated by the initial definition of virtual camera data, encompassing parameters such as pixel size, image width, height, and focal length. The images under consideration are free from distortions such as radial distortion, tangential distortion, and affine deformation. The generation of these models is predicated on the collinearity equation, a fundamental photogrammetric relationship. Arbitrary exterior orientation parameters (EOPs) are also required for the process.
In addition to stereoscopy, the applications of lidargrammetry encompass its utilisation for the measurement of infrared point data in three dimensions [
52], spatial data extraction [
53], and data orientation [
54,
55]. The present body of research utilises synthetic images in order to achieve the objectives of deep learning, specifically with regard to detection and segmentation [
56].
1.4.2. Our Approach
In this research, the concept of lidargrammetry is applied as a method for data integration in LiDAR data enhancement. In the preceding research, the application of stereoscopic model deformation theory for the vertical enhancement of LiDAR data using ground control points and the comparison of strip heights was introduced.
In this research, the concept of lidargrammetry is applied as a method for data integration in LiDAR data enhancement. In the preceding research, the application of stereoscopic model deformation theory for the vertical enhancement of LiDAR data using ground control points and the comparison of strip heights was introduced [
57].
The present paper sets forth further research results, incorporating horizontal accuracy corrections and practical considerations for the implementation of the concept of pixel–point relationships by means of ULPIs.
The paper is divided into five chapters. The initial chapter constitutes an introduction, delineating the state of the art of LiDAR adjustment procedures and the extant research context. Chapter II delineates the investigative process, encompassing the methodology, research instrumentation, and test data. The third chapter of the study presents the results and the fourth chapter include the results discussion. The concluding chapters, V and VI, present the conclusions drawn from the research and the future research plans that have been formulated.
2. Methods and Materials
2.1. Lidargrammetry—The Novel Approach
The approach to data integration and LiDAR processing is based on lidargrammetry. It was theorised that, in view of prior experience with photogrammetric and LiDAR data integration, it would be most appropriate to create a unified photogrammetric and LiDAR data format. The initial proposal was referred to as the ‘pixel–point idea’, as it represented the most fundamental element of the data. The notion was not aligned with reality; nevertheless, it constituted a foundation for conceptualisations and the pursuit of sophisticated data integration methodologies. Finally, the integration of vector (LiDAR) and raster (photogrammetry) data appeared to be a potential avenue for the advancement of lidargrammetry and its stereoscopic provenance.
In the proposed solution, lidargrams are generated in both raster and virtual image formats. Raster images comprise a representation of projected LiDAR points, accompanied by their respective RGB or intensity values. Optionally, rasters can be saved to disk. The novelty of the proposed methodology lies in the fact that the process of projecting LiDAR points onto images is lossless and reversible, and the image coordinates of these points are stored without rounding them to pixels. The list coordinates of each virtual image are stored without the application of rounding or interpolation. The utilisation of rounding and interpolation is confined to the context of optional raster generation, a process that can subsequently be employed for matching.
The points of the virtual lidargram are numbered during lidargram generation using identifiers (ULPIs) added a priori to the LiDAR points. This ensures that each point of the lidargram has a ULPI, thereby enabling the inverse procedure: calculating the points of the cloud from lidargrams using photogrammetric intersection. It is evident that each LiDAR point has the capacity to be projected onto N lidargrams. Furthermore, it is important to note that all projections share the same ULPI. The value of N is contingent upon the geometry of the block of lidargrams, incorporating factors such as image and strip overlap, image footprint size, and other relevant parameters. Despite the fact that a substantial number of points are often projected onto a single pixel of the image, they can subsequently be utilised as discrete points due to their distinctive ULPIs. This approach is advantageous for a number of reasons. This paper sets out a series of experiments that have been conducted with a view to opening up further possibilities for closer data integration and photogrammetric and LiDAR data enhancement.
While the solution may appear to be superfluous at first due to the augmented data size caused by the inclusion of additional identifiers (ULPIs), the present research will substantiate the numerous advantages of this approach.
2.2. Method Description
2.2.1. Concept of the Method
The method is grounded in the principle of aerial triangulation of lidargrams, a technique that facilitates the registration of LiDAR data or the enhancement of the accuracy of existing LiDAR data registration. The collinearity equation delineates the relationship between spatial points and image coordinates, with each point projected onto lidargrams assigned to ULPI. Furthermore, ULPIs are utilised subsequent to image adjustment in order to generate an adjusted target point cloud through the intersection. Georeferencing can be defined using 3D control points, optionally with control planes and/or discrepancies in 3D between overlapping LiDAR strips.
The method’s distinguishing feature is its avoidance of trajectory processing, a factor that facilitates its application to both archival LiDAR data in blocks or strips and newly acquired data. The functionality of the system is versatile, encompassing such purposes as global data transformation, registration enhancement, and local point cloud correction.
The method has been designed to comprise a one-step enhancement process. The integration of the following three concepts is pivotal in achieving the objective of this study.
The first concept: saved identification between the LiDAR point and its projection (ULPIs). An assignment of ULPIs to each LiDAR point constitutes a straightforward method for reversing the process, which can be achieved in two ways: firstly, as monoplotting, and secondly, as multi-intersection. The implementation of such a solution would facilitate the exploration of numerous avenues for further research and practical applications.
The second concept: Substitution of LiDAR processing methods with photogrammetric processing. It involves the utilization of photogrammetric algorithms on rasterised LiDAR data. The reverse process is predicated on an understanding of the flexibility of the traditional photogrammetric block and strips, and the implementation of this characteristic to the block or strips of lidargrams, which allows for the application of ULPIs to LiDAR data. The lossless presentation of LiDAR data facilitates the application of a variety of photogrammetric techniques. The innovative approach to the registration, transformation and correction of LiDAR geometry represents a significant aspect of research opportunities.
The third concept: Elimination of the need for trajectory data in the process. It entails the removal of trajectory processing from the methodology, thereby enhancing the flexibility of the method. The application of this technology is not limited to specific data sets; it is compatible with any data set, including those that have previously undergone block or archival data processing. Subsequent to the adjustment, the trajectory may be calculated.
Table 1 presents a concise comparison of the characteristics of TerraSolid/TerraMatch and PyLiGram.
2.2.2. Phase 1 of the Process
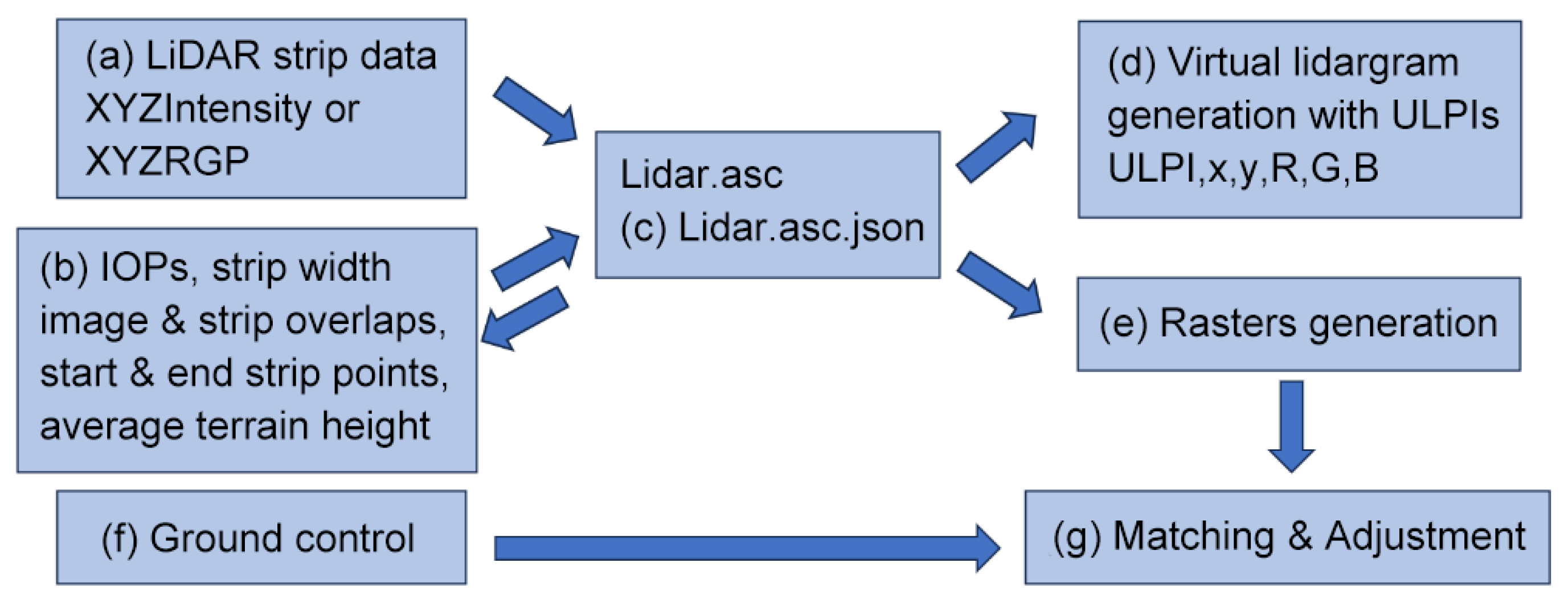
The proposed method generally can be divided into two phases as presented in
Figure 1 and
Figure 2.
As illustrated in
Figure 1, the initial phase of the process involves the preparation of the data and the subsequent matching with adjustment. The input LiDAR strips (a) are imported into the application. Furthermore, the interior orientation parameters (IOPs) of the virtual camera are arbitrary in nature and are defined based on the anticipated base-to-height ratio, with a view to enhancing the accuracy of the stereo pair geometry. The exterior orientation parameters (EOPs) are calculated using predefined interior orientation parameters (IOPs), strip width, image overlap, strip overlap, start and end point of virtual flightline, and the average terrain height. It is possible to import alternative definitions of IOPs and EOPs from real mission data. In addition, real camera IOPs and real images EOPs can also be imported. All parameters are stored and updated in JSON files for each strip (c). The initiation of the process is contingent upon the prior entry and saving of all data in JSON format.
Once collinearity equations (Equation (1)) have been employed for the calculation of image coordinates (x, y) from LiDAR points on the plane of the lidargram of IOPs (ck, x0, y0) and EOPs (X0, Y0, Z0), as well as the rotation matrix r11..r33, the virtual camera is simplified. Distortion is not applied, and the x0 and y0 coordinates are set to zero.
It is evident that all points of the virtual lidargrams are assigned ULPIs, which serve to store the unique spatial relationship between the original point of the cloud and its projection onto specific lidargram planes (image coordinates). Virtual lidargrams are defined as lists of image coordinates of all projected points with their ULPIs and RGB or intensity values.
Moreover, in the method based on image matching, rasters with their EOPs and IOPs are necessary and are generated (e). It is acknowledged that there exists a plethora of methodologies for the purpose of raster resampling. This is a topic that requires further investigation, but our preliminary findings suggest that images captured using a photographic technique may not be the most suitable for deep learning matching with models trained on typical photogrammetric data.
In the process of projecting LiDAR points onto a virtual image plane, two possible cases can be distinguished.
The primary issue pertains to the over-projection of numerous LiDAR points onto the confines of a singular pixel. In this scenario, the colour of the pixel is derived as the mean of the colors of all these points. However, it should be noted that all the points are stored separately in a virtual lidargram with their ULPIs.
The second case is that no points are projected onto the specific pixel. In this instance, the pixel is characterized by either a background colour, in which case it is set to black, or it is assigned a colour based on the supplementary parameters, in accordance with the colour of the neighbouring pixels. These supplementary parameters are employed to enhance the lidargram image, including the specification of a pixel range and the application of pixel sigma. The former assigns a colour to multiple pixels, thereby reducing the prevalence of empty pixels, while the latter utilises a Gaussian blurring technique to impart a softer quality to the image. In the event of a specific pixel being coloured by more than one neighbour pixel, the RGB values are averaged.
The coordinates of ground control points (GCPs) are imperative for the subsequent processing of external data (f). The integration of LiDAR and photogrammetric data is achieved through an approach that facilitates the conversion of point clouds to images and vice versa, ensuring the retention of all original information. Following generation, the rasters can be utilised in external matching and aerial triangulation software (g). The rasters, in conjunction with their IOPs and EOPs, are imported into external files and subsequently matched. The sole practical constraint on the method pertains to the potential for lidargrams to be matched. The adjustment is processed on the basis of matched tie points and measured GCPs. The adjustment settings are as follows: firstly, a low measurement accuracy level for tie points (approximately 2 pixels) and, secondly, a high accuracy of coordinates (0.10 m) and their measurement on a lidargram (0.5 pixel). This results in parallax discrepancies between lidargrams within a block. It is anticipated that such a situation will arise if the data are to be adjusted to GCP positions as much as possible.
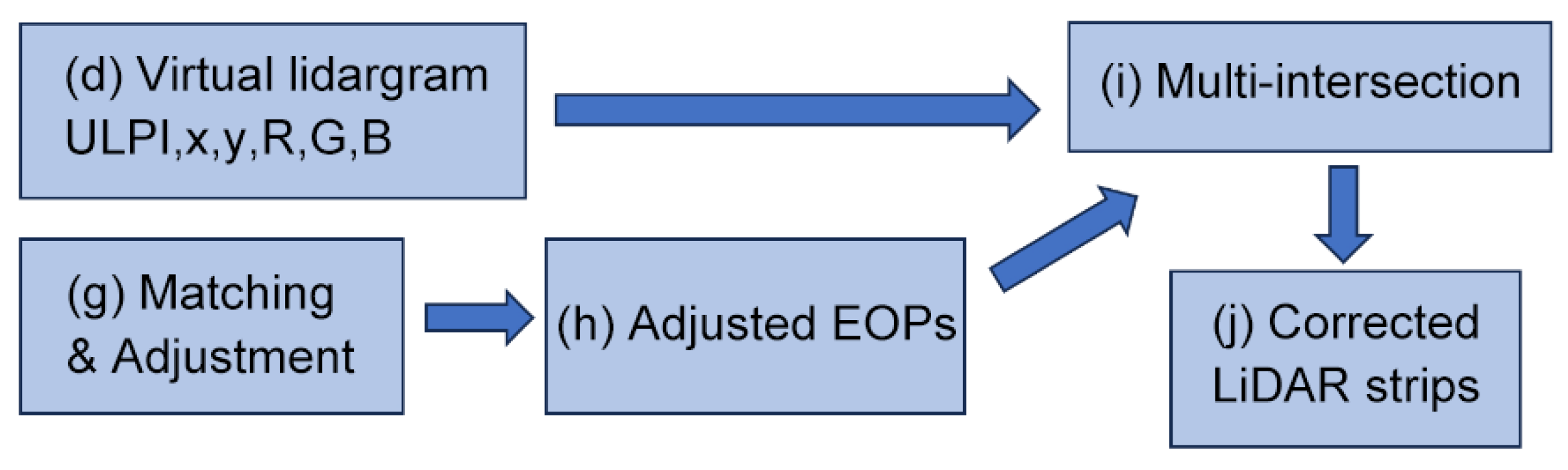
2.2.3. Phase 2 of the Process
Figure 2 illustrates the second phase of the process. The corrected EOPs (h) are exported from the external tool and subsequently imported into PyLiGram (
Appendix A).
The multi-intersection (i) of the transformed point cloud is calculated using adjusted EOPs (h) and virtual lidargrams with their ULPIs. The multi-intersection issue is resolved through the implementation of a least-squares adjustment. It was determined that the transformed point cloud was not accurate. This was due to the calculation of multiple intersections of points on the block deformed by high-accuracy GCPs, and the application of discrepancies in relative orientation. The transformation of the strips was characterised by pronounced variations in height, which were evident along the edges of the images that were considered in the multi-intersection analysis. The weighting of the position calculation was applied in order to mitigate the discontinuities of the point cloud (see Equation (2)).
The weighting function, designated as pi, is equal to one minus the quotient of the absolute value of the coordinate xi to half the aspect ratio in the direction of flight xmax. The employment of this weighting function guarantees that points located in close proximity to the centre of the virtual lidargram are assigned maximum importance, while points situated near the edge are assigned the lowest importance. Consequently, the multi-intersected points form a strip that is flexibly adjusted to the GCPs. (j).
It is important to note that there is an additional application of this method. The transformation of the point cloud can be processed by the intersection of the lidargrams using new EOPs. These EOPs are not only provided by the adjustment process, but are also derived from 3D transformation parameters of initial EOPs from one coordinate system to another.
2.2.4. PyLiGram Research Tool
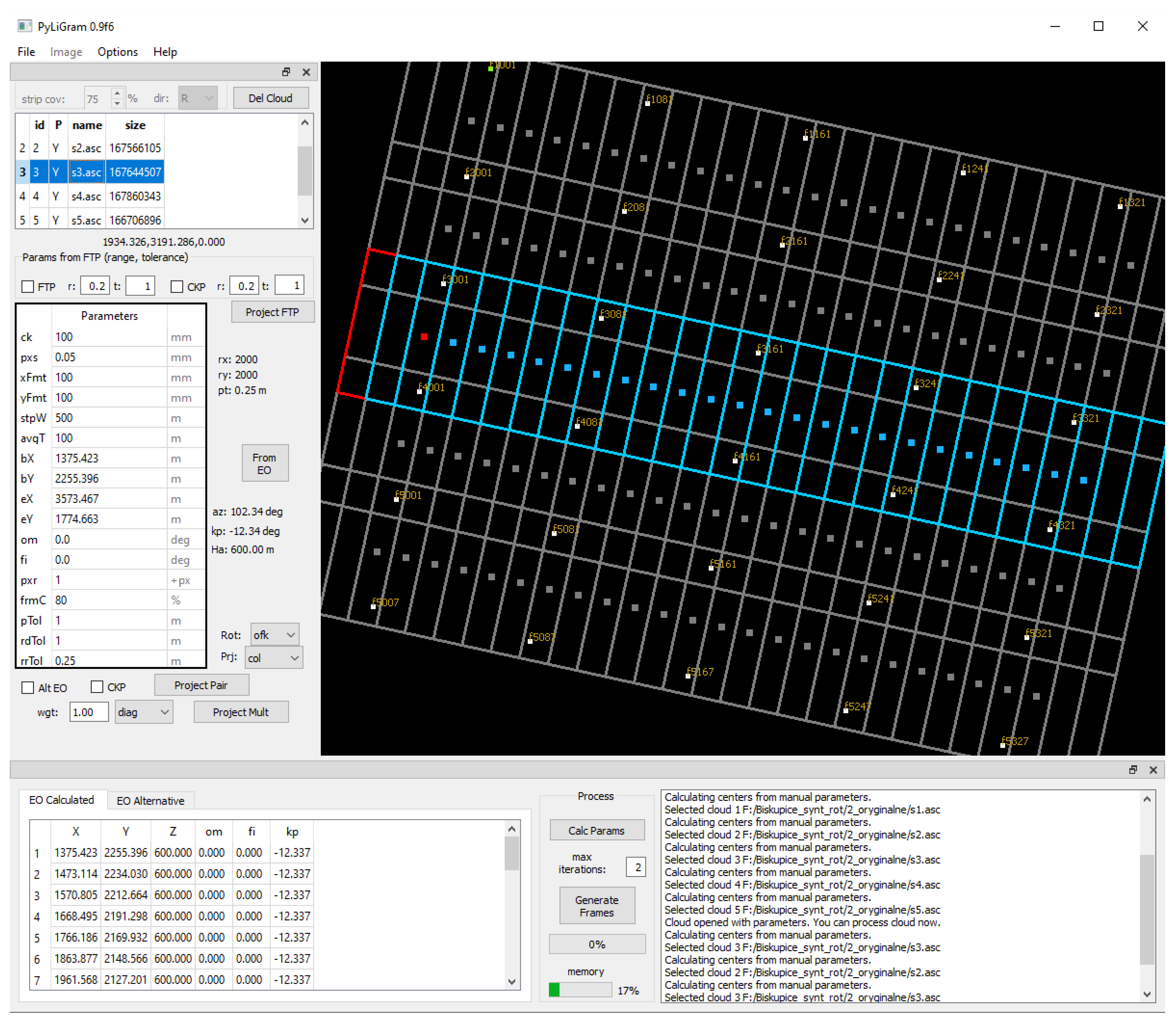
The method was implemented in a research tool named PyLiGram—Python LidarGrammetry (v. 0.9f6) (see
Figure A1). The initial functionality is delineated in the paper on stereo model vertical deformation theory employed for continuous height correction of a LiDAR strip [
57]. The second functionality is the implementation of the method presented in this paper. A further element of lidargram generation is the potential for the generation of synthetic and semisynthetic benchmark data [
58].
The PyLiGram methodology operates on LiDAR strips in discrete files, with the option of utilising GCPs. The lidargrams are of a virtual nature, manifesting as a list of image coordinates with ULPIs of the terrain points. They can be optionally saved as rasters (e.g., for further matching). The primary process encompasses the generation of lidargrams and EOP files, with the option of an additional XML file comprising GCP image coordinates subsequent to their projection onto lidargrams.
2.3. Test Data
The efficacy of the method was evaluated through the utilisation of numerous datasets. The datasets were prepared and selected based on two main requirements: firstly, the lidargrams should be matchable, and secondly, the results should be verifiable without the need for manual measurements of either GCPs or check points (CHPs) due to the limited accuracy of the manual point cloud measurements.
There are no specific requirements for the accuracy of the input data. The method has been developed for the purpose of enhancing typical errors in LiDAR external orientation.
2.3.1. Synthetic Data
The initial trials were conducted using synthetic data. The Python script was employed to generate a rectangular, flat point cloud, which was subsequently colourized by an orthophoto for later matching. The designated area was a rural region in the vicinity of the city of Kraków. The point cloud demonstrated a density of 0.25 m, which corresponded to the ground sample distance of the orthophoto. This facilitated the process of assigning colour to points. The process was conducted without the application of interpolation. The RGB colour of the orthophoto was utilised to simulate the real reflectance of the points, thereby facilitating the matching of lidargrams.
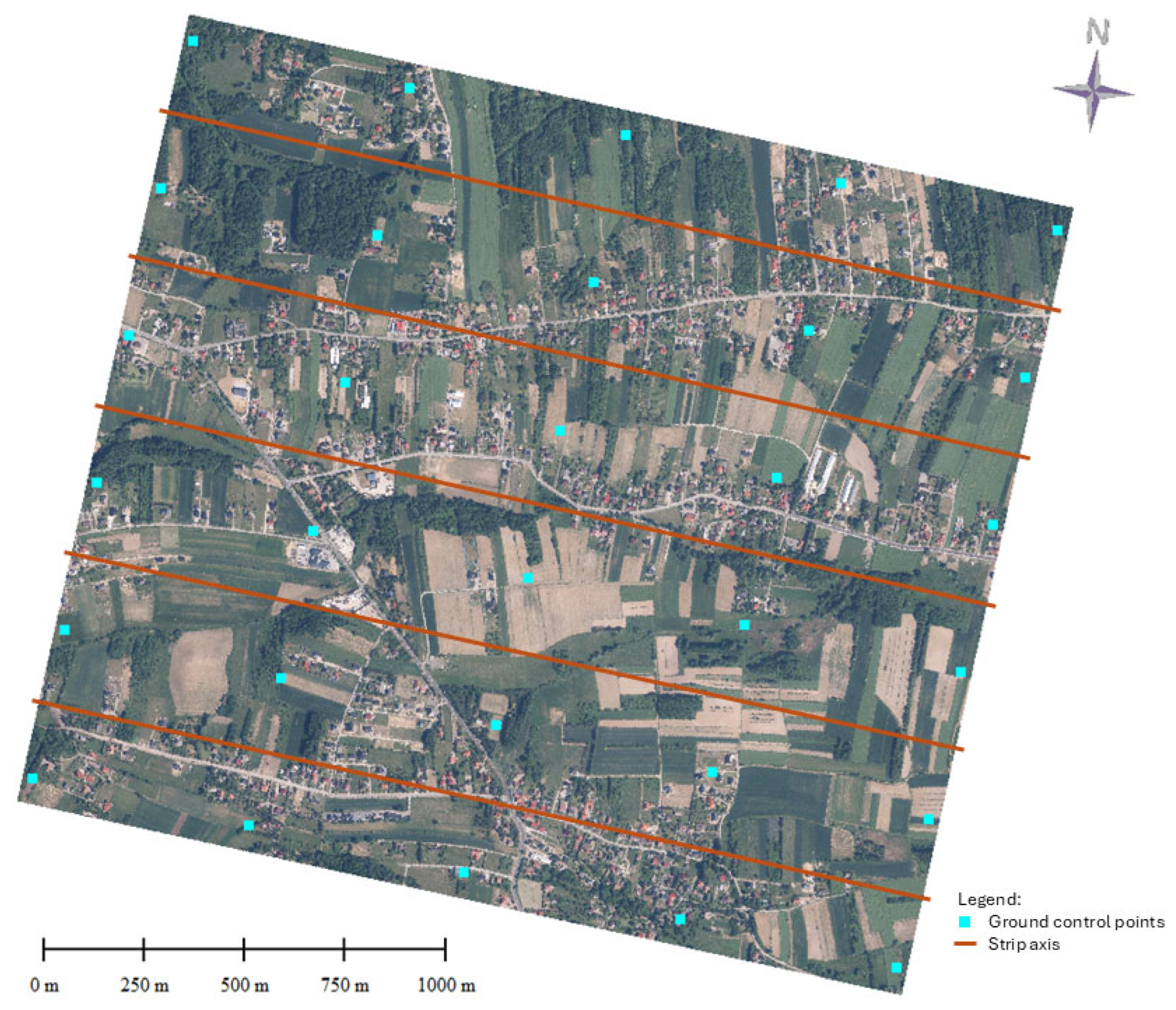
A local coordinate system was implemented, with the height of all points set to 100 m. The standard RGB point grid was saved as five overlapping strips in the latitudinal direction of the virtual flight, with each strip measuring 2300 m in length and 500 m in width (see
Figure 3).
The virtual camera utilized in this study possessed a focal length of 100 mm and a pixel size of 0.05 mm. The frame size was adjusted to 2000 × 2000 pixels in order to emulate a square format, whilst ensuring that the maximum ratio of a single LiDAR point per camera pixel was maintained. Each strip contained 10 GCPs and 233 CHPs distributed regularly in the grid, with a spacing of 68.75 m along the strip axis and 62.50 m across it. Furthermore, GCPs were subjected to randomized deviations of up to ±0.50 m in XYZ coordinates to simulate relatively large deformations of the strips. A kappa rotation was applied to all datasets (i.e., the point cloud, original and deformed GCPs, and original CHPs) in order to simulate the general case of the external orientation azimuth of the flight lines.
2.3.2. Semi-Synthetic Data
As delineated by Pargieła, Rzonca and Twardowski, the term “semi-synthetic data” pertains to data originating from real LiDAR, which is subsequently processed and tailored to meet specific testing requirements [
58]. The adaptation entailed the division of the LiDAR blocks into overlapping strips, the selection of points to be designated as GCPs with randomized 3D coordinates, and the storage of the data in ASCII files containing XYZ and RGB values only.
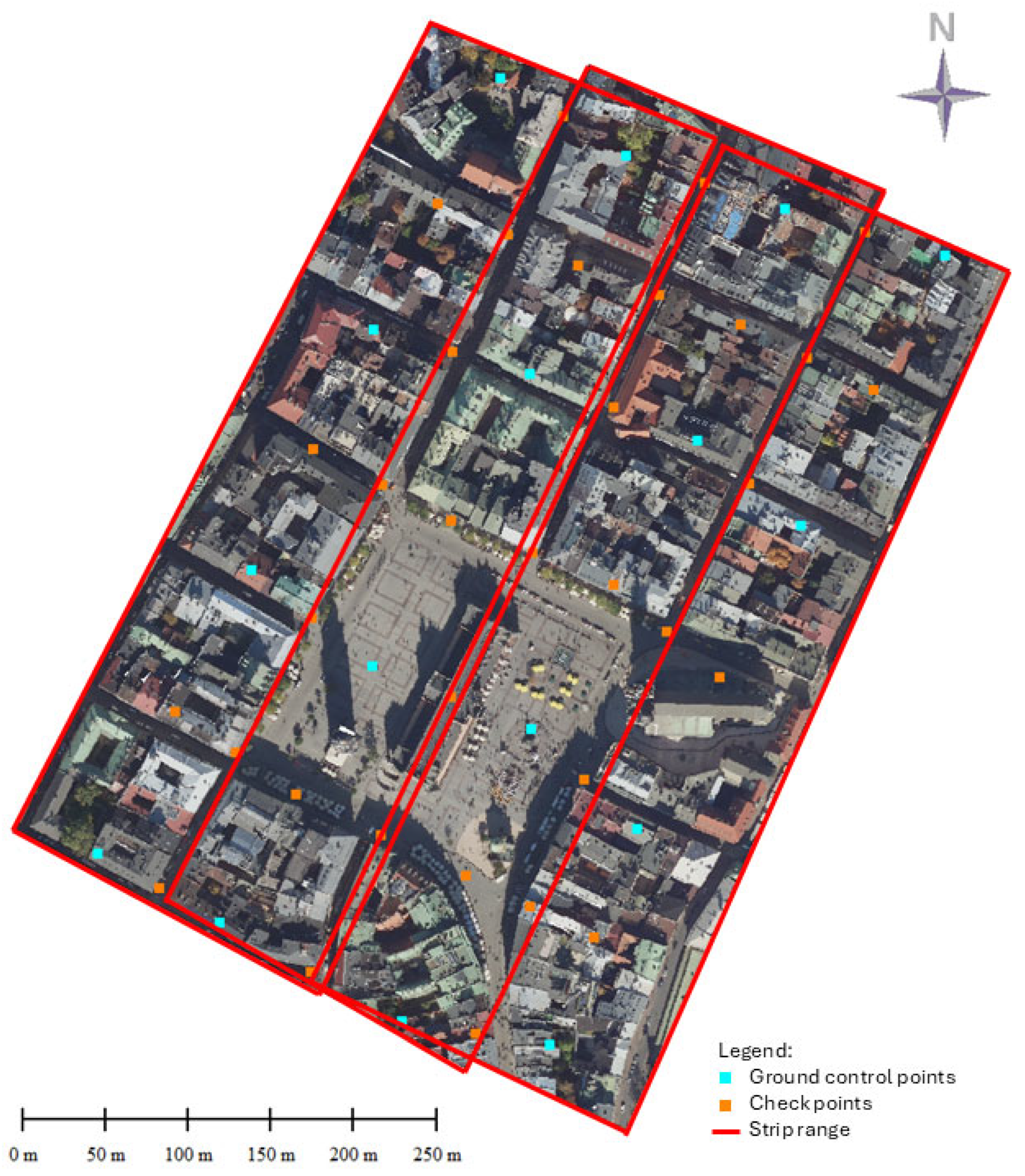
The decision to test the method on semi-synthetic data was crucial for the geometric processing of LiDAR data. The input data comprised an RGB point cloud block of Kraków from the Polish National ISOK project (ISOK). The density of LiDAR data for urban areas is typically 12 points per square metre. Sixteen GCPs and 33 CHPs were selected within three overlapping strips, each 200 m wide and 550 m long (see
Figure 4).
The creation of semi-synthetic data involved the modification of a real LiDAR block from Kraków, incorporating artificially introduced XYZ discrepancies. The data from the dense city centre area were selected to allow for strict control of discrepancies. Three strips of lidargrams were generated using a virtual camera with a focal length of 38,261 mm and a frame format of 100 × 100 mm. The experimental setup incorporated the utilisation of an ultrawide-angle camera, characterised by a focal length of 88 mm and a format size of 230 × 230 mm. This configuration was employed to simulate optimal and highly realistic geometrical conditions, thereby facilitating the analysis of the spatial intersection.
2.3.3. Real Data
The final test was conducted using authentic data. The primary objective of this test was to assess the efficiency of PyLiGram processing and the application of the method to intensity point clouds, without RGB values.
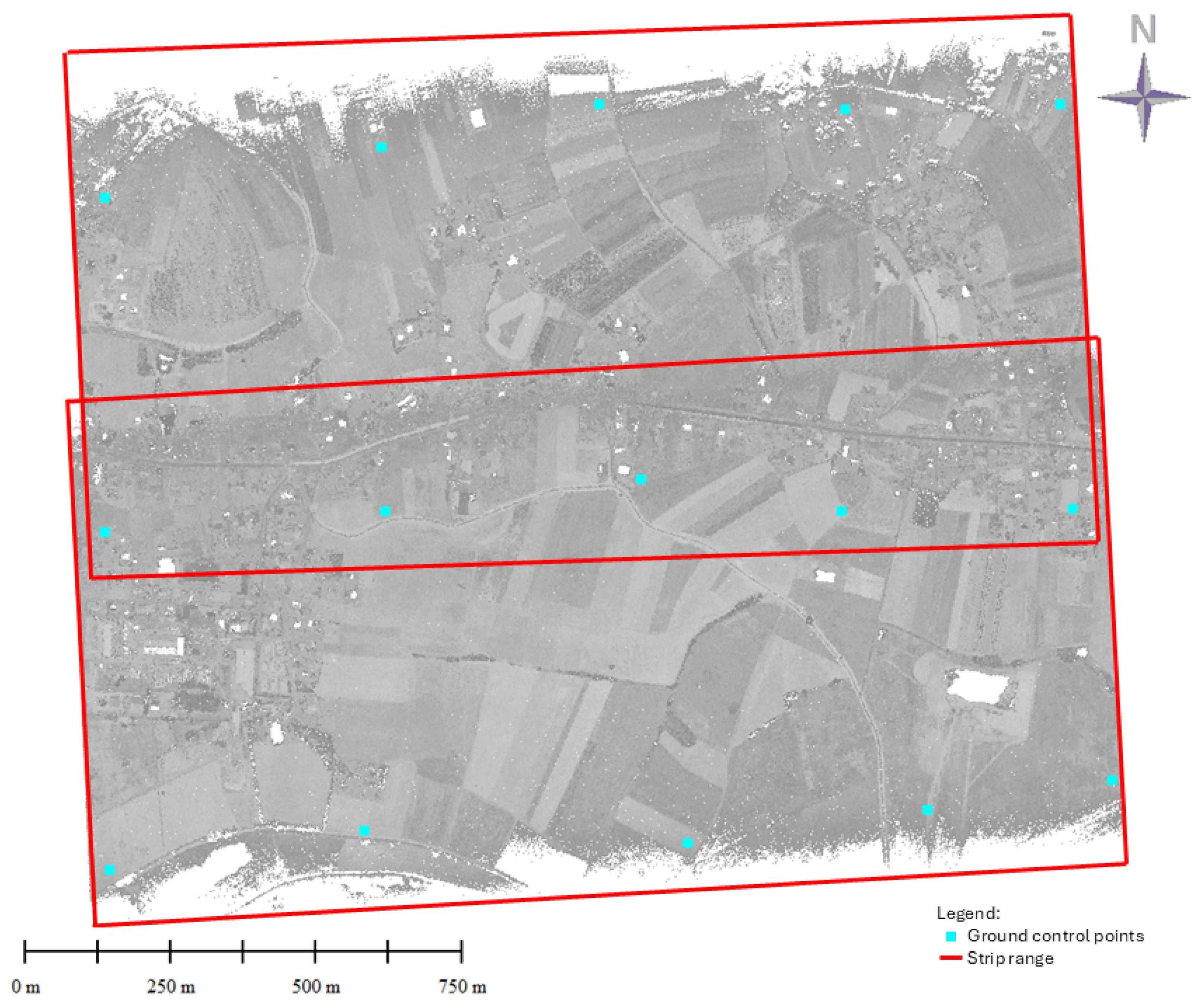
The test data comprises two original scanning strips, each measuring 1700 m in length and 770 m in width, which traverse a rural area in the vicinity of the city of Kraków. The strips exhibit an overlap of approximately 30–40%, and each contains intensity values (see
Figure 5). A total of fifteen GCPs and thirty-six CHPs were selected for the study. The original coordinates of the GCPs were subjected to randomisation in order to simulate XYZ discrepancies in the data. The original data was meticulously georeferenced, and it was necessary to simulate lower accuracy. The mean density of the point clouds was approximately 12 points per square metre, with each strip containing approximately 14 million points. The point clouds were captured by means of the Riegl VUX-100 scanner. The generation of two strips of 13 lidargrams was undertaken, with 80% overlap along the length of each strip. The virtual camera used in the test of the Kraków city centre was also employed in this instance.
2.4. Practical Testing Aspects
The inherent characteristics of point cloud data necessitate a distinct approach for the evaluation of the method and its resultant data. The accuracy of interest (in the range of a few centimetres) is approximately 10 times higher than the mean data density. It is possible to undertake a vertical accuracy evaluation even on thin point clouds using plain patches. However, the evaluation of XY accuracy of the point cloud is a significantly more arduous task and generally less precise, particularly in the case of low-density clouds in flat areas.
In accordance with the original data, original GCPs and CHPs coordinates, the following testing steps were undertaken for all test datasets in order to rigorously evaluate the presented method.
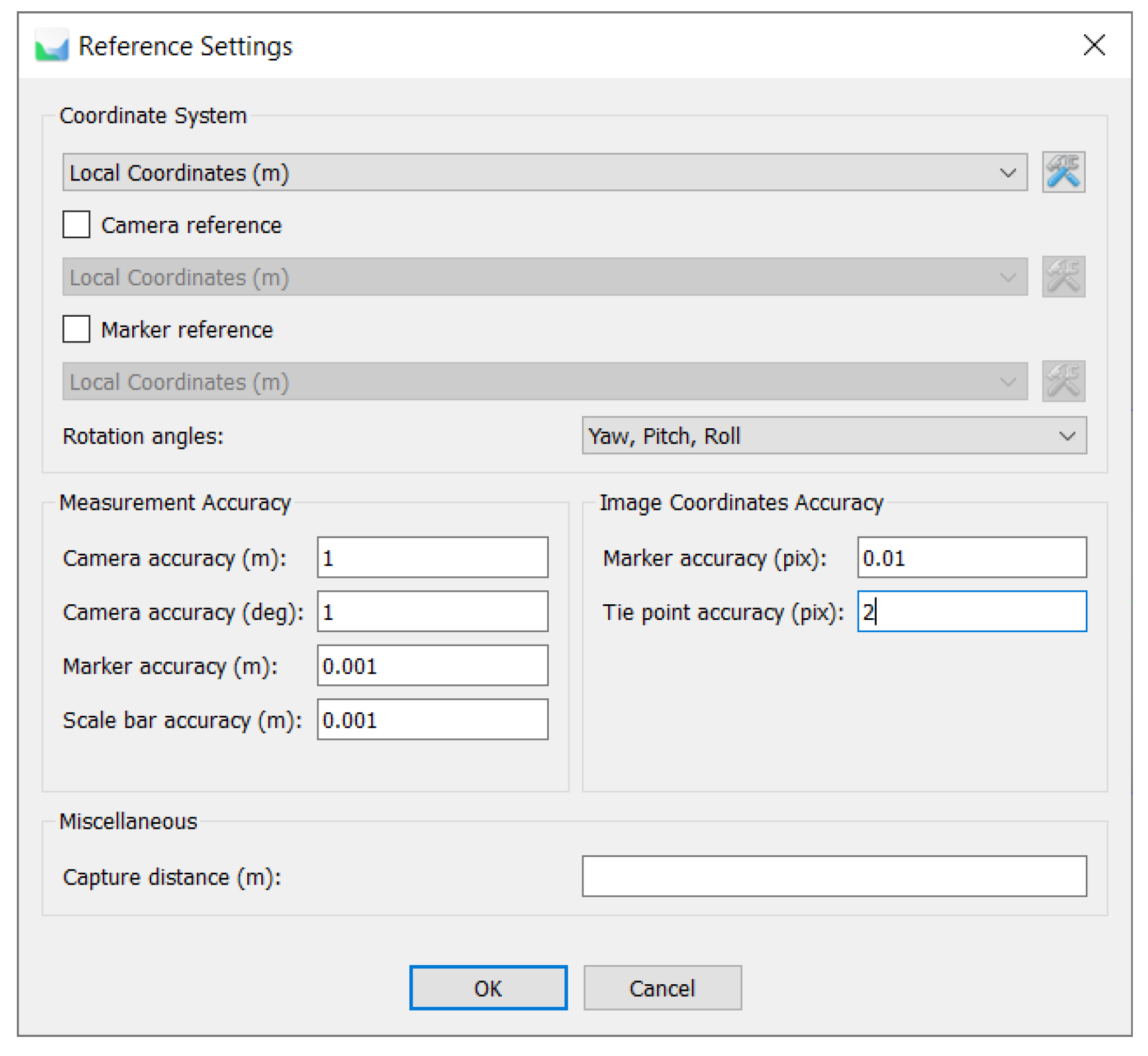
Step 1: Point Cloud Forward Transformation. The original strips and GCP coordinates were utilised to generate lidargrams with EOPs and IOPs, with the a priori parameters saved in JavaScript Object Notation (JSON) files. Virtual measurements of the GCPs on the lidargrams were stored in an XML file. The intensity point cloud lidargrams (of the real data) required contrast enhancement. It was determined that no additional radiometric alterations would be implemented. The quality of lidargrams in relation to matching results is a subject to be explored in future research. The matching and adjustment of lidargram blocks were facilitated using Agisoft Metashape (v. 1.7.3) software with the default settings (i.e., accuracy: high; generic preselection: source) [
59]. A priori errors were configured to facilitate block deformation based on the coordinates of the GCPs (
Figure 6). The accuracy of the EOPs, the measurement accuracy and the accuracy of the GCPs’ image coordinates were set at relatively elevated levels, while the accuracy of the tie points was set at a relatively low level (2 pixels). The necessity for manual measurement was negated. The adjusted EOPs were exported following the implementation of least squares estimation, and subsequently utilised to intersect new point clouds within their original strips.
Step 2 (Point Cloud Inverse Transformation): The point cloud strips generated in the preceding step were processed in a retrograde manner, as if they were original data, without the need for additional matching or adjustment. The adjusted EOPs (also from Step 1) were used to generate lidargrams, and known a priori EOPs were used as the target.
Figure 6.
Reference settings of Agisoft Metashape project before lidargrams’ block adjustment.
Figure 6.
Reference settings of Agisoft Metashape project before lidargrams’ block adjustment.
Subsequently, Steps 3 and 4 were implemented to regulate the process and method with a greater number of CHPs. The parameters of the process and the coordinates of the CHPs (a priori and deformed) were known to repeat the calculation for method analysis. The original and deformed parameters of Steps 1 and 2 were utilised for these final two steps of the process. Furthermore, the entire set of points comprising the processed point cloud (which is effectively a set of CHPs) was subjected to numbering, enabling subsequent comparison with the reference CHPs coordinates following the completion of both steps.
Step 3 (CHPs Forward Transformation): A set of CHPs as point cloud data was deformed in a manner consistent with the point cloud in Step 1, employing the same IOPs and EOPs (which are stored in JSON files) and deformed GCP coordinates.
Step 4 (CHPs Inverse Transformation): The deformed CHPs in Step 3 were processed backwards as a whole point cloud in Step 2. Furthermore, two accuracy analyses were conducted. The newly intersected coordinates of the CHPs were then compared to the following: (1) original coordinates of the CHPs, which are to be found in Step 3 of the process; and (2) corrected coordinates of the CHPs, which are to be found in Step 4 of the process. The effectiveness and accuracy of the process were evaluated by calculating the root mean square error (RMSE) and the maximum value of the difference (MAX).
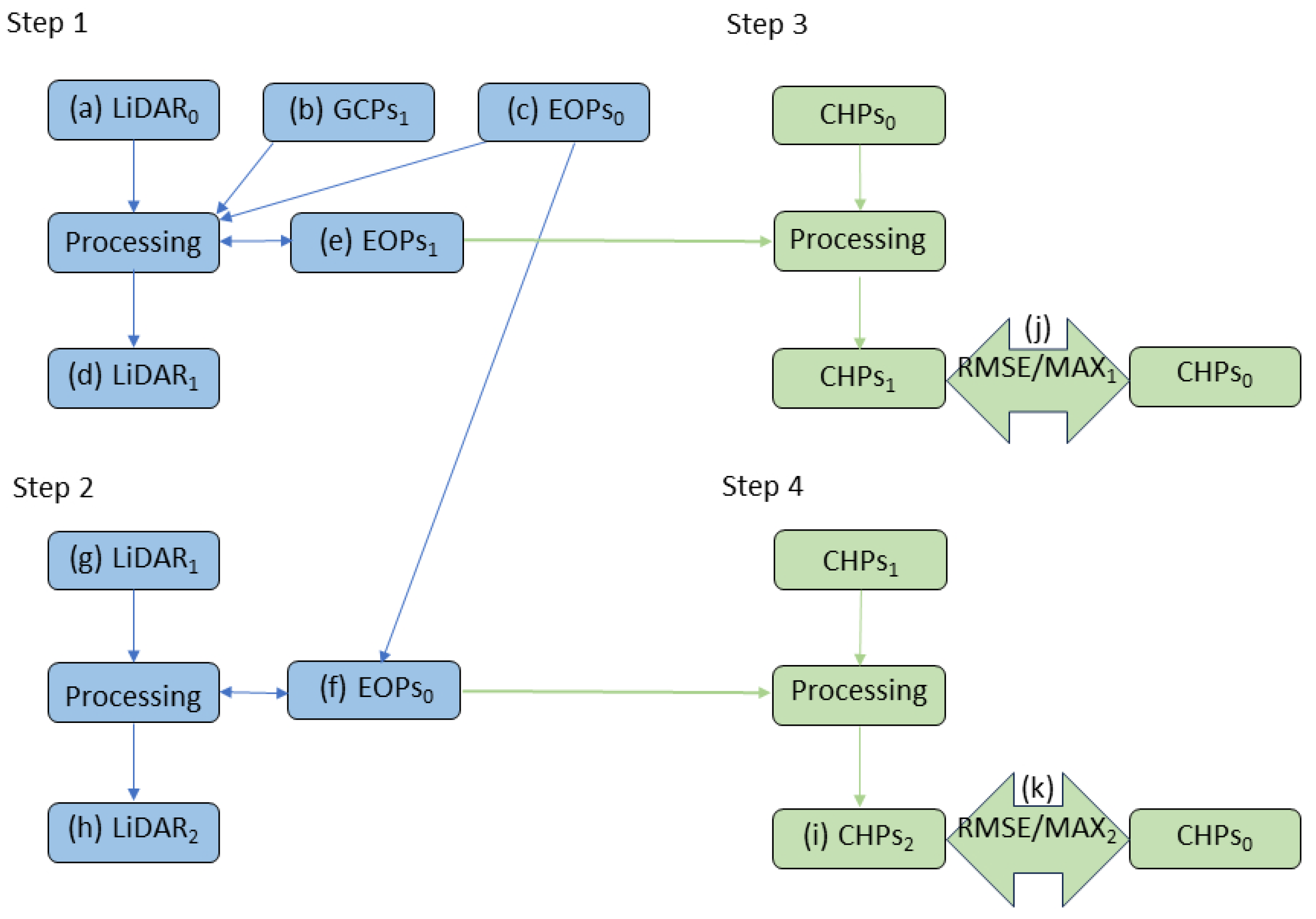
Figure 7 presents a simplified diagram of the test workflow. In the initial step, (a) LiDAR
0 data are converted to LiDAR programmes using (c) EOP
s0, and (d) LiDAR
1 data are generated after adjusting the LiDAR programmes using (b) GCP
s1 and calculating (e) EOP
s1.
In the second step of the process, the (f) EOPs0 are utilised to invert the processing of the (g) LiDAR1 data to the (h) LiDAR2 data. The fundamental evaluation of process validity entails a comparison between (a) LiDAR0 and (h) LiDAR2. It is evident that steps 3 and 4 are analogous; however, in this instance, CHPs are processed as opposed to the entire point cloud. The data from Step 1 (EOPs1) and Step 2 (EOPs0) are utilised to transform data forward and backwards, respectively, within Steps 3 and 4. The same processing parameters are utilised, yet the result (i.e., CHP2) is employed for quantitative and statistical analysis, thereby comparing a priori (j) RMSE/MAX values with a posteriori RMSE/MAX values (k).
This methodology, dedicated to the enhancement of point cloud data, facilitated the verification of its accuracy without the necessity for manual measurement. It was established that no supplementary random errors were incorporated, and an equivalent XYZ evaluation of the method was feasible.
A supplementary test was conducted to evaluate the efficacy of the methodology employed in comparison to alternative software solutions. The data obtained from Steps 3 and 4, which represented the geometrical configuration of the strips, were processed using Cloud Compare [
60]. The transformation matrix for each strip was calculated using two sets of GCPs through the Iterative Closest Point (ICP) algorithm. Subsequently, the transformation matrix was applied to the test data, and the XYZ discrepancies were calculated between the processed cloud and the target coordinates.
2.5. Evaluation Test Field
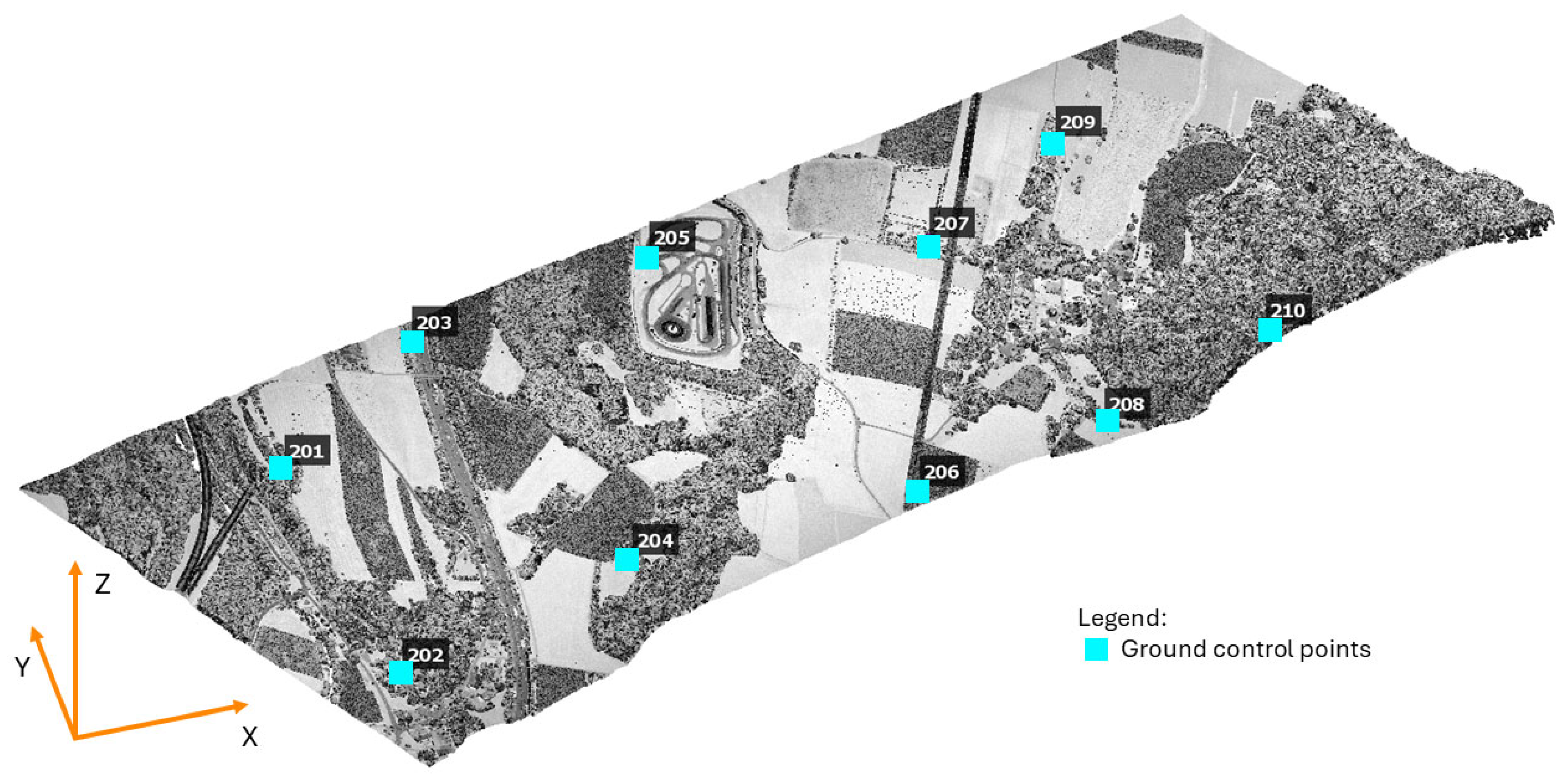
A further evaluation of the method was conducted by comparison of its results with those obtained from processing TerraScan and TerraMatch software developed by TerraSolid Company (TerraSolid Ltd., Espoo, Finland, 2022 [
2]). A segment of the LiDAR strip from the Loosdorf project was selected for analysis. The data were captured by the Riegl VQ-1560i-DW sensor platform (RIEGL Laser Measurement Systems GmbH, Riedenburgstr. 48 3580 Horn, Austria). It is evident that the utilisation of points of IR channels was the sole method employed. A total of ten control points were selected for ease of location within the point cloud. The coordinates were modified to a maximum extent of ±20 cm. The control data were then utilised to adjust the sample data. As demonstrated in
Figure 8, the evaluation data are presented with a distribution of 10 control points.
Initially, the data underwent non-rigid transformation using TerraMatch. The tie lines to XYZ known points were measured, and the fluctuations XY, Z and roll/pitch/heading were defined. The subsequent generation of the point cloud occurred subsequent to the implementation of the aforementioned corrections. The discrepancies were measured between the control and the transformed point cloud. The identical data and control points were utilized in two processes in PyLiGram. Initially, the projection of 19 lidargrams was conducted utilizing a virtual camera, which was equivalent to a PhaseOne mounted on a Riegl VQ-1560i-DW platform. The extent of image overlap was found to be 80%. Secondly, a total of 72 lidargrams were projected, utilizing a visual camera with a frame that was four times shorter in the x direction and equal in the y direction, relative to the frame of the PhaseOne camera. The overlap was set at 90%, and a substantially greater number of images (shorter in the x direction) were generated. A greater number of images would have facilitated a more precise approximation of the trajectory. The processing of both sets of lidargrams was undertaken, and the discrepancies to the control points were subsequently calculated.
3. Results
The evaluation of the proposed method and three case studies was based on the analysis of root mean square error (RMSE) values and MAX values. A thorough investigation was conducted, with each 3D coordinate being meticulously analysed to account for both horizontal and spatial discrepancies.
3.1. Test Results—Synthetic Data
The analysis of the CHPs involves examining the root mean square error (RMSE) and maximum values (MAX) for the X, Y, and Z coordinates, as well as the XY horizontal values and the XYZ spatial values.
Table 2 presents the root mean square error (RMSE) and maximum values, which represent the a priori RMSE values of the simulated deformation of the strips within Step 1/Step 3. In a similar manner, the values under discussion are presented in
Table 3 subsequent to processing within Step 2/Step 4.
The X and Y discrepancies (RMSE, MAX) were found to be similar, while the Z discrepancies (RMSE) were found to be approximately 30% larger, with the MAX values of the Z discrepancies being 40% larger. The methodology employed involves a two-step process: firstly, the data are deformed, and then corrected, with the objective of achieving near-original data recovery following processing.
A comparison of the root mean square errors (RMSEs) presented in
Table 1 and
Table 2 reveals a 38-fold decrease in the X coordinate, a 26-fold decrease in the Y coordinate, a 16-fold decrease in the Z coordinate, a 31-fold decrease in the horizontal coordinate, and a 20-fold decrease in the spatial coordinate.
The MAX values demonstrate a comparable tendency, albeit less marked than that observed in the root mean square error values. The MAX values of the discrepancies in X, Y, Z, XY and XYZ (both a priori and post-processing) decrease by a factor of 11 in X, 9 in Y, 6 in Z, 9 in XY and 7 in XYZ. Subsequent analysis indicates that the RMSEs of Z are more than twice as large as the RMSEs of X/Y, and the MAX values are three times larger for Z than for X and Y. Results obtained with synthetic data of the same height (100 m), generated from the orthophoto of a rural area, confirm the correctness of the method and its implementation. Following a thorough analysis of the results, it can be concluded that the discrepancies observed in millimeters or centimeters are negligible. The accuracy of the lidargram adjustment process results in the final point cloud after Step 2/Step 4 being different from the initial point cloud. The efficacy of this adjustment is contingent upon a number of factors, including but not limited to point cloud density, the generation algorithm employed for LiDAR grids, the parameters that define the tie point matching process, and the predetermined adjustment accuracies. The findings of the aforementioned test enabled the assessment of the method’s efficacy on more intricate data sets.
3.2. Test Results—Semi-Synthetic Data
The results obtained from the semi-synthetic data from Kraków city centre were processed in four steps, as previously outlined. In a manner consistent with the preceding steps,
Table 4 presents the RMSE and MAX values in the absence of correction, while
Table 5 demonstrates the values subsequent to processing. The root mean square error (RMSE) values demonstrate substantial decreases: The frequency of occurrence of the phenomenon was found to be 18 times in X, 17 times in Y, 8 times in Z, 8 times horizontally and 21 times in 3D.
The maximum values presented in advance in the final columns of
Table 3 and subsequent processing in
Table 4 demonstrate a reduction in the discrepancies of the positions of the CHPs: 9 times in X, 11 times in Y, 3 times in Z, 3 times horizontally and 8 times in 3D.
The findings indicate a substantial enhancement in the positioning accuracy of the CHPs. The challenges inherent in matching lidargrams within city centres, characterized by tall buildings and narrow streets, yield inferior results compared to those on flat synthetic point clouds, although the strips are better aligned. A comparison of the root mean square error (RMSE) and maximum values (MAX) prior to and following processing reveals that the enhancement in accuracy is predominantly contingent on the quality of the matching outcomes, rather than the methodology itself.
3.3. Test Results—Real Data
The real data were employed subsequent to a preliminary evaluation of their correctness, conducted using synthetic and semi-synthetic data. The same four-step procedure was used. Initially, both data strips were processed in both forward and reverse directions, with the process parameters being stored. Secondly, utilising these parameters to process solely the CHPs as a point cloud yielded the results presented in the subsequent tables.
It was necessary to apply an additional process subsequent to the generation of the intensity lidargrams and prior to their matching. In order to ensure an optimal match, it was necessary to enhance the images manually through contrast, brightness and gamma correction, with the same values of these parameters. The process of matching the block was successful, and the block was matched with a high degree of accuracy. The root mean square error (RMSE) values demonstrate a substantial decline following the implementation of the proposed methodology (see
Table 6 compared to
Table 7). This decline is evident in the X coordinate with 126 instances, the Y coordinate with 60 instances, the Z coordinate with 107 instances, and the horizontal and 3D dimensions with 101 instances.
As demonstrated in
Table 6, the maximum values presented in the final columns of
Table 5 diminish following processing. Specifically, they decrease 136 times in X, 48 times in Y, 68 times in Z, 55 times horizontally, and 67 times in 3D.
The findings derived from the analysis of authentic data substantiate the validity of the methodology and its accurate execution within the PyLiGram research apparatus. The outcomes of the greyscale (intensity) lidargram matching process were found to be successful, thus enabling the data to be processed in both forward (Step 1/Step 3) and reverse (Step 2/Step 4) directions, producing almost identical point clouds before and after the aforementioned processes. The real data results were the most successful of the three tests.
3.4. CloudCompare and PyLiGram Results Comparison
Despite the fundamental differences between the two processes (ICP as a rigid and lidargrammetric method as a non-rigid), a summary comparison was conducted. The ICP and the method under investigation were applied to all strips and then compared.
Table 7 presents a comparison of the root mean square error (RMSE) and maximum values (MAX) of discrepancies between the sample representation of the strip and the ground control in three sections: synthetic data, semi-synthetic data and real data. The initial row of each section of the table displays the discrepancies a priori, prior to processing. The second row of the table displays the results of Cloud Compare’s ICP processing, while the last row presents the outcomes of our non-rigid method. The distribution of points was found to be regular.
As predicted, the root mean square errors (RMSE) and maximum values in
Table 8 are reduced following the rigid processing of all strips in Cloud Compare when compared to the initial values. The lowest root mean square error (RMSE) and maximum values are obtained through the non-rigid transformation of PyLiGram.
A comparable trend is also demonstrated by the analysis of the results of semi-synthetic data. As illustrated in
Table 7 of the real data, the root mean square error (RMSE) and maximum (MAX) values are initially comparable to those of a rigid transformation. The distribution of 3D discrepancies exhibited a local increase in values during the rigid transformation, which is an exemplary occurrence. Nevertheless, the results of the PyLiGram process are significantly superior. The reduction of RMSE is synthetized in
Table 9.
All comparative calculations yield definitive and anticipated outcomes. The lidargrammetric method has been demonstrated to be optimal for the three-dimensional, non-rigid transformation of LiDAR strips in the absence of trajectory data.
3.5. TerraMatch and PyLiGram Results Comparison
The comparison was conducted by calculating the differences in X, Y and Z coordinates between control points and characteristic points on a processed strip. The objective was accomplished by utilising TerraScan/TerraMatch software. PyLiGram with a PhaseOne camera, and a greater quantity of PyLiGram generated with a camera frame size shorter along the virtual flight axis. Such a case would simulate superior approximation of the trajectory’s geometry thanks to a greater number of lidargrams’ projection centres. The hypothesis of this additional experiment was that the presence of more lidargrams and the adoption of more dense camera positions would result in the formation of the output LiDAR strip being more accurate.
The mean square differences for each coordinate
dX were calculated according to the Equation (3), where
XGCP is a coordinate of the ground control point (GCP),
Xi is the coordinate measured on point cloud and
n is the number of GCPs.
As demonstrated in
Table 10, the outcomes of the comparison demonstrate comparable results for both the PyLiGram methods and superior results for TerraScan/TerraMatch processing. This outcome was anticipated due to the inherent flexibility of LiDAR data adjustment as a function of trajectory. It is evident that PyLiGram does not utilise trajectory for the purpose of computing the new point cloud. The flexibility of the lidargrammetric strip of synthetic images has been demonstrated to minimise discrepancies; however. it has not been shown to reduce them to any significant extent.
4. Discussion
The efficacy of the method and its implementation were tested using three types of data: synthetic, semi-synthetic, and real. Furthermore, the method was evaluated in comparison with TerraScan/TerraMatch software as a worldwide LiDAR data processing standard.
4.1. Preliminary Results
The initial utilisation of synthetic data was for the purpose of method verification. with subsequent corrections to the implementation being made in accordance with the findings of the preliminary results. The majority of the information and insights were derived from tests based on synthetic data, which exposed errors and methodological issues. Ultimately, all issues were resolved and errors were eradicated, thereby validating the efficacy of the method and the research instrument. The presented root mean square error (RMSE) and maximum value (MAX) of discrepancies confirm the positive outcome (
Table 7). The limited consistency observed between the data before and after Steps 1/3 and Steps 2/4 can be attributed to various factors, including point cloud density, the methodologies and parameters employed in lidargram generation, and the processes of lidargram matching and adjustment. The outcomes of this process are contingent on numerous factors, including the virtual camera parameters, the accuracies defined prior to the adjustment, and the method and parameters of the adjustment itself.
4.2. Results of Dense 3D Semi-Synthetic Data
Subsequently, the lidargram generation procedure was refined for data from a tall. dense building site in an old city using semi-synthetic data. The configuration of the streets and the relative height of the buildings, as observed through the utilisation of a wide-angle virtual camera, presented a considerable challenge to the quality of the lidargrams. This necessitated the further development of the synthetic raster sampling method. The successful matching of the lidargrams served as a positive validation of the advanced sampling method. The irregular and dense data of the city centre were matched to the GCPs, with the accuracy confirmed by comparing the discrepancies with the CHPs.
4.3. Intensity Real Data Results Discussion
The test of real data constituted the third evaluation of the method. The method was applied to process raw strips, originally with intensity values, devoid of RGB colour. The process of matching and adjusting lidargrams proved to be successful, a feat facilitated by the implementation of additional image enhancement techniques, encompassing contrast, brightness, and gamma correction. The findings derived from the analysis of authentic data are highly encouraging, demonstrating a substantial improvement in performance when compared to results obtained from synthetic and semi-synthetic data sets.
4.4. Factors of the Results
It is imperative to acknowledge that a multitude of factors may influence the efficacy of the process and the precision of the outcome. A number of factors must be given full consideration.
4.4.1. Virtual Flight and Virtual Camera Parameters
Firstly, there is the overlap of the lidargrams, and secondly, the side overlap of the lidargrams strips. In addition, the parameters of the virtual camera must be given due consideration, as must the number and distribution of the GCPs and their accuracy. Furthermore, the length of the projected bases between consequent virtual projection centres must be taken into account, as must the nadir or/and oblique orientation of the lidargrams.
4.4.2. Lidargrams’ Sampling Factor
Finally, the method of lidargrams’ sampling must be considered. This finding indicates a significant area for further investigation. Despite the fact that the lidargram sampling method has been proven to be effective, further research is required to ascertain its reliability. A number of approaches have been posited for the enhancement of the quality of these images, including the utilisation of alternative optional interpolations or post-processing techniques. It is important to note that the quality of the lidargrams was not the objective of this research, as they were only used for matching and not for stereoscopic observation.
4.4.3. Ground Truth Factor
In this particular instance, the location of the GCPs in the overlap area did not have a detrimental effect on the accuracy of the process. This outcome was attributed to the congruence of the lidargrams across both strips, a phenomenon that occurred independently of the GCPs. It is imperative to emphasise the significance of appropriate weighting of the tie points, thereby enabling the strips to deform in accordance with the precise location of the GCPs. The distribution and coordinates of the GCPs in all tests were defined in order to simulate XYZ errors in the position of the point clouds. In order to align these strips, a method that was both flexible and non-rigid was required. It is evident that a flexible approach is the most effective method of minimising 3D discrepancies. The utilisation of random error values constituted a general case. The approach presented for the registration of aerial LiDAR data is based on the relationship of LiDAR points to ground truth data and does not rely on trajectory data. The ground truth data is established by the spatial coordinates of the GCPs (Ground Control Points), although point cloud control patches can also be utilised. Moreover, disparities in XYZ coordinates within overlap regions could be employed for the relative transformation of data, incorporating strip relative adjustment.
4.5. Validation of the Method and Its Implementation
The results described above constitute a subset of the real test datasets utilised during the development of the research tool. Initially, specific and simple cases were utilised (kappa = 0 and 2–3 lidargrams), with subsequent cases designed to increase complexity to facilitate error detection and address challenging scenarios. The test data presented here have been selected to illustrate the outcomes of the method and its implementation in a manner that is both representative and general. It is acknowledged that, in principle, simpler and more specific cases than those presented in these tests are also possible. Such cases may include, but are not limited to, local deformation of the block (caused by only one GCP) or 3D transformation of the data (changing the coordinate system).
The ensuing discourse on the outcomes places principal emphasis on the validation of the efficacy of the method, with specific reference to the impact of lidargram matching on the quality of the method. The utilisation of terrain LiDAR points, in conjunction with their projections on lidargrams (identifier ULPIs), has the potential to facilitate the resolution of the matching problem. In the present study, the matching and bundle adjustment processes were executed in conjunction with the utilisation of an external tool. In future iterations, the matching process will be decoupled from the overall procedure, with the integration of bundle adjustment being incorporated into the PyLiGram framework. This approach would mitigate the most significant factor contributing to the discrepancies observed in each of the test fields.
Nevertheless, the evaluation of the method by way of a comparison of the results obtained by our method and those obtained by the popular tool, TerraMatch, indicates that the trajectory adjustment method is more accurate. The PyLiGram method is dedicated to the adjustment of LiDAR data in the absence of a trajectory, or when the trajectory is affected by jamming, and when the general adjustment of the data is based on GCPs. The present study demonstrates that the system is unable to compete with the trajectory adjustment of the LiDAR strip implemented in TerraSolid software when all the necessary data are available. However, PyLiGram provides a unique solution for older data or data where GNSS is not available, when the trajectory is unknown or unreliable. The generation of flexibly transformed point clouds is achieved with precision, in accordance with the available ground truth data.
4.6. Final Remarks
The present approach is founded upon traditional methods that have been applied in a novel manner, in addition to the integration of original concepts. In addition. a conventional calculation is employed in PyLiGram, as well as for external matching and adjustment.
The limitations of the matching process, attributable to the substandard quality of the synthetic images, have precipitated the advancement of research into the application of artificial intelligence. This subsequent stage of research involves the utilization of deep learning for image matching and in-printing for image enhancement.
5. Conclusions
This paper presents a portion of the research exploring the potential of the lidargrammetric approach for processing LiDAR data using image and photogrammetric processing methods. The novel approach presented for LiDAR point cloud adjustment and transformation has been implemented in the PyLiGram research tool. A series of tests were conducted in order to verify the correctness of the concept, and its implementation was found to be satisfactory. The transformation has been executed, and the residual discrepancies measured on CHPs are significantly lower than before the implementation of the method under investigation.
The methodology employed in this study involves a lidargrammetric approach, wherein LiDAR points are projected onto virtual images with arbitrary internal and external orientation parameters (IOP and EOP). The present study introduces the concept of LiDAR point and image (lidargram) point assignment, termed the unique lidargram point identifier (ULPI). This facilitates the intersection of the new point cloud without the loss of the original LiDAR data set and without the necessity for image dense matching points. The subsequent matching and image adjustment process is necessary to estimate the EOPs that are ultimately used to intersect the new points (XYZ transformed point cloud).
It is acknowledged that external matching is contingent upon the utilisation of high-quality synthetic imagery. Furthermore, the processes of LiDAR matching and adjustment introduce errors that have the potential to reduce the accuracy of the process. The final accuracy of the matching process is influenced by several factors, including the configuration of the LiDAR block (e.g., photo overlap, strip overlap and potentially opaque photos), the matching methods and parameters employed, and the a priori defined accuracies.
The proposed methodology can be applied to any type of LiDAR data processing; however, it is particularly suitable for archival data without trajectory information, stored not only as strips but also as blocks, after the block has been divided into overlapping strips. The sole limitation pertains to the necessity for ground control and the feasibility of measuring it on point clouds. Moreover, the method can be applied to any type of vector data, not exclusively point clouds. Although not currently implemented, it is conceivable that files containing drawing primitives could be processed in an analogous manner.
The work presented can be situated within the broader context of photogrammetric and LiDAR data integration methods, as well as research into the nature and efficiency of geospatial data formats. The broader context of this research activity encompasses deep learning methodologies at multiple stages of the process, including image matching, synthetic image quality enhancement, and geometric and semantic object recognition.
6. Future Research
In the subsequent phase of the investigation. the omission of the matching phase is planned, as the image coordinates of homologous points are calculated during the lidargram generation process. The methodology entails circumventing the requisite matching step and executing an immediate adjustment to the LiDARblock. The application of ULPI facilitates the preservation of the relationship between homologous points and their original terrain points, thereby enabling their direct utilisation in the adjustment process, thus circumventing the consequences and limitations associated with matching. The outcome of the adjustment would be exterior orientation parameters (EOPs) that are more precise, unencumbered by the impact of matching errors. The corrections of EOPs would be modelled based on ground control points (GCPs) and predefined errors of the tie points and GCPs. It is imperative to enhance the measurement accuracy of the tie points while preserving the GCPs as meticulously measured points, thereby enabling the adjustment process to deform the block according to the locations of the GCPs. Although the achievement of the desired accuracy of the tie points may appear to be a somewhat abstract concept, it is nevertheless a prerequisite for allowing the block to undergo flexible deformation. During the testing phase, these accuracy settings were configured within the Agisoft Metashape software. A matching procedure must be implemented in our research tool. Subsequently, complex real data will be utilised to assess the validity of the implementation, the efficacy of the applied adjustment, and its efficiency.
It is evident that there is a discernible correlation between the quality of generated lidargrams and the ensuing outcomes of their matching. Consequently, a promising avenue for future research lies in the analysis of matching results contingent on the methodology employed in the creation of these synthetic images. The utilization of adaptive interpolation methods and deep machine learning algorithms, such as inpainting, is currently under consideration.
The subsequent stage of our research will involve the utilisation of lidargrams as intermediate data for the identification of tie points and features within LiDAR point clouds and photogrammetric images, employing deep learning methodologies. The potential exists for the execution of co-orientation of RGB photograms and lidargrams by means of efficient deep learning matching. The following data sets will be utilised: intensity lidargrams with single IR band images or CIR images, and RGB lidargrams with RGB images. This has great potential for the co-registration of LiDAR and photogrammetric data, as well as serving as a method for LiDAR enhancement based on adjusted photogrammetric data or, in reverse, the image enhancement of EOPs based on adjusted LiDAR data.
Furthermore, it could be explored as an analytical solution for multi-sensor platform calibration.
Moreover, should the aforementioned research prove successful, it would be feasible to enhance the quality of lidargrams by employing in-printing methodologies to generate lidargrams for shorter sections of the LiDAR strips. Subsequently, the trajectory could be computed through the utilization of photogrammetric resection and spline modelling.
Author Contributions
Conceptualization, A.R.; methodology, A.R.; software, M.T.; validation, A.R. and M.T.; formal analysis, A.R. and M.T.; investigation, A.R. and M.T.; resources, A.R. and M.T.; data curation, A.R. and M.T.; writing—original draft preparation, A.R. and M.T.; writing—review and editing, A.R. and M.T.; visualization, A.R. and M.T.; supervision, A.R.; project administration, A.R. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research constitutes a component of the postdoctoral research project, which is receiving partial support from the “Excellence Initiative—Research University” programme for the AGH University of Science and Technology (No. 4744). The project is being led by Antoni Rzonca.
Data Availability Statement
The original synthetic and semisynthetic data presented in the study are openly available at
https://fotogrametria.agh.edu.pl/pyligram (accessed on 30 June 2025). Restrictions apply to the availability of real data. Data were obtained from Geodimex S.A. and are available with the permission of Geodimex S.A.
Acknowledgments
We would like to express our gratitude to Krystian Pyka (AGH Kraków). Gottfried Mandlburger (TU Wien), and Johannes Otepka (TU Wien) for their valuable suggestions and creative discussions. Furthermore, the real data utilised for the testing process was provided by Gottfried Mandlburger of the Technical University of Vienna, along with Grzegorz Kuśmierz and Dariusz Fryc of Geodimex S.A.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CIR | Close Infrared |
| CHP | Check Points |
| EOP | External Orientation Parameters |
| GCP | Ground Control Points |
| GSD | Ground Sample Distance |
| ICP | Iterative Closest Point |
| IOP | Internal Orientation Parameters |
| IR | Infrared |
| LiDAR | Light Detection and Ranging |
| RMSE | Root Mean Square Error |
| ULPI | Unique LiDAR Point Identifier |
Appendix A
Figure A1.
User interface of the PyLiGram research tool.
Figure A1.
User interface of the PyLiGram research tool.
References
- Toth, C.; Jóźków, G. Remote Sensing Platforms and Sensors: A Survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Terrasolid Ltd. TerraMatch User’s Guide 2022; Terrasolid Ltd.: Jyvaskyla, Finland, 2020; pp. 169–232. [Google Scholar]
- RIEGL Laser Measurement Systems GmbH RiProcess_Datasheet_2021-05-17.Pdf 2015. Available online: https://www.laser-3d.pl/wp-content/uploads/RiProcess_Datasheet_2021-05-17.pdf (accessed on 30 June 2025).
- Hexagon HyMap. Available online: https://docs.hexagon.com/hxmap/4.5.0/ (accessed on 30 June 2025).
- Pöppl, F.; Neuner, H.; Mandlburger, G.; Pfeifer, N. Integrated Trajectory Estimation for 3D Kinematic Mapping with GNSS. INS and Imaging Sensors: A Framework and Review. ISPRS J. Photogramm. Remote Sens. 2023, 196, 287–305. [Google Scholar] [CrossRef]
- Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS—A Framework for Airborne Laser Scanning Data Analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
- Liu, X. Accuracy Assessment of Lidar Elevation Data Using Survey Marks. Surv. Rev. 2011, 43, 80–93. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of Airborne Lidar-Derived Elevation: Empirical Assessment and Error Budget. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Vosselman, G. Automated Planimetric Quality Control in High Accuracy Airborne Laser Scanning Surveys. ISPRS J. Photogramm. Remote Sens. 2012, 74, 90–100. [Google Scholar] [CrossRef]
- Soudarissanane, S.S.; van der Sande, C.J.; Khosh Elham, K. Accuracy Assessment of Airborne Laser Scanning Strips Using Planar Features. In Proceedings of the EuroCOW 2010: The Calibration and Orientation Workshop, Castelldefels, Spain, 10–12 February 2010. [Google Scholar]
- Höhle, J. The Assessment of the Absolute Planimetric Accuracy of Airborne Laserscanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5/W12, 145–150. [Google Scholar] [CrossRef]
- Ressl, C.; Kager, H.; Mandlburger, G. Quality Checking of Als Projects Using Statistics of Strip Differences. Int. Arch. Photogramm. Remote Sens. 2008, 37, 253–260. [Google Scholar]
- Bang, K.I.; Habib, A.; Kersting, A. Estimation of Biases in Lidar System Calibration Parameters Using Overlapping Strips. Can. J. Remote Sens. 2010, 36, S335–S354. [Google Scholar] [CrossRef]
- Tulldahl, H.M.; Bissmarck, F.; Larsson, H.; Grönwall, C.; Tolt, G. Accuracy Evaluation of 3D Lidar Data from Small UAV. Electro-Opt. Remote Sensing. Photonic Technol. Appl. IX 2015, 9649, 964903. [Google Scholar] [CrossRef]
- Mayr, A.; Bremer, M.; Rutzinger, M. 3D Point Errors and Change Detection Accuracy of Unmanned Aerial Vehicle Laser Scanning Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 765–772. [Google Scholar] [CrossRef]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality Assessment of Combined IMU/GNSS Data for Direct Georeferencing in the Context of UAV-Based Mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2017, 42, 355–361. [Google Scholar] [CrossRef]
- Dreier, A.; Janßen, J.; Kuhlmann, H.; Klingbeil, L. Quality Analysis of Direct Georeferencing in Aspects of Absolute Accuracy and Precision for a Uav-Based Laser Scanning System. Remote Sens. 2021, 13, 3564. [Google Scholar] [CrossRef]
- Ressl, C.; Mandlburger, G.; Pfeifer, N. Investigating Adjustment of Airborne Laser Scanning Strips Without Usage of Gnss/Imu Trajectory Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 195–200. [Google Scholar]
- Pirotti, F.; Piragnolo, M.; Vettore, A.; Guarnieri, A. Comparing Accuracy of Ultra-Dense Laser Scanner and Photogrammetry Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2022, 43, 353–359. [Google Scholar] [CrossRef]
- Bakuła, K.; Salach, A.; Zelaya Wziątek, D.; Ostrowski, W.; Górski, K.; Kurczyński, Z. Evaluation of the Accuracy of Lidar Data Acquired Using a UAS for Levee Monitoring: Preliminary Results. Int. J. Remote Sens. 2017, 38, 2921–2937. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hugenholtz, C.H.; Zou, X. ARTICLE UAV—LiDAR Accuracy in Vegetated Terrain. J. Unmanned Veh. Syst. 2018, 234, 212–234. [Google Scholar] [CrossRef]
- Salach, A.; Bakula, K.; Pilarska, M.; Ostrowski, W.; Górski, K.; Kurczynski, Z. Accuracy Assessment of Point Clouds from LidaR and Dense Image Matching Acquired Using the UAV Platform for DTM Creation. ISPRS Int. J. Geo-Inf. 2018, 7, 342. [Google Scholar] [CrossRef]
- Fuad, N.A.; Ismail, Z.; Majid, Z.; Darwin, N.; Ariff, M.F.M.; Idris, K.M.; Yusoff, A.R. Accuracy Evaluation of Digital Terrain Model Based on Different Flying Altitudes and Conditional of Terrain Using UAV LiDAR Technology. IOP Conf. Ser. Earth Environ. Sci. 2018, 169, 012100. [Google Scholar] [CrossRef]
- Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Flöry, S.; Nussbaumer, L. Concept and Performance Evaluation of a Novel UAV-Borne Topo-Bathymetric LiDAR Sensor. Remote Sens. 2020, 12, 28. [Google Scholar] [CrossRef]
- Dreier, A.; Kuhlmann, H.; Klingbeil, L. The Potential of UAV-Based Laser Scanning for Deformation Monitoring—Case Study on a Water Dam. In Proceedings of the 5th Joint International Symposium on Deformation Monitoring (JISDM), Valencia, Spain, 6–8 April 2022; 20–22 June 2022. [Google Scholar] [CrossRef]
- Li, Z.; Tan, J.; Liu, H. Rigorous Boresight Self-Calibration of Mobile and UAV LiDAR Scanning Systems by Strip Adjustment. Remote Sens. 2019, 11, 442. [Google Scholar] [CrossRef]
- Lv, J.; Xu, J.; Hu, K.; Liu, Y.; Zuo, X. Targetless Calibration of LiDAR-IMU System Based on Continuous-Time Batch Estimation. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 9968–9975. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Mandlburger, G. Rigorous Strip Adjustment of UAV-Based Laserscanning Data Including Time-Dependent Correction of Trajectory Errors. Photogramm. Eng. Remote Sens. 2016, 82, 945–954. [Google Scholar] [CrossRef]
- Yuan, W.; Choi, D.; Bolkas, D. GNSS-IMU-Assisted Colored ICP for UAV-LiDAR Point Cloud Registration of Peach Trees. Comput. Electron. Agric. 2022, 197, 106966. [Google Scholar] [CrossRef]
- Favalli, M.; Fornaciai, A.; Pareschi, M.T. LIDAR Strip Adjustment: Application to Volcanic Areas. Geomorphology 2009, 111, 123–135. [Google Scholar] [CrossRef]
- Gressin, A.; Mallet, C.; Demantké, J.Ô.; David, N. Towards 3D Lidar Point Cloud Registration Improvement Using Optimal Neighborhood Knowledge. ISPRS J. Photogramm. Remote Sens. 2013, 79, 240–251. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. Rigorous Strip Adjustment of Airborne Laserscanning Data Based on the Icp Algorithm. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 73–80. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. A Correspondence Framework for ALS Strip Adjustments Based on Variants of the ICP Algorithm. Photogramm. Fernerkund. Geoinf. 2015, 2015, 275–289. [Google Scholar] [CrossRef]
- Brun, A.; Cucci, D.A.; Skaloud, J. Lidar Point–to–Point Correspondences for Rigorous Registration of Kinematic Scanning in Dynamic Networks. ISPRS J. Photogramm. Remote Sens. 2022, 189, 185–200. [Google Scholar] [CrossRef]
- Kuçak, R.A.; Erol, S.; Erol, B. The Strip Adjustment of Mobile LiDAR Point Clouds Using Iterative Closest Point (ICP) Algorithm. Arab. J. Geosci. 2022, 15, 1017. [Google Scholar] [CrossRef]
- Csanyi, N.; Toth, C.K.; Grejner-Brzezinska, D.; Ray, J. Improvement of LiDAR Data Accuracy Using LiDAR Specific Ground Targets. In American Society for Photogrammetry and Remote Sensing-Annual Conference 2005-Geospatial Goes Global: From Your Neighborhood to the Whole Planet; American Society for Photogrammetry and Remote Sensing (ASPRS): Baton Rouge, LA, USA, 2005; Volume 1, pp. 152–162. [Google Scholar]
- Chen, Z.; Li, J.; Yang, B. A Strip Adjustment Method of Uav-Borne Lidar Point Cloud Based on Dem Features for Mountainous Area. Sensors 2021, 21, 2782. [Google Scholar] [CrossRef]
- Pentek, Q.; Kennel, P.; Allouis, T.; Fiorio, C.; Strauss, O. A Flexible Targetless LiDAR–GNSS/INS–Camera Calibration Method for UAV Platforms. ISPRS J. Photogramm. Remote Sens. 2020, 166, 294–307. [Google Scholar] [CrossRef]
- González-Aguilera, D.; Rodríguez-Gonzálvez, P.; Hernández-López, D.; Luis Lerma, J. A Robust and Hierarchical Approach for the Automatic Co-Registration of Intensity and Visible Images. Opt. Laser Technol. 2012, 44, 1915–1923. [Google Scholar] [CrossRef]
- Kim, H.; Correa, C.D.; Max, N. Automatic Registration of LiDAR and Optical Imagery Using Depth Map Stereo. In Proceedings of the 2014 IEEE International Conference on Computational Photography (ICCP), Santa Clara, CA, USA, 2–4 May 2014. [Google Scholar] [CrossRef]
- Lv, F.; Ren, K. Automatic Registration of Airborne LiDAR Point Cloud Data and Optical Imagery Depth Map Based on Line and Points Features. Infrared Phys. Technol. 2015, 71, 457–463. [Google Scholar] [CrossRef]
- Yang, B.; Chen, C. Automatic Registration of UAV-Borne Sequent Images and LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2015, 101, 262–274. [Google Scholar] [CrossRef]
- Mandlburger, G.; Wenzel, K.; Spitzer, A.; Haala, N.; Glira, P.; Pfeifer, N. Improved Topographic Models Via Concurrent Airborne Lidar and Dense Image Matching. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 259–266. [Google Scholar] [CrossRef]
- Li, J.; Yang, B.; Chen, C.; Habib, A. NRLI-UAV: Non-Rigid Registration of Sequential Raw Laser Scans and Images for Low-Cost UAV LiDAR Point Cloud Quality Improvement. ISPRS J. Photogramm. Remote Sens. 2019, 158, 123–145. [Google Scholar] [CrossRef]
- Toschi, I.; Farella, E.M.; Welponer, M.; Remondino, F. Quality-Based Registration Refinement of Airborne LiDAR and Photogrammetric Point Clouds. ISPRS J. Photogramm. Remote Sens. 2021, 172, 160–170. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Mandlburger, G. Hybrid Orientation of Airborne Lidar Point Clouds and Aerial Images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 567–574. [Google Scholar] [CrossRef]
- Haala, N.; Kölle, M.; Cramer, M.; Laupheimer, D.; Mandlburger, G.; Glira, P. Hybrid Georeferencing. Enhancement and Classification of Ultra-High Resolution Uav Lidar and Image Point Clouds for Monitoring Applications. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 727–734. [Google Scholar] [CrossRef]
- Haala, N.; Kölle, M.; Cramer, M.; Laupheimer, D.; Zimmermann, F. Hybrid Georeferencing of Images and LiDAR Data for UAV-Based Point Cloud Collection at Millimetre Accuracy. ISPRS Open J. Photogramm. Remote Sens. 2022, 4, 100014. [Google Scholar] [CrossRef]
- Cledat, E.; Skaloud, J. Fusion of Photo with Airborne Laser Scanning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 173–180. [Google Scholar] [CrossRef]
- Rzonca, A.; Majek, K. Lidarometry as a Variant of Integration of Photogrammetric and Laser Scanning Data. Meas. Autom. Monit. 2016, 62, 268–273. [Google Scholar]
- Rodríguez-Cielos, R.; Galán-García, J.L.; Padilla-Domínguez, Y.; Rodríguez-Cielos, P.; Bello-Patricio, A.B.; López-Medina, J.A. LiDARgrammetry: A New Method for Generating Synthetic Stereoscopic Products from Digital Elevation Models. Appl. Sci. 2017, 7, 906. [Google Scholar] [CrossRef]
- Teo, T.A.; Shih, T.Y.; Lin, Y.T.; Huang, C.M. The Generation of Inferred Stereo Images from Lidar Data. In Proceedings of the 31st Asian Conference on Remote Sensing, Hanoi, Vietnam, 1–5 November 2010; Volume 1, pp. 459–464.
- Fragkos, P.; Ioannidis, C. Assessment of Lidargrammetry for Spatial Data Extraction. Fourth Int. Conf. Remote Sens. Geoinf. Environ. 2016, 9688, 96881L. [Google Scholar] [CrossRef]
- Jayendra-Lakshman, M.; Devarajan, V. A New Feature Descriptor for Lidar Image Matching. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 157–162. [Google Scholar] [CrossRef]
- Jayendra-Lakshman, M. A NEW FEATURE DESCRIPTOR FOR LIDAR STRIP MATCHING. Remote Sens. Spat. Inf. Sci. 2014, II-2/W1, 157–162. [Google Scholar]
- Xianjia, Y.; Salimpour, S.; Queralta, J.P.; Westerlund, T. Analyzing General-Purpose Deep-Learning Detection and Segmentation Models with Images from a Lidar as a Camera Sensor. arXiv 2022, arXiv:2203.04064. [Google Scholar]
- Rzonca, A.; Twardowski, M. The Lidargrammetric Model Deformation Method for Altimetric UAV-ALS Data Enhancement. Remote Sens. 2022, 14, 6391. [Google Scholar] [CrossRef]
- Pargieła, K.; Rzonca, A.; Twardowski, M. The Utilization of Synthetic and Semisynthetic Point Clouds and Images for Testing Novel Approaches for Correcting Lidar Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII, 23–24. [Google Scholar] [CrossRef]
- www.agisoft.com Agisoft Mateshape. Available online: www.agisoftmetashape.com (accessed on 7 July 2025).
- www.cloudcompare.org Cloud Compare. Available online: https://www.cloudcompare.org/ (accessed on 7 July 2025).
Figure 1.
Diagram of the first phase of the processing: (a, b, f) input data, (c) data preparation, (d, e) lidargram generation and (g) matching and adjustment.
Figure 1.
Diagram of the first phase of the processing: (a, b, f) input data, (c) data preparation, (d, e) lidargram generation and (g) matching and adjustment.
Figure 2.
Diagram of the second phase of the processing: (g) matching and adjustment provides (h) adjusted EOPs; (d) virtual lidargrams and adjusted EOPs are used to (i) intersect transformed points; and (j) corrected LiDAR strips generation.
Figure 2.
Diagram of the second phase of the processing: (g) matching and adjustment provides (h) adjusted EOPs; (d) virtual lidargrams and adjusted EOPs are used to (i) intersect transformed points; and (j) corrected LiDAR strips generation.
Figure 3.
Synthetic data set—strip axis in red and distribution of GCPs.
Figure 3.
Synthetic data set—strip axis in red and distribution of GCPs.
Figure 4.
Kraków Centre semi-synthetic data set—strip footprints in red, GCPs in cyan and CHPs in orange.
Figure 4.
Kraków Centre semi-synthetic data set—strip footprints in red, GCPs in cyan and CHPs in orange.
Figure 5.
Two strips of real data.
Figure 5.
Two strips of real data.
Figure 7.
General workflow of the testing; Step 1: (a–e) all data deformation; Step 2: (f–h) back deformation; Step 3: (j) evaluation of the Step 1 deformation; Step 4: (i,k) evaluation of the back deformation.
Figure 7.
General workflow of the testing; Step 1: (a–e) all data deformation; Step 2: (f–h) back deformation; Step 3: (j) evaluation of the Step 1 deformation; Step 4: (i,k) evaluation of the back deformation.
Figure 8.
Sample of data for method evaluation.
Figure 8.
Sample of data for method evaluation.
Table 1.
Comparison of TerraSolid/TerraMatch methods and lidargrammetric method.
Table 1.
Comparison of TerraSolid/TerraMatch methods and lidargrammetric method.
| Parameter | Terrasolid/Terramatch | Pyligram |
|---|
| Input data | LiDAR strips | LiDAR strips/Vector data |
| Processing basic operation | Trajectory modification and point position recalculation | EOPs exchange
and point multi-intersection |
| Geometric representation | Trajectory-point rays | Central projection with ULPIs |
| Trajectory use | Yes | No |
| Levels of processing | Block/Strip/Point | Flexible point |
| Approach | LiDAR data processing | Image data processing |
| Degrees of freedom | All/selected by user | All |
| Ground control | XYZ Patches/XYZ GCPs | XYZ Patches/XYZ GCPs |
Table 2.
RMSE and MAX values a priori.
Table 2.
RMSE and MAX values a priori.
| | RMSE a Priori | Max Values a Priori |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.302 | 0.242 | 0.406 | 0.387 | 0.561 | 0.838 | 0.716 | 1.492 | 0.999 | 1.796 |
| 2 | 0.320 | 0.318 | 0.373 | 0.451 | 0.585 | 0.624 | 0.529 | 0.830 | 1.316 | 2.191 |
| 3 | 0.185 | 0.262 | 0.290 | 0.321 | 0.433 | 0.480 | 0.576 | 1.073 | 0.869 | 1.350 |
| 4 | 0.219 | 0.256 | 0.258 | 0.337 | 0.424 | 0.480 | 0.649 | 0.469 | 0.953 | 1.247 |
| 5 | 0.308 | 0.238 | 0.468 | 0.390 | 0.609 | 0.818 | 0.713 | 1.552 | 0.948 | 1.594 |
| Mean | 0.267 | 0.263 | 0.359 | 0.377 | 0.522 | 0.648 | 0.637 | 1.083 | 1.017 | 1.636 |
Table 3.
RMSE and MAX values after processing.
Table 3.
RMSE and MAX values after processing.
| | RMSE After Processing | Max Values After Processing |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.004 | 0.008 | 0.014 | 0.009 | 0.017 | 0.018 | 0.025 | 0.044 | 0.080 | 0.081 |
| 2 | 0.008 | 0.011 | 0.026 | 0.013 | 0.029 | 0.056 | 0.104 | 0.312 | 0.119 | 0.334 |
| 3 | 0.004 | 0.006 | 0.021 | 0.007 | 0.023 | 0.030 | 0.025 | 0.209 | 0.057 | 0.217 |
| 4 | 0.006 | 0.010 | 0.025 | 0.012 | 0.027 | 0.058 | 0.102 | 0.211 | 0.117 | 0.242 |
| 5 | 0.013 | 0.016 | 0.026 | 0.021 | 0.033 | 0.124 | 0.087 | 0.094 | 0.183 | 0.243 |
| Mean | 0.007 | 0.010 | 0.022 | 0.012 | 0.026 | 0.057 | 0.069 | 0.174 | 0.111 | 0.223 |
Table 4.
RMSE and MAX values a priori.
Table 4.
RMSE and MAX values a priori.
| | RMSE a Priori | Max Values a Priori |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.314 | 0.278 | 0.27 | 0.419 | 0.498 | 0.647 | 0.568 | 0.475 | 0.861 | 0.983 |
| 2 | 0.462 | 0.362 | 0.296 | 0.587 | 0.657 | 0.703 | 0.465 | 0.683 | 1.002 | 1.131 |
| 3 | 0.344 | 0.464 | 0.292 | 0.578 | 0.647 | 0.793 | 1.166 | 0.702 | 1.168 | 1.363 |
| Mean | 0.373 | 0.368 | 0.286 | 0.528 | 0.601 | 0.714 | 0.733 | 0.62 | 1.01 | 1.159 |
Table 5.
RMSE and MAX values after processing.
Table 5.
RMSE and MAX values after processing.
| | RMSE After Processing | Max Values After Processing |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.017 | 0.026 | 0.030 | 0.043 | 0.031 | 0.006 | 0.116 | 0.134 | 0.193 | 0.138 |
| 2 | 0.029 | 0.011 | 0.083 | 0.088 | 0.032 | 0.129 | 0.017 | 0.375 | 0.398 | 0.133 |
| 3 | 0.006 | 0.018 | 0.014 | 0.024 | 0.019 | 0.008 | 0.010 | 0.016 | 0.087 | 0.073 |
| Mean | 0.017 | 0.018 | 0.042 | 0.052 | 0.027 | 0.048 | 0.048 | 0.175 | 0.226 | 0.115 |
Table 6.
RMSE and MAX values a priori.
Table 6.
RMSE and MAX values a priori.
| | RMSE a Priori | Max Values a Priori |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.305 | 0.198 | 0.283 | 0.364 | 0.461 | 0.527 | 0.380 | 0.661 | 0.583 | 0.785 |
| 3 | 0.199 | 0.283 | 0.36 | 0.346 | 0.499 | 0.559 | 0.584 | 0.554 | 0.635 | 1.082 |
| Mean | 0.252 | 0.241 | 0.322 | 0.355 | 0.480 | 0.543 | 0.482 | 0.608 | 0.609 | 0.934 |
Table 7.
RMSE and MAX values after processing.
Table 7.
RMSE and MAX values after processing.
| | RMSE After Processing | Max Values After Processing |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| 1 | 0.001 | 0.001 | 0.001 | 0.001 | 0.002 | 0.002 | 0.002 | 0.004 | 0.002 | 0.004 |
| 3 | 0.003 | 0.006 | 0.005 | 0.006 | 0.008 | 0.006 | 0.018 | 0.013 | 0.019 | 0.023 |
| Mean | 0.002 | 0.004 | 0.003 | 0.004 | 0.005 | 0.004 | 0.01 | 0.009 | 0.011 | 0.014 |
Table 8.
RMSE and MAX values after processing—comparison of summary PyLiGram results with CloudCompare’s results.
Table 8.
RMSE and MAX values after processing—comparison of summary PyLiGram results with CloudCompare’s results.
| | RMSE After Processing | Max Values After Processing |
|---|
| Strip | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) | X (m) | Y (m) | Z (m) | XY (m) | XYZ (m) |
|---|
| Synthetic data |
| A priori | 0.267 | 0.263 | 0.359 | 0.377 | 0.522 | 0.648 | 0.637 | 1.083 | 1.017 | 1.636 |
| CC/ICP | 0.242 | 0.252 | 0.179 | 0.483 | 0.397 | 0.521 | 0.511 | 0.365 | 1.621 | 0.868 |
| PyLiGram | 0.007 | 0.010 | 0.022 | 0.012 | 0.026 | 0.057 | 0.069 | 0.174 | 0.111 | 0.223 |
| Semisynthetic data |
| A priori | 0.304 | 0.314 | 0.343 | 0.438 | 0.560 | 0.454 | 0.536 | 0.515 | 0.692 | 0.910 |
| CC/ICP | 0.290 | 0.289 | 0.398 | 0.413 | 0.576 | 0.269 | 0.226 | 0.367 | 0.541 | 0.798 |
| PyLiGram | 0.017 | 0.018 | 0.042 | 0.052 | 0.027 | 0.048 | 0.048 | 0.175 | 0.226 | 0.115 |
| Real data |
| A priori | 0.252 | 0.241 | 0.322 | 0.355 | 0.480 | 0.543 | 0.482 | 0.608 | 0.609 | 0.934 |
| CC/ICP | 0.202 | 0.310 | 0.507 | 0.370 | 0.632 | 0.400 | 0.558 | 0.456 | 0.671 | 0.908 |
| PyLiGram | 0.002 | 0.004 | 0.003 | 0.004 | 0.005 | 0.004 | 0.01 | 0.009 | 0.011 | 0.014 |
Table 9.
RMSE values reduction in %—summary PyLiGram results with CloudCompare’s results.
Table 9.
RMSE values reduction in %—summary PyLiGram results with CloudCompare’s results.
| | RMSE Reduction |
|---|
| Strip | X (%) | Y (%) | Z (%) | XY (%) | XYZ (%) |
|---|
| Synthetic data |
| CC/ICP | 90.6 | 95.8 | 49.9 | 128.1 | 76.1 |
| PyLiGram | 2.6 | 3.8 | 6.1 | 3.2 | 5.0 |
| Semisynthetic data |
| CC/ICP | 95.4 | 92.0 | 116.0 | 94.3 | 102.9 |
| PyLiGram | 5.6 | 5.7 | 12.2 | 11.9 | 4.8 |
| Real data |
| CC/ICP | 80.2 | 128.6 | 157.5 | 104.2 | 131.7 |
| PyLiGram | 0.8 | 1.7 | 0.9 | 1.1 | 1.0 |
Table 10.
Mean square differences of three methods of refinement.
Table 10.
Mean square differences of three methods of refinement.
| | Mean Square Differences |
|---|
| Process | dX (m) | dY (m) | dZ (m) | dXY (m) | dXYZ (m) |
|---|
| TerraScan/TerraMatch | 0.062 | 0.038 | 0.028 | 0.073 | 0.078 |
| PyLiGram PhaseOne | 0.077 | 0.074 | 0.083 | 0.107 | 0.136 |
| PyLiGram Trajectory | 0.098 | 0.103 | 0.075 | 0.143 | 0.161 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).