On-Orbit Calibration Method for Rotation Axis Misalignment in Rotating Mirror-Based Wide-Field Space Cameras
Abstract
1. Introduction
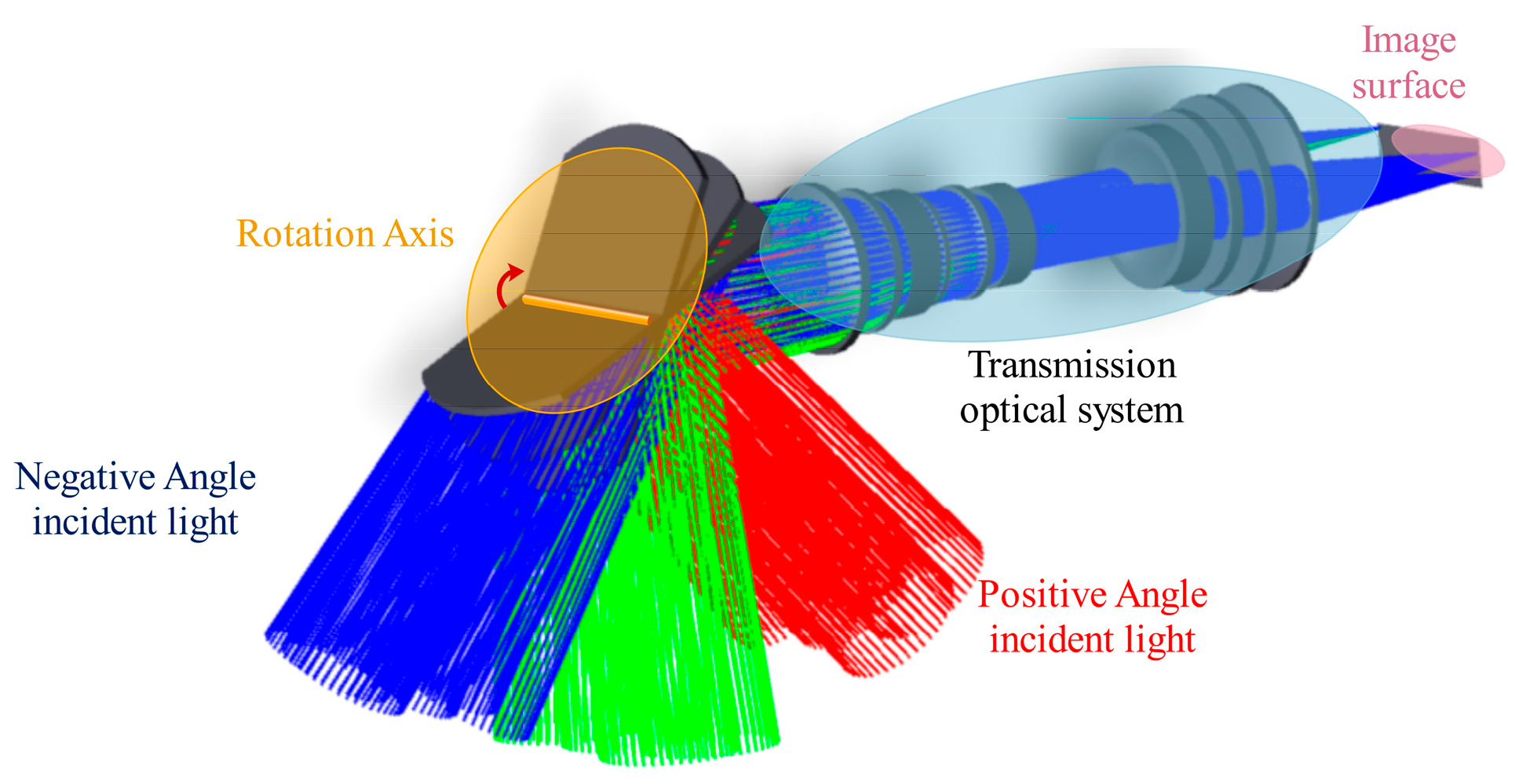
2. Imaging Mode of Rotating Mirror Wide-Field Space Camera
3. On-Orbit Calibration Method for Rotating Mirror Misalignment Based on Pointing Vector Equations
3.1. Actual Star Point Pointing Vector Model
3.2. Reference Star Pointing Vector Model
4. Simulation Analysis
4.1. Actual Star Vector Calculation
4.2. Reference Star Vector Calculation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fiete, R.D.; Tantalo, T. Comparison of snr image quality metrics for remote sensing systems. Opt. Eng. 2001, 40, 574–585. [Google Scholar] [CrossRef]
- Questad, E.J.; Antill, M.; Liu, N.; Stavros, E.N.; Townsend, P.A.; Bonfield, S.; Schimel, D. A camera-based method for collecting rapid vegetation data to support remote-sensing studies of shrubland biodiversity. Remote Sens. 2022, 14, 1933. [Google Scholar] [CrossRef]
- Meiner, H.; Stebner, K.; Kraft, T.; Gener, M.; Berger, R. Survey accuracy and spatial resolution benchmark of a camera system mounted on a fast flying drone. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 1, 261–268. [Google Scholar]
- Sun, Y.W.; Wei, Y.J.; Zhao, J. Adaptive design of long-focal-length freeform off-axis reflective space cameras with lightweight and integration of primary/tertiary mirror. Front. Phys. 2024, 12, 1481131. [Google Scholar] [CrossRef]
- Li, B.; Rui, X.T.; Wang, G.P. A simplified dynamic model and control for a multiple launch rocket system. J. Vib. Control 2022, 28, 2288–2300. [Google Scholar] [CrossRef]
- Tang, X.J.; Chen, D.K.; Xin, L.; Sun, Z.J.; Zhao, Z.Y.; Yan, Z.A.; Tian, X.; Li, X.Q. A dic method for thermal micro-deformation measurement of satellite high stability composite structure in simulated space environment. Opt. Lasers Eng. 2023, 169, 107722. [Google Scholar] [CrossRef]
- Kim, W.S.; Ansar, A.I.; Steele, R.D. Rover mast calibration, exact camera pointing, and camera handoff for visual target tracking. In Proceedings of the 12th International Conference on Advanced Robotics, Seattle, WA, USA, 17–20 July 2005; pp. 384–391. [Google Scholar]
- Chai, B.; Wei, Z.; Gao, Y. Calibration method of spatial transformations between the non-orthogonal two-axis turntable and its mounted camera. Opt. Express 2023, 31, 16952–16973. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Geneva, P.; Zuo, X.; Huang, G. Online self-calibration for visual-inertial navigation: Models, analysis, and degeneracy. IEEE Trans. Robot. 2023, 39, 3479–3498. [Google Scholar] [CrossRef]
- Cong Danh, N. The stability of a two-axis gimbal system for the camera. Sci. World J. 2021, 2021, 9958848. [Google Scholar] [CrossRef] [PubMed]
- Chustz, G.; Saripalli, S. Rooad: Rellis off-road odometry analysis dataset. In Proceedings of the 33rd IEEE Intelligent Vehicles Symposium (IEEE IV), Aachen, Germany, 5–9 June 2022; pp. 1504–1510. [Google Scholar]
- Wang, Y.; Jiang, W.-J. High precision attitude determination method for star camera based on ukf. Acta Photonica Sin. 2020, 49, 0128001. [Google Scholar] [CrossRef]
- Liu, J.; Cao, X.; Jia, X.; Ma, Y.; Li, G.; Li, T. Tool-free axis calibration method for self-rotating three-dimensional vision systems. Opt. Eng. 2023, 62, 114105. [Google Scholar] [CrossRef]
- Nissler, C.; Marton, Z.-C. Robot-to-camera calibration: A generic approach using 6d detections. In Proceedings of the 1st IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 10–12 April 2017; pp. 299–302. [Google Scholar]
- Liu, M.; Wang, H.; Wen, D.; Liu, J.; Xue, Y.; Liu, Y.; Zhao, H. A modified star map identification method suitable for astronomical camera. In Proceedings of the Conference on Applied Optics and Photonics (AOPC)—Image Processing and Analysis, Beijing, China, 5–7 May 2015. [Google Scholar]
- Liang, L.J.; Bo, Y.C.; Min, L. Low-error star pattern recognition based on point cloud matching algorithm. J. Phys. Conf. Ser. 2021, 1754, 012184. [Google Scholar] [CrossRef]
- Wei, F.; Gao, Y.; Wang, P. Research on star map matching algorithm based on image distance and image pose. J. Surv. Mapp. 2025, 50, 61–68. [Google Scholar]
- Chen, C.J.; Lin, P.D.; Jywe, W.Y. An optoelectronic measurement system for measuring 6-degree-of-freedom motion error of rotary parts. Opt. Express 2007, 15, 14601–14617. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Peng, Y.; Nie, D. A method for the installation measurement and alignment of a mirror unit in the solar dish concentrator. Appl. Sci. 2020, 10, 1511. [Google Scholar] [CrossRef]
- Cao, W.; Gorceix, N.; Coulter, R.; Coulter, A.; Goode, P.R. First light of the 1.6 meter off-axis new solar telescope at big bear solar observatory. Proc. SPIE Int. Soc. Opt. Eng. 2010, 7733, 773330–773338. [Google Scholar]
- Zheng, J.; Yan, J.; Pei, J.; Liu, G. Solar tracking error analysis of fresnel reflector. Sci. World J. 2014, 2014, 834392. [Google Scholar] [CrossRef] [PubMed]
- Lou, Z.-F.; Hao, X.-P.; Cai, Y.-D.; Lu, T.-F.; Wang, X.-D.; Fan, K.-C. An embedded sensor system for real-time detecting 5-dof error motions of rotary stages. Sensors 2019, 19, 2855. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.E.; McClelland, R.; Sayal, C.; Wilkin, P. Goes-13 stellar inertial attitude determination operational performance and impacts to overall image navigation and registration. In Proceedings of the 32nd Annual AAS Rocky Mountain Guidance and Control Conference, Breckenridge, CO, USA, 30 January–4 February 2009; p. 243. [Google Scholar]
- Kelly, P.L.; von der Linden, A.; Applegate, D.E.; Allen, M.T.; Allen, S.W.; Burchat, P.R.; Burke, D.L.; Ebeling, H.; Capak, P.; Czoske, O.; et al. Weighing the giants—Ii. Improved calibration of photometry from stellar colours and accurate photometric redshifts. Mon. Not. R. Astron. Soc. 2014, 439, 28–47. [Google Scholar] [CrossRef][Green Version]
- Lu, J.; Lei, C.; Liang, S.; Yang, Y. An all-parameter system-level calibration for stellar-inertial navigation system on ground. IEEE Trans. Instrum. Meas. 2017, 66, 2065–2073. [Google Scholar] [CrossRef]
- Xie, J.; Tang, H.; Dou, X.; Long, J. On-orbit calibration of domestic aps star tracker. In Proceedings of the 3rd International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014. [Google Scholar]
- Lv, Q.; An, X.; Wang, D.; Wu, J. Research on error online calibration method of inertial/stellar refraction integrated navigation system. In Proceedings of the China Satellite Navigation Conference (CSNC 2021) Proceedings, Nanchang, China, 22–25 May 2021. [Google Scholar]

















| Parameter | Value |
|---|---|
| Orbital Altitude | 500 km |
| Focal Length | 500 mm |
| Wavelength | 450 nm–800 nm |
| Resolution | 3.5 m |
| Field of View | 18° |
| F-number | 5 |
| Pixel Size | 3.5 μm |
| Integration Levels | 1–128 |
| Average Quantum Efficiency | 65% |
| Target Star | Right Ascension and Declination (Hour Angle) | Right Ascension and Declination (Degrees) |
|---|---|---|
| Star 1 | (18 h 00 m 00 s, −85°) | (270°, −85°) |
| Star 2 | (17 h 44 m 00 s, −88°) | (266°, −88°) |
| Star 3 | (18 h 12 m 00 s, −89.5°) | (273°, −89.5°) |
| Star 1 | Star 2 | Star 3 | ||
|---|---|---|---|---|
| Scanning Mirror Rotation Angle | 2.5° | 1° | 0.25° | |
| Celestial Coordinates of Virtual Object | RA | 270° | 270.139825° | 269.973828° |
| Dec | −10° | −3.995120° | −0.999315° | |
| Pixel Coordinates | (0, −25,189.6) | (348.6, −9977.3) | (−65.3, −2491.9) | |
| Star 1 | Star 2 | Star 3 | ||
|---|---|---|---|---|
| Scanning Mirror Rotation Angle | 2.5° | 1° | 0.25° | |
| Celestial Coordinates of Virtual Object | RA | 269.951194° | 270.094582° | 269.930266° |
| Dec | −10.029991° | −4.025219° | −1.029288° | |
| Pixel Coordinates | (−121.7, −25,266.7) | (235.8, −10,052.7) | (−173.9, −2566.6) | |
| X-Axis | Y-Axis | Z-Axis | |
|---|---|---|---|
| Preset Misalignment | 0.015° | 0.020° | −0.023° |
| Computed Misalignment of 3 Stars | 0.01503390° | 0.01990194° | −0.02311112° |
| Computed Misalignment of 4 Stars | 0.01503133° | 0.01998487° | −0.02313011° |
| Computed Misalignment of 1 Star | 0.11843954° | 3.37806788° | 3.46244602° |
| Misaligned Axis | Misalignment Amount | Star Point 1 | Star Point 2 | Star Point 3 |
|---|---|---|---|---|
| None | null | (0.0, −25,189.6) | (348.6, −9977.3) | (−65.3, −2491.9) |
| X-Axis | 20″ | (0.0, −25,218.2) | (348.6, −10,005.2) | (−65.3, −2519.6) |
| Y-Axis | 20″ | (−16.5, −25,189.6) | (333.8, −9977.4) | (−79.4, −2491.9) |
| Z-Axis | 20″ | (15.1, −25,189.6) | (363.0, −9977.3) | (−51.3, −2491.9) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Qiao, Y.; Guo, Z.; Wang, C.; Zhao, Y.; Zhang, Y.; Liu, C.; Kong, X. On-Orbit Calibration Method for Rotation Axis Misalignment in Rotating Mirror-Based Wide-Field Space Cameras. Remote Sens. 2025, 17, 2740. https://doi.org/10.3390/rs17152740
Zhang G, Qiao Y, Guo Z, Wang C, Zhao Y, Zhang Y, Liu C, Kong X. On-Orbit Calibration Method for Rotation Axis Misalignment in Rotating Mirror-Based Wide-Field Space Cameras. Remote Sensing. 2025; 17(15):2740. https://doi.org/10.3390/rs17152740
Chicago/Turabian StyleZhang, Guoxiu, Yishi Qiao, Zhenyuan Guo, Chen Wang, Yingming Zhao, Yuxin Zhang, Chunyu Liu, and Xianren Kong. 2025. "On-Orbit Calibration Method for Rotation Axis Misalignment in Rotating Mirror-Based Wide-Field Space Cameras" Remote Sensing 17, no. 15: 2740. https://doi.org/10.3390/rs17152740
APA StyleZhang, G., Qiao, Y., Guo, Z., Wang, C., Zhao, Y., Zhang, Y., Liu, C., & Kong, X. (2025). On-Orbit Calibration Method for Rotation Axis Misalignment in Rotating Mirror-Based Wide-Field Space Cameras. Remote Sensing, 17(15), 2740. https://doi.org/10.3390/rs17152740






