Improved Photosynthetic Accumulation Models for Biomass Estimation of Soybean and Cotton Using Vegetation Indices and Canopy Height
Abstract
1. Introduction
2. Materials
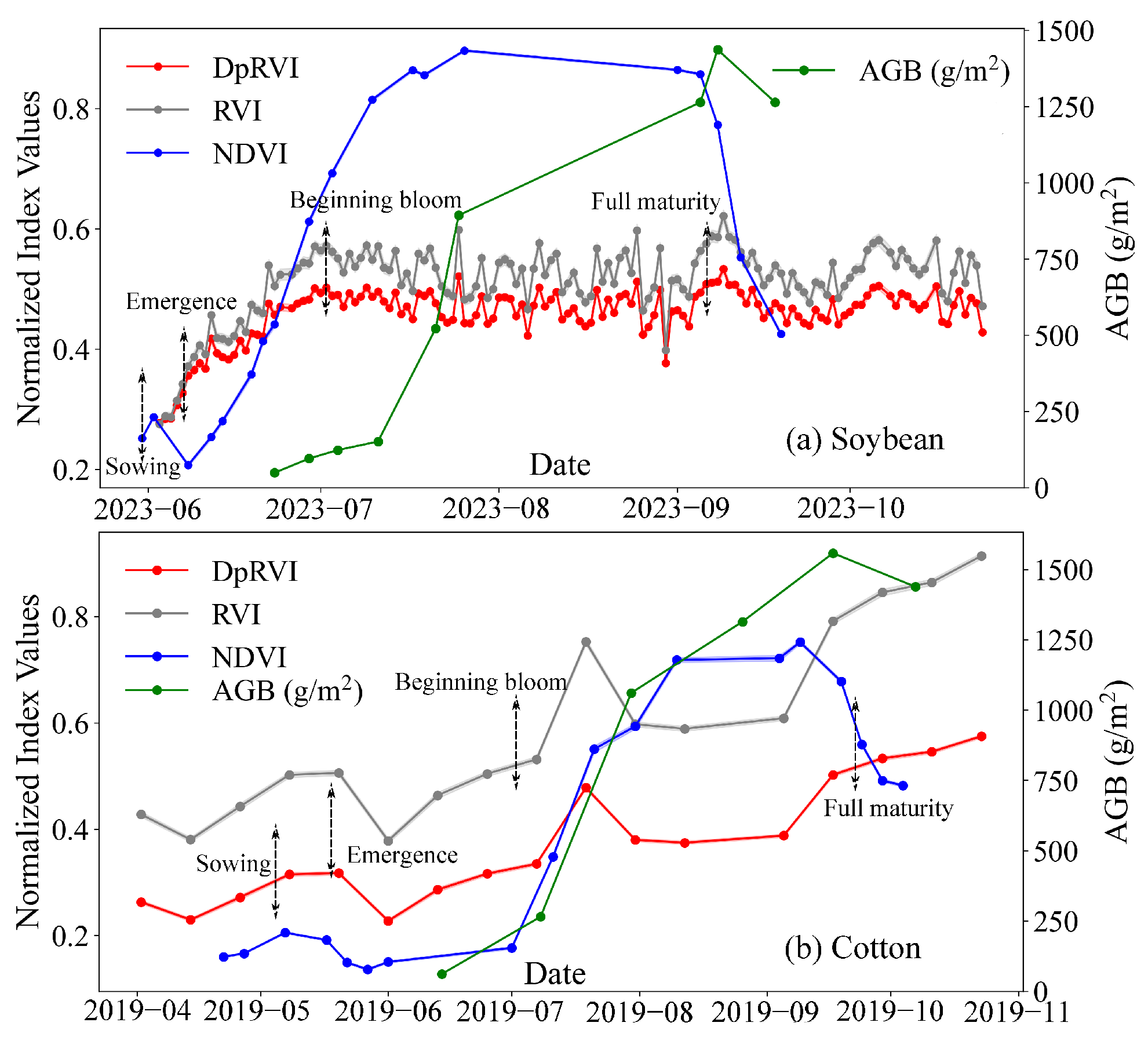
2.1. Test Site 1: Soybean
2.2. Test Site 2: Cotton
3. Methods
3.1. Introduction of Optical VIs
3.2. Photosynthesis-Based AGB Modeling in the PAM Framework
3.3. PAM Implementation and IPAM Improvements
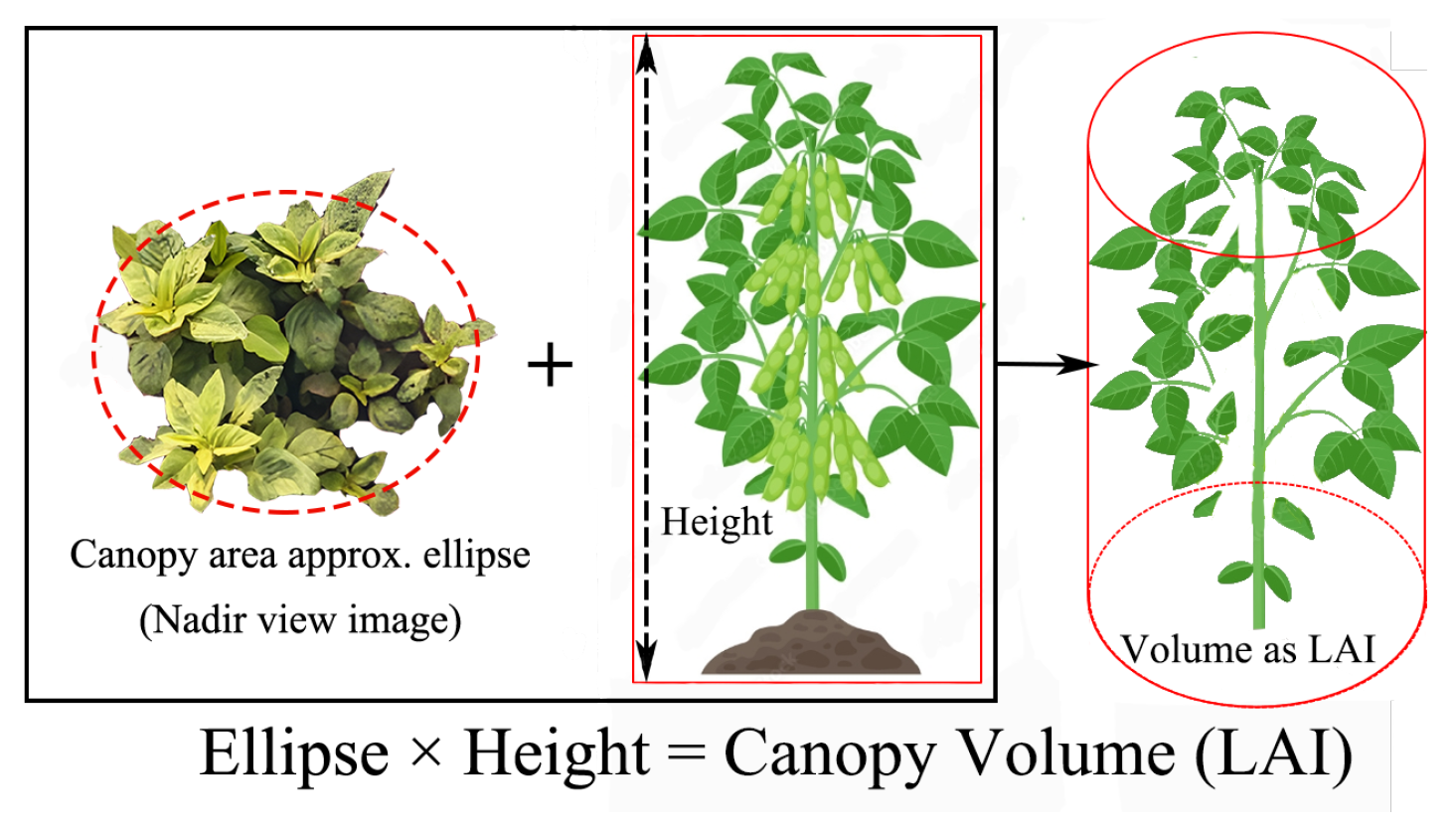
3.3.1. Numerical Integration
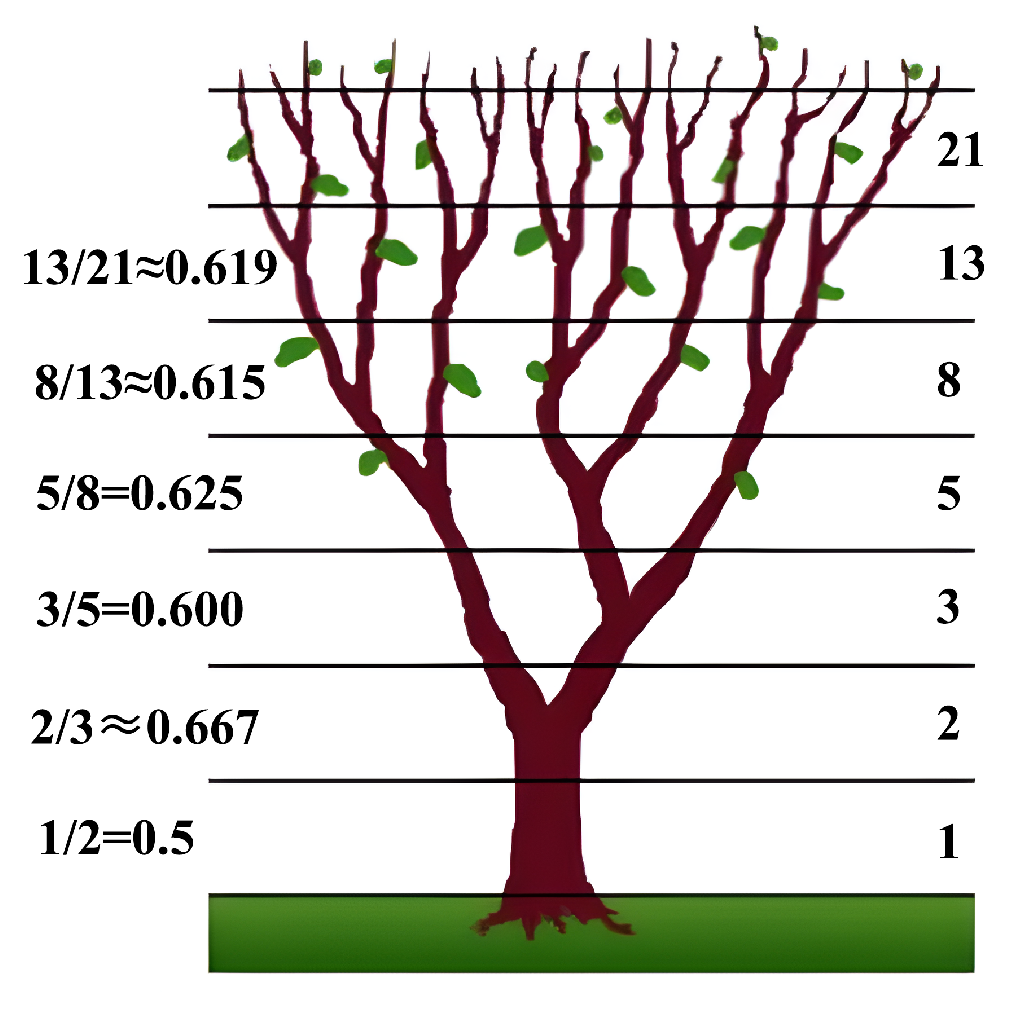
3.3.2. Fibonacci Sequence Correction Method
3.3.3. Non-Photosynthesis Area Mask
4. Results
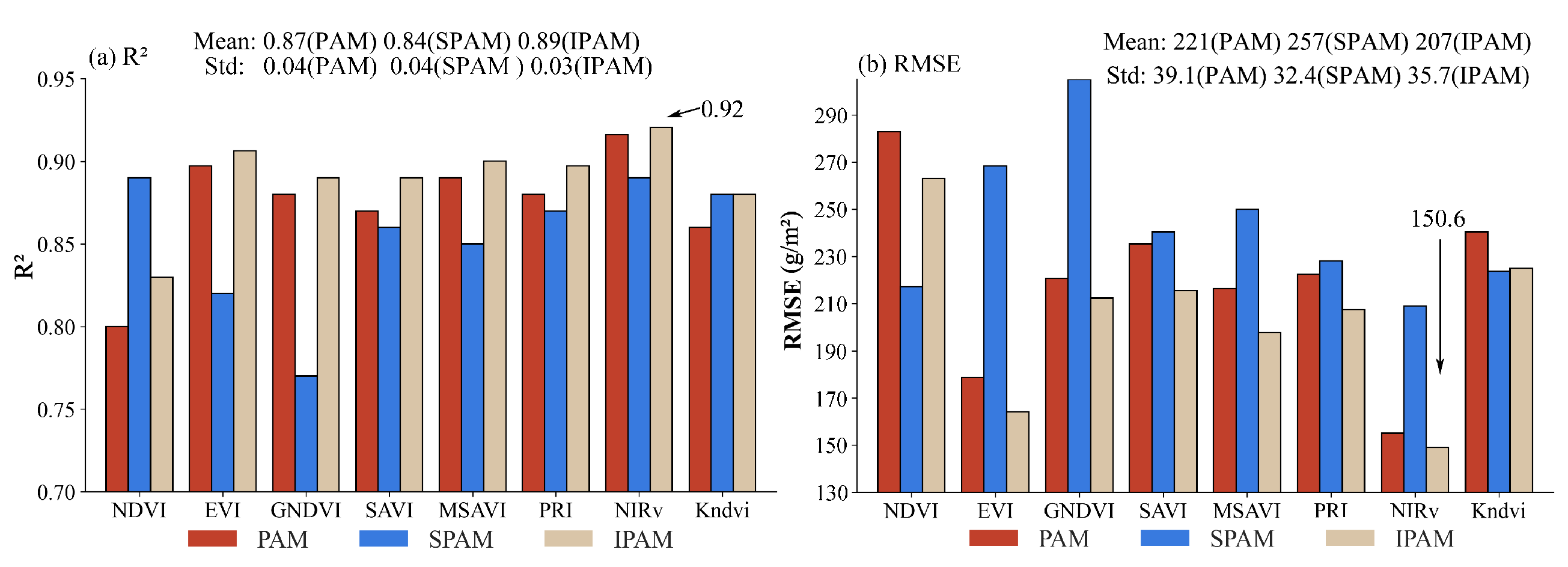
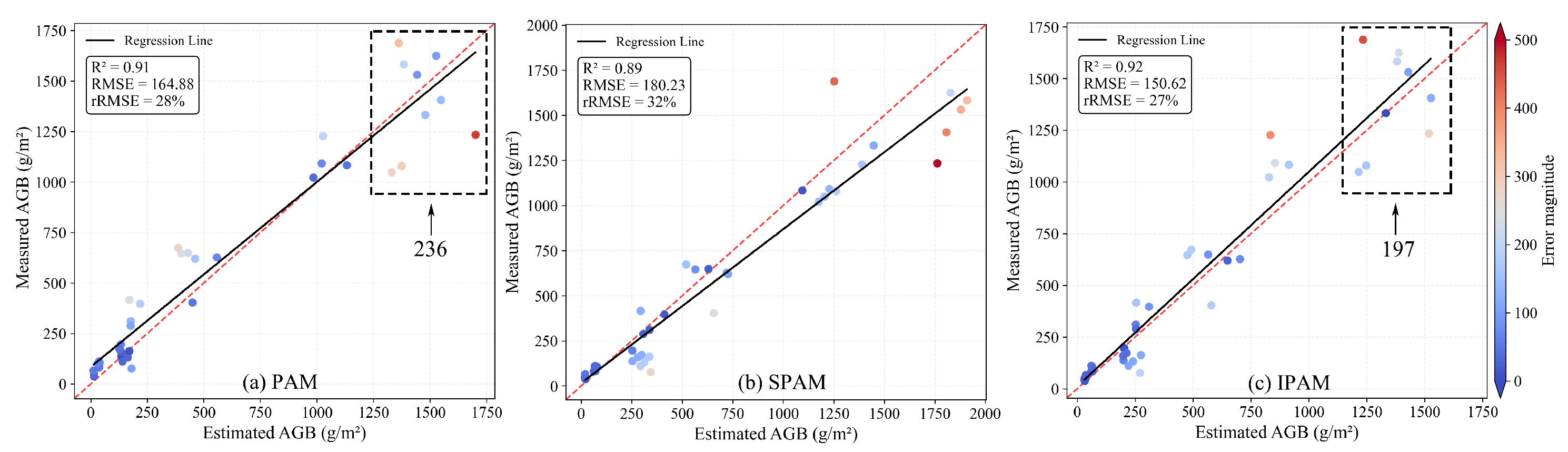
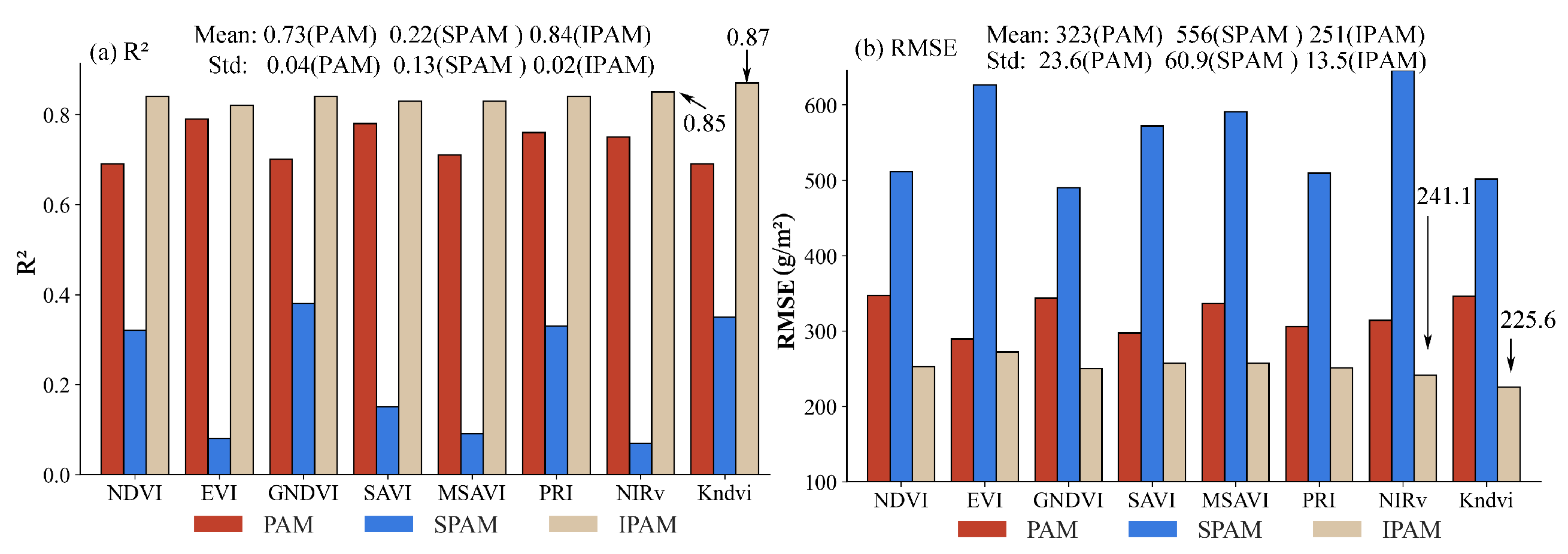
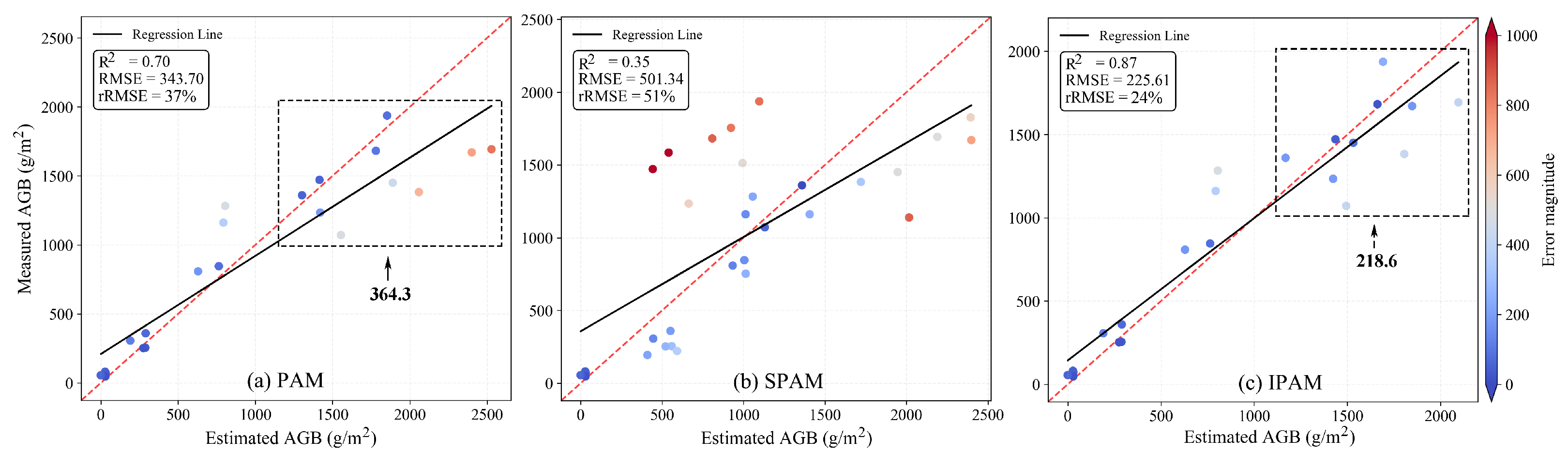
4.1. Soybean AGB Result from PAM, SPAM, and IPAM
4.2. Cotton AGB Results from PAM, SPAM, and IPAM
5. Discussion
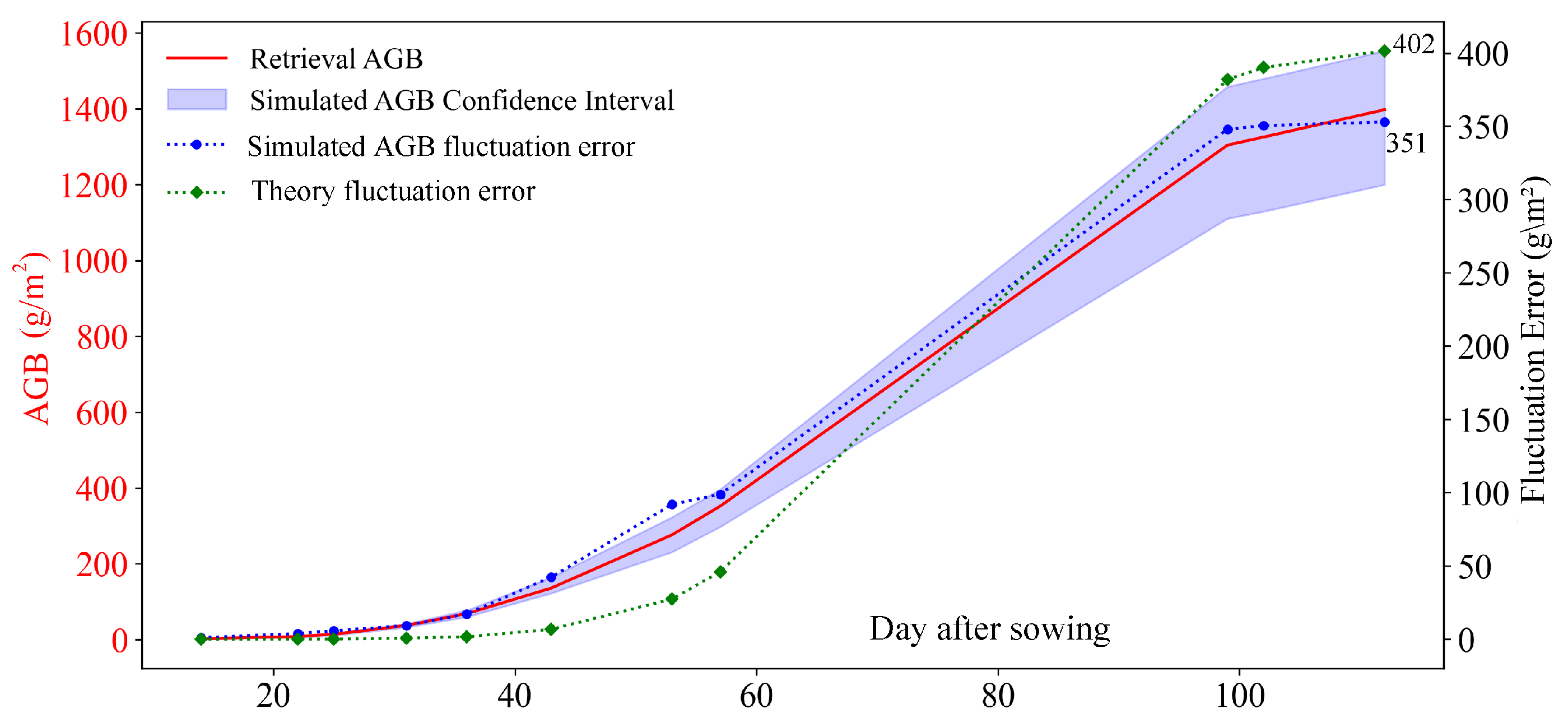
5.1. Deviation Analysis of IPAM
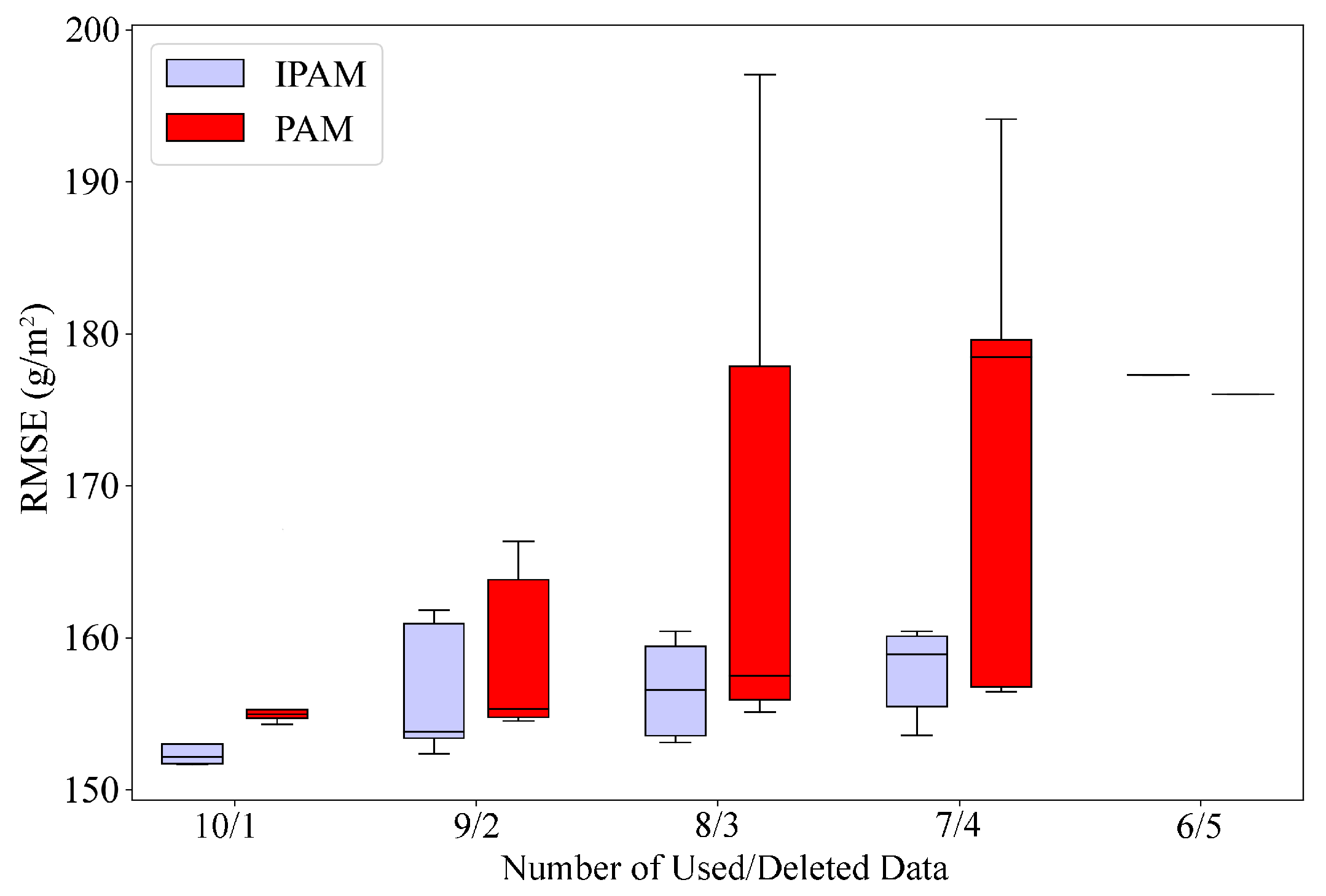
5.2. Data Reduction Impact on Model Performance
5.3. Feasibility of IPAM for Height-Free and Data-Limited Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Chao, Z.; Liu, N.; Zhang, P.; Ying, T.; Song, K. Estimation methods developing with remote sensing information for energy crop biomass: A comparative review. Biomass Bioenergy 2019, 122, 414–425. [Google Scholar] [CrossRef]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dejoux, J.F.; Huc, M.; Keravec, P.; Béziat, P.; et al. Maize and sunflower biomass estimation in southwest France using high spatial and temporal resolution remote sensing data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef]
- She, W.; Wu, Y.; Huang, H.; Chen, Z.; Cui, G.; Zheng, H.; Guan, C.; Chen, F. Integrative analysis of carbon structure and carbon sink function for major crop production in China’s typical agriculture regions. J. Clean. Prod. 2017, 162, 702–708. [Google Scholar] [CrossRef]
- G. Poley, L.; J. McDermid, G. A systematic review of the factors influencing the estimation of vegetation aboveground biomass using unmanned aerial systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
- Steffen, W.; Richardson, K.; Rockström, J.; Schellnhuber, H.J.; Dube, O.P.; Dutreuil, S.; Lenton, T.M.; Lubchenco, J. The emergence and evolution of Earth System Science. Nat. Rev. Earth Environ. 2020, 1, 54–63. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of remote sensing in precision agriculture: A review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Huete, A.; Dechant, B.; Berry, J.; Chen, J.M.; Joiner, J.; Frankenberg, C.; Bond-Lamberty, B.; Ryu, Y.; et al. Optical vegetation indices for monitoring terrestrial ecosystems globally. Nat. Rev. Earth Environ. 2022, 3, 477–493. [Google Scholar] [CrossRef]
- Anderson, G.L.; Hanson, J.D.; Haas, R.H. Evaluating Landsat Thematic Mapper derived vegetation indices for estimating above-ground biomass on semiarid rangelands. Remote Sens. Environ. 1993, 45, 165–175. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Dong, T.; Shang, J.; Liu, J.; Song, Y. Using spatio-temporal fusion of Landsat-8 and MODIS data to derive phenology, biomass and yield estimates for corn and soybean. Sci. Total Environ. 2019, 650, 1707–1721. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Saatchi, S. Sensitivity of L-band SAR backscatter to aboveground biomass of global forests. Remote Sens. 2016, 8, 522. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, 111954. [Google Scholar] [CrossRef]
- Walter, J.D.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating biomass and canopy height with LiDAR for field crop breeding. Front. Plant Sci. 2019, 10, 473161. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Anderson, K.E.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K.; Derryberry, D.R. Estimating vegetation biomass and cover across large plots in shrub and grass dominated drylands using terrestrial lidar and machine learning. Ecol. Indic. 2018, 84, 793–802. [Google Scholar] [CrossRef]
- Li, N.; Lopez-Sanchez, J.M.; Fu, H.; Zhu, J.; Han, W.; Xie, Q.; Hu, J.; Xie, Y. Rice crop height inversion from TanDEM-X PolInSAR data using the RVoG model combined with the logistic growth equation. Remote Sens. 2022, 14, 5109. [Google Scholar] [CrossRef]
- Romero-Puig, N.; Marino, A.; Lopez-Sanchez, J.M. Application of the trace coherence to HH-VV PolInSAR TanDEM-X data for vegetation height estimation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4404210. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimates of tropical mangrove forest using Sentinel-1 SAR coherence data-The superiority of deep learning over a semi-empirical model. Comput. Geosci. 2021, 150, 104737. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Zhao, K.; Valle, D.; Popescu, S.; Zhang, X.; Mallick, B. Hyperspectral remote sensing of plant biochemistry using Bayesian model averaging with variable and band selection. Remote Sens. Environ. 2013, 132, 102–119. [Google Scholar] [CrossRef]
- Chi, D.; Wang, H.; Li, X.; Liu, H.; Li, X. Assessing the effects of grazing on variations of vegetation NPP in the Xilingol Grassland, China, using a grazing pressure index. Ecol. Indic. 2018, 88, 372–383. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276, 107609. [Google Scholar] [CrossRef]
- Perry, E.M.; Morse-McNabb, E.M.; Nuttall, J.G.; O’Leary, G.J.; Clark, R. Managing wheat from space: Linking MODIS NDVI and crop models for predicting australian dryland wheat biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3724–3731. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Watson, D. The dependence of net assimilation rate on leaf-area index. Ann. Bot. 1958, 22, 37–54. [Google Scholar] [CrossRef]
- Heyneke, E.; Fernie, A.R. Metabolic regulation of photosynthesis. Biochem. Soc. Trans. 2018, 46, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Mo, J.; Luo, S.; Peng, Y.; Fang, S.; Wu, X.; Zhu, R.; Li, Y.; Yuan, N.; Zhou, C.; et al. Estimation of rice aboveground biomass by UAV imagery with photosynthetic accumulation models. Plant Phenomics 2023, 5, 0056. [Google Scholar] [CrossRef]
- Aguasca, A.; Broquetas, A.; Biscamps, J.; Fàbregas, X.; Llop, J.; Mallorquí, J.J.; Mas, M.; Palacio, H. Hydrosoil Campaign Final Report. 2021. Available online: https://earth.esa.int/eogateway/documents/d/earth-online/hydrosoil-campaign-final-report-pdf (accessed on 4 August 2025).
- Mas, M.; Aguasca, A.; Broquetas, A.; Fàbregas, X.; Mallorquí, J.J.; Llop, J.; Lopez-Sanchez, J.M.; Kubanek, J. Facility for continuous agricultural field monitoring with a GB-PolSAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11866–11876. [Google Scholar] [CrossRef]
- Aguasca, A.; Broquetas, A.; Lopez-Sanchez, J.M.; Fàbregas, X.; Mallorquí, J.J.; Mas, M. Assessment of the impact of long integration time in Geosynchronous SAR imagery of agricultural fields by means of GB-SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 1338–1347. [Google Scholar] [CrossRef]
- Coffin, A.W.; Cosh, M.H.; Pisarello, K. Two Years of Cotton (Gossypium hirsutum L.) Data from the Georgia Coastal Plain, USA. Sci. Data 2024, 11, 1037. [Google Scholar] [CrossRef] [PubMed]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Kim, J.; Hogue, T.S. Improving spatial soil moisture representation through integration of AMSR-E and MODIS products. IEEE Trans. Geosci. Remote Sens. 2011, 50, 446–460. [Google Scholar] [CrossRef]
- Bannari, A.; Khurshid, K.S.; Staenz, K.; Schwarz, J.W. A comparison of hyperspectral chlorophyll indices for wheat crop chlorophyll content estimation using laboratory reflectance measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3063–3074. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, S.; Qin, W.; Yan, G.; Gastellu-Etchegorry, J.P.; Cao, L.; Murefu, M.; Li, J.; Han, B. Potentials and limits of vegetation indices with brdf signatures for soil-noise resistance and estimation of leaf area index. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5092–5108. [Google Scholar] [CrossRef]
- Berni, J.A.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Li, D.; Chen, J.M.; Zhang, X.; Yan, Y.; Zhu, J.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; et al. Improved estimation of leaf chlorophyll content of row crops from canopy reflectance spectra through minimizing canopy structural effects and optimizing off-noon observation time. Remote Sens. Environ. 2020, 248, 111985. [Google Scholar] [CrossRef]
- Wang, D.; Fahad, S.; Saud, S.; Kamran, M.; Khan, A.; Khan, M.N.; Hammad, H.M.; Nasim, W. Morphological acclimation to agronomic manipulation in leaf dispersion and orientation to promote “Ideotype” breeding: Evidence from 3D visual modeling of “super” rice (Oryza sativa L.). Plant Physiol. Biochem. 2019, 135, 499–510. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Deng, L.; Lu, H. An improved LAI estimation method incorporating with growth characteristics of field-grown wheat. Remote Sens. 2022, 14, 4013. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Yang, C.; Xie, T.; Jiang, Z.; Hu, T.; Luo, Z.; Zhou, G.; Xie, J. Assessing the effect of real spatial resolution of in situ UAV multispectral images on seedling rapeseed growth monitoring. Remote Sens. 2020, 12, 1207. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 10th ed.; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Thompson, D.W. On Growth and Form, 2nd ed.; Dover Publications: Mineola, NY, USA, 1992; p. 1116. [Google Scholar]
- Boman, B.M.; Dinh, T.; Decker, K.; Emerick, B.; Raymond, C.; Schleiniger, G. Why do fibonacci numbers appear in patterns of growth in nature. Fib. Q. 2017, 55, 30–41. [Google Scholar] [CrossRef]
- Maselli, F.; Gilabert, M.A.; Conese, C. Integration of high and low resolution NDVI data for monitoring vegetation in Mediterranean environments. Remote Sens. Environ. 1998, 63, 208–218. [Google Scholar] [CrossRef]
- Qiao, L.; Gao, D.; Zhao, R.; Tang, W.; An, L.; Li, M.; Sun, H. Improving estimation of LAI dynamic by fusion of morphological and vegetation indices based on UAV imagery. Comput. Electron. Agric. 2022, 192, 106603. [Google Scholar] [CrossRef]
- Qiao, L.; Gao, D.; Zhang, J.; Li, M.; Sun, H.; Ma, J. Dynamic influence elimination and chlorophyll content diagnosis of maize using UAV spectral imagery. Remote Sens. 2020, 12, 2650. [Google Scholar] [CrossRef]
- Meiyan, S.; Mengyuan, S.; Qizhou, D.; Xiaohong, Y.; Baoguo, L.; Yuntao, M. Estimating the maize above-ground biomass by constructing the tridimensional concept model based on UAV-based digital and multi-spectral images. Field Crop. Res. 2022, 282, 108491. [Google Scholar] [CrossRef]
- Gaso, D.V.; de Wit, A.; Berger, A.G.; Kooistra, L. Predicting within-field soybean yield variability by coupling Sentinel-2 leaf area index with a crop growth model. Agric. For. Meteorol. 2021, 308, 108553. [Google Scholar] [CrossRef]
- Heuvelink, G.B.; Burrough, P.A.; Stein, A. Propagation of errors in spatial modelling with GIS. Int. J. Geogr. Inf. Syst. 1989, 3, 303–322. [Google Scholar] [CrossRef]
- Xie, T.; Li, J.; Yang, C.; Jiang, Z.; Chen, Y.; Guo, L.; Zhang, J. Crop height estimation based on UAV images: Methods, errors, and strategies. Comput. Electron. Agric. 2021, 185, 106155. [Google Scholar] [CrossRef]
- Fei, S.; Xiao, S.; Li, Q.; Shu, M.; Zhai, W.; Xiao, Y.; Chen, Z.; Yu, H.; Ma, Y. Enhancing leaf area index and biomass estimation in maize with feature augmentation from unmanned aerial vehicle-based nadir and cross-circling oblique photography. Comput. Electron. Agric. 2023, 215, 108462. [Google Scholar] [CrossRef]
- Zhang, L.; Grift, T.E. A LIDAR-based crop height measurement system for Miscanthus giganteus. Comput. Electron. Agric. 2012, 85, 70–76. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Erten, E.; Campos-Taberner, M.; Garcia-Haro, F.J. Retrieval of vegetation height in rice fields using polarimetric SAR interferometry with TanDEM-X data. Remote Sens. Environ. 2017, 192, 30–44. [Google Scholar] [CrossRef]
- Trudel, M.; Charbonneau, F.; Leconte, R. Using RADARSAT-2 polarimetric and ENVISAT-ASAR dual-polarization data for estimating soil moisture over agricultural fields. Can. J. Remote Sens. 2012, 38, 514–527. [Google Scholar]
- Bhogapurapu, N.; Dey, S.; Mandal, D.; Bhattacharya, A.; Karthikeyan, L.; McNairn, H.; Rao, Y. Soil moisture retrieval over croplands using dual-pol L-band GRD SAR data. Remote Sens. Environ. 2022, 271, 112900. [Google Scholar] [CrossRef]
- Gonenc, A.; Ozerdem, M.S.; Acar, E. Comparison of NDVI and RVI vegetation indices using satellite images. In Proceedings of the 2019 8th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Istanbul, Turkey, 16–19 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Mandal, D.; Kumar, V.; Ratha, D.; Lopez-Sanchez, J.M.; Bhattacharya, A.; McNairn, H.; Rao, Y.S.; Ramana, K. Assessment of rice growth conditions in a semi-arid region of India using the Generalized Radar Vegetation Index derived from RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2020, 237, 111561. [Google Scholar] [CrossRef]
- Hu, X.; Li, L.; Huang, J.; Zeng, Y.; Zhang, S.; Su, Y.; Hong, Y.; Hong, Z. Radar vegetation indices for monitoring surface vegetation: Developments, challenges, and trends. Sci. Total Environ. 2024, 945, 173974. [Google Scholar] [CrossRef]

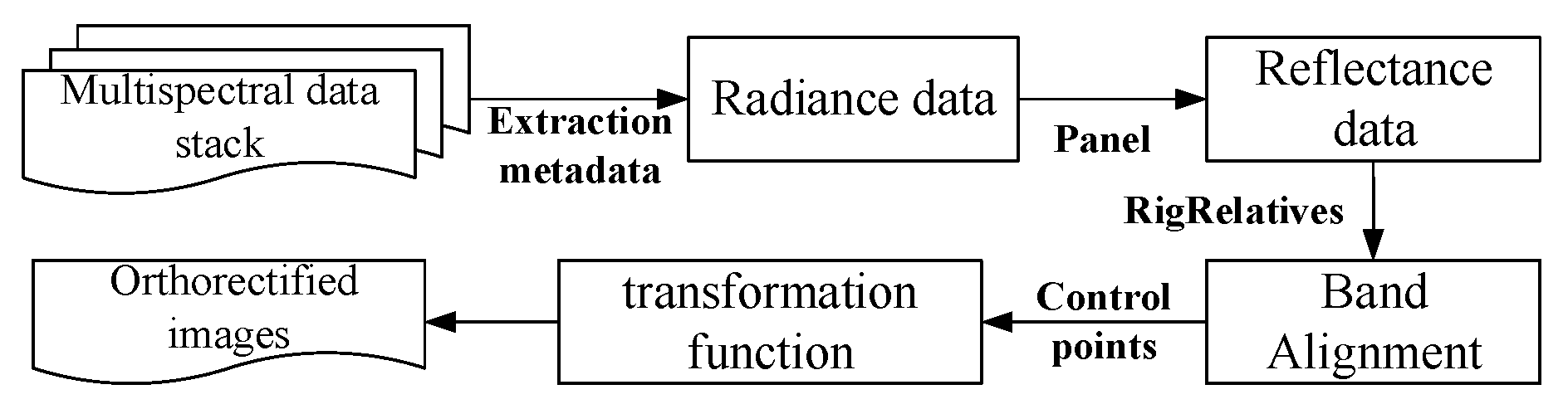
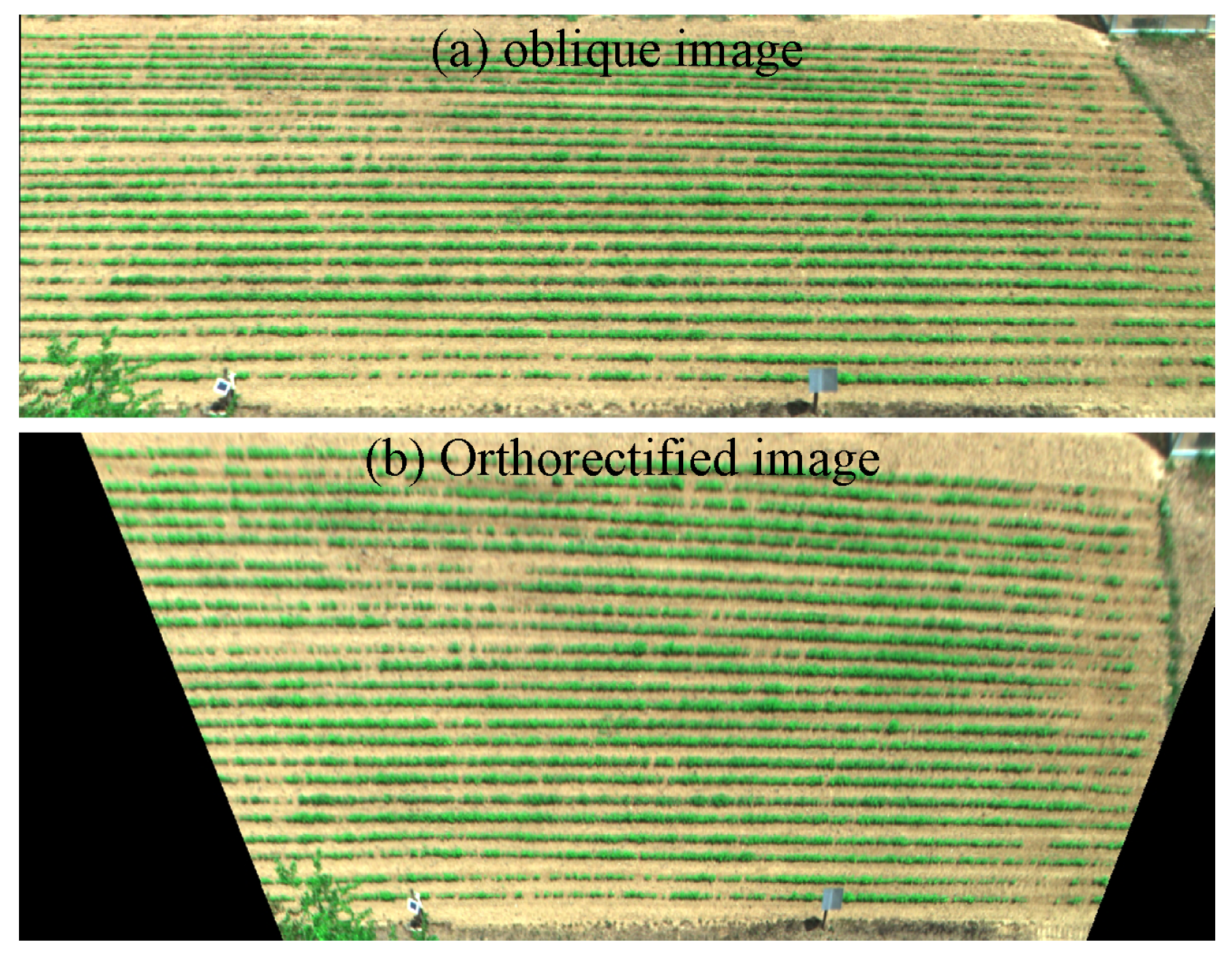
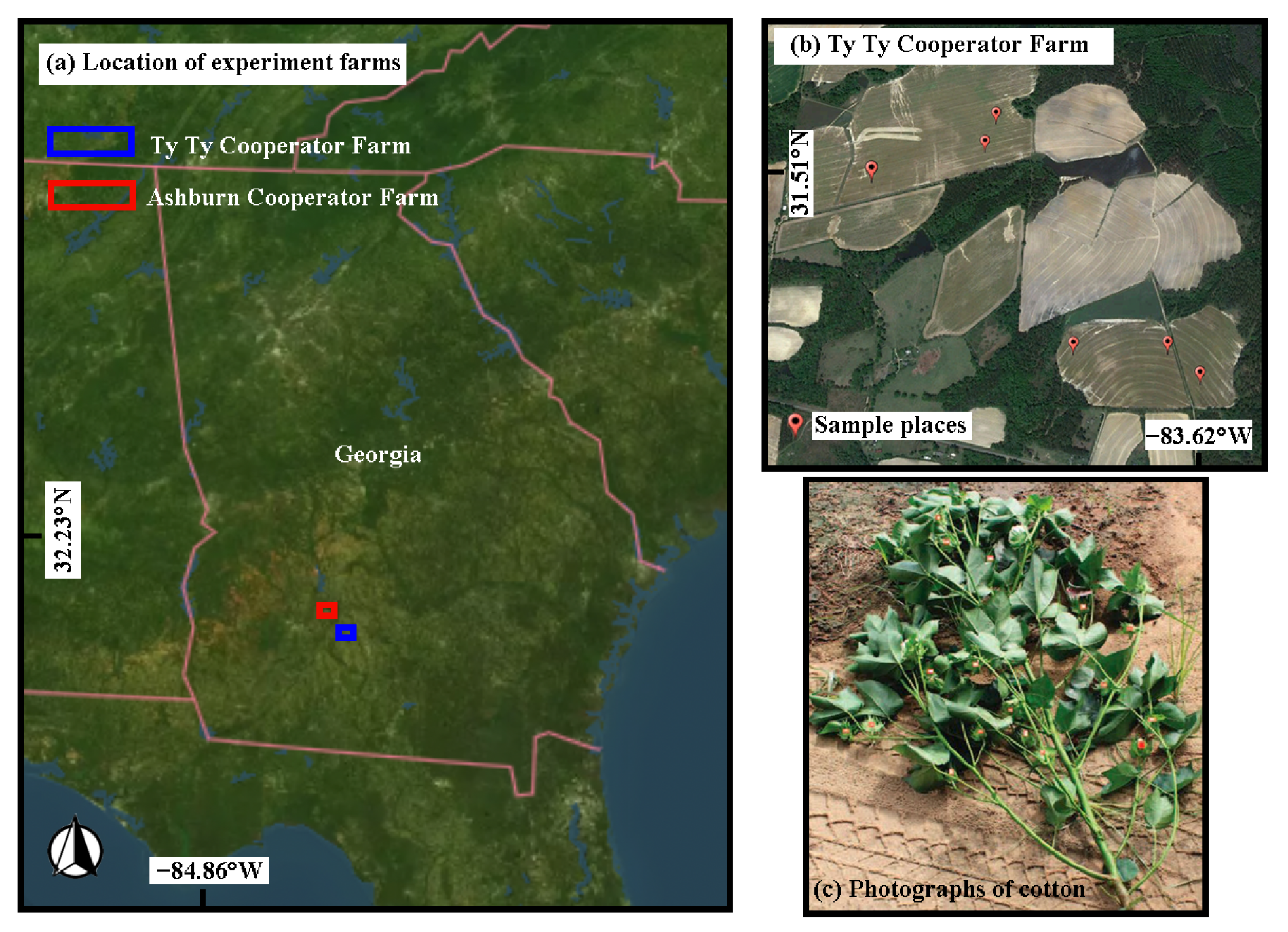
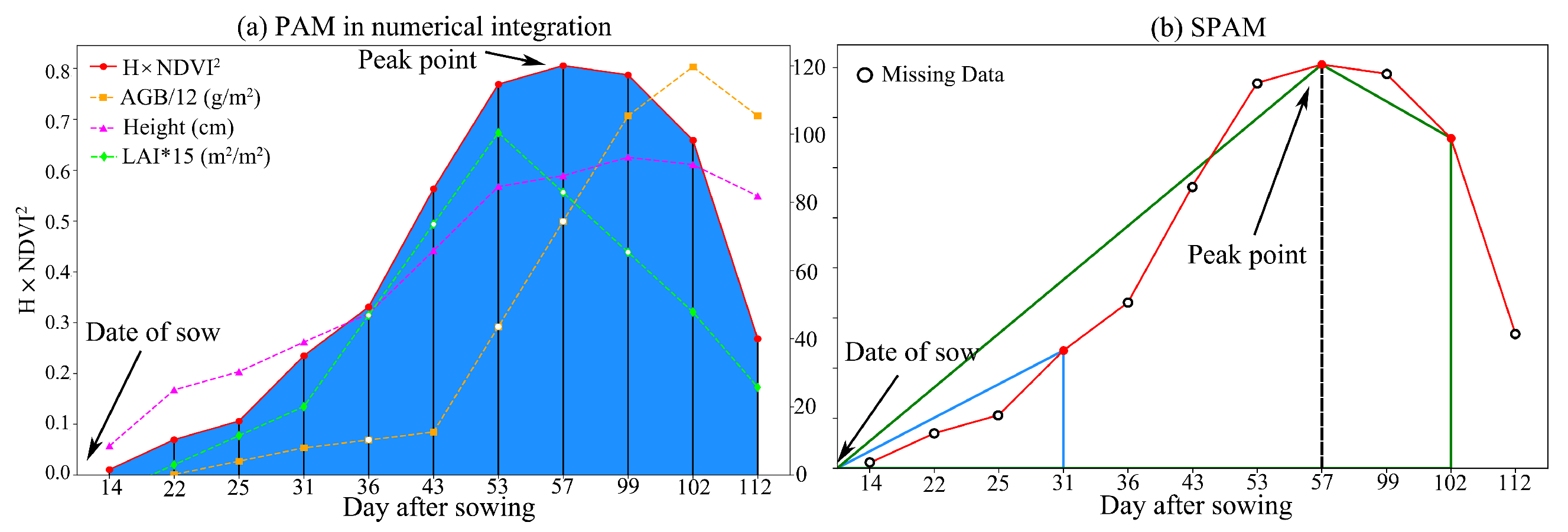
| Time | Type of Crop | Data | Data Acquisition Time |
|---|---|---|---|
| 30 May 2023–September 2023 | Soybean | MS Data | 14, 22, 25, 31, 36, 43, 49, 53, 58, 99, 102, 112 |
| Height | 14, 16, 22, 25, 31, 36, 43, 49, 53, 57, 60, 99, 102, 112 | ||
| LAI | 16, 25, 31, 46, 53, 60, 102, 112 | ||
| AGB | 25, 31, 43, 46, 60, 99, 102, 112 | ||
| 13 May 2019–October 2019 | Cotton | Sentinel 2 Data | 34, 59, 79, 109, 129, 149 |
| AGB, Height | 32, 56, 78, 105, 127, 147 |
| VIs | Formula |
|---|---|
| NDVI | |
| EVI | |
| GNDVI | |
| SAVI | |
| MSAVI | |
| PRI | |
| NIRv | |
| Kndvi |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Mallorqui, J.J.; Aguasca, A.; Fàbregas, X.; Broquetas, A.; Llop, J.; Mas, M.; Zhao, F.; Wang, Y. Improved Photosynthetic Accumulation Models for Biomass Estimation of Soybean and Cotton Using Vegetation Indices and Canopy Height. Remote Sens. 2025, 17, 2736. https://doi.org/10.3390/rs17152736
Liu J, Mallorqui JJ, Aguasca A, Fàbregas X, Broquetas A, Llop J, Mas M, Zhao F, Wang Y. Improved Photosynthetic Accumulation Models for Biomass Estimation of Soybean and Cotton Using Vegetation Indices and Canopy Height. Remote Sensing. 2025; 17(15):2736. https://doi.org/10.3390/rs17152736
Chicago/Turabian StyleLiu, Jinglong, Jordi J. Mallorqui, Albert Aguasca, Xavier Fàbregas, Antoni Broquetas, Jordi Llop, Mireia Mas, Feng Zhao, and Yanan Wang. 2025. "Improved Photosynthetic Accumulation Models for Biomass Estimation of Soybean and Cotton Using Vegetation Indices and Canopy Height" Remote Sensing 17, no. 15: 2736. https://doi.org/10.3390/rs17152736
APA StyleLiu, J., Mallorqui, J. J., Aguasca, A., Fàbregas, X., Broquetas, A., Llop, J., Mas, M., Zhao, F., & Wang, Y. (2025). Improved Photosynthetic Accumulation Models for Biomass Estimation of Soybean and Cotton Using Vegetation Indices and Canopy Height. Remote Sensing, 17(15), 2736. https://doi.org/10.3390/rs17152736






