Robust Adaptive Multiple Backtracking VBKF for In-Motion Alignment of Low-Cost SINS/GNSS
Abstract
1. Introduction
- Observation and reference vectors are constructed using the sliding window method to mitigate the accumulation of sensor errors. A weighting function is designed using a magnitude matching method to reconstruct the observation vector, enabling the detection and isolation of outliers.
- An adaptive window adjustment multiple backtracking approach is proposed to effectively utilize navigation data and significantly shorten alignment time in complex environments. This approach intelligently determines the size of the backtracking window based on an innovation gradient, which effectively improves alignment accuracy.
- An EM-based robust variational Bayesian Kalman filter is designed to accurately estimate the alignment errors in complex interference environments. Within the proposed technique, the EM and VB methods are employed to estimate the inaccurate predicted error and measurement noise covariance matrices, respectively.
2. In-Motion Alignment Model
2.1. Traditional In-Motion Alignment Method
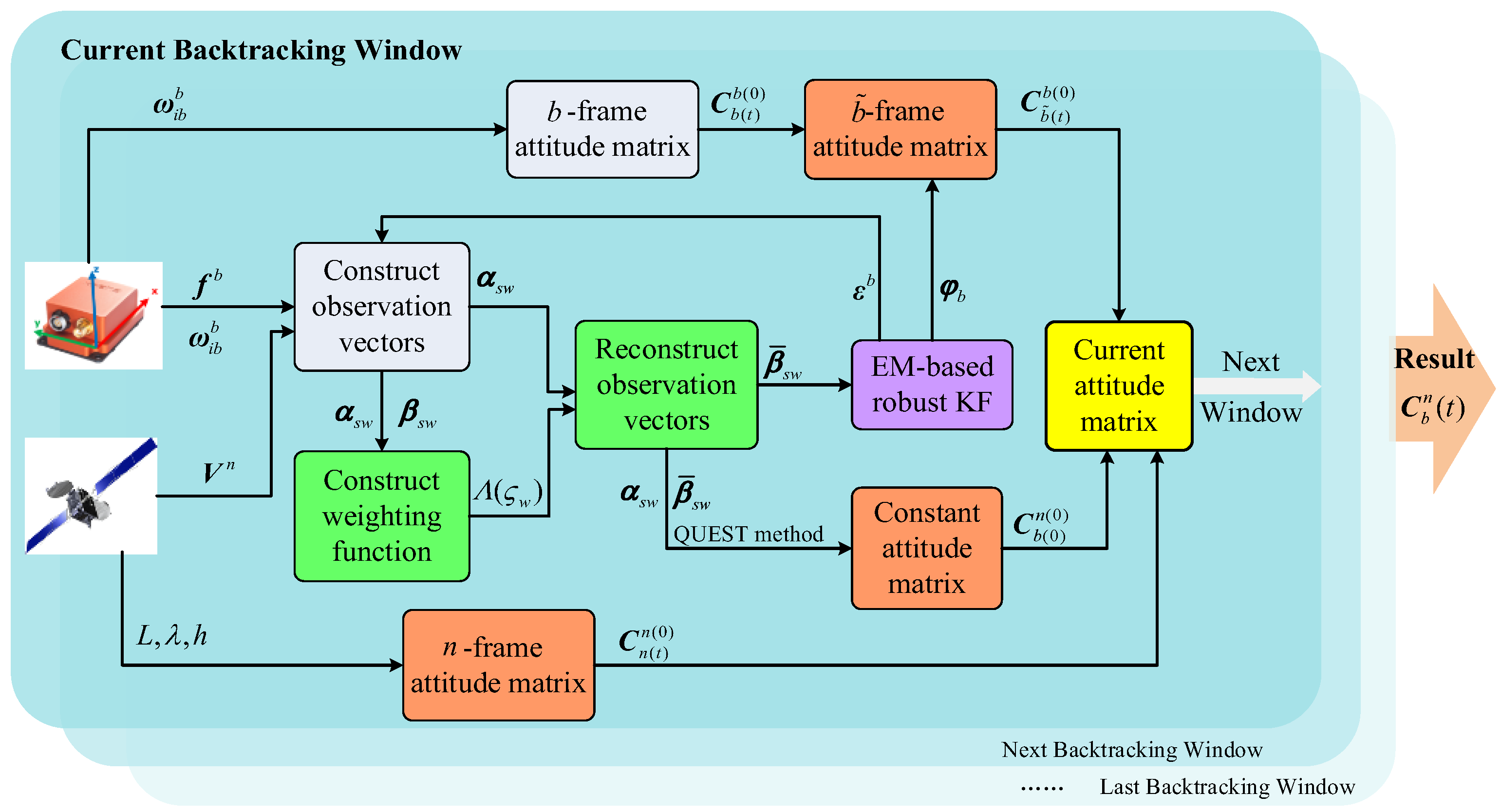
2.2. Outliers’ Isolation Based on Vector Reconstruction
2.3. Construction of State-Space Model
3. The Proposed Robust Filtering Method
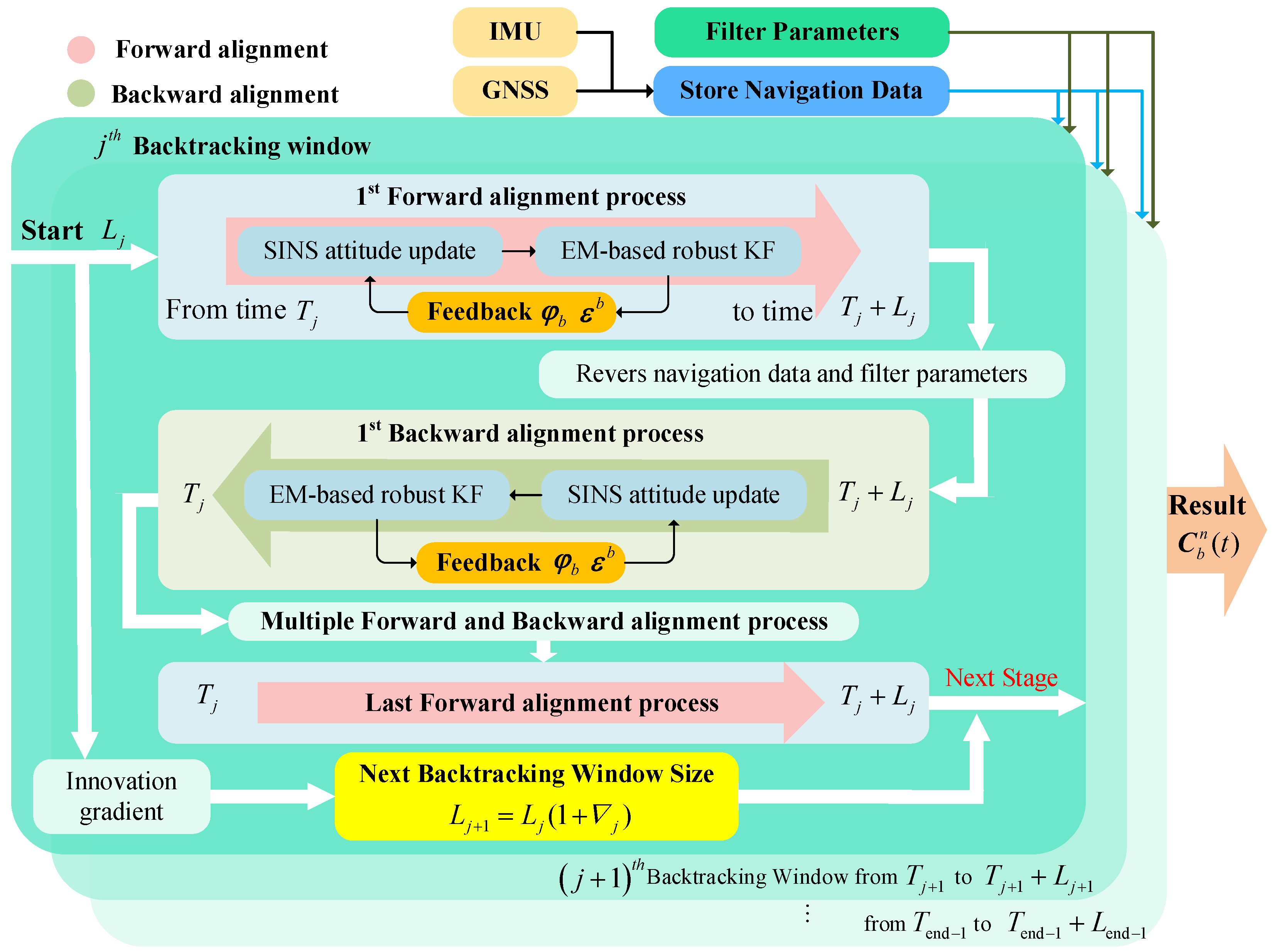
3.1. Adaptive Window Adjustment Multiple Backtracking Approach
3.2. EM-Based Robust Variational Bayesian Kalman Filter
3.3. Algorithm Summarization
| Algorithm 1: Adaptive multiple backtracking robust in-motion alignment method. |
| Initialization: , ,,. Inputs: |
| While(< IMU data length) Forward alignment for |
|
| Backward alignment |
return real-time attitude matrix |
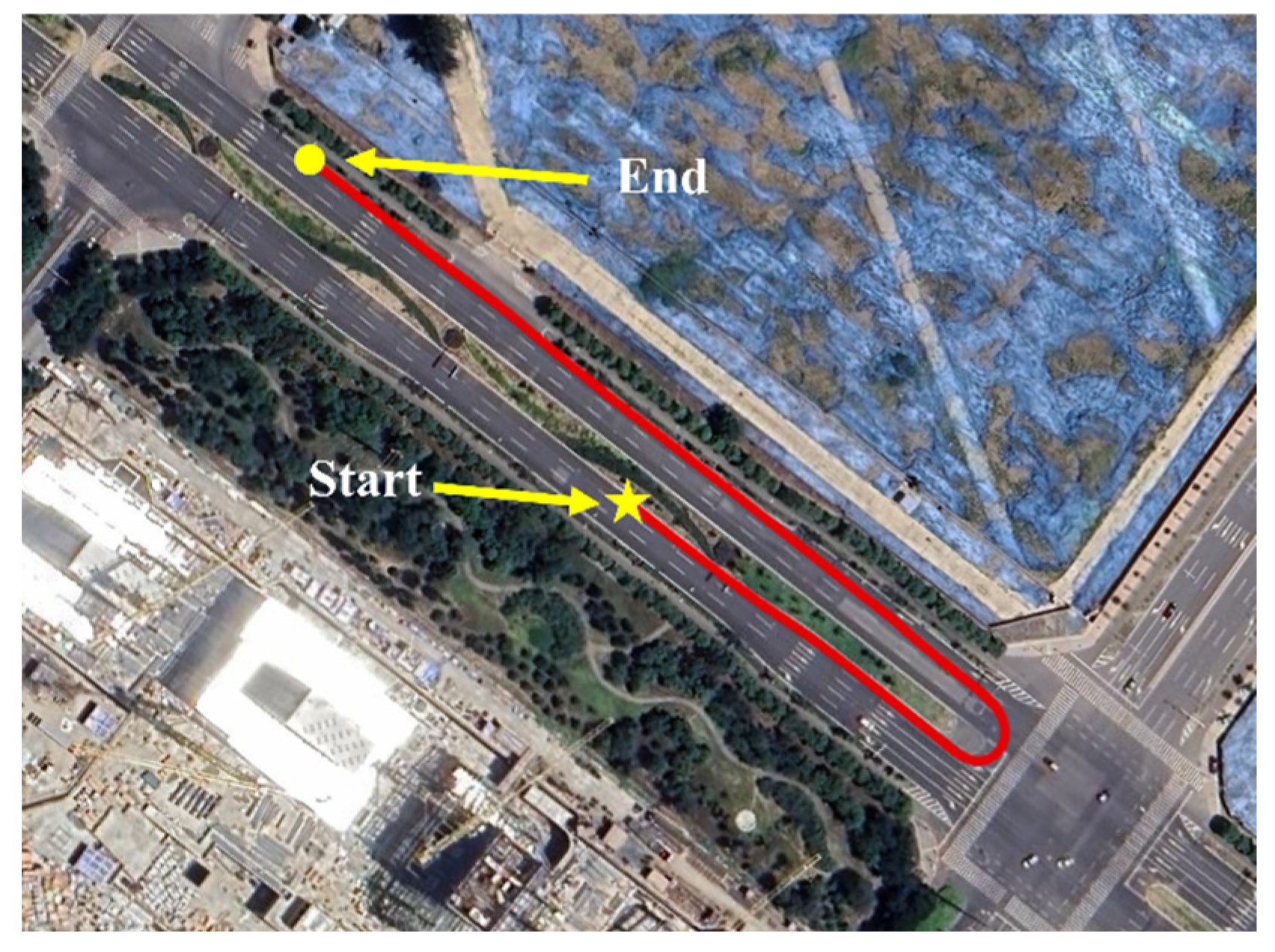
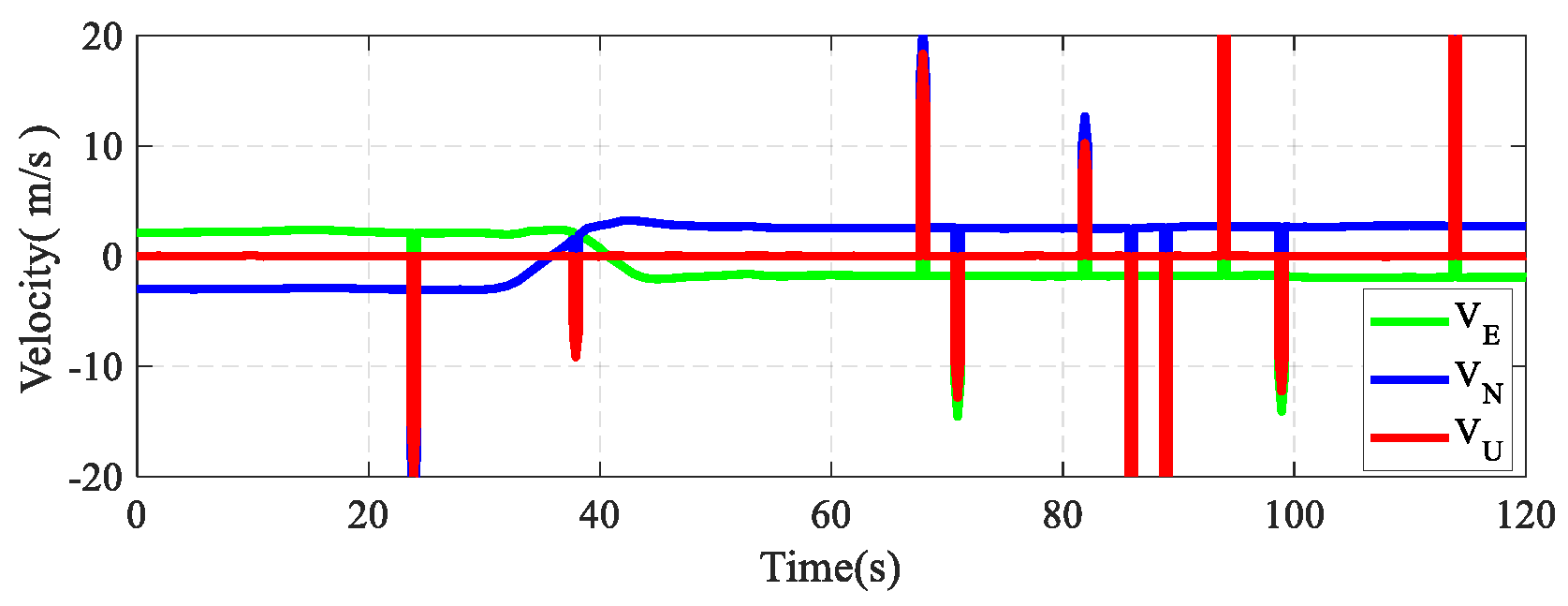
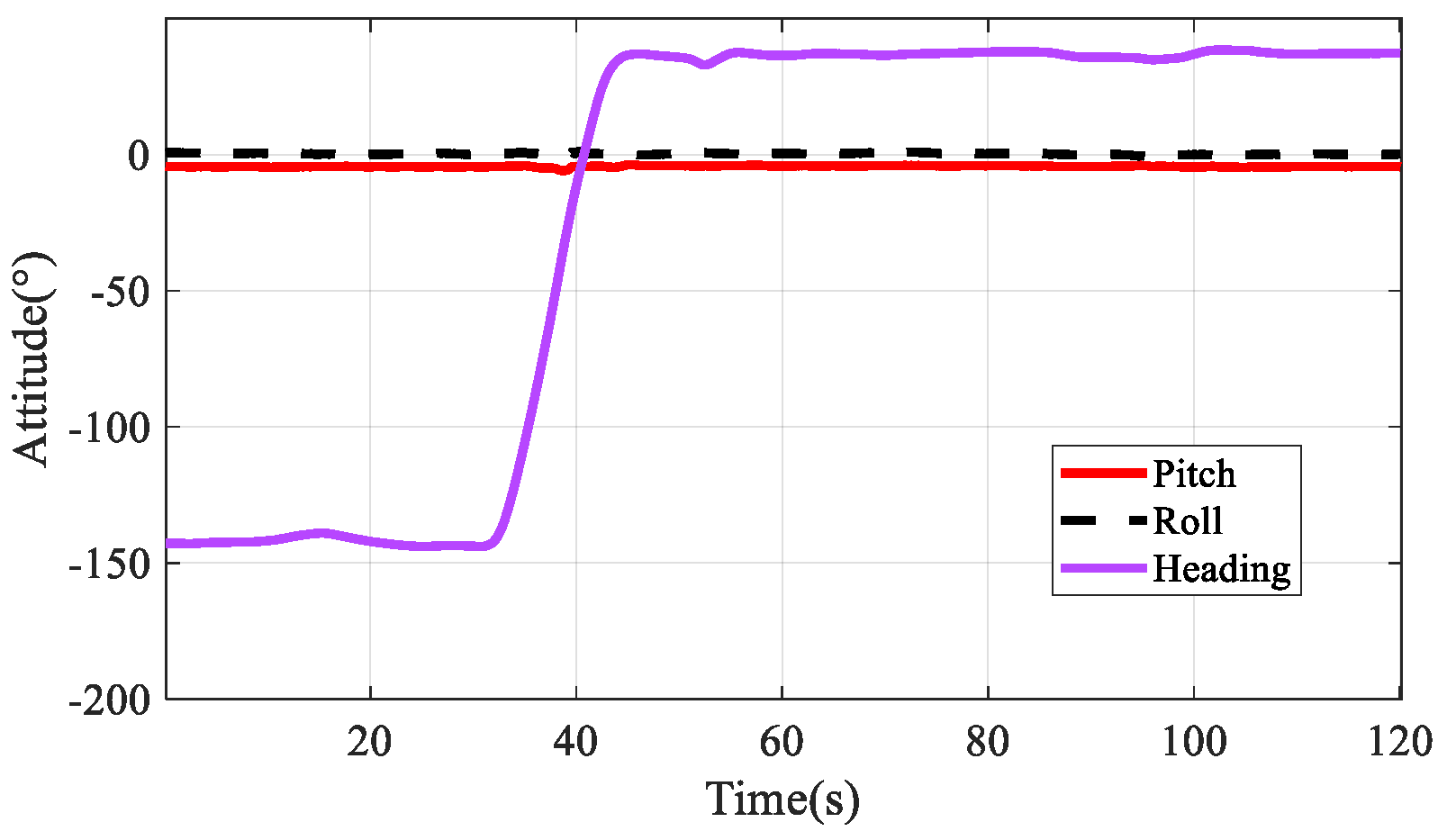
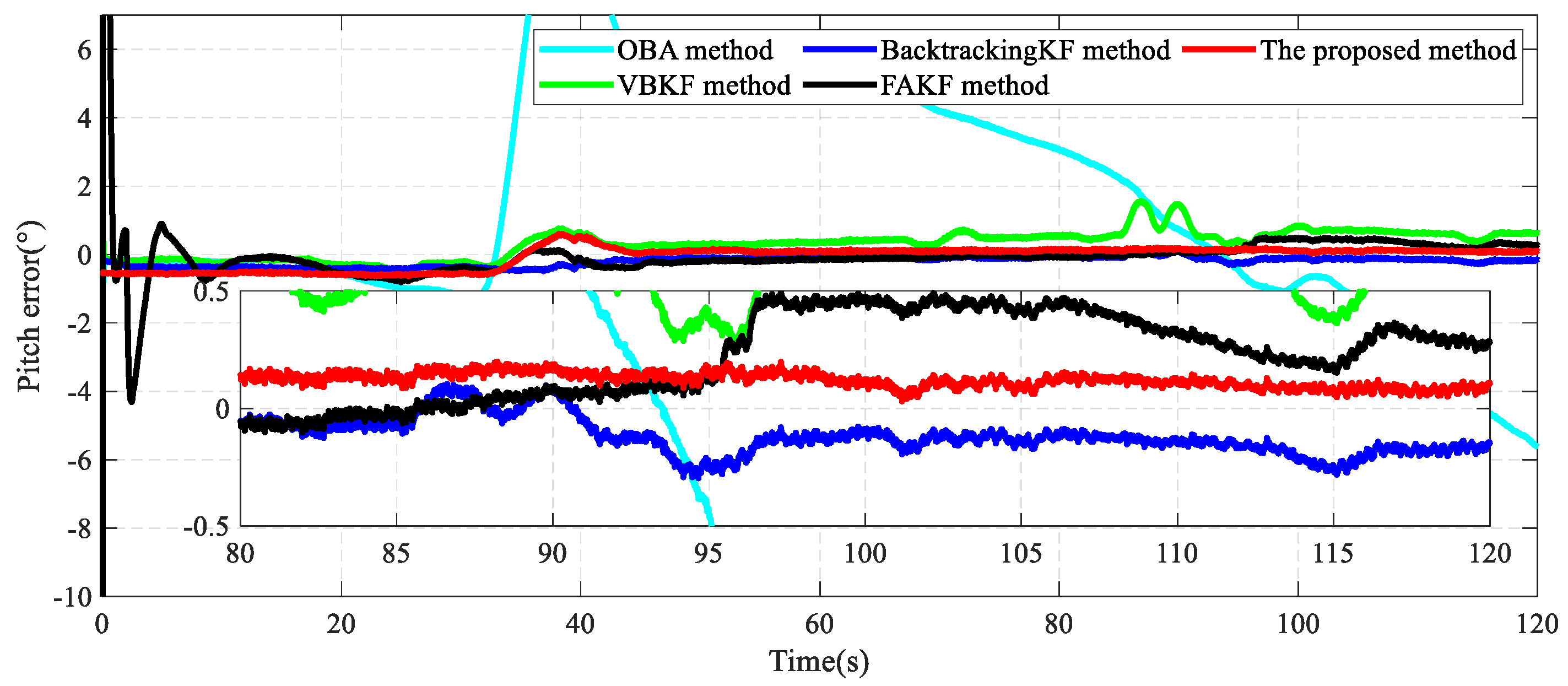
4. Results and Discussion
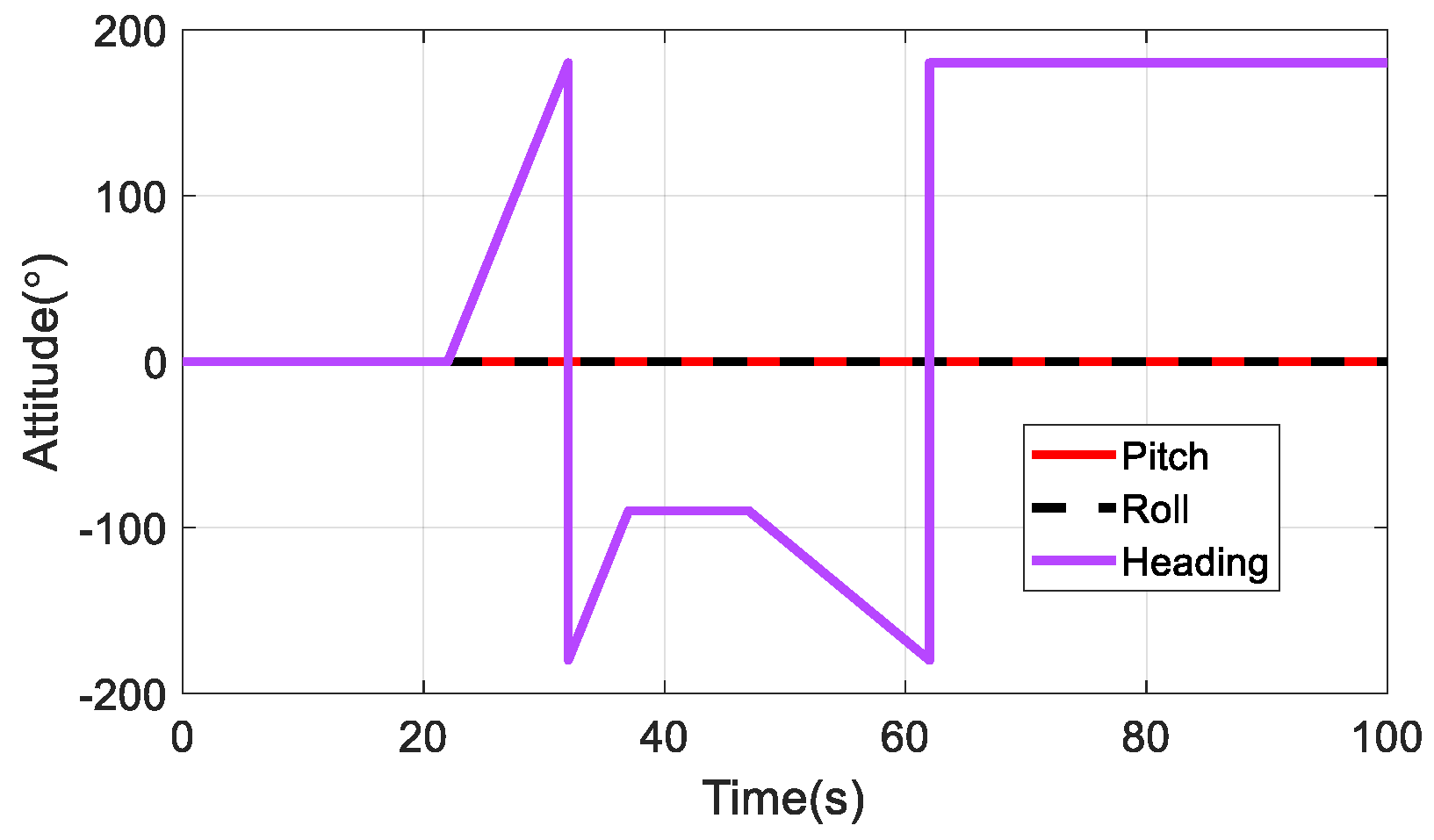
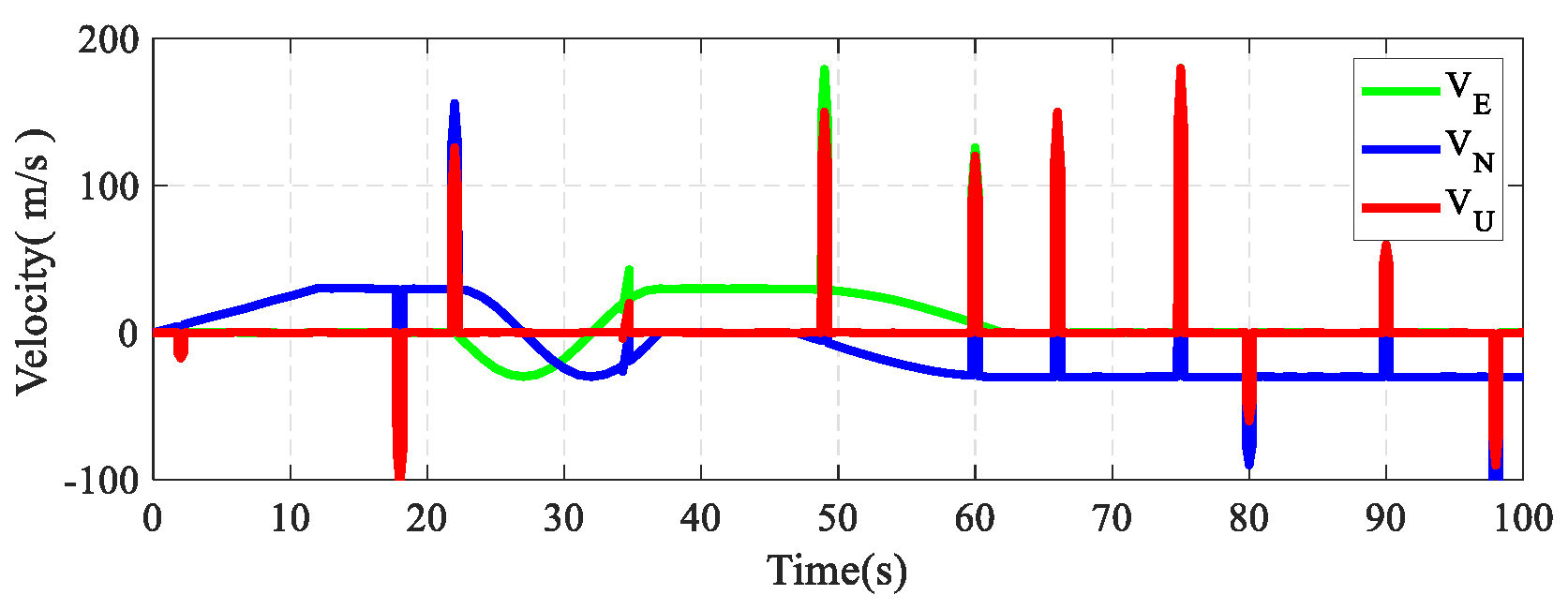
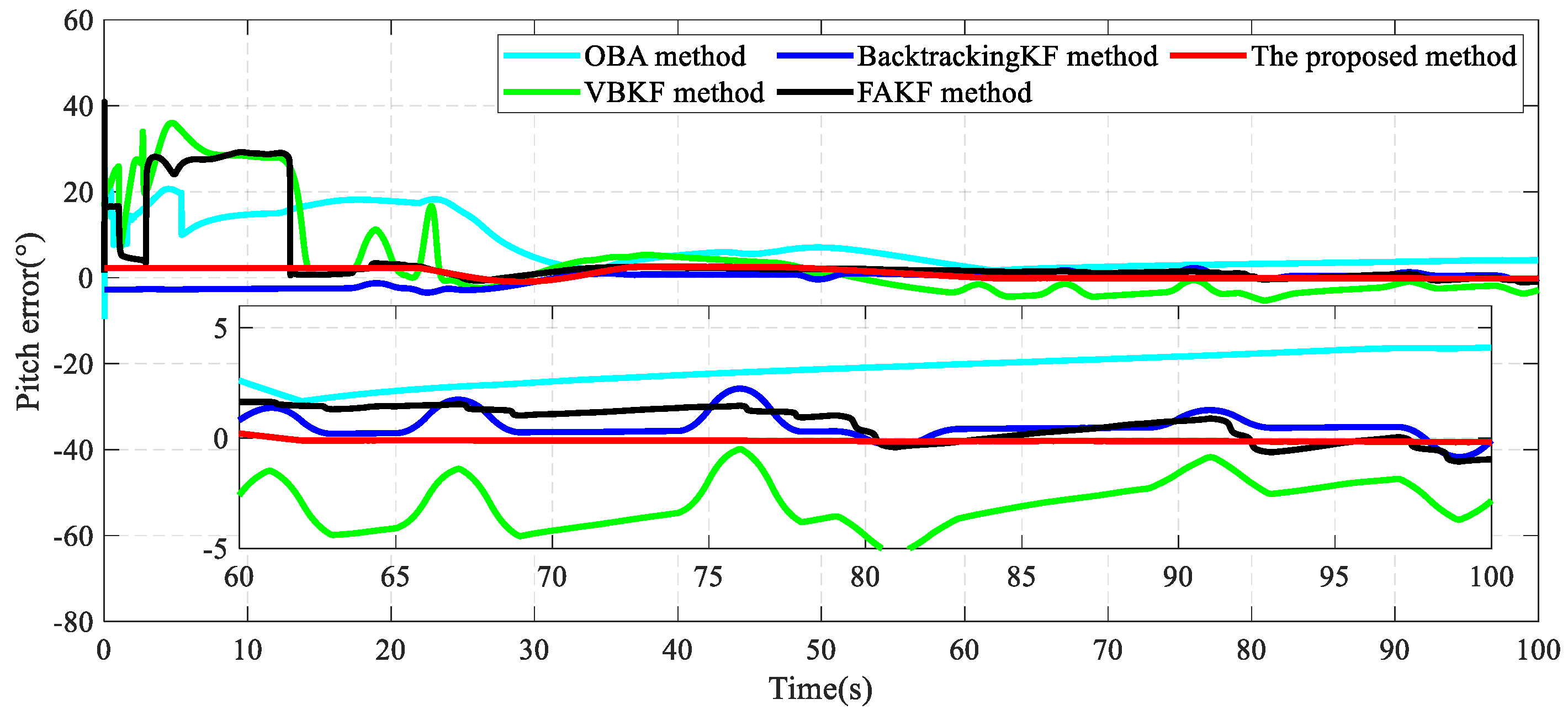
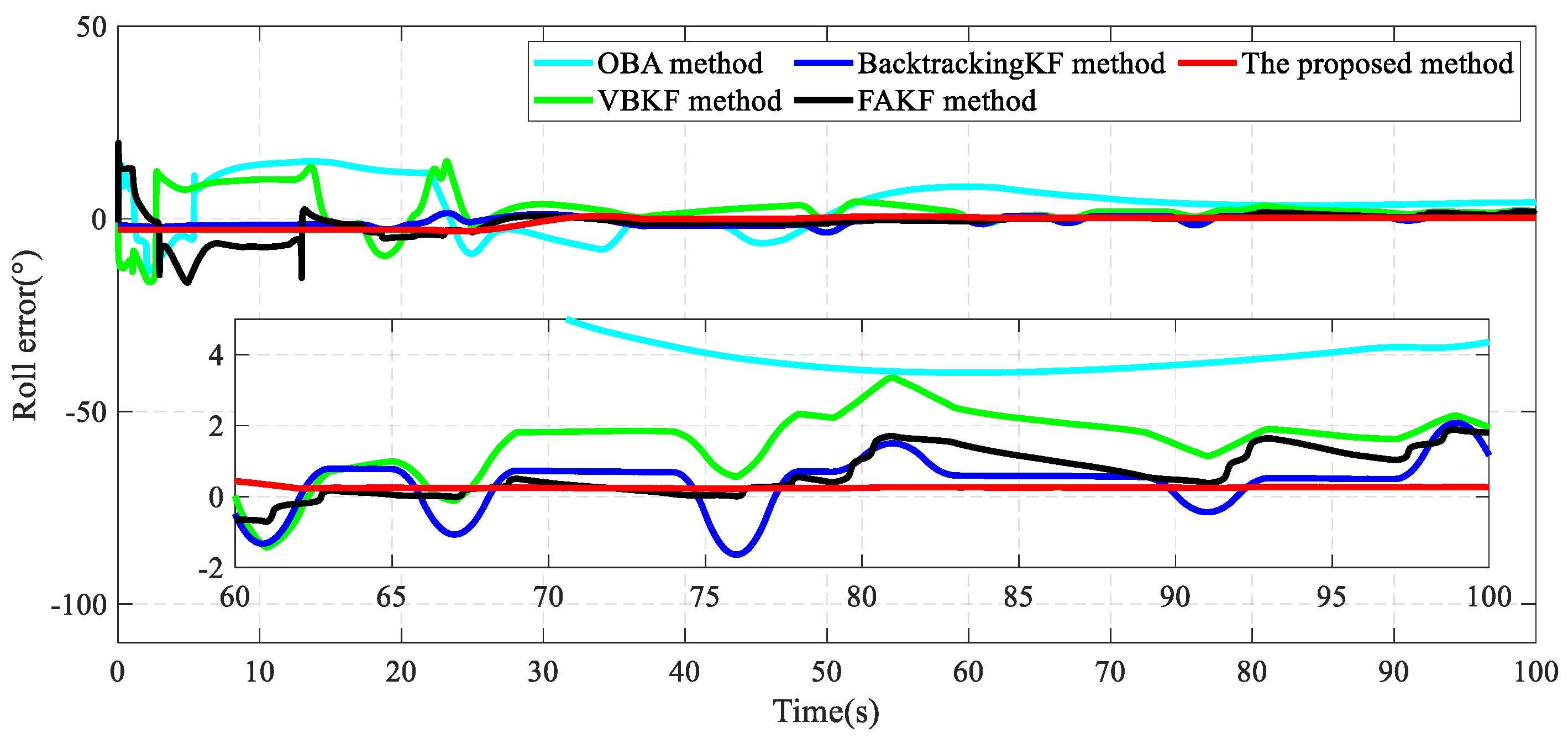
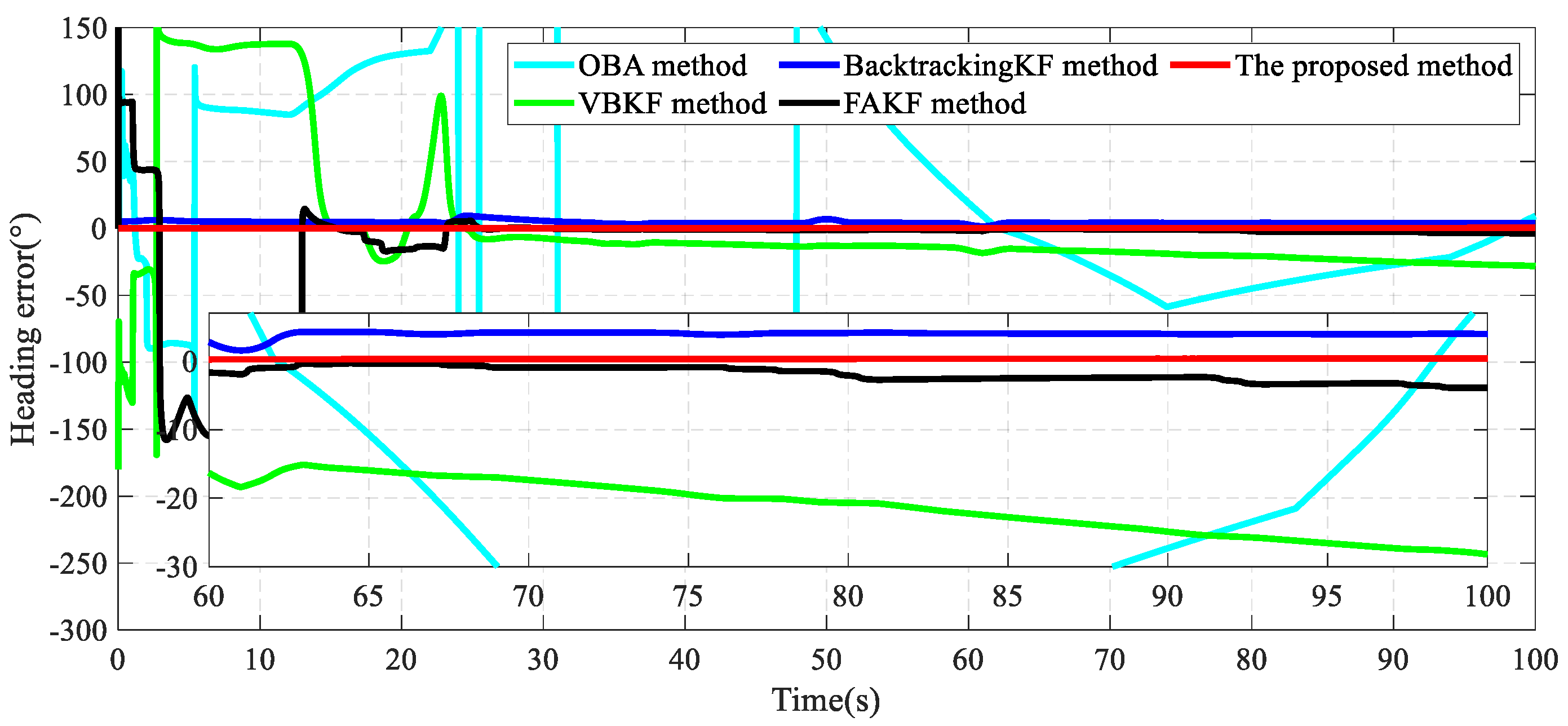
4.1. Simulation Test
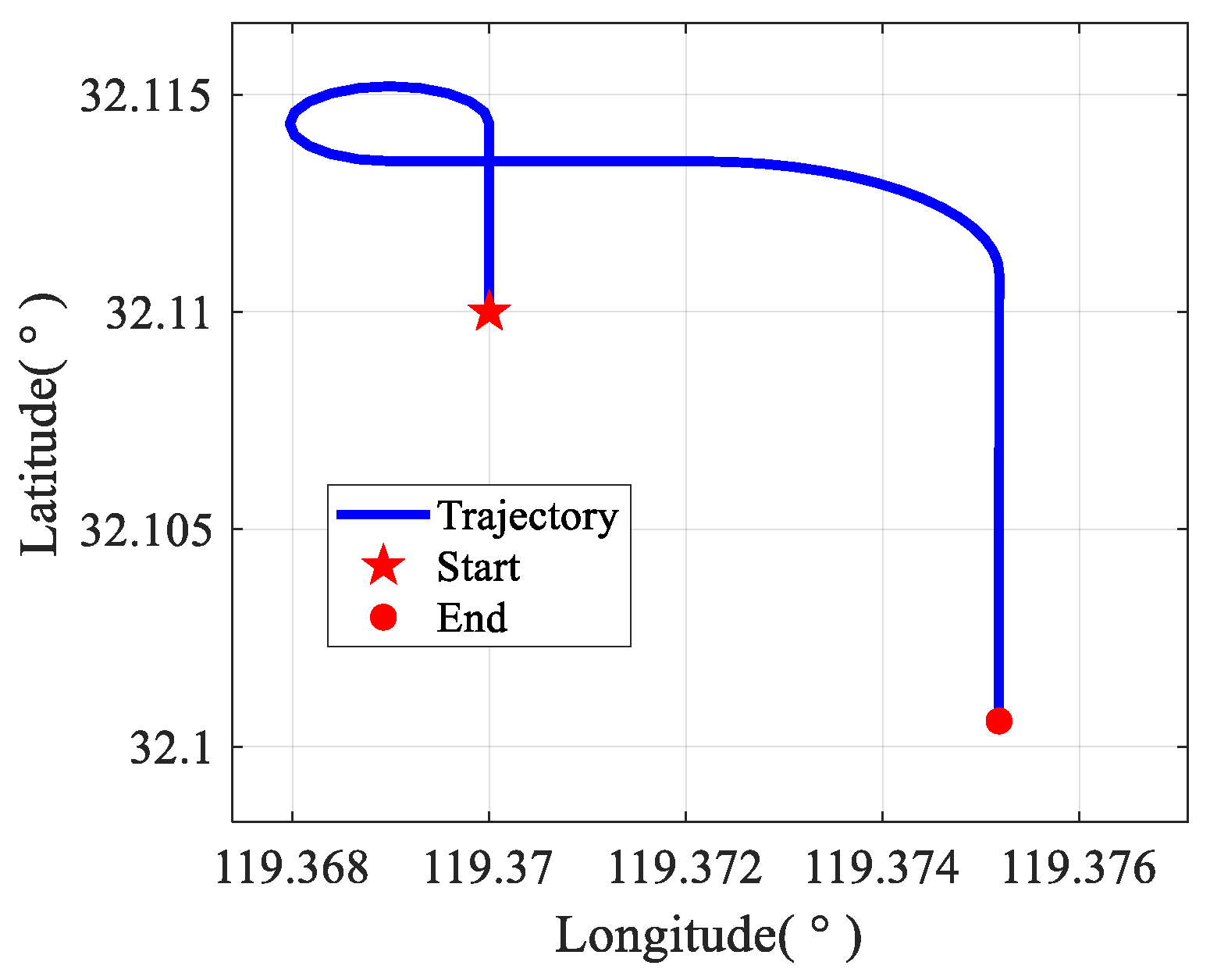
4.2. Field Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, P.; Nie, W.; Liu, Y.; Xu, T. Improving the underwater navigation performance of an IMU with acoustic long baseline calibration. Satell. Navig. 2024, 5, 7. [Google Scholar] [CrossRef]
- Han, S.; Wang, J. A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications. J. Navig. 2010, 63, 663–680. [Google Scholar] [CrossRef]
- Wang, K.; Xu, X.; Gao, W.; Wang, J. Linearized in-motion alignment for a low-cost INS. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1917–1925. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Liu, S.; Wang, S.; Yang, L. An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression. Remote Sens. 2025, 17, 1449. [Google Scholar] [CrossRef]
- Xu, X.; Gui, J.; Sun, Y.; Yao, Y.; Zhang, T. A Robust In-Motion Alignment Method With Inertial Sensors and Doppler Velocity Log. IEEE Trans. Instrum. Meas. 2021, 70, 3011873. [Google Scholar] [CrossRef]
- Xu, T.; Xu, X.; Xu, D.; Zou, Z.; Zhao, H. A new robust filtering method of GNSS/MINS integrated system for land vehicle navigation. IEEE Trans. Veh. Technol. 2022, 71, 11443–11453. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Chang, L. A New Fast In-Motion Coarse Alignment Method for GPS-Aided Low-Cost SINS. IEEE/ASME Trans. Mechatron. 2018, 23, 1303–1313. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Du, S.; Li, Y.; Zhang, Y. A high-accuracy GPS-aided coarse alignment method for MEMS-based SINS. IEEE Trans. Instrum. Meas. 2020, 69, 7914–7932. [Google Scholar] [CrossRef]
- Wei, J.; Yu, F.; Fan, S.; Zhang, Y.; Wang, Y.; Wang, Y. A Robust In-Motion Alignment Method for a DVL-Aided SINS With Latitude Uncertainty. IEEE Trans. Instrum. Meas. 2024, 73, 3341141. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, M.; Hu, J.; Li, L.; Guan, X. A Robust In-Motion Coarse Alignment Method for Low-Accuracy SINS and GPS Integrated System. IEEE/ASME Trans. Mechatron. 2025, 30, 611–622. [Google Scholar] [CrossRef]
- Sun, X.; Zhuang, Y.; Yang, X.; Huai, J.; Huang, T.; Feng, D. Tightly coupled VLP/INS integrated navigation by inclination estimation and blockage handling. Satell. Navig. 2025, 6, 7. [Google Scholar] [CrossRef]
- Xu, X.; Zheng, X.; Li, Y.; Yao, Y.; Zhou, H.; Zhu, L. An Improved In-Motion Alignment Method for SINS/GPS with the Sliding Windows Integration. IEEE Trans. Veh. Technol. 2023, 72, 12491–12499. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y.; Zhu, L.; Yao, Y. Robust attitude and positioning alignment methods for SINS/DVL integration based on sliding window improvements. IEEE Trans. Ind. Electron. 2023, 71, 8038–8046. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, T.; Cui, B.; Wei, X.; Jin, B. In-Motion Coarse Alignment for SINS/USBL Based on USBL Relative Position. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1425–1434. [Google Scholar] [CrossRef]
- Jin, S.; Camps, A.; Jia, Y.; Wang, F.; Martin-Neira, M.; Huang, F.; Yan, Q.; Zhang, S.; Li, Z.; Edokossi, K. Remote sensing and its applications using GNSS reflected signals: Advances and prospects. Satell. Navig. 2024, 5, 19. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Z.; Wang, F. A novel ML-aided methodology for SINS/GPS integrated navigation systems during GPS outages. Remote Sens. 2022, 14, 5932. [Google Scholar] [CrossRef]
- Wu, M.; Wu, Y.; Hu, X.; Hu, D. Optimization-based alignment for inertial navigation systems: Theory and algorithm. Aerosp. Sci. Technol. 2011, 15, 1–17. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, X. Velocity/position integration formula part I: Application to in-flight coarse alignment. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1006–1023. [Google Scholar] [CrossRef]
- Xu, X.; Sun, Y.; Yao, Y.; Zhang, T. A robust in-motion optimization-based alignment for SINS/GPS integration. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4362–4372. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Shao, X. An adaptive multiple backtracking UKF method based on Krein space theory for marine vehicles alignment process. IEEE Trans. Veh. Technol. 2022, 72, 3214–3226. [Google Scholar] [CrossRef]
- Cao, S.; Bian, Y.; Wang, G.; Qin, H.; Hu, M.; Cui, Q.; Ding, R. Velocity-Integral-Constraint-based In-Motion Initial Alignment for Kalman Filter-Aided Low-Cost SINS. IEEE Trans. Instrum. Meas. 2025, 74, 8506313. [Google Scholar] [CrossRef]
- Wei, X.; Li, J.; Han, D.; Wang, J.; Zhan, Y.; Wang, X.; Feng, K. An in-flight alignment method for global positioning system-assisted low cost strapdown inertial navigation system in flight body with short-endurance and high-speed rotation. Remote Sens. 2023, 15, 711. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Liu, J.; Zhu, X.; Zhong, Y. A Robust Backtracking CKF Based on Krein Space Theory for In-Motion Alignment Process. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1909–1925. [Google Scholar] [CrossRef]
- Chang, L.; Hu, B.; Li, Y. Backtracking integration for fast attitude determination-based initial alignment. IEEE Trans. Instrum. Meas. 2014, 64, 795–803. [Google Scholar] [CrossRef]
- Fu, Q.; Li, S.; Liu, Y.; Wu, F. Information-reusing alignment technology for rotating inertial navigation system. Aerosp. Sci. Technol. 2020, 99, 105747. [Google Scholar] [CrossRef]
- Lin, Y.; Miao, L.; Zhou, Z. A high-accuracy initial alignment method based on backtracking process for strapdown inertial navigation system. Measurement 2022, 201, 111712. [Google Scholar] [CrossRef]
- Wei, X.; Li, J.; Feng, K.; Zhang, D. An Improved In-flight Alignment Method Based on Backtracking Navigation for GPS-aided Low Cost SINS With Short Endurance. IEEE Robot. Autom. Lett. 2022, 7, 634–641. [Google Scholar] [CrossRef]
- Wang, D.; Wang, B.; Huang, H.; Xu, B.; Zhang, H. A Novel SINS/DVL Integrated Navigation Method Based on Different Track Models for Complex Environment. IEEE Trans. Instrum. Meas. 2024, 73, 3373066. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, T.; Wei, H. A Factor Graph Optimization-Based In-motion Alignment Method for INS/DVL Integration. IEEE Trans. Veh. Technol. 2024, 73, 18452–18459. [Google Scholar] [CrossRef]
- Jarraya, I.; Al-Batati, A.; Kadri, M.B.; Abdelkader, M.; Ammar, A.; Boulila, W.; Koubaa, A. Gnss-denied unmanned aerial vehicle navigation: Analyzing computational complexity, sensor fusion, and localization methodologies. Satell. Navig. 2025, 6, 9. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A Novel Adaptive Kalman Filter With Inaccurate Process and Measurement Noise Covariance Matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
- Du, S.; Zhu, F.; Wang, Z.; Huang, Y.; Zhang, Y. A Novel Lie Group Framework-based Student’s t Robust Filter and Its Application to INS/DVL Tightly Integrated Navigation. IEEE Trans. Instrum. Meas. 2024, 73, 3379400. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Du, Y. A novel robust adaptive Kalman filter with application to urban vehicle integrated navigation systems. Measurement 2024, 236, 114844. [Google Scholar] [CrossRef]
- Chen, H.; Sun, R.; Cheng, Q.; Yin, T.; Zhou, Y.; Ochieng, W.Y. GNSS/IMU/LO integration with a new LO error model and lateral constraint for navigation in urban areas. Satell. Navig. 2024, 5, 30. [Google Scholar] [CrossRef]
- Sun, J.; Ye, Q.; Lei, Y. In-motion alignment method of SINS based on improved Kalman filter under geographic latitude uncertainty. Remote Sens. 2022, 14, 2581. [Google Scholar] [CrossRef]
- Ge, B.; Zhang, H.; Fu, W.; Yang, J. Enhanced Redundant Measurement-Based Kalman Filter for Measurement Noise Covariance Estimation in INS/GNSS Integration. Remote Sens. 2020, 12, 3500. [Google Scholar] [CrossRef]
- Lyu, W.; Meng, F.; Jin, S.; Zeng, Q.; Wang, Y.; Wang, J. Robust In-Motion Alignment of Low-Cost SINS/GNSS for Autonomous Vehicles Using IT2 Fuzzy Logic. IEEE Internet Things J. 2025, 12, 9996–10011. [Google Scholar] [CrossRef]
- Shi, W.; Xu, J.; He, H.; Li, D.; Tang, H.; Lin, E. Fault-tolerant SINS/HSB/DVL underwater integrated navigation system based on variational Bayesian robust adaptive Kalman filter and adaptive information sharing factor. Measurement 2022, 196, 111225. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Li, N.; Wu, Z.; Chambers, J.A. A novel robust student’s t-based Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]

| Notations | Definitions |
|---|---|
| Inertial frame | |
| Navigation frame | |
| True body frame | |
| Calculated body frame | |
| Gravity vector | |
| Specific force | |
| Gyroscope constant biases | |
| Attitude matrix from frame to frame | |
| Angular rate of frame related to frame projected in | |
| Ground velocity of the SINS in frame | |
| identity matrix | |
| Skew symmetric matrix of vector | |
| Transpose operation | |
| Trace operation |
| Evaluating Indicator | Attitude Error (°) | OBA | VBKF | BKF | FAKF | Proposed |
|---|---|---|---|---|---|---|
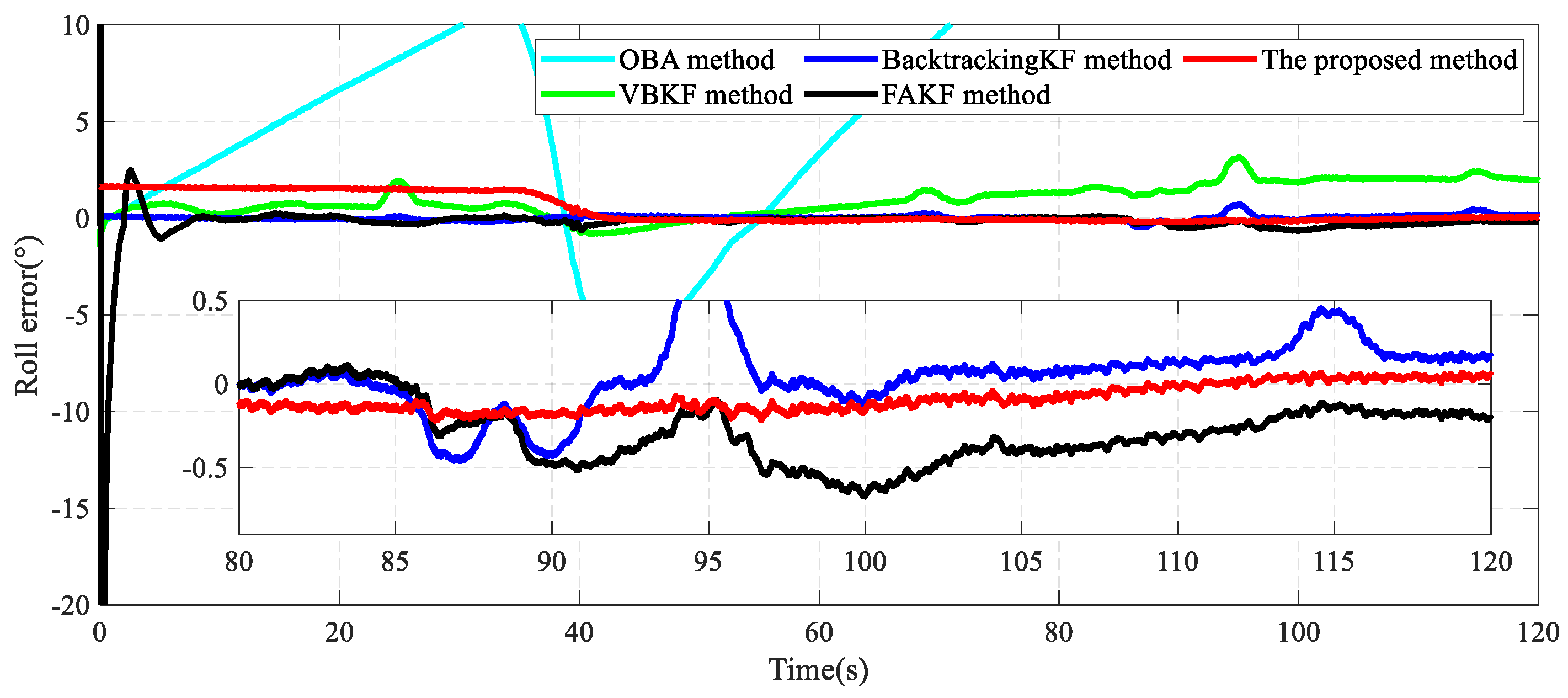
| Mean | Pitch | 5.534 | −2.956 | 0.530 | 0.636 | −0.122 |
| Roll | 4.653 | 1.561 | 0.405 | 0.669 | 0.257 | |
| Heading | −27.446 | −21.265 | 3.951 | −1.890 | 0.337 | |
| STD | Pitch | 0.274 | 1.081 | 0.566 | 0.765 | 0.049 |
| Roll | 1.414 | 0.917 | 0.735 | 0.638 | 0.026 | |
| Heading | 18.719 | 3.898 | 0.468 | 1.074 | 0.037 |
| Index | Gyroscope | Accelerometer |
|---|---|---|
| Update rate | 100 Hz | 100 Hz |
| Standard full range | ±450°/s | ±20 g |
| Initial bias error | 0.2°/s | 5 mg |
| In-run bias stability | 10°/h | 15 μg |
| Noise density | 0.01°/s/√Hz | 60 μg/√Hz |
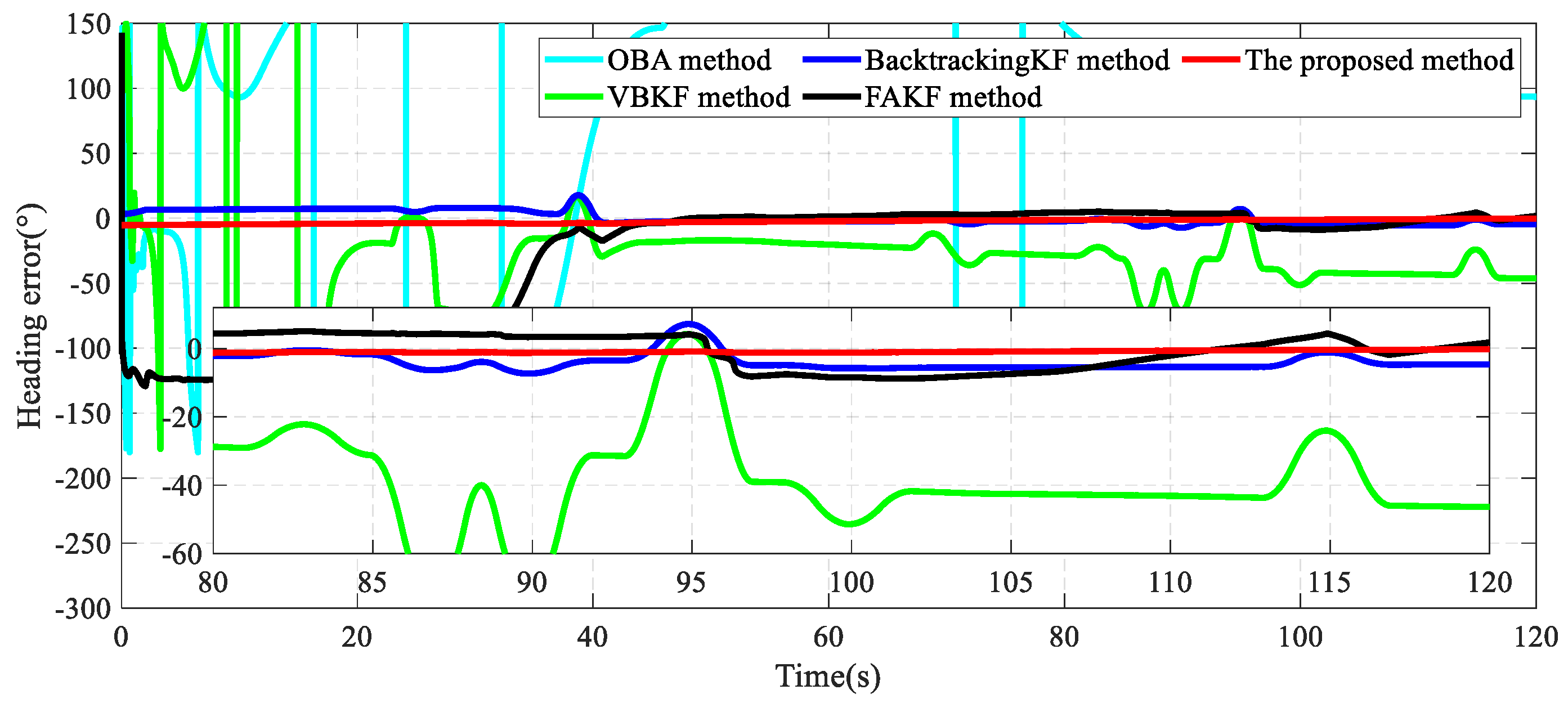
| Evaluating Indicator | Attitude Error (°) | OBA | VBKF | BKF | FAKF | Proposed |
|---|---|---|---|---|---|---|
| Mean | Pitch | −1.068 | 0.668 | −0.119 | 0.227 | 0.120 |
| Roll | 24.393 | 1.902 | 0.058 | −0.284 | −0.088 | |
| Heading | 102.960 | −39.164 | −3.869 | 4.423 | 0.870 | |
| STD | Pitch | 2.448 | 0.255 | 0.078 | 0.181 | 0.079 |
| Roll | 5.158 | 0.391 | 0.214 | 0.187 | 0.079 | |
| Heading | 11.172 | 14.398 | 2.671 | 5.034 | 0.314 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, W.; Wang, Y.; Jin, S.; Huang, H.; Tian, X.; Wang, J. Robust Adaptive Multiple Backtracking VBKF for In-Motion Alignment of Low-Cost SINS/GNSS. Remote Sens. 2025, 17, 2680. https://doi.org/10.3390/rs17152680
Lyu W, Wang Y, Jin S, Huang H, Tian X, Wang J. Robust Adaptive Multiple Backtracking VBKF for In-Motion Alignment of Low-Cost SINS/GNSS. Remote Sensing. 2025; 17(15):2680. https://doi.org/10.3390/rs17152680
Chicago/Turabian StyleLyu, Weiwei, Yingli Wang, Shuanggen Jin, Haocai Huang, Xiaojuan Tian, and Jinling Wang. 2025. "Robust Adaptive Multiple Backtracking VBKF for In-Motion Alignment of Low-Cost SINS/GNSS" Remote Sensing 17, no. 15: 2680. https://doi.org/10.3390/rs17152680
APA StyleLyu, W., Wang, Y., Jin, S., Huang, H., Tian, X., & Wang, J. (2025). Robust Adaptive Multiple Backtracking VBKF for In-Motion Alignment of Low-Cost SINS/GNSS. Remote Sensing, 17(15), 2680. https://doi.org/10.3390/rs17152680






