Across-Beam Signal Integration Approach with Ubiquitous Digital Array Radar for High-Speed Target Detection
Abstract
1. Introduction
- (1)
- Intra-beam target motion compensation: In practical scenarios, when a moving target crosses multiple beams during coherent integration, its entry and exit times from each beam cannot be pre-determined, as the target may enter the radar coverage area unexpectedly and depart after an indefinite period. Meanwhile, target motion induces across-range unit (ARU) and across-Doppler unit (ADU) effects, rendering traditional moving target detection (MTD) methods highly ineffective and causing severe performance degradation in target focusing.
- (2)
- Inter-beam signal fusion processing: Due to the tangential time-varying characteristics between target motion and different dwell beams, signal phases and envelope positions vary across beams. This necessitates addressing radar echo signal accumulation challenges across inter-beam domains.
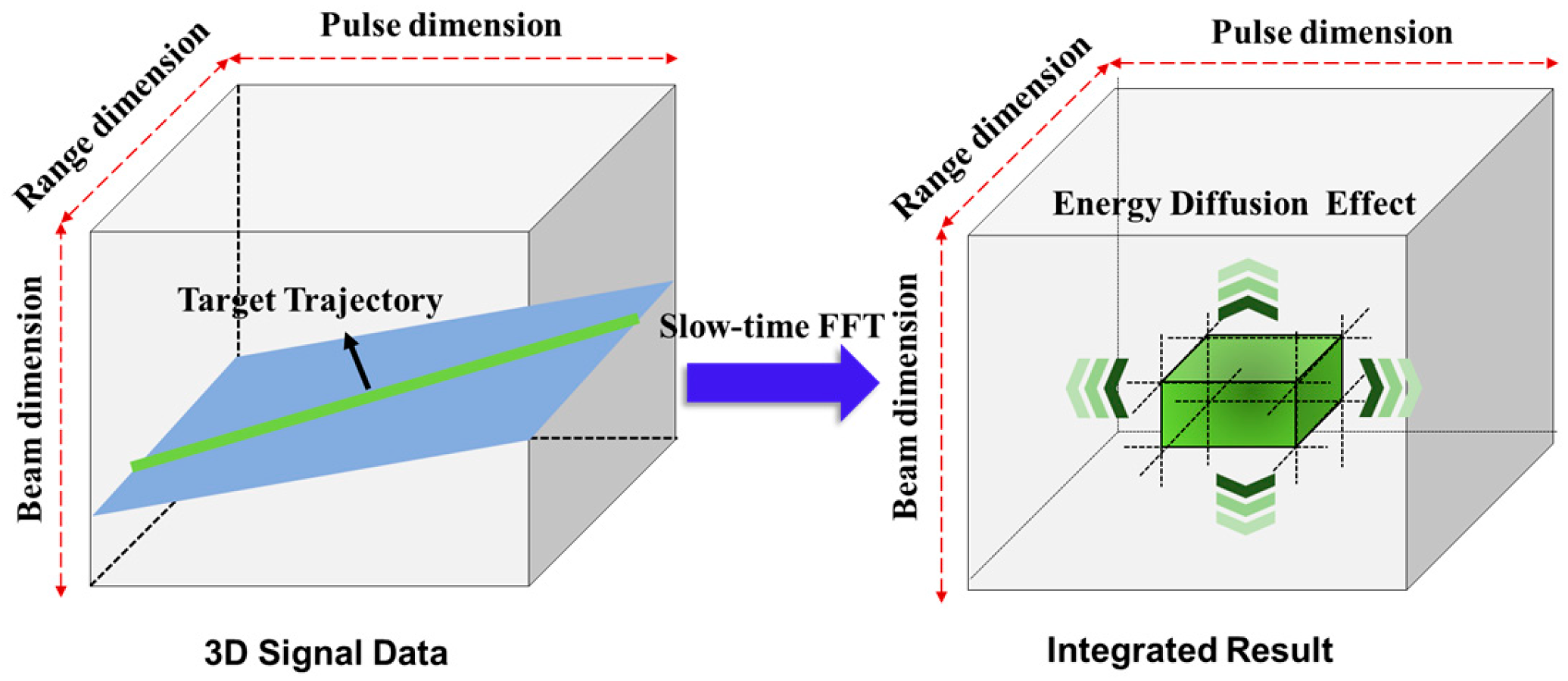
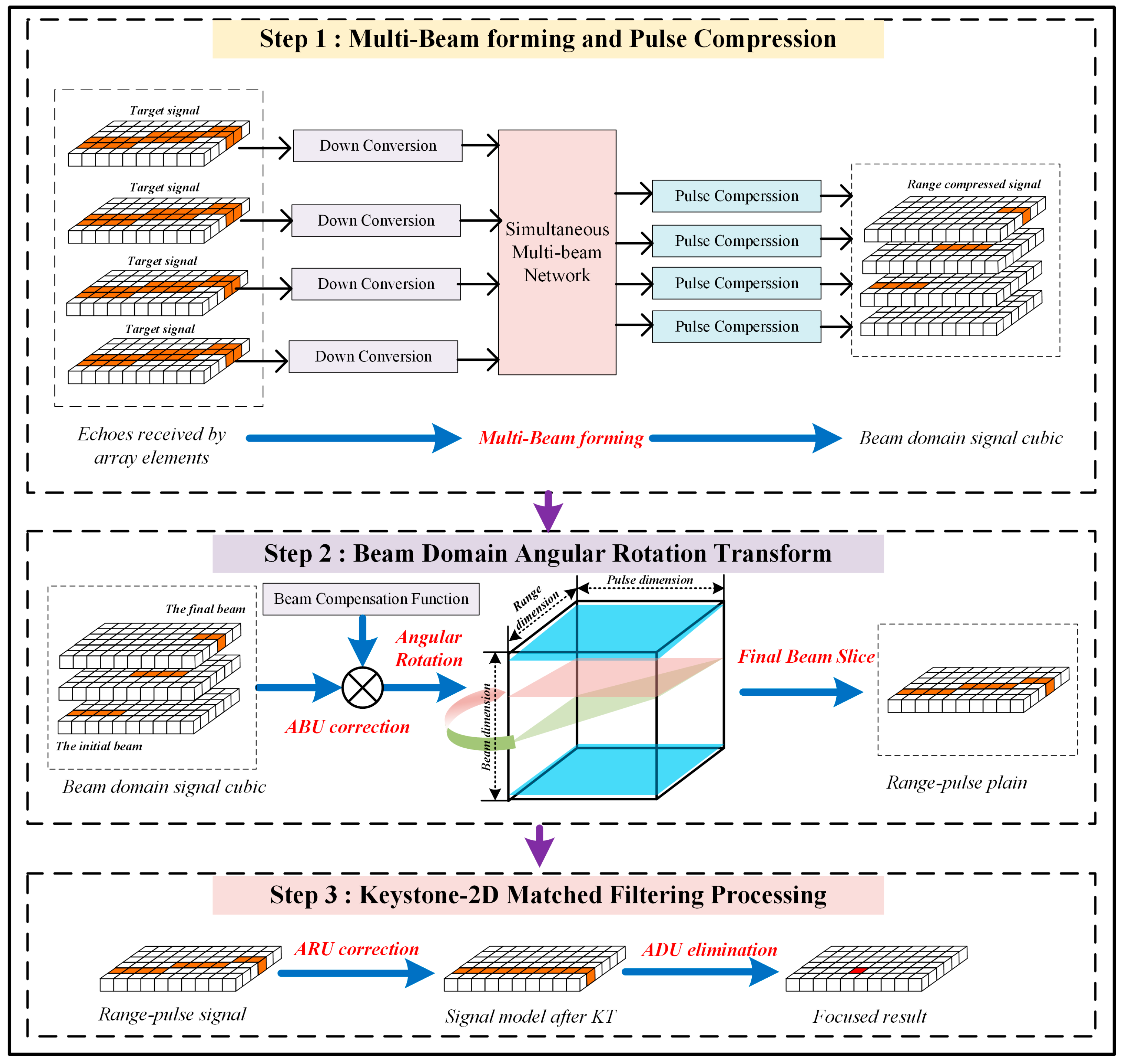
- The across-beam three-dimensional (3D) signal model for a high-speed target with UDAR is established first, illustrating the phase and envelope properties between intra-beam and inter-beam. On this basis, the beam segmentation characteristics of the across-beam received signals are described. Then, the detailed constraint conditions for the “three-crossing” effects, including the ARU, ADU, ABU, and the coherent signal constraint, are analyzed through mathematical expressions.
- Owing to the tangential angular velocity of high-speed target coupling with slow time, the target energy distribution appears as an inclined stepped platform in the 3D signal model. Then, inspired by AR-based algorithms [18,19,20,21], we propose the beam–domain rotation compensation (BARC) approach to correct the ABU effect. After dwell beam compensation and spatial angle rotation, the target energy of the beam domain can be assigned to the same beam unit. Afterwards, the keystone-matched filter method (KTMF) can be applied to remove ARU and ADU effects. It (i.e., BARC-KTMF) realizes well-focused output on the final beam, and the improved detection performance can be obtained.
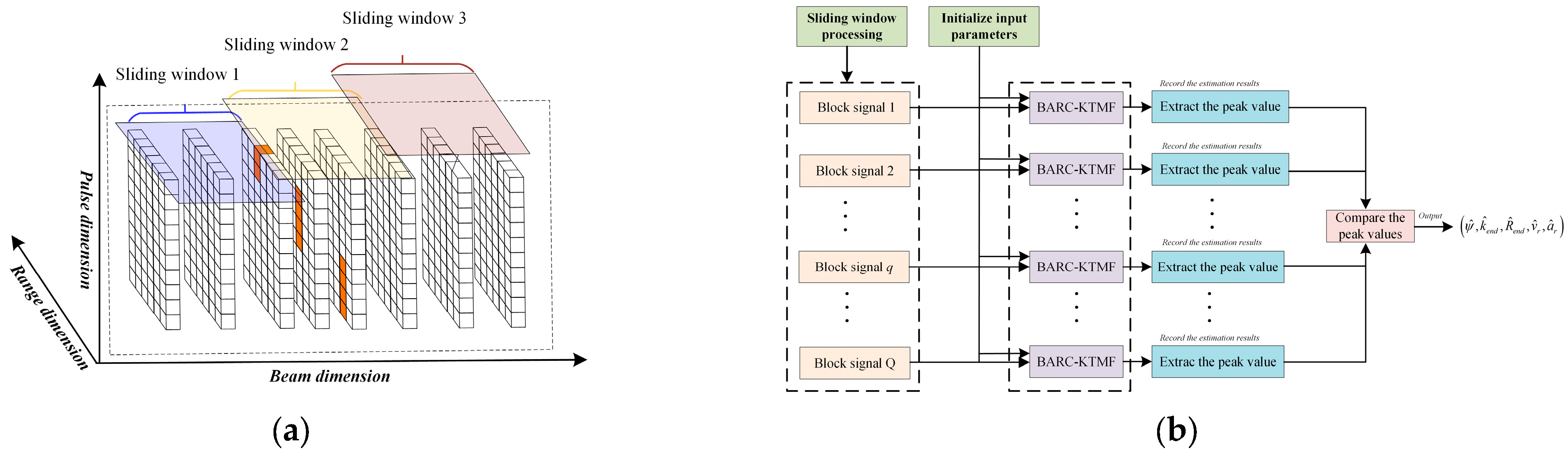
- Considering the huge computational complexity of full-beam processing, under the coherence constraint conditions, a kind of spatial windowing processing approach is developed to improve the across-beam accumulation efficiency, and the detailed execution procedures are also provided.
- In addition, to verify the validity of this algorithm, numerical simulations for different scenarios are provided to examine the performance of the proposed method, i.e., integration performance for single target, integration performance for multiple targets, detection ability comparison with some existing methods. Experiment results indicate that the accumulation and detection performance of the proposed method are significantly improved.
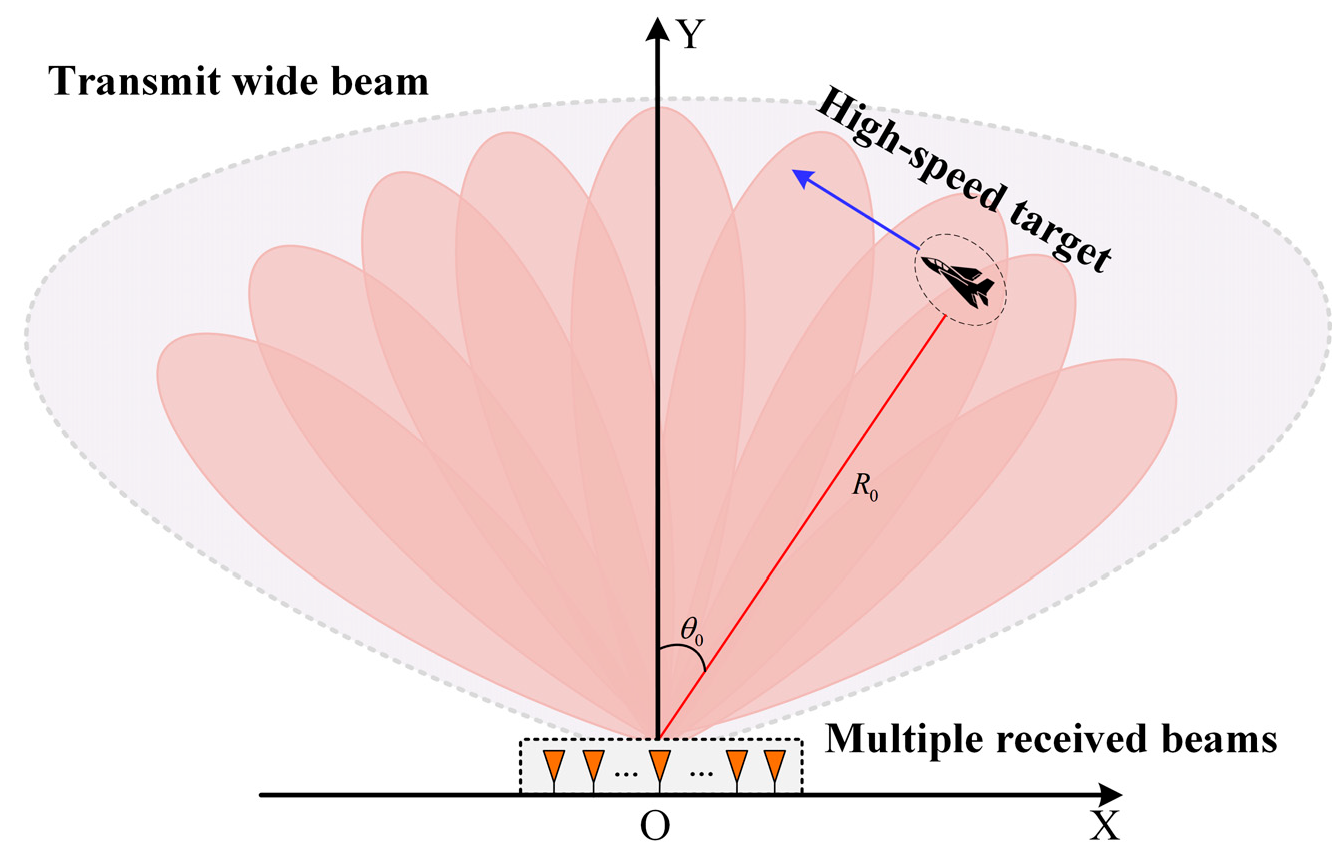
2. System Description and Model Analysis
2.1. The Across-Beam 3D Signal Model
- Part A expresses the signal envelope of range dimension and pulse dimension, where the radial velocity and radial acceleration are coupled with variable m.
- Part B is a phase term associated with the radial motion of the target.
- Part C is the envelope position term with respect to the azimuth angle, where the tangential angular velocity is also coupled with variable m, leading to the varying azimuth angle.
- Part D denotes the dwell beam phase term.
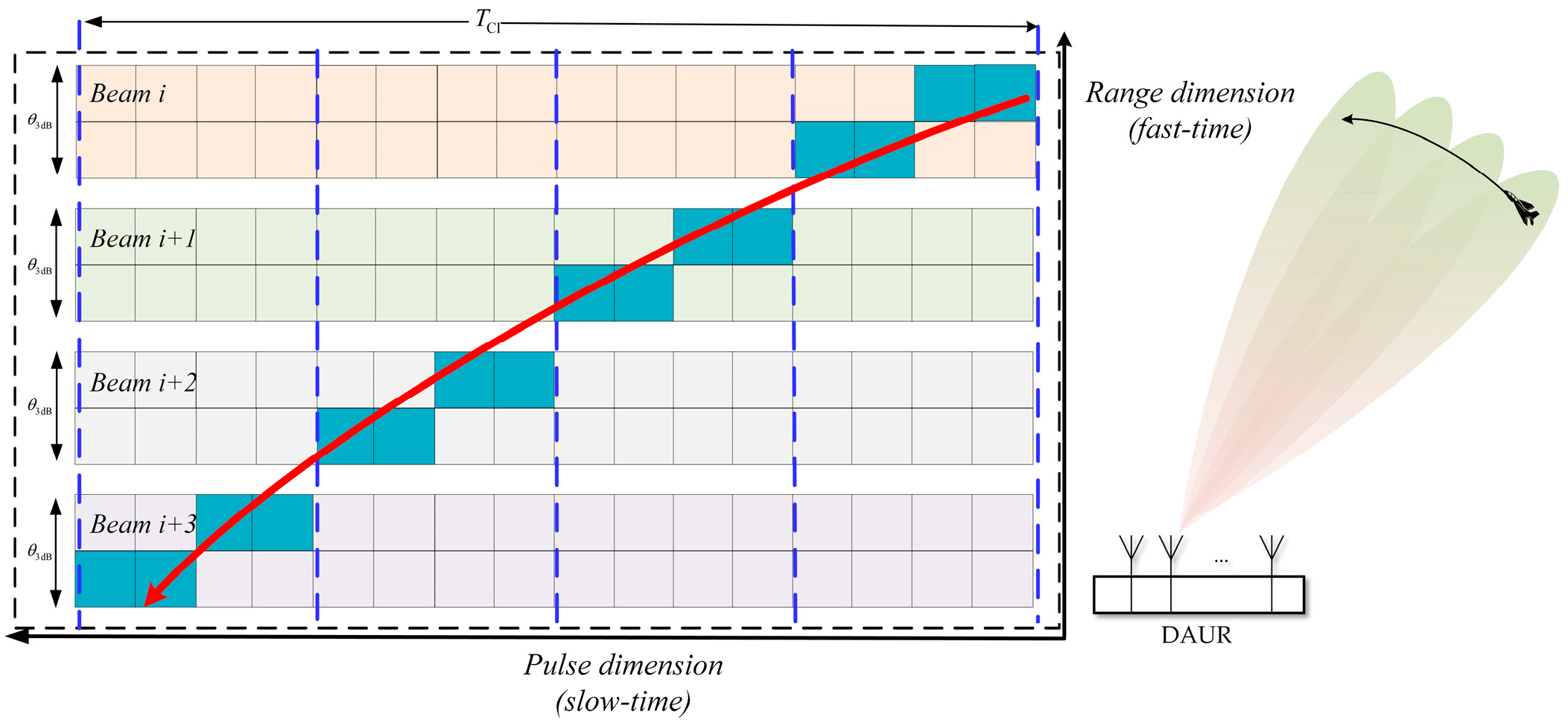
2.2. The Beam Segmentation Characteristics of the Aacross-Beam Received Signals
2.3. The Constraint Conditions for the “Three-Crossing” Effects
2.3.1. ABU Effect Analysis
2.3.2. ARU Effect Analysis
2.3.3. ADU Effect Analysis
2.3.4. The Coherent Signal Constraint
3. Proposed Method
3.1. ABU Correction Within the Inter-Beam
3.2. ARU and ADU Correction Within the Intra-Beam
- describes the term from unambiguity velocity, leading to the FRM effect.
- indicates the term of the radial acceleration, which would cause the SRM effect. Meanwhile, it would result in a Doppler spreading problem in the frequency domain, which is called the ADU effect.
- represents the residual range walk of the velocity ambiguity factor.
3.3. Detailed Implementation Steps
| Algorithm 1: The detailed procedures of the implementation approach |
 |
4. Additional Analysis for the Proposed Approach
4.1. The Analysis of Computational Complexity
4.2. The Analysis of the Output SNR
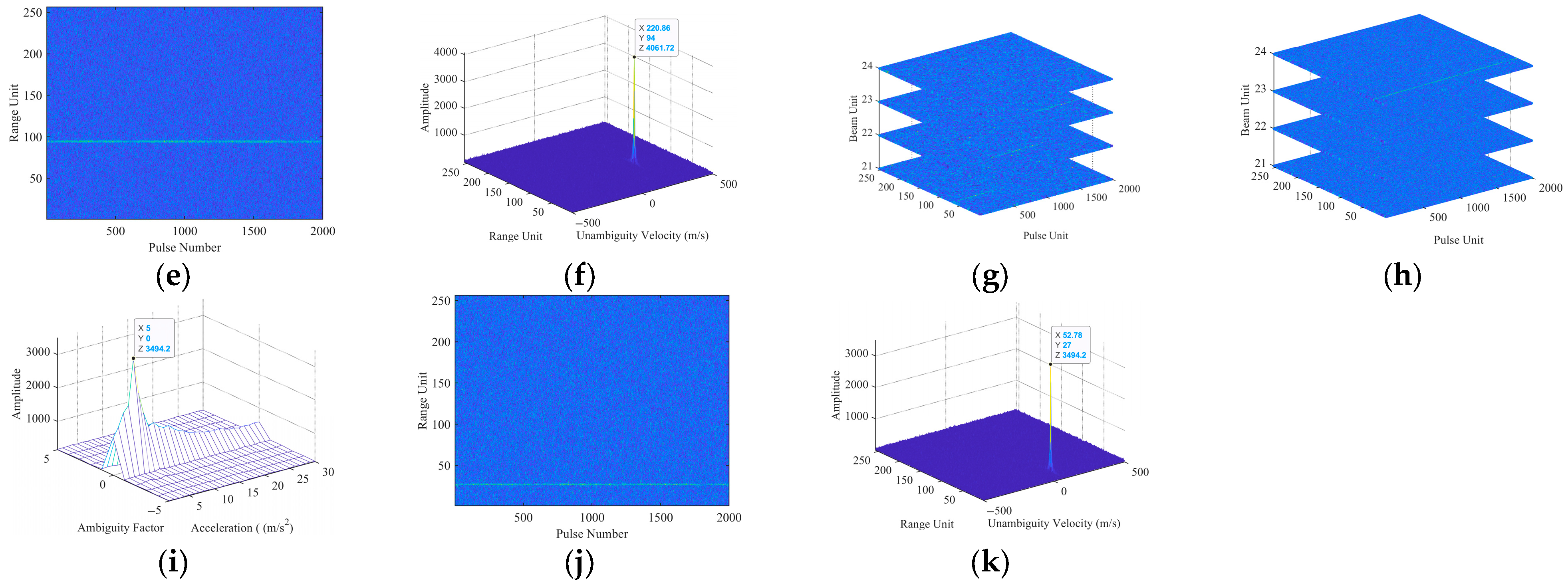
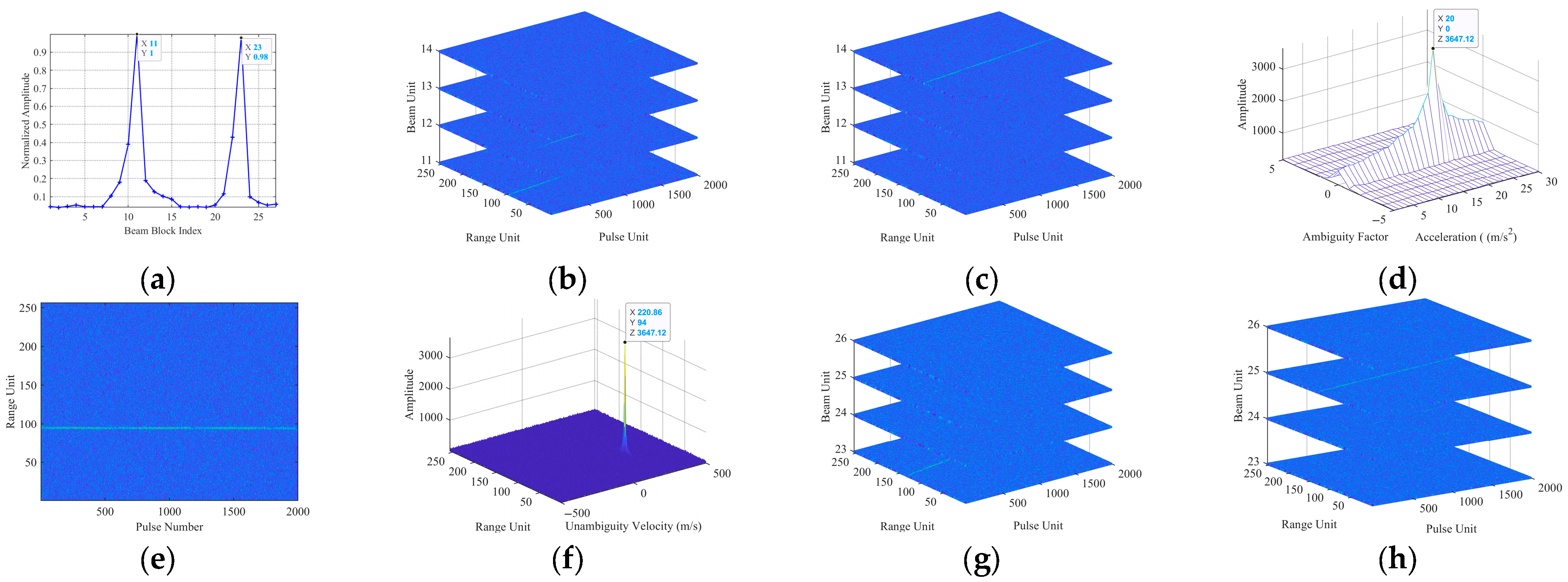
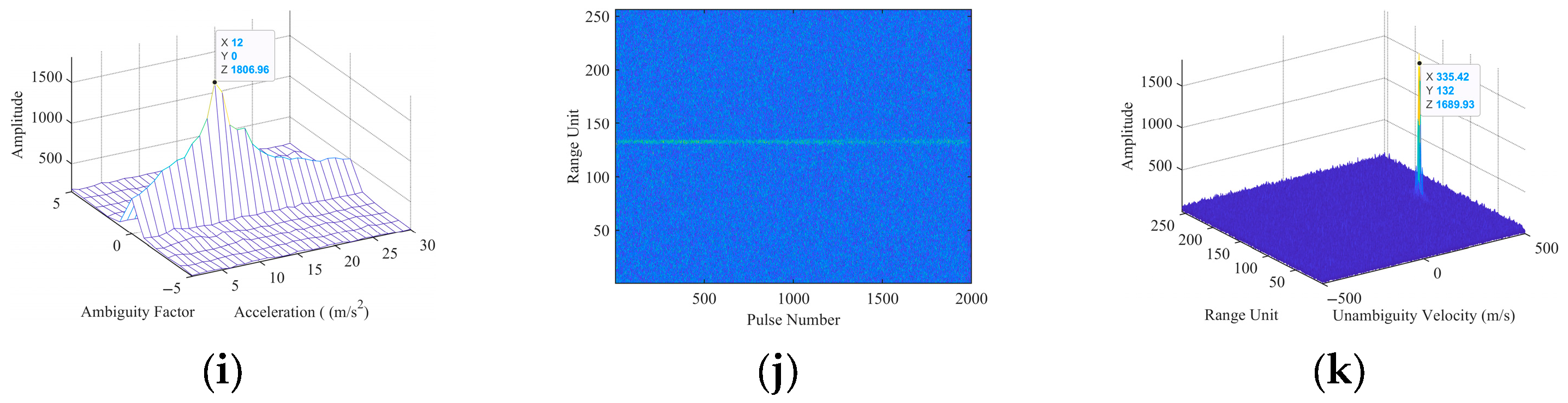
5. Simulation and Experiment Results
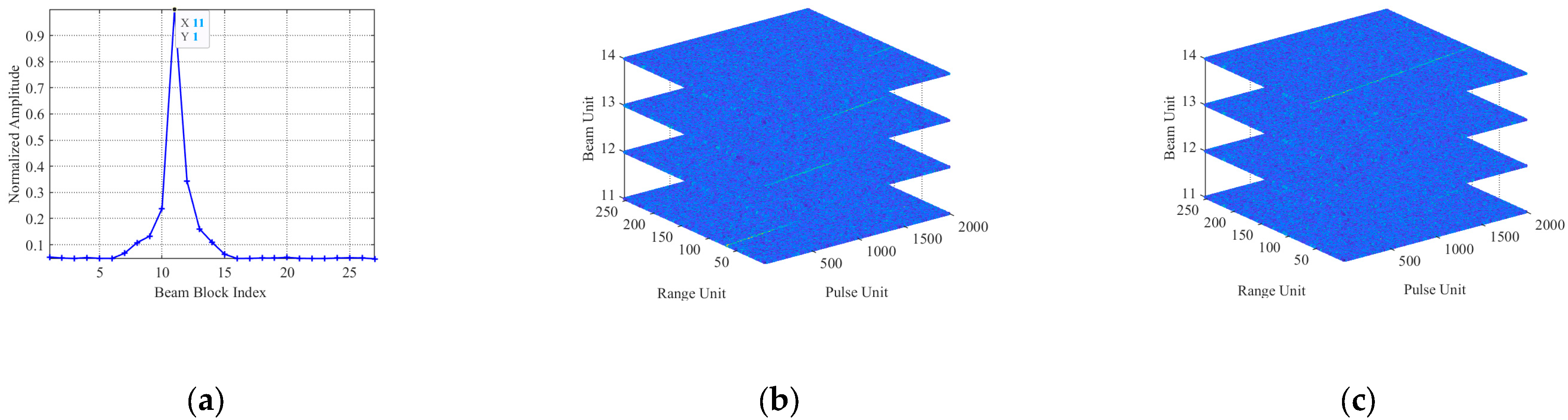
5.1. Single-Target Simulation Experimental Results
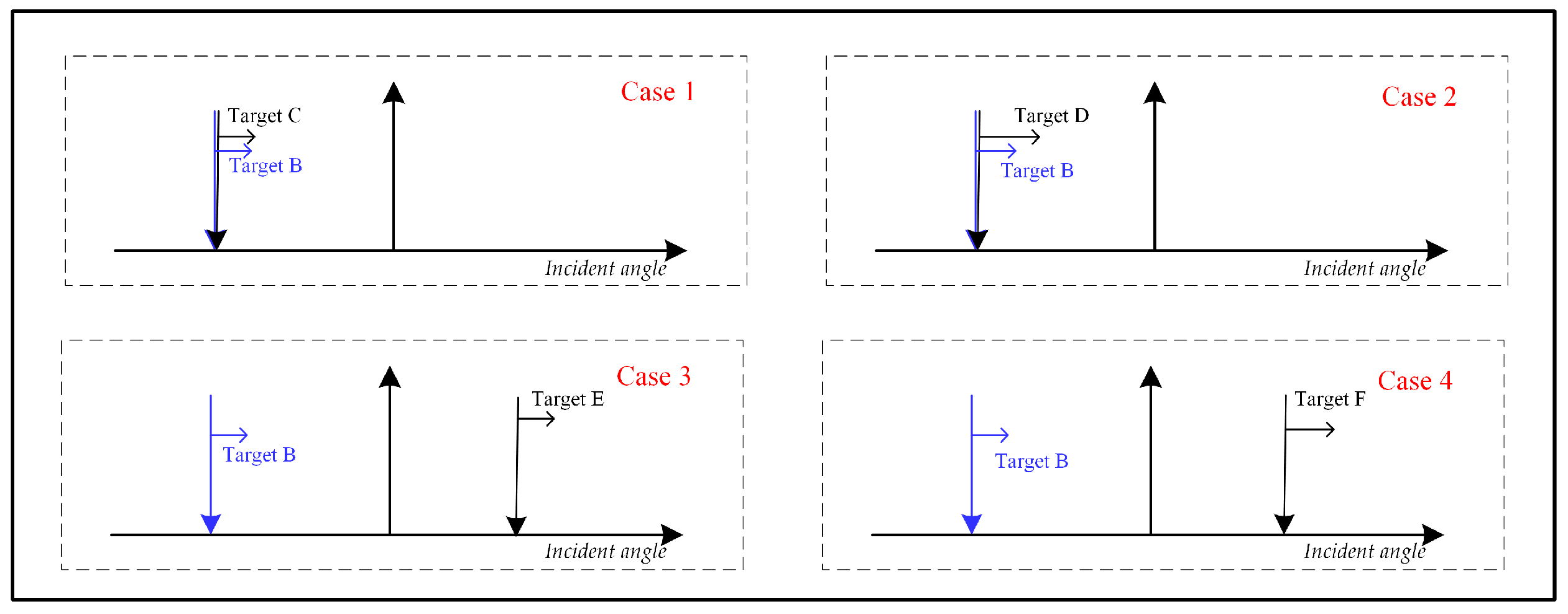
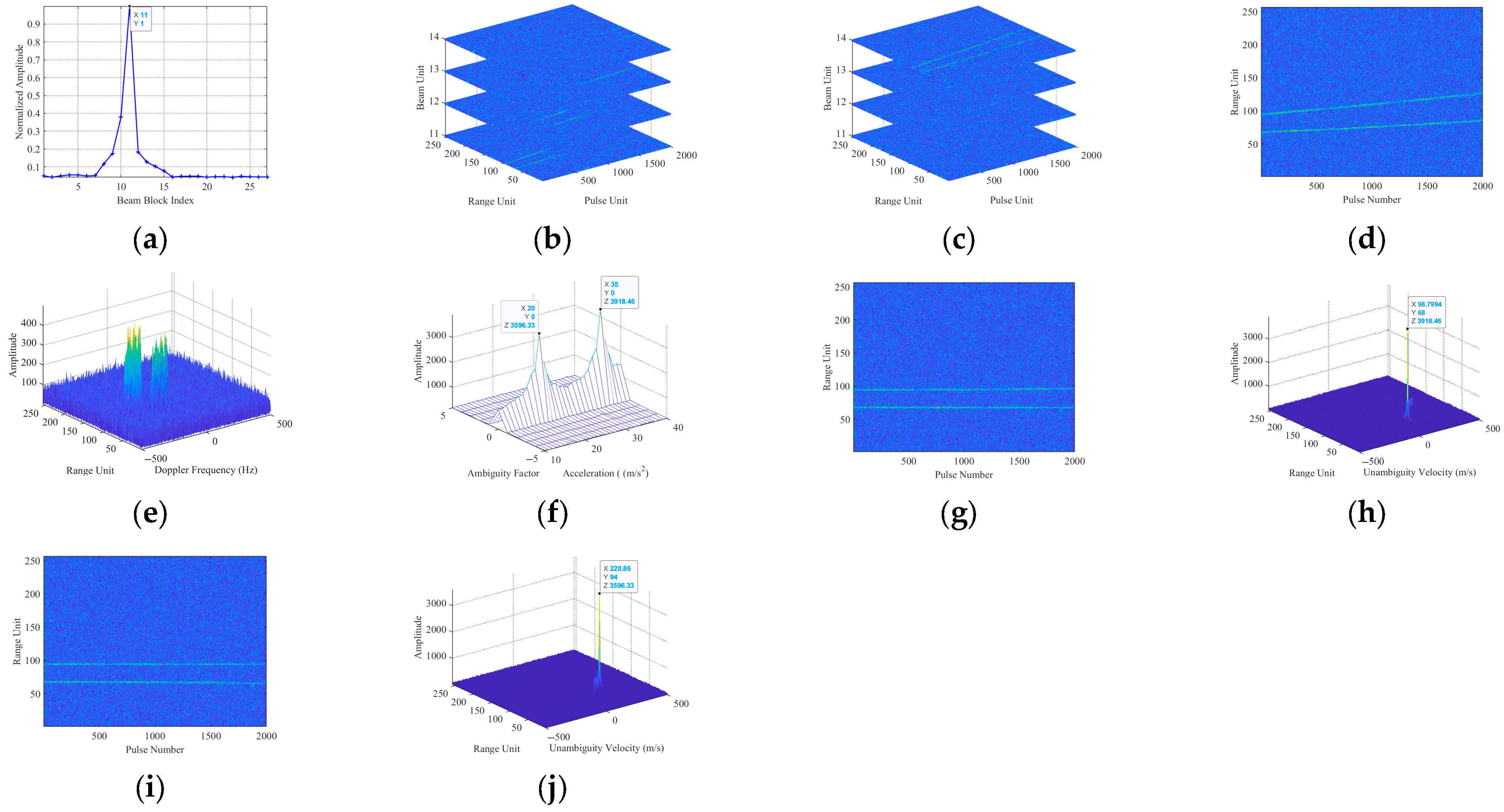
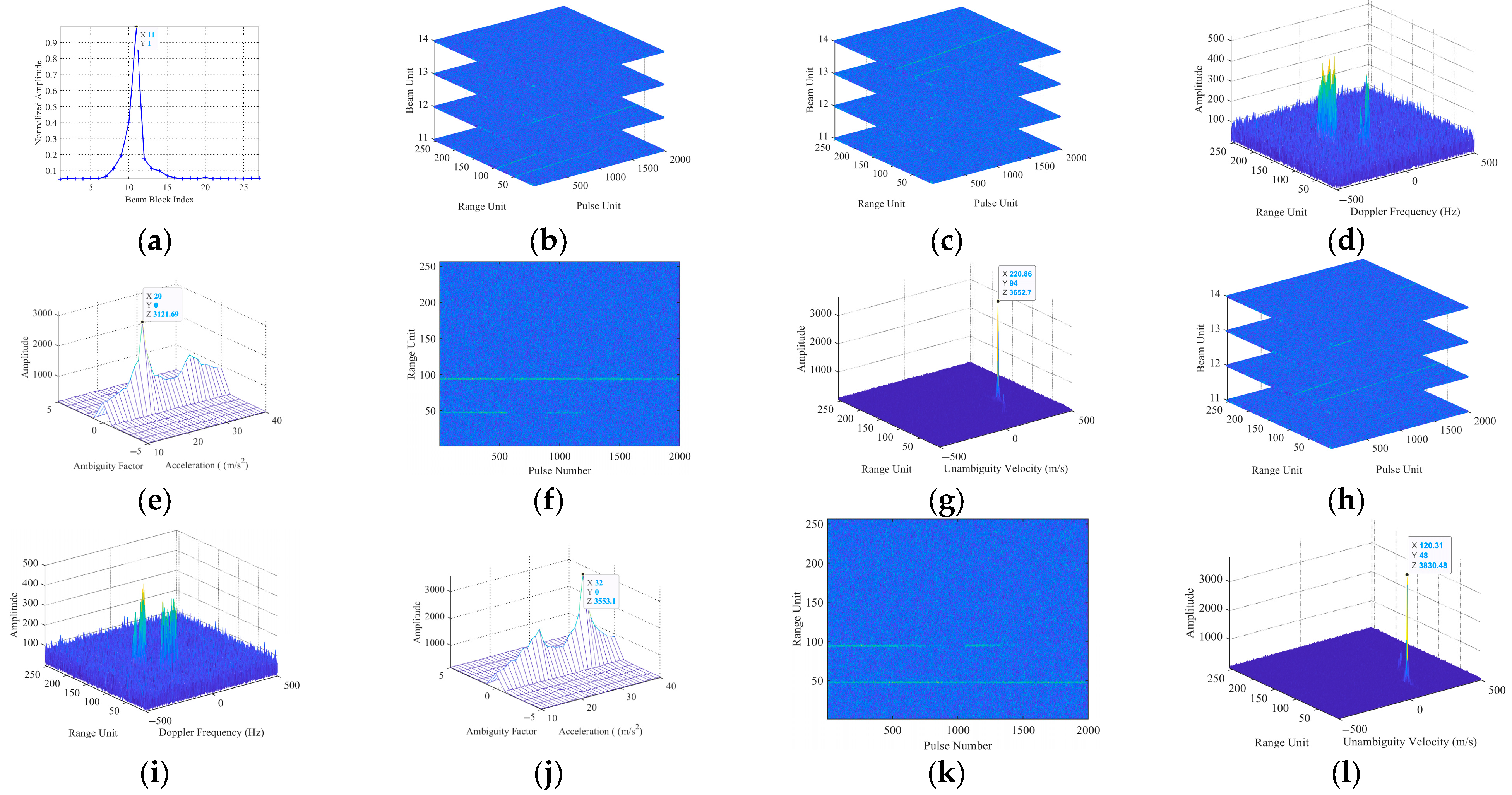
5.2. Multi-Target Simulation Experiment Results
5.3. Comparisons with the Existing Methods Under Low SNR
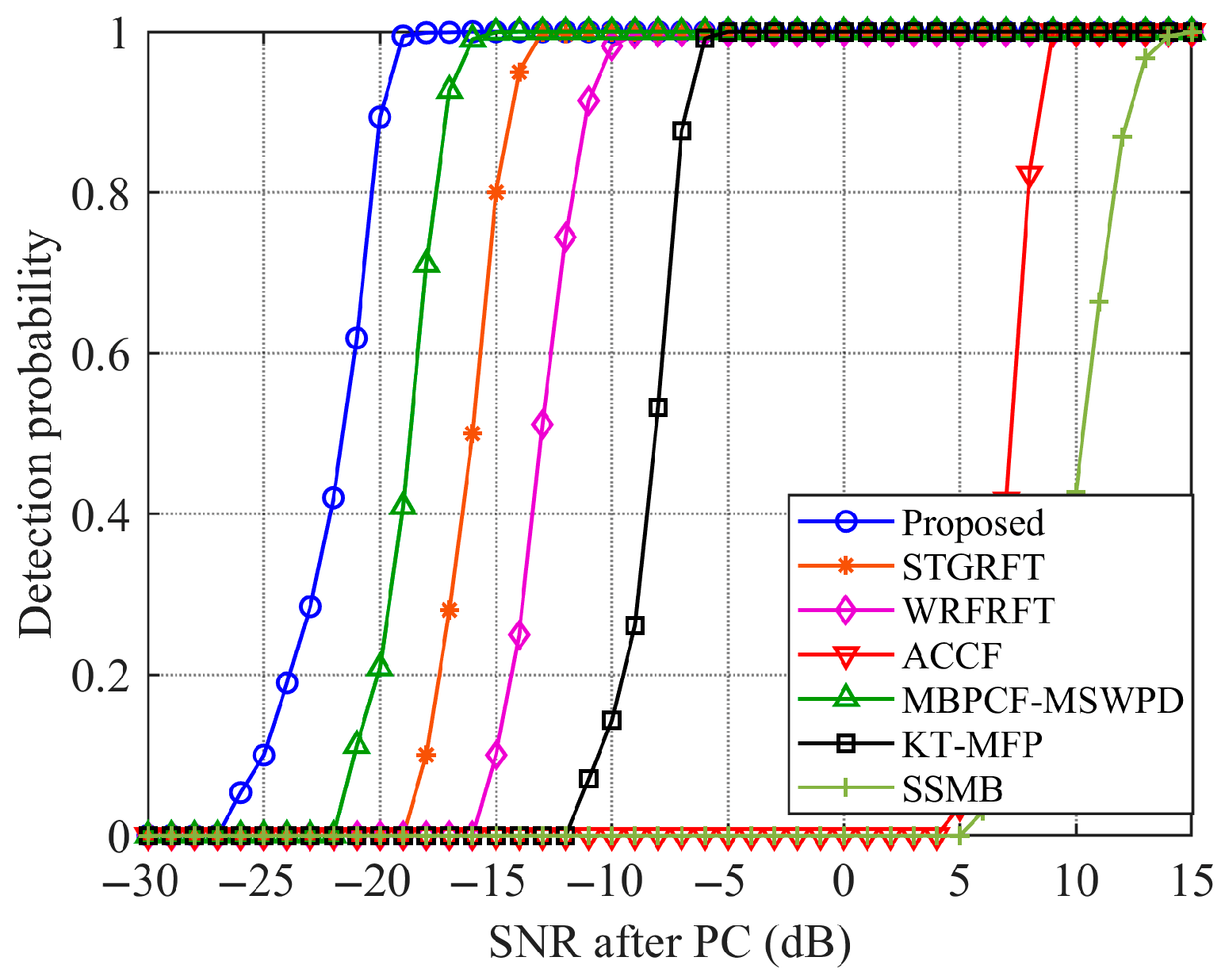
5.4. Target Detection Performance Analysis
6. Discussions
7. Conclusions
- (1)
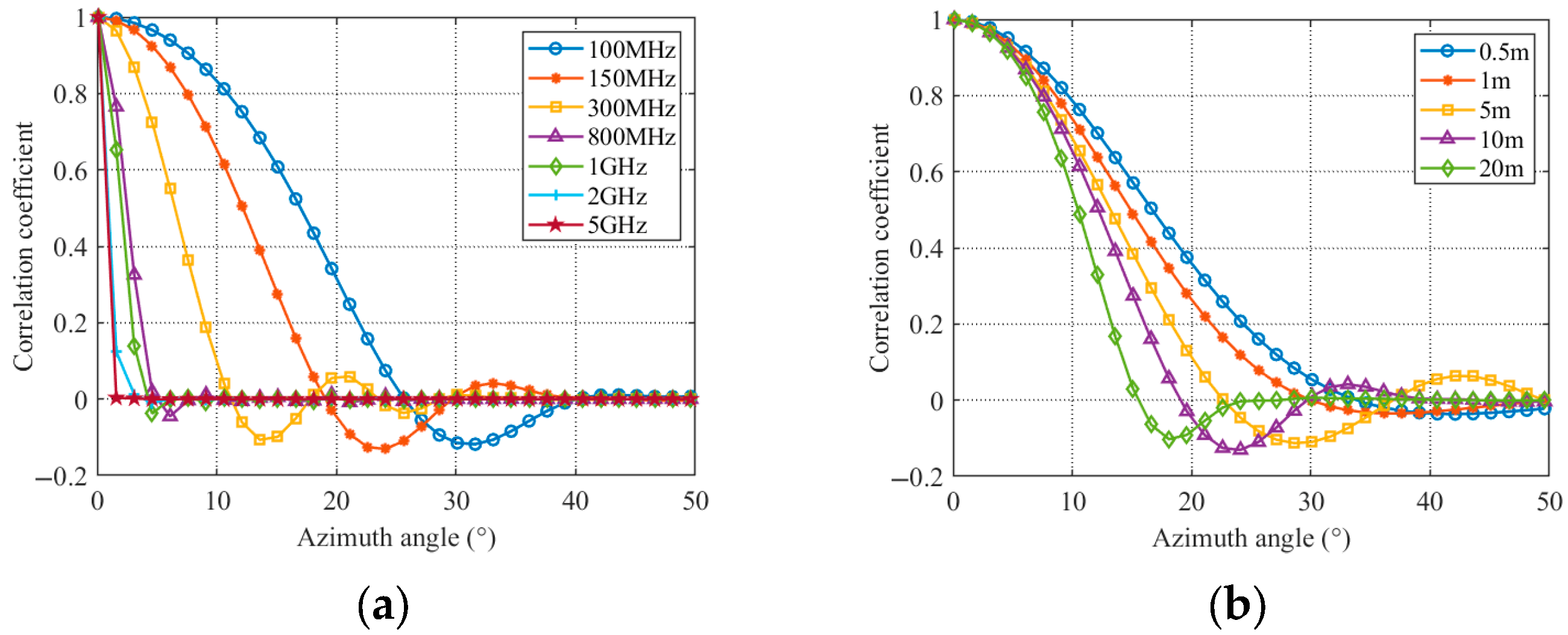
- An across-beam 3D signal model for a high-speed target with UDAR system is established to introduce “three-crossing” problems, and the detailed mathematical analysis is conducted on the constraint conditions of the ABU, ARU, and ADU effects. In addition, the multiple perspectives echo correlation experiment shows that the higher the frequency band, the greater the loss of echo correlation.
- (2)
- Compared with the representative LTCI methods that only perform radial parameter estimation, by utilizing a three-dimensional search based on the spatial domain angle, ambiguity factor, and radial angular velocity, the proposed algorithm realizes excellent accumulation ability, and the tangential and radial motion characteristics of high-speed targets can be obtained.
- (3)
- We develop a kind of spatial windowing processing approach to accelerate the computational efficiency with multiple beam blocks. Owing to the flexible division of beam blocks, simulation experiments verify that the proposed algorithm possesses the ability to distinguish multiple targets in the spatial domain.
- (4)
- Moreover, the proposed algorithm effectively corrects the across-beam signal to the final beam unit. It can output angle information that is closer to the true spatial position of the target when the target flies out of the illumination area, which is particularly critical in complex scenarios for high-speed target detection.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hussain, M.; Ahmed, R.; Cheema, H.M. Segmented Radon Fourier Transform for Long-Time Coherent Radars. IEEE Sens. J. 2023, 23, 9582–9594. [Google Scholar] [CrossRef]
- Xu, J.; Peng, Y.; Xia, X. Focus-before-detection radar signal processing: Part I—Challenges and methods. IEEE Trans. Aerosp. Electron. Syst. 2017, 32, 48–59. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Zhang, L.; Liu, B.; Xu, H.-X. Joint Power, Bandwidth, and Subchannel Allocation in a UAV-Assisted DFRC Network. IEEE Internet Things J. 2025, 12, 11633–11651. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Liu, B. Joint Customer Assignment, Power Allocation, and Subchannel Allocation in a UAV-Based Joint Radar and Communication Network. IEEE Internet Things J. 2024, 11, 29643–29660. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, P.; Zeng, H.; Chen, J. Moving Target Detection Using GNSS-Based Passive Bistatic Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3356. [Google Scholar] [CrossRef]
- Li, D.; Zhan, M.; Liu, H.; Liao, G. A robust translational motion compensation method for ISAR imaging based on keystone transform and fractional Fourier transform under low SNR environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2140–2156. [Google Scholar] [CrossRef]
- Liu, G.; Tian, Y.; Wen, B.; Liu, C. Combined Coherent and Non-Coherent Long-Time Integration Method for High-Speed Target Detection Using High-Frequency Radar. Remote Sens. 2024, 16, 2139. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Fei, T. A Robust Joint Frequency Spectrum and Power Allocation Strategy in a Coexisting Radar and Communication System. Chin. J. Aeronaut. 2024, 37, 393–409. [Google Scholar] [CrossRef]
- De Quevedo, A.D.; Urzaiz, F.I.; Menoyo, J.G.; Lopez, A.A. Drone Detection and RCS Measurements with Ubiquitous Radar. In Proceedings of the 2018 International Conference on Radar, Brisbane, Australia, 27–31 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Massardo, M.; Stallone, R. Experimental Validation of a Frustum of Cone Antenna Applied to Omega 360 Ubiquitous 2D Radar. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace, Padua, Italy, 21–23 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 36–39. [Google Scholar]
- Zheng, J.; Su, T.; Zhu, W.; He, X.; Liu, Q.H. Radar High-Speed Target Detection Based on the Scaled Inverse Fourier Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 1108–1119. [Google Scholar] [CrossRef]
- Zheng, J.; Su, T.; Liu, H.; Liao, G.; Liu, Z.; Liu, Q.H. Radar High-Speed Target Detection Based on the Frequency-Domain Deramp-Keystone Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 285–294. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A Fast Maneuvering Target Motion Parameters Estimation Algorithm Based on ACCF. IEEE Signal Process. Lett. 2015, 22, 270–274. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Sequence-Reversing Transform-Based Coherent Integration for High-Speed Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1573–1580. [Google Scholar] [CrossRef]
- Wan, J.; He, Z.; Tan, X.; Li, D.; Liu, H.; Shu, Y.; Chen, Z. Coherent Integration for Maneuvering Target Detection via Fast Nonparametric Estimation Method. Signal Process. 2023, 203, 108820. [Google Scholar] [CrossRef]
- Niu, Z.; Zheng, J.; Su, T.; Zhang, J. Fast Implementation of Scaled Inverse Fourier Transform for High-speed Radar Target Detection. Electron. lett. 2017, 53, 1142–1144. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.-G.; Ma, J.-T.; Ma, J. Long-Time Coherent Integration for Weak Maneuvering Target Detection and High-Order Motion Parameter Estimation Based on Keystone Transform. IEEE Trans. Signal Process. 2016, 64, 4013–4026. [Google Scholar] [CrossRef]
- Rao, X.; Tao, H.; Su, J.; Guo, X.; Zhang, J. Axis Rotation MTD Algorithm for Weak Target Detection. Digit. Signal Process. 2014, 26, 81–86. [Google Scholar] [CrossRef]
- Wang, L.; Tao, H.; Yang, A.; Yang, F. Coherent Integration Method for High-speed Target Detection Using Angular Inverse Rotation Transform. Electron. lett. 2024, 60, e70087. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Yi, W.; Cui, G.; Kong, L. A Coherent Detection and Velocity Estimation Algorithm for the High-Speed Target Based on the Modified Location Rotation Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2346–2361. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Y.; Zhang, L.; Chen, Z.; Zhang, L. Detection and Fast Motion Parameter Estimation for Target with Range Walk Effect Based on New Axis Rotation Moving Target Detection. Digit. Signal Process. 2022, 120, 103274. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.-N.; Xia, X.-G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yan, L.; Zhou, X.; Long, T.; Xia, X.-G.; Wang, Y.-L.; Farina, A. Adaptive Radon–Fourier Transform for Weak Radar Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1641–1663. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A Keystone Transform Without Interpolation for SAR Ground Moving-Target Imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Xu, J.; Xia, X.-G.; Peng, S.-B.; Yu, J.; Peng, Y.-N.; Qian, L.-C. Radar Maneuvering Target Motion Estimation Based on Generalized Radon-Fourier Transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration. IEEE Trans. Signal Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-Linear Canonical Ambiguity Function-Based Detection and Estimation Method for Marine Target With Micromotion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Deng, J.; Sun, Z.; Liu, W.; Li, X.; Cui, G. Blind Source Separation-Based High-Speed Weak Target Coherent Detection Method Under Strong Target BSSL Covering Situation. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 7987–7994. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Radar Detection and Parameter Estimation of High-Speed Target Based on MART-LVT. IEEE Sens. J. 2019, 19, 1478–1486. [Google Scholar] [CrossRef]
- Rao, X.; Tao, H.; Xie, J.; Su, J.; Li, W. Long-time Coherent Integration Detection of Weak Manoeuvring Target via Integration Algorithm, Improved Axis Rotation Discrete chirp-Fourier Transform. IET Radar. Sonar. Amp. Navig. 2015, 9, 917–926. [Google Scholar] [CrossRef]
- Rao, X.; Tao, H.; Su, J.; Xie, J.; Zhang, X. Detection of Constant Radial Acceleration Weak Target via IAR-FRFT. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3242–3253. [Google Scholar] [CrossRef]
- Zeng, C.; Li, D.; Luo, X.; Song, D.; Liu, H.; Su, J. Ground Maneuvering Targets Imaging for Synthetic Aperture Radar Based on Second-Order Keystone Transform and High-Order Motion Parameter Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4486–4501. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Yi, W.; Cui, G.; Kong, L. Detection of Weak Maneuvering Target Based on Keystone Transform and Matched Filtering Process. Signal Process. 2017, 140, 127–138. [Google Scholar] [CrossRef]
- Zhan, M.; Huang, P.; Zhu, S.; Liu, X.; Liao, G.; Sheng, J.; Li, S. A Modified Keystone Transform Matched Filtering Method for Space-Moving Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. An Airborne SAR Moving Target Imaging and Motion Parameters Estimation Algorithm With Azimuth-Dechirping and the Second-Order Keystone Transform Applied. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3967–3976. [Google Scholar]
- Zhang, Q.; Zhang, Y.; Sun, B.; Dong, Z.; Yu, L. Motion Parameters Estimation and HRRP Reconstruction of Maneuvering Weak Target for Wideband Radar Based on SKT-ELVD. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2752–2763. [Google Scholar] [CrossRef]
- Fang, X.; Xiao, G.; Cao, Z.; Min, R.; Pi, Y. Migration Correction Algorithm for Coherent Integration of Low-Observable Target with Uniform Radial Acceleration. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Wang, L.; Tao, H.; Yang, A.; Yang, F.; Wang, X. A Fast Non-Searching Method for Maneuvering Weak Target Detection Using Ubiquitous Radar. In Proceedings of the 2023 6th International Conference on Information Communication and Signal Processing, Xi’an, China, 23–25 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 512–516. [Google Scholar]
- Lin, L.; Sun, G.; Cheng, Z.; He, Z. Long-Time Coherent Integration for Maneuvering Target Detection Based on ITRT-MRFT. IEEE Sens. J. 2020, 20, 3718–3731. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, J.; Du, X.; Liu, Q.H. Radar High-Speed Maneuvering Target Detection Based on Three-Dimensional Scaled Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2821–2833. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.-G.; Liu, X.; Liao, G. Refocusing and Motion Parameter Estimation for Ground Moving Targets Based on Improved Axis Rotation-Time Reversal Transform. IEEE Trans. Comput. Imaging 2018, 4, 479–494. [Google Scholar] [CrossRef]
- Rao, X.; Sun, Z.Y.; Tao, H.H. Multi-Beam Associated Coherent Integration Algorithm for Weak Target Detection. Radioengineering 2024, 33, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Yeo, T.S.; Zhang, T.; Yi, W.; Cui, G.; Kong, L. STGRFT for Detection of Maneuvering Weak Target with Multiple Motion Models. IEEE Trans. Signal Process. 2019, 67, 1902–1917. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Zhang, T.; Yi, W.; Cui, G.; Kong, L. WRFRFT-Based Coherent Detection and Parameter Estimation of Radar Moving Target with Unknown Entry/Departure Time. Signal Process. 2020, 166, 107228. [Google Scholar] [CrossRef]
- Hu, R.; Li, D.; Wan, J.; Kang, X.; Liu, Q.; Chen, Z.; Yang, X. Integration and Detection of a Moving Target with Multiple Beams Based on Multi-Scale Sliding Windowed Phase Difference and Spatial Projection. Remote Sens. 2023, 15, 4429. [Google Scholar] [CrossRef]
- Wang, L.; Tao, H.; Yang, A.; Yang, F.; Ma, H.; Su, J. Radar High-Speed Moving Target Coherent Integration and Parameter Estimation Algorithm Using PSA-FAIR-NUFFT. IEEE Sens. J. 2025, 25, 24712–24730. [Google Scholar] [CrossRef]
- Niu, Z. Research on Energy Focusing and Detection Technology of Range Migrating Radar Target; Xidian University: Xi’an, China, 2020. [Google Scholar]
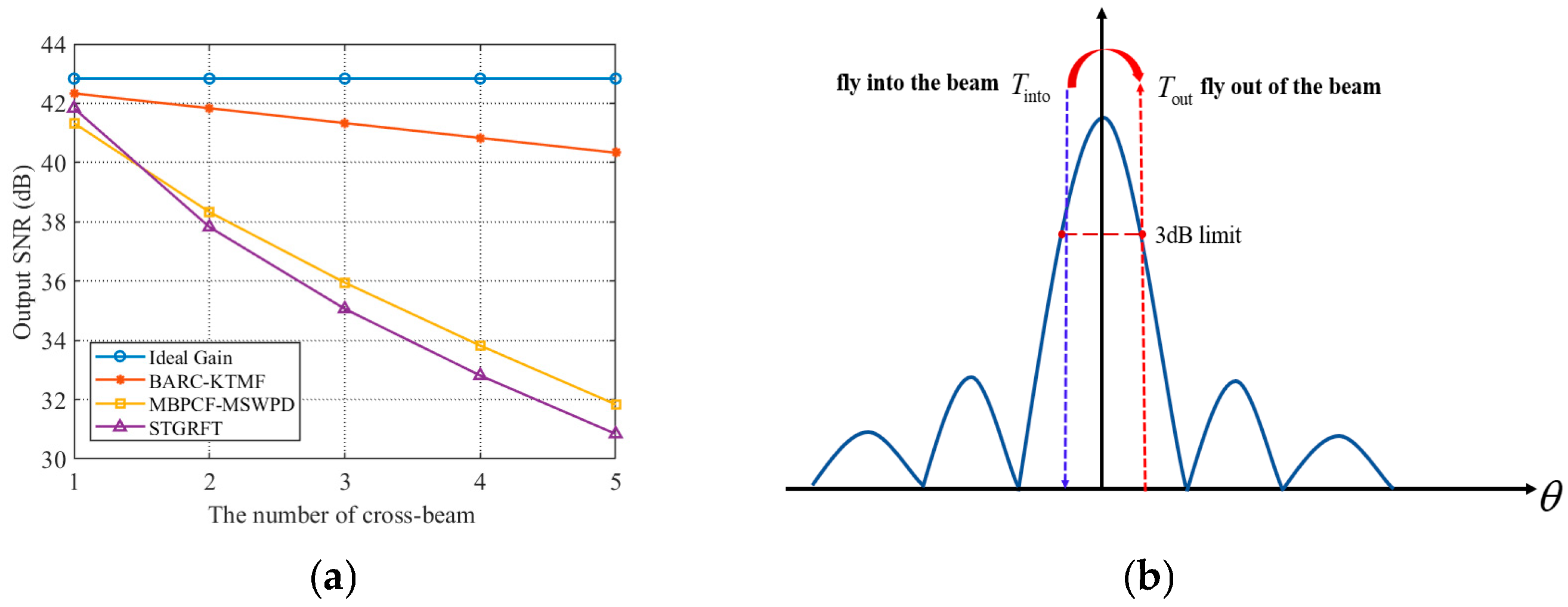

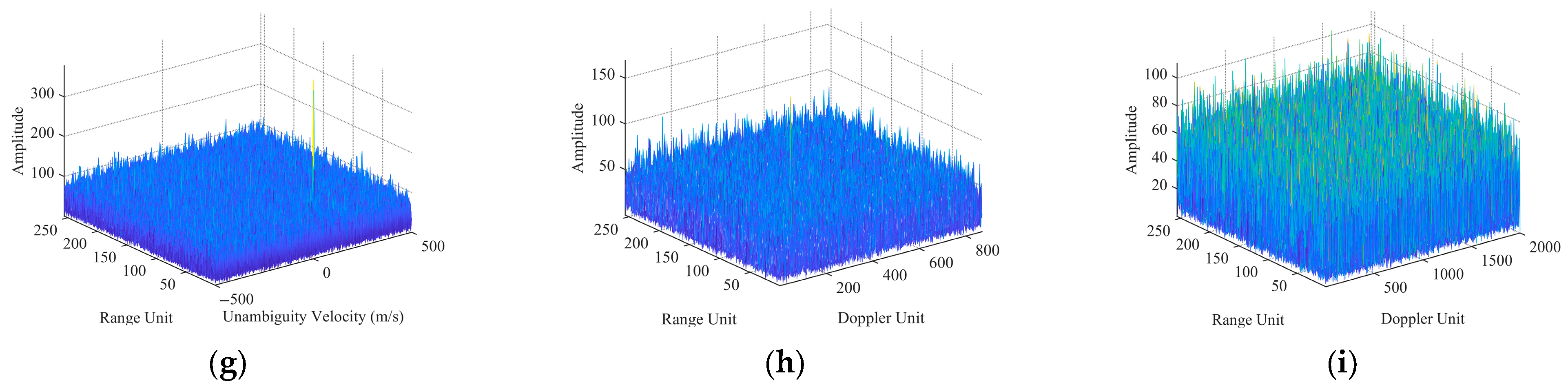
| Methods | Output SNRs | Remarks |
| Ideal Gain | ||
| BARC-KTMF | ||
| MBPCF-MSWPD | ||
| STGRFT |
| Parameter Name | Symbol | Parameter Value | Parameter Name | Symbol | Parameter Value |
|---|---|---|---|---|---|
| Carrier frequency | 150 MHz | Pulse duration | 10 μs | ||
| Bandwidth | 10 MHz | Array element number | 48 | ||
| Range unit number | 256 | Element spacing | 1 m | ||
| Pulse repetition frequency | 1000 Hz | Receive beam number | 31 | ||
| Pulse number | 2000 | Receive beam range | - | [−30°: 2°: 30°] | |
| Sampling rate | 10 MHz | Beam width | 2° |
| Parameter Name | Symbol | Target A |
|---|---|---|
| Azimuth angular velocity | 0.0571 rad/s | |
| Incident angle | −11° | |
| Initial radial range | 21,000 m | |
| Radial velocity | 200 m/s | |
| Radial acceleration | 60 m/s2 |
| Parameter Name | Target B | Target C | Target D | Target E | Target F |
|---|---|---|---|---|---|
| Azimuth angular velocity | 0.057 rad/s | 0.057 rad/s | 0.029 rad/s | 0.057 rad/s | 0.046 rad/s |
| Incident angle | −11° | −11° | −11° | 9° | 13° |
| Initial range | 21,200 m | 20,800 m | 20,500 m | 20,187 m | 21,774 m |
| Radial velocity | 220 m/s | 98 m/s | 120 m/s | 52 m/s | 335 m/s |
| Radial acceleration | 20 m/s2 | 35 m/s2 | 32 m/s2 | 5 m/s2 | 12 m/s2 |
| SNR before DBF | −30 dB | −30 dB | −32 dB | −31 dB | −33 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Tao, H.; Yang, A.; Yang, F.; Xu, X.; Ma, H.; Su, J. Across-Beam Signal Integration Approach with Ubiquitous Digital Array Radar for High-Speed Target Detection. Remote Sens. 2025, 17, 2597. https://doi.org/10.3390/rs17152597
Wang L, Tao H, Yang A, Yang F, Xu X, Ma H, Su J. Across-Beam Signal Integration Approach with Ubiquitous Digital Array Radar for High-Speed Target Detection. Remote Sensing. 2025; 17(15):2597. https://doi.org/10.3390/rs17152597
Chicago/Turabian StyleWang, Le, Haihong Tao, Aodi Yang, Fusen Yang, Xiaoyu Xu, Huihui Ma, and Jia Su. 2025. "Across-Beam Signal Integration Approach with Ubiquitous Digital Array Radar for High-Speed Target Detection" Remote Sensing 17, no. 15: 2597. https://doi.org/10.3390/rs17152597
APA StyleWang, L., Tao, H., Yang, A., Yang, F., Xu, X., Ma, H., & Su, J. (2025). Across-Beam Signal Integration Approach with Ubiquitous Digital Array Radar for High-Speed Target Detection. Remote Sensing, 17(15), 2597. https://doi.org/10.3390/rs17152597






