Snow Depth Retrieval Using Sentinel-1 Radar Data: A Comparative Analysis of Random Forest and Support Vector Machine Models with Simulated Annealing Optimization
Abstract
1. Introduction
2. Materials and Methods
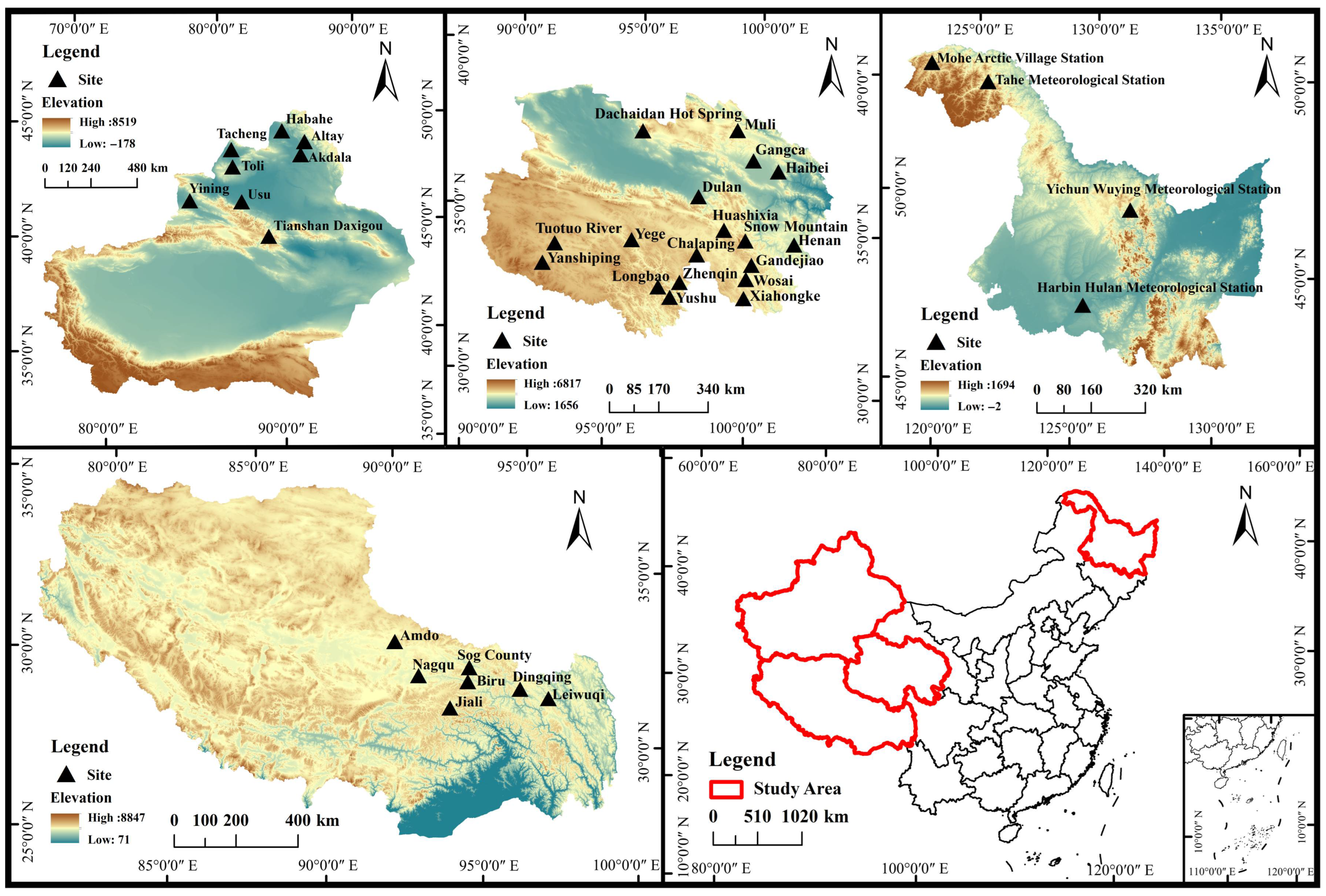
2.1. Data Source
2.1.1. Radar Data
2.1.2. In Situ Measurement Data
2.1.3. Snow Depth Products
2.2. Research Methods
2.2.1. Feature Data Processing
2.2.2. Selection of Optimal Feature Parameters
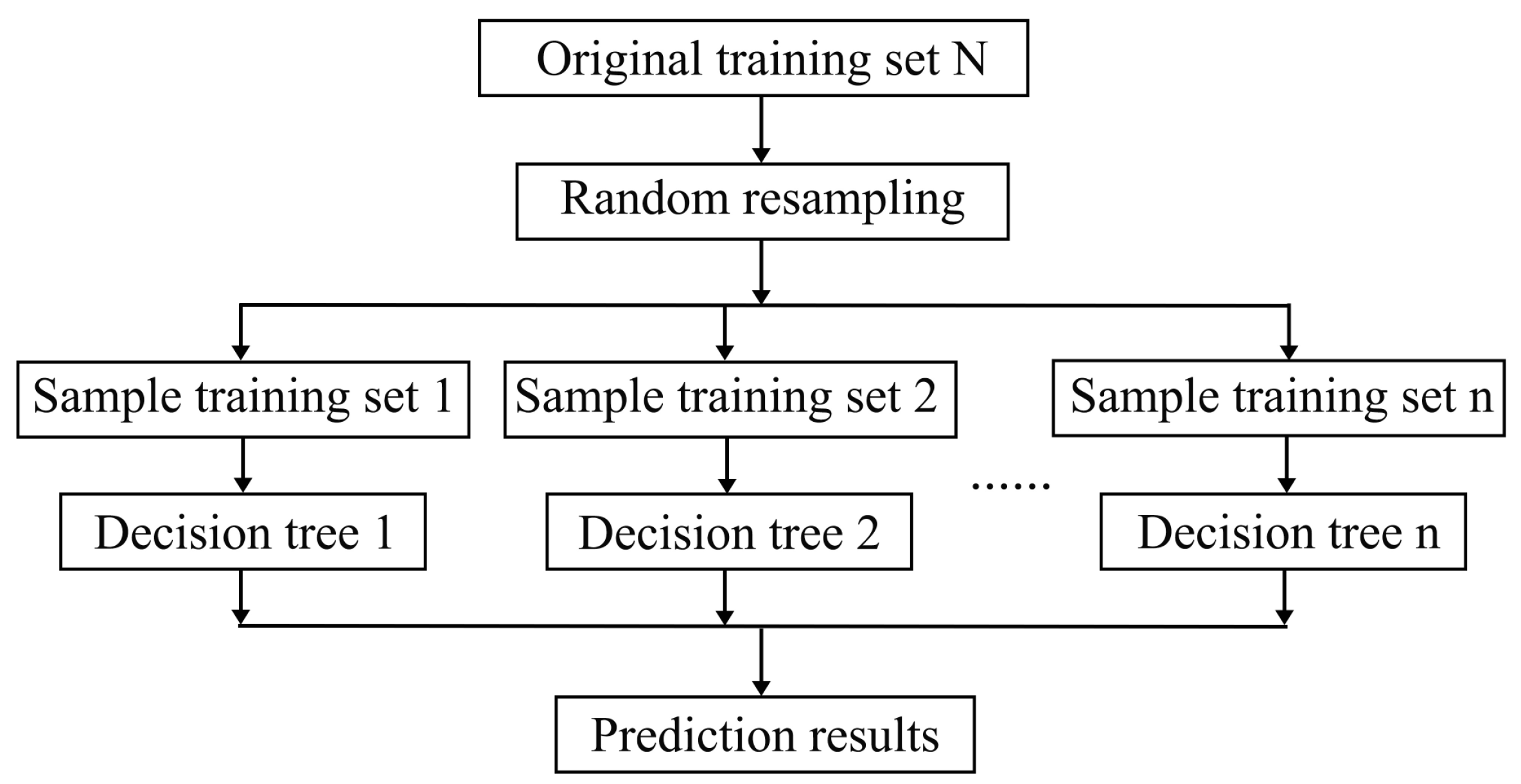
2.2.3. Random Forest Model
2.2.4. Support Vector Regression Model
2.2.5. Accuracy Validation
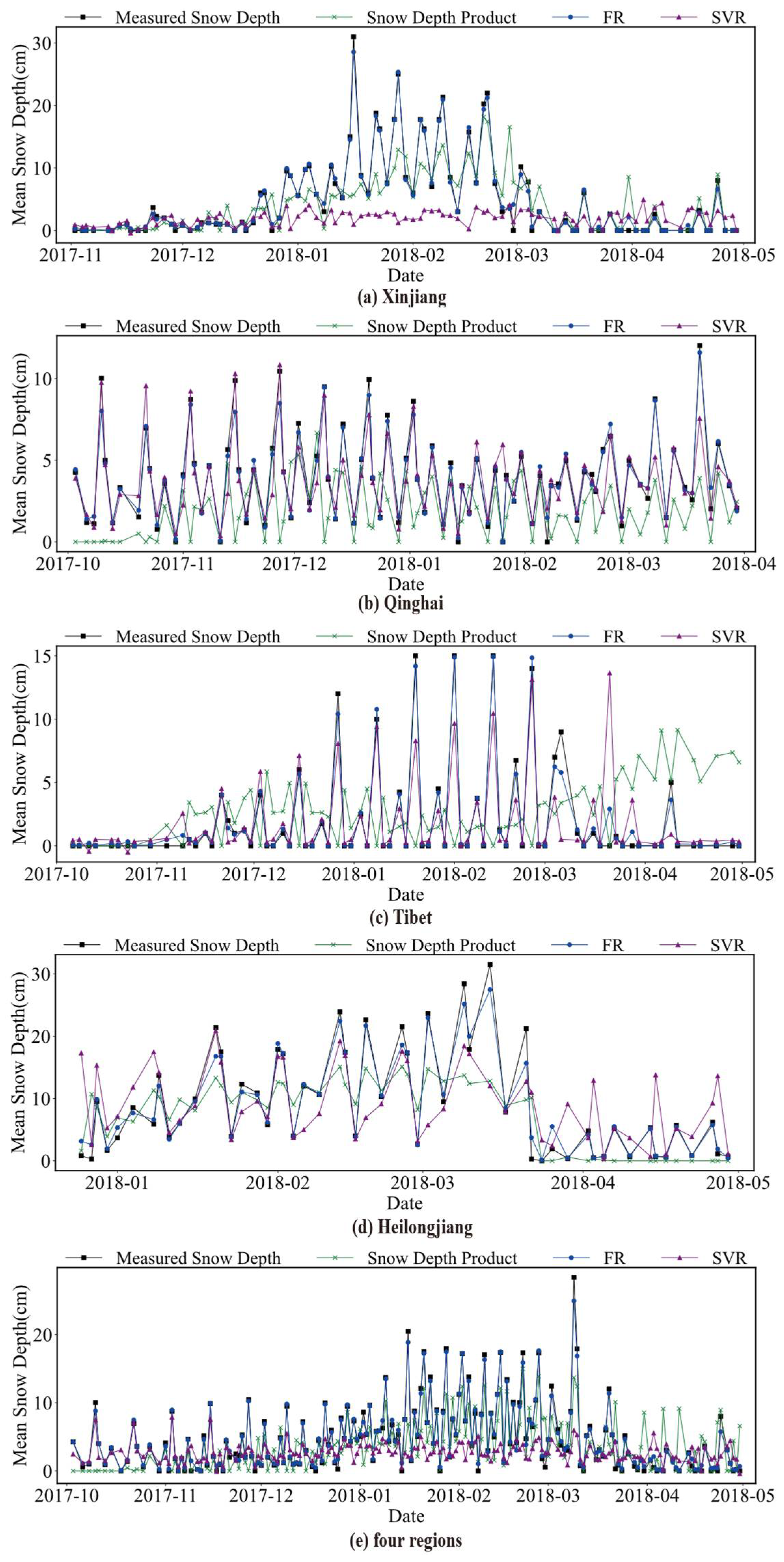
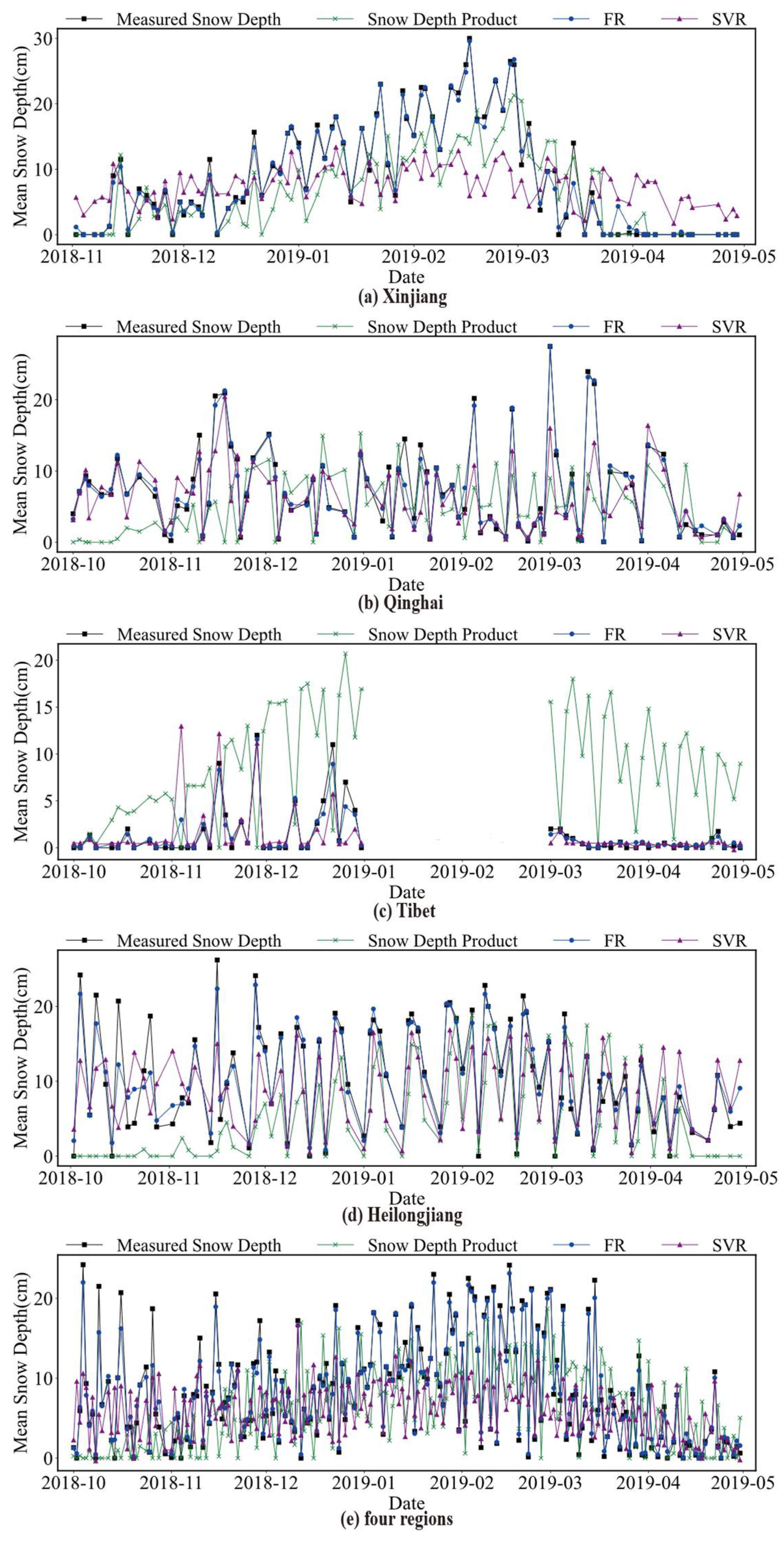
3. Results
4. Discussion
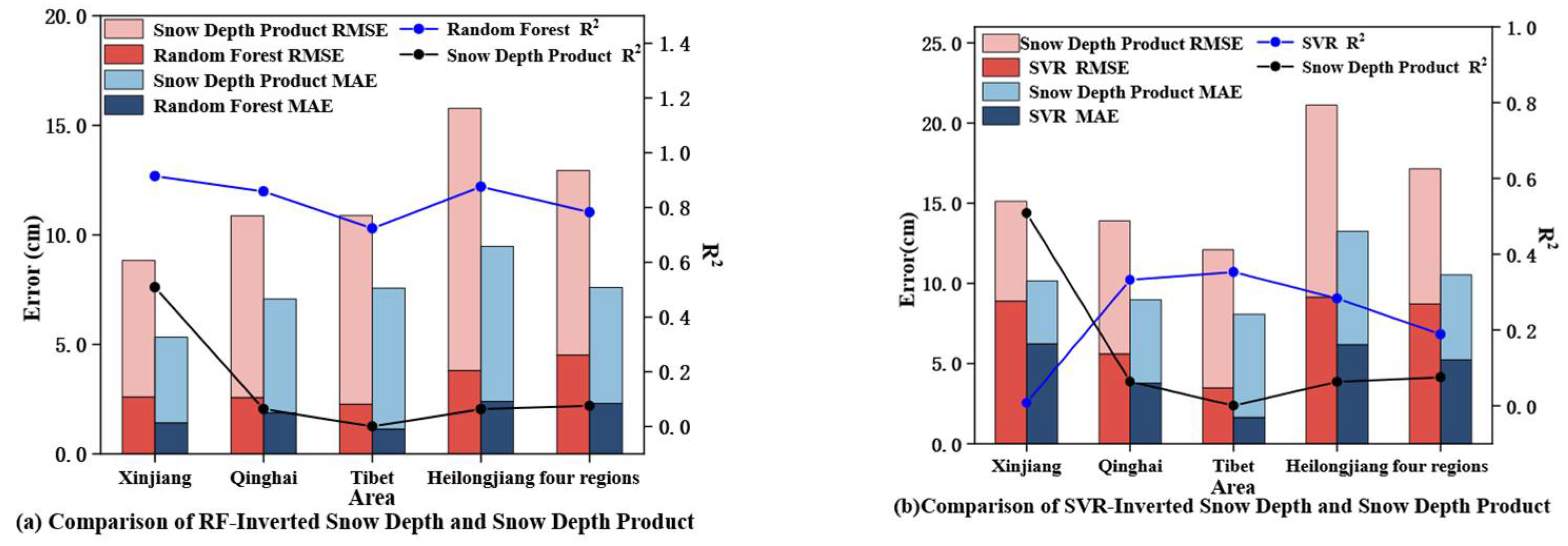
4.1. Comparison of Model Inversion Results with Snow Depth Product Results
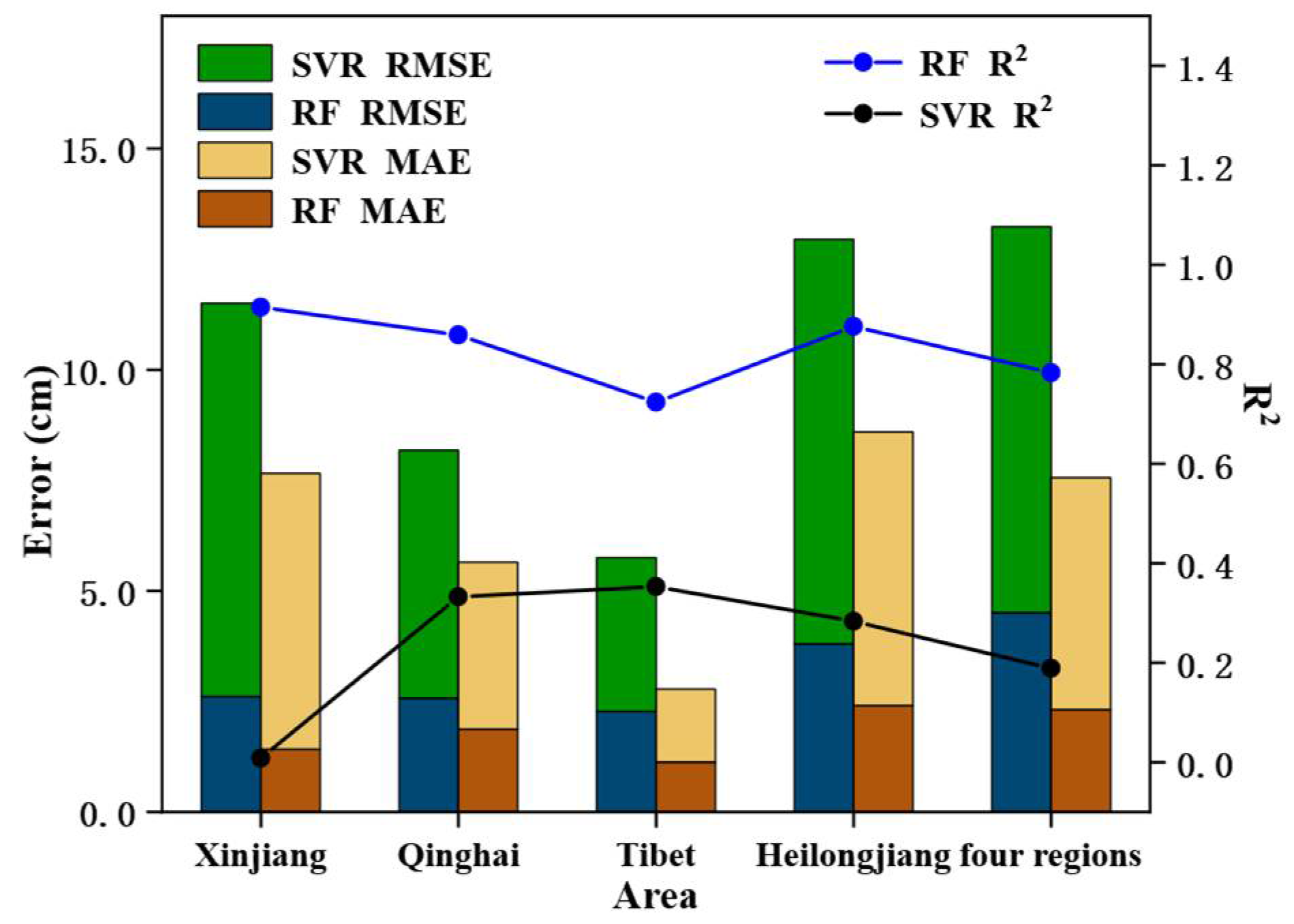
4.2. Comparison of Model Inversion Results
5. Conclusions
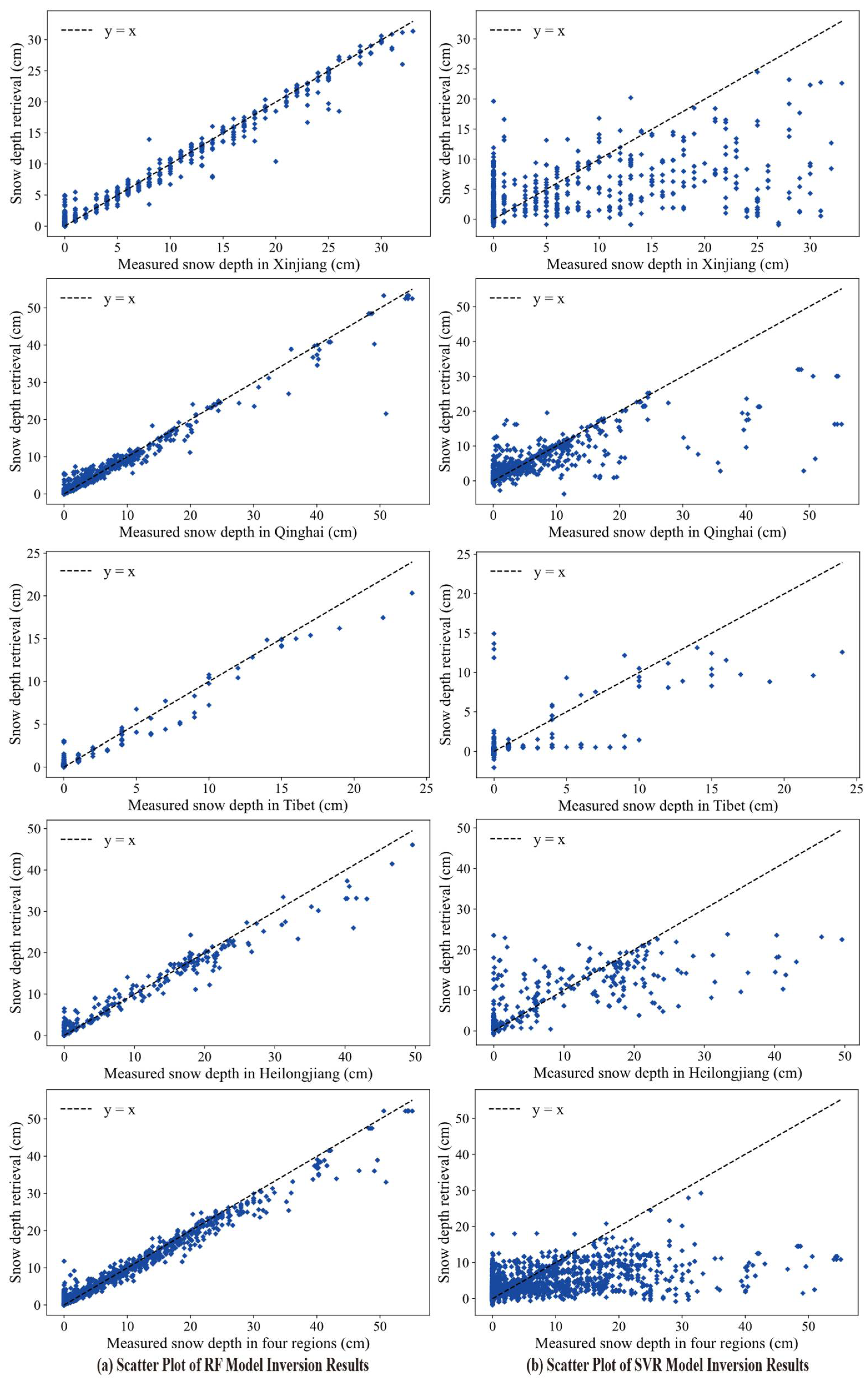
- The RF model demonstrates superior inversion accuracy and regional adaptability, achieving consistently high goodness-of-fit values (R2) across all study areas, most notably in Xinjiang (R2 = 0.915) while maintaining strong overall performance (R2 = 0.78) across all four regions. This represents a significant improvement over both SVR and conventional snow depth products, as evidenced by substantially lower RMSE and MAE values that confirm the RF model’s enhanced generalization capability under diverse terrain and snow conditions;
- While the SVR model shows marginal improvements over snow depth products in certain regions (Qinghai, Tibet, and Heilongjiang), its overall performance proves inconsistent, particularly in Xinjiang, where it underperforms even the baseline products. The model’s generally elevated error metrics (RMSE and MAE) across all regions highlight fundamental limitations in prediction accuracy and stability compared to the RF approach;
- Comparative analysis reveals the RF model’s distinct advantages over existing snow depth products, which exhibit systematic underestimation/overestimation issues evidenced by negative R2 values in some regions. The RF methodology’s superior accuracy and reliability establish it as a valuable reference for high-precision snow depth inversion applications;
- Notably, region-specific modeling demonstrates clear advantages over unified approaches, with the RF model’s aggregate regional performance (R2 = 0.78) falling below the average accuracy of individual regional models. This performance gap becomes even more pronounced for SVR (overall R2 = 0.09), emphasizing the importance of accounting for regional variations in terrain, climate, and vegetation characteristics through localized factor selection and modeling strategies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Area | ID | Station Name | Longitude (E) | Latitude (N) | Altitude (m) |
|---|---|---|---|---|---|
| Xinjiang | 1 | Altay | 88°4′48″ | 47°43′48″ | 735 |
| 2 | Tianshan Daxigou | 86°49′48″ | 43°6′0″ | 3539 | |
| 3 | Yining | 81°19′48″ | 43°57′0″ | 663 | |
| 4 | Usu | 84°40′12″ | 44°25′48″ | 479 | |
| 5 | Toli | 83°36′0″ | 45°55′48″ | 1094 | |
| 6 | Tacheng | 83°0′0″ | 46°43′48″ | 535 | |
| 7 | Akdala | 87°58′12″ | 47°6′0″ | 563 | |
| 8 | Habahe | 86°24′0″ | 48°3′0″ | 533 | |
| Qinghai | 9 | Gangca | 99°51′33.22″ | 37°15′40.15″ | 3133 |
| 10 | Henan | 101°34′59″ | 34°44′7″ | 3509 | |
| 11 | Huashixia | 98°51′23.86″ | 35°5′39.16″ | 4255 | |
| 12 | Wosai | 99°47′53.37″ | 33°37′19.84″ | 4033 | |
| 13 | Chalaping | 97°53′2.01″ | 34°16′44.89″ | 4625 | |
| 14 | Snow Mountain | 99°42′5.05″ | 34°47′57.52″ | 3848 | |
| 15 | Muli | 99°9′46.07″ | 38°9′52.37″ | 3988 | |
| 16 | Dachaidan Hot Spring | 95°22′34.32″ | 37°55′56.91″ | 3572 | |
| 17 | Yushu | 96°36′58″ | 33°9′10″ | 4245 | |
| 18 | Zhenqin | 97°18′10.44″ | 33°24′11.52″ | 4265 | |
| 19 | Yege | 95°20′59.64″ | 34°34′57.36″ | 4271 | |
| 20 | Yanshiping | 92°4′12″ | 33°34′51.96″ | 4713 | |
| 21 | Dulan | 97°47′36″ | 36°3′34″ | 3001 | |
| 22 | Tuotuo River | 92°26′19″ | 34°12′58″ | 4533 | |
| 23 | Longbao | 96°30′29″ | 33°12′42″ | 4600 | |
| 24 | Gandejiao | 99°52′18.14″ | 33°57′49.71″ | 4107 | |
| 25 | Haibei | 100°51′32.09″ | 36°57′31.8″ | 3132 | |
| 26 | Xiakongke | 99°41′23.46″ | 32°48′1.08″ | 4001 | |
| Tibet | 27 | Amdo | 91°6′0″ | 32°21′0″ | 4800 |
| 28 | Nagqu | 92°4′0″ | 31°29′0″ | 4507 | |
| 29 | Sog County | 93°47′0″ | 31°53′0″ | 4023 | |
| 30 | Biru | 93°47′0″ | 31°29′0″ | 3940 | |
| 31 | Dingqing | 95°36′0″ | 31°25′0″ | 3873 | |
| 32 | Leiwuqi | 96°36′0″ | 31°13′0″ | 3810 | |
| 33 | Jiali | 93°17′0″ | 30°40′0″ | 4489 | |
| Heilongjiang | 34 | Haerbin Hulan Meteorological Station | 126°34′53.33″ | 45°56′2.62″ | 115 |
| 35 | Yichun Wuying Meteorological Station | 129°13′44.4″ | 48°6′45.58″ | 307 | |
| 36 | Mohe Arctic Village Station | 122°20′47.65″ | 53°28′17.15″ | 296 | |
| 37 | Tahe Meteorological Station | 124°43′22.8″ | 52°21′0.72″ | 357 |
References
- Grippa, M.; Mognard, N.; Le Toan, T.; Josberger, E.G. Siberia Snow Depth Climatology Derived from SSM/I Data Using a Combined Dynamic and Static Algorithm. Remote Sens. Environ. 2004, 93, 30–41. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Gao, F. Estimation of Snow Water Equivalent in the Tibetan Plateau Using Passive Microwave Remote Sensing Data (SSM/I). J. Glaciol. Geocryol. 2004, 26, 363–368. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Wang, G.; Zhao, K.; Zheng, X.; Jiang, T. Based on Snow Cover Survey Data of Accuracy Verification and Analysis of Passive Microwave Snow Cover Remote Sensing Products in Northeast China. Remote Sens. Technol. Appl. 2019, 34, 1181–1189. [Google Scholar]
- Chen, F.; Chang, L.; Feng, G. Inversion of Snow Depth in Alaska Based on GNSS-R Technology and Its Application. Chin. J. Polar Res. 2023, 35, 197–211. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Huang, C. Assimilating Passive Microwave Remote Sensing Data into a Land Surface Model to Improve the Estimation of Snow Depth. Remote Sens. Environ. 2014, 143, 54–63. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Cui, C.; Xie, G. Snow Depth Retrieval Based on AMSR-E Data in Northern Xinjiang Region, China. J. Glaciol. Geocryol. 2013, 35, 40–47. [Google Scholar]
- Deng, G.; Tang, Z.; Dong, C.; Shao, D.; Wang, X. Development and Evaluation of a Cloud-Gap-Filled MODIS Normalized Difference Snow Index Product over High Mountain Asia. Remote Sens. 2024, 16, 192. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Z.; Deng, G.; Hu, G.; You, Y.; Zhao, Y. Landsat Satellites Observed Dynamics of Snowline Altitude at the End of the Melting Season, Himalayas, 1991–2022. Remote Sens. 2023, 15, 2534. [Google Scholar] [CrossRef]
- Min, W.; Pen, J.; Li, S. The Evaluation of FY-3C Snow Products in the Tibetan Plateau. Remote Sens. Nat. Resour. 2021, 33, 145–151. [Google Scholar] [CrossRef]
- Liang, Z.; Yu, Z.; Hong, Y.; Yamin, H.; Ming, X.; Jian, G. A dynamic approach to retrieving snow depth based on the technology of integrating satellite remote sensing and in situ data. Acta Meteorol. Sin. 2013, 71, 769–782. [Google Scholar] [CrossRef]
- Tanis, C.M.; Lindgren, E.; Frey, A.; Latva, L.; Arslan, A.N.; Luojus, K. Use of Webcams in Support of Operational Snow Monitoring. Geosciences 2023, 13, 92. [Google Scholar] [CrossRef]
- Jenssen, R.; Eckerstorfer, M.; Jacobsen, S. Drone-Mounted Ultrawideband Radar for Retrieval of Snowpack Properties. IEEE Trans. Instrum. Meas. 2020, 69, 221–230. [Google Scholar] [CrossRef]
- Gao, F.; Li, X.; Armstrong, R.; Wang, J.; Che, T.; Xu, W. Operational Snow Monitoring on the Tibetan Plateau by Using SSM/I Data and Algorithm Validation. In Proceedings of the Third International Asia-Pacific Environmental Remote Sensing Remote Sensing of the Atmosphere, Ocean, Environment, and Space, Hangzhou, China, 30 April 2003; Volume 4894, pp. 456–463. [Google Scholar]
- Jiang, L.; Wang, P.; Zhang, L.; Yang, H.; Yang, J. Improvement of Snow Depth Retrieval for FY3B-MWRI in China. Sci. China Earth Sci. 2014, 57, 1278–1292. [Google Scholar] [CrossRef]
- Gao, S.; Wu, Y.; Qian, B. Retrieval of Snow Depth from FY-3B/MWRI Data over the Qinghai-Tibetan Plateau. Prog. Geophys. 2020, 35, 399–405. [Google Scholar] [CrossRef]
- Josberger, E.; Mognard, N. Passive Microwave Snow Depth Algorithm with a Proxy for Snow Metamorphism. Hydrol. Process. 2002, 16, 1557–1568. [Google Scholar] [CrossRef]
- Wu, J.; Yao, T.; Dai, Y.; Chen, W. Evaluation of Passive Microwave Snow-Depth Retrieval Algorithm in Selin Co and Nam Co. Remote Sens. Technol. Appl. 2022, 37, 1339–1349. [Google Scholar]
- Xiao, X.; Zhang, T. Passive Microwave Remote Sensing of Snow Depth and Snow Water Equivalent: Overview. Adv. Earth Sci. 2018, 33, 590. [Google Scholar] [CrossRef]
- Wen, J.; Dai, M.; Jean, P. Extent and Depth of Snow Cover over the Nyainqêntanghla Range Derived from ASAR and MODIS Data. J. Glaciol. Geocryol. 2006, 28, 54–61. [Google Scholar]
- Pulliainen, J.; Grandell, J.; Hallikainen, M. HUT Snow Emission Model and Its Applicability to Snow Water Equivalent Retrieval. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1378–1390. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.; Chang, A.T.C.; Guo, J.; Ding, K. Dense Media Radiative Transfer Theory Based on Quasicrystalline Approximation with Applications to Passive Microwave Remote Sensing of Snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Che, T.; Dai, L.; Zheng, X.; Li, X.; Zhao, K. Estimation of snow depth from passive microwave brightness temperature data in forest regions of northeast China. Remote Sens. Environ. 2016, 183, 334–349. [Google Scholar] [CrossRef]
- Deng, G.; Liu, X.; Shen, Q.; Zhang, T.; Chen, Q.; Tang, Z. Remote Sensing Data Assimilation to Improve the Seasonal Snow Cover Simulations Over the Heihe River Basin, Northwest China. Int. J. Climatol. 2024, 44, 5621–5640. [Google Scholar] [CrossRef]
- Bi, Y.; He, W.; Long, F.; Chen, H.; Li, C. Improvement of the Snow-Depth Retrieval Algorithm Using Passive Microwave Remote Sensing over the Arxan Region Inner Mongolia. Clim. Environ. Res. 2020, 25, 410–418. [Google Scholar] [CrossRef]
- Yao, H.; Zhang, Y.; Jiang, L.; Ewe, H.; Ng, M. Snow Parameters Inversion from Passive Microwave Remote Sensing Measurements by Deep Convolutional Neural Networks. Sensors 2022, 22, 4769. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Li, X.; Gu, L.; Zheng, X.; Jiang, T.; Zheng, Z. A Fine-Resolution Snow Depth Retrieval Algorithm From Enhanced-Resolution Passive Microwave Brightness Temperature Using Machine Learning in Northeast China. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, Q.; Yang, T.; Zhang, F.; Qi, Z.; Li, L. Snow Depth Reconstruction over Last Century: Trend and Distribution in the Tianshan Mountains, China. Glob. Planet. Change 2019, 173, 73–82. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support Vector Regression Snow-Depth Retrieval Algorithm Using Passive Microwave Remote Sensing Data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, L.; Zhang, Y.; Kan, X.; Liu, X.; Cao, H.; Wang, J. Downscaling Machine Learning Snow Depth Inversion on the Qinghai-Xizang Plateau Based on FY-3B Passive Microwave Data. J. Glaciol. Geocryol. 2024, 46, 539–554. [Google Scholar] [CrossRef]
- Dai, L.; Che, T. Estimating snow depth or snow water equivalent from space. Sci. Cold Arid. Reg. 2022, 14, 79–90. [Google Scholar]
- Yu, X.; Hu, X.; Wang, G.; Wang, K.; Chen, X. Machine-Learning Estimation of Snow Depth in 2021 Texas Statewide Winter Storm Using SAR Imagery. Geophys. Res. Lett. 2022, 49, e99119. [Google Scholar] [CrossRef]
- Yang, Y.; Fang, S.; Wu, H.; Du, J.; Wang, X.; Chen, R.; Liu, Y.; Wang, H. High-Resolution Inversion Method for the Snow Water Equivalent Based on the GF-3 Satellite and Optimized EQeau Model. Remote Sens. 2022, 14, 4931. [Google Scholar] [CrossRef]
- Dozier, J.; Shi, J. Estimation of Snow Water Equivalence Using SIR-C/X-SAR. I. Inferring Snow Density and Subsurface Properties. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2465–2474. [Google Scholar] [CrossRef]
- Dozier, J.; Shi, J. Estimation of Snow Water Equivalence Using SIR-C/X-SAR. II. Inferring Snow Depth and Particle Size. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2475–2488. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Sentinel-1 SAR GRD: C-Band Synthetic Aperture Radar Ground Range Detected. Google Earth Engine Dataset. 2023. Available online: https://developers.google.com/earth-engine/datasets/catalog/COPERNICUS_S1_GRD (accessed on 6 July 2025).
- Farr, T.; Rosen, P.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Li, L.; Che, T.; Liu, Y.; Li, X. Snow Depth Dataset from Common Station in the Typical Regions of China during 2017–2019. 2021. [Google Scholar] [CrossRef]
- Che, T.; Dai, L.; Li, X. Long-Term Series of Daily Snow Depth Dataset in China (1979–2024). Natl. Tibet. Plateau Data Cent. 2015. [Google Scholar] [CrossRef]
- King, J.; Kelly, R.; Kasurak, A.; Duguay, C.; Gunn, G.; Rutter, N.; Watts, T.; Derksen, C. Spatio-Temporal Influence of Tundra Snow Properties on Ku-Band (17.2 GHz) Backscatter. J. Glaciol. 2015, 61, 267–279. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Derksen, C.; Toose, P.; Proksch, M.; Pulliainen, J.; Kontu, A.; Rautiainen, K.; Seppänen, J.; Hallikainen, M. Simulating Seasonally and Spatially Varying Snow Cover Brightness Temperature Using HUT Snow Emission Model and Retrieval of a Microwave Effective Grain Size. Remote Sens. Environ. 2015, 156, 71–95. [Google Scholar] [CrossRef]
- Loew, A.; Mauser, W. Generation of Geometrically and Radiometrically Terrain Corrected SAR Image Products. Remote Sens. Environ. 2007, 106, 337–349. [Google Scholar] [CrossRef]
- Lievens, H.; Demuzere, M.; Marshall, H.-P.; Reichle, R.H.; Brucker, L.; Brangers, I.; de Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow Depth Variability in the Northern Hemisphere Mountains Observed from Space. Nat. Commun. 2019, 10, 4629. [Google Scholar] [CrossRef] [PubMed]
- Bo, Y.; Feng, X. The Retrieval of Snow-Depth Using SSM/I Remotely Sensed Data and Its Results Assessment in Qinghai-Xizang (Tibet) Plateau. In Proceedings of the IGARSS 2000, IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; Volume 2, pp. 509–511. [Google Scholar] [CrossRef]
- Deng, G.; Tang, Z.; Hu, G.; Wang, J.; Sang, G.; Li, J. Spatiotemporal Dynamics of Snowline Altitude and Their Responses to Climate Change in the Tienshan Mountains, Central Asia, during 2001–2019. Sustainability 2021, 13, 3992. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Deng, G.; Wang, X.; Jiang, Z.; Sang, G. Spatiotemporal Variation of Snowline Altitude at the End of Melting Season across High Mountain Asia, Using MODIS Snow Cover Product. Adv. Space Res. 2020, 66, 2629–2645. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Zhou, M.; Liu, C.; Huang, X. Retrieved Snow Depth over the Tibetan Plateau Using Random Forest Algorithm with AMSR2 Passive Microwave Data. J. Glaciol. Geocryol. 2020, 42, 1077–1086. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, X.; Tang, B. Application of Feature Optimization and Convolutional Neural Network in Crop Classification. J. Geo-Inf. Sci. 2021, 23, 1071–1081. [Google Scholar] [CrossRef]
- Habibi, A.; Delavar, M.R.; Nazari, B.; Pirasteh, S.; Sadeghian, M.S. A Novel Approach for Flood Hazard Assessment Using Hybridized Ensemble Models and Feature Selection Algorithms. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103443. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial Neural Network-Based Techniques for the Retrieval of SWE and Snow Depth from SSM/I Data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
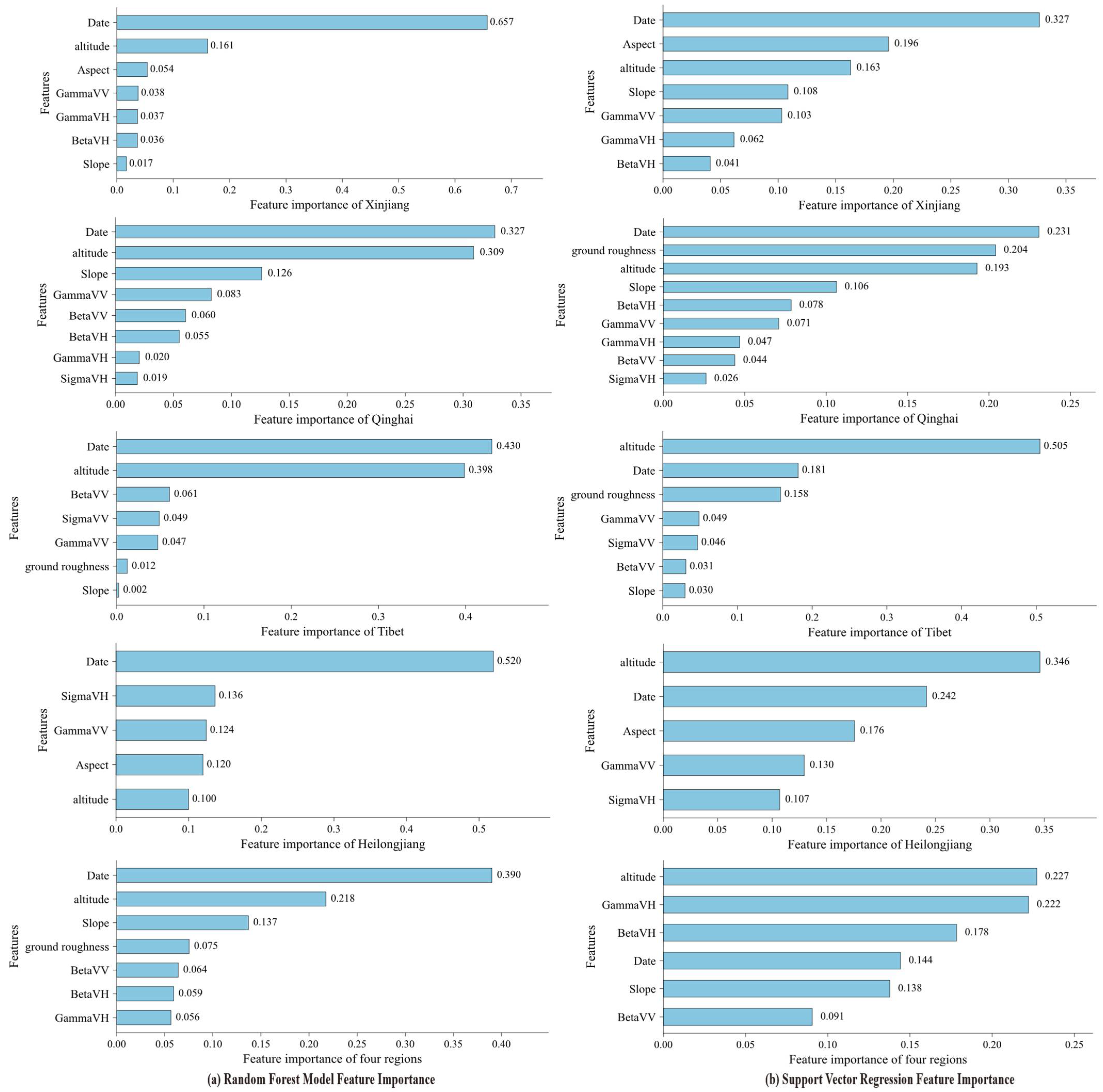
| Model Parameters | Feature Variables |
|---|---|
| Radar feature parameters | , , , , , , |
| Spatiotemporal geographical parameters | altitude, ground roughness, slope, aspect, date |
| Area | Radar Feature Parameters | Spatiotemporal Geographical Parameters |
|---|---|---|
| Xinjiang | , , | altitude, slope, aspect, date |
| Qinghai | , , , , , | altitude, slope, date |
| Tibet | , , | altitude, ground roughness, slope, date |
| Heilongjiang | , | altitude, aspect, date |
| Four regions | , , | altitude, slope, date |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Chen, S.; Mo, G.; Ji, D.; Lv, L.; Fu, J. Snow Depth Retrieval Using Sentinel-1 Radar Data: A Comparative Analysis of Random Forest and Support Vector Machine Models with Simulated Annealing Optimization. Remote Sens. 2025, 17, 2584. https://doi.org/10.3390/rs17152584
Cui Y, Chen S, Mo G, Ji D, Lv L, Fu J. Snow Depth Retrieval Using Sentinel-1 Radar Data: A Comparative Analysis of Random Forest and Support Vector Machine Models with Simulated Annealing Optimization. Remote Sensing. 2025; 17(15):2584. https://doi.org/10.3390/rs17152584
Chicago/Turabian StyleCui, Yurong, Sixuan Chen, Guiquan Mo, Dabin Ji, Lansong Lv, and Juan Fu. 2025. "Snow Depth Retrieval Using Sentinel-1 Radar Data: A Comparative Analysis of Random Forest and Support Vector Machine Models with Simulated Annealing Optimization" Remote Sensing 17, no. 15: 2584. https://doi.org/10.3390/rs17152584
APA StyleCui, Y., Chen, S., Mo, G., Ji, D., Lv, L., & Fu, J. (2025). Snow Depth Retrieval Using Sentinel-1 Radar Data: A Comparative Analysis of Random Forest and Support Vector Machine Models with Simulated Annealing Optimization. Remote Sensing, 17(15), 2584. https://doi.org/10.3390/rs17152584








