Abstract
The spatial distribution of ephemeral and perennial dryland plant species is increasingly modified and restricted by ever-changing climates and development expansion. At the interface of biodiversity conservation and developmental planning in desert landscapes is the growing need for adaptable tools in identifying and monitoring these ecologically fragile plant assemblages, habitats, and, often, heritage sites. This study evaluates usage of Sentinel-2 time series composite imagery to discriminate vegetation assemblages in a hyper-arid landscape. Spatial predictor spaces were compared to classify different vegetation communities: spectral components (PCs), vegetation indices (VIs), and their combination. Further, the uncertainty in discriminating field-verified vegetation assemblages is assessed using Shannon entropy and intensity analysis. Lastly, the intensity analysis helped to decipher and quantify class transitions between maps from different spatial predictors. We mapped plant assemblages in 2022 from combined PCs and VIs at an overall accuracy of 82.71% (95% CI: 81.08, 84.28). A high overall accuracy did not directly translate to high class prediction probabilities. Prediction by spectral components, with comparably lower accuracy (80.32, 95% CI: 78.60, 81.96), showed lower class uncertainty. Class disagreement or transition between classification models was mainly contributed by class exchange (a component of spatial allocation) and less so from quantity disagreement. Different artefacts of vegetation classes are associated with the predictor space—spectral components versus vegetation indices. This study contributes insights into using feature extraction (VIs) versus feature selection (PCs) for pixel-based classification of plant assemblages. Emphasising the ecologically sensitive vegetation in desert landscapes, the study contributes uncertainty considerations in translating optical satellite imagery to vegetation maps of arid landscapes. These are perceived to inform and support vegetation map creation and interpretation for operational management and conservation of plant biodiversity and habitats in such landscapes.
1. Introduction
Dryland vegetation communities endure remarkable ecological resilience and adaptation strategies that are increasingly challenged by uncertain climate patterns and changing ecological conditions. Globally, drylands comprising arid and hyper-arid regions have been estimated at 27% of the terrestrial surface area [1]. Local-scale mapping and conservation of often heritage and ecologically unique arid plant communities is gaining global attention, considering the upsurge in developmental actions that undermine the spatial and temporal shifts in plant habitats due to changing climates. The differentiation of environmental conditions at local scale is an important determinant of plant biodiversity and distribution [2,3]. Such differentiation, mediated by variability in topography, promotes the formation of micro-refugia for plant species [4]—stressing the importance of microtopographic variability. Variability in the spatial configuration of terrain contributes to diversifying potential plant habitats, on one hand. On the other hand, by decreasing the spatial range of individual habitats and their likely connectivity, it mitigates inter-species competition (for limited space and resources), thus contributing to plant micro-refugia and species richness [4,5,6]. The mapping of these refugia and vegetation assemblages is imperative for monitoring spatial changes and in planning the protection and conservation of their contributed and heritage biodiversity.
Land use and land cover maps, by and large, are increasingly serving as support tools for both research and end-user applications for predicting the impacts of climate crisis and for planning development or management strategies [7,8,9,10]. Since maps are a simplified representation of ground reality, errors and uncertainties are inevitable in their production. These errors vary in magnitude depending on one of several, often compounding, factors, including data quality, data processing, and analysis procedure [11]. Thus, an important consideration of such maps is their reliability or uncertainty—often evaluated by metrics of map quality or accuracy. For effective remote sensing application, different approaches have been suggested for accounting and reporting uncertainties in classification at the pixel level [12], for object-based classification [13,14,15], and for scale-based classification or spatial uncertainty [16,17]. In general, different analyses and target applications of land use and land cover, whether pixel- or object-based, warrant a corresponding scale of accuracy assessment [18]. Thus, approaches combining multi-features (several indices, texture, etc.) at high spatiotemporal resolution are promising in differentiating classes of mixed vegetation or land cover [19,20,21,22], which may inform several intended conservation and management endeavours in drylands and desert landscapes.
In remote sensing of vegetation, the use of vegetation indices (VIs) has been largely successful in mapping high and dense vegetation [19,22]. Such vegetation retains leaf and related phenological cycles over prolonged periods, which feeds the sensitivity of VIs and other proxies as feature texture. Leaf phenology and texture are captured in aerial or satellite images and across time series to inform the differentiation and mapping of different and mixed vegetation [15,21,22,23,24]. However, such proxies of vegetation may be applicable and reliable in arid and desert landscapes to a lesser extent. In arid and desert landscapes, permanent vegetation prevails in cultivated farms and active oases, in existent montane forests, and sparse woodlands. A considerable proportion of the vegetation has ephemeral distribution, with very brief periods of green leaf phenology—chlorophyll retention—during periods of rainfall and water flushes into the Wadis (water channels and catchments). Since these periods of vegetation proliferation are often erratic and short-lived, field observations of vegetation occurrence and distribution may not be readily reflected in remote sensing-based proxies of vegetation status. And these proxies may be less sensitive, or lack sensitivity entirely, in relation to observed non-green, dried, and sparse vegetation [25,26,27]. Usage of spectral-based VIs as spatial predictors to map and monitor arid vegetation is increasingly questionable [11,26,28] and may be unreliable for different and specific landscapes [11,20,25,27,29,30,31]. Thus, for ephemeral and mostly dry vegetation in arid landscapes, it is unreasonable to continuously apply or assume unverified reliance on vegetation index (VI) proxy from multi-spectral remote sensing data. Such a proxy may be reliable under certain landscape specifics—such as in areas with persistent vegetation cover—and in other circumstances may provide only complementary information in discriminating vegetation assemblages and mapping their distribution.
The spatial and temporal heterogeneity of dryland vegetation is a key contributor to errors in mapping its distribution. Nonetheless, literature on remote sensing of such vegetation has overlooked quantifying the uncertainties in vegetation mapping from spatial features of spectral signatures and vegetation indices. Different methods have been suggested in assessing the accuracy or errors of remote sensing classification of vegetation and land cover at the pixel-based level [32,33], local spatial scale [34], object-based feature extraction [35], and map change classification [36,37]. In addition to classification error and confusion, spatial consideration of unknown space, for which no reference predictor information is available, is essential in estimating the area of applicability of map outputs [16,17]. The application of remote sensing in pixel-based (soft) classification produces errors that vary across space. Thus, usage of overall accuracy estimates and related metrics as Kappa provides less intuitive visual clues to and interpretation of the spatial variability and patterns in classification errors [32,38].
Uncertainties in mapping vegetation have been largely overlooked in remote sensing of vegetation in arid, semi-arid, and desert landscapes [39,40,41,42]. And, there is scant literature that either validates or benchmarks the reliability and spatial extent of VI-based mapping of desert plant communities for applications such as biodiversity conservation and development planning. This study, therefore, questions and dissociates, based on quantified classification uncertainties and spatial disagreement, the contribution of VI proxies versus principal spectral information in discriminating and mapping vegetation assemblages in desert landscapes. Using a dense time series of Sentinel-2 imagery and the random forest (ensemble features) classification algorithm, we quantify classification error from both per-pixel class uncertainty by Shannon entropy (information loss) and feature-based uncertainty by intensity analysis of class transition across classification models.
2. Materials and Methods
2.1. Study Area
The study landscape is Wadi Ashar in AlUla County (in the Al Madinah District) of the Kingdom of Saudi Arabia. The landscape’s physical structure and geology comprise a mix of several spectacular natural features and landforms (sandstone massifs, harrat plateaux, steep gorges, sand dunes, sandy plains, open Wadis, or seasonal drainage channels) and land uses (irrigated farms, date palm orchards, animal camps, etc.). The elevation across the landscape ranges between 760 m a.s.l. in the Wadis and 1240 m a.s.l. on the Harrat plateaus, while the terrains have a slope range of 0 to 75 degrees. The administrative boundary covers a surface area of about 3046 ha (Figure 1), and the landscape has established and planned development strategies and facilities of public, touristic, and regal interests—e.g., exquisite hotel resorts. In this landscape, the iconic Maraya Concert Hall is the central structure of a developed chain of exquisite desert resorts, which are punctuated by heritage landscape features and touristic attractions.
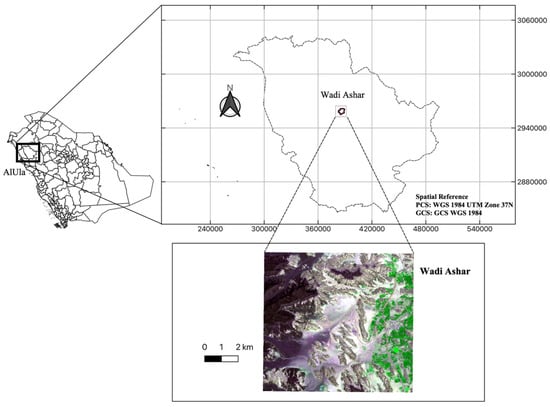
Figure 1.
Location map of the study landscape as viewed on Sentinel-2 imagery (false colour RGB composite: green, NIR, and red spectral bands).
2.2. Vegetation Classification and Mapping
In detecting and mapping the different field-surveyed vegetation communities or assemblages, we implemented supervised classifications based on the random forest ensemble (bagging and decision tree) algorithm [43]. As predictors for the classifier algorithm, we explored the spatial information of spectral bands and their derivative vegetation indices from time-series Sentinel-2 multi-spectral imagery. The details of the reference ground truth data, spatial data, and classification procedure are provided in the following subsections.
2.2.1. Plant Survey (Field) Data
Field data and observations are initially a mosaic of different key vegetation types in the study area. The vegetation types were preliminarily categorised into a high order based on three major habitats: sandy plains, sand dunes, and harrats. To better understand these habitats and generate vegetation descriptions and maps, extensive field data were sampled during field surveys—the surveys were conducted from November to December 2021 and in September 2022. During the surveys, two types of plant data were collected: 1. plot data—a complete list of the plants in a delimited plot of vegetation, with information on species cover, substrate, and other abiotic features; 2. general observations—to ensure that we capture as wide a variety of plant species found on the site as possible.
To ascertain and describe the vegetation community on surveyed locations, which had associated identified plants, the plant species data, recorded as species abundance (values from 0 to 5 coded according to a DAFOR scale), were subjected to hierarchical cluster analysis (HCA). The HCA helped define the reference classes, or types of vegetation communities, in the study area. Further visual observation in Google Earth enabled extracting additional reference points identified for roads, settlements, and other farms or agricultural areas. These, in addition to the vegetation survey points, serve as ground truth data (Table 1) for remote sensing data extraction and classification model training. The reference spatial data were extracted using reference polygons for the identified vegetation classes (described in Table S1 of the online Supplementary Material).

Table 1.
Summary of reference pixels and areas (m2) for the vegetation and land cover classes.
2.2.2. Spatial Data and Processing
As for spatial information, we explored Sentinel-2 (S-2) multi-spectral image archives provided by the European Space Agency. Available S-2 images covering the study areas were accessed using the Google Earth Engine (GEE) cloud computing platform, and the time-series images were filtered for images acquired for the area of interest in the period between 1 January 2021 and 15 September 2022 with a cloudy pixel percentage of <5% for each image. A total of 85 images (temporal series) were accessed following this filtering criteria, and each image collection was processed to compute 5 different vegetation indices (VIs) that provide proxies for vegetation status and cover: NDVI: Normalised Difference Vegetation Index [44], EVI: Enhanced Vegetation Index [45,46,47]. SAVI: Soil-Adjusted Vegetation Index [48], MSAVI2: Modified Soil-Adjusted Vegetation Index—2 [49], and GSAVI: Green Soil-Adjusted Vegetation Index [50]. For each computed VI, we estimated and retained the max values for each pixel across the time series [51]. Thus, the pre-processing of spatial data resulted in 5 raster images for the vegetation indices.
In addition to spatial information from VIs, we explored information lurking in the spectral signatures (for both vegetation and non-vegetation) to potentially improve the classification based on VIs. For each of the computed VIs, we extracted the corresponding spectral bands to create a raster stack of spectral signatures. A total of 20 spectral bands (4 from each VI corresponding to the blue, green, red, and near-infrared bands) were subjected to a Principal Component Analysis (PCA) data reduction procedure to obtain a set of uncorrelated spatial features. Based on the PCA, 5 principal components (PCs) explained about 99% of the variance in the spectral signatures for the study area (Table 2), of which 4 were most significant [52]. The PC (raster layers) estimation procedure is illustrated in Figure 2. The PC raster layers served as additional explanatory variables for vegetation and land cover classification. Thus, in total, we used 10 raster layers (5 PCs and 5 VIs) as the spatial predictors or environmental space for vegetation classification.

Table 2.
Explained variance by the 5 principal components (PCs) of PCA on the 20 spectral bands.
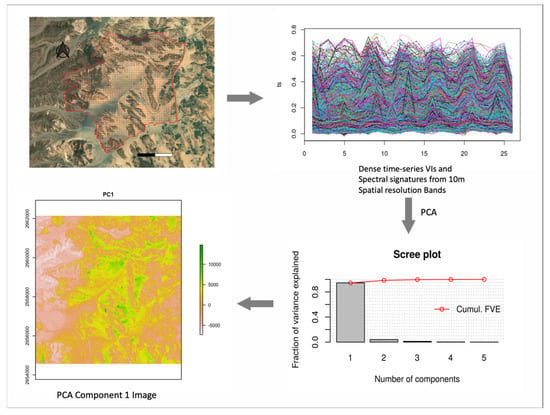
Figure 2.
Workflow for extracting principal spectral information from Sentinel-2 image dense time series. Top left panel: regular grid points for extracting time-series data. Top right: illustration of a sample VI time series from 84 images that met the image filtering criteria.
2.2.3. Vegetation Type Classification and Validation
To map the vegetation assemblages (and land cover) in study landscapes, the random forest classification algorithm was implemented to delineate the clusters of vegetation types hitherto identified and group them as clusters of plant assemblages. The reference polygons for the vegetation assemblages or land cover classes (Table 1) were used to extract training data from the stack of raster layers (10 explanatory or predictor rasters in total). Considering disparities in both the number and size of reference polygons for each class, the extracted training data, or pixels, were unbalanced across the considered classes.
We trained random forest classification models to learn distinguishing features of plant assemblages based on the ten (10) raster predictors. As additional model tuning, the parameter number of trees (ntree) was set to 500 for building the decision trees, while the best possible number of features (variable) to split each node (mtry) of a decision tree was estimated to be 2, and the Gini index-based identification of variable importance was used. Considering the unbalanced tally of reference clusters and extracted spatial data between the target vegetation and land cover classes, as well as potential biases of Gini-based importance towards correlated predictors, we tuned the hyper-parameters for the random forest classification algorithm in combination with applying forward feature selection (FFS) and targeted spatial cross-validation (CV) procedures [16]. Thus, we used forward feature selection (FFS) in conjunction with target-oriented CV to reduce spatial over-fitting. We used a spatial 5-fold cross-validation (k = 5), and the ground truth data had the minimum of 5 reference polygons for the “Bare rock” class, thus ensuring each fold in cross-validation contains data from each reference class. Based on the unique IDs for each reference polygon, we implemented a spatial cross-validation, using the Leave-Location-Out Cross-Validation (LLO-CV) procedure, which specifies that data from the same polygon are always grouped to prevent usage in both model training and testing [16] procedures by leaving the location out at each iteration of model training.
2.2.4. Classification Error and Area of Applicability
The dissimilarity index (DI) was used to assess the area of applicability (AOA) of the final classification map. As suggested by [16], we considered areas with predictor space (VI and spectral features) that are unknown to the classification model and thus are termed “Unknown spaces” and identified by a high dissimilarity index. The dissimilarity index was computed based on the weighted distance of a new prediction space and the average (threshold) distance within the spatial cross-validated prediction space in the trained model. Thus, for model prediction, areas or pixels with a DI < Threshold were classified to be within the Area of Applicability (AOA) for model prediction. The predictions within the AOA were based on the DI map and threshold (Figure 3).
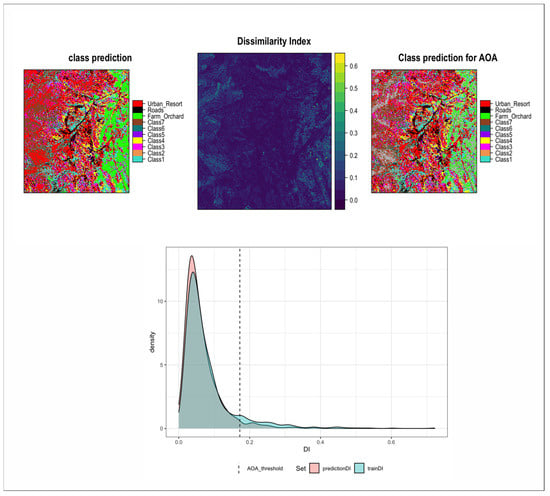
Figure 3.
Spatial consideration and estimation of unknown space for map predictions within the area of applicability (AOA) of the classification model. The top left panel shows predictions for known and unknown environmental space. The dissimilarity index (DI) was estimated and is mapped (top middle panel) as a measurement threshold for unknown environmental space. The DI was used as the basis for model prediction within the AOA (map at top right panel)— a pixel with DI above the AOA threshold (dotted line in bottom panel) is mapped as outside the AOA (unclassified areas).
2.3. Quantifying Uncertainty (Information) in Class Prediction
There is an unreliable common practice in remote sensing literature to overlook the details of the sampling scheme and size for accuracy assessment [18]. This is especially the case for object-based image analysis (OBIA) and less likely so for pixel-level classifications. To ascertain and delineate the contribution of spectral signature versus vegetation indices to discriminate vegetation assemblages, we compare three models or scenarios of predictor (explanatory) remote sensing variables: (1) Model VI: Using vegetation indices (VIs)—5 raster images; (2) Model PC: Using principal components (PCs) of time-series spectral signatures—5 raster images; and (3) Model VIPC: Using both VIs and PCs as predictor features—10 raster images.
In quantifying the uncertainty in the pixel-based classification, a measure of uncertainty, the Shannon Entropy (H), computed from predicted class probability, was applied to evaluate information gained from the use of different spatial predictors. For pixel-based classification, the Shannon entropy or cross-entropy has been applied in remote sensing for edge detection [53], in measuring class error [21], and in quantifying land use change and dynamics [54,55,56].
The entropy of a random variable, according to information theory [57], is the average level of “information”, “surprise”, or “uncertainty” inherent to the variable’s possible outcomes. Given a discrete random variable X, which takes values in the alphabet X and is distributed according to p: X → [0, 1], the Shannon entropy (information content, surprisal, or self-information) is estimated as follows:
where H(X) is the total amount of information in an entire probability distribution, p(xi) is the probability of classifying a pixel as class i, log is logarithm, and b is the base of the log and changing its value modifies the unit of estimated entropy. The choice of base for log, the logarithm, depends on the following applications: base 2 = unit of bits or “Shannon” unit, base e = “natural units” nat, and base 10 = units of “dits” or “bans”.
To ascertain the level of information or uncertainty in class predictions, the Shannon entropy was employed as a measure of the reliability in the predicted probabilities (class votes) by the random forest ensemble models. The estimated Shannon entropy (uncertainty) was compared between classes and across the different models (predictor features). To evaluate the within-class variability in uncertainty, we applied the Kernel density (distribution) profiles and the non-parametric Kruskal–Wallis test with mean comparison based on the Dunn test pairwise comparison and the Bonferroni p-value adjustment.
2.4. Dissociating the Contribution of Predictor Features: Intensity Analysis
Intensity analysis provides a procedure for analysing land use change and transition at three different levels: time interval, category, and transition level [58,59,60]. The three successive levels of analysis form a hierarchical framework to decipher increasing details in change patterns at specific time intervals (or between maps), assuming that the spatial extent is identical at each time point and class categories between comparable maps. To assess class uncertainty and accuracy between the three classification models, we applied the categorical and transition-level intensity analysis.
The category-level intensity analysis examines how the loss intensity, Lti, from category i and the gain intensity, Gtj, to category j compare to a uniform intensity, St, during each map interval [Mt, Mt+1]. If Lti < St, then Lti is dormant, i.e., category i experiences loss less intensively than if the changes during map interval [Mt, Mt+1] were uniformly distributed across the spatial extent. If Lti > St, then Lti is active, implying that category i experiences loss more intensively than if the changes during map interval [Mt, Mt+1] had a uniform distribution across the analysis domain or spatial extent of map. Likewise, for the gain intensity, if Gtj < St, then Gtj is dormant, and Gtj is active if Gtj > St. The computation of St, Lti, and Gtj is illustrated in Equation (3), Equation (4), and Equation (5), respectively.
At the transition level, the analysis examines how the transition intensity, Rtij, from category i to category j compares to a uniform transition intensity Wtj, given the gain of category j during interval [Mt, Mt+1]. If Rtij < Wtj, then the gain of j transitions from i less intensively during time interval [Mt, Mt+1] than if the gain of j were to have transitioned uniformly from the space that is not j at time Mt—i.e., the gain of j avoids i. Conversely, If Rtij > Wtj, this implies the gain of j transitions from i more intensively during time interval [Mt, Mt+1] than if the gain of j were to have transitioned uniformly from the space that is not j at time Mt, i.e., the gain of j target i. Equations (6) and (7) illustrate, respectively, the estimates of Rtij and Wtj. The order of subscripts j and i in Ctji of the denominator of Equation (7) allows that the summation over i subtracts category j at the initial time Mt. The relationship among the different equations and intensity estimates is illustrated in Table 3 and Table 4.

Table 3.
Mathematical notation of intensity estimates as adapted from the literature [38,61].

Table 4.
Illustration of the confusion matrix and the relationship between the estimated intensity components.
The conceptual organisation of the various intensities and land use dynamic degrees during time intervals [Mt, Mt+1] is presented in Table 4. At the transition level, the intensity analysis determines if the gain of a category j either avoids or targets its transition from another category I; thus, the intensity analysis compares a uniform transition intensity (Wti) to its corresponding transition intensities within each column j, Rtij. For the category-level analysis, a comparison is made between the change percentage in the time interval St and both the loss intensities (Lti) and the gain intensities (Gtj) to determine whether each loss and gain is dormant or active.
The image classification, uncertainty analysis, and intensity analyses were conducted within the R Studio (version 2023.06.0+421) environment using several available libraries of the R programming language [62,63,64]. The overall analysis design and procedure of data collection, image processing and classification, and assessment of class spatial allocation entropy are graphically illustrated in Figure 4.
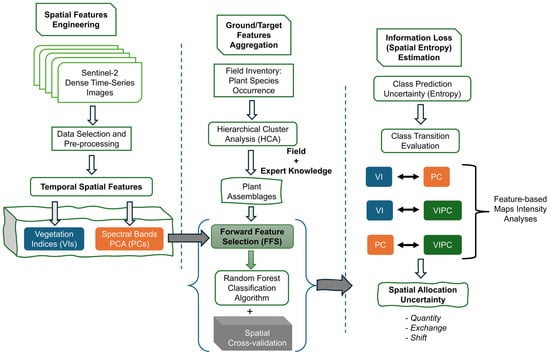
Figure 4.
Graphical illustration of analysis design highlighting key steps of spatial and field data collation, image processing, classification map comparison, and class transition estimation.
3. Results
3.1. Vegetation and Land Cover Classification
Plant assemblages (or communities) were discriminated based on the time series of both spectral information and vegetation indices with reliable accuracy. Overall, the different vegetation types were predicted with an overall accuracy of 0.834 (95% CI: 0.8178, 0.8493), a Kappa of 0.699, and a global F1-Score of 0.535, as detailed in Table 5. The classification error was within the reported reasonable range in remote sensing of vegetation in arid landscapes [41,65,66]. However, there was high variability in individual class accuracy across different classification models. All the models showed a high specificity and sensitivity in discriminating the monoculture farmlands and orchards (Table 6). For mixed plant assemblages, the classification uncertainty and accuracy were variable between the different models. The thematic maps of 11 vegetation and land cover categories, including the unclassified areas outside the AOA, for the three classification models are depicted in Figure 5.

Table 5.
Summary statistics of the RF classification models from different predictor variables.

Table 6.
Plant assemblage (vegetation) classification model statistics.
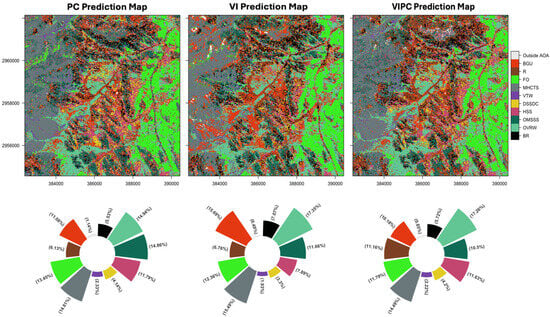
Figure 5.
Thematic maps of plant assemblages land cover categories based on the three classification models (top row) and the class (pixel) proportions in the respective maps (bottom row).
Contrary to the other vegetation and land cover categories, the class-specific accuracy for farms and orchards (FO) did not vary as much with the choice of spatial predictors. Our results highlight that the VI-based classification, with comparably high overall accuracy (Kappa of 65.91%), had high variability in class-specific prediction probability. Vegetation assemblages with low height and density showed inconsistency in reliable (low uncertainty) prediction across the classification models. This uncertain accuracy reflects temporal and spatial variability in combination with vegetation structural and phenological traits. In desert landscapes, most vegetation has distinctive spatial patterns—its type and mechanism of formation are modulated by geomorphic processes, amongst other landscape processes [67]. Most of the vegetation communities are a mixture of different species, with often different growth forms, providing different functions. Thus, distinctive plant assemblages often inhabit different niches distributed across micro-habitats in a landscape. The high uncertainty and quantity disagreement observed for vegetation index-based classification model are indicative of typical vegetation structures and forms that superpose variability in the vegetation index. In an arid landscape in Africa, Ref. [30] observed that spatial and temporal variations in species dominance are likely a noise contributor in the modelling relationship between NDVI and biomass.
3.2. Classification Uncertainty
The Kernel density distribution, within the quantile range of 2.5 to 97.5%, of the estimated Shannon entropy (classification uncertainty) for the vegetation categories is reported in Figure 6. A low classification uncertainty is observed for the class representing mono-specific plant assemblages and/or their mosaic structure in farms or orchards (FO). For all the other considered categories, the distribution of the uncertainty is either skewed or multi-modal across the different classification models (top row of Figure 6). The classification model based on vegetation indices (top middle panel in Figure 6) showed a normal distribution in the range of uncertainty (information complexity) for both uniform (FO) and high (VTW) vegetation categories. The range of statistics representing the vegetation proxy and spectral information of the FO class was wide enough to reliably predict the spatial and structural variability in the class. In general, the kernel distribution of Shannon entropy (H) is indicative of high variability in classification uncertainty for some vegetation assemblages, both in the pixel domain and at the local spatial levels. For the FO category, using VIs as predictors showed the lowest uncertainty estimate (4.76%) in comparison to using the spectral components—PCs (6.13%)—and the combined predictors—VIPC (11.16%).
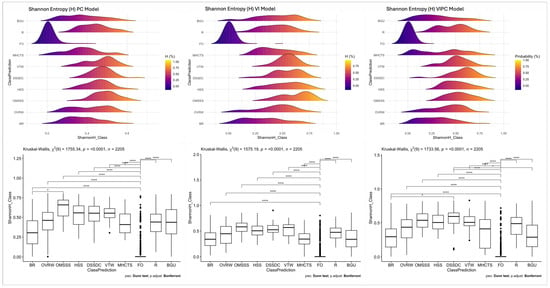
Figure 6.
Distribution of information uncertainty (Shannon entropy) based on non-parametric probability (kernel) distribution estimates (top row) and boxplots with a non-parametric mean comparison of uncertainty (bottom row) for the predicted vegetation assemblages and land cover. Categories with significantly different mean entropy are indicated with an asterisk.
3.3. Comparison of Classification Methods: Change Intensity
Overall differences in class quantity and allocation (exchange and shift) between the classification models (maps) are presented in Figure 7. The exchange component represents the allocation difference due to pairwise confusions, while the shift component estimates the allocation difference from non-pairwise confusions. The class allocation components, exchange, and shift accounted for most of the difference between all three thematic maps. The highest class disagreement was observed between the thematic maps from the spectral components (PCs) and vegetation indices (VIs); compared to the latter, the former had a lower allocation difference to map predictions based on combined predictors (VIPCs). Although the overall accuracy of the VI-based map was higher than that based on the PC predictors, the latter showed more consistency in discriminating other vegetation assemblages except for farms and orchards. With reference to the combined (VIPC) model, the overall quantity disagreement in the PC-based classification (7.60%) was less than that observed in the VI-based classification (9.68%). For the PC to VI map transition, the quantity component derives largely from a net gain of two non-vegetation categories—R and BR, and the net loss in two vegetation categories—OVRW and OMSSS (Figure 8). The contribution of such classes to the quantity component is backed by the heterogeneous nature and distribution of vegetation in the desert landscapes as modulated by major landforms and topography. Such spatial heterogeneity in vegetation and landforms is well captured in class entropy (uncertainty) distribution across the different classification models (Figure 6). Thus, in comparing transitions between thematic maps, class entropy distribution provides insights into class predictability and the magnitude of contribution to pairwise (exchange) and non-pairwise (shift) confusions.
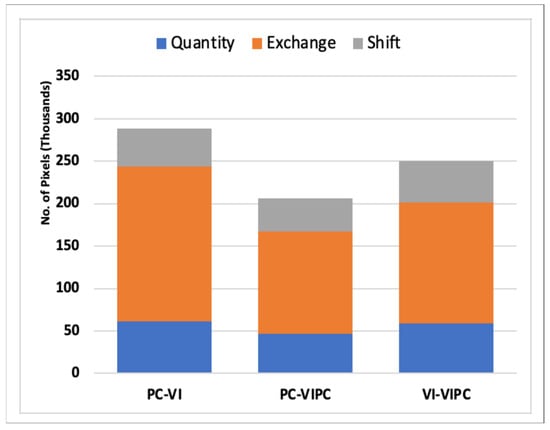
Figure 7.
Overall difference in class prediction between maps, as estimated by disagreements in class quantity and the spatial allocation or configuration (exchange and shift).
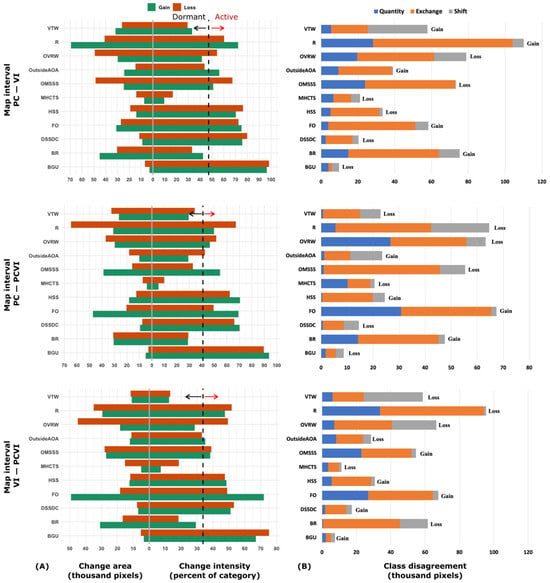
Figure 8.
Land cover/use category-level change intensity and class disagreement for the three predicted maps: (A) Graphs on the left show the change in intensity. The mapped categories are indicated as a pair of bars for the loss and gain between the map intervals. Bars that extend to the left of the 0 axis are the sizes (no. of pixels) of the loss or gain, and those that extend to the right are the intensities (proportions) of loss Lti or gain Gtj—each the size of the corresponding bar to the left of the 0 line divided by the category’s total size. For each map interval, the black dashed line represents the value of uniform spatial intensity St. If a bar extends above the uniform intensity line, the change in intensity for the category is active. If a bar stops below the uniform intensity line, then the category is dormant. (B) Graphs show the three different class disagreements for the transition-level change intensity between each reference and comparison map. Labels for each category indicate the overall quantity difference between maps (the gain is the sum of pixels at the reference or final map minus the persistence, while the loss is the sum at the comparison or initial map minus the persistence).
The class-level change intensity between the map predictions is presented in Figure 8A. In general, we observed an active change in intensity (gain and loss) for most classes across the different models. However, for some classes, large change intensity is attributable to their comparably small change area (size) in the comparison (initial) map compared to the reference map. Such as is observed for the following classes: HSS, DSSDC, BGU, and OutsideAOA. Figure 8B presents the three components of the quantified disagreement between the reference and comparison maps: quantity, exchange, and shift. The components are stacked to highlight their respective contribution to overall class disagreement between the reference maps and comparison maps. In other words, their joint contribution conveys, for the purpose of this analysis, the proportion of correctly classified pixels (often calculated as 1—total proportion of disagreement). Thus, uncertainty in class predictions is based on the spectral components versus vegetation indices centred around class allocation disagreements and less so on proportion correction (quantity disagreement).
4. Discussion
4.1. Vegetation Discrimination Accuracy
The classification models had accuracies in the range widely reported in the remote sensing literature [18]. However, reliance on class accuracy to validate land use maps is a subject of increasing debate. Controversies in the acceptable range of classification accuracy hinge on complexities in validation related to (1) variability in mapping goals, (2) the errors of mapping as a function of the target classes, (3) heterogeneity within and between landscapes, and (4) the highly variable quality of remotely sensed data between classification experiments [68]. Thus, as a guideline to aim for with classification results, a generic accuracy threshold is not feasible across studies [18]. A widely used metric for accuracy assessment is the Kappa statistic, which compares the observed accuracy to a baseline of random accuracy—to be properly estimated as a proportion correct for each class equalling one over the number of considered categories. This comparison is usually irrelevant and misleading, as random classification is not usually the alternative scenario in mapping experiments [38]. Based on accuracy and Kappa statistics, the VI-based classification had a higher overall accuracy that would imply better classification and reliability. Similarly, an accuracy of 66% was reported using higher-resolution multi-spectral imagery to map 28 vegetation classes in arid landscapes [41]. However, for classification based on VIs, the results in this study emphasise class uncertainty (or entropy) distribution and class allocation (or configuration) disagreement when compared to the classification by combination of feature selection and extraction (Figure 6 and Figure 9). Besides confirming the high variability of pixel-based (soft) classification error across space, the Shannon Entropy distribution also communicates spatial uncertainty in individual class predictions. Such variability and uncertainty in class allocation is largely overlooked by mere usage and reliance on accuracy values of pixel-based land use classification.
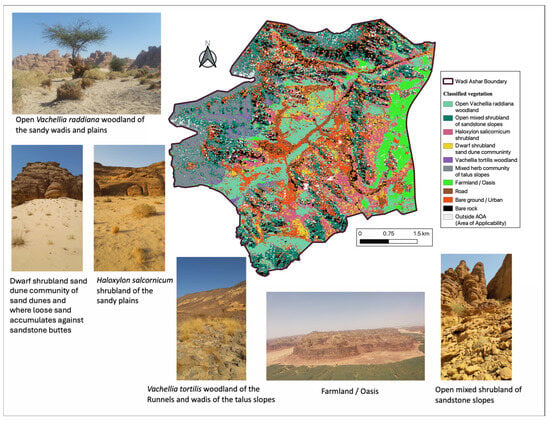
Figure 9.
Thematic map illustration of the distribution of plant assemblages in the study area. The pictures illustrate some main vegetation assemblages observed during field surveys.
The application of vegetation indices to spatially discriminate and map vegetation types, from landscape level to global scales, abounds in the literature. The widely used vegetation indices, such as those in our analysis, rely on the NIR band to distinguish specific vegetation types and to assess their status and structural changes in space and time. However, arid and hyper-arid landscapes exhibit a predominantly sparse vegetation distribution that is characterised by spasmodic photosynthetic phases—largely greyer to brown than green foliage, relative to either the phases of plant senescence or adaptation strategies. These features present challenges to the vegetation index approach of vegetation identification and discrimination in such landscapes. Thus, sporadic spatial and temporal congruence between VIs and vegetation phenological status may explain the high uncertainty and variability of the VI-based classification model (Figure 5). This is especially observable in categories with low vegetation, short-lived photosynthetic activity, and extensively sparse or non-vegetative states—e.g., MHCTS, OMSSS, and DSSDC. As these vegetation assemblages comprise herbaceous cover, shrub mosaics, and woodlands with comparably short-lived leafy or green states, they may convey little to no sensitivity of legacy proxies developed and tailored to capture more permanent and dense vegetation. The disconnect or link between conventional vegetation indices and different vegetation types and structures warrants discussion. For instance, research reports inconsistencies between RGB-only vegetation indices and actual crop health or NDVI [69]. Their observations were, however, based on a comparison of vegetation in agricultural fields (corn versus rice). There is a need for alternative, non-NIR-reliant approaches to discriminating arid or rangeland vegetation for a wide range of applications in landscapes and other jurisdictional levels. Our results support and compound the need to reconsider vegetation mapping by tailoring and handcrafting spectral information to landscape specifics, especially from the standpoint of discriminating and monitoring the sparse and ecologically fragile vegetation in hyper-arid landscapes.
Contrary to the other vegetation and land cover categories, the class-specific accuracy for farms and orchards (FO) did not vary as much with the choice of spatial predictors. Our results highlight that the VI-based classification, with a comparably high overall accuracy (Kappa of 65.91%), had high variability in class-specific prediction probability. Vegetation assemblages with low height and density showed inconsistency in reliable (low uncertainty) prediction across the classification models. This uncertain accuracy reflects temporal and spatial variability in the combination of vegetation structure and phenological cycles. In desert landscapes, most vegetation has distinctive spatial patterns—its type and mechanism of formation are modulated by geomorphic processes, amongst other landscape processes [67]. Most of the vegetation communities are a mixture of different species, with often different growth forms, providing different functions. Thus, distinctive plant assemblages often inhabit different niches distributed across micro-habitats in a landscape. The high uncertainty and quantity disagreement observed for the vegetation index-based classification model are indicative of typical vegetation structure and forms that superpose variability in the vegetation index. In an arid landscape in Africa, Ref. [30] observed that spatial and temporal variations in species dominance are likely a noise contributor in the modelling relationship between NDVI and biomass.
Several factors may explain the variability in classification accuracy or classification confusion (Table 6). Class confusion may be linked to either the status of the vegetation at field sampling, spatial variability in class spectral and VI signature, or the resultant information from the temporal image composite medley within a spectrum from green to dried-out vegetation. On one hand, class error or uncertainty is attributable to the low sensitivity (or the lack thereof) of some vegetation indices. For instance, as is remarkable in vegetation classes with short-lived green leaf phenology. On the other hand, confusion can be a product of the status of vegetation assemblages across temporal and spatial scales—e.g., a characteristic mixed spectral signature, which may derive transitional spectral information or indices between one or more classes. In arid landscapes, the vegetation distribution is largely contracted, modulated by temperature and moisture regimes. Thus, variability in class prediction accuracy and predictability (entropy) may result from one or a combination of the following: spatial location, the vegetation structure at field sampling and across seasons, and changes resulting from previous and on-going developmental and maintenance landscaping.
Based on the entropy distribution for each class (Figure 6), we observed variable predictability for some classes, while others are predictable with low uncertainty across the models. Developmental and landscaping works, captured within the image time-series window, result in roads and buildings of different types and statuses. These contribute complexities in spectral information at both the individual class levels and spatial context. Such observations may help explain the high uncertainty and mis-classification of the road and build-up areas in the study landscape. Moreover, heterogeneity in vegetation structure has been reported to be prominent during periods of high vegetation growth [70]; however, such a scenario is less intuitive in arid or desert landscapes. Colour similarities between desert plant assemblages in a non-green (non-photosynthesising) state and non-vegetation areas may explain the low accuracy or misclassification using vegetation indices and the ambiguity in discriminating these classes. Variabilities in spectral information and indices are reflected in the wide distribution of class uncertainties or Shannon entropy (Figure 6). Though such temporal variabilities hold true for the vegetation classes, regardless of landscaping activities to either suppress or enhance the growth of some vegetation categories, the high uncertainties derive from structural and phenological heterogeneity in time and space. The period covered by the time-series image composite provided adequate spatial information and features to capture temporal variations in both intra- and inter-annual vegetation distribution. Using vegetation proxies in assessing vegetation sensitivity to climate change, studies suggest parabolic variations along the aridity index gradient and differences between vegetation types in arid and semi-arid regions [71]. We observed a low but variable class uncertainty in the FO class—representing monospecific vegetation assemblages and/or their mosaic (Figure 5). For this class, the prediction uncertainty (entropy) and sensitivity of vegetation proxies is attributable to differing degrees of anthropogenic activities, predominantly the changes in the structure and pattern of crops and trees, irrigation and fallow regimes, and land use management.
4.2. Class Uncertainty Distribution
The classification uncertainty was estimated as the Shannon entropy of the distribution of class probability votes for each pixel. This was extrapolated to the estimated (average) uncertainty in the class predictions for different classification models (or predictor variables). The distribution of uncertainty (entropy) varied for the different land cover/use categories across the classification models. Based on the dense time-series spectral information and vegetation indices at each pixel (in image composites), the estimate of uncertainty is interpreted as representative of the probable distribution error relating to the sampling for each considered vegetation assemblage or land cover class. In making inferences about population statistics, sampling may provide different estimates of target population parameters. Thus, the kernel distribution may reflect and be interpreted as variation in the Shannon entropy or class uncertainty due to the sampling procedure for the distribution of reference vegetation assemblages. The VI-based classification shows a narrow distribution of class uncertainty for the high vegetation categories, i.e., FO and VTW. For the other considered classes, high variability in uncertainty was observed for low vegetation and non-vegetation categories. The model thus reasonably captures the spatial variability in high vegetation categories (Figure 6), although less so for the low and mixed vegetation classes. The latter classes may be potential targets for sampling tailored to aim at improving classification error, i.e., sampling mainly areas with features (spectral and indices values) that are unknown or not learnt by the classification algorithms. Nonetheless, the observed uncertainty distribution is not interpreted to be exhaustive for each considered class and the study landscape, as it is considered as the accuracy of the classification algorithm. Though the random forest algorithm is known to outperform other algorithms used in vegetation classification [66], there is a lack of literature confirming such performance for desert vegetation. Our results, while reducing this information void, highlight considerations in optimal feature selection relating to the context of analysis, vegetation specifics, and expected model performance. A high variability in class-specific accuracy was observable across all considered classification models, which reflects an improvement in the reported classification accuracies for similar landscapes [41,66].
The map prediction from spectral components, with a comparable lower accuracy and Kappa (80.32% and 65.42%, respectively), showed lower prediction uncertainty for individual classes (Figure 6). The performance of spectral components from multispectral bands has been reliable in land cover/use mapping based on images from different sensors and feature selection [72]; however, the measured performance has been limited to accuracy measures. While revealing the performance of spectral components over spectral indices for the study landscape, our results complement concerns of misleading reliance on accuracy and Kappa value in remote sensing applications [38]. The classifier model with spectral components, deriving from principal component analysis of time-series spectral signatures, is representative of data dimension reduction approaches or feature selections. In the scenarios of limited sample size and spectral indices, feature selection through Recursive Feature Elimination (RFE) improves LC classification accuracy in arid areas by removing redundant variables [65]. In our analysis, redundant spectral information was eliminated through principal component dimensionality reduction—e.g., with the spectral components (PCs). A merit of multispectral data reduction by feature selection (principal components) is the non-reliance on specific spectral bands and the reliability in differentiating both natural (including vegetation) and artificial features [72]. By contrast, application of vegetation indices as a feature extraction approach is constrained by the selection of specific spectral bands to match the analysis objectives and target features. The wavelength range of spectral bands may vary when merging images captured by different sensors. Thus, the selection of VI proxies will often provide a constrained or limited sensitivity range in relation to specific landscape features and their variability in space and time.
4.3. Class Spatial Allocation and Intensity
To resolve the contribution of vegetation indices versus spectral signature (principal) components in class predictions, intensity analysis was applied to assess the spatial configuration of vegetation classes or land cover [58,59]. This enabled quantifying the class change and dynamics between the classification models and the underlying change patterns and intensity related to the spatial predictors. The marginal difference in overall accuracies between the classification models supports direct comparison of class prediction and spatial allocation in the respective thematic maps (Figure 5). The change pattern in the predicted class supports our understanding of the contribution of the different predictor features, or their interaction, to pixel classes at different spatial scales.
Overall, the change in each map interval was accounted for mostly by allocation differences due to class exchange. The VI–VIPC map interval had the smallest quantity differences but the largest proportion of allocation (exchange and shift) differences (Figure 7). Most of this quantity difference is contributed by the FO and OVRW categories (Figure 8B); while the former category has an overall quantity gain, the latter is a net quantity loss. Each bar in Figure 8B demonstrates that less than a quarter of the overall disagreement is attributable to quantity disagreement. Quantity disagreement refers to the amount of difference between the reference map and a comparison map that is due to the less than perfect match in the proportions of the categories. An objective in this study was to estimate and compare the contribution of predictor variables to land use/cover change based on the three classification models; in this regard, class allocation transition due to class exchange and shift disagreements were of much less significance. Thus, although the overall classification error is in the range of 17.29% to 19.68% across the classification models, this compares with merely reported accuracies for land use/cover mapping in similar landscapes [41,66]. As observable in Figure 8, pairs of categories may contribute to exchange disagreement between maps. Thus, it is useful to separate overall change into its constituent components given that each component is interpretable in relation to application specifics. For instance, in change characterisation, error assessment, and map comparison. Insights into the effect of category aggregation on model performance can help eliminate less contributing or informative variables to model performance. The observed performance in map comparisons and the contributions to class quantity and allocation transitions (Figure 8) suggest that spectral information may provide optimal spatial features in discriminating and mapping vegetation assemblages in arid and hyper-arid landscapes. The results are reliable for both the purpose of analysis and as a reference distribution map (Figure 9) for different intended practical applications.
5. Conclusions
The need for monitoring and managing vegetation assemblages in desert and arid landscapes has gained country-specific and international attention due to spreading developmental actions that impact the ecological heritage in these landscapes, besides ubiquitous ecological challenges elicited by erratic climate patterns. In this study, we question and quantify the uncertainty associated with, or contributed by, using vegetation indices versus spectral information from Sentinel-2 imagery as proxies for mapping the vegetation communities of drylands. The results suggest considerations in translating multi-spectral remote sensing data to context-specific vegetation mapping, with emphasis on the ephemeral and ecologically erratic vegetation distribution in desert landscapes. Our findings underscore the distribution of classification uncertainty and spatial difference (quantity and spatial allocation) related to the choice of predictor features between spectral information and vegetation indices.
Discriminating and mapping plant species distribution on drylands from remote sensing data, modulated by environmental variables such as soil and topography, depends on the choice of spatial predictor variables or metrics, besides other parameters relating to model selection, the desired level of map details, complexities in the target landscapes, etc. Thus, to reliably map vegetation types in arid landscapes, the choice of predictor variables constitutes persistent burdens and challenges to resource managers, who require informed guidance relating to available reference data, the scale of analysis, and to reliably match models and/or knowledge with context. Questioning the reliability of classic metrics or indices for vegetation in desert landscapes, this study suggests considerations of feature extraction versus feature selection in mapping and quantifying vegetation communities in arid landscapes. Thus, with consideration of landscape specifics of ephemeral and contracted vegetation distribution in most desert landscapes, the findings highlight a rethinking in (a) combining predictors for different features for vegetation mapping and (b) using information loss (entropy) to decipher spatial uncertainties in class allocation. Though the resultant maps are not perceived as potential inputs for models that seek to maximise overall accuracy, the results contribute relevant insights into the characterisation and mapping of desert vegetation communities and woodlands by integrating remote-sensing data.
The analysis and quantification of class uncertainty may lend a priori information in understanding the application and limits of remotely sensed data to landscape specifics. In quantifying the level of uncertainty in mapping vegetation assemblages using different spatial predictors, the presented analyses fall short of considering an exhaustive number of possible proxies in identifying and mapping the considered vegetation communities. Nonetheless, this study contributes insights into using and optimising feature extraction (VIs) versus feature selection (PCs) for pixel-based classification of arid vegetation communities. These results are perceived to leverage usage of Sentinel-2 satellite imagery to inform and support the interpretation of vegetation maps intended for operational management and developmental planning in hyper-arid landscapes.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs17152553/s1, Figure S1: Illustration of the 5 raster bands (maximum VIs) used as explanatory variables for mapping the vegetation types or assemblages; Figure S2: Illustration of the 5 principal components images (of time series spectral signatures) used as both separate and complementary spatial variables; Table S1: Description of vegetation assemblages as identified from field surveys and reference data collection, plant species groupings; Table S2: Classification statistics (Precision, Recall, and F1-Scores) for the three RF Classification Models; Table S3: Classification confusion matrix (of training data or pixels) for the considered classes and different classifier models; Figure S3: Predictor variable importance for the PC-based Classifier; Figure S4: Predictor variable importance for the VIs-based Classifier; Figure S5: Predictor variable importance for the combined VIPC-based Classifier; Figure S6: Cumulative density of class uncertainty (Shannon entropy) for the PC-based Classification model; Figure S7: Cumulative density of class uncertainty (Shannon entropy) for the VI-based Classification model; Figure S8: Cumulative density of class uncertainty (Shannon entropy) for the VIPC-based Classification model; Table S4: Size (No. Pixels) of class transitions between the different classifier-model-based maps.
Funding
This research received no external funding.
Data Availability Statement
The spatial data (processed time-series satellite images) that support the findings of this study are available from the corresponding author upon reasonable request. However, the plant inventory data analysed in this study were generated by the Royal Botanic Garden Edinburgh (RBGE) in collaboration with the Royal Commission for AlUla (RCU). The data and thematic map may be shared, upon request, by the respective institutions.
Acknowledgments
Fieldwork and plant surveys were conducted by scientists at the Centre for Middle Eastern Plants (CMEP) of the Royal Botanic Garden Edinburgh (RBGE). This work was supported by the Royal Commission for AlUla (RCU). Plant identification during field surveys was conducted principally by Tony Miller and Sophie Neale. They provided key contributions in project administration, interpreting the vegetation clusters, and describing the plant assemblages. The following RCU and CMEP researchers also provided worthy contributions and support during field surveys and plant species identification: Ayman A. Abdulkareem, Mohammed J. Darwish, Gail Stott, and Frederick N. Numbisi.
We thank the independent reviewers for their insightful comments and suggestions, which guided the revision of our manuscript and enhanced its content and quality.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AOA | Area of Applicability |
| DI | Dissimilarity Index |
| FFS | Forward Feature Selection |
| HCA | Hierarchical Cluster Analysis |
| PCA | Principal Component Analysis |
| PCs | Principal Component images |
| RF | Random Forest |
| RFE | Recursive Feature Elimination |
| VIs | Vegetation Indices |
References
- Zomer, R.J.; Xu, J.; Trabucco, A. Version 3 of the Global Aridity Index and Potential Evapotranspiration Database. Sci. Data 2022, 9, 409. [Google Scholar] [CrossRef] [PubMed]
- Deutschewitz, K.; Lausch, A.; Kühn, I.; Klotz, S. Native and alien plant species richness in relation to spatial heterogeneity on a regional scale in Germany. Glob. Ecol. Biogeogr. 2003, 12, 299–311. [Google Scholar] [CrossRef]
- Lundholm, J.T. Plant species diversity and environmental heterogeneity: Spatial scale and competing hypotheses. J. Veg. Sci. 2009, 20, 377–391. [Google Scholar] [CrossRef]
- Opedal, Ø.H.; Armbruster, W.S.; Graae, B.J. Linking small-scale topography with microclimate, plant species diversity and intra-specific trait variation in an alpine landscape. Plant Ecol. Divers. 2015, 8, 305–315. [Google Scholar] [CrossRef]
- Dobrowski, S.Z. A climatic basis for microrefugia: The influence of terrain on climate: A Climatic Basis for Microrefugia. Glob. Change Biol. 2011, 17, 1022–1035. [Google Scholar] [CrossRef]
- Dufour, A.; Gadallah, F.; Wagner, H.H.; Guisan, A.; Buttler, A. Plant species richness and environmental heterogeneity in a mountain landscape: Effects of variability and spatial configuration. Ecography 2006, 29, 573–584. [Google Scholar] [CrossRef]
- Aburas, M.M.; Abdullah, S.H.; Ramli, M.F.; Ash’aari, Z.H. Measuring Land Cover Change in Seremban, Malaysia Using NDVI Index. Procedia Environ. Sci. 2015, 30, 238–243. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Feature Extraction using Normalized Difference Vegetation Index (NDVI): A Case Study of Jabalpur City. Procedia Technol. 2012, 6, 612–621. [Google Scholar] [CrossRef]
- Bharathkumar, L.; Mohammed-Aslam, M.A. Crop Pattern Mapping of Tumkur Taluk Using NDVI Technique: A Remote Sensing and GIS Approach. Aquat. Procedia 2015, 4, 1397–1404. [Google Scholar] [CrossRef]
- Hammond, W.M.; Williams, A.P.; Abatzoglou, J.T.; Adams, H.D.; Klein, T.; López, R.; Sáenz-Romero, C.; Hartmann, H.; Breshears, D.D.; Allen, C.D. Global field observations of tree die-off reveal hotter-drought fingerprint for Earth’s forests. Nat. Commun. 2022, 13, 1761. [Google Scholar] [CrossRef] [PubMed]
- Yengoh, G.T.; Dent, D.; Olsson, L.; Tengberg, A.E.; Tucker, C.J. Limits to the Use of NDVI in Land Degradation Assessment. In Use of the Normalized Difference Vegetation Index (NDVI) to Assess Land Degradation at Multiple Scales; Springer International Publishing: Cham, Switzerland, 2015; pp. 27–30. [Google Scholar]
- Beckschäfer, P. Obtaining rubber plantation age information from very dense Landsat TM & ETM + time series data and pixel-based image compositing. Remote Sens. Environ. 2017, 196, 89–100. [Google Scholar] [CrossRef]
- Galletti, C.; Myint, S. Land-Use Mapping in a Mixed Urban-Agricultural Arid Landscape Using Object-Based Image Analysis: A Case Study from Maricopa, Arizona. Remote Sens. 2014, 6, 6089–6110. [Google Scholar] [CrossRef]
- Mishra, N.B.; Crews, K.A. Mapping vegetation morphology types in a dry savanna ecosystem: Integrating hierarchical object-based image analysis with Random Forest. Int. J. Remote Sens. 2014, 35, 1175–1198. [Google Scholar] [CrossRef]
- Wang, S.; Waldner, F.; Lobell, D.B. Unlocking large-scale crop field delineation in smallholder farming systems with transfer learning and weak supervision. Remote Sens. 2022, 14, 5738. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 1620–1633. [Google Scholar] [CrossRef]
- Ye, S.; Pontius, R.G.; Rakshit, R. A review of accuracy assessment for object-based image analysis: From per-pixel to per-polygon approaches. ISPRS J. Photogramm. Remote Sens. 2018, 141, 137–147. [Google Scholar] [CrossRef]
- Ganem, K.A.; Xue, Y.; Rodrigues, A.D.A.; Franca-Rocha, W.; Oliveira, M.T.D.; Carvalho, N.S.D.; Cayo, E.Y.T.; Rosa, M.R.; Dutra, A.C.; Shimabukuro, Y.E. Mapping South America’s Drylands through Remote Sensing—A Review of the Methodological Trends and Current Challenges. Remote Sens. 2022, 14, 736. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and Land Surface Temperature for Drought Assessment: Merits and Limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Numbisi, F.N.; Van Coillie, F.M.B.; De Wulf, R. Delineation of Cocoa Agroforests Using Multiseason Sentinel-1 SAR Images: A Low Grey Level Range Reduces Uncertainties in GLCM Texture-Based Mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 179. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Almalki, R.; Khaki, M.; Saco, P.M.; Rodriguez, J.F. Monitoring and Mapping Vegetation Cover Changes in Arid and Semi-Arid Areas Using Remote Sensing Technology: A Review. Remote Sens. 2022, 14, 5143. [Google Scholar] [CrossRef]
- Gil, A.; Yu, Q.; Lobo, A.; Lourenço, P.; Silva, L.; Calado, H. Assessing the effectiveness of high resolution satellite imagery for vegetation mapping in small islands protected areas. J. Coast. Res. 2011, 64, 1663–1667. [Google Scholar]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.; Neigh, C.; Reichstein, M. Trend Change Detection in NDVI Time Series: Effects of Inter-Annual Variability and Methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, S.; Yin, T.; Chavanon, E.; Lauret, N.; Guilleux, J.; Henke, M.; Qin, W.; Cao, L.; Li, J.; et al. Using the Negative Soil Adjustment Factor of Soil Adjusted Vegetation Index (SAVI) to Resist Saturation Effects and Estimate Leaf Area Index (LAI) in Dense Vegetation Areas. Sensors 2021, 21, 2115. [Google Scholar] [CrossRef] [PubMed]
- Pellat, F.P.; Sanchez, M.E.R.; Vélez, E.P.; González, M.B.; Lazalde, J.R.V. Alcances Y Limitaciones de Los Índices Espectrales de La Vegetación: Análisis de Índices de Banda Ancha. Terra Latinoam. 2015, 33, 27–49. [Google Scholar]
- Loranty, M.; Davydov, S.; Kropp, H.; Alexander, H.; Mack, M.; Natali, S.; Zimov, N. Vegetation Indices Do Not Capture Forest Cover Variation in Upland Siberian Larch Forests. Remote Sens. 2018, 10, 1686. [Google Scholar] [CrossRef]
- Mbow, C.; Fensholt, R.; Rasmussen, K.; Diop, D. Can vegetation productivity be derived from greenness in a semi-arid environment? Evidence from ground-based measurements. J. Arid Environ. 2013, 97, 56–65. [Google Scholar] [CrossRef]
- Smith, W.K.; Dannenberg, M.P.; Yan, D.; Herrmann, S.; Barnes, M.L.; Barron-Gafford, G.A.; Biederman, J.A.; Ferrenberg, S.; Fox, A.M.; Hudson, A.; et al. Remote sensing of dryland ecosystem structure and function: Progress, challenges, and opportunities. Remote Sens. Environ. 2019, 233, 111401. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. Predicting individual pixel error in remote sensing soft classification. Remote Sens. Environ. 2017, 199, 401–414. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Mei, Y.; Yang, W. Geostatistical characterization of local accuracies in remotely sensed land cover change categorization with complexly configured reference samples. Remote Sens. Environ. 2019, 223, 63–81. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P.; Hu, X. Novel Classification Uncertainty Measurement Model Integrating Spatial Information for Remote Sensing Image. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-3-2020, 723–730. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy Assessment Measures for Object-based Image Segmentation Goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Arora, A.; Pandey, M.; Mishra, V.N.; Kumar, R.; Rai, P.K.; Costache, R.; Punia, M.; Di, L. Comparative evaluation of geospatial scenario-based land change simulation models using landscape metrics. Ecol. Indic. 2021, 128, 107810. [Google Scholar] [CrossRef]
- Tsutsumida, N.; Rodríguez-Veiga, P.; Harris, P.; Balzter, H.; Comber, A. Investigating spatial error structures in continuous raster data. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 259–268. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.S. Classifying and mapping of vegetated area in Al- Baha region, Saudi Arabia using remote sensing. I. Extent and distribution of ground vegetated cover categories. Indian J. Appl. Res. 2020, 10, 75–80. [Google Scholar] [CrossRef]
- Al-Rowaily, S.R.; Assaeed, A.M.; Al-Khateeb, S.A.; Al-Qarawi, A.A.; Al Arifi, F.S. Vegetation and condition of arid rangeland ecosystem in Central Saudi Arabia. Saudi J. Biol. Sci. 2018, 25, 1022–1026. [Google Scholar] [CrossRef] [PubMed]
- Malatesta, L.; Attorre, F.; Altobelli, A.; Adeeb, A.; De Sanctis, M.; Taleb, N.M.; Scholte, P.T.; Vitale, M. Vegetation mapping from high-resolution satellite images in the heterogeneous arid environments of Socotra Island (Yemen). J. Appl. Remote Sens. 2013, 7, 073527. [Google Scholar] [CrossRef]
- Roy, P.S.; Behera, M.D.; Murthy, M.S.R.; Roy, A.; Singh, S.; Kushwaha, S.P.S.; Jha, C.S.; Sudhakar, S.; Joshi, P.K.; Reddy, C.S.; et al. New vegetation type map of India prepared using satellite remote sensing: Comparison with global vegetation maps and utilities. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 142–159. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rouse, W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the 3rd Earth Resources Technology Satellite-1 Symposium, Greenbelt, NASASP-351, Washington, DC, USA, 10–14 December 1973; NASA: Washington, DC, USA, 1974; pp. 3010–3017. [Google Scholar]
- Huete, A. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial Color Infrared Photography for Determining Early In-Season Nitrogen Requirements in Corn. Agron. J. 2006, 98, 968–977. [Google Scholar] [CrossRef]
- Tassi, A.; Vizzari, M. Object-Oriented LULC Classification in Google Earth Engine Combining SNIC, GLCM, and Machine Learning Algorithms. Remote Sens. 2020, 12, 3776. [Google Scholar] [CrossRef]
- Kaiser, H.F. The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Kiani, A.; Sahebi, M.R. Edge detection based on the Shannon Entropy by piecewise thresholding on remote sensing images. IET Comput. Vis. 2015, 9, 758–768. [Google Scholar] [CrossRef]
- Deribew, K.T. Spatiotemporal analysis of urban growth on forest and agricultural land using geospatial techniques and Shannon entropy method in the satellite town of Ethiopia, the western fringe of Addis Ababa city. Ecol. Process. 2020, 9, 46. [Google Scholar] [CrossRef]
- Patra, P.K.; Behera, D.; Goswami, S. Relative Shannon’s Entropy Approach for Quantifying Urban Growth Using Remote Sensing and GIS: A Case Study of Cuttack City, Odisha, India. J. Indian Soc. Remote Sens. 2022, 50, 747–762. [Google Scholar] [CrossRef]
- Yulianto, F.; Fitriana, H.L.; Sukowati, K.A.D. Integration of remote sensing, GIS, and Shannon’s entropy approach to conduct trend analysis of the dynamics change in urban/built-up areas in the Upper Citarum River Basin, West Java, Indonesia. Model. Earth Syst. Environ. 2020, 6, 383–395. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Aldwaik, S.Z.; Pontius, R.G., Jr. Map errors that could account for deviations from a uniform intensity of land change. Int. J. Geogr. Inf. Sci. 2013, 27, 1717–1739. [Google Scholar] [CrossRef]
- Aldwaik, S.Z.; Pontius, R.G. Intensity analysis to unify measurements of size and stationarity of land changes by interval, category, and transition. Landsc. Urban Plan. 2012, 106, 103–114. [Google Scholar] [CrossRef]
- Pontius, R.G.; Santacruz, A. Quantity, exchange, and shift components of difference in a square contingency table. Int. J. Remote Sens. 2014, 35, 7543–7554. [Google Scholar] [CrossRef]
- Huang, B.; Huang, J.; Gilmore Pontius, R.; Tu, Z. Comparison of Intensity Analysis and the land use dynamic degrees to measure land changes outside versus inside the coastal zone of Longhai, China. Ecol. Indic. 2018, 89, 336–347. [Google Scholar] [CrossRef]
- Meyer, H.; Milà, C.; Ludwig, M.; Linnenbrink, J. CAST: “Caret” Applications for Spatial-Temporal Models. Available online: https://CRAN.R-project.org/package=CAST (accessed on 20 July 2023).
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 15 June 2023).
- Pontius, R.G., Jr.; Santacruz, A. diffeR-package: Metrics of Difference for Comparing Pairs of Maps or Pairs of Variables. Available online: https://CRAN.R-project.org/package=diffeR (accessed on 1 September 2023).
- Saeed, M.; Ahmad, A.; Mohd, O. Optimal Land-cover Classification Feature Selection in Arid Areas based on Sentinel-2 Imagery and Spectral Indices. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 106–112. [Google Scholar] [CrossRef]
- Silver, M.; Tiwari, A.; Karnieli, A. Identifying Vegetation in Arid Regions Using Object-Based Image Analysis with RGB-Only Aerial Imagery. Remote Sens. 2019, 11, 2308. [Google Scholar] [CrossRef]
- Wainwright, J. Desert Ecogeomorphology. In Geomorphology of Desert Environments; Parsons, A.J., Abrahams, A.D., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 21–66. [Google Scholar]
- Foody, G.M. Harshness in image classification accuracy assessment. Int. J. Remote Sens. 2008, 29, 3137–3158. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Xu, X.; Liu, L.; Han, P.; Gong, X.; Zhang, Q. Accuracy of Vegetation Indices in Assessing Different Grades of Grassland Desertification from UAV. Int. J. Environ. Res. Public Health 2022, 19, 16793. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yang, H.; Jin, T.; Wu, K. Assessment of terrestrial ecosystem sensitivity to climate change in arid, semi-arid, sub-humid, and humid regions using EVI, LAI, and SIF products. Ecol. Indic. 2024, 158, 111511. [Google Scholar] [CrossRef]
- Palanisamy, P.A.; Jain, K.; Bonafoni, S. Machine Learning Classifier Evaluation for Different Input Combinations: A Case Study with Landsat 9 and Sentinel-2 Data. Remote Sens. 2023, 15, 3241. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).