Abstract
Marine heatwaves (MHWs) and Marine cold spells (MCSs) are oceanic events characterized by prolonged periods of anomalously warm or cold sea surface temperatures, which pose significant ecological and socio-economic threats on a global scale. These extreme temperature events exhibit an asymmetric trend under ongoing climate change in recent decades: MHWs have increased markedly in both frequency and intensity, whereas MCSs have shown an overall decline. Among the potential drivers, mesoscale eddies play a critical role in modulating sea surface temperature anomalies (SSTAs). Anticyclonic eddies (AEs) promote downwelling, generating positive SSTAs that potentially favor MHWs, while cyclonic eddies (CEs) enhance upwelling and negative anomalies that are potentially related to MCSs. In this paper, we investigate the relationship between mesoscale eddies and MHWs/MCSs using global satellite-derived datasets from 2010 to 2019. By analyzing the spatial overlap and intensity correlation between eddies and MHWs/MCSs, it is found that 12.2% of MHWs are accompanied by AEs, and 13.4% of MCSs by CEs, with a high degree of spatial containment where approximately 90.2% of MHW events are found within the mean eddy contour of AEs, and about 93.1% of MCS events fall inside the mean eddy contour of CEs. Stronger eddies tend to be associated with more intense MHWs/MCSs. This study provides new insights into the role of mesoscale eddies in regulating extreme oceanic temperature events, offering valuable information for future predictions in the context of climate change.
1. Introduction
Ocean temperature variability is a critical component of the Earth’s climate system. Studying these variations and extreme events is essential for understanding the balance and health of global marine ecosystems [1,2,3,4]. Extreme ocean temperature events, such as marine heatwaves (MHWs) and marine cold spells (MCSs), are defined as prolonged periods of sea surface temperature anomalies (SSTAs) that are significantly warmer or cooler than baseline climatic conditions [3,5,6]. These events have become key indicators of climate change and variability [7]. Under ongoing global warming, the frequency and intensity of MHWs have risen markedly [8,9,10,11,12,13], whereas the occurrence of MCSs has shown an overall decline [14,15]—an asymmetric trend that has profound ecological consequences, including coral bleaching [16,17,18,19,20,21], shifts in species distribution [3,22,23], and significant disturbances to fisheries productivity [24,25,26,27]. Additionally, these events significantly affect the Earth’s climate system by altering air–sea interactions [3,28,29,30,31,32,33,34]. For example, MHWs can intensify air–sea heat fluxes, while MCSs can influence sea ice expansion and melting patterns through sustained cooling effects [35].
These extreme events are further modulated by dynamic ocean processes such as mesoscale eddies. Mesoscale eddies are dynamic, rotating ocean currents typically about 100 km in diameter, and are widely distributed across the global oceans [36,37,38]. In the Northern Hemisphere, they generally rotate clockwise and counterclockwise, known as anticyclonic eddies (AEs) and cyclonic eddies (CEs), respectively, with opposite rotational directions in the Southern Hemisphere. These eddies transport large volumes of water with distinct characteristics, playing a key role in the movement of heat, salinity, and nutrients throughout the ocean [39,40,41]. They are critical in maintaining the global ocean heat balance [42,43,44] by regulating both vertical and horizontal heat transport, which significantly affects the distribution of sea surface temperature (SST) [41,44,45,46,47,48]. AEs induce downward motion and depress the thermocline, leading to localized increases in SST. While stronger and more coherent AEs may also advect warmer water masses within their cores, the major contribution to SST anomalies arises from thermocline displacement [49,50,51,52]. In contrast, CEs enhance upwelling and elevate the thermocline, resulting in localized SST decreases [51,52,53,54]. Similarly, stronger CEs can advect colder subsurface water toward the surface, further amplifying the cooling effect. As a result, AEs can promote the occurrence of MHWs [15,55,56,57], while CEs can intensify the development of MCSs [15,57,58,59].
Although extensive research [39,40,42,45,60,61,62] has examined mesoscale eddies and their impact on sea surface temperature anomaly (SSTA), studies directly linking mesoscale eddies with extreme temperature events, such as MHWs and MCSs, remain relatively limited. Unlike previous studies focusing on SST anomalies, we specifically quantify the spatial overlap and intensity correlations between mesoscale eddies and MHWs/MCSs on a global scale. This detailed investigation of their direct linkage, particularly regarding the precise spatial and intensity relationships during extreme events, has not been thoroughly explored [55,63,64,65].
This study, based on global SST and eddy trajectory data from 2010 to 2019, investigates the statistical relation between MHWs/MCSs and mesoscale eddies over the globe. By quantifying these spatial and intensity relationships, the study aims to provide a fresh physical perspective on eddy-modulated extreme temperature anomalies and to lay a theoretical foundation for improving their prediction in the context of future climate change. The remainder of this paper is organized as follows: Section 2 presents the data and methods used in this work. Section 3 outlines the main results. Section 4 provides a discussion of the mechanisms linking eddies and heatwaves/cold spells. Finally, Section 5 concludes with a summary of this study.
2. Material and Methods
2.1. Sea Surface Temperature
This study uses the Optimum Interpolation SST data provided by the National Oceanic and Atmospheric Administration (NOAA OISST V2.1), covering the period from 1 January 1982, to 31 December 2019 for the detection of MHWs/MCSs [66]. The climate reference period used in this study spans from 1 January 1982 to 31 December 2012, providing a long-term baseline for SST analysis. The detection period for MHWs and MCSs ranges from 1 January 2010 to 31 December 2019. The OISST V2.1 dataset integrates satellite observations, in-situ measurements (such as buoy and ship data), and advanced optimal interpolation techniques. It has a spatial resolution of 0.25° × 0.25° and a temporal resolution of one day [67]. Due to its extensive spatiotemporal coverage and high resolution, this dataset has been widely used for monitoring and trend analysis of MHWs and MCSs [4,10,12,15,46,68,69,70,71,72,73,74], with its effectiveness being repeatedly validated.
2.2. Mesoscale Eddy Trajectory Data
This study uses the two-satellite version of the META3.2 DT dataset to detect the location of mesoscale eddies and capture their geometrical characteristics. The data, produced by SSALTO/DUACS in collaboration with IMEDEA and released by AVISO+ (https://aviso.altimetry.fr), is supported by CNES and is a widely used product for eddy tracking. The dataset is based on sea level anomalies (SLAs) and uses an automated eddy detection algorithm to track mesoscale eddy signals from January 1993 to the present; for this study, the period under investigation spans from 1 January 2010 to 31 December 2019. This product provides core characteristics of the eddies, including location, radius, type (anticyclonic or cyclonic), amplitude, and more. The temporal resolution is daily, and the spatial resolution is 0.25° × 0.25° (consistent with AVISO SLA data). The two-satellite version of the data exhibits high stability and consistency, making it particularly suitable for long-term climate analysis and dynamic monitoring of mesoscale eddies. Because it is based on dual-satellite data (C3S), it provides more uniform eddy tracking results in both spatial and temporal dimensions [75,76]. The META3.2 DT dataset, known for its high quality and consistency, is widely used in research on the global distribution of mesoscale eddies, their intensity variations, and their associations with other oceanic processes [77,78,79,80].
2.3. Definition of MHWs/MCSs
In this study, MHWs are defined as events where the daily average SST exceeds the 90th percentile of the climatic baseline (typically over a 30-year period). MCSs are defined as events where the daily average SST falls below the 10th percentile. Each event must last for at least 5 days, and to distinguish independent events, there must be a gap of at least 2 days between consecutive MHW/MCS events [3,5]. We used the detect function from the M_MHW toolbox in MATLAB R2025a to identify the characteristics of all MHW and MCS events between 2010 and 2019, following the definitions and methods outlined by Hobday et al. [5], using a fixed climatic baseline. Figure 1 presents examples of an MHW observed at 42.675°N, 36.5°W, and an MCS observed at 43.875°N, 13.625°W in 2010. The intensity of the MHW/MCS is defined as the difference between the SST (black line in Figure 1) and the climatic mean (green line in Figure 1). The daily intensity reflects the magnitude of abnormal warming (for MCSs, cooling). The cumulative intensity is given by integrating the shaded area (red for MHWs and blue for MCSs).
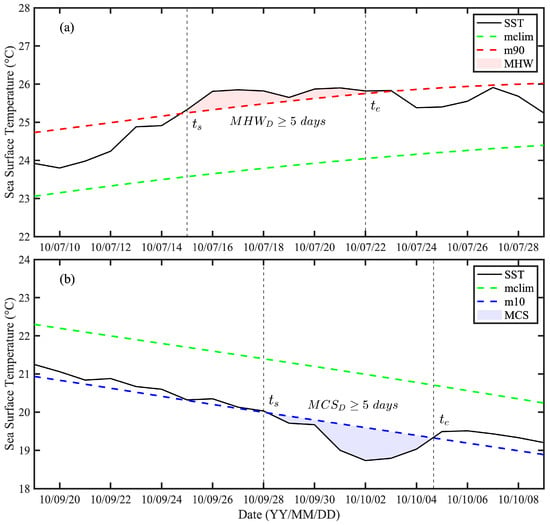
Figure 1.
Schematic diagram of an MHW (42.675°N, 36.5°W) (a) and an MCS (43.875°N, 13.625°W) (b) observed at an arbitrary location in 2010. The black curve represents the SST, the green line represents the climate mean, and the blue line indicates the threshold for determining MHW/MCS events. (a) MHW is the 90th percentile of the climate baseline, (b) MCS is the 10th percentile of the climate baseline. The red shaded area represents an MHW event, and the blue shaded area represents an MCS event.
2.4. Definition of an MHW/MCS Accompanied by an Eddy
In this study, a metric based on the overlap area was used to match mesoscale eddies (anticyclonic and cyclonic) associated with MHWs and MCSs. The specific steps are as follows. For the calculation of overlap area, we directly compute the overlap area () between each MHW and AE, or each MCS and CE, and compare it with the total area of the MHW or MCS (). The overlap ratio is then defined as follows (1):
The area of each MHW is derived based on the definition provided in Section 2.1. Specifically, MHWs are defined as events where the daily average SST exceeds the 90th percentile of the climatic baseline. The area of each MHW is then calculated based on the spatial extent of these temperature anomalies. Similarly, MCSs are defined as events where the daily average SST falls below the 10th percentile, and their area is calculated based on the corresponding spatial extent of cooling anomalies. The calculation of MHW/MCS areas takes both the spatial and temporal extent of the events into account. The overlapping match criterion is as follows: when the overlap ratio between an MHW or MCS and a given eddy exceeds 50%, the eddy is considered to be significantly associated with the corresponding MHW/MCS. If the overlap ratio between an MHW (MCS) and an AE (CE) meets this condition, the MHW (MCS) is considered to be associated with that AE (CE). The 50% threshold was chosen to ensure that the majority of the MHW/MCS overlaps spatially and temporally with the eddy, making the association both meaningful and interpretable.
For events that meet the match criteria, we further calculate the geometric center of the MHW or MCS, which serves as the central point of the event (x, y). The formula for calculating the centroid is as follows (2):
This formula is used to calculate the geometric of the MHW or MCS event by considering the coordinates of all points along the event’s contour. The centroid represents the average position of the event, accounting for the spatial distribution of all points involved. Specifically, is the x-coordinate of the i-th point, and is the y-coordinate of the i-th point on the contour line. N is the number of individual points that define the boundary or outline of the event.
Figure 2 illustrates the match process. The red area represents the spatial extent of the MHW or MCS, the blue area represents the mesoscale eddy, and the purple shaded region indicates the overlap between the two. When the overlap area exceeds 50% of the total area of the MHW or MCS, the MHW/MCS event is considered matched. If the eddy lies entirely within the MHW/MCS area, this case is excluded from the analysis.
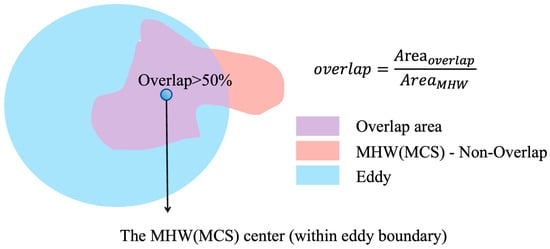
Figure 2.
Schematic diagram of the overlap-based match process. The red area represents the spatial extent of MHWs or MCSs, the blue area represents the mesoscale eddy (anticyclonic or cyclonic) region, and the purple shaded area represents the overlapping region between the two. The match criterion is that the overlapping region must account for more than 50% of the total area of the MHW/MCS.
2.5. Relocating MHWs/MCSs Relative to Eddies
In this study, the coordinates of the unmatched MHW and MCS events were normalized to analyze their relative position distribution characteristics within the corresponding mesoscale eddy structures. Specifically, each MHW or MCS event is paired with a corresponding mesoscale eddy (anticyclonic or cyclonic). Based on the eddy’s center coordinates (xeddy, yeddy) and radius (R), the coordinates (x, y) of the MHW or MCS events are normalized. The formula for this normalization is as follows (3):
where xnormalized and ynormalized are the normalized coordinates of the MHW/MCS, x and y are the original coordinates of the MHW/MCS, xeddy and yeddy are the original coordinates of the eddy, and R is the radius of the eddy.
3. Results
3.1. Global Distribution of MHWs, MCSs, and Their Association with Eddies
In this section, we present the spatial distribution characteristics of MHWs, MCSs, and their associated mesoscale eddies (AEs and CEs) during the period from 2010 to 2019. The location of each MHW, MCS, and mesoscale eddy is determined by the central position and the boundary contour of the event. These locations are then gridded with a 1° by 1° spatial resolution to perform the spatial distribution analysis. Each event’s centroid is assigned to a specific grid cell, and the distribution is statistically processed by counting the number of occurrences of MHWs, MCSs, and eddies in each grid cell. This approach allows for the visualization of the global spatial distribution of MHWs, MCSs, and their associated eddies. Figure 3 and Figure 4 show the occurrence counts of MHWs/MCSs and AEs/CEs, respectively.
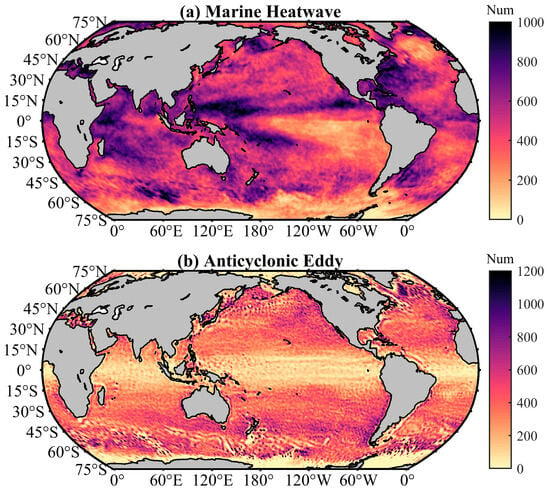
Figure 3.
Global distribution of the MHW (a) and AE (b) counts from 2010 to 2019.
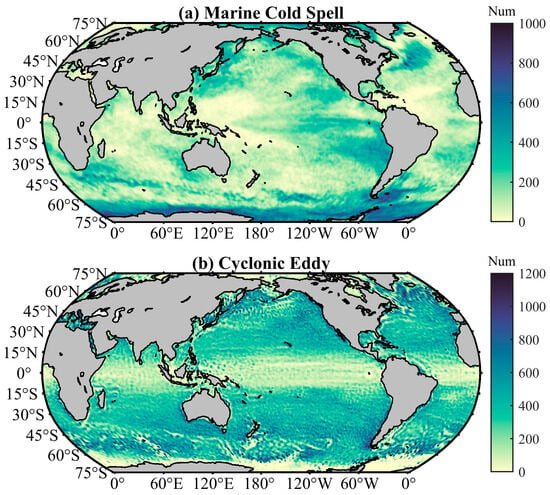
Figure 4.
Global distribution of the MCS (a) and CE (b) counts from 2010 to 2019.
3.1.1. MHWs and AEs
Figure 3a shows the global spatial distribution of MHWs. It is evident that the occurrence counts of MHWs are particularly high in the North Pacific, especially in the western Pacific warm pool. This is likely closely related to the SSTA caused by the El Niño phenomenon [31,81,82,83]. In addition, higher frequencies of MHWs are observed in the mid- to high-latitude regions between 30°S and 60°S. The positive SSTAs in these areas may be closely related to changes of Southern Hemisphere westerlies [58,84]. Regions such as the Gulf Stream (GS) and Kuroshio Extension (KE) also show higher frequencies of MHWs, which may be influenced by regional oceanic current dynamics [85].
By contrast, the global distribution of AEs shows similar patterns to the MHW counts distribution (Figure 3b). The spatial distribution of AEs exhibits distinct regional characteristics. The occurrence counts of AEs are higher in the mid- to high-latitude regions between 30°S and 60°S. Additionally, higher counts of AEs are also observed at regions with strong currents, such as along the coasts of the Gulf of Mexico, California Bay, and the KE region.
From the spatial distribution perspective, MHWs and AEs exhibit significant overlap in several regions. Particularly in the North Pacific, North Atlantic, and mid- to high-latitude regions of the Southern Hemisphere, both MHWs and AEs show higher occurrence counts. This consistency suggests that AEs may play an important role in the formation and maintenance of MHWs.
3.1.2. MCSs and CEs
Figure 4a shows that the Gulf of Mexico, the KE region, and the cold tongue area of the Eastern Pacific are high-frequency zones for MCSs. This is particularly evident in the equatorial Eastern Pacific, which is closely associated with the upwelling processes in the region and La Niña events. Additionally, higher counts of MCSs are observed in the mid- to high-latitude regions of the Southern Hemisphere, such as the South Pacific and South Atlantic, forming significant high-frequency cold spell zones. This suggests that the SST variations in these regions may be influenced by large-scale atmosphere-ocean interactions.
In Figure 4b, the distribution of CEs is similar to that of AEs, especially in the mid- to high-latitude regions between 30°S and 60°S, where the occurrence counts of CEs are higher. This is consistent with the strong oceanic dynamics and the characteristics of the Southern Ocean circulation in this region. Additionally, higher counts of CEs are observed in the regions surrounding the Gulf of Mexico and California Bay, as well as in the KE region, showing a certain degree of spatial consistency with the distribution of MCSs.
MCSs and CEs exhibit a highly overlapping distribution pattern in several regions, particularly in the KE region, the Gulf of Mexico, and the mid- to high-latitude areas between 30°S and 60°S. This phenomenon may suggest that CEs play a key role in the formation of MCSs, such as by enhancing upwelling, promoting cold water upwelling, and other mechanisms that lower SST, thereby increasing the probability of MCS occurrences.
3.2. Global Distribution of Matched MHWs and MCSs
In Section 2.5, we applied an overlap-based filtering method to match MHW and MCS events associated with AEs and CEs. In this section, we will present the distribution of the matched MHWs and MCSs during the period from 2010 to 2019. The spatial distribution of these events is analyzed by gridding the data onto a 1° by 1° resolution grid, and the occurrence of MHWs and MCSs in each grid cell is calculated.
From Figure 5, it is evident that the distribution characteristics of the matched MHWs exhibit significant spatial heterogeneity. First, the GS and KE regions in the Northern Hemisphere (located approximately at 30°N, 80°W and 30°N, 140°E) show concentrated high-frequency MHW zones, with higher counts of MHWs in these areas. Additionally, the mid- to high-latitude regions of the Southern Hemisphere (located between approximately 50°S, 60°E to 90°E in the South Indian Ocean and around 50°S, 60°W in the South Atlantic Ocean, particularly near the southern coast of Australia) exhibit significantly higher counts of MHWs.
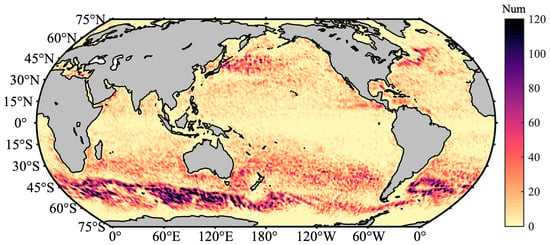
Figure 5.
The distribution of the unmatched MHW counts globally from 2010 to 2019.
From Figure 6, it is evident that the matched MCSs exhibit a high spatial overlap with the matched MHWs shown in Figure 5. Both are concentrated in the GS and KE regions (approximately at 30°N, 80°W and 30°N, 140°E) as well as the mid- to high-latitude regions of the Southern Hemisphere (located between approximately 50°S, 60°E to 90°E in the South Indian Ocean and around 50°S, 60°W in the South Atlantic Ocean, particularly near the southern coast of Australia).
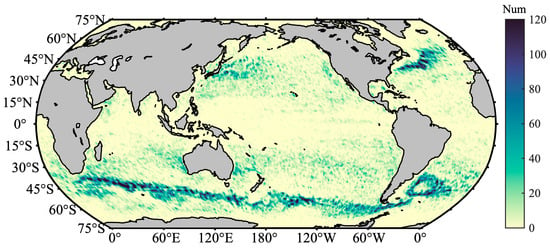
Figure 6.
The distribution of the matched MCS counts globally from 2010 to 2019.
3.3. Comparison of Matched and Unmatched MHWs/MCSs
In Section 2.4, we applied an overlap-based match criterion to identify mesoscale eddies associated with MHWs and MCSs. To further assess the effectiveness of this match criterion, we compare the probability density distributions of eddy amplitude and radius between the matched and unmatched eddies. This comparison reveals how the match criterion affects the identification of eddies with different distribution characteristics.
Overall, there is a clear difference between the matched cases (Figure 7a,c) and the unmatched cases (Figure 7b,d) in terms of the 0.90 cumulative probability regions. Specifically, for the matched cases (Figure 7a,c), these regions are predominantly found within log10 amplitude values ranging from −1.8 to −0.3 and log10 radius values ranging from 4.6 to 5.2. Conversely, in the unmatched cases (Figure 7b,d), the 90% cumulative probability regions are concentrated at smaller log10 amplitude values, ranging from −2.3 to −1.7, and smaller log10 radius values, ranging from 4.4 to 4.8. This distinct shift in the distribution ranges highlights that the match criterion effectively selects for eddies with higher intensity and larger spatial scales.
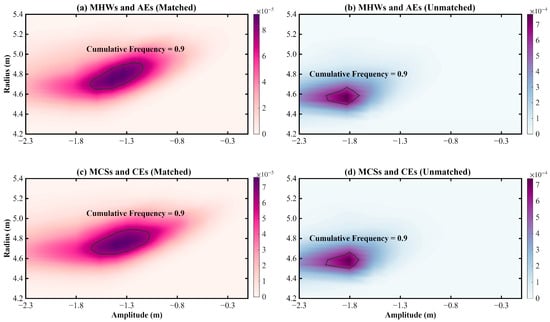
Figure 7.
Probability density distributions of the amplitude and radius for AEs associated with MHWs (a) and CEs associated with MCSs (c) as matched by the 2.4 criterion, as well as for unmatched AEs (b) and unmatched CEs (d) for MHWs and MCSs, respectively. The x-axis represents the logarithmic value of the eddy amplitude, and the y-axis represents the logarithmic value of the eddy radius. Both amplitude and radius are measured in meters (m). The color shading in each subplot indicates the frequency of occurrence for different combinations of amplitude and radius. A black closed contour line represents the 0.90 cumulative density level.
In Figure 7a, we can observe the probability density distribution of AEs associated with MHWs. The data suggest that the highest probability densities are associated with larger amplitudes (log10 amplitude ranging from −1.8 to −0.3) and larger radii (log10 radius ranging from 4.6 to 5.2). This indicates that AE linked to MHWs generally exhibit higher intensity (larger amplitude) and larger spatial scales (larger radius). This relationship highlights the characteristic nature of AEs during MHW events, supporting the notion that stronger and more expansive AEs are key features of MHWs.
In Figure 7b, the unmatched case, the density of both MHWs and AEs significantly decreases, especially when compared to the matched case. The probability distribution becomes more dispersed, covering a broader range of amplitude and radius. The highest probability densities are now more concentrated around smaller amplitudes (log10 amplitude ranging from −2.3 to −1.7) and smaller radii (log10 radius ranging from 4.4 to 4.8). This suggests that, in the unmatched scenario, the eddies typically have lower intensity (smaller amplitude) and smaller spatial scales (smaller radius), indicating they are less likely to be associated with extreme ocean temperature events like MHWs.
In Figure 7c, this panel, representing CEs associated with MCSs, shows a similar distribution to that observed in Figure 7a. The matched MCSs and CEs also exhibit higher probability densities in regions with larger amplitudes (log10 amplitude between −1.8 and −0.3) and larger radii (log10 radius between 4.6 and 5.2). This confirms that CEs associated with MCSs share similar characteristics with AEs in terms of amplitude and radius, suggesting that these eddies are also more likely to be associated with extreme temperature events like MCSs. This emphasizes the importance of larger, more intense eddies in these systems.
In Figure 7d, the unmatched case for MCSs and CEs, we again observe a similar pattern to Figure 7b. The density is lower, and the distribution is broader. The highest probability densities are concentrated around smaller amplitudes (log10 amplitude ranging from −2.3 to −1.7) and smaller radii (log10 radius ranging from 4.4 to 4.8). This further emphasizes that CEs in the unmatched scenario are less likely to be associated with extreme ocean events.
The results indicate that larger and more intense eddies, including both anticyclonic and cyclonic, are typically associated with extreme oceanic events such as MHWs and MCSs. In contrast, the unmatched cases exhibit greater variability, with weaker correlations between the eddy characteristics (amplitude and radius) and these extreme events. This suggests that smaller, less intense eddies are less likely to be associated with such phenomena.
3.4. MHW/MCS Locations Relative to Eddies
This section analyzes the normalized spatial distribution of MHW and MCS events from 2010 to 2019 within mesoscale AEs and CEs that meet the match criteria. Using the normalization method described in Section 2.5, the center of each eddy is set as the origin, and the eddy radius is used as the standard scale. The locations of MHW and MCS events are normalized to enable comparison of eddies with different radii and intensities within the same coordinate system. The main objective of this section is to reveal the typical distribution patterns of MHWs and MCSs within their respective eddies.
Figure 8a illustrates the spatial distribution of MHWs within AEs. Darker shading indicates that MHW events are concentrated in eddy cores, where the probability density is higher. The concentration of MHW events aligns with the 10th percentile eddy contour (gray dash-dot line), suggesting that these extreme temperature events are more likely to occur in the central part of the eddy. As we move outward from the core, the probability density of MHWs gradually decreases, and the distribution becomes more diffuse in the outer regions, indicating that the central part of the AE exerts a stronger influence on MHWs. Additionally, a westward shift in the distribution of MHW events is noticeable, indicating that the structural dynamics of the AE may cause these extreme temperature events to be more concentrated on the western side of the eddy. The orange-red contour line representing the 50th percentile of MHWs further highlights that 50% of the MHW events fall within this boundary, providing additional insight into the central concentration of these extreme events within the AE.
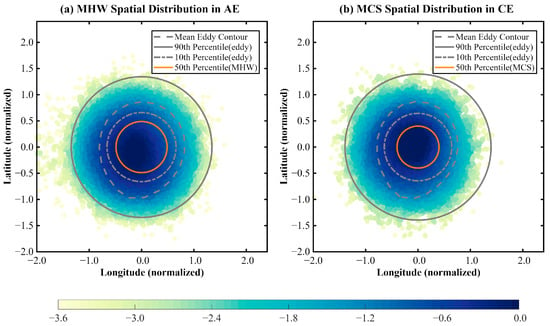
Figure 8.
Normalized probability density spatial distribution of (a) MHW events within AEs and (b) MCS events within CEs across all study years. The x- and y-axes represent the normalized longitude and latitude relative to the center of the eddy, respectively. The color shading indicates the probability density of MHW and MCS events, with darker regions representing higher probability densities, indicating a more concentrated distribution of the respective events, and lighter regions representing lower probability densities. The probability density is shown on a log10 scale. The gray contour lines depict the contours of mesoscale eddies, with the AE contour on the left for MHW and the CE contour on the right for MCS. The gray dashed line represents the 90th percentile boundary contour, the gray dash-dot line represents the 10th percentile boundary contour, and the gray solid line represents the average eddy contour. Additionally, the orange-red contour line represents the 50th percentile of MHW events, indicating that 50% of the MHW events fall within this boundary.
Statistical analysis reveals that approximately 90.2% of the MHW events are contained within the “mean eddy contour of the AE, further confirming the central concentration of these events within the AE’s core.
Figure 8b shows the spatial distribution of MCS events within CEs. MCS events are similarly concentrated in the core region of the CE, with higher probability densities (darker regions) indicating a higher frequency of occurrence within the core. However, in contrast to the westward shift seen in MHWs within AEs, the distribution of MCSs within CEs is more symmetric. This suggests that MCSs are more uniformly distributed across the eddy, without the directional bias observed in the case of MHWs. As with MHWs, the density of MCS events decreases as we move away from the core, with fewer MCS events in the outer regions of the CE. This further reinforces the idea that the central region of the CE has a more significant role in driving the occurrence of MCS events.
Statistical analysis also indicates that approximately 93.1% of the MCS events are contained within the mean eddy contour of the CE, supporting the central concentration of MCSs within the core of the CE.
In summary, both MHWs and MCSs are most concentrated within the core regions of their respective eddies, with the density of both events diminishing as we move toward the outer edges of the eddies. While MHWs in AEs exhibit a distinct westward shift, MCSs in CEs show a more symmetrical distribution. These patterns suggest that the structural dynamics of the eddies—such as their core intensity—play a crucial role in influencing the spatial distribution of extreme temperature events like MHWs and MCSs.
4. Discussion
This study analyzed the spatial distribution of MHW and MCS events within mesoscale eddies during the period from 2010 to 2019, revealing the influence of eddy strength and structure on these extreme temperature events. By employing a normalization method, we standardized eddies of varying radii onto a common coordinate system for comparison, providing novel insights into the relationship between eddy dynamics and extreme climate events.
In this study, we defined an eddy as “accompanying” an MHW or MCS event when their spatial overlap exceeds 50% of the event’s area. This threshold was chosen to enable quantitative analysis. The eddy region, as defined by the contour of maximum speed in the eddy data, is considered a conservative definition. Dynamically, the actual influence region of an eddy can extend beyond this specific contour, and precisely quantifying this larger region is challenging. Consequently, adopting a 100% overlap threshold based on this conservative definition would likely underestimate the number of MHWs/MCSs associated with eddies. Therefore, a 50% overlap threshold was adopted as a pragmatic choice, guided by intuitive considerations and common sense. Further supporting this choice, Figure 8 illustrates that the centroids of these MHWs/MCSs are almost entirely (>90%) located within the mean eddy radius, indicating the reasonableness of this value.
However, recognizing that the choice of overlap threshold may influence the stability and interpretation of the results, we conducted a sensitivity analysis of the threshold. By adjusting the threshold from 50% to 75%, we observed that the proportion of MHWs associated with AEs decreased from 12.2% to 9.39%, and the proportion of MCSs associated with CEs decreased from 13.4% to 10.94%. This adjustment confirms that increasing the threshold indeed results in a lower spatial overlap between eddies and extreme temperature events, which may introduce some bias in interpreting the association between mesoscale eddies and MHW/MCS events.
AEs trap heat within their cores due to subsidence, leading to localized SST increases, which can enhance and intensify MHWs [49,50,51,52]. In contrast, CEs bring deep cold waters to the surface through upwelling, causing localized cooling and promoting the formation and intensification of MCSs [51,52,53,54]. Normalized distributions not only confirm the close coupling between MHWs/MCSs and eddies but also provide a new physical perspective on the specific role of oceanic eddies in the formation of extreme temperature events.
While our study primarily focused on observation-based statistical relationships, our findings align with recent high-resolution modeling work that further elucidates the underlying physical mechanisms. For instance, Bian et al. (2023) [64] utilized an eddy-resolving climate model to demonstrate that heat flux convergence by oceanic mesoscale eddies (HFC-E) acts as a dominant driver of MHW life cycles. They found that HFC-E, largely governed by quasi-geostrophic horizontal advection, makes an important contribution to the growth and decay phases of MHWs. Vertical transport, while locally important, plays a secondary role in this process. Furthermore, their work suggests that MHWs primarily driven by mesoscale eddies tend to have a relatively shorter duration compared to those influenced by mean flows, contributing to the overall characteristics of the MHW life cycle. This highlights how mesoscale eddies crucially influence not only the intensity but also the temporal evolution of these extreme events. Our observation-based results provide the first global-scale empirical support for these mechanisms derived from real-world data, reinforcing the significance of mesoscale eddies in modulating extreme surface temperature events. Thus, our normalized distributions not only confirm the close coupling between MHWs/MCSs and eddies but also provide a new physical perspective on the specific role of oceanic eddies in the formation of extreme temperature events.
In addition to normal AEs and CEs, which typically cause positive (negative) SSTAs, we also considered the impact of abnormal AEs and CEs, which lead to negative (positive) SSTAs. These “abnormal” eddies, specifically known as cold-core anticyclonic eddies and warm-core cyclonic eddies, have been found to be surprisingly abundant in the global ocean, accounting for approximately 20% of all observed eddies [52]. Their formation mechanisms often deviate from the traditional vertical pumping, involving processes such as relative wind-stress-induced Ekman pumping, surface mixed layer depth variations, vertical entrainment [86], or complex interactions with salinity stratification and temperature gradients [87]. Consequently, their interactions with MHWs and MCSs may differ from the normal cases. To explore this, we analyzed the relationship between MHWs and CEs, as well as MCSs and AEs. Our results revealed that MHWs associated with CEs occurred at a rate of 2.93%, and MCSs associated with AEs occurred at a rate of 1.19%. These findings suggest that while normal AEs and CEs are the dominant contributors to MHWs and MCSs, abnormal eddies also play a role in modulating extreme temperature events. This broadens our understanding of the complex interactions between MHWs/MCSs and mesoscale eddies, highlighting the complexity of these dynamics.
Furthermore, the normalization analysis demonstrates the varying spatial extent of eddy impacts on extreme temperature events based on their intensity. We found that stronger eddies, whether anticyclonic or cyclonic, generate more significant temperature anomalies in their core regions, and their influence extends over a broader area. This highlights the critical role of eddy strength in modulating the spatial scope of extreme climate events. Strong mesoscale eddies not only intensify SSTAs within their core regions but also enlarge the affected area, thereby causing broader oceanic temperature deviations.
Finally, future research should further explore the physical mechanisms behind MHWs within AEs, as well as investigate the role of abnormal eddies in modulating these extreme temperature events. By integrating atmospheric-ocean coupled models and expanding the analysis to include abnormal eddies, it will be possible to better understand the dynamic processes behind these shifts and assess their implications on global climate patterns. Moreover, it is crucial to consider the temporal scope of such investigations. While our current analysis focuses on the 2010–2019 period, satellite data for mesoscale eddies and extreme temperature events are available for a longer duration, typically from 1993 to 2019. To contextualize the coverage of our study, we assessed the proportion of events within our 2010–2019 timeframe relative to the broader 1993–2019 period. Our analysis revealed that the events captured in our study period represent approximately 36.93% of total CEs and 36.89% of AEs observed between 1993 and 2019. For extreme temperature events, our period covers about 44.30% of MCSs and 28.67% of MHWs during the same longer interval. These percentages indicate that while our study period does not cover the entire available record, it still represents a substantial and recent segment. The insights gained from this decade into the mechanisms governing mesoscale eddy and extreme temperature event interactions are valuable, and these fundamental relationships are likely to be robust across different temporal scales, even if the overall frequency of events varies.
Therefore, comprehensive long-term trend analyses, encompassing the full satellite record and incorporating both normal and abnormal eddies, would provide a more robust foundation for spatial predictions of future oceanic extreme temperature events, improving the accuracy and reliability of these predictions.
5. Conclusions
In this study, we investigated the relationship between mesoscale eddies and MHW/MCS events using global observational data from 2010 to 2019. By applying an overlap-based analytical approach, we derived the following key findings:
Firstly, a significant positive correlation was found between the intensity of matched mesoscale eddies and the strength of MHWs/MCSs, with the correlation between MHW intensity and AE strength being notably stronger than that between MCS intensity and CE strength (through statistical analysis). As the intensity (i.e., amplitude) of mesoscale eddies increases, the intensity of both MHWs and MCSs tends to increase as well.
Furthermore, this study analyzed the probability density distributions of eddy amplitude and radius to further validate the influence range of eddy strength on extreme temperature events. Stronger AEs, which typically have larger amplitudes and radii, have a more significant impact on MHWs in their core regions. In contrast, unmatched AEs exhibit a broader spatial distribution, indicating that these weaker eddies are highly likely to have a smaller effect on MHWs. Similarly, the impact of CEs is closely related to their amplitude and radius; stronger CEs tend to exert a greater influence on MCSs, while weaker CEs have a more limited effect.
The results also reveal that AEs and CEs influence the spatial distribution of extreme temperature events through their distinct dynamical mechanisms. MHWs are primarily concentrated in the core regions of AEs but exhibit a clear westward shift, whereas MCSs are more frequent in the core regions of CEs, with no westward displacement.
In conclusion, this study, through a detailed normalized spatial analysis, provides new insights into the role of mesoscale eddies in modulating MHWs and MCSs. Eddy intensity, size, and structure regulate the spatial patterns of these extreme climate events. These results offer a new physical perspective on the interactions between oceanic eddies and extreme temperature anomalies and provide a theoretical basis for predicting such events in the context of future climate change.
Author Contributions
Conceptualization, J.D. and S.S.; methodology, J.D., W.S. and S.S.; software, Y.-X.F. and S.S.; validation, J.D., S.S. and Y.-X.F.; formal analysis, Y.-X.F. and S.S.; investigation, S.S. and Y.-X.F.; resources, Y.-X.F. and S.S.; data curation, S.S. and Y.-X.F.; writing—original draft preparation, S.S. and Y.-X.F.; writing—review and editing, J.D., W.S., S.S. and Y.-X.F.; visualization, Y.-X.F. and S.S.; supervision, J.D.; project administration, J.D.; funding acquisition, W.S. and J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China, grant number 42192562 and the Science and Technology Innovation Project of Laoshan Laboratory under contract LSKJ202400203.
Data Availability Statement
All data utilized in this study are publicly available. The daily Optimum Interpolation Sea-Surface Temperature (OISST) v2.1 dataset, produced by the National Oceanic and Atmospheric Administration—National Centers for Environmental Information (NOAA/NCEI), can be downloaded from https://www.ncei.noaa.gov/data/sea-surface-temperature-optimum-interpolation/v2.1/access/avhrr/ (accessed on 25 April 2025). The Global Mesoscale Eddy Trajectory Atlas META 3.2 DT (two-satellite version), produced by SSALTO/DUACS and distributed by AVISO+ with support from CNES and in collaboration with IMEDEA, is available at https://www.aviso.altimetry.fr/en/data/products/value-added-products/global-mesoscale-eddy-trajectory-product/meta3-2-dt.html (accessed on 25 April 2025).
Acknowledgments
We sincerely thank the four anonymous reviewers for their constructive comments and valuable suggestions, which have improved the quality of this paper. We also thank Zijie Zhao for providing the main function code used to detect MHWs and MCSs (https://github.com/ZijieZhaoMMHW/m_mhw1.0, accessed on 25 April 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MHW | Marine Heatwave |
| MCS | Marine Cold Spell |
| SLA | Sea Level Anomaly |
| SST | Sea Surface Temperature |
| SSTA | Sea Surface Temperature Anomaly |
| AE | Anticyclonic Eddy |
| CE | Cyclonic Eddy |
| C3S | Copernicus Climate Change Service |
| KE | Kuroshio Extension |
| GS | Gulf Stream |
| HFC-E | Heat Flux Convergence by Oceanic Mesoscale Eddies |
References
- Wernberg, T.; Smale, D.A.; Tuya, F.; Thomsen, M.S.; Langlois, T.J.; De Bettignies, T.; Bennett, S.; Rousseaux, C.S. An Extreme Climatic Event Alters Marine Ecosystem Structure in a Global Biodiversity Hotspot. Nat. Clim. Change 2013, 3, 78–82. [Google Scholar] [CrossRef]
- Smale, D.A.; Wernberg, T.; Oliver, E.C.J.; Thomsen, M.; Harvey, B.P.; Straub, S.C.; Burrows, M.T.; Alexander, L.V.; Benthuysen, J.A.; Donat, M.G.; et al. Marine Heatwaves Threaten Global Biodiversity and the Provision of Ecosystem Services. Nat. Clim. Change 2019, 9, 306–312. [Google Scholar] [CrossRef]
- Schlegel, R.W.; Darmaraki, S.; Benthuysen, J.A.; Filbee-Dexter, K.; Oliver, E.C.J. Marine Cold-Spells. Prog. Oceanogr. 2021, 198, 102684. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, C.; Fu, Y. Global Marine Heatwaves and Cold-Spells in Present Climate to Future Projections. Earths Future 2022, 10, e2022EF002787. [Google Scholar] [CrossRef]
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.J.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M.; et al. A Hierarchical Approach to Defining Marine Heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef]
- Amaya, D.J.; Jacox, M.G.; Fewings, M.R.; Saba, V.S.; Stuecker, M.F.; Rykaczewski, R.R.; Ross, A.C.; Stock, C.A.; Capotondi, A.; Petrik, C.M.; et al. Marine Heatwaves Need Clear Definitions so Coastal Communities Can Adapt. Nature 2023, 616, 29–32. [Google Scholar] [CrossRef] [PubMed]
- Beaugrand, G.; Edwards, M.; Brander, K.; Luczak, C.; Ibanez, F. Causes and Projections of Abrupt Climate-driven Ecosystem Shifts in the North Atlantic. Ecol. Lett. 2008, 11, 1157–1168. [Google Scholar] [CrossRef] [PubMed]
- Scannell, H.A.; Pershing, A.J.; Alexander, M.A.; Thomas, A.C.; Mills, K.E. Frequency of Marine Heatwaves in the North Atlantic and North Pacific since 1950. Geophys. Res. Lett. 2016, 43, 2069–2076. [Google Scholar] [CrossRef]
- Frölicher, T.L.; Fischer, E.M.; Gruber, N. Marine Heatwaves under Global Warming. Nature 2018, 560, 360–364. [Google Scholar] [CrossRef] [PubMed]
- Chiswell, S.M. Global Trends in Marine Heatwaves and Cold Spells: The Impacts of Fixed Versus Changing Baselines. J. Geophys. Res. Oceans 2022, 127, e2022JC018757. [Google Scholar] [CrossRef]
- Han, W.; Zhang, L.; Meehl, G.A.; Kido, S.; Tozuka, T.; Li, Y.; McPhaden, M.J.; Hu, A.; Cazenave, A.; Rosenbloom, N.; et al. Sea Level Extremes and Compounding Marine Heatwaves in Coastal Indonesia. Nat. Commun. 2022, 13, 6410. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Shan, H.; Liang, J.-H.; Dong, C. Assessment and Projections of Marine Heatwaves in the Northwest Pacific Based on CMIP6 Models. Remote Sens. 2023, 15, 2957. [Google Scholar] [CrossRef]
- Sun, D.; Li, F.; Jing, Z.; Hu, S.; Zhang, B. Frequent Marine Heatwaves Hidden below the Surface of the Global Ocean. Nat. Geosci. 2023, 16, 1099–1104. [Google Scholar] [CrossRef]
- Song, Q.; Yao, Y.; Wang, C. Response of Future Summer Marine Heatwaves in the South China Sea to Enhanced Western Pacific Subtropical High. Geophys. Res. Lett. 2023, 50, e2023GL103667. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Yang, Y.; Yang, J.; Ji, J.; Dong, C. Marine Heatwaves/Cold-Spells Associated With Mixed Layer Depth Variation Globally. Geophys. Res. Lett. 2024, 51, e2024GL112325. [Google Scholar] [CrossRef]
- Brown, C.J.; Mellin, C.; Edgar, G.J.; Campbell, M.D.; Stuart-Smith, R.D. Direct and Indirect Effects of Heatwaves on a Coral Reef Fishery. Glob. Change Biol. 2021, 27, 1214–1225. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Bethel, B.J.; Dong, C.; Zhao, H.; Yao, Y.; Yu, Y. Marine Heatwave Events near Weizhou Island, Beibu Gulf in 2020 and Their Possible Relations to Coral Bleaching. Sci. Total Environ. 2022, 823, 153414. [Google Scholar] [CrossRef] [PubMed]
- Le Nohaïc, M.; Ross, C.L.; Cornwall, C.E.; Comeau, S.; Lowe, R.; McCulloch, M.T.; Schoepf, V. Marine Heatwave Causes Unprecedented Regional Mass Bleaching of Thermally Resistant Corals in Northwestern Australia. Sci. Rep. 2017, 7, 14999. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.R.; Gonçalves Neto, A.H.; Vieira, E.A.; Longo, G.O. The Severe 2020 Coral Bleaching Event in the Tropical Atlantic Linked to Marine Heatwaves. Commun. Earth Environ. 2025, 6, 208. [Google Scholar] [CrossRef]
- Donovan, M.K.; Burkepile, D.E.; Kratochwill, C.; Shlesinger, T.; Sully, S.; Oliver, T.A.; Hodgson, G.; Freiwald, J.; Van Woesik, R. Local Conditions Magnify Coral Loss after Marine Heatwaves. Science 2021, 372, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Bainbridge, S.J. Temperature and Light Patterns at Four Reefs along the Great Barrier Reef during the 2015–2016 Austral Summer: Understanding Patterns of Observed Coral Bleaching. J. Oper. Oceanogr. 2017, 10, 16–29. [Google Scholar] [CrossRef]
- Welch, H.; Savoca, M.S.; Brodie, S.; Jacox, M.G.; Muhling, B.A.; Clay, T.A.; Cimino, M.A.; Benson, S.R.; Block, B.A.; Conners, M.G.; et al. Impacts of Marine Heatwaves on Top Predator Distributions Are Variable but Predictable. Nat. Commun. 2023, 14, 5188. [Google Scholar] [CrossRef] [PubMed]
- Smith, K.E.; Aubin, M.; Burrows, M.T.; Filbee-Dexter, K.; Hobday, A.J.; Holbrook, N.J.; King, N.G.; Moore, P.J.; Sen Gupta, A.; Thomsen, M.; et al. Global Impacts of Marine Heatwaves on Coastal Foundation Species. Nat. Commun. 2024, 15, 5052. [Google Scholar] [CrossRef] [PubMed]
- Brander, K. Impacts of Climate Change on Fisheries. J. Mar. Syst. 2010, 79, 389–402. [Google Scholar] [CrossRef]
- Cheung, W.W.L.; Frölicher, T.L. Marine Heatwaves Exacerbate Climate Change Impacts for Fisheries in the Northeast Pacific. Sci. Rep. 2020, 10, 6678. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Caputi, N.; Chandrapavan, A.; Chen, M.; Hart, A.; Kangas, M. Multi-Year Marine Cold-Spells off the West Coast of Australia and Effects on Fisheries. J. Mar. Syst. 2021, 214, 103473. [Google Scholar] [CrossRef]
- Marshak, A.R.; Link, J.S. Responses of Fisheries Ecosystems to Marine Heatwaves and Other Extreme Events. PLoS ONE 2024, 19, e0315224. [Google Scholar] [CrossRef] [PubMed]
- Tozuka, T.; Oettli, P. Asymmetric Cloud-Shortwave Radiation-Sea Surface Temperature Feedback of Ningaloo Niño/Niña. Geophys. Res. Lett. 2018, 45, 9870–9879. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Sen Gupta, A. Marine Heatwaves. Annu. Rev. Mar. Sci. 2021, 13, 313–342. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Luo, J.-J.; Xu, H.; Ma, J.; Deng, J.; Zhang, L.; Bi, D.; Chen, X. Robust Regional Differences in Marine Heatwaves between Transient and Stabilization Responses at 1.5 °C Global Warming. Weather Clim. Extrem. 2021, 32, 100316. [Google Scholar] [CrossRef]
- Gregory, C.H.; Artana, C.; Lama, S.; León-FonFay, D.; Sala, J.; Xiao, F.; Xu, T.; Capotondi, A.; Martinez-Villalobos, C.; Holbrook, N.J. Global Marine Heatwaves Under Different Flavors of ENSO. Geophys. Res. Lett. 2024, 51, e2024GL110399. [Google Scholar] [CrossRef]
- Choi, H.-Y.; Park, M.-S.; Kim, H.-S.; Lee, S. Marine Heatwave Events Strengthen the Intensity of Tropical Cyclones. Commun. Earth Environ. 2024, 5, 69. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, B.; Shan, H. Predictability Assessment of Marine Heatwaves in the Northeast Pacific Based on SEAS5. Weather Clim. Extrem. 2025, 48, 100773. [Google Scholar] [CrossRef]
- Zhang, N.; Lan, J.; Sun, W.; Dong, C. Contrasting Impacts of Two Types of El Niño on Interannual Variations of Marine Heatwaves in the South China Sea. J. Geophys. Res. Oceans 2025, 130, e2024JC021991. [Google Scholar] [CrossRef]
- Carnat, G.; Brabant, F.; Dumont, I.; Vancoppenolle, M.; Ackley, S.F.; Fritsen, C.; Delille, B.; Tison, J.-L. Influence of Short-Term Synoptic Events and Snow Depth on DMS, DMSP, and DMSO Dynamics in Antarctic Spring Sea Ice. Elem. Sci. Anthr. 2016, 4, 000135. [Google Scholar] [CrossRef]
- Rhines, P.B. Mesoscale Eddies. In Encyclopedia of Ocean Sciences; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1717–1730. ISBN 978-0-12-227430-5. [Google Scholar]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; De Szoeke, R.A. Global Observations of Large Oceanic Eddies. Geophys. Res. Lett. 2007, 34, 2007GL030812. [Google Scholar] [CrossRef]
- Dong, C.; You, Z.; Dong, J.; Ji, J.; Sun, W.; Xu, G.; Lu, X.; Xie, H.; Teng, F.; Liu, Y.; et al. Oceanic Mesoscale Eddies. Ocean-Land-Atmosphere Res. 2025, 4, 0081. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The Observed Signature of Mesoscale Eddies in Sea Surface Temperature and the Associated Heat Transport. Deep Sea Res. Part Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic Mass Transport by Mesoscale Eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global Heat and Salt Transports by Eddy Movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, C.L.; Cessi, P.; McClean, J.L.; Maltrud, M.E. Vertical Heat Transport in Eddying Ocean Models. Geophys. Res. Lett. 2008, 35, 2008GL036138. [Google Scholar] [CrossRef]
- Bashmachnikov, I.L.; Raj, R.P.; Golubkin, P.; Kozlov, I.E. Heat Transport by Mesoscale Eddies in the Norwegian and Greenland Seas. J. Geophys. Res. Oceans 2023, 128, e2022JC018987. [Google Scholar] [CrossRef]
- Dong, D.; Brandt, P.; Chang, P.; Schütte, F.; Yang, X.; Yan, J.; Zeng, J. Mesoscale Eddies in the Northwestern Pacific Ocean: Three-Dimensional Eddy Structures and Heat/Salt Transports. J. Geophys. Res. Oceans 2017, 122, 9795–9813. [Google Scholar] [CrossRef]
- Yang, G.; Yu, W.; Yuan, Y.; Zhao, X.; Wang, F.; Chen, G.; Liu, L.; Duan, Y. Characteristics, Vertical Structures, and Heat/Salt Transports of Mesoscale Eddies in the Southeastern Tropical I Ndian O Cean. J. Geophys. Res. Oceans 2015, 120, 6733–6750. [Google Scholar] [CrossRef]
- Sun, W.; Dong, C.; Wang, R.; Liu, Y.; Yu, K. Vertical Structure Anomalies of Oceanic Eddies in the Kuroshio Extension Region: 3-D EDDY IN THE KUROSHIO EXTENSION REGION. J. Geophys. Res. Oceans 2017, 122, 1476–1496. [Google Scholar] [CrossRef]
- Stanley, Z.; Bachman, S.D.; Grooms, I. Vertical Structure of Ocean Mesoscale Eddies with Implications for Parameterizations of Tracer Transport. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002151. [Google Scholar] [CrossRef]
- Wang, Q.; Dong, C.; Dong, J.; Zhang, H.; Yang, J. Submesoscale Processes-Induced Vertical Heat Transport Modulated by Oceanic Mesoscale Eddies. Deep Sea Res. Part II Top. Stud. Oceanogr. 2022, 202, 105138. [Google Scholar] [CrossRef]
- Brannigan, L. Intense Submesoscale Upwelling in Anticyclonic Eddies. Geophys. Res. Lett. 2016, 43, 3360–3369. [Google Scholar] [CrossRef]
- Chen, Y.L.; Chen, H.-Y.; Jan, S.; Lin, Y.-H.; Kuo, T.-H.; Hung, J.-J. Biologically Active Warm-Core Anticyclonic Eddies in the Marginal Seas of the Western Pacific Ocean. Deep Sea Res. Part Oceanogr. Res. Pap. 2015, 106, 68–84. [Google Scholar] [CrossRef]
- Mizobata, K.; Saitoh, S.I.; Shiomoto, A.; Miyamura, T.; Shiga, N.; Imai, K.; Toratani, M.; Kajiwara, Y.; Sasaoka, K. Bering Sea Cyclonic and Anticyclonic Eddies Observed during Summer 2000 and 2001. Prog. Oceanogr. 2002, 55, 65–75. [Google Scholar] [CrossRef]
- Ni, Q.; Zhai, X.; Jiang, X.; Chen, D. Abundant Cold Anticyclonic Eddies and Warm Cyclonic Eddies in the Global Ocean. J. Phys. Oceanogr. 2021, 51, 2793–2806. [Google Scholar] [CrossRef]
- Barton, E.D.; Arístegui, J.; Tett, P.; Cantón, M.; García-Braun, J.; Hernández-León, S.; Nykjaer, L.; Almeida, C.; Almunia, J.; Ballesteros, S.; et al. The Transition Zone of the Canary Current Upwelling Region. Prog. Oceanogr. 1998, 41, 455–504. [Google Scholar] [CrossRef]
- Vukovich, F.M.; Maul, G.A. Cyclonic Eddies in the Eastern Gulf of Mexico. J. Phys. Oceanogr. 1985, 15, 105–117. [Google Scholar] [CrossRef]
- Li, J.; Roughan, M.; Hemming, M. Interactions between Cold Cyclonic Eddies and a Western Boundary Current Modulate Marine Heatwaves. Commun. Earth Environ. 2023, 4, 380. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, Y.; Feng, M.; Hobday, A.J. Vertical Structures of Marine Heatwaves. Nat. Commun. 2023, 14, 6483. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Zhan, W.; Feng, M.; Gong, Y.; Cai, S.; Zhan, H. Common Occurrences of Subsurface Heatwaves and Cold Spells in Ocean Eddies. Nature 2024, 634, 1111–1117. [Google Scholar] [CrossRef] [PubMed]
- Beech, N.; Rackow, T.; Semmler, T.; Danilov, S.; Wang, Q.; Jung, T. Long-Term Evolution of Ocean Eddy Activity in a Warming World. Nat. Clim. Change 2022, 12, 910–917. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, J.; Hu, Y. Climatic Interactions between Cold Surges in the South China Sea and North Pacific Extratropical Cyclones. Meteorol. Appl. 2024, 31, e2182. [Google Scholar] [CrossRef]
- Melnichenko, O.; Amores, A.; Maximenko, N.; Hacker, P.; Potemra, J. Signature of Mesoscale Eddies in Satellite Sea Surface Salinity Data: SSS SIGNATURE OF MESOSCALE EDDIES. J. Geophys. Res. Oceans 2017, 122, 1416–1424. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, L.; Chen, G. Characterization of Sea Surface Temperature and Air-Sea Heat Flux Anomalies Associated With Mesoscale Eddies in the South China Sea. J. Geophys. Res. Oceans 2020, 125, e2019JC015470. [Google Scholar] [CrossRef]
- Lv, M.; Wang, F.; Li, Y.; Zhang, Z.; Zhu, Y. Structure of Sea Surface Temperature Anomaly Induced by Mesoscale Eddies in the North Pacific Ocean. J. Geophys. Res. Oceans 2022, 127, e2021JC017581. [Google Scholar] [CrossRef]
- Schaeffer, A.; Sen Gupta, A.; Roughan, M. Seasonal Stratification and Complex Local Dynamics Control the Sub-Surface Structure of Marine Heatwaves in Eastern Australian Coastal Waters. Commun. Earth Environ. 2023, 4, 304. [Google Scholar] [CrossRef]
- Bian, C.; Jing, Z.; Wang, H.; Wu, L.; Chen, Z.; Gan, B.; Yang, H. Oceanic Mesoscale Eddies as Crucial Drivers of Global Marine Heatwaves. Nat. Commun. 2023, 14, 2970. [Google Scholar] [CrossRef] [PubMed]
- Wyatt, A.S.J.; Leichter, J.J.; Washburn, L.; Kui, L.; Edmunds, P.J.; Burgess, S.C. Hidden Heatwaves and Severe Coral Bleaching Linked to Mesoscale Eddies and Thermocline Dynamics. Nat. Commun. 2023, 14, 25. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.-M. Improvements of the Daily Optimum Interpolation Sea Surface Temperature (DOISST) Version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Li, C.; Sun, W.; Ji, J.; Zhu, Y. Historical Marine Cold Spells in the South China Sea: Characteristics and Trends. Remote Sens. 2024, 16, 1171. [Google Scholar] [CrossRef]
- Cao, M.; Mao, K.; Yan, Y.; Shi, J.; Wang, H.; Xu, T.; Fang, S.; Yuan, Z. A New Global Gridded Sea Surface Temperature Data Product Based on Multisource Data. Earth Syst. Sci. Data 2021, 13, 2111–2134. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, F.; Zhu, J.; Chen, X. Observed Frequent Occurrences of Marine Heatwaves in Most Ocean Regions during the Last Two Decades. Adv. Atmospheric Sci. 2022, 39, 1579–1587. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, S.; Yang, J.; Gao, X.; Ji, J.; Dong, C. Artificial Intelligence Forecasting of Marine Heatwaves in the South China Sea Using a Combined U-Net and ConvLSTM System. Remote Sens. 2023, 15, 4068. [Google Scholar] [CrossRef]
- Sun, W.; Yin, L.; Pei, Y.; Shen, C.; Yang, Y.; Ji, J.; Yang, J.; Dong, C. Marine Heatwaves in the Western North Pacific Region: Historical Characteristics and Future Projections. Deep Sea Res. Part Oceanogr. Res. Pap. 2023, 200, 104161. [Google Scholar] [CrossRef]
- Sun, W.; Yang, Y.; Wang, Y.; Yang, J.; Ji, J.; Dong, C. Characterization and Future Projection of Marine Heatwaves under Climate Change in the South China Sea. Ocean Model. 2024, 188, 102322. [Google Scholar] [CrossRef]
- Pan, Y.; Sun, W.; Bao, S.; Xie, M.; Jiang, L.; Ji, J.; Yu, Y.; Dong, C. Global Variability and Future Projections of Marine Heatwave Onset and Decline Rates. Remote Sens. 2025, 17, 1362. [Google Scholar] [CrossRef]
- Mason, E.; Pascual, A.; McWilliams, J.C. A New Sea Surface Height–Based Code for Oceanic Mesoscale Eddy Tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Pegliasco, C.; Delepoulle, A.; Mason, E.; Morrow, R.; Faugère, Y.; Dibarboure, G. META3.1exp: A New Global Mesoscale Eddy Trajectory Atlas Derived from Altimetry. Earth Syst. Sci. Data 2022, 14, 1087–1107. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Liu, Y.; Ma, L.; Wang, H.; Ren, K.; Chen, S. Parametric Model for Eddies-Induced Sound Speed Anomaly in Five Active Mesoscale Eddy Regions. J. Geophys. Res. Oceans 2022, 127, e2022JC018408. [Google Scholar] [CrossRef]
- Rocha, C.B.; Simoes-Sousa, I.T. Compact Mesoscale Eddies in the South Brazil Bight. Remote Sens. 2022, 14, 5781. [Google Scholar] [CrossRef]
- Erickson, Z.K.; Fields, E.; Johnson, L.; Thompson, A.F.; Dove, L.A.; D’Asaro, E.; Siegel, D.A. Eddy Tracking From In Situ and Satellite Observations. J. Geophys. Res. Oceans 2023, 128, e2023JC019701. [Google Scholar] [CrossRef]
- Ioannou, A.; Guez, L.; Laxenaire, R.; Speich, S. Global Assessment of Mesoscale Eddies with TOEddies: Comparison Between Multiple Datasets and Colocation with In Situ Measurements. Remote Sens. 2024, 16, 4336. [Google Scholar] [CrossRef]
- Holbrook, N.J.; Claar, D.C.; Hobday, A.J.; McInnes, K.L.; Oliver, E.C.J.; Gupta, A.S.; Widlansky, M.J.; Zhang, X. ENSO-Driven Ocean Extremes and Their Ecosystem Impacts. In Geophysical Monograph Series; McPhaden, M.J., Santoso, A., Cai, W., Eds.; Wiley: Oxford, UK, 2020; pp. 409–428. ISBN 978-1-119-54812-6. [Google Scholar]
- Capotondi, A.; Newman, M.; Xu, T.; Di Lorenzo, E. An Optimal Precursor of Northeast Pacific Marine Heatwaves and Central Pacific El Niño Events. Geophys. Res. Lett. 2022, 49, e2021GL097350. [Google Scholar] [CrossRef]
- Ma, J.; Xu, H.; Dong, C.; Luo, J.-J. The Forecast Skills and Predictability Sources of Marine Heatwaves in the NUIST-CFS1.0 Hindcasts. Adv. Atmos. Sci. 2024, 41, 1589–1600. [Google Scholar] [CrossRef]
- Chapman, C.C.; Monselesan, D.P.; Risbey, J.S.; Feng, M.; Sloyan, B.M. A Large-Scale View of Marine Heatwaves Revealed by Archetype Analysis. Nat. Commun. 2022, 13, 7843. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Liu, K.; Wang, H.; Chen, X. Vertical Structures and Drivers of Marine Heatwaves and Cold-Spells in the Kuroshio Extension Region. Environ. Res. Lett. 2024, 19, 054015. [Google Scholar] [CrossRef]
- Ni, Q.; Zhai, X.; Yang, Z.; Chen, D. Generation of Cold Anticyclonic Eddies and Warm Cyclonic Eddies in the Tropical Oceans. J. Phys. Oceanogr. 2023, 53, 1485–1498. [Google Scholar] [CrossRef]
- He, Q.; Zhan, H.; Cai, S. Anticyclonic Eddies Enhance the Winter Barrier Layer and Surface Cooling in the Bay of Bengal. J. Geophys. Res. Oceans 2020, 125, e2020JC016524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).