A Multi-Task Learning Framework with Enhanced Cross-Level Semantic Consistency for Multi-Level Land Cover Classification
Abstract
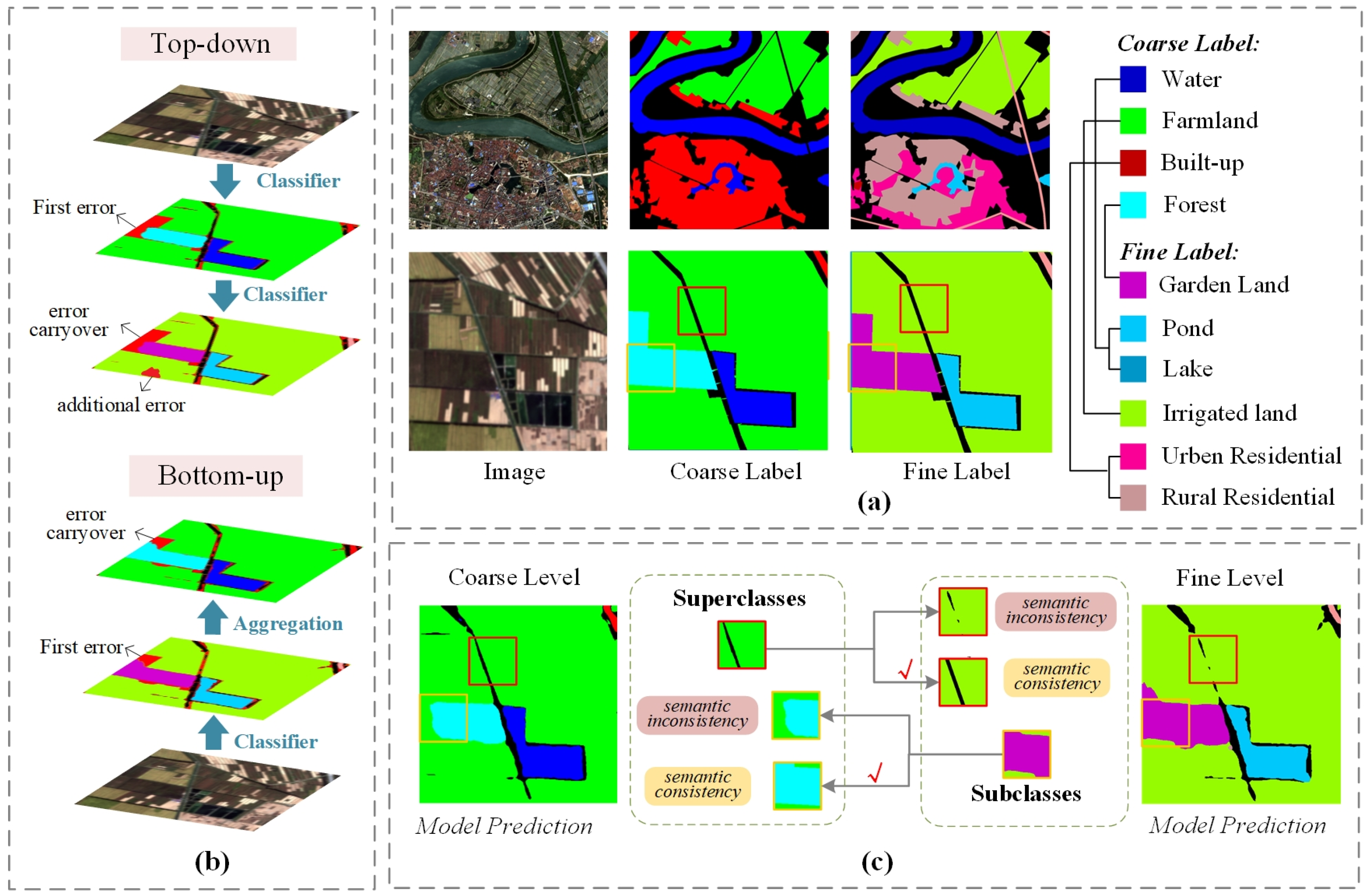
1. Introduction
- (1)
- It achieves information sharing and mutual constraints between semantic layers through shared encoder and feature cascade, while independent decoders generate their respective classification maps, effectively preventing the accumulation and propagation of prediction errors across layers.
- (2)
- A hierarchical structure is incorporated into the loss function to explicitly model category dependencies, where a hierarchical regularization term, combined with task-specific losses, penalizes inconsistent predictions across semantic levels, thereby enhancing semantic coherence while maintaining high classification accuracy.
- (3)
- Two novel evaluation metrics, Semantic Alignment Deviation (SAD) and Enhancing Semantic Alignment Deviation (ESAD), are introduced to quantify semantic consistency across hierarchical levels by measuring the alignment of predictions with the taxonomic structure, offering a comprehensive assessment of both accuracy and coherence.
2. Related Work
2.1. Classification with Hierarchical Class Structures
2.2. Multi-Level Land Cover Classification
2.3. Deep Multi-Task Learning
3. Methodology
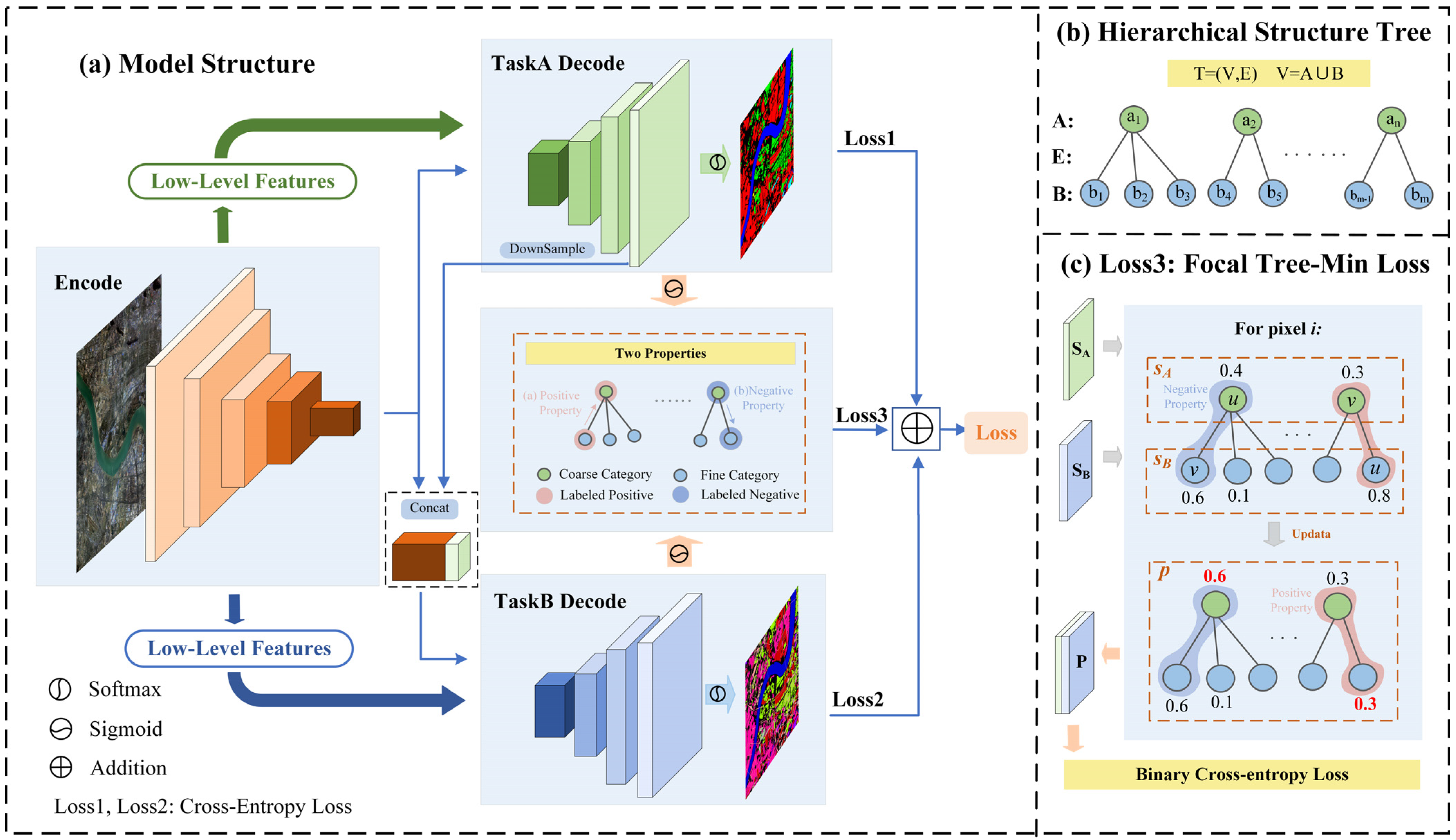
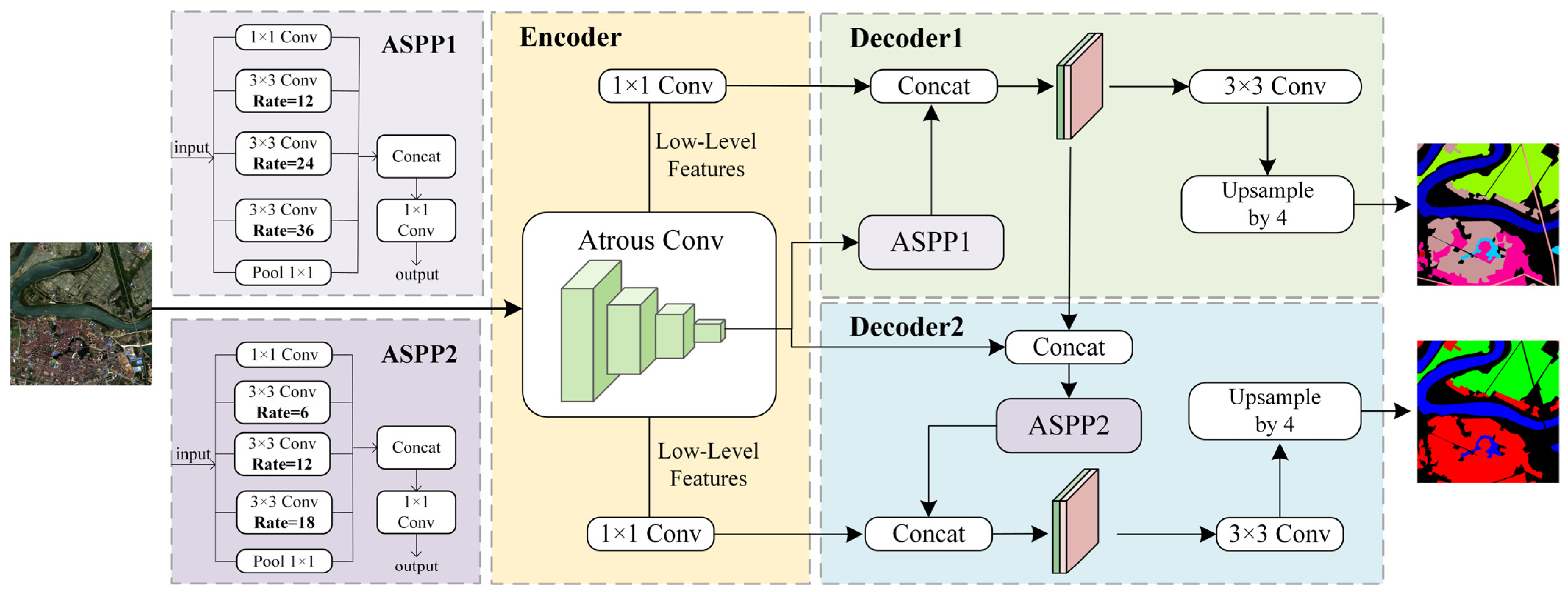
3.1. Encode–Decode Structure
- (1)
- Encoder component
- (2)
- Decoder1: Coarse-level segmentation
- (3)
- Decoder2: Fine-level segmentation
- (4)
- Feature cascade
3.2. Hierarchical Loss Functions
3.2.1. Focal Tree-Min Loss
- (1)
- Positive Property: For each pixel, if a class is labeled positive, all its ancestor nodes (i.e., superclasses) should be labeled positive.
- (2)
- Negative Property: For each pixel, if a class is labeled negative, all its child nodes (i.e., subclasses) should be labeled negative.
- (1)
- Positive -Constraint: For each pixel , if class is labeled as positive (belongs to this class), and , then it should hold that .
- (2)
- Negative -Constraint: For each pixel , if class is labeled as negative (does not belong to this class), and , then it should hold that .
3.2.2. Joint Loss Function
4. Experiments and Results
4.1. Experimental Setup
4.1.1. Dataset
4.1.2. Parameter Settings
4.2. Evaluation Metrics
4.2.1. Segmentation Accuracy Metrics
4.2.2. Semantic Consistency Metrics
4.3. Ablation Experiment
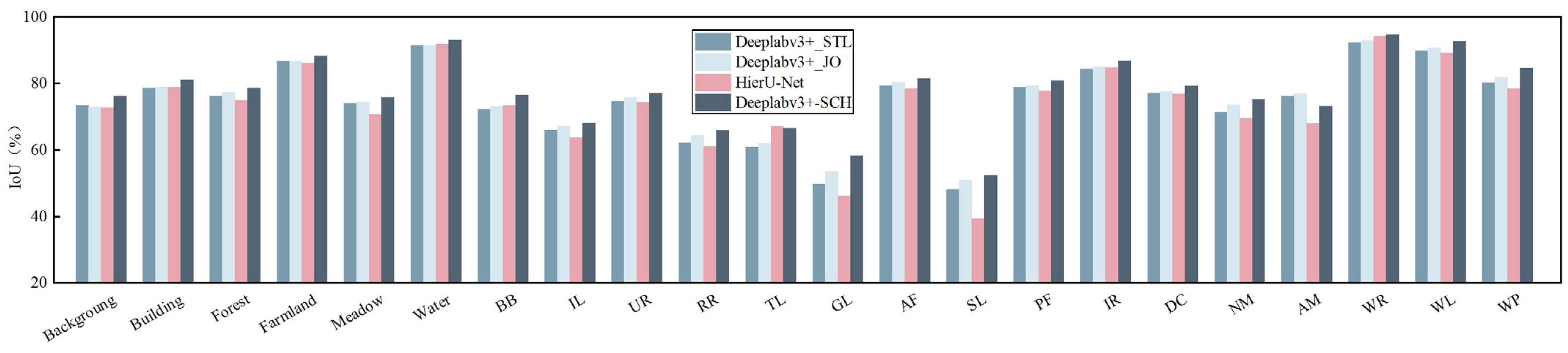
4.4. Experiments on the GID Dataset
4.4.1. Comparative Experiments
4.4.2. Generalization Analysis
4.5. Experiments on the STB Dataset
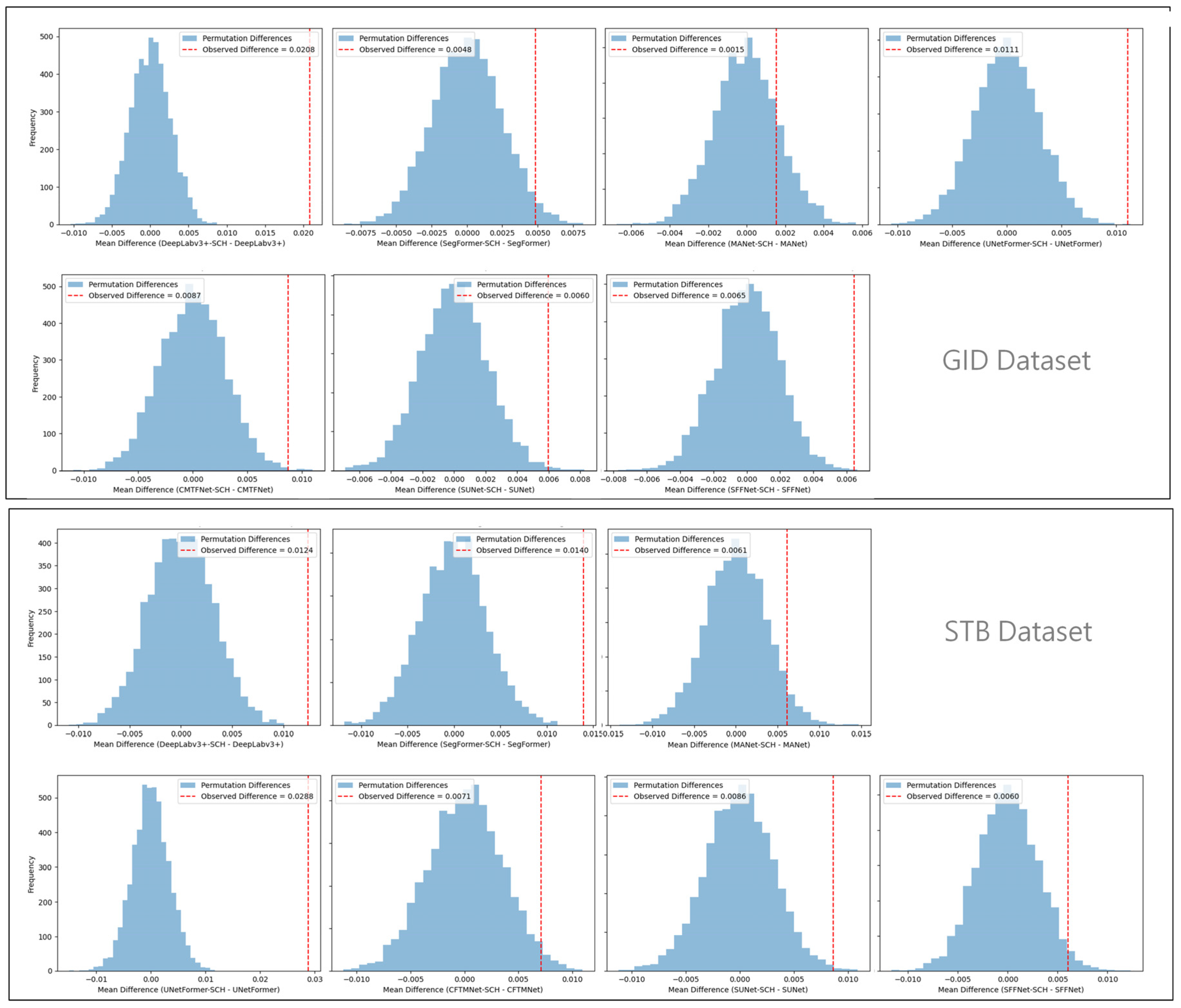
4.6. Statistical Significance Analysis
4.7. Semantic Consistency Analysis
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, F.; Wang, C.; Zhang, H.; Li, J.; Li, L.; Chen, W.; Zhang, B. Built-up area mapping in China from GF-3 SAR imagery based on the framework of deep learning. Remote Sens. Environ. 2021, 262, 112515. [Google Scholar] [CrossRef]
- Albarakati, H.M.; Khan, M.A.; Hamza, A.; Khan, F.; Kraiem, N.; Jamel, L.; Almuqren, L.; Alroobaea, R. A Novel Deep Learning Architecture for Agriculture Land Cover and Land Use Classification from Remote Sensing Images Based on Network-Level Fusion of Self-Attention Architecture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6338–6353. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, J.; Hunjra, A.I.; Zhao, S.; Bouri, E. How Does Urban Land Use Efficiency Improve Resource and Environment Carrying Capacity? Socio-Econ. Plan. Sci. 2024, 91, 101760. [Google Scholar] [CrossRef]
- Anderson, J.R. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Colorado, CO, USA, 1976.
- Bossard, M.; Feranec, J.; Otahel, J. CORINE Land Cover Technical Guide: Addendum 2000; European Environment Agency Copenhagen: Denmark, Copenhagen, 2000. [Google Scholar]
- Di Gregorio, A. Land Cover Classification System: Classification Concepts and User Manual: LCCS; Food & Agriculture Org: Rome, Italy, 2005. [Google Scholar]
- Zafari, A.; Zurita-Milla, R.; Izquierdo-Verdiguier, E. Land Cover Classification Using Extremely Randomized Trees: A Kernel Perspective. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1702–1706. [Google Scholar] [CrossRef]
- Tatsumi, K.; Yamashiki, Y.; Torres, M.A.C.; Taipe, C.L.R. Crop Classification of Upland Fields Using Random Forest of Time-Series Landsat 7 ETM+ Data. Comput. Electron. Agric. 2015, 115, 171–179. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A Hybrid MLP-CNN Classifier for Very Fine Resolution Remotely Sensed Image Classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef]
- Li, J.; Zhang, B.; Huang, X. A Hierarchical Category Structure Based Convolutional Recurrent Neural Network (HCS-ConvRNN) for Land-Cover Classification Using Dense MODIS Time-Series Data. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102744. [Google Scholar] [CrossRef]
- Gavish, Y.; O’Connell, J.; Marsh, C.J.; Tarantino, C.; Blonda, P.; Tomaselli, V.; Kunin, W.E. Comparing the Performance of Flat and Hierarchical Habitat/Land-Cover Classification Models in a NATURA 2000 Site. ISPRS J. Photogramm. Remote Sens. 2018, 136, 1–12. [Google Scholar] [CrossRef]
- Demirkan, D.Ç.; Koz, A.; Düzgün, H.Ş. Hierarchical Classification of Sentinel 2-a Images for Land Use and Land Cover Mapping and Its Use for the CORINE System. J. Appl. Remote Sens. 2020, 14, 026524. [Google Scholar] [CrossRef]
- Yang, C.; Rottensteiner, F.; Heipke, C. Exploring Semantic Relationships for Hierarchical Land Use Classification Based on Convolutional Neural Networks. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 2, 599–607. [Google Scholar] [CrossRef]
- Waśniewski, A.; Hościło, A.; Chmielewska, M. Can a Hierarchical Classification of Sentinel-2 Data Improve Land Cover Mapping? Remote Sens. 2022, 14, 989. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Friedl, M.A.; Krankina, O.N.; Baccini, A.; Woodcock, C.E.; Sibley, A.; Sun, G.; Kharuk, V.; Elsakov, V. Hierarchical Mapping of Northern Eurasian Land Cover Using MODIS Data. Remote Sens. Environ. 2011, 115, 392–403. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer Resolution Observation and Monitoring of Global Land Cover: First Mapping Results with Landsat TM and ETM+ Data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global Land-Cover Product with Fine Classification System at 30 m Using Time-Series Landsat Imagery. Earth Syst. Sci. Data Discuss. 2020, 2020, 2753–2776. [Google Scholar] [CrossRef]
- Xie, S.; Liu, L.; Zhang, X.; Yang, J.; Chen, X.; Gao, Y. Automatic Land-Cover Mapping Using Landsat Time-Series Data Based on Google Earth Engine. Remote Sens. 2019, 11, 3023. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Zhang, C.; Duan, C.; Su, J.; Wang, L.; Atkinson, P.M. Multiattention Network for Semantic Segmentation of Fine-Resolution Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5607713. [Google Scholar] [CrossRef]
- TANG, B.; PALIDAN, T.; BAI, J.; QI, R. Land Cover Classification Method for Remote Sensing Images Using CNN and Transformer. Microelectron. Comput. 2024, 41, 64–73. [Google Scholar]
- Xia, J.; Yokoya, N.; Adriano, B.; Broni-Bediako, C. Openearthmap: A Benchmark Dataset for Global High-Resolution Land Cover Mapping. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Tucson, AZ, USA, 2–7 January 2023; pp. 6254–6264. [Google Scholar] [CrossRef]
- Tong, X.-Y.; Xia, G.-S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-Cover Classification with High-Resolution Remote Sensing Images Using Transferable Deep Models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- ISPRS Potsdam 2D Semantic Labeling Dataset. Available online: https://www.isprs.org/resources/datasets/benchmarks/UrbanSemLab/2d-sem-label-potsdam.aspx (accessed on 22 December 2021).
- ISPRS Vaihingen 2D Semantic Labeling Dataset. Available online: https://www.isprs.org/resources/datasets/benchmarks/UrbanSemLab/2d-sem-label-vaihingen.aspx (accessed on 22 December 2021).
- Fu, Y.; Zhang, X.; Wang, M. DSHNet: A Semantic Segmentation Model of Remote Sensing Images Based on Dual Stream Hybrid Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4164–4175. [Google Scholar] [CrossRef]
- Cao, Y.; Huo, C.; Xiang, S.; Pan, C. GFFNet: Global Feature Fusion Network for Semantic Segmentation of Large-Scale Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 4222–4234. [Google Scholar] [CrossRef]
- Yang, K.; Tong, X.-Y.; Xia, G.-S.; Shen, W.; Zhang, L. Hidden Path Selection Network for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5628115. [Google Scholar] [CrossRef]
- Li, Z.; Bao, W.; Zheng, J.; Xu, C. Deep Grouping Model for Unified Perceptual Parsing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Los Alamitos, CA, USA, 14–19 June 2020; pp. 4053–4063. [Google Scholar] [CrossRef]
- Liang, X.; Xing, E.; Zhou, H. Dynamic-Structured Semantic Propagation Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 752–761. [Google Scholar]
- Deng, J.; Ding, N.; Jia, Y.; Frome, A.; Murphy, K.; Bengio, S.; Li, Y.; Neven, H.; Adam, H. Large-Scale Object Classification Using Label Relation Graphs. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 48–64. [Google Scholar] [CrossRef]
- Chen, J.; Qian, Y. Hierarchical Multi-Label Ship Recognition in Remote Sensing Images Using Label Relation Graphs. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4968–4971. [Google Scholar] [CrossRef]
- Zhang, X.; Hong, W.; Li, Z.; Cheng, X.; Tang, X.; Zhou, H.; Jiao, L. Hierarchical Knowledge Graph for Multilabel Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5645714. [Google Scholar] [CrossRef]
- Jo, S.; Shin, D.; Na, B.; Jang, J.; Moon, I.-C. Hierarchical Multi-Label Classification with Partial Labels and Unknown Hierarchy. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham UK, 21–25 October 2023; pp. 1025–1034. [Google Scholar] [CrossRef]
- Patel, D.; Dangati, P.; Lee, J.-Y.; Boratko, M.; McCallum, A. Modeling Label Space Interactions in Multi-Label Classification Using Box Embeddings. ICLR 2022 Poster 2022. [Google Scholar]
- Giunchiglia, E.; Lukasiewicz, T. Coherent Hierarchical Multi-Label Classification Networks. Adv. Neural Inf. Process. Syst. 2020, 33, 9662–9673. [Google Scholar]
- Li, L.; Zhou, T.; Wang, W.; Li, J.; Yang, Y. Deep Hierarchical Semantic Segmentation. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 1236–1247. [Google Scholar] [CrossRef]
- Sulla-Menashe, D.; Gray, J.M.; Abercrombie, S.P.; Friedl, M.A. Hierarchical Mapping of Annual Global Land Cover 2001 to Present: The MODIS Collection 6 Land Cover Product. Remote Sens. Environ. 2019, 222, 183–194. [Google Scholar] [CrossRef]
- Liu, L.; Tong, Z.; Cai, Z.; Wu, H.; Zhang, R.; Le Bris, A.; Olteanu-Raimond, A.-M. HierU-Net: A Hierarchical Semantic Segmentation Method for Land Cover Mapping. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4404614. [Google Scholar] [CrossRef]
- Yang, C.; Rottensteiner, F.; Heipke, C. A Hierarchical Deep Learning Framework for the Consistent Classification of Land Use Objects in Geospatial Databases. ISPRS J. Photogramm. Remote Sens. 2021, 177, 38–56. [Google Scholar] [CrossRef]
- Gbodjo, Y.J.E.; Ienco, D.; Leroux, L.; Interdonato, R.; Gaetano, R.; Ndao, B. Object-Based Multi-Temporal and Multi-Source Land Cover Mapping Leveraging Hierarchical Class Relationships. Remote Sens. 2020, 12, 2814. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A Survey on Multi-Task Learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Kokkinos, I. Ubernet: Training a Universal Convolutional Neural Network for Low-, Mid-, and High-Level Vision Using Diverse Datasets and Limited Memory. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6129–6138. [Google Scholar]
- Xu, D.; Ouyang, W.; Wang, X.; Sebe, N. Pad-Net: Multi-Tasks Guided Prediction-and-Distillation Network for Simultaneous Depth Estimation and Scene Parsing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 675–684. [Google Scholar]
- Vandenhende, S.; Georgoulis, S.; Van Gool, L. MTI-Net: Multi-Scale Task Interaction Networks for Multi-Task Learning. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2020; Volume 12349, pp. 527–543. [Google Scholar] [CrossRef]
- Misra, I.; Shrivastava, A.; Gupta, A.; Hebert, M. Cross-Stitch Networks for Multi-Task Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3994–4003. [Google Scholar] [CrossRef]
- Ruder, S.; Bingel, J.; Augenstein, I.; Søgaard, A. Latent Multi-Task Architecture Learning. Proc. AAAI Conf. Artif. Intell. 2019, 33, 4822–4829. [Google Scholar] [CrossRef]
- Liu, S.; Johns, E.; Davison, A.J. End-to-End Multi-Task Learning with Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1871–1880. [Google Scholar] [CrossRef]
- Lopes, I.; Vu, T.-H.; de Charette, R. Cross-Task Attention Mechanism for Dense Multi-Task Learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 2329–2338. [Google Scholar] [CrossRef]
- Goncalves, D.N.; Marcato, J.; Zamboni, P.; Pistori, H.; Li, J.; Nogueira, K.; Goncalves, W.N. MTLSegFormer: Multi-Task Learning with Transformers for Semantic Segmentation in Precision Agriculture. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 6290–6298. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like Transformer for Efficient Semantic Segmentation of Remote Sensing Urban Scene Imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Wu, H.; Huang, P.; Zhang, M.; Tang, W.; Yu, X. CMTFNet: CNN and Multiscale Transformer Fusion Network for Remote-Sensing Image Semantic Segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 2004612. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-Like Pure Transformer for Medical Image Segmentation. In Computer Vision—ECCV 2022 Workshops; Karlinsky, L., Michaeli, T., Nishino, K., Eds.; Lecture Notes in Computer Science; Springer Nature: Cham, Switzerland, 2023; Volume 13803, pp. 205–218. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, G.; Li, J. Sffnet: A Wavelet-Based Spatial and Frequency Domain Fusion Network for Remote Sensing Segmentation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3000617. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Garcia-Rodriguez, J.A. Review on Deep Learning Techniques Applied to Semantic Segmentation. arXiv 2017, arXiv:1704.06857. [Google Scholar] [CrossRef]
- Ernst, M.D. Permutation Methods: A Basis for Exact Inference. Stat. Sci. 2004, 19, 676–685. [Google Scholar] [CrossRef]

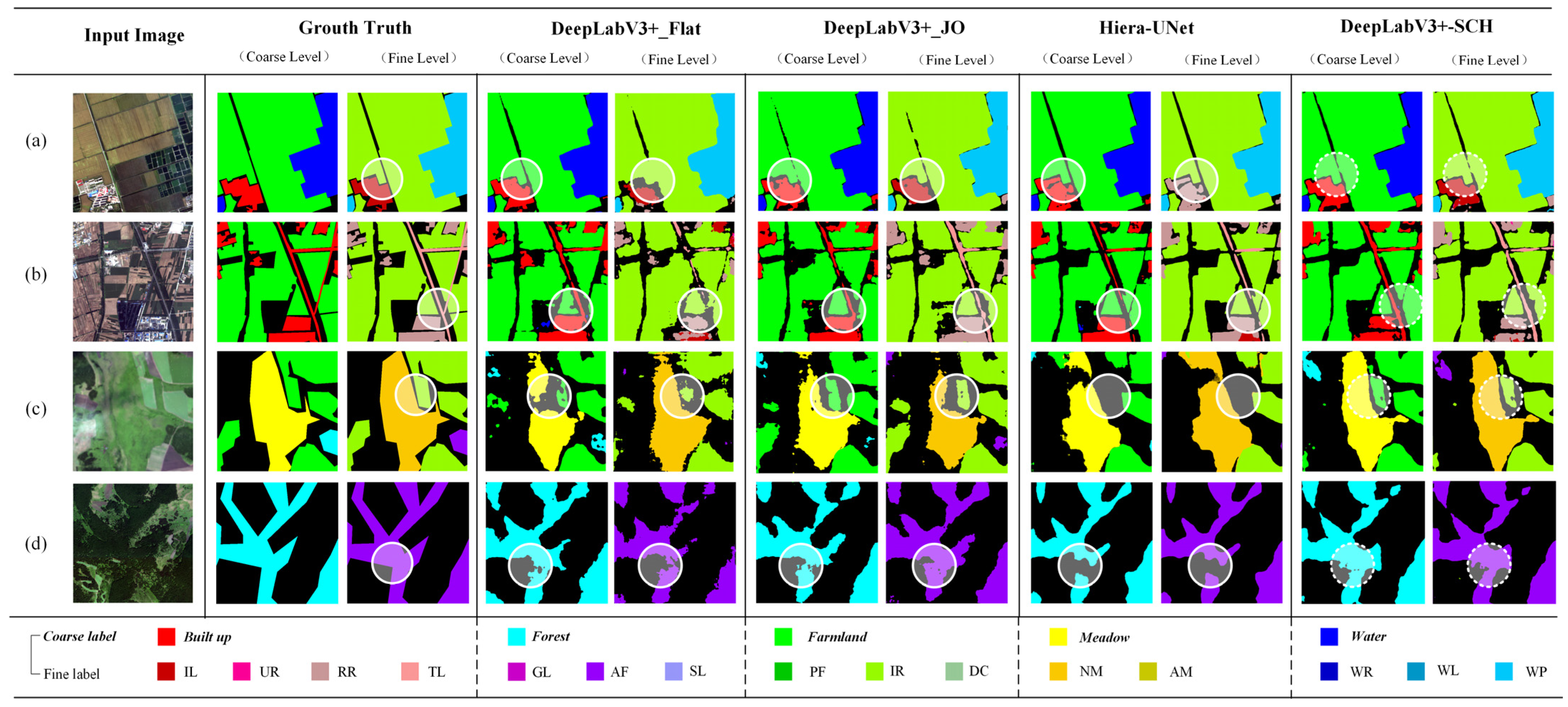
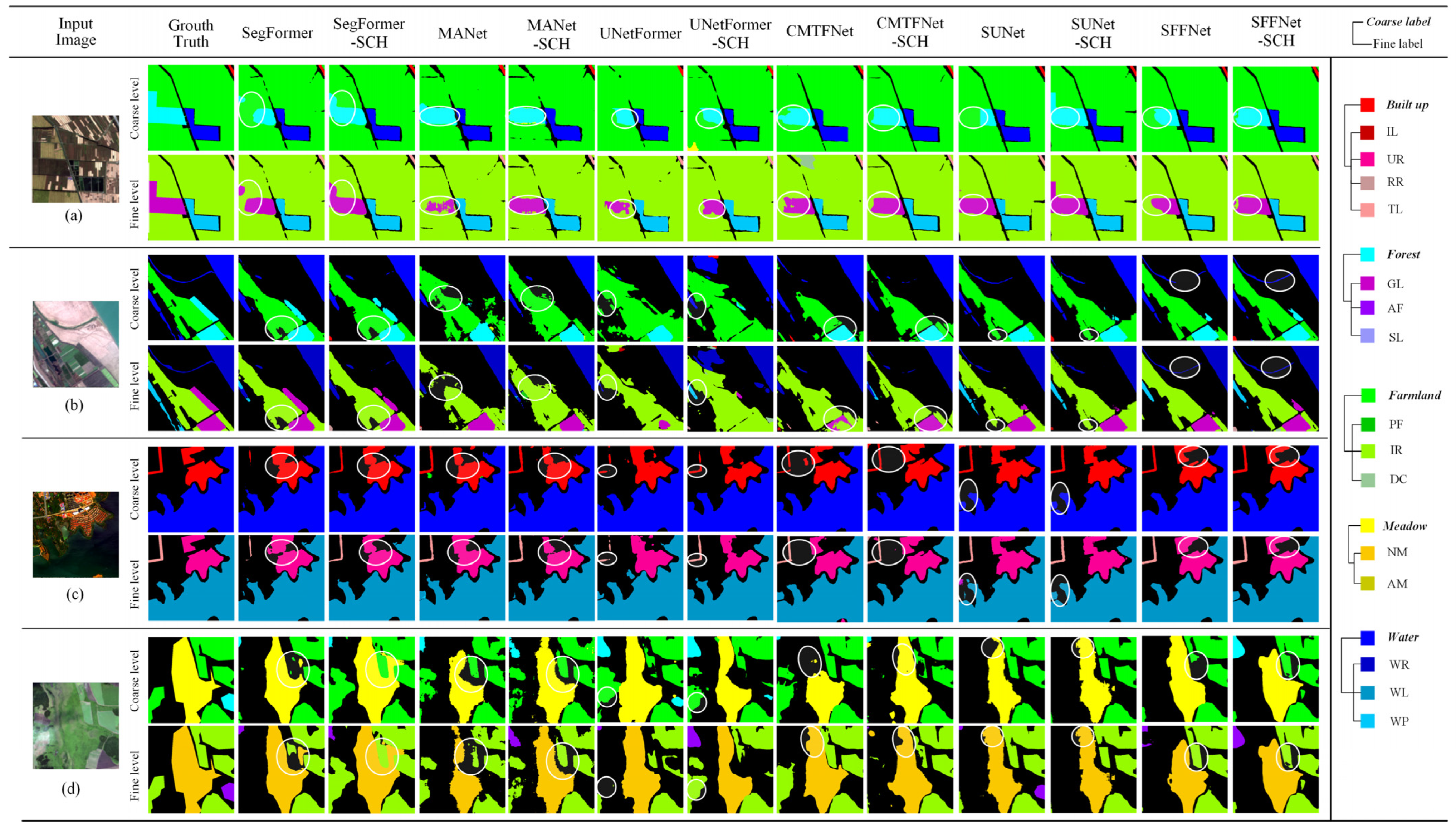
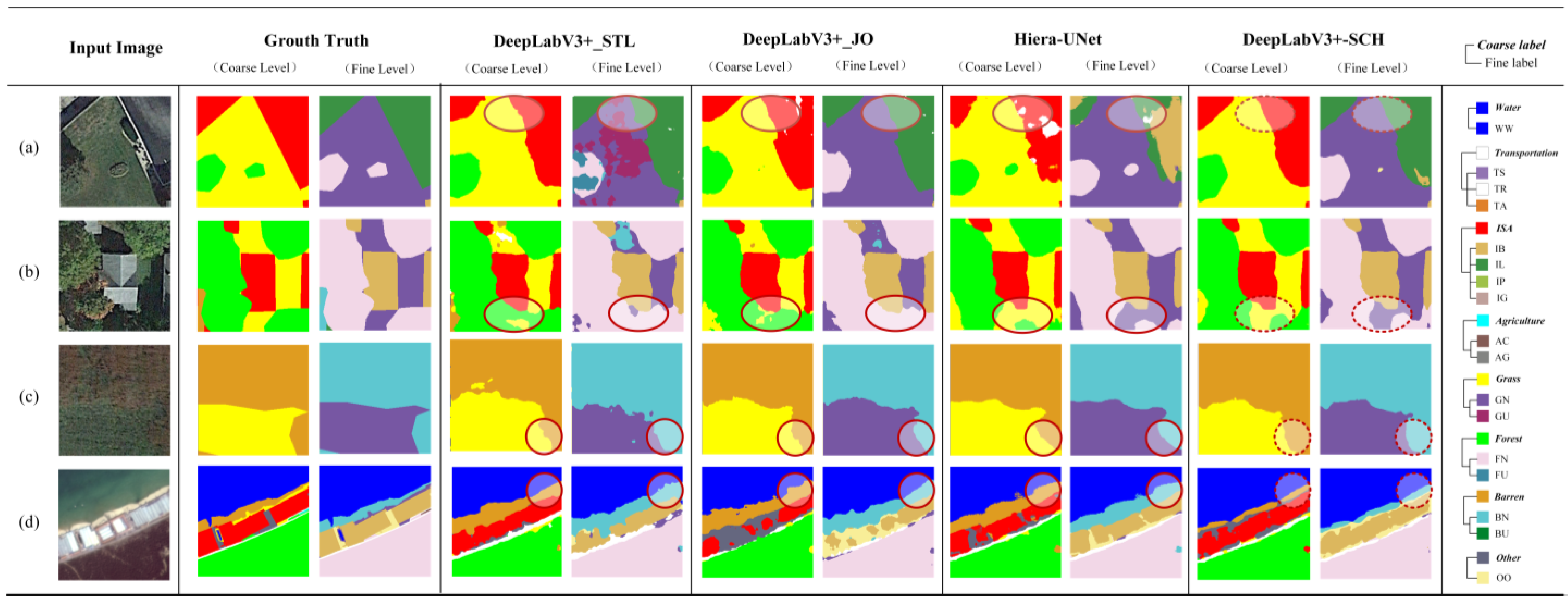
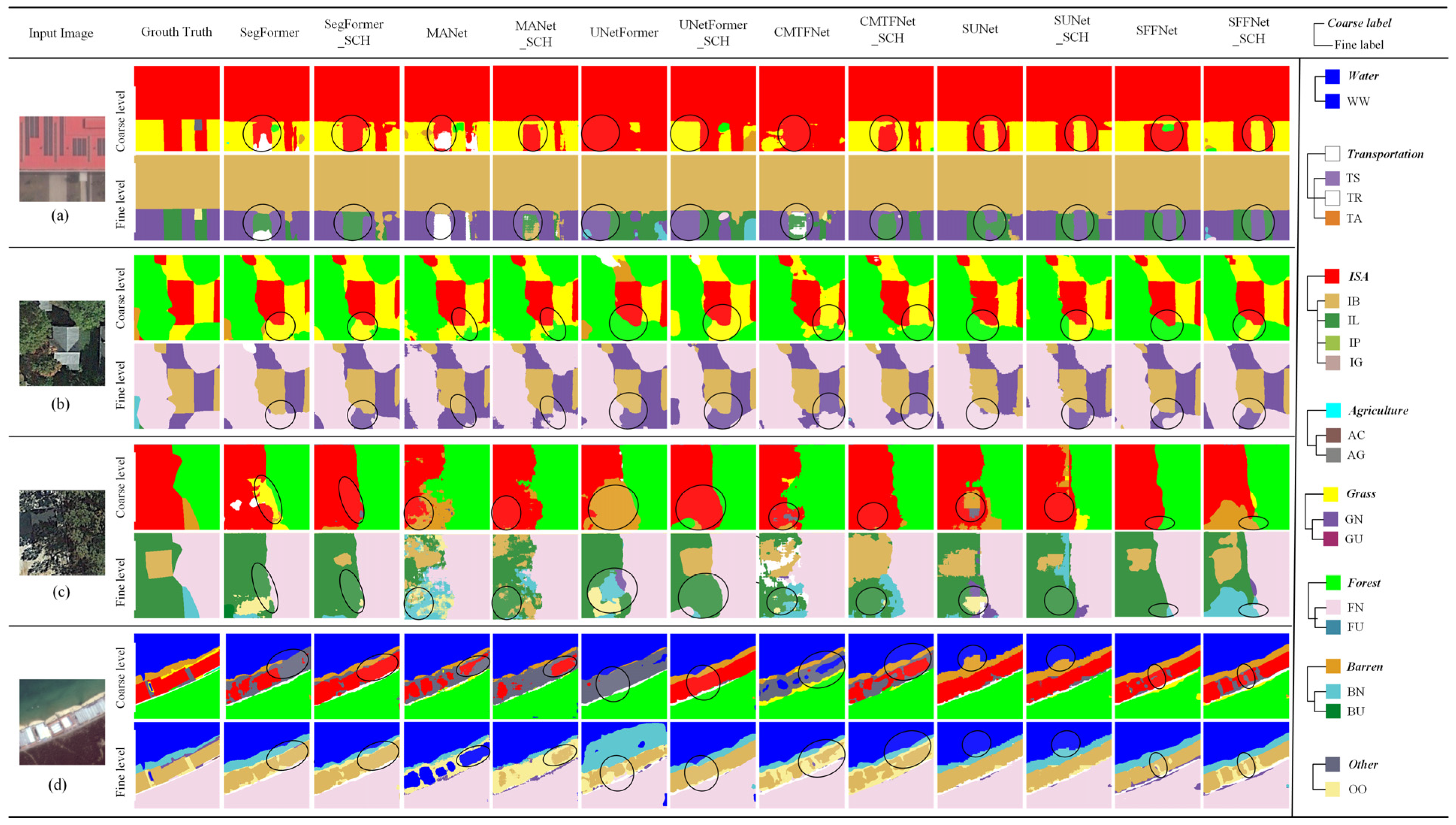

| 6-Class | 16-Class |
|---|---|
| Background | Background (BB) |
| Built-Up | Industrial Land (IL), Urban Residential (UR), Rural Residential (RR), Traffic Land (TL) |
| Forest | Garden Land (GL), Arbor Forest (AF), Shrub Land (SL) |
| Farmland | Paddy Field (PF), Irrigated Land (IR), Dry Cropland (DC) |
| Meadow | Natural Meadow (NM), Artificial Meadow (AM) |
| Water | River (WR), Lake (WL), Pond (WP) |
| 8-Class | 17-Class |
|---|---|
| Water | Water (WW) |
| Transportation | Road (TR), Airport (TA), Railway Station (TS) |
| Impervious Surface (ISA) | Building (IB), Parking Lot (IL), Photovoltaic (IP), Playground (IG) |
| Agriculture | Cultivated Land (AC), Agriculture Greenhouse (AG) |
| Grass | Natural Grass (GN), Unnatural Grass (GU) |
| Forest | Natural Forest (FN), Unnatural Forest (FU) |
| Barren | Natural Bare Soil (BN), Unnatural Bare Soil (BU) |
| Other | Other (OO) |
| Coarse Level | Fine Level | |||||
|---|---|---|---|---|---|---|
| OA | MIoU | FWIoU | OA | MIoU | FWIoU | |
| γ = 0 | 90.24 | 82.37 | 82.35 | 88.46 | 75.80 | 79.49 |
| γ = 1 | 90.12 | 82.33 | 82.21 | 88.44 | 76.52 | 79.52 |
| γ = 2 | 90.09 | 82.27 | 82.12 | 88.34 | 75.92 | 79.37 |
| γ = 3 | 89.88 | 82.00 | 81.75 | 88.17 | 75.93 | 79.02 |
| Baseline | Share Feature | Cascade | Hierarchical Loss | Coarse Level | Fine Level | ||||
|---|---|---|---|---|---|---|---|---|---|
| OA | MIoU | FWIoU | OA | MIoU | FWIoU | ||||
| √ | 88.66 | 80.14 | 79.83 | 86.25 | 72.8 | 76.13 | |||
| √ | √ | 89.46 | 81.26 | 81.11 | 87.6 | 74.5 | 78.17 | ||
| √ | √ | √ | 89.59 | 81.66 | 81.26 | 87.84 | 75.22 | 78.48 | |
| √ | √ | √ | √ | 90.12 | 82.33 | 82.21 | 88.44 | 76.52 | 79.52 |
| FPS | Params (M) | Method | Backbone | Coarse Level | Fine Level | SAD | ESAD | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | MIoU | FWIoU | OA | MIoU | FWIoU | ||||||
| 13.60 | 39.64 | Deeplabv3+_STL | ResNet50 | 88.66 | 80.14 | 79.83 | 86.25 | 72.80 | 76.13 | 12.06 | 21.07 |
| 6.40 | 56.01 | Deeplabv3+_JO | ResNet50 | 88.69 | 80.36 | 79.83 | 86.91 | 74.16 | 77.09 | 6.65 | 16.26 |
| 4.00 | 287.23 | HierU-Net | ResNet50 | 88.37 | 79.27 | 79.34 | 86.45 | 71.51 | 76.45 | 1.96 | 14.55 |
| 7.38 | 56.06 | Deeplabv3+-SCH | ResNet50 | 90.12 | 82.33 | 82.21 | 88.44 | 76.52 | 79.52 | 2.21 | 12.52 |
| Encode | Decode | Params (M) | Method | Coarse Level | Fine Level | ||||
|---|---|---|---|---|---|---|---|---|---|
| OA | MIoU | FWIoU | OA | MIoU | FWIoU | ||||
| MiT-B5 | MLP | 84.60 | SegFormer | 89.63 | 81.53 | 81.42 | 88.09 | 76.2 | 78.97 |
| 87.76 | SegFormer-SCH | 90.37 | 82.67 | 82.63 | 88.57 | 77.06 | 79.74 | ||
| ResNet50 | Attention | 35.86 | MANet | 87.82 | 78.8 | 78.52 | 85.92 | 71.51 | 75.64 |
| 42.97 | MANet-SCH | 88.71 | 80.38 | 79.93 | 86.49 | 72.79 | 76.53 | ||
| ResNet50 | Transformer | 24.24 | UNetFormer | 87.26 | 77.96 | 77.54 | 84.93 | 70.31 | 74.24 |
| 4.98 | UNetFormer-SCH | 87.61 | 78.5 | 78.17 | 86.03 | 72.31 | 75.84 | ||
| ResNet50 | Attention | 30.75 | CMTFNet | 87.37 | 76.66 | 77.78 | 86.20 | 71.90 | 76.03 |
| 36.64 | CMTFNet -SCH | 89.00 | 80.77 | 80.36 | 87.07 | 74.45 | 77.43 | ||
| Swin Transformer | Swin Transformer | 31.82 | SUNet | 90.94 | 83.29 | 83.55 | 89.95 | 79.55 | 81.94 |
| 36.12 | SUNet-SCH | 91.91 | 85.25 | 85.17 | 90.54 | 81.41 | 82.92 | ||
| ConvNext | Spatial and Frequency Domain Fusion | 34.18 | SFFNet | 92.49 | 86.26 | 86.16 | 91.79 | 82.57 | 84.95 |
| 34.35 | SFFNet-SCH | 93.45 | 87.81 | 87.79 | 92.44 | 84.48 | 86.06 | ||
| Method | Coarse Level | Fine Level | ||||
|---|---|---|---|---|---|---|
| OA | MIoU | FWIoU | OA | MIoU | FWIoU | |
| DeepLabv3+_STL | 79.27 | 60.71 | 66.26 | 75.79 | 46.23 | 61.84 |
| DeepLabv3+_JO | 77.98 | 58.67 | 64.36 | 73.78 | 43.99 | 59.16 |
| HierU-Net | 77.85 | 59.07 | 64.60 | 74.15 | 43.57 | 60.01 |
| DeepLabv3+-SCH | 80.38 | 62.90 | 67.83 | 77.03 | 48.22 | 63.48 |
| SegFormer | 77.39 | 57.56 | 63.68 | 72.35 | 41.86 | 57.51 |
| SegFormer-SCH | 78.40 | 59.40 | 64.99 | 74.13 | 43.73 | 59.40 |
| MANet | 75.77 | 55.86 | 61.50 | 71.15 | 39.64 | 56.05 |
| MANet-SCH | 76.61 | 56.95 | 62.70 | 71.76 | 41.24 | 57.07 |
| UNetFormer | 76.11 | 55.70 | 62.29 | 71.81 | 41.72 | 57.42 |
| UNetFormer-SCH | 78.81 | 60.08 | 65.77 | 74.69 | 44.39 | 60.63 |
| CMTFNet | 76.93 | 57.45 | 63.28 | 73.21 | 43.19 | 58.73 |
| CMTFNet -SCH | 78.56 | 59.66 | 65.43 | 73.92 | 43.58 | 59.45 |
| SUNet | 79.93 | 61.55 | 67.23 | 77.54 | 48.72 | 64.17 |
| SUNet-SCH | 81.71 | 65.15 | 69.75 | 78.41 | 50.02 | 65.37 |
| SFFNet | 80.72 | 62.73 | 68.27 | 77.85 | 48.75 | 64.45 |
| SFFNet-SCH | 81.46 | 64.24 | 69.37 | 78.36 | 49.88 | 65.27 |
| Backbone Model | GID Dataset | STB Dataset | ||||
|---|---|---|---|---|---|---|
| mIoU Difference | p-Value | Significant (p < 0.05) | mIoU Difference | p-Value | Significant (p < 0.05) | |
| DeepLabv3+ | 3.72 | <0.0001 | ✓ | 1.99 | <0.0001 | ✓ |
| SegFormer | 0.86 | 0.0244 | ✓ | 1.87 | <0.0001 | ✓ |
| MANet | 1.28 | 0.1712 | ✗ | 0.9 | 0.0438 | ✓ |
| UNetFormer | 2.00 | 0.0002 | ✓ | 2.67 | <0.0001 | ✓ |
| CMTFNet | 2.55 | 0.0018 | ✓ | 0.39 | 0.0214 | ✓ |
| SUNet | 1.86 | 0.0040 | ✓ | 1.82 | 0.0030 | ✓ |
| SFFNet | 1.91 | 0.0002 | ✓ | 1.13 | 0.0222 | ✓ |
| Method | STB Dataset | GID Dataset | ||
|---|---|---|---|---|
| SAD (%) | ESAD (%) | SAD (%) | ESAD (%) | |
| DeepLabv3+ | 14.22 | 29.71 | 12.06 | 21.07 |
| DeepLabv3+-SCH | 4.45 | 24.62 | 2.21 | 12.52 |
| Difference | 9.77 | 5.09 | 9.85 | 8.55 |
| SegFormer | 17.56 | 33.59 | 5.90 | 14.12 |
| SegFormer-SCH | 1.92 | 26.55 | 1.37 | 11.71 |
| Difference | 15.64 | 7.04 | 4.53 | 2.41 |
| MANet | 18.09 | 35.38 | 9.37 | 18.57 |
| MANet-SCH | 7.40 | 30.96 | 3.63 | 15.98 |
| Difference | 10.69 | 4.42 | 5.74 | 2.59 |
| UNetFormer | 18.45 | 35.24 | 11.6 | 20.47 |
| UNetFormer-SCH | 4.87 | 27.09 | 4.59 | 16.42 |
| Difference | 13.58 | 8.15 | 7.01 | 4.05 |
| CMTFNet | 20.23 | 37.2 | 9.99 | 18.99 |
| CMTFNet-SCH | 11.28 | 30.93 | 3.79 | 14.74 |
| Difference | 8.95 | 6.27 | 6.2 | 4.25 |
| SUNet | 14.52 | 28.8 | 6.92 | 13.56 |
| SUNet-MTL | 2.83 | 22.62 | 1.61 | 10.18 |
| Difference | 11.69 | 6.18 | 5.31 | 3.38 |
| SFFNet | 14.46 | 27.91 | 6.00 | 10.88 |
| SFFNet-SCH | 1.61 | 22.26 | 0.45 | 7.78 |
| Difference | 12.85 | 5.65 | 5.55 | 3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, S.; Fu, H.; Yang, R.; Wang, L. A Multi-Task Learning Framework with Enhanced Cross-Level Semantic Consistency for Multi-Level Land Cover Classification. Remote Sens. 2025, 17, 2442. https://doi.org/10.3390/rs17142442
Tao S, Fu H, Yang R, Wang L. A Multi-Task Learning Framework with Enhanced Cross-Level Semantic Consistency for Multi-Level Land Cover Classification. Remote Sensing. 2025; 17(14):2442. https://doi.org/10.3390/rs17142442
Chicago/Turabian StyleTao, Shilin, Haoyu Fu, Ruiqi Yang, and Leiguang Wang. 2025. "A Multi-Task Learning Framework with Enhanced Cross-Level Semantic Consistency for Multi-Level Land Cover Classification" Remote Sensing 17, no. 14: 2442. https://doi.org/10.3390/rs17142442
APA StyleTao, S., Fu, H., Yang, R., & Wang, L. (2025). A Multi-Task Learning Framework with Enhanced Cross-Level Semantic Consistency for Multi-Level Land Cover Classification. Remote Sensing, 17(14), 2442. https://doi.org/10.3390/rs17142442





