Debris-Flow Erosion Volume Estimation Using a Single High-Resolution Optical Satellite Image
Abstract
1. Introduction
- An NPC constraint is introduced using a random permutation operator to handle heterogeneous albedo distributions.
- The adaptability of the SFS-based depth super-resolution is extended, using publicly available global DEM as the initial reference, enabling terrain estimation under more complex surface conditions.
- High-resolution GF-6 optical satellite data are used for debris-flow erosion volume estimation, and results are quantitatively compared with airborne LiDAR-derived erosion volumes.
2. Methodology
2.1. Background of SRSFS
2.1.1. Imaging Model
2.1.2. Piecewise Constant Albedo
2.2. NPC SRSFS
| Algorithm 1 Update of the non-local piecewise smooth constrained albedo. |
| Input: Image , parameters , where is the iteration tolerance, is the dimensionality of the image, step factors |
| 1. Initialize: |
| %%main loops |
| 2. while do |
| %Dual ascent in |
| 3. |
| 4. |
| 5. |
| 6. |
| %Primal descent in |
| 7. |
| 8. |
| %Auxiliary variables update step |
| 9. |
| 10. |
| end while |
| Output: albedo |
| Algorithm 2 NPC SRSFS. |
| Input: Image , low-resolution , parameters weight of the augmented Lagrangian |
| 1. Initialize: |
| %%main steps of ADMM |
| 2. while do |
| %Albedo update |
| 3. Update using the primal-dual method as |
| %Lighting update |
| 4. Estimate using pseudo-inverse as |
| %Auxiliary variable update |
| 5. Update using L-BFGS as |
| %Depth update |
| 6. Refine by the conjugate gradient method as |
| %Extrapolation step |
| 7. Perform extrapolation as |
| end while |
| Output: estimated |
2.3. Debris-Flow Erosion Volume Estimation
| Algorithm 3 Debris-flow erosion volume estimation. |
| Input: Post-disaster image, Pre-disaster image (optional), GDEM |
| Main steps: |
| %Post-disaster image processing |
| 1. Generate the debris-flow area mask |
| 2. Estimate the post-disaster DSM using NPC SRSFS |
| %Pre-disaster image processing (optional) |
| 3. Estimate the pre-disaster DSM using NPC SRSFS (or simply interpolate from GDEM) |
| %DSM differencing |
| 4. Compute the difference between post-disaster and pre-disaster DSMs |
| %Volume calculation |
| 5. Calculate debris-flow erosion volume within the left area |
| Output: estimated debris-flow erosion volume |
3. Experiments and Discussion
3.1. Research Area and Datasets
3.2. Experimental Results
3.3. Parameter Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Orthographic Camera Model

Appendix A.2. Update of Albedo with NPC
References
- Metternicht, G.; Hurni, L.; Gogu, R. Remote sensing of landslides: An analysis of the potential contribution to geo-spatial systems for hazard assessment in mountainous environments. Remote Sens. Environ. 2005, 98, 284–303. [Google Scholar] [CrossRef]
- Jakob, M.; Hungr, O. Debris-Flow Hazards and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2005; Volume 739. [Google Scholar]
- Arattano, M.; Bertoldi, G.; Cavalli, M.; Comiti, F.; D’Agostino, V.; Theule, J. Comparison of Methods and Procedures for Debris-Flow Volume Estimation. In Engineering Geology for Society and Territory, Vol 3: River Basins, Reservoir Sedimentation and Water Resources; Springer International Publishing: Geneva, Switzerland, 2015; pp. 115–119. [Google Scholar] [CrossRef]
- Schimmel, A.; Coviello, V.; Comiti, F. Debris flow velocity and volume estimations based on seismic data. Nat. Hazards Earth Syst. Sci. 2022, 22, 1955–1968. [Google Scholar] [CrossRef]
- Zhu, L.; Jia, Y.; Huang, S.; Meyer, N.; Wieser, A.; Schindler, K.; Aaron, J. DeFlow: Self-supervised 3D Motion Estimation of Debris Flow. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 6508–6517. [Google Scholar]
- Orland, E.; Kirschbaum, D.; Stanley, T. A Scalable Framework for Post Fire Debris Flow Hazard Assessment Using Satellite Precipitation Data. Geophys. Res. Lett. 2022, 49, 1–9. [Google Scholar] [CrossRef]
- He, C.; Ye, B. Automatic Extraction of Potential Debris Flow Based on Gf-2 Satellite Data. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (Igarss 2019), Yokohama, Japan, 28 July–10 August 2019; pp. 9705–9708. [Google Scholar] [CrossRef]
- Miura, H. Fusion Analysis of Optical Satellite Images and Digital Elevation Model for Quantifying Volume in Debris Flow Disaster. Remote Sens. 2019, 11, 1096. [Google Scholar] [CrossRef]
- Li, Y.; Ma, C.; Wang, Y. Landslides and debris flows caused by an extreme rainstorm on 21 July 2012 in mountains near Beijing, China. Bull. Eng. Geol. Environ. 2017, 78, 1265–1280. [Google Scholar] [CrossRef]
- Huang, J.; Hales, T.C.; Huang, R.; Ju, N.; Li, Q.; Huang, Y. A hybrid machine-learning model to estimate potential debris-flow volumes. Geomorphology 2020, 367, 107333. [Google Scholar] [CrossRef]
- Hu, X.; Yang, F.; Hu, K.; Ding, M.; Liu, S.; Wei, L. Estimating the debris-flow magnitude using landslide sediment connectivity, Qipan catchment, Wenchuan County, China. Catena 2023, 220, 106689. [Google Scholar] [CrossRef]
- Ding, C.; Feng, G.; Liao, M.; Tao, P.; Zhang, L.; Xu, Q. Displacement history and potential triggering factors of Baige landslides, China revealed by optical imagery time series. Remote Sens. Environ. 2021, 254, 112253. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Wu, T.; Hao, J.; Wu, X.; Ma, X.; Zhu, X.; Lou, P.; Zhang, L. Activity and Kinematics of Two Adjacent Freeze–Thaw-Related Landslides Revealed by Multisource Remote Sensing of Qilian Mountain. Remote Sens. 2022, 14, 5059. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Ge, D.; Deng, Y.; Wang, R. Improved offset tracking for predisaster deformation monitoring of the 2018 Jinsha River landslide (Tibet, China). Remote Sens. Environ. 2020, 247, 111899. [Google Scholar] [CrossRef]
- Cucchiaro, S.; Maset, E.; Fusiello, A.; Cazorzi, F. 4d-Sfm Photogrammetry for Monitoring Sediment Dynamics in a Debris-Flow Catchment: Software Testing and Results Comparison. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 281–288. [Google Scholar] [CrossRef]
- Miura, H.; Tanizaki, T. UAV Observations for Soil Volume Estimation of Debris Flows. In Proceedings of the IGARSS 2022––2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7771–7774. [Google Scholar]
- Liang, R.; Dai, K.; Xu, Q.; Pirasteh, S.; Li, Z.; Li, T.; Wen, N.; Deng, J.; Fan, X. Utilizing a single-temporal full polarimetric Gaofen-3 SAR image to map coseismic landslide inventory following the 2017 Mw 7.0 Jiuzhaigou earthquake (China). Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103657. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Zhou, Y.; Wang, F.; Zhang, R.; Zhao, Q. Three-dimensional information extraction from GaoFen-1 satellite images for landslide monitoring. Geomorphology 2018, 309, 77–85. [Google Scholar] [CrossRef]
- Chen, L.; Letu, H.; Fan, M.; Shang, H.; Tao, J.; Wu, L.; Zhang, Y.; Yu, C.; Gu, J.; Zhang, N.; et al. An Introduction to the Chinese High-Resolution Earth Observation System: Gaofen-1~7 Civilian Satellites. J. Remote Sens. 2022, 2022, 9769536. [Google Scholar] [CrossRef]
- Wang, P.; Shi, L.; Chen, B.; Hu, Z.; Qiao, J.; Dong, Q. Pursuing 3-D scene structures with optical satellite images from affine reconstruction to Euclidean reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Hu, Z.; Tao, P.; Long, X.; Wang, H. Shading aware DSM generation from high resolution multi-view satellite images. Geo-spatial Inf. Sci. 2022, 27, 398–407. [Google Scholar] [CrossRef]
- Mertan, A.; Duff, D.J.; Unal, G. Single image depth estimation: An overview. Digit. Signal Process. 2022, 123, 103441. [Google Scholar] [CrossRef]
- Shao, J.; Yang, Y.; Zhou, H.; Zhang, Y.; Shen, Y.; Guizilini, V.; Wang, Y.; Poggi, M.; Liao, Y. Learning temporally consistent video depth from video diffusion priors. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 22841–22852. [Google Scholar]
- Xu, H.; Peng, S.; Wang, F.; Blum, H.; Barath, D.; Geiger, A.; Pollefeys, M. Depthsplat: Connecting gaussian splatting and depth. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 16453–16463. [Google Scholar]
- Ke, B.; Obukhov, A.; Huang, S.; Metzger, N.; Daudt, R.C.; Schindler, K. Repurposing diffusion-based image generators for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 9492–9502. [Google Scholar]
- Piccinelli, L.; Yang, Y.-H.; Sakaridis, C.; Segu, M.; Li, S.; Van Gool, L.; Yu, F. UniDepth: Universal monocular metric depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 10106–10116. [Google Scholar]
- Tian, P.; Yao, M.; Xiao, X.; Zheng, B.; Cao, T.; Xi, Y.; Liu, H.; Cui, H. 3D semantic terrain reconstruction of monocular close-up images of Martian terrains. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar]
- Panagiotou, E.; Chochlakis, G.; Grammatikopoulos, L.; Charou, E. Generating Elevation Surface from a Single RGB Remotely Sensed Image Using Deep Learning. Remote Sens. 2020, 12, 2002. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Yan, B.; Yue, L.; Wang, L. Global DEMs vary from one to another: An evaluation of newly released Copernicus, NASA and AW3D30 DEM on selected terrains of China using ICESat-2 altimetry data. Int. J. Digit. Earth 2022, 15, 1149–1168. [Google Scholar] [CrossRef]
- Guan, L.; Hu, J.; Pan, H.; Wu, W.; Sun, Q.; Chen, S.; Fan, H. Fusion of public DEMs based on sparse representation and adaptive regularization variation model. ISPRS J. Photogramm. Remote Sens. 2020, 169, 125–134. [Google Scholar] [CrossRef]
- Okolie, C.J.; Smit, J.L. A systematic review and meta-analysis of Digital elevation model (DEM) fusion: Pre-processing, methods and applications. ISPRS J. Photogramm. Remote Sens. 2022, 188, 1–29. [Google Scholar] [CrossRef]
- Basri, R.; Jacobs, D.W. Lambertian reflectance and linear subspaces. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 218–233. [Google Scholar] [CrossRef]
- Haefner, B.; Queau, Y.; Mollenhoff, T.; Cremers, D. Fight Ill-Posedness with Ill-Posedness: Single-shot Variational Depth Super-Resolution from Shading. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 164–174. [Google Scholar]
- Bonneel, N.; Kovacs, B.; Paris, S.; Bala, K. Intrinsic Decompositions for Image Editing. Comput Graph. Forum 2017, 36, 593–609. [Google Scholar] [CrossRef]
- Jin, X.; Gu, Y.; Liu, T. Intrinsic Image Recovery From Remote Sensing Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 224–238. [Google Scholar] [CrossRef]
- Haefner, B.; Peng, S.; Verma, A.; Queau, Y.; Cremers, D. Photometric Depth Super-Resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2453–2464. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, Q.; Lin, L.; Liu, Q.; Zhan, W. DEM densification using perspective shape from shading through multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2012, 10, 145–149. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, Y.; Shan, J. Shading-based DEM refinement under a comprehensive imaging model. ISPRS J. Photogramm. Remote Sens. 2015, 110, 24–33. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.C.; Grumpe, A.; Wöhler, C. Construction of pixel-level resolution DEMs from monocular images by shape and albedo from shading constrained with low-resolution DEM. ISPRS J. Photogramm. Remote Sens. 2018, 140, 3–19. [Google Scholar] [CrossRef]
- Douté, S.; Jiang, C. Small-scale topographical characterization of the Martian surface with in-orbit imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 447–460. [Google Scholar] [CrossRef]
- Tao, Y.; Douté, S.; Muller, J.-P.; Conway, S.J.; Thomas, N.; Cremonese, G. Ultra-high-resolution 1 m/pixel CaSSIS DTM using super-resolution restoration and shape-from-shading: Demonstration over oxia planum on Mars. Remote Sens. 2021, 13, 2185. [Google Scholar] [CrossRef]
- Strekalovskiy, E.; Cremers, D. Real-time minimization of the piecewise smooth Mumford-Shah functional. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part II 13. pp. 127–141. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the 2005 Ieee Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Meka, A.; Zollhöfer, M.; Richardt, C.; Theobalt, C. Live intrinsic video. ACM Trans. Graph. 2016, 35, 1–14. [Google Scholar] [CrossRef]
- Graber, G.; Balzer, J.; Soatto, S.; Pock, T. Efficient minimal-surface regularization of perspective depth maps in variational stereo. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 511–520. [Google Scholar]
- Wang, Z.; Li, Z.; Wang, Y.; Zheng, X.; Deng, X. Building green infrastructure for mitigating urban flood risk in Beijing, China. Urban For. Urban Green. 2024, 93, 128218. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]




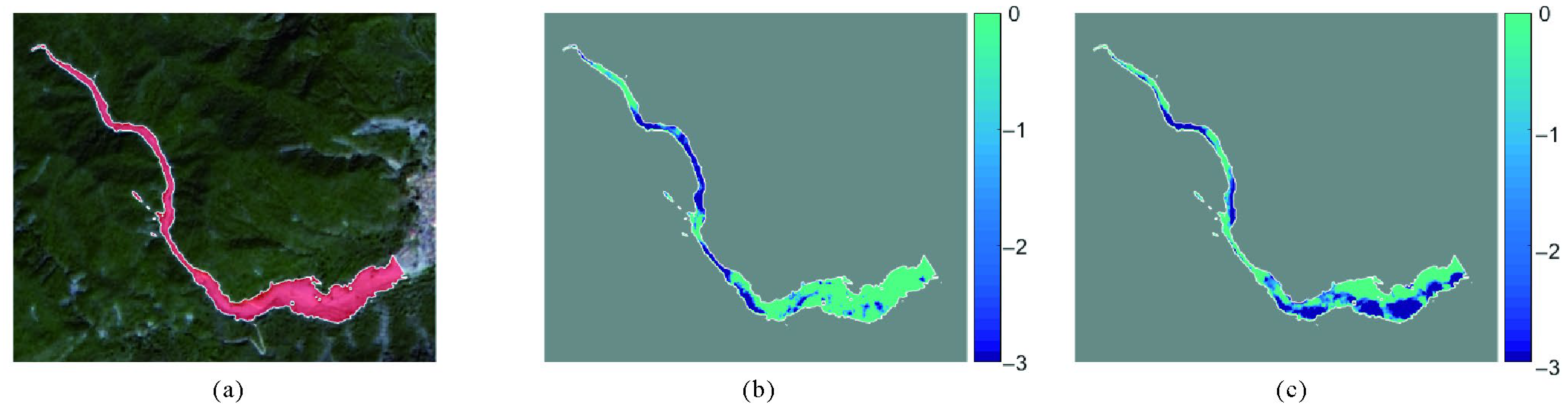

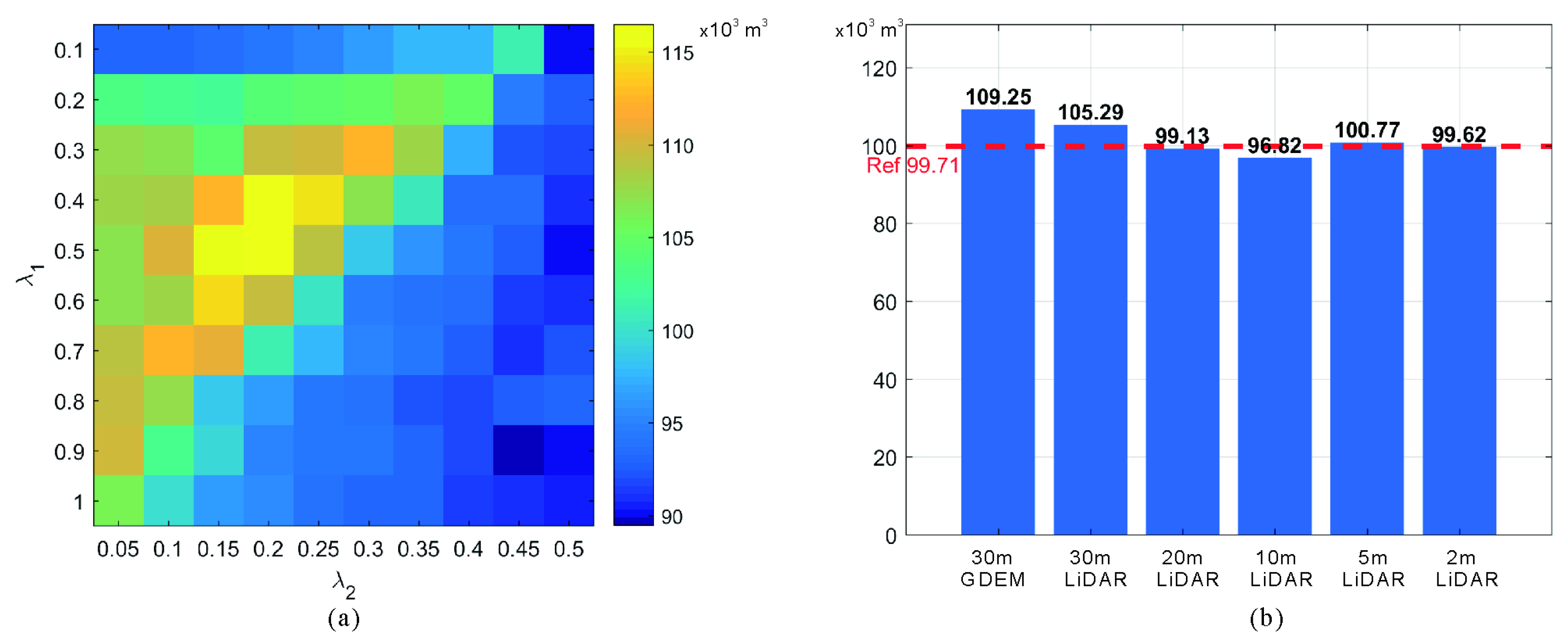
| Method | Calculation Approach | Erosion Volume (m3) | Relative Error (%) |
|---|---|---|---|
| SRSFS | Post-event DSM–GDEM | 52.07 × 103 | −47.78 |
| Post-event DSM–Pre-event DSM | 59.38 × 103 | −40.45 | |
| NPC SRSFS | Post-event DSM–GDEM | 106.41 × 103 | +6.72 |
| Post-event DSM–Pre-event DSM | 109.25 × 103 | +9.57 | |
| Aerial LiDAR | Post-event DSM–Pre-event DSM | 99.71 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wang, S.; Zhou, G.; Zheng, Y.; Li, K.; Ji, L. Debris-Flow Erosion Volume Estimation Using a Single High-Resolution Optical Satellite Image. Remote Sens. 2025, 17, 2413. https://doi.org/10.3390/rs17142413
Zhang P, Wang S, Zhou G, Zheng Y, Li K, Ji L. Debris-Flow Erosion Volume Estimation Using a Single High-Resolution Optical Satellite Image. Remote Sensing. 2025; 17(14):2413. https://doi.org/10.3390/rs17142413
Chicago/Turabian StyleZhang, Peng, Shang Wang, Guangyao Zhou, Yueze Zheng, Kexin Li, and Luyan Ji. 2025. "Debris-Flow Erosion Volume Estimation Using a Single High-Resolution Optical Satellite Image" Remote Sensing 17, no. 14: 2413. https://doi.org/10.3390/rs17142413
APA StyleZhang, P., Wang, S., Zhou, G., Zheng, Y., Li, K., & Ji, L. (2025). Debris-Flow Erosion Volume Estimation Using a Single High-Resolution Optical Satellite Image. Remote Sensing, 17(14), 2413. https://doi.org/10.3390/rs17142413





