An Integrated Approach for Emergency Response and Long-Term Prevention for Rainfall-Induced Landslide Clusters
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. OTSU Threshold Segmentation Method
3.2. Estimation of Landslide Thickness Using the SLBL Model
3.3. R.avaflow Model
3.4. Landslide Susceptibility Assessment
3.4.1. Selection of Evaluation Factors and Data Preprocessing
- (1)
- Topographic factors: derived from 5 m resolution DEM;
- (2)
- Geological factors: obtained from national geological maps at 1:100,000 and 1:50,000 scales;
- (3)
- Soil texture factors: including sand, silt, and clay content, sourced from national soil texture spatial datasets;
- (4)
- Vegetation factor (NDVI): derived from 10 m resolution Sentinel-2 imagery;
- (5)
- Road network factor: interpreted from 1 m resolution Google imagery;
- (6)
- Land use factor: obtained from the 2020 China National Land Use and Cover Change (CNLUCC) dataset;
- (7)
- Human activity factors: including human modification intensity and population density, both retrieved from public datasets on the GEE platform.
3.4.2. Susceptibility Mapping Units
3.4.3. Selection of Machine Learning Algorithms
4. Results
4.1. Landslide Identification
4.1.1. Landslide Distribution
4.1.2. Landslide Identification Validation
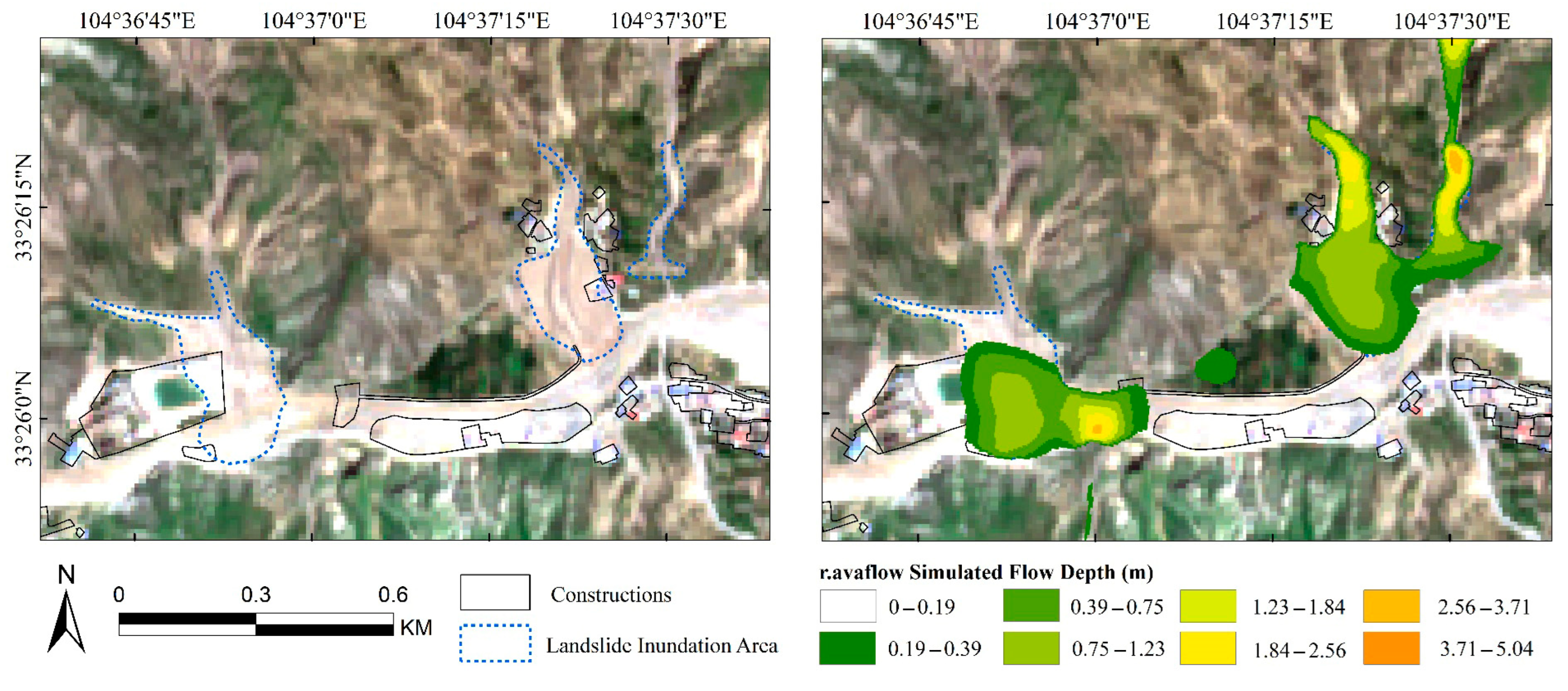
4.2. Post-Disaster Emergency Simulation
4.3. Landslide Susceptibility Assessment Results
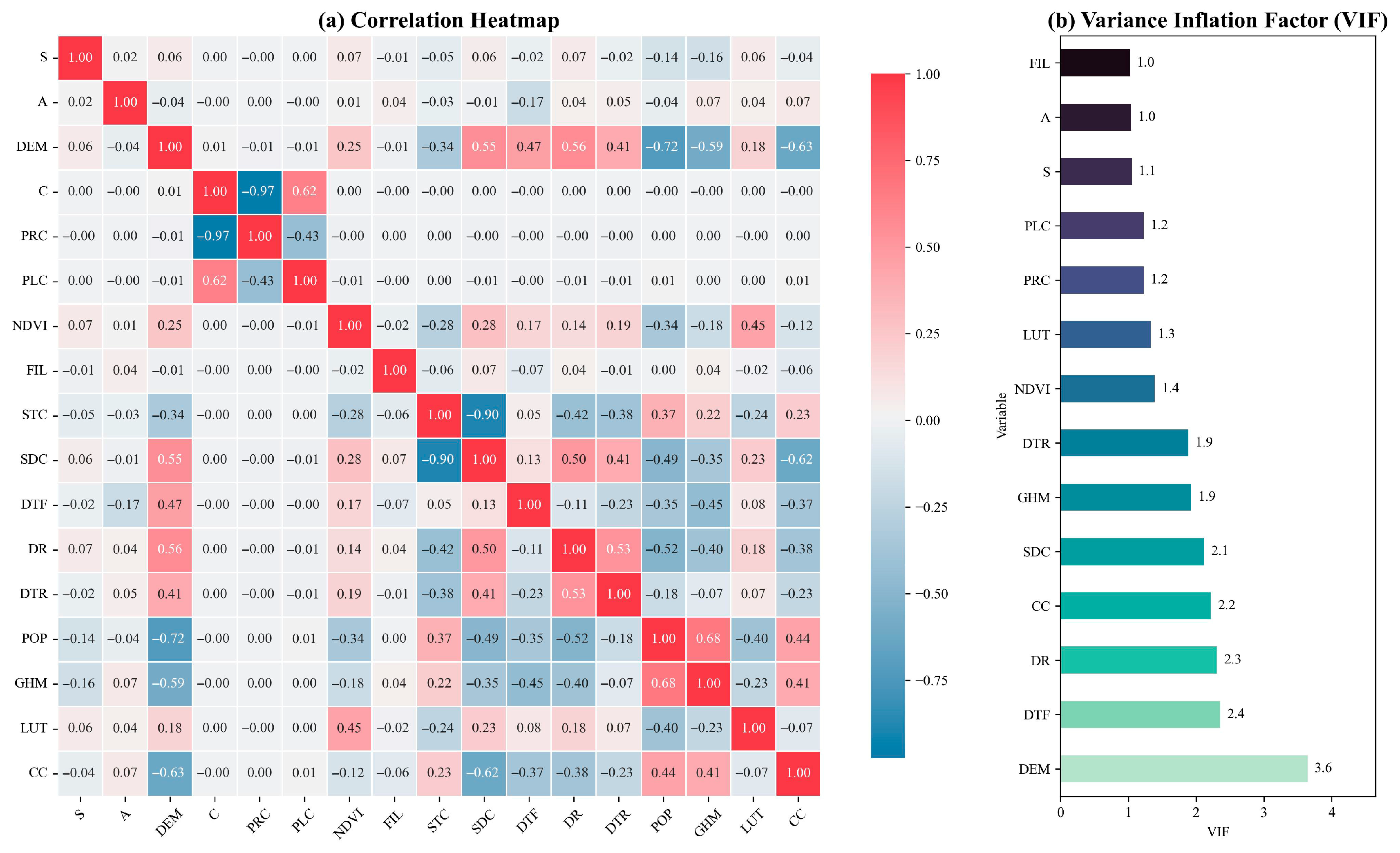
4.3.1. Multicollinearity Analysis of Environmental Factors
4.3.2. Model Evaluation and Optimization
4.4. Delineation of Impact Areas and Identification of Hazardous Slopes
4.4.1. Delineation of Impact Areas
4.4.2. Identification of Hazardous Slopes
5. Discussion
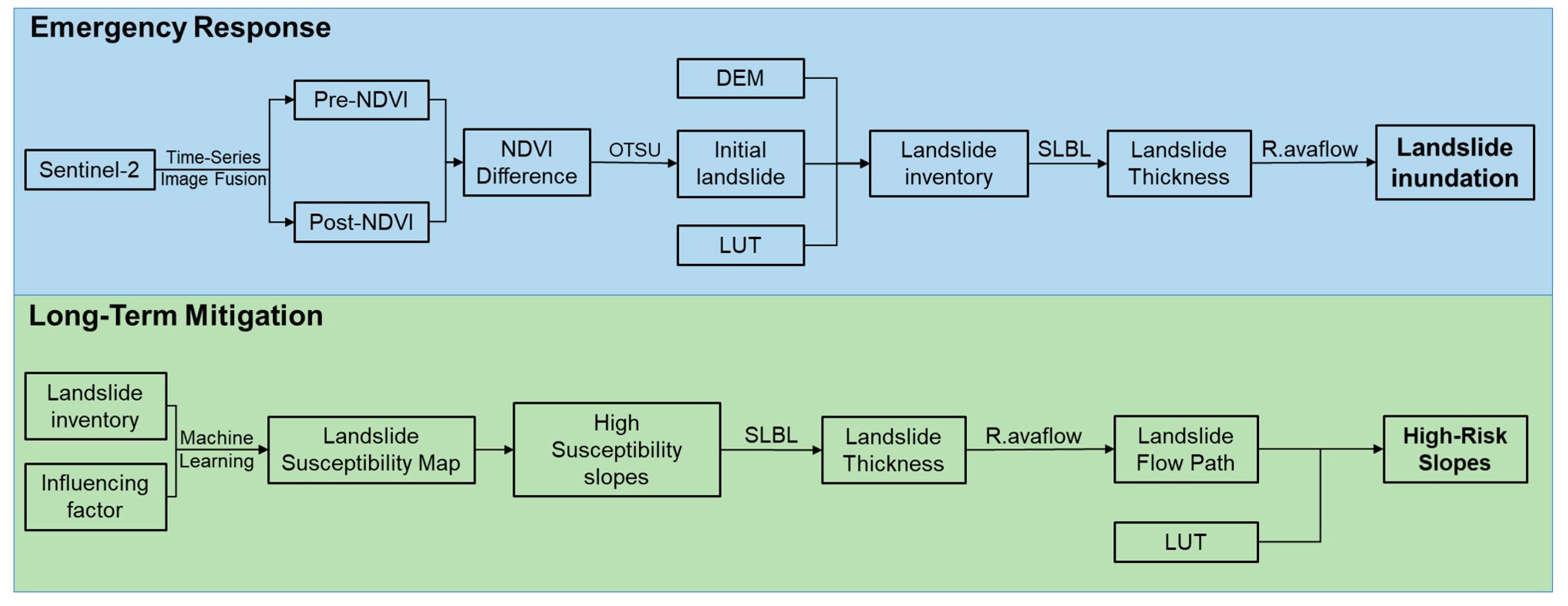
5.1. An Integrated Approach to Risk Management of Rainfall-Induced Landslides
5.2. Insights from Parameter Sensitivity in Numerical Simulation
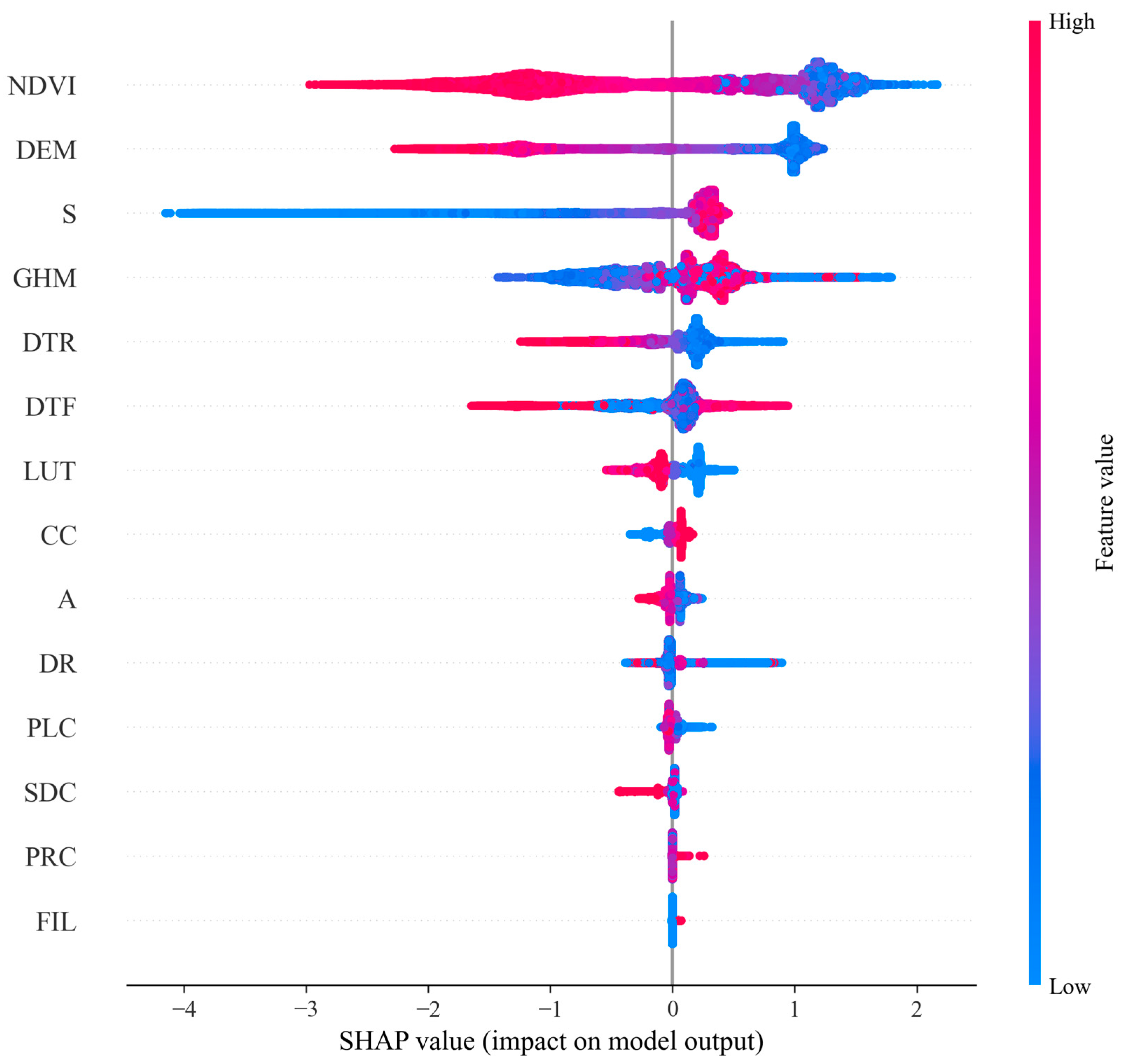
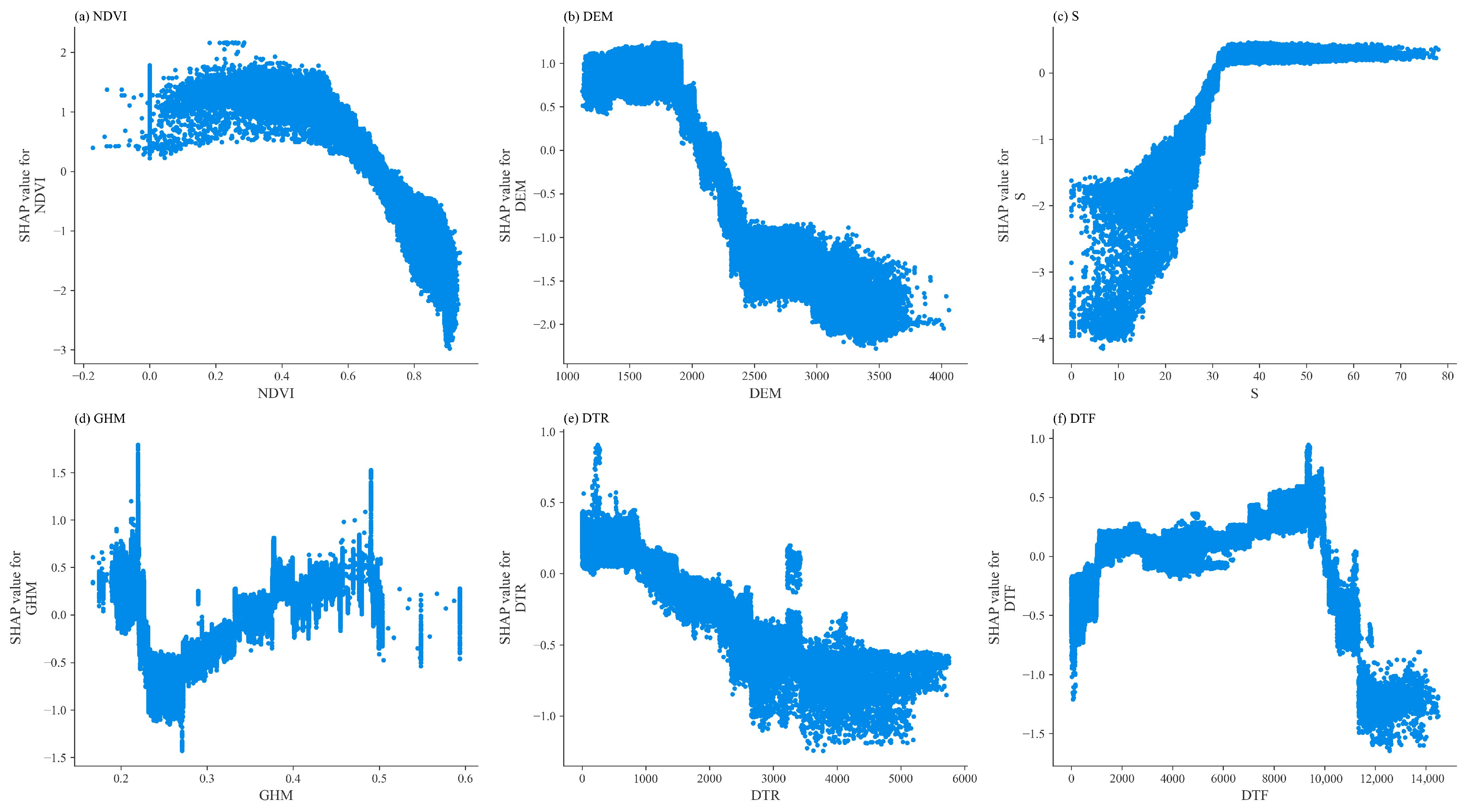
5.3. Insights from Feature Importance Analysis of the Susceptibility Evaluation Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Touma, D.; Stevenson, S.; Swain, D.L.; Singh, D.; Kalashnikov, D.A.; Huang, X. Climate Change Increases Risk of Extreme Rainfall Following Wildfire in the Western United States. Sci. Adv. 2022, 8, eabm0320. [Google Scholar] [CrossRef] [PubMed]
- Wasko, C.; Nathan, R.; Stein, L.; O’Shea, D. Evidence of Shorter More Extreme Rainfalls and Increased Flood Variability under Climate Change. J. Hydrol. 2021, 603, 126994. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Wiatr, T.; Fernández-Steeger, T.M.; Reicherter, K.; Rodrigues, D.M.M.; Azzam, R. Landslide Hazard and Cascading Effects Following the Extreme Rainfall Event on Madeira Island (February 2010). Nat. Hazards 2013, 65, 635–652. [Google Scholar] [CrossRef]
- Suradi, M.; Fourie, A.B.; Saynor, M.J. An Experimental and Numerical Study of a Landslide Triggered by an Extreme Rainfall Event in Northern Australia. Landslides 2016, 13, 1125–1138. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M. Landslide Disasters Triggered by Extreme Rainfall Events: The Case of Montescaglioso (Basilicata, Southern Italy). Geosciences 2018, 8, 377. [Google Scholar] [CrossRef]
- Araújo, J.R.; Ramos, A.M.; Soares, P.M.M.; Melo, R.; Oliveira, S.C.; Trigo, R.M. Impact of Extreme Rainfall Events on Landslide Activity in Portugal under Climate Change Scenarios. Landslides 2022, 19, 2279–2293. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Kapnick, S.B.; Stanley, T.; Pascale, S. Changes in Extreme Precipitation and Landslides Over High Mountain Asia. Geophys. Res. Lett. 2020, 47, e2019GL085347. [Google Scholar] [CrossRef]
- Donnini, M.; Santangelo, M.; Gariano, S.L.; Bucci, F.; Peruccacci, S.; Alvioli, M.; Althuwaynee, O.; Ardizzone, F.; Bianchi, C.; Bornaetxea, T.; et al. Landslides Triggered by an Extraordinary Rainfall Event in Central Italy on September 15, 2022. Landslides 2023, 20, 2199–2211. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S. Landslide Mobility and Hazards: Implications of the 2014 Oso Disaster. Earth Planet. Sci. Lett. 2015, 412, 197–208. [Google Scholar] [CrossRef]
- Rossi, M.; Guzzetti, F.; Salvati, P.; Donnini, M.; Napolitano, E.; Bianchi, C. A Predictive Model of Societal Landslide Risk in Italy. Earth-Sci. Rev. 2019, 196, 102849. [Google Scholar] [CrossRef]
- Caleca, F.; Tofani, V.; Segoni, S.; Raspini, F.; Franceschini, R.; Rosi, A. How Can Landslide Risk Maps Be Validated? Potential Solutions with Open-Source Databases. Front. Earth Sci. 2022, 10, 998885. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, H.; Liao, H.; Li, W.; Su, L.; He, W.; Zeng, L.; Qin, H.; Dhital, M.R. Emergency Response to the Reactivated Aniangzhai Landslide Resulting from a Rainstorm-Triggered Debris Flow, Sichuan Province, China. Landslides 2021, 18, 1115–1130. [Google Scholar] [CrossRef]
- Huang, B.; Zheng, W.; Yu, Z.; Liu, G. A Successful Case of Emergency Landslide Response—The Sept. 2, 2014, Shanshucao Landslide, Three Gorges Reservoir, China. Geoenviron. Disasters 2015, 2, 18. [Google Scholar] [CrossRef][Green Version]
- Robinson, T.R.; Rosser, N.J.; Densmore, A.L.; Williams, J.G.; Kincey, M.E.; Benjamin, J.; Bell, H.J. Rapid Post-Earthquake Modelling of Coseismic Landslide Intensity and Distribution for Emergency Response Decision Support. Nat. Hazards Earth Syst. Sci. 2017, 17, 1521–1540. [Google Scholar] [CrossRef]
- An, J.; Bai, X.; Xu, J.; Nie, G.; Wang, X. Prediction of Highway Blockage Caused by Earthquake-Induced Landslides for Improving Earthquake Emergency Response. Nat. Hazards 2015, 79, 511–536. [Google Scholar] [CrossRef]
- Chen, X.Q.; Cui, P.; Li, Y.; Zhao, W.Y. Emergency Response to the Tangjiashan Landslide-Dammed Lake Resulting from the 2008 Wenchuan Earthquake, China. Landslides 2011, 8, 91–98. [Google Scholar] [CrossRef]
- Dikau, R. The Recognition of Landslides. In Floods and Landslides: Integrated Risk Assessment; Casale, R., Margottini, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–44. ISBN 978-3-642-63664-6. [Google Scholar]
- Saba, S.B.; van der Meijde, M.; van der Werff, H. Spatiotemporal Landslide Detection for the 2005 Kashmir Earthquake Region. Geomorphology 2010, 124, 17–25. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Shyu, J.B.H.; Gao, M.; Tan, X.; Ran, Y.; Zheng, W. Landslides Triggered by the 20 April 2013 Lushan, China, Mw 6.6 Earthquake from Field Investigations and Preliminary Analyses. Landslides 2015, 12, 365–385. [Google Scholar] [CrossRef]
- Murillo-García, F.G.; Alcántara-Ayala, I.; Ardizzone, F.; Cardinali, M.; Fiourucci, F.; Guzzetti, F. Satellite Stereoscopic Pair Images of Very High Resolution: A Step Forward for the Development of Landslide Inventories. Landslides 2015, 12, 277–291. [Google Scholar] [CrossRef]
- Đurić, D.; Mladenović, A.; Pešić-Georgiadis, M.; Marjanović, M.; Abolmasov, B. Using Multiresolution and Multitemporal Satellite Data for Post-Disaster Landslide Inventory in the Republic of Serbia. Landslides 2017, 14, 1467–1482. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Domènech, G.; Yang, F.; Guo, X.; Dai, L.; He, C.; Xu, Q.; Huang, R. Two Multi-Temporal Datasets That Track the Enhanced Landsliding after the 2008 Wenchuan Earthquake. Earth Syst. Sci. Data 2019, 11, 35–55. [Google Scholar] [CrossRef]
- Yang, W.; Wang, M.; Shi, P. Using MODIS NDVI Time Series to Identify Geographic Patterns of Landslides in Vegetated Regions. IEEE Geosci. Remote Sens. Lett. 2012, 10, 707–710. [Google Scholar] [CrossRef]
- Tavakkoli Piralilou, S.; Shahabi, H.; Jarihani, B.; Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Aryal, J. Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sens. 2019, 11, 2575. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Shahabi, H.; Crivellari, A.; Homayouni, S.; Blaschke, T.; Ghamisi, P. Landslide Detection Using Deep Learning and Object-Based Image Analysis. Landslides 2022, 19, 929–939. [Google Scholar] [CrossRef]
- Meena, S.R.; Soares, L.P.; Grohmann, C.H.; Van Westen, C.; Bhuyan, K.; Singh, R.P.; Floris, M.; Catani, F. Landslide Detection in the Himalayas Using Machine Learning Algorithms and U-Net. Landslides 2022, 19, 1209–1229. [Google Scholar] [CrossRef]
- Zhou, W.; Qiu, H.; Wang, L.; Pei, Y.; Tang, B.; Ma, S.; Yang, D.; Cao, M. Combining Rainfall-Induced Shallow Landslides and Subsequent Debris Flows for Hazard Chain Prediction. Catena 2022, 213, 106199. [Google Scholar] [CrossRef]
- Tayyebi, S.M.; Pastor, M.; Stickle, M.M.; Yagüe, Á.; Manzanal, D.; Molinos, M.; Navas, P. Two-Phase SPH Modelling of a Real Debris Avalanche and Analysis of Its Impact on Bottom Drainage Screens. Landslides 2022, 19, 421–435. [Google Scholar] [CrossRef]
- Sajwan, A.; Mhaski, S.; Pandey, A.; Vangla, P.; Ramana, G.V. A Multi-Scale Approach for Deterministic Analysis of Landslide Triggering and Mass Flow Mechanism at Kaliasaur (Rudraprayag). Landslides 2024, 21, 393–409. [Google Scholar] [CrossRef]
- Ahmad, N.; Shafique, M.; Hussain, M.L.; Ullah, I. Integrated Debris Flow Hazard and Risk Assessment Using UAV Data and RAMMS, a Case Study in Northern Pakistan. Nat. Hazards 2025, 121, 1463–1487. [Google Scholar] [CrossRef]
- Bhagya, S.B.; Sumi, A.S.; Balaji, S.; Danumah, J.H.; Costache, R.; Rajaneesh, A.; Gokul, A.; Chandrasenan, C.P.; Quevedo, R.P.; Johny, A. Landslide Susceptibility Assessment of a Part of the Western Ghats (India) Employing the AHP and F-AHP Models and Comparison with Existing Susceptibility Maps. Land 2023, 12, 468. [Google Scholar] [CrossRef]
- Chanu, M.L.; Bakimchandra, O. Landslide Susceptibility Assessment Using AHP Model and Multi Resolution DEMs along a Highway in Manipur, India. Environ. Earth Sci. 2022, 81, 156. [Google Scholar] [CrossRef]
- Zhou, J.; Tan, S.; Li, J.; Xu, J.; Wang, C.; Ye, H. Landslide Susceptibility Assessment Using the Analytic Hierarchy Process (AHP): A Case Study of a Construction Site for Photovoltaic Power Generation in Yunxian County, Southwest China. Sustainability 2023, 15, 5281. [Google Scholar] [CrossRef]
- Malakar, S.; Rai, A.K. Estimating Seismic Vulnerability in West Bengal by AHP-WSM and AHP-VIKOR. Nat. Hazards Res. 2023, 3, 464–473. [Google Scholar] [CrossRef]
- Parvin, F.; Najmul Islam Hashmi, S.; Ali, S.A. Appraisal of Infrastructural Amenities to Analyze Spatial Backwardness of Murshidabad District Using WSM and GIS-Based Kernel Estimation. GeoJournal 2021, 86, 19–41. [Google Scholar] [CrossRef]
- Saha, A.; Villuri, V.G.K.; Bhardwaj, A.; Kumar, S. A Multi-Criteria Decision Analysis (MCDA) Approach for Landslide Susceptibility Mapping of a Part of Darjeeling District in North-East Himalaya, India. Appl. Sci. 2023, 13, 5062. [Google Scholar] [CrossRef]
- Beigh, I.H.; Bukhari, S.K. Landslide Susceptibility Assessment Using GIS-Based Multicriteria Decision Analysis (MCDA) along a Part of National Highway-1, Kashmir- Himalayas, India. Appl. Geomat. 2024, 16, 451–469. [Google Scholar] [CrossRef]
- He, J.; Qiu, H.; Qu, F.; Hu, S.; Yang, D.; Shen, Y.; Zhang, Y.; Sun, H.; Cao, M. Prediction of Spatiotemporal Stability and Rainfall Threshold of Shallow Landslides Using the TRIGRS and Scoops3D Models. Catena 2021, 197, 104999. [Google Scholar] [CrossRef]
- Raimondi, L.; Pepe, G.; Firpo, M.; Calcaterra, D.; Cevasco, A. An Open-Source and QGIS-Integrated Physically Based Model for Spatial Prediction of Rainfall-Induced Shallow Landslides (SPRIn-SL). Environ. Model. Softw. 2023, 160, 105587. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, F. Three-Dimensional Seismic Slope Stability Assessment with the Application of Scoops3D and GIS: A Case Study in Atsuma, Hokkaido. Geoenviron. Disasters 2019, 6, 9. [Google Scholar] [CrossRef]
- Ermini, L.; Catani, F.; Casagli, N. Artificial Neural Networks Applied to Landslide Susceptibility Assessment. Geomorphology 2005, 66, 327–343. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Comparison of Landslide Susceptibility Based on a Decision-Tree Model and Actual Landslide Occurrence: The Akaishi Mountains, Japan. Geomorphology 2009, 109, 108–121. [Google Scholar] [CrossRef]
- Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests Techniques for Shallow Landslide Susceptibility Assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
- Nikoobakht, S.; Azarafza, M.; Akgün, H.; Derakhshani, R. Landslide Susceptibility Assessment by Using Convolutional Neural Network. Appl. Sci. 2022, 12, 5992. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide Susceptibility Assessment Using SVM Machine Learning Algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, C.-W.; Lee, S.; Lee, M.-J. Landslide Susceptibility Mapping and Comparison Using Decision Tree Models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on Landslide Susceptibility Mapping Using Support Vector Machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Pradhan, B.; Dikshit, A.; Lee, S.; Kim, H. An Explainable AI (XAI) Model for Landslide Susceptibility Modeling. Appl. Soft Comput. 2023, 142, 110324. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.-L.; Huang, F.; Huang, L.; Wang, X.-M. Machine Learning-Based Landslide Susceptibility Assessment with Optimized Ratio of Landslide to Non-Landslide Samples. Gondwana Res. 2023, 123, 198–216. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into Geospatial Heterogeneity of Landslide Susceptibility Based on the SHAP-XGBoost Model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Rong, G.; Li, K.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Population Amount Risk Assessment of Extreme Precipitation-Induced Landslides Based on Integrated Machine Learning Model and Scenario Simulation. Geosci. Front. 2023, 14, 101541. [Google Scholar] [CrossRef]
- Gabet, E.J.; Mudd, S.M. The Mobilization of Debris Flows from Shallow Landslides. Geomorphology 2006, 74, 207–218. [Google Scholar] [CrossRef]
- Cui, P.; Zhou, G.G.; Zhu, X.H.; Zhang, J.Q. Scale Amplification of Natural Debris Flows Caused by Cascading Landslide Dam Failures. Geomorphology 2013, 182, 173–189. [Google Scholar] [CrossRef]
- Trancoso Gomes, R.A.; Guimarães, R.F.; de Carvalho Júnior, O.A.; Fernandes, N.F.; Vargas do Amaral Júnior, E. Combining Spatial Models for Shallow Landslides and Debris-Flows Prediction. Remote Sens. 2013, 5, 2219–2237. [Google Scholar] [CrossRef]
- Luu, C.; Ha, H.; Thong Tran, X.; Ha Vu, T.; Duy Bui, Q. Landslide Susceptibility and Building Exposure Assessment Using Machine Learning Models and Geospatial Analysis Techniques. Adv. Space Res. 2024, 74, 5489–5513. [Google Scholar] [CrossRef]
- Ma, S.; Xu, C.; Shao, X. Spatial Prediction Strategy for Landslides Triggered by Large Earthquakes Oriented to Emergency Response, Mid-Term Resettlement and Later Reconstruction. Int. J. Disaster Risk Reduct. 2020, 43, 101362. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Chigira, M.; Arai, N.; Derron, M.-H.; Rudaz, B.; Tsou, C.-Y. Testing a Failure Surface Prediction and Deposit Reconstruction Method for a Landslide Cluster That Occurred during Typhoon Talas (Japan). Earth Surf. Dyn. 2019, 7, 439–458. [Google Scholar] [CrossRef]
- Sun, X.; Zeng, P.; Li, T.; Zhang, L.; Jimenez, R.; Dong, X.; Xu, Q. A Bayesian Approach to Develop Simple Run-out Distance Models: Loess Landslides in Heifangtai Terrace, Gansu Province, China. Landslides 2023, 20, 77–95. [Google Scholar] [CrossRef]
- Wang, Y.; Hutter, K.; Pudasaini, S.P. The Savage-Hutter Theory: A System of Partial Differential Equations for Avalanche Flows of Snow, Debris, and Mud. ZAMM—J. Appl. Math. Mech. Z. Für Angew. Math. Mech. 2004, 84, 507–527. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Mergili, M. A Multi-Phase Mass Flow Model. J. Geophys. Res. Earth Surf. 2019, 124, 2920–2942. [Google Scholar] [CrossRef]
- Baggio, T.; Mergili, M.; D’Agostino, V. Advances in the Simulation of Debris Flow Erosion: The Case Study of the Rio Gere (Italy) Event of the 4th August 2017. Geomorphology 2021, 381, 107664. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Fischer, J.-T. A Mechanical Erosion Model for Two-Phase Mass Flows. Int. J. Multiph. Flow 2020, 132, 103416. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Krautblatter, M. The Mechanics of Landslide Mobility with Erosion. Nat. Commun. 2021, 12, 6793. [Google Scholar] [CrossRef] [PubMed]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Mondini, A.C.; Santangelo, M.; Rocchetti, M.; Rossetto, E.; Manconi, A.; Monserrat, O. Sentinel-1 SAR Amplitude Imagery for Rapid Landslide Detection. Remote Sens. 2019, 11, 760. [Google Scholar] [CrossRef]
- Barra, A.; Monserrat, O.; Mazzanti, P.; Esposito, C.; Crosetto, M.; Scarascia Mugnozza, G. First Insights on the Potential of Sentinel-1 for Landslides Detection. Geomat. Nat. Hazards Risk 2016, 7, 1874–1883. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Didehban, K.; Rasouli, H.; Kamran, K.V.; Feizizadeh, B.; Blaschke, T. An Application of Sentinel-1, Sentinel-2, and GNSS Data for Landslide Susceptibility Mapping. ISPRS Int. J. Geo-Inf. 2020, 9, 561. [Google Scholar] [CrossRef]
- Dabiri, Z.; Hölbling, D.; Abad, L.; Helgason, J.K.; Sæmundsson, Þ.; Tiede, D. Assessment of Landslide-Induced Geomorphological Changes in Hítardalur Valley, Iceland, Using Sentinel-1 and Sentinel-2 Data. Appl. Sci. 2020, 10, 5848. [Google Scholar] [CrossRef]



| Factor Type | Evaluation Factors and Abbreviations |
|---|---|
| Topographic Factors | Slope (S), Aspect (A), Elevation (DEM), Profile Curvature (PRC), Plan Curvature (PLC), Curvature (C) |
| Geological Factors | Distance to Faults (DF), Distance to Rivers (DTR), Clay Content (CC), Sand Content (SDC), Silt Content (STC), NDVI, Formation Intensity Level (FIL) |
| Human Activity Factors | Distance to Roads (DR), Land Use Type (LUT), Population Density (POP), Global Human Modification Index (GHM) |
| Model Name | Characteristics | Source |
|---|---|---|
| Logistic Regression | Suitable for binary classification; simple and efficient; best for linearly separable data. | scikit-learn |
| Random Forest | Ensemble of decision trees using majority voting; good for nonlinear data; prevents overfitting. | scikit-learn |
| Gradient Boosting | Sequentially improves weak learners; good for complex nonlinear problems; longer training time. | scikit-learn |
| Extra Trees | Similar to Random Forest but with random split thresholds; increases randomness and generalization. | scikit-learn |
| Extreme Gradient Boosting (XGBoost) | Highly efficient gradient boosting algorithm; supports parallel computation; robust and scalable. | XGBoost |
| Light Gradient Boosting (LightGBM) | Fast, memory-efficient framework; performs well with high-dimensional data. | LightGBM |
| Categorical Boosting (CatBoost) | Handles categorical variables well; requires less parameter tuning. | CatBoost |
| SGD Classifier | Linear model optimized by stochastic gradient descent; suitable for large-scale or online learning. | scikit-learn |
| Gaussian Naive Bayes | Based on Bayes’ theorem; assumes feature independence and Gaussian distribution; best for small, simple datasets. | scikit-learn |
| Landslide Detection | Landslide Detection (m2) | Percentage (%) | |
|---|---|---|---|
| Visual Interpretation | 469,049.93 | 100 | |
| Automated Detection | Total Area | 461,113.58 | 98.30 |
| Perfect Match | 304,835.55 | 64.99 | |
| False Positives | 31,520.16 | 6.72 | |
| Missed Detections | 5910.03 | 1.26 | |
| Correct Detections | 450,428.65 | 96.03 |
| Phase | θ (°) | φ (°) | Uws (kg/m3) | EM | CE (kg−1) |
|---|---|---|---|---|---|
| Solid | 10 | 36 | 2200 | 2 | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Li, Y.; Huang, Y.; Li, G.; Ma, F.; Zhang, J.; Wang, M.; Zhao, Y.; Chen, G.; Meng, X.; et al. An Integrated Approach for Emergency Response and Long-Term Prevention for Rainfall-Induced Landslide Clusters. Remote Sens. 2025, 17, 2406. https://doi.org/10.3390/rs17142406
Zhao W, Li Y, Huang Y, Li G, Ma F, Zhang J, Wang M, Zhao Y, Chen G, Meng X, et al. An Integrated Approach for Emergency Response and Long-Term Prevention for Rainfall-Induced Landslide Clusters. Remote Sensing. 2025; 17(14):2406. https://doi.org/10.3390/rs17142406
Chicago/Turabian StyleZhao, Wenxin, Yajun Li, Yunfei Huang, Guowei Li, Fukang Ma, Jun Zhang, Mengyu Wang, Yan Zhao, Guan Chen, Xingmin Meng, and et al. 2025. "An Integrated Approach for Emergency Response and Long-Term Prevention for Rainfall-Induced Landslide Clusters" Remote Sensing 17, no. 14: 2406. https://doi.org/10.3390/rs17142406
APA StyleZhao, W., Li, Y., Huang, Y., Li, G., Ma, F., Zhang, J., Wang, M., Zhao, Y., Chen, G., Meng, X., Guo, F., & Yue, D. (2025). An Integrated Approach for Emergency Response and Long-Term Prevention for Rainfall-Induced Landslide Clusters. Remote Sensing, 17(14), 2406. https://doi.org/10.3390/rs17142406








