1. Introduction
Radar echo extrapolation technology plays a crucial role in short-term precipitation forecasting, weather modification, and operational effect assessment [
1]. In the field of radar meteorology, rapid and accurate echo extrapolation has always been a focus of attention. Radar echo extrapolation involves constructing a time series using consecutive radar data periods, analyzing the distribution, movement speed, and directional changes of echoes, and employing a series of algorithms to predict the echo state for a future period [
2]. Compared to numerical weather prediction, radar echo extrapolation technology can provide more timely and accurate predictions within 0–2 h, making it widely used by meteorological departments for monitoring and forecasting precipitation processes [
3].
The main traditional techniques for radar echo extrapolation include cross-correlation methods [
4,
5], centroid tracking methods [
6,
7], and optical flow methods [
8,
9]. Cross-correlation is one of the most commonly used algorithms in echo extrapolation. The algorithm calculates the correlation coefficient of small regions in the radar echo image and determines the relative movement of the radar based on the size of the correlation between these regions. Zhang Yaping et al. [
10] proposed DITREC, which offers better temporal and spatial continuity compared to TREC. The centroid tracking method primarily extracts features from radar echo cells, identifying significant characteristics such as the centroid and volume of the echo cells, but it performs poorly for weather processes involving multiple strong convective systems. The optical flow method, proposed by Gibson in 1979, infers the movement velocity of each pixel in both horizontal and vertical directions by analyzing the brightness changes of pixels in adjacent image frames, forming an optical flow field. This method performs better than cross-correlation in predicting complex weather situations. Bechini et al. [
11] applied a multi-scale HS optical flow method, Cao Yong et al. [
12] used the LK (Lucas–Kanade) optical flow method with image pyramid techniques, Pulkkinen et al. [
13] applied the LK feature optical flow method to extrapolate rain band motion vectors, and Zhang Lei et al. [
14] used RPM-SL for optical flow. These improvements have enhanced the computational efficiency and accuracy of optical flow methods.
However, traditional extrapolation methods face challenges when modeling complex, nonlinear processes such as short-term precipitation forecasting, as their modeling capabilities are insufficient to accurately capture the evolution trends of radar echoes.
In the era of meteorological big data, deep learning has found extensive applications in the field of meteorology [
15,
16,
17,
18,
19,
20,
21,
22,
23], particularly experiencing rapid development in the area of radar echo extrapolation. Shi et al. proposed an end-to-end model by combining Convolutional Neural Networks (CNN) [
24] and Long Short-Term Memory networks (LSTM) [
25], resulting in the Convolutional LSTM Network (ConvLSTM) [
26]. Building upon this, they introduced the Trajectory Gated Recurrent Unit (TrajGRU) [
2], which more accurately captures the spatiotemporal evolution of radar echoes. Subsequently, various improved extrapolation models derived from ConvLSTM have been proposed. The RDCNN (Regional Deep Convolutional Neural Network) [
27], an extrapolation method based on CNNs, incorporates a recurrent dynamic subnetwork and a probabilistic prediction layer. By leveraging the recurrent structure of convolutional layers, it enhances processing capabilities, demonstrating higher accuracy and extended prediction horizons compared to traditional methods. Du et al. [
28] proposed a model combining a temporal attention Encoder–Decoder with a Bidirectional Long Short-Term Memory (Bi-LSTM), which adaptively learns multivariate temporal features and hidden correlations to improve extrapolation performance. Bonnet et al. [
29] utilized a video prediction deep learning model (VPDL-PredRNN++) to forecast 1 h reflectivity image sequences in São Paulo, Brazil, achieving significant improvements in precipitation nowcasting. Huang Xingyou et al. [
30] employed a ConvLSTM neural network trained with a weighted loss function using multi-year radar detection datasets. Their extrapolation results outperformed traditional optical flow methods, particularly in stratiform cloud precipitation forecasting compared to convective cloud scenarios. He et al. [
31] proposed an improved Multi-Convolutional Gated Recurrent Unit (M-ConvGRU), which performs convolutional operations on input data and previous outputs of the GRU network to more effectively capture spatiotemporal correlations in radar echo images. Yang et al. [
32] introduced a self-attention mechanism, embedding global spatiotemporal features into the original Spatiotemporal Long Short-Term Memory (ST-LSTM) to construct a self-attention integrated recurrent unit. Stacking multiple such units formed a radar echo extrapolation network, experimentally proven to outperform other models. Guo et al. [
33] proposed a 3D-UNet-LSTM model based on the Extractor-Forecaster architecture, which uses a 3D UNet to extract spatiotemporal features from input radar images and models them via a Seq2Seq network, demonstrating superior capture of strong echo spatiotemporal variations.
Chen et al. [
34] proposed a novel radar image extrapolation algorithm—Dynamic Multiscale Fusion Generative Adversarial Network (DMSF-GAN)—which effectively captures both the future location and structural patterns of radar echoes. Yao et al. [
35] developed a prediction refinement neural network based on DyConvGRU and U-Net, which leverages dynamic convolution and a prediction refinement framework to enhance the model’s capability in predicting high-reflectivity echoes. He et al. [
36] introduced a spatiotemporal LSTM model enhanced by multiscale contextual fusion and attention mechanisms, enabling the model to extract short-term contextual features across different radar image scales, thereby improving its perception of historical echo sequences.
In 2014, Goodfellow et al. proposed Generative Adversarial Networks (GANs) [
37], which significantly improve the quality of predicted images by reducing blurriness. Since then, numerous GAN-based extrapolation models have emerged. Given that conventional deep learning models often suffer from detail loss and blurred outputs due to the mean squared error (MSE) loss function, Jing et al. [
38] introduced the Adversarial Extrapolation Neural Network (AENN), which incorporates a conditional generator and two discriminators trained via adversarial optimization, demonstrating great potential for short-term weather forecasting. Yan et al. [
39] proposed the Conditional Latent Generative Adversarial Network (CLGAN), which shows strong performance in capturing heavy precipitation events. Xu et al. [
40] presented the UA-GAN model, which improves both image details and precipitation prediction accuracy. Zheng et al. [
41] developed a spatiotemporal process reinforcement model (GAN-argcPredNet v1.0), which enhances prior information to reduce loss and improve prediction performance for heavy precipitation. Addressing the “spatial blurring” issue in deep learning-based radar nowcasting—caused by inadequate representation of spatial variability—Gong et al. [
42] proposed the SVRE (Spatial Variability Representation Enhancement) loss function and the AGAN (Attentional Generative Adversarial Network) model. Ablation and comparative experiments confirmed the effectiveness of this method in improving nowcasting accuracy.
Despite these advances, most of the aforementioned models fundamentally rely on convolutional operations, which inevitably lead to increased blurriness over longer extrapolation periods due to the smoothing nature of convolutions. Furthermore, their inputs are typically not raw radar base data but instead pseudo-colored echo intensities ranging from −5 to 70 dBZ (with a resolution of 5 dBZ), which are converted to 0–255 grayscale images. This preprocessing causes substantial loss of echo details, limiting the models’ ability to capture complex and rapidly evolving precipitation patterns. Moreover, radar-based extrapolation models often lack physical constraints derived from atmospheric dynamics, thermodynamics, and microphysics. As a result, forecasting errors accumulate over time, particularly impairing the prediction of echo initiation and dissipation—issues that cannot be resolved through algorithmic improvements alone.
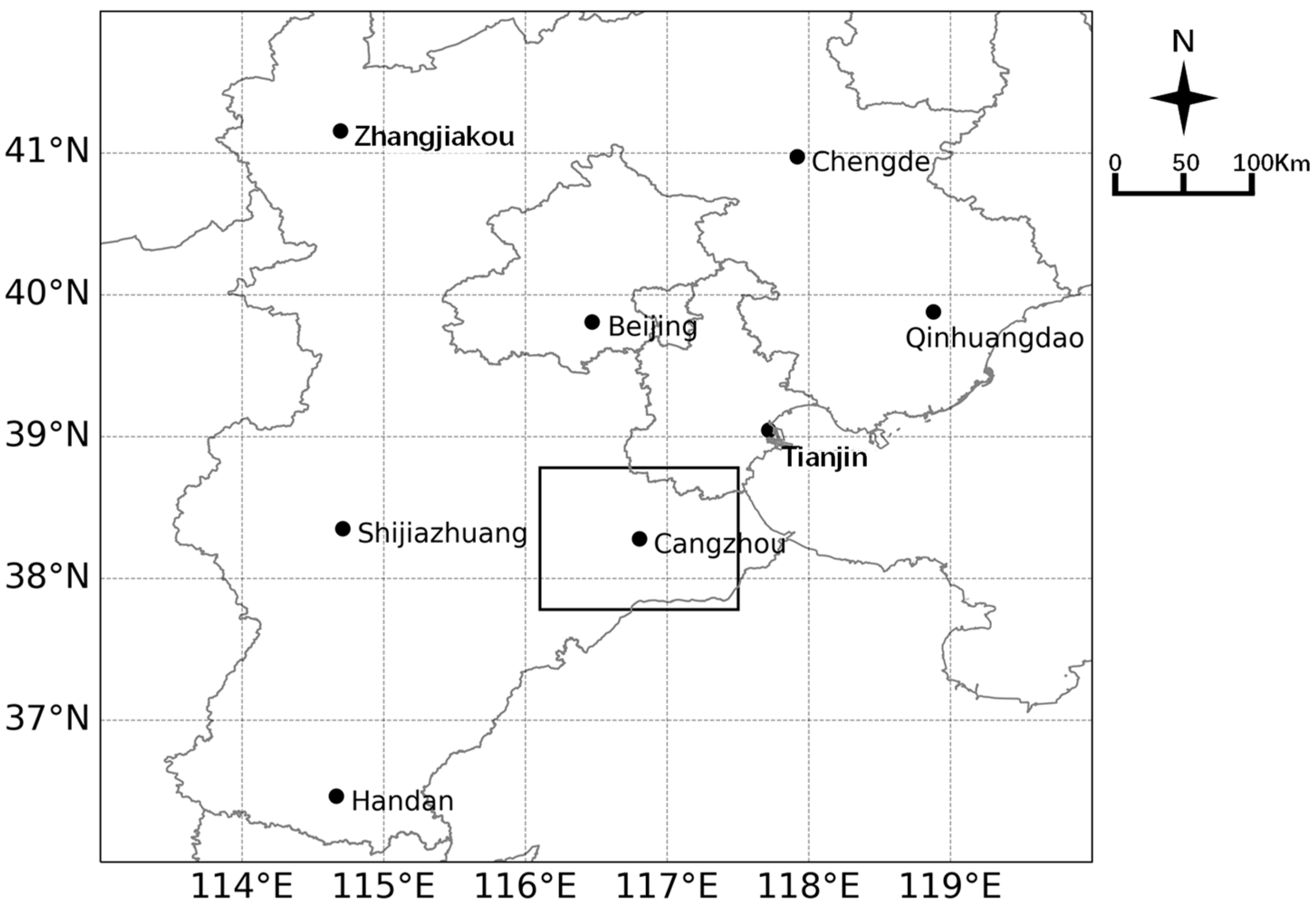
Benefiting from advancements in integrated meteorological observation systems, multi-source real-time data fusion analysis, and multiscale numerical forecasting models, regional meteorological centers in Beijing, Shanghai, Guangdong, and other areas in China have developed rapid update analysis and forecasting systems with a temporal resolution of 10–12 min and spatial resolution of 1 km. These systems provide initial fields capable of depicting real-time weather backgrounds with spatiotemporal resolutions comparable to radar observations. Therefore, effectively integrating such physical background information into deep learning-based radar echo extrapolation models—by fusing radar echoes with meteorological physical variables—can greatly enhance prediction accuracy.
To address the above challenges and leverage the emerging high-resolution weather background data, this study is motivated by two key objectives: (1) overcoming the blurriness and detail loss caused by conventional convolutional operations; (2) integrating physical constraints from meteorological background fields to improve the prediction of echo dynamics. The main contributions are as follows:
A fusion-encoder–decoder framework is designed for radar echo extrapolation, which couples deep convolutional generative adversarial networks (DCGAN) with time-series modeling to reduce echo blurriness and preserve fine-scale features.
Real-time weather background data (e.g., from RMAPS-NOW) are innovatively integrated into the deep learning model, providing physical constraints that mitigate error accumulation in long-term extrapolation.
The model assigns adaptive weights to long time sequences and strong echoes, significantly improving prediction accuracy for complex precipitation patterns, as validated by comprehensive experiments.
3. Network Architecture Design and Model Training
3.1. ConvLSTM
Radar echoes are not only temporally interrelated, but more importantly, they also exhibit spatial correlation. Therefore, this study designs a network architecture that incorporates weather backgrounds based on the ConvLSTM framework, which has good capabilities for extracting temporal and spatial features. ConvLSTM is a neural network model that combines Convolutional Neural Networks (CNN) and LSTM. LSTM, a variant of Recurrent Neural Network (RNN), demonstrates strong long-term dependency modeling capabilities when processing sequential data. It selectively forgets and updates information through gating units, enabling better capture of long-term dependencies in time series. ConvLSTM, an extension of LSTM, introduces convolutional operations, allowing it to process both spatial and temporal information simultaneously (Equation (2)).
In the equation, ∗ denotes the convolution operation, is the input gate at time step t, is the input data at time step t (typically a convolved feature map); is the forget gate at time step t, with parameters similar to those of the input gate; is the output gate at time step t; and are the cell states at time steps t and t − 1, respectively; is the fused information at time step t; and are the hidden states at time steps t and t − 1, respectively; W represents the corresponding convolutional kernel parameters; b is the bias term; σ is the sigmoid activation function, which avoids gradient vanishing and offers good convergence and computational efficiency; tanh is the hyperbolic tangent activation function, whose nonlinear transformation characteristics endow the network with the ability to learn complex relationships.
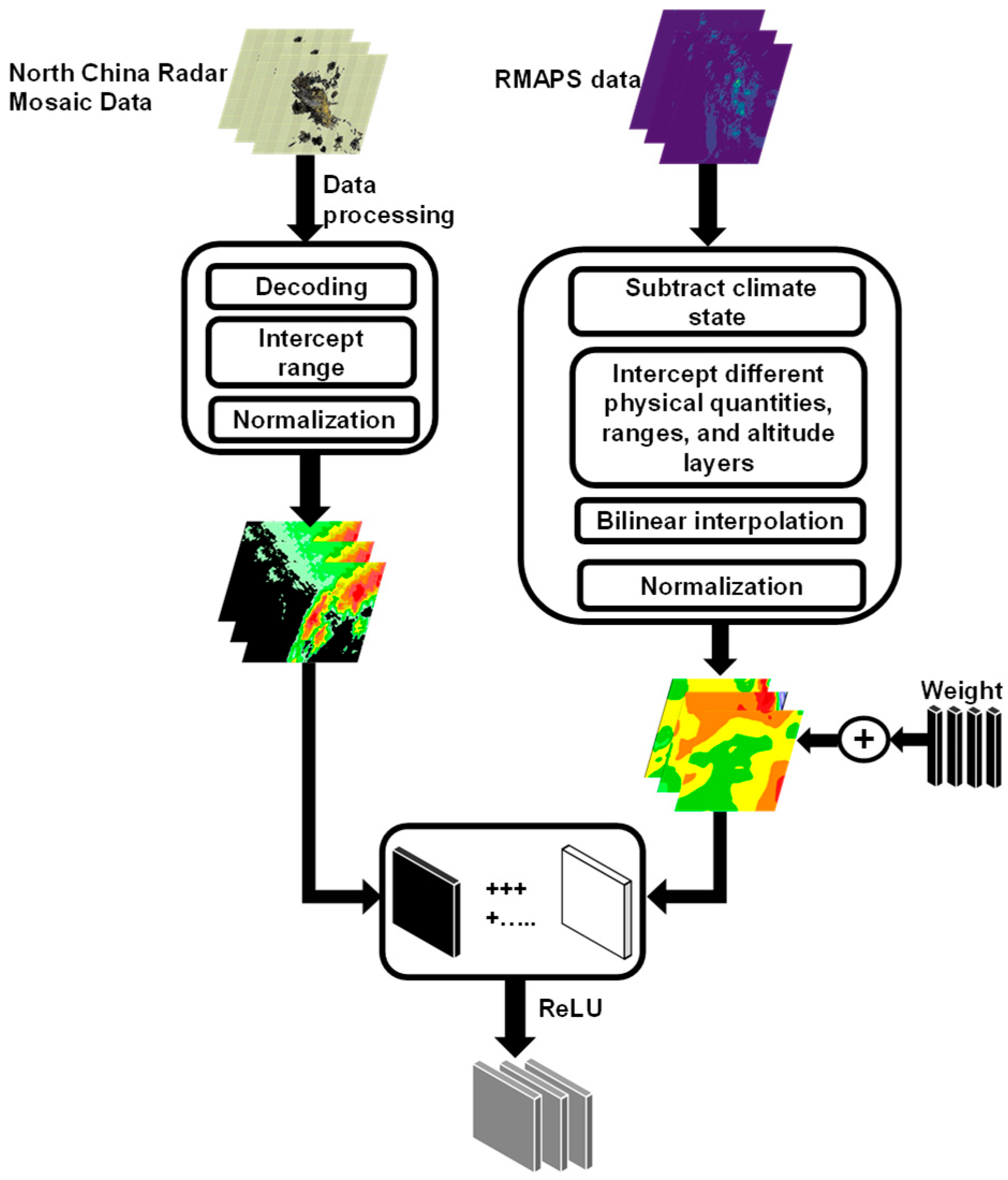
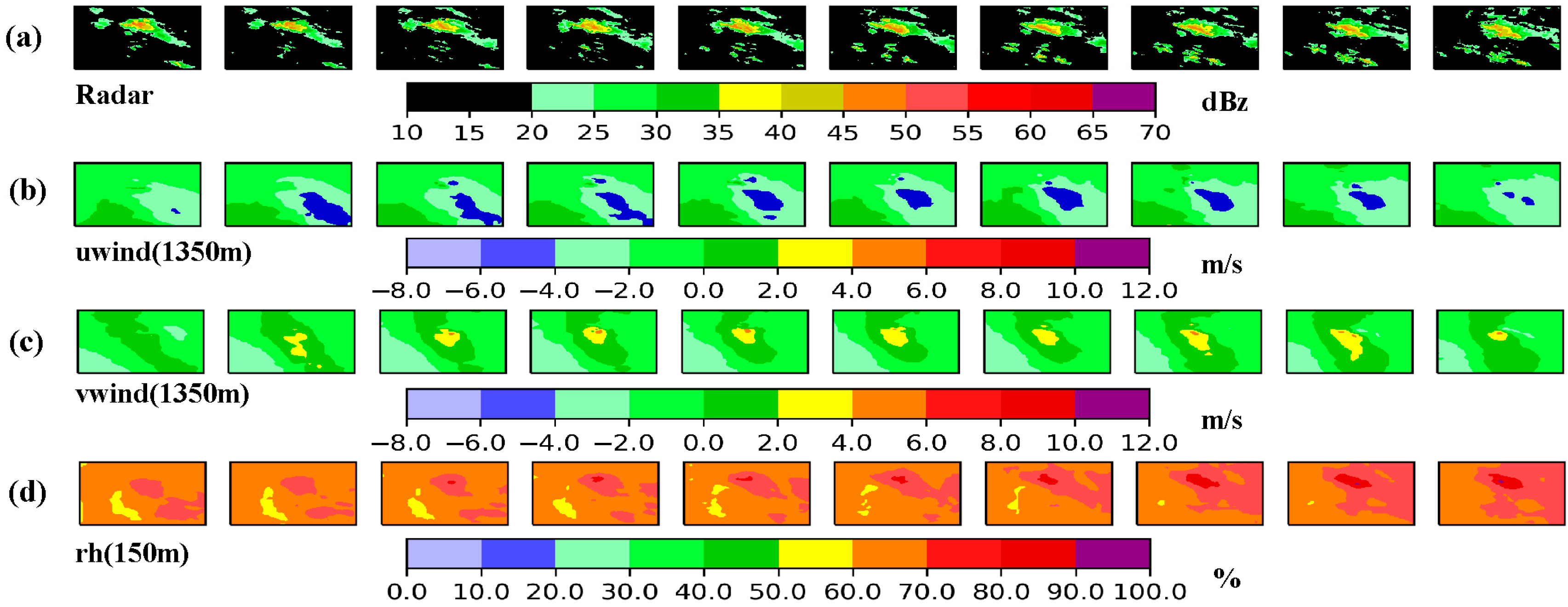
3.2. Radar Cell Encoding
A radar cell was constructed by multiplying a given physical variable (e.g., relative humidity, u-wind, or v-wind) by an initially assigned weight and stacking it with the corresponding radar echo intensity matrix, thereby integrating information from a single physical variable (
Figure 2). The weight is automatically optimized during the model training process. The formulation of the radar cell is given in Equation (3):
In this equation, represents the matrix resulting from the fusion of weather background information and radar echoes, reflecting the influence of external meteorological factors on the radar data. denotes the learnable weight parameters, represents the input physical variables, and is a trainable bias term introduced to enhance the model’s adaptability. The ReLU activation function is applied to ensure non-negative outputs, thereby enforcing that the fusion process only introduces positive corrections to the data without introducing negative interference.
For each physical variable, 1 to 3 grid fields at different vertical levels were selected (see
Table 1 for details). A scaling parameter (Scale) was used to adjust the relative weights of different physical variables. These variables were then fused with the corresponding radar echo sequences to generate multiple radar cells, each incorporating distinct background meteorological information. After applying weighting and normalization to each radar cell, they were further encoded into ConvLSTM cells based on the ConvLSTM architecture, and used as the input sequence for the ConvLSTM network.
Batch normalization was applied to both the previous hidden state and the input ConvLSTM cell to enhance the model’s generalization ability and to mitigate issues such as gradient vanishing or explosion, thereby improving training efficiency and model performance. The ConvLSTM cell served as the input gate, performing forward propagation using convolutional operations, allowing spatially dependent information to flow across time steps through the computation and activation of various gates and cell states.
Finally, a Squeeze-and-Excitation Layer (SELayer) was introduced to return the attention-weighted hidden state and the updated cell state . The self-attention mechanism applied to the hidden state enhances the model’s ability to learn important channel features, thereby improving its representational capacity.
3.3. MR-DCGAN Network Architecture
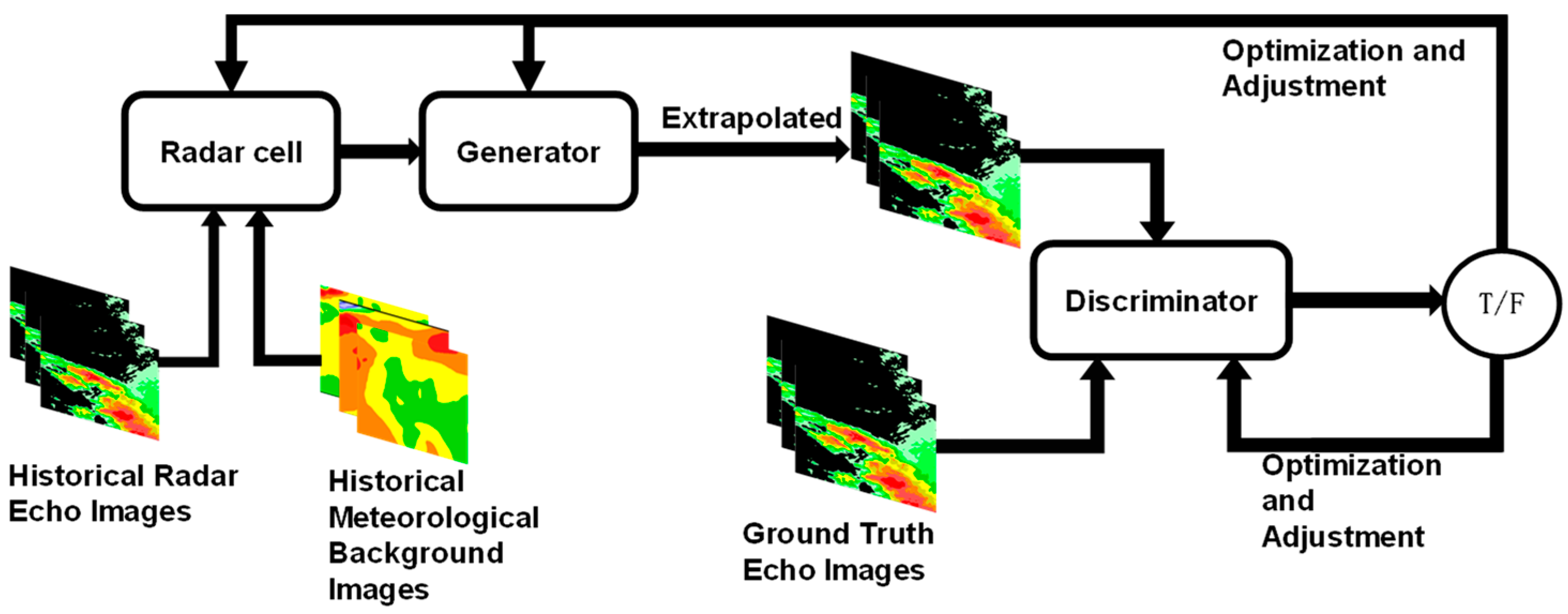
In traditional radar echo extrapolation, the quality of predicted echoes significantly deteriorates as the forecast lead time increases, leading to issues such as difficulties in echo tracking, increased uncertainty in identification, and greater complexity in data processing. Moreover, deep learning-based echo extrapolation models typically rely on pixel-wise loss functions, which often result in image distortion during prediction. Deep Convolutional Generative Adversarial Networks (DCGANs) are capable of effectively capturing the spatial features of radar echo images and reconstructing them in a reverse manner, thereby alleviating the blurring problem commonly observed in extrapolated outputs.
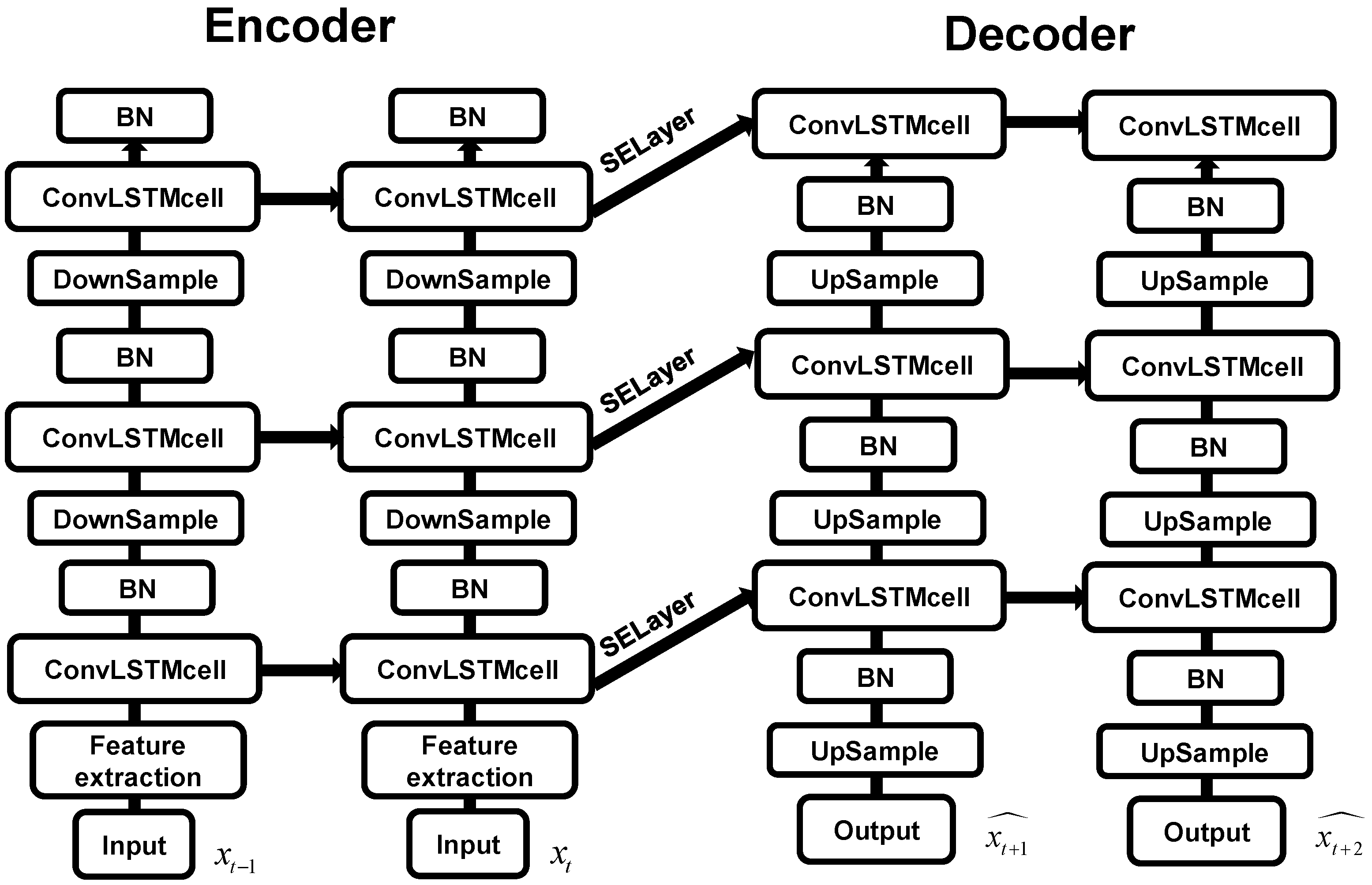
A generative adversarial network primarily consists of a generator and a discriminator The MR-DCGAN network architecture proposed in this study (
Figure 3) builds upon the MR-ConvLSTM model (
Figure 4) developed by Wang Shanhao et al. [
43]. In this architecture, we employed an Encoder–Decoder framework to predict spatio-temporal sequences. Building upon this structure, we integrated ConvLSTM cells constructed from multiple radar units of RMAPS-NOW into the encoder–decoder architecture, further developing the MR-ConvLSTM network architecture.
The encoder consists of three downsampling layers and three ConvLSTM cell layers. It transforms the input hidden states into a fixed-length vector encapsulating information from the input sequence. The hidden state from the final encoding step initializes the decoder’s hidden states. After each encoding step, the input to the ConvLSTM cells is downsampled via convolution to extract critical spatial features, enabling the ConvLSTM cells to better learn radar echo characteristics integrated with weather background information. Batch normalization is applied after each ConvLSTM cell layer to enhance model generalization. The Leaky-ReLU activation function is used to mitigate the vanishing gradient issue in the negative region.
The decoder prediction module comprises three upsampling layers and three ConvLSTM cell layers. At the input of each ConvLSTM cell layer, an SELayer (Squeeze-and-Excitation Layer) is introduced to strengthen skip connections between the encoder and decoder. The decoder processes the context vector from the encoder, using the last frame of the encoded input as its initial input. Through an attention mechanism, it learns features to generate the target sequence, achieving spatio-temporal prediction. After each decoding step, deconvolution (upsampling) is performed to expand the feature maps, allowing the ConvLSTM cells to learn upsampled features and reconstruct future radar echo sequences. Batch normalization is also applied after each ConvLSTM cell layer.
Finally, the output sequences are stacked and dimension-transformed. A CNN is applied at the decoder’s final stage to further adjust feature dimensions and enhance representational capacity, generating the predicted output. This process iterates to produce the final radar echo extrapolation sequence.
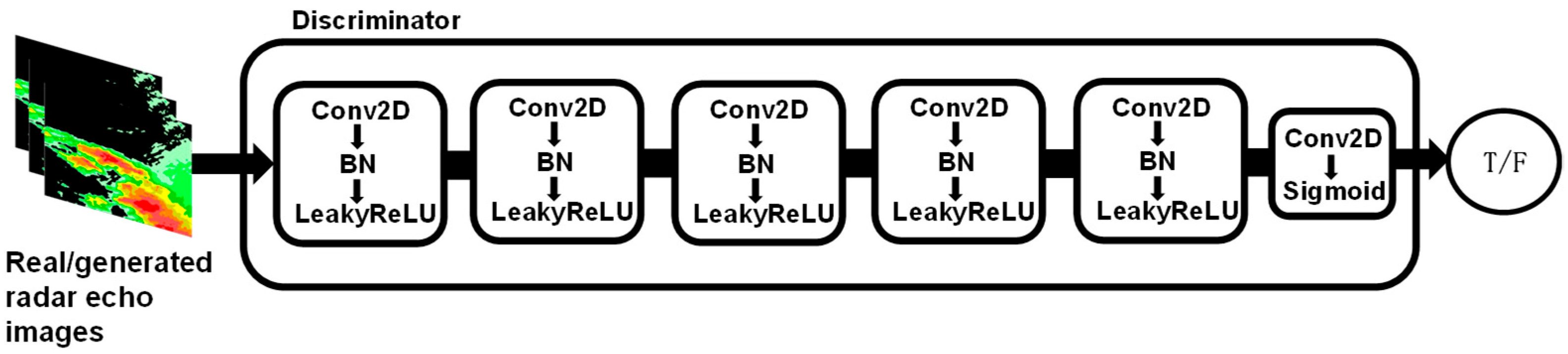
The discriminator is used to assess the authenticity of the input images. The network structure of the discriminator (
Figure 5) consists of six layers. The first to fifth layers are composed of convolutional blocks, while the sixth layer includes a Conv2D convolutional layer followed by a Sigmoid activation function layer. Each convolutional block consists of a Conv2D convolutional layer, a BatchNorm layer for batch normalization, and a LeakyReLU activation function. This structure effectively extracts local features from the echo images and continuously optimizes the generator during training, ensuring that the generated echo predictions are more consistent with the ground truth. Additionally, it enhances the accuracy and stability of long-term extrapolation.
In this study, an alternating optimization strategy will be employed for model training to achieve a dynamic game relationship between the generator and the discriminator, thereby improving the quality and authenticity of the generated results. The training process consists of the following two main stages:
Discriminator Training Stage: During the discriminator training, the generator network and the module parameters for integrating weather background variables are kept fixed. The generator network, based on its own structure and parameters, generates simulated radar echo data from specific random noise or latent features. The module that integrates weather background variables takes into account various meteorological factors and generates data by fusing weather background physical variables with radar echo data through radar cells. This fusion ensures that the generated data better aligns with actual meteorological conditions. The real radar echo data and the simulated data generated by the generator are then input into the discriminator network. The discriminator network analyzes the input data features and determines whether the data is real radar echo data or simulated data. It uses an optimization algorithm to adjust its parameters to minimize the discrimination error. After multiple iterations of training, the discriminator’s parameters are continuously optimized, and its ability to discriminate improves, ultimately enabling accurate identification of real radar echo images, thereby providing feedback for generator training.
Generator Training Stage: During the generator training, the parameters of the discriminator network are fixed. The main task of the generator network is to generate radar echo image data based on the input random noise and latent features. The radar cells are responsible for fusing weather background physical variables with the radar echo data during the generation process, thereby enhancing the authenticity and plausibility of the output data. During training, the generator continuously generates new radar echo image data and inputs these data into the discriminator with fixed parameters for evaluation. The discriminator provides feedback on the authenticity of the generated data based on its judgment criteria. The generator then uses this feedback and optimization algorithms to adjust its parameters, allowing it to generate radar echo images that are as close as possible to real radar echoes, thus improving the spatiotemporal consistency and structural integrity of the generated samples.
Through alternating training of the generator and discriminator, the discriminator continuously improves its ability to distinguish between real and generated data, while the generator progressively optimizes itself during the adversarial process, causing the generated radar echo data to approach the real echo distribution. Ultimately, this process leads the model to reach a Nash Equilibrium, where the discriminator can no longer effectively distinguish between real and generated data, ensuring that the extrapolated results maintain consistency with real radar echoes in terms of data distribution, thereby improving the accuracy of long-term sequence predictions.
3.4. Custom Loss Function
In the Generative Adversarial Network (GAN), the discriminator is a logistic regression model, and thus the loss function is defined as binary cross-entropy loss, as shown in Equation (4):
where
N is the number of samples,
is the label value,
is the predicted probability, and
is the spatial dimension weight loss function (Equation (7)). For the discriminator, when
=
0, real samples are used to train the discriminator, with
being the real value; when
=
1, generated samples are used to train the discriminator, with
being the fake value; and when
=
2, generated samples are used to train the generator, with
being the real value. The loss functions for the discriminator and generator used in this chapter are shown in Equations (5) and (6), respectively:
To further improve the extrapolation performance of long time series, this chapter independently trains the model for each forecast time step based on different physical quantity inputs, thereby constructing 20 sub-models for extrapolation at different time steps. This time-step-specific training strategy allows the model to optimize at each time step, enabling each sub-model to more accurately learn the specific echo features within its corresponding time step. This approach reduces the mutual interference between different time steps, lowers model complexity, enhances the local generalization ability, and simultaneously improves the model’s adaptability to echo evolution across different time scales.
Although this method has higher computational requirements, fine-tuning parameters and optimization strategies can significantly improve overall prediction accuracy, especially in terms of maintaining strong echoes and restoring spatial details. Finally, through extensive experiments and tests, the optimal time-step weight matrix was determined, as shown in
Table 2. The vertical dimension of this matrix represents the forecast time steps, while the horizontal dimension corresponds to different echo intensity ranges. This matrix is used to adjust the weights of each part in the loss function, further enhancing the extrapolation model’s prediction stability and accuracy across different echo intensity ranges.
3.5. Model Training
The focus of this study is to validate the performance of the radar echo extrapolation model, which incorporates weather background information, when integrating DCGAN and time-sequencing modeling methods. Therefore, in the comparative experiments, Unet and ConvLSTM models, which do not include weather background information, were selected as benchmark models to assess the improvements in extrapolation results brought about by the optimizations presented in this chapter. Considering computational constraints, no further algorithms were included for comparison to avoid introducing too many variables, which could impact the interpretability of the experimental results.
The experiments were based on MR-DCGAN, ConvLSTM, and Unet structures without the inclusion of physical quantities. Five different input encoding schemes were designed, and except for the ConvLSTM and Unet models that did not include physical quantities, the other architectures each trained 20 time-sequencing models. The experimental extrapolation models are shown in
Table 3 below:
All experiments were conducted with the same hyperparameter configuration to ensure the comparability of the results. The initial learning rate was set to 0.0001, the batch size was 5, and the maximum number of iterations was 400. To prevent overfitting, an early stopping mechanism was implemented. If the loss function was not optimized over 30 consecutive epochs, the training process was prematurely terminated, and the best model parameters were saved. The Adam optimizer was used during the optimization process to further improve the model’s convergence and stability.
3.6. Evaluation Indicators
A binary classification model based on predefined thresholds, commonly used in meteorological operations, is employed to assess the model’s performance. The reflectivity thresholds are selected as 20, 30, and 35 dBZ, with a forecast time interval of 6 min. The model’s ability to correctly predict is evaluated using the Probability of Detection (POD), the False Alarm Rate (FAR) is used to assess erroneous predictions of events that did not occur, and the Critical Success Index (CSI) is used to measure the overall performance of the model (Equation (8)).
In Equation (8), each value is calculated from the confusion matrix (
Table 4). The True Positives (TP) represent the points where both the predicted value and the actual value exceed the threshold, False Negatives (FN) represent the points where the predicted value exceeds the threshold but the actual value does not, False Positives (FP) represent the points where the predicted value is below the threshold but the actual value exceeds the threshold, and True Negatives (TN) represent the points where both the predicted and actual values are below the threshold.
By comparing the predicted values with the observed values for each grid point, the classification for each point is determined, and the evaluation metrics are then calculated. The methods for calculating POD, FAR, and CSI are shown in Equation (8). Higher values of POD and CSI indicate more accurate predictions, while a lower FAR value indicates better prediction accuracy.
To more comprehensively evaluate the model, the Structural Similarity (SSIM) index was further introduced to assess the visual quality and structural preservation capabilities between predicted radar echo images and actual observational data. SSIM integrates luminance, contrast, and structural information of images. By calculating the similarity between predicted and real images across these features, it quantifies the model’s ability to retain fine-grained echo details. The SSIM formula is presented in Equation (9):
where
x and
y denote the real radar echo image and predicted echo image, respectively;
and
represent the pixel-wise means of
x and
y;
and
are their pixel variances;
is the pixel covariance between them; constants
C1 and
C2 are primarily used to enhance numerical stability.
4. Model Evaluation
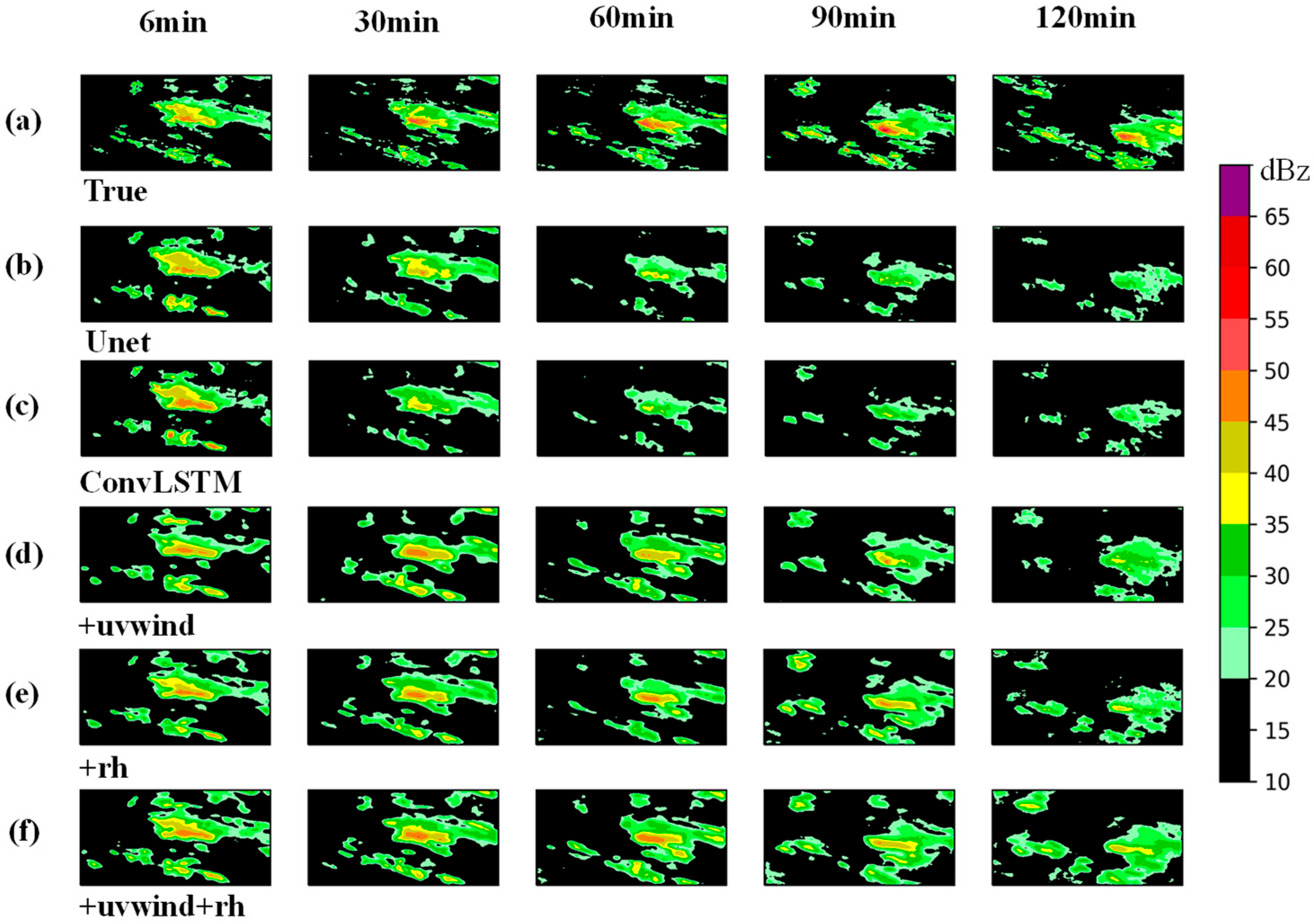
In this study, a total of 20 radar echo extrapolation models were trained based on three network architectures—Unet, ConvLSTM, and MR-DCGAN—and five different input encoding schemes. These models were then evaluated using a testing dataset to perform radar echo extrapolation and assess model performance.
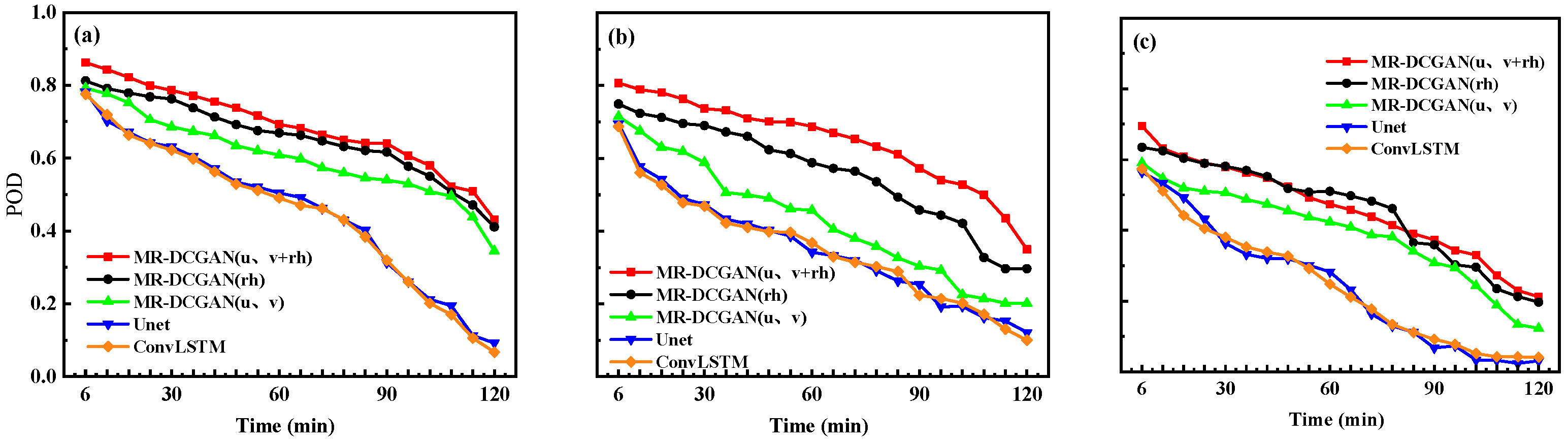
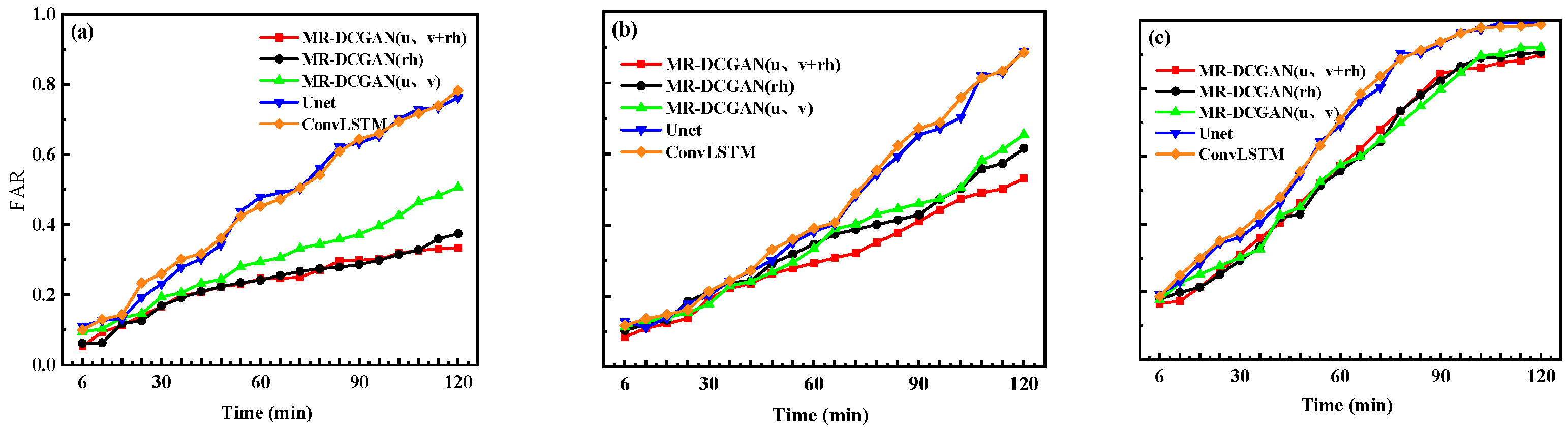
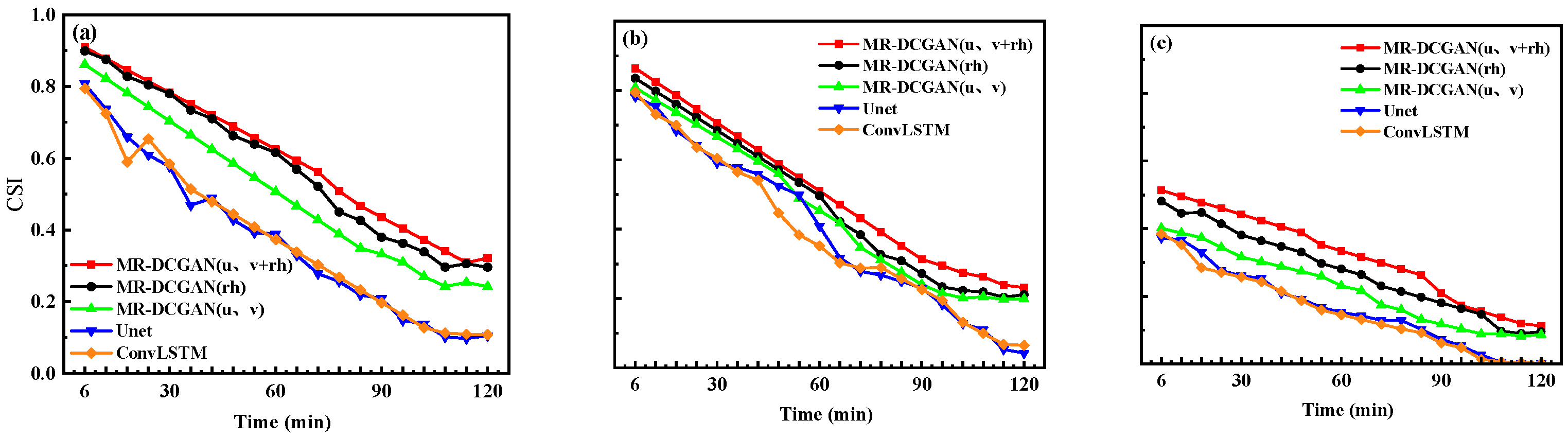
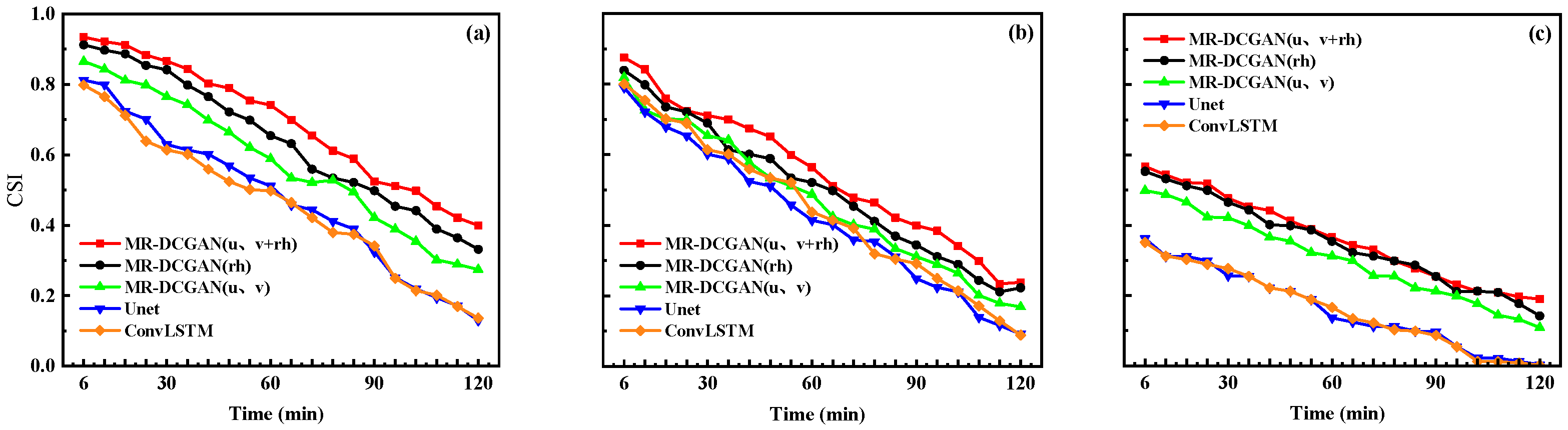
To comprehensively evaluate the extrapolation performance, radar echo intensity thresholds of 20, 30, and 35 dBZ were selected. For each threshold, the Probability of Detection (POD), False Alarm Rate (FAR), and Critical Success Index (CSI) were calculated for the different models on the test set.
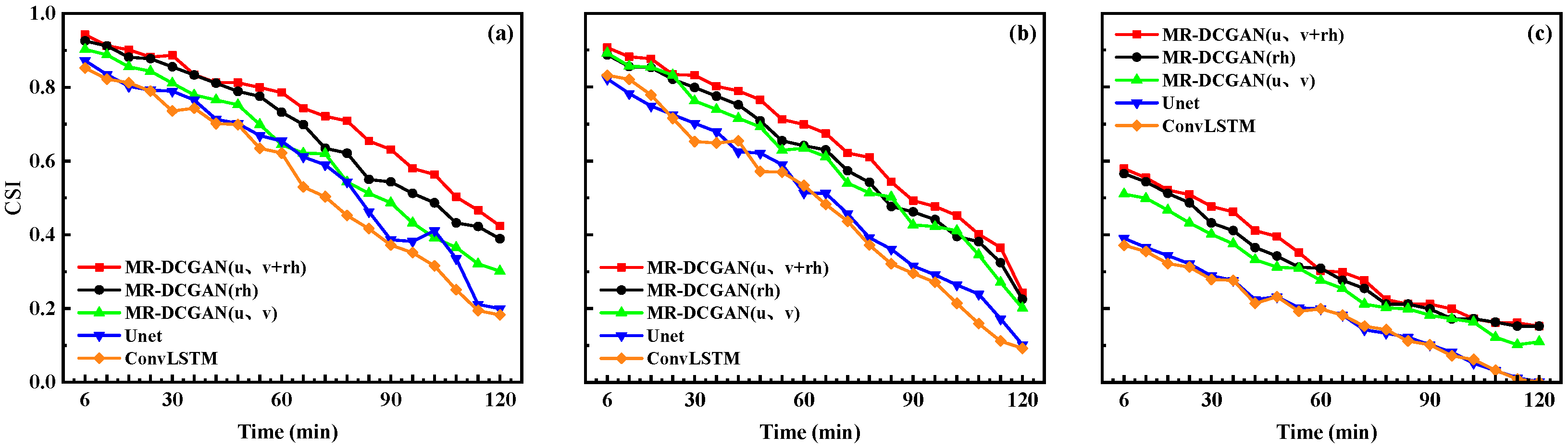
Figure 6,
Figure 7 and
Figure 8 illustrate the extrapolation performance metrics over successive 6 min intervals for models trained with different input encodings based on the MR-DCGAN, Unet, and ConvLSTM architectures (without incorporating physical variables).
Table 5 further presents the average values of POD, FAR, and CSI for the 120 min extrapolation horizon.
As shown in
Figure 6,
Figure 7 and
Figure 8, and
Table 5, with increasing radar echo intensity thresholds, both POD and CSI exhibit a declining trend, while FAR increases. In comparison to the Unet and ConvLSTM models, the extrapolation models trained with MR-DCGAN demonstrate significant improvements in CSI and POD across all thresholds, along with a marked reduction in FAR. Specifically, the CSI values of the MR-DCGAN model increase by 18.59%, 8.76%, and 11.28% over the Unet and ConvLSTM models at thresholds of 20 dBZ, 30 dBZ, and 35 dBZ, respectively. The corresponding improvements in POD are 19.46%, 19.21%, and 19.18%, while FAR is reduced by 19.85%, 11.48%, and 9.88%, respectively. These results indicate that incorporating physical variables can effectively enhance the accuracy of radar echo extrapolation and improve the model’s predictive capability under various echo intensity levels.
According to the results summarized in
Table 4, the MR-DCGAN model incorporating three physical variables (
u,
v wind components, and relative humidity) significantly outperforms the models without physical variable integration across different radar reflectivity thresholds. Specifically, the Critical Success Index (CSI) and Probability of Detection (POD) show average improvements of 16.75% and 24.75%, respectively, while the False Alarm Ratio (FAR) decreases by an average of 15.36%.
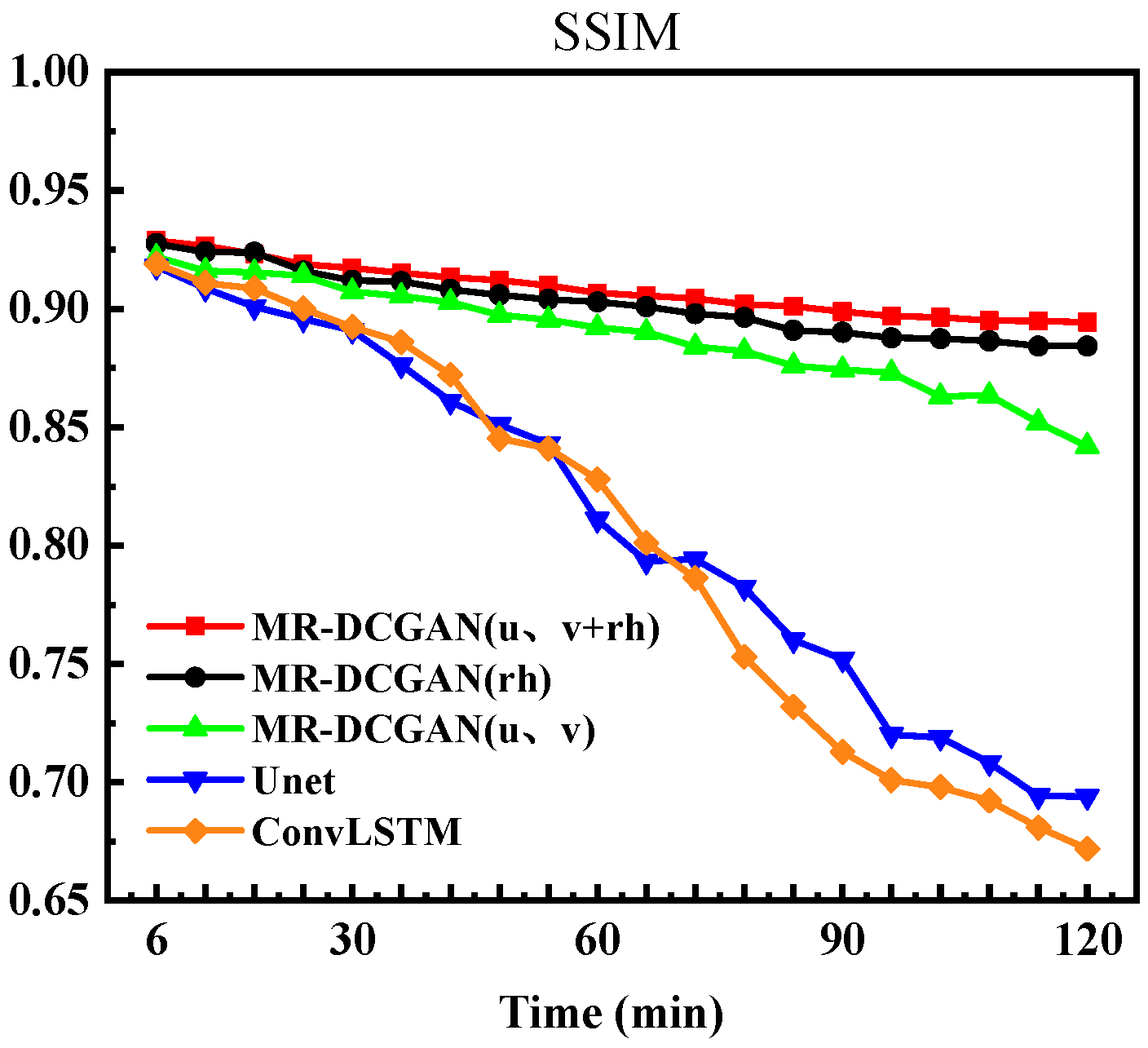
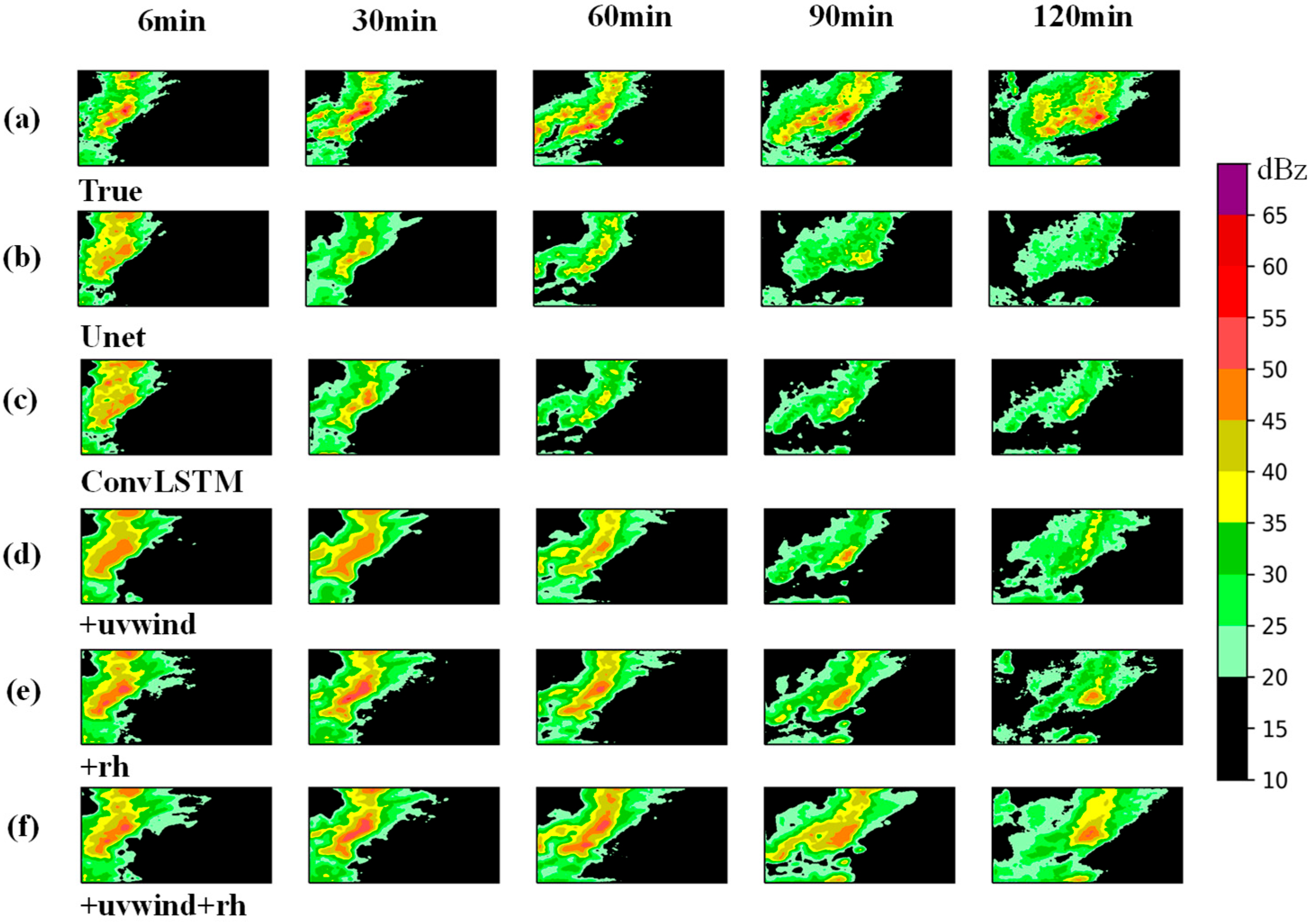
To further evaluate the visual quality of predicted images, this study introduced the SSIM metric for analysis. The variation curves of SSIM values over 20 time steps are presented in
Figure 9. As shown in the figure, the SSIM values of all models gradually decline over time. Notably, the MR-DCGAN model proposed in this research exhibits a slower and more stable decay throughout the extrapolation process, with its superiority becoming particularly pronounced in the latter half of the prediction horizon. Among all configurations, the model integrating
u/
v and rh physical variables demonstrates the optimal performance.
These findings indicate that integrating complex physical variables can effectively enhance the model’s extrapolation capability for varying reflectivity intensities, leading to predictions that are more physically consistent and spatiotemporally coherent.
6. Comparative Experiment
To better demonstrate the advantages of the MR-DCGAN architecture in radar echo extrapolation, a comparative experiment was conducted by selecting the MR-ConvLSTM [
43] architecture for comparison with the proposed architecture in this paper. The comparative model adopted was the MR-ConvLSTM (
u,
v + rh) model with the best test performance, while the MR-DCGAN (
u,
v + rh) model with the optimal performance in this study was also chosen for intuitive result presentation. The test dataset was the same as the echo extrapolation model’s test data for the Cangzhou region used in this paper. To eliminate the influence of different data dimensions, all selected data were uniformly normalized, which effectively improved the comparability of the data and the stability of model training, ensuring the scientificity and rigor of testing the generalization ability of the MR-DCGAN (
u,
v + rh) model.
In the comparative experiment, POD (Probability of Detection), FAR (False Alarm Rate), CSI (Critical Success Index), and SSIM (Structural Similarity Index) were selected as evaluation metrics. These metrics not only enable quantitative evaluation of the models’ precipitation prediction capabilities but also comprehensively reflect the similarity between the predicted images and the real echo images. By using these four numerical indicators, the extrapolation performance of the models can be tested more objectively.
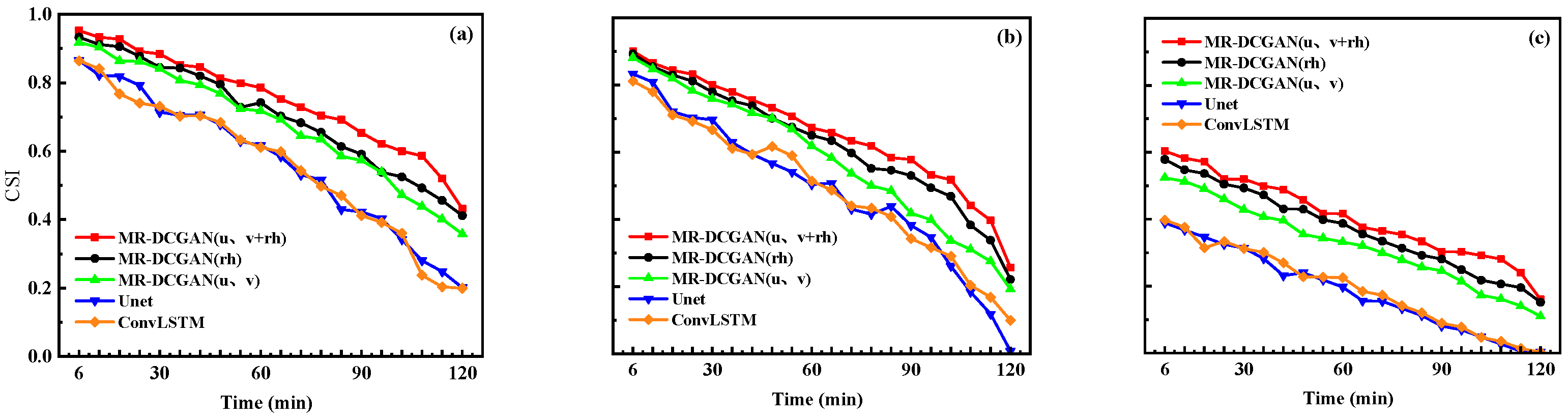
According to
Table 6, the CSI of the MR-DCGAN (
u,
v + rh) model was on average 4.08%, 3.79%, and 3.15% higher than that of the MR-ConvLSTM (
u,
v + rh) model under the reflectivity thresholds of 20 dBZ, 30 dBZ, and 35 dBZ, respectively. The POD increased by 2.24%, 1.72%, and 2.99%, while the FAR decreased by 2.39%, 1.47%, and 4.19%. These experimental data demonstrate that the MR-DCGAN (
u,
v + rh) model outperforms the MR-ConvLSTM (
u,
v + rh) model in radar echo extrapolation tasks under the same test dataset. It can improve the prediction rate while reducing the false alarm rate, further indicating that the MR-DCGAN (
u,
v + rh) model has better extrapolation performance.
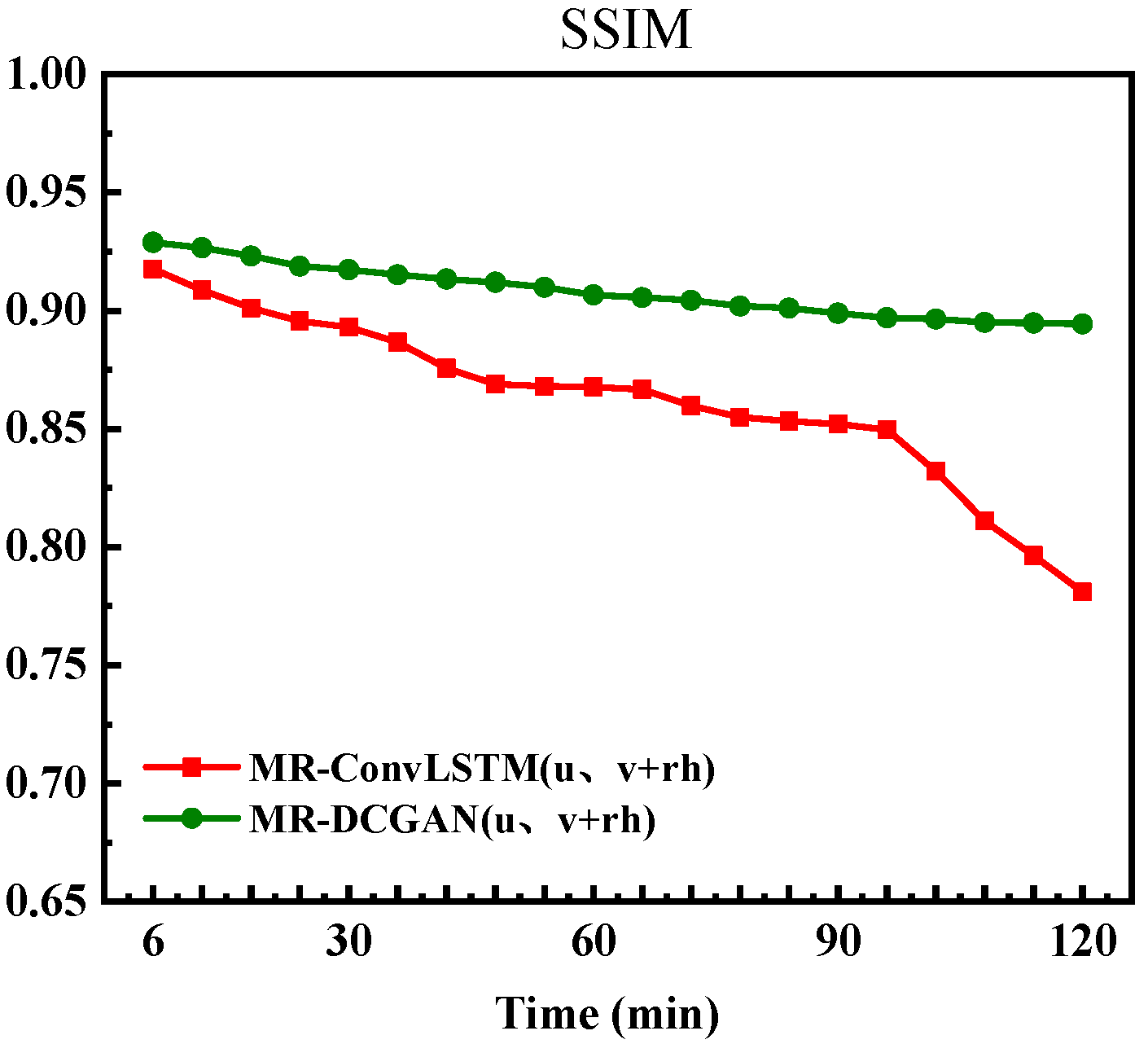
Figure 17 shows the variation trend of the Structural Similarity Index (SSIM) for the two models in radar echo prediction tasks. It can be seen that the decay process of the SSIM index is relatively smooth for both the MR-DCGAN (
u,
v + rh) and MR-ConvLSTM (
u,
v + rh) models, indicating that both models can maintain a certain structural similarity during prediction. In the initial stage of prediction, the echo images generated by the MR-DCGAN (
u,
v + rh) model exhibit higher similarity to the real echoes, suggesting that this model has better structural fidelity in short-term prediction.
In summary, the MR-DCGAN (u, v + rh) model exhibits superior performance in short-term prediction and demonstrates strong generalization capabilities across various time intervals in extrapolation tasks. It can adapt more stably to diverse meteorological conditions, thereby enhancing the reliability and applicability of radar echo prediction.