Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO
Abstract
1. Introduction
2. Correction Analysis
2.1. PPP-B2b Correction Accuracy Analysis
2.2. PPP-B2b Orbit Accuracy Analysis
2.2.1. Satellite Orbit Error Evaluation Methods
2.2.2. Satellite Orbit Accuracy Analysis
2.3. PPP-B2b Clock Error Accuracy Analysis
2.3.1. Evaluation Method for Satellite Clock Error
2.3.2. Analysis of Satellite Clock Error Accuracy
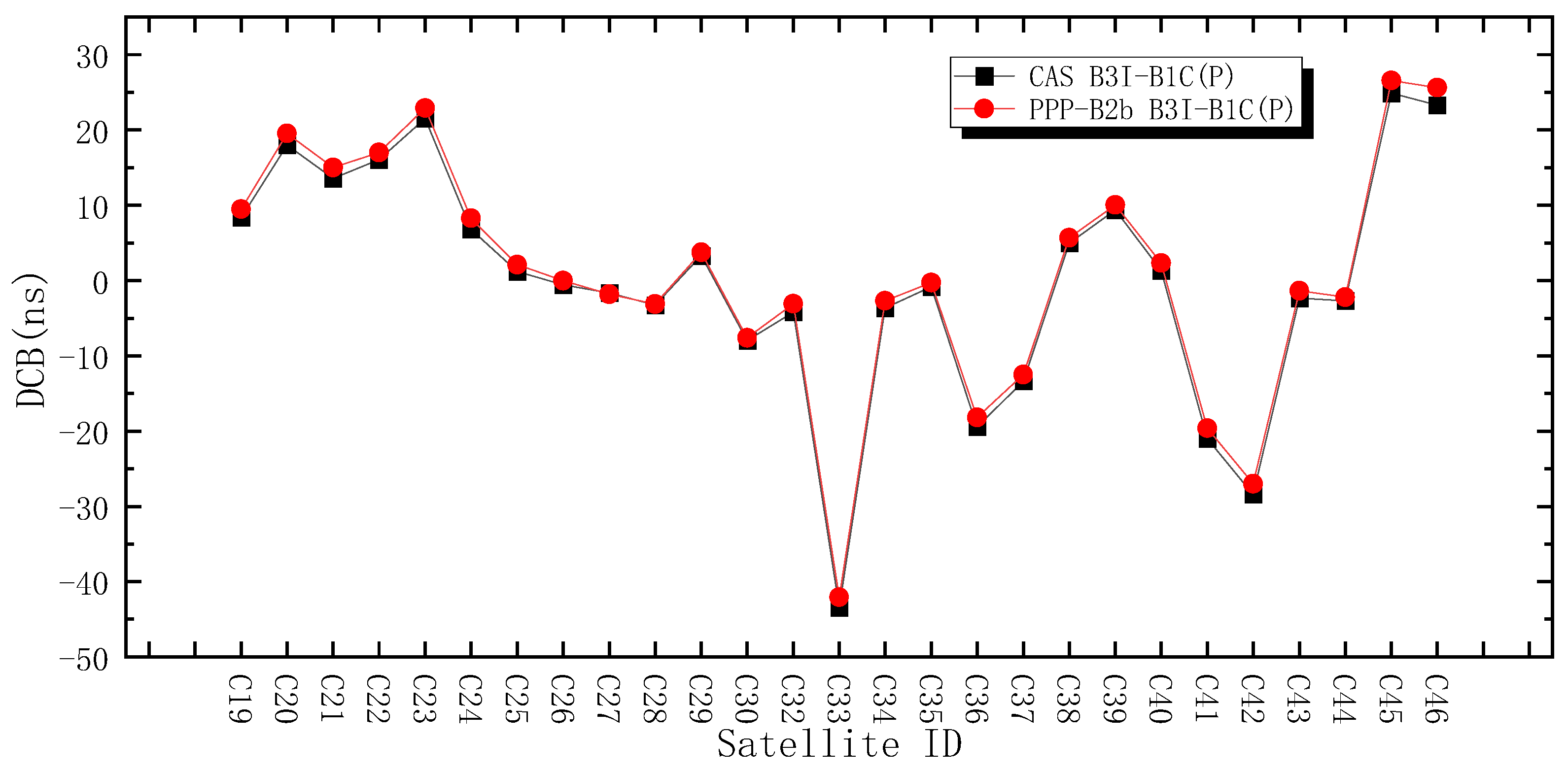
2.4. PPP-B2b Code Deviation Accuracy
3. PPP-B2b Time Comparison
3.1. PPP-B2b Time Comparison Processing Strategy
3.2. PPP-B2b Time Comparison Analysis
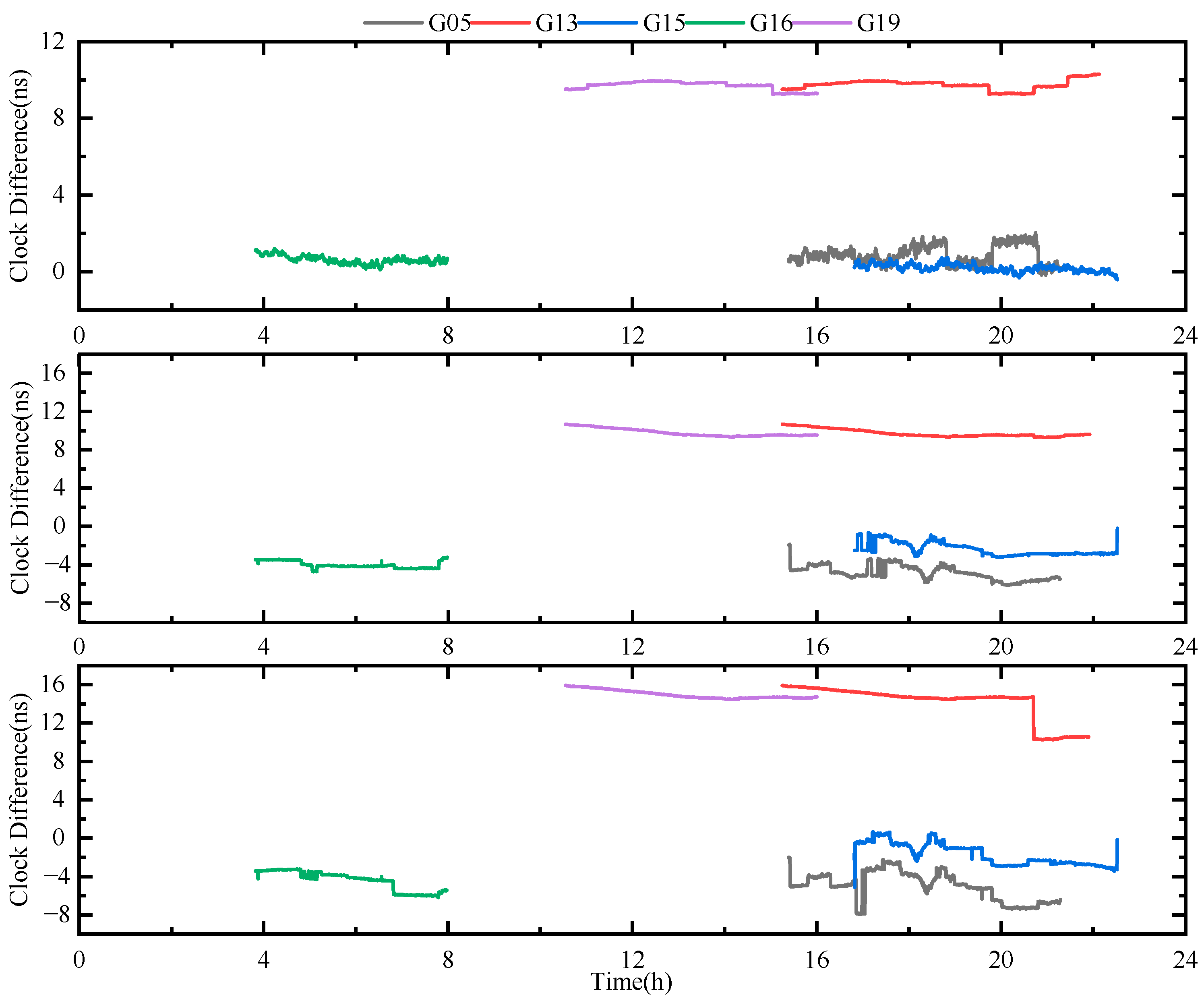
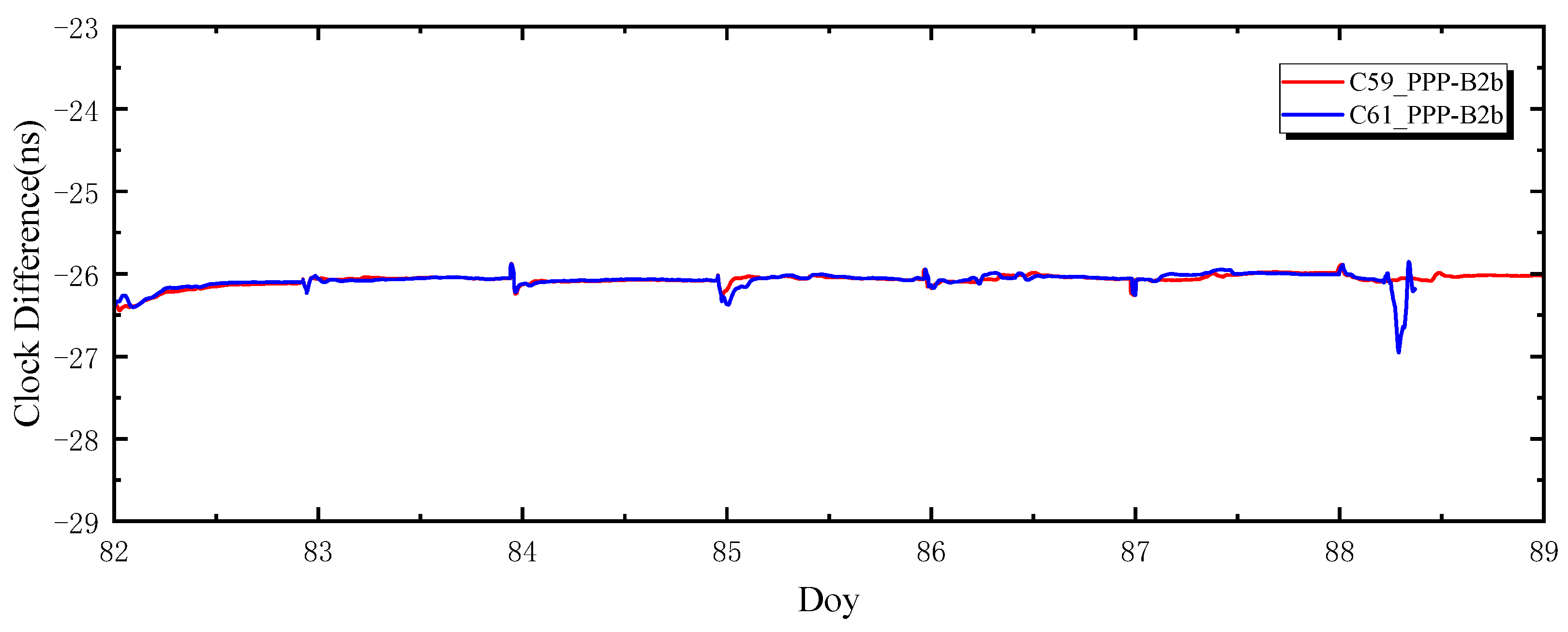
3.2.1. Zero-Baseline PPP-B2b Time Comparison
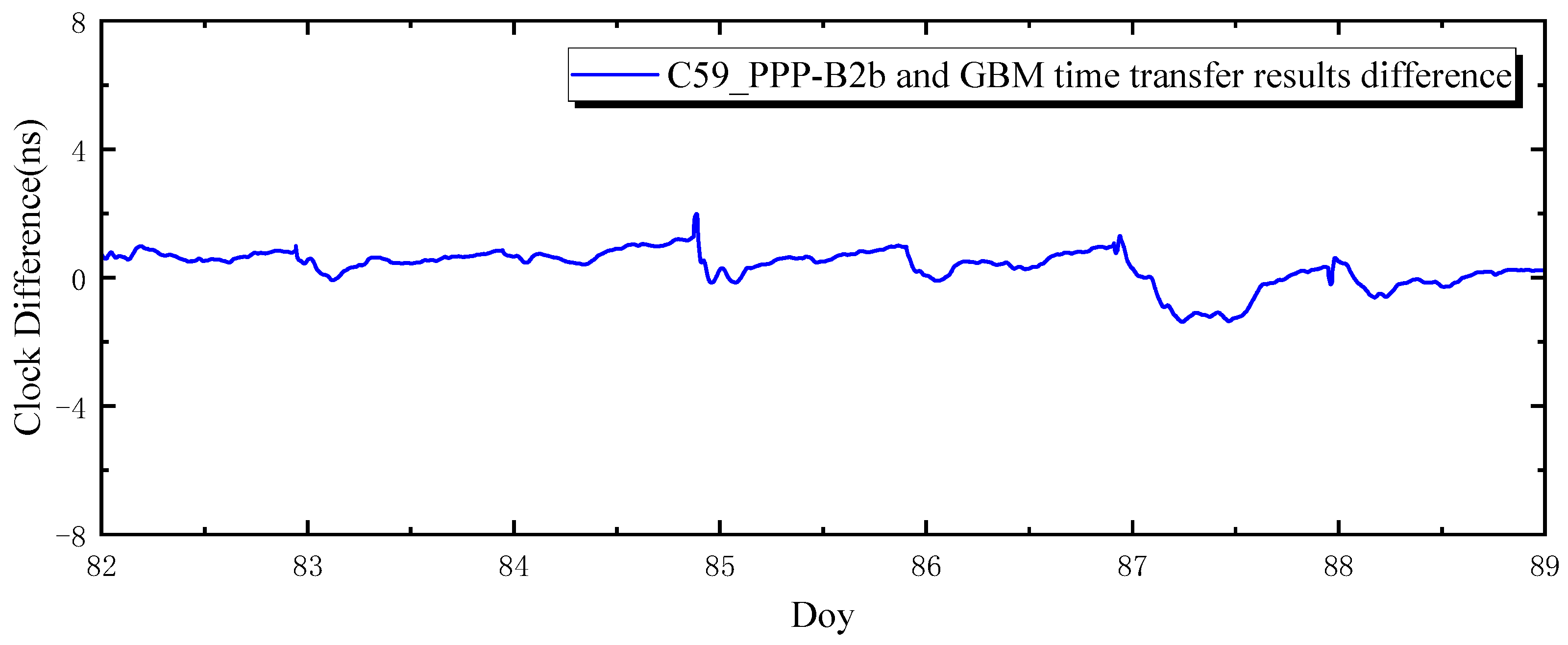
3.2.2. Long-Baseline PPP-B2b Time Comparison
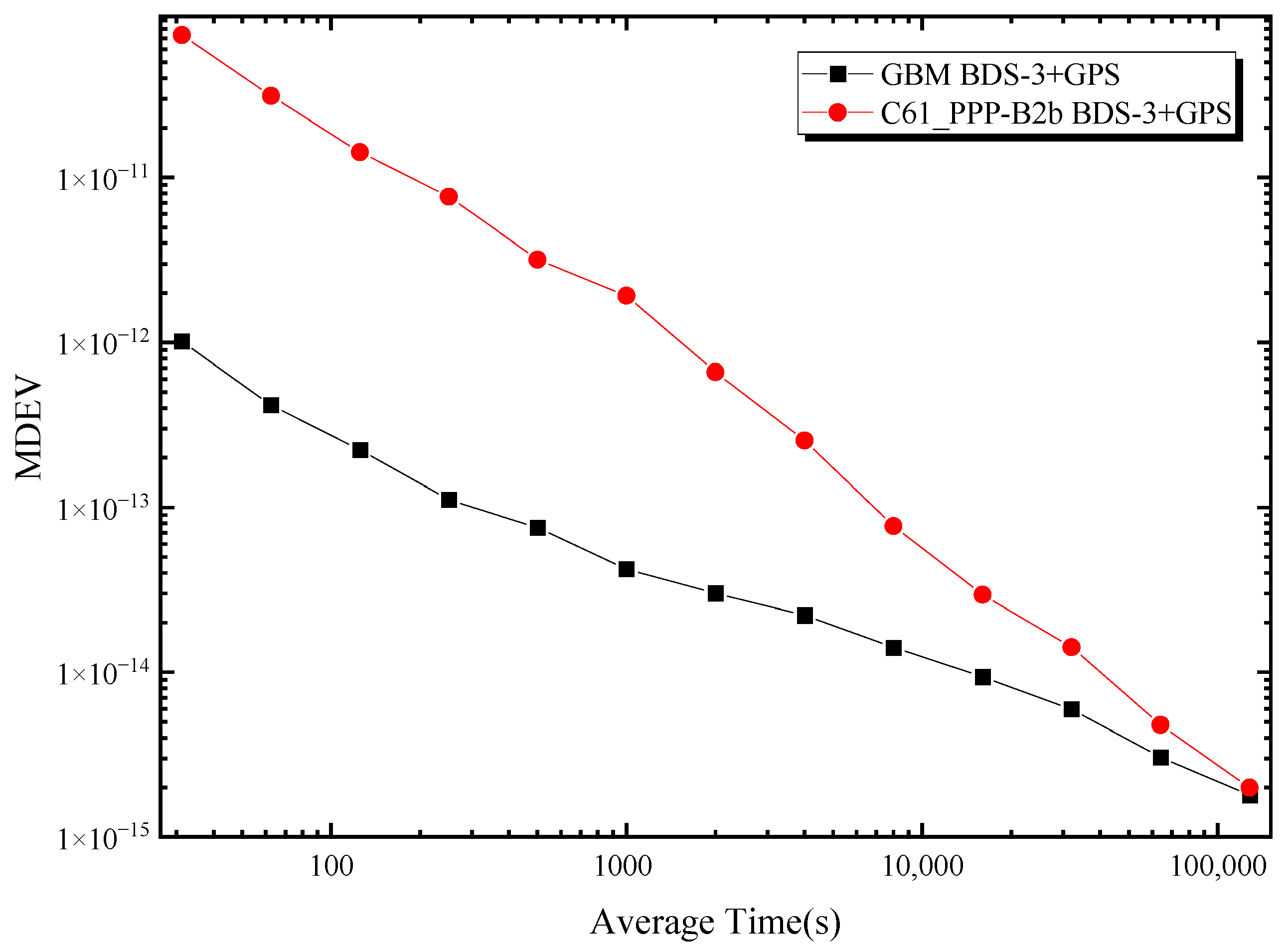
3.2.3. Comparison of Time Transfer Links
4. PPP-B2b Positioning
4.1. PPP-B2b Positioning Processing Strategy
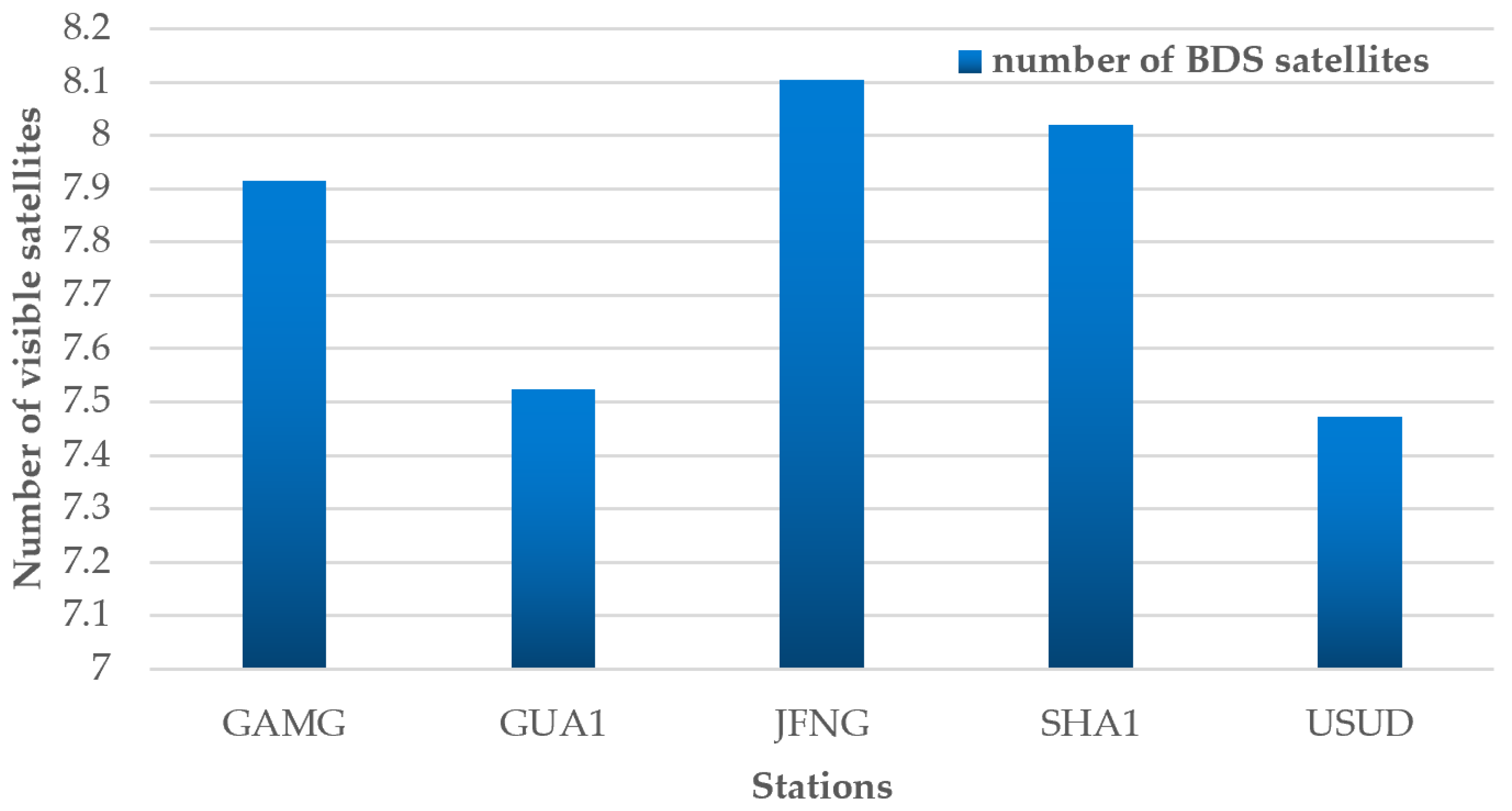
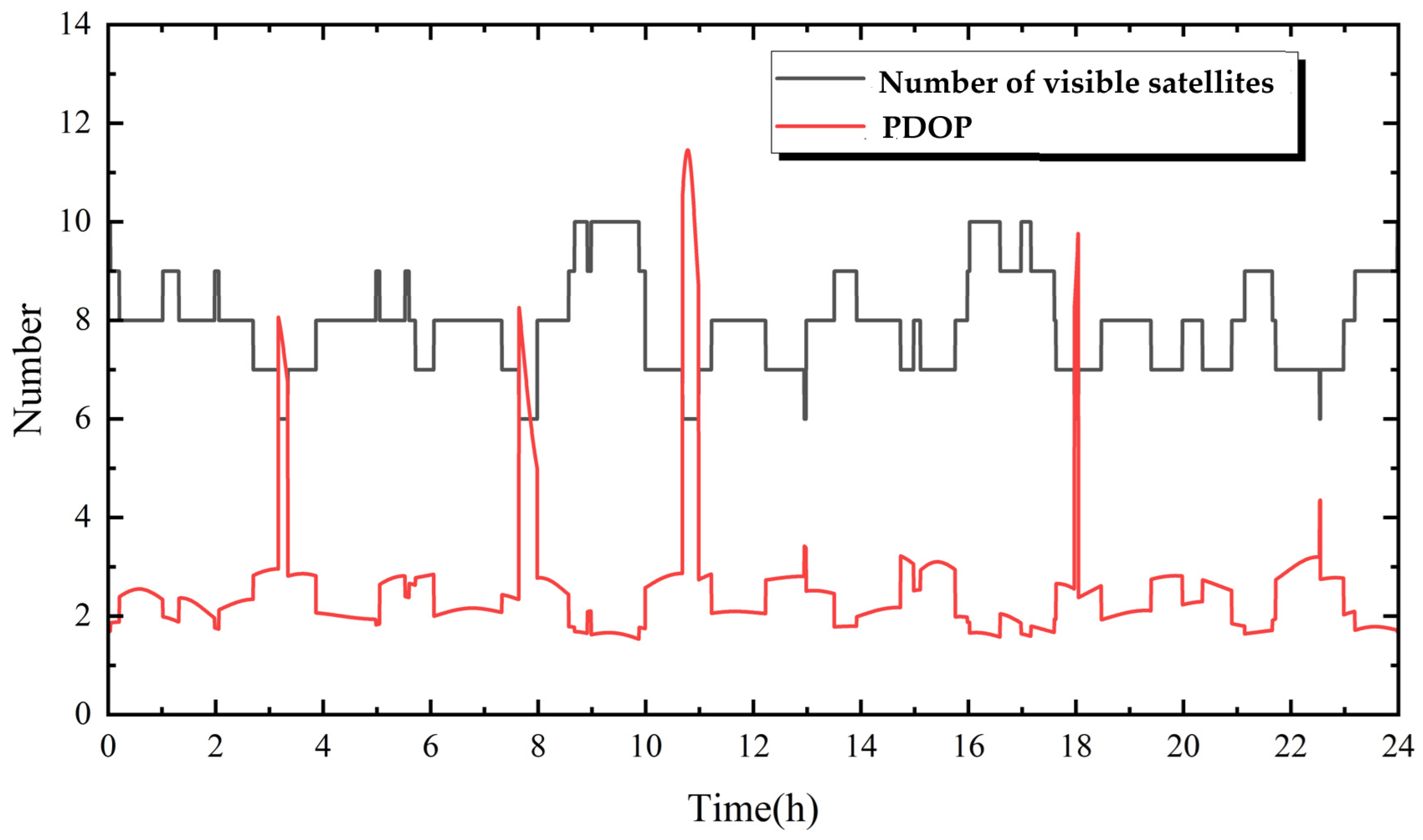
4.2. BDS-3 PPP-B2b Positioning Research
4.2.1. BDS-3 PPP-B2b Static Positioning
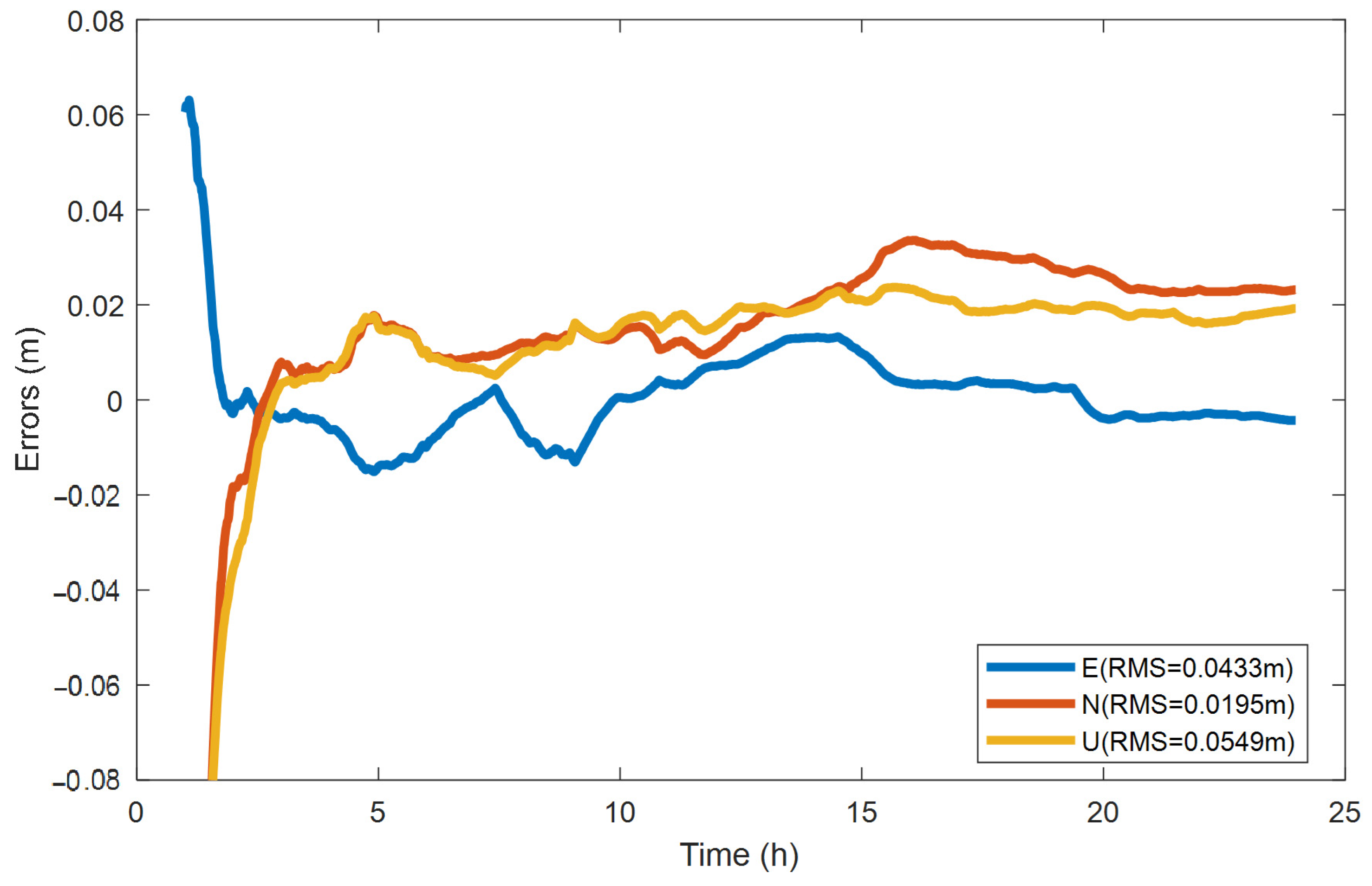
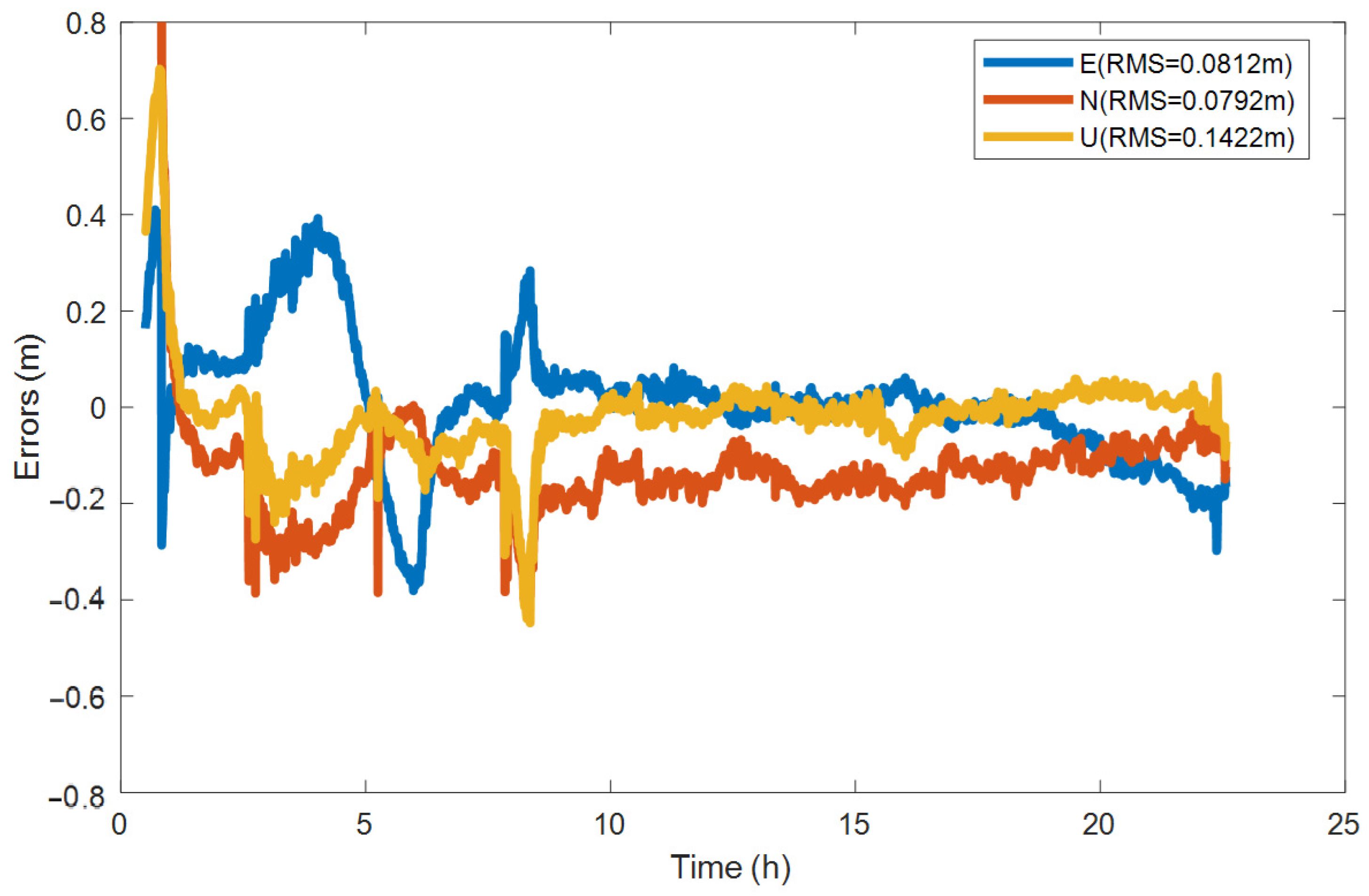
4.2.2. BDS-3 PPP-B2b Kinematic Positioning
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, B.; Ai, Q.; Yuan, Y. Analysis of Precise Orbit Determination of BDS-3 MEO and IGSO Satellites Based on Several Dual-Frequency Measurement Combinations. Remote Sens. 2022, 14, 6030. [Google Scholar]
- Yang, Y.; Liu, L.; Li, J.; Yang, Y.; Ren, X. Featured services and performance of BDS-3. Sci. Bull. 2021, 66, 2135–2143. [Google Scholar]
- Zhao, Q.; Guo, J.; Liu, S.; Tao, J.; Hu, Z.; Chen, G. A variant of raw observation approach for BDS/GNSS precise point positioning with fast integer ambiguity resolution. Satell. Navig. 2021, 2, 29. [Google Scholar] [CrossRef]
- de Oliveira, P.S.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef]
- Goss, A.; Hernández-Pajares, M.; Schmidt, M.; Roma-Dollase, D.; Seitz, F. High-Resolution Ionosphere Corrections for Single-Frequency Positioning. Remote Sens. 2020, 13, 12. [Google Scholar]
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document Open Service Signal B2b (Version 1.0), China Satellite Navigation Office: Beijing, China, July 2020. Available online: http://www.beidou.gov.cn/xt/gfxz/202008/P020230516558683155109.pdf (accessed on 6 July 2025).
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document Precise Point Positioning Service Signal PPP-B2b (Version 1.0), China Satellite Navigation Office: Beijing, China, July 2020. Available online: http://www.beidou.gov.cn/xt/gfxz/202008/P020230516574071340728.pdf (accessed on 6 July 2025).
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and performance analysis of precise time transfer based on BDS triple-frequency un-combined observations. J. Geod. 2019, 93, 837–847. [Google Scholar] [CrossRef]
- Yang, H.; Ren, X.; Liu, M.; Zhang, X. Dual-frequency to five-frequency real-time precise point positioning using new BDS-3 PPP-B2b service. Earth Planets Space 2024, 76, 82. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Han, J. Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations. GPS Solut. 2020, 24, 40. [Google Scholar] [CrossRef]
- Xu, W.; Yan, C.; Chen, J. Performance evaluation of BDS-2/BDS-3 combined precise time transfer with B1I/B2I/B3I/B1C/B2a five-frequency observations. GPS Solut. 2022, 26, 80. [Google Scholar] [CrossRef]
- Ge, Y.; Zhou, F.; Liu, T.; Qin, W.; Wang, S.; Yang, X. Enhancing real-time precise point positioning time and frequency transfer with receiver clock modeling. GPS Solut. 2018, 23, 20. [Google Scholar] [CrossRef]
- Kazmierski, K.; Zajdel, R.; Sośnica, K. Evolution of orbit and clock quality for real-time multi-GNSS solutions. GPS Solut. 2020, 24, 111. [Google Scholar] [CrossRef]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling. Remote Sens. 2019, 11, 347. [Google Scholar]
- Wang, L.; Li, Z.; Ge, M.; Neitzel, F.; Wang, Z.; Yuan, H. Validation and Assessment of Multi-GNSS Real-Time Precise Point Positioning in Simulated Kinematic Mode Using IGS Real-Time Service. Remote Sens. 2018, 10, 337. [Google Scholar]
- Wang, S.L.; Ge, Y.L.; Meng, X.L.; Shen, P.L.; Wang, K.D.; Ke, F.Y. Modelling and Assessment of Single-Frequency PPP Time Transfer with BDS-3 B1I and B1C Observations. Remote Sens. 2022, 14, 1146. [Google Scholar] [CrossRef]
- Tao, J.; Liu, J.; Hu, Z.; Zhao, Q.; Chen, G.; Ju, B. Initial Assessment of the BDS-3 PPP-B2b RTS compared with the CNES RTS. GPS Solut. 2021, 25, 131. [Google Scholar] [CrossRef]
- Sun, S.; Wang, M.; Liu, C.; Meng, X.; Ji, R. Long-term performance analysis of BDS-3 precise point positioning (PPP-B2b) service. GPS Solut. 2023, 27, 69. [Google Scholar] [CrossRef]
- Ren, Z.; Gong, H.; Peng, J.; Tang, C.; Huang, X.; Sun, G. Performance assessment of real-time precise point positioning using BDS PPP-B2b service signal. Adv. Space Res. 2021, 68, 3242–3254. [Google Scholar] [CrossRef]
- Zhang, R.; He, Z.; Ma, L.; Xiao, G.; Guang, W.; Ge, Y.; Zhang, X.; Zhang, J.; Tang, J.; Li, X. Analysis of BDS-3 PPP-B2b Positioning and Time Transfer Service. Remote Sens. 2022, 14, 2769. [Google Scholar] [CrossRef]
- Nie, Z.; Xu, X.; Wang, Z.; Du, J. Initial Assessment of BDS PPP-B2b Service: Precision of Orbit and Clock Corrections, and PPP Performance. Remote Sens. 2021, 13, 2050. [Google Scholar] [CrossRef]
- Dai, W.; Liu, N.; Zhang, Z.; Tang, C.; Zhang, Z.; Yang, Y.; Pan, L. BDS-3/GPS uncombined real-time PPP with PPP-B2b precise products: Modeling and its long-term performance evaluation. Adv. Space Res. 2025, 75, 7212–7225. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document Open Service Signal B1I (Version 3.0), China Satellite Navigation Office: Beijing, China, February 2019. Available online: http://www.beidou.gov.cn/xt/gfxz/201902/P020190227593621142475.pdf (accessed on 6 July 2025).
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document Open Service Signal B3I (Version 1.0), China Satellite Navigation Office: Beijing, China, February 2018. Available online: http://www.beidou.gov.cn/xt/gfxz/201802/P020180209623601401189.pdf (accessed on 6 July 2025).
- Tang, J.; Lyu, D.; Zeng, F.; Ge, Y.; Zhang, R. Modelling and Assessment of BDS-3 Real-Time Precise Point Positioning Time Transfer Based on PPP-B2b Service. Math. Probl. Eng. 2022, 2022, 4054179. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Zhang, M. Comprehensive Analyses of PPP-B2b Performance in China and Surrounding Areas. Remote Sens. 2022, 14, 643. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1C (Version 1.0); ChinaSatellite Navigation Office: Beijing, China, December 2017. Available online: http://www.beidou.gov.cn/xt/gfxz/201712/P020171226741342013031.pdf (accessed on 6 July 2025).
- Xu, Y.; Yang, Y.; Li, J. Performance evaluation of BDS-3 PPP-B2b precise point positioning service. GPS Solut. 2021, 25, 142. [Google Scholar] [CrossRef]
- NTSCCAS. National Time Service Center of the Chinese Academy of Sciences, Global Ground Station GPS Navigation Information Data (Jilin Station). 1.0; National Space Science Data Center: Beijing, China, 2025. [Google Scholar]
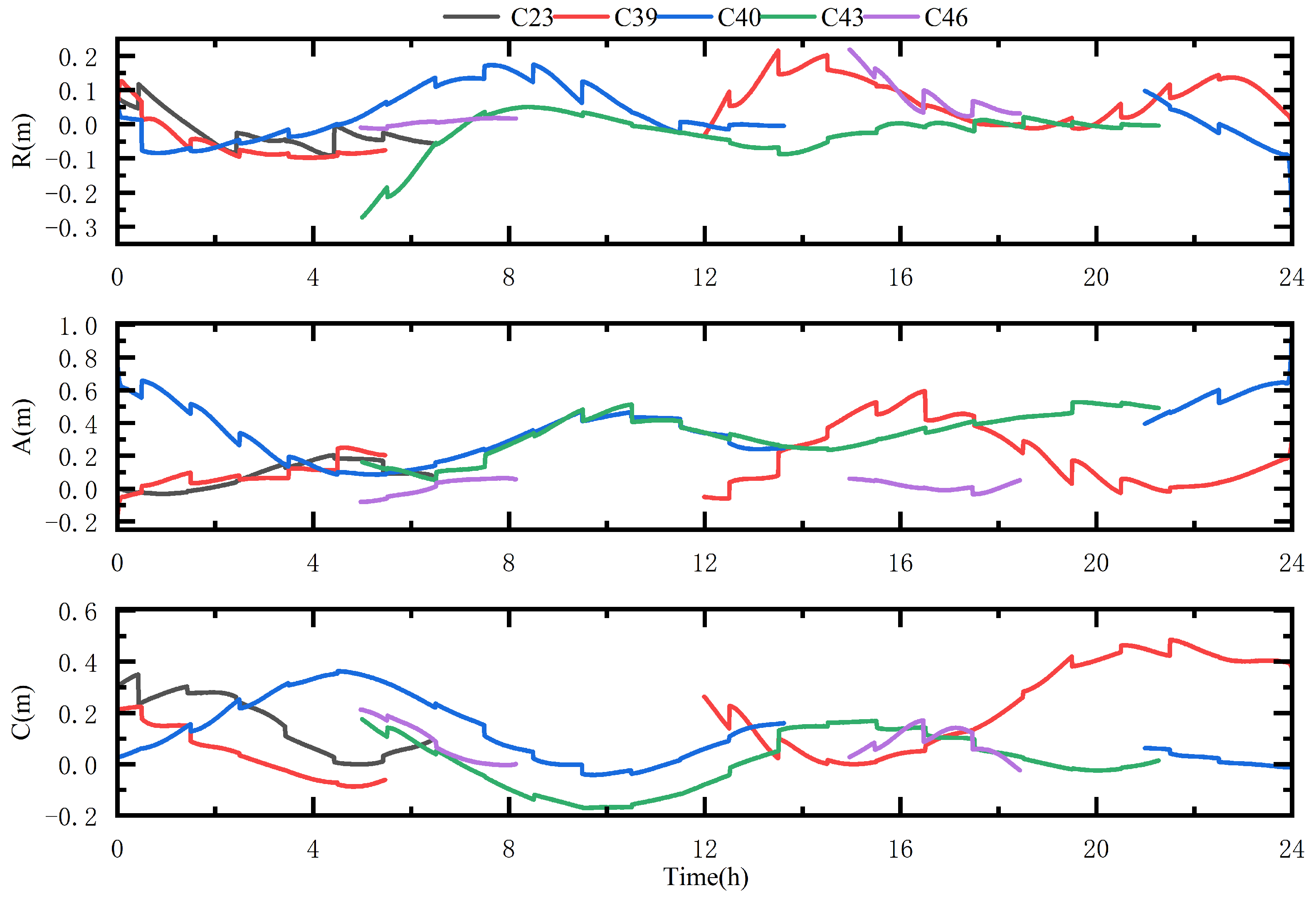
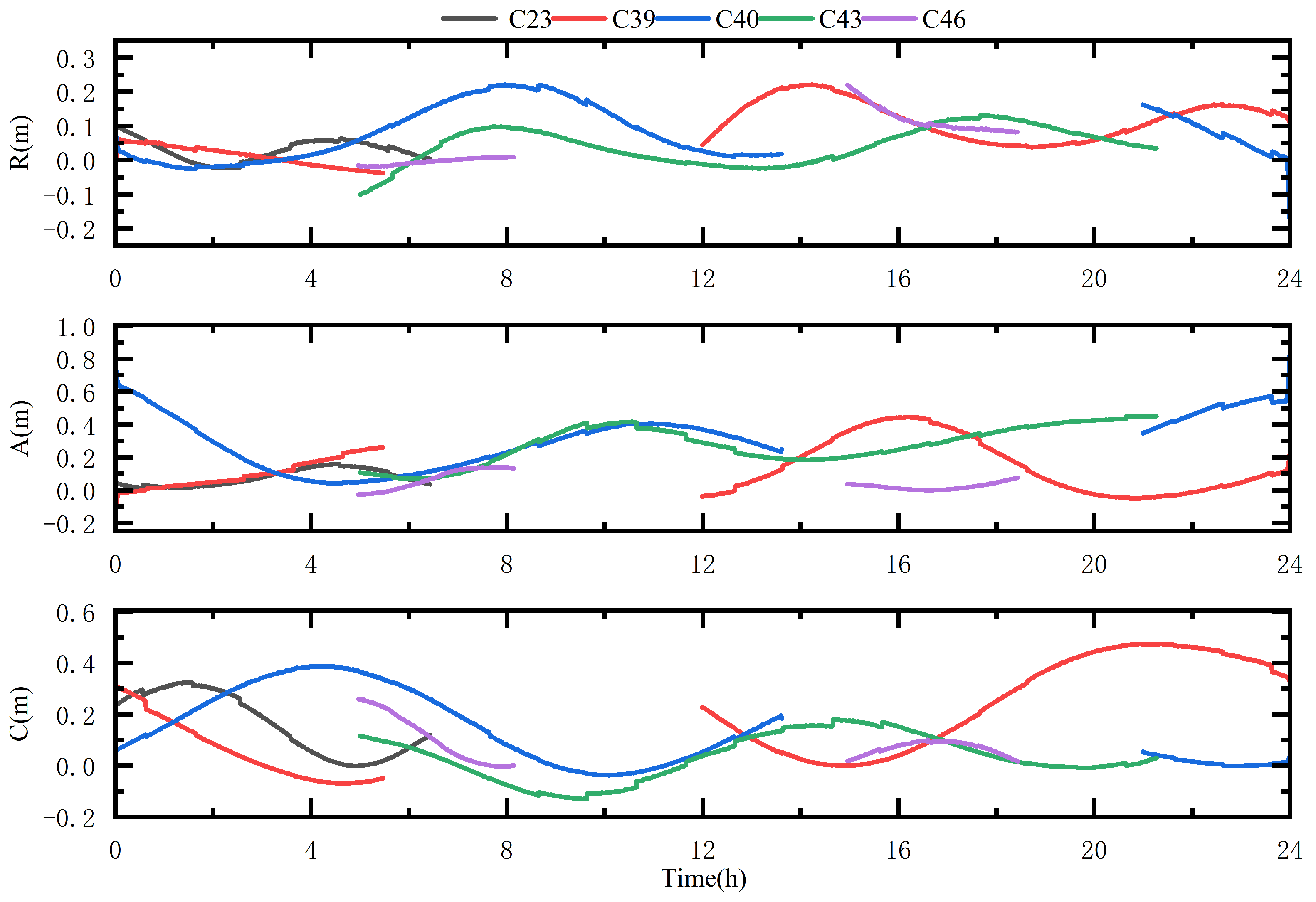


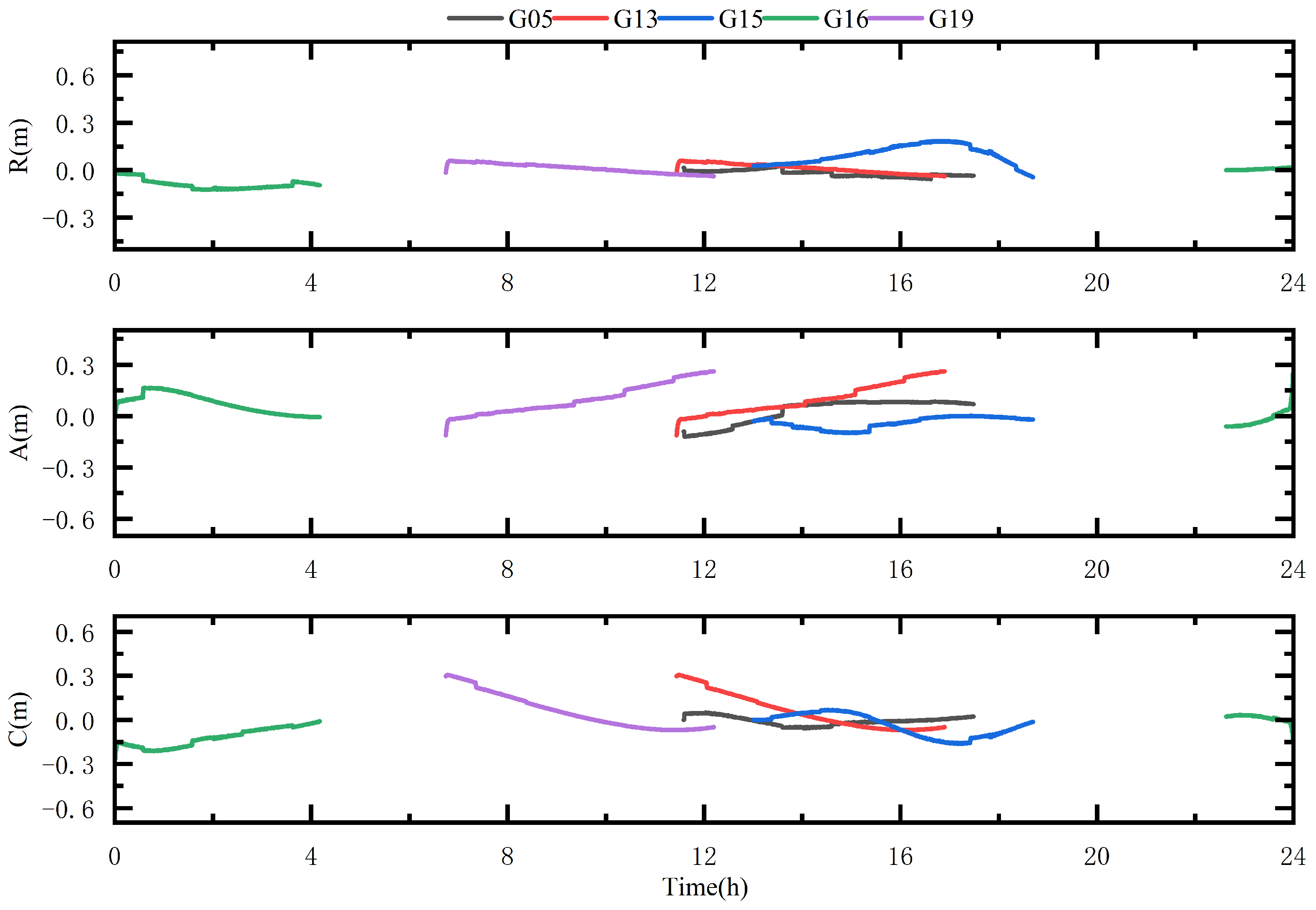
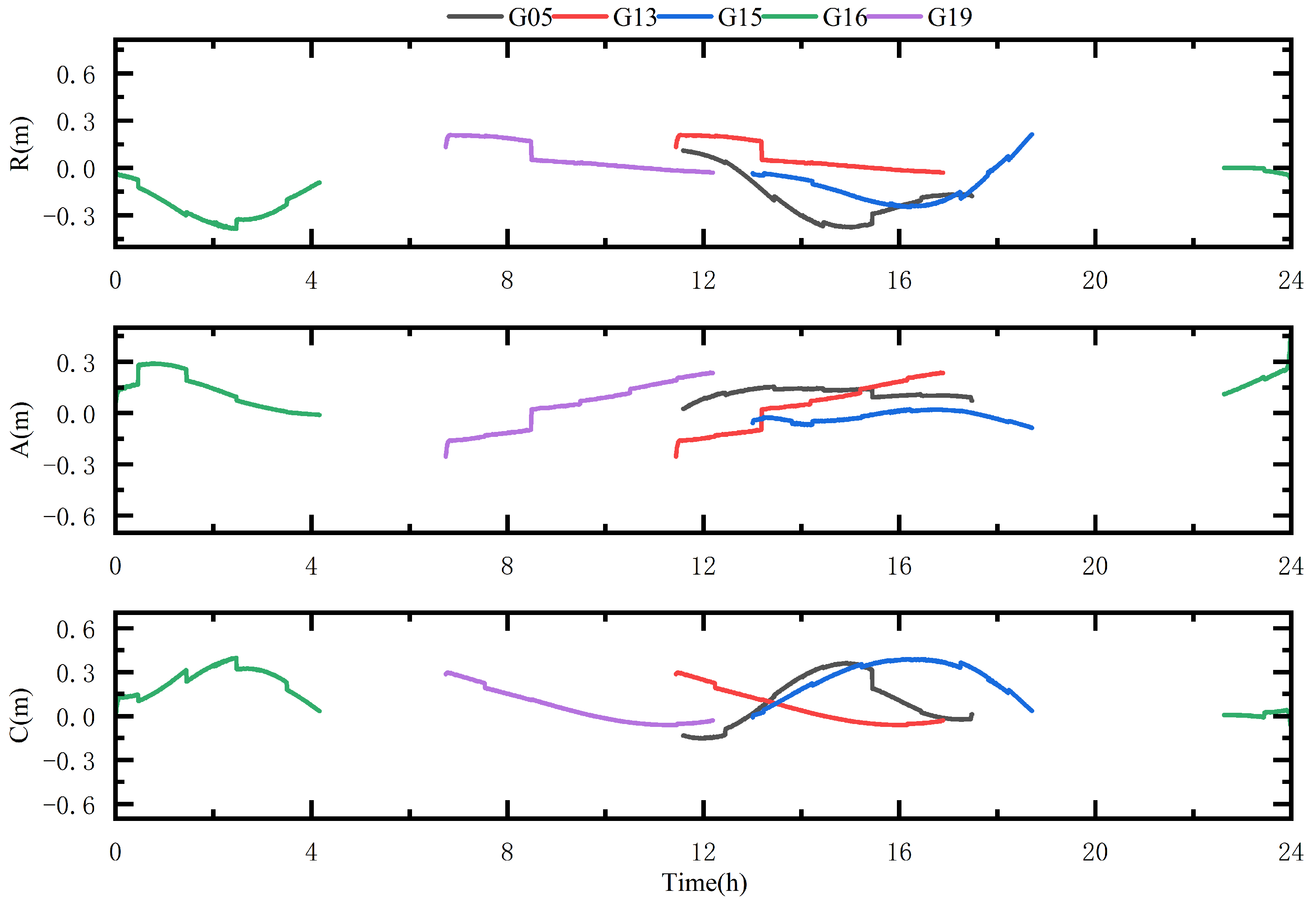








| Items | Radial (cm) | Tangential (cm) | Normal (cm) |
|---|---|---|---|
| BDS-3 CNAV1 | 8.34 | 23.05 | 17.46 |
| BDS-3 C59_PPP-B2b | 7.83 | 20.46 | 17.16 |
| BDS-3 C61_PPP-B2b | 8.14 | 19.88 | 18.46 |
| GPS LNAV | 15.46 | 22.49 | 19.05 |
| GPS C59_PPP-B2b | 6.83 | 9.73 | 8.94 |
| GPS C61_PPP-B2b | 9.86 | 11.57 | 15.49 |
| Items | STD (ns) |
|---|---|
| BDS-3 CNAV1 | 0.64 |
| BDS-3 C59_PPP-B2b | 0.22 |
| BDS-3 C61_PPP-B2b | 0.24 |
| GPS LNAV | 0.31 |
| GPS C59_PPP-B2b | 0.61 |
| Station Name | Station Category | Receiver Model | Antenna Model | External Clock |
|---|---|---|---|---|
| XIA6 | NTSC | Sept Polarx5TR | SEPCHOKE_B3E6 | UTC(NTSC) |
| SE22 | NTSC | Sept Polarx5TR | SEPCHOKE_B3E6 | UTC(NTSC) |
| JLJI | NTSC | TRIMBLE ALLOY | SEPCHOKE_B3E6 | H-Maser |
| Error Terms | Processing Model |
|---|---|
| Precise ephemeris and clock bias | PPP-B2b Precision Orbit and Clock Error |
| Ionospheric delay | Dual-frequency ionosphere-free combination |
| Tropospheric time delay | ZTD estimation |
| Observations | B1I/B3I, L1/L2 code pseudorange and carrier phase |
| Elevation mask | 15° |
| Solid tide correction | IERS 2010 |
| Antenna phase center | igs14.atx |
| Parameter estimation | Extended Kalman filter |
| Receiver position model | Static model |
| Receiver clock bias model | White noise |
| Observation value sampling interval | 30 s |
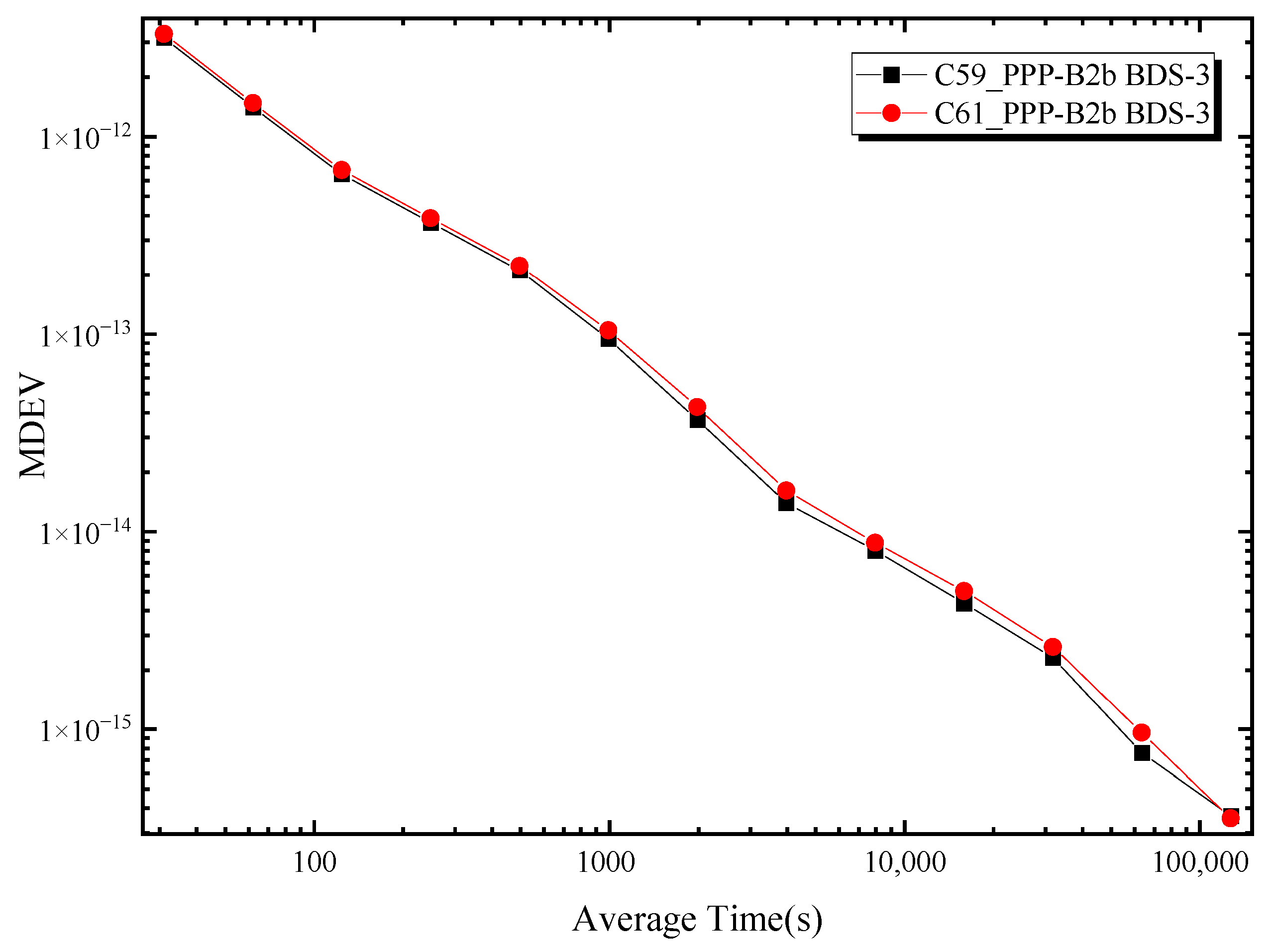
| Items | PPP-B2b | Time Comparison STD (ns) | Correct Allen’s Variance |
|---|---|---|---|
| XIA6-SE22 | C59 | 0.071 | 3.56 × 10−16 |
| C61 | 0.094 | 3.67 × 10−16 | |
| XIA6-JLJI | C59 | 0.544 | 3.87 × 10−15 |
| C61 | 0.511 | 1.99 × 10−15 |
| Station Name | Station Category | Receiver Model | Antenna Model | External Clock |
|---|---|---|---|---|
| GAMG | IGS | Sept Polarx5TR | LEIAR25.R4 LEIT | Internal |
| GUA1 | IGMAS | MGR_iGMAS | Geodetic-GNSS | Rubidium |
| JFNG | IGS | TRIMBLE ALLOY | TRM59800.00 | Internal |
| SHA1 | IGMAS | Unicore UB4B0 | NOV750.R4 NOVS | Rubidium |
| USUD | IGS | Sept Polarx5 | AOAD/M_T JPLA | H-Maser |
| Error Terms | Processing Model |
|---|---|
| Precise ephemeris and clock bias | PPP-B2b Precision Orbit and Clock Error |
| Ionospheric delay | Dual-frequency ionosphere-free combination |
| Tropospheric time delay | ZTD estimation |
| Observations | B1I/B3I, L1/L2 code pseudorange and carrier phase |
| Elevation mask | 15° |
| Solid tide correction | IERS 2010 |
| Antenna phase center | igs14.atx |
| Parameter estimation | Extended Kalman filter, least squares estimation |
| Receiver position model | Constant model |
| Receiver clock bias model | White noise |
| Observation value sampling interval | 30 s |
| Station | C59_PPP-B2b | C61_PPP-B2b | ||||
|---|---|---|---|---|---|---|
| E (cm) | N (cm) | U (cm) | E (cm) | N (cm) | U (cm) | |
| GAMG | 0.68 | 0.87 | 2.62 | 0.89 | 1.16 | 2.81 |
| GUA1 | 2.53 | 0.88 | 1.93 | 2.31 | 0.84 | 1.92 |
| JFNG | 0.87 | 1.7 | 7.07 | 1.03 | 1.92 | 6.86 |
| SHA1 | 2.72 | 2.05 | 4.98 | 2.51 | 2.04 | 5.23 |
| USUD | 5.66 | 3.72 | 8.51 | 5.99 | 3.86 | 8.81 |
| Station | C59_PPP-B2b | C61_PPP-B2b | ||||
|---|---|---|---|---|---|---|
| E (cm) | N (cm) | U (cm) | E (cm) | N (cm) | U (cm) | |
| GAMG | 0.68 | 0.87 | 2.62 | 0.89 | 1.16 | 2.81 |
| GUA1 | 2.53 | 0.88 | 1.93 | 2.31 | 0.84 | 1.92 |
| JFNG | 0.87 | 1.7 | 7.07 | 1.03 | 1.92 | 6.86 |
| SHA1 | 2.72 | 2.05 | 4.98 | 2.51 | 2.04 | 5.23 |
| USUD | 5.66 | 3.72 | 8.51 | 5.99 | 3.86 | 8.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Yang, J.; Guan, X.; Wu, J.; Wu, H. Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO. Remote Sens. 2025, 17, 2351. https://doi.org/10.3390/rs17142351
Ma H, Yang J, Guan X, Wu J, Wu H. Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO. Remote Sensing. 2025; 17(14):2351. https://doi.org/10.3390/rs17142351
Chicago/Turabian StyleMa, Hongjiao, Jinming Yang, Xiaolong Guan, Jianfeng Wu, and Huabing Wu. 2025. "Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO" Remote Sensing 17, no. 14: 2351. https://doi.org/10.3390/rs17142351
APA StyleMa, H., Yang, J., Guan, X., Wu, J., & Wu, H. (2025). Differences in Time Comparison and Positioning of BDS-3 PPP-B2b Signal Broadcast Through GEO. Remote Sensing, 17(14), 2351. https://doi.org/10.3390/rs17142351






