Beyond the Grid: GLRT-Based TomoSAR Fast Detection for Retrieving Height and Thermal Dilation
Abstract
1. Introduction
2. TomoSAR Detection
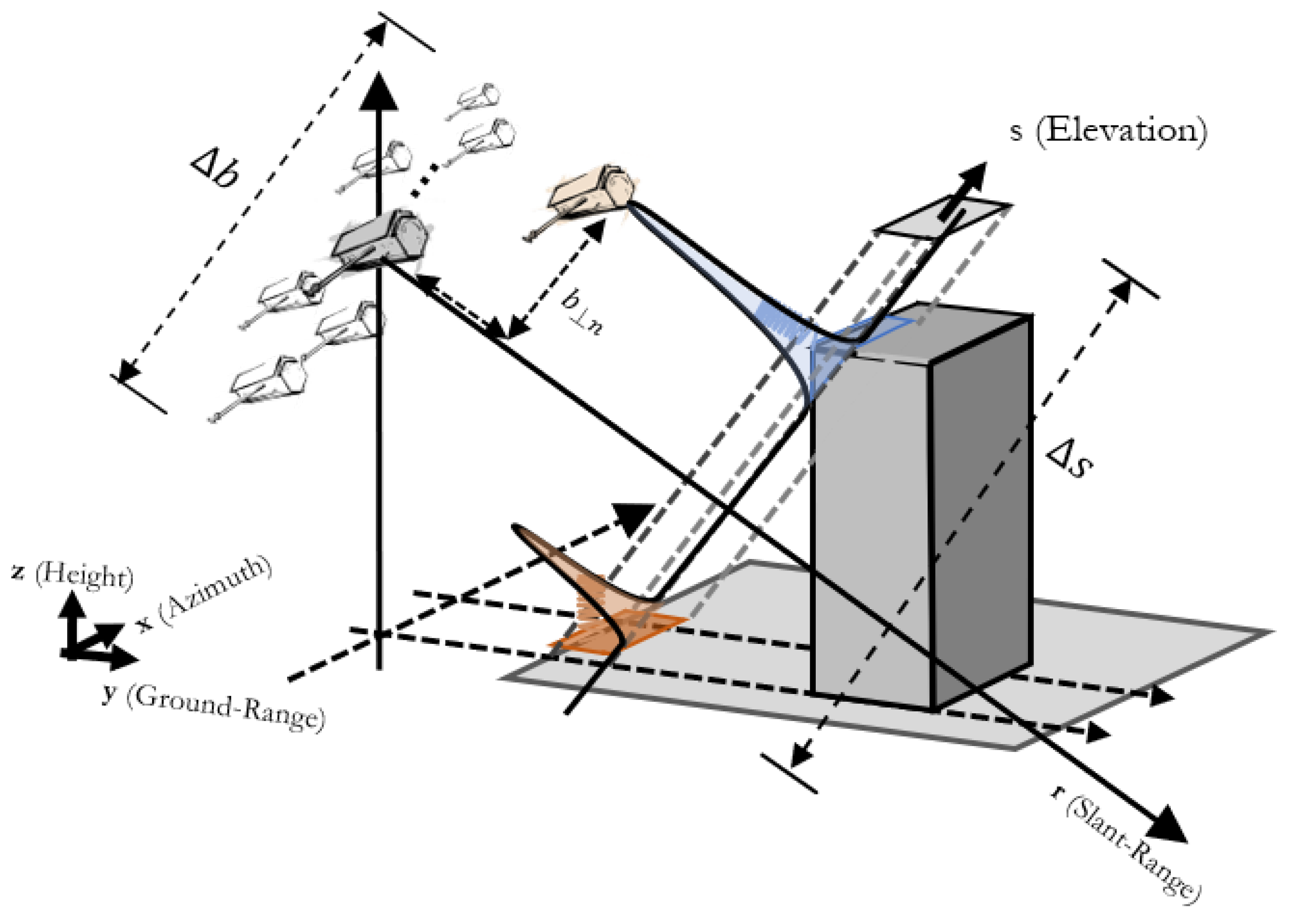
2.1. TomoSAR Configuration
- : the measurement vector of dimension .
- : the discretized reflectivity function of dimension whose elements are the samples . At a fixed range and azimuth position, is sampled at N points corresponding to all the triplets associated with the discrete samples distributed over the (elevation, thermal dilation, velocity) domain. In other words, is the number of discretized values of s, , and v.
- : the steering matrix of dimension whose -vector element is expressed as:where and denote, respectively, the angular, thermal, and velocity frequencies whose analytical expressions are , , and (note that and account, respectively, for the wavelength and radar to ground distance).
- : the noise vector of dimension .
2.2. GLRT Detection
- : the optimal p-sparse support set .
- : the projection operator onto the orthogonal complement of the subspace spanned by the columns indexed by . Its formulas is .
- : the predefined threshold for the test. Monte Carlo simulations provide a way to empirically estimate it by simulating the distribution of the GLRT statistic under the different hypotheses and selecting the value that corresponds to the desired false alarm rate.
2.3. Optimal Support Set
- Exhaustive search: where all possible support sets of size p are examined, in other words, all combinations. This variant of GLRT, known as Support GLRT, guarantees finding the global minimum of the objective function. However, its computational complexity is prohibitive for large values of N and p. This makes the exhaustive search approach impractical in high-dimensional scenarios, where the search space becomes challenging.
- Sequential search: where the support set is built iteratively by adding one element at a time. At each step i (), the index is selected so that the objective function is minimized, where . This variant of GLRT, known as Fast-Sup GLRT, greatly reduces the computational burden compared to exhaustive search by making locally optimal decisions at each iteration. However, since the search is greedy in nature, it may converge to a suboptimal local minimum rather than the global optimum. Its effectiveness depends on the structure of the problem and the quality of the locally optimal choices. While it significantly improves computational efficiency, especially for large-scale problems, its performance can be sensitive to noise and acquisition geometry.
3. Proposed Method
| Algorithm 1 Procedure for the estimation of the support and the corresponding matrix |
 |
- Initial sequential selection: The first stage of our methodology harnesses the strength of the Fast-Sup GLRT search to efficiently identify an initial estimate of the support set. This is achieved by minimizing . By doing so, the search is guided toward a promising region in the solution space.
- Quasi-Newton optimization and refinement: Following the initial estimation, we employ a quasi-Newton optimization approach. The objective function to be minimized is:where with formulated as , or in simplified manner as .The analytic gradients of the objective function with respect to the parameter vectors are:To calculate these gradients, we first need to derive , , and . Before simplification, they can be expressed by ([37]):Using properties of the pseudoinverse and projection orthogonality, they become:The derivative of , with respect to the parameters, affects only the corresponding column:The steering vector derivatives are:The complete gradient expressions for the objective function are:For implementation purposes, we adopt the Broyden–Fletcher–Goldfarb–Shanno (BFGS) update strategy [38], implemented via MATLAB’s fminunc [39]. At each iteration , the objective function is minimized in the updated support, refined by the previous optimization, with parameter updates expressed as:where the following parameters account for:
- : the optimization variable at iteration j whose elements are
- : the gradient of the objective function at iteration j having as elements
- : the step size determined via a line search.
- : the search direction expressed as .
- : the Hessian approximation.
The Hessian approximation is updated in each iteration using the BFGS formula:where and denote the step vector and the difference in gradients whose expressions are and , respectively.Since inverting at each iteration is computationally expensive, alternatively, one may directly update the inverse Hessian approximation () using: - Support Expansion: After each optimization cycle, the support set is expanded by incorporating an additional scatterer position identified through Fast-Sup GLRT while keeping the previously optimized positions. All identified scatterers then undergo re-optimization through the quasi-Newton optimization on the complete parameter set. This process of support expansion followed by joint re-optimization continues iteratively until the maximum number of scatterers is identified and localized.
4. Results
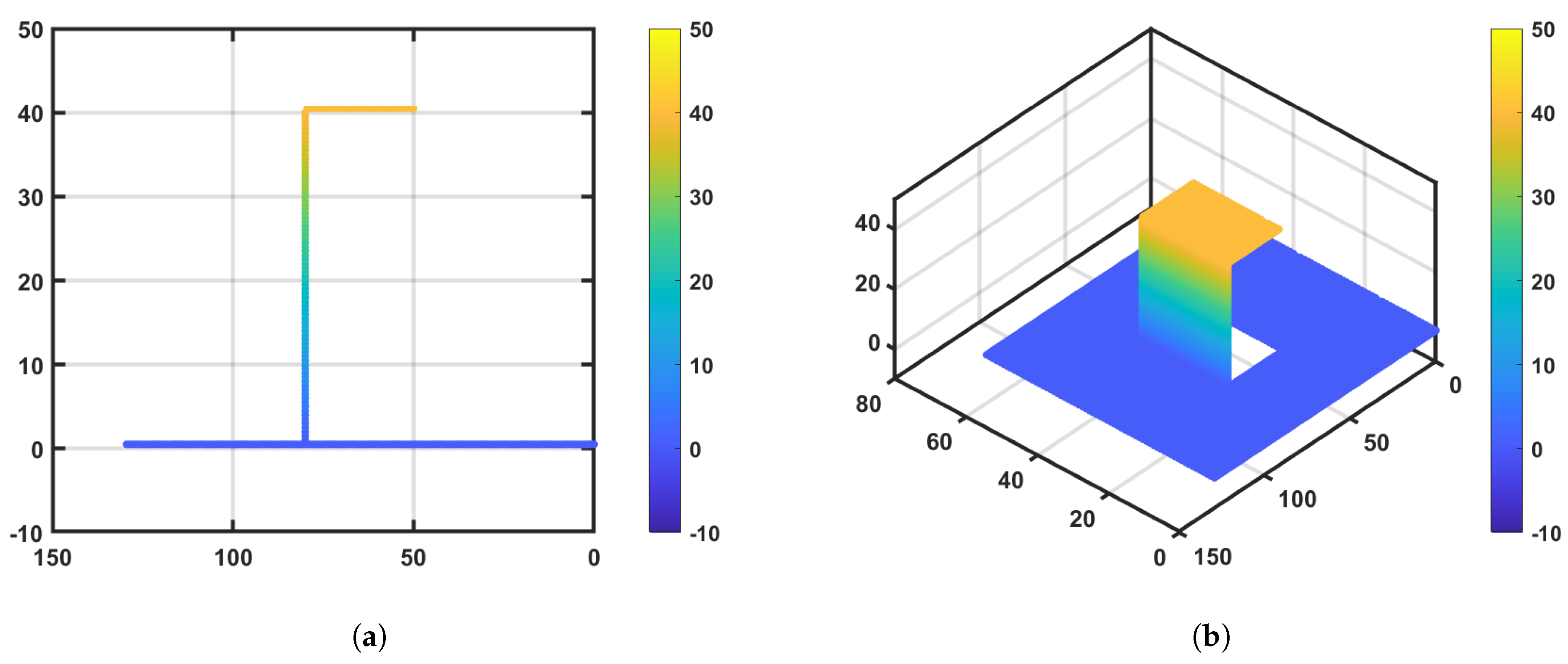
4.1. Simulated Results
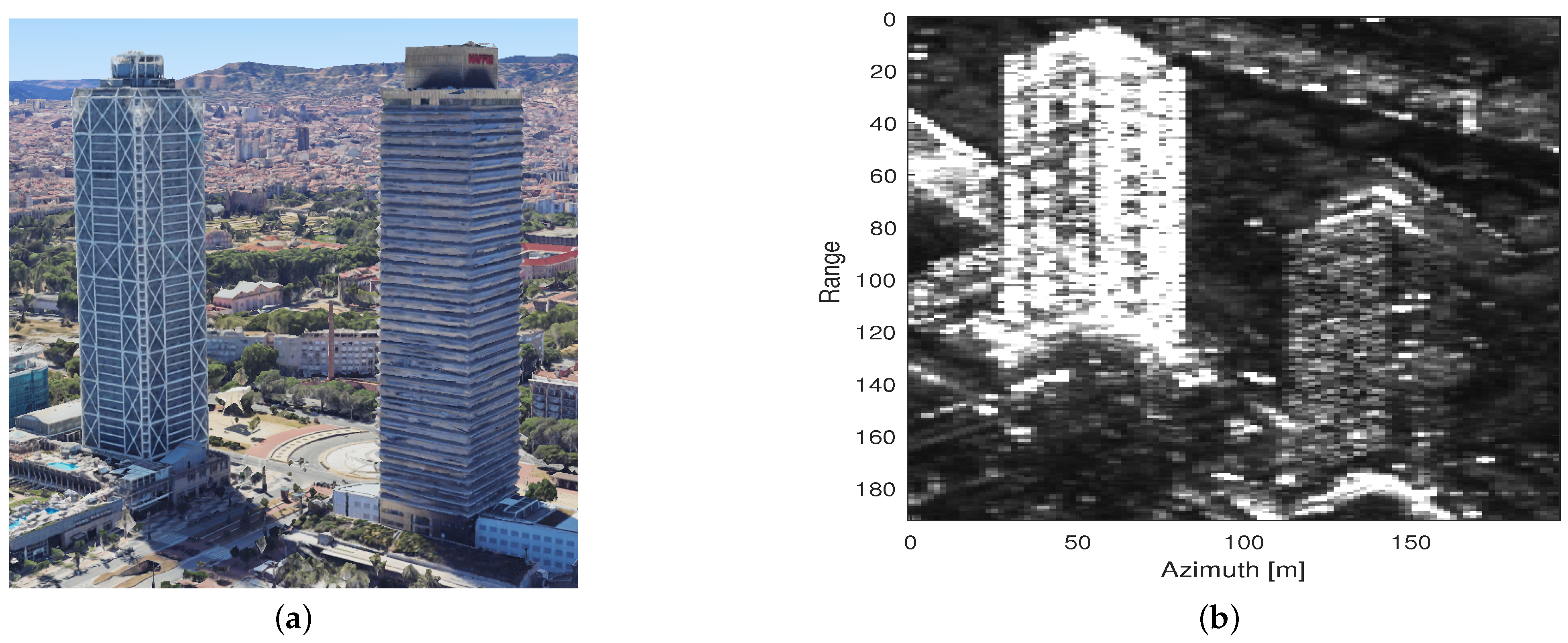
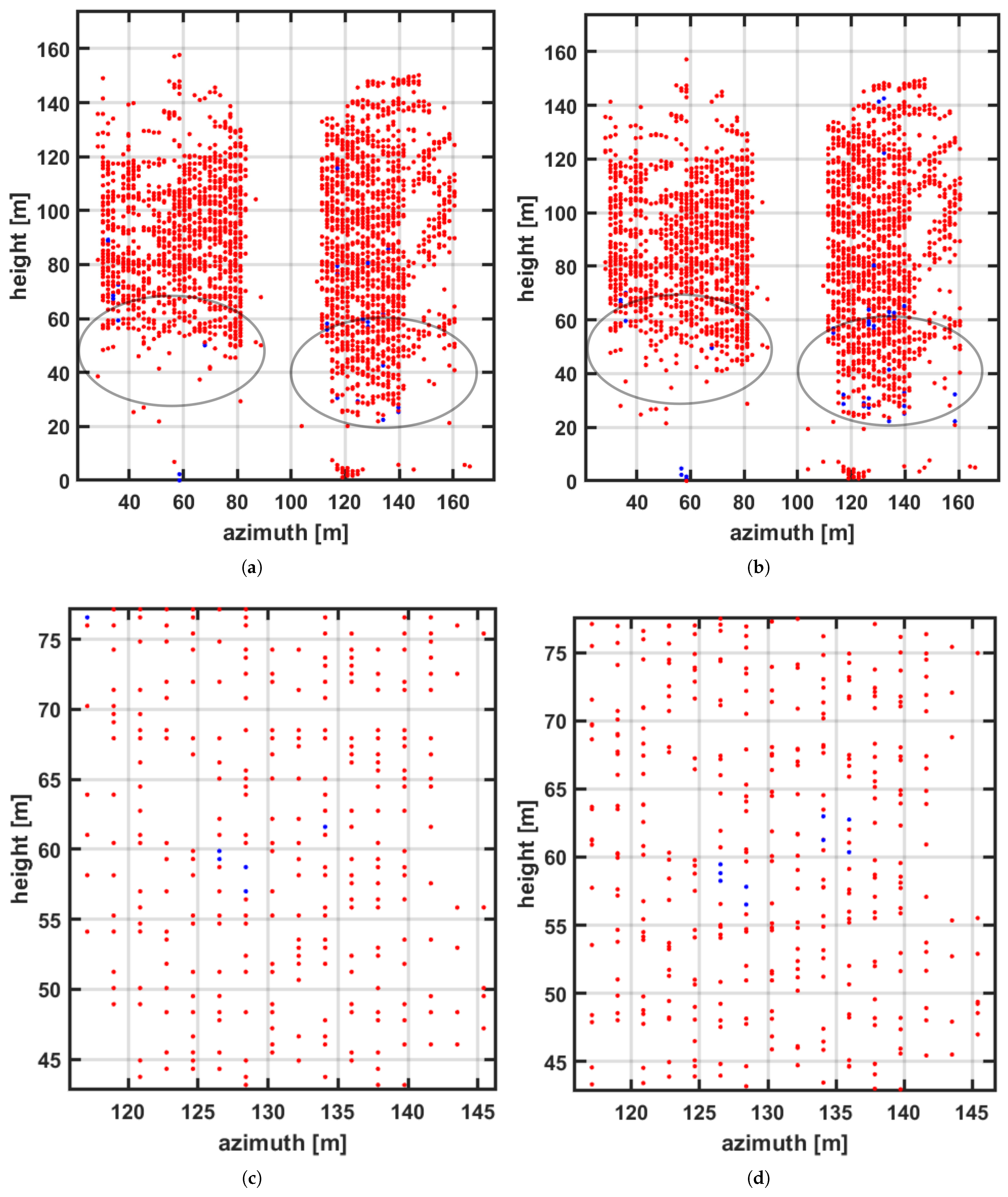
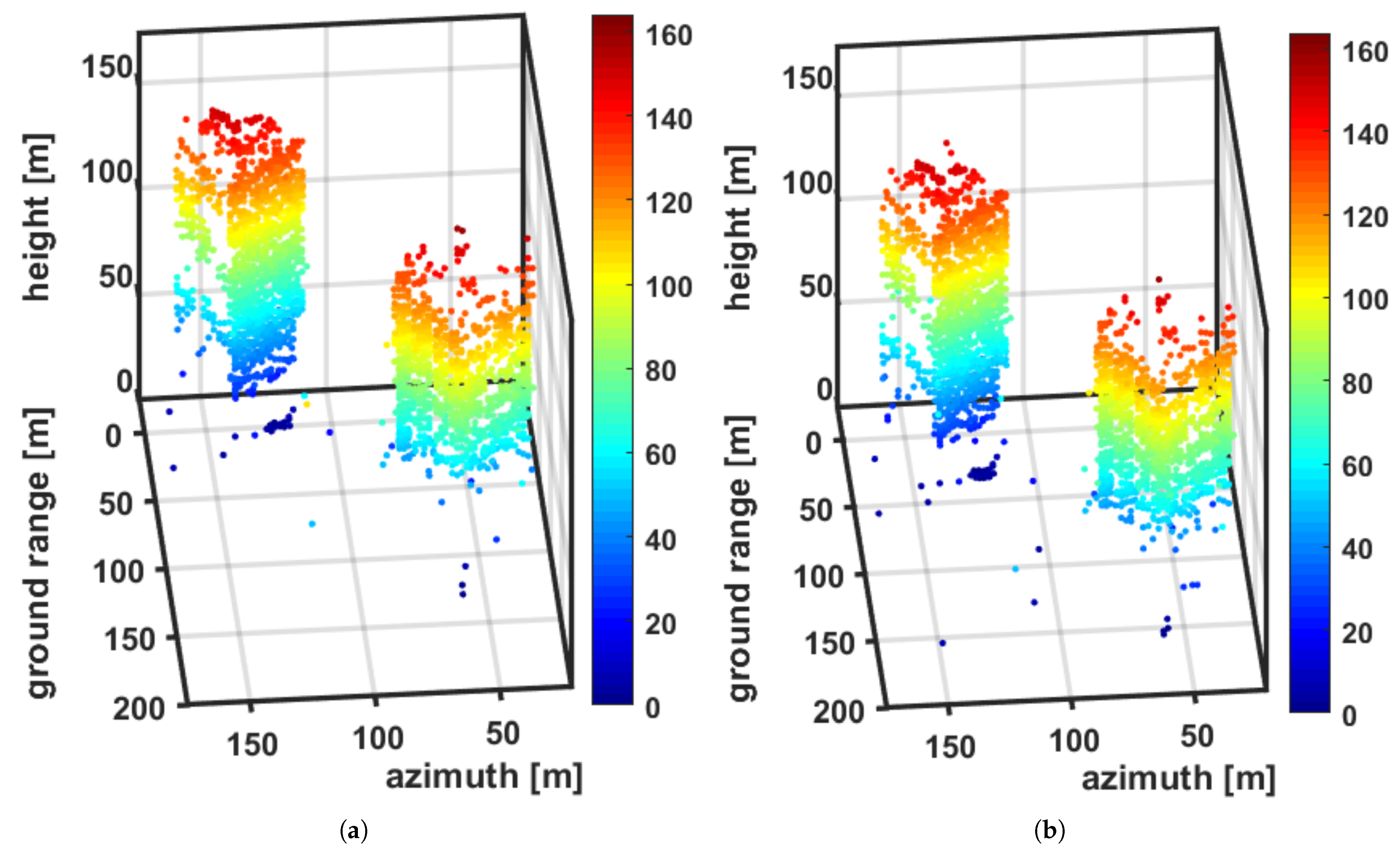
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Budillon, A.; Schirinzi, G. Remote monitoring of civil infrastructure based on TomoSAR. Infrastructures 2022, 7, 52. [Google Scholar] [CrossRef]
- Fornaro, G.; Pauciullo, A.; Pascazio, V.; Schirinzi, G.; Reale, D. Multi-Dimensional Imaging with Synthetic Aperture Radar; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Rambour, C.; Budillon, A.; Johnsy, A.C.; Denis, L.; Tupin, F.; Schirinzi, G. From Interferometric to Tomographic SAR: A Review of Synthetic Aperture Radar Tomography-Processing Techniques for Scatterer Unmixing in Urban Areas. IEEE Geosci. Remote Sens. Mag. 2020, 8, 6–29. [Google Scholar] [CrossRef]
- Omati, M.; Sahebi, M.R.; Aghababaei, H. Evaluation of nonparametric SAR tomography methods for urban building reconstruction. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4013605. [Google Scholar] [CrossRef]
- Hadj-Rabah, K.; Schirinzi, G.; Budillon, A.; Hocine, F.; Belhadj-Aissa, A. Non-Parametric Tomographic SAR Reconstruction via Improved Regularized MUSIC. Remote Sens. 2023, 15, 1599. [Google Scholar] [CrossRef]
- Schmitt, M.; Stilla, U. Maximum-likelihood-based approach for single-pass synthetic aperture radar tomography over urban areas. IET Radar Sonar Navig. 2014, 8, 1145–1153. [Google Scholar] [CrossRef]
- Haddad, N.; Bouaraba, A.; Hadj-Rabah, K.; Budillon, A.; Harkati, L.; Schirinzi, G. Generalized Parametric Iterative Approach for Tomographic SAR Reconstruction. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4011005. [Google Scholar] [CrossRef]
- Armeshi, H.; Sahebi, M.R.; Aghababaei, H. A deterministic descriptive regularization-based method for SAR tomography in urban areas. Int. J. Remote Sens. 2024, 45, 1884–1903. [Google Scholar] [CrossRef]
- Budillon, A.; Evangelista, A.; Schirinzi, G. Three-Dimensional SAR Focusing From Multipass Signals Using Compressive Sampling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 488–499. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Tomographic SAR inversion by L1-norm regularization—The compressive sensing approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3839–3846. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Let’s do the time warp: Multicomponent nonlinear motion estimation in differential SAR tomography. IEEE Geosci. Remote Sens. Lett. 2011, 8, 735–739. [Google Scholar] [CrossRef]
- De Maio, A.; Fornaro, G.; Pauciullo, A. Detection of single scatterers in multidimensional SAR imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2284–2297. [Google Scholar] [CrossRef]
- Pauciullo, A.; Reale, D.; De Maio, A.; Fornaro, G. Detection of double scatterers in SAR tomography. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3567–3586. [Google Scholar] [CrossRef]
- Budillon, A.; Schirinzi, G. GLRT based on support estimation for multiple scatterers detection in SAR tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 1086–1094. [Google Scholar] [CrossRef]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. A fast support detector for superresolution localization of multiple scatterers in SAR tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2768–2779. [Google Scholar] [CrossRef]
- Reale, D.; Fornaro, G.; Pauciullo, A. Extension of 4-D SAR imaging to the monitoring of thermally dilating scatterers. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5296–5306. [Google Scholar] [CrossRef]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. 4-D SAR Support Based Tomographic Imaging. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–4. [Google Scholar]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. Support-detection 5-D SAR tomography. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7407–7410. [Google Scholar]
- Budillon, A.; Johnsy, A.C.; Schirinzi, G. Extension of a fast GLRT algorithm to 5D SAR tomography of Urban areas. Remote Sens. 2017, 9, 844. [Google Scholar] [CrossRef]
- Pauciullo, A.; Reale, D.; Franzé, W.; Fornaro, G. Multi-look in GLRT-based detection of single and double persistent scatterers. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5125–5137. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Dong, Z.; Yu, A.; Zhang, Y.; Zhu, X. Super-resolved multiple scatterers detection in SAR tomography based on compressive sensing generalized likelihood ratio test (CS-GLRT). Remote Sens. 2019, 11, 1930. [Google Scholar] [CrossRef]
- Luo, H.; Dong, Z.; Li, Z.; Yu, A. Iterative-SGLRT for multiple-scatterer detection in SAR tomography. IEEE Geosci. Remote Sens. Lett. 2020, 18, 122–126. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, A.; Dong, Z.; Wu, M.; Liu, Q. Off-grid correction for improving scatterer localization performance in compressive sampling SAR tomography. Sci. China Inf. Sci. 2021, 64, 129302. [Google Scholar] [CrossRef]
- Budillon, A.; Ferraioli, G.; Schirinzi, G. Localization performance of multiple scatterers in compressive sampling SAR tomography: Results on COSMO-SkyMed data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2902–2910. [Google Scholar] [CrossRef]
- Bang, D.; Xiaolan, Q.; Zhe, Z.; Bin, L.; Chibiao, D. L1 Minimization with Perturbation for Off-grid Tomographic SAR Imaging. J. Radars 2021, 11, 62–70. [Google Scholar]
- Guo, Q.; Liang, X.; Li, Y.; Dai, Y. A Novel Method for Airborne Array-InSAR Tomography Based on Off-grid Target Modeling and Group Sparsity. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3505205. [Google Scholar] [CrossRef]
- Yu, L.; Feng, D.; Wang, J.; Huang, X. An efficient reconstruction approach based on atomic norm minimization for coprime tomographic SAR. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4503705. [Google Scholar] [CrossRef]
- Wang, X.; Xu, F. Tomographic SAR Inversion by Atomic-Norm Minimization—The Gridless Compressive Sensing Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5239113. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Z.; Zhang, B.; Wu, Y. Gridless tomographic SAR imaging based on accelerated atomic norm minimization with efficiency. In Proceedings of the International Conference on Radar Systems (RADAR 2022), Hybrid Conference, Edinburgh, UK, 24–27 October 2022. [Google Scholar]
- Wang, X.; Xu, F. Efficient ADMM Algorithm for Atomic Norm Minimization in SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5211415. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Y.; Ding, Z.; Li, L.; Zeng, T. Atomic Norm Minimization Based Fast Off-Grid Tomographic SAR Imaging with Nonuniform Sampling. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5203517. [Google Scholar] [CrossRef]
- Shao, M.; Zhang, Z.; Li, J.; Kang, J.; Zhang, B. TADCG: A Novel Gridless Tomographic SAR Imaging Approach based on the Alternate Descent Conditional Gradient Algorithm with Robustness and Efficiency. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5201213. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, Z.; Qiu, X.; Ding, C. A Novel Gradient Descent Least Squares (GDLS) Algorithm for Efficient Gridless Line Spectrum Estimation with Applications in Tomographic SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5208313. [Google Scholar] [CrossRef]
- Haddad, N.; Budillon, A.; Hadj-Rabah, K.; Bouaraba, A.; Harkati, L.; Benbouzid, M.A.; Schirinzi, G. Gridless GLRT for Tomographic SAR Detection Using Particle Swarm Optimization Algorithm. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4019205. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Luzi, G.; Crippa, B. Measuring thermal expansion using X-band persistent scatterer interferometry. ISPRS J. Photogramm. Remote Sens. 2015, 100, 84–91. [Google Scholar] [CrossRef]
- Seker, I.; Lavalle, M. Tomographic performance of multi-static radar formations: Theory and simulations. Remote Sens. 2021, 13, 737. [Google Scholar] [CrossRef]
- Golub, G.H.; Pereyra, V. The differentiation of pseudo-inverses and nonlinear least squares problems whose variables separate. SIAM J. Numer. Anal. 1973, 10, 413–432. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- The MathWorks Inc. Optimization Toolbox User’s Guide, Version 9.4 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022; Available online: https://www.mathworks.com/help/optim/ (accessed on 9 March 2025).





| Parameter | Quantity |
|---|---|
| Wavelength | [m] |
| Incidence angle | ° |
| Range Distance | [km] |
| Number of images | 27 |
| Total Baseline | [m] |
| Detector | Height Accuracy | Height Completeness | Thermal Dilation Accuracy | Computational Time |
|---|---|---|---|---|
| [m] | [m] | [mm/°C] | [s] | |
| Fast-Sup | 0.6689 | 0.8239 | 0.02895 | 1335.7 |
| Proposed | 0.2446 | 0.2387 | 0.01031 | 511.4 |
| Parameter | Quantity |
|---|---|
| Wavelength | [m] |
| Range Distance | 618 [km] |
| Number of images | 28 |
| Total Baseline | [m] |
| Vertical Resolution | 19 [m] |
| Fast-Sup | Proposed | |
|---|---|---|
| Single Scatterers | 2624 | 2708 |
| Double Scatterers | 18 | 23 |
| Detector | Time [s] | Completeness | R-Squared |
|---|---|---|---|
| Fast-Sup | 5856.4 | 0.1324 | 0.9813 |
| Proposed | 1235.1 | 0.1151 | 0.9946 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddad, N.; Hadj-Rabah, K.; Budillon, A.; Schirinzi, G. Beyond the Grid: GLRT-Based TomoSAR Fast Detection for Retrieving Height and Thermal Dilation. Remote Sens. 2025, 17, 2334. https://doi.org/10.3390/rs17142334
Haddad N, Hadj-Rabah K, Budillon A, Schirinzi G. Beyond the Grid: GLRT-Based TomoSAR Fast Detection for Retrieving Height and Thermal Dilation. Remote Sensing. 2025; 17(14):2334. https://doi.org/10.3390/rs17142334
Chicago/Turabian StyleHaddad, Nabil, Karima Hadj-Rabah, Alessandra Budillon, and Gilda Schirinzi. 2025. "Beyond the Grid: GLRT-Based TomoSAR Fast Detection for Retrieving Height and Thermal Dilation" Remote Sensing 17, no. 14: 2334. https://doi.org/10.3390/rs17142334
APA StyleHaddad, N., Hadj-Rabah, K., Budillon, A., & Schirinzi, G. (2025). Beyond the Grid: GLRT-Based TomoSAR Fast Detection for Retrieving Height and Thermal Dilation. Remote Sensing, 17(14), 2334. https://doi.org/10.3390/rs17142334









