Principles of Correction for Long-Term Orbital Observations of Atmospheric Composition, Applied to AIRS v.6 CH₄ and CO Data

Abstract

This study considers methods for assessing the quality of orbital observations, quantifying drift over time, and the application of correction methods to long-term series. AIRS v6 (IR-only) satellite methane (CH₄) and carbon monoxide (CO) total column (TC) measurements were compared with NDACC ground station data from 2003 to 2022. For CH₄, negative trends were observed in the difference between satellite and ground measurements (AIRS-GR) at all 18 stations (mean drift: 1.69 × 10¹⁴ ± 0.31 × 10¹⁴ molecules/cm² per day), suggesting a shift in the orbital spectrometer parameters is probable. The application of a dynamic correction based on this drift coefficient significantly improved the correlation with satellite data for both daily means and trends at all stations. In contrast, AIRS v6 CO measurements showed a strong initial correlation (R = 0.93 for the entire dataset, and R ~ 0.8–0.95 for separate stations) without systematic drift, i.e., the trends of AIRS-GR at individual sites were oppositely directed and statistically insignificant. Therefore, the AIRS v6 CO TC satellite product does not require additional correction within this method. The developed methodology for satellite data verification and correction is supposed to be universal and applicable to other long-term orbital observations.

1. Introduction

Satellite observations cover large areas of land, seas and oceans and provide experimental information on atmospheric composition and parameters in inaccessible and sparsely populated areas, i.e., where ground-based monitoring stations are not available. Orbital remote sensing data are widely used by various research teams to solve the problems of studying the dynamics of atmospheric composition and climate, the variability and transport of greenhouse gases and climate-active substances in the atmosphere in different regions of the Earth.

There are currently a large number of scientific satellites in Earth orbit, such as Terra (https://terra.nasa.gov (accessed on 2 February 2025)), Aqua (https://aqua.nasa.gov (accessed on 1 March 2024)), AURA (https://aura.gsfc.nasa.gov (accessed on 2 February 2025)), Sentinel 5P (https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-5P (accessed on 2 February 2025)), the OCO series [1,2], and others, equipped with various orbital instruments and providing a large amount of information on the composition and parameters of the Earth’s atmosphere and surface. In terms of sophistication, performance and time in orbit, these instruments can be roughly divided into “older generation instruments” and “high spatial resolution instruments” or “modern orbital systems”. For example, MOPITT, MODIS, AIRS, and OMI were launched at the turn of the millennium and have been providing information on the composition and parameters of the atmosphere for two or more decades (depending on the instrument). These orbital observing systems can also be called “long-flying”. These instruments have some limitations compared to modern high spatial resolution instruments. However, they have a very important advantage precisely because of their long time in orbit.

Despite some shortcomings (e.g., relatively low spatial resolution), older-generation instruments are essential for assessing regional and global long-term changes in atmospheric composition [3,4,5,6,7,8], especially in areas of the globe not covered by ground-based monitoring networks, for studying the long-range transport of pollutants [9,10,11]. The advantages of these orbital instruments (MOPITT, AIRS, IASI, OMI) also include the careful, multifaceted validation of measurement data carried out by many research teams [3,12,13,14].

The AIRS BAE Systems infrared sounder (https://airs.jpl.nasa.gov (accessed on 1 March 2024)), equipped with a hyperspectral instrument with 2378 infrared channels (more on the spectrometer at https://airs.jpl.nasa.gov/mission/airs-project-instrument-suite/airs/spectrometer-optics (accessed on 1 March 2024)), is one of six instruments aboard NASA’s AQUA satellite, launched on 4 May 2002. It is operated by NASA’s Jet Propulsion Laboratory in Pasadena, California.

AIRS is designed to support climate research and improve weather forecasting. In addition to meteorological parameters, the instrument measures the content and concentration of selected atmospheric trace gases. AIRS uses infrared technology to produce 3D maps of air and surface temperature, water vapor and cloud properties and measures trace gases such as ozone, carbon monoxide and methane. The AIRS spectrometer records absorption spectra of the Earth’s own infrared radiation in the spectral range from 3.75 to 15.4 µm. The scanner has a swath of 800 km on either side of the ground track, allowing measurements to cover more than 80 percent of the Earth’s surface [15].

The AIRS retrieval algorithm uses 36 channels between 2181 and 2221 cm⁻¹ (gas band center is ~4.5 μm) for CO and 58 channels between 1220 and 1356 cm⁻¹ (gas band center is ~7.7 μm) for the CH₄ retrieval [16]; at the same time, the methane band resides inside the broad 6.7 μm H₂O band, which imposes additional complexities and uncertainties on the calculations [16]. In the tropics, the most sensitive layer of AIRS channels to CH₄ is at about 200–300 hPa, and it decreases in altitude to about 400–500 hPa in the polar region [16]. Temperature and humidity profiles significantly affect the weighting function, and the vertical sensitivity of AIRS retrieval has significant geographic and seasonal variability [16]. Similarly, the level of greatest AIRS sensitivity to CO was found to be in the middle troposphere and close to 510 hPa [13]; this study also reported that the AIRS CO mixing ratio in the lower troposphere was biased by ∼20% in summer compared to aircraft profiles.

AQUA crosses the equator at approximately 1:30 and 13:30 local time. The correlation of the CH₄ TC daily values measured by AIRS with ground-based data is quite high: the correlation coefficient (hereinafter R) is equal to ~0.6–0.8 at most sites [17]. For CO TC, even higher correlations are observed [18] both at separate stations and for the whole dataset, which is further reflected in this work.

AIRS atmospheric composition data of different versions (v5, v6 and v7) have been successfully used to assess emissions of various pollutants, such as CO emissions from wildfires [6,19,20,21], as well as to study global and regional CO and CH₄ trends [22,23,24,25,26]. As there is no alternative for studying the distribution of long-term trends in CH₄ (the measurement series of other, newer space-based monitoring tools are much shorter), scientists continue to validate and use the measurement data from the so-called “long-flying” satellite systems.

Different product levels are available to users: L1, L2, L3 (levels 1, 2, 3) of different versions (the latest version is v.7). The daily product of level L3 uses data from all orbits and averages them over the corresponding cells of the entire Earth’s surface. The levels and data structure are described in more detail in [27]. L3 products are the most adapted for use and are based on L2 data that have passed quality control, been filtered, distributed over 1° × 1° grid cells, and contain mean values, standard deviation, and amount of L2 data for each cell and for all measured parameters.

The relative disadvantages of AIRS are not only low spatial resolution but also insufficient sensitivity in the lower troposphere, which leads to underestimation of the admixture content under regions with intense surface emissions (e.g., in areas of megacities and wildfires [18,20]). Similar conclusions about the sensitivity of AIRS CH₄ retrievals in the lower troposphere have been confirmed in other studies [23,28,29,30]. Similarly, [13] reported that the AIRS CO mixing ratio in the lower troposphere was biased by ∼20% in summer compared to aircraft profiles. In addition, in our earlier work, we found that the ‘long-flying’ AIRS underestimated the evaluations of CH₄ trends (up to 1.5 times) compared to estimates based on ground-based data [24]. The same result (underestimated CH₄ trends by AIRS v6) was obtained in [23]. The latter circumstance allowed us to assume that the parameters of the orbital instrument change over time, leading to the aforementioned underestimation and also, apparently, to a deterioration in the characteristics of the agreement between AIRS data and ground-based measurements. The aim of our work was to test this assumption and to develop methods for correcting orbital data associated with long-term changes in the quality of satellite observations. Firstly, we tested the estimates of the long-term drift of the difference between AIRS and ground-based data for daily CO and CH₄ total content observations.

At this stage, the most important aspect for us was to have longer and statistically robust data series. Therefore, in this work, we have used AIRS version 6 (v6) and NDACC network data on CO and CH₄ total content (TC), but not data on averaged volume mixing ratio VMR or X[GAS], which are presented in both v6 and the latest v7.

2. Materials and Methods

In this study, the CH₄ and CO TC orbital measurements of AIRS (version v6 Standard L3 v.6 IR AIRS Only Daily) for the period from 2003 to 2022 are validated for 18 sites corresponding to the locations of the measurement stations of the NDACC atmospheric monitoring network stations (https://ndacc.larc.nasa.gov (accessed on 30 September 2024)). The coordinates of each ground station are the center of the 1° × 1° satellite measurement cell.

The NDACC network started its own observations in 1991—significantly earlier than TCCON [31], which provides column averaging kernels; similarly, NDACC spectroscopic datasets [32] are significantly longer and statistically more robust.

Both AIRS v6 and NDACC present CO and CH₄ data as total content, i.e., recalculations (such as [31,33]) are not required when comparing data; this avoids additional errors that are inevitable when performing recalculations.

The validated AIRS v6 L3 product is publicly available (NASA website: https://airs.jpl.nasa.gov/data/get-data/standard-data (accessed on 1 March 2024)). AIRS satellite spectrometer data for each station were extracted from the primary .hdf files using a custom software package, TROPOMI_tools, version 7.01 [34]. We used data from daytime AIRS measurements only (from ascending orbit, “ascending only”), i.e., around 13:30 local time for each cell and each day, which (usually) coincides with the time of the ground-based spectroscopic measurements with an accuracy of 2–3 h. The description of the satellite products used in this work is given in

Table 1. Information about version and spatial resolution of data, encoding of the satellite products CH₄ and CO TC of the AIRS orbital spectrometer, and the names and description of the variables used.

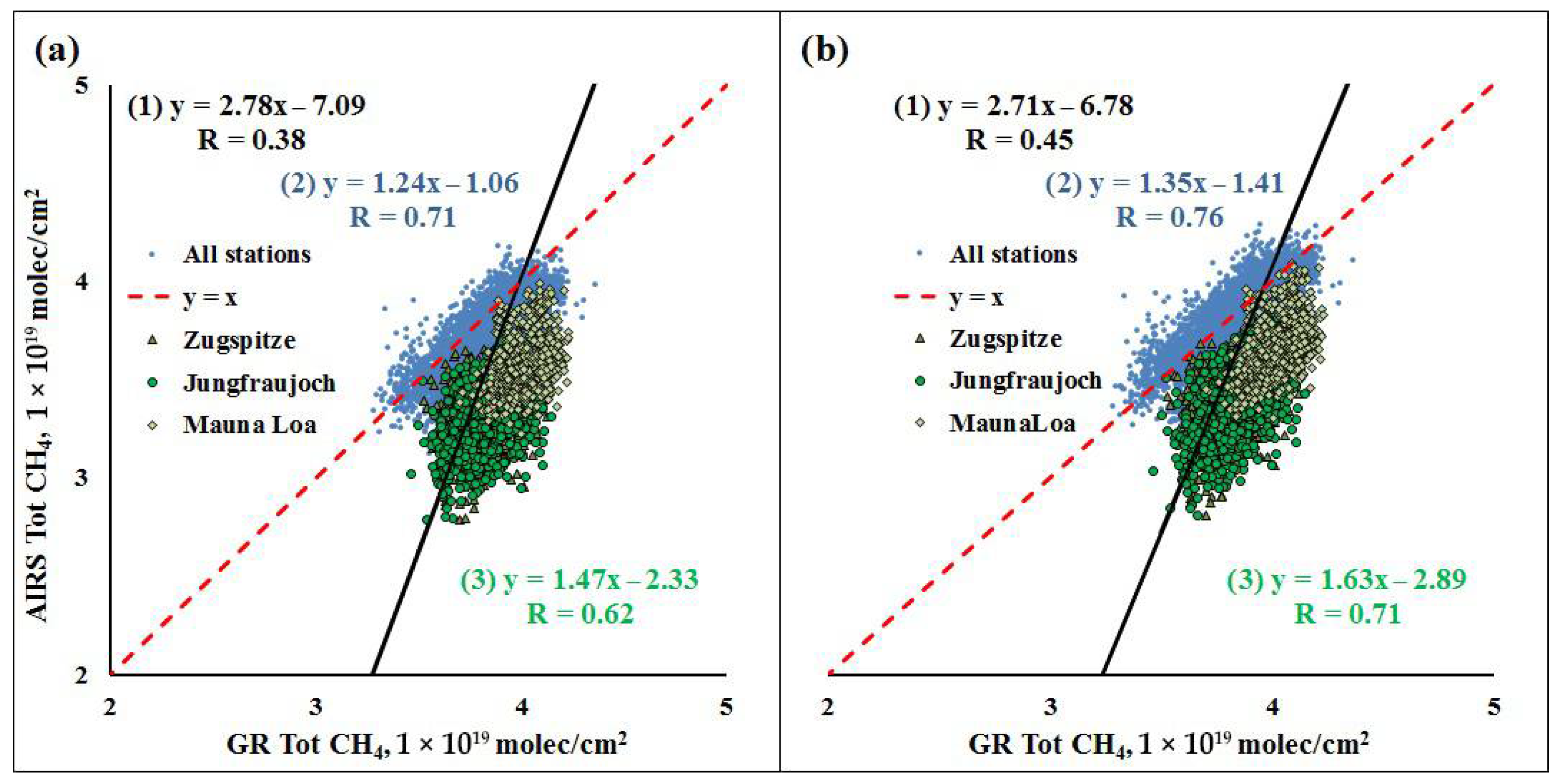
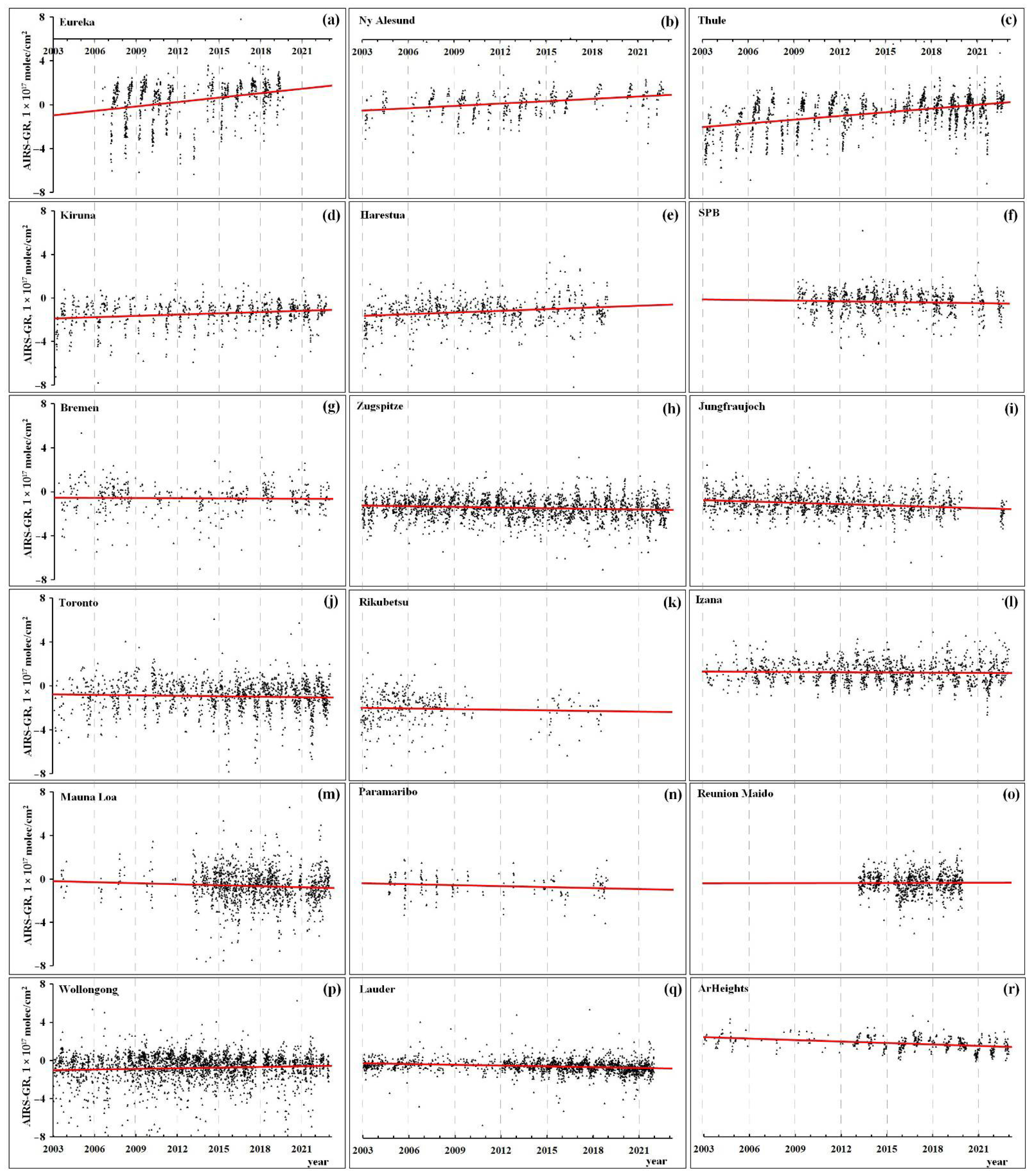
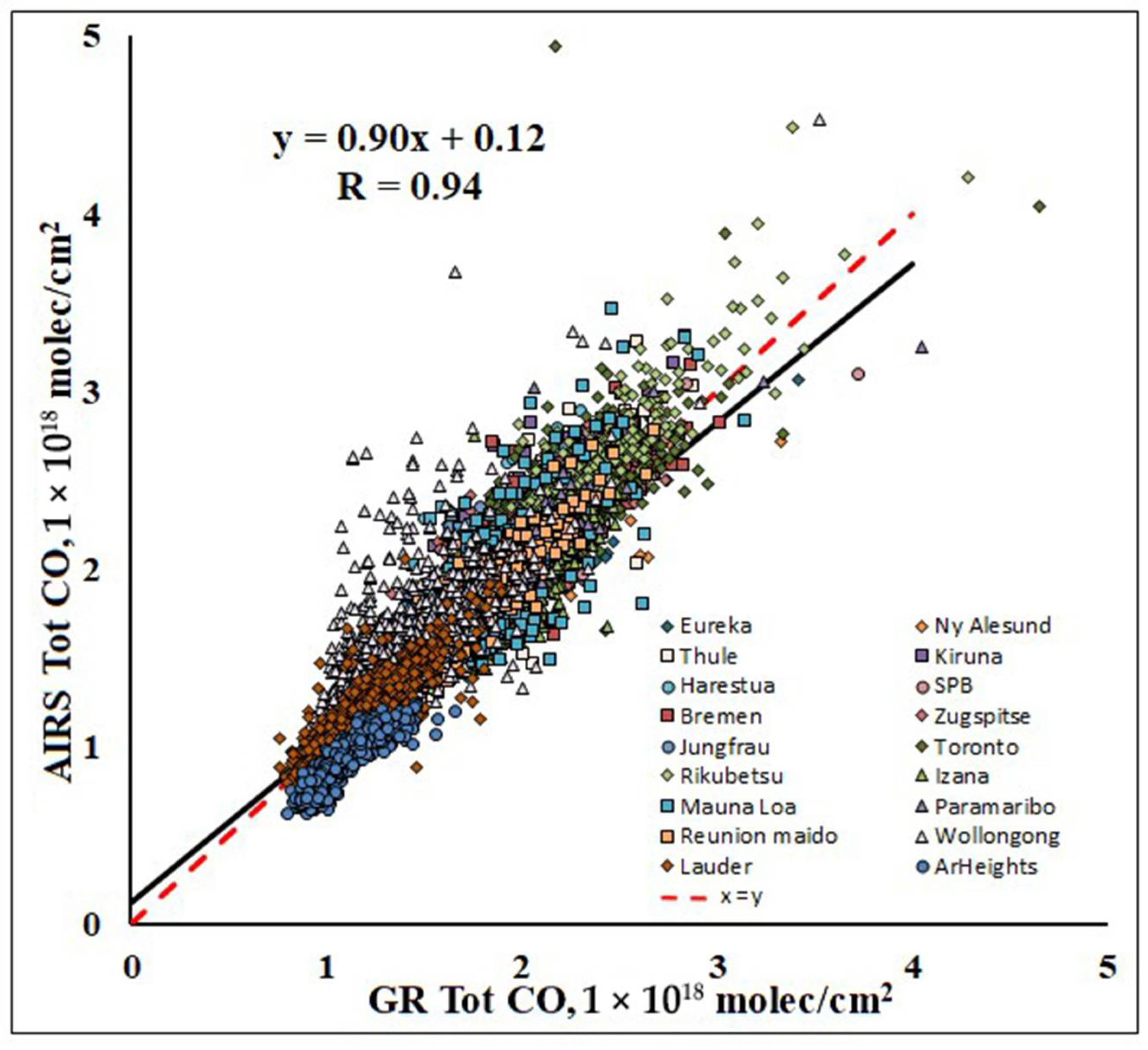
Parameter	Satellite Product	Encoding	Variable for Extraction
CH4 TC	Standard L3 v.6 IR AIRS Only Daily	AIRS3STD	TotCH4_A * Total column CH4, ascending, 1° × 1° resolution, molecules/cm2
CO TC	Standard L3 *IR AIRS Only Daily	AIRS3STD	TotCO_A. Total CO column, ascending, 1° × 1° resolution, molecules/cm2
Altitude	-	-	Topography Topography of the Earth in meters above the geoid, resolution 1° × 1°, m

* Ascending, i.e., only the ascending part of the orbit.

.

As reference values for the TC of both trace gases, spectroscopic measurements from NDACC stations of those points in the network equipped with high-resolution solar Fourier spectrometers and with long series of measurements [32] are adopted. The accuracy of a single measurement of the gas content in the atmospheric column of these spectrometers is estimated to be 0.1–5% for the main anthropogenic greenhouse gases (CO₂, CH₄, N₂O, tropospheric ozone, CO) depending on the gas [35,36,37,38].

The actual location of the NDACC monitoring network measurement stations used in this work is shown in Figure 1; a list of the stations, their coordinates and altitude, conversion factors from ground measurements to sea level to match the satellite data, and the measurement periods for each of the considered gases are shown in

Table 2. List of the NDACC network stations involved in the analysis, indicating their geographical location, altitude, sea level conversion factors, and considered periods of observations.

№	Station	Latitude/Longitude, °	Altitude, m a.s.l.	Sea Level Conversion Factor	Measur. Period	Measured Parameter
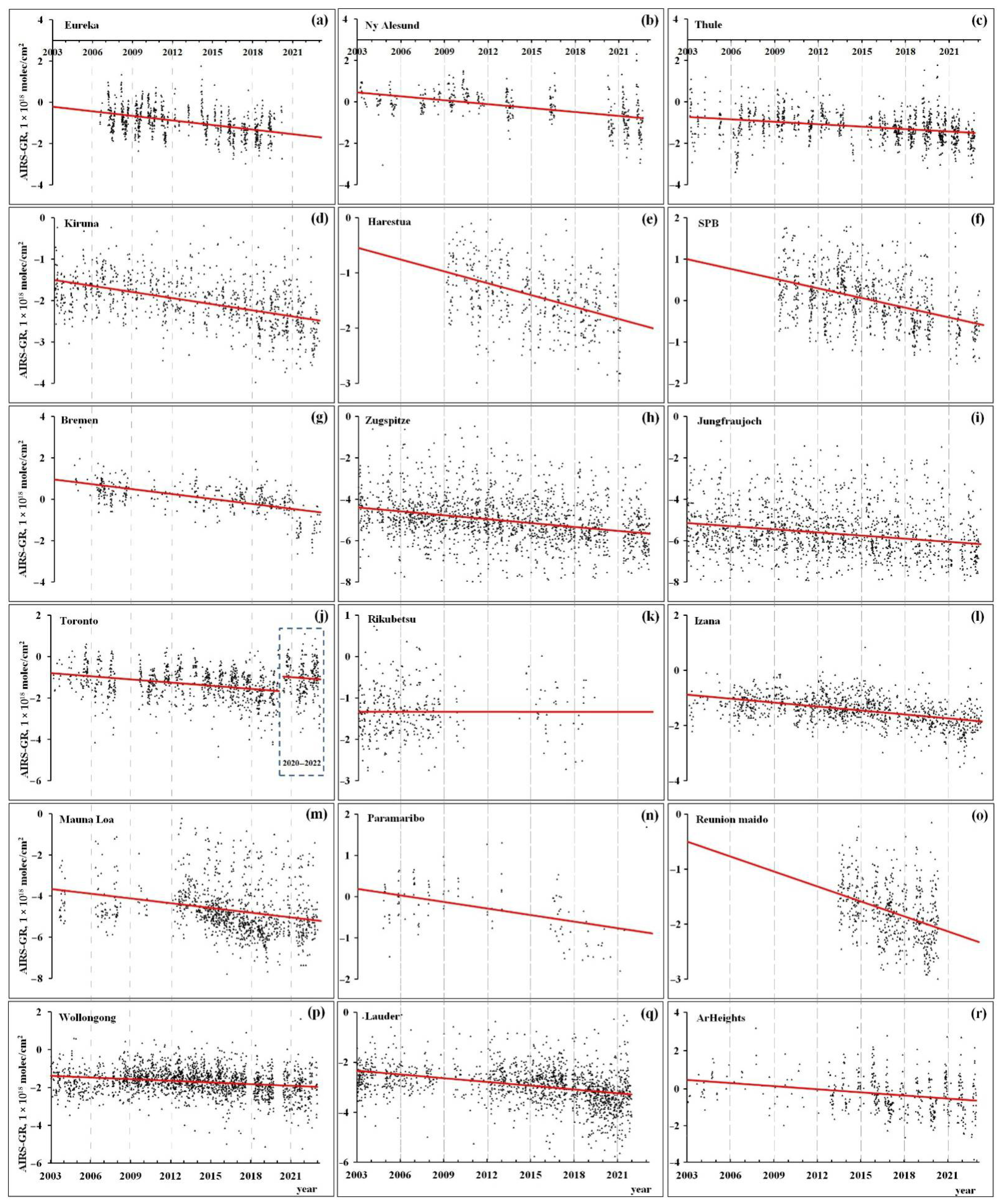
1	Eureka, Canada	80.0N/86.4W	610	0.926	2006–2020	CH4/CO
2	Ny Ålesund, Norway	78.9N/11.9E	15	0.998	2003–2022	CH4/CO
3	Thule, Greenland	76.5N/68.7W	220 *	0.973	2003–2022	CH4/CO
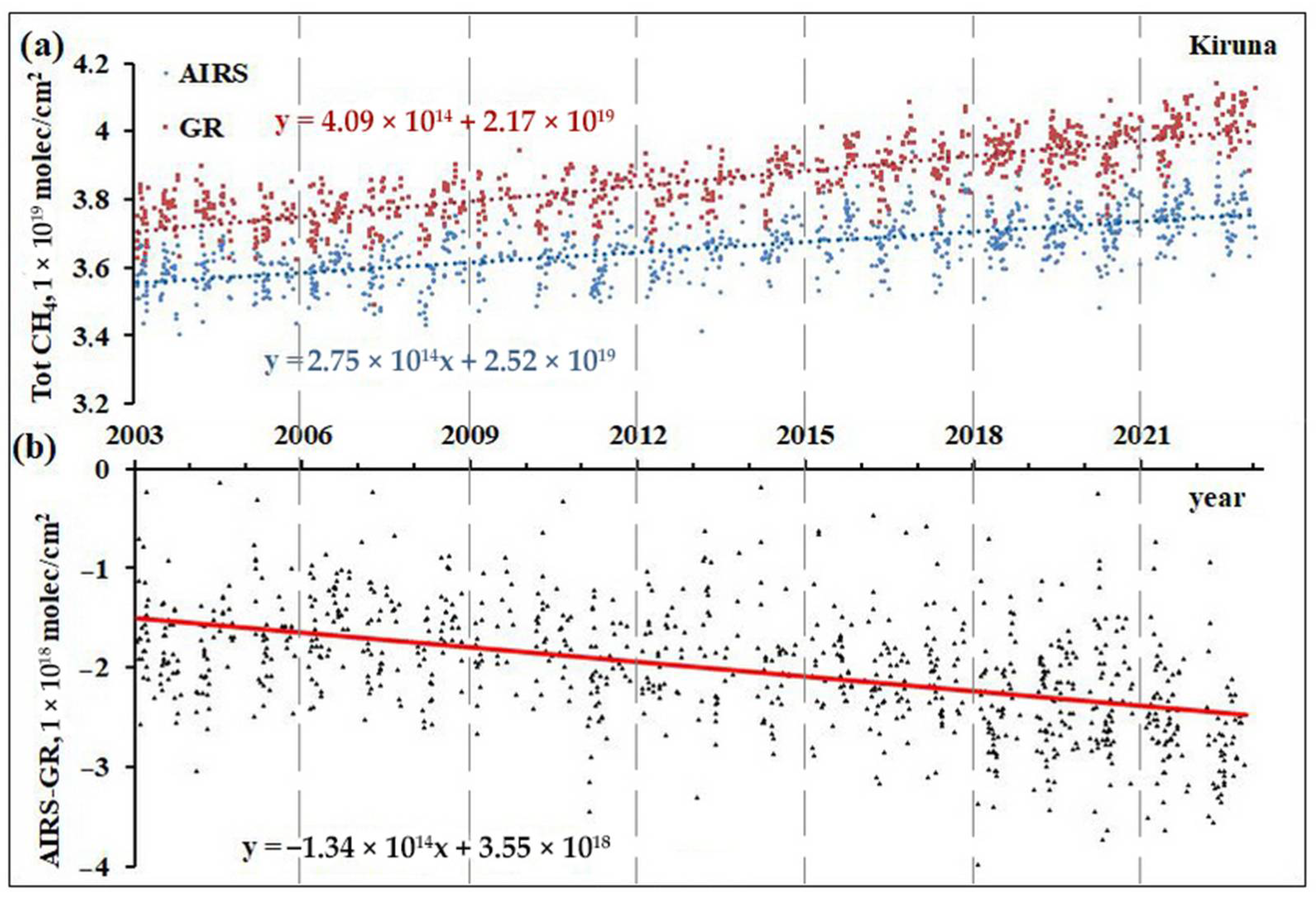
4	Kiruna, Sweden	67.8N/20.4E	419	0.949	2003–2022	CH4/CO
5	Harestua, Norway	60.2N/10.8E	596	0.928	2009–2020	CH4
					2003–2018	CO
6	St. Petersburg, Russian Federation	59.9N/29.8E	20	0.997	2009–2022	CH4/CO
7	Bremen, Germany	53.1N/8.8E	27	0.997	2003–2022	CH4/CO
8	Zugspitze, Germany	47.4N/11.0E	2964	0.690	2003–2022	CH4/CO
9	Jungfraujoch, Switzerland	46.5N/8.0E	3580	0.638	2003–2022	CH4/CO
10	Toronto—TAO, Canada	43.7N/79.4W	174	0.978	2002–2019 **	CH4
					2003–2022	CO
11	Rikubetsu, Japan	43.5N/143.8E	380	0.953	2003–2019	CH4
					2003–2018	CO
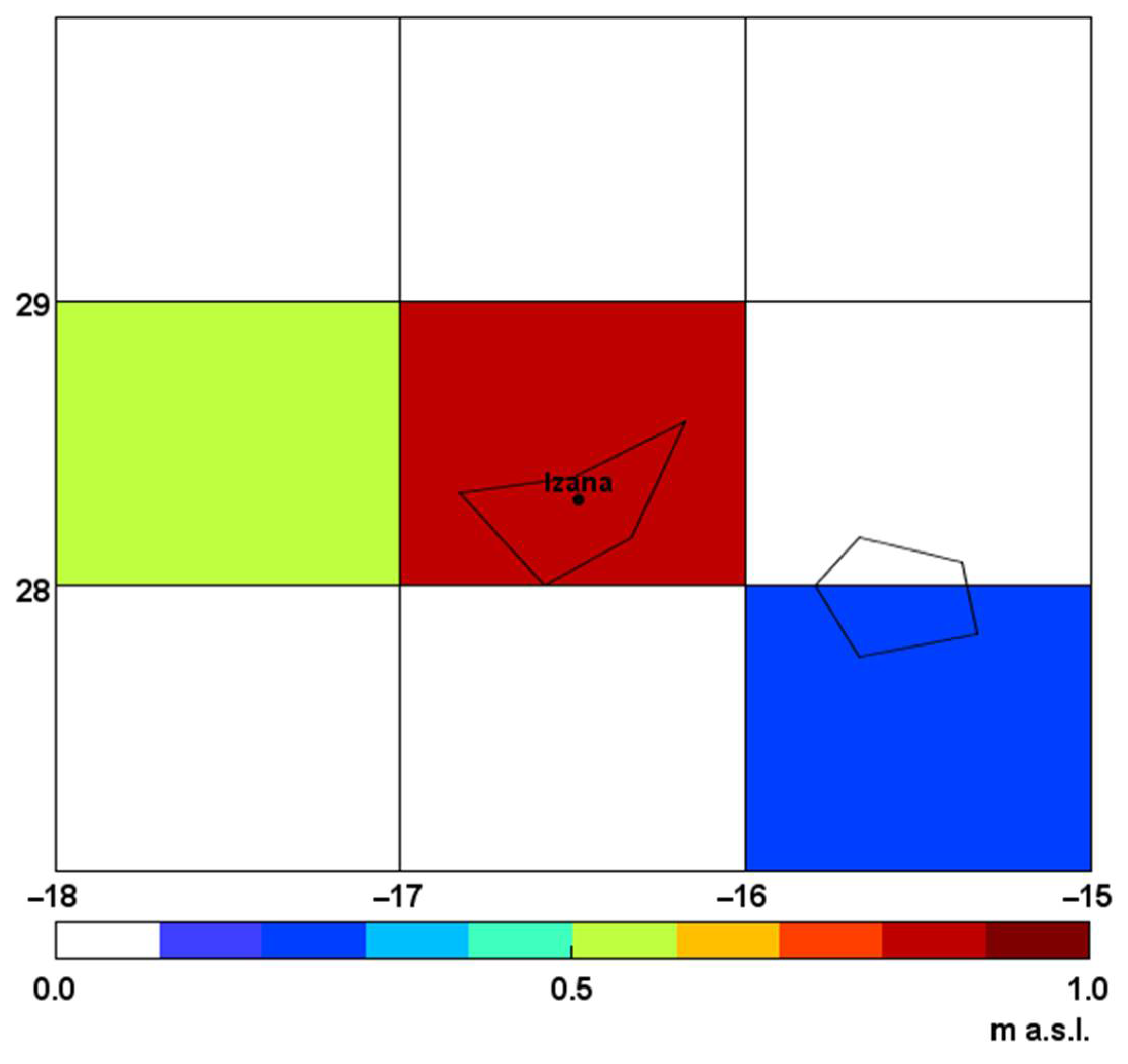
12	Izaña, Tenerife, Spain	28.3N/16.5W	2367	0.743	2003–2022	CH4/CO
13	Mauna Loa, HI, United States	19.5N/155.9W	3397	0.653	2003–2022	CH4/CO
14	Paramaribo, Suriname	5.7N/55.2W	23	0.997	2004–2022	CH4
					2004–2018	CO
15	Reunion Island, Maido, France	21.1S/55.4E	2155	0.763	2013–2019	CH4/CO
16	Wollongong, Australia	34.4S/150.9E	30	0.996	2003–2022	CH4/CO
17	Lauder, New Zealand	45.0S/169.7E	370	0.955	2003–2021	CH4/CO
18	Arrival Heights, Antarctica	77.8S/166.7E	184	0.977	2003–2022	CH4/CO

* On the NDACC website (https://ndacc.larc.nasa.gov/stations/thule-greenland, accessed 30 September 2024), the altitude of the Thule station in Greenland is given as 30–220 m above sea level (https://ndacc.larc.nasa.gov/stations/thule-greenland, accessed 30 September 2024). The official website of the station [https://www.thuleatmos-it.it/index.php, accessed 30 September 2024] states that the FTIR is located in building #1971 at an altitude of 220 m. The TC conversion factor for both impurities for the Thule station is calculated based on this information. ** At the Toronto TAO site in Canada, CH₄ TC data are available through 2022. However, in recent years (since 2020), the methane data from this site have raised questions (see additionally Figure 2 and Figure 3j). During the initial assessment of the quality of the Toronto measurements, a sharp shift (a “step”) in the measurement series was detected in 2020. In this work, a shorter CH₄ TC time series (from 2003 to 2019) was used in the calculation for Toronto.

.

At the first stage of the study, all available NDACC stations with the longest, most uniform, and statistically representative data series for the period coinciding with the measurement series of the AIRS satellite spectrometer were selected. Furthermore, the series of each NDACC ground station and the AIRS orbital spectrometer were synchronized, i.e., pairs of daily averages were selected. Thus, only those days were used where both the ground-based instrument and the orbiting spectrometer measured at each location, similar to [24].

After assessing the uniformity of the data distribution in the time series, the Rikubetsu and Paramaribo stations were excluded from the calculation of the average drift coefficient due to their statistical inadequacy. Not only is the number of comparison pairs (364 and 122, respectively, from 2003 to 2022) important, but also the regularity of the measurements during the study period. The number of comparison pairs for each monitoring site is shown in

Table 3. Slope coefficient of the linear regression (diurnal drift of the discrepancy) and ±95% confidence interval for the AIRS-GR CH₄ TC difference for each monitoring site and the number of pairs of comparisons for each monitoring site.

No.	Monitoring Site	Slope of Difference Trend, Molecules/cm2 (×10)13	Number of Synchronised Measurements (Pairs)
1	Eureka	−2.02 ± 2.86	810
2	Ny Alesund	−1.82 ± 3.05	417
3	Thule	−1.07 ± 2.02	1027
4	Kiruna	−1.34 ± 1.54	907
5	Harestua	−1.98 ± 4.50	462
6	SPB	−2.18 ± 3.02	859
7	Bremen	−2.42 ± 2.97	356
8	Zugspitze	−1.75 ± 2.76	1721
9	Jungfraujoch	−1.40 ± 3.27	1441
10	Toronto	−1.43 ± 2.96	863
11	Rikubetsu	ND *	364
12	Izana	−1.33 ± 1.48	1081
13	Mauna Loa	−2.14 ± 4.63	1082
14	Paramaribo	ND*	122
15	Reunion Maido	−2.54 ± 5.64	542
16	Wollongong	−0.81 ± 1.67	1963
17	Lauder	−1.37 ± 1.81	1578
18	Arrival Heights	−1.49 ± 5.06	492
	Average	−1.69 ± 3.08

* Not determined. Insufficient amount of data or uneven measurements prevent a correct assessment of the trend.

.

It is also worth mentioning the Bremen station, where the number of paired measurements is only 356, i.e., even less than at the Rikubetsu measurement point. However, the data here are evenly distributed over the time scale, which allows the station to be used in further calculations, while for the Rikubetsu monitoring station, the main number of measurements falls on 2003–2008 (306 pairs of values)—and only 58 pairs fall on the remaining years, which does not allow a reliable determination of the trend of the difference between satellite and ground measurements for the period under study.

Since the NDACC data on the total content are given for the altitude at which a specific instrument is located, and the AIRS Standard L3 v.6 IR AIRS Only Daily product provides the value of this parameter for sea level, for a correct comparison of the series and determination of the value of the AIRS-GR difference in physical terms, it was necessary to convert the ground-based measurement data to sea level using the barometric formula [39]. For this purpose, using information on the altitude of the station, the conversion factors K were determined (see Table 2) and calculated as follows:

$$K={\displaystyle \frac{P}{P_0}}$$

where:

• P—atmospheric pressure at the station level, mbar
• P₀—atmospheric pressure at sea level equal to 1013 mbar

The station level pressure is calculated as follows:

$$P=P_0\ast exp\left[-Mg{\displaystyle \frac{h-h_0}{RT}}\right]$$

where:

• P is pressure in the layer of given height h;
• P₀—pressure at sea level;
• h − h₀—height difference equal to h when calculated for sea level, m;
• R—universal gas constant;
• T—absolute temperature in Kelvin degrees;
• M—molar mass of air;
• g—gravitational acceleration.

Thus, the conversion factor of the value of total column content to sea level is equal to:

$$K=exp\left[-Mg{\displaystyle \frac{h-h_0}{RT}}\right]$$

NDACC network data are freely available. It should be noted that data from individual sites are not always regularly entered into Internet databases: some stations provide measurements almost in real time, others with a delay of one year or more, which also determines the choice of the analysis period from 2003 to 2022.

No outlier elimination methods (filtering of random values) were applied to the ground-based and satellite data series, i.e., all daily values were used except for a few unrealistic values, such as 1.95 × 10¹⁹ molecules/cm² in the original ground-based data series from the Bremen measurement site (NDACC).

Regression analysis (linear and orthogonal regression methods) was used to examine the parameters of correspondence between satellite measurements and ground-based data. When describing the distribution of the dataset, the equations of linear and orthogonal regression look the same: y = ax + b, where:

• a is the slope coefficient (hereinafter SC) of the regression
• b is the shift coefficient (error term) of the regression.

The orthogonal regression method is better suited for determining the dependence of two measurement series with an unknown spread of values. The linear regression equation mathematically models the unknown or dependent variable and the known or independent variable as a linear equation, so it is best suited for determining the TC trend and the AIRS-GR difference trend over a given time period. In this case, if the R between the compared data is close to 1, then both linear and orthogonal regressions will provide similar reliable results. The smaller the correlation coefficient, the greater the angle between the graphical displays of the linear and orthogonal regressions, and the greater the physical error in the dependence reflected by the simple linear regression equation. In this context, we used orthogonal regression analysis to assess the correlation parameters and linear regression to determine the trend with time dependence.

3. Results

3.1. AIRS v.6 CH₄ TC Product

As was previously noted [24], this discrepancy was manifested in the value of the linear trend. Based on the analysis of a shorter period (2003–2018), attention was drawn to the underestimation of CH₄ trends according to AIRS data. However, no study of the AIRS–GR difference was conducted before the present work (see also Figure 2).

The slope of the linear trend of the difference in CH₄ TC (AIRS-GR) calculated for all monitoring sites for the available periods is shown in Table 3 (given in [molecules/cm²/day ± 95% confidence interval]) and in Figure 3. For all analyzed monitoring sites, these values are negative and close to each other; the trend’s confidence interval for each site was smaller than the estimated trend’s value. The obtained results indicate a change in the AIRS spectrometer parameters over time. The observed pattern can be characterized as a pronounced and stable unidirectional drift of the satellite instrument readings. This systematic error requires dynamic correction of the AIRS data and subsequent comparisons to assess the quality of the result obtained.

It should be noted that the drift of the satellite instrument affects the fit parameters for both the daily and monthly mean series. In addition, the satellite instrument systematically underestimates the absolute values (e.g., Figure 2a) and, with them, the trend estimates (by a factor of about 1.5) at all the sites studied, compared to the results obtained from ground observations.

At some stations, including those at high latitudes, there is evidence of a seasonal variation in the difference, but due to the climatic characteristics at these points, there are significant gaps in the data series during each year. This is due to the fact that the stations have significantly fewer days suitable for spectroscopic measurements. In addition, the developers’ documentation and some researchers note a deterioration in the quality of AIRS measurements at high latitudes [12,40,41]. It is not possible to precisely determine the amplitude of the variations and the seasonal variation of the difference, but it can be said that for the Northern Hemisphere, the minimum values occur in May–June and the winter maximum is observed approximately in January–February (Eureca—80.05°N, Figure 3a; Ny Alesund—78.92°N, Figure 3b (but the station with the least data) and Thule—76.53°N, Figure 3c). In the Southern Hemisphere (Ar Height 77.83°S, Figure 3r), a mirror image situation is observed: the minimum falls on the winter months (January–February), and the maximum is shifted to October–November. It is known that in the Northern Hemisphere, at high latitudes, methane concentrations reach their maximum in winter and their minimum in summer (in the Southern Hemisphere, on the contrary) [42,43].

In order to perform a general and universal correction of orbital series, the average value of the drift of the discrepancy between satellite and ground series on CH₄ TC per day for the period from 2003 to 2022 was calculated—satellite spectrometer drift (SSD), equal to 1.69 × 10¹⁴ ± 3.08 × 10¹³ molecules/cm² per day (± 95% confidence interval). Station-by-station values of the difference trend with confidence intervals are given in Table 3.

In addition, a series of AIRS v6 L3 satellite measurements were dynamically (i.e., daily) corrected for the value of “discrepancy” drift, starting on 1 January 2003. The correction was applied as follows:

CH₄ TC SSD = CH₄ TC + (N − 1) × SSD

where:

CH₄ TC SSD—corrected daily satellite value of CH₄ TC, molecules/cm²

CH₄ TC—CH₄ total content, molecules/cm² AIRS V6 L3

N—ordinal number of the day starting from 01.01.2003

SSD is the drift coefficient of the satellite spectrometer, 1.69 × 10¹⁴ molecules/cm² per day.

The obtained new (corrected) series of satellite measurements were further used to determine the correlation parameters with ground-based data, as well as to estimate the CH₄ TC trends for the period 2003–2022. The correlation parameters between the orbital and ground data obtained for each site before and after correction are presented in

Table 4. Values of correlation coefficients R and orthogonal regression equation for different stations without applying the drift coefficient to the satellite data and with its application to all available pairs for the study period.

No.	Monitoring Site	Original Data		Corrected Data
		Correlation, R	Orthogonal Regression Equation	Correlation, R	Orthogonal Regression Equation
1	Eureka	0.62	0.62x + 1.35 × 1019	0.72	0.83x + 6.00 × 1018
2	Ny Alesund	0.74	0.65x + 1.31 × 1019	0.82	0.97x + 1.74 × 1018
3	Thule	0.66	0.86x + 3.99 × 1018	0.76	1.22x − 8.74 × 1018
4	Kiruna	0.84	0.78x + 6.54 × 1018	0.90	1.07x − 4.07 × 1018
5	Harestua	0.58	1.20x − 1.22 × 1019	0.75	0.91x + 2.63 × 1018
6	SPB	0.69	0.85x + 5.70 × 1018	0.78	1.06x − 1.53 × 1018
7	Bremen	0.81	0.62x + 1.48 × 1019	0.88	0.89x + 4.97 × 1018
8	Zugspitze	0.48	1.32x − 1.74 × 1019	0.61	1.53x − 2.49 × 1019
9	Jungfraujoch	0.46	1.39x − 2.08 × 1019	0.58	1.61x − 2.85 × 1019
10	Toronto	0.58	0.56x + 1.61 × 1019	0.67	0.89x + 3.72 × 1018
11	Rikubetsu	0.61	1.24x − 1.03 × 1019	0.67	1.61x − 2.43 × 1019
12	Izana	0.83	0.81x + 6.15 × 1018	0.90	1.14x − 6.51 × 1018
13	Mauna Loa	0.36	2.02x − 4.57 × 1019	0.49	2.01x − 4.44 × 1019
14	Paranaribo	0.58	0.37x + 2.41 × 1019	0.68	0.76x + 9.40 × 1018
15	Reunion Maido	0.46	1.36x − 1.63 × 1019	0.59	1.52x − 2.16 × 1019
16	Wollongong	0.69	1.04x − 3.34 × 1018	0.78	1.38x − 1.53 × 1019
17	Lauder	0.65	1.08x − 6.05 × 1018	0.77	1.36x − 1.58 × 1019
18	Arrival Heights	0.38	1.29x − 1.04 × 1019	0.53	1.58x − 1.99 × 1019

.

The application of this technique had a positive effect on the correlation of the studied series of orbital and ground-based data. At all stations, an increase in the correlation coefficient R was observed after the application of the dynamic correction, even at those points where the correlation was initially high (see Table 4). The relatively low correlation (R ~ 0.4–0.5) observed at the original series of four high-altitude stations (Zugspitze, Jungfraujoch, Mauna Loa and Reunion Maido) increased to R ~ 0.5–0.6 after the correction. The correlation at the high-altitude station of Arrival Heights, which initially had the lowest R of all the stations studied, also increased significantly.

At the lowland stations, as well as at Izana, the correlation increased to R ~ 0.7–0.9. The lower correlation coefficient at the high-altitude stations can be explained by the error in converting the measured TC value to sea level, as well as by the error of the satellite measurements themselves, related to the uncertainties at high altitude and the complex surface relief in the area of these stations.

The quality and peculiarities of the methane total content data from AIRS Only Ascending v.6 L3 require further investigation. When examining the parameters of agreement between satellite and ground measurements, it is worth mentioning separately the high-altitude stations above 1000 m a.s.l., for which the satellite incorrectly determines the altitude (

Table 5. Differences between actual altitude of NDACC monitoring sites and AIRS-based altitude.

No.	Monitoring Site	Actual Altitude, m a.s.l.	AIRS-Based Altitude, m a.s.l.
1	Zugspitze	2964	1264
2	Jungfraujoch	3580	1551
3	Izana	2367	1
4	Mauna Loa	3397	1301
5	Reunion Maido	2155	0

).

If we estimate the altitude of the 1° × 1° cell, in the center of which the measurement point under consideration is located, this value is close to sea level according to the AIRS L3 topography data (Topography variable) for the Izana and Reunion Maido stations, whereas the NDACC stations are actually high-mountain (see Table 5 and Figure 4 for Izana according to AIRS topography). They are located at an altitude of 2367 m and 2155 m, respectively, on small islands (about 50 km) surrounded by the sea. Since the coordinates of the measurement points for the AIRS spectrometer are the centers of a 1° × 1° cell, an error occurs in the determination of the parameter when the altitude values are averaged over the whole area. In this case, the vertical profile of the recalculation of the satellite values to sea level should probably not be applied in these cells, but nevertheless, the series of measurements obtained at these two stations fit quite well into the general dataset, together with other studied measurement points located below 1000 m above sea level (Figure 5). The application of the correction technique improved the observed general picture of correlation in this array from R = 0.71 to R = 0.76.

For the remaining three high-altitude stations (Zugspitze, Jungfraujoch, Mauna Loa), there is a significant underestimation of altitude due to the complex topography around the stations. This may lead to errors in determining AIRS CH₄ TC in some areas when using the universal vertical profile of methane distribution. Due to their location, these three stations should be classified as continental, i.e., on land (the Mauna Loa station is located in the center of a large island; the 1° × 1° cell in the center of which the station is located is almost entirely on land). At the same time, all three data series fit well into a separate dataset (Figure 5), which has its own initially high correlation (R = 0.62). Using the methodology developed by the authors, the correlation coefficient in this dataset improved further to R = 0.71.

As mentioned above, the measurements from all the analysed stations plotted on a correlation plot do not fit into a single dataset (see Figure 5a). In this case, the correlation parameters are also unsatisfactory (SC = 2.78, R = 0.38). Using a universal correction factor for the discrepancy drift did not solve the problem completely (SC = 2.71, R = 0.45 after correction, see Figure 5b). However, for the general dataset excluding the Zugspitze, Jungfraujoch and Mauna Loa stations, the technique was highly efficient for all individual stations (see Table 4).

Table 6. Estimated CH₄ TC trends (trend ± 95% confidence interval) for the studied stations from 2003 to 2022 for the original AIRS v6-GR NDAAC data series and with drift correction of the AIRS satellite spectrometer.

No.	Monitoring Site	Initial Trend, %/Year			Trend After Drift Correction, %/Year
		AIRS	GR	Δ, AIRS-GR	AIRS	Δ, AIRS-GR
1	Eureka	0.14 ± 0.03	0.33 ± 0.03	−0.19	0.30 ± 0.03	0.03
2	Ny Alesund	0.27 ± 0.03	0.44 ± 0.03	−0.17	0.42 ± 0.03	0.02
3	Thule	0.21 ± 0.02	0.31 ± 0.02	−0.10	0.37 ± 0.02	0.06
4	Kiruna	0.27 ± 0.02	0.39 ± 0.02	−0.11	0.43 ± 0.02	0.05
5	Harestua	0.25 ± 0.05	0.46 ± 0.05	−0.21	0.44 ± 0.04	−0.02
6	SPB	0.28 ± 0.03	0.48 ± 0.03	−0.20	0.43 ± 0.03	−0.05
7	Bremen	0.30 ± 0.03	0.53 ± 0.03	−0.23	0.46 ± 0.03	−0.07
8	Zugspitze	0.29 ± 0.03	0.42 ± 0.01	−0.13	0.47 ± 0.03	0.05
9	Jungfraujoch	0.33 ± 0.03	0.41 ± 0.02	−0.08	0.51 ± 0.03	0.10
10	Toronto	0.24 ± 0.02	0.37 ± 0.03	−0.12	0.40 ± 0.02	0.03
11	Rikubetsu	0.27 ± 0.04	0.26 ± 0.03	0.01	0.43 ± 0.04	0.18
12	Izana	0.32 ± 0.01	0.43 ± 0.01	−0.11	0.48 ± 0.01	0.04
13	Mauna Loa	0.30 ± 0.05	0.46 ± 0.02	−0.16	0.46 ± 0.04	0.01
14	Paranaribo	0.20 ± 0.03	0.35 ± 0.06	−0.15	0.35 ± 0.03	0
15	Reunion Maido	0.28 ± 0.05	0.50 ± 0.02	−0.22	0.44 ± 0.05	−0.06
16	Wollongong	0.33 ± 0.02	0.39 ± 0.01	−0.06	0.49 ± 0.02	0.10
17	Lauder	0.24 ± 0.02	0.36 ± 0.01	−0.11	0.41 ± 0.02	0.06
18	Arrival Heights	0.25 ± 0.05	0.40 ± 0.03	−0.15	0.41 ± 0.05	0.01
	Average	0.26 ± 0.03	0.40 ± 0.02		0.43 ± 0.03

shows the calculated values of the CH₄ TC trend based on the original and corrected data series.

When assessing trends based on AIRS v.6 data for the period 2003 to 2022, a systematic underestimation of the trend value by the satellite is observed, on average by ~1.5 times relative to the estimates based on ground-based measurements at NDACC stations. When the dynamic correction for the “discrepancy” drift of the satellite spectrometer is applied using a universal coefficient, the trend estimates based on the orbital and ground-based series almost match at each site (with accuracy up to the 95% confidence interval, see Table 6). The overall discrepancy in the average trend estimates for all CH₄ TC stations after correction is within 10% of the trend value, indicating the effectiveness of the technique developed.

We also investigated the seasonal features of the AIRS-GR CH₄ TC discrepancy drift. As it turned out, for all four seasons, the drift characteristics were close in both direction and magnitude to a similar estimate obtained for the entire time series (see Table S1 in the Supplementary Materials).

Thus, only for the winter and spring months, the average relative difference of the obtained drift with the annual estimate was 8% for winter and 6.5% for spring, which is explained by the absence of high-latitude stations in the analysis, where measurements are not carried out under polar night conditions. In summer and autumn, the differences were 4% and 0%, respectively. The seasonal estimates of the AIRS-GR CH₄ TC discrepancy drift obtained are close to similar estimates based on complete measurement series, thus confirming our initial conclusion.

To illustrate our results, the CH₄ TC trend distributions for the Northern Hemisphere and the period 2003–2022 and their confidence intervals according to AIRS v6 before and after the application of the correction are shown in Supplementary Materials, Figures S1 and S2.

3.2. AIRS v.6 CO TC Product

Another satellite product analyzed during the work was the AIRS v6 CO TC. As in the case of the CH₄ TC, in order to determine the quality of the satellite data, the slope of the linear trend of the AIRS-GR difference was determined for all available periods (given in [molecules/cm²/day]) for each measurement site from Table 2. The analysis showed that the slopes of the AIRS-GR values for different sites have different directions, vary significantly in magnitude and are not statistically significant at most stations, i.e., the confidence interval exceeds the estimated value of the trend (see Figure 6,

Table 7. Slope coefficient of linear regression ± 95% confidence interval for AIRS-GR CO TC difference, correlation coefficient R, and AIRS and Gr trends (± 95% confidence interval) for each monitoring site for all available periods.

No.	Monitoring Site	Slope of Difference, Molecules/cm2 (×10)12	R	AIRS Trend, %/Year	GR Trend, %/Year	Δ, AIRS-GR	Number of Compared Pairs
1	Eureka	36.8 ± 8.20	0.80	−0.13 ± 0.18	−0.84 ± 0.26	0.70	777
2	NY Alesund	19.2 ± 5.61	0.95	−0.79 ± 0.24	−1.15 ± 0.30	0.36	415
3	Thule	30.3 ± 3.28	0.93	−0.60 ± 0.10	−1.15 ± 0.14	0.54	1315
4	Kiruna	10.1 ± 3.72	0.92	−0.80 ± 0.14	−0.93 ± 0.16	0.13	752
5	Harestua	13.8 ± 5.39	0.91	−1.19 ± 0.20	−1.37 ± 0.21	0.18	681
6	SPB	−4.89 ± 5.25	0.93	−0.89 ± 0.25	−0.80 ± 0.26	0.10	793
7	Bremen	−1.33 ± 6.12	0.90	−0.98 ± 0.23	−0.93 ± 0.22	0.05	428
8	Zugspitse	−5.59 ± 1.99	0.91	−0.78 ± 0.10	−0.61 ± 0.09	0.17	2137
9	Jungfrau	−10.9 ± 2.78	0.92	−1.11 ± 0.15	−0.82 ± 0.14	0.29	1219
10	Toronto	−3.93 ± 4.45	0.85	−0.87 ± 0.14	−0.76 ± 0.14	0.11	1479
11	Rikubetsu	−5.17 ± 11.2	0.93	−1.40 ± 0.42	−1.21 ± 0.43	0.19	352
12	Izana	−1.88 ± 3.16	0.88	−0.45 ± 0.13	−0.43 ± 0.13	0.01	1154
13	Mauna Loa	−8.64 ± 7.18	0.85	−0.95 ± 0.26	−0.73 ± 0.30	0.23	1278
14	Paramaribo	−8.14 ± 11.1	0.87	−0.89 ± 0.39	−0.71 ± 0.37	0.17	175
15	Reunion maido	0.76 ± 8.95	0.94	1.27 ± 0.59	1.23 ± 0.62	0.04	818
16	Wollongong	6.28 ± 3.80	0.79	−0.33 ± 0.13	−0.48 ± 0.16	0.15	2579
17	Lauder	−7.81 ± 1.96	0.89	−0.03 ± 0.13	0.22 ± 0.14	0.25	1695
18	Arrival Heights	−14.2 ± 3.22	0.90	−0.28 ± 0.26	0.24 ± 0.31	0.52	483
	Average			−0.62 ± 0.22	−0.62 ± 0.24

).

The reason for such results is the CO TC pronounced seasonal variations (background CO content has a maximum in February–March and a minimum in summer months and September [12,43,44,45]), which makes the factor of statistical representativeness and uniformity of the data over the study period important. For stations where the poor statistical availability is caused by the absence of data for certain seasons (e.g., high-latitude stations such as Eureka, NY Alesund, Thule and Arrival Heights, where ground measurements are only made for half of the calendar year due to the polar night), the slope value of the AIRS-GR difference is only a seasonal estimate, which may have an error up to its sign.

In general, it is impossible to define the observed situation as the drift of the satellite instrument. In this case, it is more appropriate to speak about the systematic error of the measurements in one or the other direction for each station separately, which is related to a complex set of factors, including the peculiarities of the sensitivity of the AIRS spectrometer at different altitudes, at middle or high latitudes, and under different conditions (background or polluted atmosphere), as well as the sensitivity of the AIRS satellite spectrometer to significant anthropogenic influences, including emissions from fires. This is indirectly confirmed by the fact that on the AIRS-GR difference plots for the CO TC, the presence of seasonal fluctuations is observed at almost all stations with good statistical representativeness, which requires further investigation.

Thus, the AIRS v6 CO TC Standard L3 Only Daily satellite product is an example of the inapplicability of the developed methodology, as the validation of these data requires a different approach for a number of reasons described above.

Furthermore, the estimates indicate that the AIRS v.6 L3 CO TC data reflect the observed picture quite well. Note the high correlation of the initial series (i.e., without removing the “artefact” values) of the ground-based and satellite measurements, both between stations (the correlation coefficient R varies from 0.80 to 0.95) and in the general dataset for all the stations studied (correlation coefficient R = 0.94, see Figure 7, Table 7).

The data fit well into a single series, with the slope coefficient of the orthogonal regression line close to 1 and equal to 0.90 (see Figure 7). The residual analysis plot for AIRS-GR difference for CO TC data, at all stations and for the full time period 2003–2022 (see Figure S4 from the Supplementary Materials), provides an additional explanation of Figure 7. This demonstrates that the distribution points are randomly located around zero and that the residual analysis graph does not indicate the presence of any other patterns.

An assessment of the trends based on the original series of satellite and ground measurements is given in Table 7. As can be seen, the trends are unidirectional and correlate well with each other for stations with uniform statistical data. The mean trend of both ground-based and satellite measurements for all stations used in the study is in agreement up to one-tenth of the confidence interval (AIRS −0.62 ± 0.22; GR −0.62 ± 0.24).

The reasons for the differences in trend estimates obtained from satellite and ground-based data at local levels may be different and require separate, detailed study. These reasons may include discrepancies between the a priori profiles included in the calculations and the actual profiles, or inaccuracies in accounting for the absorption of other gases within the used spectral range. In addition, knowing the features of the altitude sensitivity function of the AIRS, future studies should pay attention to the level of pollution in the areas of specific stations, the processes of long-range transport of pollution from areas with intense emissions (for example, areas of natural fires), as well as the height of the atmospheric boundary layer.

The seasonal features of the AIRS-GR CO TC discrepancy drift for all four seasons were close in direction and magnitude to similar estimates obtained for the entire time series of all ground sites (see Table S2 in the Supplementary Materials). As can be seen in Table S2, the CO TC drift at different stations has different directions and, as a rule, low statistical significance.

To demonstrate our results, the CO TC trend distribution for the Northern Hemisphere and the period 2003–2022 and its confidence intervals are given in Supplementary Materials, Figure S3.

4. Discussion

The comparisons performed revealed that the conformity characteristics of the CH₄ AIRS V6 measurements with the NDACC ground data, as well as the AIRS-GR difference, change over time. The trends of these changes were found to be statistically significant and unidirectional at all comparison points. However, a similar effect was not observed for CO AIRS measurements. Put briefly, when measuring two different impurities with the same orbital instrument, degradation of the quality of measurements was established in one case, but not in the other.

There may be several reasons for this. Note that the CH₄ and CO measurements are carried out in different spectral channels and ranges that are quite widely spaced from each other (4.5 µm and 7.7 µm). We could not find any information in the AIRS documentation suggesting that different radiation receivers or adaptive and amplifying paths are used for these ranges. However, this is usually the case in ground spectrometers. According to our main assumption, the parameters of the instrument changed in the 8 μm spectral area, where methane is measured. The causes and sources of this change are unclear and require further study. We are not suggesting that there is only one possible reason; there may be several. In this case, we simply state the fact that there is a drift in the characteristics of compliance and argue that such studies could be relevant to many other orbital measurements and products.

Another possible reason for the deterioration in the fit between AIRS CH₄ measurements and ground-based data could be the insufficient consideration of spatial and temporal variability and trends in water vapour content and profiles in the AIRS calculation algorithm. As discussed above, AIRS uses a spectral interval centered around 7.7 μm for methane, which largely overlaps with the H₂O absorption band [16] and significantly complicates the calculations. The dependence on H₂O content is weaker for CO due to the greater isolation of the CO absorption band in the ~4.5 μm spectral region (free of strong H₂O absorption bands), as confirmed indirectly by the better correlation between satellite and ground-based measurements. However, the seasonal dependence of the AIRS-GR difference, evident at many comparison points (see Figure 6), indicates the need for thorough investigation of this issue for CO as well. For example, it was found that the global increase in water vapour was 0.21% per year between 2005 and 2020, while regional trends varied significantly (from a slight decrease at a rate of up to 0.1% per year to an increase of ~1% per year [46]). At the same time, detailed and representative data on long-term moisture content variability are not available in the scientific literature.

Thus, another possible explanation for the results we obtained is that they are due to long-term and/or seasonal changes in the content and vertical profiles of atmospheric gases whose absorption bands are contained in the spectral intervals used by the satellite, and these perhaps are not taken into account sufficiently in the calculation algorithms. Clarifying this issue is beyond the scope of this article and would require additional, careful study. We propose a fairly simple and effective method for correcting orbital data in the event of the detection of long-term, unidirectional drift in the discrepancy between satellite sensor readings and those of reference ground-based instruments.

In addition, we note that the magnitude of the free term A of the linear (this type of analysis was used to study trends) and orthogonal (this type of analysis was used to calculate correlation characteristics) regression in the station-by-station comparison of orbital and ground-based series, for both the original and corrected data, turned out to be different in magnitude and direction for both impurities and individual sites. This parameter (A) has little effect on the estimates of the difference trend; therefore, the slope coefficient of the difference is used to estimate the discrepancy between satellite and ground-based measurements, since it is precisely this coefficient that is responsible for the possible drift of the satellite instrument in this case. The reasons and sources of differences in parameter A for different sites cannot be analyzed at the moment and require additional research and possible consideration in our future work.

To sum up, we note that the main reason for the differences is the different spectral resolution of ground-based and orbital instruments, different forms of the vertical sensitivity function, and even different spectral regions. Thus, the AIRS instrument uses a region of about 7.7 μm for methane measurements, while NDACC spectrometers measure methane in the region of 3.5 μm [47]. In addition, AIRS has low sensitivity in the surface layers of the atmosphere. The difference in slope values between different comparison sites depends on seasonal features, the observation period, the uniformity of the ground series, landscape complexity, and the pollution level (polluted, slightly polluted, or background conditions) of each measurement site.

5. Conclusions

Significant long-term changes in the parameters of correspondence between the orbital data of the CH₄ AIRS Standard L3 v.6 IR AIRS Only Daily and the ground-based observations of the NDACC stations have been identified.

The trend of the “discrepancy” (the difference between measurements of the AIRS v6 L3 orbital spectrometer and ground measurements of the NDACC network stations) for the CH₄ TC for the period 2003 to 2022 for all available paired values is negative at all studied sites and is defined as a long-term drift of the satellite instrument parameters.

The average slope coefficient of the discrepancy trend line for the CH₄ TC in physical terms (SSD), calculated on the basis of an analysis of data from 18 measurement sites, was determined to be 1.69 × 10¹⁴ molecules/cm² per day.

A method for dynamic correction of the data series of CH₄ orbital measurements with a correction for the universal coefficient (daily drift of the “discrepancy”) has been developed and successfully applied.

After the correction, a significant improvement in the correlation parameters between the corrected orbital and ground-based data was obtained. In addition, the discrepancy between the CH₄ TC trend estimates obtained using the corrected orbital series and those based on ground-based measurements became significantly smaller for each station individually and practically identical on average for all stations: AIRS: 0.43 ± 0.03%/yr; GR: 0.40 ± 0.02%/yr; compared to the original AIRS estimate of 0.26 ± 0.03%/yr.

For the CO TC orbital data, no drift of the satellite instrument parameters was found. The coefficient of difference between satellite and ground measurements AIRS—GR can have different signs and is statistically insignificant for most stations.

The data do not require any correction within the developed methodology, since the initial series of total CO concentration without filtering have a good correlation in the whole dataset (R = 0.94, the slope of the orthogonal regression line is 0.9), and the average trend of the CO total content for 18 studied sites coincides according to the estimates of satellite and ground-based measurements and is equal to −0.62 ± 0.22 and −0.62 ± 0.24, respectively.

The developed method is universal, i.e., it can be used in validation studies of other long-term orbital measurements if required.