Underwater Sound Speed Profile Inversion Based on Res-SACNN from Different Spatiotemporal Dimensions
Abstract
1. Introduction
- By designing a dual-channel CNN architecture, multi-source data fusion with spatiotemporal mismatch is achieved, which extracts spatiotemporal features of sea-surface parameters.
- By integrating the residual network and self-attention mechanism into the CNN framework, a nonlinear mapping model between surface parameters and sound speed field is established, which improves the SSP inversion accuracy.
- By conducting multi-regional and seasonal evaluations of the deep learning model, spatiotemporal generalization capabilities are enhanced, which mitigates the spatiotemporal sensitivity limitations of sEOF-r methods.
2. Materials and Methods
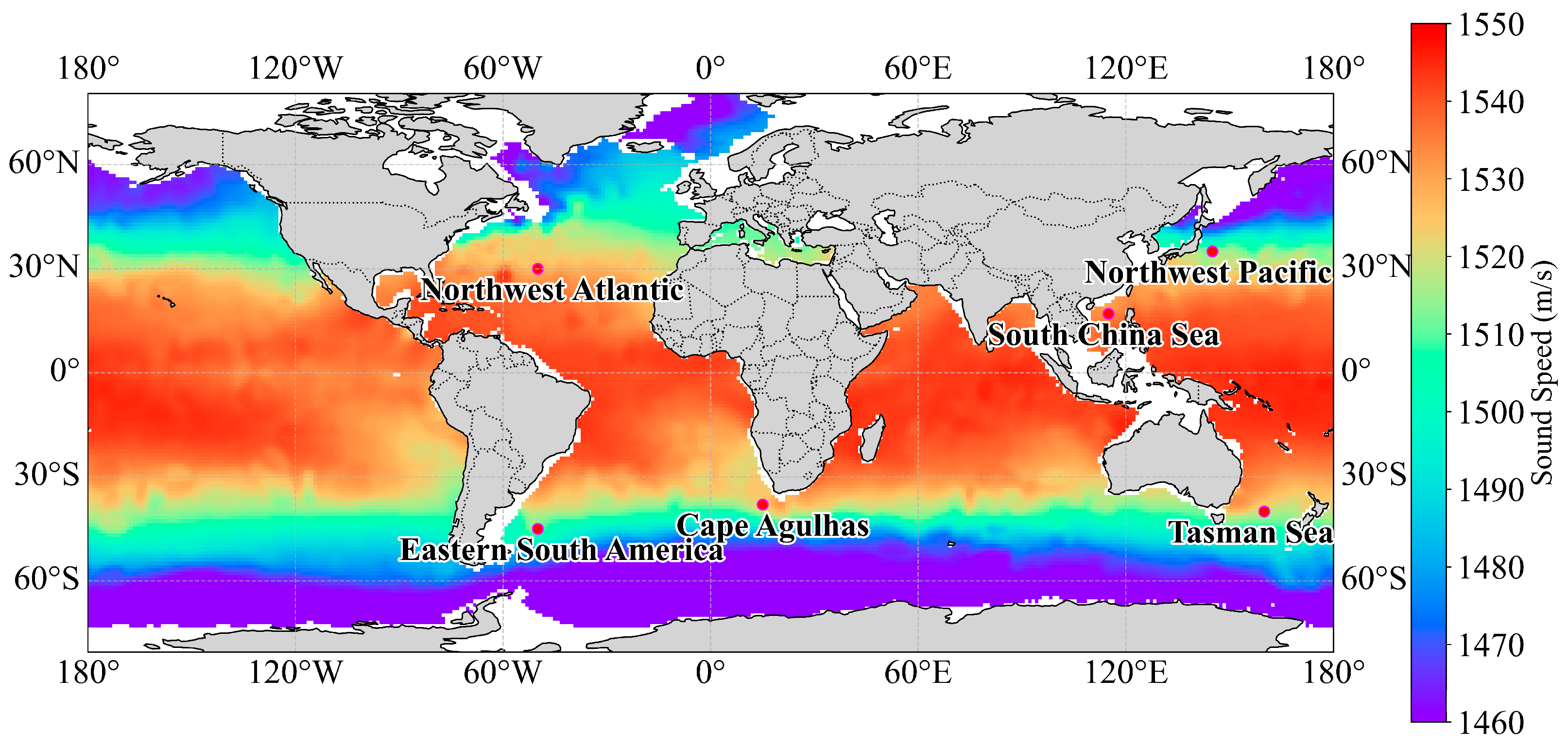
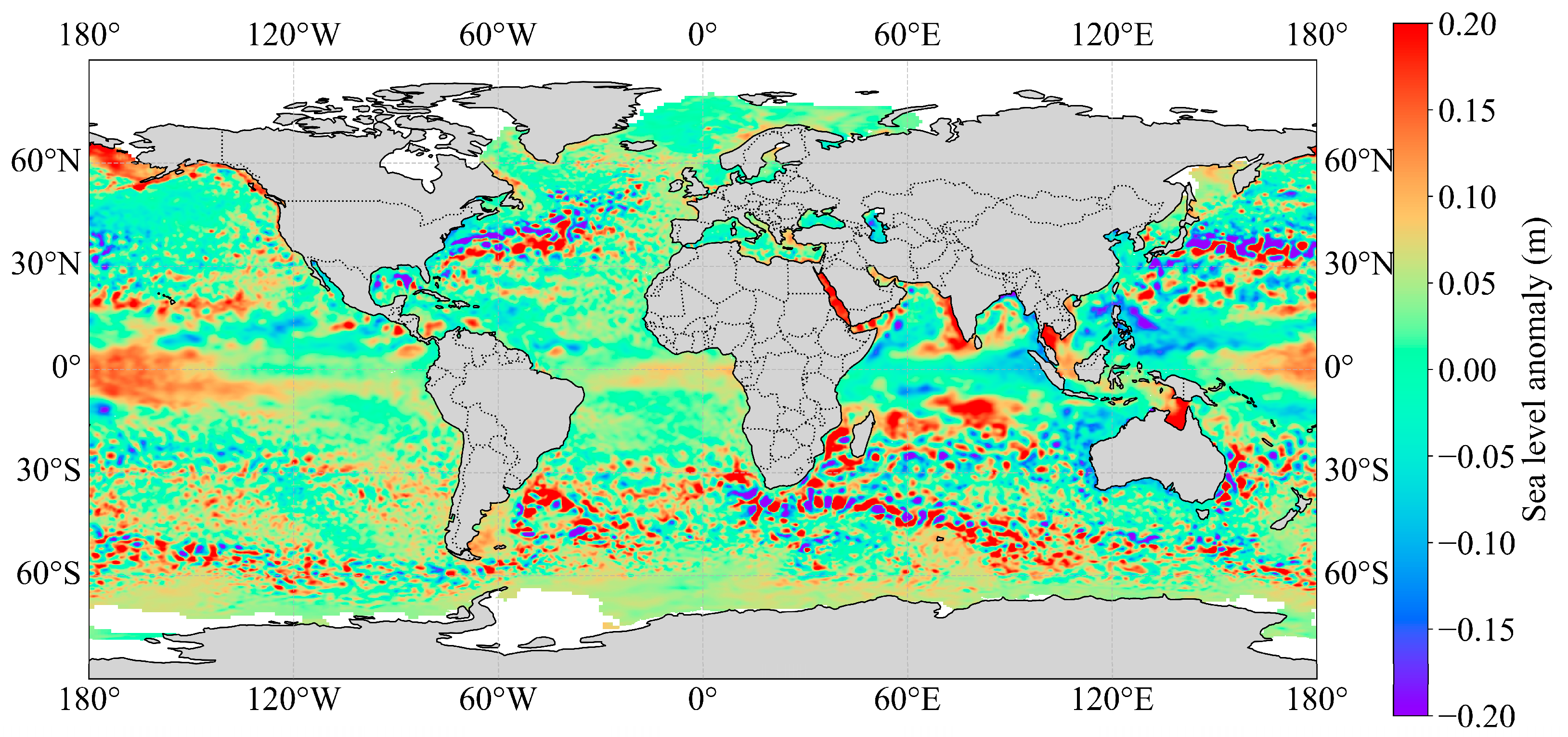
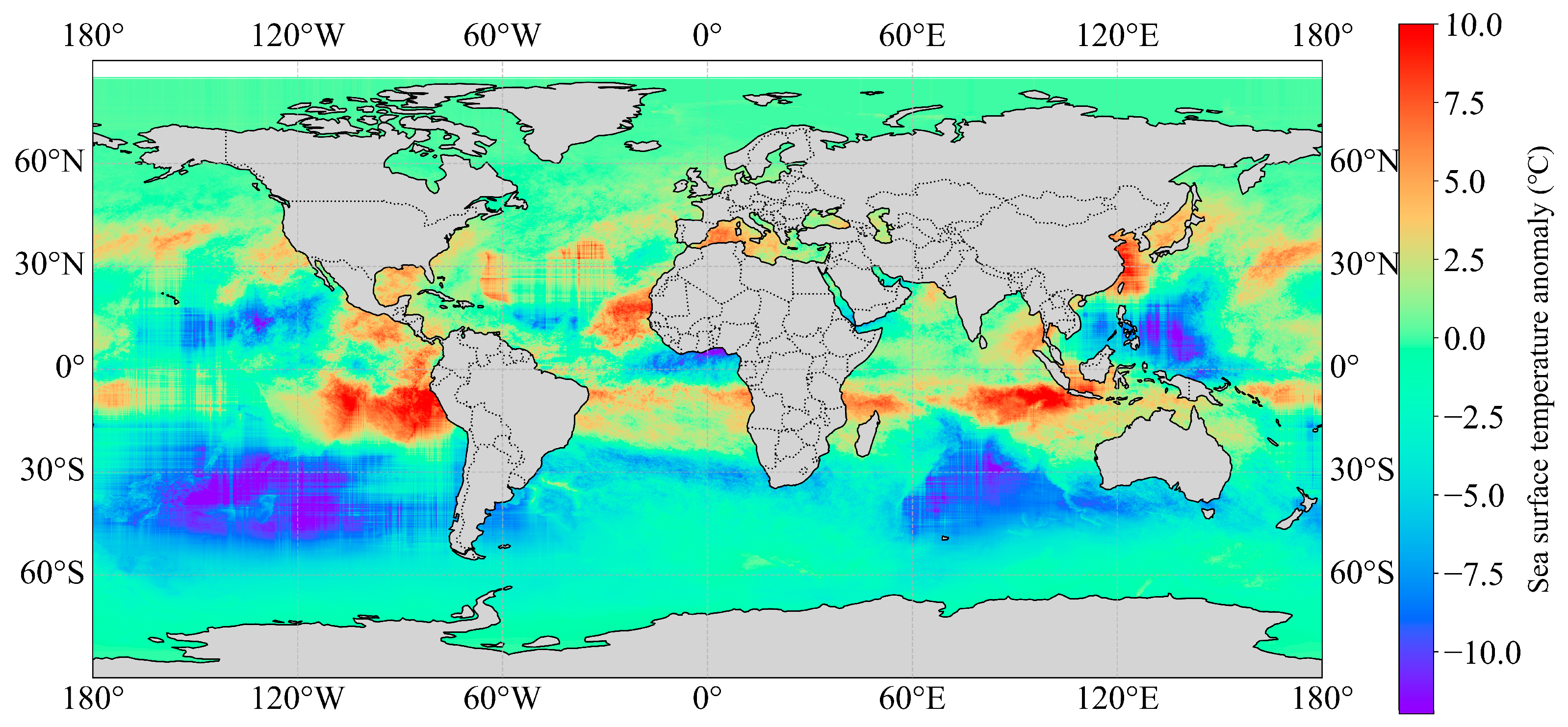
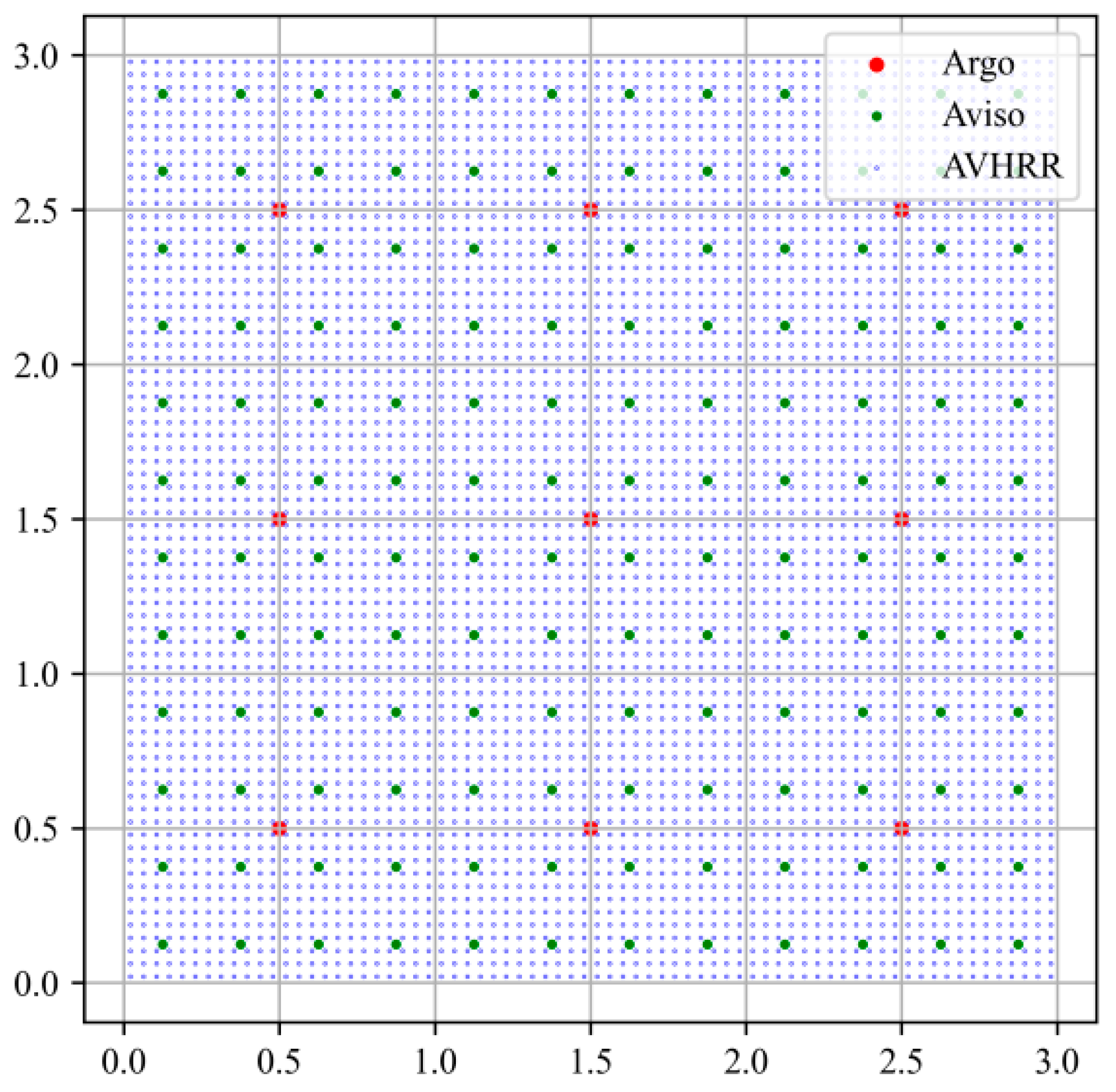
2.1. Data Preparation and Preprocessing
- Average the two SST observations of AVHRR per day and store them as the SST data of that day.
- Conduct a separate study for each month. Take the monthly average SST of that month, and subtract the monthly average SST from the SST of that day stored in the previous step to obtain the SSTA of each day.
- Save the SSTA data in a manner of monthly averaging.
2.2. Single Empirical Orthogonal Function Regression Method
2.3. Res-SACNN Model
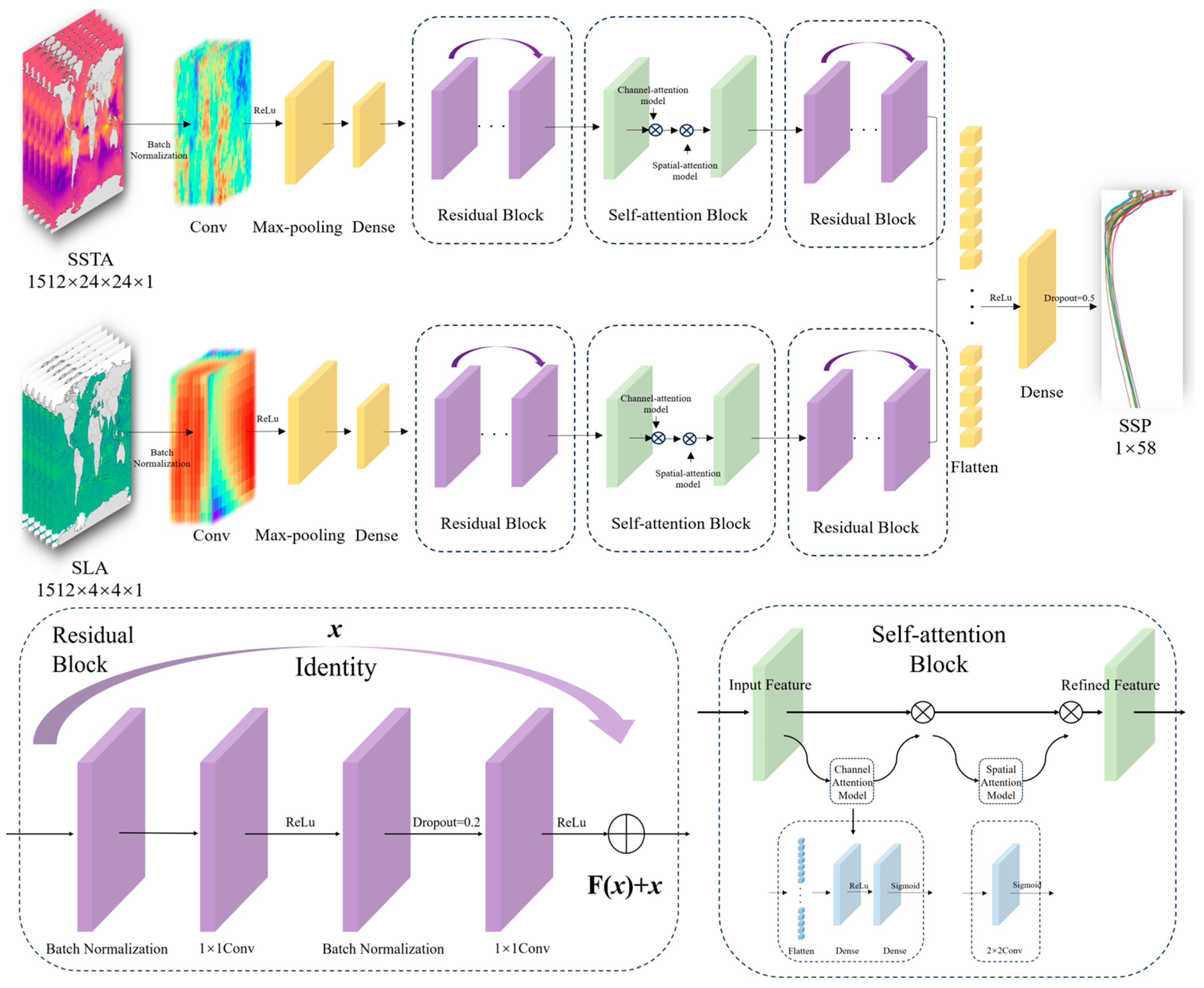
2.3.1. Construction of the Res-SACNN Model
2.3.2. Multi-Source Data Fusion
2.3.3. The Training Process of the Res-SACNN Model
- Data Normalization: Normalization processing is a common data preprocessing method in machine learning. Due to the different magnitudes and large data values of the three types of data, SLA, SSTA, and SSP, to ensure the convergence of the model, we use the Min–Max normalization method to constrain the training data within the [0, 1] interval to facilitate the effect of feature extraction. The normalization calculation formula is as follows:where is the normalized datais the normalized data, X is the original data, is the minimum value of the original data, and is the maximum value of the original data.
- Feature Extraction: We use convolution operations and max-pooling operations to extract features from SLA and SSTA. The convolution operation is mainly used to extract local features from the input data, and the max-pooling operation is a down-sampling method that captures local patterns by sliding the convolution kernel to generate multi-level feature representations; then, the down-sampling operation is used to reduce redundant information and enhance the translation invariance and robustness of the features. In this model, the data sizes of SLA and SSTA are different. Therefore, in the process of feature extraction, different convolution kernels and pooling kernels are adopted for the two channels for feature extraction.
- Residual Network Module [33]: The design of the residual network module is an important part of this model. Its structure contains two convolutional layers and two batch normalization layers. In this module, we also introduce a regularization layer to reduce the dependence between neurons and thereby effectively suppress the occurrence of overfitting. The generalization ability of the model can be improved, making it more adaptable and stable when dealing with complex data.
- Self-Attention Mechanism [34]: This mechanism mainly consists of two core modules, the channel module and the spatial module. Among them, the core structure of the channel module includes one unfolding layer and two fully connected layers. This design can effectively capture the global information association between different channels, thereby enhancing the richness of feature expression. The spatial module is implemented by a convolutional layer with a convolution kernel size of 2 × 2, which is mainly used to extract local spatial features and capture the spatial dependence between pixels. These two modules work together to enable the model to better understand the feature distribution of the input data on multiple scales.
- Dual-Channel Weight Setting: In the design of this model, differentiated weight settings are made for the dual-channel data (SLA and SSTA). SLA is a key input variable and plays a more important role in the SSP inversion process [27], and its impact on the model performance is particularly significant; while SSTA also provides valuable information, but its role is relatively more auxiliary. Based on this characteristic, we assigned different weights to SLA and SSTA and set the weight ratio of the two to 1.5:1. This design highlights the dominant position of SLA, while taking into account the supplementary role of SSTA, thereby more effectively capturing the complex nonlinear relationship between sea surface parameters and SSP.
- Model Evaluation: In order to comprehensively and objectively reflect the inversion performance of this model, we use MSE as the loss function and RMSE as the error indicator. The calculation formulas are as follows:where is the true value, and is the predicted value.
3. Results
3.1. Experimental Design
- Experiments in different time domains.
- Experiments in different geographical regions domains.
3.2. Comprehensive Experiments
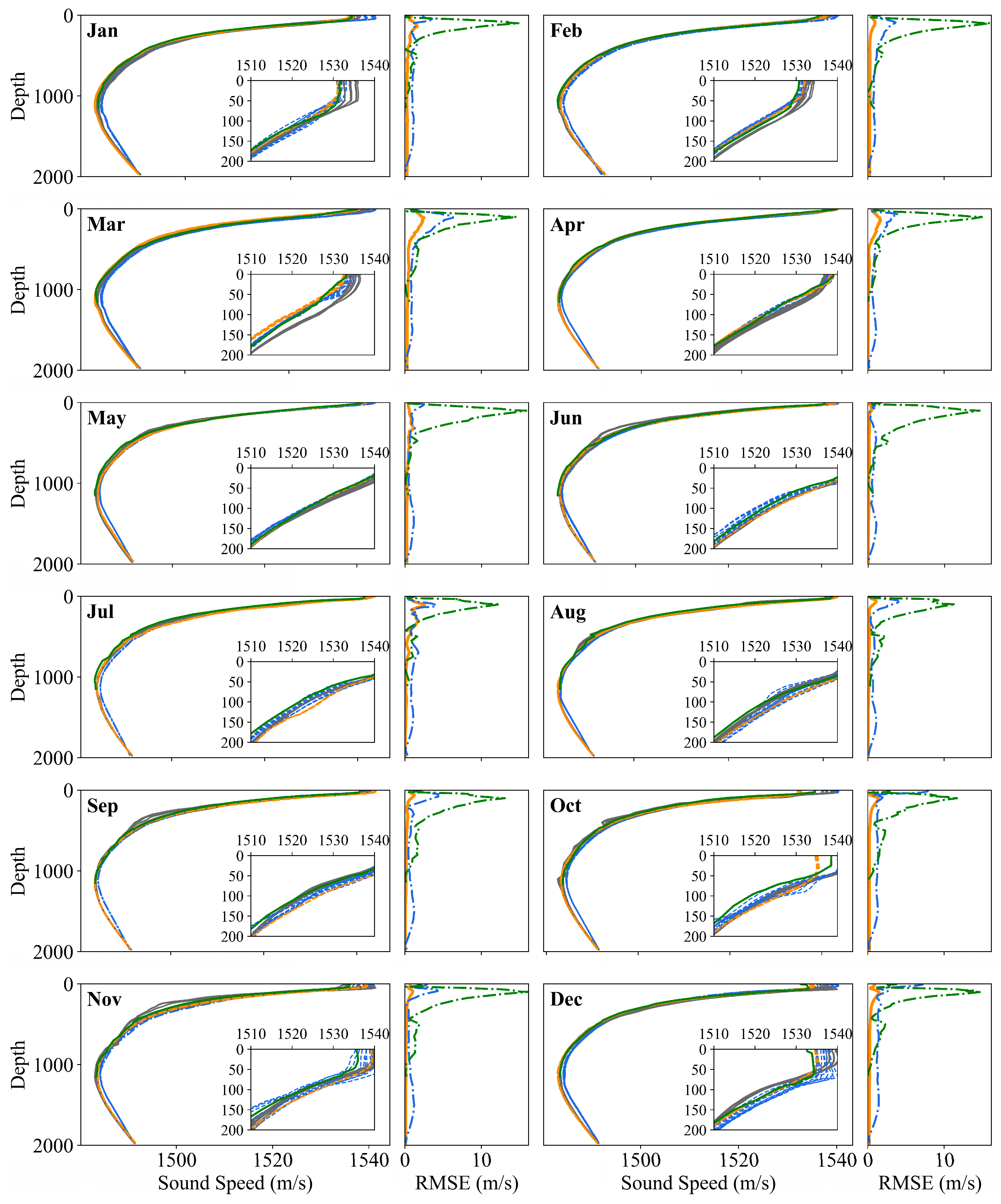
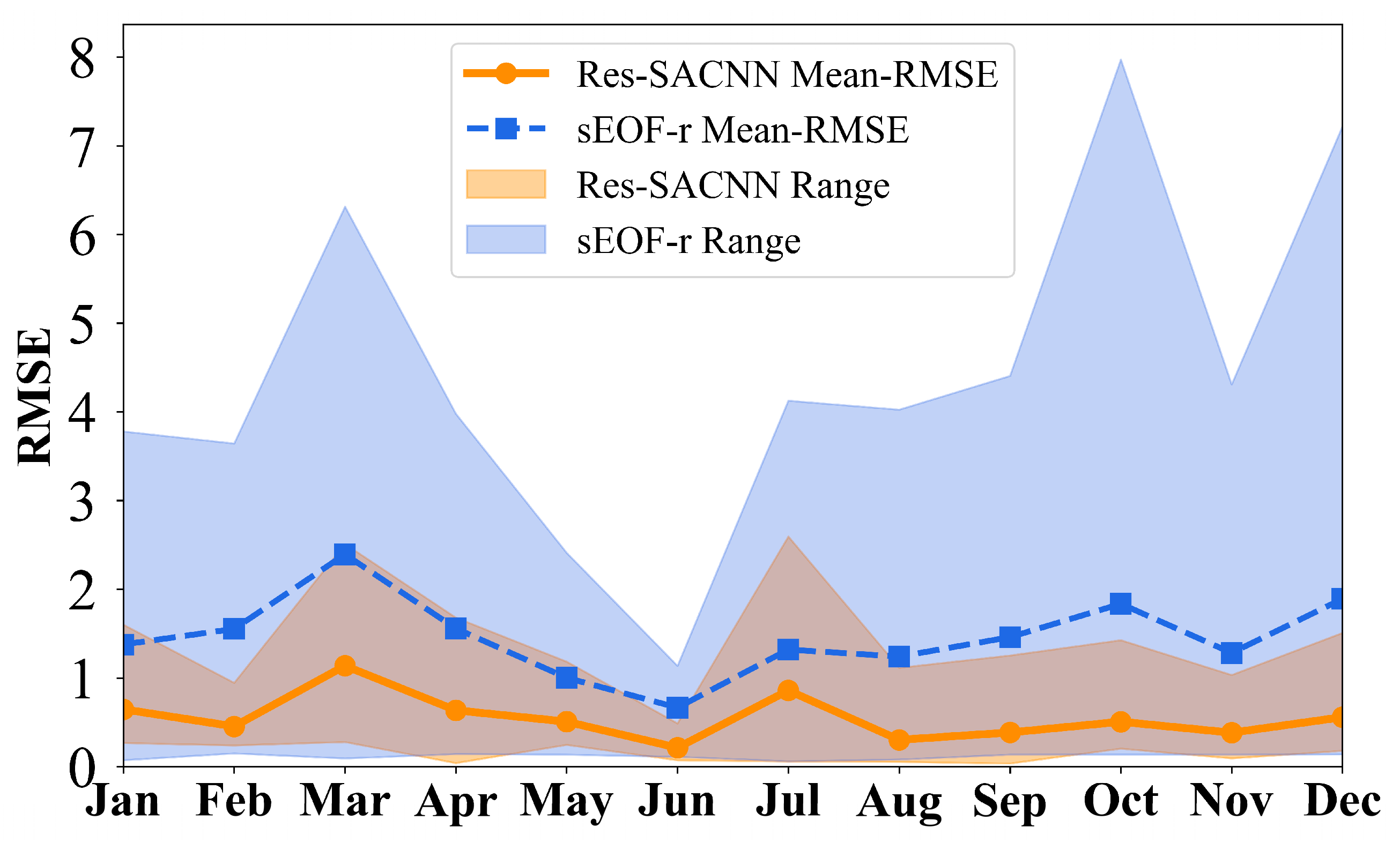
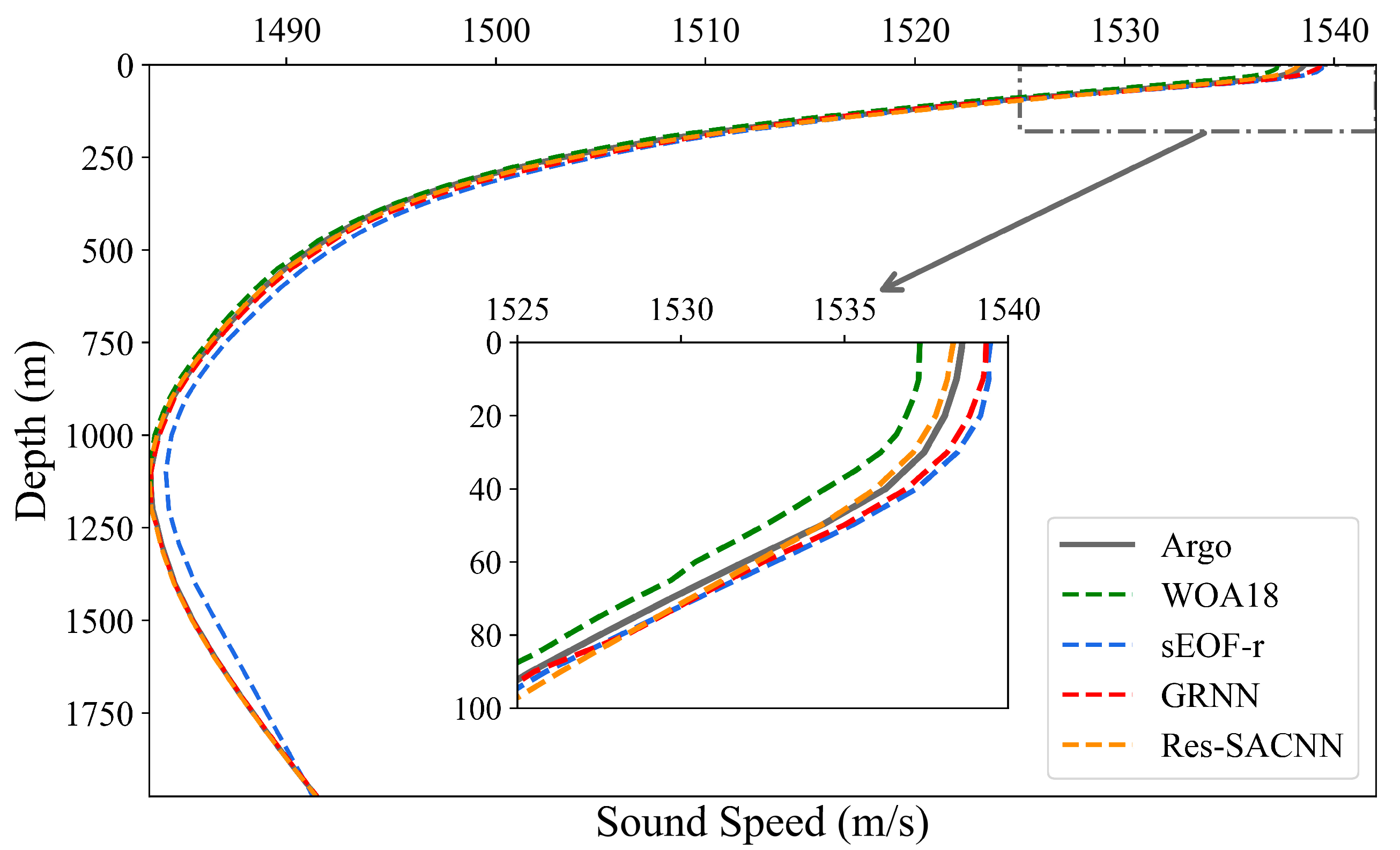
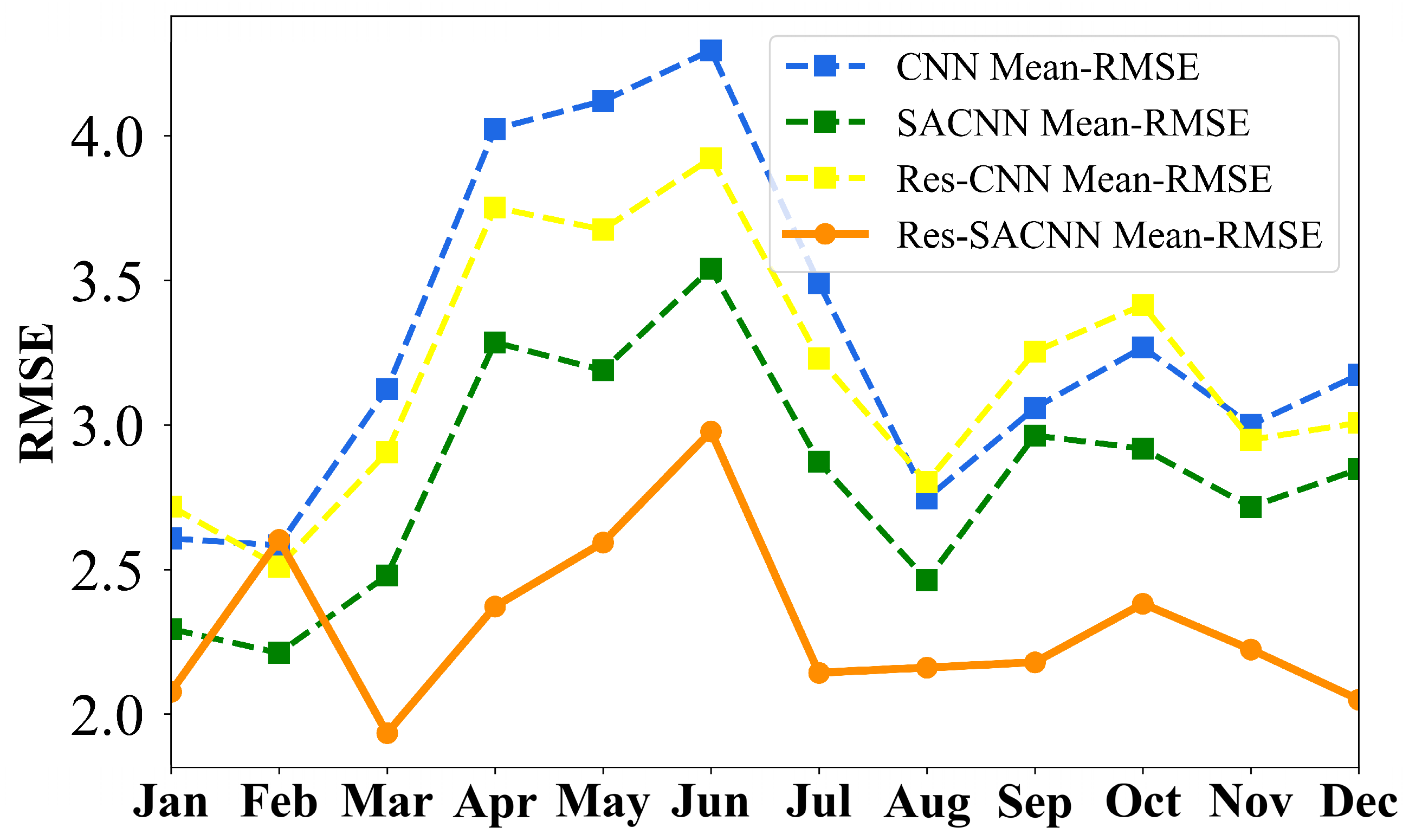
3.2.1. Experiments in Different Time Domains
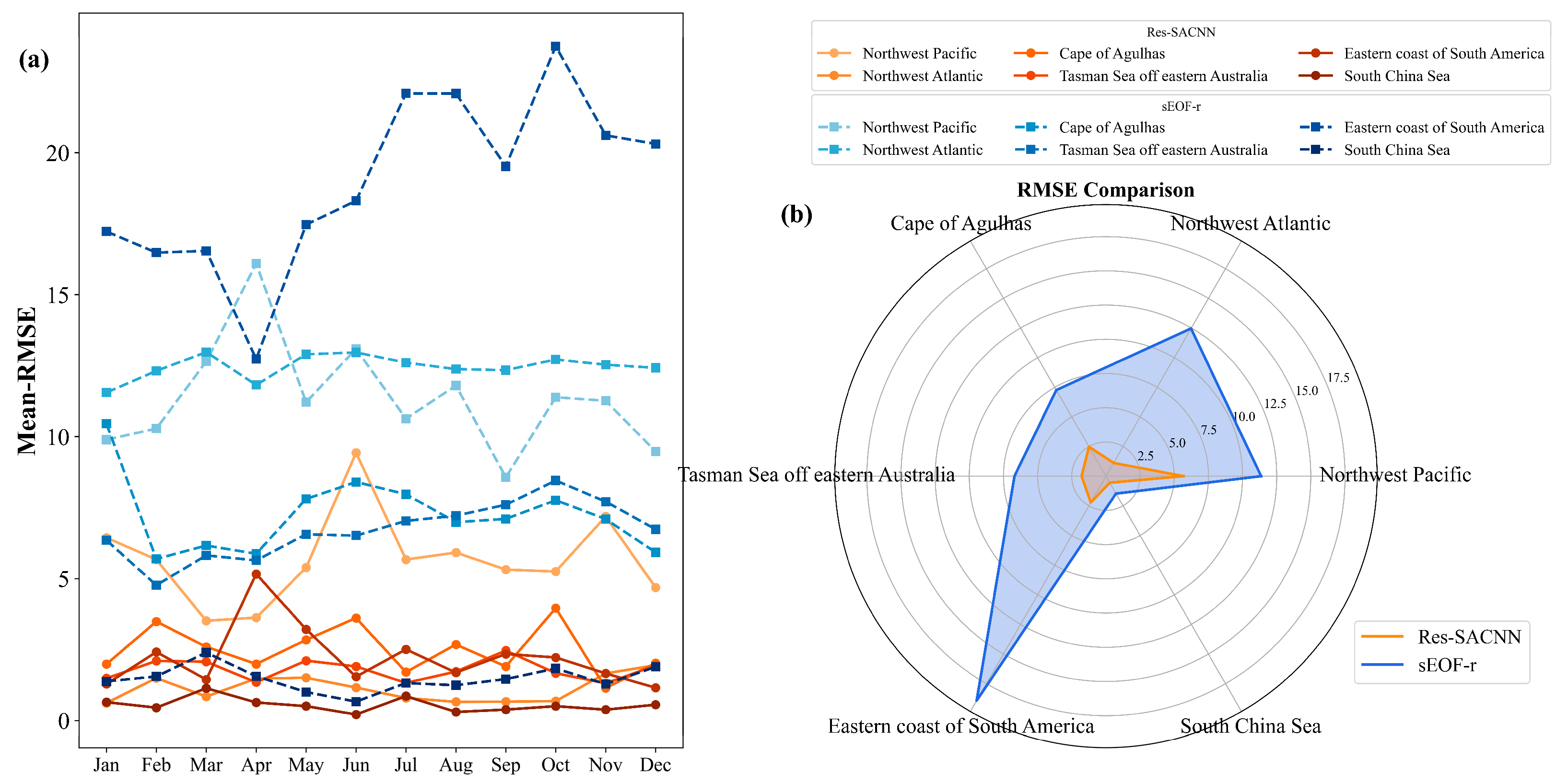
3.2.2. Experiments in Different Regions
3.3. Experimental Summary
4. Discussion
4.1. Model Evaluation
4.2. Limitations and Future Work
5. Conclusions
- Improve Inversion Accuracy: The Res-SACNN model shows a significant reduction in RMSE (average of 7.39 m/s) across six ocean regions, with an optimization ratio of 71.8%. Notably, accuracy is exceptional in areas with large sound speed gradients, like the Northwest Pacific and Cape of Agulhas region.
- Strong Generalization: The model performs well in both complex, dynamic environments and stable regions (e.g., South China Sea), achieving a 62.5% optimization ratio, demonstrating adaptability to diverse marine conditions.
- Real-Time and Robust: By integrating residual networks and self-attention mechanisms, the model enhances spatiotemporal feature capture and computational efficiency. Combined with satellite remote sensing data, it ensures real-time response and robust performance in variable marine environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chu, X.; Zhao, F.; Wang, Z.; Qian, Y.; Yang, G. Acoustic Wave Propagation in Depth Evolving Sound Speed Field Using the Lattice Boltzmann Method. Phys. Fluids 2024, 36, 097118. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, C.; Feng, X. Investigating the Reliable Acoustic Path Properties in a Global Scale. Front. Mar. Sci. 2023, 10, 1213002. [Google Scholar] [CrossRef]
- Xue, S.; Li, B.; Xiao, Z.; Sun, Y.; Li, J. Centimeter-level-precision Seafloor Geodetic Positioning Model with Self-structured Empirical Sound Speed Profile. Satell. Navig. 2023, 4, 30. [Google Scholar] [CrossRef]
- Carnes, M.R.; Mitchell, J.L.; de Witt, P.W. Synthetic Temperature Profiles Derived from Geosat Altimetry: Comparison with Air-dropped Expendable Bathythermograph Profiles. J. Geophys. Res. Ocean. 1990, 95, 17979–17992. [Google Scholar] [CrossRef]
- Davis, R.E. Predictability of Sea Surface Temperature and Sea Level Pressure Anomalies over the North Pacific Ocean. J. Phys. Oceanogr. 1976, 6, 249–266. [Google Scholar] [CrossRef]
- Shen, Y.; Ma, Y.; Tu, Q.; Jiang, X. Feasibility of Describing the Sound Speed Profile in Shallow Water via Empirical Orthogonal Function. J. Appl. Acoust. 1999, 18, 21–25. [Google Scholar] [CrossRef]
- Chen, C.; Ma, Y.; Liu, Y. Reconstructing Global Sound Speed Profiles Using Sea Surface Data. Appl. Ocean Res. 2018, 77, 26–33. [Google Scholar] [CrossRef]
- Huang, J.; Luo, Y.; Shi, J.; Ma, X.; Li, Q.-Q.; Li, Y.-Y. Rapid Modeling of the Sound Speed Field in the South China Sea Based on a Comprehensive Optimal LM-BP Artificial Neural Network. J. Mar. Sci. Eng. 2021, 9, 488. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Zhang, H.; Xu, T.; Yin, F. A Meta-deep-learning Framework for Spatial-temporal Underwater SSP Inversion. Front. Mar. Sci. 2023, 10, 1146333. [Google Scholar] [CrossRef]
- Huang, W.; Zhou, J.; Gao, F.; Wang, J.; Xu, T. Experimental Results of Underwater Sound Speed Profile Inversion by Few-Shot Multi-Task Learning. Remote Sens. 2023, 16, 167. [Google Scholar] [CrossRef]
- Feng, X.; Tian, T.; Zhou, M.; Sun, H.; Li, D.; Tian, F.; Lin, R. Sound Speed Inversion Based on Multi-Source Ocean Remote Sensing Observations and Machine Learning. Remote Sens. 2024, 16, 814. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Chen, W.; Meng, Z. Inversion of Sound Speed Profile in the Luzon Strait by Combining Single Empirical Orthogonal Function and Generalized Regression Neural Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1502405. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, P.; Li, G.; Ou, Z.; Qu, K. Reconstructing the Sound Speed Profile of South China Sea Using Remote Sensing Data and Long Short-term Memory Neural Networks. Front. Mar. Sci. 2024, 11, 1375766. [Google Scholar] [CrossRef]
- Tolstoy, A.; Diachok, O.; Frazer, L. Acoustic Tomography via Matched Field Processing. J. Acoust. Soc. Am. 1991, 89, 1119–1127. [Google Scholar] [CrossRef]
- Choo, Y.; Seong, W. Compressive Sound Speed Profile Inversion Using Beamforming Results. Remote Sens. 2018, 10, 704. [Google Scholar] [CrossRef]
- Li, Q.; Shi, J.; Li, Z.; Luo, Y.; Yang, F.; Zhang, K. Acoustic Sound Speed Profile Inversion Based on Orthogonal Matching Pursuit. Acta Oceanol. Sin. 2019, 38, 149–157. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Jiang, P. Underwater Sound Speed Inversion by Joint Artificial Neural Network and Ray Theory. In Proceedings of the Thirteenth ACM International Conference on Underwater Networks & Systems, Shenzhen, China, 3–5 December 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Stephan, Y.; Thiria, S.; Badran, F. Inverting Tomographic Data with Neural Nets. In Proceedings of the Challenges of Our Changing Global Environment Conference, OCEANS’ 95 MTS/IEEE, San Diego, CA, USA, 9–12 October 1995; Volume 3, pp. 1501–1504. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, S.; Bian, G.; Cui, Y.; Peng, C.; Xia, H. A Method for Sound Speed Profile Prediction Based on CNN-BiLSTM-Attention Network. J. Mar. Sci. Eng. 2024, 12, 414. [Google Scholar] [CrossRef]
- Cui, X.; Liu, X.; Li, J.; Li, L.; Jiang, B.; Li, S.; Liu, J. Adaptive Sound Velocity Profile Prediction Method Based on Deep Reinforcement Learning. IEEE Sens. Lett. 2024, 8, 6002704. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.; Chen, Z. An Estimation Method of Sound Speed Profile Based on Grouped Dilated Convolution Informer Model. Front. Mar. Sci. 2025, 12, 1484098. [Google Scholar] [CrossRef]
- Lu, J.; Huang, W.; Zhang, H. Dynamic Prediction of Full-Ocean Depth SSP by a Hierarchical LSTM: An Experimental Result. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1501105. [Google Scholar] [CrossRef]
- Ou, Z.; Qu, K.; Liu, C. Estimation of Sound Speed Profiles Using a Random Forest Model with Satellite Surface Observations. Shock Vib. 2022, 2022, 2653791. [Google Scholar] [CrossRef]
- Ou, Z.; Qu, K.; Shi, M.; Wang, Y.; Zhou, J. Estimation of Sound Speed Profiles Based on Remote Sensing Parameters Using a Scalable End-to-end Tree Boosting Model. Front. Mar. Sci. 2022, 9, 1051820. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, H.; Shi, Y.; Lu, J.; Li, S.; Huang, W.; Tang, N.; Wang, S. Real-time estimation of underwater sound speed profiles with a data fusion convolutional neural network model. Appl. Ocean. Res. 2024, 150, 104088. [Google Scholar] [CrossRef]
- Yuan Liu, Y.; Tang, Q.; Li, J.; Chen, G.; Cai, W. ST-LSTM-SA: A Novel Ocean Sound Velocity Field Prediction Model Based on Deep Learning. Adv. Atmos. Sci. 2024, 41, 1364–1378. [Google Scholar] [CrossRef]
- Chen, W.; Ren, K.; Zhang, Y.; Liu, Y.; Chen, Y.; Ma, L.; Chen, S. Reconstruction of the Sound Speed Profile in Typical Sea Areas Based on the Single Empirical Orthogonal Function Regression Method. J. Mar. Sci. Eng. 2023, 11, 841. [Google Scholar] [CrossRef]
- Wilson, W.D. Equation for the Speed of Sound in Seawater. J. Acoust. Soc. Am. 1960, 32, 1357. [Google Scholar] [CrossRef]
- Medwin, H. Speed of Sound in Water: A Simple Equation for Realistic Parameters. J. Acoust. Soc. Am. 1975, 58, 1318–1319. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Meng, Z.; Chen, W. Performance of Single Empirical Orthogonal Function Regression Method in Global Sound Speed Profile Inversion and Sound Field Prediction. Appl. Ocean Res. 2023, 136, 103598. [Google Scholar] [CrossRef]
- Karol, G.; Ivo, D.; Alex, G.; Danilo, J.R.; Daan, W. DRAW: A Recurrent Neural Network for Image Generation. arXiv 2015. [Google Scholar] [CrossRef]
- Fnu, N.; Deepshikha, B.; Deepak, K.; Md, A. From Classical Techniques to Convolution-based Models: A Review of Object Detection Algorithms. In Proceedings of the 2025 IEEE 6th International Conference on Image Processing, Applications and Systems (IPAS), Lyon, France, 9–11 January 2025. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Dzmitry, B.; Kyunghyun, C.; Yoshua, B. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014. [Google Scholar] [CrossRef]
- Samanta, D.; Goodkin, N.F.; Karnauskas, K.B. Volume and Heat Transport in the South China Sea and Maritime Continent at Present and the End of the 21st Century. Journal of Geophysical Research. Oceans 2021, 126, e2020JC016901. [Google Scholar] [CrossRef]
- Chen, C.; Yang, K.; Duan, R.; Ma, Y. Acoustic Propagation Analysis with a Sound Speed Feature Model in the Front Area of Kuroshio Extension. Appl. Ocean Res. 2017, 68, 1–10. [Google Scholar] [CrossRef]
- Matano, R.; Combes, V.; Palma, E.D.; Strub, P.T. Circulation and Cross-Shelf Exchanges in the Agulhas Bank Region. J. Geophys. Res. Ocean. 2025, 130, e2023JC020234. [Google Scholar] [CrossRef]
- Iain, M.S.; Jock, W.Y.; Mark, E.B.; Roughan, M.; Everett, J.D.; Brassington, G.B.; Byrne, M.; Condie, S.A.; Hartog, J.R.; Hassler, C.S.; et al. The Strengthening East Australian Current, its Eddies and Biological Effects—An Introduction and Overview. Deep Sea Res. Part II Top. Stud. Oceanogr. 2011, 58, 538–546. [Google Scholar] [CrossRef]
- Alejandro, H.O.; Thomas, W.; Worth, D.N. On the Meridional Extent and Fronts of the Antarctic Circumpolar Current. Deep Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 641–673. [Google Scholar] [CrossRef]
- Alice, A.; Chiara, S.; Stefano, S. Ocean Sound Propagation in a Changing Climate: Global Sound Speed Changes and Identification of Acoustic Hotspots. Earth’s Future 2022, 10, e2021EF002099. [Google Scholar] [CrossRef]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Inference. arXiv 2017. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficient-Net: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2019. [Google Scholar] [CrossRef]


| Researchers | Models/Methods | Datasets/Resources | Research Region |
|---|---|---|---|
| Zhang et al. [19] | CNN-BiLSTM-Attention network | Argo gridded dataset | Western Pacific Ocean |
| Cui et al. [20] | Adaptive sound velocity profile prediction method premised on deep reinforcement learning (DRL-ASP) | Measured dataset | the South China Sea Arctic Ocean Southern Ocean |
| Qin et al. [21] | Grouped dilated convolution (GDC) | Argo gridded dataset EOF decomposition data Geographic location Temporal information Historical SSP data | Andaman Sea South China Sea Red Sea Western Pacific Ocean |
| Lu et al. [22] | Hierarchical long short-term memory (H-LSTM) neural network | Argo gridded dataset Ocean experiments dataset | South China Sea |
| Ou et al. [23] | Random forest (RF) | SSTA(NOAA) SSHA(AVISO) WOA13 dataset Argo dataset | South China Sea |
| Hyperparameter | Value | |
|---|---|---|
| Residual Block | Kernel size | (1, 1) |
| Strides | 1 | |
| Learning rate | 0.001 | |
| Dropout | 0.2 | |
| Self-attention Block | Reduction | 8 |
| Kernel size | (2, 2) | |
| Strides | 1 | |
| Learning rate | 0.0001 | |
| Dilation rate | 2 | |
| Res-SACNN Fitting | Epochs | 2000 |
| Batch-size | 64 | |
| Early Stopping Patience | 40 |
| Layer | SLA Channel | SSTA Channel | ||||||
|---|---|---|---|---|---|---|---|---|
| Input | Type | HP | Output | Input | Type | HP | Output | |
| 1 | (1512, 4, 4, 1) | Batch Normalization | / | (1512, 4, 4, 1) | (1512, 24, 24, 1) | Batch Normalization | / | (1512, 24, 24, 1) |
| 2 | (1512, 4, 4, 1) | Conv2D | (1, 1) | (1512, 4, 4, 64) | (1512, 24, 24, 1) | Conv2D | (1, 1) | (1512, 24, 24, 128) |
| 3 | (1512, 4, 4, 64) | MaxPool2D | (2, 2) | (1512, 2, 2, 64) | (1512, 24, 24, 128) | MaxPool2D | (3, 3) | (1512, 8, 8, 128) |
| 4 | (1512, 2, 2, 64) | Dense | Relu | (1512, 2, 2, 32) | (1512, 8, 8, 64) | Dense | Relu | (1512, 8, 8, 32) |
| 5 | (1512, 2, 2, 32) | Batch Normalization | / | (1512, 2, 2, 32) | (1512, 8, 8, 32) | Batch Normalization | / | (1512, 8, 8, 32) |
| 6 | (1512, 2, 2, 32) | Residual block | / | (1512, 2, 2, 64) | (1512, 8, 8, 64) | Residual block | / | (1512, 8, 8, 128) |
| 7 | (1512, 2, 2, 64) | Self-attention block | / | (1512, 2, 2, 64) | (1512, 8, 8, 128) | Self-attention block | / | (1512, 8, 8, 128) |
| 8 | (1512, 2, 2, 64) | Residual block | / | (1512, 2, 2, 64) | (1512, 8, 8, 128) | Residual block | / | (1512, 8, 8, 128) |
| 9 | (1512, 2, 2, 64) | GlobalAveragePooling2D | / | (6048, 64) | (1512, 8, 8, 128) | GlobalAveragePooling2D | / | (96,768, 128) |
| Month | Res-SACNN (m/s) | sEOF-r (m/s) | ||||
|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | |
| Jan | 1.60 | 0.27 | 0.65 | 3.78 | 0.07 | 1.38 |
| Feb | 0.95 | 0.24 | 0.45 | 3.64 | 0.15 | 1.55 |
| Mar | 2.51 | 0.28 | 1.14 | 6.31 | 0.09 | 2.39 |
| Apr | 1.68 | 0.04 | 0.64 | 3.98 | 0.14 | 1.56 |
| May | 1.18 | 0.25 | 0.51 | 2.41 | 0.14 | 1.00 |
| Jun | 0.49 | 0.07 | 0.21 | 1.14 | 0.11 | 0.67 |
| Jul | 2.59 | 0.06 | 0.86 | 4.13 | 0.06 | 1.32 |
| Aug | 1.12 | 0.05 | 0.30 | 4.03 | 0.08 | 1.24 |
| Sep | 1.25 | 0.04 | 0.39 | 4.41 | 0.14 | 1.46 |
| Oct | 1.43 | 0.20 | 0.51 | 7.97 | 0.14 | 1.84 |
| Nov | 1.03 | 0.09 | 0.38 | 4.31 | 0.14 | 1.28 |
| Dec | 1.51 | 0.18 | 0.56 | 7.22 | 0.14 | 1.89 |
| Mean | 1.45 | 0.15 | 0.55 | 4.44 | 0.12 | 1.47 |
| Region | Optimization Ratio | Decrease |
|---|---|---|
| Northwest Pacific | 50.1% | 5.69 |
| Northwest Atlantic | 91.0% | 11.34 |
| Cape of Agulhas region | 65.7% | 4.78 |
| Tasman Sea off eastern Australia | 73.3% | 4.91 |
| Eastern coast of South America | 88.3% | 16.71 |
| South China Sea | 62.5% | 0.92 |
| Mean | 71.8% | 7.39 |
| Model | FLOPs (M) | Params (M) |
|---|---|---|
| CNN | 0.12 | 0.05 |
| SACNN | 1.19 | 0.07 |
| Res-CNN | 4.41 | 0.16 |
| Res-SACNN | 8.67 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xu, F.; Liu, Y.; Chen, Y.; Liu, S. Underwater Sound Speed Profile Inversion Based on Res-SACNN from Different Spatiotemporal Dimensions. Remote Sens. 2025, 17, 2293. https://doi.org/10.3390/rs17132293
Wang J, Xu F, Liu Y, Chen Y, Liu S. Underwater Sound Speed Profile Inversion Based on Res-SACNN from Different Spatiotemporal Dimensions. Remote Sensing. 2025; 17(13):2293. https://doi.org/10.3390/rs17132293
Chicago/Turabian StyleWang, Jiru, Fangze Xu, Yuyao Liu, Yu Chen, and Shu Liu. 2025. "Underwater Sound Speed Profile Inversion Based on Res-SACNN from Different Spatiotemporal Dimensions" Remote Sensing 17, no. 13: 2293. https://doi.org/10.3390/rs17132293
APA StyleWang, J., Xu, F., Liu, Y., Chen, Y., & Liu, S. (2025). Underwater Sound Speed Profile Inversion Based on Res-SACNN from Different Spatiotemporal Dimensions. Remote Sensing, 17(13), 2293. https://doi.org/10.3390/rs17132293




