Nearshore Depth Inversion Bathymetry from Coastal Webcam: A Novel Technique Based on Wave Celerity Estimation
Abstract
1. Introduction
2. Methods
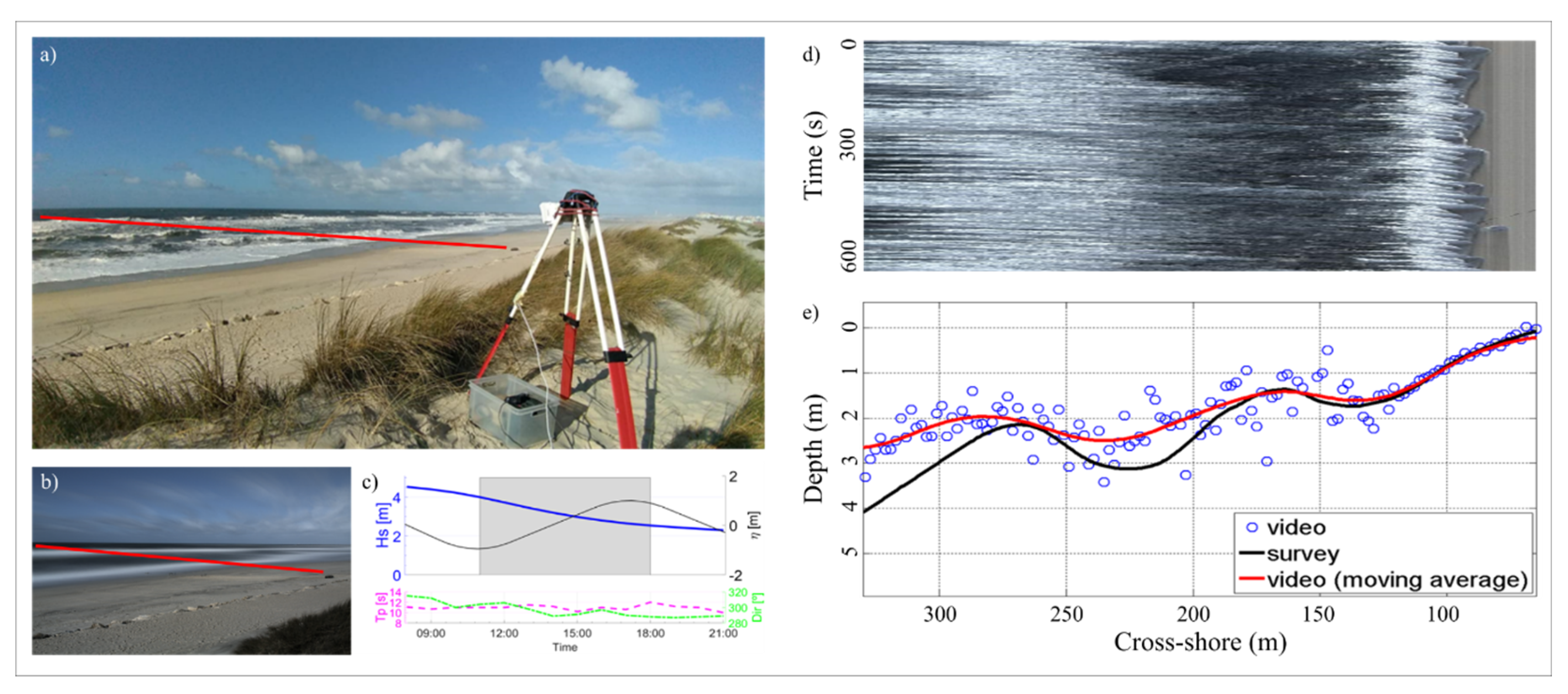
2.1. Study Site and Video Data
2.2. Wave Celerity Assessment from Timestack
2.3. Depth Inversion
3. Results
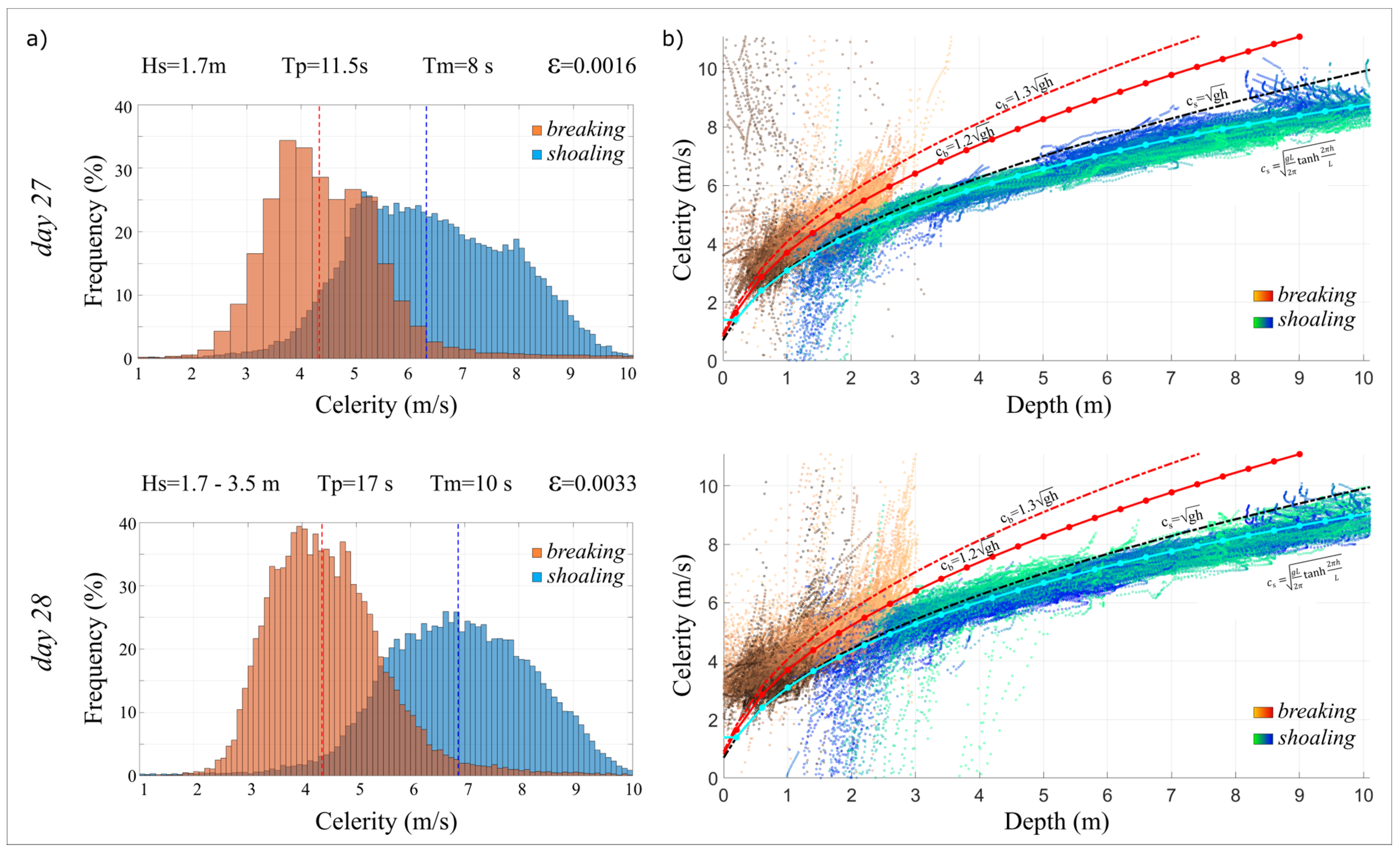
3.1. Wave Celerity
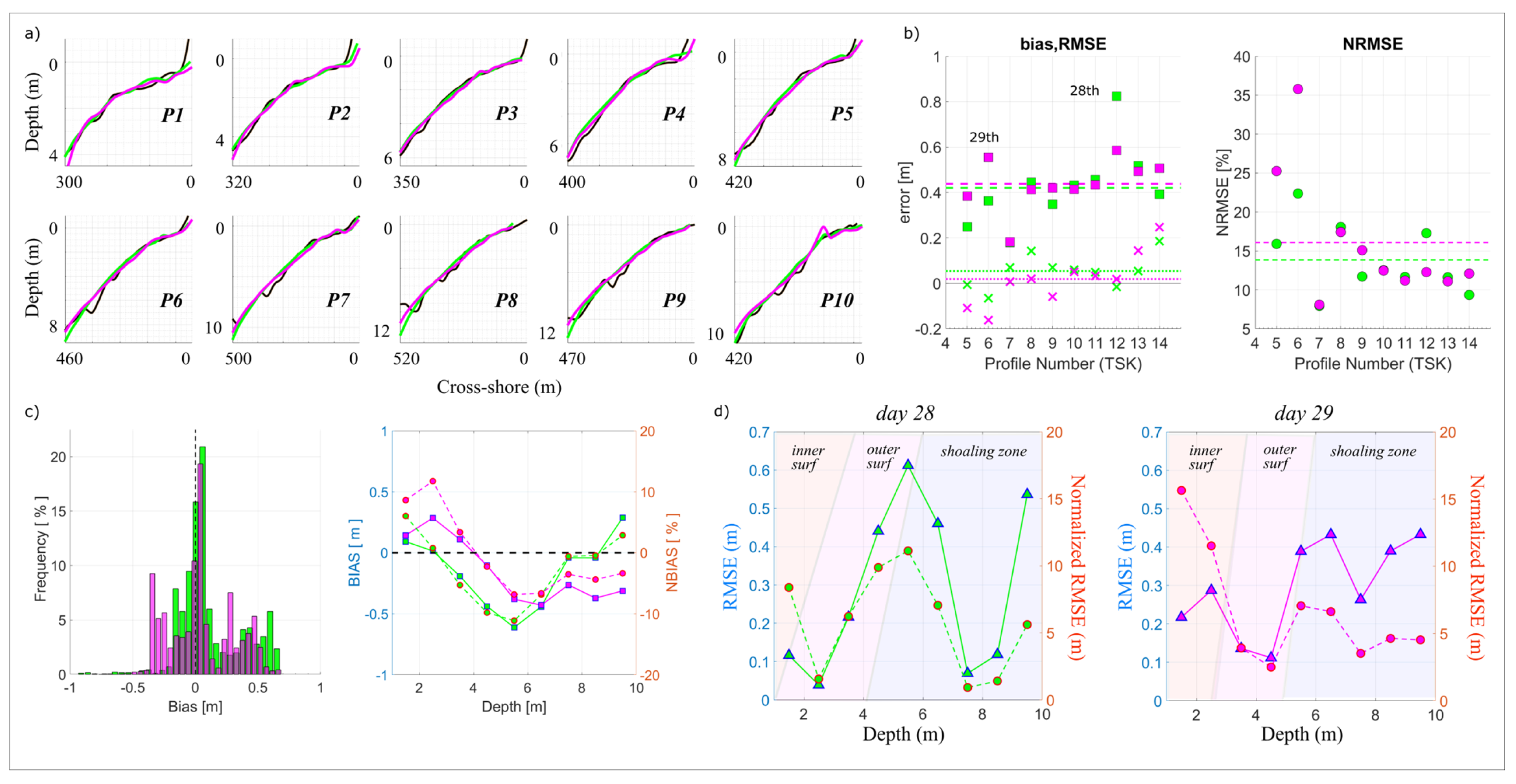
3.2. Video-Derived Bathymetry
4. Discussion
4.1. Wave Celerity
4.2. Depth Inversion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fontán-Bouzas, Á.; Alcántara-Carrió, J.; Albarracín, S.; Baptista, P.; Silva, P.A.; Portz, L.; Manzolli, R.P. Multiannual shore morphodynamics of a Cuspate Foreland: Maspalomas (Gran Canaria, Canary Islands). J. Mar. Sci. Eng. 2019, 7, 416. [Google Scholar] [CrossRef]
- Melet, A.; Teatini, P.; Le Cozannet, G.; Jamet, C.; Conversi, A.; Benveniste, J.; Almar, R. Earth Observations for Monitoring Marine Coastal Hazards and Their Drivers. Surv. Geophys. 2020, 41, 1489–1534. [Google Scholar] [CrossRef]
- Mendes, D.; Pinto, J.P.; Pires-Silva, A.A.; Fortunato, A.B. Infragravity wave energy changes on a dissipative barred beach: A numerical study. Coast. Eng. 2018, 140, 136–146. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.H.; Ris, R.C. The “Swan” Wave Model for Shallow Water. Coast. Eng. 1997, 1, 510–516. [Google Scholar]
- Ciavola, P.; Ferreira, O.; Van Dongeren, A.; Van Thiel de Vries, J.; Armaroli, C.; Harley, M. Prediction of Storm Impacts on Beach and Dune Systems. In Hydrometeorological Hazards: Interfacing Science and Policy; John Wiley and Sons: Hoboken, NJ, USA, 2014; Volume 9781118629, pp. 227–252. ISBN 9781118629567. [Google Scholar]
- Garnier, E.; Ciavola, P.; Spencer, T.; Ferreira, O.; Armaroli, C.; McIvor, A. Historical analysis of storm events: Case studies in France, England, Portugal and Italy. Coast. Eng. 2018, 134, 10–23. [Google Scholar] [CrossRef]
- Matias, A.; Rita Carrasco, A.; Loureiro, C.; Masselink, G.; Andriolo, U.; McCall, R.; Ferreira, Ó.; Plomaritis, T.A.; Pacheco, A.; Guerreiro, M. Field measurements and hydrodynamic modelling to evaluate the importance of factors controlling overwash. Coast. Eng. 2019, 152, 103523. [Google Scholar] [CrossRef]
- Ferreira, Ó. Modelling Risk Reduction Measures to Minimise Future Impacts of Storms at Coastal Areas. In Springer Climate; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef]
- Masselink, G.; Van Heteren, S. Response of wave-dominated and mixed-energy barriers to storms. Mar. Geol. 2014, 352, 321–347. [Google Scholar] [CrossRef]
- Fontán, A.; Alcántara-Carrió, J.; Correa, I.D. Combined beach—Inner shelf erosion in short and medium term (Maspalomas, Canary Islands). Geol. Acta 2012, 10, 411–426. [Google Scholar]
- Salameh, E.; Frappart, F.; Almar, R.; Baptista, P.; Heygster, G.; Lubac, B.; Raucoules, D.; Almeida, L.P.; Bergsma, E.W.J.; Capo, S.; et al. Monitoring Beach Topography and Nearshore Bathymetry Using Spaceborne Remote Sensing: A Review. Remote Sens. 2019, 11, 2212. [Google Scholar] [CrossRef]
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters—A 50 year retrospective and future directions. Remote Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Almeida, L.P.; Almar, R. Application of remote sensing methods to monitor coastal zones. J. Mar. Sci. Eng. 2020, 8, 391. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C. Ferreira Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Almar, R.; Bergsma, E.W.J. Satellite optical imagery in Coastal Engineering. Coast. Eng. 2021, 167, 103919. [Google Scholar] [CrossRef]
- Catalán, P.; Haller, M.C. Nonlinear phase speeds and depth inversions. Coast. Dyn. 2005 Proc. Fifth Coast. Dyn. Int. Conf. 2006, 1–14. [Google Scholar]
- Almar, R.; Bergsma, E.W.J.; Thoumyre, G.; Baba, M.W.; Cesbron, G.; Daly, C.; Garlan, T.; Lifermann, A. Global satellite-based coastal bathymetry from waves. Remote Sens. 2021, 13, 4628. [Google Scholar] [CrossRef]
- Andriolo, U.; Sánchez-García, E.; Taborda, R. Operational use of surfcam online streaming images for coastal morphodynamic studies. Remote Sens. 2019, 11, 78. [Google Scholar] [CrossRef]
- Splinter, K.D.; Harley, M.D.; Turner, I.L. Remote sensing is changing our view of the coast: Insights from 40 years of monitoring at Narrabeen-Collaroy, Australias. Remote Sens. 2018, 10, 1744. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. Ocean. 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Zikra, M. Development of Video Image Analysis Methods for Estimating Bathymetry and the Directional Wave Spectrum in Shallow Water Areas. Ph.D. Thesis, Kyushu university, Fukuoka, Japan, 2012. [Google Scholar]
- Holman, R.; Plant, N.; Holland, T. CBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. Ocean. 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Catálan, P.A.; Haller, M.C. Remote sensing of breaking wave phase speeds with application to non-linear depth inversions. Coast. Eng. 2008, 55, 93–111. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D.; Luque, P.; Orfila, A.; Ribas, F. UBathy: A new approach for bathymetric inversion from video imagery. Remote Sens. 2019, 11, 2722. [Google Scholar] [CrossRef]
- Gawehn, M.; De Vries, S.; Aarninkhof, S. A self-adaptive method for mapping coastal bathymetry on-the-fly from wave field video. Remote Sens. 2021, 13, 4742. [Google Scholar] [CrossRef]
- Santos, D.; Abreu, T.; Silva, P.A.; Baptista, P. Estimation of coastal bathymetry using wavelets. J. Mar. Sci. Eng. 2020, 8, 772. [Google Scholar] [CrossRef]
- Santos, D.; Abreu, T.; Silva, P.A.; Santos, F.; Baptista, P. Nearshore Bathymetry Retrieval from Wave-Based Inversion for Video Imagery. Remote Sens. 2022, 14, 2155. [Google Scholar] [CrossRef]
- Almar, R.; Cienfuegos, R.; Catalán, P.A.; Birrien, F.; Castelle, B.; Michallet, H. Nearshore bathymetric inversion from video using a fully non-linear Boussinesq wave model. J. Coast. Res. 2011, 64, 3–7. [Google Scholar]
- Liu, H.; Arii, M.; Sato, S.; Tajima, Y. Long-Term Nearshore Bathymetry Evolution From Video Imagery: A Case Study in the Miyazaki Coast. Coast. Eng. Proc. 2012, 1, 60. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave Celerity From Video Imaging: A New Method. Coast. Eng. 2009, 661–673. [Google Scholar]
- Almar, R. Morphodynamique Littorale Haute Fréquence par Imagerie Vidéo. Ph.D. Thesis, Université de Rouen, Mont-Saint-Aignan, France, 2009. [Google Scholar]
- Abessolo, G.O.; Almar, R.; Bonou, F.; Bergsma, E. Error Proxies in Video-Based Depth Inversion: Temporal Celerity Estimation. J. Coast. Res. 2020, 95, 1101. [Google Scholar] [CrossRef]
- Thuan, D.H.; Almar, R.; Marchesiello, P.; Viet, N.T. Video Sensing of Nearshore Bathymetry Evolution with Error Estimate. J. Mar. Sci. Eng. 2019, 7, 233. [Google Scholar] [CrossRef]
- Tsukada, F.; Shimozono, T.; Matsuba, Y. UAV-based mapping of nearshore bathymetry over broad areas. Coast. Eng. J. 2020, 62, 285–298. [Google Scholar] [CrossRef]
- Hashimoto, K.; Shimozono, T.; Matsuba, Y.; Okabe, T. Unmanned aerial vehicle depth inversion to monitor river-mouth bar dynamics. Remote Sens. 2021, 13, 412. [Google Scholar] [CrossRef]
- Yoo, J.; Fritz, H.M.; Haas, K.A.; Work, P.A.; Barnes, C.F. Depth Inversion in the Surf Zone with Inclusion of Wave Nonlinearity Using Video-Derived Celerity. J. Waterw. Port. Coast. Ocean. Eng. 2011, 137, 95–106. [Google Scholar] [CrossRef]
- Yoo, J.; Fritz, H. Nonlinear Bathymetry Inversion Based on Wave Property Estimation from Nearshore Video Imagery. Civ. Environ. Engng. 2007. [Google Scholar]
- Matsuba, Y.; Sato, S. Nearshore bathymetry estimation using UAV. Coast. Eng. J. 2018, 60, 51–59. [Google Scholar] [CrossRef]
- Palmsten, M.L.; Brodie, K.L. The Coastal Imaging Research Network (CIRN). Remote Sens. 2022, 14, 453. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef]
- Rodríguez-Padilla, I.; Castelle, B.; Marieu, V.; Morichon, D. Video-Based Nearshore Bathymetric Inversion on a Geologically Constrained Mesotidal Beach during Storm Events. Remote Sens. 2022, 14, 3850. [Google Scholar] [CrossRef]
- Bouvier, C.; Balouin, Y.; Castelle, B.; Valentini, N. Video Depth Inversion at a Microtidal Site Exposed to Prevailing Low-energy Short-period Waves and Episodic Severe Storms. J. Coast. Res. 2020, 95, 1021–1026. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.J.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138, 199–209. [Google Scholar] [CrossRef]
- Taborda, R.; Silva, A. COSMOS: A lightweight coastal video monitoring system. Comput. Geosci. 2012, 49, 248–255. [Google Scholar] [CrossRef]
- Sánchez-García, E.; Balaguer-Beser, A.; Pardo-Pascual, J.E. C-Pro: A coastal projector monitoring system using terrestrial photogrammetry with a geometric horizon constraint. ISPRS J. Photogramm. Remote Sens. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Andriolo, U. Nearshore Hydrodynamics and Morphology Derived from Video Imagery; Faculdade de Ciências da Universidade de Lisboa: Lisbon, Portugal, 2018. [Google Scholar]
- Andriolo, U.; Mendes, D.; Taborda, R. Breaking wave height estimation from timex images: Two methods for coastal video monitoring systems. Remote Sens. 2020, 12, 204. [Google Scholar] [CrossRef]
- Andriolo, U. Nearshore wave transformation domains from video imagery. J. Mar. Sci. Eng. 2019, 7, 186. [Google Scholar] [CrossRef]
- Almar, R.; Cienfuegos, R.; Catalán, P.A.; Michallet, H.; Castelle, B.; Bonneton, P.; Marieu, V. A new breaking wave height direct estimator from video imagery. Coast. Eng. 2012, 61, 42–48. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; Melo de Almeida, L.P.; Sall, M. On the operational use of UAVs for video-derived bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R.; Schäffer, H.A. Surf zone dynamics simulated by a Boussinesq type model. Part II: Surf beat and swash oscillations for wave groups and irregular waves. Coast. Eng. 1997, 32, 289–319. [Google Scholar] [CrossRef]
- Postacchini, M.; Brocchini, M. A wave-by-wave analysis for the evaluation of the breaking-wave celerity. Appl. Ocean. Res. 2014, 46, 15–27. [Google Scholar] [CrossRef]
- Tissier, M.; Bonneton, P.; Almar, R.; Castelle, B.; Bonneton, N.; Nahon, A. Field measurements and non-linear prediction of wave celerity in the surf zone. Eur. J. Mech. B/Fluids 2011, 30, 635–641. [Google Scholar] [CrossRef]
- Perugini, E.; Soldini, L.; Palmsten, M.L.; Calantoni, J.; Brocchini, M. Linear depth inversion sensitivity to wave viewing angle using synthetic optical video. Coast. Eng. 2019, 152, 103535. [Google Scholar] [CrossRef]
- Osorio, A.F.; Montoya-Vargas, S.; Cartagena, C.A.; Espinosa, J.; Orfila, A.; Winter, C. Virtual BUOY: A video-based approach for measuring near-shore wave peak period. Comput. Geosci. 2019, 133, 104302. [Google Scholar] [CrossRef]
- Sun, S.-H.; Chuang, W.-L.; Chang, K.-A.; Young Kim, J.; Kaihatu, J.; Huff, T.; Feagin, R. Imaging-Based Nearshore Bathymetry Measurement Using an Unmanned Aircraft System. J. Waterw. Port. Coast. Ocean. Eng. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Gonçalves, G.; Gonçalves, D.; Gómez-gutiérrez, Á.; Andriolo, U.; Pérez-alvárez, J.A. 3D reconstruction of coastal cliffs from fixed-wing and multi-rotor uas: Impact of sfm-mvs processing parameters, image redundancy and acquisition geometry. Remote Sens. 2021, 13, 1222. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gonçalves, G.; Pérez-Alvávez, J.A.; Andriolo, U. On the 3D Reconstruction of Coastal Structures by Unmanned Aerial Systems with Onboard Global Navigation Satellite System and Real-Time Kinematics and Terrestrial Laser Scanning. Remote Sens. 2022, 14, 1485. [Google Scholar] [CrossRef]
- Andriolo, U.; Garcia-Garin, O.; Vighi, M.; Borrell, A.; Gonçalves, G. Beached and Floating Litter Surveys by Unmanned Aerial Vehicles: Operational Analogies and Differences. Remote Sens. 2022, 14, 1336. [Google Scholar] [CrossRef]
- Gonçalves, D.; Gonçalves, G.; Pérez-Alvárez, J.A.; Andriolo, U. 3D cliff reconstruction by drone: An in-depth analysis of the image network. Meas. J. Int. Meas. Confed. 2023, 222, 113606. [Google Scholar] [CrossRef]
- Catalán, P.A.; Haller, M.C.; Holman, R.A.; Plant, W.J. Optical and microwave detection of wave breaking in the surf zone. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1879–1893. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andriolo, U.; Azevedo, A.; Gonçalves, G.; Taborda, R. Nearshore Depth Inversion Bathymetry from Coastal Webcam: A Novel Technique Based on Wave Celerity Estimation. Remote Sens. 2025, 17, 2274. https://doi.org/10.3390/rs17132274
Andriolo U, Azevedo A, Gonçalves G, Taborda R. Nearshore Depth Inversion Bathymetry from Coastal Webcam: A Novel Technique Based on Wave Celerity Estimation. Remote Sensing. 2025; 17(13):2274. https://doi.org/10.3390/rs17132274
Chicago/Turabian StyleAndriolo, Umberto, Alberto Azevedo, Gil Gonçalves, and Rui Taborda. 2025. "Nearshore Depth Inversion Bathymetry from Coastal Webcam: A Novel Technique Based on Wave Celerity Estimation" Remote Sensing 17, no. 13: 2274. https://doi.org/10.3390/rs17132274
APA StyleAndriolo, U., Azevedo, A., Gonçalves, G., & Taborda, R. (2025). Nearshore Depth Inversion Bathymetry from Coastal Webcam: A Novel Technique Based on Wave Celerity Estimation. Remote Sensing, 17(13), 2274. https://doi.org/10.3390/rs17132274






