Abstract
Tidal creeks play a vital role in influencing geospatial evolution and marsh ecological communities in coastal landscapes. However, evaluating the geospatial characteristics of numerous creeks across a site and understanding their ecological relationships pose significant challenges due to the labor-intensive nature of manual delineation from imagery. Traditional methods rely on manual annotation in GIS interfaces, which is slow and tedious. This study explores the application of Attention-based Dense U-Net (ADU-Net), a deep learning image segmentation model, for automatically classifying creek pixels in high-resolution (0.5 m) orthorectified aerial imagery in coastal Georgia, USA. We observed that ADU-Net achieved an outstanding F1 score of in identifying creek pixels, demonstrating its ability in tidal creek mapping. The study highlights the potential of deep learning models for automated tidal creek mapping, opening avenues for future investigations into the role of creeks in marshes’ response to environmental changes.
1. Introduction
Around the world, the spatial extent and patterning of coastal wetlands are changing due to anthropogenic interventions (e.g., damming of rivers and limiting sediment supply to estuaries [1], urban development in coastal zones [2], groundwater withdrawal [3]) and natural influences (natural redistribution of sediments [4], drought or climatic events [5], and storms [6]). These intertidal, vegetated landscapes, which form at the interface of land and sea, provide vital economic (fisheries [7], recreational activity [8]) and ecosystem services (biodiversity [9], carbon sequestration [10]). Past studies have highlighted the importance of understanding the nature of geospatial change in salt marshes, mangrove forests, and other coastal wetlands so that they can be better preserved and restored [11]. Within these systems, the areas experiencing particularly high rates of change are often the boundaries between lower elevation channel and creek networks that convey water throughout wetland systems and the adjacent vegetated habitats [12].
Tidal creeks and channels form vast, dendritic networks throughout the world’s wetlands [13,14]. These geomorphic features deliver water, nutrients, and sediments to interior locations via tidal and storm flooding, which sustain robust vegetation growth [15], build elevation (e.g., development of natural levee systems [16]), and alter ecosystem services of the larger landscape (e.g., fish foraging, dispersal of larvae, enhanced biodiversity [17]). The spatial scale of these features can range from sub-meter to several km wide and tens of m to hundreds of km long [14]. These dendritic networks can have relatively high rates of change in spatial extent (1–10 m per year) over annual or decadal time scales. The hydrodynamic conditions of the system, paired with the local geology (i.e., erodibility or depositional patterns), can define their evolution [18]. Resolving the current distribution of tidal creek features as well as how they are changing (with direct effects on the rate and pattern of change in the wetlands they intersect) is vital to advancing understanding of the overall function and stability of these high-value coastal landscapes [19]. Despite increasing awareness that creek–marsh boundaries are where change is often most rapid, most approaches to quantify coastal tidal creek expansion (on landscape scales) rely on manual delineation of features in a limited spatial extent [20]. Thus, a need remains to differentiate creeks and channels at higher resolution and at large spatial scales to extract vital information about the location and pace of coastal wetland change.
Several studies have been conducted in coastal wetland mapping over the years [21,22]. Existing methods can be categorized into heuristic approaches, genetic algorithms, and machine learning techniques. A heuristic approach such as the Normalized Difference Water Index (NDWI) is combined with Maximum Between-Class Variance (Otsu) [23] classification to delineate the wide tidal creeks in Sentinel-2A data [24]. Then, a Modified Fuzzy C-Means (MFCM) algorithm was used to effectively suppress the differences between the targeted features and the background caused by spatial heterogeneity in the tidal flat environment. In [25], the NDWI, in conjunction with edge detection algorithms such as the Canny algorithm, morphological expansion algorithm, and Graham Scanning Method, is used to delineate tidal creek features in Landsat 8 data. A different approach focuses on genetic algorithms (GAs). In [26], the GA utilizes predictors from LiDAR-UAV, digital aerial photogrammetry (DAP)-UAV, and RGB datasets to determine vegetation characteristics. The fitness function of the GA is calibrated based on the target population data, and the algorithm aims to minimize the Root Mean Square Error (RMSE) in fitting the input data. Other methods have been developed to delineate creek networks using the digital elevation model alone or combined with raster images. A combination of a threshold for the bed elevation and curvature has often been adopted to delineate the network planimetric profile [27,28,29]. However, these approaches usually require a threshold for bed elevation and curvature for delineation.
With the advancement of machine learning, many machine learning models have been applied to map coastal wetlands. To predict freshwater wetlands coverage in Poyang Lake (China), Dronova et al. [30] developed an object-based image analysis to delineate functional plant groups and compared the results from the following classifiers: Bayesian [31], Logistic [32], Neural Network [33,34,35,36], Decision Trees [37], K-Nearest Neighbors (KNN) [38], and Support Vector Machines (SVM) [39]. These models were developed to predict a three-class classification problem and a six-class classification problem. The model utilized Landsat 5 TM data as input and was corrected to surface reflectance. The input channels were Landsat TM bands 3, 4, 5, and 7, and the normalized difference vegetation index (NDVI) and NDWI. They found no clear improvements when incorporating textures in the object-based image analysis, possibly due to Landsat’s larger pixel size of 30 m resolution. Whyte et al. [40] created an object-based image analysis model to delineate South Africa’s most extensive estuary wetlands. They utilized the SRTM digital elevation model, Sentinel-1 (C-Band Radar, VV + VH), and Sentinel-2 ( blue, green, red, NIR, and SWIR) as inputs for their model.
Unlike early machine learning models, which often relied on handcrafted features, deep learning models can automatically learn hierarchical representations from raw data. U-net has been extensively used to classify remote sensing images of coastal wetlands. Li et al. [41] developed a robust U-Net model to classify coastal wetlands in South Carolina (USA). The model input was Sentintel-2 satellite bands 2–8 and 11–12 and derived index layers with a 10 m or 20 m resolution. They considered the spatial heterogeneity of the coastal environment. They examined two NOAA National Estuarine Research Reserves (NERRs) in South Carolina: the North Inlet–Winyah Bay (NIWB) NERR for model training and the ACE Basin NERR for testing. A high-resolution land cover map in the NIWB was used for the training process. Ground reference points recorded by the NERR and Google Earth were utilized for accuracy assessment. This work was a multi-class classification problem separated into groups: water, low marsh, high marsh, forest, and others. The best performance of their model was 90% accuracy, but they demonstrated the challenge in coastal wetland delineation whereby spectral signatures of different classes may be considerable. In other research [42], the authors utilized a U-Net deep learning architecture to classify bi-temporal, high-resolution, county-scale aerial images to determine the spatial extent and changes in land cover classes impacting tidal marshes. U-Net was compared with two machine learning classifiers, random tree (RT) and SVM. The results indicate that the U-Net model outperformed the other two classifiers regarding Overall Accuracy ( for U-Net compared to for SVM and for RF). Zheng et al. [43] conducted a study on the quantitative analysis of tidal creek evolution and vegetation variation in silting muddy flats on the Yellow Sea. The focus of this study was to understand the factors influencing the evolution of tidal creeks in coastal wetland ecosystems facing challenges from rapid economic development, climate change, and sea level rise. They applied various classification methods, including random forest, maximum likelihood, SVM, and the U-Net convolutional neural network, in their research. The experiments suggested that the U-Net convolutional neural network algorithm demonstrated the highest overall accuracy and kappa coefficient compared to other classification methods, with an overall accuracy of and a kappa coefficient of . In other research, Huang et al. [44] utilized a U-Net convolutional neural network model to extract habitat information and the expansion of Spartina alterniflora in Suaeda salsa-dominated coastal wetlands. To study the sea level rise, shifts in plant and animal distributions, and other drivers of change [45] investigated the multi-year data. Similarly, in [46,47,48], U-net is applied to enhance the classification accuracy of tidal creeks within the Yancheng wetlands.
Another research study employed a WetSegNet, a novel convolutional neural network model inspired by ResNet [49], for binary classification tasks, distinguishing between “wetlands” and “not” categories within freshwater wetland areas situated in Illinois (USA). This model used high-resolution (1 m) aerial imagery (NAIP) and digital elevation models to predict the binary class problem. In all variants of the WetSegNet model (seven in total), the accuracy ranged from (based on area under the curve) 89.15% to a peak of 93.44%. This model significantly improved the quality of wetland predictions and could predict at high resolution (1 m) levels compared to previous models that utilized Landsat (30 m resolution). Wang et al. [50] provide a detailed investigation into the application of drone LiDAR leveraging deep learning of point clouds for mapping 3D marshes in an intertidal estuary dominated by Spartina alterniflora. By leveraging deep learning algorithms, such as the RandLA-Net model, the drone LiDAR point cloud can be classified into different categories (e.g., ground, low vegetation, high vegetation) with an overall accuracy of around 84.13%. This classification process is essential for accurately delineating bare earth surfaces and marsh features in intertidal estuaries. However, the U-Net architecture performed best because of its ability to capture both local details and global context simultaneously.
In this study, we aim to develop a machine model to segment creek features from the adjacent wetland landscape using high-resolution aerial imagery for wetland cover-type prediction. Specifically, we seek to create a deep neural network capable of precisely identifying tidal creeks within 0.5 m resolution aerial images found in Georgia, USA. These segments are categorized as “creek” or “not creek” pixels. The model will recognize creek features across a diverse spectrum of scales, encompassing the fine-grained details at the pixel level within the marsh landscape (less than 1 m) to the more extensive open water bodies, ranging from 10 m to kms in width. Segmenting tidal creek footprints in high-resolution aerial imagery (with a resolution of 0.5 m) is notably challenging due to intricate landscape details and noisy features. We employed an Attention-based Dense U-Net model (ADU-Net) to address this challenge. The outcomes of this research lay the groundwork for a better understanding of the intricate network structure of tidal creeks within salt marshes and other coastal wetlands. This, in turn, supports future research endeavors focused on assessing the rates and patterns of geospatial changes within tidal creek marshes through analyses of aerial imagery time series and landscape-scale assessments of the provisioning of ecosystem functions and services that are influenced by the relationships between tidal creeks and adjacent vegetated marsh areas.
2. Materials and Methods
2.1. Study Site Characteristics
The study site is situated in the region between Blackbeard Creek (northern end) and the Altamaha River (southern end) in coastal, southeastern Georgia, USA (refer to Figure 1). The dataset encompasses an area of approximately 255 square km along the coastline. This region includes diverse ecosystems, including extensive fresh, brackish, and salt marsh habitats and a chain of barrier islands providing habitats for different marine and terrestrial wildlife. This study site was chosen because it offers a wide spectrum of creek features in terms of spatial scale, spectral properties, geomorphologies, and landscape textures.
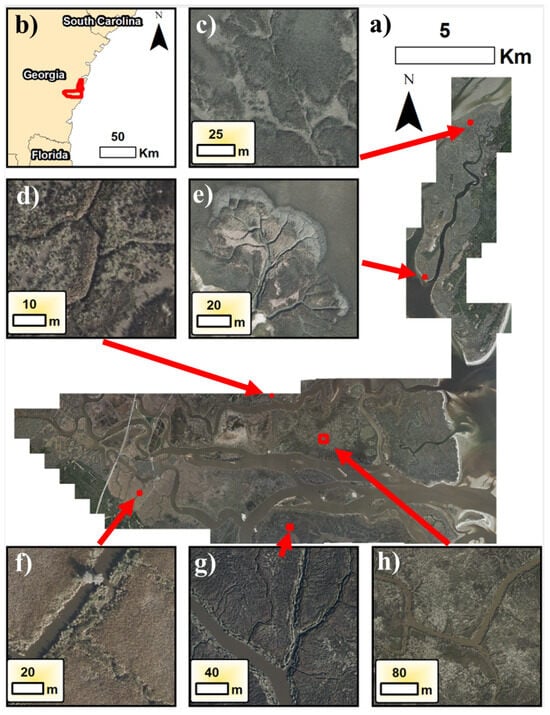
Figure 1.
(a) Aerial imagery dataset (entire extents) used to predict pixels for this study. (b) Study extents (red box) indicate the study extents concerning Georgia, USA. (c–h) Zooms of different locations across the domain show representative variations in creeks (shape, scale, and background textures). These regions were labeled in ArcGIS 10.7 to create the overall training, validation, and test datasets for quantitative results.
For instance, in salt marsh regions closer to the ocean, the intertidal wetland is dominated by smooth cordgrass (Spartina alterniflora) and upland treed hammocks. The density and height of Spartina alterniflora vary with elevation and hydroperiod (the time inundated per day or tidal period), with the densest and tallest grasses (over 200 cm in height) prospering at creek banks and low marsh areas [26,51]. Moving further from the water sources, the stem height (ranging from 10 to 100 cm) and density of vegetation are further reduced, allowing for differentiation of rough zonation by eye in aerial or satellite imagery. Closer to freshwater sources such as the Altamaha River, which is the primary water source in our study area, Juncus romerianus has become the dominant plant species. Juncus romerianus exhibits a distinct appearance from Spartina alterniflora in the input dataset [52].
Figure 1a shows the extent of labeled data we developed to train the model and a representative range of features and landscape textures. For example, Figure 1c,e both contain prominent mudflat features (grayish areas), which are caused by both crab grazing (i.e., removal of surficial vegetation) or high inundation periods [13]. In Figure 1f, the landscape looks much different as this region becomes dominated by Juncus plants. Figure 1g can be characterized by its sharper gradients in color and, notably, many small, fractured marsh areas along the creekbanks. Lastly, in Figure 1f, the site can be characterized by the water area appearing more like the background textures.
This diverse array of landscape features within our study area provides a dataset for training and evaluating the ADU-Net model, enabling accurate delineation and classification of creek networks across varying environmental conditions and spatial scales.
2.2. Dataset Characteristics
The input dataset for this study consisted of high-resolution ortho-images with a spatial resolution of 0.5 m, acquired in November 2017 using the Leica ADS100 aerial imagery system. The dataset contains four channels: blue (435–495 nm), green (525–584 nm), red (wavelength of 619–651 nm), and near-infrared (808–882 nm). We did not incorporate digital elevation models because they are often unreliable (i.e., low vertical accuracy) or coarse spatial resolution (10–30 m) in coastal marsh areas. The data underwent a geo-rectification process, employing ground control points provided and maintained by the Georgia Coastal Ecosystems Long-Term Ecological Research (LTER) site. Subsequently, all images were mosaicked together in the .sid format. Figure 1 offers an overview of the complete dataset and its image extents. The overall image (Figure 1a) is provided in GeoTIFF tiles encompassing the entire area. In this work, we utilized 5000 × 5000 pixel segments from these images, resulting in 383 images. The dataset includes a substantial 165,000 × 155,000 pixels, including NaNs (indicating missing or undefined values).
The labels were manually digitized in ArcMap 10.7 utilizing the ArcScan feature and polygon geospatial operations from the imported image dataset. Creeks and water features were manually labeled and exported to GeoTIFF rasters. In Figure 1c–h, the different training datasets delineated are shown, which were selected to represent broad patterns of creek features found throughout the coastal landscape. The training data locations were determined based on expert knowledge of the system variation of vegetation dynamics to fully capture the range of marshes from fresher to saltier. Furthermore, sufficient data were needed in areas with upland forests as these regions initially produced considerable amounts of noise when doing preliminary tests in model development. The model is coded in Python 3.1.
2.3. Proposed Architecture: Attention-Based Dense U-Net Model (ADU-Net)
We have proposed an Attention-based Dense U-Net model (ADU-Net) to segment tidal creek features from high-resolution aerial imagery. The different components of the proposed architecture are highlighted in Figure 2. ADU-Net maps the complex creek networks by combining the strengths of U-Net architecture with dense connectivity and attention mechanisms.
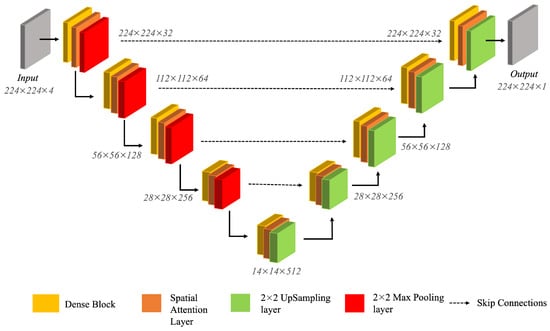
Figure 2.
The architecture of the proposed ADU-Net model.
- U-Net: The U-Net model, proposed by Ronneberger et al. in 2015 [53], is a basic architecture for semantic segmentation tasks, consisting of two main components: the encoder (left half) and the decoder (right half). The encoder encompasses downsampling layers, progressively increasing the filters in each step and extracting high-level feature representations from the input image. The decoder involves upsampling operations to reconstruct the original image size. Additionally, U-Net uses skip connections, significantly improving the reconstruction quality. The downsampling operations in the encoder can lead to the loss of fine-grained spatial information. Thus, skip connections enable the decoder to preserve the spatial details by providing a direct pathway for information to bypass the downsampling layers. Thus, the U-Net model’s elegance lies in its ability to harness the local features effectively, its distinctive “U” shape, and the incorporation of skip connections. U-Net retains fine-detailed information by integrating skip connections, enabling accurate feature extraction and reconstruction. Thus, leveraging global and local context facilitates precise pixel-level classification and segmentation tasks.
- Dense Layers: ADU-Net incorporates DenseNet architecture to enhance feature extraction and address gradient-related issues. The Dense Net is a variation of a traditional convolutional neural network (CNN) [54] introducing dense connections between layers. With the conventional CNN, as the network size increases, it can face either an exploding or vanishing gradient problem. DenseNet adopts a unique characteristic known as dense connectivity to address these issues.In the DenseNet architecture, feature maps from preceding layers are not simply passed sequentially but concatenated to subsequent layers. Figure 3 illustrates this dense connectivity pattern. Within each dense block, comprising three 2-D CNN layers, the input to the layer consists of the concatenated features from layers . This dense connectivity promotes feature reuse, effectively addressing the vanishing gradient problem and fostering enhanced information flow throughout the network. By integrating dense connections, DenseNet enables the model to capture and leverage essential features from all levels of the network, contributing to improved performance.
 Figure 3. The illustration of Dense Block used in ADU-Net.ADU-Net comprises 9 dense blocks with three 2D convolutional layers as depicted in Figure 3. The encoder has 5 dense blocks. After each dense block in the encoder, a max-pooling layer is applied to reduce the spatial resolution. As we obtain the latent space representation, the spatial resolution decreases, and the feature map increases. In the decoder, there are four dense blocks, and an upsampling layer is applied before each dense block.
Figure 3. The illustration of Dense Block used in ADU-Net.ADU-Net comprises 9 dense blocks with three 2D convolutional layers as depicted in Figure 3. The encoder has 5 dense blocks. After each dense block in the encoder, a max-pooling layer is applied to reduce the spatial resolution. As we obtain the latent space representation, the spatial resolution decreases, and the feature map increases. In the decoder, there are four dense blocks, and an upsampling layer is applied before each dense block. - Attention Layers: The ADU-Net architecture the incorporates Convolutional Block Attention Module (CBAM) [55] in its encoder and decoder components to emphasize salient spatial regions (refer to Figure 4). We have incorporated the spatial attention mechanism to enhance the network’s focus on essential areas within the input data. The spatial attention is computed by applying average-pooling and max-pooling operations along every channel and concatenating them. The pooling operation highlights the relevant information present in the input.
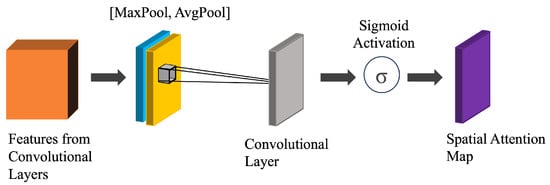 Figure 4. The architecture of Spatial Attention incorporated within ADU-Net (CBAM [55]).In the ADU-Net design, the attention layer is strategically placed after each dense block, allowing for selective emphasis on significant features within the densely connected layers. This placement ensures that attention is applied just before the upsampling operation in the decoder phase. The network obtains attention-normalized features before expanding the spatial resolution by incorporating the attention layer prior to upsampling. This strategic integration of the attention layer facilitates U-Net’s ability to discern and prioritize relevant spatial information during encoding and decoding processes. It improves the model’s capacity to capture and leverage critical features, leading to more effective and contextually rich representations in the final output.
Figure 4. The architecture of Spatial Attention incorporated within ADU-Net (CBAM [55]).In the ADU-Net design, the attention layer is strategically placed after each dense block, allowing for selective emphasis on significant features within the densely connected layers. This placement ensures that attention is applied just before the upsampling operation in the decoder phase. The network obtains attention-normalized features before expanding the spatial resolution by incorporating the attention layer prior to upsampling. This strategic integration of the attention layer facilitates U-Net’s ability to discern and prioritize relevant spatial information during encoding and decoding processes. It improves the model’s capacity to capture and leverage critical features, leading to more effective and contextually rich representations in the final output.
2.4. Model Experiments
We used 6012 input samples for the training of the U-Net model. Each input sample has a dimensionality of . However, the model is prone to overfitting due to a large number of parameters and a smaller number of training samples. This can result in poor generalization on the test dataset. To mitigate this issue, we implemented data augmentation by flipping the input images vertically and horizontally and applying a 90-degree rotation.
The data were split into training, validation, and testing sets. Training images that contained the most creek features (e.g., not large open waterbody areas) were oversampled at a ratio of to for open waterbody images. The resulting test dataset was split again into the test and validation datasets.
We used a range of metrics such as F1 score, dice score, user accuracy (also known as precision), producer accuracy (or recall), and kappa coefficients to evaluate the quantitative performance of the model. Here are some terms used to define these metrics. True positives (TP) are the actual positives that are correctly predicted positives. True negatives (TN) are actual negatives that are correctly predicted negatives. False positives (FP) are actual negatives that are wrongly predicted positives. False Negatives (FN) are actual positives that are wrongly predicted negatives. The user accuracy or precision (Equation (1)) calculates the proportion of correctly predicted positive observations (true positives) out of all predicted positive observations (true positives and false positives).
The producer accuracy or recall (Equation (2)) calculates the proportion of actual positive instances (e.g., creek pixels) that the model correctly identifies. It quantifies the number of positive class predictions (true positives) made from all positive examples (true positives and false negatives) in the dataset.
The F1 score (Equation (3)) is the harmonic mean of precision and recall. It provides a balanced measure of the model’s performance by considering precision and recall.
The dice score, or the Dice Similarity Coefficient (Equation (4)), is the spatial overlap between the predicted segmentation and the ground truth. Its value ranges between 0 and 1, with 1 being the perfect overlap.
where is the number of pixels correctly classified as target objects in both ground-truth and prediction masks. and are the total number of pixels classified as belonging to target objects in ground-truth and predicted masks, respectively. The kappa coefficient, or Cohen’s kappa (Equation (5)), is a statistical measure of inter-rater agreement for categorical items. The kappa coefficient provides a measure of agreement between predicted segmentation and ground-truth segmentation [56].
These metrics collectively provide insights into different aspects of the model’s performance.
We used 5-fold cross-validation to train the model. The model was trained for 30 epochs in each fold with a batch size of 32. The learning rate was set to . The model was trained using binary cross-entropy loss. A Monte Carlo experiment was conducted 5 times to obtain an accurate performance estimate. The Adam optimizer [57] was used to train the model, an algorithm for first-order gradient-based optimization of stochastic objective functions. Adam optimizer is advantageous compared to other optimizers due to the adaptive learning rates, which means that it is computationally efficient and requires less memory than other algorithms. In each experiment, of samples were randomly selected for training and the other for testing. All experiments were executed on an NVIDIA A100 GPU equipped with 80 GB of GPU memory.
3. Results
The model’s performance is compared with the vanilla U-Net model, a commonly used baseline architecture for semantic segmentation tasks. The vanilla U-Net model was applied in [41] to map a salt marsh along coastal South Carolina. The comparative analysis is presented in Table 1, which compares the model’s performance using different metrics.

Table 1.
This table shows the comparison of performance metrics among different variants of the ADU-Net model.
From the results, we can conclude that ADU-Net shows exceptional results. ADU-Net has a kernel size of 5 and an F1 score and a dice score of and , respectively, showcasing its effectiveness in capturing relevant features for classification tasks. Similarly, the model has a user and producer accuracy of and , showing the model’s effectiveness in accurately identifying and categorizing important data attributes.
We have shown the results of ADU-net on test samples in Figure 5. To evaluate the results, we computed and reported the dice coefficient of these figures. Figure 5a and Figure 5b, characterized by lower densities of Sesarma crabs, achieve high dice coefficients of and , respectively. Similarly, Figure 5c, Figure 5d, and Figure 5e attain dice coefficients of , , and , respectively. The high dice coefficients indicate the strong segmentation performance of the ADU-Net model. It is efficient in delineating creek features amidst varying densities of Sesarma crabs.

Figure 5.
(a–e) shows the different levels of creekhead grazing by Sesarma reticulatum crabs. Creek images from test data are shown (left), the ground truth is marked on the original images (middle), and the predictions from ADU-Net are marked on the original images (right).
Figure 6 and Figure 7 show a region of creeks with extensive grazing and mudflat formation. We can observe that in Figure 8, the model is able to identify most parts of the creeks. Especially in the blue region, the model has effectively captured all the creek pixels. However, in the red-bounding box, not all the creek pixels are identified. Figure 9 shows a Juncus-dominated marsh adjacent to the mainland. This region is primarily impacted by human development as there is extensive canal ditching throughout. In the lower left region, the model recognizes certain man-made structures as creek pixels, highlighting a challenge for future model improvements to handle uncertainties and unseen image scenarios more effectively. These images illustrate large spatial creeks, which would be time-consuming to label manually. Therefore, we provide visual interpretations of the segmentation results. Our study highlights that ADU-Net excels in accurately identifying and mapping creek features. It performs well, especially in challenging environments. However, there is room for improvement in handling more complex situations. This suggests opportunities for refining and enhancing the model to better tackle diverse environmental scenarios.

Figure 6.
(a) Larger spatial creek area with extensive grazing and mudflat formations. (b) Prediction results from ADU-Net.

Figure 7.
(a) Larger spatial creek area with extensive grazing. (b) Prediction results from ADU-Net.
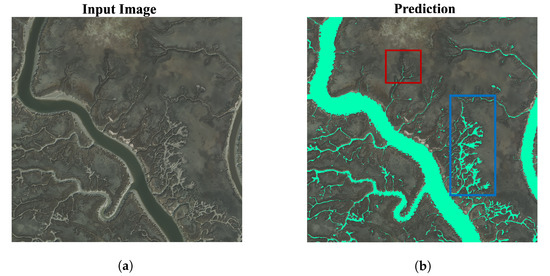
Figure 8.
(a) Larger spatial creek area dominated by Spartina alterniflora. with extensive grazing. The figure shows both creeks with extensive grazing and mudflat formation. (b) Prediction results from ADU-Net. In the red bounding box, we can see that not all creek pixels are identified. However, all the intricate pixels are effectively identified by ADU-Net in the blue bounding box.

Figure 9.
(a) Marsh area connected to the mainland containing fresher marshes and man-made drainage ditches. These locations are dominated by Juncus-dominated marsh. (b) Prediction results from ADU-Net.
3.1. Sensitivity Analysis
Kernel Size-Attention: We conducted a sensitivity analysis on the validation set to explore the impact of different kernel sizes on the performance of the attention module and determine the optimal configuration for the attention mechanism, as illustrated in Table 2. A larger kernel takes into account a larger receptive field to determine a pixel’s relevance. A larger kernel also increases the number of neural network parameters. On the other hand, a smaller kernel does not have enough spatial neighborhood information to determine its relevance in the entire spatial feature map. However, a smaller kernel keeps the number of parameters low. Therefore, an optimal kernel size is required, which is most suitable for the network. This analysis allowed us to assess how variations in kernel size affect the attention mechanism’s ability to capture relevant features and enhance the model’s overall performance.

Table 2.
Sensitivity analysis of different kernel size (k) to the performance of the model.
The results are summarized in Table 2 and in Figure 10; four metrics (F-1 score, dice coefficient, user accuracy, and producer accuracy) are plotted for different kernel sizes. These results show that is optimal for this task. Based on the results from the table and plots, we can conclude that the ADU-Net model achieves optimal performance with a kernel size of . This configuration strikes a balance between capturing relevant spatial context without becoming overly sensitive to fine details and maintaining computational efficiency, enhancing the model’s effectiveness.
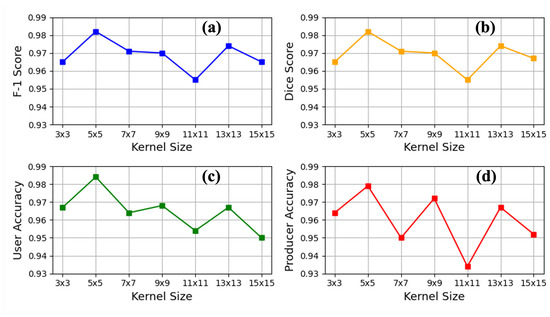
Figure 10.
Performance metrics (a) F-1 score, (b) dice score, (c) user accuracy, and (d) producer accuracy plotted against different kernel sizes (3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, 13 × 13, 15 × 15) for the ADU-Net model.
3.2. Ablation Study
We performed an ablation study to observe the performance of four different variants of the U-Net model: the ADU-Net model (with no attention and dense layers) or vanilla U-Net, the ADU-Net model (with no attention layers), the ADU-Net model (with no dense layers), and ADU-Net. The findings are illustrated in Table 1. The ablation study reveals a consistent trend in the performance metrics as we progress from the ADU-Net model (with no attention and dense layers) to the ADU-Net model (with no attention), the ADU-Net model (with no dense layers), and finally, to the ADU-Net model. The results are evaluated using metrics such as F1 score, dice score, user accuracy, producer accuracy, and kappa coefficient. All the metrics indicate that ADU-Net performs best among all these U-Net model variants. For instance, comparing the F1 score, we observe an increase from for vanilla U-Net to for ADU-Net. Similarly, the dice score shows a similar trend, with values increasing from for vanilla U-Net to for ADU-Net. This consistent improvement across multiple metrics indicates that the enhancements introduced in each successive model iteration contribute positively to overall performance. Similarly, there is an enhancement in both user and producer accuracy, indicating the model’s ability to identify and classify critical features in the dataset accurately.
These findings highlight how the synergistic combination of attention and dense layers helps accurately predict creek pixels. They demonstrate the effectiveness of spatial attention in capturing and leveraging crucial spatial information for segmentation tasks while also showcasing the efficacy of DenseNet in enhancing model performance.
4. Discussion
Our findings demonstrate that the ADU-Net model exhibits optimal performance across various metrics, including F1 score, dice score, user accuracy, producer accuracy, and kappa coefficient. This enhancement is attributed to the synergistic combination of attention mechanisms and dense layers, significantly improving the model’s ability to capture and leverage essential spatial information for segmentation tasks, thereby accurately delineating creek features from aerial imagery.
Our methodology’s primary advantage is its ability to capture features at high resolution. Lower resolution datasets, such as those from the Sentinel mission at 10 m × 10 m pixels, may fail to capture creek features that often exist on scales of tens of centimeters to a few meters. This increased fidelity of extracted data allows for identifying detailed patterns that were previously too time-intensive to digitize manually. Spatial patterns at these scales may influence the ecological–geomorphic interactions and vice versa. The inclusion of these data with high fidelity has the potential to understand the inter-dynamics of these systems better and produce a sufficient sample size for statistical analysis. For example, with crab and mussel-dominated creek systems, there can be high variation in geomorphic structure (e.g., sinuosity, bifurcation angle, creek–marsh area ratios), and it can be difficult to discern which are driving factors of these patterns. However, given a large sample size (this dataset within), it has the potential to capture wide variability and could reveal potential drivers and mechanisms of these geospatial patterns. Our model surpasses traditional manual methods, limited by the human capacity to digitize extensive creek networks. The ADU-Net model’s ability to efficiently extract large networks, potentially encompassing thousands of creeks, represents a significant advancement. Furthermore, the high accuracy of our model’s results reduces the need for manual post-processing, thus enabling the dataset to be readily available for subsequent analyses.
Figure 5 shows the different levels of creekhead grazing by Sesarma reticulatum crabs. Sesarma crabs are widespread throughout most marshes, although some areas, such as in Figure 5a,b in the image, show lower densities. These crabs play a dual role in shaping the creeks, particularly the creekheads [12,58]. They accomplish this by consuming vegetation and creating extensive burrows in the ground. This combined activity increases the soil’s erodibility, leading to the formation of distinct creeks like Figure 5c–e. The gray areas represent mud flats where vegetation has been stripped away, resulting in weak soil that can cause sinking when stepped on. In [12], the impact of crab grazing on marsh evolution is investigated. According to their finding, the marshes in the region are evolving the most, where there are the highest densities of Sesarma. The ADU-Net model can precisely extract the creek networks, potentially encompassing thousands of creeks. Our ongoing research aims to extract and analyze tens of thousands of creeks from the marshland, facilitating statistical investigations into creek evolution and structure.
Despite the model’s success, Figure 9 shows misclassification issues in a Juncus-dominated marsh adjacent to the mainland. This region is primarily impacted by human development as there is extensive canal ditching throughout. The model misclassified particular man-made objects as creeks. Therefore, in our future work, we must address this problem by training the model to detect these outliers effectively.
In future work, we also aim to extend the applicability of the ADU-Net model to datasets from multiple years without necessitating model retraining. This presents challenges because the dataset from year 2014 shows a drought year with widespread vegetation die-back and noticeable mudflats, unlike the 2017 dataset, where mudflats were less common. This difference in environmental conditions across years poses a significant challenge for using the same model across different datasets. Using a model trained on data from one year to analyze subsequent years presents challenges due to the varying distribution of denuded and mudflat areas within interior marsh regions. Additionally, seasonal changes can cause significant shifts in the landscape’s spectral characteristics, making it difficult to ensure consistent model performance over time. To address these challenges effectively, we will focus on developing adaptive strategies that enable the ADU-Net model to generalize across diverse temporal conditions.
5. Conclusions
Tidal creek segmentation is crucial for distinguishing creeks and channels at higher resolutions and larger spatial scales, enabling the extraction of vital insights into the rate of change in coastal wetlands. We evaluated a new deep neural network model, ADU-Net, for creek segmentation on data having a m spatial resolution and 4-band spectral resolution (red, green, blue, and near-infrared). The DenseNet architecture plays a crucial role in retaining both low-level and high-level features (feature reuse), preventing the need for a large number of filters in the network. By incorporating DenseNet modules, we mitigate issues like vanishing gradients from earlier layers. At the same time, the integrated attention mechanism extracts salient spatial regions and propagates this information to the decoder. ADU-Net can achieve a high F1 score of compared to vanilla U-Net, which has an F1 score of . Additionally, when compared across other metrics, ADU-Net demonstrates improvements: the dice coefficient increases by , producer accuracy by , user accuracy by , and kappa coefficient by . Accurate prediction of the multi-scale water features can expand the sample size for geospatial analyses, enabling the mapping of the entire coastal region in hours with limited user intervention. Future work will improve this model to avoid uncertainties in unseen test data, such as man-made structures, and incorporate imagery from different years. This will allow multi-temporal change analyses to identify patterns of marsh evolution. We also plan to include SAR imagery in addition to the current dataset for segmenting targets on intertidal flats.
Author Contributions
Methodology, R.D.; Data curation, C.O.; Writing—original draft, R.D.; Writing—review & editing, C.O., W.H., Z.C.C., C.A., A.C. and Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
Aerial imagery datasets were collected by Kucera International and quality controlled under the direction of Clark Alexander, with support from the Georgia Coastal Ecosystems Long-Term Ecological Research Program (NSF Award #1237140). R.D., W.H., Z.C.C., and Z.J. were supported by the NSF CRII project with grant Nos. IIS-2147908, IIS-2207072, CNS-1951974, and OAC-2152085. C.O. and C.A. were supported by a grant from the National Science Foundation (NSF-CBET #1652628).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Syvitski, J.P.; Vorosmarty, C.J.; Kettner, A.J.; Green, P. Impact of humans on the flux of terrestrial sediment to the global coastal ocean. Science 2005, 308, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Kennish, M.J. Coastal salt marsh systems in the US: A review of anthropogenic impacts. J. Coast. Res. 2001, 17, 731–748. [Google Scholar]
- Barlow, P.M.; Reichard, E.G. Saltwater intrusion in coastal regions of North America. Hydrogeol. J. 2010, 18, 247. [Google Scholar] [CrossRef]
- French, J.R.; Spencer, T. Dynamics of sedimentation in a tide-dominated backbarrier salt marsh, Norfolk, UK. Mar. Geol. 1993, 110, 315–331. [Google Scholar] [CrossRef]
- Hughes, A.L.; Wilson, A.M.; Morris, J.T. Hydrologic variability in a salt marsh: Assessing the links between drought and acute marsh dieback. Estuar. Coast. Shelf Sci. 2012, 111, 95–106. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; Van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Altieri, A.H.; Bertness, M.D.; Coverdale, T.C.; Herrmann, N.C.; Angelini, C. A trophic cascade triggers collapse of a salt-marsh ecosystem with intensive recreational fishing. Ecology 2012, 93, 1402–1410. [Google Scholar] [CrossRef]
- Kelleway, J.J.; Cavanaugh, K.; Rogers, K.; Feller, I.C.; Ens, E.; Doughty, C.; Saintilan, N. Review of the ecosystem service implications of mangrove encroachment into salt marshes. Glob. Chang. Biol. 2017, 23, 3967–3983. [Google Scholar] [CrossRef] [PubMed]
- Barbier, E.B.; Georgiou, I.Y.; Enchelmeyer, B.; Reed, D.J. The value of wetlands in protecting southeast Louisiana from hurricane storm surges. PLoS ONE 2013, 8, e58715. [Google Scholar] [CrossRef]
- Chmura, G.L.; Anisfeld, S.C.; Cahoon, D.R.; Lynch, J.C. Global carbon sequestration in tidal, saline wetland soils. Glob. Biogeochem. Cycles 2003, 17, 1111. [Google Scholar] [CrossRef]
- Crotty, S.M.; Pinton, D.; Canestrelli, A.; Fischman, H.S.; Ortals, C.; Dahl, N.R.; Williams, S.; Bouma, T.J.; Angelini, C. Faunal engineering stimulates landscape-scale accretion in southeastern US salt marshes. Nat. Commun. 2023, 14, 881. [Google Scholar] [CrossRef]
- Crotty, S.M.; Ortals, C.; Pettengill, T.M.; Shi, L.; Olabarrieta, M.; Joyce, M.A.; Altieri, A.H.; Morrison, E.; Bianchi, T.S.; Craft, C.; et al. Sea-level rise and the emergence of a keystone grazer alter the geomorphic evolution and ecology of southeast US salt marshes. Proc. Natl. Acad. Sci. USA 2020, 117, 17891–17902. [Google Scholar] [CrossRef]
- Ortals, C.; Cordero, O.; Valle-Levinson, A.; Angelini, C. Flows, transport, and effective drag in intertidal salt marsh creeks. J. Geophys. Res. Ocean. 2021, 126, e2021JC017357. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Hannion, M.; D’Odorico, P. Geomorphic structure of tidal hydrodynamics in salt marsh creeks. Water Resour. Res. 2008, 44, W02419. [Google Scholar] [CrossRef]
- Christiansen, T.; Wiberg, P.; Milligan, T. Flow and sediment transport on a tidal salt marsh surface. Estuar. Coast. Shelf Sci. 2000, 50, 315–331. [Google Scholar] [CrossRef]
- Temmerman, S.; Bouma, T.; Govers, G.; Lauwaet, D. Flow paths of water and sediment in a tidal marsh: Relations with marsh developmental stage and tidal inundation height. Estuaries 2005, 28, 338–352. [Google Scholar] [CrossRef]
- Angelini, C.; van Montfrans, S.G.; Hensel, M.J.; He, Q.; Silliman, B.R. The importance of an underestimated grazer under climate change: How crab density, consumer competition, and physical stress affect salt marsh resilience. Oecologia 2018, 187, 205–217. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Kirwan, M.L.; Mudd, S.M.; Guntenspergen, G.R.; Temmerman, S.; D’Alpaos, A.; Van De Koppel, J.; Rybczyk, J.M.; Reyes, E.; Craft, C.; et al. Numerical models of salt marsh evolution: Ecological, geomorphic, and climatic factors. Rev. Geophys. 2012, 50, RG1002. [Google Scholar] [CrossRef]
- Kirwan, M.L.; Megonigal, J.P. Tidal wetland stability in the face of human impacts and sea-level rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef]
- Burns, C.J.; Alexander, C.R.; Alber, M. Assessing long-term trends in lateral salt-marsh shoreline change along a US east coast latitudinal gradient. J. Coast. Res. 2021, 37, 291–301. [Google Scholar]
- Mou, K.; Gong, Z.; Qiu, H. Spatiotemporal differentiation and development process of tidal creek network morphological characteristics in the Yellow River Delta. J. Geogr. Sci. 2021, 31, 1633–1654. [Google Scholar] [CrossRef]
- Chen, C.; Tian, B.; Schwarz, C.; Zhang, C.; Guo, L.; Xu, F.; Zhou, Y.; He, Q. Quantifying delta channel network changes with Landsat time-series data. J. Hydrol. 2021, 600, 126688. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Gong, Z.; Wang, Q.; Guan, H.; Zhou, D.; Zhang, L.; Jing, R.; Wang, X.; Li, Z. Extracting tidal creek features in a heterogeneous background using Sentinel-2 imagery: A case study in the Yellow River Delta, China. Int. J. Remote Sens. 2020, 41, 3653–3676. [Google Scholar] [CrossRef]
- Gong, Z.; Mou, K.; Wang, Q.; Qiu, H.; Zhang, C.; Zhou, D. Parameterizing the Yellow River Delta tidal creek morphology using automated extraction from remote sensing images. Sci. Total Environ. 2021, 769, 144572. [Google Scholar] [CrossRef]
- Pinton, D.; Canestrelli, A.; Wilkinson, B.; Ifju, P.; Ortega, A. Estimating ground elevation and vegetation characteristics in coastal salt marshes using UAV-based LiDAR and digital aerial photogrammetry. Remote Sens. 2021, 13, 4506. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, M.; Zhao, S.; Zhan, W.; Yang, K.; Li, M. Automated extraction of tidal creeks from airborne laser altimetry data. J. Hydrol. 2015, 527, 1006–1020. [Google Scholar] [CrossRef]
- Geng, L.; Gong, Z.; Lanzoni, S.; D’Alpaos, A. A new method for automatic definition of tidal creek networks. J. Coast. Res. 2018, 85, 156–160. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Bortoluzzi, A.; Dietrich, W.E.; Adami, A.; Lanzoni, S.; Marani, M.; Rinaldo, A. Tidal networks: 1. Automatic network extraction and preliminary scaling features from digital terrain maps. Water Resour. Res. 1999, 35, 3891–3904. [Google Scholar] [CrossRef]
- Dronova, I.; Gong, P.; Clinton, N.E.; Wang, L.; Fu, W.; Qi, S.; Liu, Y. Landscape analysis of wetland plant functional types: The effects of image segmentation scale, vegetation classes and classification methods. Remote Sens. Environ. 2012, 127, 357–369. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Cambridge, MA, USA, 1988. [Google Scholar]
- Cramer, J.S. The Origins of Logistic Regression; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron, a Perceiving and Recognizing Automaton Project Para; Cornell Aeronautical Laboratory: Buffalo, NY, USA, 1957. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Committee on Applied Mathematics, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3/E; Pearson Education: Bengaluru, India, 2009. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Fix, E. Discriminatory Analysis: Nonparametric Discrimination, Consistency Properties; USAF School of Aviation Medicine: Dayton, OH, USA, 1985; Volume 1. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Whyte, A.; Ferentinos, K.P.; Petropoulos, G.P. A new synergistic approach for monitoring wetlands using Sentinels-1 and 2 data with object-based machine learning algorithms. Environ. Model. Softw. 2018, 104, 40–54. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Cui, Y.; Hodgson, M. Mapping salt marsh along coastal South Carolina using U-Net. ISPRS J. Photogramm. Remote Sens. 2021, 179, 121–132. [Google Scholar] [CrossRef]
- Morgan, G.R.; Wang, C.; Li, Z.; Schill, S.R.; Morgan, D.R. Deep learning of high-resolution aerial imagery for coastal marsh change detection: A comparative study. ISPRS Int. J. Geo-Inf. 2022, 11, 100. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, Y.; Zhao, C.; Dai, W.; Kattel, G.R.; Zhou, D. Quantitative Analysis of Tidal Creek Evolution and Vegetation Variation in Silting Muddy Flats on the Yellow Sea. Remote Sens. 2023, 15, 5107. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Z.; Zheng, G.; Zhao, C. Identification of Spartina alterniflora habitat expansion in a Suaeda salsa dominated coastal wetlands. Ecol. Indic. 2022, 145, 109704. [Google Scholar] [CrossRef]
- Lv, Z.; Nunez, K.; Brewer, E.; Runfola, D. Mapping the tidal marshes of coastal Virginia: A hierarchical transfer learning approach. GIScience Remote Sens. 2024, 61, 2287291. [Google Scholar] [CrossRef]
- Dang, K.B.; Nguyen, M.H.; Nguyen, D.A.; Phan, T.T.H.; Giang, T.L.; Pham, H.H.; Nguyen, T.N.; Tran, T.T.V.; Bui, D.T. Coastal wetland classification with deep u-net convolutional networks and sentinel-2 imagery: A case study at the tien yen estuary of vietnam. Remote Sens. 2020, 12, 3270. [Google Scholar] [CrossRef]
- Li, R.; Liu, W.; Yang, L.; Sun, S.; Hu, W.; Zhang, F.; Li, W. DeepUNet: A deep fully convolutional network for pixel-level sea-land segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3954–3962. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Yu, J.; Li, Y.; Guan, B.; Zhou, J.; Ling, Y.; Ma, Y. Distribution of tidal channels in different landscape types in coastal wetlands of the Yellow River estuary. Chin. J. Ecol. 2023, 42, 2218. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wang, C.; Morgan, G.R.; Morris, J.T. Drone Lidar Deep Learning for Fine-Scale Bare Earth Surface and 3D Marsh Mapping in Intertidal Estuaries. Sustainability 2023, 15, 15823. [Google Scholar] [CrossRef]
- Pinton, D.; Canestrelli, A.; Wilkinson, B.; Ifju, P.; Ortega, A. A new algorithm for estimating ground elevation and vegetation characteristics in coastal salt marshes from high-resolution UAV-based LiDAR point clouds. Earth Surf. Process. Landforms 2020, 45, 3687–3701. [Google Scholar] [CrossRef]
- Hladik, C.; Schalles, J.; Alber, M. Salt marsh elevation and habitat mapping using hyperspectral and LIDAR data. Remote Sens. Environ. 2013, 139, 318–330. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhang, Y.D.; Pan, C.; Chen, X.; Wang, F. Abnormal breast identification by nine-layer convolutional neural network with parametric rectified linear unit and rank-based stochastic pooling. J. Comput. Sci. 2018, 27, 57–68. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews correlation coefficient (MCC) is more informative than Cohen’s Kappa and Brier score in binary classification assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Morrison, E.S.; Bianchi, T.S.; Kenney, W.F.; Brenner, M.; Prince, K.; Williams, S.; Ortals, C.; Cordero, O.; Crotty, S.M.; Angelini, C. Influence of the Keystone Grazer, Sesarma reticulatum, on the Hydrology and Organic Matter Cycling in Salt Marshes of the Southeastern USA. Estuaries Coasts 2024, 47, 994–1011. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).