Comparative Analysis of Machine Learning and Deep Learning Models for Individual Tree Structure Segmentation Using Terrestrial LiDAR Point Cloud Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition
2.3. Methodology
2.4. PCD Preprocessing and Individual Tree Data Construction
2.4.1. Point Cloud Registration and Geometric Correction
2.4.2. Individual Tree Extraction
2.4.3. PCD Noise Removal
2.5. Label Data Construction for Tree Structure Segmentation
2.5.1. Manual Segmentation of Tree Structures
2.5.2. Dataset Construction Based on Downsampling Conditions
2.6. Model Construction for Tree Structure Segmentation
2.6.1. Selection of Input Features
2.6.2. Model Selection and Training Configuration
2.7. Evaluation of Tree Structure Segmentation Models
3. Results
3.1. Dataset Construction for Individual Tree Structure Segmentation
3.2. Hyperparameter Optimization and Feature Importance Analysis of XGBoost
3.3. Accuracy Evaluation Under Different Input Feature Combinations
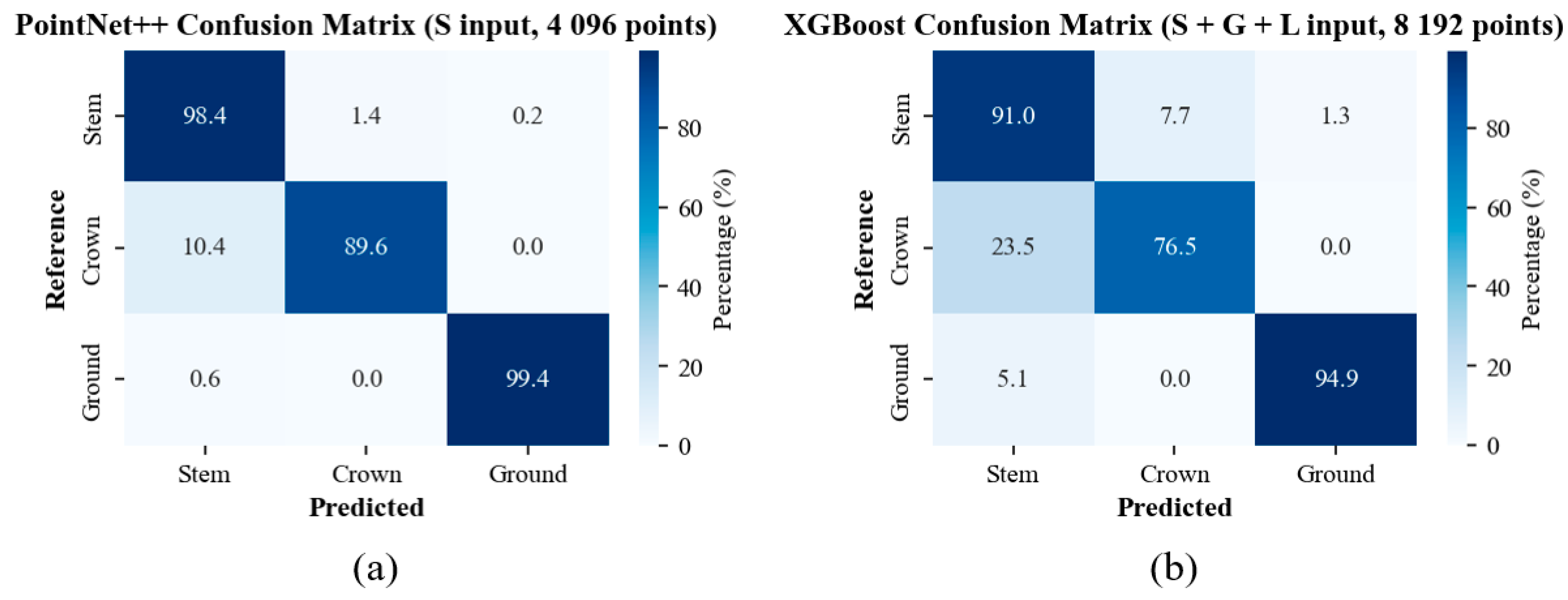
3.4. Class-Wise Tree Structure Segmentation Accuracy by ML and DL Models
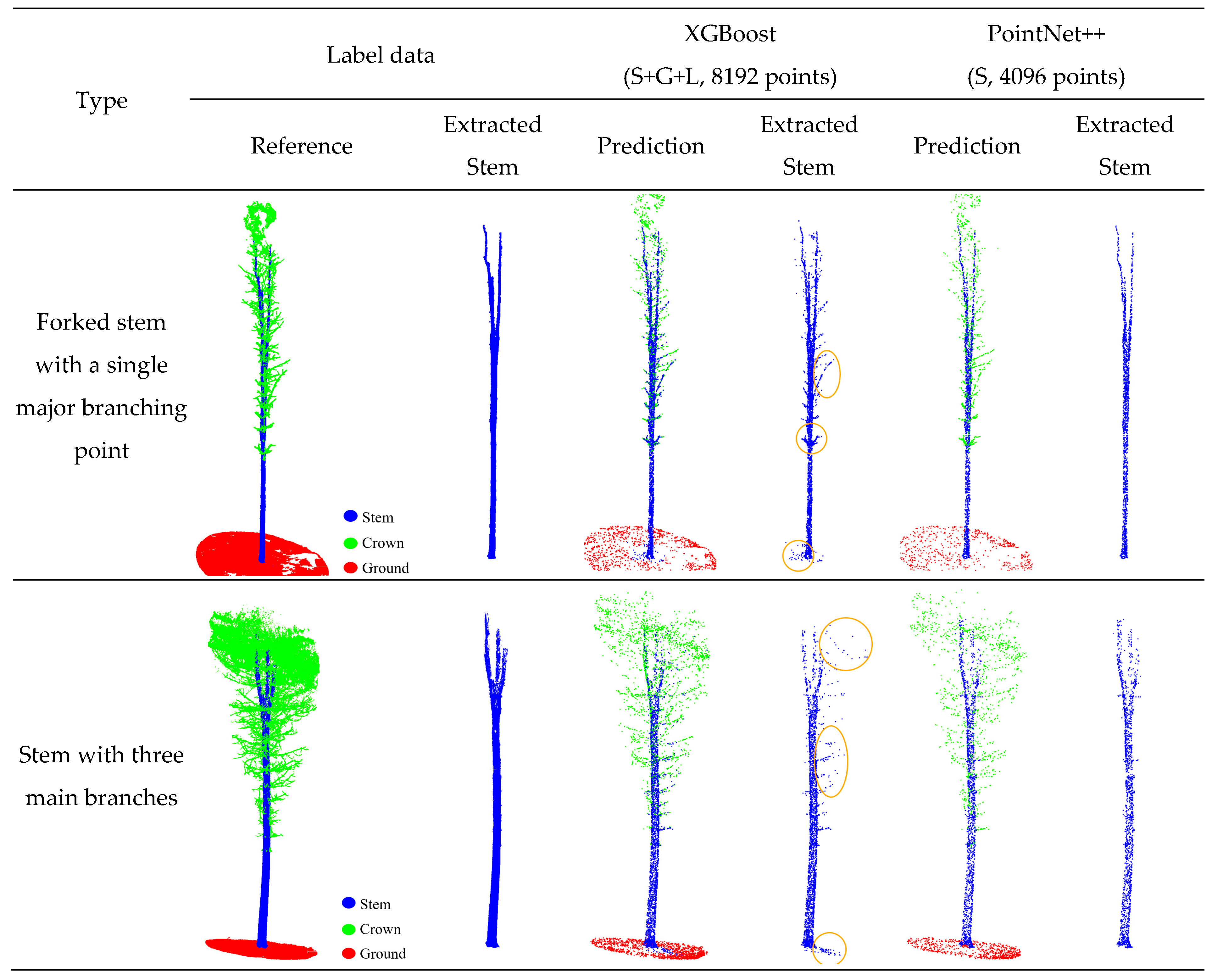
3.5. Analysis of Missegmentation Cases in Tree Structure Segmentation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Psistaki, K.; Tsantopoulos, G.; Paschalidou, A.K. An overview of the role of forests in climate change mitigation. Sustainability 2024, 16, 6089. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, D.; Yao, X.; Wang, S.; Chi, T.; Meng, Y. Forest emissions reduction assessment using optical satellite imagery and space LiDAR fusion for carbon stock estimation. Remote Sens. 2023, 15, 1410. [Google Scholar] [CrossRef]
- Sparks, A.M.; Smith, A.M. Accuracy of a lidar-based individual tree detection and attribute measurement algorithm developed to inform forest products supply chain and resource management. Forests 2021, 13, 3. [Google Scholar] [CrossRef]
- Ko, C.U.; Kang, J.T.; Park, J.M.; Lee, M.W. Assessing forest resources with terrestrial and backpack LiDAR: A case study on leaf-on and leaf-off conditions in Gari Mountain, Hongcheon, Republic of Korea. Forests 2024, 15, 2230. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Kim, D.Y.; Choi, Y.W.; Lee, G.S.; Cho, G.S. Extracting individual number and height of tree using airborne LiDAR data. J. Cadastre Land Inf. 2016, 46, 87–100. [Google Scholar]
- Seo, S.H.; Park, K.M.; Jung, T.Y. Study on tree volume measurement using terrestrial and airborne laser scanners. J. Korean Inst. Landsc. Archit. 2024, 52, 42–52. [Google Scholar] [CrossRef]
- Woo, H.; Cho, S.; Jung, G.; Park, J. Precision forestry using remote sensing techniques: Opportunities and limitations of remote sensing application in forestry. Korean J. Remote Sens. 2019, 35, 1067–1082. [Google Scholar] [CrossRef]
- Korea Forest Service. Forest Master Plans, 6th ed.; Korea Forest Service: Daejeon, Republic of Korea, 2018; p. 27. [Google Scholar]
- Jo, S.H.; Ban, S.H.; Lee, H.J.; Choi, S.K. Individual tree detection in natural forest using high density airborne laser scanning. J. Korean Soc. Geospat. Inf. Sci. 2023, 31, 29–38. [Google Scholar] [CrossRef]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2015, II-3/W4, 189–196. [Google Scholar] [CrossRef]
- Sheppard, J.; Morhart, C.; Hackenberg, J.; Spiecker, H. Terrestrial laser scanning as a tool for assessing tree growth. iForest 2017, 10, 172–179. [Google Scholar] [CrossRef]
- Boucher, P.B.; Paynter, I.; Orwig, D.A.; Valencius, I.; Schaaf, C. Sampling forests with terrestrial laser scanning. Ann. Bot. 2021, 128, 689–708. [Google Scholar] [CrossRef] [PubMed]
- Campos, M.B.; Litkey, P.; Wang, Y.; Chen, Y.; Hyyti, H.; Hyyppä, J.; Puttonen, E. A long-term terrestrial laser scanning measurement station to continuously monitor structural and phenological dynamics of boreal forest canopy. Front. Plant Sci. 2021, 11, 606752. [Google Scholar] [CrossRef]
- Hackenberg, J.; Spiecker, H.; Calders, K.; Disney, M.; Raumonen, P. SimpleTree—An efficient open source tool to build tree models from TLS clouds. Forests 2015, 6, 4245–4294. [Google Scholar] [CrossRef]
- Wang, D.; Liang, X.; Mofack, G.I.; Martin-Ducup, O. Individual tree extraction from terrestrial laser scanning data via graph pathing. For. Ecosyst. 2021, 8, 67. [Google Scholar] [CrossRef]
- De Paula Pires, R.; Olofsson, K.; Persson, H.J.; Lindberg, E.; Holmgren, J. Individual tree detection and estimation of stem attributes with mobile laser scanning along boreal forest roads. ISPRS J. Photogramm. Remote Sens. 2022, 187, 211–224. [Google Scholar] [CrossRef]
- Wilkes, P.; Disney, M.; Armston, J.; Bartholomeus, H.; Bentley, L.; Brede, B.; Burt, A.; Calders, K.; Chavana-Bryant, C.; Clewley, D.; et al. TLS2trees: A scalable tree segmentation pipeline for TLS data. Methods Ecol. Evol. 2023, 14, 3083–3099. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar] [CrossRef]
- Su, Z.; Li, S.; Liu, H.; Liu, Y. Extracting wood point cloud of individual trees based on geometric features. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1294–1298. [Google Scholar] [CrossRef]
- Neuville, R.; Bates, J.S.; Jonard, F. Estimating forest structure from UAV-mounted LiDAR point cloud using machine learning. Remote Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Tarsha Kurdi, F.; Campbell, G. Review of automatic processing of topography and surface feature identification LiDAR data using machine learning techniques. Remote Sens. 2022, 14, 4685. [Google Scholar] [CrossRef]
- Windrim, L.; Bryson, M. Detection, segmentation, and model fitting of individual tree stems from airborne laser scanning of forests using deep learning. Remote Sens. 2020, 12, 1469. [Google Scholar] [CrossRef]
- Daif, H.; Marzouk, M. Point cloud classification and part segmentation of steel structure elements. Neural Comput. Appl. 2025, 37, 4387–4407. [Google Scholar] [CrossRef]
- Itakura, K.; Miyatani, S.; Hosoi, F. Estimating tree structural parameters via automatic tree segmentation from LiDAR point cloud data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 15, 555–564. [Google Scholar] [CrossRef]
- Zhang, W.; Wan, P.; Wang, T.; Cai, S.; Chen, Y.; Jin, X.; Yan, G. A novel approach for the detection of standing tree stems from plot-level terrestrial laser scanning data. Remote Sens. 2019, 11, 211. [Google Scholar] [CrossRef]
- Shao, J.; Lin, Y.C.; Wingren, C.; Shin, S.Y.; Fei, W.; Carpenter, J.; Habib, A.; Fei, S. Large-scale inventory in natural forests with mobile LiDAR point clouds. Sci. Remote Sens. 2024, 10, 100168. [Google Scholar] [CrossRef]
- Korea Forest Service and Korea Forestry Promotion Institute. The 8th National Forest Inventory and Forest Health Monitoring. -Field Manual-; Korea Forestry Promotion Institute: Seoul, Republic of Korea, 2021; pp. 7–8. [Google Scholar]
- National Institute of Forest Science (NIFoS). Guidelines for Using Terrestrial LiDAR for Digital Forest Resource Inventory; NIFoS: Seoul, Republic of Korea, 2022. [Google Scholar]
- Pavelka, K.; Zahradnik, D.; Sedina, J. New measurement methods for structure deformation and objects exact dimension determination. IOP Conf. Ser. Earth Environ. Sci. 2021, 906, 012060. [Google Scholar] [CrossRef]
- Lopatin, E.; Vaatainen, K.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Holmström, E.; Sikanen, L.; Nuutinen, Y.; Routa, J. Unlocking digitalization in forest operations with viewshed analysis to improve GNSS positioning accuracy. Forests 2023, 14, 689. [Google Scholar] [CrossRef]
- Panella, F.; Roecklinger, N.; Vojnovic, L.; Loo, Y.; Boehm, J. Cost–benefit analysis of rail tunnel inspection for photogrammetry and laser scanning. ISPRS Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 1137–1144. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Cheng, F.; Ma, W.; Liu, Q.; Liu, G. Natural forest ALS–TLS point cloud data registration without control points. J. For. Res. 2023, 34, 809–820. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Duan, D.; Deng, Y.; Zhang, J.; Wang, J.; Dong, P. Influence of VF and SOR-filtering methods on tree height inversion using unmanned aerial vehicle LiDAR data. Drones 2024, 8, 119. [Google Scholar] [CrossRef]
- Tai, H.; Xia, Y.; Yan, M.; Li, C.; Kong, X. Construction of artificial forest point clouds by laser SLAM technology and estimation of carbon storage. Appl. Sci. 2022, 12, 10838. [Google Scholar] [CrossRef]
- Wang, D.; Momo Takoudjou, S.; Casella, E. LeWoS: A universal leaf–wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Kim, D.H.; Ko, C.U.; Kim, D.G.; Kang, J.T.; Park, J.M.; Cho, H.J. Automated segmentation of individual tree structures using deep learning over LiDAR point cloud data. Forests 2023, 14, 1159. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Gharineiat, Z.; Lewandowicz, E.; Shan, J. Modeling the geometry of tree trunks using LiDAR data. Forests 2024, 15, 368. [Google Scholar] [CrossRef]
- Liu, B.; Chen, S.; Huang, H.; Tian, X. Tree species classification of backpack laser scanning data using the PointNet++ point cloud deep learning method. Remote Sens. 2022, 14, 3809. [Google Scholar] [CrossRef]
- Pan, L.; Chen, X.; Cai, Z.; Zhang, J.; Zhao, H.; Yi, S.; Liu, Z. Variational relational point completion network for robust 3D classification. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11340–11351. [Google Scholar] [CrossRef]
- Sun, P.; Yuan, X.; Li, D. Classification of individual tree species using UAV LiDAR based on transformer. Forests 2023, 14, 484. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Learning semantic segmentation of large-scale point clouds with random sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8338–8354. [Google Scholar] [CrossRef]
- Han, T.; Sánchez-Azofeifa, G.A. A deep learning time series approach for leaf and wood classification from terrestrial LiDAR point clouds. Remote Sens. 2022, 14, 3157. [Google Scholar] [CrossRef]
- Van den Broeck, W.A.J.; Terryn, L.; Cherlet, W.; Cooper, Z.T.; Calders, K. Three-dimensional deep learning for leaf–wood segmentation of tropical tree point clouds. ISPRS Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-1/W2-2023, 765–770. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, Z.; Liu, H.; Wu, J.; Lin, W. Individual tree species identification for complex coniferous and broad-leaved mixed forests based on deep learning combined with UAV LiDAR data and RGB images. Forests 2024, 15, 293. [Google Scholar] [CrossRef]
- Weinmann, M.; Urban, S.; Hinz, S.; Jutzi, B.; Mallet, C. Distinctive 2D and 3D features for automated large-scale scene analysis in urban areas. Comput. Graph. 2015, 49, 47–57. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Pan, J.; Mu, F.; Zhao, L. Stem detection from terrestrial laser scanning data with features selected via stem-based evaluation. Forests 2023, 14, 2035. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, Q.; Liu, S.; Liang, C.; Dai, L.; Zhang, Z.; Wang, Y. LWSNet: A point-based segmentation network for leaf–wood separation of individual trees. Forests 2023, 14, 1303. [Google Scholar] [CrossRef]
- Xianyi, W.; Yanqiu, X.; Haotian, Y.; Tao, X.; Su, S. TLS point cloud classification of forest based on nearby geometric features. J. Beijing For. Univ. 2019, 41, 138–146. [Google Scholar] [CrossRef]
- Rust, S.; Stoinski, B. Enhancing Tree Species Identification in Forestry and Urban Forests through Light Detection and Ranging Point Cloud Structural Features and Machine Learning. Forests 2024, 15, 188. [Google Scholar] [CrossRef]
- Han, T.; Sánchez-Azofeifa, G.A. Extraction of liana stems using geometric features from terrestrial laser scanning point clouds. Remote Sens. 2022, 14, 4039. [Google Scholar] [CrossRef]
- Fan, Z.; Wei, J.; Zhang, R.; Zhang, W. Tree species classification based on PointNet++ and airborne laser survey point cloud data enhancement. Forests 2023, 14, 1246. [Google Scholar] [CrossRef]
- Moorthy, S.M.K.; Bao, Y.; Calders, K.; Schnitzer, S.A.; Verbeeck, H. Semi-automatic extraction of liana stems from terrestrial LiDAR point clouds of tropical rainforests. ISPRS J. Photogramm. Remote Sens. 2019, 154, 114–126. [Google Scholar] [CrossRef]
- Yu, J.W.; Yoon, Y.W.; Baek, W.K.; Jung, H.S. Forest vertical structure mapping using two-seasonal optic images and LiDAR DSM acquired from UAV platform through random forest, XGBoost, and support vector machine approaches. Remote Sens. 2021, 13, 4282. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Li, W.; Chen, Y.; Wang, C.; Nurunnabi, A.A.M.; Li, J. Detection of individual trees in UAV LiDAR point clouds using a deep learning framework based on multichannel representation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5701715. [Google Scholar] [CrossRef]
- Han, J.W.; Synn, D.J.; Kim, T.H.; Chung, H.C.; Kim, J.K. Feature based sampling: A fast and robust sampling method for tasks using 3D point cloud. IEEE Access 2022, 10, 58062–58070. [Google Scholar] [CrossRef]
- Lee, Y.K.; Lee, S.J.; Lee, J.S. Comparison and evaluation of classification accuracy for Pinus koraiensis and Larix kaempferi based on LiDAR platforms and deep learning models. Korean J. For. Sci. 2023, 112, 195–208. [Google Scholar] [CrossRef]
- Ge, B.; Chen, S.; He, W.; Qiang, X.; Li, J.; Teng, G.; Huang, F. Tree Completion Net: A novel vegetation point clouds completion model based on deep learning. Remote Sens. 2024, 16, 3763. [Google Scholar] [CrossRef]
- Soydaner, D. A comparison of optimization algorithms for deep learning. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2052013. [Google Scholar] [CrossRef]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Münzinger, M.; Prechtel, N.; Behnisch, M. Mapping the urban forest in detail: From LiDAR point clouds to 3D tree models. Urban For. Urban Green. 2022, 74, 127637. [Google Scholar] [CrossRef]
- Cherlet, W.; Cooper, Z.; Van Den Broeck, W.A.; Disney, M.; Origo, N.; Calders, K. Benchmarking instance segmentation in terrestrial laser scanning forest point clouds. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 4511–4515. [Google Scholar] [CrossRef]
- Mathes, T.; Seidel, D.; Häberle, K.H.; Pretzsch, H.; Annighöfer, P. What are we missing? Occlusion in laser scanning point clouds and its impact on the detection of single-tree morphologies and stand structural variables. Remote Sens. 2023, 15, 450. [Google Scholar] [CrossRef]
- Ou, J.; Tian, Y.; Zhang, Q.; Xie, X.; Zhang, Y.; Tao, J.; Lin, J. Coupling UAV hyperspectral and LiDAR data for mangrove classification using XGBoost in China’s Pinglu Canal Estuary. Forests 2023, 14, 1838. [Google Scholar] [CrossRef]
- Kulicki, M.; Cabo, C.; Trzciński, T.; Będkowski, J.; Stereńczak, K. Artificial intelligence and terrestrial point clouds for forest monitoring. Curr. For. Rep. 2024, 11, 5. [Google Scholar] [CrossRef]
- Ma, Z.; Dong, Y.; Zi, J.; Xu, F.; Chen, F. Forest-PointNet: A deep learning model for vertical structure segmentation in complex forest scenes. Remote Sens. 2023, 15, 4793. [Google Scholar] [CrossRef]
- Moorthy, S.M.K.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved supervised learning-based approach for leaf and wood classification from LiDAR point clouds of forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef]
- Puliti, S.; Pearse, G.; Surový, P.; Wallace, L.; Hollaus, M.; Wielgosz, M.; Astrup, R. For-instance: A uav laser scanning benchmark dataset for semantic and instance segmentation of individual trees. arXiv 2023, arXiv:2309.01279. [Google Scholar] [CrossRef]
- Puliti, S.; Lines, E.R.; Müllerová, J.; Frey, J.; Schindler, Z.; Straker, A.; Allen, M.J.; Winiwarter, L.; Rehush, N.; Hristova, H.; et al. Benchmarking tree species classification from proximally sensed laser scanning data: Introducing the FOR-species20K dataset. Methods Ecol. Evol. 2025, 16, 801–818. [Google Scholar] [CrossRef]



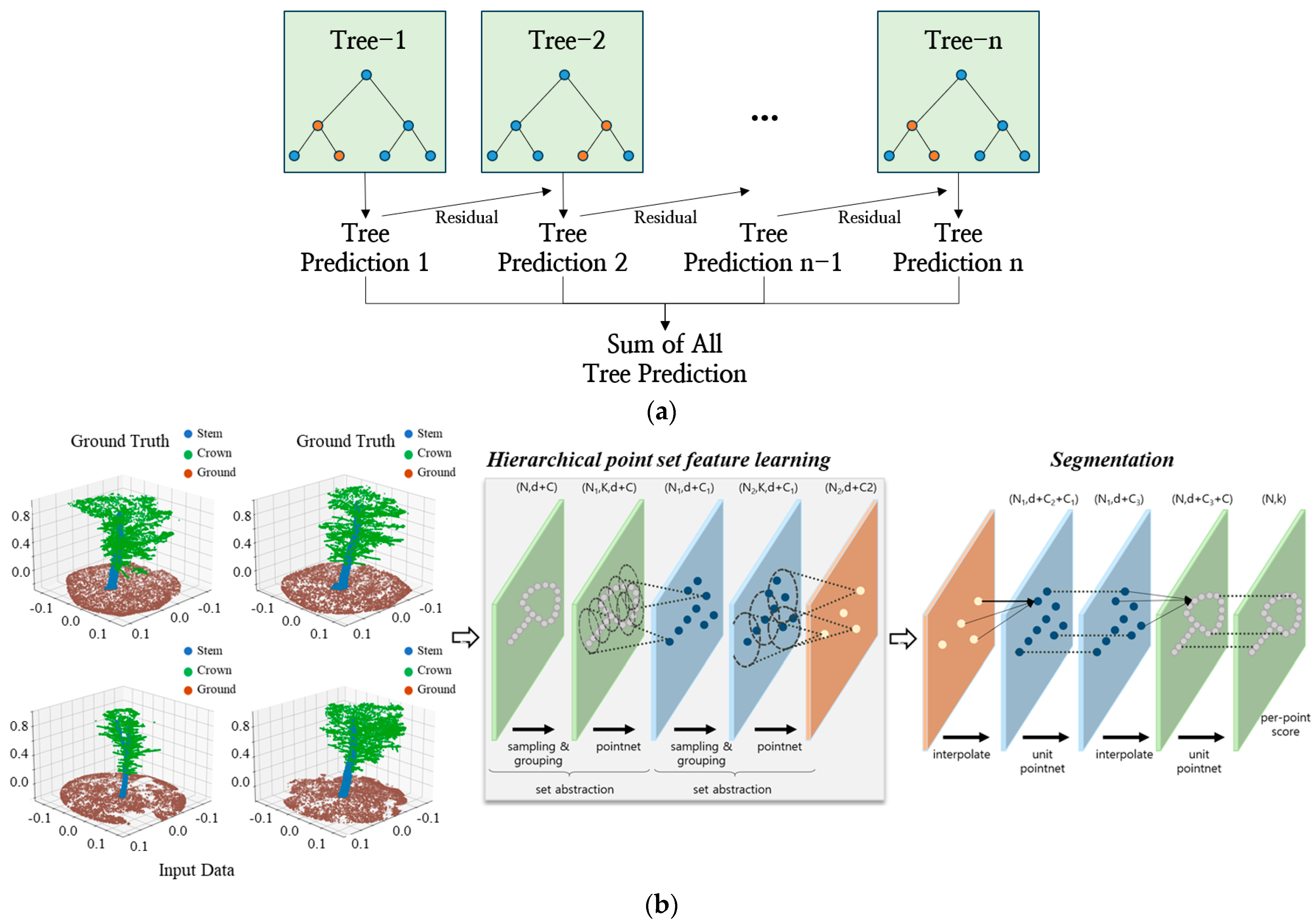
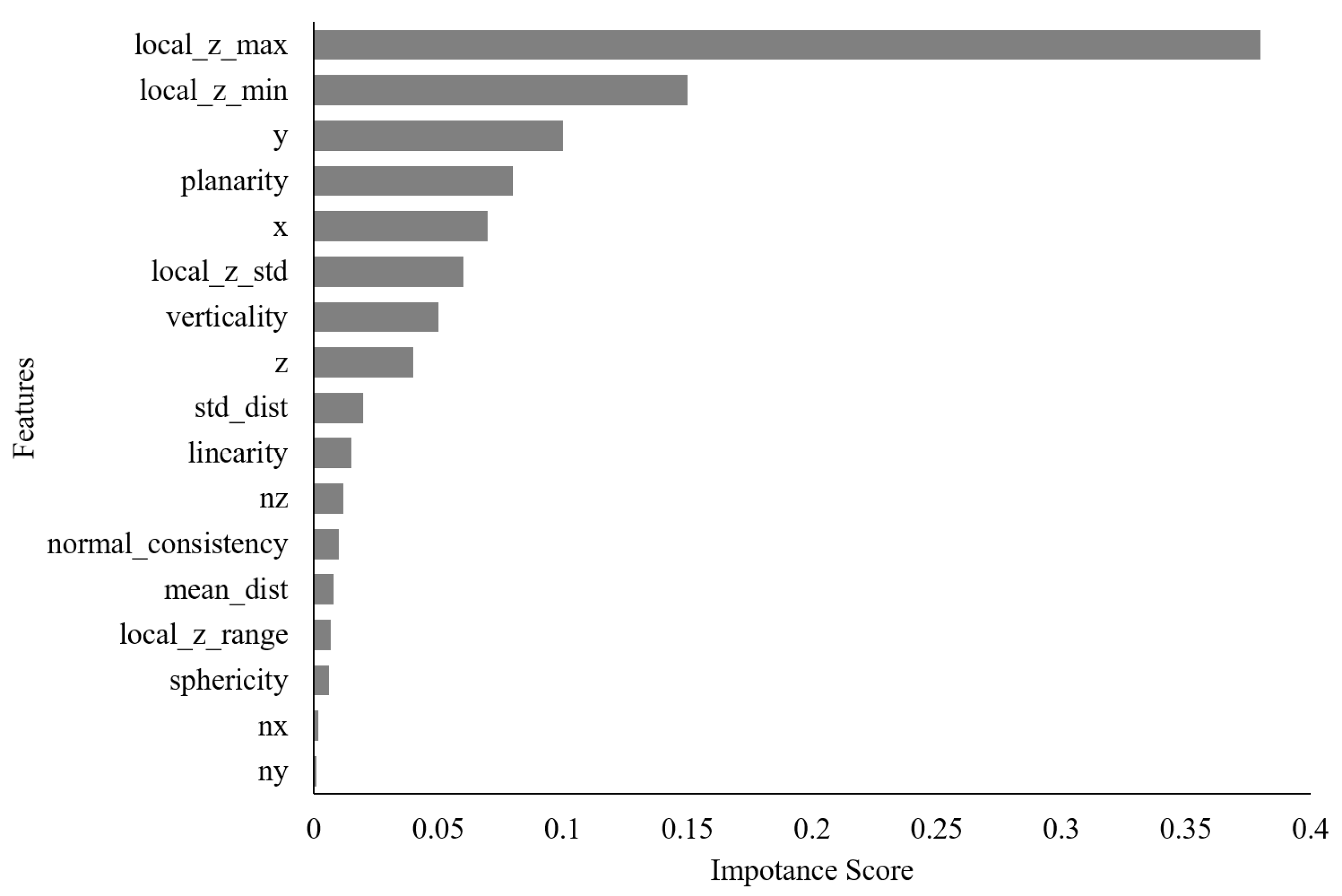
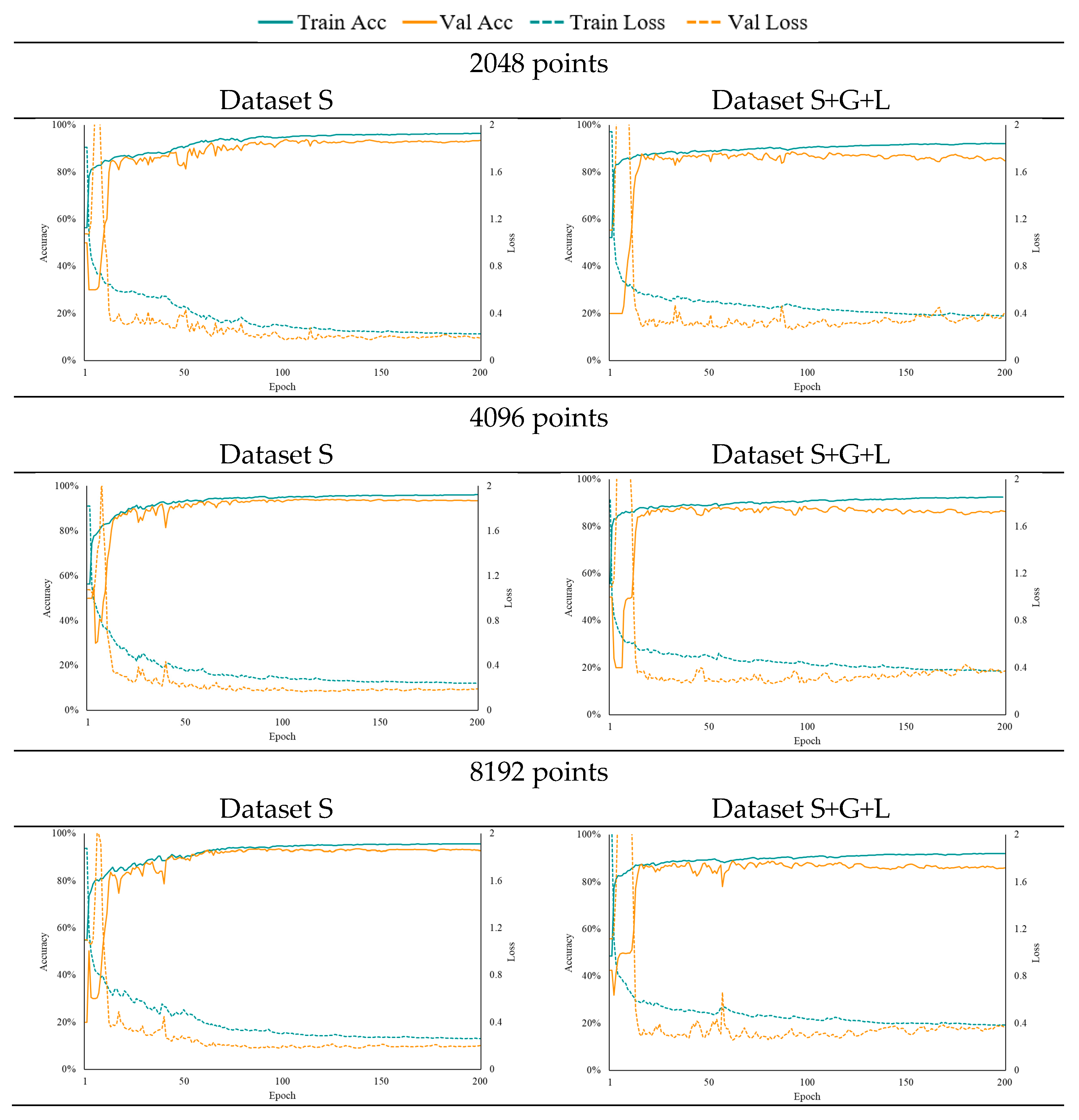
| Plot | No. of Trees | DBH (cm) | Tree Height (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Std | Min | Max | Mean | Std | ||
| 1 | 52 | 12.0 | 45.0 | 26.4 | 6.3 | 14.9 | 24.7 | 18.5 | 1.8 |
| 2 | 46 | 13.6 | 48.4 | 27.0 | 6.7 | 13.4 | 23.0 | 18.6 | 2.0 |
| 3 | 36 | 13.9 | 43.1 | 28.1 | 8.1 | 14.7 | 22.5 | 20.0 | 1.9 |
| 4 | 29 | 12.6 | 51.3 | 29.5 | 8.5 | 14.7 | 29.2 | 20.3 | 2.3 |
| Feature | Definition | Formula | |
|---|---|---|---|
| spatial coordinates and normal (Dataset S) | x | 3D x-coordinate of point | - |
| y | 3D y-coordinate of point | - | |
| z | 3D z-coordinate of point | - | |
| x component of normal vector indicating surface direction | - | ||
| y component of normal vector indicating surface direction | - | ||
| z component of normal vector indicating surface direction | - | ||
| geometric structure features (Dataset G) | Degree of linear arrangement of point cloud (Linearity) | ||
| Degree of planar arrangement of point cloud (Planarity) | |||
| Degree of spherical protrusion of point cloud (Sphericity) | |||
| Degree of vertical arrangement of point cloud (Verticality) | |||
| local distribution features (Dataset L) | Maximum height of neighboring points | ||
| Minimum height of neighboring points | |||
| Height range of neighboring points | |||
| Standard deviation of neighboring points’ heights | |||
| Average distance to neighboring points | |||
| Standard deviation of distances to neighboring points | |||
| Normal vector consistency of neighboring points | |||
| Structure | Number of Points (n = 163) | Point Density | |||
|---|---|---|---|---|---|
| Min | Max | Mean | SD | Pts/m2 | |
| Overall Trees | 265,148 | 13,252,547 | 4,742,683 | 2,654,630 | 1407 |
| Stem | 127,211 | 2,767,364 | 766,735 | 393,653 | 6970 |
| Crown | 63,204 | 4,950,873 | 872,765 | 694,291 | 508 |
| Ground | 74,733 | 8,891,581 | 3,103,183 | 1,975,605 | 908 |
| Downsampling | Dataset | n_Estimators (500, 750, 1000) | Max_Depth (6, 8, 10) | Learning_Rate (0.001, 0.01, 0.1) |
|---|---|---|---|---|
| 2048 | S | 750 | 6 | 0.01 |
| S+G | 750 | 6 | 0.01 | |
| S+L | 1000 | 6 | 0.01 | |
| S+G+L | 1000 | 6 | 0.01 | |
| 4096 | S | 750 | 6 | 0.01 |
| S+G | 750 | 6 | 0.01 | |
| S+L | 750 | 6 | 0.01 | |
| S+G+L | 1000 | 6 | 0.01 | |
| 8192 | S | 750 | 6 | 0.01 |
| S+G | 1000 | 6 | 0.01 | |
| S+L | 1000 | 6 | 0.01 | |
| S+G+L | 1000 | 6 | 0.01 |
| Model | Down Sampling | Dataset | Overall Accuracy (%) | F1-Score (%) | Runtime (min) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Val | Test | Train | Val | Test | ||||
| XGBoost | 2048 | S | 81.8 | 80.8 | 80.2 | 82.0 | 81.2 | 80.3 | 10 |
| S+G | 84.9 | 84.3 | 83.9 | 85.4 | 84.9 | 84.4 | 12 | ||
| S+L | 87.7 | 86.3 | 86.2 | 88.4 | 87.0 | 86.9 | 14 | ||
| S+G+L | 88.3 | 87.3 | 87.1 | 89.0 | 87.9 | 87.7 | 16 | ||
| 4096 | S | 82.0 | 80.8 | 80.2 | 82.2 | 81.3 | 80.4 | 17 | |
| S+G | 84.9 | 84.1 | 83.8 | 85.5 | 84.8 | 84.3 | 20 | ||
| S+L | 87.4 | 86.1 | 86.2 | 88.1 | 86.8 | 86.9 | 22 | ||
| S+G+L | 88.3 | 87.1 | 87.0 | 89.0 | 87.8 | 87.7 | 26 | ||
| 8192 | S | 82.2 | 81.2 | 80.5 | 82.5 | 81.7 | 80.7 | 32 | |
| S+G | 85.3 | 84.4 | 84.2 | 85.9 | 85.1 | 84.7 | 35 | ||
| S+L | 87.5 | 86.5 | 86.5 | 88.2 | 87.2 | 87.2 | 39 | ||
| S+G+L | 88.3 | 87.4 | 87.3 | 89.0 | 88.2 | 88.0 | 47 | ||
| PointNet++ | 2048 | S | 96.4 | 93.4 | 92.1 | 96.7 | 93.9 | 92.8 | 51 |
| S+G | 92.8 | 86.9 | 85.2 | 92.7 | 87.9 | 86.3 | 59 | ||
| S+L | 95.3 | 91.8 | 89.7 | 95.6 | 92.3 | 90.5 | 49 | ||
| S+G+L | 91.4 | 84.8 | 83.8 | 92.1 | 86.1 | 85.1 | 55 | ||
| 4096 | S | 95.6 | 93.4 | 92.2 | 96.3 | 93.9 | 93.0 | 65 | |
| S+G | 92.4 | 86.0 | 85.6 | 93.0 | 87.3 | 86.7 | 71 | ||
| S+L | 94.8 | 90.8 | 89.3 | 95.2 | 91.6 | 90.4 | 65 | ||
| S+G+L | 92.5 | 86.3 | 95.9 | 93.1 | 87.6 | 87.0 | 68 | ||
| 8192 | S | 95.7 | 92.8 | 92.0 | 96.0 | 93.4 | 92.7 | 166 | |
| S+G | 91.9 | 84.9 | 83.6 | 97.8 | 86.3 | 85.1 | 168 | ||
| S+L | 95.0 | 91.1 | 90.1 | 95.0 | 91.1 | 91.1 | 167 | ||
| S+G+L | 92.1 | 86.0 | 85.4 | 92.7 | 87.2 | 86.5 | 167 | ||
| Section | Model | Condition | Structure | Precision (%) | Recall (%) | F1-Score (%) | |
|---|---|---|---|---|---|---|---|
| Downsampling | Dataset | ||||||
| (a) | XGBoost | 8192 | S+G+L | Stem | 84.7 | 81.1 | 87.8 |
| Crown | 85.3 | 77.8 | 81.3 | ||||
| Ground | 97.6 | 92.2 | 94.8 | ||||
| PointNet++ | 4096 | S | Stem | 93.4 | 90.9 | 92.1 | |
| Crown | 86.8 | 89.8 | 88.3 | ||||
| Ground | 97.7 | 99.3 | 98.5 | ||||
| (b) | XGBoost | 8192 | S+G+L | Stem | 84.7 | 81.1 | 87.8 |
| Crown | 85.3 | 77.8 | 81.3 | ||||
| Ground | 97.6 | 92.2 | 94.8 | ||||
| PointNet++ | 8192 | S+G+L | Stem | 87.5 | 82.5 | 84.9 | |
| Crown | 77.6 | 80.7 | 79.1 | ||||
| Ground | 91.8 | 99.5 | 95.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Sim, W.; Lee, Y.; Park, J.; Kang, J.; Lee, J. Comparative Analysis of Machine Learning and Deep Learning Models for Individual Tree Structure Segmentation Using Terrestrial LiDAR Point Cloud Data. Remote Sens. 2025, 17, 2245. https://doi.org/10.3390/rs17132245
Lee S, Sim W, Lee Y, Park J, Kang J, Lee J. Comparative Analysis of Machine Learning and Deep Learning Models for Individual Tree Structure Segmentation Using Terrestrial LiDAR Point Cloud Data. Remote Sensing. 2025; 17(13):2245. https://doi.org/10.3390/rs17132245
Chicago/Turabian StyleLee, Sangjin, Woodam Sim, Yongkyu Lee, Jeongmook Park, Jintaek Kang, and Jungsoo Lee. 2025. "Comparative Analysis of Machine Learning and Deep Learning Models for Individual Tree Structure Segmentation Using Terrestrial LiDAR Point Cloud Data" Remote Sensing 17, no. 13: 2245. https://doi.org/10.3390/rs17132245
APA StyleLee, S., Sim, W., Lee, Y., Park, J., Kang, J., & Lee, J. (2025). Comparative Analysis of Machine Learning and Deep Learning Models for Individual Tree Structure Segmentation Using Terrestrial LiDAR Point Cloud Data. Remote Sensing, 17(13), 2245. https://doi.org/10.3390/rs17132245







