VOX-LIO: An Effective and Robust LiDAR-Inertial Odometry System Based on Surfel Voxels
Abstract
1. Introduction
- We propose a point cloud matching strategy based on adaptive hash voxels that incorporate surfel features and planarity. This method classifies spatial voxels into surfel and common classes based on planarity. To enhance efficiency, surfels consistently observed over time are reused to constrain optimization. This approach also supports incremental refinement of surfel features within surfel voxels, enabling accurate and efficient map updates.
- We propose a weighted fusion strategy that integrates LiDAR-IMU data measurements on the manifold space. This approach compensates for motion distortion, especially during rapid LiDAR movement. To ensure stability, the fusion method may leverage robust kernel functions in conjunction with advanced optimization techniques.
- We integrate a loop closure module into VOX-LIO to enhance global consistency. Comprehensive experiments on public datasets and our robotic platforms demonstrate the system’s effectiveness in pose estimation accuracy and global map consistency. On the kitti_05 sequence, VOX-LIO reduces the mean APE by 63.9% compared to Faster-LIO, while VOX-LIOM further reduces it by 55.5% over VOX-LIO, demonstrating significant improvements in pose estimation accuracy. Furthermore, on our private dataset, the integration of the loop closure module enables VOX-LIOM to maintain globally consistent maps during extended operation.
2. Related Work
2.1. Point Cloud Registration and Data Association
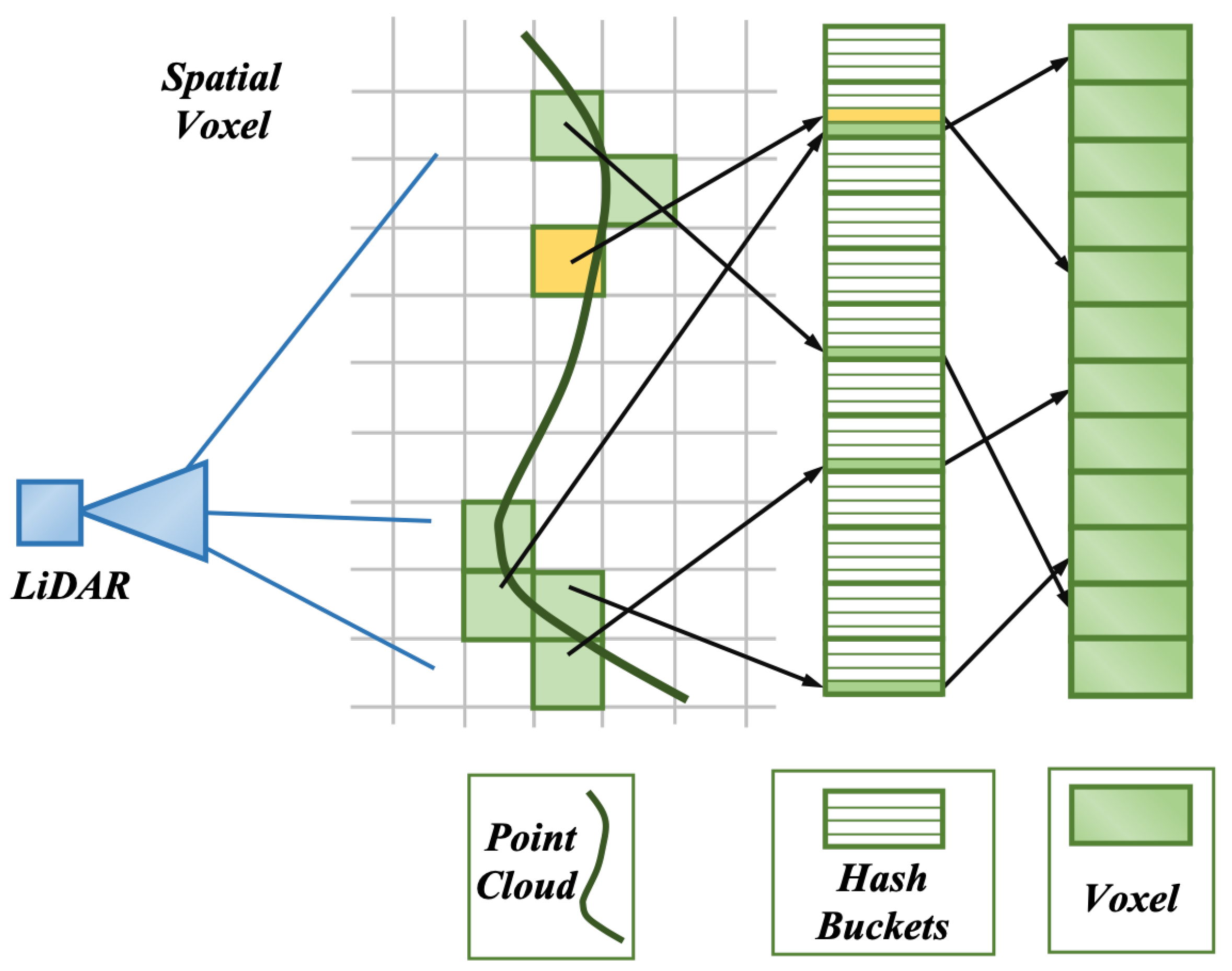
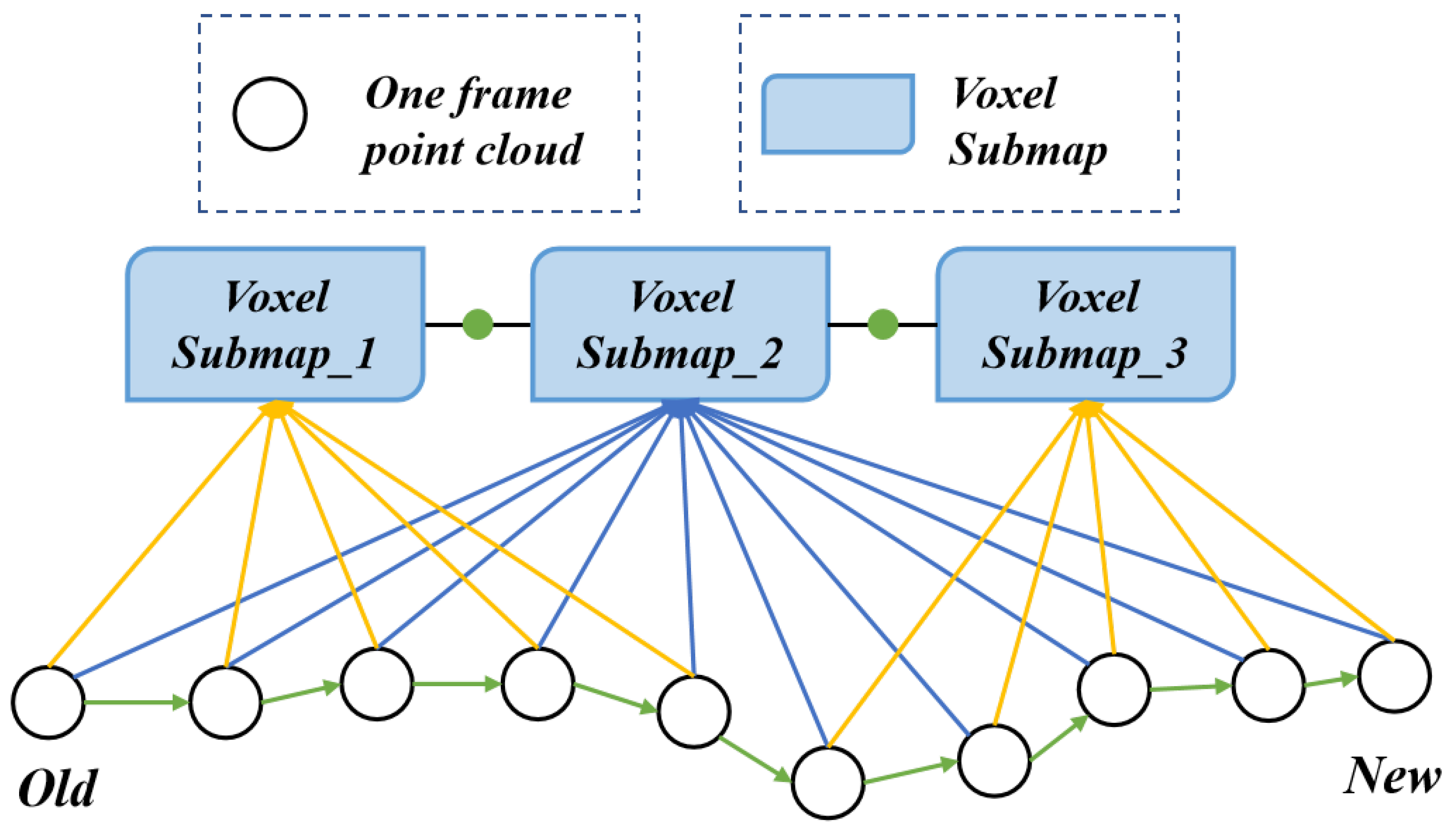
2.2. Point Cloud Map Management
2.3. Multi-Modal Sensor Fusion for State Estimation
2.4. Loop Closure Detection and Global Optimization
3. Methods
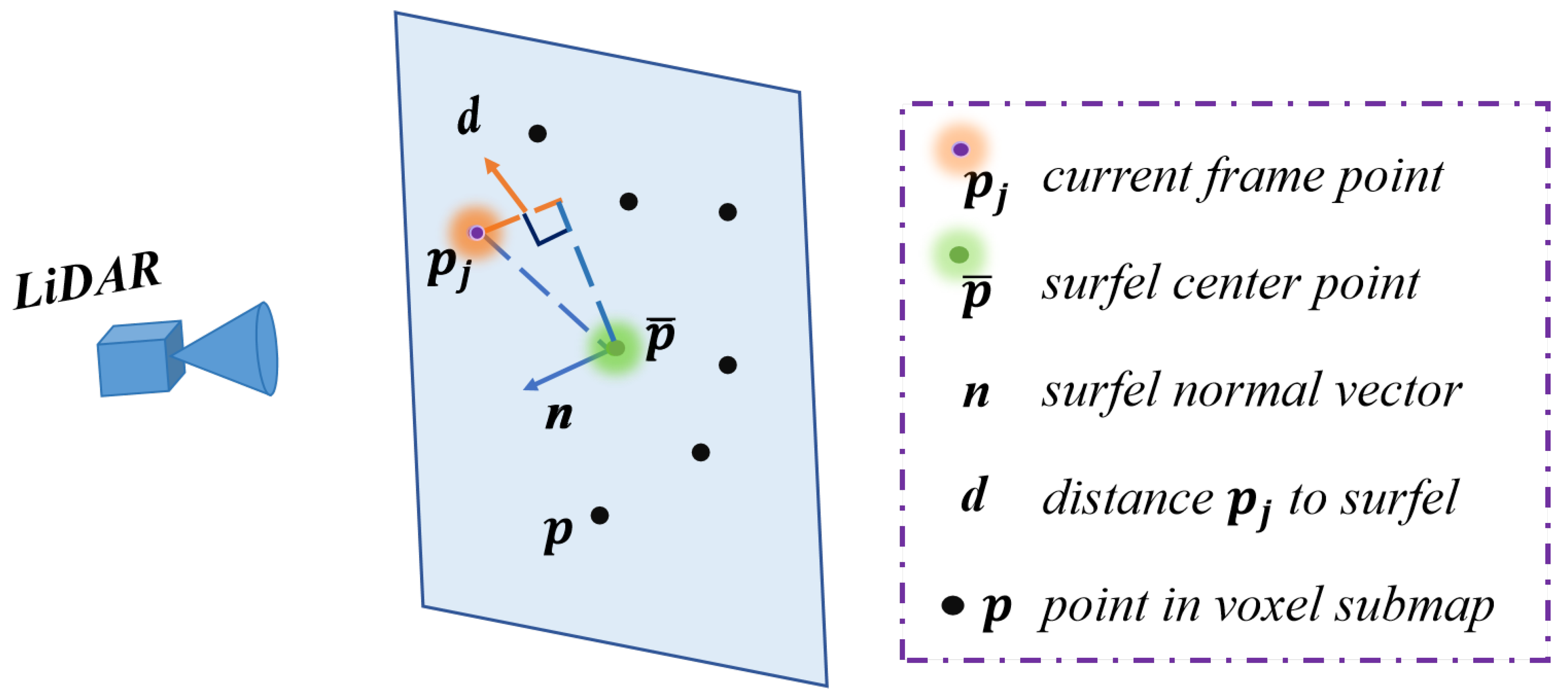
3.1. Probabilistic Model-Based Surfel Feature Fitting
3.1.1. Definition of Surfel Feature
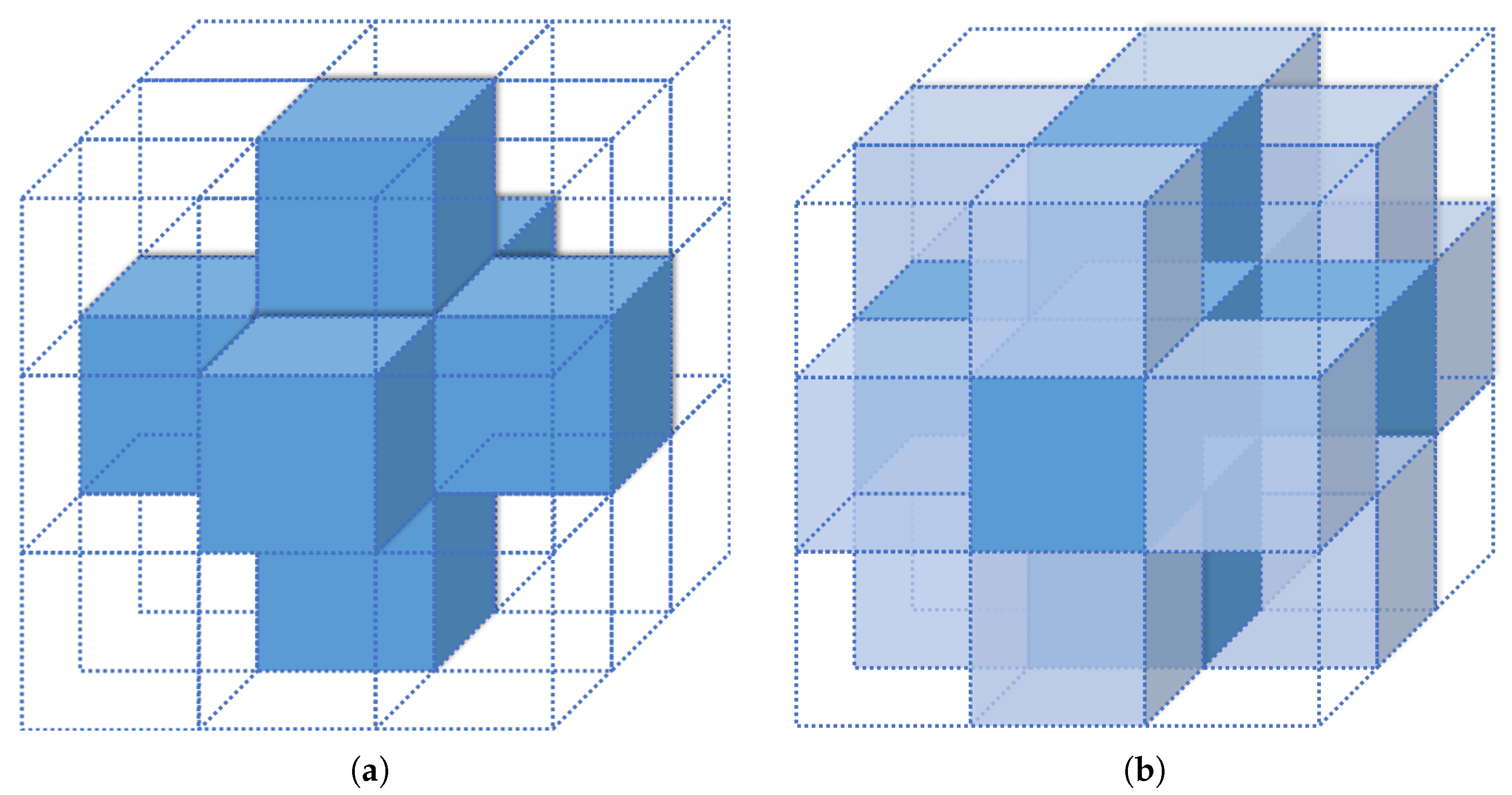
3.1.2. Surfel Feature Updating and Map Maintenance
3.2. Real-Time Pose Estimation
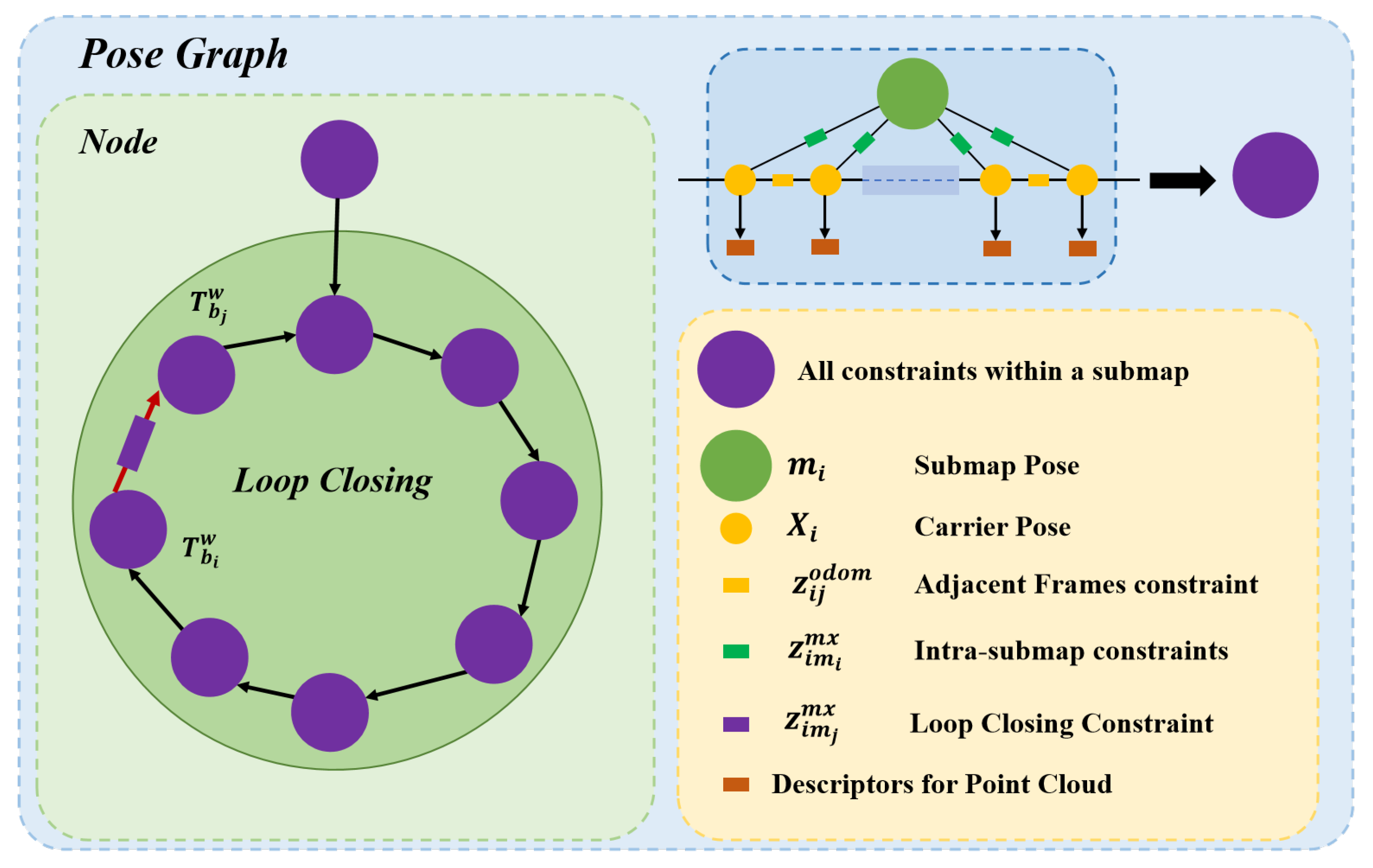
3.3. Loop Closing and Global Optimization
4. Experiment and Discussion
4.1. Experimental Design and Platforms
4.2. Evaluation Metrics
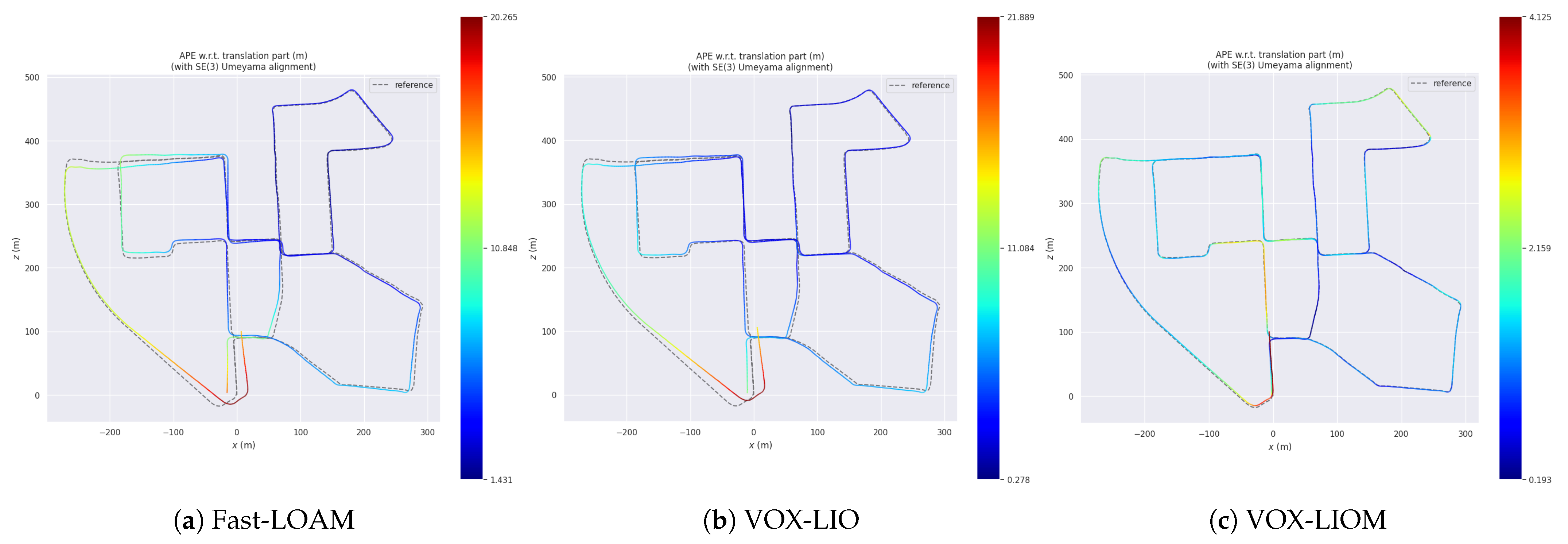
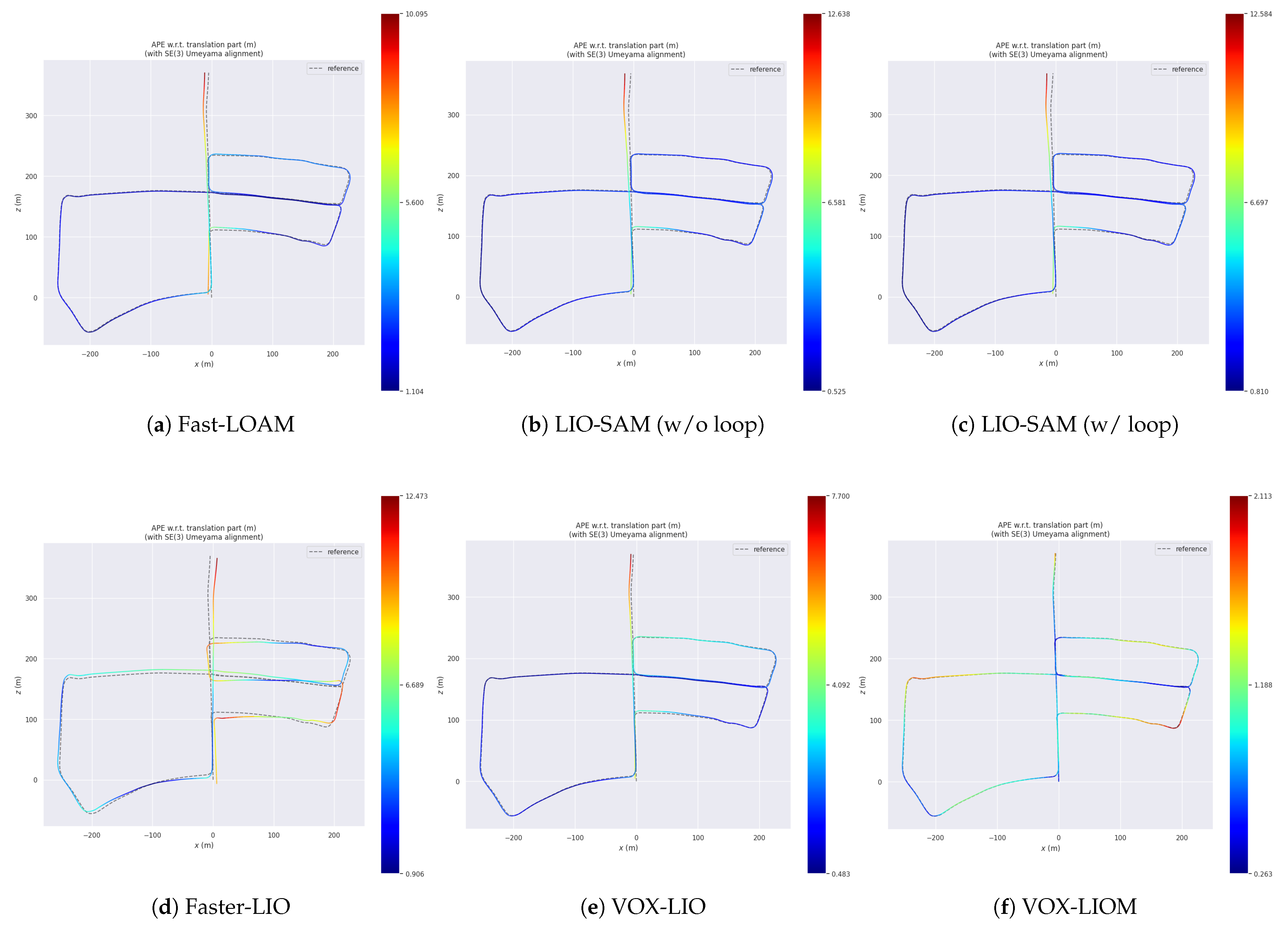
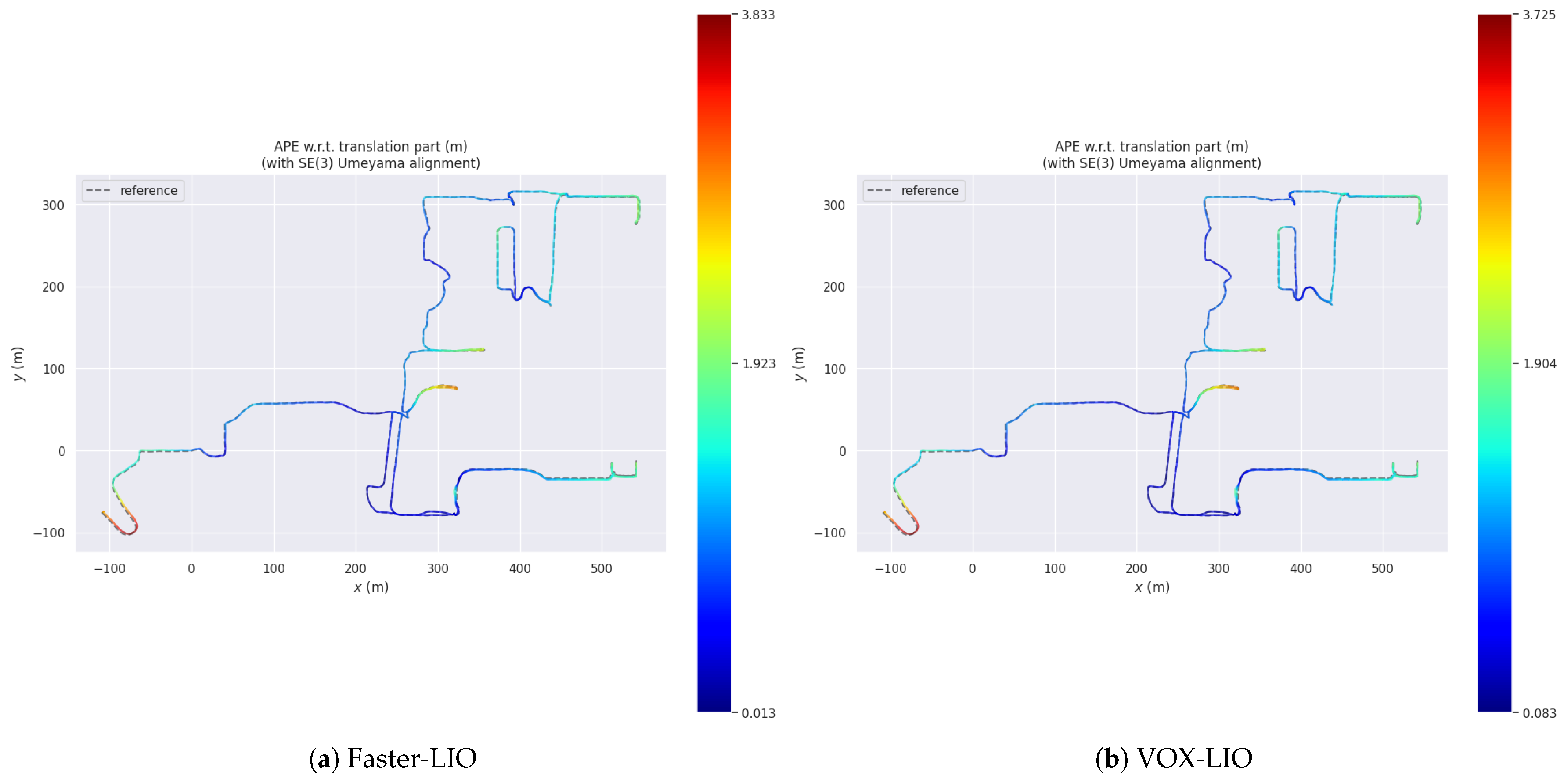
4.3. Pose Estimation Accuracy Experiment
4.4. Mapping and Loop Closing Performance
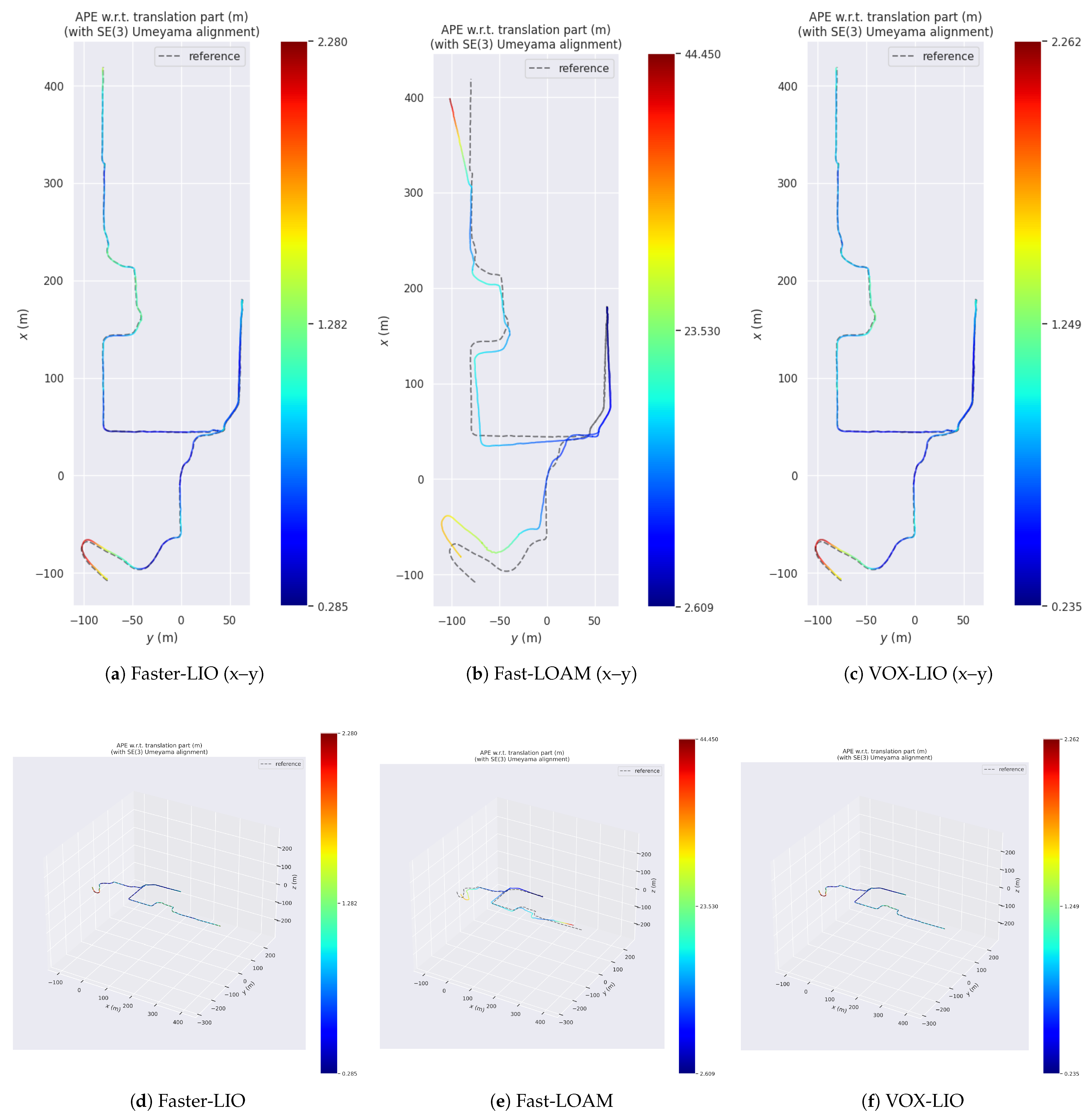
4.5. Generalization Experiments
4.5.1. Experiments of the Four-Wheeled Robot Platform
4.5.2. Experiments of the Quadruped Robot Platform
4.6. Efficiency Experiments
4.6.1. Surfel Voxel-Based Matching Efficiency
4.6.2. Surfel Voxel-Based Acceleration for Runtime Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Gauss–Newton Method for Solving Linear Least Squares
Appendix B. Algorithm for Surfel Feature Matching
| Algorithm A1 Surfel Voxel-based Association and Pose Optimization |
|
References
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems Conference, Berkeley, CA, USA, 12–13 July 2014; Volume 2, pp. 1–9. [Google Scholar]
- Wang, H.; Wang, C.; Chen, C.; Xie, L. F-LOAM: Fast LiDAR Odometry And Mapping. arXiv 2021, arXiv:2107.00822. [Google Scholar]
- Xu, W.; Zhang, F. Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- He, D.; Xu, W.; Zhang, F. Kalman Filters on Differentiable Manifolds. arXiv 2021, arXiv:2102.03804. [Google Scholar]
- Shan, T.; Englot, B.J.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. arXiv 2020, arXiv:2007.00258. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Censi, A. An ICP variant using a point-to-line metric. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 19–25. [Google Scholar]
- Serafin, J.; Grisetti, G. NICP: Dense normal based point cloud registration. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 742–749. [Google Scholar]
- Deschaud, J.E. IMLS-SLAM: Scan-to-model matching based on 3D data. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2480–2485. [Google Scholar]
- Low, K.L. Linear Least-Squares Optimization for Point-To-Plane Icp Surface Registration; University of North Carolina: Chapel Hill, NC, USA, 2004; Volume 4, pp. 1–3. [Google Scholar]
- Cho, H.; Kim, E.K.; Kim, S. Indoor SLAM application using geometric and ICP matching methods based on line features. Robot. Auton. Syst. 2018, 100, 206–224. [Google Scholar] [CrossRef]
- Magnusson, M.; Andreasson, H.; Nuchter, A.; Lilienthal, A.J. Appearance-based loop detection from 3D laser data using the normal distributions transform. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 23–28. [Google Scholar]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Behley, J.; Stachniss, C. Efficient Surfel-Based SLAM using 3D Laser Range Data in Urban Environments. In Proceedings of the Robotics: Science and Systems, Pittsburgh, PA, USA, 26–30 June 2018; Volume 2018, p. 59. [Google Scholar]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguère, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-based Semantic SLAM. arXiv 2021, arXiv:2105.11320. [Google Scholar]
- Skrodzki, M. The k-d tree data structure and a proof for neighborhood computation in expected logarithmic time. arXiv 2019, arXiv:1903.04936. [Google Scholar]
- Cai, Y.; Xu, W.; Zhang, F. ikd-Tree: An incremental KD tree for robotic applications. arXiv 2021, arXiv:2102.10808. [Google Scholar]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improving grid-based slam with rao-blackwellized particle filters by adaptive proposals and selective resampling. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2432–2437. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME Ser. D. J. Basic Engrg. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Tang, J.; Chen, Y.; Kaartinen, H.; Kukko, A.; Zhu, L.; Liang, X.; Chen, L.; Hyyppä, J. An integrated GNSS/INS/LiDAR-SLAM positioning method for highly accurate forest stem mapping. Remote Sens. 2016, 9, 3. [Google Scholar] [CrossRef]
- Gao, J.; Sha, J.; Wang, Y.; Wang, X.; Tan, C. A fast and stable GNSS-LiDAR-inertial state estimator from coarse to fine by iterated error-state Kalman filter. Robot. Auton. Syst. 2024, 175, 104675. [Google Scholar] [CrossRef]
- Dellaert, F.; Fox, D.; Burgard, W.; Thrun, S. Monte carlo localization for mobile robots. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 2, pp. 1322–1328. [Google Scholar]
- Ye, H.; Chen, Y.; Liu, M. Tightly coupled 3d lidar inertial odometry and mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Lin, J.; Zhang, F. R3LIVE: A Robust, Real-time, RGB-colored, LiDAR-Inertial-Visual tightly-coupled state Estimation and mapping package. arXiv 2021, arXiv:2109.07982. [Google Scholar]
- Kim, G.; Kim, A. Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4802–4809. [Google Scholar]
- Wang, Y.; Sun, Z.; Xu, C.Z.; Sarma, S.E.; Yang, J.; Kong, H. Lidar iris for loop-closure detection. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 5769–5775. [Google Scholar]
- Konolige, K.; Grisetti, G.; Kümmerle, R.; Burgard, W.; Limketkai, B.; Vincent, R. Efficient sparse pose adjustment for 2D mapping. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 22–29. [Google Scholar]
- Dellaert, F.; Kaess, M. Square root SAM: Simultaneous localization and mapping via square root information smoothing. Int. J. Robot. Res. 2006, 25, 1181–1203. [Google Scholar] [CrossRef]
- Yin, H.; Xu, X.; Lu, S.; Chen, X.; Xiong, R.; Shen, S.; Stachniss, C.; Wang, Y. A Survey on Global LiDAR Localization: Challenges, Advances and Open Problems. arXiv 2024, arXiv:2302.07433. [Google Scholar] [CrossRef]
- Daun, K.; Kohlbrecher, S.; Sturm, J.; von Stryk, O. Large scale 2d laser slam using truncated signed distance functions. In Proceedings of the 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Wurzburg, Germany, 2–4 September 2019; pp. 222–228. [Google Scholar]
- Teschner, M. Optimized Spatial Hashing for Collision Detection of Deformable Objects. VMV 2003, 3, 47–54. [Google Scholar]
- Yuan, C.; Xu, W.; Liu, X.; Hong, X.; Zhang, F. Efficient and probabilistic adaptive voxel mapping for accurate online lidar odometry. IEEE Robot. Autom. Lett. 2022, 7, 8518–8525. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, Y.; Dong, J.; Sun, H.; Zhu, F. Link3d: Linear keypoints representation for 3d lidar point cloud. arXiv 2022, arXiv:2206.05927. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2015, 35, 1023–1035. [Google Scholar] [CrossRef]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 13 May 2025).
- Feng, Y.; Jiang, Z.; Shi, Y.; Feng, Y.; Chen, X.; Zhao, H.; Zhou, G. Block-Map-Based Localization in Large-Scale Environment. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 1709–1715. [Google Scholar] [CrossRef]




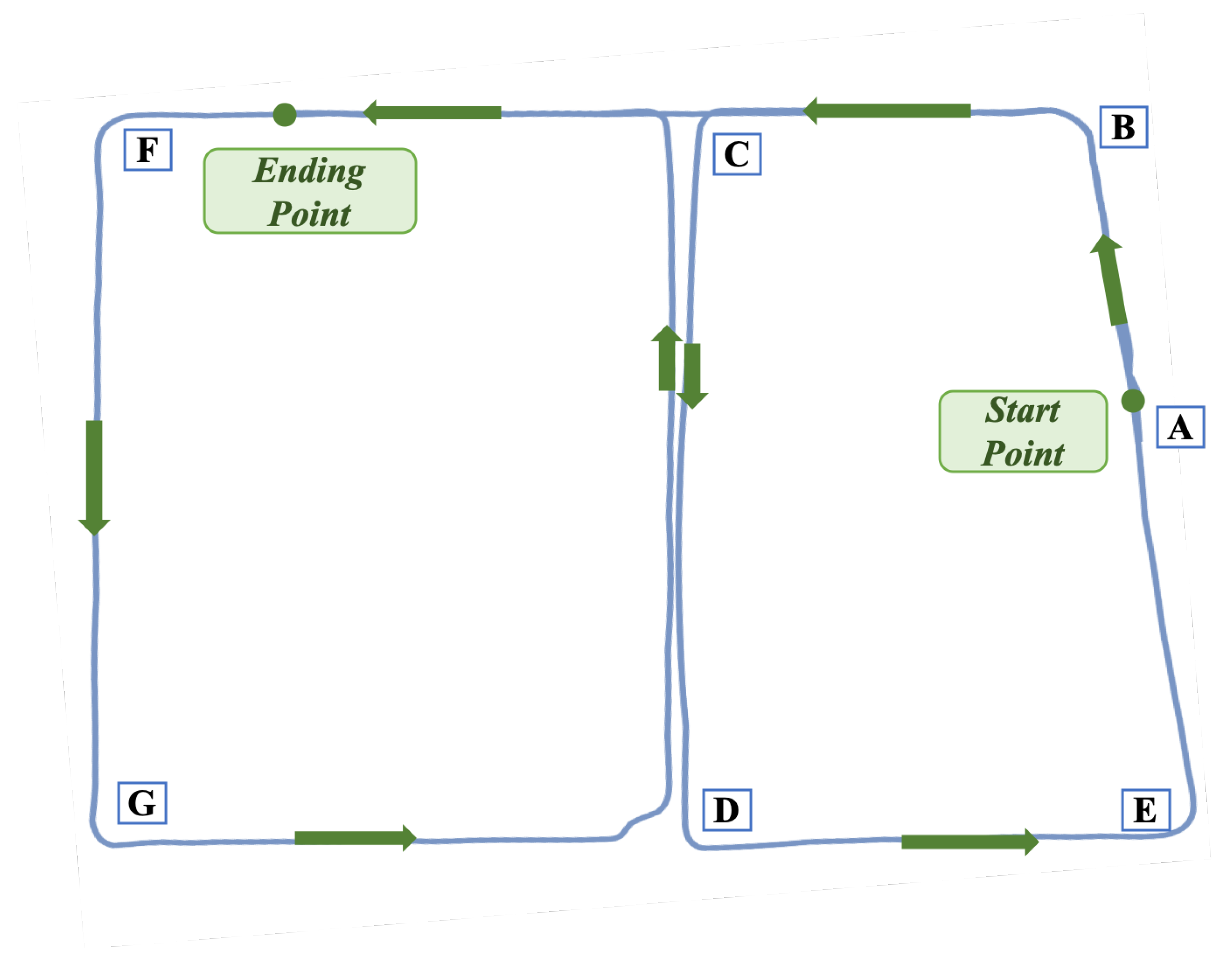
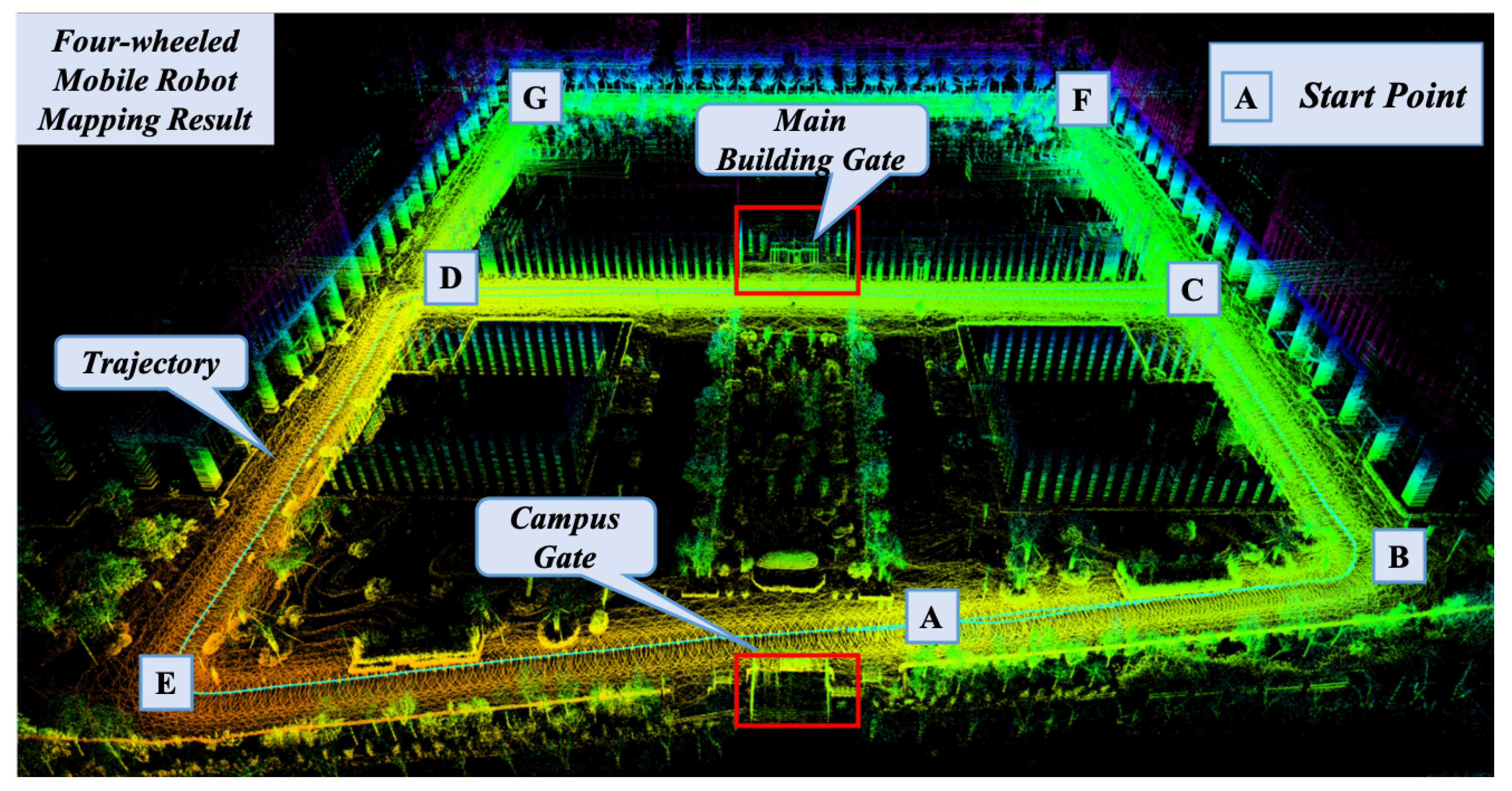


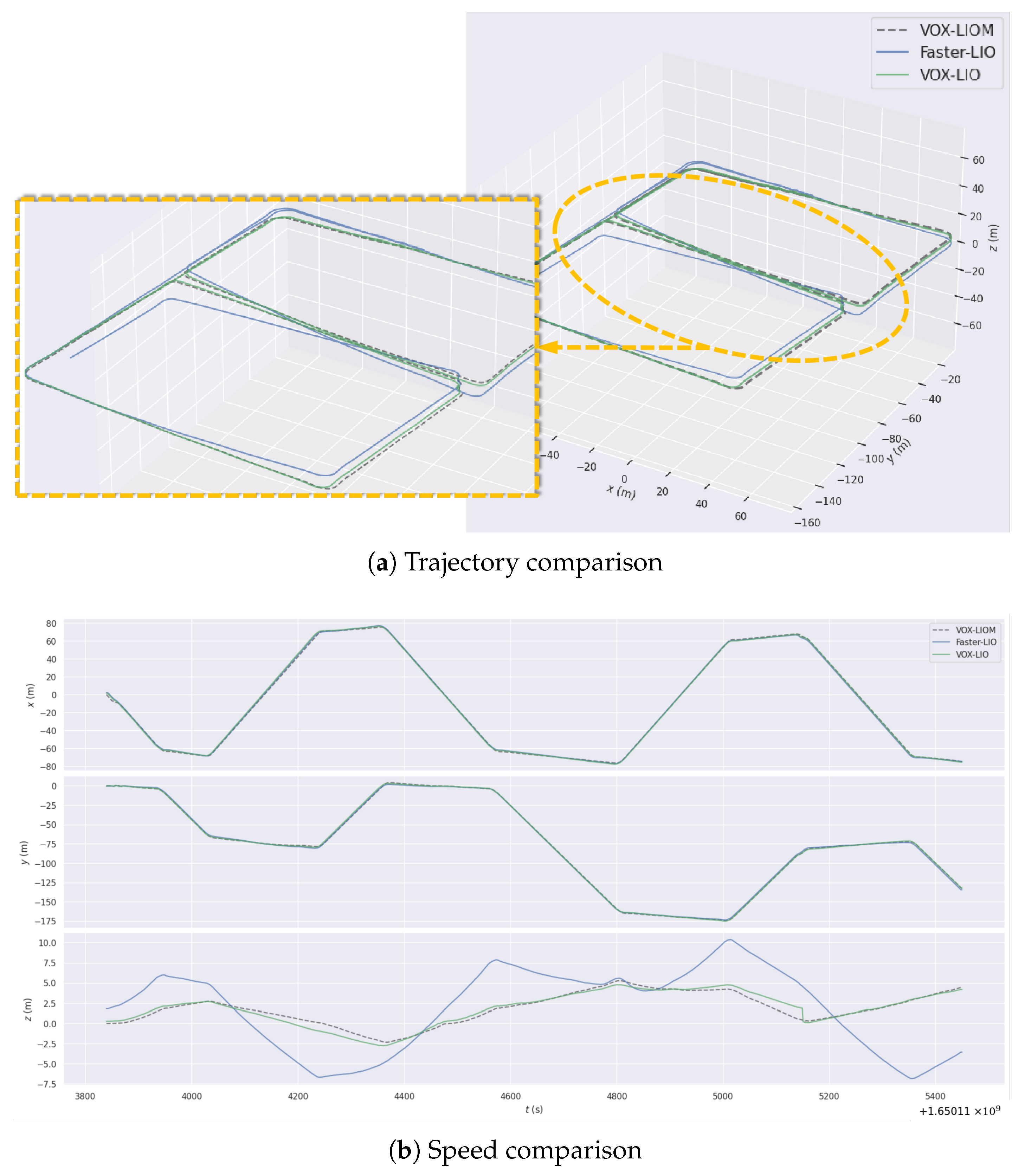

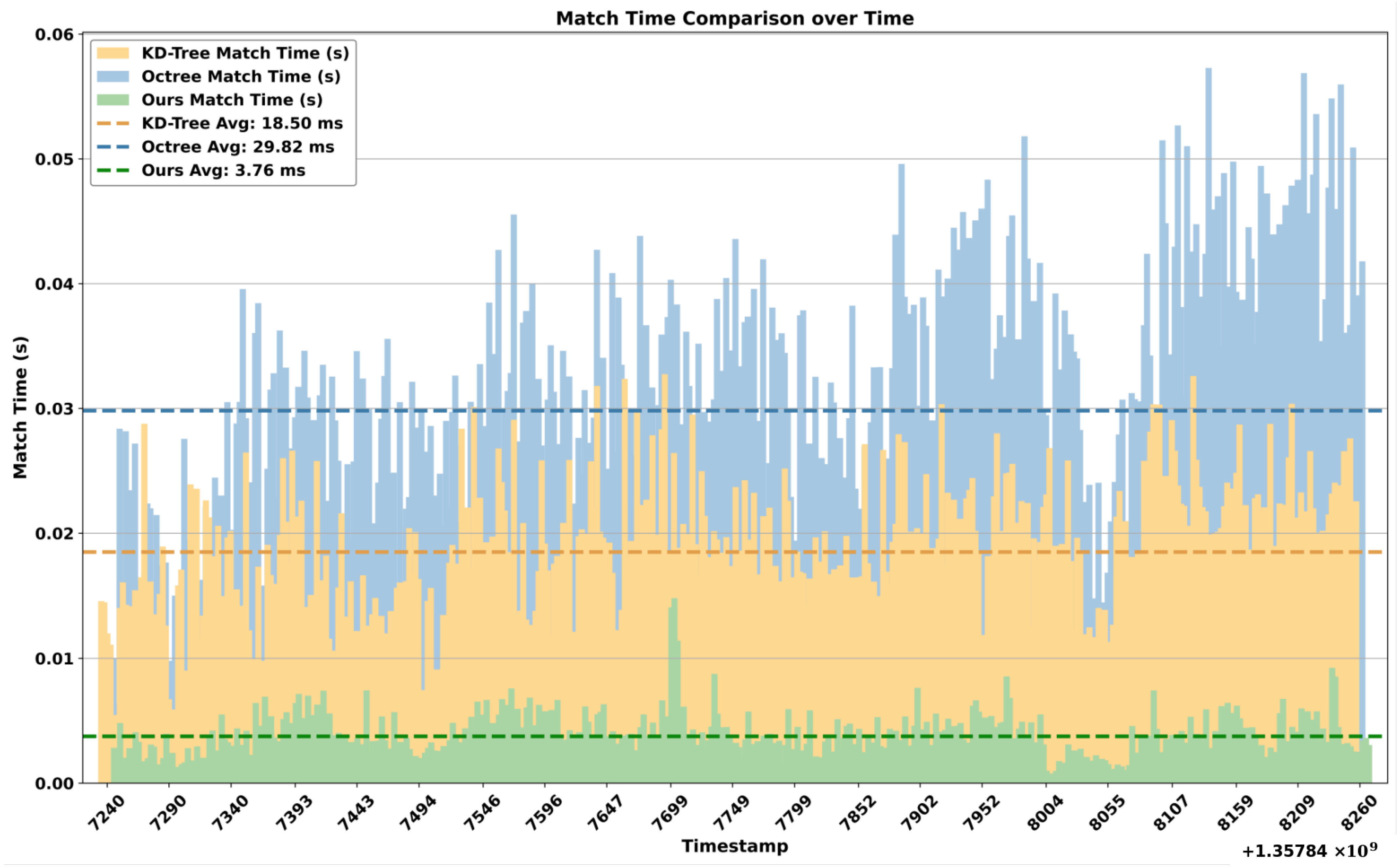
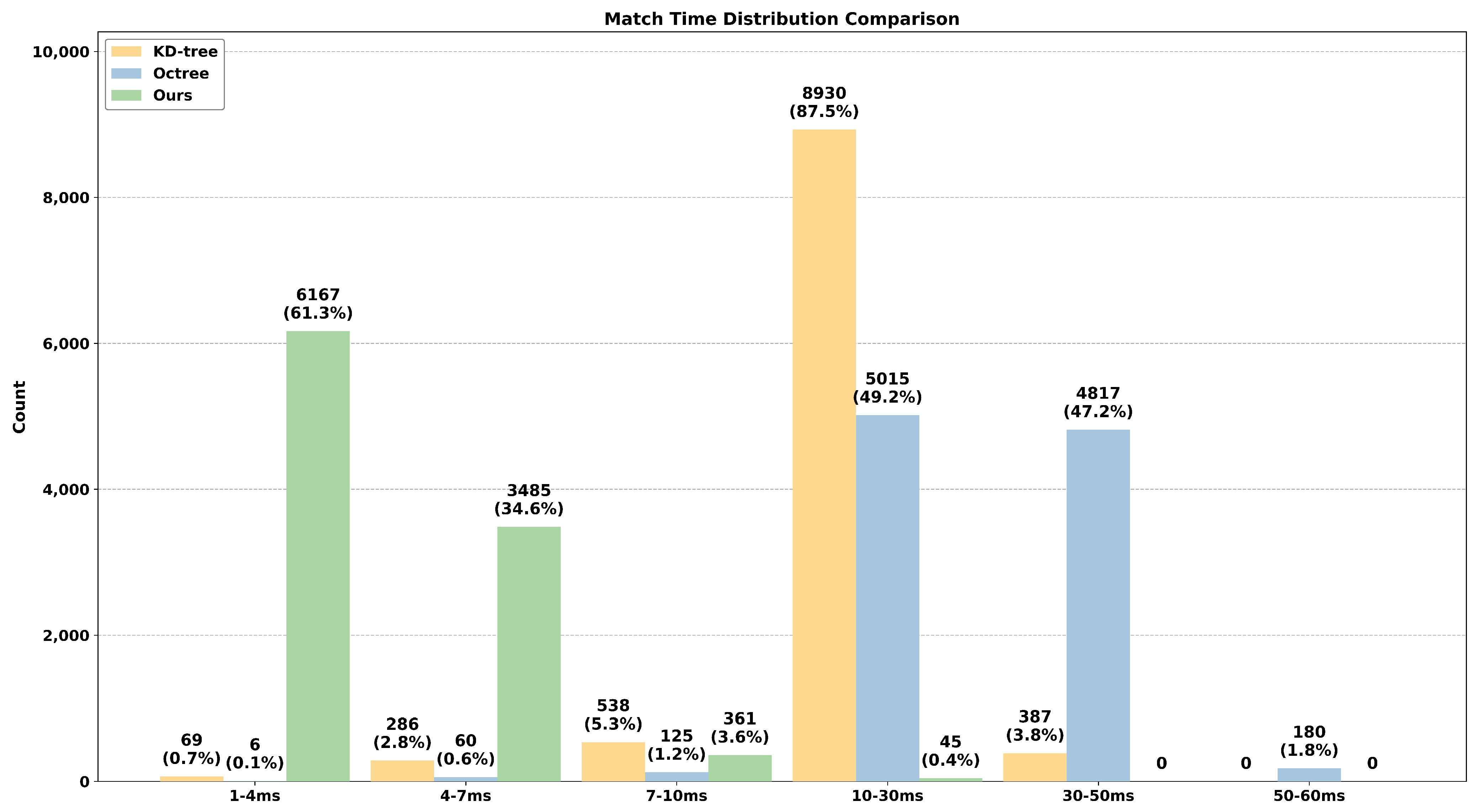
| Seq. | Capture Time | Duration (s) | Point Cloud Frames | Trajectory Length (m) | Weather | Snowy |
|---|---|---|---|---|---|---|
| kitti_00 | 3 October 2011 | 470 | 4544 | 3700 | Partly cloudy | No |
| kitti_05 | 30 September 2011 | 270 | 2762 | 2200 | Cloudy | No |
| nclt_01 | 10 January 2013 | 1025 | 7775 | 1100 | Overcast | Yes |
| nclt_02 | 29 April 2012 | 2600 | 25,819 | 3100 | Sunny | No |
| Platform | Duration (s) | Frames | Length (m) | Characteristics |
|---|---|---|---|---|
| Four-Wheeled | 1611 | 15,980 | 1050 | Steady |
| Quadruped | 295 | 2926 | 267 | Bumps |
| Seq. | Method | Max (m) | Mean (m) | Median (m) | RMSE (m) | Std (m) |
|---|---|---|---|---|---|---|
| kitti_00 | VOX-LIO | 21.74 | 5.59 | 4.56 | 7.10 | 4.37 |
| VOX-LIOM | 4.13 | 1.48 | 1.35 | 1.66 | 0.76 | |
| Fast-LOAM | 20.27 | 6.87 | 5.56 | 8.18 | 4.45 | |
| LIO-SAM | × | × | × | × | × | |
| kitti_05 | VOX-LIO | 7.70 | 2.20 | 2.00 | 2.58 | 1.35 |
| VOX-LIOM | 2.11 | 0.98 | 0.93 | 1.06 | 0.39 | |
| Fast-LOAM | 10.10 | 3.06 | 2.42 | 3.58 | 1.86 | |
| Faster-LIO | 12.47 | 6.10 | 5.56 | 6.60 | 2.54 | |
| LIO-SAM (w/o loop) | 12.95 | 4.02 | 3.66 | 4.41 | 1.82 | |
| LIO-SAM (w/loop) | 4.71 | 3.30 | 3.20 | 3.38 | 0.71 | |
| nclt_01 | VOX-LIO | 2.26 | 0.84 | 0.80 | 0.93 | 0.38 |
| Faster-LIO | 2.28 | 0.89 | 0.83 | 0.96 | 0.38 | |
| Fast-LOAM | 44.4 | 15.3 | 14.6 | 17.7 | 8.7 | |
| LIO-SAM | × | × | × | × | × | |
| nclt_02 | VOX-LIO | 3.72 | 1.10 | 0.99 | 1.28 | 0.64 |
| Faster-LIO | 3.83 | 1.15 | 1.04 | 1.32 | 0.66 | |
| Fast-LOAM | × | × | × | × | × | |
| LIO-SAM | × | × | × | × | × |
| Dataset | VOX-LIO | Faster-LIO | Fast-LOAM | |||
|---|---|---|---|---|---|---|
| Pre. (ms) | Est. (ms) | Pre. (ms) | Est. (ms) | Pre. (ms) | Est. (ms) | |
| nclt_01 | 6.60 | 13.08 | 6.8 | 20.78 | 6.71 | 37.23 |
| nclt_02 | 6.25 | 11.45 | 6.35 | 17.89 | 5.87 | 35.29 |
| Four-wheeled | 5.80 | 12.27 | 5.72 | 18.17 | 5.61 | 27.16 |
| Mean | 6.22 | 12.26 | 6.29 | 18.95 | 6.06 | 33.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Liu, Y.; Yang, Y.; He, X.; Zhang, W. VOX-LIO: An Effective and Robust LiDAR-Inertial Odometry System Based on Surfel Voxels. Remote Sens. 2025, 17, 2214. https://doi.org/10.3390/rs17132214
Guo M, Liu Y, Yang Y, He X, Zhang W. VOX-LIO: An Effective and Robust LiDAR-Inertial Odometry System Based on Surfel Voxels. Remote Sensing. 2025; 17(13):2214. https://doi.org/10.3390/rs17132214
Chicago/Turabian StyleGuo, Meijun, Yonghui Liu, Yuhang Yang, Xiaohai He, and Weimin Zhang. 2025. "VOX-LIO: An Effective and Robust LiDAR-Inertial Odometry System Based on Surfel Voxels" Remote Sensing 17, no. 13: 2214. https://doi.org/10.3390/rs17132214
APA StyleGuo, M., Liu, Y., Yang, Y., He, X., & Zhang, W. (2025). VOX-LIO: An Effective and Robust LiDAR-Inertial Odometry System Based on Surfel Voxels. Remote Sensing, 17(13), 2214. https://doi.org/10.3390/rs17132214







