Joint SAR–Optical Image Compression with Tunable Progressive Attentive Fusion

Abstract

Remote sensing tasks, such as land cover classification, are increasingly becoming multimodal problems, where information from multiple imaging devices, complementing each other, can be fused. In particular, synergies between optical and synthetic aperture radar (SAR) are widely recognized to be beneficial in a variety of tasks. At the same time, archival of multimodal imagery for global coverage poses significant storage requirements due to the multitude of available sensors, and their increasingly higher resolutions. In this paper, we exploit redundancies between SAR and optical imaging modalities to create a joint encoding that improves storage efficiency. A novel neural network design with progressive attentive fusion modules is proposed for joint compression. The model is also promptable at test time with a desired tradeoff between the input modalities, to enable flexibility in the fidelity of the joint representation to each of them. Moreover, we show how end-to-end optimization of the joint compression model, including its modality tradeoff prompt, allows for better accuracy on downstream tasks leveraging multimodal inference when a constraint on the rate is to be met.

1. Introduction

Remote sensing of the Earth largely relies on imagery acquired by a variety of imaging devices onboard satellites. Multiple kinds of imaging devices are adopted in order to capture different features of interest, and exhibit different tradeoffs in their operations. As an example, in the optical imaging realm, very high resolution panchromatic images may be suitable to detect and monitor small subjects of interest, hyperspectral images with limited spatial resolution and very high spectral resolution may provide large-scale insights on material properties, while multispectral images may represent a good compromise of spectral information and spatial resolution. At the same time, synthetic aperture radar (SAR) captures a different view of the Earth at microwave frequencies, eliciting different material responses and having operational advantages such as not being affected by clouds.

Indeed, it is widely recognized in the literature that combining SAR and optical images provides a fuller picture and helps image analysis tasks. Existing works design neural network architectures and training procedures to effectively fuse SAR and optical data [1,2,3,4,5] for tasks such as land monitoring [6], urban mapping [7], change detection [8], disaster assessment [9]. In general, a multimodal model will solve an inference task by leveraging a dual input composed of an optical image and a SAR image of the same scene.

However, storage of such multimodal data is becoming challenging due to the larger and larger amounts of images that are captured. In fact, global high-resolution coverage, from multiple missions and sensors, as well as multitemporal information to trace content in time and detect change, pose enormous demands on storage and retrieval systems. This calls for improved image compression methods that can effectively reduce storage requirements without compromising image quality. In particular, more efficient representations that better leverage the redundancies across data modalities appear to be an interesting direction. This motivates the study of joint multimodal compression methods that depart from the existing approach of independently compressing each image modality.

In this paper, we propose a method for joint compression of SAR and optical images based on a novel design of a deep neural network. The encoder of the proposed model processes both input modalities at the same time to extract a compressed joint latent representation. This encoder is based on a novel neural network architecture design that progressively fuses the latent features of the two modalities into joint features by means of attention mechanisms. While the compression task managed by the encoder is joint over both modalities, we ensure that decompression can reconstruct the optical or the SAR image independently. This is desirable when a downstream application only requires one of the two. Moreover, we design a prompting mechanism that works as an extra user-defined input parameter to decide, at test-time, the desired tradeoff between the SAR and optical modalities. This allows a user to prioritize the faithfulness of one modality over the other for a target rate.

At the same time, the emergent coding-for–machines paradigm [10] seeks to develop data compression models that are not necessarily optimized for human consumption but rather preserve features that are relevant for the models solving downstream problems, such as image classification. The proposed development of a joint multimodal compressor becomes especially interesting when paired with downstream tasks and models that are designed to exploit multimodal information. These are becoming more and more prevalent in remote sensing [1,2,3,4,5] because it has been observed that integrating SAR and optical data can lead to improved accuracy in various detection tasks. Therefore, we present an end-to-end optimization of the proposed compression model together with a state-of-the-art joint SAR–optical deep model for land use segmentation [11]. The end-to-end optimization process allows the compressor to only preserve joint features that are useful to the downstream model for the land segmentation task, as well as to directly optimize the tradeoff in quality between the two modalities to maximize segmentation performance.

Experiments have been conducted on the recently introduced WHU-OPT-SAR-dataset [11] and on the SEN12MS dataset [12], which have registered SAR and optical images of a set of scenes, as well as land usage labels for classification. The results show that the proposed joint compression method improves rate-distortion performance over state-of-the-art independent compressors. Moreover, we show that end-to-end optimization boosts the rate-accuracy performance of multimodal land use segmentation.

In summary, the main contributions of this paper are as follows:

• A novel exploration of the topic of joint SAR–optical image compression, which has so far received little attention, despite the potential gains to be had from joint encoding methods.
• A novel neural network design for joint SAR–optical compression that leverages a progressive attention mechanism to slowly fuse the features of the two modalities into a joint representation.
• A functionality to test-time prompts the compression model with a user-input tradeoff between the SAR and optical modalities to prioritize faithfulness of one or the other for a given rate. This tradeoff prompt can also be end-to-end optimized for a downstream task.

2. Related Work

The field of image compression has witnessed rapid evolution in recent decades, transitioning from traditional model-based methods to learning-based approaches. Model-based methods either relied on transform coding approaches (e.g., JPEG or JPEG2000), where an image presents a compact representation in the transformed domain, or leverage predictive coding (e.g., CCSDS-123 B 2 [13]) to only encode pixelwise prediction errors. These techniques, while effective for many applications, are based on hand-crafted models that may not fully exploit the underlying data distribution.

Recent advances in deep learning have spurred a transformative shift towards neural network-based image compression. The seminal work by Theis et al. [14] introduced the idea of utilizing convolutional neural networks (CNNs) to learn image codecs. By optimizing an encoder, decoder, and entropy model, these frameworks are capable of achieving higher compression ratios while maintaining or even improving perceptual quality compared to traditional methods. Alternatively, Toderici et al. [15] explored the use of recurrent neural networks (RNNs) for progressive image compression.

Subsequent research expanded on this foundation by incorporating more sophisticated network architectures and probabilistic models. Ballé et al. [16,17] proposed a variational autoencoder (VAE)-based approach that employs a hyperprior to capture spatial dependencies in the latent representation, significantly improving rate-distortion performance. Their framework marked an important step in bridging the gap between conventional codecs and neural network-based models, providing a flexible mechanism for adaptively encoding image features.

More recent research [18,19,20,21,22] has aimed to further refine the neural architectures of encoders and decoders, while also addressing the computational complexity of the entropy model. ELIC [23] significantly reduces the complexity of the joint backward-and-forward adaptive entropy modeling while presenting state-of-the-art rate-distortion performance.

Despite the remarkable progress achieved through these neural network-based methods, some areas of research remain yet largely unexplored. Notably, this is the case of joint multimodal compression, where redundancies across modalities could be exploited to further improve compression performance, which is especially relevant int he context of remote sensing. The closest to what is presented in this paper for this topic is the work by Lu et al. [24]. They developed a multimodal codec that processes visible and infrared images. However, compared to our work, their setting focuses on using the infrared image to aid the compression of the visible image rather than truly jointly compressing them with an arbitrary tradeoff between the two modalities.

3. Method

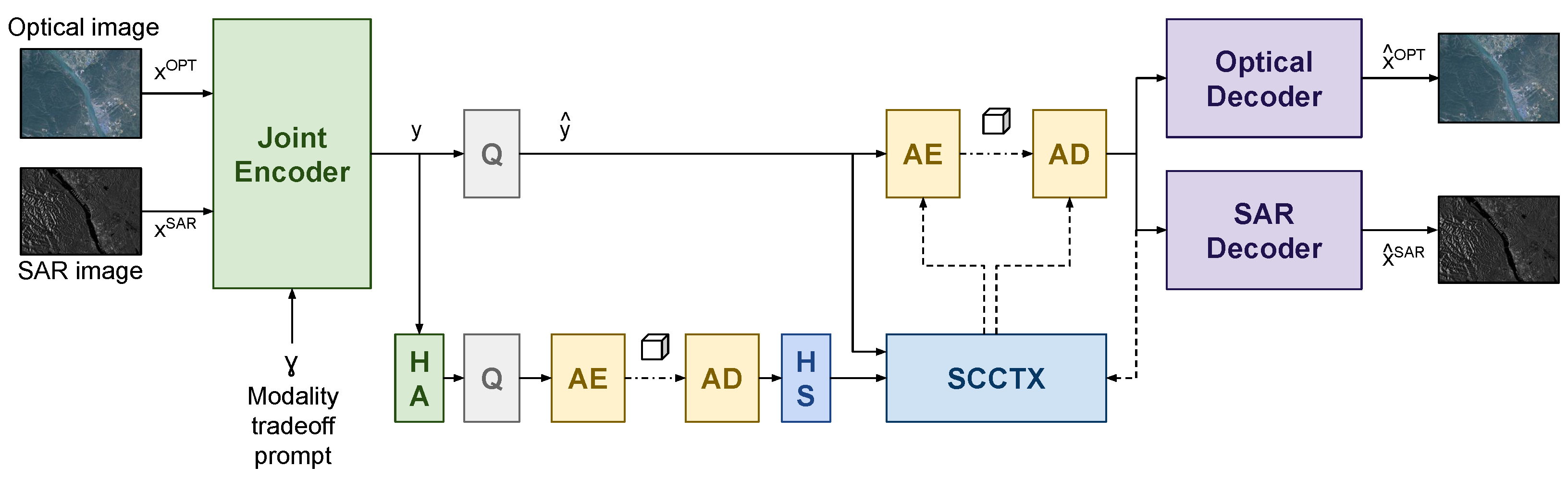
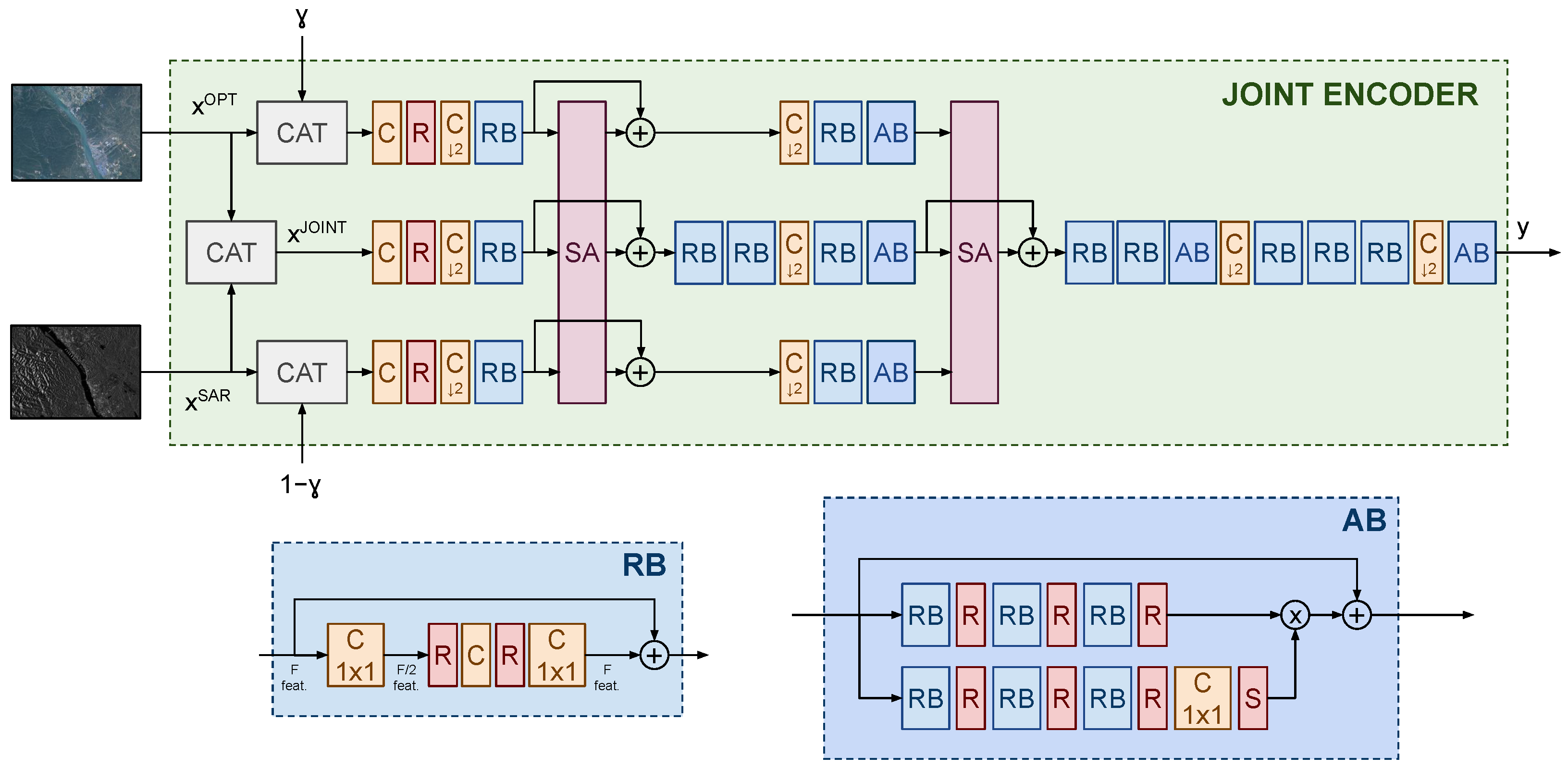
This section introduces the proposed joint SAR–optical image compression method. A high-level overview of the joint encoder and independent decoders is shown in Figure 1, while Figure 2 shows the details of the joint encoder architecture.

3.1. Architecture

The architecture generalizes a backbone based on ELIC [23] to the task of joint multimodal compression. As can be seen in the overview block diagram in Figure 1, the SAR image $x^{\mathrm{SAR}}$ and the optical image $x^{\mathrm{OPT}}$ of a given scene serve as input to the model encoder. The joint encoder extracts a joint latent representation y which is used by the hyper-analysis/synthesis transforms to derive the hyperprior model. Following ELIC [23] the entropy model uses an efficient Space-Channel ConTeXt model (SCCTX) to model the distribution of the quantized version of y. The independent decoders process the compressed latent to either reconstruct the SAR image or the optical image. Independent decoders rather than a single joint decoder are desirable to allow reconstruction of a single modality for single-modal tasks, without incurring in the computational cost of always reconstructing both.

Details of the novel joint encoder are presented in Figure 2. The main idea is to progressively fuse the features of the two modalities at various scales and levels of abstraction. Importantly, the fusion operations leverage attention mechanisms that, by cross-correlating the modalities features with the joint features, adaptively ensure the use of the most relevant modality on a per-input and per spatial position basis. More in detail, a joint tensor is immediately created by concatenation along the channel dimension, which serves as the starting point of what will become the joint latent representation. Parallel extraction of features from the optical, SAR, and joint representations is performed by means of convolutional layers and residual blocks. A self-attention operation is then used to adaptively mix the three branches, allowing the exchange of deep features. We denote as $h^{\mathrm{OPT}}\in {\mathbb{R}}^{F\times H\times W}$, $h^{\mathrm{SAR}}\in {\mathbb{R}}^{F\times H\times W}$ and $h^{\mathrm{joint}}\in {\mathbb{R}}^{F\times H\times W}$ the feature maps of the three branches. The self-attention operation assembles all the pixels in the feature maps as a batch of sequences of length 3 with F features to obtain $z_i\in {\mathbb{R}}^{F\times 3}=[h_i^{\mathrm{OPT}};h_i^{\mathrm{joint}};h_i^{\mathrm{SAR}}]$ for all $i=1,\dots ,HW$. This is performed for inter-modality fusion of each individual spatial location, so that a spatially varying mixing could be achieved. This is useful as different modalities may be more or less informative depending on the specific spatial location. Projections of the sequences into key, query, and value sequences are then obtained via

$$\begin{array}{cc}\hfill k_i& =W_k{z}_i\hfill \\ \hfill q_i& =W_q{z}_i\hfill \\ \hfill v_i& =W_v{z}_i\hfill \end{array}$$

(1)

and attention scores are computed to mix the modalities:

$$\begin{array}{c}\hfill h_i=\mathrm{softmax}\left({\displaystyle \frac{q_i^T{k}_i}{\sqrt{F}}}\right)v_i\end{array}$$

(2)

The resulting length 3 sequence collects transformed versions of the features of each original branch, which are carried forward for further processing, following the diagram in Figure 2.

The decoders follow the same design presented in [23] for the sake of fairness of comparisons.

3.2. Modality Tradeoff Prompting and Training

When compressing different modalities independently, one could choose the desired target rate or quality for each of them. The design of a joint multimodal compressor needs to capture this fact as well, leaving the user the option to decide the desired tradeoff between modalities. In fact, it is conceivable that, depending on the application, some modalities might be more relevant than others, and so it might be desirable to prioritize their fidelity. It is also desirable that this option is provided as a user input test-time parameter, rather than requiring multiple models trained for different tradeoffs.

We propose to prompt the encoder network by including an extra scalar input, named $\gamma$, valued between 0 and 1, which represents the optical-SAR tradeoff. By convention, a value close to 1 will prioritize the quality of the optical image, while a value close to 0 will prioritize the quality of the SAR image, for a given rate. The $\gamma$ parameter is replicated spatially to match the size of the input images. After size matching, $\gamma$ is concatenated as an extra channel to the optical image and $1-\gamma$ is concatenated as an extra channel to the SAR image, before feature processing.

Since an arbitrary $\gamma$ prompt can be supplied at test time, the training process needs to optimize the tradeoff for any $\gamma \in (0,1)$. This is achieved by randomly sampling a value of $\gamma$ from the uniform distribution on the unit interval for each minibatch used in the training process. The parameter is also used in the rate-distortion loss function to trade the optical distortion against the SAR distortion. Therefore, the overall loss function is as follows:

$$\begin{array}{c}\hfill \mathcal{L}={\mathbb{E}}_{\gamma \sim \mathcal{U}(0,1)}\left[R\left(\widehat{y}\right)+\lambda \left(\gamma D(x^{\mathrm{OPT}},{\widehat{x}}^{\mathrm{OPT}})+(1-\gamma )D(x^{\mathrm{SAR}},{\widehat{x}}^{\mathrm{SAR}})\right)\right].\end{array}$$

(3)

$R\left(\widehat{y}\right)$ is the rate of the discrete coding symbols obtained by quantizing the output of the joint encoder, as estimated by the entropy model [23]. D is a measure of distortion, such as mean squared error (MSE), between the reconstructions produced by the decoder and the original images. We can notice that $\gamma$ creates a convex combination of the optical and SAR distortion to implement the desired tradeoff. In this work, we use MSE as the distortion metric, but other metrics such as SSIM or perceptual metrics like LPIPS could be used, without loss of generality. The Lagrange multiplier $\lambda$ sets the rate-distortion operating point of the model. In this work, we train a different model for each operating point, but variable-rate training techniques could also be applied without loss of generality.

3.3. End-to-End Training for Downstream Tasks with Optimal Tradeoff

When a specific downstream inference task is targeted, it is possible to optimize compression for such a task rather than visual consumption. Since nowadays more and more inference problems leverage joint multimodal models, it is only natural to optimize a joint multimodal compression method to maximize the performance on the task, for a given rate, in an end-to-end fashion.

Figure 3 shows a diagram of the proposed joint compression model interfacing with a detection model, e.g., for land cover classification. All the building blocks of the detection and compression model can be finetuned with a rate-constrained task-specific objective. For example, in a typical segmentation problem, a Lagrangian loss accounting for rate and cross-entropy with respect to the pixel class labels would serve as the natural optimization target for finetuning. Let us denote as $\mathcal{E}$, ${\mathcal{D}}_{\mathrm{OPT}}$, ${\mathcal{D}}_{\mathrm{SAR}}$, $\mathcal{C}$ the joint encoder, optical decoder, SAR decoder, and classifier models, respectively, and, as v, the ground truth classification labels. The end-to-end optimization process would then train the parameters of those models as follows:

$$\begin{array}{cc}\hfill & {\gamma }^{*},{\theta }_{\mathcal{E}}^{*},{\theta }_{{\mathcal{D}}_{\mathrm{OPT}}}^{*},{\theta }_{{\mathcal{D}}_{\mathrm{SAR}}}^{*},{\theta }_{\mathcal{C}}^{*}=arg\underset{\gamma ,{\theta }_{\mathcal{E}},{\theta }_{{\mathcal{D}}_{\mathrm{OPT}}},{\theta }_{{\mathcal{D}}_{\mathrm{SAR}}},{\theta }_{\mathcal{C}}}{min}R\left(\mathcal{E}(\gamma ,x^{\mathrm{OPT}},x^{\mathrm{SAR}})\right)+\hfill \\ \hfill & \lambda \mathrm{CE}\left[v,\mathcal{C}({\mathcal{D}}_{\mathrm{OPT}}\left(\mathcal{E}(\gamma ,x^{\mathrm{OPT}},x^{\mathrm{SAR}})\right),{\mathcal{D}}_{\mathrm{SAR}}\left(\mathcal{E}(\gamma ,x^{\mathrm{OPT}},x^{\mathrm{SAR}})\right))\right],\hfill \end{array}$$

(4)

being CE the cross-entropy cost function. Notice that the tradeoff parameter $\gamma$ is also optimized in an end-to-end fashion. This allows to discover the optimal balance between modalities to maximize the task performance, since, in general, one modality may contribute more than the other to the final result.

4. Experimental Results

This section presents the experimental assessment of the proposed method. Two main experiments present the rate-distortion and rate-accuracy performance of the proposed joint compression method, when its task is to reconstruct the original images or solve a land cover classification problem, respectively. Moreover, we analyze the behavior of the model concerning the modality tradeoff prompt.

4.1. Experimental Setting

The experimental evaluation adopts two datasets, namely WHU-SAR-OPT [11] and SEN12MS [12]. WHU-SAR-OPT is a recently proposed dataset with optical RGB-NIR and SAR images of the same scenes from the Hubei Province in China. The optical images are produced by the Gaofen-1 satellite, while the SAR images are produced by the Gaofen-3 satellite. The dataset comprises 100 images of size $5556\times 3704$ with a standard train and test split. For the purposes of training and testing our models, the images are split into non-overlapping patches of size $512\times 512$. The dataset also provides pixel-level ground truth annotations for land use classification with eight possible classes (background, farmland, city, village, water, forest, road, and other). The availability of land use labels allows us to test end-to-end training for rate-constrained classification as well as pure compression of the images. SEN12MS is a similar dataset composed of multispectral images from the Sentinel-2 satellite and SAR images from the Sentinel-1 satellite. For the purpose of this paper, we use a subset of the original data, namely the “Spring” regions of interest for which we create a training set with 8000 images of size $256\times 256$ and a test set with 2000 images of the same size. For the optical data, we keep only the four RGB-NIR bands. SEN12MS also provides whole-image land classification labels with 10 possible classes (International Geosphere-Biosphere Programme classification scheme).

The main experiment on rate-distortion performance of the proposed joint model trains the model for approximately 100 epochs with a batch size of eight. A learning rate equal to ${10}^{-3}$ is used and manually decayed to ${10}^{-4}$ after 80 epochs. Four models with different rate-distortion operating points are trained, corresponding to Lagrange multiplier values $\lambda =\{0.0064,0.0128,0.0256,0.0512\}$ in Equation (3). MSE is used as distortion metric for training.

Concerning the experiments on end-to-end optimized rate-constrained classification, for the per-pixel land cover classification task on WHU-SAR-OPT, we use the recently proposed MCANet [11] as a multimodal classification model. For the whole-image classification task on SEN12MS we use instead a ResNet-18 model. The proposed joint compressor and the classification model (MCANet or ResNet-18) are finetuned from their pretrained weights for approximately 10 epochs with the rate-cross-entropy loss in Equation (4) and a batch size of 8. The learning rate is ${10}^{-4}$ for the model weights and ${10}^{-2}$ for the $\gamma$ parameter. All experiments are run on single NVIDIA A40 or L40S GPUs.

The previously indicated hyperparameter values have been set according to typically used values and do not exhibit a strong sensitivity. Note that the $\gamma$ parameter in the end-to-end experiment needs a larger learning rate, due to it being close to the input and potentially receiving weaker gradients.

4.2. Compression Performance

The main experiment we report investigates the rate-distortion performance of the joint model compared to state-of-the-art models independently encoding the two modalities. Performance is measured in terms of Peak Signal-to-Noise Ratio (PSNR) and Multi-Scale Structural Similarity Index Measure (MS-SSIM) as a function of coding rate. The joint PSNR or MS-SSIM of the two modalities has been defined as the average of the individual PSNRs or MS-SSIMs. The rate is measured in bits-per-pixel and it is computed by dividing the total number of bits used to encode both modalities by the total number of pixels (i.e., twice the spatial size of a single image). The performance curves report the envelope of achievable rate-PSNR or rate-SSIM points from various tradeoffs between modalities.

The results are shown in Figure 4 and Figure 5 in terms of rate-PSNR and rate-SSIM curves, on the WHU-SAR-OPT and SEN12MS datasets, respectively. We compare the proposed joint coding method with a number of state-of-the-art and baseline deep learning methods. In particular, the state-of-the-art ELIC [23] offers a fair assessment of the advantage of joint instead of independent compression, since several components in our design are based on ELIC. Additionally, we present results using well-known models that are widely adopted in the image compression literature, namely the mean-scale hyperprior model by Balle et al. [25] and the model leveraging self-attention by Cheng et al. [26]. It can be noticed that the proposed joint compression outperforms all the tested methods both on the PSNR and MS-SSIM metrics. The Bjontegaard Delta (BD-Rate) of joint compression with respect to independent compression with ELIC is measured as $-4.22\%$ on the WHU-SAR-OPT dataset and $-5.21\%$ on the SEN12MS dataset. Figure 6 and Figure 7 report some visual results of SAR and optical images compressed with the tested methods, at similar rate points.

4.3. Tradeoff Prompt Effectiveness

We now analyze whether the prompting mechanism controlled by parameter $\gamma$ is effective at tuning the tradeoff between the quality of the optical or SAR image. This assessment is performed by providing three different values $\gamma =\{0.1,0.5,0.9\}$ at test-time. Figure 8 reports the rate-PSNR and rate-SSIM curves obtained for each of these values, decoupled into the quality of the optical image and the quality of the SAR image. We noticed that for $\gamma =0.5$ the reconstructed optical and SAR images have similar quality level, confirming that the model does not significantly prioritize one over the other. Conversely, it is clear that $\gamma =0.9$ prioritizes minimization of the distortion of the optical image, while $\gamma =0.1$ prioritizes minimization of the distortion of the SAR image.

4.4. Computational Complexity

The computational complexity of the joint compression model is only slightly larger to that of two independent models based on ELIC. As a term of comparison, training two independent models for optical and SAR requires approximately 1.5 days on a single NVIDIA A40 GPU while the joint model requires 2 GPU days.

Table 1. Computational complexity.

	Training Time (A40 h)	Inference Time (ms)
Joint (proposed)	47.5	51
Indep. ELIC (SAR + opt.) [23]	32.4	34
Indep. Balle Hyperprior (SAR + opt.) [25]	25.7	26
Indep. Cheng et al. [26] (SAR + opt.)	29.2	31

reports training and inference times for an input image of size $512\times 512$. Notice that independent compression needs to train or run two models so the table reports the total time for both models.

4.5. Rate-Constrained Land Cover Classification Performance

This experiment analyzes the performance of the end-to-end training scheme presented in Section 3.3 where the joint compression algorithm is trained in conjunction with a multimodal classification model. In particular, we are interested in the performance of the land use classification task under a rate constraint. For pixel-level classification on the WHU-SAR-OPT data, we assess performance of the land use classifier in terms of overall accuracy and Cohen’s Kappa coefficient as a function of the rate of the compressed images, while for whole-image classification on SEN12MS we evaluate accuracy as a function of the rate of the compressed images. For fairness of comparisons we also end-to-end finetune the independent compression baseline by training two independent encoders with the same $\lambda$ parameter and the land cover classification model. Figure 9 and Figure 10 show the results for the proposed joint compression method and for independent compression by means of ELIC on the WHU-SAR-OPT data and SEN12MS data, respectively. We found that for both datasets, joint compression outperforms independent compression by providing better classification results under the rate constraint. For example, on WHU-SAR-OPT, at a rate of approximately 0.07 bpp, we observe a significant improvement in overall accuracy of 0.2 percentage points. A qualitative example of improved land cover classification is shown in Figure 11. In this example, artifacts introduced by independent compression models lead to misclassification of an area of farmland as water, while joint compression accurately classifies it. We report that the performance of the uncompressed system, i.e., when the original uncompressed images are provided to the classification model, as a benchmark of the ideal system performance when no rate constraint is to be met. Introducing lossy compression will always degrade the performance but will allow to substantially reduce storage requirements. We also remark that the specific choice of classification models (MCANet or ResNet-18) is not important for our experiment, as we are only interested in the relative difference between the rate-accuracy performance of joint compression against independent compression. A better classification model will improve all accuracy values but will not change the ranking of compression methods.

Moreover,

Table 2. Optimal modality compression tradeoff for land use classification.

WHU-SAR-OPT	Rate (bpp)	0.0214	0.0326	0.0636	0.1004
	${\gamma }^{*}$	0.82	0.86	0.87	0.91
SEN12MS	Rate (bpp)	0.0103	0.0134	0.0171	0.0212
	${\gamma }^{*}$	0.54	0.48	0.42	0.44

shows the value of the $\gamma$ tradeoff parameter as optimized by the finetuning procedure. This parameter is initialized to $\gamma =0.5$. For the WHU-SAR-OPT dataset, the finetuning procedure deems a higher value is needed to maximize performance. Notice that the optimal $\gamma$ value slightly changes with rate. This could be related to the higher difficulty of compressing SAR images compared to optical images, so that at lower rates it becomes necessary to be more careful in representing the SAR image with enough fidelity. At higher rates, higher $\gamma$ values show that more important information for the classification problem is carried by the optical image. For the SEN12MS dataset, the optimal value for $\gamma$ is closer to the initial 0.5, meaning that on these data and for the whole-image classification task there is no substantial preference for optical or SAR image quality.

5. Conclusions

We presented an investigation into the relatively unexplored topic of joint multimodal compression, where coding efficiency can be enhanced thanks to the partial redundancy of features in the multiple modalities.

In particular, we considered the problem of jointly compressing optical and SAR images. We proposed a deep learning approach where a joint encoder derives a single representation for the two input images by progressively fusing them to create joint features. Independent decoders were proposed to maintain flexibility of decoding individual modalities. Moreover, the proposed method is promptable at test time with a user-specified parameter that controls the tradeoff between the quality of the optical and the quality of the SAR image for a given rate. The proposed joint compression outperforms state-of-the-art models based on independent compression.

Finally, we also showed how a joint multimodal compressor is naturally suited to be optimized end-to-end with multimodal models for downstream tasks, e.g., land use classification. The proposed approach provided superior classification performance under a rate constraint, underlining the advantage of joint coding and optimizing the tradeoff between the importance of the two modalities.

A limitation of the method could lie in the need for paired training data with both modalities. Although this is a requirement for inference, collecting large amounts of paired data for training could be challenging. Future work could address training procedures leveraging unpaired data.